北师大版九年级上期相似三角形单元检测卷

合集下载

2022-2023学年北师大版九年级数学上册《4-4探索三角形相似的条件》同步达标测试题(附答案)

2022-2023学年北师大版九年级数学上册《4.4探索三角形相似的条件》同步达标测试题（附答案）一．选择题（共12小题，满分48分）1．图形中，每个小网格均为正方形网格，带阴影部分的三角形中与如图△A1B1C1相似的是（）A．B．C．D．2．如图，在△ABC中，D，E两点分别在BC，AC上，且AD平分∠BAC，若∠ABE＝∠C，BE与AD相交于点F，则图中与△ABD相似的是（）A．△ABC B．△ABF C．△BFD D．△AEF3．如图，在△ABC中，点D、E分别在AB、AC边上，DE与BC不平行，那么下列条件中，不能判断△ADE∽△ACB的是（）A．∠ADE＝∠C B．∠AED＝∠B C．＝D．＝4．已知△ABC三边长是，，2，与△ABC相似的三角形三边长可能是（）A．1，，B．1，，C．1，，D．1，，5．如图，D是△ABC边AB上一点，添加一个条件后，仍然不能使△ACD∽△ABC的是（）A．∠ACB＝∠ADC B．∠ACD＝∠ABC C．D．6．已知Rt△ABC中，∠C＝90°，∠A≠∠B，点P是边AC上一点（不与A、C重合），过P点的一条直线与△ABC的边相交，所构成的三角形与原三角形相似，这样的直线有（）条．A．1B．2C．3D．47．如图，△ABC中，点D、E分别在AB、AC边上，则下列条件中，不一定能使△AED∽△ABC的是（）A．∠2＝∠B B．∠1＝∠C C．D．8．如图：点D在△ABC的边AB上，连接CD，下列条件：①∠ACD＝∠B；②∠ADC＝∠ACB；③AC2＝AD•AB；④AB•CD＝AC•BC．其中能判定△ACD∽△ABC的共有（）A．1个B．2个C．3个D．4个9．如图，在△ABC中，点D、E分别在边AB、AC上，则在下列四个条件中：①∠AED＝∠B；②DE∥BC；③；④AD•BC＝DE•AC，能满足△ADE∽△ACB的条件有（）A．1个B．2个C．3个D．4个10．如图，在△ABC中，AB＝AC＝8，BC＝6，点P从点B出发以1个单位/s的速度向点A运动，同时点Q从点C出发以2个单位/s的速度向点B运动．当以B，P，Q为顶点的三角形与△ABC相似时，运动时间为（）A．s B．s C．s或s D．以上均不对11．如图，在△ABC中，点D、E分别在边AB、AC上，则在下列五个条件中：①∠AED＝∠B；②DE∥BC；③＝；④AD•BC＝DE•AC；⑤∠ADE＝∠C，能满足△ADE∽△ACB的条件有（）A．1个B．2个C．3个D．4个12．如图，正方形ABCD中，F为AB上一点，E是BC延长线上一点，且AF＝EC，连接EF，DE，DF，M是FE中点，连接MC，设FE与DC相交于点N．则4个结论：①DN ＝DG；②△BFG∽△EDG∽△BDE；③CM垂直BD；④若MC＝，则BF＝2；正确的结论有（）个A．4B．3C．2D．1二．填空题（共4小题，满分20分）13．如图，∠B＝∠D，请你添加一个条件，使得△ABC∽△ADE，这个条件可以是．14．如图，在边长为4的正方形ABCD中，点E、F分别是BC、CD的中点，DE、AF交于点G，AF的中点为H，连接BG、DH．给出下列结论：①AF⊥DE；②DG＝；③HD∥BG；④△ABG∽△DHF．其中正确的结论有．（请填上所有正确结论的序号）15．如图，在△ABC中，AB≠AC．D、E分别为边AB、AC上的点．AC＝3AD，AB＝3AE，点F为BC边上一点，添加一个条件：，可以使得△FDB与△ADE 相似．（只需写出一个）16．如图，在△ABC中，P为AB上一点，在下列四个条件中：①∠ACP＝∠B；②∠APC ＝∠ACB；③AC2＝AP•AB；④AB•CP＝AP•CB，能满足△APC与△ACB相似的条件是（只填序号）．三．解答题（共8小题，满分52分）17．已知：如图，点C，D在线段AB上，△PCD是等边三角形，且AC＝1，CD＝2，DB ＝4．求证：△ACP∽△PDB．18．如图，已知∠1＝∠2，∠AED＝∠C，求证：△ABC∽△ADE．19．如图，AB•AE＝AD•AC，且∠1＝∠2，求证：△ABC∽△ADE．20．如图，点E是四边形ABCD的对角线BD上一点，且∠BAC＝∠BDC＝∠DAE．求证：△ABE∽△ACD．21．如图，在△ABC中，BD平分∠ABC，交AC于点D，点E是AB上一点，连接DE，BD2＝BC•BE．证明：△BCD∽△BDE．22．如图，在△ABC中，AB＝8cm，BC＝16cm，点P从点A开始沿AB向B以2cm/s的速度移动，点Q从点B开始沿BC向C点以4cm/s的速度移动．如果P，Q分别从A，B同时出发，经过几秒钟△PBQ与△ABC相似？23．如图，已知AD•AC＝AB•AE．求证：△ADE∽△ABC．24．如图，在△ABC中，AB＝AC＝1，BC＝，在AC边上截取AD＝BC，连接BD．（1）通过计算，判断AD2与AC•CD的大小关系；（2）求∠ABD的度数．参考答案一．选择题（共12小题，满分48分）1．解：因为△A1B1C1中有一个角是135°，选项中，有135°角的三角形只有B，且满足两边成比例夹角相等，故选：B．2．解：在△ABE与△ACB中，∠ABE＝∠C，∠BAE＝∠CAB，∴△ABE∽△ACB，∴∠AEB＝∠ABC，∵AD平分∠BAC，∴∠BAD＝∠EAF，∴△ABD∽△AEF．故选：D．3．解：∵∠DAE＝∠CAB，∴当∠ADE＝∠C时，△ADE∽△ACB；当∠AED＝∠B时，△ADE∽△ACB；当＝时，△ADE∽△ACB．故选：C．4．解：∵△ABC三边长是，，2，∴△ABC三边长的比为：2：＝1：：，∴△ABC相似的三角形三边长可能是1，，，故选：A．5．解：A、当∠ACB＝∠ADC时，再由∠A＝∠A，可得出△ACD∽△ABC，故此选项不合题意；B、当∠ACD＝∠ABC时，再由∠A＝∠A，可得出△ACD∽△ABC，故此选项不合题意；C、当＝时，再由∠A＝∠A，可得出△ACD∽△ABC，故此选项不合题意；D、当＝时，无法得出△ACD∽△ABC，故此选项符合题意；故选：D．6．解：如图，过点P作AB的平行线，或作BC的平行线，或作AB的垂线，或作∠CPD＝∠B，共4条直线，故选：D．7．解：∠A＝∠A，A、若添加∠2＝∠B，可利用两角法判定△AED∽△ABC，故本选项错误；B、若添加∠1＝∠C，可利用两角法判定△AED∽△ABC，故本选项错误；C、若添加＝，可利用两边及其夹角法判定△AED∽△ABC，故本选项错误；D、若添加＝，不能判定△AED∽△ABC，故本选项正确；故选：D．8．解：①∠A＝∠A，∠ACD＝∠B，∴△ACD∽△ABC，②∵∠A＝∠A，∠ADC＝∠ACB，∴△ACD∽△ABC，③∵AC2＝AD•AB，∴，∵∠A＝∠A，∴△ACD∽△ABC，④条件不符合，不能判定△ACD∽△ABC，故选：C．9．解：①∠B＝∠AED，∠A＝∠A，则可判断△ADE∽△ACB，故①符合题意；②DE∥BC，则△ADE∽△ABC，故②不符合题意，③，且夹角∠A＝∠A，能确定△ADE∽△ACB，故③符合题意；④由AD•BC＝DE•AC可得＝，此时不确定∠ADE＝∠ACB，故不能确定△ADE∽△ACB，故④不符合题意，故选：B．10．解：设运动时间为t秒．BP＝t，CQ＝2t，BQ＝BC﹣CQ＝6﹣2t，当△BAC∽△BPQ，＝，即＝，解得t＝；当△BCA∽△BPQ，＝，即＝，解得t＝，综上所述，当以B，P，Q为顶点的三角形与△ABC相似时，运动时间为s或s，故选：C．11．解：①∠B＝∠AED，∠A＝∠A，则可判断△ADE∽△ACB，故①符合题意；②DE∥BC，则△ADE∽△ABC，故②不符合题意，③，且夹角∠A＝∠A，能确定△ADE∽△ACB，故③符合题意；④由AD•BC＝DE•AC可得，此时不确定∠ADE＝∠ACB，故不能确定△ADE∽△ACB；故④不符合题意，⑤∠ADE＝∠C，∠A＝∠A，则可判断△ADE∽△ACB，故⑤符合题意；故选：C．12．解：正方形ABCD中，AD＝CD，在△ADF和△CDE中，，∴△ADF≌△CDE（SAS），∴∠ADF＝∠CDE，DE＝DF，∴∠EDF＝∠FDC+∠CDE＝∠FDC+∠ADF＝∠ADC＝90°，∴∠DEF＝45°，∵∠DGN＝45°+∠FDG，∠DNG＝45°+∠CDE，∠FDG≠∠CDE，而∠FDG与∠CDE不一定相等，∴∠DGN与∠DNG不一定相等，故判断出①错误；∵△DEF是等腰直角三角形，∵∠ABD＝∠DEF＝45°，∠BGF＝∠EGD（对顶角相等），∴△BFG∽△EDG，∵∠DBE＝∠DEF＝45°，∠BDE＝∠EDG，∴△EDG∽△BDE，∴△BFG∽△EDG∽△BDE，故②正确；连接BM、DM．∵△AFD≌△CED，∴∠FDA＝∠EDC，DF＝DE，∴∠FDE＝∠ADC＝90°，∵M是EF的中点，∴MD＝EF，∵BM＝EF，∴MD＝MB，在△DCM与△BCM中，，∴△DCM≌△BCM（SSS），∴∠BCM＝∠DCM，∴CM在正方形ABCD的角平分线AC上，∴MC垂直平分BD；故③正确；过点M作MH⊥BC于H，则∠MCH＝45°，∵MC＝，∴MH＝＝1，∵M是EF的中点，BF⊥BC，MH⊥BC，∴MH是△BEF的中位线，∴BF＝2MH＝2，故④正确；综上所述，正确的结论有②③④．故选：B．二．填空题（共4小题，满分20分）13．解：∵∠B＝∠D，∴添加∠C＝∠E或∠BAC＝∠DAE或∠BAD＝∠CAE或＝，可证△ABC∽△ADE．故答案为：∠C＝∠E或∠BAC＝∠DAE或∠BAD＝∠CAE或＝．14．解：∵四边形ABCD为正方形，∴∠ADC＝∠BCD＝90°，AD＝CD，∵E和F分别为BC和CD中点，∴DF＝EC＝2，∴△ADF≌△DCE（SAS），∴∠AFD＝∠DEC，∠F AD＝∠EDC，∵∠EDC+∠DEC＝90°，∴∠EDC+∠AFD＝90°，∴∠DGF＝90°，即DE⊥AF，故①正确；∵AD＝4，DF＝CD＝2，∴AF＝，∴DG＝AD×DF÷AF＝，故②错误；∵H为AF中点，∴HD＝HF＝AF＝，∴∠HDF＝∠HFD，∵AB∥DC，∴∠HDF＝∠HFD＝∠BAG，∵AG＝＝，AB＝4，∴，∴△ABG∽△DHF，故④正确；∴∠ABG＝∠DHF，而AB≠AG，则∠ABG和∠AGB不相等，故∠AGB≠∠DHF，故HD与BG不平行，故③错误；故答案为：①④．15．解：DF∥AC，或∠BFD＝∠A．理由：∵∠A＝∠A，＝＝，∴△ADE∽△ACB，∴①当DF∥AC时，△BDF∽△BAC，∴△BDF∽△EAD．②当∠BFD＝∠A时，∵∠B＝∠AED，∴△FBD∽△AED．故答案为DF∥AC，或∠BFD＝∠A．16．解：前三项正确，因为他们分别符合有两组角对应相等的两个三角形相似；两组对应边的比相等且相应的夹角相等的两个三角形相似．故相似的条件是①，②，③．三．解答题（共8小题，满分52分）17．证明：∵△PCD是等边三角形，∴∠PCD＝∠PDC＝60°，PC＝CD＝PD＝2，∴∠PCA＝∠PDB＝120°，∵AC＝1，BD＝4，∴，＝，∴＝，∴△ACP∽△PDB．18．证明：∵∠1＝∠2，∴∠1+∠BAE＝∠2+∠BAE，即∠DAE＝∠BAC，∵∠AED＝∠C，∴△ABC∽△ADE．19．证明：如图，∵AB•AE＝AD•AC，∴＝．又∵∠1＝∠2，∴∠2+∠BAE＝∠1+∠BAE，即∠BAC＝∠DAE，∴△ABC∽△ADE．20．解：∵∠BAC＝∠BDC，∠AOB＝∠DOC，∴∠ABE＝∠ACD又∵∠BAC＝∠DAE∴∠BAC+∠EAC＝∠DAE+∠EAC∴∠DAC＝∠EAB∴△ABE∽△ACD．21．证明：∵BD平分∠ABC，∴∠DBE＝∠CBD．∵BD2＝BC•BE，∴，∴△BCD∽△BDE．22．解：设在开始运动后第x秒，△BPQ与△BAC相似，由题意得：AP＝2xcm，PB＝（8﹣2x）cm，BQ＝4x，分两种情况考虑：当∠BPQ＝∠C，∠B＝∠B时，△PBQ∽△CBA，∴，即解得：x＝0.8，当x＝0.8秒时，△BPQ与△BAC相似；当∠BPQ＝∠A，∠B＝∠B时，△BPQ∽△BAC，∴，即，解得：x＝2，当x＝2秒时，△BPQ与△BAC相似．综上，当x＝0.8秒或2秒时，△BPQ与△BAC相似．23．证明：∵AD•AC＝AE•AB，∴＝在△ABC与△ADE中∵＝，∠A＝∠A，∴△ABC∽△ADE．24．解：（1）∵AD＝BC，BC＝，∴AD＝，DC＝1﹣＝．∴AD2＝＝，AC•CD＝1×＝．∴AD2＝AC•CD．（2）∵AD＝BC，AD2＝AC•CD，∴BC2＝AC•CD，即．又∵∠C＝∠C，∴△BCD∽△ACB．∴，∠DBC＝∠A．∴DB＝CB＝AD．∴∠A＝∠ABD，∠C＝∠BDC．设∠A＝x，则∠ABD＝x，∠DBC＝x，∠C＝2x．∵∠A+∠ABC+∠C＝180°，∴x+2x+2x＝180°．解得：x＝36°．∴∠ABD＝36°．。

北师大版九年级上册相似测试题

相似三角形测试题一．填空题：（每题3分，共30分） 1．点C 在线段AB 上，AC ∶CB=3∶4，则AB ∶CB = ；2．在比例尺1∶8000000的地图上，量得太原到北京的距离为6.4厘米，则太原到北京的实际距离为公里；3．已知：a ，b ，c ，d 是成比例线段，其中a =3cm ，b =2cm ， c =6cm ，则d = cm ； 4．已知：2=yx ，则=+y yx ，=-x y x ； 5．已知)0(5≠++===g f e g c f b e a ，则=++++g f e cb a ；第（6）题图第（7）题图 6．已知如图，D 是△ABC 的AB 边上一点，要使△ABC ∽△ACD则还须具备一个条件是__ __.或； 7．如图，已知△ADE ∽△ABC ，AD=6cm ，DB=3cm ，BC=9.9cm, ∠B=50°,则∠ADE= ，DE = cm ； 8．若两个相似三角形面积比为9:4，则它们的周长比是；9．已知：Rt △ABC 中，∠ACB=90°， CD ⊥AB 于D ，若BC=5，AC=12，则AD=__________，BD=________ ．10、点P 是△ABC 中AB 边上的一点，过P 作直线（不与AB 重合）截△ABC ，使截得的三角形与原三角形相似，满足条件的直线最多有条. 二．选择题：（每题3分，共30分） 11．下列说法正确的是（）A .所有的等腰三角形都相似 B.所有的直角三角形都相似C.所有的等腰直角三角形都相似D.有一个角相等的两个等腰三角形都相似BCC12．已知：如图，小明在打网球时，要使球恰好能打过网，而且落在离网5米的位置上，则球拍球的高度h 应为( ) ) （A ） 2.7m （B ） 1.8m （C ） 0.9m （D ） 6m13.如图，在△ABC 中，D 、E 分别是AB 、AC 上一点，且DE ∥BC ，下面有四个结论中错误的是( ) (A)AC AEAB AD =(B)ACECAB DB =(C) ECAEDB AD = (D)BCDEDB AD =14．在相同时刻的物高与影长成比例，如果高为1.5米的测竿的影长为2.5米，那么影长为30米的旗杆的高是 ( )（A.） 20米（B.） 18米（C. ） 16米（D.）15米 15．在矩形ABCD 中，E 、F 分别是CD 、BC 上的点，若∠AEF=90°，则一定有 ( ) (A) ΔADE ∽ΔAEF (B) ΔECF ∽ΔAEF (C)ΔADE ∽ΔECF (D) ΔAEF ∽ΔABF16如图,∠ACB=∠ADC=90°,BC=a,AC=b,AB=c,要使⊿ABC ∽⊿CAD,只要CD 等于( )A.c b 2B.a b 2C.c abD.ca 217．两个相似三角形的对应边分别是cm 15和cm 23，它们的周长相差cm 40，则这两个三角形的周长分别是( )（A ）cm 75，cm 115（B ）cm 60，cm 100（C ）cm 85，cm 125（D ）cm 45，cm 85 18．两个相似三角形的相似比是2：3，其中较小的三角形的面积是12，则另一个三角形的面积是（）（A ）8 （B ）16 （C ）24 （D ）27 19．下列说法正确的是（）A .所有的等腰三角形都相似 B.所有的直角三角形都相似C.所有的等腰直角三角形都相似D.有一个角相等的两个等腰三角形都相似ABCQM D N PE20．如图，在平行四边形ABCD 中，E 为BC 边上的点，若BE ：EC ＝4：5，AE 交BD 于F ，则S ΔBEF ：S ΔDAF 等于（）A 、4：5B 、16：25C 、4：9D 、16：81三．解答题：（40分） 21 已知432zy x ==，且1832=-+z y x ，求x ，y ，z 的值。

北师大版九年级数学上册相似三角形的性质同步测试卷

北师大版九年级数学测试卷（考试题）4.7 相似三角形的性质1．若△ABC ∽△A`B`C`，则相似比k 等于（）A ．A`B`:AB B ．∠A: ∠A`C ．S △ABC ：S △A`B`C`D ．△ABC 周长：△A`B`C`周长2．把一个三角形改成和它相似的三角形，如果面积扩大到原来的100倍，那么边长扩大到原来的（）A ．10000倍B ．10倍C ．100倍D ．1000倍3．两个相似三角形，其周长之比为3：2，则其面积比为（）A ．2:3B ．3：2C ．9：4D ．不能确定4．把一个五边形改成和它相似的五边形，如果面积扩大到原来的49倍，那么对应的对角线扩大到原来的（）A ．49倍B ．7倍C ．50倍D ．8倍5．两个相似多边形的一组对应边分别为3cm 和4.5cm ，如果它们的面积和为78cm 2，那么较大多边形的面积为（）A ．46.8 cm 2B ．42 cm 2C ．52 cm 2D ．54 cm 26．两个多边形的面积之比为5，周长之比为m ，则m5为（） A ．1 B ．55 C ．5 D ．5 7．在一张1：10000的地图上，一块多边形地区的面积为6cm 2，则这块多边形地区的实际面积为（）A ．6m 2B ．60000m 2C ．600m 2D ．6000m 28．已知△ABC ∽△A`B`C`，且BC ：B`C`＝3：2，△ABC 的周长为24，则△A`B`C`的周长为_______.9．两个相似三角形面积之比为2：7，较大三角形一边上的高为2，则较小三角形的对应边上的高为_______.10．两个相似多边形最长的的边分为10cm 和25cm ，它们的周长之差为60cm ，则这两个多边形的周长分别为_______.11．四边形ABCD ∽四边形A`B`C`D`，他们的面积之比为36：25，他们的相似比_____,若四边形A`B`C`D`的周长为15cm ，则四边形ABCD 的周长为________.12．如图，矩形ABCD 中，E ，F 分别在BC ，AD 上，矩形ABCD ∽矩形ECDF ，且AB ＝2，S矩形ABCD ＝3S 矩形ECDF 。

2024-2025北师大九年级数学(上)第四章图形的相似单元测试卷(含答案)

第四章测试卷(时间:100分钟满分:120分)一、选择题(每小题3分，共30分，)题号12345678910答案B C A D B C C C A C1.下列形状分别为正方形、矩形、正三角形、圆的边框，其中不一定是相似图形的是( )2.在比例尺为1：500000的交通地图上，玉林到灵山的长度约为 23.6cm ，则它的实际长度约为( )A.0.118km B.1.18km C.118km D.1180km3.如图，以A ，B ，C 为顶点的三角形与以D ，E ，F 为顶点的三角形相似，则这两个三角形的相似比为( )A.2:1B.3:1C.4:3D.3:24.在△ABC 中,D 是AB 中点,E 是AC 中点,若△ADE 的面积是3，则△ABC 的面积是 ( )A.3 B.6 C.9 D.125.如图,在△ABC 中,点D 在AB 边上,过点 D 作DE ∥BC 交AC 于点E,DF ∥AC 交BC 于F,若AE:DF=2:3,则BF:BC 的值是 ( )A. 23 B. 35 C. 12D. 256.如图,在四边形ABCD 中,如果∠ADC=∠BAC,那么下列条件中不能判定△ADC 和△BAC 相似的是 ( )A.∠DAC=∠ABC B. AC 是∠BCD 的平分线 C.AC²=BC ⋅CD D.ADAB =DCAC7. 若△ABC 的各边都分别扩大到原来的 2 倍，得到△A ₁B ₁C ₁，下列结论正确的是 ( )A.△ABC 与△A ₁B ₁C ₁的对应角不相等 B.△ABC 与△A ₁B ₁C ₁不一定相似C.△ABC 与△A ₁B ₁C ₁的相似比为1:2 D.△ABC 与△A ₁B ₁C ₁的相似比为2:18.如图,点 E 是▱ABCD 的边 BC 延长线上的一点,AE 和CD 交于点G ，AC 是▱ABCD 的对角线，则图中相似三角形共有 ( )A.2 对B.3 对C.4 对D.5 对9.如图,已知E(-4,2),F(--2,--2),以O 为位似中心,把△EFO 缩小到原来的 12，则点E 的对应点的坐标为( )A.(2,一1)或(-2,1)B.(8,一4)或(一8,4)C.(2,-1)D.(8,-4)10.如图,在正方形 ABCD 中,点 E 、F 分别在边AD 和CD 上,AF ⊥BE,垂足为G,若 AEED =2,则 AGGF 的值为( )A. 45B. 56C.67D.78二、填空题(每小题3分，共15分)11.若△ABC ∽△A'B'C',且相似比为3:5,已知△ABC 的周长为21,则△A'B'C'的周长为 .12.如图是一架梯子的示意图，其中 AA₁‖BB₁‖CC₁‖DD₁,且AB=BC=CD.为使其更稳固，在A ，D ₁间加绑一条安全绳( 线段AD ₁),量得 AE=0.4m,则 AD₁= m13.如图，阳光通过窗口照到室内，在地上留下3m 宽的亮区.已知亮区一边到窗下的墙角的距离CE=7m ，窗口高AB=1.8m,那么窗口底边离地面的高BC 等于 m.14.如图，已知每个小方格的边长均为1，则△ABC 与△CDE 的面积比为 .15.如图,在正方形ABCD 中,E 是BC 的中点,F 是CD 上一点，且 CF =14CD,下列结论:①∠BAE=30°,②△ABE ∽△ECF,③AE ⊥EF,④△ADF ∽△ECF.其中正确的结论是 (填序号).三、解答题(本大题8个小题，共75 分)16.(8分)根据下列条件,判断△ABC 与△A'B'C'是否相似,并说明理由. AB =3,BC =4,AC =5,A 'B '=12,B 'C '=16,C 'A '=2017.(9分)如图,D 是△ABC 的边AC 上的一点,连接BD,已知∠ABD=∠C,BC=6,BD=4,如果△ABD 的面积为4,求△BC D 的面积.18.(9分)在平面直角坐标系中,△ABC 的三个顶点的坐标分别是 A(1，3)，B(4,1),C(1,1).(1)画出△ABC 关于x 轴成轴对称的△A ₁B ₁C ₁;(2)画出△ABC 以点O 为位似中心,相似比为 1:2的△A ₂B ₂C ₂.19.(9分)如图,四边形ABCD 是菱形,AF ⊥BC 交BD 于E,交 BC 于F.求证: AD 2=12DE ⋅DB.20.(10分)周末，小华和小亮想用所学的数学知识测量家门前小河的宽.测量时，他们选择了河对岸边的一颗大树，将其底部作为点 A，在他们所在的岸边选择了 B，使得AB与河岸垂直，并在B点竖起标杆BC，再在AB 的延长线上选择点 D 竖起标杆DE，使得点 E 与点C、A共线.已知:CB⊥AD,ED⊥AD,测得 BC=1m,DE=1.5m,BD=8.5m，测量示意图如图所示.请根据相关测量信息，求河宽 AB.21.(10分)如图,E是平行四边形ABCD的边 DA 延长线上一点,连结 EC 交AB 于 P.(1)写出图中的三对相似三角形(不添加辅助线)；(2)请在你所写的相似三角形中选一对，说明相似的理由.22.(10分)阅读与计算：请阅读以下材料，并完成相应的问题.角平分线分线段成比例定理：如图1，在△ABC中，AD平分∠BAC,则ABAC =BDCD.下面是这个定理的部分证明过程.证明:如图2,过点C作CE∥DA,交 BA的延长线于点 E⋯任务：(1)请按照上面的证明思路，写出该证明过程的剩余部分；(2)如图3,在△ABC中,AD是角平分线,AB=5cm ,AC=4 cm,BC=7 cm.求 BD的长.23.(10分)在矩形 ABCD中,点 E 是对角线AC 上一动点,连接 DE,过点 E 作EF⊥DE 交AB 于点 F.(1)如图1,当DE=DA时,求证:AF=EF;(2)如图2，点E 在运动过程中，DEEF的值是否发生变化?请说明理由.第四章测试卷答案一、选择题1、B2、C3、A4、D5、B6、C7、C8、C9、A 10、C 二、填空题11、35 12、1.2m 13、2.4m 14、4:1 15、②③三、解答题16、解：相似，理由： ∵AB A 'B '=312=14,BC B 'C '=416=14,AC A 'C '=520=14,∴ABA 'B'=BCB 'C '=ACA 'C ',∴ABC ∽A 'B 'C '.17、解:∵∠ABD=∠C,又∠A=∠A,∴△ABD ∽△ACB,S ABD S ACB=(BD CB )2=(46)2=49,18、解：如图所示19、证明:连接AC 交 BD 于点O,∵四边形ABCD 为菱形,∴AC ⊥BD,BO=OD,∵AE ⊥AD,∴△AOD ∽△EAD, ∴AD OD=ED AD,∴A D 2=ED ⋅OD,即 A D 2=12DE ⋅DB.20、解:∵CB ⊥AD,ED ⊥AD, ∴∠CBA =∠EDA =90°.∵∠CAB=∠EAD, ∴ABCOADE,∴AB AD=BC DE,∴AB AB +8.5=11.5,∴AB =17,.∴河宽为17m.21、解:(1)△EAP ∽△CBP,△AEP ∽△DEC,△BCP ∽△DEC.(2)选. △EAPO △CBP,理由如下:在▱ABCD 中AD ∥BC,∴∠EAP=∠B.又∵∠APE=∠BPC,∴△EAP ∽△CBP.22、解:(1)证明:如图2,过点C作CE∥DA,交BA的延长线于点E, ∵CEDA,∴BDCD =BAEA,∠CAD=∠ACE,∠BAD=∠E,∵AD平分∠BAC,∴∠BAD=∠CAD, ∠ACE=∠E,∴AE=AC,∴ABAC =BDCD；(2)∵AD是角平分线, ∴ABAC =BDCD,AB=5 cm,AC=4 cm,BC=7 cm, C.54=BD7−BD,解得BD=359cm.23、解:(1)证明:如图,连接 DF，在矩形ABCD 中,∠DAF=90°,又∵DE⊥EF,∴∠DEF=90°,∵AD=DE,DF=DF,∴Rt△DAF≌Rt△DEF(HL),∴AF=EF;(2)DEEF 的值不变.如图,过点E作EM⊥AD于点M,过点E 作EN⊥AB 于点 N,∵EM∥CD,EN∥BC,∴EMCD =AEAC,ENBC=AEAC,∴EMEN=CDBC,∵∠DEF=∠MEN=90°,∴∠DEM=∠FEN,又·∴∠DME=∠ENF=90°,∴△DME⊗△FNE,∴DEEF =EMEN,∴DEEF=CDBC,∵CD 与BC 的长度不变, ∴DEFF的长度不变.。

新北师大版九年级上册第四章《相似三角形》名校调研检测题及解答

新北师大版九年级上册第四章《相似三角形》名校单元检测题(时间：120分钟满分：120分)一、选择题(每小题3分，共30分)1．下列说法正确的是()A．对应边都成比例的多边形相似B．对应角都相等的多边形相似C．边数相同的正多边形相似D．矩形都相似2．已知△ABC∽△DEF，相似比为3∶1，且△ABC的周长为18，则△DEF的周长为() A．2B．3C．6D．54 3．如图，已知BC∥DE，则下列说法不正确的是()A．两个三角形是位似图形B．点A是两个三角形的位似中心C．AE∶AD是相似比D．点B与点E，点C与点D是对应位似点4．如图，身高为1.6 m的吴格霆想测量学校旗杆的高度，当她站在C处时，她头顶端的影子正好与旗杆顶端的影子重合，并测得AC＝2.0 m，BC＝8.0 m，则旗杆的高度是() A．6.4 m B．7.0 m C．8.0 m D．9.0 m,第3题图),第4题图),第5题图),第6题图)5．如图，为估算某河的宽度，在河对岸选定一个目标点，在近岸取点B，C，D，使得AB⊥BC，CD⊥BC，点E在BC上，并且点A，E，D在同一条直线上．若测得BE＝20 m，CE＝10 m，CD＝20 m，则河的宽度AB等于()A．60 m B．40 m C．30 m D．20 m6．“标准对数视力表”对我们来说并不陌生，如图是视力表的一部分，其中最上面较大的“E”与下面四个较小“E”中的哪一个是位似图形()A．左上B．左下C．右上D．右下7．如图，点A，B，C，D的坐标分别是(1，7)，(1，1)，(4，1)，(6，1)，以点C，D，E 为顶点的三角形与△ABC相似，则点E的坐标不可能是()A．(6，0) B．(6，3) C．(6，5) D．(4，2),第7题图) ,第8题图),第10题图),第9题图)8．如图，梯形ABCD 中，AD ∥BC ，∠B ＝∠ACD ＝90°，AB ＝2，DC ＝3，则△ABC 与△DCA 的面积比为( )A ．2∶3B ．2∶5C ．4∶9 D.2∶ 39．如图，在△ABC 中，∠A ＝36°，AB ＝AC ，AB 的垂直平分线OD 交AB 于点O ，交AC 于点D ，连接BD .下列结论错误的是( )A ．∠C ＝2∠AB ．BD 平分∠ABCC ．S △BCD ＝S △BOD D ．点D 为线段AC 的黄金分割点10．如图，在直角梯形ABCD 中，AD ∥BC ，∠ABC ＝90°，AB ＝8，AD ＝3，BC ＝4，点P 为AB 边上一动点，若△P AD 与△PBC 是相似三角形，则满足条件的点P 的个数是( )A ．1个B ．2个C ．3个D ．4个二、填空题(每小题3分，共18分)11．若x y ＝m n ＝45(y ≠n )，则x －m y －n＝____．12．如图是两个形状相同的红绿灯图案，则根据图中给出的部分数值，得到x 的值是___． 13．如图，在△ABC 中，点P 是AC 上一点，连接BP .要使△ABP ∽△ACB ，则必须有∠ABP ＝____或∠APB ＝__ __或ABAP ＝____．,第12题图) ,第13题图) ,第14题图) ,第15题图)14．如图，矩形ABCD 中，AB ＝2，BC ＝3，点E 是AD 的中点，CF ⊥BE 于点F ，则CF ＝____．15．如图所示，一条河的两岸有一段是平行的，在河的南岸边每隔5米有一棵树，在北岸边每隔50米有一根电线杆，小丽站在离南岸边15米的点P 处看北岸，发现北岸相邻的两根电线杆恰好被南岸的两棵树遮住，并且在这两棵树之间还有三棵树，则河宽为____米．16．劳技课上小敏拿出了一个腰长为8厘米，底边为6厘米的等腰三角形，她想用这个等腰三角形加工出一个边长比是1∶2的平行四边形，平行四边形的一个内角恰好是这个等腰三角形的底角，平行四边形的其他顶点均在三角形的边上，则这个平行四边形的较短的边长为__ cm__．三、解答题(共72分)17．(10分)如图，点D是△ABC的边AC上的一点，连接BD，已知∠ABD＝∠C，AB＝6，AD＝4，求线段CD的长．18．(10分)一个钢筋三角架三边长分别是20厘米、50厘米、60厘米，现在再做一个与其相似的钢筋三角架，而只有长为30厘米和50厘米的两根钢筋，要求以其中一根为一边，从另一根上截下两段(允许有余料)作为两边，则不同的截法有多少种？写出你的设计方案，并说明理由．19．(10分)如图，在平面直角坐标系中，已知△ABC三个顶点的坐标分别为A(－1，2)，B(－3，4)，C(－2，6)．(1)画出△ABC绕点A顺时针旋转90°后得到的△A1B1C1；(2)在网格内以原点O为位似中心，画出将△A1B1C1三条边放大为原来的2倍后的△A2B2C2.20．(10分)如图，矩形ABCD为台球桌面．AD＝260 cm，AB＝130 cm.球目前在E点位置，AE＝60 cm.如果小丁瞄准了BC边上的点F将球打进去，经过反弹后，球刚好弹到D点位置．(1)求证：△BEF∽△CDF；(2)求CF的长．21．(10分)已知，如图，△ABC中，AD是中线，且CD2＝BE·BA.求证：ED·AB＝AD·BD.22．(10分)如图，在平行四边形ABCD中，过点A作AE⊥BC，垂足为点E，连接DE，点F为线段DE上一点，且∠AFE＝∠B.(1)求证：△ADF∽△DEC；(2)若AB＝8，AD＝63，AF＝43，求AE的长．23．(12分)将一副三角尺如图①摆放(在Rt △ABC 中，∠ACB ＝90°，∠B ＝60°；在Rt △DEF 中，∠EDF ＝90°，∠E ＝45°)点D 为AB 的中点，DE 交AC 于点P ，DF 经过点C .(1)求∠ADE 的度数；(2)如图②，将△DEF 绕点D 顺时针方向旋转角α(0°<α<60°)，此时的等腰直角三角尺记为△DE ′F ′，DE ′交AC 于点M ，DF ′交BC 于点N ，试判断PMCN 的值是否随着α的变化而变化？如果不变，请求出PMCN 的值；反之，请说明理由．参考答案：一、选择题(每小题3分，共30分) 1． ( C ) 2． ( C ) 3． ( C ) 4． ( C ) 5． ( B ) 6． ( B ) 7． ( B ) 8．（ C ) 9． ( C ) 10 ( C )二、填空题(每小题3分，共18分)11． __45__．12． __16__．13．∠ABP ＝__∠C __或∠APB ＝__∠ABC __或AB AP ＝__ACAB__． 14． __125__． 15.__2.4_cm 或2411_cm __．三、解答题(共72分) 17．．解：在△ABD 和△ACB 中，∠ABD ＝∠C ，∠A ＝∠A ，∴△ABD ∽△ACB ，∴AB AC ＝ADAB，∵AB ＝6，AD ＝4，∴AC ＝AB 2AD ＝364＝9，则CD ＝AC －AD ＝9－4＝518．解：两种截法：①30厘米与60厘米的两根钢筋为对应边，把50厘米的钢筋按10厘米与25厘米两部分截，则有1020＝2550＝3060＝12，从而两个三角形相似；②30厘米与50厘米长的两根钢筋为对应边，把50厘米分截出12厘米和36厘米两部分，则有2012＝5030＝6036＝53，从而两三角形相似19．解：20．解：(1)证明：∵FG ⊥BC ，∠EFG ＝∠DFG ，∴∠BFE ＝∠CFD ，又∵∠B ＝∠C ＝90°，∴△BEF ∽△CDF(2)解：设CF ＝x ，则BF ＝260－x ，∵AB ＝130，AE ＝60，BE ＝70，由(1)得：△BEF ∽△CDF ，∴BE CD ＝BF CF ，即70130＝260－xx ，∴x ＝169 cm ，即CF ＝169 cm21．证明：∵AD 是中线，∴BD ＝CD ，又CD 2＝BE ·BA ，∴BD 2＝BE ·BA ，即BE BD ＝BDAB，又∠B＝∠B ，∴△BED ∽△BDA ，∴ED AD ＝BDAB，∴ED ·AB ＝AD ·BD22．解：(1)证明：∵四边形ABCD 是平行四边形，∴AB ∥CD ，AD ∥BC.∴∠C ＋∠B ＝180°，∠ADF ＝∠DEC.∵∠AFD ＋∠AFE ＝180°，∠AFE ＝∠B ，∴∠AFD ＝∠C.∴△ADF ∽△DEC (2)∵四边形ABCD 是平行四边形，∴CD ＝AB ＝8.由(1)知△ADF ∽△DEC ，∴AD DE ＝AF CD .∴DE ＝AD ·CDAF ＝63×843＝12.在Rt △ADE 中，由勾股定理得AE ＝DE 2－AD 2＝122－（63）2＝623．(12分)．解：(1)由题意知：CD 是Rt △ABC 中斜边AB 上的中线，∴AD ＝BD ＝CD ，∵在△BCD 中，BD ＝CD 且∠B ＝60°，∴△BCD 是等边三角形，∴∠BCD ＝∠BDC ＝60°，∴∠ADE ＝180°－∠BDC －∠EDF ＝180°－60°－90°＝30°(2)PMCN的值不会随着α的变化而变化，理由如下：∵△APD 的外角∠MPD ＝∠A ＋∠ADE ＝30°＋30°＝60°，∴∠MPD ＝∠BCD ＝60°，∵在△MPD 和△NCD 中，∠MPD ＝∠NCD ＝60°，∠PDM ＝∠CDN ＝α，∴△MPD ∽△NCD ，PM CN ＝PDCD ，又∵由(1)知AD ＝CD ，∴∠ACD ＝∠A ＝30°，即∠PCD ＝30°.在Rt △PCD 中，∠PCD ＝30°，∴PD CD ＝13＝33，∴PM CN ＝PD CD ＝33。

北师大版九年级数学上册《4.7相似三角形的性质》同步测试题带答案

北师大版九年级数学上册《4.7相似三角形的性质》同步测试题带答案学校:___________班级：___________姓名：___________考号：___________【基础达标】1.两个相似三角形的对应边之比为3∶4,那么它们对应高线的比为()A.√3∶4B.3∶4C.√3∶2D.2∶√32.已知△ABC∽△DEF,相似比为3∶1,且△ABC的周长为18,则△DEF的周长为()A.2B.3C.6D.543.已知两个相似三角形的相似比为2∶3,则它们的面积比为()A.2∶3B.4∶9C.3∶2D.√2∶√34.如图,△ADE∽△ABC,若AD=1,BD=2,则△ADE与△ABC的相似比是()A.1∶2B.1∶3C.2∶3D.3∶25.若相似三角形对应角平分线的比为3∶2,则它们对应中线的比为.6.已知△ABC的三边长分别为√2,√6,2,△A'B'C'的两边长分别是1和√3,如果△ABC与△A'B'C'相似,那么△A'B'C'的第三边长应该是√2.7.两个相似三角形的面积之比为1∶2,则相似比为√2.【能力巩固】8.如图,△AOB∽△COD,OA∶OC=9∶7,∠A=x°,∠C=y°,△AOB与△COD的面积分别是S1和S2,△AOB与△COD的周长分别是C1和C2,则下列等式一定成立的是()A.BO=9CDB.7x=9yC.7S1=9S2D.7C1=9C29.如图,在正方形网格中,每个小正方形的边长均为1,△ABC和△DEF的顶点都在网格线的交点的值为.上.设△ABC的面积为S1,△DEF的面积为S2,则S1S210.如图,在△ABC中,D、E分别是AB、AC的中点,M是DE的中点,CM的延长线交边AB于点的值为.N,那么S△DMNS四边形DBCM11.在平面直角坐标系中,已知O(0,0),A(2,0),B(0,4),C(0,3),D为x轴上一点.若以D、O、C为顶点的三角形与△AOB相似,这样的D点有()A.2个B.3个C.4个D.5个12.已知△ABC∽△A'B'C',它们的周长之差为20,面积比为4∶1,求△ABC和△A'B'C'的周长.【素养拓展】13.如图,矩形ABCD的一条边AD=8,将矩形ABCD折叠,使得顶点B落在CD边上的P点处.已知折痕与边BC交于点O,连接AP、OP、OA.(1)求证:△OCP∽△PDA.(2)若△OCP与△PDA的周长之比为1∶2,求边AB的长.参考答案【基础达标】1.B2.C3.B4.B5.3∶26.√27.1∶√2【能力巩固】8.D9.1210.11511.C12.解:∵△ABC∽△A'B'C',面积比为4∶1∴相似比为2∶1,周长比为2∶1.∵周长比相差1,而周长之差为20∴每份周长为20∴△ABC的周长是2×20=40,△A'B'C'的周长是1×20=20.【素养拓展】13.解:(1)证明:∵四边形ABCD是矩形,∴AD=BC,DC=AB,∠DAB=∠B=∠C=∠D=90°.由折叠可得AP=AB,PO=BO,∠PAO=∠BAO,∠APO=∠B∴∠APO=90°,∴∠APD=90°-∠CPO=∠POC.∵∠D=∠C,∠APD=∠POC∴△OCP∽△PDA.(2)∵△OCP与△PDA的周长之比为1∶2∴OPPA =CPDA=12,∴DA=2CP.∵AD=8,∴CP=4,CB=8.设OP=x,则OB=x,CO=8-x.在Rt△PCO中,∠C=90°,CP=4,OP=x 则OB=x,CO=8-x∴x2=(8-x)2+42,解得x=5.∵OPPA =12,∴AB=AP=2OP=10∴边AB的长为10.。

北师版数学九年级上第四章相似三角形单元测试(含答案)

北师版数学九年级相似三角形单元测试班级姓名成绩（时间：120分钟，满分120分）一、（选择题，只有一个是正确的，认真选一选，能选对的）（每题4分，共计44分） 1、若43=y x ，则下列各式中不成立的是。

A 、47=+y y x B 、14=-x y y C 、41=-y y x D 、3112=+x y x 2、已知△ABC∽△DEF，且AB ：DE=1：2，则△ABC 的面积与△DEF 的面积之比为(A)1：2 (B)1：4 (C)2：1 (D)4：13、若△ABC ∽△DEF, △ABC 与△DEF 的相似比为１∶2，则△ABC 与△DEF 的周长比为（） A ．1∶4B ．1∶2C ．2∶1D 24、2009年杭州市）如果一个直角三角形的两条边长分别是6和8，另一个与它相似的直角三角形边长分别是3和4及x ，那么x 的值（）A ．只有1个B ．可以有2个C ．有2个以上但有限D ．有无数个 5、如图1所示，给出下列条件：①B ACD ∠=∠；②ADC ACB ∠=∠；③AC AB CD BC=；④2AC AD AB =．其中单独能够判定ABC ACD △∽△的个数为（） A ．1 B ．2 C ．3 D ．46、如图2所示，小东用长为3.2m 的竹竿做测量工具测量学校旗杆的高度，移动竹竿，使竹竿、旗杆顶端的影子恰好落在地面的同一点．此时，竹竿与这一点相距8m 、与旗杆相距22m ，则旗杆的高为（） A ．12m B ．10m C ．8m D ．7m7、如图3，小正方形的边长均为1，则下列图中的三角形（阴影部分）与ABC △相似的是（）8、如图4， ABC △中，CD AB ⊥于D ，一定能确定ABC △为直角三角形的条件的个数是（）①1A ∠=∠，②CD DBAD CD =，③290B ∠+∠=°， ④345BC AC AB =∶∶∶∶，⑤CD AC BD AC ∙=∙A ．1B ．2C ．3D ．49、如图5，正五边形FGHMN 是由正五边形ABCDE 经过位似变换得到的，若AB:FG=2:3，则下列结论正确的是（） A ．2DE=3MN ， B ．3DE=2MN ， C ． 3∠A=2∠F D ．2∠A=3∠F10、若一个图形的面积为2，那么将它与成中心对称的图形放大为原来的两倍后的图形面积为（） A. 8 B. 6 C. 4 D. 211、如图，丁轩同学在晚上由路灯AC 走向路灯BD ，当他走到点P 时，发现身后他影子的顶部刚好接触到路灯AC 的底部，当他向前再步行20m 到达Q 点时，发现身前他影子的顶部刚好接触到路灯BD 的底部，已知丁轩同学的身高是1.5m ，两个路灯的高度都是9m ，则两路灯之间的距离是A ．24mB ．25mC ．28mD ．30m二、填空题（仔细填，注意答案医药是最简的形式）（每题3分，共计18分） 12、已知x ：y ：z=4：5：6，则（x-2y+3z ）：（2x+3y-z ）= 。

4.7 相似三角形的性质数学北师大版九年级上册同步测试(含答案)

《相似三角形的性质》同步测试1. 下列说法中正确的是( )A. 位似图形可以通过平移而相互得到B. 位似图形的对应边平行且相等C. 位似图形的位似中心不只有一个D. 位似中心到对应点的距离之比都相等2. 如下图，ABCD 是正方形，E 是CD 的中点，P 是BC 边上的一点，下列条件中，不能推出△ABP 与△ECP 相似的是（）A.∠APB ＝∠EPC B. ∠APE ＝90° C. P 是BC 的中点 D. BP ︰BC ＝2︰33. 如下图,Rt △ABC 中，AB ⊥AC ，AB =3，AC =4，P 是BC 边上一点，作PE ⊥AB 于E ，PD ⊥AC 于D ，设BP ＝x ，则PD+PE ＝（）A.B.C.D.4. 如图，在内有边长分别为a ，b ，c 的三个正方形．则a 、b 、c 满足的关系式是（）A.B.C.D.5. 如右上图，一人拿着一支厘米小尺，站在距电线杆约30米的地方，把手臂向前伸直，小尺竖直，看到尺上12厘米的长度恰好遮住电线杆，已知手臂长约60厘米，则电线杆的高为。

6. 已知一本书的宽与长之比为黄金比，且这本书的长是20 cm ，则它的宽为_____cm 。

（结果保留根号）7. 顶角为36°的等腰三角形称为黄金三角形，如图，在△ABC 中，AB ＝AC ＝1，∠A ＝36°，BD 是三角形ABC 的角平分线，那么AD ＝。

8. 已知：如图，ΔABC 中，AB=AC ，D 为BC 边上一点，且∠BDE=∠CDF 。

求证：S ΔBDF =S ΔCDE 。

9．如图，在平面直角坐标系中，△ABC 的三个顶点坐标分别为A(－2，1)，B(－1，4)，C(－3，2)。

(1)以原点O 为位似中心，相似比为1∶2，在y 轴的左侧，画出△ABC 放大后的图形△A 1B 1C 1，并直接写出C 1点的坐标；(2)若点D(a ，b)在线段AB 上，请直接写出经过(1)的变化后点D 的对应点D 1的坐标。

第四章图形的相似单元测试北师大版2024—2025学年秋季九年级上册

第四章图形的相似单元测试北师大版2024—2025学年秋季九年级上册考生注意：本试卷共三道大题，23道小题，满分120分，时量120分钟注意事项:1.本试卷分第I卷(选择题)和第II卷(非选择题)两部分。

笞卷前，考生务必将自己的姓名、准考证号填写在答题卡上。

2.回答第I卷时，选出每小题答案后，把答案填写在答题卡上对应题目的位置，填空题填写在答题卡相应的位置写在本试卷上无效。

3.回答第II卷时，将答案写在第II卷答题卡上。

4.考试结束后，将本试卷和答题卡一并交回。

第I卷一、选择题（每题只有一个正确选项，每小题3分，满分36分）1.在比例尺是1：8000的地图上，中山路的长度约为25cm，该路段实际长度约为（）A．3200m B．3000m C．2400m D．2000m2.如图，用放大镜将贺兰山旅游图标放大，这两个图形之间属于以下哪种图形变换（）A．相似B．平移C．轴对称D．旋转3．已知＝，则下列式子中正确的是（）A．a：b＝c2：d2B．a：d＝c：bC．a：b＝（a+c）：（b+d）D．a：b＝（a﹣d）：（b﹣d）4．下列说法中，不正确的是（）A．等边三角形都相似B．等腰直角三角形都相似C．矩形都相似D．正八边形都相似5．以下四组线段中，成比例的是（）A．3，4，6，8B．2，3，4，5C．1，2，3，4D．5，6，7，8 6．如果两个相似三角形的相似比是1：2，那么它们的周长比是（）A．2：1B．1：4C．1：D．1：27．如图，每个小正方形边长均为1，则下列图中的三角形（阴影部分）与图中△ABC相似的是（）A．B．C．D．8．如图，在平面直角坐标系中，正方形ABCD与正方形BEFG是以原点O为位似中心的位似图形，且相似比为，点A，B，E在x轴上．若正方形ABCD的边长为2，则点F坐标为（）A．（8，6）B．（9，6）C．D．（10，6）9．如图，在▱ABCD中，E是AB边的中点，则S△AEG：S平行四边形ABCD的值为（）A．B．C．D．10．如图，在矩形ABCD中，E、F分别在BC、CD上运动（不与端点重合），连接BF、AE，交于点P，且满足．连接CP，若AB＝4，BC＝6，则CP的最小值为（）A．2﹣3B．2﹣2C．5D．3二．填空题（6小题，每题3分，共18分）11．若，则＝．12．如图，已知AC∥EF∥BD，如果AE：EB＝2：3，CD＝6，那么DF的长等于.13．如图，在▱ABCD中，AD＝16，∠ABC的平分线交AD于点F，交CD的延长线于点E，若S△EDF：S四边形FBCD＝9：55，则AB＝．14．若，则k＝．15．如图，△ABC∽△CBD，AB＝9，BD＝25，则BC＝．16．如图，矩形ABCD中，AB＝3，BC＝10，点P是AD上的一个动点，若以A，P，B为顶点的三角形与△PDC相似，则AP＝．第II卷第四章图形的相似单元测试北师大版2024—2025学年秋季九年级上册姓名：____________ 学号：____________准考证号：___________一、选择题12345678910题号答案二、填空题11、_______ 12、______13、_______ 14、______15、_______ 16、______三、解答题解答题（17、18、19题每题6分，20、21每题8分，22、23每题9分，24、25每题10分，共计72分，解答题要有必要的文字说明）17．已知，求的值．18．如图，AB∥CD∥EF，BF＝20．（1）若AC＝3，CE＝5，求DF的长；（2）若AC：CE＝2：3，求DF的长．19.在△ABC中，∠BAC＝90°，AB＝AC，点D是BC边上一点，过点D作∠ADE＝45°，DE交AC于点E，求证：△ABD∽△DCE．20.如图，在△ABC中，AD是角平分线，点E在边AC上，且AD2＝AE•AB，连接DE．（1）求证：△ABD∽△ADE；（2）若CD＝3，CE＝2，求AE的长．21.如图，△ABC中，D、E两点分别在BC、AD上，且AD为∠BAC的角平分线，若∠ABE＝∠C，＝．（1）求证：△AEB∽△ADC．（2）求△BDE与△ABC的面积比．22.如图，在正方形ABCD中，点E在边AD上，过点D作DK⊥BE于K，且DK＝．（1）若AE＝ED，求正方形ABCD的周长；（2）若∠EDK＝22.5°，求正方形ABCD的面积．23.如图，AB＝4，CD＝6，F在BD上，BC、AD相交于点E，且AB∥CD∥EF．（1）若AE＝3，求ED的长．（2）求EF的长．24.如图，四边形ABCD中，AC平分∠DAB，∠ADC＝∠ACB＝90°，E为AB的中点．（1）求证：AC2＝AB•AD；（2）求证：CE∥AD；（3）若AD＝8，AB＝12．求的值．25．问题1：如图①，在△ABC中，AB＝4，D是AB上一点（不与A，B重合），DE∥BC，交AC于点E，连接CD．设△ABC的面积为S，△DEC的面积为S′．（1）当AD＝3时，＝；（2）设AD＝m，请你用含字母m的代数式表示．问题2：如图②，在四边形ABCD中，AB＝4，AD∥BC，AD＝BC，E是AB上一点（不与A，B重合），EF∥BC，交CD于点F，连接CE．设AE＝n，四边形ABCD的面积为S，△EFC的面积为S′．请你利用问题1的解法或结论，用含字母n的代数式表示．。

北师大版九年级数学上册第四章相似三角形单元测试卷(PDF版,无答案)

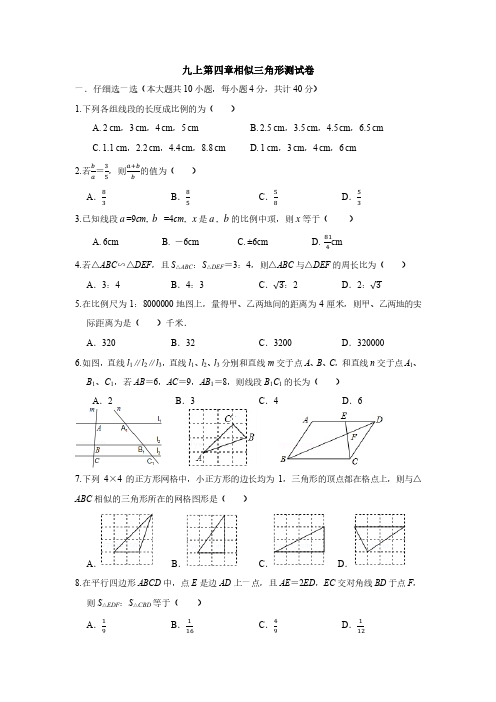
九上第四章相似三角形测试卷一．仔细选一选（本大题共10小题，每小题4分，共计40分）1.下列各组线段的长度成比例的为（）A. 2 cm，3 cm，4 cm，5 cmB. 2.5 cm，3.5 cm，4.5 cm，6.5 cmC. 1.1 cm，2.2 cm，4.4 cm，8.8 cmD. 1 cm，3 cm，4 cm，6 cm2.若ba ＝35，则a+bb的值为（）A．83B．85C．58D．533.已知线段a=9cm, b=4cm, x是a, b的比例中项，则x等于（）A. 6cmB. －6cmC. ±6cmD. 814cm4.若△ABC∽△DEF，且S△ABC：S△DEF＝3：4，则△ABC与△DEF的周长比为（）A．3：4B．4：3C．√3：2D．2：√35.在比例尺为1：8000000地图上，量得甲、乙两地间的距离为4厘米，则甲、乙两地的实际距离为是（）千米．A．320B．32C．3200D．3200006.如图，直线l1∥l2∥l3，直线l1、l2、l3分别和直线m交于点A、B、C，和直线n交于点A1、B1、C1，若AB＝6，AC＝9，AB1＝8，则线段B1C1的长为（）A．2B．3C．4D．67.下列4×4的正方形网格中，小正方形的边长均为1，三角形的顶点都在格点上，则与△ABC相似的三角形所在的网格图形是（）A．B．C．D．8.在平行四边形ABCD中，点E是边AD上一点，且AE＝2ED，EC交对角线BD于点F，则S△EDF：S△CBD等于（）A．19B．116C．49D．1129.在矩形ABCD中，AB＝6，AD＝9，点E为线段AD上一点，且DE＝2AE，点G是线段AB上的动点，EF⊥EG交BC所在直线于点F，连接GF．则GF的最小值是（）A．3B．6C．6√2D．3√510．如图1，若△ABC内一点P满足∠P AC＝∠PBA＝∠PCB，则点P为△ABC的布洛卡点，三角形的布洛卡点是法国数学家和数学教育家克洛尔于1816年首次发现，但他的发现并未被当时的人们所注意，1875年，布洛卡点被一个数学爱好者法国军官布洛卡重新发现，并用他的名字命名．问题：如图2，在等腰△DEF中，DF＝EF，FG是△DEF的中线，若点Q为△DEF的布洛卡点，FQ＝9，FG＝√2，则DQ+EQ＝（）DEA．10B．9+9√2C．6+6√3D．7√22二．认真填一填（本大题有6小题，每小题5分，共30分）11.若线段AB＝2cm，C是AB的黄金分割点(AC>BC)，则线段AC＝cm．12．如图，△ADE∽△ABC，AD＝3，AE＝4，BE＝5，CA的长为．13.如图，在△ABC中，D是AB边上的一点，连接CD，请添加一个适当的条件，使△ABC∽△ACD．（只填一个即可）14.如图，AD是△ABC的中线，点E是线段AD上的一点，且AE＝1AD，CE交AB于点3F．若AF＝2cm，则AB＝cm．15.如图，在△ABC中，AB＝BC．以AB为直径的圆O交AC于点D．交BC于点E连结AE，DE．若AB＝√2AC，则S△CDE：S△ABE的值为．16.如图，直线l1∥l2∥l3，且l1与l2的距离为1，l2与l3的距离为2，等腰△ABC的顶点分别在直线l1、l2，l3上，AB=AC，∠BAC=120°，则等腰三角形的腰长为.班级__________ 姓名____________ 试场所在教室__________座位号＿＿＿＿＿＿＿＿＿＿＿ --------------------------------------------------------------------密-------------------------------------封-------------------------------线------------------------------------------------------------开放双语九上第四章相似三角形测试卷九年级数学答题卷一、选择题（本大题有10小题，每小题4分，共40分）1 2345678910二、填空题（本大题有6小题，每小题5分，共30分）11、________________； 12、________________； 13、________________；14、________________； 15、________________； 16、________________；三、解答题（17-20每题8分，21题10分，22,23题12分，24题14 分，共80分） 17.如图．在平面直角坐标系中，△ABC 的三个顶点坐标分别为A （﹣2，1），B （﹣1，4），C （﹣3，2），(1)以O 为位似中心，在第二象限内把△ABC 扩大到原来的两倍，得则△A 2B 2C 2，画出△A 2B 2C 2；(2)△ABC 的面积为．(直接写出答案)18.如图，正方形ABCD 中，M 为BC 上一点，F 是AM 的中点，EF ⊥AM ，垂足为F ，交AD 的延长线于点E ，交DC 于点N ．（1）求证：△ABM ∽△EFA ；（2）若AB ＝12，BM ＝5，求DE 的长．19.小明用如图所示的方式测量一幢楼高：线段AB、EF、CD分别表示人、竹、竿、楼房的高度，且A、C、E在一条直线上．测得人和竹竿的水平距离为1.5m，人和楼房的水平距离为20m，人的高度为1.6m，竹竿的离度为2.8m，求这幢楼的高度．20.如图，BD、AC相交于点P，连接AB、BC、CD、DA，∠1＝∠2（1）求证：DP∙BP=AP∙PC（2）若AB＝8，CD＝4，DP＝3，求AP的长．21.在一个直角三角形的内部作一个矩形ABCD，其顶点A和点D分别在两直角边上，BC在斜边上．（1）设矩形的一边BC为x，那么AB边的长度如何表示？（2）设矩形的面积为y平方米，当x取何值时，y的最大值为多少？EF22.定义：从三角形（不是等腰三角形）一个顶点引出一条射线与对边相交，顶点与交点之间的线段把这个三角形分割成两个小三角形，如果分得的两个小三角形中一个为等腰三角形，另一个与原三角形相似，我们把这条线段叫做这个三角形的完美分割线例如：如图①，AD把△ABC分成△ABD与△ADC，若△ABD是等腰三角形，且△ADC∽△BAC，那么AD 就是△ABC的完美分割线．解答下列问题：(1)如图②，在△ABC中，∠B＝40°，AD是△ABC的完美分割线，且△ABD 是以AD为底边的等腰三角形，则∠CAD＝度．(2)在△ABC中，∠B＝42°，AD是△ABC的完美分割线，且△ABD是等腰三角形，求∠BAC 的度数．23.如图，在正方形ABCD中，E是CD上一点，连接AE．过点D作DM⊥AE，垂足为M，⊙O经过点A，B，M，与AD相交于点F．（1）求证：△ABM∽△DFM；（2）若正方形ABCD的边长为5，⊙O的直径为√29，求DE的长．24.如图，抛物线y＝−12x2+32x+2与x轴交于点A，B，与y轴交于点C．(1)试求A，B，C的坐标；(2)将△ABC绕AB中点M旋转180°，得到△BAD．①求点D的坐标；②判断四边形ADBC的形状，并说明理由；(3)在该抛物线对称轴上是否存在点P，使△BMP与△BAD相似？若存在，请直接写出所有满足条件的P点的坐标；若不存在，请说明理由．。

北师版九年级上册第四章相似三角形单元考试测试卷(无答案)

北师版九年级上册第四章单元测试卷(时间：100分钟满分：120分)一、选择题(12小题，每小题3分，共36分) 1. 已知2x ＝3y ，则下列比例式成立的是( )A .x 2＝3yB .x ＋y y ＝43 C .x 3＝y 2 D .x ＋y x ＝352.下列四组线段中，不能成比例的是（）.A. a ＝3，b ＝6，c ＝2，d ＝4B. a ＝1，b ＝3，c ＝2，d ＝6C. a ＝4，b ＝6，c ＝5，d ＝10D. a ＝2，b ＝5，c ＝4，d ＝103. 如图，直线a ，b ，c 分别与直线m ，n 交于点A ，B ，C ，D ，E ，F.已知直线a ∥b ∥c ，若AB ＝2，BC ＝3，则DE EF 的值为( ) A .23 B .32 C .25 D .354. 如图，点D ，E 分别是△ABC 的边AB ，AC 上的中点，如果△ADE 的周长是6，则△ABC 的周长是( ) A ．6 B ．12 C ．18 D ．245.如图，在△ABC 中，已知DE ∥BC ，AD ＝3，DB ＝6，DE ＝2，则BC ＝（）.A. 4B. 6C. 10D. 8EDCBA6.如图所示，在△ABC 中D 为AC 边上一点，若∠DBC ＝∠A ，6 BC ，AC ＝3，则CD 长为（） A ．1B ．23 C ．2 D ．257.把一张矩形的纸片对折后和原矩形相似，那么大矩形与小矩形的相似比是（）.A. 2 ∶1B. 4∶1C. 3∶1D. 2∶1 8. 如图，小正方形的边长均为1，则图中三角形（阴影部分）与△ABC 相似的是（）9.如图，在△ABC 中，∠BAC ＝90°，D 是BC 中点，AE ⊥AD 交CB 的延长线于E ，则下列结论正确的是（）A.△AED ∽△ACBB. △AEB ∽△ACDC.△BAE ∽△ACED.△AEC ∽△DAC10.在平面直角坐标系中，已知点A （﹣4，2），B （﹣2，﹣2），以原点O 为位似中心，相似比为12，把△AOB 缩小，则点A 的对应点A′的坐标是（）A ．（﹣2，1）B ．（﹣8，4）C ．（﹣8，4）或（8，﹣4）D ．（﹣2，1）或（2，﹣1）11.如图，已知正方形ABCD 的边长为4，E 是BC 边上的一个动点，AE ⊥EF ，EF 交DC 于点F ，设BE ＝x ，FC ＝y ，则当点E 从点B 运动到点C 时，关于x 的函数图像是（）12. 如图，在△ABC 中，∠A ＝36°，AB ＝AC ，AB 的垂直平分线OD 交AB 于点O ，交AC 于点D ，连接BD.下列结论错误的是( )A ．∠C ＝2∠AB ．BD 平分∠ABC C ．S △BCD ＝S △BOD D ．点D 为线段AC 的黄金分割点二、填空：（6小题，每小题4分，共24分）13. 若1，2，3，x 是成比例线段，则x ＝6. 14. 若x y ＝m n ＝45(y≠n)，则x －m y －n＝ .15. 如图，在△ABC 中，点D ，E 分别为AB ，AC 上的点，若DE∥BC，AD AB ＝13，则AD ＋DE ＋AE AB ＋BC ＋AC＝ . 16.如图所示，身高1.6m 的小华站在距路灯杆5m 的C 点处，测得她在灯光下的影长CD 为2.5m ，则路灯的高度AB 为______．xyx yx yxy 2224442221114221OOO O17．如图是一位同学设计的用手电筒来测量某古城墙高度的示意图．点P 处放一水平的平面镜，光线从点A 出发经平面镜反射后刚好到古城墙CD 的顶端C 处，已知AB ⊥BD ，CD ⊥BD ，测得AB=2米，BP=3米，PD=12米，那么该古城墙的高度CD 是米．18. 如图，这是圆桌正上方的灯泡（看作一个点）发出的光线照射桌面后，在地上形成阴影（圆形）的示意图，已知桌面的直径为1.2米，桌面距地面1米，灯泡距地面3米，则地上阴影部分的面积是______.三、解答题（共60分）19.(7分) 如图，若点P 在线段AB 上，点Q 在线段AB 的延长线上，AB ＝10，AP BP ＝AQ BQ ＝32，求线段PQ 的长．20．(8分)如图，在平面直角坐标系中，已知△ABC 三个顶点的坐标分别为A(－1，2)，B(－3，4)，C(－2，6)．(1)画出△ABC 绕点A 顺时针旋转90°后得到的△A 1B 1C 1；(2)在网格内以原点O 为位似中心，画出将△A 1B 1C 1三条边放大为原来的2倍后的△A 2B 2C 2.21.(7分)如图，点C 、D 在线段AB 上，△PCD 是等边三角形. ⑴当AC 、CD 、DB 满足怎样的关系式时，△ACP ∽△PDB ？ ⑵当△AC P ∽△PDB 时，求∠APB 的度数.22.(8分)如图，在△ABC 中，AB ＝10cm ，BC ＝20cm ，点P 从点A 开始沿AB 边向B 点以2cm/s 的速度移动，点Q 从点B 开始沿BC 边向点C 以4cm/s 的速度移动，如果点P 、Q 分别从A 、B 同时出发，问经过几秒钟，△PBQ 与△ABC 相似.C23.(10分)如图，△ABC与△ADE都是等腰三角形，AD=AE，AB=AC，∠DAB=∠CAE.求证：△ABC∽△ADE.24. (10分)如图，点D是△ABC的边AC上的一点，连接BD，已知∠ABD＝∠C，AB＝6，AD ＝4，求线段CD的长．25．(10分)如图，在平行四边形ABCD中，过点A作AE⊥BC，垂足为点E，连接DE，点F为线段DE上一点，且∠AFE＝∠B.(1)求证：△ADF∽△DEC；(2)若AB＝8，AD＝63，AF＝43，求AE的长．。

北师大-九年级上相似图形单元测试-(带答案)

2009-2010学年云南省曲靖市师宗二中八年级（下）单元试卷（第4章相似图形）九年级上第3章相似图形单元试卷一、细心填一填（每小题3分，共30分）1．已知：AB=3m，CD=30cm，则AB：CD=_________．2．两个三角形相似，其中一个三角形的两个内角是40°、60°．那么另一个三角形的最大角是_________度，最小角是_________度．3．一个主持人站在舞台的黄金分割点处最自然得体，如果舞台AB长为20米，一个主持人现在站在A处，则他应至少再走________米才最理想．4．某一时刻，一根4米长的旗杆的影子长6米，同一时刻一座建筑物的影子长36米，则这座建筑物的高度为_________米．5．已知△ABC∽△DEF，S△ABC ：S△DEF=1：9，△ABC的周长为18厘米，则△DEF的周长为_______厘米．6．在比例尺为1：6000000的中华人民共和国地图上，玉溪到昆明的图上距离是1.4厘米，则玉溪到昆明的实际距离是_________千米．7．已知，如下图1，ED∥BC，且，则=_________．8．（昆明）如上图2，在△ABC中，AC＞AB，点D在AC边上，（点D不与A、C重合），若再增加一个条件就能使△ABD∽△ACB，则这个条件可以是_________．9．如上图3，△ABC中，D、E分别为AB、AC边上的中点，若DE=6，则BC=_________．10．（梅州）在中国地理地图册上，连接上海、香港、台湾三地构成一个三角形，用刻度尺测得它们之间的距离如上图4所示．飞机从台湾直飞上海的距离约为1 286千米，那么飞机从台湾绕道香港再到上海的飞行距离约为_________千米．二、用心选一选（每小题3分，共30分）11．如果，则=（） A． B． C． D．12．（云南）已知，则（b+d≠0）的值等于（）A． B． C． D．13．若△ABC∽△DEF，则相似比等于（）A．DE：AB B．∠A：∠D C．S△ABC：S△DEF D．C△ABC：C△DEF14．下列说法错误的是（）A．任意两个直角三角形一定相似 B．任意两个正方形一定相似C．位似图形一定是相似图形 D．位似图形每一组对应点到位似中心的距离之比都等于位似比15．若a、b、c、d是互不相等的正数，且，则下列式子错误的是（）A． B． C． D．16．已知△ABC∽△DEF，AB=6cm，BC=4cm，AC=9cm，且△DEF的最短边边长为8cm，则最长边边长为（）A．16cm B．18cm C．4.5cm D．13cm17．△ABC∽△DEF，它们的周长之比为：1，则它们的对应高比及面积比分别为（）A．1：，2：1 B．：1，2：1 C．2：1，：1 D．1：2，：118．已知：如图在△ABC中，AE=ED=DC，FE∥MD∥BC，FD的延长线交BC的延长线于N，则为（）A． B． C． D．19．如上图2，△ABC中，D为BC中点，E为AD的中点，BE的延长线交AC于F，则为（）A．1：5 B．1：4 C．1：3 D．1：220．已知：如图在△ABC中，DE∥BC，，则=（）A． B． C．D．三、耐心做一做（共60分）21．如图，已知∠ADC=∠BAC，BC=16cm，AC=12cm，求DC的长．22．如图，已知BE、CF分别是△ABC的边AC、AB的高．试说明：AC•BE=AB•CF．23．如图，已知∠1=∠3，∠B=∠D，AB=DE=5cm，BC=4cm．（1）△ABC∽△ADE吗？说明理由．（2）求AD的长．24．（云南）已知：如图，在△ABC中，∠ACB的平分线CD交AB于D，过B作BE∥CD交AC的延长线于点E．（1）求证：BC=CE；（2）求证：．25．如图，平行四边形ABCD中，AE：EB=1：2，求△AEF与△CDF的周长的比．如果S△AEF=6cm2，求S△CDF．26．一条河的两岸有一段是平行的，在该河岸的这一段每隔5米有一颗树，河对岸每隔50米有一根电线杆．在这岸离开岸边25米处看对岸，看到对岸相邻的两根电线杆恰好被这岸的两颗树遮住，且这两颗树之间还有3棵树，求河的宽度．九年级（上）单元试卷（第4章相似图形）参考答案与试题解析一、细心填一填（每小题3分，共30分）1．故答案为：10：1．2．故答案为：80，40．3．①若AC是BC与AB的比例中项：则=，即x：（20﹣x）=（﹣1）：2解得x=30﹣10；②若BC是AC与AB的比例中项：则=，即（20﹣x）：x=（﹣1）：2；解得x=10﹣10．∵30﹣10＜10﹣10，∴他应至少再走（30﹣10）米才最理想．故答案为：30﹣10．4．故答案为：24．5．故答案为：54．6．故答案为：84．7．故答案为：．8．解答：解：连接BD，若①∠ABD=∠ACB，∵∠ABD=∠ACB，∠BAD=∠CAB，∴△ABD∽△ACB．若②∠ADB=∠ABC，∵∠ADB=∠ABC，∠BAD=∠CAB，∴△ABD∽△ACB．若③=，∵=，∠BAD=∠CAB，∴△ABD∽△ACB．9．解答：解：如图所示，∵D、E分别为AB、AC边上的中点，∴DE是△ABC的中位线，∴DE=BC，∴BC=12．故答案是12．10．解答：解：根据图上距离，发现：飞机从台湾绕道香港再到上海的飞行的图上距离是飞机从台湾直飞上海的图上距离的3倍，所以飞机从台湾绕道香港再到上海的飞行的实际距离设为x（千米），=，解得x=3858（千米），故填3858．二、用心选一选（每小题3分，共30分）11．故选C．12．故选B．13．故选D．14．故选A．15．故选D．16．故选B．17．故选B．18．故选C．19．解答：解：过D作BF的平行线，交AC边于G，如下图所示：∵D为BC中点，DG∥BF；∴∠CGD=∠CFB；又∵∠C=∠C；∴△CDG∽△CBF；∴==，即：CG=CF=FG；又E为AD的中点，BE的延长线交AC于F，DG∥BF；同理可得：△AEF∽△ADG；∴==，即：AF=AG=FG；∴AF=FG=GC；∴===1：2；故选：D；．20．解答：解：∵AD：BD=1：3，∴AD：AB=1：4；∵DE∥BC，∴△ADE∽△ABC；∴DE：BC=AD：AB=1：4；故选C．三、耐心做一做（共60分）21．解答：解：∵∠ADC=∠BAC，∠C=∠C，∴△ADC∽△BAC，∴，∵BC=16cm，AC=12cm，∴DC==9cm．22．解答：证明：∵BE、CF分别是△ABC的边AC、AB的高，∴∠AEB=∠AFC=90°，又∵∠A=∠A，∴△ABE∽△ACF，∴=，∴AC•BE=AB•CF．23．解答：解：（1）△ABC∽△ADE．理由：∵∠1=∠3，∴1+∠2=∠3+∠2，即∠BAC=∠DAE．∵∠B=∠D，∴△ABC∽△ADE．（2）∵△ABC∽△ADE，∴AB：AD=BC：DE，即 5：AD=4：5，∴AD=（cm）．24．解答：证明：（1）∵CD平分∠ACB，∴∠ACD=∠BCD．又∵BE∥CD，∴∠CBE=∠B CD，∠CEB=∠ACD．∵∠ACD=∠BCD，∴∠CBE=∠CEB．故△BCE是等腰三角形，BC=CE．（2）∵BE∥CD，根据平行线分线段成比例定理可得=，又∵BC=CE，∴=．25．解答：解：由AE：EB=1：2得=，又∵ABCD是平行四边形，∴△AEF∽△CDF，由AB=CD得=，所以△AEF与△CDF周长的比等于相似比等于1：3．由=（相似三角形面积比是相似比的平方）由S△AEF =6cm2解得S△CDF=54cm2．26．解答：解：如上所示：AF=25m，BC=5×4=20m，DE=50m．因为BC∥DE，所以=，即=，解得：FG=37.5m．经检验FG=37.5符合题意．故河宽37.5m．。

1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

D A C
120°E
D
C
B
A C
A
B
八年级相似三角形单元检测卷
A 卷（100分，时间60分钟）
一、选择题（每题3分，共30分）
1．在比例尺为1:500000的地图上，A 、B 两个城市之间的距离为6㎝，那A 、B 两个城市之间的实际距离是（）
A.30 km
B. 3km
C. 300 km
D. 3000km
2.下列各组线段（单位：㎝）中，四条线段成比例的是（）
A ．1、3、4、6 B.2、3、6、9 C. 3、5、9、12 D. 3、4、5、6 3.已知△ABC ∽△DEF ，则下列等式正确的是（）
A ．A
B EF DE A
C ⋅=⋅ B ．AB BC DE EF ⋅=⋅ C ．BC DF AC EF ⋅=⋅
D ．AC DF BC DF ⋅=⋅ 4．ABC △中，D
E BC ∥，且2
3
AD DB =
，4DE =cm ，则BC =（）
Ａ．14cm Ｂ．12cm
Ｃ．10cm Ｄ．8cm
5．某天同时同地，甲同学测得2m 的测竿在地面上的影长为1.6m ，乙同学测得国旗旗杆在地面上的影长为9.6m ，则国旗旗杆的高度为（）m A. 10 B.12 C. 13 D. 15
6．五边形ABCDE ∽五边形E D C B A ''''',且最长边分别为AB=10㎝和B A ''=8㎝，如果五边形ABCDE 的周长为35㎝，则五边形E D C B A '''''的周长为（）㎝ A ．28㎝ B. 24㎝ C. 56㎝ D. 30㎝ 7.下列判断正确的是（）
A ．等腰三角形都相似
B ．正方形都相似
C ．直角三角形形都相似
D ．对应角都分别相等的多边形相似 8.如图，在直角△ABC 中，∠ACB=900
，CD ⊥AB 与点D.则下列结论错误的是（）
A.AC 2=AD ·AB
B.BC 2
=BD ·AB
C.CD 2=AD ·BD
D.AC 2：BC 2=AD 2：BD 2
9. 如图所示，△ABC 是等边三角形，∠DAE=120°，D 、B 、C 、E 共线，则图中相似三角形的对数至少为（） A ．一对 B ．二对 C ．三对 D ．四对
10．1．如图，小正方形的边长均为1，则下列图中的三角形（阴影部分）与△ABC 相似的是（）
A
B
C D E
C
B
B A
A
B
C
D
二、填空题（每题4分，共20分）
11.若3x-2y=0, 则y x
=。

若a= 2 ，b=3, c= 8 则成比例线段a 、b 、c 、d 中的d= .
12. 如图在△ABC 中，点D 为AB 之中点，DE ∥BC, △ADE 的面积为S 1，四边形DBCE 的面积为S 2，则S 1 ：S 2=
13. 如图，小明在地面上放置一个平面镜E 来测量铁塔AB 的高度，镜子与铁塔的距离EB=20米，镜子与小明的距离ED=2米时，小明刚好从镜子中看到铁塔顶端点A ，已知小明的眼睛距地面的高度CD=1.5米，则铁塔AB 的高度是_________米.
14.如图，在△ABC 中，点D 为边BC 上一点，请你填写一个条件，，可使△ABC ∽△DBA 。

15．若53
=
=
=
f
e d
c b
a
，则f d b e c a +-+-=，5232--+--+f d b e c a =.
三、解答题(16—21题每题7分，22题8分)
16. 若等腰三角形ABC 中，AB=AC, ∠A=120°,AD 为高，求AD:BC 的值。

17. 若5
32
c
b a ==，且3a-2b+5c=50,求a,b,
c 的值
A
C
18. 已知线段AB=20cm ，点M 为AB 的黄金分割点，求BM 的长。

19. 如图，在平面直角坐标系中，已知△ABC 三个顶点的坐标分别为A （﹣1，2），
B （﹣3，4）
C （﹣2，6）（1）画出△ABC 绕点A 顺时针旋转90°后得到的△A 1B 1C 1
（2）以原点O 为位似中心，画出将△A 1B 1C 1三条边放大为原来的2倍后的△A 2B 2C 2．
20.如图，在△ABC 中∠C=900
，在AB 边上取一点D ，使BD=BC,过D 作DE ⊥AB 交AC 于点E ，AC=8，BC=6，求DE 的长。

E
C B
A
21. 如图，□ABCD 中，E 是CD 的延长线上一点，BE 与AD 交于点F ，CD DE 2
1。

⑴求证：△ABF ∽△CEB;
⑵若△DEF 的面积为2，求□ABCD 的面积。

22. 如图，Rt △ABC 中，∠BAC=90°，AB=AC=2，点D 在BC 上运动. （不到达B 、C ），过D 作∠ADE=45°交于AC 于E. （1）求证：△ABD ∽△DCE.
（2）当△ADE 是等腰三角形时，求AE 的长.
C E
D B A 第21题图 F A
D E
B C
B 卷
（满分50分，时间40分钟）
一．填空题（每题4分，共20分）
1．若k b a c c a b c b a =+=+=+，
则k 的值为________；直线y kx k =-必定经过第________象限。

2．如图，ABC △是一块锐角三角形余料，边120BC =mm ，高80AD =mm ，要把它加工成长方形零件PQMN ，使长方形PQMN 的边QM 在BC 上，其余两个顶点P N ，分别在AB AC ，上．
则求这个长方形零件PQMN 面积S 的最大值=.；
3．.如图，在正方形ABCD 中，P 是BC 上一点，BP=3PC ，Q 为CD 之中点，QE ⊥AP 于E 。

则AQ:QP=; AE ：EP=.
4．如图，身高1.8米的小明某晚站在两个一样高的相距24米的路灯下的EF 处，此时，他左边的影长为4米，他在右边的影长为6米，则路灯的高为米。

H
G
F E
D
C
B
A
B
N
E P
A
B 5．.如图，在矩形ABCD 中，AB=12cm,BC=6cm,点P 沿AB 边从点A 开始向点B 以2cm/s 的速度移动;点Q 从点D 开始向点A 以1cm/S 移动，如果P 、Q 同时出发，用t(s)表示移动时间，那么：当t=时，△QAP 为
等腰直角三角形；当t=时，以点Q 、A 、P 为顶点的三角形与△ABC 相似。

二．解答题
6．某同学想测量一棵树AB 的高度。

他在某时刻测得1米的竹竿竖直时影长为1.5米。

在同一时刻测树的影长时，因为树靠近一面墙体，影子不全落在地上，有一部分落在墙上，他测得地上影长为30米，墙上影长为5米，如图所示，请你帮他求出树的高度。

（5分）
7．如图所示，△ABC 中，AB=9，AC=6，BC=12，点M 在AB 边上，且AM=3，过点M 作直线MN 与三角形的另一边交于点N ，若截得的三角形与原三角形相似，试求MN 的长。

（6分）
Q
D C
B
A
D
8．如图，四边形ABCD中，AD＝CD，∠DAB＝∠ACB＝90°，过点D作DE⊥AC，垂足为F，DE与AB相交于点E.
（1）求证：AB·AF＝CB·CD
（2）已知AB＝15cm，BC＝9cm，P是射线DE上的动点.设DP＝xcm（x＞0），四边形BCDP 的面积为ycm2.
①求y关于x的函数关系式；
②当x为何值时，△PBC的周长最小，并求出此时y的值.
9．已知：如图，在平面直角坐标系中，△ABC是直角三角形，∠ACB=90°，点A、C的坐标分别
为A（－3，0），C（1，0），BC
AC
=
4
3.
（1）求过点A、B的直线的函数表达式；
（2）在x轴上找一点D，连接DB，使得以点A、D、B为顶点的三角形与△ABC相似（不包括全等），并求点D的坐标；
（3）在（2）的条件下，如P、Q分别是AB和AD上的动点，连接PQ，设AP=DQ=m，问是否存在这样的m使A得以点A、P、Q为顶点的三角形与△ADB相似，如存在，请求出m的值；如不存在，请说明理由. （10分）。

北师大版九年级上期相似三角形单元检测卷

2022-2023学年北师大版九年级数学上册《4-4探索三角形相似的条件》同步达标测试题(附答案)

北师大版九年级上册相似测试题

北师大版九年级数学上册相似三角形的性质同步测试卷

2024-2025北师大九年级数学(上)第四章图形的相似单元测试卷(含答案)

新北师大版九年级上册第四章《相似三角形》名校调研检测题及解答

北师大版九年级数学上册《4.7相似三角形的性质》同步测试题带答案

北师版数学九年级上第四章相似三角形单元测试(含答案)

4.7 相似三角形的性质数学北师大版九年级上册同步测试(含答案)

第四章图形的相似单元测试北师大版2024—2025学年秋季九年级上册

北师大版九年级数学上册第四章相似三角形单元测试卷(PDF版,无答案)

最新北师大九年级上册相似三角形单元测试题

最新北师大版九年级上册相似三角形单元测试试题(基础+拔高各一套)

北师版九年级上册第四章相似三角形单元考试测试卷(无答案)

北师大-九年级上相似图形单元测试-(带答案)

北师大版九年级上期相似三角形单元检测卷

2022-2023学年北师大版九年级数学上册《4-4探索三角形相似的条件》同步达标测试题(附答案)

北师大版九年级上册相似测试题

北师大版九年级数学上册相似三角形的性质同步测试卷

2024-2025北师大九年级数学(上)第四章图形的相似单元测试卷(含答案)

新北师大版九年级上册第四章《相似三角形》名校调研检测题及解答

北师大版九年级数学上册《4.7相似三角形的性质》同步测试题带答案

北师版数学九年级上第四章 相似三角形单元测试(含答案)

4.7 相似三角形的性质 数学北师大版九年级上册同步测试(含答案)

第四章图形的相似单元测试北师大版2024—2025学年秋季九年级上册

北师大版九年级数学上册第四章 相似三角形 单元测试卷(PDF版,无答案)

最新北师大九年级上册相似三角形单元测试题

最新北师大版九年级上册相似三角形单元测试试题(基础+拔高各一套)

北师版九年级上册第四章相似三角形 单元考试测试卷(无答案)

北师大-九年级上相似图形单元测试-(带答案)

北师版数学九年级上第四章相似三角形单元测试(含答案)

4.7 相似三角形的性质数学北师大版九年级上册同步测试(含答案)

北师大版九年级数学上册第四章相似三角形单元测试卷(PDF版,无答案)

北师版九年级上册第四章相似三角形单元考试测试卷(无答案)