山东省淄博市2020版高二下学期期中数学试卷(理科)(II)卷
山东省淄博市高二下学期数学期中考试试卷

山东省淄博市高二下学期数学期中考试试卷姓名:________ 班级:________ 成绩:________一、选择题:本大题共12小题,每小题5分,共60分. (共12题;共60分)1. (5分) (2020高二下·天津期中) 4名同学分别报名参加学校的手工、绘画、机器人设计三个校本课程,每人限报其中一个课程,不同报法的种数是()A . 81B . 64C . 24D . 162. (5分) (2017高二下·沈阳期末) 定义在R上的可导函数f(x),f ′(x)是其导函数.则下列结论中错误的是()A . 若f(x)是偶函数,则f ′(x)必是奇函数B . 若f(x)是奇函数,则f ′(x)必是偶函数C . 若f ′(x)是偶函数,则f(x)必是奇函数D . 若f ′(x)是奇函数,则f(x)必是偶函数3. (5分)离散型随机变量X的分布列为P(X=k)=pkq1﹣k(k=0,1,p+q=1),则EX与DX依次为()A . 0和1B . p和p2C . p和1﹣pD . p和p(1﹣p)4. (5分) (2019高二下·拉萨月考) 从5名男生和4名女生中选出4人参加比赛,如果4人中须既有男生又有女生,选法有()种A . 21B . 120C . 60D . 915. (5分)从6名男同学,3名女同学中任选3名参加体能测试,则选到的3名同学中既有男同学又有女同学的概率为()A .B .C .D .6. (5分)对于上可导的任意函数,若满足,则必有()A .B .C .D .7. (5分)在研究吸烟与患肺癌的关系中,通过收集数据、整理分析数据得“吸烟与患肺癌有关”的结论,并且有99%以上的把握认为这个结论是成立的,则下列说法中正确的是()A . 100个吸烟者中至少有99人患有肺癌B . 1个人吸烟,那么这人有99%的概率患有肺癌C . 在100个吸烟者中一定有患肺癌的人D . 在100个吸烟者中可能一个患肺癌的人也没有8. (5分) (2016高二下·吉林期中) 在10个球中有6个红球和4个白球(各不相同),不放回地依次摸出2个球,在第一次摸出红球的条件下,第2次也摸到红球的概率为()A .B .C .D .9. (5分)某班选派6人参加两项志愿者活动,每项活动最多安排4人,则不同的安排方法有()A . 50种B . 70种C . 35种D . 55种10. (5分)定义:如果函数在区间上存在,满足则称函数在区间上的一个双中值函数,已知函数是区间上的双中值函数,则实数的取值范围是()A .B .C .D .11. (5分) (2015高二下·张掖期中) 下列说法正确的是()A . 类比推理是由特殊到一般的推理B . 演绎推理是特殊到一般的推理C . 归纳推理是个别到一般的推理D . 合情推理可以作为证明的步骤12. (5分)函数的最大值为()A .B .C .D .二、填空题:本大题共4小题,每小题5分,共20分。
山东省淄博市淄川中学2020学年高二数学下学期期中试题

山东省淄博市淄川中学2020学年高二数学下学期期中试题时间150分钟分值150分第Ⅰ卷(共60分)一、选择题:本大题共12个小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的.1.设复数满足,则()A. B. C. D.2.某工厂生产的零件外直径(单位:)服从正态分布,今从该厂上、下午生产的零件中各随机取出一个,测得其外直径分别为和,则可认为()A.上午生产情况异常,下午生产情况正常B.上午生产情况正常,下午生产情况异常C.上、下午生产情况均正常D.上、下午生产情况均异常3.将一枚质地均匀的硬币抛掷四次,设为正面向上的次数,则等于()A. B. C. D.4.为了弘扬我国优秀传统文化,某中学广播站在春节、元宵节、清明节、端午节、中秋节五个中国传统节日中,随机选取两个节日来讲解其文化内涵,那么春节和端午节恰有一个被选中的概率是()A. B. C. D.5.在报名的名男生和名女生中,选取5人参加义务劳动,要求男生、女生都有,则不同的选取方式的种数为( ).A. 120 B. 126 C. 240 D.2526.已知随机变量服从正态分布,若,则()A. B. C. D.7.函数,则在点处的切线方程为()A. B. C. D.8.在二项式的展开式中,各项系数之和为,二项式系数之和为,若,则()A. B. C. D.9.一个盒子里装有大小、形状、质地相同的个球,其中黄球个,篮球个,绿球个.现从盒子中随机取出两个球,记事件为“取出的两个球颜色不同”,事件为“取出一个黄球,一个绿球”,则()A. B. C. D.10.已知是定义在上的可导函数,的图象如下图所示,则的单调减区间是()A. B. C. D.11.甲、乙、丙、丁、戊五名同学参加某种技术竞赛,决出了第一名到第五名的五个名次,甲、乙去询问成绩,组织者对甲说:“很遗憾,你和乙都未拿到冠军”;对乙说:“你当然不会是最差的”.从组织者的回答分析,这五个人的名次排列的不同情形种数共有()A. B. C. D.12.已知定义在上的函数的导函数为,满足,且,则不等式的解集为()A. B. C. D.第Ⅱ卷(共90分)二、填空题(每题5分,满分20分,将答案填在答题纸上)13.随机变量,变量,则.14.二项式展开式中含项的系数是.15.已知函数的导函数为,且满足,则.16.设,若随机变量的分布列是:则当变化时,的极大值是.三、解答题(本大题共6小题,共70分.解答应写出文字说明、证明过程或演算步骤.)17.已知的展开式中所有项的系数和为.(1)求的展开式中二项式系数最大的项;(2)求的展开式中的常数项.18. 已知函数,且当时,函数取得极值为.(1)求的解析式;(2)若关于的方程在上有两个不同的实数解,求实数的取值范围.19. 实力相等的甲、乙两队参加乒乓球团体比赛,规定5局3胜制(即5局内谁先赢3局就算胜出并停止比赛).⑴试求甲打完5局才能取胜的概率.⑵按比赛规则甲获胜的概率20.某校从学生会宣传部6名成员(其中男生4人,女生2人)中,任选3人参加某省举办的演讲比赛活动.(1)设所选3人中女生人数为ξ,求ξ的分布列;(2)求男生甲或女生乙被选中的概率;(3)设“男生甲被选中”为事件A,“女生乙被选中”为事件B,求P(B)和P(B|A).21.某公司计划购买2台机器,该种机器使用三年后即被淘汰.机器有一易损零件,在购进机器时,可以额外购买这种零件作为备件,每个200元.在机器使用期间,如果备件不足再购买,则每个500元.现需决策在购买机器时应同时购买几个易损零件,为此搜集并整理了100台这种机器在三年使用期内更换的易损零件数,得下面柱状图:以这100台机器更换的易损零件数的频率代替1台机器更换的易损零件数发生的概率,记表示2台机器三年内共需更换的易损零件数,表示购买2台机器的同时购买的易损零件数.(I)求的分布列;(II)若要求,确定的最小值;(III)以购买易损零件所需费用的期望值为决策依据,在与之中选其一,应选用哪个?22.已知函数=e x(e x﹣a)﹣a2x.(1)讨论的单调性;(2)若,求a的取值范围.高二数学试卷答案一、选择题本大题共12个小题,每小题5分,共60分1-5:DBCCA 6-10:CAADB 11、D 12、A二、填空题13. 14. 15. 16.三、解答题17.解:(1)由题意,令得,即,所以展开式中二项式系数最大的项是第项,即(2)展开式的第项为.由,得;由,得.所以的展开式中的常数项为18.解:(1),由题意得,即解得∴.(2)由有两个不同的实数解,得在上有两个不同的实数解,设,则,由,得或,当时,,则在上递增,当时,,则在上递减,由题意得即解得,所以,实数的取值范围是.19. 甲、乙两队实力相等,所以每局比赛甲获胜的概率为,乙获胜的概率为.⑴甲打完5局才能取胜,相当于进行5次独立重复试验,且甲第5局比赛取胜,前4局恰好2胜2负∴甲打完5局才能取胜的概率.(2) 记事件 “甲打完3局才能取胜”,记事件=“甲打完4局才能取胜”,记事件=“甲打完5局才能取胜”.事件=“按比赛规则甲获胜”,则,又因为事件、、彼此互斥,故.答:按比赛规则甲获胜的概率为20. (1)ξ的所有可能取值为0,1,2,依题意得P (ξ=0)=63=51,P (ξ=1)=63=53,P (ξ=2)=63=51.∴ξ的分布列为(2)设“甲、乙都不被选中”为事件C ,则P (C )=63=204=51.∴所求概率为P ()=1-P (C )=1-51=54.(3)P (B )=63=2010=21;P (B |A )=52=104=52.21.【答案】(I )见解析(II )19(III )22.【答案】(1)当,在单调递增;当,在单调递减,在单调递增;当,在单调递减,在单调递增;(2).【解析】试题分析:(1)分,,分别讨论函数的单调性;(2)分,,分别解,从而确定a 的取值范围. 试题解析:(1)函数的定义域为,,①若,则,在单调递增.②若,则由得.当时,;当时,,所以在单调递减,在单调递增.③若,则由得.当时,;当时,,故在单调递减,在单调递增.。
山东省淄博市淄博中学2023-2024学年高二下学期期中考试数学试题(含解析)

淄博中学2023-2024学年第二学期高二期中考试数学试题一、单选题(每小题5分,共40分,只有一个正确选项)1.已知函数,则( )A .B .1CD2.是等差数列a 的前项和,,,则首项( )A .1B .2C .3D .43.在数列中,若,则( )A .B .2C .1D .4.某同学是个数学迷,他在设置手机的数字密码时,打算将圆周率的前六个数字3、1、4、1、5、9进行某种排列得到密码,要求两个1必须相邻,那么可以设置的不同密码有( )A .120B .240C .60D .305.数学家杨辉在其专著《详解九章算术法》和《算法通变本末》中,提出了一些新的高阶等差数列,其中二阶等差数列是一个常见的等差数列,如数列2,4,7,11,16,从第二项起,每一项与前一项的差组成新数列2,3,4,5,新数列2,3,4,5为等差数列,则称数列2,4,7,11,16为二阶等差数列,现有二阶等差数列,其中前几项分别为2,5,10,17,26,37,记该数列的后一项与前一项之差组成新数列,则( )A .15B .17C .18D .196.设,函数的导函数是,若是奇函数,则曲线在处的切线方程为( )A .B .C .D .7.如图,用四种不同颜色给矩形A 、B 、C 、D 涂色,要求相邻的矩形涂不同的颜色,则不同的涂色方法共有()A .12种B .24种C .48种D .72种8.已知函数在区间上单调递减,则a 的值可能为()()cos f x x =066lim x f x f xππ∆→⎛⎫⎛⎫+∆- ⎪ ⎪⎝⎭⎝⎭=∆12-n S {}n a 3412a a +=749S =1a ={}n a 11a =-()1121n n a n a -=≥-2024a =1-12{}n a {}n b 8b =a R ∈()()4323f x x a x ax =-++()f x '()f x '()y f x =1x =31y x =-+2y x=-24y x =+24y x =-+()ln x f x ae x =-()1,2A .B .C .D .e二、多选题(每小题6分,共18分,选错得0分)9.下列求导运算正确的是()A .若,则B .若,则C .若,则D .若,则10.为弘扬我国古代的“六艺文化”,某夏令营主办单位计划利用暑假开设“礼”、“乐”、“射”、“御”、“书”、“数”六门体验课程,每周一门,连续开设六周,则下列说法正确的是( )A .某学生从中选2门课程学习,共有15种选法B .课程“乐”“射”排在相邻的两周,共有240种排法C .课程“御”“书”“数”排在不相邻的三周,共有72种排法D .课程“礼”不排在第一周,课程“数”不排在最后一周,共有504种排法11.已知数列的通项公式为,,记为数列的前n 项和,则下列说法正确的是( )A .B .C .若,则D .若,则三、填空题(每小题5分,共15分)12.函数在上的最大值为______.13.已知数列为等比数列,,公比,若是数列的前n 项积,则取最大值时,n 的值为______.14.已知函数有两个不同的零点,则实数a 的取值范围是______.四、解答题(本大题共77分)15.(13分)某医院有内科医生7名,外科医生5名,现选派4名参加赈灾医疗队,其中,(1)甲、乙有且仅有一人参加,有多少种选法?2e2e-3e-()()cos 21f x x =+()()2sin 21f x x '=+()23x f x e -+=()232x f x e -+'=-()x x f x e =()1x xf x e +'=()lg f x x x =()1lg ln10f x x '=+{}n a ()214n n a π-=tan n n b a =n S {}n a ()11n n b -=-()1123112n n b b b b -+-++++=n n n c a b =()12314nnn c c c c π-++++=n n n d b S =()2123224n d d d d n n π++++=-+ ()ln f x x x =-(]0,e {}n a 164a =12q =n T {}n a n T ()()ln 2f x x ax a =-+∈R(2)队中至少有一名内科医生和一名外科医生,有几种选法?16.(15分)设函数,曲线在点处的切线斜率为1.(1)求a 的值;(2)设函数,求的最小值;17.(15分)已知等比数列中,且是和的等差中项.(1)求数列的通项公式;(2)若函数,满足,求的前n 项和.18.(17分)已知数列的前n 项和为,满足.(1)求的通项公式;(2)删去数列的第3i 项(其中),将剩余的项按从小到大的顺序排成新数列,设的前n 项和为,请写出的前6项,并求出和.19.(17分)已知函数(,e 为自然对数的底数).(1)若在处的切线与直线垂直,求a 的值;(2)讨论函数的单调性;(3)当时,求证:.淄博中学2023-2024学年第二学期高二期中考试数学试题答案一、单选题(每小题5分,共40分,只有一个正确选项)1.【答案】,选A 2.【答案】得所以选A3.【答案】,,,所以周期为3,所以选D ()()()2ln 1f x x x ax =++-()y f x =()()0,0f ()()g x f x ='()g x {}n a 12a =22a 3a 14a {}n a {}n b ()22n n b n a n N *=+∈{}n b n S {}n a n S 22n n S a =-{}n a {}n a 1,2,3,i = {}n b {}n b n T {}n b 6T 2n T ()()21x f x axe x =-+a ∈R ()f x 0x =y ax =()f x 21a e≥()2ln 2f x x x x ≥---()sin f x x =-'()016limsin 662x f x f x f x πππ∆→⎛⎫+∆- ⎪⎛⎫⎝'⎭==-=- ⎪∆⎝⎭3471249a a S +=⎧⎨=⎩112a d =⎧⎨=⎩11a =-212a =32a =41a =-{}n a 2024212a a ==4.【答案】,选A5.【答案】前几项为3、5、7、9、11,所以,所以,所以选B 6.【答案】因为是奇函数所以所以所以切点为所以所以选B7.【答案】选C 8.【答案】因为,所以,因为在区间上单调递减,所以在上恒成立,即在上恒成立,当时,因为在上恒成立,故上式成立,满足题意;当时,则在上恒成立,令,,所以在上恒成立,所以在上单调递增,又,故,即,选C 二、多选题(每小题6分,共18分,选错得0分)9.【答案】A .B .55120A ={}n b 21n b n =+817b =()()324332f x x a x ax +'=-+()f x '3a =-()423f x x x =-()1,2-()12f '=-2y x =-432248⨯⨯⨯=()()ln 0x f x ae x x =->()1x f x ae x'=-()f x ()1,2()10xf x ae x =-≤'()1,21x a xe≤()1,20a ≤10xxe >()1,20a >1x xe a≥()1,2()x g x xe =()1,2x ∈()()10x g x x e =+>'()1,2()g x ()1,2()()222g x g e <=212e a ≥2102a e<≤()()2sin 21f x x =-+'()232x f x e -+'=-C .D . 选BD 10.【答案】A .B .C .D .选ABD11.【答案】由可知是以,的等差数列。
山东省2020版高二下学期期中数学试卷(理科)(II)卷(新版)

山东省2020版高二下学期期中数学试卷(理科)(II)卷姓名:________ 班级:________ 成绩:________一、选择题 (共12题;共24分)1. (2分)已知,其中m,n是实数,i是虚数单位,则m+n=()A . 1+2iB . 1﹣2iC . 2+iD . 2﹣i2. (2分)(2020·成都模拟) 已知,函数在区间上恰有个极值点,则正实数的取值范围为()A .B .C .D .3. (2分)设,则下列关系式成立的是()A .B .C .D .4. (2分) (2016高二下·咸阳期末) 设a=n(n﹣1)(n﹣2)…(n﹣50),则a可表示为()A .B .C .D .5. (2分)规定[x]表示不超过x的最大整数,例如:[3.1]=3,[-2.6]=-3,[-2]=-2;若f'(x)是函数f(x)=ln|x|导函数,设g(x)=f(x)f'(x),则函数y=[g(x)]+[g(-x)]的值域是()A . {偶数}B . {0,1}C . {0}D . {-1,0}6. (2分)欧拉(LeonhardEuler,国籍瑞士)是科学史上最多产的一位杰出的数学家,他发明的公式eix=cosx+isinx(i为虚数单位),将指数函数的定义域扩大到复数,建立了三角函数和指数函数的关系,这个公式在复变函数理论中占有非常重要的地位,被誉为“数学中的天桥”.根据此公式可知,表示的复数在复平面内位于()A . 第一象限B . 第二象限C . 第三象限D . 第四象限7. (2分)已知是虚数单位,若复数是纯虚数,则实数等于()A .B .C .D .8. (2分)(2014·辽宁理) 6把椅子排成一排,3人随机就座,任何两人不相邻的坐法种数为()A . 144B . 120C . 72D . 249. (2分) (2017高三下·河北开学考) 若,则a等于()A . ﹣1B . 1C . 2D . 410. (2分)若方程的根在区间上,则K的值为()A . -1B . 1C . -1或2D . -1或111. (2分)(2017·达州模拟) 的展开式的所有二项式系数之和为128,则n为()A . 5B . 6C . 7D . 812. (2分) (2016高二下·东莞期中) 函数函数f(x)=(x﹣3)ex的单调递增区间是()A . (﹣∞,2)B . (0,3)C . (1,4)D . (2,+∞)二、填空题 (共4题;共4分)13. (1分) (2016高二上·大庆期中) 设双曲线的一条渐近线与抛物线y=x2+1 只有一个公共点,则双曲线的离心率为________.14. (1分)(2016·中山模拟) 已知m=3 sinxdx,则二项式(a+2b﹣3c)m的展开式中ab2cm﹣3的系数为________.15. (1分) (2016高二下·黄冈期末) 某校开设9门课程供学生选修,其中A,B,C3门课由于上课时间相同,至多选1门,若学校规定每位学生选修4门,则不同选修方案共有________种.16. (1分)函数的单调增区间是________.三、解答题 (共6题;共55分)17. (10分)(2020·镇江模拟) 定义:若数列满足所有的项均由构成且其中-1有m个,1有p 个,则称为“ ﹣数列”.(1)为“ ﹣数列” 中的任意三项,则使得的取法有多少种?(2)为“ ﹣数列” 中的任意三项,则存在多少正整数对使得且的概率为 .18. (15分)(2013·福建理) 已知函数f(x)=sin(wx+φ)(w>0,0<φ<π)的周期为π,图象的一个对称中心为(,0),将函数f(x)图象上所有点的横坐标伸长到原来的2倍(纵坐标不变),再将得到的图象向右平移个单位长度后得到函数g(x)的图象.(1)求函数f(x)与g(x)的解析式(2)是否存在x0∈(),使得f(x0),g(x0),f(x0)g(x0)按照某种顺序成等差数列?若存在,请确定x0的个数,若不存在,说明理由;(3)求实数a与正整数n,使得F(x)=f(x)+ag(x)在(0,nπ)内恰有2013个零点.19. (10分) (2018高二上·宁夏期末) 已知函数(1)求这个函数的导数;(2)求这个函数的图像在处的切线方程.20. (10分) (2016高一上·佛山期中) 已知函数f(x)=ax﹣(a,b∈N*),f(1)= 且f(2)<2.(1)求a,b的值;(2)判断并证明函数y=f(x)在区间(﹣1,+∞)上的单调性.21. (5分)已知在的展开式中,第4项为常数项,(1)求f(x)的展开式中含x﹣3的项的系数;(2)求f(x)的展开式中系数最大的项.22. (5分) (2018高三上·汕头模拟) 设函数 .(Ⅰ)求证:;(Ⅱ)当时,函数恒成立,求实数的取值范围.参考答案一、选择题 (共12题;共24分)答案:1-1、考点:解析:答案:2-1、考点:解析:答案:3-1、考点:解析:答案:4-1、考点:解析:答案:5-1、考点:解析:答案:6-1、考点:解析:答案:7-1、考点:解析:答案:8-1、考点:解析:答案:9-1、考点:解析:答案:10-1、考点:解析:答案:11-1、考点:解析:答案:12-1、考点:解析:二、填空题 (共4题;共4分)答案:13-1、考点:解析:答案:14-1、考点:解析:答案:15-1、考点:解析:答案:16-1、考点:解析:三、解答题 (共6题;共55分)答案:17-1、考点:解析:答案:18-1、答案:18-2、答案:18-3、考点:解析:答案:19-1、答案:19-2、考点:解析:答案:20-1、答案:20-2、考点:解析:答案:21-1、考点:解析:答案:22-1、考点:解析:。
山东省2020版高二下学期期中数学试卷(理科)(II)卷
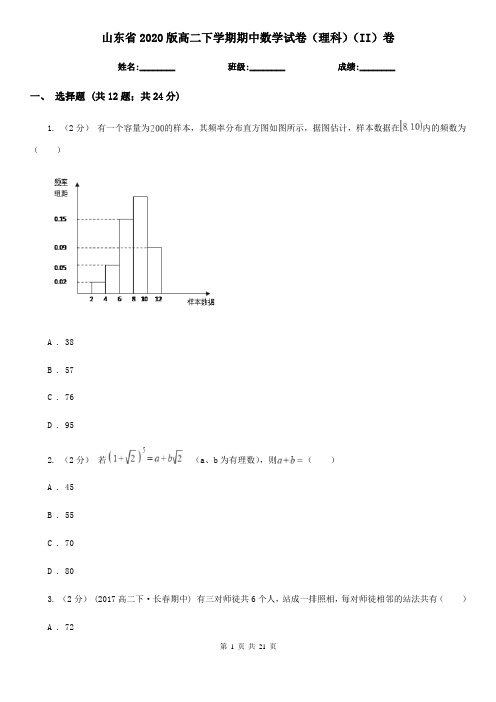
山东省2020版高二下学期期中数学试卷(理科)(II)卷姓名:________ 班级:________ 成绩:________一、选择题 (共12题;共24分)1. (2分)有一个容量为的样本,其频率分布直方图如图所示,据图估计,样本数据在内的频数为()A . 38B . 57C . 76D . 952. (2分)若(a、b为有理数),则()A . 45B . 55C . 70D . 803. (2分) (2017高二下·长春期中) 有三对师徒共6个人,站成一排照相,每对师徒相邻的站法共有()A . 72B . 54C . 48D . 84. (2分)如图是高尔顿板的改造装置,当小球从B自由下落时,进入槽口A处的概率为()A .B .C .D .5. (2分)利用随机模拟方法计算y=x2+1与y=5围成的面积时,先利用计算器产生两组0~1之间的均匀随机数a1=RAND,b1=RAND,然后进行平移与伸缩变换a=4a1﹣2,b=4b1+1,实验进行了1000次,前998次中落在所求面积区域内的样本点数为624,若最后两次实验产生的0~1之间的均匀随机数为(0.3,0.1),(0.9,0.7),则本次模拟得到的面积的估计值是()A . 10B .C .D .6. (2分)线性回归方程=bx+a必过()B . (, 0)点C . (0,)点D . (,)点7. (2分) (2018高三上·重庆月考) 下列说法中错误的是()A . 先把高二年级的2000名学生编号为1到2000,再从编号为1到50的50名学生中随机抽取1名学生,其编号为,然后抽取编号为,,的学生,这样的抽样方法是系统抽样法;B . 独立性检验中,越大,则越有把握说两个变量有关;C . 若两个随机变量的线性相关性越强,则相关系数的值越接近于1;D . 若一组数据1、a、3的平均数是2,则该组数据的方差是 .8. (2分)某班有50名学生,一次数学考试的成绩ξ服从正态分布N(105,102),已知P(95≤ξ≤105)=0.32,估计该班学生数学成绩在115分以上的人数为()A . 10B . 9C . 8D . 79. (2分) (2019高三上·吉安月考) 某种植基地将编号分别为1,2,3,4,5,6的六个不同品种的马铃薯种在如图所示的A B C D E F这六块实验田上进行对比试验,要求这六块实验田分别种植不同品种的马铃薯,若种植时要求编号1,3,5的三个品种的马铃薯中至少有两个相邻,且2号品种的马铃薯不能种植在A、F这两块实验田上,则不同的种植方法有()B . 432种C . 456种D . 480种10. (2分) (2018高二上·鹤岗月考) 设,则()A . -B .C . -D .11. (2分) (2015高二上·河北期末) 在高校自主招生中,某学校获得5个推荐名额,其中清华大学2名,北京大学2名,复旦大学1名.并且北京大学和清华大学都要求必须有男生参加.学校通过选拔定下3男2女共5个推荐对象,则不同的推荐方法共有()A . 20种B . 22种C . 24种D . 36种12. (2分)在[0,π]上随机取一个数x,则事件“2sin cos+cosx≥”发生的概率为()A .B .C .D .二、填空题 (共4题;共4分)13. (1分) (2017高二上·钦州港月考) 某校高中生共有900人,其中高一年级300人,高二年级200人,高三年级400人,现采用分层抽样法抽取一个容量为45的样本,那么从高一、高二、高三各年级抽取人数分别为________.14. (1分) (2018高二下·顺德期末) 位同学在一次聚会活动中进行纪念品的交换,任意两位同学之间最多交换一次,进行交换的两位同学互赠一份纪念品。
山东省淄博市高二数学下学期期中联考试题理(扫描版)

山东省淄博市2016-2017学年高二数学下学期期中联考试题理(扫描版)数学答案(科学倾向)一、选择题:DBDDB CBCCD BC 二、填空题:112++n n 2 -20 ),(323三、解答题:17.【解析】(1)∵21021010(3)33310i i i z i i i +--====-++,∴z =(2)∵2(3)(3)(3)(3)83i i ai i a a a i b --+=-+-=+-+,∴83(6)113a b a a b +==-⎧⎧⇒⎨⎨-+==-⎩⎩.18.(Ⅰ)当1a =时,32()1f x x x x =-+++,得(2)1f =- 1分 且2()321f x x x '=-++,(2)7f '=-. 3分所以,曲线32()21f x x x x =-+-+在点(2(2))f ,处的切线方程是17(2)y x +=--, 5分整理得7130x y +-=. 6分 (Ⅱ)解:322()1f x x ax a x =-+++,22()32(3)()f x x ax a x a x a '=-++=-+-.令()0f x '=,解得3ax =-或x a =. 8分 若0a >,当x 变化时,()f x '的正负如下表:因此,函数()f x 在3ax =-处取得极小值3a f ⎛⎫- ⎪⎝⎭,且351327a f a ⎛⎫-=- ⎪⎝⎭;函数()f x 在x a =处取得极大值()f a ,且3()1f a a =+. 12分19.【解析】证明:证法一(综合法):因为a>0,b>0()a b=+==-2=≥≥.证法二(分析法)≥,即证()0a b-≥,因为a>0,b>0,a-b所以()a b-≥≥20.【解析】设小正方形的边长为x cm,则盒子底面长为(82x-)cm,宽为(52x-)cm,32(82)(52)42640V x x x x x x=--=-+,()x<<52 4分210125240,0,1().3V x x V x x''=-+===令得或舍去(1)18V V==极大值,在定义域内仅有一个极大值,maxV∴=18 10分即小正方形边长为1cm时,盒子容积最大为cm318 12分21.试题解析:(ⅰ)当1=n时,左边=1112=,右边=3411214=+⨯⨯,左边<右边,即不等式成立;(ⅱ)假设)(*Nkkn∈=时,不等式成立,即222211114123421kk k++++⋅⋅⋅+<+则当1+=kn时,22222211111411234(1)21(1)kk k k k++++⋅⋅⋅++<++++问题可通过证明1)1(2)1(4)1(11242+++<+++kkkkk来实现要证:32441)1(2)1(4)1(11242++=+++<+++k k k k k k k 只需证:1243244)1(12+-++<+k k k k k ,只需证:)12)(32(4)1(12++<+k k k 只需证:2)1(4)32)(12(+<++k k k ,只需证:4124312422++<++k k k k ∵43<,∴1)1(2)1(4)1(11242+++<+++k k k k k 即当1+=k n 是不等式也成立.综上:由(ⅰ)(ⅱ)可得,对于一切的*∈N n 不等式恒成立.22. (1)解:求导函数,可得f′(x )= 221xax x +-(Ⅱ) 当a=2时,,的定义域是(0,+)∞,2221ln 21ln 211)('xx x x x x x x g --=⋅--= 令,,,递增,又时,,,递减,当时,,,递增,;(Ⅲ)证明:由(Ⅱ)得,时,,令,则,()()122ln )12)12(212)12(2122ln(2212111221+=++⋅⋅⋅++⋅+>+++-=∑n n n n nk k k。
山东省淄博市高二数学下学期期中联考试题 理(扫描版)

山东省淄博市2016-2017学年高二数学下学期期中联考试题理(扫描版)数学答案(科学倾向)一、选择题:DBDDB CBCCD BC 二、填空题:112++n n 2 -20 ),(323三、解答题:17.【解析】(1)∵21021010(3)33310i i i z i i i +--====-++,∴z =(2)∵2(3)(3)(3)(3)83ii ai i a a a i b--+=-+-=+-+,∴83(6)113a b a a b +==-⎧⎧⇒⎨⎨-+==-⎩⎩.18.(Ⅰ)当1a =时,32()1f x x x x =-+++,得(2)1f =- 1分 且2()321f x x x '=-++,(2)7f '=-. 3分所以,曲线32()21f x x x x =-+-+在点(2(2))f ,处的切线方程是17(2)y x +=--, 5分整理得7130x y +-=. 6分 (Ⅱ)解:322()1f x x ax a x =-+++,22()32(3)()f x x ax a x a x a '=-++=-+-.令()0f x '=,解得3ax =-或x a =. 8分 若0a >,当x 变化时,()f x '的正负如下表:因此,函数()f x 在3ax =-处取得极小值3a f ⎛⎫- ⎪⎝⎭,且351327a f a ⎛⎫-=- ⎪⎝⎭;函数()f x 在x a =处取得极大值()f a ,且3()1f a a =+. 12分19.【解析】证明:证法一(综合法):因为a>0,b>0+-()a b=+==-2=≥≥.证法二(分析法)≥≥即证()0a b-≥,因为a>0,b>0,a-b所以()a b-≥≥20.【解析】设小正方形的边长为x cm,则盒子底面长为(82x-)cm,宽为(52x-)cm,32(82)(52)42640V x x x x x x=--=-+,()x<<52 4分210125240,0,1().3V x x V x x''=-+===令得或舍去(1)18V V==极大值,在定义域内仅有一个极大值,maxV∴=18 10分即小正方形边长为1cm时,盒子容积最大为cm318 12分21.试题解析:(ⅰ)当1=n时,左边=1112=,右边=3411214=+⨯⨯,左边<右边,即不等式成立;(ⅱ)假设)(*Nkkn∈=时,不等式成立,即222211114123421kk k++++⋅⋅⋅+<+则当1+=kn时,22222211111411234(1)21(1)kk k k k++++⋅⋅⋅++<++++问题可通过证明1)1(2)1(4)1(11242+++<+++kkkkk来实现要证:32441)1(2)1(4)1(11242++=+++<+++k k k k k k k 只需证:1243244)1(12+-++<+k k k k k ,只需证:)12)(32(4)1(12++<+k k k 只需证:2)1(4)32)(12(+<++k k k ,只需证:4124312422++<++k k k k ∵43<,∴1)1(2)1(4)1(11242+++<+++k k k k k 即当1+=k n 是不等式也成立.综上:由(ⅰ)(ⅱ)可得,对于一切的*∈N n 不等式恒成立.22. (1)解:求导函数,可得f′(x )= 221xax x +-(Ⅱ) 当a=2时,,的定义域是(0,+)∞,2221ln 21ln 211)('xx x x x x x x g --=⋅--= 令,,,递增,又时,,,递减,当时,,,递增,;(Ⅲ)证明:由(Ⅱ)得,时,,令,则,()()122ln )12)12(212)12(2122ln(2212111221+=++⋅⋅⋅++⋅+>+++-=∑nn n n nk k k。
山东省淄博市2020年(春秋版)数学高二下学期理数期中考试试卷(II)卷

山东省淄博市2020年(春秋版)数学高二下学期理数期中考试试卷(II)卷姓名:________ 班级:________ 成绩:________一、单选题 (共10题;共20分)1. (2分)(2020·顺德模拟) 复数()A . 1B . -1C .D .2. (2分) (2020高二下·新余期末) 用反证法证明命题“三角形的内角中至少有一个角不大于”时,应假设()A . 三角形的三个内角都不大于B . 三角形的三个内角都大于C . 三角形的三个内角至多有一个大于D . 三角形的三个内角至少有两个大于3. (2分)已知复数是z的共轭复数,则=()A .B .C . 1D . 24. (2分)如下图为一串白黑相间排列的珠子,按这种规律往下排起来,那么第36颗珠子应是什么颜色的()A . 白色B . 黑色C . 白色可能性大D . 黑色可能性大5. (2分)已知为定义在上的可导函数,且对于任意恒成立,则()A .B .C .D .6. (2分)(2016·太原模拟) 某台小型晚会由6个节目组成,演出顺序有如下要求:节目甲必须排在前两位、节目乙不能排在第一位,节目丙必须排在最后一位,该台晚会节目演出顺序的编排方案共有()A . 36种B . 42种C . 48种D . 54种7. (2分)定积分的值为()A .B .D .8. (2分)设函数f (x)=x3-4x+a,0<a<2.若f (x)的三个零点为x1 , x2 , x3 ,且x1<x2<x3 ,则()A . x1>-1B . x2<0C . x2>0D . x3>29. (2分)把1,3,6,10,15,21,…这些数叫做三角形数,这是因为这些数目的点子可以排成一个正三角形,则第七个三角形数是()A . 21B . 28C . 32D . 3610. (2分)(2020·上饶模拟) 已知函数和函数,关于这两个函数图像的交点个数,下列四个结论:①当时,两个函数图像没有交点;②当时,两个函数图像恰有三个交点;③当时,两个函数图像恰有两个交点;④当时,两个函数图像恰有四个交点.正确结论的个数为()A . 1B . 2C . 3二、填空题 (共5题;共6分)11. (1分)函数f(x)=excosx的图象在点(0,f(0))处的切线的倾斜角为________12. (1分)(2020·淮北模拟) 展开式中项的系数是________.13. (1分)(2019·宁波模拟) 五一假期从5月1日至4日调休4天,某班6名同学准备五一期间去参加社会实践做志愿者,每人社会实践一天,且甲乙两人不在同一天的不同安排方案有________种(用数字作答).14. (1分) (2016高二下·民勤期中) 定义一种运算如下: =ad﹣bc,则复数的共轭复数是________.15. (2分)对于三次函数,定义:设是函数的导数的导数,若方程有实数解,则称点为函数的“拐点”.有同学发现“任何一个三次函数都有‘拐点’;任何一个三次函数都有对称中心;且‘拐点’就是对称中心.”请你将这一发现视为条件,若函数,则它的对称中心为________;并计算________.三、解答题 (共4题;共35分)16. (10分)综合题。
山东省淄博第一中学2020年学年高中高二数学下学期期中试卷试题理
淄博一中2020学年第二学期期中考试数学试题(理科)注意事项:1.本试题分第Ⅰ卷和第Ⅱ卷两部分。
第Ⅰ卷为选择题,共60分;第Ⅱ卷为非选择题,共90分,满分150分,考试时间为120分钟。
2.第Ⅰ卷共12小题,每题5分;请将选出的答案标号(A、B、C、D)涂在答卷纸上。
第Ⅰ卷(共60分)一、选择题(本大题共12个小题,每题5分,满分60分,每题只有一个正确答案)1、已知i是虚数单位,则复数7i=()3i(A)2–i(B)2+i(C)-2+i(D)-2-i2、如图1—1,是全集,、、是I 的3个子集,则暗影部分所表示的会合是()I MPS(A).(M∩P)∩S(B).(M∩P)∪S图1—1(C).(M∩P)∩IS(D).(M∩P)∪IS开始3、设Sn是数列{an}的前n项和,且Sn=n2,则{an}是()A.等比数列,但不是等差数列B.等差数列,但不是等比数列输入xC.等差数列,并且也是等比数列 D.既非等比数列又非等差数列否4、阅读右侧的程序框图,运转相应的程序,当输入x的值为-25|x|>1?时,输出x的值为()是(A)-1(B)1x|x|1(C)3(D)95、某几何体的三视图以以下图所示,它的体积为()(A)12(B).45x=2x+1(C).81(D).57输出x6、“”是“方程表示椭圆”结束的(A).充足不用要条件(B).必需不充足条件(C).充要条件(D).既不充足也不用要条件7、已知随机变量Z 听从正态散布N (0,e 2),若P(Z>2)=0.023,则P(-2≤Z ≤2)=()8、二项式 睁开式中的常数项是(A).第9项(B). 第10项 (C). 第8 项(D).第7 项9、要排出某班一天中语文、数学、政治、英语、体育、艺术 6堂课的课程表,要求数学课排在上午前4节,体育课排在下午 后2节,不一样排法种数为(A).144(B).192(C).360(D).72010、设坐标原点为,抛物线y2=2 与过焦点的直线交于、 B两点,则OA ·OB 等于()OxA(A).3(B).-3(C).3(D).-34411、已知圆C:(x ―2)2+(y ―3)2=1和圆C:(x ―3)2+(y ―4)2=9,此中M ,N 分别是圆C ,1 21 C 2上的动点,P 为x 轴上的动点,则|PM|+|PN|的最小值为( )(A).17(B).17―4 (C).6―2 2 (D).5 2―412、已知函数f(x)=2sin( 3x +6)+2,对随意的a ∈[1,2),方程f(x)-a=2(0≤x<m)有两个不一样的实数根,则m 的取值范围是()(A)(2,6](B)[2,6](C)(2,7](D)[2,7]第Ⅱ卷(非选择题 共90分)二、填空题(本大题共 4个小题,每题 5分,满分20分)13、设f(x) 是定义在R 上的奇函数,若当 x ≥0时,f(x)=log 3(1+x ),则f(-2)=14、已知两个单位向量a,b 的夹角为,c ttb 若b,则__________.15、下边有五个命题:①函数y=sin 4x-cos4x的最小正周期是.②终边在y轴上的角的会合是{|=k,k Z}.2③在同一坐标系中,函数y=sinx的图象和函数y=x的图象有三个公共点.④把函数y=3sin(2x+3)的图象向右平移6获得y=3sin2x的图象.⑤函数y=sin(x-2)在(0,)上是减函数.此中真命题的序号是lnx,x0,D是由x轴和曲线y f(x)及该曲线在点(1,0)处的16、设函数f(x)1,x2x0切线所围成的关闭地区,则z x2y在D上的最大值为三、解答题(本大题共 6小题,共70分.解答应写出文字说明、证明过程或演算步骤)17、(本小题满分11分)如图,在ABC中, ABC,AB,BC,P为ABC内一点,BPC.若PB,求PA;若APB,求PBA.18、(本小题满分11分)四棱锥S ABCD中,底面ABCD为平行四边形,侧面SBC底面ABCD.已知∠ABC45o,AB 2,BC22,SASB3.S(Ⅰ)证明SA BC;(Ⅱ)求直线SD与平面所成角的正弦值.CSABBD A19、(本小题满分12分)已知等差数列{a n}前三项的和为3,前三项的积为8.(Ⅰ)求等差数列{a n}的通项公式;(Ⅱ)若a2,a3,a1成等比数列,求数列{|a n|}的前n项和.20、(本小题满分12分)共享单车是指由公司在校园、公交站点、商业区、公共服务区等场所供给的自行车单车共享服务,因为其依靠“互联网+”,切合“低碳出行”的理念,已越来越多地惹起了人们的关注.某部门为了对该城市共享单车增强看管,随机选用了50人就该城市共享单车的实行状况进行问卷检查,并将问卷中的这 50人依据其满意度评分值(百分制)依据[50,60),[60,70),,[90,100]分红5组,请依据下边还没有达成并有局部污损的频次散布表和频次散布直方图(以下图)的解决以下问题:(I)求出a,b,x的值;(II)若在满意度评分值为[80,100]的人中随机抽取2人进行会谈,设所抽取的2人中来自第5组的人数记为,求的散布列和数学希望.21、(本小题满分12分)已知点分别是椭圆的左、右极点,F为其右焦点,与的等比中项是求椭圆C的方程;设可是原点O的直线l与椭圆C交于数列,求面积的取值范围.,椭圆的离心率为两点,若直线.的斜率挨次成等比22、(本小题满分12若函数在设,且分)已知函数上为单一增函数,求,求证.a的取值范围;.。
山东省淄博市2020年高二下学期期中数学试卷(理科)D卷

山东省淄博市2020年高二下学期期中数学试卷(理科)D卷姓名:________ 班级:________ 成绩:________一、选择题 (共12题;共24分)1. (2分)设(x1,y1),(x2,y2),…,(xn,yn),是变量x:和y的n个样本点,直线Z是由这些样本点通过最小二乘法得到的线性回归方程(如图),以下结论中正确的是()A . x和y正相关B . y和y的相关系数为直线I的斜率C . x和y的相关系数在-1到O之间D . 当n为偶数时,分布在l两侧的样本点的个数一定相同2. (2分)已知,且A中至少有一个奇数,则这样的集合A共有()A . 11个B . 12个C . 15个D . 16个3. (2分)(2018·中原模拟) 如图为2017年3-11月某市接待游客人数及与上年同期相比增速图,根据该图,给出下列结论:①2017年11月该市共接待旅客35万人次,同比下降了3.1%;②整体看来,该市2017年3-11月接待游客数量与上年同期相比都处于下降状态;③2017年10月该市接待游客人数与9月相比的增幅小于2017年5月接待游客人数与4月相比的增幅.其中正确结论的个数为()A . 0B . 1C . 2D . 34. (2分)已知、都是定义在R上的函数,,,,,则关于的方程有两个不同实根的概率为()A .B .C .D .5. (2分)(2020·上饶模拟) 上海地铁号线早高峰时每隔分钟一班,其中含列车在车站停留的分钟,假设乘客到达站台的时刻是随机的,则该乘客到达站台立即能乘上车的概率为()A .B .C .D .6. (2分)已知变量x与y负相关,且由观测数据算得样本平均数 =3, =3.5,则由该观测数据算得的线性回归方程可能是()A . =0.4x+2.3B . =2x﹣2.4C . =﹣2x+9.5D . =﹣0.4x+4.47. (2分)在2011年十四中“校园十佳歌手”大赛中,七位评委为一选手打出的分数如下:90 89 90 95 93 94 93去掉一个最高分和一个最低分后,所剩数据的平均值和方差分别为()A . 92,2B . 93,2C . 92,2.8D . 93,2.88. (2分)某学校在校学生2 000人,为了学生的“德、智、体”全面发展,学校举行了跑步和登山比赛活动,每人都参加而且只参与其中一项比赛,各年级参与比赛的人数情况如下表:高一年级高二年级高三年级跑步人数a b c登山人数x y z其中a∶b∶c=2∶5∶3,全校参与登山的人数占总人数的 .为了了解学生对本次活动的满意程度,从中抽取一个200人的样本进行调查,则应从高三年级参与跑步的学生中抽取()A . 15人B . 30人C . 40人D . 45人9. (2分)某班选派6人参加两项志愿者活动,每项活动最多安排4人,则不同的安排方法有()A . 50种B . 70种C . 35种D . 55种10. (2分)设随机变量ξ~N(0,1),记Φ(x)=P(ξ<x),则P(﹣1<ξ<1)等于()A . 2Φ(1)﹣1B . 2Φ(﹣1)﹣1C .D . Φ(1)+Φ(﹣1)11. (2分) (2017高二下·钦州港期末) 已知随机变量ξ服从正态分布N(3,σ2),若P(ξ<2)=0.3,则P(2<ξ<4)的值等于()A . 0.5B . 0.2C . 0.3D . 0.412. (2分)数列1,3,6,10,…的一个通项公式是()A .B .C . an=D . an=二、填空题 (共4题;共4分)13. (1分) (2016高二下·海南期末) 设p为非负实数,随机变量ξ的分布列为:ξ012P﹣p p则D(ξ)的最大值为________.14. (1分) (2019高三上·城关期中) 甲、乙两校各有3名教师报名支教.若从这6名教师中任选2名,选出的2名教师来自同一学校的概率为________.15. (1分)(2014·浙江理) 在8张奖券中有一、二、三等奖各1张,其余5张无奖.将这8张奖券分配给4个人,每人2张,不同的获奖情况有________种(用数字作答).16. (1分) (2017高二下·赣州期末) 四根绳子上共挂有10只气球,绳子上的球数依次为1,2,3,4,每枪只能打破一只球,而且规定只有打破下面的球才能打上面的球,则将这些气球都打破的不同打法数是________.三、解答题 (共6题;共60分)17. (15分)(2017·枣庄模拟) 为了调查每天人们使用手机的时间,我校某课外兴趣小组在天府广场随机采访男性、女性用户各50 名,其中每天玩手机超过6小时的用户列为“手机控”,否则称其为“非手机控”,调查结果如下:手机控非手机控合计男性262450女性302050合计5644100(1)根据以上数据,能否有60%的把握认为“手机控”与“性别”有关?(2)现从调查的女性用户中按分层抽样的方法选出5人,求所抽取5人中“手机控”和“非手机控”的人数;(3)从(2)中抽取的5人中再随机抽取3人,记这3人中“手机控”的人数为X,试求X的分布列与数学期望.参考公式:.参考数据:P(K2≥k0)0.500.400.250.050.0250.010k00.456[0.708 1.321 3.840 5.024 6.63518. (5分)一汽车厂生产A,B,C三类轿车,某月的产量如下表(单位:辆):类别A B C数量400600a按分层抽样的方法在这个月生产的轿车中抽取50辆,其中有A类轿车10辆.(Ⅰ)求a的值;(Ⅱ)用分层抽样的方法在A,B类轿车中抽取一个容量为5的样本.将该样本看成一个总体,从中任取2辆,求至少有1辆A类轿车的概率;(Ⅲ)用随机抽样的方法从A,B两类轿车中各抽取4辆,进行综合指标评分,经检测它们的得分如图,比较哪类轿车综合评分比较稳定.19. (15分)已知在的展开式中,第6项为常数项.(1)求;(2)求含项的系数;(3)求展开式中所有的有理项.20. (5分)(2018·凯里模拟) 某地有一企业2007年建厂并开始投资生产,年份代号为7,2008年年份代号为8,依次类推.经连续统计9年的收入情况如下表(经数据分析可用线性回归模型拟合与的关系):年份代号()789101112131415当年收入(千万元)131418202122242829(Ⅰ)求关于的线性回归方程;(Ⅱ)试预测2020年该企业的收入.(参考公式:,)21. (10分)某市A,B两所中学的学生组队参加辩论赛,A中学推荐3名男生,2名女生,B中学推荐了3名男生,4名女生,两校推荐的学生一起参加集训,由于集训后队员的水平相当,从参加集训的男生中随机抽取3人,女生中随机抽取3人组成代表队。
山东省2020版高二下学期期中数学试卷(理科)(II)卷

山东省2020版高二下学期期中数学试卷(理科)(II)卷姓名:________ 班级:________ 成绩:________一、选择题: (共12题;共24分)1. (2分)(2014·山东理) 已知a,b∈R,i是虚数单位,若a﹣i与2+bi互为共轭复数,则(a+bi)2=()A . 5﹣4iB . 5+4iC . 3﹣4iD . 3+4i2. (2分) (2019高二下·浙江期末) 已知数列的前项和为,且满足,则下列结论中()①数列是等差数列;② ;③A . 仅有①②正确B . 仅有①③正确C . 仅有②③正确D . ①②③均正确3. (2分)已知命题p:;命题q:,若是真命题,则实数a的取值范围为()A .B . 且C . 或D .4. (2分)(2018·南充模拟) 已知函数,则函数的图像大致是()A .B .C .D .5. (2分) (2016高二下·郑州期末) 以下数表的构造思路源于我国南宋数学家杨辉所著的《详解九章算术》一书中的“杨辉三角性”.该表由若干行数字组成,从第二行起,每一行中的数字均等于其“肩上”两数之和,表中最后一行仅有一个数,则这个数为()A . 2017×22015B . 2017×22014C . 2016×22015D . 2016×220146. (2分)(2014·天津理) 如图,△ABC是圆的内接三角形,∠BAC的平分线交圆于点D,交BC于E,过点B的圆的切线与AD的延长线交于点F,在上述条件下,给出下列四个结论:①BD平分∠CBF;②FB2=FD•FA;③AE•CE=BE•DE;④AF•BD=AB•BF.所有正确结论的序号是()A . ①②B . ③④C . ①②③D . ①②④7. (2分)在等比数列{an}中,,则a4=()A . ±16B . ±4C . 16D . 48. (2分)在100个零件中,有一级品20个,二级品30个,三级品50个,从中抽取20个作为样本:①采用随机抽样法,将零件编号为00,01,02,…,99,抽出20个;②采用系统抽样法,将所有零件分成20组,每组5个,然后每组中随机抽取1个;③采用分层抽样法,随机从一级品中抽取4个,二级品中抽取6个,三级品中抽取10个;则()A . 不论采取哪种抽样方法,这100个零件中每个被抽到的概率都是B . ①②两种抽样方法,这100个零件中每个被抽到的概率都是,③并非如此C . ①③两种抽样方法,这100个零件中每个被抽到的概率都是,②并非如此D . 采用不同的抽样方法,这100个零件中每个被抽到的概率各不相同9. (2分) (2016高一下·平罗期末) 下列命题中,正确的是()A . 经过两条相交直线,有且只有一个平面B . 经过一条直线和一点,有且只有一个平面C . 若平面α与平面β相交,则它们只有有限个公共点D . 若两个平面有三个公共点,则这两个平面重合10. (2分) (2016高二上·包头期中) 已知方程﹣ =1表示双曲线,那么k的取值范围是()A . k>5B . ﹣2<k<2C . k>2或k<﹣2D . k>5或﹣2<k<211. (2分)设函数,曲线 y=g(x) 在点处的切线方程为 y=2x+1 ,则曲线y=f(x) 在点处切线的斜率是()A . 4B .C . 2D .12. (2分) (2019高一上·上饶期中) 已知函数,其定义域是,则下列说法正确的是()A . 有最大值,无最小值B . 有最大值,最小值C . 有最大值,无最小值D . 无最大值,最小值二、填空题: (共4题;共4分)13. (1分) (2016高二下·抚州期中) 用0,1,2,3,4组成没有重复数字的全部五位数中,若按从小到大的顺序排列,则数字12340应是第________个数.14. (1分)(2016·上海文) 在的二项式中,所有项的二项式系数之和为256,则常数项等于________.15. (1分)设a,b都是正数,且满足+=cosxdx,则使a+b>c恒成立的实数c的取值范围是________16. (1分) (2016高一上·南京期中) 若函数(a,b,c,d∈R),其图象如图所示,则a:b:c:d=________三、解答题: (共6题;共60分)17. (10分) (2018高二下·葫芦岛期中) 已知(n∈N*)的展开式中第五项的系数与第三项的系数的比是10∶1.(1)求展开式中各项系数的和;(2)求展开式中含的项.18. (5分) (2016高三上·嘉兴期末) 已知抛物线与直线交于两点,,点在抛物线上,.(Ⅰ)求的值;(Ⅱ)求点的坐标.19. (15分)如图,在四棱锥P﹣ABCD中,底面ABCD是平行四边形,∠ADC=45°,AD=AC=1,O为AC的中点,PO⊥平面ABCD,PO=2,M为PD的中点.(1)证明:PB∥平面ACM;(2)证明:AD⊥平面PAC;(3)求四面体PACM的体积.20. (10分)(2017·孝义模拟) 数列{an}满足an+5an+1=36n+18,n∈N* ,且a1=4.(1)写出{an}的前3项,并猜想其通项公式;(2)用数学归纳法证明你的猜想.21. (10分)(2017·乌鲁木齐模拟) 椭圆C: + =1(a>b>0)的离心率为,过左焦点任作直线l,交椭圆的上半部分于点M,当l的斜率为时,|FM|= .(1)求椭圆C的方程;(2)椭圆C上两点A,B关于直线l对称,求△AOB面积的最大值.22. (10分) (2015高二下·上饶期中) f(x)=lnx﹣ax+1.(1)求f(x)的单调增区间.(2)求出f(x)的极值.参考答案一、选择题: (共12题;共24分)1-1、2-1、3-1、4-1、5-1、6-1、7-1、8-1、9-1、10-1、11-1、12-1、二、填空题: (共4题;共4分)13-1、14-1、15-1、16-1、三、解答题: (共6题;共60分)17-1、17-2、18-1、19-1、19-2、19-3、20-1、20-2、21-1、21-2、22-1、22-2、。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
山东省淄博市2020版高二下学期期中数学试卷(理科)(II)卷
姓名:________ 班级:________ 成绩:________
一、选择题 (共12题;共24分)
1. (2分) (2017高二上·长沙月考) 已知集合,则()
A .
B .
C .
D .
2. (2分) (2016高二下·黔南期末) i是虚数单位,若复数z满足zi=﹣1+i,则复数z的实部与虚部的和是()
A . 0
B . 1
C . 2
D . 3
3. (2分) (2018高二下·抚顺期末) 某班准备从甲、乙、丙等6人中选出4人参加某项活动,要求甲、乙、丙三人中至少有两人参加,那么不同的方法有()
A . 18种
B . 12种
C . 432种
D . 288种
4. (2分)设是三个不重合的平面,l是直线,给出下列命题:
①若,则;②若则
③若l上存在两点到的距离相等,则;④若l不在内,且,则
其中正确的命题是()
A . ①②
B . ②③
C . ②④
D . ③④
5. (2分) (2016高三上·清城期中) 下列说法正确的是()
A . 命题“若x2=1,则x=1”的否命题为:“x2=1,则x≠1”
B . 若命题p:∃x∈R,x2﹣x+1<0,则命题¬p:∀x∈R,x2﹣x+1>0
C . 命题“若x=y,则sinx=siny”的逆否命题为真命题
D . “x2﹣5x﹣6=0”必要不充分条件是“x=﹣1”
6. (2分) (2017高三下·平谷模拟) 已知实数、满足:,则的最大值为().
A .
B .
C .
D .
7. (2分) (2015高三上·太原期末) 执行如图的程序框图输出的T的值为()
A . 4
B . 6
C . 8
D . 10
8. (2分) (2017高一上·焦作期末) 如图为一个几何体的三视图,三视图中的两个不同的正方形的边长分别为1和2,则该几何体的体积为()
A . 6
B . 7
C . 8
D . 9
9. (2分)曲线y= 上点M处的切线与直线y=3﹣x垂直,则切线方程为()
A . 5x﹣5y﹣4=0
B . 5x+5y﹣4=0
C . 5x+5y﹣4=0或5x+5y+4=0
D . 5x﹣5y﹣4=0或5x﹣5y+4=0
10. (2分) (2017高二下·晋中期末) 已知椭圆E:,圆O:x2+y2=a2与y轴正半轴交于点B,过点B的直线与椭圆E相切,且与圆O交于另一点A,若∠AOB=60°,则椭圆E的离心率为()
A .
B .
C .
D .
11. (2分) (2019高一上·嘉善月考) 若函数为定义在R上的奇函数,且在内是增函数,又
,则不等式的解集为()
A .
B .
C .
D .
12. (2分) (2016高二上·黄骅期中) 如图,已知椭圆C的中心为原点O,F(﹣2 ,0)为C的左焦点,P为C上一点,满足|OP|=|OF|且|PF|=4,则椭圆C的方程为()
A . =1
B . =1
C . =1
D . =1
二、填空题 (共4题;共4分)
13. (1分) (2018高二下·牡丹江期末) 设命题,,则为________.
14. (1分)(2018·孝义模拟) 已知向量与的夹角是,且,则向量与的夹角是________.
15. (1分)(2017·南通模拟) 已知a,b∈R,a>b,若2a2﹣ab﹣b2﹣4=0,则2a﹣b的最小值为________.
16. (1分) (2016高一下·大丰期中) 若一个长方体的长、宽、高分别为,,1,则它的外接球的表面积是________.
三、解答题:解答应写出文字说明、证明过程或演算步骤. (共6题;共55分)
17. (10分)(2012·浙江理) 在△ABC中,内角A,B,C的对边分别为a,b,c.已知cosA= ,sinB=
C.
(1)求tanC的值;
(2)若a= ,求△ABC的面积.
18. (10分) (2016高二下·揭阳期中) 已知.
(1)求f(x)的周期及其图象的对称中心;
(2)△ABC中,角A、B、C所对的边分别是a、b、c,满足(2a﹣c)cosB=bcosC,求f(B)的值.
19. (10分) (2016高三上·黄冈期中) 在等比数列{an}中,an>0,(n∈N*),公比q∈(0,1),且a1a5+2a3a5+a2a8=25,a3与a5的等比中项为2.
(1)求数列{an}的通项公式;
(2)设bn=log2an,数列{bn}的前n项和为Sn,当最大时,求n的值.
20. (10分) (2019高二下·涟水月考) 如图,已知矩形所在平面垂直于直角梯形所在平面于直线,且,,,且 .
(1)求平面与平面所成的二面角的余弦值;
(2)线段上是否存在一点,使得直线与平面所成角的正弦值等于?若存在,试确定点的位置;若不存在,请说明理由.
21. (10分) (2018高二上·宁夏期末) 已知椭圆:的一个顶点为,离心率为,直线与椭圆交于不同的两点 .
(1)求椭圆的方程;
(2)当的面积为时,求的值.
22. (5分) (2016高二上·淮南期中) 已知函数g(x)= +lnx在[1,+∞)上为增函数,且θ∈(0,π),f(x)=mx﹣﹣lnx(m∈R).
(Ⅰ)求θ的值;
(Ⅱ)若f(x)﹣g(x)在[1,+∞)上为单调函数,求m的取值范围;
(Ⅲ)设h(x)= ,若在[1,e]上至少存在一个x0 ,使得f(x0)﹣g(x0)>h(x0)成立,求m的取值范围.
参考答案
一、选择题 (共12题;共24分)
1、答案:略
2-1、
3-1、
4-1、
5-1、
6-1、
7-1、
8-1、
9-1、
10-1、
11-1、
12-1、
二、填空题 (共4题;共4分)
13-1、
14-1、
15-1、
16-1、
三、解答题:解答应写出文字说明、证明过程或演算步骤. (共6题;共55分) 17-1、
17-2、
18-1、
18-2、
19-1、19-2、
20-1、
20-2、
21-1、
21-2、
22-1、。
