函数的极限PPT课件
合集下载
《极限的运算》课件

重要的作用。
无穷小量的运算包括无穷小量的加法、 减法、乘法和除法。在运算过程中,无 穷小量可以与其他量进行加减乘除运算
,但需要注意运算结果的极限状态。
无穷小量在极限运算中常常用于等价变 换和泰勒展开等技巧,可以帮助我们简
化复杂的极限问题。
极限运算的注意事项
01
02
03
04
在进行极限运算时,需要注意 一些关键的点,以确保结果的
极限存在定理的证明方法
极限存在定理可以通过多种方法证明,如数学归纳法、反证法、直接证明法等 。这些方法都基于实数完备性定理,通过排除不可能的情况来证明极限的存在 。
极限存在定理的应用
函数极限的求解
极限存在定理是求解函数极限的基础 ,通过判断函数在某点的极限是否存 在,可以进一步研究函数的性质和变 化趋势。
极限的性质
极限具有一些重要的性质,如 唯一性、局部有界性、局部保 号性等。
这些性质在研究函数的极限行 为时非常重要,可以帮助我们 推导一些重要的结论和定理。
了解和掌握这些性质对于深入 理解极限的概念和应用极限的 方法具有重要意义。
02
极限的四则运算
极限的四则运算法则
加法法则
如果lim(x→a) f(x) = M1 和 lim(x→a) g(x) = M2,那么 lim(x→a) [f(x) + g(x)] = M1 + M2。
这种定义方式具有高度的严谨性 和精确性,是数学分析中研究函
数的重要基础。
极限的直观理解
极限的直观理解可以描述为函数在某一点附近的变化趋势。
当x逐渐接近这一特定点时,函数值会逐渐接近其极限值,或者保持一定的距离,或 者趋近于无穷。
这种变化趋势可以通过图形或表格进行可视化,帮助我们更好地理解极限的概念。
无穷小量的运算包括无穷小量的加法、 减法、乘法和除法。在运算过程中,无 穷小量可以与其他量进行加减乘除运算
,但需要注意运算结果的极限状态。
无穷小量在极限运算中常常用于等价变 换和泰勒展开等技巧,可以帮助我们简
化复杂的极限问题。
极限运算的注意事项
01
02
03
04
在进行极限运算时,需要注意 一些关键的点,以确保结果的
极限存在定理的证明方法
极限存在定理可以通过多种方法证明,如数学归纳法、反证法、直接证明法等 。这些方法都基于实数完备性定理,通过排除不可能的情况来证明极限的存在 。
极限存在定理的应用
函数极限的求解
极限存在定理是求解函数极限的基础 ,通过判断函数在某点的极限是否存 在,可以进一步研究函数的性质和变 化趋势。
极限的性质
极限具有一些重要的性质,如 唯一性、局部有界性、局部保 号性等。
这些性质在研究函数的极限行 为时非常重要,可以帮助我们 推导一些重要的结论和定理。
了解和掌握这些性质对于深入 理解极限的概念和应用极限的 方法具有重要意义。
02
极限的四则运算
极限的四则运算法则
加法法则
如果lim(x→a) f(x) = M1 和 lim(x→a) g(x) = M2,那么 lim(x→a) [f(x) + g(x)] = M1 + M2。
这种定义方式具有高度的严谨性 和精确性,是数学分析中研究函
数的重要基础。
极限的直观理解
极限的直观理解可以描述为函数在某一点附近的变化趋势。
当x逐渐接近这一特定点时,函数值会逐渐接近其极限值,或者保持一定的距离,或 者趋近于无穷。
这种变化趋势可以通过图形或表格进行可视化,帮助我们更好地理解极限的概念。
《高等数学极限》课件

THANK YOU
无穷级数与无穷积分的收敛性
总结词
收敛性是无穷级数和无穷积分最重要的性质之一,它 表示无穷级数或无穷积分的和是有限的。收敛性的判 定是高等数学中的一个重要问题,需要用到多种数学 方法和技巧。
详细描述
收敛性是无穷级数和无穷积分最重要的性质之一,它 表示无穷级数或无穷积分的和是有限的。如果一个无 穷级数或无穷积分是收敛的,那么它的和就是有限的 ,否则就是发散的。收敛性的判定是高等数学中的一 个重要问题,需要用到多种数学方法和技巧,如比较 判别法、柯西判别法、阿贝尔判别法等。对于不同的 级数和积分,需要采用不同的方法和技巧进行收敛性 的判定。
03
导数与连续性
导数的定义与性质
导数的定义
导数是函数在某一点的变化率的极限 ,表示函数在该点的切线斜率。
导数的性质
导数具有线性、可加性、可乘性和链 式法则等性质,这些性质在研究函数 的单调性、极值和曲线的几何特性等 方面具有重要应用。
导数的计算方法
基本初等函数的导数
对于常数、幂函数、指数函数、三角函数和反三角函 数等基本初等函数,需要熟记其导数公式。
限的。
无穷积分的定义与性质
总结词
无穷积分是数学中另一个重要的概念,它是由无穷多个 定积分的和组成的积分。无穷积分具有一些重要的性质 ,如可加性、可乘性和可微性等。
详细描述
无穷积分是由无穷多个定积分的和组成的积分,这些定 积分可以是积分限不同的积分。无穷积分在数学中也有 着广泛的应用,如求解面积、体积和曲线长度等。无穷 积分具有一些重要的性质,如可加性、可乘性和可微性 等。其中,可加性表示无穷积分可以拆分成若干个部分 的和,可乘性和可微性则表示无穷积分可以与函数进行 运算和求导。
《函数的极限与连续》课件

示例
考虑函数$f(x) = x^2$,在区间 $[0, 1]$上连续且单调增加。如果 $f(0) < c < f(1)$,则可以证明$c < frac{f(0) + f(1)}{2}$。
利用连续性求函数的零点
要点一
总结词
利用函数的连续性可以找到函数的零 点。
要点二
详细描述
如果函数在某区间上连续,且在该区 间上从正变负或从负变正,则可以利 用函数的连续性找到函数的零点。这 是因为函数在这一点上从增加变为减 少或从减少变为增加,的定义
函数在某点连续的定义
如果函数在某点的左右极限相等且等于该点的函数值,则函数在该点连续。
函数在区间上连续的定义
如果函数在区间内的每一点都连续,则函数在该区间上连续。
连续性的性质
连续函数的和、差、积、商(分母不为零)仍为连续函数。
复合函数在复合点连续的定义:如果一个复合函数在某点的极限等于该点的函数值,则复合函数在该点 连续。
与其他数学知识的联系
探讨函数极限与连续性与中学数学、微积分等其他 数学知识的联系,理解其在数学体系中的地位。
理论严谨性
深入思考函数极限与连续性理论的严谨性和 完备性,理解数学严密性的重要性。
对后续学习的展望
导数与微分
预告后续将学习函数的导数与微分概念,了解它们与 极限和连续性的关系。
级数与积分
简要介绍级数和积分的基本概念,理解其在数学中的 重要性和应用。
01
和差运算性质
若$lim f(x)=A$且$lim g(x)=B$ ,则$lim [f(x)pm g(x)]=Apm B$。
02
03
乘积运算性质
幂运算性质
若$lim f(x)=A$且$lim g(x)=B$ ,则$lim [f(x)cdot g(x)]=Acdot B$。
高等数学(同济第六版)课件 第一章 3.函数的极限(一)

且a >b, (或a<b)
则正数X, 当x<-X时, 都有f(x) >b . (或f(x)<b) 当x>X时, 当|x|>X时,
(4) 充要条件:
lim lim lim f ( x ) A x f ( x ) A且 x f ( x ) A.
x
证: " " 0, X 1 0, 当x>X1 时,成立 f ( x ) A .
得 | x x0 |
x0
当 | x x0 | x0 时,才能使x>0, 取 min{ x0 , x0 } 当 0 x x0 时, 成立 | x x0 |
lim x
x x0
x0
" "定义
x x0
lim f ( x ) A
2 x2 x 1 3 lim x 1 x 1 2 x2 x 1 3 | 2 | x 1 | ( x 1) 0, | x 1 2 x2 x 1 3 | 当x与1多么接近时? | x 1 | x 1 | 2
2 x2 x 1 0, 当 0 | x 1 | 时, 成立 | 3 | 2 x 1
lim f ( x ) 0, 则 lim f ( x ) g( x ) 0
x x
1 x (7) 重要极限:lim (1 ) e x x
特点:(1)1 型 (2)底数减1等于指数的倒数 。
例2 求下列极限
2 x3 3 x2 5 (1) lim 3 2 x 7 x 4 x 1
二、 自变量趋向有限值时函数的极限 若当x无限接近于x0时,函数f(x)无限接近于常数A, 称常数A为当x趋于x0时,函数f(x)的极限。 记作 lim f ( x ) A
函数的极限【高等数学PPT课件】

A(或f
( x0
0)
A)
右极限: 定理1
lim
xx0
f (x)
A(或f (x0
0)
A)
lim f (x) A lim f (x) lim f (x) A
xx0
xx0
xx0
x sin x, x 0
例1
试问函数f ( x)
10, x 0
(c) Sketch the graph of F.
例2 lim sin x不存在 x
lim sin 1 不存在.
x0
x
y sin 1 x
思考与练习
1. 若极限 lim f ( x) 存在, 是否一定有
x x0
lim f ( x) f ( x0 ) ?
x x0
2. 设函数 f ( x) a x2, x 1 且 2x 1, x 1
lim f ( x)
x1
存在, 则 a 3 .
3.Let F (x) x 2 1 .
x 1
(a) Find (i) lim F (x) x 2 1 .
x1
x 1
(ii) lim x1
F(x)
x2 1 .
x 1
(b) Does lim F(x). exist?
x1
lim f ( x) lim f ( x) lim f ( x) 不存在.
x0
x0
x0
二、函数极限的性质
1.惟一性
定理1 (极限的惟一性) 如果函数极限
存在,则极限值惟一.
2.有界性
定理2 (局部有界性)
如果极限 lim f (x) xx0
考研高数总复习函数的极限(讲义)PPT课件

无穷小是函数极限的必要条件,即如果函数在某点的极限存在,那么函数在该点的值必定是无穷小。
无穷小与函数极限的关系是相互依存的,无穷小是函数极限的一种表现形式,而函数极限又是无穷小的 一种表现形式。
无穷小在求极限中的应用
利用无穷小的性质,可以将复杂的函数极限转化为简单的无穷小量,从而 简化计算过程。
在求函数极限时,可以利用等价无穷小替换,将复杂的函数表达式替换为 简单的无穷小量,从而得到更易处理的极限表达式。
利用极限的四则运算法则,消去零因子,化 简函数形式,再求极限。
利用两个重要极限求解
利用重要极限$lim_{x to 0} frac{sin x}{x} = 1$求解:当函数 形式为$frac{sin x}{x}$时,可以利用此重要极限求解。
利用重要极限$lim_{x to infty} frac{1}{x} = 0$求解:当函数 形式为$frac{1}{x}$时,可以利用此重要极限求解。
考研高数总复习函数的极限(讲义 )ppt课件
contents
目录
• 函数极限的基本概念 • 函数极限的求解方法 • 函数极限的应用 • 函数极限的深入理解 • 总结与展望
01 函数极限的基本概念
函数极限的定义
1 2
函数极限的定义
当自变量趋近某一特定值时,函数值的变化趋势。
函数极限的表示方法
lim f(x) = A,表示当x趋近于某个值时,f(x)趋 近于A。
THANKS FOR WATCHING
感谢您的观看
在物理学中,函数极限被用来描述物体运动的速度、加速度等概念;在 工程中,函数极限被用来描述信号的变化趋势;在经济中,函数极限被
用来描述市场的变化趋势。
通过对函数极限的学习,我们可以更好地理解和应用这些概念,为未来 的学习和工作打下坚实的基础。
无穷小与函数极限的关系是相互依存的,无穷小是函数极限的一种表现形式,而函数极限又是无穷小的 一种表现形式。
无穷小在求极限中的应用
利用无穷小的性质,可以将复杂的函数极限转化为简单的无穷小量,从而 简化计算过程。
在求函数极限时,可以利用等价无穷小替换,将复杂的函数表达式替换为 简单的无穷小量,从而得到更易处理的极限表达式。
利用极限的四则运算法则,消去零因子,化 简函数形式,再求极限。
利用两个重要极限求解
利用重要极限$lim_{x to 0} frac{sin x}{x} = 1$求解:当函数 形式为$frac{sin x}{x}$时,可以利用此重要极限求解。
利用重要极限$lim_{x to infty} frac{1}{x} = 0$求解:当函数 形式为$frac{1}{x}$时,可以利用此重要极限求解。
考研高数总复习函数的极限(讲义 )ppt课件
contents
目录
• 函数极限的基本概念 • 函数极限的求解方法 • 函数极限的应用 • 函数极限的深入理解 • 总结与展望
01 函数极限的基本概念
函数极限的定义
1 2
函数极限的定义
当自变量趋近某一特定值时,函数值的变化趋势。
函数极限的表示方法
lim f(x) = A,表示当x趋近于某个值时,f(x)趋 近于A。
THANKS FOR WATCHING
感谢您的观看
在物理学中,函数极限被用来描述物体运动的速度、加速度等概念;在 工程中,函数极限被用来描述信号的变化趋势;在经济中,函数极限被
用来描述市场的变化趋势。
通过对函数极限的学习,我们可以更好地理解和应用这些概念,为未来 的学习和工作打下坚实的基础。
函数的极限(二)PPT课件

复习引入
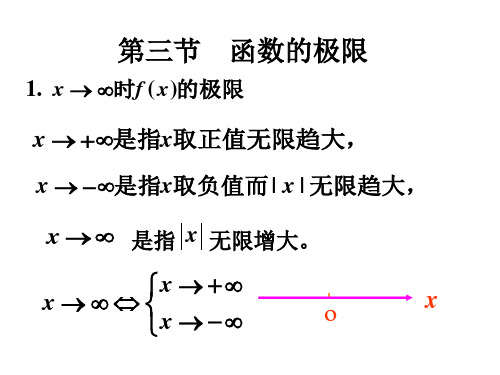
1 .当自变量 x 取正值并且无限增大时,如果函数 f(x) 无限趋近于一个常数a,就说当x趋向于正无穷大时, 函数f(x)的极限是a,记作 。 2.当自变量x取负值并且绝对值无限增大时,如果函数 f(x)无限趋近于一个常数a,就说当x趋向于负无穷大时, 函数f(x)的极限是a,记作 。 3.如果 且 ,就说当x趋向于无穷 大时,函数f(x)的极限是a,记作: 。 4.常数函数f(x)=c(c∈R)有 。
2.研讨当x无限趋近于1(但不等于1)时,函数 的变化趋势 (1)图象 y=x+1 (x∈R,x≠1)
y
2 1 -1 0 1 x
(2)结论:自变量x从x轴上点x=1的左右两边无限趋近 于1,函数 的值无限趋近于2.
3.研讨当x无限趋近于0时分段函数 变化趋势?
(1)图象
的
(2) 结论: x从0的左边无限趋近于0时,y值无限趋近于-1 x从0的右边无限趋近于0时,y值无限趋近于1
(二)函数在一点处的极限与左、右极限 1.当自变量x无限趋近于常数x0(但x不等于x0)时, 如果函数f(x)无限趋近于一个常数a,就说当x趋近于x0 时,函数f(x)的极限是a,记作 或当x→x0时 f(x)→a。 2.当x从点x0左侧(即x﹤x0)无限趋近于x0时, 函数f(x)无限趋近于一个常数a,就说a是函数f(x) 在点x0处的左极限,记作 。 3.如果当x从点x0右侧(即x﹥x0)无限趋近于x0 时,函数f(x)无限趋近于常数a,就说a是函数f(x) 在点x0处的右极限,记作 。 4.常数函数f(x)=c在点x=x0处的极限有 .
注意: (1) 中x无限趋近于x0,但不包含x=x0即x≠x0, 所以函数f(x)的极限是a仅与函数f(x)在点x0附近的函数 值的变化有关,而与函数f(x)在点x0的值无关(x0可以 不属于f(x)的定义域) (2) 而 极限,
1 .当自变量 x 取正值并且无限增大时,如果函数 f(x) 无限趋近于一个常数a,就说当x趋向于正无穷大时, 函数f(x)的极限是a,记作 。 2.当自变量x取负值并且绝对值无限增大时,如果函数 f(x)无限趋近于一个常数a,就说当x趋向于负无穷大时, 函数f(x)的极限是a,记作 。 3.如果 且 ,就说当x趋向于无穷 大时,函数f(x)的极限是a,记作: 。 4.常数函数f(x)=c(c∈R)有 。
2.研讨当x无限趋近于1(但不等于1)时,函数 的变化趋势 (1)图象 y=x+1 (x∈R,x≠1)
y
2 1 -1 0 1 x
(2)结论:自变量x从x轴上点x=1的左右两边无限趋近 于1,函数 的值无限趋近于2.
3.研讨当x无限趋近于0时分段函数 变化趋势?
(1)图象
的
(2) 结论: x从0的左边无限趋近于0时,y值无限趋近于-1 x从0的右边无限趋近于0时,y值无限趋近于1
(二)函数在一点处的极限与左、右极限 1.当自变量x无限趋近于常数x0(但x不等于x0)时, 如果函数f(x)无限趋近于一个常数a,就说当x趋近于x0 时,函数f(x)的极限是a,记作 或当x→x0时 f(x)→a。 2.当x从点x0左侧(即x﹤x0)无限趋近于x0时, 函数f(x)无限趋近于一个常数a,就说a是函数f(x) 在点x0处的左极限,记作 。 3.如果当x从点x0右侧(即x﹥x0)无限趋近于x0 时,函数f(x)无限趋近于常数a,就说a是函数f(x) 在点x0处的右极限,记作 。 4.常数函数f(x)=c在点x=x0处的极限有 .
注意: (1) 中x无限趋近于x0,但不包含x=x0即x≠x0, 所以函数f(x)的极限是a仅与函数f(x)在点x0附近的函数 值的变化有关,而与函数f(x)在点x0的值无关(x0可以 不属于f(x)的定义域) (2) 而 极限,
《极限定理教学》课件

02
无穷小和无穷大在极限理论中有 着重要的应用,如极限的定义、 性质和计算等。
06
极限定理的深化理解
极限定理的几何解释
极限定理的几何解释
通过几何图形和图形的变化趋势,深入 理解极限的概念和性质。例如,通过观 察函数图像的变化趋势,理解函数在某 点的极限值。
VS
动态演示
利用动画或动态图演示函数的变化趋势, 帮助学生直观地理解极限的概念。
注意事项
强调在求幂函数的极限时需要注意 的要点,例如n不能为负数且分母不 能为零等。
指数函数的极限
指数函数的形式
指数函数的一般形式为a^x( a>0且a≠1),其极限值取决于a
的值。
举例说明
通过具体例子演示如何求指数函 数的极限,例如求lim(x->∞) a^x的极限值,其中a>1和 0<a<1的情况。
在微积分中,极限的应用可以帮助我们更好地理解微积分 的本质和思想,解决微积分中的问题,如求解函数的极值 、求解定积分等。
04
极限的运算
极限的四则运算
极限的四则运算法则
注意事项
极限的四则运算法则是极限运算的基 础,包括加法、减法、乘法和除法的 极限运算规则。
强调在运用极限的四则运算法则时需 要注意的要点,例如分母不能为零等 。
左极限与右极限
根据函数在某点处的左右两侧的变化 趋势,可以将极限分为左极限和右极 限。
单侧极限与双侧极限
根据函数在某点处是否只有一个方向 上的变化趋势,可以将极限分为单侧 极限和双侧极限总结词
单调有界定理是极限理论中的基本定理之一,它表明如果一 个数列单调递增且有上界或单调递减且有下界,则该数列收 敛。
无穷大的定义与性质
函数的极限-课件

函数的极限-PPT课件
通过这个PPT课件,我们将深入了解函数的极限,探讨其定义、性质、求解方 法、连续性以及应用领域,帮助您更好地理解和应用相关知识。
什么是函数的极限
函数的极限是指随着自变量趋近某个特定值,函数取值的趋势。我们将讨论 其定义和概念,以及极限的基本性质。
如何求解函数的极限
重要极限公式、极限的运算法则以及夹逼定理等是求解函数极限的关键工 具。我们将学习它们的应用方法。
参考资料
常用函数极限表格
提供常见函数的极限值和性质的表格,作为学 习和记忆的参考。
相关专业书籍和资料
推荐一些深入学习函数极限的专业书籍和学术 资料,供进一步研究使用。
函数的极ห้องสมุดไป่ตู้与连续性
极限存在的充分条件
我们将研究函数极限存在的条件,并探讨它们与函 数连续性之间的关系。
极限与函数的连续性
了解极限与函数连续性之间的关联,以及在函数图 像上的表现。
函数极限的应用
1 极限与导数的关系
探索函数的极限与导数之间的联系,以及这种联系在微积分中的重要性。
2 极限在微积分中的应用
了解如何使用函数极限解决微积分问题,例如求曲线的切线、曲线的变率等。
3 极限在实际问题中的应用
通过实际问题案例,展示函数极限在科学、工程、经济等领域的实际应用。
练习与总结
练习题解析
通过解析一些典型练习题,加深对函数极限的理解 和应用能力。
总结和回顾
总结已学习的知识点,回顾整个课程,确保对函数 的极限有全面的理解。
通过这个PPT课件,我们将深入了解函数的极限,探讨其定义、性质、求解方 法、连续性以及应用领域,帮助您更好地理解和应用相关知识。
什么是函数的极限
函数的极限是指随着自变量趋近某个特定值,函数取值的趋势。我们将讨论 其定义和概念,以及极限的基本性质。
如何求解函数的极限
重要极限公式、极限的运算法则以及夹逼定理等是求解函数极限的关键工 具。我们将学习它们的应用方法。
参考资料
常用函数极限表格
提供常见函数的极限值和性质的表格,作为学 习和记忆的参考。
相关专业书籍和资料
推荐一些深入学习函数极限的专业书籍和学术 资料,供进一步研究使用。
函数的极ห้องสมุดไป่ตู้与连续性
极限存在的充分条件
我们将研究函数极限存在的条件,并探讨它们与函 数连续性之间的关系。
极限与函数的连续性
了解极限与函数连续性之间的关联,以及在函数图 像上的表现。
函数极限的应用
1 极限与导数的关系
探索函数的极限与导数之间的联系,以及这种联系在微积分中的重要性。
2 极限在微积分中的应用
了解如何使用函数极限解决微积分问题,例如求曲线的切线、曲线的变率等。
3 极限在实际问题中的应用
通过实际问题案例,展示函数极限在科学、工程、经济等领域的实际应用。
练习与总结
练习题解析
通过解析一些典型练习题,加深对函数极限的理解 和应用能力。
总结和回顾
总结已学习的知识点,回顾整个课程,确保对函数 的极限有全面的理解。
函数的极限函数的连续性PPT教学课件

一暴( pu) 十寒:
比喻做事不坚持,无 恒心
拒人千里:
形容对人态度傲慢
鲁国打算让乐正子治理国政。 孟子说:“听到这消息,我喜欢得睡不着觉。” 孟子的学生公孙丑问:“乐正子很有能力吗?有智慧 有远见吗?见闻广博吗?” 孟子说:“不是。” 公孙丑问:“那您为什么喜欢得睡不着呢?” 孟子回答说:“因为他能听取别人的意见。能听取别 人的意见就足以治理天下,四面八方的人会不远千里 赶来提意见;听不進别人的意见,说:‘喔喔,你说 的我早就知道了!’‘喔喔’的声音和脸色就会把别 人拒绝在千里之外。有志之士在千里之外停滞不前, 而那些阿谀奉承的人就会到来,想治理好国家,能办 得到吗?”
xx0
lim C C
x x0
lim
x x0
x
x0
lim f (x) a lim f (x) lim f (x) a
xx0
xx0
xx0
其趋中近于xlxim0x时0 f的(x左) 极 a限表,示当x从左侧
于xxl0im时x0 的f (右x)极 a限表示当x从右侧趋近
对于函数极限有如下的运算法则:
C.自己不喜欢做的事更 不应强加于人 D.准备充分才能做事完美 E.对人要守诚信 F.为人要光明磊落
G.要管好别人首先要 管好自己
H.兴趣是学习最好 的推动力
孟子名言
1.恻隐之心, 人皆有之 2.生于忧患,死于安乐 3.尽 信 书 不 如 无 书 4.不以规矩,不成方圆 5.仁者无敌 6.君子不怨天,不尤人 7.爱人者,人恒爱之; 敬人者,人恒敬之
室.他为何要在我家弹瑟啊? "
登堂入室:
表示学业已达一定程度 或是已得到老师专授指点
有人指责孟子不尽力帮助齐王。孟子便解 释说:“比如说,天下有些易活的植物, 假如把它放在太阳下晒一天,然后再把它 放在阴冷的地方冻十天,即使是生命力再 强的植物也会死。我见到齐王的机会少之 又少,即使给了他些良好的影响与帮助, 我一离开,一些和我主张不同的人,又带 给他许多不好影响。我怎么能使齐王的思 想、品质好起来呢?”
比喻做事不坚持,无 恒心
拒人千里:
形容对人态度傲慢
鲁国打算让乐正子治理国政。 孟子说:“听到这消息,我喜欢得睡不着觉。” 孟子的学生公孙丑问:“乐正子很有能力吗?有智慧 有远见吗?见闻广博吗?” 孟子说:“不是。” 公孙丑问:“那您为什么喜欢得睡不着呢?” 孟子回答说:“因为他能听取别人的意见。能听取别 人的意见就足以治理天下,四面八方的人会不远千里 赶来提意见;听不進别人的意见,说:‘喔喔,你说 的我早就知道了!’‘喔喔’的声音和脸色就会把别 人拒绝在千里之外。有志之士在千里之外停滞不前, 而那些阿谀奉承的人就会到来,想治理好国家,能办 得到吗?”
xx0
lim C C
x x0
lim
x x0
x
x0
lim f (x) a lim f (x) lim f (x) a
xx0
xx0
xx0
其趋中近于xlxim0x时0 f的(x左) 极 a限表,示当x从左侧
于xxl0im时x0 的f (右x)极 a限表示当x从右侧趋近
对于函数极限有如下的运算法则:
C.自己不喜欢做的事更 不应强加于人 D.准备充分才能做事完美 E.对人要守诚信 F.为人要光明磊落
G.要管好别人首先要 管好自己
H.兴趣是学习最好 的推动力
孟子名言
1.恻隐之心, 人皆有之 2.生于忧患,死于安乐 3.尽 信 书 不 如 无 书 4.不以规矩,不成方圆 5.仁者无敌 6.君子不怨天,不尤人 7.爱人者,人恒爱之; 敬人者,人恒敬之
室.他为何要在我家弹瑟啊? "
登堂入室:
表示学业已达一定程度 或是已得到老师专授指点
有人指责孟子不尽力帮助齐王。孟子便解 释说:“比如说,天下有些易活的植物, 假如把它放在太阳下晒一天,然后再把它 放在阴冷的地方冻十天,即使是生命力再 强的植物也会死。我见到齐王的机会少之 又少,即使给了他些良好的影响与帮助, 我一离开,一些和我主张不同的人,又带 给他许多不好影响。我怎么能使齐王的思 想、品质好起来呢?”
函数的极限PPT课件

详细描述
函数极限的唯一性是函数极限的一个重要性质,它表明在某一点附近,函数的 极限值是唯一的。这个性质在研究函数的连续性和可导性等方面有着重要的应 用。
函数极限的局部有界性
总结词
函数极限的局部有界性是指,如果函数$f(x)$在点$x_0$处有极限,那么在点$x_0$的某个邻域内,函 数$f(x)$是有界的。
详细描述
函数极限的保号性是函数极限的一个重要性质,它表明在函数极限存在的区域内,函数 的符号与极限值的符号保持一致。这个性质在研究函数的单调性和不等式证明等方面有
着重要的应用。
03 函数极限的计算方法
直接代入法
总结词
直接代入法适用于求函数在某点的极限 值,当函数在该点的值已知时,可以直 接代入计算。
VS
详细描述
直接代入法是最基本的求函数极限的方法 。当函数在某点的值已知时,我们可以直 接将该点的值代入函数表达式中,得到该 点的极限值。这种方法适用于一些简单的 函数,如常数函数、一次函数等。
抓大头法
总结词
抓大头法适用于求函数在某点的极限值,当 函数在该点的值未知,但存在一个较大的项 或几个项的组合可以确定函数的极限值时。
详细描述
函数极限的局部有界性是函数极限的一个重要性质,它表明在函数极限存在的区域内,函数值是有界 的。这个性质在研究函数的单调性和收敛性等方面有着重要的应用。
函数极限的保号性
总结词
函数极限的保号性是指,如果函数$f(x)$在点$x_0$处的极限值大于0,那么在点$x_0$ 的某个邻域内,函数$f(x)$的值也大于0;如果极限值小于0,那么函数值也小于0。
详细描述
等价无穷小替换法是一种通过将函数中的某 些项替换为等价的无穷小量来估算函数的极 限值的方法。这种方法适用于一些复杂的函 数,如幂函数、三角函数等。在等价无穷小 替换法中,常用的等价无穷小量包括x→0时,
函数极限的唯一性是函数极限的一个重要性质,它表明在某一点附近,函数的 极限值是唯一的。这个性质在研究函数的连续性和可导性等方面有着重要的应 用。
函数极限的局部有界性
总结词
函数极限的局部有界性是指,如果函数$f(x)$在点$x_0$处有极限,那么在点$x_0$的某个邻域内,函 数$f(x)$是有界的。
详细描述
函数极限的保号性是函数极限的一个重要性质,它表明在函数极限存在的区域内,函数 的符号与极限值的符号保持一致。这个性质在研究函数的单调性和不等式证明等方面有
着重要的应用。
03 函数极限的计算方法
直接代入法
总结词
直接代入法适用于求函数在某点的极限 值,当函数在该点的值已知时,可以直 接代入计算。
VS
详细描述
直接代入法是最基本的求函数极限的方法 。当函数在某点的值已知时,我们可以直 接将该点的值代入函数表达式中,得到该 点的极限值。这种方法适用于一些简单的 函数,如常数函数、一次函数等。
抓大头法
总结词
抓大头法适用于求函数在某点的极限值,当 函数在该点的值未知,但存在一个较大的项 或几个项的组合可以确定函数的极限值时。
详细描述
函数极限的局部有界性是函数极限的一个重要性质,它表明在函数极限存在的区域内,函数值是有界 的。这个性质在研究函数的单调性和收敛性等方面有着重要的应用。
函数极限的保号性
总结词
函数极限的保号性是指,如果函数$f(x)$在点$x_0$处的极限值大于0,那么在点$x_0$ 的某个邻域内,函数$f(x)$的值也大于0;如果极限值小于0,那么函数值也小于0。
详细描述
等价无穷小替换法是一种通过将函数中的某 些项替换为等价的无穷小量来估算函数的极 限值的方法。这种方法适用于一些复杂的函 数,如幂函数、三角函数等。在等价无穷小 替换法中,常用的等价无穷小量包括x→0时,
高等数学函数的极限课程课件
则称当x x0时,函数f ( x)以a为极限,记作
lim f ( x) a 或
x x0
f (x) a(x x0 )
此时, 亦称当 x x0 时 f ( x) 存在极限
(或收 敛且收 敛 于 a ).
注 1 : 定义中的“0 | x x0 | ”表明: 当 x x0 时, f ( x) 有无极限以及极限值为多少均与 f ( x) 在 x0 有无定义无关.
xk
1
但 lim f ( x)不 存 在
2
xk
函数极限与数列极限的联系(某个桥梁):
定理3.1(Heine定理)
设f
: N ( x0 )
R为一函数,则 lim x x0
f (x)
a的
充要条件为对于N ( x0 )中的任何数列xn,
只要xn x0 (n ),
相应的函数值数列f ( xn )都收敛于a.
例3.2 问limarctanx是否存在? x
解 因为 lim arctan x ,
x
2
lim arctan x ,
x
2
lim arctan x lim arctan x,
x +
x
所以 limarctanx不存在.
x
y arctanx图象如图:
y
2
y arctan x
o
x
2
2. x x0时f ( x)的极限
都有 | f ( x) | L.
证明 设 lim f ( x) a, x x0 对 1, 0, 当0 x x0 时,
有 | f ( x) a | 1
所以当x ( x0 , x0 ) ( x0, x0 ) 时,
有a 1 f ( x) a 1
函数极限ppt课件

在常数A 对于任意给定的正数e 总存在正数d 使得当x
满足不等式0<|x-x0|d 时 对应的函数值f(x)都满足不等式 |f(x)-A|e
那么常数A就叫做函数f(x)当xx0时的极限 记为
lim
x x0
f(x)A
或
f(x) A(当
x
x0
)
•定义的简记形式
lim
x x0
f(x)A或fe(x>)0 Ad(x>0x当0)。0<|x-x0|<d
但f(g(x))在x0时无极 . 限
取 x n 2 n 1,x n 0 ,而 y n f( g ( x n ) )f( 0 ) 0 .
取 x n 2 n1 +,x n 0 ,而 y n f(g (x n ) )f(2 n+ 2 ) 1 . 2
取 xnn22(n1,2, )n , +, xn +, 且s有 inxnsin n)(0 0.
取xn(2n+2)2(n1,2, ),n+ ,xn+ ,
且有 sinxn
sin2n(+)11.
2
首页
上页
返回
下页
结束
铃
❖收敛函数的运算法则 •定理5(四则运算法则)
自变量的同一变化过程中,若lim f(x)A lim g(x)B 那么
返回
下页
结束
铃
例例33
求 lim
x3
x-3 x2 -9
解解 lim x - 3 lim x - 3 lim 1 x 3 x 2 - 9 x 3 (x - 3)(x + 3) x 3 x + 3
lim 1
x3
1
满足不等式0<|x-x0|d 时 对应的函数值f(x)都满足不等式 |f(x)-A|e
那么常数A就叫做函数f(x)当xx0时的极限 记为
lim
x x0
f(x)A
或
f(x) A(当
x
x0
)
•定义的简记形式
lim
x x0
f(x)A或fe(x>)0 Ad(x>0x当0)。0<|x-x0|<d
但f(g(x))在x0时无极 . 限
取 x n 2 n 1,x n 0 ,而 y n f( g ( x n ) )f( 0 ) 0 .
取 x n 2 n1 +,x n 0 ,而 y n f(g (x n ) )f(2 n+ 2 ) 1 . 2
取 xnn22(n1,2, )n , +, xn +, 且s有 inxnsin n)(0 0.
取xn(2n+2)2(n1,2, ),n+ ,xn+ ,
且有 sinxn
sin2n(+)11.
2
首页
上页
返回
下页
结束
铃
❖收敛函数的运算法则 •定理5(四则运算法则)
自变量的同一变化过程中,若lim f(x)A lim g(x)B 那么
返回
下页
结束
铃
例例33
求 lim
x3
x-3 x2 -9
解解 lim x - 3 lim x - 3 lim 1 x 3 x 2 - 9 x 3 (x - 3)(x + 3) x 3 x + 3
lim 1
x3
1
函数的极限(左右极限)ppt课件

记作: lim f (x) a x
◆定义(2):
一般地,当自变量x取负值并且绝对值无限增大时, 函数f(x)的值无限趋近于一个常数a,就说当x趋 向于负无穷大时,函数f(x)的极限是a,
记作: lim f (x) a
x
3
◆定义(3)
如果 lim f (x) a且 lim f (x) a
限是4.记作:limx 2 4 x 2 强调:x→2,包括分别从左、右两侧趋近于2.
即: “x→2”是指以任何方式无限趋近于2,(分别从
左、右两侧或左、右两侧交替地无限趋近于2).7
2. 考察函数 y x 2 1 (x≠1),当x无限趋近于1(但 x 1
不等于1)时,函数的变化趋势
(1)图象 y=x+1 (x∈R,x≠1)
y 4 1.75 0.39 0.04 0.004 0.0004 0.00004 ……
x
2.5 2.1 2.01 2.001 2.0001 2.00001 ……
y=x2 6.25 4.41 4.04 4.004 4.0004 4.00004 ……
y 4 2.25 0.41 0.04 0.004 0.0004 0.00004 ……
函数在一点处的极限与左、右极限的定义 10
函数在一点处的极限与左、右极限
1.当自变量x无限趋近于常数x0(但x不等于x0)时,如
果函数f(x)无限趋近于一个常数a,就说当x趋近于x0时,
函 数 f(x) 的 极 限 是 a , 记 作 f(x)→a。
lim f( x) a 或 当 x→x0 时
x x 0
(2)lim f(x) 是x从x0的两侧无限趋近于x0,是双侧极限,
xx0
高数课件-函数的极限

对任意给定的正数 ε(不论 ε 多么小),作两条水平直 线 y=A-ε,y=A+ε,则总存在一个正数 X,使得在区间 (-∞,-X)与(X,+∞)内,函数 f(x)的图形介于这两 条水平直线之间(见图)。
25-15
注 2:X 的相应性 一般说,X 是随着ε的变小而变大的, 可写成 X= X(ε),但是这种写法并不意味着 X 是由ε唯一确
例 2.2.4 证明 lim ax 0 ,其中常数a 1 . x
证 对于任意给定的正数 (0 1) ,要使得 ax 0 ax ,
只须 x lg a lg ,即 x lg ,故取 X lg 0 ,当 x X 时,
lg a
lg a
恒有
ax 0
成立,所以 lim ax 0 . x
lim
x x0
sin
x
sin
x0
.
25-27
注
在利用定义来验证函数极限时,也可考虑对 |f(x) -A|进行放大,放大的原则与数列时的情形完全相同。此外还须注意
x=x 此时是在
0的附近考察问题的,对于“附近”应如何理解,请揣摩一
下。
单侧极限:
自变量 x 是指 x 无限增大.
如果只考察 x 0 , x 无限增大,就称 x 趋向正无穷大,
f
(x) .
25-30
极限自变量x的li某m变化过程 f (x) A 的整体刻画:
如果对于任意给定的正数 ε,当自变量 x 变化到一定的程 度时,恒有
| f (x) A |
成立,则有
lim
自变量x的某变化过程
f
(x)
A。
25-31
lim f (x) A
x
0,X 0,使当x X时,恒有 f (x) A lim f (x) A
25-15
注 2:X 的相应性 一般说,X 是随着ε的变小而变大的, 可写成 X= X(ε),但是这种写法并不意味着 X 是由ε唯一确
例 2.2.4 证明 lim ax 0 ,其中常数a 1 . x
证 对于任意给定的正数 (0 1) ,要使得 ax 0 ax ,
只须 x lg a lg ,即 x lg ,故取 X lg 0 ,当 x X 时,
lg a
lg a
恒有
ax 0
成立,所以 lim ax 0 . x
lim
x x0
sin
x
sin
x0
.
25-27
注
在利用定义来验证函数极限时,也可考虑对 |f(x) -A|进行放大,放大的原则与数列时的情形完全相同。此外还须注意
x=x 此时是在
0的附近考察问题的,对于“附近”应如何理解,请揣摩一
下。
单侧极限:
自变量 x 是指 x 无限增大.
如果只考察 x 0 , x 无限增大,就称 x 趋向正无穷大,
f
(x) .
25-30
极限自变量x的li某m变化过程 f (x) A 的整体刻画:
如果对于任意给定的正数 ε,当自变量 x 变化到一定的程 度时,恒有
| f (x) A |
成立,则有
lim
自变量x的某变化过程
f
(x)
A。
25-31
lim f (x) A
x
0,X 0,使当x X时,恒有 f (x) A lim f (x) A
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
数列极限复习
定义:
一般地,如果当项数n无限增大时, 无穷数列{an}的项an无限地趋 近于某个常数a,(既|an-a|无 限地接近于0),那么就说数列 {an}以a为极限,或者说数列 {an}的极限是a 记着:
lim an a
n
重要结论
(1)常数c的极限等于 它本身,
即 (2)
lim C C
n
lim a
n n
(3)
A1n A2 n …… lim t t 1 n B n B n …… 1 2
s
s 1
(1)当
x
时
函数f(x)的极限
x
1 y x
1
10
100
1000
10000
100000
y
1
0.1
0.01
0.001
0.0001
0.00001
一定存在吗???
问题???
若
x
lim f ( x)
和
x
lim f ( x)
存在
它们的值一定相等吗???
定义(3)
如果
x
lim f ( x) a
且
x
lim f ( x) a
那么就说 当x趋向于无穷大时,函数f(x)的极 限是a,记着:
lim f ( x ) a
0
但两个极限值不相等
0
lim f ( x ) lim f ( x) ( 3) 与 x x 可以都存在, x x0
且两个极限值相等
谢谢欣赏
欢迎督查指导
x x0
0
lim f ( x) a
lim f ( x ) 也叫做函数f(x)在点x=x0处的极限 x x
x无限趋近于常数x0,是指x从x0的左、右两边趋近于x0
lim C C 一般地,设C为常数,则 x x
x 1 2 由例2及 lim , x 1 x 1 你能总结出一般性结论吗?
x x0
x x0
lim f ( x) lim f ( x) a
x x0
练习1:P83练习1、2 练习2: P83习题1
举例说明:
f ( x) 可以都不存在 lim f ( x) 与 xlim ( 1) x xx
0
0
lim f ( x ) lim f ( x) ( 2) 与 x x 可以都存在, x x0
当自变量x取正值并无限增大时(即x趋向于正无穷大 时),函数y的值无限趋近于0,即|y-o|可以变得任意 小. 同样地,当自变量x取负值并且它的绝对值无限 增大时(即x趋向于负无穷大时),函数y的值也无 限趋近于0,
定义(1): 一般地,当自变量x取正值并无限增大时,函数f(x) 的值无限趋近于一个常数a,就说当x趋向于正无穷 大时,函数f(x)的极限是a,记着:
x无限趋近于x0,应理解为x可以用任何方式 无限趋近于x0
阅读:P80例2 练习: P81练习2
想一想:
可以总结出什么规律?
左极限定义: 一般地如果当x从点x0左侧(即x<x0)无限趋近 于x0时,函数f(x)无限趋近于常数a,就说a是函数 f(x)在点x0处的左极限,记作
右极限定义:
x x0
lim f ( x) a
一般地如果当x从点x0右侧(即x<x0)无限趋近 于x0时,函数f(x)无限趋近于常数a,就说a是函数 f(x)在点x0处的右极限,记作
x x0
lim f ( x) a
根据函数在一点处的极限、左 极限、右极限的定义,可以得 出:
lim f ( x) a
2
0
本节课主要学 习了哪些问题?
第二课时
函数的左、右极限
说出下列函数极限的定义:
(1)
x x
lim f ( x) a
(2) (3)
lim f ( x) a lim f ( x ) a
x
(4)
x x0
lim f ( x) a
定义(1):
x
lim f ( x) a
一般地,当自变量x取正值并无限增大时, 函数f(x)的值无限趋近于一个常数a,就 说当x趋向于正无穷大时,函数f(x)的极 限是a,记着:
定义(2):
x
lim f ( x) a
一般地,当自变量x取负值并且绝对值无 限增大时,函数f(x)的值无限趋近于一 个常数a,就说当x趋向于负无穷大时,函 数f(x)的极限是a,记着:
函数
yx
2
的变化趋势:
lim x 4
2 x2
2
问题(1):讨论当x无限趋近于1 (从左、右两边)
x 1 y 的变化趋势: x 1
时,函数
x 1 lim 2 x 1 x 12Fra bibliotek问题???
当 x从x0的左、右两边趋近于x0时, f(x)的极限一定相等吗?
你能否举例说明?
(
)
定义(4) 一般地,当自变量x无限趋近于常数x0时(但x不等 于x0),如果函数f(x) 无限趋近于一个常数a,就 说当x趋近于x0时时,函数f(x)的极限是a,记着:
x
注意:必须两个条件都满足, 才能说-------
对于常数函数f(x)=c(x∈R), 也有 lim
x
f ( x) C
x
重要结论:
x
lim a ?
x
x
lim a ?
记忆方法:数形结合法(指数函 数的图象)
(2)当
x x0
时
函数f(x)的极限
问题(1):讨论当x无限趋近于2(从左、右两边)时,
定义(3)
lim f ( x ) a
x
lim f ( x ) a lim f ( x ) a 如果 x 且 x
那么就说 当x趋向于无穷大时,函 数f(x)的极限是a,记着:
定义(4)(函数在一点处的极限)
x x0
lim f ( x) a
一般地,当自变量x无限趋近于常数 x0时(但x不等于x0),如果函数f(x) 无限趋近于一个常数a,就说当x趋近于 x0时时,函数f(x)的极限是a,记着:
x
lim f ( x) a
定义(2):
一般地,当自变量x取负值并且绝对值无限增大时, 函数f(x)的值无限趋近于一个常数a,就说当x趋向 于负无穷大时,函数f(x)的极限是a,记着:
x
lim f ( x) a
问题???
x
lim f ( x)
和
x
lim f ( x)
定义:
一般地,如果当项数n无限增大时, 无穷数列{an}的项an无限地趋 近于某个常数a,(既|an-a|无 限地接近于0),那么就说数列 {an}以a为极限,或者说数列 {an}的极限是a 记着:
lim an a
n
重要结论
(1)常数c的极限等于 它本身,
即 (2)
lim C C
n
lim a
n n
(3)
A1n A2 n …… lim t t 1 n B n B n …… 1 2
s
s 1
(1)当
x
时
函数f(x)的极限
x
1 y x
1
10
100
1000
10000
100000
y
1
0.1
0.01
0.001
0.0001
0.00001
一定存在吗???
问题???
若
x
lim f ( x)
和
x
lim f ( x)
存在
它们的值一定相等吗???
定义(3)
如果
x
lim f ( x) a
且
x
lim f ( x) a
那么就说 当x趋向于无穷大时,函数f(x)的极 限是a,记着:
lim f ( x ) a
0
但两个极限值不相等
0
lim f ( x ) lim f ( x) ( 3) 与 x x 可以都存在, x x0
且两个极限值相等
谢谢欣赏
欢迎督查指导
x x0
0
lim f ( x) a
lim f ( x ) 也叫做函数f(x)在点x=x0处的极限 x x
x无限趋近于常数x0,是指x从x0的左、右两边趋近于x0
lim C C 一般地,设C为常数,则 x x
x 1 2 由例2及 lim , x 1 x 1 你能总结出一般性结论吗?
x x0
x x0
lim f ( x) lim f ( x) a
x x0
练习1:P83练习1、2 练习2: P83习题1
举例说明:
f ( x) 可以都不存在 lim f ( x) 与 xlim ( 1) x xx
0
0
lim f ( x ) lim f ( x) ( 2) 与 x x 可以都存在, x x0
当自变量x取正值并无限增大时(即x趋向于正无穷大 时),函数y的值无限趋近于0,即|y-o|可以变得任意 小. 同样地,当自变量x取负值并且它的绝对值无限 增大时(即x趋向于负无穷大时),函数y的值也无 限趋近于0,
定义(1): 一般地,当自变量x取正值并无限增大时,函数f(x) 的值无限趋近于一个常数a,就说当x趋向于正无穷 大时,函数f(x)的极限是a,记着:
x无限趋近于x0,应理解为x可以用任何方式 无限趋近于x0
阅读:P80例2 练习: P81练习2
想一想:
可以总结出什么规律?
左极限定义: 一般地如果当x从点x0左侧(即x<x0)无限趋近 于x0时,函数f(x)无限趋近于常数a,就说a是函数 f(x)在点x0处的左极限,记作
右极限定义:
x x0
lim f ( x) a
一般地如果当x从点x0右侧(即x<x0)无限趋近 于x0时,函数f(x)无限趋近于常数a,就说a是函数 f(x)在点x0处的右极限,记作
x x0
lim f ( x) a
根据函数在一点处的极限、左 极限、右极限的定义,可以得 出:
lim f ( x) a
2
0
本节课主要学 习了哪些问题?
第二课时
函数的左、右极限
说出下列函数极限的定义:
(1)
x x
lim f ( x) a
(2) (3)
lim f ( x) a lim f ( x ) a
x
(4)
x x0
lim f ( x) a
定义(1):
x
lim f ( x) a
一般地,当自变量x取正值并无限增大时, 函数f(x)的值无限趋近于一个常数a,就 说当x趋向于正无穷大时,函数f(x)的极 限是a,记着:
定义(2):
x
lim f ( x) a
一般地,当自变量x取负值并且绝对值无 限增大时,函数f(x)的值无限趋近于一 个常数a,就说当x趋向于负无穷大时,函 数f(x)的极限是a,记着:
函数
yx
2
的变化趋势:
lim x 4
2 x2
2
问题(1):讨论当x无限趋近于1 (从左、右两边)
x 1 y 的变化趋势: x 1
时,函数
x 1 lim 2 x 1 x 12Fra bibliotek问题???
当 x从x0的左、右两边趋近于x0时, f(x)的极限一定相等吗?
你能否举例说明?
(
)
定义(4) 一般地,当自变量x无限趋近于常数x0时(但x不等 于x0),如果函数f(x) 无限趋近于一个常数a,就 说当x趋近于x0时时,函数f(x)的极限是a,记着:
x
注意:必须两个条件都满足, 才能说-------
对于常数函数f(x)=c(x∈R), 也有 lim
x
f ( x) C
x
重要结论:
x
lim a ?
x
x
lim a ?
记忆方法:数形结合法(指数函 数的图象)
(2)当
x x0
时
函数f(x)的极限
问题(1):讨论当x无限趋近于2(从左、右两边)时,
定义(3)
lim f ( x ) a
x
lim f ( x ) a lim f ( x ) a 如果 x 且 x
那么就说 当x趋向于无穷大时,函 数f(x)的极限是a,记着:
定义(4)(函数在一点处的极限)
x x0
lim f ( x) a
一般地,当自变量x无限趋近于常数 x0时(但x不等于x0),如果函数f(x) 无限趋近于一个常数a,就说当x趋近于 x0时时,函数f(x)的极限是a,记着:
x
lim f ( x) a
定义(2):
一般地,当自变量x取负值并且绝对值无限增大时, 函数f(x)的值无限趋近于一个常数a,就说当x趋向 于负无穷大时,函数f(x)的极限是a,记着:
x
lim f ( x) a
问题???
x
lim f ( x)
和
x
lim f ( x)
