中心对称课件ppt
合集下载
九年级数学中心对称图形课件

正方形中心对称图形的面积计算
总结词
正方形中心对称图形的面积计算与矩形类似,也是通过 计算一个正方形面积再除以2得到。
详细描述
正方形作为特殊的矩形,其中心对称图形的面积计算方 法与矩形相同。将正方形分成两个完全相同的部分,然 后计算一个正方形的面积,最后将结果除以2即可得到整 个中心对称图形的面积。假设正方形边长为a,则其面积 为a^2。所以,中心对称图形的面积为(a^2)/2。
THANKS
感谢观看
03
中心对称图形的判定
通过旋转判定中心对称图形
总结词
旋转法是判定中心对称图形的一种常 用方法。
详细描述
将图形绕着某点旋转180度,如果旋 转后的图形与原图形重合,则该图形 是中心对称图形。例如,正方形、圆 、正六边形等都是中心对称图形。
通过反射判定中心对称图形
总结词
反射法是通过图形的对称性来判定中心对称图形的方法。
05
中心对称图形的面积计算
矩形中心对称图形的面积计算
要点一
总结词
要点二
详细描述
矩形中心对称图形的面积计算相对简单,可以通过计算一 个矩形面积再除以2得到。
对于矩形中心对称图形,我们可以将其分成两个完全相同 的矩形,然后计算一个矩形的面积,最后将结果除以2即可 得到整个中心对称图形的面积。假设矩形长为a,宽为b, 则其面积为ab。所以,中心对称图形的面积为(ab)/2。
九年级数学中心对称图形ppt课件
目 录
• 中心对称图形的定义 • 中心对称图形的性质 • 中心对称图形的判定 • 中心对称图形的作图 • 中心对称图形的面积计算
01
中心对称图形的定义
中心对称图形的文字定义
总结词:简明扼要
23.2.1 中心对称(共43张PPT)
15 8
2
OF
15 8
同理OE 15 ,即 OF OE OF 15
8
4
A
D
C′
D′
O 重合
B′
A′
B
C
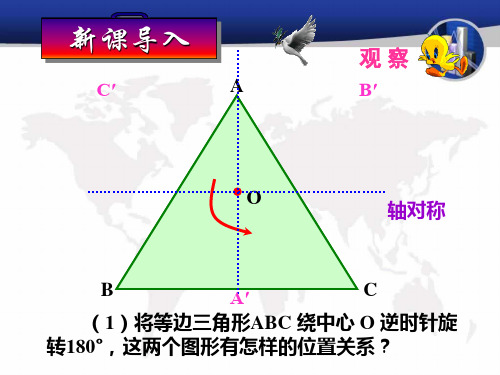
(4)将平行四边形ABCD绕中心O逆时针旋 转180°,这两个图形有怎样的位置关系?
有的轴对称, 有的重合。
绕中心旋转180°,旋转后的图 形与原图的位置关系有什么不同?
教学目标
【知识与能力】
了解中心对称、对称中心、关于中心的对称 点等概念。 通过具体实例认识两个图形关于某一点成中 心对称的本质:就是一个图形绕一点旋转180° 而成。 作出中心对称的图形。
它是轴对称图形吗? 不是轴对称图形。
这个图形是否能够通过某种图形运动与自 身重合?
探究
下列图形是否能够通过某种图形运动与自
身重合?图旋Biblioteka 形转绕后中与
线段绕中点旋转180°
心原 旋图
旋转后与原图重合
转重
180 合
°
知识要点
把一个图形绕着某一个点旋转180°, 如果它能够与另一个图形重合,那么就说 这两个图形关于这个点对称或中心对称 (central symmetry),这个点叫做对称中 心。这两个图形中的对应点叫做关于中心 的对称点。
经历对日常生活中与中心对称有关的图形进行 观察、分析、欣赏、动手操作、画图等过程,发 展审美能力,增强对图形的欣赏意识。
从图形变化过程中,树立正确的辩证唯物主义 观点。
认识几何图形的对称美,培养学生热爱数学, 热爱生活。
教学重难点
利用中心对称、对称中心、关于中心的 对称点的概念解决一些问题。 从一般旋转中导入中心对称。 中心对称的性质及初步应用。 中心对称与旋转之间的关系。
九年级数学上册 23.2.2 中心对称图形 课件(共24张PPT)

(2)中心对称图形的对称点
O
连线被_对__称__中__心__平__分__
C
B
性质:中心对称图形上的每一对对称点的连线都经过对称
中心且被对称中心平分.
知识归纳
中心对称图形的性质
知识点二
中心对称与中心对称图形的区别与联系:
中心对称
中心对称图形
1.针对两个图形而言的
1.针对一个图形而言的
区 2.是指两个图形的(位置)关系2.是指具有某种性质的一个图形
探究新知
中心对称图形的概念
【问题】将下面的图形绕O点旋转,你有什么发现?
知识点一
AO B
O
O
O
共同点:(1)都绕一点旋转了180度; (2)都与原图形完全重合.
中心对称图形的定义 注意 中心对称图形是指一个图形.
把一个图形绕某个点旋转180º,如果旋转后的图形能与原来的图 形重合,那么这个图形叫做中心对称图形,这个点叫做它的对称中
ABCDEFGH I J KLM
NOPQRSTUVWXYZ
2.在线段、角、等腰三角形、等边三角形、等腰梯形、平行四 边形、矩形、菱形、正方形、正六边形、圆中,既是轴对称图形, 又是中心对称图形的图形有( D ) A.3个 B.4个 C.5个 D.6个
针对训练
中心对称图形的概念
知识点一
3.下列图形中,既是轴对称图形,又是中心对称图形的是( B )
分别交AD和BC于点E,F,AB=2,BC=3,则图中阴影部分的面积为_3__.
A
ED
O
BF
C
针对训练
中心对称图形的性质
知识点二
1.如图,有一个平行四边形请你用无刻度的直尺画一条直线把他
中心对称--PPT课件

如图,已知△ABC与△A’B’C’中心对称,求出它们 的对称中心O。
C
B A
A’ B’
C’
王母娘娘被考神说服,她表示作出下面这道题就解除对
懒星和美星的惩罚,就让她们见面,大家一起来帮帮她们 吧!
小结:
• 这节课你有那些收获?
• 请你说给大家听听
最后通过大家的帮助懒星和美星两姐妹终于又到了 一起!
结论:
1.关于中心对称的两个图形,对称点所连线段都经过对称 中心,而且被对称中心所平分.
2.关于中心对称的两个图形是全等图形.
△ABC与△ADE就是成中心对称的两个三角形,点 A是对称中心,点B关于对称中心A的对称点为点 ___D______,点C关于对称中心A的对称点为点 ___E_______。
23.2.1中心对称
你能给出中心对称的定义吗?
定义: 把一个图形绕着某一个点旋转180度,如果它能够与
另一个图形重合,那么就说这两个图形关于这个点对称或 中心对称,这个点叫做对称中心.
思考:如何作出已知图形关于某点的对称图形?
作该图形绕该点旋转180度后的图形即为 所求!
善良的你能帮助懒星根据自己和天宫找到她妹妹美星的 位置吗?
.
懒星
天宫
作出ΔABC关于点O的对称图形ΔDEF并说明作图
步骤
A
. 0
B
C
F E
D
辩一辩哪组同学的作图方法更好一点:
自己动手量一量,比一比,看一看你能得出哪些结论?
Ao=__O_D_____ BO=_O_E ______ co=__O_F______
ΔABC__≌___ΔDEF
中心对称图形课件(共20张PPT)人教版数学九年级上册

(中心对称图形的特点:绕某一点旋转180°后能与自身重合.中心对称图形 上每一对对称点所连线段都被对称中心平分(合理即可);中心对称图形是 指一个图形本身是中心对称的,反映了一个图形的本质特征,而中心对称 是指两个图形关于某一点对称,表示的是两个图形之间的一种关系)
小组讨论 1.我们已经知道,平行四边形是中心对称图形,你能根据中心 对称图形的性质验证平行四边形的哪些性质? (平行四边形的对边互相平行且相等; 平行四边形的对角相等; 平行四边形的对角线互相平分) 2.试着总结中心对称图形的性质
【题型二】中心对称与中心对称图形的区别和联系 例3: 下列说法中,正确的是( A) ①中心对称与中心对称图形是两个不同的概念;②中心对称与 中心对称图形都只有一个对称中心;③中心对称图形是指两个 图形之间的一种关系;④中心对称的两个图形 ,对称点所连线段 的中点刚好是对称中心. A.①②④ B.①②③ C.①③④ D.②③④
(点A,B,C,D的对应点分别是点C,D,A,B ; 重合)
③上述两个旋转的共同点是什么? (都是绕某一点旋转180°,旋转后的图形能与原图形重合)
自主探究
2.请同学们阅读课本67页,并勾画中心对称图形的概念. 3.你还能说出其他的中心对称图形吗?
(正方形 长方形 正六边形等) 4.说说中心对称图形具有哪些特点?它与中心对称有什么区 别和联系?
图形名称 线段 角 等腰三 等边三 直角三 平行四 矩形 菱形 正方 等腰 直角 圆
角形 角形 角形 边形
形 梯形 梯形
是否是轴对 是 是 是 是 否 否 是 是 是 是 否 是
称图形
是否是中心 是 否 否
对称图形
否 否是 是 是 是否 否 是
板书设计
联 ①把中心对称的两个图形看成一个“整体”,则为中心对称图形; 系 ②把中心对称图形的两部分看成两个图形,则它们中心对称
小组讨论 1.我们已经知道,平行四边形是中心对称图形,你能根据中心 对称图形的性质验证平行四边形的哪些性质? (平行四边形的对边互相平行且相等; 平行四边形的对角相等; 平行四边形的对角线互相平分) 2.试着总结中心对称图形的性质
【题型二】中心对称与中心对称图形的区别和联系 例3: 下列说法中,正确的是( A) ①中心对称与中心对称图形是两个不同的概念;②中心对称与 中心对称图形都只有一个对称中心;③中心对称图形是指两个 图形之间的一种关系;④中心对称的两个图形 ,对称点所连线段 的中点刚好是对称中心. A.①②④ B.①②③ C.①③④ D.②③④
(点A,B,C,D的对应点分别是点C,D,A,B ; 重合)
③上述两个旋转的共同点是什么? (都是绕某一点旋转180°,旋转后的图形能与原图形重合)
自主探究
2.请同学们阅读课本67页,并勾画中心对称图形的概念. 3.你还能说出其他的中心对称图形吗?
(正方形 长方形 正六边形等) 4.说说中心对称图形具有哪些特点?它与中心对称有什么区 别和联系?
图形名称 线段 角 等腰三 等边三 直角三 平行四 矩形 菱形 正方 等腰 直角 圆
角形 角形 角形 边形
形 梯形 梯形
是否是轴对 是 是 是 是 否 否 是 是 是 是 否 是
称图形
是否是中心 是 否 否
对称图形
否 否是 是 是 是否 否 是
板书设计
联 ①把中心对称的两个图形看成一个“整体”,则为中心对称图形; 系 ②把中心对称图形的两部分看成两个图形,则它们中心对称
人教版九年级上册数学中心对称图形优秀ppt课件

中心对称图形形状匀称美观,很多建筑物和工艺品上 常采用这种图形作装饰图案.另外,具有中心对称图形形 状的物体,能够在平面内绕对称中心平稳地旋转,在生 产中旋转的零部件的形状常设计成中心对称图形,如水 泵叶轮等.
人教版九年级上册数数学学中心对23称.2图.2形中优心秀对p称pt图课形件(共36张PPT)
人教版九年级上册数数学学中心对23称.2图.2形中优心秀对p称pt图课形件(共36张PPT)
返回
旋转
人教版九年级上册数数学学中心对23称.2图.2形中优心秀对p称pt图课形件(共36张PPT) 人教版九年级上册数数学学中心对23称.2图.2形中优心秀对p称pt图课形件(共36张PPT)
o O
人教版九年级上册数数学学中心对23称.2图.2形中优心秀对p称pt图课形件(共36张PPT)
人教版九年级上册 数学 23.2.2中心对称图形(共36张PPT) 人教版九年级上册 数学 23.2.2中心对称图形(共36张PPT)
人教版九年级上册 数学 23.2.2中心对称图形(共36张PPT) 人教版九年级上册 数学 23.2.2中心对称图形(共36张PPT)
人教版九年级上册 数学 23.2.2中心对称图形(共36张PPT)
中心对称图形
1什么是中心对称?
2中心对称有什么性质?
A
定义: 把一个图形绕着 某一点旋转180 °,如 果它能够与另一个图 形重合,那么就说这 两个图形关于这个点 对称或中心对称,这 个点叫做对称中心, 能够互相重合的一对 点叫做对称点。
C`
B`
O
B
C
A`
性质: ①两个图形全等;
②对应点所连线段都经过对称中 心,并且被对称中心平分
中心对称与中心对称图形有什么区别与联系?
人教版九年级上册数数学学中心对23称.2图.2形中优心秀对p称pt图课形件(共36张PPT)
人教版九年级上册数数学学中心对23称.2图.2形中优心秀对p称pt图课形件(共36张PPT)
返回
旋转
人教版九年级上册数数学学中心对23称.2图.2形中优心秀对p称pt图课形件(共36张PPT) 人教版九年级上册数数学学中心对23称.2图.2形中优心秀对p称pt图课形件(共36张PPT)
o O
人教版九年级上册数数学学中心对23称.2图.2形中优心秀对p称pt图课形件(共36张PPT)
人教版九年级上册 数学 23.2.2中心对称图形(共36张PPT) 人教版九年级上册 数学 23.2.2中心对称图形(共36张PPT)
人教版九年级上册 数学 23.2.2中心对称图形(共36张PPT) 人教版九年级上册 数学 23.2.2中心对称图形(共36张PPT)
人教版九年级上册 数学 23.2.2中心对称图形(共36张PPT)
中心对称图形
1什么是中心对称?
2中心对称有什么性质?
A
定义: 把一个图形绕着 某一点旋转180 °,如 果它能够与另一个图 形重合,那么就说这 两个图形关于这个点 对称或中心对称,这 个点叫做对称中心, 能够互相重合的一对 点叫做对称点。
C`
B`
O
B
C
A`
性质: ①两个图形全等;
②对应点所连线段都经过对称中 心,并且被对称中心平分
中心对称与中心对称图形有什么区别与联系?
16.4 中心对称图形课件(共17张PPT)

A
3.如图,△ABO与△CDO关于点O成中心对称,点E,F在线段AC 上,且AF=CE.求证:FD=BE.
证明:∵△ABO与△CDO关于点O成中心对称∴AB=CD,∠A=∠C∵AF=CE∴AF+FE=CE+FE即AE=CF在△ABE和△CDF中∵AB=CE∠A=∠CAE=CF∴△ABE≌△CDF(SAS)∴FD=BE
知识点3 中心对称的性质
在成中心对称的两个图形中,对应点的连线经过对称中心,并且被对称中心平分.
中心对称的性质
例题解析
例 如图,已知线段AB和点O,画出线段AB关于点O的中心对称图形.
解:如图.(1)连接AO,BO,并延长AO到点C,延长BO到点D,使得OC=OA,OD=OB.(2)连接CD.线段CD即为所求.
第十六章 轴对称和中心对称16.4 中心对称图形
学习目标
学习重难点
重点
难点
1.认识并能够辨析中心对称图形和两个图形成中心对称.2.理解中心对称的基本性质,并会利用性质作图.
能够辨析中心对称图形和两个图形成中心对称.
理解中心对称的基本性质,并会利用性质作图.
观察这几幅图片,将它们分别绕各自标示的“中心点”旋转180°后,能不能与它们自身重合?
知识点2 成中心对称
中心对称图形是指一个图形的中心对称性,两个图形之间往往也具有这种对称关系.
如果一个图形绕某一点旋转180°后与另一个图形重合,我们就把这两个图形叫做成中心对称,这个点叫做对称中心,其中成中心对称的点、线段和角,分别叫做对应点、对应线段和对应角.
随堂练习
1.下列图案都是由字母“m”经过变形、组合 而成的,其中不是中心对称图形的是( )A B C D
B
2.如图,是一个中心对称图形,A为对称中心,若∠C=90°,∠B=30°,AB=3,则AB'的长为 .
3.如图,△ABO与△CDO关于点O成中心对称,点E,F在线段AC 上,且AF=CE.求证:FD=BE.
证明:∵△ABO与△CDO关于点O成中心对称∴AB=CD,∠A=∠C∵AF=CE∴AF+FE=CE+FE即AE=CF在△ABE和△CDF中∵AB=CE∠A=∠CAE=CF∴△ABE≌△CDF(SAS)∴FD=BE
知识点3 中心对称的性质
在成中心对称的两个图形中,对应点的连线经过对称中心,并且被对称中心平分.
中心对称的性质
例题解析
例 如图,已知线段AB和点O,画出线段AB关于点O的中心对称图形.
解:如图.(1)连接AO,BO,并延长AO到点C,延长BO到点D,使得OC=OA,OD=OB.(2)连接CD.线段CD即为所求.
第十六章 轴对称和中心对称16.4 中心对称图形
学习目标
学习重难点
重点
难点
1.认识并能够辨析中心对称图形和两个图形成中心对称.2.理解中心对称的基本性质,并会利用性质作图.
能够辨析中心对称图形和两个图形成中心对称.
理解中心对称的基本性质,并会利用性质作图.
观察这几幅图片,将它们分别绕各自标示的“中心点”旋转180°后,能不能与它们自身重合?
知识点2 成中心对称
中心对称图形是指一个图形的中心对称性,两个图形之间往往也具有这种对称关系.
如果一个图形绕某一点旋转180°后与另一个图形重合,我们就把这两个图形叫做成中心对称,这个点叫做对称中心,其中成中心对称的点、线段和角,分别叫做对应点、对应线段和对应角.
随堂练习
1.下列图案都是由字母“m”经过变形、组合 而成的,其中不是中心对称图形的是( )A B C D
B
2.如图,是一个中心对称图形,A为对称中心,若∠C=90°,∠B=30°,AB=3,则AB'的长为 .
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
形,这个点叫做它的对称中心。
(2)这些图形都可以绕某个点旋 特旋转征 转哪: 18个(0°1角)后度中与后心自与对身称原重图来合形;的绕(图着2形)它重中的合心中对心? 称点
图形也是一种特殊的旋转对称图形。
❖ 线段、三角形、平行四边形、长方形、正 方形、圆是中心对称图形吗?如果是,那 么对称中心又在哪里?
观察
(1)把其中一个图案绕点O旋转180°,你有什么发现?
(2)线段AC,BD相交于点O,OA=OC,OB=OD.把 △OCD绕点O旋转180°,你有什么发现?
重合
重合
像这样把一个图形绕
C
着某一点旋转180度,如
果它能够和 另一个图
形重合,那么,我们就说
这两个图形关于这个
B
A A
D 点成中心对称,这个
点就叫对称中心,这
两个图形中的对应点你探究
中心对称图形与中心对称的区别:
不同点 相同点
中心对称图形 中心对称
❖请你动手:将一个三角板放在纸上,
画出△ABC,再将三角板绕一个顶点旋 转180o,画出△A’B’C’,移开三角 板,画出的△ABC与△A’B’C’关于点 O对称。分别连接对称点AA’ 、BB’、 CC’,点O在线段AA’上吗?如果在, 在什么位置? △ABC与 △A’B’C’有 什么关系?
下图中△A′B′C′与△ABC关于 点O是成中心对称的,你能从图中 找到哪些等量关系?
(1)OA=OA′、OB=OB′、 OC=OC′ (2)成中心对称的两图形形状、大小一样,对应线段 相等,对应角相等
归纳:
在成中心对称的两个图形中,连接对称点的 线段都经过对称中心,并且被对称中心平分.
反过来,如果两个图形的对应点连成的线段 都经过某一点,并且都被该点平分,那么这两 个图形一定关于这一点成中心对称.
应用拓展 :已知四边形ABCD和点O(下图),
画四边形A’B’C’D’,使它与已知四边形关
于点O对称. D
A
画法:1. 连结AO并延长到A’,使
OA’=OA,得到点A的对称点A’.
C B
.o
2. 同样画B、C、D的对称点 B’、C’、D’.
C’
B’
3. 顺次连结A’、B’、C’、D’ 各点.
A’
四边形A’B’C’D’就是所求的四边形.
F
B
B.
M
A
O
G
CA
C
E
D
D
小结: 今天你学到了什么 ?
1、回顾本节课的活动过程 。 观察——分析——探索 ——概括——应用 2、本节课学到了哪些知识? (1)中心对称图形与中心对称的定义 (2)中心对称的性质 (3)我们所学的多边形中有哪些是中心对称图形 (4)中心对称的应用
课后作业
自己设计一个中心对称图形,并画出它关于某点 成中心对称的图形。
学习目标
❖ 1、理解中心对称图形和中心对称的概念,知 道两者之间的辩证关系,并掌握它们的性质 和判定。
❖ 2、会画一个图形关于某一点的对称图形。
观察:下列图形,绕中心点旋转多少度能与自身
重合?它们的旋转角度有什么相同点?
在平面内,一个图形绕某个点旋转180o,能
与(自1)身这重些合,图那形么有这什个么图共形同叫做的中特心征对?称图
试一试:如果△ABC和△EDF关于点O成中
心对称,写出相等的线段和相等的角。
D E
F
灵活运用,体会内涵 1、点的中心对称点的作法
以点O为对称中心,作出点A的对称点A′;
AO
A′
点A′即为所求的点
2、线段的中心对称线段的作法
以点O为对称中心,作出线段AB的对称线段点A′B′
A
B′
O
B
A′
线段A′B′就是所求的线段
D’
巩固练习:如图23.2-5,选择点O为对称中心,画 出与△ABC关于点O对称的△A’B’C’.
能力提高 : 已知四边形ABCD,画四边形
A’B’C’D’,使它与已知四边形关于点A对
称。
D
C
A B
达标检测一
1、判断下列图形是否是中心对称图形?
达标检测二
2、画一个与已知四边形ABCD中心对称图形。 (1)以顶点A为对称中心; (2)以BC边的中点为对称中心。 N
(2)这些图形都可以绕某个点旋 特旋转征 转哪: 18个(0°1角)后度中与后心自与对身称原重图来合形;的绕(图着2形)它重中的合心中对心? 称点
图形也是一种特殊的旋转对称图形。
❖ 线段、三角形、平行四边形、长方形、正 方形、圆是中心对称图形吗?如果是,那 么对称中心又在哪里?
观察
(1)把其中一个图案绕点O旋转180°,你有什么发现?
(2)线段AC,BD相交于点O,OA=OC,OB=OD.把 △OCD绕点O旋转180°,你有什么发现?
重合
重合
像这样把一个图形绕
C
着某一点旋转180度,如
果它能够和 另一个图
形重合,那么,我们就说
这两个图形关于这个
B
A A
D 点成中心对称,这个
点就叫对称中心,这
两个图形中的对应点你探究
中心对称图形与中心对称的区别:
不同点 相同点
中心对称图形 中心对称
❖请你动手:将一个三角板放在纸上,
画出△ABC,再将三角板绕一个顶点旋 转180o,画出△A’B’C’,移开三角 板,画出的△ABC与△A’B’C’关于点 O对称。分别连接对称点AA’ 、BB’、 CC’,点O在线段AA’上吗?如果在, 在什么位置? △ABC与 △A’B’C’有 什么关系?
下图中△A′B′C′与△ABC关于 点O是成中心对称的,你能从图中 找到哪些等量关系?
(1)OA=OA′、OB=OB′、 OC=OC′ (2)成中心对称的两图形形状、大小一样,对应线段 相等,对应角相等
归纳:
在成中心对称的两个图形中,连接对称点的 线段都经过对称中心,并且被对称中心平分.
反过来,如果两个图形的对应点连成的线段 都经过某一点,并且都被该点平分,那么这两 个图形一定关于这一点成中心对称.
应用拓展 :已知四边形ABCD和点O(下图),
画四边形A’B’C’D’,使它与已知四边形关
于点O对称. D
A
画法:1. 连结AO并延长到A’,使
OA’=OA,得到点A的对称点A’.
C B
.o
2. 同样画B、C、D的对称点 B’、C’、D’.
C’
B’
3. 顺次连结A’、B’、C’、D’ 各点.
A’
四边形A’B’C’D’就是所求的四边形.
F
B
B.
M
A
O
G
CA
C
E
D
D
小结: 今天你学到了什么 ?
1、回顾本节课的活动过程 。 观察——分析——探索 ——概括——应用 2、本节课学到了哪些知识? (1)中心对称图形与中心对称的定义 (2)中心对称的性质 (3)我们所学的多边形中有哪些是中心对称图形 (4)中心对称的应用
课后作业
自己设计一个中心对称图形,并画出它关于某点 成中心对称的图形。
学习目标
❖ 1、理解中心对称图形和中心对称的概念,知 道两者之间的辩证关系,并掌握它们的性质 和判定。
❖ 2、会画一个图形关于某一点的对称图形。
观察:下列图形,绕中心点旋转多少度能与自身
重合?它们的旋转角度有什么相同点?
在平面内,一个图形绕某个点旋转180o,能
与(自1)身这重些合,图那形么有这什个么图共形同叫做的中特心征对?称图
试一试:如果△ABC和△EDF关于点O成中
心对称,写出相等的线段和相等的角。
D E
F
灵活运用,体会内涵 1、点的中心对称点的作法
以点O为对称中心,作出点A的对称点A′;
AO
A′
点A′即为所求的点
2、线段的中心对称线段的作法
以点O为对称中心,作出线段AB的对称线段点A′B′
A
B′
O
B
A′
线段A′B′就是所求的线段
D’
巩固练习:如图23.2-5,选择点O为对称中心,画 出与△ABC关于点O对称的△A’B’C’.
能力提高 : 已知四边形ABCD,画四边形
A’B’C’D’,使它与已知四边形关于点A对
称。
D
C
A B
达标检测一
1、判断下列图形是否是中心对称图形?
达标检测二
2、画一个与已知四边形ABCD中心对称图形。 (1)以顶点A为对称中心; (2)以BC边的中点为对称中心。 N
