基于邻接矩阵的最短路径算法
应用邻接矩阵求有向图的最短路径

0 0 O 6
数 ,…,B k = ( b ( i , t . t 1 , 2 , 叫 √) ) = : 一 1 0A 其中
bk =l 商n l + 【 , , 6 2+ 2 ,,…
,
6 m 与%都不为零 ,t ≠J ,否则6 为o t k 为
b k 抽 + a U I
黑河学院学报
2 0 1 7 年第4 期 ( 2 0 1 7 年0 4 月)
J O U R N A L OF HE I H E U N I V E R S I T Y
N o. 4 201 7
d o i :1 0 . 3 9 6 9  ̄. i s s n . 1 6 7 4 — 9 4 9 9 . 2 0 1 7 . 0 4 . 1 0 4
关键词 :矩 阵运 算 ;邻接 矩阵; 有 向图
中 图分类号 :O1 5 1 . 2 1
文献标 志码 :A
文章编号 :1 6 7 4 — 9 4 9 9 ( 2 0 1 7 ) 0 4 — 0 2 1 7 — 0 2
地理选址 、交通 网络布控 、计算机数据结构等很多领域 算 法 定 义 6 = r r &a n + 口 2 + 口 2 ’ ’ ’a f n + a l , j, n + a l j 2 + Ⅱ 2 r . , a f + a l j n 个 项 中最 小 的 序数 为 t 1 ,… , 都能用到有 向图 。由于有 向图的可 以应用到很多领域 ,因 a
,
算法 一 :B 1 =b ( i , t 1 , ) _ A0 其 中
二 、应 用举 例
b I ( i , t 1 , ) = Ⅱ 血a 订 + a 1 f , a f 2 + a 2 , , …,a f n + a 1 f j ,
邻接矩阵求带权图中最短通路

第 4期
黄9 币 化: 邻接矩阵求带权 图中最短通路
・2 7・
最 短 通 路 时 进 行 回 溯 ,构 造 出 一 个 矩 阵 D = ( d i , ) …, 其中d , 表示顶 点 到 f 之 间最 短通 路
的 步长 。 A 的构造 过程 分为两 步 :
第一 步 : 初步计算 4 , A = A ・ +A =
( Ⅱ : ) , z = 2 , 3 , 4 , …, n一 1 。
邻 接矩 阵 求 两 个 不 同点 间最 短 通 路 的思 想
是: 在构造 A = ( 0 ) …, z=2 , 3 , 4, …, n一1的
收 稿 日期 :2 0 l 3— 0 5—2 9 作者简介 :黄师化 , 女, 安徽太湖人 , 安庆师范学院计算机 信息学院讲师 , 研究方 向: 智能计算。
两 点不 连通 , 可 以理 解距 离为 无穷大 。 最后 求得 的 矩 阵 D, 其 中元素 d , 代 表 的就是顶 点 与 之 问
最 短通 路 的步长 。
2 两点间最短通路及距离的求解算法
带权邻 接 矩阵求 两个 不 同点之 间距 离 的思 想 是: 在 两点 问步 长 为 1 , 2 , , 3 …, 凡一 l的通 路 中找
邻 接矩 阵求 带 权 图 中最 短通 路
黄 师 化
( 安庆师范学院 计算机与信息学院 , 安徽 安庆 2 4 6 1 3 3 )
摘
要 :通 过对带权邻接矩阵定义一种运算 , 计算 n阶简单带权 图中任意两点之间步长为 l , 2 , …, n—l的最短通路
长度, 逐 步比较 , 确定通路所过各边权值之和最小的即最短路径 。 在汁算 的过 程中用矩阵记 下最短路径 所经过 的所有 结 点, 最后验证 了其在无 向和有向简单带权 图中的有效性 。 关键词:带权邻接矩 阵; 带权图 ; 最短通路 ; 矩阵算法 中图分类号 :0 1 5 7 . 5 文献标识码 :A 文章编号 :1 0 0 7— 4 2 6 0 ( 2 0 1 3 ) 0 4— 0 0 2 6—0 3
floyd算法求解邻接矩阵的最短距离矩阵

文章编号:001主题:探讨floyd算法求解邻接矩阵的最短距离矩阵在计算机算法中,图论一直是一个重要的研究领域。
而其中,最短路径算法一直是图论中的热门话题之一。
在众多的最短路径算法中,floyd算法因其简洁高效的特点而备受青睐。
本文将深入探讨floyd算法在求解邻接矩阵的最短距离矩阵中的应用,并分析其实现原理及优缺点。
一、floyd算法简介Floyd算法是一种用于寻找加权图中顶点之间最短路径的动态规划算法。
它的基本思想是每次引入一个新的顶点,看看这个新顶点能不能对原来两个顶点之间的距离产生改变,如果可能,就进行更新。
通过多次迭代,最终得到所有顶点之间的最短路径。
二、floyd算法的实现步骤1. 初始化邻接矩阵在使用floyd算法求解最短路径时,首先需要初始化邻接矩阵。
邻接矩阵的每个元素代表图中两个顶点之间的距禋,如果两个顶点之间没有直接连接,则距离设为无穷大。
如果两个顶点直接相连,则距离设为两个顶点之间的权值。
2. 动态规划求解最短路径接下来,利用动态规划的思想,通过逐渐引入新的顶点,不断更新已有的最短路径。
具体做法是,对于每对顶点i和j,检查它们之间是否存在顶点k,使得从i到j的最短路径可以经过顶点k。
如果存在这样的顶点k,那么更新i到j的最短路径为i到k和k到j的距离之间的较小值。
3. 递推过程重复上述步骤,通过逐渐引入新的顶点k,直到遍历完所有顶点,就可以得到最终的最短距离矩阵。
三、floyd算法的优缺点1. 优点floyd算法可以求解任意两点之间的最短路径,且适用于有向图和无向图。
并且可以方便地求出最短路径的具体路径。
算法简单易懂,实现起来也比较容易。
2. 缺点floyd算法的时间复杂度较高,为O(n^3),当n较大时,计算量会非常庞大。
另外,在处理稀疏图时,可能会造成大量的计算浪费,因为floyd算法会对所有的顶点对进行遍历,而对于稀疏图来说,很多顶点对之间并不存在直接连接的边。
四、个人观点和理解在实际应用中,floyd算法通常适用于节点数量不是特别大,但边的数量非常大或者需要求解任意两点之间最短路径的情况。
邻接矩阵存储法和Floyd算法求解任意两个顶点的最短路径数据结构报告

数据结构上机报告(2) 姓名:张可心学号:14030188030 班级:1403018一、题目描述一个图的存储矩阵如下所示(顶点分别是0、1、2、3、4、5):0,12,18,∞,17,∞12, 0,10,3,∞,518,10,0,∞,21,11∞,3,∞,0,∞,817,∞,21,∞,0,16∞,5,11,8,16,0试用邻接矩阵存储法和Floyd算法求解任意两个顶点的最短路径。
输入:输入数据第一行为1个正整:顶点个数n(顶点将分别按0,1,…,n-1进行编号)。
后面有n+1行,前n行都有n个整数(第i行第j个数表示顶点i-1和顶点j-1之间的边长,用10000来表示两个顶点之间无边);第n+1行输入一对顶点x和y输出:x和y顶点的最短路径长度和最短路径(路径换行输出,只输出顶点编号序列)。
示例输入(1):60 12 18 10000 17 1000012 0 10 3 10000 518 10 0 10000 21 1110000 3 10000 0 10000 817 10000 21 10000 0 1610000 5 11 8 16 00 1示例输出(1):1201示例输入(2):60 12 18 10000 17 1000012 0 10 3 10000 518 10 0 10000 21 1110000 3 10000 0 10000 817 10000 21 10000 0 1610000 5 11 8 16 02 3示例输出(2):13213示例输入(3):60 12 18 10000 17 1000012 0 10 3 10000 518 10 0 10000 21 1110000 3 10000 0 10000 817 10000 21 10000 0 1610000 5 11 8 16 01 4示例输出(3):21154示例输入(in和out文件的内容):60 12 18 10000 17 1000012 0 10 3 10000 518 10 0 10000 21 1110000 3 10000 0 10000 817 10000 21 10000 0 1610000 5 11 8 16 03 4示例输出:24354二、解题思路先用邻接矩阵存储法构建矩阵输入,分别输入顶点数,路径长度矩阵,邻接矩阵,再通过Floyd算法求解任意两个顶点的最短路径,具体代码如下。
迪杰斯特拉算法计算最短路径

利用Dijkstra算法计算最短路径摘要福格环游地球问题是一个十分典型的最短路径求解问题,题设给出了当时世界上主要交通网络图及交通通畅的城市之间来往所需时长,并限定了福格的出行方向(福格选择的是往东走),给出起止地点后要求找出福格环游世界天数最短的最佳路径。
我们认为,这个问题的实质在于最短路径的求解和优化。
我们对比图论中的多种最短路径算法,决定利用Dijkstra算法解决这个问题。
由于Dijkstra算法要求输入图G的关联矩阵,且图G为二维赋权图,而题中给出的地图可看成是三维环状地图,因此,我们对题设地图做相关处理,将其从起点处“切断”并展开为二维图,然后根据此图建立关联矩阵。
同时,我们考虑到最短路径可能会与切断线有交点,在切断线以西找出若干地点一分为二,修改关联矩阵。
对于题目中缺失的两处数据,本文将以当时的交通数据为基础,经过合理的数据处理,结合Google Earth测距软件与题目数据的合理类比,补充缺失数据,完成关联矩阵。
得到关联矩阵后,我们分别以伦敦、纽约和上海作为起点,调整关联矩阵起点和终点,用matlab编程进行求解得到最短环游时间和最短路径,进而判断出所选择的路径是否能让他赢得赌注。
根据我们的求解结果,在这三个城市,福格均能在80天内环游地球,赢得赌注。
本文进一步对此种算法的优缺点、灵敏度与推广性进行了分析,同时初步提出了两种优化方法。
关键词:最短路径算法 dijkstra算法算法优化一、问题重述儒勒•凡尔纳的著名小说《环游世界80天》中,英国绅士福格在伦敦与人打赌能够在80天内环游世界,这在当时的1872年是一个了不起的壮举。
当时最快的旅行方式是火车和轮船,然而世界上大部分地区还是靠马车、大象、驴子或者步行来旅行。
下面是一个从伦敦环游世界不同路线的交通网络图,福格选择的是往东走,每段路线所需要的天数显示在图上(见附录一),旅行的时间基于1872年能采用的旅行方式以及距离。
我们将解决以下问题:1.我们将设计一个算法为福格选择一条最佳路径,即环游世界天数最短,并判断所选择的路径是否能让他赢得赌注。
Dijkstra算法(邻接矩阵存储)

Dijkstra算法(邻接矩阵存储)⾸先我们需要熟悉Dijkstra算法的原理:从某个源点到其余各顶点的最短路径,即单源点最短路径。
单源点最短路径是指:给定带权有向图G和源点v,求从v到G中其余各顶点的最短路径。
迪杰斯特拉(Dijkstra)提出了按路径长度递增的顺序产⽣各顶点的最短路径算法。
该算法的基本思想是:(1)设置两个顶点的集合S和T=V-S,集合S中存放已找到最短路径的顶点,集合T存放当前还未找到最短路径的顶点;(2)初始状态时,集合S中只包含源点v0;(3)从集合T中选取到某个顶点vi(要求vi到v0的路径长度最⼩)加⼊到S中;(4)S中每加⼊⼀个顶点vi,都要修改顶点v0到T中剩余顶点的最短路径长度值,它们的值为原来值与新值的较⼩者,新值是vi的最短路径长度加上vi到该顶点的路径长度;(5)不断重复(3)和(4),直到S包含全部顶点。
算法的代码实现很巧妙:1.⾸先函数⾥⾯运⽤数组D[n]表⽰源点到节点n的最短距离,s[n]表⽰某⼀节点n是否已经进⼊集合S,如果进⼊则将s[i]置为1.P[n]表⽰当前节点n的前驱节点(⽤来输出路径)。
2.在开始遍历之前,⾸先给数组D[n]赋值为源点到该点的距离,这样便能第⼀次找到源点到相邻节点的最短距离(D[i]=C[v1][i];)。
3.下⾯找出最短距离:if((!S[j])&&(D[j]<min)){min=D[j];k=j;}4.更新各节点的最短距离:for(j=0;j<n;j++){if((!S[j])&&(D[j]>D[k]+C[k][j]))//调整各节点(未进⼊集合S)的距离值{D[j]=D[k]+C[k][j]; //修改蓝点j+1的距离P[j]=k+1; //k+1是j+1的前趋}}4.代码实现:1 #include<stdio.h>2#define maxsize 1000 //表⽰两点间不可达,距离为⽆穷远3#define n 7 //结点的数⽬4void dijkstra(int C[][n],int v);//求原点v到其余顶点的最短路径及其长度5void main()6 {78//对邻接矩阵进⾏赋值,没有直接连通的赋值为maxsize9int C[n][n]=10 {11 {maxsize,13,8,maxsize,30,maxsize,32},12 {maxsize,maxsize,maxsize,maxsize,maxsize,9,7},13 {maxsize,maxsize,maxsize,5,maxsize,maxsize,maxsize},14 {maxsize,maxsize,maxsize,maxsize,6,maxsize,maxsize},15 {maxsize,maxsize,maxsize,maxsize,maxsize,2,maxsize},16 {maxsize,maxsize,maxsize,maxsize,maxsize,maxsize,17},17 {maxsize,maxsize,maxsize,maxsize,maxsize,maxsize,maxsize}18 },v=1,i,j;1920 dijkstra(C,v);//迪杰斯特拉算法2122 }23void dijkstra(int C[][n],int v)//求原点v到其余顶点的最短路径及其长度24 {252627int D[n];//⽤来存储从起点到某⼀节点的最短距离28int P[n],S[n];//p[n]表⽰某⼀节点的⽗亲,s[n]相当于标志数组29int i,j,k,v1,pre;30int min,max=maxsize,inf=1200;31 v1=v-1;//节点号和存储的数⽬差132333435for(i=0;i<n;i++)36 {37 D[i]=C[v1][i]; //置初始距离值38if(D[i]!=max) //说明存在边39 P[i]=v;//把⽗亲置为v40else41 P[i]=0;//否则⽗亲置为042 }43444546for(i=0;i<n;i++)47 S[i]=0; //如果某点i被访问则把该点值置为1,否则为048495051 S[v1]=1;//已经被访问置为152 D[v1]=0; //源点v送S53545556for(i=0;i<n-1;i++) //扩充红点集57 {585960 min=inf;//令inf>max,保证距离值为max的蓝点能扩充到S中 61for(j=0;j<n;j++)//在当前蓝点中选距离值最⼩的点k+162 {63if((!S[j])&&(D[j]<min))64 {65 min=D[j];//找从起点开始的最⼩权值66 k=j;67 }68 }697071 S[k]=1; //已经被访问,置为1727374for(j=0;j<n;j++)75 {76if((!S[j])&&(D[j]>D[k]+C[k][j]))//调整各蓝点的距离值77 {78 D[j]=D[k]+C[k][j]; //修改蓝点j+1的距离79 P[j]=k+1; //k+1是j+1的前趋80 }81 }828384 } //所有顶点均已扩充到S中858687for(i=0;i<n;i++)//输出结果和最短路径88 {89 printf("%d到%d的最短距离为",v,i+1);90 printf("%d\n",D[i]); //打印结果91 pre=P[i];92 printf("路径:%d",i+1);93while(pre!=0) //继续找前趋顶点94 {95 printf("<——%d",pre);96 pre=P[pre-1];97 }98 printf("\n");99 }100101102 }。
最短路径之dijkstra算法

} }
for(j=0; j<5; j++) path[i][j] = path[v][j];
path[i][i] = TRUE;
这整个相当于更改已知的顶点0到顶点i的最 短路径经过的顶点
更新后,现在的图如左边所示(因为在之前0→2的距 离为MAXVALUE,而今有0→1→2 = 60,所以在现在 已知的情况我们认为从0→2 的最短距离为60,即 distance[2] = 60;)
10
1
50
0 100
30
Hale Waihona Puke 41060
2
3
20
有了上面的准备后,我们就可以开始求顶点0到其它顶点的最短路径啦~
4、开始主循环
当然顶点0到顶点0的最短距离就不用求啦,直接found[0] = TRUE; 接着求顶点0到其它顶点的最短距离…
建临时的变量min与v,分别记录当前所知离顶点0的最近距离与所对应的顶点。 初始值设为MAXVALUE;
printf("目地点------最短路径------路径长度\n");
for(i=0; i<5; i++) {
count = 0; printf("%-12d", i); for(j=0; j<5; j++) {
if(path[i][j] == TRUE) {
printf("%d ",j); count += 2; } } for(j=0; j<14-count; j++) printf(" ");
int distance[5]; int path[5][5];
matlab floyd算法

matlab floyd算法
一、算法思想
Floyd算法是一种用于解决最短路径问题的算法,它可以找出任意两点之间的最短路径。
它由西班牙数学家Robert Floyd在1960年提出,是一种动态规划的应用,其可以求出任意两点之间的最短路径问题,由此可以证明,Floyd算法具备时间复杂度为O(n^3)的性质。
二、算法步骤
1、初始化:根据邻接矩阵表示图,初始化Floyd算法的距离矩阵。
2、迭代:使用Floyd算法的迭代式更新距离矩阵。
3、最短路径:最后获得的距离矩阵就是最短路径矩阵,可以求出任意两点之间的最短距离。
三、MATLAB实现
1、首先我们需要输入一个无向图的邻接矩阵,形如:
A=[0 1 inf 1;
1 0 1 inf;
inf 1 0 2;
1 inf
2 0];
2、利用matlab实现floyd算法,代码如下:
function dist = Floyd(A)
%A是图的邻接矩阵
n=size(A,1);
dist=A;
for i=1:n
for j=1:n
for k=1:n
if dist(j,k)>dist(j,i)+dist(i,k)
dist(j,k)=dist(j,i)+dist(i,k);
end
end
end
end
end
3、运行如下:
dist = Floyd(A)
dist =
0 1 3 1
1 0 1 2
3 1 0 2
1 2 2 0
即得到任意两点之间的最短路径,起点到终点最短路径长度为dist(i,j)。
实验7 基于Dijsktra算法的最短路径求解_数据结构习题解析与实验指导_[共2页]
![实验7 基于Dijsktra算法的最短路径求解_数据结构习题解析与实验指导_[共2页]](https://img.taocdn.com/s3/m/7eca77fae2bd960590c677f8.png)
实验 7
基于 Dijsktra 算法的最短路径求解
【实验目的】 1.掌握图的邻接矩阵表示法,掌握采用邻接矩阵表示法创建图的算法。 2.掌握求解最短路径的 Dijsktra 算法。 【实验内容】 问题描述 一张地图包括 n 个城市,假设城市间有 m 条路径(有向图),每条路径的长度已知。给定地 图的一个起点城市和终点城市,利用 Dijsktra 算法求出起点到终点之间的最短路径。 输入要求 多组数据,每组数据有 m+3 行。第一行为两个整数 n 和 m,分别代表城市个数 n 和路径条数 m。第二行有 n 个字符,代表每个城市的名字。第三行到第 m+2 行每行有两个字符 a 和 b 和一个 整数 d,代表从城市 a 到城市 b 有一条距离为 d 的路。最后一行为两个字符,代表待求最短路径 的城市起点和终点。当 n 和 m 都等于 0 时,输入结束。 输出要求 每组数据输出 2 行。第 1 行为一个整数,为从起点到终点之间最短路的长度。第 2 行为一串 字符串,代表该路径。每两个字符之间用空格隔开。 输入样例 33 ABC AB1 BC1 CA3 AC 68 ABCDEF A F 100 A E 30 A C 10 BC5 C D 50 D E 2
floyd算法求解邻接矩阵的最短距离矩阵

floyd算法求解邻接矩阵的最短距离矩阵摘要:1.Floyd 算法简介2.邻接矩阵的概念3.最短距离矩阵的计算方法4.Floyd 算法的应用实例5.总结正文:【1.Floyd 算法简介】Floyd 算法是一种用于寻找加权图中所有顶点之间最短路径的算法,由Robert C.Floyd 于1968 年提出。
该算法主要应用于计算邻接矩阵的最短距离矩阵,适用于存在负权边的图,但不适用于存在负权环的图。
【2.邻接矩阵的概念】邻接矩阵是一种用于表示有向图或无向图中顶点之间关系的矩阵。
设图G 有n 个顶点,用A 表示邻接矩阵,则A 是一个n×n 的矩阵,其中A[i][j] 表示顶点i 到顶点j 的边的权值。
如果顶点i 到顶点j 没有边相连,则A[i][j] 为无穷大或一个很大的数。
【3.最短距离矩阵的计算方法】最短距离矩阵是用于表示图中所有顶点之间最短路径长度的矩阵。
设D 为最短距离矩阵,则D[i][j] 表示顶点i 到顶点j 的最短路径长度。
通过Floyd 算法,可以计算出邻接矩阵A 的最短距离矩阵D,计算方法如下:1.初始化D 为单位矩阵,即D[i][j]=1(i≠j);2.遍历所有顶点k,对于每条边(i, k) 和(k, j),更新D[i][j] =min(D[i][j], D[i][k] + D[k][j]);3.当遍历完所有顶点后,D[i][j] 即为顶点i 到顶点j 的最短路径长度。
【4.Floyd 算法的应用实例】假设有一个无向图,共有4 个顶点A、B、C、D,边的权值如下:- A 到B 的权值为1;- A 到C 的权值为4;- B 到C 的权值为2;- B 到D 的权值为5;- C 到D 的权值为1。
通过Floyd 算法计算最短距离矩阵,结果如下:- D[A][B] = 1;- D[A][C] = 5;- D[A][D] = 6;- D[B][C] = 3;- D[B][D] = 6;- D[C][D] = 2。
以邻接表和邻接矩阵做存储结构求最短路径

}//endif
p=p->next;//找vi的下一邻接点
}//endwhile
}//endwhile
}//end of shortestpath
dist[p->adjvex]++;
pre[p->adjvex]=i;
visited[P->adjvex]=TRUE;
EnQueue(&Q,p->adjvex);//访问过的vk人队
}//endif
答:
(1)求顶点vi到顶点vj(i<>j)的最短路径
int shortestpath(ALGraph*G,int i,int j)
{// 对邻接表表示的图G,求顶点vi到顶点vj(i<>j)的最短路径
int dist[MaxVertexNum];
}
}//endwhile
}//BFSM
(2)求源点vi到其余各顶点的最短路径
void shortestpath(ALGraph*G,int i)
{// 对邻接表表示的图G,求顶点vi到顶点vj(i<>j)的最短路径
int dist[MaxVertexNum];
int BFSM(MGraph *G,int i,int j)
{// 对邻接链表表示的图G,求顶点vi到顶点vj(i<>j)的最短路径
i Q;
initQueue(&Q);
floyd算法求解邻接矩阵的最短距离矩阵

floyd算法求解邻接矩阵的最短距离矩阵Floyd算法用于求解任意两个顶点之间的最短路径。
给定一个有向图的邻接矩阵,算法通过不断迭代更新矩阵中的元素来计算最短距离矩阵。
首先,初始化最短距离矩阵为邻接矩阵本身。
然后,通过对每一个中间顶点进行遍历,如果存在一条路径经过中间顶点使得路径长度更短,则更新最短距离矩阵中的相应元素。
以下是Floyd算法的Python实现:```pythondef floyd(adj_matrix):num_vertices = len(adj_matrix)dist_matrix = adj_matrix.copy()for k in range(num_vertices):for i in range(num_vertices):for j in range(num_vertices):if dist_matrix[i][j] > dist_matrix[i][k] + dist_matrix[k][j]: dist_matrix[i][j] = dist_matrix[i][k] + dist_matrix[k][j] return dist_matrix```其中,adj_matrix是一个包含顶点间距离的邻接矩阵,dist_matrix是一个用于存储最短距离的矩阵。
示例:假设有一个有向图G,顶点集合为{A, B, C, D},邻接矩阵为:```A B C DA 0 3 ∞ 7B ∞ 0 2 ∞C 5 ∞ 0 1D ∞ ∞ ∞ 0```运行floyd(G)将得到最短距离矩阵:```A B C DA 0 3 5 6B ∞ 0 2 3C 5 8 0 1D ∞ ∞ ∞ 0```最终得到的dist_matrix中,dist_matrix[i][j]表示从顶点i到顶点j的最短距离。
如果顶点i和顶点j之间不存在路径,则对应元素为无穷大。
基于邻接矩阵的最短路径算法

基于邻接矩阵的最短路径算法
周石林;尹建平;冯豫华
【期刊名称】《软件导刊》
【年(卷),期】2010(009)009
【摘要】以邻接矩阵为出发点,并根据邻接矩阵运算得到的可达矩阵判断是否存在从源点到目标点通路,然后从可达矩阵出发进行最短路径的搜索,这样的好处是减少了无效的搜索,从而减少了搜索时间;同时,以深度搜索优先首先找到一条通路,采用每次新加边长为可加边长中最短的原则,采用了新的定界手段,使用这些手段可以删除更多的活节点,从而减少算法计算量.结合这几个要点提出了一种新的最短路径算法.【总页数】2页(P68-69)
【作者】周石林;尹建平;冯豫华
【作者单位】南昌大学,信息工程学院,江西,南昌,330031;南昌大学,信息工程学院,江西,南昌,330031;南昌大学,信息工程学院,江西,南昌,330031
【正文语种】中文
【中图分类】TP312
【相关文献】
1.基于邻接矩阵的最短路径算法 [J], 周石林;尹建平;冯豫华
2.基于邻接矩阵的网络拓扑自动生成方法 [J], 王健;宋春咏;李佳雨;高国涛
3.基于有向邻接矩阵的配电网拓扑检测与识别 [J], 许栋梁;赵健;王小宇;茅东华;裘瑾怡
4.基于邻接矩阵的低压配电网故障区段定位方法 [J], 姚永峰;王启哲;王慧萍;贾佳;
夏西宾
5.一种基于汉明矩阵和连杆邻接矩阵的运动链同构识别方法 [J], 吴昌军;许辉;邓涛;张露;华叙彬
因版权原因,仅展示原文概要,查看原文内容请购买。
实验9 无向网的邻接矩阵存储与最短路径的实现

实验9 无向网的邻接矩阵存储与最短路径的实现(1)完成对邻接矩阵的如下操作:1. 创建图2.判断2个顶点是不是相邻3.计算1个顶点的度4.显示矩阵*5.用input文件创建图*6.利用迪杰斯特拉算法求单源最短路径0.退出(2)预编译命令与类型定义#define INFINITY 1000 //充当无穷大值#define MAX_VERTEX_NUM 20Typedef int Status;typedef int VRType;typedef char VertexType;typedef enum {DG,DN,UDG,UDN} GraphKind;typedef struct ArcCell{VRType adj;char *info;} ArcCell,AdjMatrix[MAX_VERTEX_NUM][MAX_VERTEX_NUM];typedef struct {VertexType vexs[MAX_VERTEX_NUM];AdjMatrix arcs;int vexnum, arcnum;GraphKind kind;}MGraph;(3)通过读文件的方法构造无向网的函数,文件input.txt存放无向网的顶点和边的信息,Status InputCreateUDN(MGraph &G){int i,j,k,IncInfo;VertexType v1,v2;VRType w;FILE * fp;fp=fopen("input.txt","rb");fscanf(fp,"%d %d",&G.vexnum,&G.arcnum);fseek(fp,5L,0);for(i=0;i<G.vexnum;++i)fscanf(fp,"%c",&G.vexs[i]);fseek(fp,2*sizeof(char),1);for(i = 0;i < G.vexnum;++i)for(j = 0;j < G.vexnum;++j){G.arcs[i][j].adj= INFINITY;G.arcs[i][j].info= NULL;}for(k = 0;k < G.arcnum;++k){fscanf(fp,"%c %c %d %d",&v1,&v2,&w,&IncInfo);fseek(fp,2*sizeof(char),1);i=LocateVex(G,v1);j=LocateVex(G,v2);G.arcs[i][j].adj=w;if(IncInfo)scanf("%s",G.arcs[i][j].info);G.arcs[j][i] = G.arcs[i][j];}return OK;}6、拓扑排序算法的C语言实现#include "stdio.h"#define MAX_VERTEX_NUM 20#include "conio.h"#include "stdlib.h"#define STACK_INIT_SIZE 16#define STACKINCREMENT 5typedef int SElemType;typedef char VertexType;typedef struct{SElemType *base;SElemType *top;int stacksize;}SqStack;//我们依然用邻接表来作图的存储结构typedef struct ArcNode{int adjvex;struct ArcNode *nextarc;int info;}ArcNode; //表结点类型typedef struct VNode{VertexType data;int count;ArcNode *firstarc;}VNode,AdjList[MAX_VERTEX_NUM]; //头结点typedef struct{AdjList vertices; //邻接表int vexnum,arcnum;}ALGraph;int InitStack(SqStack &S){S.base=(SElemType*)malloc(STACK_INIT_SIZE*sizeof(SElemType));if(!S.base) exit(-1);S.top=S.base;S.stacksize=STACK_INIT_SIZE;return 1;}//InitStackint Push(SqStack &S,SElemType e){if((S.top-S.base)>=S.stacksize){S.base=(SElemType*)realloc(S.base,(S.stacksize+STACKINCREMENT)*sizeof(SElemType)); if(!S.base) exit(-1);S.top=S.base+S.stacksize;S.stacksize+=STACKINCREMENT;}//if*(S.top)=e;S.top++;return 1;}//Pushint Pop(SqStack &S,SElemType &e){if(S.top==S.base) return 0;--S.top;e=*S.top;return 1;}//Popint StackEmpty(SqStack &S){if(S.top==S.base) return 1;else return 0;}//StackEmptyint LocateVex(ALGraph G,char u){int i;for (i=0;i<G.vexnum;i++){ if(u==G.vertices[i].data) return i; }if (i==G.vexnum) {printf("Error u!\n");exit(1);}return 0;}void CreateALGraph_adjlist(ALGraph &G){int i,j,k,w;char v1,v2,enter;ArcNode *p;printf("Input vexnum & arcnum:\n");scanf("%d",&G.vexnum);scanf("%d",&G.arcnum);printf("Input Vertices(以回车隔开各个数据):\n");for (i=0;i<G.vexnum;i++){ scanf("%c%c",&enter,&G.vertices[i].data);//注意点,解说G.vertices[i].firstarc=NULL;}//forprintf("Input Arcs(v1,v2,w)以回车分开各个数据:\n");for (k=0;k<G.arcnum;k++){scanf("%c%c",&enter,&v1);scanf("%c%c",&enter,&v2);//scanf("%d",&w);i=LocateVex(G,v1);j=LocateVex(G,v2);p=(ArcNode*)malloc(sizeof(ArcNode));p->adjvex=j;//p->info = w;p->nextarc=G.vertices[i].firstarc; //前插法,即每次都插入到头结点的后面G.vertices[i].firstarc=p;printf("Next\n");}//forreturn;}//CreateALGraph_adjlistvoid FindInDegree(ALGraph &G){int i,j;for(i=0;i<G.vexnum;i++){G.vertices[i].count=0;}//forfor(j=0;j<G.vexnum;j++){//G.vertices[i].count++;for(ArcNode *p=G.vertices[j].firstarc;p;p=p->nextarc)G.vertices[p->adjvex].count++;}//for}//FindInDegreeint TopoSort(ALGraph &G){SqStack S;FindInDegree(G);InitStack(S);for(int i=0;i<G.vexnum;i++)if(G.vertices[i].count==0) Push(S,i);int countt=0;while(!StackEmpty(S)){int i,m;m=Pop(S,i);printf(" %c",G.vertices[i].data); ++countt;for(ArcNode *p=G.vertices[i].firstarc;p;p=p->nextarc){ int k;k=p->adjvex;if(!(--G.vertices[k].count)) Push(S,k);}//for}//whileif(countt<G.vexnum) return 0;else return 1;}//TopoSortint main(){ALGraph G;CreateALGraph_adjlist(G);TopoSort(G);return 1;}。
邻接矩阵求最短路径c语言

邻接矩阵求最短路径c语言
邻接矩阵是图论中的一个重要概念,它用于表示一个图的结构。
在计算机科学中,邻接矩阵经常用于表示有向图和无向图。
而求最短路径是图论中的一个基本问题,也是很多实际问题的核心。
在c语言中,可以通过邻接矩阵来求解最短路径问题。
具体步骤如下:
1. 首先,需要定义一个邻接矩阵,该矩阵应该包含所有节点之
间的距离信息。
如果两个节点之间没有边相连,则距离为无穷大。
2. 接下来,可以使用Floyd算法来计算最短路径。
Floyd算法
是一种动态规划算法,可以通过多次迭代来逐步缩小两个节点之间的距离。
3. 最后,可以输出最短路径矩阵,该矩阵包含了所有节点之间
的最短路径信息。
通过以上步骤,就可以在c语言中求解邻接矩阵的最短路径问题。
- 1 -。
邻接矩阵求最短距离
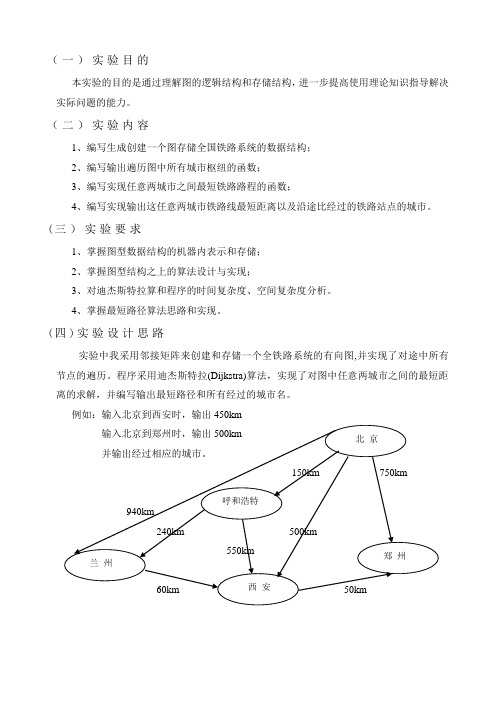
(一)实验目的本实验的目的是通过理解图的逻辑结构和存储结构,进一步提高使用理论知识指导解决实际问题的能力。
(二)实验内容1、编写生成创建一个图存储全国铁路系统的数据结构;2、编写输出遍历图中所有城市枢纽的函数;3、编写实现任意两城市之间最短铁路路程的函数;4、编写实现输出这任意两城市铁路线最短距离以及沿途比经过的铁路站点的城市。
(三)实验要求1、掌握图型数据结构的机器内表示和存储;2、掌握图型结构之上的算法设计与实现;3、对迪杰斯特拉算和程序的时间复杂度、空间复杂度分析。
4、掌握最短路径算法思路和实现。
(四)实验设计思路实验中我采用邻接矩阵来创建和存储一个全铁路系统的有向图,并实现了对途中所有节点的遍历。
程序采用迪杰斯特拉(Dijkstra)算法,实现了对图中任意两城市之间的最短距离的求解,并编写输出最短路径和所有经过的城市名。
例如:输入北京到西安时,输出450km(四)程序清单#i n c l u d e<s t d i o.h>#i n c l u d e<s t d l i b.h>#i n c l u d e<s t r i n g.h>#d e f i n e I N F I N I T Y10000#d e f i n e m a x100#d e f i n e l e n20#d e f i n e N U L L0s t r u c t v e r t e x{i n t n u m;c h a rd a t a[le n];};s t r u c t g r a p h{i n t n,e;v e r t e x v e x s[m a x];i n t e d g e s[m a x][m a x];};v o i d c r e a t e g r a p h(g r a p h*g r a){i n t i,j,k,w;c h a r b[l e n],t[l e n];p r i n t f("请输入全国铁路枢纽城市个数:\n");s c a n f("%d",&g r a->n);p r i n t f("请输入全部枢纽城市之间的干线数:\n");s c a n f("%d",&g r a->e);f o r(i=0;i<g r a->n;i++){p r i n t f("请输入第%d个城市名称:\n",i+1);s c a n f("%s",g r a->v e x s[i].d a t a);g r a->v e x s[i].n u m=i;}f o r(i=0;i<g r a->n;i++)f o r(j=0;j<g r a->n;j++)g r a->e d g e s[i][j]=I N F I N I T Y;f o r(k=0;k<g r a->e;k++){p r i n t f("输入第%d条铁路干线的信息:\n",k+1);p r i n t f("起点站序号:\n");s c a n f("%s",b);p r i n t f("终点站序号:\n");s c a n f("%s",t);p r i n t f("起始站和终点站干线长度:");s c a n f("%d",&w);i=0;w h i l e(i<g r a->n&&s t r c m p(g r a->v e x s[i].d a t a,b)!=N U L L) i++;i f(i>=g r a->n){p r i n t f("输入起点的城市不正确!\n");e x i t(1);}j=0;w h i l e(j<g r a->n&&s t r c m p(g r a->v e x s[j].d a t a,t)!=N U L L) j++;i f(i>=g r a->n){p r i n t f("输入终点的城市不正确!\n");e x i t(2);}g r a->e d g e s[i][j]=w;}}v o i d d i s p l a y(g r a p h*g r a){i n t i,j,f l a g=0;d o u b le s u m=0;i f(!g r a->v e x s[0].d a t a)p r i n t f("没有铁路城市信息!请先创建铁路信息.\n");e l s e{p r i n t f("全国铁路枢纽城市的信息如下:\n");f o r(i=0;i<g r a->n;i++){f o r(j=0;j<g r a->n;j++)s u m+=g r a->e d g e s[i][j];i f(((i n t)s u m/g r a->n)>=I N F I N I T Y)f l a g=1;p r i n t f("城市名称\t序号\n");p r i n t f("%s\t\t%d\n",g r a->v e x s[i].d a t a,i);i f(f l a g)p r i n t f("\t该城市不可达其他城市.\n");e l s e{p r i n t f("\t\t可达以下城市:\n");p r i n t f("\t城市名称\t\t序号\t\t铁路线距离\n");f o r(j=0;j<g r a->n;j++){i f(g r a->e d g e s[i][j]<I N F I N I T Y)p r i n t f("\t%s\t\t\t%d\t\t\t%l d(K m)\n",g r a->v e x s[j].d a t a,g r a->v e x s[j].n u m,g r a->e d g e s[i][j]);}}f l a g=0;s u m=0;p r i n t f("\n");}}}v o i d s h o r t P a t h(g r a p h*g r a,i n t v0,i n t p[][m a x],i n t d[m a x]) {i n t v,w,i,j,m i n;i n t f i n a l[m a x];f o r(v=0;v<g r a->n;v++){f i n a l[v]=0;d[v]=g r a->e d g e s[v0][v];f o r(w=0;w<m a x;w++)p[v][w]=-1;i f(d[v]<I N F I N I T Y){p[v][0]=v0;p[v][1]=v;}}d[v0]=0;f i n a l[v0]=1;f o r(i=1;i<g r a->n;i++){m i n=I N F I N I T Y;f o r(w=0;w<g r a->n;w++){i f(!f i n a l[w]){i f(d[w]<m i n){v=w;m i n=d[w];}}}f i n a l[v]=1;f o r(w=0;w<g r a->n;w++){i f(!f i n a l[w]&&(m i n+g r a->e d g e s[v][w]<d[w])){d[w]=m i n+g r a->e d g e s[v][w];f o r(j=0;p[v][j]>-1&&j<g r a->n;j++){p[w][j]=p[v][j];}p[w][j]=w;}}}}v o i d f i n d p a t h(g r a p h*g r a){i n t i,j,v0,v e n d,f l a g1=0,f l a g2=0;i n t d[m a x],p[m a x][m a x];c h a r s c i t y[l e n],e c i t y[l e n];p r i n t f("输入铁路起始站城市名称:\n");s c a n f("%s",s c i t y);p r i n t f("输入铁路终止站城市名称:\n");s c a n f("%s",e c i t y);f o r(i=0;i<g r a->n;i++){i f(s t r c m p(g r a->v e x s[i].d a t a,s c i t y)==N U L L){v0=g r a->v e x s[i].n u m;f l a g1=1;}i f(s t r c m p(g r a->v e x s[i].d a t a,e c i t y)==N U L L){v e n d=g r a->v e x s[i].n u m;f l a g2=1;}}i f(f l a g1==N U L L){p r i n t f("输入的起始站错误!");e x i t(1);}i f(f l a g2==N U L L){p r i n t f("输入的终止站错误!");e x i t(2);}e l s e{s h o r t P a t h(g r a,v0,p,d);f o r(i=0;i<g r a->n;i++){i f(i==v e n d){i f(d[i]>=I N F I N I T Y)p r i n t f("从%s到%s不可达!\n",g r a->v e x s[v0].d a t a,g r a->v e x s[v e n d].d a t a);e l s e{p r i n t f("从%s城市出发到%s城市最短路径经过的城市为:\n",g r a->v e x s[v0].d a t a,g r a->v e x s[v e n d].d a t a);i f(p[i][v0]>-1){f o r(j=0;p[i][j]!=-1;j++){i f(j!=0)p r i n t f("->");p r i n t f("%5s",g r a->v e x s[p[i][j]].d a t a);}p r i n t f("\n");}p r i n t f("最短路径长为:%l d(k m)\n",d[i]);p r i n t f("\n");}}}}}i n t m a i n(){g r a p h g r a;c h a r c h;d o{p r i n t f("┌———————————————————─┐\n");p r i n t f("│┈┈☆☆欢迎使用铁路查询系统☆☆┈┈│\n");p r i n t f("│请选择下面操作│\n");p r i n t f("│ 1.创建铁路系统2.查看全部铁路信息│\n");p r i n t f("│ 3.任意两城市铁路信息查询4.退出铁路系统│\n");p r i n t f("└——————————————————─┘\n\t");s c a n f("%c",&c h);s w i t c h(c h){c a s e'1':c r e a t e g r a p h(&g r a);g e t c h a r();b r e a k;c a s e'2':d i s p l a y(&g r a);ge t c h a r();b r e a k;c a s e'3':f i n d p a t h(&g r a);g e t ch a r();b r e a k;c a s e'4':p r i n t f("┈┈┈☆☆欢迎下次使用铁路信息系统☆☆┈┈┈┈┈\n");b r e a k;}}w h i l e(c h!='4');r e t u r n0;}(五)实验结果1创建铁路系统:2.查询全部铁路信息:3.任意两城市信息查询:(六)实验思考实验采用邻接表存储有向图,怎么具体实现迪杰斯特拉算法?先定义一个数组对每个顶点到其余城市可达距离,其余和邻接矩阵迪杰斯特拉算法相同。
