离散数学(软件)课程第16章
离散数学(第16讲)

1 2 3 4 1 2 3 4 2 4 1 3 (1 2 4 3), 3 2 4 1 ( 3 4 1), (1 2 4 3)(3 4 1) ( 2 4)
2018/11/12 计算机学院 15
例6.3
设
1 2 3 4 5 6 1 2 3 4 5 6 1 1 3 6 5 4 2 , 2 2 1 3 5 6 4
2018/11/12
f2={<a,1>,<b,2>}; f4={<a,2>,<b,2>}。
计算机学院 6
常将从A到B的一切函数构成的集合记为BA:BA={f|f:A→B}
函数相等
定义6.2 f=g。 设 f和g :X→Y是两个函数,如果对
xX ,都有f(x)=g(x), 则称f与g相等,记为
2018/11/12
2018/11/12 计算机学院 14
循环的积
一个置换可能由一个单一的循环表示出来, 也可能由多个循环连接在一起表示,称之为循 环的积(置换的复合)。 当两个循环没有公共元素时,它们的积仍是 原来的两个循环;当两个循环有公共元素时, 它们的积按照复合的意义变成了新的循环的积。 例如
1 2 3 4 5 6 0 3 1 6 4 2 5 (1 3 6 5 2)
2018/11/12 计算机学院 3ຫໍສະໝຸດ §6.1 一般集合的函数概念
定义6.1 设f是集合A到B的关系,如果对每个x∈A,都 存在惟一的y∈B,使得<x,y>∈f,则称关系f为A到B 的函数(或映射、变换),记为f:A→B。当 <x,y>∈f时,通常记为y=f(x),这时称x为函数的自 变量,称y为x在f下的函数值(或映像)。 由函数的定义显然有: 1) domf=A,称为函数f的定义域; 2) ranf=B,称为函数f的值域,并称f(A)为A在f下的像; 3) <x,y>∈f∧<x,z>∈f y=z; 4) |f|=|A|。
离散数学sec16-17 群

模 6 加群 <Z6, >中 由 2 生成的子群 <2> = { 0, 2, 4 }
21
特殊子群2
例 设G为群,令C是与G中所有的可交换的元素构 成的集合,即 C={a|a∈G∧x∈G(ax=xa)} 则C是G的子群,称为G的中心。
限群。 群G的基数称为群G的阶,有限群G的阶记作|G|。
(2)只含单位元的群称为平凡群。
(3)若群G中的二元运算是可交换的,则称G为交 换群或阿贝尔(Abel)群。
11
群论中常用的概念-元素的n次幂
定义 设G是群,a∈G,n∈Z,则a的n次幂 P250 定义17.4
e a n a n1a
(a 1 )n
换 σ∈Sn,逆置换σ1是σ 的逆元. 这就证明了Sn关于置换的乘法构成一个群,称为 n
元对称群. n元对称群的子群称为 n元置换群.
31
例 设 S = {1, 2, 3},3元对称群
S3的对称群是? 运算表? S3的子群?
32
n元置换的分解式
• k阶轮换与轮换分解方法 定义11.11 P258
定义 设<G,>是代数系统,为二元运算。如果运 算是可结合的,存在单位元e∈G,并且对G中 的任何元素x都有x-1∈G,则称G为群(group)。 (P249定义17.1)
例 <Z,+>,<Q,+>,<R,+>,<Z+,+>,<N,+>是不是群?
<Zn,>是群?
8
14.4+16离散数学

13
有向图关联矩阵的性质: 有向图关联矩阵的性质:
14
有向图关联矩阵的性质: 有向图关联矩阵的性质:
(1)∑ m ij = 0( j = 1,2,⋯, m ) ,从而 ∑ ∑ m ij = 0 ,这说明 j=1 i =1 i =1 有向图关联矩阵中所有元素之和为0。
n
m
n
0 0 0 − 1 1 1 −1 1 0 0 0 0 0 1 1 0 0 − 1 − 1 − 1
(1 ) i = 1 j= 1
n
n
长度为1的通路的总数。 长度为1的通路的总数。 而 中环的个数, 中长度为1的回路总数。 ∑ a ii 为D中环的个数,即D中长度为1的回路总数。
(1 ) i =1 n
24
问下图中有多少条长度为2、3、4…. 的通路?
25
0 0 0 ' A = 0 0 0 0
0 0 0 0
2 1 0 0 1 0 0 0 1 0 1 1
∑a
j= 1
n
(1 ) ij
,于是 n n a (1) = n d + ( v ) = m = d ( v i )(i = 1,2,⋯, n ) ∑ ∑ ij ∑ i
+
i =1 j=1 i =1
∑a
i =1
4
强连通图和单向连通图的判别定理 定理14 14. 定理14.8 有向图D是强连通图当且仅当D中 存在经过每个顶点至少一次的回路。 定理14.9 有向图D是单向连通图当且仅当D 定理14.9 中存在经过每个顶点至少一次的通路。
5
例
(1)
(2)
(3)
(1)是强连通图 (2)是单向连通图 (3)是弱连通图
离散数学 图论-树

中序遍历(次序:左-根-右) 前序遍历(次序:根-左-右) 后序遍历(次序:左-右-根) b 中序遍历: c b e d g f a I k h j 前序遍历: a b c d e f g h i k j 后序遍历: c e g f d b k i j h a
例:给定二叉树,写出三种访问 结点的序列
是否为根树
(a) (no)
(b) (no)
(c) (yes)
从树根到T的任意顶点v的通 路(路径)长度称为v的层数。 v5的层数为 层。
层数最大顶点的层数称为树 高.将平凡树也称为根树。 右图中树高为( )。
v1
v2 v3
v4 v8v5Fra bibliotekv6v7 v10
v9
在根树中,由于各有向边的方向是一 致的,所以画根树时可以省去各边上的所 有箭头,并将树根画在最上方.
等长码:0-000;1-001;2-010;3-011;4-100; 5-101;6-110;7-111. 总权值: W2=3*100=300
4、二叉树的周游(遍历)
二叉树的周游:对于一棵二叉树的每一个结点都访问一次且 仅一次的操作 1)做一条绕行整个二叉树的行走路线(不能穿过树枝) 2)按行走路线经过结点的位臵(左边、下边、右边) 得到周游的方法有三种: 中序遍历(路线经过结点下边时访问结点) 访问的次序:左子树-根-右子树 前序遍历(路线经过结点左边时访问结点) 访问的次序:根-左子树-右子树 后序遍历(路线经过结点右边时访问结点) 访问的次序:左子树-右子树-根
2、根树中顶点的关系
定义:设T为一棵非平凡的根树, v2 ∀vi,vj∈V(T),若vi可达vj,则称vi为 vj的祖先,vj为vi的后代; v4 v5 若vi邻接到vj(即<vi,vj>∈E(T),称 vi为vj的父亲,而vj为vi的儿子 v8 若vj,vk的父亲相同,则称vj与vk是兄 弟
离散数学(第16-17章)陈瑜

定理16.1(移项法则)设<R,+, *>是一个环, θ是加法幺元,对任意a,b,c R有: a+b=c a+b-c=θ
2019/1/16
计算机学院
9/128
定理16.2设<R,+, *>是一个环,θ是加法幺 元,对任意a,b,c R有: ① a*θ=θ*a=θ(加法幺元是乘法零元) ② (-a)*b=a*(-b)=-(a*b) ③ (-a) *(-b)=a*b ④ (b-c) *a=b*a-c*a ⑤ a* (b-c)=a*b-a*c
2019/1/16 计算机学院 7/128
例 16.2 设 Zk 表示整数集 Z 上的模 k 剩余类集 合,即: Zk={[0],[1],[2],…,[k-1]} <Zk ,>是群(剩余类加群), <Zk ,>是半群(剩余类乘半群), ∵ 对 [i],[j],[k] Zk 有[i]([j][k])=[i(j+k)]=[ij+ik] =[ij][ik] =([i][j])([i][k]) ∴ <Zk ,,>是环,称为(模k)剩余类环。 特别, k=2时,称为布尔环。
2019/1/16 计算机学院 6/128
例 16.2 设 Zk 表示整数集 Z 上的模 k 剩余类集 合,即: Zk={[0],[1],[2],…,[k-1]} <Zk ,>是群(剩余类加群), <Zk ,>是半群(剩余类乘半群), ∵ 对 [i],[j],[k] Zk 有[i]([j][k])=[i(j+k)]=[ij+ik] =[ij][ik] =([i][j])([i][k]) ∴ <Zk ,,>是环,称为(模k)剩余类环。 特别, k=2时,称为布尔环。
离散数学课件16.1-2无向树和生成树

生成树
❖ 设G=<V,E>是无向连通图,T是G的 生成子图,并且T是树,则称T是G的生 成树.
❖ G在T中的边称为T的树枝, ❖ G不在T中的边称为T的弦. ❖ T的所有弦的集合的导出子图称为T
的余树.
(2)为(1)的一棵生成树T,(3)为T 的余树,注意余树不一定是树.
定理 任何连通图G至少存在一棵生成 树.
推论1 设n阶无向连通图G有m条边,则 m≥n-1.
推论2 设n阶无向连通图G有m条边,T 是G的生成树,T'是T的余树,则T'中有 m-n+1条边.
图
基本回路
在图中,实边所示的子图是图G的一 棵生成树T,d,e,f为T的树枝,a,b,c 为T的弦.在T上加弦a,产生G的一 个初级回路aed.在T上加弦b,产生 G的一个初级回路bdf.在T上加弦 c,产生G的一个初级回路cef.这3 个回路中每一个回路都只含一条 弦,其余的边都是树枝,这样的回 路称为基本回路.
定义 设T是n阶连通图G=<V,E>的 一棵生成树,称T的n-1个树枝对应的 G的n-1个割集(每个割集只含一个 树枝,其余的边都是弦)S1,S2,···,Sn-1 为对应生成树T的G的基本割集,称 {S1,S2,···,Sn-1}为对应生成树T的基 本割集系统.
对一个n阶连通图G来说,对应 不同的生成树的基本割集可能 不一样,但基本割集的个数必为 n-1个,这也是G的固有特性.
T有5个树枝a,b,c,d,e,因而有5个基本割 集: Sa={a,g,f}; Sb={b,g,h}; Sc={c,f,h}; Sd={d,i,h}; Se={e,f,i};
《离散数学》课件-第16章树

18
16.3 根树及其应用
19
定义(有向树)设D是有向图,如果D的基图是无向 树,则称D为有向树。
在有向树中最重要的是根树。 定义16.6(根树)一棵非平凡的有向树,如果恰有 一个顶点的入度为O,其余所有顶点的入度均为1,则称该 树为根树。 入度为0的顶点称为树根,入度为1出度为0的顶点称 为树叶,入度为1出度不为0的点称为内点,内点和树根统 称为分支点。 树根到一个顶点的有向通路的长度称为该顶点的层数。 层数最大顶点的层数称为树高。 平凡树也称为根树。
2
16.1 树及其性质
3
定义16.1(树和森林) 连通且无回路的无向图称为无向树,简称为树,常用
T表示树。 平凡图为树,称为平凡树。 非连通且每个连通分支是树的无向图称为森林。 T中度数为1的顶点(悬挂顶点)称为树叶,度数大于
1的顶点称为分支点。 称只有一个分支点,且分支点的度数为n-1的n(n≥3)
定义16.8(子树)设T为一棵根树,则其任一顶点v 及其后代导若将层数相同的顶点都 标定次序,则称T为有序树。
根据每个分支点的儿子数以及是否有序,可将根树 分成如下若干类:
定义(跟树分类)设T为一棵根树 (1)若T的每个分支点至多有r个儿子,则称T为r叉 树。又若r叉树是有序的,则称它为r叉有序树。 (2)若T的每个分支点恰好有r个儿子,则称T为r叉 正则树。又若r叉正则树是有序的,则称它为r叉正则有 序树。 (3)若T为r叉正则树,且每个树叶的层数均为树高, 则称T为r叉完全正则树。又若r叉完全正则树是有序的, 则称它为r叉完全正则有序树。
8
平均编码长度为:L = ∑ P( i )× l( i ) = 2.53bit i=1
离散数学——树ppt课件

无向树的性质
定理16.2 设T是n阶非平凡的无向树,则T中至少有两片树叶。
证明
设T有x片树叶,由握手定理及定理16.1可知,
2(n 1) d(vi ) x 2(n x)
由上式解出x≥2。
12
例16.1
例16.1 画出6阶所有非同构的无向树。
解答 设Ti是6阶无向树。 由定理16.1可知,Ti的边数mi=5, 由握手定理可知,∑dTi(vj)=10,且δ(Ti)≥1,△(Ti)≤5。 于是Ti的度数列必为以下情况之一。
(1) 1,1,1,1,1,5 (2) 1,1,1,1,2,4 (3) 1,1,1,1,3,3 (4) 1,1,1,2,2,3 (5) 1,1,2,2,2,2
(4)对应两棵非同构的树, 在一棵树中两个2度顶点相邻, 在另一棵树中不相邻, 其他情况均能画出一棵非同构 的树。
13
例16.1
人们常称只有一个分支点,且分支点的度数为n-1的 n(n≥3)阶无向树为星形图,称唯一的分支点为星心。
知,G-e已不是连通图, 所以,e为桥。
9
(5)(6)
如果G是连通的且G中任何边均为桥,则G中没有回路,但在任 何两个不同的顶点之间加一条新边,在所得图中得到唯一的 一个含新边的圈。
因为G中每条边均为桥,删掉任何边,将使G变成不连通图, 所以,G中没有回路,也即G中无圈。
又由于G连通,所以G为树,由(1) (2)可知,
u,v∈V,且u≠v,则u与v之间存在唯一的路径Г,
则Г∪(u,v)((u,v)为加的新边)为G中的圈, 显然圈是唯一的。
10
(6)(1)
如果G中没有回路,但在任何两个不同的顶点之间加一条新边, 在所得图中得到唯一的一个含新边的圈,则G是树。
《离散数学》讲义(胡盛)

小结
合式公式(命题公式)及其判定 自然语言的翻译(符号化形式)
列出原子命题,并符号化 不同的原子命题使用不同的符号,符号使用最少 选择合适的联结词,根据命题表达的真实含义,而不 拘泥于形式
离散数学
30
1-3 命题公式与翻译
P12(3)(5)ad(7)
离散数学
31
第一章 数理逻辑 1-4 真值表与等价公式
(PQ) (PQ) T F F T
35
1、真值表
例题4 给出(PQ)(PQ)的真值表 公式不论命题变元做何种指派,其真值永为真, 我们把这类公式记为T。
P Q PQ (PQ) P Q PQ T T T F F T F F T F F F F T T T F F T T F T F T F T T T (PQ)( PQ) T T T T
定义1-5.1
给定一命题公式,若无论对分量作怎样的指派,其对 应的真值永为T,则称该命题公式为重言式或永真公 式。 例如:表1-4.4
明天下雨
2. 我们去看电影
房间里有十张凳子
二元运算
离散数学 17
1-2 联结词
析取(),其定义可用如下真值表表示
P T T F Q T F T PQ T T T 今天我在家看电视或去剧场看戏
她可能是100米或400米赛跑的冠军
他昨天作了二十或三十道习题 可兼或
F
F
F
排斥或
二元运算
离散数学 18
它可以是有意义的一般论证,也可以是科学理论中的数学证 明或结论。建立逻辑学的主要目的在于探索出一套完整的规 则,按照这些规则,就可以确定任何特定论证是否有效。这 些规则,通常称为推理规则。
离散数学
6
离散数学 16章

CHAPTER Fourteen
先证G中无回路 中无回路。 中存在某个结点v上的环 ②⇒③ 先证 中无回路。若G中存在某个结点 上的环, 中存在某个结点 上的环, 存在一条路L ∀u∈V,由条件知 到v存在一条路 1:u…v, ∈ ,由条件知u到 存在一条路 , 有另一条路L 则u到v有另一条路 2:u…vv,矛盾。 到 有另一条路 ,矛盾。 中存在长度大于等于2的一条回路 若G中存在长度大于等于 的一条回路,则回路上两个结点之间存 中存在长度大于等于 的一条回路, 在不同的路, 矛盾。所以G中无回路 中无回路。 在不同的路 矛盾。所以 中无回路。 以下用归纳法证明m=n–1。 。 以下用归纳法证明 为平凡图, 当n=1时,G为平凡图,m=0=1–1=n–1。结论成立。 时 为平凡图 。结论成立。 设n≤k时,结论成立。下证 时 结论成立。下证n=k+1时,结论也成立。 时 结论也成立。 中的一条边, 中无回路, 设e=(u,v)是G中的一条边,由于 中无回路,所以 e有两个连 是 中的一条边 由于G中无回路 所以G- 通分支G 设它们的结点数和边数分别为: 通分支 1和G2,设它们的结点数和边数分别为:n1,m1和n2,m2。 于是有n 和 于是有 1≤k和n2≤k,由归纳假设知:m1=n1–1和m2=n2-1, ,由归纳假设知: 和 , m=m1+m2+1=n1-1+n2-1+1=n-1。 + + 。
3/7/2011 8:48 AM
Discrete Math. , huang liujia
8
例题
CHAPTER Fourteen
已知无向树T有 片树叶 度与 度顶点各1个 片树叶, 度与3度顶点各 例2 已知无向树 有5片树叶 2度与 度顶点各 个, 其余顶点的度 数均为4. 求T的阶数 并画出满足要求的所有非同构的无向树. 数均为 的阶数n, 并画出满足要求的所有非同构的无向树 的阶数 的阶数为n, 度顶点的个数为n− 解 设T的阶数为 则边数为 −1, 4度顶点的个数为 −7. 由握手定 的阶数为 则边数为n− 度顶点的个数为 理得 2m=2(n−1)=5×1+2×1+3×1+4(n−7) − × × × − 解出n=8, 4度顶点为 个. 度顶点为1个 解出 度顶点为 T的度数列为 的度数列为1,1,1,1,1,2,3,4 的度数列为 有3棵非同构的无向树 棵非同构的无向树
离散数学第十六章课件省名师优质课赛课获奖课件市赛课一等奖课件

Sc={c,f,h}
g
h
i
Sd={d,h,i}
Se={e,f,i}
基本割集系统为:{Sa , Sb , Sc , Sd , Se}
割集秩为5.
14
实例
例 下图实线边所示为生成树,求基本回路系统与基本割集系统
解 弦e, f, g相应旳基本回路分别为 Ce=e b c, Cf=f a b c, Cg=g a b c d, C基={Ce, Cf, Cg}.
所求最小生成树如 图所示,W(T)=38.
17
16.3 根树及其应用
定义16.6 有向树T ——基图为无向树旳有向图。 (1) T 为根树——T 中一种顶点入度为0,其他顶点入度均为1
旳有向树. (2) 树根——入度为0旳顶点 (3) 树叶——入度为1,出度为0旳顶点 (4) 内点——入度为1,出度不为0旳顶点 (5) 分支点——树根与内点旳总称 (6) 顶点v旳层数——从树根到任意顶点v旳途径旳长度(即
途径中旳边数) (7) 树高——T 中全部顶点旳最大层数 (8) 平凡根树——平凡图
18
根树实例
根树旳画法:树根放上方,省去全部有向边上旳箭头 如右图所示
a是树根 b,e,f,h,i是树叶 c,d,g是内点 a,c,d,g是分支点 a为0层;1层有b,c; 2层有d,e,f; 3层有g,h; 4层有i. 树高为4
6
子图
定义14.8 G=<V,E>, G =<V ,E >
(1) G G —— G 为G旳子图,G为G 旳母图
(2) 若G G且V =V,则称G 为G旳生成子图
(3) 若V V或E E,称G 为G旳真子图
(4) V (V V且V
)旳导出子图,记作G[V ]
《离散数学》教学大纲

《离散数学》教学大纲(Discrete Mathematics)适用专业:电子信息类课程类别:学科基础课课程学时:48课程学分:3.0先修课程:高等数学、线性代数等一、课程简介离散数学是研究离散量的结构及其相互关系的数学学科,是现代数学的一个重要分支,是计算机科学中基础理论的核心课程,是计算机科学与技术的支撑学科。
它在计算机科学与技术领域有着广泛的应用,同时离散数学也是计算机专业的许多专业课程,如程序设计语言、数据结构、操作系统、编译技术、人工智能与机器人、数据库、网络、计算机图形学、算法设计与分析、理论计算机科学基础等必不可少的先行课程。
通过离散数学的学习,不但可以掌握离散结构的描述工具和处理方法,为后续课程的学习创造条件,而且可以提高抽象思维和严格的逻辑推理能力,为将来参与创新性的研究和开发工作打下坚实的基础。
二、教学目的与任务离散数学是一门培养学生缜密思维、严格推理,具有综合归纳分析能力的课程。
通过本课程的学习,使学生有一定的严格逻辑推理与抽象思维能力,掌握离散量的处理及运算技能,能够将离散数学应用到解决计算机技术中的实际问题中。
不仅能为学生奠定计算机科学的专业基础,并且能为将后续课程的学习及将来开发软、硬件技术及研究、应用提供有力的工具。
三、课程内容第1章命题逻辑的基本概念1.1命题与联结词1.2命题公式及其赋值第2章命题逻辑等值演算2.1等值式2.2析取范式与合取范式* 2.3联结词的完备集* 2.4可满足性问题与消解法第3章命题逻辑的推理理论3.1推理的形式结构3.2自然推理系统P3.3消解证明法第4章一阶逻辑基本概念4.1一阶逻辑命题符号化4.2一阶逻辑公式及其解释第5章一阶逻辑等值演算与推理5.1一阶逻辑等值式与置换规则5.2一阶逻辑前束范式* 5.3一阶逻辑的推理理论第6章集合代数6.1集合的基本概念6.2集合的运算6.3有穷集的计数6.4集合恒等式第7章二元关系7.1有序对与笛卡儿积7.2二元关系7.3关系的运算7.4关系的性质7.5关系的闭包7.6等价关系与划分7.7偏序关系第8章函数8.1函数的定义与性质8.2函数的复合与反函数* 8.3双射函数与集合的基数* 8.4一个电话系统的描述实例第14章图的基本概念14.1图14.2通路与回路14.3图的连通性14.4图的矩阵表示* 14.5图的运算第15章欧拉图与哈密顿图15.1欧拉图15.2哈密顿图15.3最短路问题、中国邮递员问题与货郎担问题第16章树16.1无向树及其性质16.2生成树16.3根树及其应用三、课程学时分配、教学内容与教学基本要求四、教学方法与教学手段说明该课程教学方式主要有:课堂教学、交互学习、课后作业。
离散数学16教案讲稿
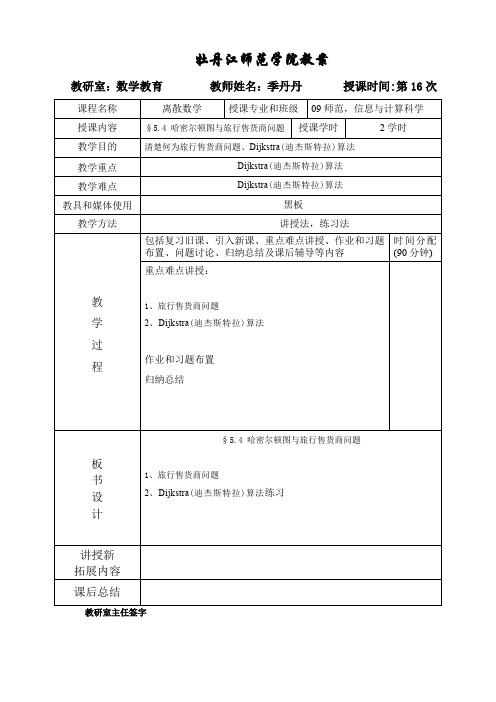
Dijkstra(迪杰斯特拉)算法:
Dijkstra(迪杰斯特拉)算法是典型的单源最短路径算法,用于计算一个节点到其他所有节点的最短路径.主要特点是以起始点为中心向外层层扩展,直到扩展到终点为止.Dijkstra算法是很有代表性的最短路径算法,在很多专业课程中都作为基本内容有详细的介绍,如数据结构,运筹学等等.Dijkstra一般的表述通常有两种方式,一种用永久和临时标号方式,一种是用OPEN,CLOSE表的方式,这里均采用永久和临时标号的方式.注意该算法要求图中不存在负权边.
1.设置 , , , ( , 是永久标号,其余标号均为临时标号)
2.循环所有与 关联的临时标号的顶点
1)如果 ( 是 与 两顶点间边的权值)
那么设置
2)计算 且有临时标号
置 为永久标号
3)如果
那么设置 ,
3.对每一个顶点 , ,利用 从 开始回溯找到 到 的最短路径
4.算法结束.
如果用本算法求一个图中全部的最短路,则要以每个点为源点调用一次Dijkstra算法.至今还没有找到解决货郎担问题的更有效算法,它是众多NP难解问题中的一个.
例4在带权图5-4-7中,求从 到其余各点的最短路径和距离.
解 ,
,
,
, .
例5现有一电脑代理商要从她所在城市出发,乘飞机去5个城市,然后回到出发点.如图5-4-8所示,顶点代表城市. 是她所在的城市.边代表城市间的直达航线.她怎么才能访问每个城市恰巧一次,最后回到出发点呢?
解从图中我们可以看出,销售代表要到达城市 ,只能经由 或 ,因此她的飞行路线必须包括 和 .这就使得她必须走路线 ,否则她就得走路线 ,但这样一来就提早的形成了一个圈 .同理,她也不能走路线 .再通过简单的分析,找到两条可行的路线: , , 和 , , .从而得到她的这个行程应为: 或者 .当然,她还可以将顺序颠倒,得到4条不同的巡回路线.
《离散数学》完整课件

第三节 复合关系与逆关系
本节讨论关系的复合运算与逆运算极其 性质;主要考虑了下列问题:
1.关系的复合是否满足交换律、结合律、 关系的复合对于集合的并(交)是否有分 配律;
2.关系的复合运算与逆运算在关系图和 关系矩阵上的反应;
3.关系的复合运算与关系的逆运算之间 的运算规律.
返回本章首页
11 2021/6/7
|A|<|B|三条中有且仅有一条成立;
2.Bernstein定理:设A,B是两个集合,若|A|≥|B| 且|A| ≤ |B|,则集合A,B等势;
3.设A是任意集合,P(A)为A的幂集,则P(A)的基 数大于A的基数.
返回本章首页
23 2021/6/7
本章小结
本章的主要内容有:集合的等势、有限 集与无限集、可数集与不可数集、较为 常见的集合的基数等.集合的基数反映了 集合的元素的多少,它是集合的一种性 质,一种与该集合等势的集合构成的集 合族的共同性质.
返回本章首页
17 2021/6/7
第九节 复合映射与逆映射
映射的复合就是关系的复合,须注意的是 复合的次序,主要内容有:
1.映射的复合具有结合律,但不符合交换律; 2.区分了左逆与右逆;给出里左逆、右逆
与单射、满射之间的关系; 3.可逆与左、右逆之间的关系.
返回本章首页
18 2021/6/7
本章小结
1.本节首先给出了公式的蕴涵关系的三个等价定 义,及蕴涵关系具有的性质,给出了15个基本蕴 涵式;
2.把蕴涵概念推广,得到公式的逻辑结果的定义;
3.为了研究推理,还引进演绎的概念;
4.用实例说明推理方法.
返回本章首页
30 2021/6/7
第六节 形式演绎
精品课程《离散数学》PPT课件(全)

言1
为什么学习离散数学?
离散数学是现代数学的一个重要分支,是计算机科学与技术 的理论基础,所以又称为计算机数学,是计算机科学与技术 专业的核心、骨干课程。
它以研究离散量的结构和相互间的关系为主要目标,其研 究对象一般是有限个或可数个元素,因此它充分描述了计算 机科学离散性的特点。
离散数学是什么课?
真值为1
25
1.1 命题符号化及联结词
以下命题中出现的a是给定的一个正整数: (3) 只有 a能被2整除, a才能被4整除。
(4) 只有 a能被4整除, a才能被2整除。
解: 令r: a能被4整除, s: a能被2整除。 真值不确定 (3)符号化为 s r (4)符号化为 r s
真值为1
26
19
1.1 命题符号化及联结词
3.析取词 设p,q为二命题,复合命题“p或q” 称为p与q的析取式,记作p ∨ q,符号∨称 为析取联结词。 运算规则:
p 0 0 1 1 q 0 1 0 1 p∨q 0 1 1 1
20
1.1 命题符号化及联结词
析取运算特点:只有参与运算的二命题全为假时,运算结果才 为假,否则为真。 相容或:二者至少有一个发生,也可二者都发生 排斥或:二者只有一个发生,即非此即彼 例如: (1)小王爱打球或爱跑步。 设p:小王爱打球。 q:小王爱跑步。 则上述命题可符号化为:p ∨ q (2)张晓静是江西人或湖南人。 设p:江西人。 q:湖南人。 则上述命题就不可简单符号化为:p ∨ q 而应描述为(p∧ q) ∨( p∧q)(也可用异或联接词∨)
(1)星期天天气好,带儿子去了动物园; (2)星期天天气好,却没带儿子去动物园; (3)星期天天气不好,却带儿子去了动物园; (4)星期天天气不好,没带儿子去动物园。
离散数学_第16章_树

无向连通图G的割集秩与生成树的选取无关,但不同生成 树对应的基本割集系统可能不同。
三、最小生成树 1. 定义 定义 16.5 T 是 G=<V ,E , W>的生成树 (1)W(T)——T 各边权之和 (2)最小生成树——G 的所有生成树中权最小的 2.求最小生成树的一个算法 避圈法(Kruskal)设 G=<V , E , W>,将 G 中非环边按权从小到大 排序:e1 , e2, …, em. (1)取 e1 在 T 中 (2)查 e2 ,若 e2 与 e1 不构成回路,取 e2 也在 T 中,否则弃 e2. (3)再查 e3 , …, 直到得到生成树为止.
(2)(3)
如果G中任意两个顶点之间存在唯一的路径, 则G中无回路且m=n-1。 其次证明 m=n-1。(归纳法) n=1时,G为平凡图,结论显然成立。 设n≤k(k≥1)时结论成立, 当n=k+1时,设e=(u,v)为G中的一条边, 由于G中无回路,所以G-e为两个连通分支G1、G2。 设ni、mi分别为Gi中的顶点数和边数,则ni≤k ,i=1,2, 由归纳假设可知mi=ni-1,于是 m=m1+m2+1=n1-1+n2-1+1=n1+n2-1=n-1。
此图的圈秩为5,基本回路系统为{C1,C2,C3,C4,C5}。
说 明
无向连通图G的圈秩与生成树的选取无关,但不同生成树 对应的基本回路系统可能不同。
2.基本割集与基本割集系统 (1)定义基本割集的基础 定理 16.5 设 T 是连通图 G 的一棵生成树,e 为 T 的树枝,则 G 中存在只含树枝 e,其余边都是弦的割集,且不同的树枝对应 的割集也不同. 证 由定理 16.1 可知,e 是 T 的桥,因而 Te 有两个连通分支 T1 和 T2,令 Se={e | eE(G)且 e 的两个端点分别属于 V(T1)和 V(T2)}, 由构造显然可知 Se 为 G 的割集,eSe 且 Se 中除 e 外都是弦, 所以 Se 为所求. 显然不同的树枝对应的割集不同.
离散数学完整版课件全套ppt教学教程最全整套电子讲义幻灯片(最新)

1.1 命题及联结词
运算符“析取” 与汉语的“或”几乎一致但有 区别:哪些老师讲离散数学?有人回答如下:
(16)“讲离散数学的老师是杨老师或吴老师”, 分解为
“讲离散数学的老师是杨老师”或 “讲离散数学的老师是吴老师”, 这两个原子命题有可能都是对的, 这种“或”称为“可同时为真的或”, 或简称为“可兼或”。 这种“或”表示可表 示为“析取”
1.1 命题及联结词
定义1.4条件:当p是1 ,q是0时,pq为0,即10 为0,其他情况为1。
逻辑运算符“如果…那么”, 如老妈说:“如果期终考了年级前10 名,那么奖励1000元”。 p:期终考了年级前10名 q:奖励1000元 则上面的语句表示为pq。 先考虑值为0即假的情况: 当p为1即“期终考了年级前10”, 且q为0即“没有奖励1000元” 这时老妈的话是假话空话,
这个例题有点不正点! “郎才当且仅当女貌”,
可以表示为“郎才女貌”
1.2命题公式
对错明确的陈述语句称为命题,其真值t/f 0/1 C运算:加+、减-、乘x、除/、余数%, 命题逻辑:合、析、否定、条件、双条件(版) C语言中用变量x表示某些数,如x*x+x+10是表达式,
命题逻辑中用变量p,q,r表示任意命题,由命题常元与 此类变量所构成表达式,称为“命题公式”。
无论p/q取何值,这两个公式的值,与前面各例 不同,此表是将运算结果写在联结词的下方!
1.3 等值式
定义1.3.1等值: 对于合法的命题公式A、B, 若无论其中的命题变元取何值,A 、B值总相等, 称为两个公式等值,记为AB (边播边板)
目的:
1.掌握离散数学五大核心内容(集合论、数 理逻辑、代数结构、图论、组合数学)的基本概 念、基本理论、基本方法,训练提高学生的概括 抽象能力、逻辑思维能力、归纳构造能力,培养 学生严谨、完整、规范的科学态度和学习思维习 惯。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
例3 求最小生成树。
4 21 3
21 3
解:n=8,执行7次,12 11 5 6
8
56 8
9
79
10
W(T)=1+2+3+5+6+8+9=34
11
求最小生成树的算法——避圈法 (Kruskal) 设G=<V,E,W>, 将非环边按权从小到大排序:e1,
e2, …, em. (1) 取e1在T中 (2) 检查e2, 若e2与e1不构成回路, 则将e2加入T中, 否
则弃去e2. (3) 检查e3,…, 重复进行直至得到生成树为止.
12
例4 求图的一棵最小生成树
W(T)=38
13
16.3 根树及其应用
有向树及有关概念 家族树 根树的分类 最优2元树与Huffman算法 前缀码 遍历
14
1、有向树与根树的定义
有向树:基图为无向树的有向图。 根树:有一个顶点入度为0, 其余的入度均为1的非
平凡的有向树。 树根:有向树中入度为0的顶点。 树叶:有向树中入度为1, 出度为0的顶点。 内点:有向树中入度为1, 出度大于0的顶点。 分支点:树根与内点的总称。 顶点v的层数:从树根到v的通路长度。 树高:有向树中顶点的最大层数。
15
例如下图,有向树
T1
T2
T3
T4
16
根树的画法:树根放上方,省去所有有向边的箭头。 如右图所示
G1
G2
G3
G4
3
2、无向树的性质
定理16.1 设G=<V, E>是n阶m条边的无向图,则下 面各命题是等价的:
(1)G是树(连通无回路); (2)G中任意两个顶点之间存在惟一的路径; (3)G中无回路且m=n1; (4)G是连通的且m=n1; (5)G是连通的且G中任何边均为桥; (6)G中没有回路, 但在任何两个不同的顶点之间
加一条新边后所得图中有惟一的一个含新边的圈.
4
定理16.2 设T 是 n 阶非平凡的无向树,则T中至少 有两片树叶.
例2 设树T有1个3度顶点,2个2度顶点,其余均为树 叶,求树叶数,画出非同构的无向树。
解:用树的性质m=n1和握手定理. 设有x片树叶,于是 n=1+2+x=3+x, 2m=2(n1)=2(2+x)=13+22+x 解出x=3,故T有3片树叶. T的度数列为1, 1, 1, 2, 2, 3
6
16.2 生成树
生成树 性质 最小生成树
7
1、生成树
设G为无向连通图 G的生成树:G的生成子图并且是树。 生成树T的树枝:G在T中的边。 生成树T的弦:G不在T中的边。
生成树T的余树 T :所有弦的集合的导出子图。 注意:T 不一定连通,也不一定不含回路。
右图黑边构成生成树 红边构成余树
解: (1) {2, 3, 4, 4, 5, 5, 7}
5
8
10
(2) {4, 4, 5, 5, 5, 7} (3) {5, 5, 5, 7, 8} (4) {5, 7, 8, 10} (5) {8, 10, 12}
2 34 45 5 (1) (2) (3) 30
12
18
12 18
(6) {12, 18}
有2棵非同构的无向树,如图所示。
5
例3 已知无向树T有5片树叶, 2度与3度顶点各1个, 其 余顶点的度数均为4. 求T的阶数n, 并画出满足要 求的所有非同构的无向树.
解:设T的阶数为n,则边数为n1,4度顶点的个数 为n7。由握手定理得 2m=2(n1)=51+21+31+4(n7) 解出n=8,4度顶点为1个。 T的度数列为1,1,1,1,1,2,3,4 有3棵非同构的无向树。
a是树根
0层
b, e, f, h, i是树叶
1层
c, d, g是内点
2层
a, c, d, g是分支点
a为0层;1层有b,c;
3层
2层有d, e, f ;
3层有g, h;4层有i.
4层
树高为4
17
2、家族树
定义 把根树看作一棵家族树: (1) 若顶点 a 邻接到顶点 b, 则称 b 是 a 的儿子, a 是
19
(a)2叉树
(b)3叉树
(c)3叉正则树
O
A
D
B CE
G
F
HI J
(d)2叉正则树 (e)2叉完全正则树 (f)3叉有序树
20
4、最优2叉树
t
定义 树T的权:WW((Tt) wil(vi )
i1
其中 l(vi)是vi的层数。
最优 2叉树: —— Haffman算法 P314
21
例1 构造关于权{2, 3, 4, 4, 5, 5, 7}的最优2叉树。
8
例1 画生成树
一般地,图G的生成树不唯一。
9
2、性质
定理 任何无向连通图都有生成树. 推论 设n阶无向连通图有m条边, 则mn1.
例2 某地要兴建5个工厂,拟修筑道路连接这5处, 经勘测其道路可依上图的无向边铺设,为使这5 处都相通,问至少要铺几条路?
10
3、最小生成树
T的权:T是无向连通带权图G=<V, E, W>的一棵生 成树,T的各边权之和。
第十六章 树 16.1 无向树
无向树及相关概念 性质
1
1、无向树
无向树:连通无回路的无向图,用T表示 平凡树:平凡图 森林:每个连通分支都是树的非连通的无向图 树叶:树中度数为1的顶点(悬挂顶点) 分支点:树中度数2的顶点
如右图,
图(a)是森林,
图(b)为一棵12阶树。 (a)
(b)
2
例1 判断下列各图是否为树?
5
8 10 5
8 10
7
7
23 (4)
4455 2 3 4455
(5)
(6)
22
最优2叉树如前图。 wi 2 3 7 4 4 5 5 l(vi) 3 3 2 3 3 3 3
∴ W(T)=2×3+3×3+7×2+4×3+4×3 +5×3+5×3=83
最优2叉树不是唯一的,但Huffman算法 得到的树一定是最优2叉树。
b 的父亲; (2) 若b和c为同一个顶点的儿子, 则称b和c是兄弟; (3) 若ab且a可达b, 则称a是b的祖先, b是a的后代.
设v为根树的一个顶点且不是树根, 称v及其所有后 代的导出子图为以v为根的根子树.
18
3、根树的分类
有序树:将根树同层上的顶点规定次序。 r叉树:根树的每个分支点至多有r个儿子。 r叉正则树:根树的每个分支点恰有r个儿子。 r叉完全正则树:树叶层数相同的r元正则树。 r叉有序树:有序的r元树。 r叉正则有序树:有序的r元正则树。 r叉完全正则有序树:有序的r元完全正则树。
