沪科版九年级数学综合培优讲义(含答案)

合集下载

沪教版九年级(下)学期同步讲义第1讲相似三角形(学生版)

一、比和比例一般来说，两个数或两个同类的量a与b相除，叫做a与b的比，记作:a b（或表示为ab ）；如果::a b c d=（或a cb d=），那么就说a、b、c、d成比例．二、比例的性质（1）基本性质：如果a cb d=，那么ad bc=；如果a cb d=，那么b da c=，a bc d=，c da b=．（2）合比性质：如果a cb d=，那么a b c db d++=；如果a cb d=，那么a b c db d--=．（3）等比性质：如果a ckb d==，那么a c a ckb d b d+===+．相似三角形知识结构模块一：比例线段知识精讲2 / 17三、比例线段的概念对于四条线段a 、b 、c 、d ，如果::a b c d =（或表示为a cb d=），那么a 、b 、c 、d 叫做成比例线段，简称比例线段．四、黄金分割如果点P 把线段AB 分割成AP 和PB （AP PB >）两段（如下图），其中AP 是AB 和PB 的比例中项，那么称这种分割为黄金分割，点P 称为线段AB 的黄金分割点．其中，510.6182AP AB -=≈，称为黄金分割数，简称黄金数．五、三角形一边的平行线性质定理平行于三角形一边的直线截其他两边所在的直线，截得的对应线段成比例．如图，已知ABC ∆，直线l // BC ，且与AB 、AC 所在直线交于点D 和点E ，那么AD AEDB EC =．六、三角形一边的平行线性质定理推论平行于三角形一边的直线截其他两边所在的直线，截得的三角形的三边与原三角形的三边对应成比例．如图，点D 、E 分别在ABC ∆的边AB 、AC 上，如果DE // BC ，那么DE AD AEBC AB AC ==．七、三角形的重心定义：三角形三条中线交于一点，三条中线交点叫三角形的重心．性质：三角形重心到一个顶点的距离，等于它到这个顶点对边中点的距离的两倍．八、三角形一边的平行线判定定理如果一条直线截三角形的两边所得的对应线段成比例，那么这条直线平行于三角形的第三边．九、三角形一边的平行线判定定理推论如果一条直线截三角形的两边的延长线（这两边的延长线在第三边的同侧）所得的对应线段成比例，那么这条直线平行于三角形的第三边．APBlAB CDEAB CDE ABC DE ll ABCD EA BCDE如图，在ABC ∆中，直线l 与AB 、AC 所在直线交于点D 和点E ，如果AD AEDB EC=，那么l //BC ．十、平行线分线段成比例定理两条直线被三条平行的直线所截，截得的对应线段成比例．如图，直线1l //2l //3l ，直线m 与直线n 被直线1l 、2l 、3l 所截，那么DF EGFB GC=．十一、平行线等分线段定理两条直线被三条平行的直线所截，如果一条直线上截得的线段相等，那么另一条直线上截得的线段也相等．【例1】如图，点D 、E 分别在ABC ∆的边AB 和BC 上．下列所给的四个条件中，不一定能得到DE // AC 的条件是（）A ．BE BC BD BA =B ．CE AD BE BD =C ．BD DEBA AC=D ．BC CEAB AD=【例2】在比例尺为1 : 40000的一张地图上，量得A 、B 两地的距离是37 cm ，那么A 、B两地的实际距离是______km ．例题解析ABCDEABCDEABCDEBC D E FG4 / 17BCDE FG A【例3】（2015学年·普陀区二模·第5题）如图，已知1l //2l //3l ，DE = 4，DF = 6，那么下列结论正确的是（） A ．BC : EF = 1 : 1 B ．BC : AB = 1 : 2 C ．AD : EF = 2 : 3 D ．BE : CF = 2 : 3【例4】如果线段a = 4 cm ，b = 9 cm ，那么它们的比例中项是______cm ．【例5】四边形ABCD 是平行四边形，点E 在边BA 的延长线上，CE 交边AD 于点F ，交对角线BD 于点G ．求证：CG 是EG 与FG 的比例中项．【例6】（2014学年·长宁区二模·第16题）已知线段AB = 10，P 是线段AB 的黄金分割点（AP > PB ），则AP =______．【例7】已知23a c eb d f ===，18ac e =--，0bd f ++≠，求b d f ++的值．【例8】如果直角三角形的斜边长为18，那么这个三角形的重心到直角顶点的距离为FEDAB CMAFBECD ABCDEFMAB C DE FA BCDEFG______．【例9】（2015学年·浦东新区二模·第15题）如图，已知AD // EF // BC ，AE = 3BE ，AD = 2，EF = 5，那么BC =______．【例10】（2015学年·普陀区二模·第17题）如图，点E 、F 分别在正方形ABCD 的边AB 、BC 上，EF 与对角线BD 交于点G ，如果BE = 5，BF = 3，那么FG : EF 的比值是_______．【例11】（2015学年·长宁区、金山区二模·第23题）如图，BD 是ABC ∆的角平分线，点E 、F 分别在BC 、AB 上，且DE // AB ，DEF A ∠=∠．（1）求证：BE = AF ；（2）设BD 与EF 交于点M ，联结AE ，交BD 于点N ，求证：BN MD BD ND =．【例12】（2013学年·宝山区、嘉定区二模·第23题）如图，在直角梯形ABCD 中，AD // BC ，90DAB ABC ∠=∠=︒，E 为CD 的中点，联结AE 并延长交BC 的延长线于F ；（1）联结BE ，求证BE = EF ．（2）联结BD 交AE 于M ，当AD = 1，AB =2，AM = EM 时，求CD 的长．6/ 17一、相似三角形的定义如果一个三角形的三个角与另一个三角形的三个角对应相等，且它们各有的三边对应成比例，那么这两个三角形叫做相似三角形．如图，DE 是ABC ∆的中位线，那么在ADE ∆与ABC ∆中， A A ∠=∠， ADE B ∠=∠，AED C ∠=∠；12AD DE AE AB BC AC ===．由相似三角形的定义，可知这两个三角形相似．用符号来表示，记作ADE ∆∽ABC ∆，其中点A 与点A 、点D 与点B 、点E 与点C 分别是对应顶点；符号“∽”读作“相似于”．用符号表示两个相似三角形时，通常把对应顶点的字母分别写在三角形记号“∆”后相应的位置上．根据相似三角形的定义，可以得出：（1）相似三角形的对应角相等，对应边成比例；两个相似三角形的对应边的比，叫做这两个三角形的相似比（或相似系数）．（2）如果两个三角形分别与同一个三角形相似，那么这两个三角形也相似．二、相似三角形的预备定理平行于三角形一边的直线截其他两边所在的直线，截得的三角形与原三角形相似．如图，已知直线l 与ABC ∆的两边AB 、AC 所在直线分别交于点D 和点E ，则ADE ∆∽ABC ∆．A BCDEABCDEABCDEDABCE知识精讲模块二：相似三角形8 / 17ABCA 1B 1C 1AB C A 1B 1C 1三、相似三角形判定定理1如果一个三角形的两角与另一个三角形的两角对应相等，那么这两个三角形相似．可简述为：两角对应相等，两个三角形相似．如图，在ABC ∆与111A B C ∆中，如果1A A ∠=∠、1B B ∠=∠，那么ABC ∆∽111A B C ∆．常见模型如下：四、相似三角形判定定理2如果一个三角形的两边与另一个三角形的两边对应成比例，并且夹角相等，那么这两个三角形相似．可简述为：两边对应成比例且夹角相等，两个三角形相似．如图，在ABC ∆与111A B C ∆中，1A A ∠=∠，1111AB ACA B AC =，那么ABC ∆∽111A B C ∆．ABCA 1B 1C 1五、相似三角形判定定理 3如果一个三角形的三条边与另一个三角形的三条边对应成比例，那么这两个三角形相似．可简述为：三边对应成比例，两个三角形相似．如图，在ABC ∆与111A B C ∆中，如果111111AB BC CAA B B C C A ==，那么ABC ∆∽111A B C ∆．六、直角三角形相似的判定定理如果一个直角三角形的斜边及一条直角边与另一个直角三角形的斜边及一条直角边对应成比例，那么这两个直角三角形相似．可简述为：斜边和直角边对应成比例，两个直角三角形相似．如图，在Rt ABC ∆和111Rt A B C ∆中，如果190C C ∠=∠=︒，1111AB BCA B B C =，那么ABC ∆∽111A B C ∆．七、相似三角形性质定理相似三角形性质定理1：相似三角形对应高的比、对应中线的比和对应角平分线的比都等于相似比．相似三角形性质定理2：相似三角形周长的比等于相似比．相似三角形性质定理3：相似三角形的面积的比等于相似比的平方．ABCA 1B 1C 110 / 17AB CDA B C D EFABCDE FAB CDE【例13】（2014学年·普陀区二模·第6题）在下列44⨯的正方形网格图中，每个小正方形的边长都是1，三角形的顶点都在格点上，那么与图1中ABC ∆相似的三角形所在的网格图是（）A ．B ．C ．D ．【例14】（2013学年·普陀区二模·第11题）已知ABC ∆∽DEF ∆，且相似比为3 : 4，2ABC S ∆=cm 2，则DEF S ∆=______ cm 2．【例15】如图，已知点D 是ABC ∆中的边BC 上的一点，BAD C ∠=∠，ABC ∠的平分线交边AC 于点E ，交AD 于F ，那么下列结论中错误的是（） A ．BAC ∆∽BDA ∆ B ．BFA ∆∽BEC ∆ C ．BDF ∆∽BEC ∆D ．BDF ∆∽BAE ∆【例16】如图，已知点D 在ABC ∆的边AB 上，且ACD B ∠=∠，:1:3ACD DBC S S ∆∆=．求ACAB的值．【例17】如图，已知点E 、F 分别在矩形ABCD 的边BC 和CD 上，EF AE ⊥，BE = 3 cm ，AB = 6 cm ，矩形ABCD 的周长为28 cm ，求CF 的长．【例18】（2015学年·静安区二模·第5题）如图，已知点D 、E 分别在ABC ∆边AB 、AC 上，DE // BC ，BD = 2AD ，那么:DEB EBC S S ∆∆等于（） A ．1 : 2B ．1 : 3C ．1 : 4D ．2 : 3例题解析图1AB C DM GA B C DEFA BCDEF【例19】（2014学年·杨浦区二模·第13题）如图，ABC ∆中，如果AB = AC ，AD ⊥BC 于点D ，M 为AC 中点，AD 与BM 交于点G ，那么:GDM GAB S S ∆∆的值为_______．【例20】如图，已知ABC ∆中，AB = AC ，CD 是边AB 上的高，且CD = 2，AD = 1，四边形BDEF 是正方形．CEF ∆和BDC ∆相似吗？试证明你的结论．【例21】（2013学年·奉贤区二模·第23题）已知：如图，点E 是四边形ABCD 的对角线BD 上一点，且BAC BDC DAE ∠=∠=∠．（1）求证：ABE ∆∽ACD ∆；（2）求证：BC AD DE AC =．【例22】（2015学年·浦东新区二模·第23题）如图，已知：四边形ABCD 是平行四边形，点E 在边BA 的延长线上，CE 交AD 于点F ，ECA D ∠=∠．（1）求证：ECA ∆∽ECB ∆；（2）若DF = AF ，求AC : BC 的值．EDCBA12 / 17ABCD EFGHADE F【例23】（2015学年·宝山区、嘉定区二模·第23题）如图，BD 是平行四边形ABCD 的对角线，若45DBC ∠=︒，DE BC ⊥于E ，BF CD ⊥于F ，DE 与BF 相交于H ，BF 与AD 的延长线相交于G ．求证：（1）CD = BH ；（2）AB 是AG 和HE 的比例中项．【例24】（2015学年·松江区二模·第23题）如图，已知等腰ABC ∆中，AB = AC ，AD ⊥BC ，CE ⊥AB ，垂足分别为D 、E . （1）求证：CAD ECB ∠=∠；（2）点F 是AC 的中点，联结DF ，求证：2BD FC BE =．【例25】（2014学年·闵行区二模·第23题）如图，已知在梯形ABCD 中，AD // BC ，90A ∠=︒，AB = AD ．点E 在边AB 上，且DE CD ⊥，DF 平分EDC ∠，交BC 于点F ，联结CE 、EF ．（1）求证：DE = DC ；（2）如果2BE BF BC =，求证：BEF CEF ∠=∠．【例26】（2013学年·静安区二模·第23题）已知：如图，在ABC ∆中，AB = AC ，点D 、E 分别是边AC 、AB 的中点，DF ⊥AC ，DF 与CE 相交于点F ，AF 的延长线与BD 相交于点G ．CB AD EFA BCDEFABCD EFGABCPQ（1）求证：2AD DG BD =；（2）联结CG ，求证：ECB DCG ∠=∠．【例27】（2015学年·闸北区二模·第23题）如图，直角梯形ABCD 中，90B ∠=︒，AD // BC ，BC = 2AD ，点E 为边BC 的中点．（1）求证：四边形AECD 为平行四边形；（2）在CD 边上取一点F ，联结AF 、AC 、EF ，设AC 与EF 交于点G ，且EAF CAD ∠=∠．求证：AEC ∆∽ADF ∆；（3）在（2）的条件下，当45ECA ∠=︒时，求：FG : EG 的比值．【例28】如图，已知在ABC ∆中，P 是边BC 上的一个动点，PQ // AC ，PQ 与边AB 相交于点Q ，AB = AC = 10，BC = 16，BP = x ，APQ ∆的面积为y ．（1）求y 关于x 的函数解析式；（2）试探索：APQ ∆与ABP ∆能否相似？如果能相似，请求出x 的值，如果不能相似，请说明理由．14 / 17ABCDE FOP ABCMN【习题1】如果两个相似三角形的面积的比为4 : 9，那么它们对应的角平分线的比是______．【习题2】（2014学年·浦东新区二模·第6题）如图，ABC ∆和AMN ∆都是等边三角形，点M 是ABC ∆的重心，那么AMN ABCSS ∆∆的值为（）A ．23B ．13C ．14D ．49【习题3】（2013学年·虹口区二模·第16题）如图，AB // DC ，DE = 2AE ，CF = 2BF ，且DC = 5，AB = 8，则EF =______．【习题4】已知，如图，D 、E 、F 分别是ABC ∆的边BC 、AB 、AC 的中点，AD 与EF 相交于点O ，线段CO 的延长线交AB 于点P ，求证：AB = 3AP ．【习题5】（2013学年·杨浦区二模·第23题）如图，在平行四边形ABCD 中，AE ⊥BC 于E ，AF ⊥CD 于F ．（1）求证：CD DF BC BE =；（2）若M 、N 分别是AB 、AD 中点，且60B ∠=︒，求证：EM // FN ．随堂检测ABC DEFABCDF EABCDEF【习题6】（2013学年·黄浦区二模·第23题）如图，Rt ABC ∆中，90ACB ∠=︒，D 是边BC上一点，点E 、F 分别是线段AB 、AD 中点，联结CE 、CF 、EF . （1）求证：CEF ∆≌AEF ∆；（2）联结DE ，当BD = 2CD 时，求证：DE = AF .【习题7】（2015学年·崇明县二模·第23题）已知正方形ABCD 的对角线相交于点O ，CAB ∠的平分线分别交BD 、BC 于点E 、F ，作BH AF ⊥，垂足为H ，BH 的延长线分别交AC 、CD 于点G 、P ．（1）求证：AE = BG ；（2）求证：GO AG CG AO =．ABCDP G OF HE16 / 17ABC DEFP ABCDE FABCDE FO【作业1】（2013学年·长宁区二模·第4题）若ABC ∆∽111A B C ∆（其中点A 和1A 、B 和1B 、C 和1C 分别对应），且AB = 4，11A B = 6，则ABC ∆的周长和111A B C ∆的周长之比是（） A ．9 : 4B ．4 : 9C ．2 : 3D ．3 : 2【作业2】已知，如图，在Rt ABC ∆中，90ACB ∠=︒，点D 为AB 的中点，BE CD ⊥，垂足为点F ，BE 交AC 于点E ，CE = 1cm ，AE = 3 cm ．求证：（1）ECB ∆∽BCA ∆；（2）求斜边AB 的长．【作业3】（2013学年·金山区二模·第23题）已知：如图，线段AB // CD ，AC CD ⊥，AC 、BD 相交于点P ，E 、F 分别是线段BP 和DP 的中点．（1）求证：AE // CF ；（2）如果AE 和DC 的延长线相交于点Q ，M 、N 分别是线段AP 和DQ 的中点，求证：MN = CE ．【作业4】（2015学年·普陀区二模·第23题）如图，已知在四边形ABCD 中，AD // BC ，对角线AC 、BD 相交于点O ，BD 平分ABC ∠，过点D 作DF // AB ，分别交AC 、BC 于点E 、F ．（1）求证：四边形ABFD 是菱形；（2）设AC AB ⊥，求证：AC OE AB EF =．课后作业AB CDEFH【作业5】（2015学年·静安区、青浦区二模·第23题）已知：如图，四边形ABCD 是菱形，点E 在边CD 上，点F 在BC 的延长线上，CF = DE ，AE 的延长线与DF 相交于点G ．（1）求证：CDF DAE ∠=∠；（2）如果DE = CE ，求证：AE = 3EG ．【作业6】（2013学年·浦东新区二模·第23题）已知：如图，在正方形ABCD 中，点E 是边AD 的中点，联结BE ，过点A 作AF BE ⊥,分别交BE 、CD 于点H 、F ，联结BF ．（1）求证：BE = BF ；（2）联结BD ，交AF 于点O ，联结OE ．求证：AEB DEO ∠=∠．EDCG FAB。

沪教版九年级数学暑假同步讲义第9讲相似三角形的章节复习(解析版)

相似三角形是初中数学九年级上学期第一章的内容，在本章中，我们学习了比例线段的相关性质，相似三角形的概念、判定及性质和平面向量的线性运算．重点是灵活运用相似三角形的判定定理和性质定理，难点是利用辅助线解决相似三角形问题以及相似三角形与动点问题相结合的类型。

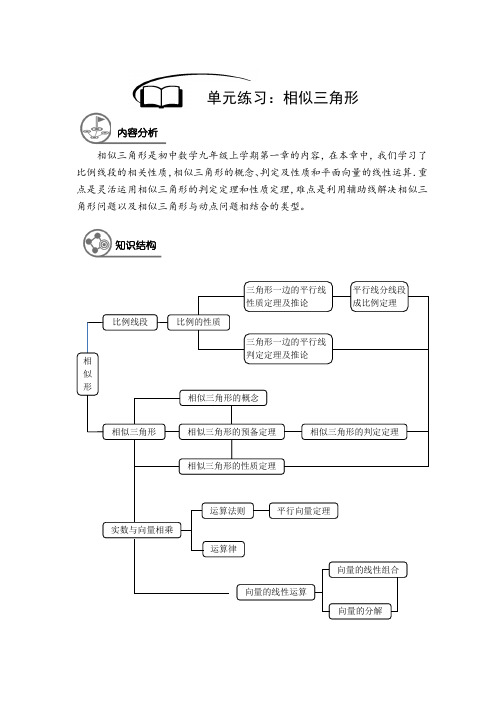
比例线段运算法则比例的性质向量的分解平行向量定理运算律实数与向量相乘向量的线性组合向量的线性运算相似三角形的概念相似三角形的预备定理相似三角形的判定定理相似三角形的性质定理三角形一边的平行线性质定理及推论三角形一边的平行线判定定理及推论平行线分线段成比例定理相似形相似三角形单元练习：相似三角形内容分析知识结构步同级年九2 / 17A B CDO【练习1】下列图形：①两个等腰三角形；②两个直角三角形；③两个正方形；④两个矩形；⑤两个菱形；⑥两个正五边形．其中一定相似的有（） A ．2组B ．3组C ．4组D ．5组【答案】A【解析】判定相似有2个条件：对应角相等，且对应边成比例，两个矩形对应角相等，但长和宽的不一定成比例，两个（等腰三角形）菱形对应边成比例，但对应角又不一定相等，只有③⑥一定相似．【总结】考查学生对相似几何图形性质的理解，对应角相等和对应边成比例两个条件缺一不可．【练习2】若a cb d=，下列各式中正确的个数有（） ①a c d b =；②::d c b a =；③22a a b b =；④55a c b d +=+；⑤a a c b a d +=+；⑥c ma d mb=．A ．1个B ．2个C ．3个D ．4个【答案】A【解析】考查比和比例的基本性质，以“内项积等于外项积”检验①不成立，②是对的；比的基本性质是前项和后项同时乘以（或除以）同一个不为零的数，比值不变，③是不成立的；比例线段的等比性质及合并性质也需要学生理解到位；其中⑥不正确的原因是0m ≠．【总结】考查比和比例的基本性质．【练习3】已知AB //CD ，AD 、BC 相交于点O ，下列比例式中正确的是（）A ．AB OA CD AD = B ．OA OBOD BC= C ．AB OB CD OC= D ．BC OBAD OD= 【答案】C【解析】∵AB CD ，∴AB AO BODC DO CO ==,对应关系要弄清楚．【总结】考查“平行型”的A 字模型．【练习4】下列条件中能判定ABC ∆∽DEF ∆的有（）①45A ∠=︒，12AB =，15AC =，45D ∠=︒，16DE =，40DF =； ②12AB =，15BC =，24AC =，20DE =，25EF =，40DF =；选择题DA BCPA B C DE 1 2③47A ∠=︒，15AB =，20AC =，47E ∠=︒，28DE =，21EF =． A ．0个B ．1个C ．2个D ．3个【答案】C【解析】对应角相等，但对应边不成比例，①不成立；三边对应成比例，可以判定②成立；两边对应成比例及夹角相等判定③成立．【总结】考查相似三角形的判定定理．【练习5】如图，已知12∠=∠，那么添加一个条件后，仍无法判定ABC ∆∽ADE ∆的是（）A ．AB AC AD AE =B ．AB BCAD DE=C ．BD ∠=∠D ．C AED ∠=∠【答案】B【解析】已知一组对应角相等，再添加任意一组对应角相等都可以判定相似，添加对应边成比例需要对应角的夹边成比例．【总结】考查相似三角形判定定理．【练习6】如图，已知，电灯P 在横杆AB 的正上方，AB 在灯光下的影子为CD ，AB //CD ，AB = 2m ，CD = 5m ，点P 到CD 的距离是3m ，则P 到AB 的距离是（）A ．56mB ．67mC ．65mD ．103m【答案】C【解析】相似比等于对应高之比，设P 到AB 的距离为xcm ，列等量关系253x =，解得65x =．【总结】考查相似三角形的性质，相似比等于对应高之比．【练习7】如图，厨房角柜的台面是三角形，如果把各边中点的连线所围成的三角形铺成黑色的大理石（图中阴影部分），其余部分铺成白色大理石，那么黑色大理石的面积与白色大理石的面积之比是（）A ．14B ．41C ．13D【答案】CABCOAB CD E 【解析】相似三角形面积之比是相似比的平方，联结三角形三边中点，将原三角形的面积四等分，所以黑色面积与白色面积之比是13．【总结】考查相似三角形的性质．【练习8】如图，在O中，向量OB，OC，AO是（）A．有相同起点的向量B．单位向量C．长度相等的向量D．相等的向量【答案】C【解析】同圆的半径相等，所以OB，OC，AO的长度是相等的．【总结】考查向量的方向、长度及相等向量的概念．【练习9】若a是任一非零向量，b是单位向量，下列各式中，正确的是（）①a b>；②a//b；③0a>；④1b=±．A．①④B．③C．①②③D．②③【答案】B【解析】单位向量的长度是单位1，方向是任意的，b是单位向量，但并没有讲是向量a方向上的单位向量，所以②是不对的．【总结】考查单位向量的概念．【练习10】如图，在ABC∆中，DE//BC，BC = 6cm，:1:4ADE ABCS S∆∆=，那么DE的长为（）A．1.5cm B．2cm C．2.5cm D．3cm【答案】D【解析】∵:1:4ADE ABCS S∆∆=，∴12DEBC=，∵BC＝6cm，∴DE＝3cm．【总结】考查相似三角形性质的应用．a x cb A ．B ．a xc b C ．axc b D ．axc bAB CP【练习11】已知线段a ，b ，c ，求作线段x ，使bx = ac ，以下方法中不正确的是（）【答案】B【解析】利用平行线分线段成比例，可以验证A 、C 、D 都成立，B 选项不成立的原因是从作图的角度看，不能保证延长线段a 与线段c 相交成的线段长度一定为所求作x ．【总结】考查利用比例线段求作第四条线段的作图方法．【练习12】如图，若P 为ABC ∆的边AB 上一点（AB >AC ），则下列条件不一定能保证ACP ∆∽ABC ∆的有（）A ．ACPB ∠=∠B ．APC ACB ∠=∠C ．AC AP AB AC =D ．PC AC BC AB=【答案】D【解析】如图，两个三角形已经有一组公共角，添加角度条件一定可以判定相似，若是添加对应边成比例不能使用到公共角的对边，所以D 选项不能判定ACP ∆∽ABC ∆．【总结】考查相似三角形的判定定理．【练习13】过三角形一边上一点画直线，使直线与另一边相交，且截得的三角形与原三角形相似，那么最多可画这样的直线的条数是（） A ．1条B ．2条C ．3条D ．4条【答案】D【解析】过三角形一边上一点画直线与另一边相交，截得的三角形与原三角形相似，这样的直线最多可画4条，每条边上两条，其中包括“平行型”和“斜交型”，如图所示．（当这个点是直角三角形斜边上一点时，最多可以画三条符合题意的直线）【总结】考查相似基本图形．【练习14】已知P 为线段AB 的黄金分割点，且AP <PB ，则（）A ．2AP AB PB = B ．2AB AP PB =C ．2PB AP AB =D ．222AP BP AB +=【答案】C【解析】线段的黄金分割点有两个，是对称的，其中三条线段之间存在一个黄金比例关系，=较短较长较长全长，即AP BPBP AB =,即2BP AP AB =．【总结】考查线段的黄金分割．AB CDEOOB DC C 'A【练习15】如图，在ABC ∆中，高BD 、CE 交于点O ，下列结论错误的是（）A ．CO CE CD CA =B ．AD AC AE AB = C ．OE OC OD OB =D ．CO DO BO EO =【答案】D【解析】基本图形“双垂型”，图中有4个三角形两两相似，都可以用“AA”来判定，ABD ACE OBE OCD ∆∆∆∆，对应边成比例换成等积式，其中D 选项比例关系不对．【总结】考查相似模型之“双垂型”．【练习16】如图，AD 是ABC ∆的中线，45ADC ∠=︒，把ADC ∆沿AD 对折，点C 落在'C 的位置，则'BC BC 的值为（）A ．14B ．13 CD ．1 【答案】C【解析】联结'CC ,因为翻折，所以'CC AD ⊥，设交点为O ，因为∠ADC ＝45°，所以∠OCD ＝45°，又因为',DB DC DC ==根据三角形内角和可以证明'90BC C ∠=，所以'BC C ∆为等腰直角三角形，即'BC BC =．【总结】考查翻折的性质及等腰直角三角形的性质．【练习17】把平面上所有单位向量归结到共同的始点，那么这些向量的终点所构成的图形是（） A ．一条线段B ．一个圆面C ．圆上的一群孤点D ．一个圆【答案】D【解析】单位向量的长度是一样的，方向是任意的，将同一平面内的单位向量的起点归为同一点，它们的终点汇聚成了一个单位圆，到定点的距离等于定长的点的轨迹是圆．【总结】考查单位向量的性质及圆的定义．【练习18】下面几个命题中，真命题的个数是（）（1）若a b =，则a b =；（2）两个向量a 、b 相等，则a b =，a //b ；（3）若AB DC =，则四边形ABCD 是平行四边形；（4）若四边形ABCD 是平行四边形，则AB DC =；（5）若a b =，b c =，则a c =；（6）若a //b ，b //c ，则a //c ． A ．4个B ．3个C ．2个D ．1个【答案】B【解析】长度相等的向量，方向不一定相同，所以（1）不正确；若AB DC =，则四边形ABCD 是平行四边形，这句话也是有漏洞的，当A 、B 、C 、D 四点共线时，构不成平行四边形，不过它的逆命题是正确的；其它选项都是正确的．【总结】考查平面向量的有关概念与性质．AB CP【练习19】 A 、B 两地的实际距离是200千米，地图上的比例尺为1 : 1000000，则A 、B两地在地图上的距离是______厘米．【答案】20厘米．【解析】厘米和千米的进率为：1100000km cm =，设图上距离为x 厘米，由题意，得1:1000000:20000000x =，解得20x =．【总结】考查比例尺的运用．【练习20】 2、3、5再配上一个比它们都大的数组成比例式，这个数是______．【答案】152．【解析】设这个数为x ，若其它三个比例项分别为,,a b c ，且abx c=，要使x 最大，则ab 取最大值，c 取最小值，所以351522x ⨯==，若x 的取值没有要求，这样的x （与2、3、5组成比例式）有三个．【总结】考查比例的基本性质．【练习21】若x : y : z = 2 : 7 : 5，且x - 2y + 3z = 6，则x =____，y =____，z =____．【答案】41410x y z ===，，．【解析】∵::2:7:5x y z =，设275x k y k z k ===，，，则227356k k k -⨯+⨯=，解得2k =，∴4,14,10x y z ===．【总结】考查学生对设“k ”法的理解应用．【练习22】已知线段a = 8厘米，b = 9厘米，则线段a 和b 的比例中项是______．【答案】62cm ．【解析】a b ，的比例中项c ab =±，当a b ，为线段长时，c 取正值．【总结】考查比例中项的定义．【练习23】如图，已知ACP B ∠=∠，AC = 4，AP = 2，则AB = ______．【答案】AB ＝8．【解析】∵ACP B ∠=∠，且A A ∠=∠，∴ACP ABC ∆∆填空题8米4米0．8米hABD 则AC APAB AC=,∵42AC AP==，，∴8AB=．【总结】考查相似三角形的判定与性质．【练习24】如图，小智在打网球时，击球点距离球网的距离是8米，已知网高是0．8米，要使球恰好能打过网，且落在离网4米的位置，则球拍击球的高度h为______米．【答案】2.4米．【解析】根据平行线分线段成比例，得0.8412h=，解得 2.4h=．【总结】考查平行线分线段成比例的应用，也可以用相似三角形的性质求解h．【练习25】如图，AB是斜靠在墙角的长梯，梯脚B距墙80厘米，梯上点D距墙70厘米，BD长55厘米，则梯子长为______．【答案】440厘米．【解析】设,AB x=根据平行线分线段成比例，得70,80ADAB=即5578xx-=，解得440x=，所以梯子的长为440厘米．【总结】考查平行线分线段成比例的应用．【练习26】若两个相似三角形的面积比为2 : 9，则这两个三角形的对应中线的比是______．3．．【总结】考查相似三角形的性质：面积比是相似比的平方比，相似比也是对应中线之比．【练习27】在边长为1的正方形ABCD 中，设AB a =，BC b =，AC c =，则a b c ++=______；a c b +-=______；c a b --=______．【答案】20；．【解析】（1）2a b c AB BC AC AC ++=++=,因为正方形边长为1，所以AC =即a b c ++=（2）2a c b AB AC BC AB AC CB AB +-=+-=++=,即2a c b +-=；（3）0c a b AC AB BC BC BC --=--=-=，即0c a b --=．【总结】考查平面向量的线性运算．【练习28】计算：()()325232a b a b +--=______．【答案】19b ．【解析】()()325232a b a b +--=6156419a b a b b +-+=．【总结】考查实数与向量相乘及平面向量的加减运算．【练习29】若()()::a b x y x y =+-，则:x y =______．【答案】a ba b+-．【解析】设()()a b k x y a b k x y +=+-=-，，解得22a b x k a b y k +⎧=⎪⎪⎨-⎪=⎪⎩，所以:a b x y a b +=-．【总结】考查设“k ”法的理解应用．【练习30】点P 是线段AB 的黄金分割点，且AP =2，则AB =______．31+．【解析】（1）当AP为较长的线段时，AP AB =1AB ；（2）当AP为较短的线段时，AP BP =解得1BP =，123AB =+=．【总结】考查线段的黄金分割，等量关系=短长长全，一条线段的黄金分割点有两个，需要学生具有分类讨论的思想．【练习31】过直角三角形的斜边上一点画直线，使直线与另一边相交，且截得的三角形与原三角形相似，那么最多可画______条这样的直线；过直角三角形的直角边上一点画直线，使直线与另一边相交，且截得的三角形与原三角形相似，那么最多可画______条这样的直线．【答案】3条；4条．【解析】当这个点在直角边上时，可以画4条这样的直线使得截得的三角形与原三角形相似；当这个点在斜边上时，可以画3条（有2条重合在一起）这样的直线使得截得的三角形与原三角形相似，如图所示．【总结】考查相似基本图形，结论是“直4斜3”．ABCD EF KH【练习32】如图，AD = DE = EC ，且AB // DF // EH ，AH 交DF 于K ，则EHKF=______．【答案】23EH KF =．【解析】∵DK EH ，∴AD DKAE EH =， ∵EH DF ，∴CE EHCD DF=, ∵AD DE EC ==, ∴1122DK EH EH DF ==，, 设DK k =，则24EH k DF k ==，， ∴23EH KF =．【总结】考查平行线分线段成比例的性质运用．【练习33】在等边三角形ABC 中，点D 、E 分别在AB 、AC 上，且DE // BC ，如果BC = 8厘米，AD : AB = 1 : 4，那么ADE ∆的周长为_________．【答案】6厘米．【解析】∵DE BC ,∴ADE ABC ∆∆，∵:1:4AD AB =，∴:1:4ADE ABC C C ∆∆=,因为8BC =，所以24ABC C ∆=，12464ADE C ∆=⨯=．【总结】考查相似三角形的性质运用．【练习34】如果直角三角形的斜边长为18，那么这个直角三角形的重心到直角顶点的距离为______．【答案】6．【解析】直角三角形的斜边长为18，则斜边上的中线为9，根据三角形重心的性质，重心到直角顶点的距离是斜边中线的23．【总结】考查直角三角形重心的性质运用．AB CD【练习35】如图，在平行四边形ABCD中，AB a=，CB b=，则向量AO为______．（结果用a和b表示）【答案】1122a b-．【解析】∵平行四边形对角线互相平分，∴11()22AO AC AB BC==+，∵AB a CB b==，，∴1122AO a b=-．【总结】考查平面向量的线性分解及运算，结合平行四边形的性质．【练习36】如图，将①BAD C∠=∠；②ADB CAB∠=∠；③2AB BD BC=；④CA ABAD DB=；⑤BC ACBA DA=；⑥BC DABA AC=中的一个作为条件，另一个作为结论，组成一个真命题，则条件是______，结论是______．（只填序号）【答案】答案不唯一，比如条件是①，结论是③．【解析】这是一个典型的相似基本图形“母子型”，其中可以作为条件的选择不唯一，结论自然也不一，情况如下：（1）当条件为①时，结论可以是②③④⑤；（2）当条件为②时，结论可以是①③④⑤；（3）当条件为③时，结论可以是①②④⑤．【总结】考查相似三角形的判定和性质运用以及对基本图形“母子型”的理解运用．A BCDOAB CD【练习1】已知23a c eb d f ===，18ac e =--，0bd f ++≠，求b d f ++的值．【答案】27b d f ++=．【解析】∵203a c e b d f b d f ===++≠，，∴23a c eb d f ++=++，又∵18ac e ++=， ∴27bd f ++=．【总结】考查等比性质的运用．【练习2】已知b c c a a bx a b c+++===，求x 的值．【答案】21x =-或．【解析】（1）当0a b c ++=时，b c a c a b a b c +=-+=-+=-，，，∴1ax a-==-；（2）当0a b c ++≠时，b c c a a bx a b c+++===，根据等比性质， 2()2b c c a a b a b c x a b c a b c+++++++===++++；综上，12x =-或．【总结】考查等比性质的运用，需要学生理解等比性质成立的条件，以及有分类的思想．【练习3】如图，已知点D 在ABC ∆的边AB 上，且ACD B ∠=∠，:1:3ACD DBC S S ∆∆=．求ACAB的值．【答案】12AC AB =．【解析】∵,ACD B A A ∠=∠∠=∠,∴ACD ABC∆∆ ∵:1:3ACD BCD S S ∆∆=，∴:1:4ACD ABC S S ∆∆=，∴12AC AB =．【总结】考查相似三角形的判定与性质，需要理解相似三角形的相似比与面积比的关系．【练习4】如图，已知点E 、F 分别在矩形ABCD 的边BC 和CD 上，EF AE ⊥，BE = 3cm ，AB = 6cm ，矩形ABCD 的周长为28cm ，求CF 的长．解答题AB CDEFAB CDE FOPAB CDEF【答案】52CF cm=．【解析】∵矩形ABCD，628AB C==，周长，∴8BC=，∵AE EF⊥,AB BC DC BC⊥⊥，，可证ABE ECF∆∆,∴AB BEEC EC=，∵63835AB BE EC===-=，，，∴52CF cm=．【总结】本题在矩形背景下考查“一线三直角”模型．【练习5】如图，已知ABC∆中，AB = AC，CD是边AB上的高，且CD = 2，AD = 1，四边形BDEF是正方形．CEF∆和BDC∆相似吗？试证明你的结论．【答案】CEF BDC∆∆，证明略．【解析】1290AD CD ADC AC==∠=∴=，，，1AB AC AB BD=∴==，，1ABCD BD DE EF∴===正方形，，∴21)3CE=-=∴BDEC==CDEF=，即BD CDEC EF=，又∵90BDC CEF∠=∠=，∴BDC CEF∆∆．【总结】本题结合直角三角形的性质考查相似三角形的判定，同时需要学生扎实的运算功底．【练习6】如图，D、E、F分别是ABC∆的边BC、AB、AC的中点，AD与EF相交于点O，线段CO的延长线交AB于点P．求证：AB = 3AP．【答案】证明略．【解析】∵E F AB AC、分别是、的中点，∴12EF BC EF BC=，，ABCEF∴12AE EO AB BD ==，∵D 是BC 的中点，∴14EO BC =， ∵EO BC ，∴14PE EO PB BC ==，设PE k =，则4PB k =，3BE k =，∴26AB EB k ==，2AP AB PB k =-=，∴:6:23AB AP k k ==，即3AB AP =．【总结】考查平行线分线段成比例的综合运用．【练习7】如图，在Rt ABC ∆中，90ACB ∠=︒，点D 为AB 的中点，BE CD ⊥，垂足为点F ，BE 交AC 于点E ，CE = 1cm ，AE = 3cm ．（1）求证：ECB ∆∽BCA ∆；（2）求斜边AB 的长．【答案】（1）证明略；（2）AB =【解析】（1）∵90,ACB ∠=D AB 为的中点，∴DA DC =，∴A ECF ∠=∠,∵BE CD ⊥,∴90FCB CFB ∠+∠=，∵90FCE ECF ∠+∠=，∴ECF CBF ∠=∠， ∴A CBE ∠=∠,∵ECB BCA ∠=∠,∴ECB BCA ∆∆；（2）∵ECB BCA ∆∆，∴EC CBBC CA=,∵14EC AC AE EC ==+=，，∴2BC =， ∵90ACB ∠=，∴AB = 【总结】考查相似三角形的判定和性质的综合运用．。

沪教版九年级数学暑假同步讲义第14讲锐角的三角比章节复习培优 (解析版)

锐角的三角比是九年级数学上学期第二章的内容．本章的基本要求是理解锐角三角比的概念，会求特殊锐角的三角比的值，会解直角三角形，需理解仰角、俯角、方向角、坡度和坡角等概念，并能解决有关的实际问题．重点是应用锐角三角比的意义及运用解直角三角形的方法进行有关的几何计算．难点是解直角三角形的应用．已知锐角，求三角比已知锐角的三角比，求锐角锐角的三角比的概念已知一边和一个锐角已知两边直角三角形中的边角关系解直角三角形解直角三角形的应用单元练习：锐角的三角比内容分析知识结构步同级年九2 / 19【练习1】下列不等式成立的是（）A ．sin60sin45sin30︒<︒<︒B ．cos60cos45cos30︒>︒>︒C ．tan60tan45tan30︒<︒<︒D ．cot60cot 45cot30︒<︒<︒【答案】D【解析】通过计算特殊角的锐角三角比的值，可以判断D 正确．【总结】当锐角的度数逐渐增大时，正切值和正弦值也逐渐增大，而余切值和余弦值反而逐渐减小．【练习2】在Rt ABC ∆中，90C ∠=︒，下列条件中不能解直角三角形的是（）A ．已知c 和aB ．已知b 和A ∠C ．已知a 和bD ．已知A ∠和B ∠ 【答案】D【解析】考查解直角三角形的条件．【总结】要解直角三角形，必须至少知道一条边．【练习3】已知AD 是Rt ABC ∆的斜边BC 边上的高，BC = a ，B β∠=，那么AD 等于（） A ．2sin a βB ．2cos a βC ．sin cos a ββD ．sin tan a ββ【答案】C【解析】解：在ABC Rt △中，BCAB=βcos ，∴βcos a AB =．在ABD Rt △中，ABAD=βsin ∴βββsin cos sin a AB AD ==．【总结】本题主要考查利用锐角三角比解直角三角形．选择题【练习4】如果等腰三角形的底角为30°，腰长为6厘米，则这个三角形的面积为（）A ．4.5平方厘米 B． C．平方厘米D ．36平方厘米【答案】B【解析】解：根据题意解直角三角形可得：等腰三角形的高为3，底边长为36，则三角形的面积为3933621=⨯⨯．【总结】本题主要考查30°角的锐角三角比的值．【练习5】如图，设点A （m ，n ）是锐角α的一条边上的任意一点，则mn的值（） A ．只与角α的大小有关B ．只与点A 在角α的边上的位置有关C ．与角α的大小及点A 在角α的边上的位置有关D ．与角α的大小及点A 在角α的边上的位置无关【答案】A【解析】=cot mn α，所以只与角α的大小有关．【总结】本题主要考查锐角三角比的概念及相关性质．【练习6】等腰三角形的两条边分别为5和6，关于底角A 下列等式中成立的是（）A ．3sin 5A =B ．3cos 5A =C ．3sin 5A =或512D ．3cos 5A =或512【答案】D【解析】①等腰三角形的两腰为5，底为6时，3cos 5A =； ②等腰三角形的两腰为6，底为5时，5cos 12A =．【总结】本题主要考查锐角三角比的概念，注意要分类讨论．【练习7】如图，CD 是平面镜，光线从点A 出发经CD 上点E 反射后照射到点B ，若入步同级年九4 / 19射角为α，AC ⊥CD ，BD ⊥CD ，垂足分别为C 、D ，且AC = 3，BD = 6，CD = 11，则tan α的值为（）A ．113B ．311C ．911D ．119【答案】D【解析】解：由光线反射定律可知：BED AEC ∠=∠．则BED AEC ∠=∠tan tan ． ∴DE BDCE AC =． ∴CE CE -=1163，解得：311=CE ． ∴9113311tan tan ====AC CE A α．【总结】本题主要是跟物理知识相结合，注意反射角等于入射角的运用．【练习8】菱形的边长为4，有一个内角为40°，则较短的对角线是（）A ．4sin40︒B ．4sin20︒C ．8sin20︒D ．8cos20︒【答案】C【解析】考查菱形对角线平分一组内角和解直角三角形基础知识．【练习9】如图，在ABC ∆中，30A ∠=︒，E 为AC 上一点，且AE : EC = 3 : 1，EF ⊥AB于点F ，连接FC ，则cot CFB ∠的值为（）A 136B 132C 433D 134【答案】DABCDαE【解析】过C 作CG ⊥AB ．∵EF ⊥AB ，CG ⊥AB ，∴EF ∥CG ∴43===AG AF GC EF AC AE ．设a FE 3=，则a CG 4=．在AEF Rt △中，AF EF A =tan ，∴AFa333=，∴a AF 33=． ∵43=AG AF ，∴a GF 3= ∴在GFC Rt △中，4343cot ===∠a a CG FG CFB ．【总结】本题主要考查通过添加辅助线将所要求的锐角放到直角三角形中求解．【练习10】在ABC ∆中，AD 是BC 边上的高，且AD BD ==CD = 1，那么BAC ∠的大小可能是（） A ．15° B ．75° C ．15°，75° D ．105°【答案】C【解析】解：在ABD Rt △中，133tan ===∠AD BD BAD ，∴︒=∠45BAD ．在ACD Rt △中，3331tan ===∠AD CD CAD ，∴︒=∠30CAD ． ∴①︒=︒+︒=∠+∠=∠753045DAC BAD BAC ； ②︒=︒-︒=∠-∠=∠153045DAC BAD BAC ．【总结】本题主要考查解直角三角形，注意分类讨论．步同级年九6 / 19A B CDABCDE【练习11】如图，沿AC 方向开山修路，为了加快施工进度，要在小山的另一边同时施工，从AC 上一点B ，取145ABD ∠=︒，BD = 500米，55D ∠=︒，要使A 、C 、E 成一直线，那么开挖点E 离点D 的距离是（）米 A ．500sin55︒ B ．500cos55︒C ．500tan55︒D ．500cot55︒【答案】B【解析】解：∵145ABD ∠=︒，∴︒=∠35CBD ．∵55D ∠=︒，∴︒=∠90E ．在BED Rt △中，BD EDD =cos ，∴︒=55cos 500ED ．【总结】本题主要考查解直角三角形的运用，注意分析题目中的条件．【练习12】如图，四边形ABCD 中，=135A ∠︒，90B D ∠=∠=︒，23BC =，AD = 2，则四边形ABCD 的面积是（） A ．42B ．3C ．4D ．6【答案】C【解析】延长CD 和BA 交于点E ．∵=135A ∠︒，90B D ∠=∠=︒，∴45C EAD ∠=∠=．∴()4221322121212222=⨯-⨯=-=AD BC S ABCD 四边形．【总结】本题主要考查通过解直角三角形求几何图形的面积．【练习13】如图，在梯形ABCD 中，AD // BC ，AC ⊥AB ，AD = CD ，4cos 5DCA ∠=， BC = 10，则AB 的值是（） A ．3 B ．6 C ．8 D ．9【答案】BA BCABC D EF 【解析】解：∵AD = CD ，∴DCA DAC ∠=∠．∵AD // BC ，∴ACB DAC ∠=∠， ∴ACB DCA ∠=∠． ∴BCA DCA ∠=∠cos cos 在ABC Rt △中，BCACACB =∠cos ， ∴1054AC =，解得：8=AC ． ∴68102222=-=-=AC BC AB ．【总结】当两个锐角相等时，它们的相应的锐角三角比的值也相等．【练习14】如图，某地夏季中午，当太阳移至房顶上方偏南时，光线与地面成80°角，房屋朝南的窗子高AB = 1.8米，要在窗子外面上方安装水平当光板AC ，使午间光线不能直接射入室内，则挡光板的宽度AC 为（） A ．1.8sin80︒B ．1.8cos80︒C ． 1.8sin80︒D ．以上都不对【答案】D【解析】正确答案为︒80cot 8.1．【总结】本题主要考查锐角三角比的准确运用．【练习15】如图，已知矩形ABCD 的两边AB 与BC 的比为4 : 5，E 是AB 上的一点，沿CE 将EBC ∆向上翻折，若点B 恰好落在边AD 上的点F ，则tan AEF ∠等于（）A ．34B ． 43C ．35D ． 53 【答案】B【解析】解：设x DC 4=，x BC 5=．∵△CBE ≌△CFE ， ∴x CF 5=．在DFC Rt △中，()()x x x DC FC DF 3452222=-=-=．∵︒=∠+∠90AFE AEF ，︒=∠+∠90DFC AFE ， ∴DFC AEF ∠=∠， ∴4343tan tan ===∠=∠x x DF DC DFC AEF ．【总结】本题一方面考查翻折的性质，另一方面考查等角的锐角三角比的相关性质．【练习16】菱形的两条对角线长为23和6，则菱形较小的内角为______．【答案】60°．【解析】∵菱形的对角线互相垂直且每条对角线平分一组内角， ∴最小内角一半的正切值是33， ∴最小内角一半为30°，∴最小内角为60°．【总结】本题主要考查特殊角的锐角三角比的值以及菱形的性质．【练习17】如果24cos 8cos 30αα-+=，那么锐角α= ______．【答案】60°．【解析】解方程可得：23cos =α或21cos =α，∵1cos 0<<α，∴21cos =α，∴︒=60α．【总结】本题主要考查特殊角的锐角三角比的值．【练习18】校园内有两棵树，相距12米，一棵树高13米，另一棵树高8米，一只小鸟从一棵树的顶端飞到另一棵树的顶端，小鸟至少要飞______米．【答案】13．【解析】如图，AB =8，CD =13，BD =12．过A 作AE ⊥DC ，则四边形ABDE 为矩形． ∴AB =DE =8，BD =AE =12，∴135122222=+=+=CE AE AC ．【总结】本题主要考查根据题目中的已知条件求直角三角形的斜边．填空题ABC D【练习19】等腰三角形ABC中，AB = AC，BC = 10，ABCS∆=，那么A∠=______．【答案】120°．【解析】∵12ABCS BC h∆=⋅⋅=，BC = 10，∴335=h．∴33533521tan===BChB，∴︒=∠30B．∴︒=∠-︒=∠1202180BA．【总结】本题主要考查特殊角的锐角三角比的值以及等腰三角形的性质．【练习20】ABC∆中，90C∠=︒，斜边上的中线CD = 6，sin A =13，则ABCS∆= _____．【答案】【解析】∵90C∠=︒，斜边上的中线CD = 6，∴AB = 2CD = 12．∵sin A =13，∴31=ABBC．∴4=BC．∴284122222=-=-=CBABAC．∴11422ABCS AC BC==⨯⨯=【总结】本题主要考查解直角三角形以及直角三角形的性质．【练习21】如图，在C处测得铁塔AB的塔顶A的仰角为30°，向塔前进10米到达D处，在D处测得A的仰角为45°，则铁塔的高为______．【答案】535+．【解析】由题意，可设xBDAB==．在ABCRt△中，33tan==BCABC，∴xCB3=．∴xx310=+，解得：535+=x．【总结】本题主要考查解直角三角形与仰角结合的应用．【练习22】某拦水坝的横截面为梯形ABCD，其中斜面AB的坡比为1 : 3，如果自A向B 走了米，那么升高的高度为______米．【答案】10．【解析】设斜面AB 的垂直高度为x ，则水平高度为x 3， ∴()101010322==+x x x ，解：10=x∴升高的高度为10米．【总结】本题主要考查解直角三角形在坡比问题中的应用．【练习23】如图，在平地上种植树木时，要求株距（相邻两树间的水平距离）为4米．如果在坡度为1：34的山坡上种树，也要求株距为4米，则相邻两树间的坡面距离是______．【答案】5．【解析】考查坡度的定义．【练习24】用高为h 的测角仪测得铁塔AB 的顶点A 的仰角为α，测角仪到铁塔距离为m ，那么铁塔高度为____________．【答案】αtan m h +．【解析】考查仰角的定义．【练习25】如图，某人从A 点沿西南方向行了B 点后观察到原点O 在它的南偏东60°的方向上，则原来A 的坐标为______．【答案】04⎛+⎝，．步同级年九12 / 19ABP'A'P【解析】由题意可知：︒=∠45A ，︒=∠60AOB ，24=AB ．过B 作BC ⊥AO ．在ABC Rt △中，22sin ==BA CA A ， ∴4=CA ，4=BC ．在OBC Rt △中，3tan ==∠OC CB AOB ， ∴334=CO ． ∴3344+=OA ．∴A 点的坐标为⎪⎭⎫ ⎝⎛+33440，．【总结】本题主要考查通过添垂线将特殊角放在直角三角形中，然后进行求解．【练习26】如图，如果APB ∆绕点B 按逆时针方向旋转30°后得到''A P B ∆，且BP = 2，那么'PP 的长为______．（62sin15-︒=）【答案】26-．【解析】联结'PP ，过B 作BD ⊥'BP ． ∵︒=∠30'PBP ，'BP BP =， ∴︒=∠15PBD ．∴在BPD Rt △中，PB DP PBD =∠sin ，∴2426DP =-，∴226-=PD ． ∴262'-==PD PP ．【总结】本题主要考查通过添垂线将特殊角放在直角三角形中，然后进行求解，另外还考查了旋转的性质．【练习27】 ABC ∆中，AB = 5，AC = 8，30C ∠=︒，则ABC ∆的面积是______．【答案】638±．【解析】过A 作AD ⊥BC ，垂足为D ．ABCDM在ACD Rt △中，421==AC AD ． ∴34482222=-=-=AD AC CD ．在Rt ABD △中，3452222=-=-=AD AB BD ．()63843342121+=⋅+⋅=⋅⋅=AD BC S ABC △； ②()638433421211-=⋅-⋅=⋅⋅=AD C B S ABC △．【总结】本题主要考查根据已知条件解直角三角形，另外要注意进行分类讨论．【练习28】如图，在Rt ABC ∆中，90ACB ∠=︒，A B ∠<∠，沿ABC ∆的中线CM 将CMA ∆折叠，使点A 落在点D 处，若CD 恰好与MB 垂直，则tan A 的值为______．【答案】33．【解析】∵△AMC ≌△DMC ，∴D A ∠=∠，DCM ACM ∠=∠． ∵CM 为Rt ABC ∆的中线， ∴ACM A ∠=∠． ∵CD 恰好与MB 垂直，∴︒=∠+∠90DCB B ．又∵︒=∠+∠90A B ， ∴A DCB ∠=∠． ∴DCM ACM DCB ∠=∠=∠．∵︒=∠+∠+∠90DCM ACM DCB ， ∴︒=∠30ACM ．∴︒=∠30A ，∴33tan =A ．【总结】本题综合性较强，主要考查翻折的性质以及直角三角形的性质和特殊角的锐角三角比的值．解答题步同级年九14 / 19【练习29】计算：cos 45sin 301cos60tan 452︒-︒︒+︒．【答案】212-．【解析】解：原式=212121212122-=⨯+-．【总结】本题主要考查特殊角的锐角三角比的值及代数式求值．【练习30】已知α为锐角，且11tan α-无意义，求()()2cos 15615sin ααα+︒-︒的值．【答案】21-．【解析】∵α为锐角，且11tan α-无意义．∴1tan =α，∴︒=45α．∴原式=212223621245sin 30cos 660cos 2-=⨯⨯-⨯=︒︒-︒．【总结】本题主要考查特殊角的锐角三角比的值以及分式无意义的条件．【练习31】如图，在ABC ∆中，90C ∠=︒，AC = BC ，BD 为AC 边上的中线．求sin ABD ∠和tan ABD ∠的值．【答案】1010，31．【解析】过D 作DE ⊥AB ，垂足为E ．设AE =DE =x ，则x AD 2=．∵BD 为AC 边上的中线， ∴x AC 22=．∴x AC AB 42==． ∴x BE 3=． ∴x BE DE BD 1022=+=．∴101010sin ===∠xx DB DE ABD ，313tan ===∠x x EB DE ABD ．【总结】本题主要考查解直角三角形以及锐角三角比的概念．【练习32】如图，等腰梯形ABCD ，AD // BC ，45DBC ∠=︒，翻折梯形ABCD ，使点B重合于点D ，折痕分别交AB 、BC 于点F 、E ，若AD = 2，BC = 8．求：（1）BE 的长；（2）CDE ∠的正切值．【答案】（1）5；（2）53．【解析】∵EF 垂直平分BD ， ∴DE BE =． ∴︒=∠=∠45BDE DBC ， ∴︒=∠90DEB ．过A 作AG ⊥BC ，由等腰梯形的性质可得：3==EC BG ． ∴538=-=-=EC BC BE ． ∴5==BE DE ．∴在DEC Rt △中，53tan ==∠DE CE CDE ．【总结】本题综合性较强，主要考查翻折的性质以及等腰梯形的性质和特殊角的锐角三角比的值．【练习33】如图，已知梯形ABCD 中，AD // BC ，90ABC ∠=︒，45C ∠=︒，BE ⊥CD 于点E ，AD = 1，CD =．求BE 的长．【答案】223．【解析】过D 作DF ⊥BC ，垂足为F ，则可得四边形ABFD 为矩形．A B CDE FG AB CDEF∵在DCF Rt △中，DC DFC =sin ，∴2222DF =，∴2=FD ． ∴2=CF ． ∴2=AB ，1==AD BF ． ∴3=BC ．∵在BCE Rt △中，BC BEC =sin ，∴322BE =，∴223=BE ．【总结】本题主要考查解直角三角形，注意通过添加垂线，将特殊角放到直角三角形中．【练习34】如图，在电线杆上的C 处引拉线CE 、CF 固定电线杆，拉线CE 和地面成60°．在离电线杆6米的B 处安置测角仪，在A 处测得C 处的仰角为30°，已知测角仪高AB 为1.5米，求拉线CE 的长．【答案】34+．【解析】过A 作AG ⊥CD ，垂足为G ．由题意可得：︒=∠30CAG ，︒=∠60CED ，6==BD AG ．∵在ACG Rt △中，AG CGCAG =∠tan ，∴633CG =，∴32=CG ， ∴2332+=CD ．∵在CED Rt △中，CECDCED =∠sin ， ∴CE233223+=，∴34+=CE ．【总结】本题主要考查解直角三角形在仰角问题中的应用．【练习35】如图，有一朝向为正南方向的居民楼CD ，该居民楼的一楼是高6米的超市，超市以上是居民住房，在该楼的前面15米处要盖一栋高20米的新楼AB ，当冬季正午阳光与水平线的夹角为30°时．（1）问超市以上的居民住房采光是否有影响？为什么？（2）若要超市采光不受影响，两楼应相距多少米？【答案】（1）不受影响，理由见解析；（2）320．EAB CEFG【解析】（1）由题意可知：︒=∠30AEF ，15=EF ．在CED Rt △中，∵FE AF AEF =∠tan ，∴1533AF=，∴35=AF ． ∵636.113520>≈-==BF EC ，∴超市以上的居民住房采光不受影响．（2）当︒=∠30ACB 时，超市采光不受影响，在ACB Rt △中，BCABACB =∠tan ， ∴BC2033=，∴320=BC ． ∴两楼至少相距320米．【总结】本题主要考查解直角三角形在实际生活中的应用．【练习36】如图，拦水坝的横截面为梯形ABCD ，坝顶宽BC 为6米，坝高为3.2米，为提高拦水能力，需要将水坝加高2米，并保持坝顶宽度不变，迎水坡CD 的坡度不变，但背水坡坡度由原来的1 : 2变成1 : 2.5．求加高后的坝底HD 的长为多少？【答案】29.4米．【解析】解：∵BH =3.2， ∴加高后MF =EN =5.2，MN =EF =BC =6，在HMF Rt △和EDN Rt △中，5.21=HM FM ，21=DN EN ∴HM =2.5MF =13， DN =2EN =10.4 ，∴HD =13+6+10.4=29.4．【总结】本题主要考查解直角三角形在坡度问题中的应用．【练习37】近日A 市气象局测得沙尘暴中心在A 市正西300公里的B 处，并以107 公里/小时的速度向南偏东60°的BF 方向移动，距沙尘暴中心200公里的范围是受沙尘暴影响的区域．（1）A 市是否受到本次沙尘暴的影响？（2）若A 市受沙尘暴影响，求受影响的时间有多长？【答案】（1）是；（2）10小时．【解析】如图，点C 为台风离A 市最近的地方． D 为A 市是开始受到沙尘暴影响，E 为A 市不受沙尘暴影响．在ABC Rt △中，20015021<==AB AC ．∴A 市会受到本次沙尘暴影响．（2）由题意可知：AD =AE =200．在ADC Rt △中，7501502002222=-=-=CA DA DC ，∴71002==DC DE ．∴107107100==t ．【总结】本题主要考查解直角三角形在方位角问题中的应用．【练习38】如图，在ABC ∆中，120BAC ∠=︒，AB = 10，【答案】143．【解析】解：过C 作CD ⊥AB ，垂足为D ，过B 作BE ⊥AC ，垂足为E ．∵120BAC ∠=︒，∴︒=∠=∠60EAB DAC ．在ABE Rt △中，521==AB AE ，∴355102222=-=-=AE BA EB ．在ADC Rt △中，2521==AC AD ．∴2352552222=⎪⎭⎫ ⎝⎛-=-=AD CA DC ．在CBE Rt △中，()7510352222=+=+=CE BE CB ，∴在BDC Rt △中，72375325sin ===BC DC B ．在BEC Rt △中，737535sin ===BC BE C ；∴33sin sin =142B C ．【总结】本题主要考查解直角三角形的应用，综合性较强，要注意去寻找包含所求锐角的直角三角形．。

沪科版数学九年级下册综合训练50题含参考答案

沪科版数学九年级下册综合训练50题含答案（填空、解答题）一、填空题1．“任意买一张电影票，座位号是2的倍数”，此事件是______事件．（填“确定”或“不确定”）．【答案】不确定【分析】根据确定事件和随机事件的定义来区分判断即可，必然事件和不可能事件统称确定性事件．随机事件：在一定条件下，可能发生也可能不发生的事件称为随机事件．【详解】根据题意，座位号可能是奇数可能是偶数，所以此事件是随机事件，即不确定事件．故答案为：不确定．【点睛】本题考查了确定事件和随机事件，理解定义是解题的关键．2．一个不透明的箱子里装有红球、蓝球、黄球共20个，除颜色外，形状、大小、质地等完全相同．通过大量摸球试验，小明发现摸到红球、黄球的频率分别稳定在10%、15%，则估计箱子里蓝球有__个．【答案】15【分析】利用频率估计概率，可得到摸到红色、黄色球的概率为10%和15%，则摸到蓝球的概率为75%，然后根据概率公式可计算出口袋中蓝色球的个数．⨯--=（个），【详解】解：估计箱子里蓝球有20(110%15%)15故答案为：15．【点睛】本题考查了利用频率估计概率：大量重复实验时，事件发生的频率在某个固定位置左右摆动，并且摆动的幅度越来越小，根据这个频率稳定性定理，可以用频率的集中趋势来估计概率，这个固定的近似值就是这个事件的概率．用频率估计概率得到的是近似值，随实验次数的增多，值越来越精确．3．如图所示，：AB AB=，∴________=________.【答案】 APB ∠ AMB ∠【分析】根据同弧所对的圆周角相等即可解答.【详解】AB AB =∴APB ∠=AMB ∠故答案为APB ∠，AMB ∠【点睛】本题考查的是“同弧所对的圆周角相等”，熟练掌握这一结论是关键. 4．一个不透明的袋中装有3个红球，2个黄球，1个白球，每个球除颜色外都相同，从袋中任意摸出一球，则摸到__________球的可能性最大．（填“红色”、“黄色”或“白色”）5．如图，CD 为∴O 的直径，弦AB ∴CD 于点E ，CE ＝1，AB ＝10，则直径CD ＝__________．【答案】26【分析】连接OA ，先根据垂径定理，求出AE 的长，再设出圆的半径OA 为x ，表示出OE ，根据勾股定理建立关于x 的方程，求出方程的解即可得到x 的值即可得到答案．【详解】解：连接OA ，∵DE ⊥AB ，且AB ＝10，∴AE ＝BE ＝5，设圆O 的半径OA 的长为x ，则OC ＝OD ＝x∵CE ＝1，∴OE ＝x ﹣1，在直角三角形AOC 中，根据勾股定理得：x 2﹣（x ﹣1）2＝52，解得：x ＝13，所以CD ＝26．故答案为：26．【点睛】此题考查了学生对垂径定理的运用与掌握，注意构建以圆的半径，弦的一半及弦心距的直角三角形是解题关键．6．某声讯台综艺节目接到热线电话3000个，现要从中抽取“幸运听众”10名，刘强同学打通了一次热线电话，那么她成为“幸运听众”的概率为________．7．如图，A 、C 、D 为O 上的点，35D ∠=，则AOC ∠=________°．【答案】70【分析】由圆周角定理即可得出答案．【详解】解：∴∴D =35°，∴∴AOC =2∴D =70°．故答案为70．【点睛】本题考查了圆周角定理：在同圆或等圆中，同弧或等弧所对的圆周角相等，都等于这条弧所对的圆心角的一半．8．如图，四边形ABCD 内接于∴O ，点M 在AD 的延长线上，71∠︒=CDM ，则AOC ∠=___．【答案】142︒【分析】先求出∴ADC=180°-∴CDM=109°，然后求出∴B=180°-∴ADC=71°，再由圆周角定理求解即可．【详解】解：∴∴CDM=71°，∴∴ADC=180°-∴CDM=109°，∴四边形ABCD是圆内接四边形，∴∴B=180°-∴ADC=71°，∴∴AOC=2∴B=142°，故答案为：142°．【点睛】本题主要考查了圆内接四边形，圆周角定理，熟知相关知识是解题的关键．9．如图，三个同心圆扇形的圆心角∴AOB为120o，半径OA为6cm，C、D是圆弧AB的三等分点，则阴影部分的面积等于_____cm2．10．直角三角形的两直角边分别3，4；则它的外接圆半径R=___________．【答案】2.511．“早发现，早报告，早隔离，早治疗”是我国抗击“新冠肺炎”的宝贵经验，其中“早”字出现的频率是_______．12．寒假即将来临，小明要从甲、乙、丙三个社区中随机选取一个社区参加综合实践活动，那么小明选择到甲社区参加实践活动的可能性为__________．13．如图，小明向图中的格盘中随意投掷一枚棋子，该棋子落在三角形内的概率是__________；A B C分别14．三个正方形方格在扇形中的位置如图所示，点O为扇形的圆心，格点,,在扇形的两条半径和弧上，已知每个方格的边长为1，则图中阴影部分面积为________．15．边长为6的正三角形的外接圆半径是________．16．已知ABC三边长为3，4，5，则ABC外接圆的直径为______．【答案】5【分析】先根据勾股定理的逆定理得出ABC为直角三角形，根据直径所对的圆周角为直角，即可得出结论．【详解】解：∴222+=，345∴ABC为直角三角形，∴ABC外接圆的直径为5．故答案为：5．【点睛】本题主要考查了勾股定理的逆定理以及直径所对的圆周角为直角，解题的关键是熟练掌握相关内容．17．在ABC 中，90C ∠=︒，3AC =，4BC =，则ABC 的内切圆的半径为__________．【答案】1【详解】如图，设△ABC 的内切圆与各边相切于D ，E ，F ，连接OD ，OE ，OF ，则OE∴BC ，OF∴AB ，OD∴AC ，设半径为r ，CD=r ，∴∴C=90°，BC=4，AC=3，∴AB=5，∴BE=BF=4-r ，AF=AD=3-r ，∴4-r+3-r=5，∴r=1．∴∴ABC 的内切圆的半径为 1．18．如图，ABC 内接于半径为2的O ，ABC ∠、ACB ∠的平分线交于点I ，110BIC ∠=︒，则劣弧BC 的长为______．19．如图，四边形ABCD是∴O的内接正方形，若正方形的面积等于4，则∴O的面积等于_______．【答案】2π．【分析】根据正方形的面积公式求得半径，然后根据圆的面积公式求解．20．如图，已知反比例函数过A，B两点，A点坐标(2,3)，直线AB经过原点，将线段AB绕点B顺时针旋转90°得到线段BC，则C点坐标为________．，证明ABD CBE≌从而求得，反比例：k yx =AB BC⊥ABD∠+∠CBE∴∠= AB BC=ABD∴△≌△4BE AD ∴==，6CE BD ==∴(4,7)C -．故答案为：(4,7)-．【点睛】本题考查一次函数与反比例函数的综合运用、三角形全等，平面内点的坐标，图形的旋转．解题的关键是掌握一次函数与反比例函数的相关性质和数形结合思想．21．已知在平面直角坐标系中，∴ABC 三个顶点的坐标分别为（0，4）、（6，4）、（0，﹣1），则这个三角形的外接圆的圆心坐标为_____．记住直角三角形的外接圆的圆心是斜边的中点．22．如图，在Rt△ABC中，∴C＝90°，CB＝2，CA＝4，线段AD由线段AB绕点A逆时针方向旋转90°得到，△EFG由△ABC沿CB方向平移得到，当直线EF恰好经过点D时，CG的长等于_____．故答案为5．【点睛】考查了旋转的性质：对应点到旋转中心的距离相等；对应点与旋转中心所连线段的夹角等于旋转角；旋转前、后的图形全等．也考查了等腰直角三角形的性质和正方形的性质．也考查了平移的性质．23．P 为∴O 内一点，且OP ＝8 cm ，过P 的最长弦长为20 cm ，则过P 的最矩弦长为________．24．如图，在菱形ABCD 中，AB ＝1，60BAD ∠=︒ ，把菱形ABCD 绕点A 顺时针旋转30°得到菱形AB C D ''' ，其中点C 的运动路径为CC ' ，边AB 、BC 、'AD 、''C D 及点C 的路径所围成的阴影区域的周长为 _____．_____．26．如图，扇形OAB的圆心角为2α，点P为弧AB上一点，将此扇形翻折，当点O和点P重合时折痕恰巧过点B，且65ABPB=，则α正切值为_______．PB点OC AB⊥AC BC ∴=122αα=，Rt BOC 中，2OB BC =-34BC BOC OC ∠==． 3tan 4α=．故答案为34．27．如图，一副含30︒和45︒角的三角板ABC 和EDF 拼合在一个平面上，边AC 与EF 重合，12AC cm =.当点E 从点A 出发沿AC 方向滑动时，点F 同时从点C 出发沿射线BC 方向滑动.当点E 从点A 滑动到点C 时，点D 运动的路径长为______cm .28．如图，在平面直角坐标系中，∴ABC的顶点坐标分别为A（﹣1，1），B（0，﹣2），C（1，0），点P（0，2）绕点A旋转180°得到点P1，点P1绕点B旋转180°得到点P2，点P2绕点C旋转180°得到点P3，点P3绕点A旋转180°得到点P4，…，按此作法进行下去，则点P2018的坐标为_____．【详解】解：如图所示，P1（﹣2，0），P2（2，﹣4），P3（0，4），P4（﹣2，﹣2），P5（2，﹣2），P6（0，2），发现6次一个循环．∴2018÷6=336…2，∴点P2018的坐标与P2的坐标相同，即P2018（2，﹣4）．故答案为（2，﹣4）．点睛：本题考查了坐标与图形的性质、点的坐标等知识，解题的关键是循环探究问题的方法，属于中考常考题型．29．如图，矩形OABC 的顶点B 在O 上，点A 、C 在弦DE 上，且3,6OA OD ==，则sin ODA ∠=__________．30．如图，∴ABC为等边三角形，AB＝2，若P为∴ABC内一动点，且满足∴P AB＝∴ACP，则点P运动的路径长为_________．∴OA＝OC，二、解答题31．如图，C是∴O直径AB上一点，过C作弦DE，使DC=OC，∴AOD=40°，求∴BOE的度数．【答案】120°．【分析】根据等腰三角形的性质：等边对等角以及三角形的外角等于不相邻的两个内角的和即可求解．【详解】解：∴DC=OC，∴∴D=∴AOD=40°，∴∴OCE=∴D+∴AOD=40°+40°=80°，∴OD=OE，∴∴E=∴D=40°．∴∴BOE=∴E+∴OCE=40°+80°=120°．故答案为120°．【点睛】本题考查等腰三角形的性质，三角形的外角的性质，以及同圆半径相等的性质，理解性质是关键．32．如图，请找出4组相等的圆周角．【答案】（1）AEB ADB ACB ∠=∠=∠；（2）BAC BEC BDC ∠=∠=∠；（3）CAD CBD CED ∠=∠=∠；（4）DAE DBE DCE ∠=∠=∠；（5）EBA ECA EDA ∠=∠=∠．【分析】根据圆周角定理即可求解．【详解】由AB 可得AEB ADB ACB ∠=∠=∠；由BC 可得BAC BEC BDC ∠=∠=∠；由CD 可得CAD CBD CED ∠=∠=∠；由DE 可得DAE DBE DCE ∠=∠=∠；由AE 可得EBA ECA EDA ∠=∠=∠．【点睛】此题主要考查圆周角定理，解题的关键是熟知同弧所对的圆周角相等． 33．如图，在∴O 中,弧AC ＝弧BC ，CD∴OA 于D ，CE∴OB 于E ，请问：CD 与CE 的大小有什么关系？为什么？【答案】CD ＝CE.理由见解析. 【详解】试题分析：同弧或者等弧所对的圆心角相等，可得∴COA ＝∴COB，易证∴CDO ∴∴CEO，所以CD ＝CE.试题解析：解：CD ＝CE .理由如下：连接OC .(1分)∴＝，∴∴COA ＝∴COB .(3分)∴CD ∴OA ，CE ∴OB ，∴∴CDO ＝∴CEO ＝90°.(5分)又∴OC ＝OC ，∴∴CDO ∴∴CEO ，∴CD＝CE.(8分)34．某品牌洗衣产品分为洗衣粉、洗衣液、洗衣片、洗衣凝珠四种类型（分别用A，B，C，D依次表示这四种类型）．小洁和小静计划每人购买一种该品牌洗衣产品，上述四种类型洗衣产品中的每一种被选中的可能性均相同．(1)小洁随机选择一种洗衣产品，选的是洗衣凝珠的概率是．(2)请你用列表法或树状图法表示出两人购买洗衣产品所有可能的结果，求两人选择同一种类型洗衣产品的概率．件．用到的知识点为：概率＝所求情况数与总情况数之比．35．如图，在平面直角坐标系中，ABC ∆的三个顶点坐标分别为()0,1A ，()1,1B -，()1,3C -（1）画出ABC ∆关于x 轴对称的111A B C ∆，并写出点1C 的坐标；（2）画出ABC ∆绕原点O 顺时针方向旋转90︒后得到的222A B C ∆，并写出点2C 的坐标；（3）将222A B C ∆平移得到333A B C ∆，使点2A 的对应点是3A ，点2B 的对应点时3B ，点2C 的对应点是()34,1C -，在坐标系中画出333A B C ∆，并写出点3A ，3B 的坐标.【答案】（1）图详见解析，()11,3C --；（2）图详见解析，()23,1C ；（3）图详见解析，()32,2A - ()32,1B -【分析】（1）从三角形的各点向对称轴引垂线并延长相同单位得到各点的对应点，顺次连接即可，然后从坐标中读出各点的坐标；（2）让三角形的各顶点都绕点O 顺时针旋转90°后得到对应点，顺次连接即可；（3）将222A B C ∆平移得到333A B C ∆，使点2A 的对应点是3A ，点2B 的对应点是3B ，点2C 的对应点是3C (4，−1)，在坐标系中画出333A B C ∆，并写出点3A ，3B 的坐标；【详解】解：（1）（2）（3）如图所示：（1）根据图形结合坐标系可得：()113C --，；（2）根据图形结合坐标系可得：点2C (3，1)；（3）根据图形结合坐标系可得：()322A -，，()321B -，；【点睛】本题主要考查了作图-旋转变换，作图-轴对称变换，掌握作图-旋转变换，作图-轴对称变换是解题的关键.36．口袋里有红球4个、绿球5个和黄球若干个，任意摸出一个球是黄色球的概率是14. 求：（1）口袋里黄球的个数；（2）任意摸出一个球是红色的概率．37．如图，在单位长度为1的正方形网格图中，一条圆弧经过网格点A （0，4）、B （4，4）、C （6，2）三点，请在网格中进行下列操作：（1）在图中确定该圆弧所在圆的圆心D 点的位置，写出D 点坐标为．（2）连接AD 、CD ，求∴D 的半径及弧AC 的长．R中，t DECt R AOD中，tan∴OADt R CDE中，tan∴EDC∴∴OAD＝∴EDC，∴∴OAD+∴ODA＝90°∴∴EDC+∴ODA∴∴ADC＝90°，9018038．已知△ABC在平面直角坐标系中的位置如图所示．(1)画出△ABC关于原点O对称的△A1B1C1；(2)直接写出A1，B1，C1三点的坐标．【答案】(1)见解析(2)A1（3，-5），B1（4，-2），C1（-2，-3）【分析】（1）根据旋转的性质即可画出△ABC关于原点O对称的△A1B1C1；（2）结合（1）即可写出A1，B1，C1三点的坐标．（1）解：如图，△A1B1C1即为所求；（2）解：由图象得：A1（3，-5），B1（4，-2），C1（-2，-3）．【点睛】本题考查了作图-旋转变换，解决本题的关键是掌握旋转的性质．39．如图，点A、B、C、D在∴O上，AB=DC，AC与BD相等吗？为什么？【答案】AC=BD.【分析】由AB=DC，根据在同圆或等圆中，如果两个圆心角以及它们对应的两条弧、两条弦中有一组量相等，则另外两组量也对应相等得到AB CD=，即有=，因此AC与BD相等．AB BC BC CD+=+，即AC BD【详解】AC与BD相等．理由如下：∴AB=DC，∴AB CD=，∴AB BC BC CD+=+，即AC BD=，∴AC=BD．【点睛】本题考查了在同圆或等圆中，如果两个圆心角以及它们对应的两条弧、两条弦中有一组量相等，则另外两组量也对应相等．在圆中经常利用此结论把圆心角、弧、弦之间进行转化．40．如图，在∴O中，AB为直径，D．E为圆上两点，C为圆外一点，且∴E+∴C=90°．（1）求证：BC为∴O的切线．（2）若sinA=35，BC=6，求∴O的半径．41．在迎新年班会上，老师随机给同学们派送新年礼物，当轮到小明和小红时，还剩下2本笔记本和1本书共三份礼物问：（1）若先轮到小明，则他收到一本笔记本的概率是多少？（2）请借助树状图或列表的方式分析，求小明和小红两人都收到一本笔记本的概率．42．如图，O是ABC的外接圆，AE是O的直径，点B是CE的中点，过点B的切线与AC的延长线交于点D．(1)求证：BD AD⊥；(2)若9AC=，3tan4ABC∠=，求O的半径．【答案】(1)见解析；为O的切线，得到D即可；90∠（2）连接CE，根据圆周角定理得到ACE∠=∠12AECtan tanEC=，根据勾股定理求出为O的切线，OBD=︒，90为CE的中点，BE，∠，2∴90D，即BD AD⊥；（2）连接CE，AE是O的直径，ACE=︒，90AEC ABC=∠AEC=∠tan3，4Rt ACE中，2AE=+912∴O的半径为【点睛】此题考查了证明直线是圆的切线，圆周角定理，勾股定理，锐角三角函数，正确掌握圆周角定理是解题的关键．43．如图，O 的直径2AB =，AM 和BN 是它的两条切线，DE 切于E ，交AM 于D ，交BN 于C ．设AD x =，BC y =．（1）求证：//AM BN ．（2）探究y 与x 的函数关系．是O 的两条切线，90，，是O 的两条切线，切O 于E ，xCE CB ==CE x y =+，Rt DFC 中，由勾股定理得：2()x y +=整理为：1y x=与x 的函数关系为：【点睛】本题考查了圆中的线段位置关系和数量关系，综合性较强，中等难度44．某中学为了解学生对新闻，体育，娱乐，动画四类电视节目的喜爱情况，进行了统计调查．随机调查了某班所有同学最喜欢的节目(每名学生必选且只能选择四类节目中的一类)，并将调查结果绘成如下不完整的统计图．根据两图提供的信息，回答下列问题：（1）本次调查了多少人？（2）请补全条形统计图；（3）根据抽样调查结果，若该校有1000名学生，请你估计该校有多少名学生最喜欢“新闻”类节目；（4）在全班同学中，甲，乙，丙，丁等同学最喜欢体育类节，班主任打算从甲，乙，丙，丁4名同学中选取2人参加学校组织的体育知识竞赛，请用列表法或树状图求同时选中甲，乙两同学的概率．645．如图，已知四边形APBC 中，60ACB APB ∠=∠=︒，过A ，B ，C 三点的O 与P A 相切．(1)求证：PB 是O 的切线；(2)若O 的半径长为4cm ，求图中阴影部分的面积．【答案】(1)见解析∴O 与P A 相切，90OAP ∠=四边形AOBP AOB ∠+∠90OBP ∠=PB 是O 的切线）解：连接OP PB 是∴O 的切线，APO ＝12∴APB APO 中，tan30°=AOP S S -【点睛】此题考查了切线的性质与判定、解直角三角函数、扇形面积公式等知识．此题难度不大，解题的关键是注意数形结合思想的应用．46．已知布袋中有红、黄、蓝色小球各一个，用画树状图或列表的方法求下列事件的概率.（1）如果摸出第一个球后，不放回，再摸出第二球，求摸出的球颜色是“一黄一蓝”的概率.（2）随机从中摸出一个小球，记录下球的颜色后，把球放回，然后再摸出一个球，记录下球的颜色，求得到的球颜色是“一黄一蓝”的概率.47．如图，在Rt ABC中，90C∠=︒，AD平分BAC∠交BC于点D，O为AB上一点，经过点A，D的O分别交AB，AC于点E，F，连接OF交AD于点G．（1）求证：ABD ADF∽；（2）若2BE=，3sin5B=，求AD的长．5548．有两个内角分别是它们对角的一半的四边形叫做半对角四边形．（1）如图1，在半对角四边形ABCD中，∠B＝12∠D，∠C＝12∠A，求∠B与∠C的度数之和；（2）如图2，锐角∠ABC内接于∠O，若边AB上存在一点D，使得BD＝BO．∠OBA的平分线交OA于点E，连结DE并延长交AC于点F，∠AFE＝2∠EAF．求证：四边形DBCF 是半对角四边形；（3）如图3，在（2）的条件下，过点D 作DG∠OB 于点H ，交BC 于点G ．当DH ＝BG 时，求∠BGH 与∠ABC 的面积之比．ABC ∆49．如图，AB 是O 的直径，弦CD AB ⊥于点E ，G 是AD 上一动点（不与点A ，点D 重合），以AG ，CG 为边构造平行四边形AFCG ，交O 于点H ，交AB 于点M ，若CD =1BE =．(1)求证：F ACD ∠=∠．(2)当CF 与O 相切时，求AG 的长．(3)∴当AMG 中有一个角与HCF ∠相等时，求AG 的长．∴若点H 关于AC 的对称点H '落在ACG 的内部（不包括ACG 的边界），求CH 的取值范围（直接写出答案）．，首先证明()OCE OAK AAS ≌，再结合垂径定理即可求得AG 的长；，设O 半径为，由勾股定理可解得 4.5x =，AC CHF AGC =∠经过O 点，即O 、，再证明MGA ADC ∽，由相似三角形的性质可解得AMG 中有一个角与HCF ∠相等时，即当AMG ∠H 关于AC H '落在ACG 的内部（不包括ACG 的边界）H '落在边上时和当H '落在边AG 上时CH 的长，即可获得答案．【详解】（）证明：如下图，连接AD ，是O 的直径，12DE CD =AD ，ACD ADC =∠AC ，与O 相切，为O 半径，CF ，四边形AFCG 为平行四边形，AG ，AG ，AB ⊥，∴()OCE OAK AAS ≌CE AK =，12CE DE CD ==， 2CD CE =，OK AG ⊥，1设O 半径为Rt OCE 中，由勾股定理可得22)(x +-4.51 3.5=-=OA OE =+Rt OCE 中，由勾股定理可得四边形AGCH 内接于O ，CHF AGC F =∠；经过O 点，即O 、M 重合时，如下图，∴MGA ADC ∽，AM AG CA CD=，即4.5623AG =，当AMG 中有一个角与若点H 关于AC 的对称点落在ACG 的内部（不包括ACG 的边界）值范围为33，理由如下：H '落在边CG 上时，如下图，连接HH '交，连接AH '，∴(HAN H CN AAS '≌132AN CN AC ===HH AC '⊥，HH '经过圆心O ，OH 在Rt OAN 中，ON OH ON =-CNH △中，落在边AG∴(CHF CH G AAS '≌CF CG =，四边形AFCG 为菱形，GF AC ⊥，且AQ =GF 经过点O ， Rt CGQ 中，四边形AFCG 为菱形，36CG ==CHF AGC =∠3CF ==落在ACG 的内部（不包括ACG 的边界）【点睛】本题主要考查了垂径定理、平行四边形的性质、圆周角定理的推论、切线的性质、圆内接四边形的性质、勾股定理、全等三角形的判定与性质、相似三角形的判定与性质、菱形的判定与性质、轴对称的性质等知识，综合性强，难度较大，熟练掌50．如图1，正方形ABCD 中，E 、F 分别是边CD 、AD 上的点，45EBF ∠=︒．(1)小聪同学通过将BAF △绕点B 顺时针旋转90︒至BCG ，得到45EBG EBF ∠=∠=︒．∴请直接写出线段CE 、EF 、AF 之间的数量关系：______（用等式表示）； ∴若2AB =，E 为CD 边中点，求AF ．(2)如图2，将正方形ABCD 改为矩形，且2AB =，3BC =，其他条件不变，即：E 、F 分别是边CD 、AD 上的点，45EBF ∠=︒．∴记EF y =，CE AF x +=，试探究y 与x 之间的数量关系（用等式表示）； ∴当BF EF ⊥时，求线段EF 的长． ≌BCG ，所以≌(SAS BGE EC CG EC +=1=，设AF ，2DF =-中，90D ，利用勾股定理建立关于将ABF △绕点B 顺时针旋转90︒至PBM ，延长MH DN ⊥于点H ，连接，由旋转可得，ABF PBM ∠∠=，易证四边形PMNC BEF ≌(BEM SAS 22EH EM =，代入数据可得结论；是等腰直角三角形，则FB FE =，∠≌(DFE AAS 1=，由勾股定理可得由题意可知△≌BCG ，BG ，AF CG =EBG EBF ∠∠==BE BE =，BFE ∴≌(BGE SAS EF EG ∴=，EG EC CG EC =+=，EF EC AF ∴=+，故答案为：EF EC =②若点E 为DE EC ∴=设AF x =D，由勾股定理可得，中，902AF=．3至PBM，延长∠=BCN∴四边形PM CH∴=∴+CE CHFBE∠=∴∠+ABF=BF BMBEM SAS∴≌(BEF∴==，EM EF y在Rt MHE△中，由勾股定理可得，222∴+=，即y=1x y∠②BF EF⊥，EBF∴是等腰直角三角形，BFEFB FE∴=，∠+∠AFB ABF∴∠=∠ABF DFEA D∠=∠=DFE AAS∴≌(ABF=∴=，AF DE2DF∴=．5EF【点睛】本题主要考查全等三角形的性质与判定，矩形的性质，勾股定理，旋转的性质等知识，解题的关键是利用类比思想作出正确的辅助线，将所求线段放在同一个三角形中．。

沪科版九年级数学中考复习（含答案）

沪科版九年级数学中考复习一次方程(组)和分式方程汇编（含答案）1、一次方程组一、选择题1. (·杭州)设x ，y ，c 是实数．( ) A. 若x ＝y ，则x ＋c ＝y －c B. 若x ＝y ，则xc ＝yc C. 若x ＝y ，则x c ＝ycD. 若x 2c ＝y3c，则2x ＝3y2. (·南充)如果a ＋3＝0，那么a 的值是( ) A. 3 B. －3 C. 13 D. －133. (·永州)已知x ＝1是关于x 的方程2x －a ＝0的解，则a 的值是( )A. －2B. 2C. －1D. 1 4. (·天津)方程组⎩⎨⎧y ＝2x ，3x ＋y ＝15的解是( )A. ⎩⎨⎧x ＝2，y ＝3B. ⎩⎨⎧x ＝4，y ＝3C. ⎩⎨⎧x ＝4，y ＝8D. ⎩⎨⎧x ＝3，y ＝65. (·衢州)二元一次方程组⎩⎨⎧x ＋y ＝6，x －3y ＝－2的解是( )A. ⎩⎨⎧x ＝5，y ＝1B. ⎩⎨⎧x ＝4，y ＝2C. ⎩⎨⎧x ＝－5，y ＝－1D. ⎩⎨⎧x ＝－4，y ＝－26. (·舟山)若二元一次方程组⎩⎨⎧x ＋y ＝3，3x －5y ＝4的解为⎩⎨⎧x ＝a ，y ＝b ，则a－b 的值为( ) A. 1 B. 3 C. －14 D. 747. (·眉山)已知关于x ，y 的二元一次方程组⎩⎨⎧2ax ＋by ＝3，ax －by ＝1的解为⎩⎨⎧x ＝1，y ＝－1，则a －2b 的值是( )A. －2B. 2C. 3D. －38. (·巴中)若方程组⎩⎨⎧2x ＋y ＝1－3k ，x ＋2y ＝2的解满足x ＋y ＝0，则k的值为( )A. －1B. 1C. 0D. 无法确定二、填空题9. (·云南)已知关于x 的方程2x ＋a ＋5＝0的解是 x ＝1，则a 的值为________．10. (·崇左)若4a 2b 2n ＋1与a m b 3是同类项，则m ＋n 的值为________．11. (·长沙)方程组⎩⎨⎧x ＋y ＝1，3x －y ＝3的解是________．12. (·乐山)二元一次方程组x ＋y 2＝2x －y3＝x ＋2的解是________．13. (·南宁)已知⎩⎨⎧x ＝a ，y ＝b 是方程组⎩⎨⎧x －2y ＝0，2x ＋y ＝5的解，则3a －b ＝________．14. (·包头)若关于x ，y 的二元一次方程组⎩⎨⎧x ＋y ＝3，2x －ay ＝5的解是⎩⎨⎧x ＝b ，y ＝1，则a b 的值为________． 15. (·枣庄)已知⎩⎨⎧x ＝2，y ＝－3是方程组⎩⎨⎧ax ＋by ＝2，bx ＋ay ＝3的解，则a 2－b 2＝________．16. (·镇江)若实数a 满足||a －12＝32，则a 对应于图中数轴上的点可以是A ，B ，C 三点中的点________．第16题17. (·荆州)若单项式－5x 4y 2m ＋n与2 017x m －n y 2是同类项，则m －7n 的算术平方根是________．三、解答题18. (·柳州)解方程：2x －7＝0.19. (·武汉)解方程：4x －3＝2(x －1)．20. (·湖州)对于任意实数a ，b ，定义关于“⊗”的一种运算如下：a ⊗b ＝2a －b.例如：5⊗2＝2×5－2＝8，(－3)⊗4＝2×(－3)－4＝－10.若3⊗x ＝－2 011，求x 的值．21. (·荆州)解方程组⎩⎨⎧y ＝2x －3，3x ＋2y ＝8.22. (·桂林)解二元一次方程组⎩⎨⎧2x ＋y ＝3，5x ＋y ＝9.23. (·镇江)解方程组⎩⎨⎧x －y ＝4，2x ＋y ＝5.24. (·广州)解方程组⎩⎨⎧x ＋y ＝5，2x ＋3y ＝11.25. (·重庆)对任意一个三位数n ，如果n 满足各数位上的数字互不相同，且都不为零，那么称这个数为“相异数”．将一个“相异数”任意两个数位上的数字对调后可以得到三个不同的新三位数，把这三个新三位数的和与111的商记为F(n)．例如n ＝123，对调百位与十位上的数字得到213，对调百位与个位上的数字得到321，对调十位与个位上的数字得到132，这三个新三位数的和为213＋321＋132＝666，666÷111＝6，所以F(123)＝6. (1) 计算：F(243)，F(617)．(2) 若s ，t 都是“相异数”，其中s ＝100x ＋32，t ＝150＋y(1≤x≤9，1≤y≤9，x ，y 都是正整数)，规定：k ＝F （s ）F （t ）.当F(s)＋F(t)＝18时，求k 的最大值．2. 分式方程一、选择题1. (·河南)解分式方程1x－1－2＝31－x，去分母，得()A. 1－2(x－1)＝－3B. 1－2(x－1)＝3C. 1－2x－2＝－3D. 1－2x＋2＝32. (·哈尔滨)方程2x＋3＝1x－1的解为()A. x＝3B. x＝4C. x＝5D. x＝－53. (·黔东南州)分式方程3x（x＋1）＝1－3x＋1的根为()A. －1或3B. －1C. 3D. 1或－34. (·岳阳)解分式方程2x－1－2xx－1＝1，可知方程的解为()A. x＝1B. x＝3C. x＝12 D. 无解5. (·滨州)分式方程xx－1－1＝3（x－1）（x＋2）的解为()A. x＝1B. x＝－1C. 无解D. x＝－26. (·成都)已知x＝3是分式方程kxx－1－2k－1x＝2的解，那么实数k的值为()A. －1B. 0C. 1D. 27. (·毕节)已知关于x的分式方程7xx－1＋5＝2m－1x－1有增根，则m的值为()A. 1B. 3C. 4D. 58. (·聊城)如果解关于x的分式方程mx－2－2x2－x＝1时出现增根，那么m的值为()A. －2B. 2C. 4D. －49. (·七台河)已知关于x的分式方程3x－ax－3＝13的解是非负数，那么a的取值范围是()A. a>1B. a≥1C. a≥1且a≠9D. a≤110. (·重庆)若实数a使关于x的分式方程2x－1＋a1－x＝4的解为正数，且使关于y的不等式组⎩⎨⎧y＋23－y2>1，2（y－a）≤0的解集为y<－2，则符合条件的所有整数a的和为()A. 10B. 12C. 14D. 16二、填空题11. (·淮安)方程2x－1＝1的解是________．12. (·宁波)分式方程2x＋13－x＝32的解是________．13. (·常德)分式方程2x＋1＝4x的解为________．14. (·襄阳)分式方程2x－3＝3x的解是________．15. (·株洲)分式方程4x－1x＋2＝0的解为________．16. (·南京)方程2x＋2－1x＝0的解是________．17. (·威海)方程3－xx－4＋14－x＝1的解是________．18. (·黄石)分式方程xx－1＝32（x－1）－2的解为________．19. (·绵阳)分式方程2x－1－1x＋1＝11－x的解是________．20. (·六盘水)方程2x2－1－1x－1＝1的解为x＝________.21. (·泰安)已知分式7x－2与x2－x的和为4，则x的值为________．22. (·宿迁)若关于x的分式方程mx－2＝1－x2－x－3有增根，则实数m的值是________．23. (·荆州)若关于x的分式方程k－1x＋1＝2的解为负数，则k的取值范围为________．24.(·泸州)若关于x 的分式方程x ＋m x －2＋2m2－x＝3的解为正实数，则实数m 的取值范围是____________．三、解答题25. (·无锡)解方程：52x －1＝3x ＋2.26. (·常州)解方程：2x －5x －2＝3x －3x －2－3.27. (·湖州)解方程：2x －1＝1x －1＋1.28. (·宁夏)解方程：x ＋3x －3－4x ＋3＝1.29. (·眉山)解方程：1x －2＋2＝1－x 2－x .30. (·泰州)解方程：x ＋1x －1＋41－x 2＝1.31. (·随州)解分式方程：3x 2－x ＋1＝xx －1.32. (·上海)解方程：3x 2－3x －1x －3＝1.1. 一次方程(组)一、 1. B 2. B 3. B 4. D 5. B 6. D 7. B 8. B 二、 9. －7 10. 3 11.⎩⎨⎧x ＝1，y ＝0 12.⎩⎨⎧x ＝－5，y ＝－1 13. 514. 115. 1 16. B 17. 4 三、 18. x ＝72 19. x ＝1220. 根据题意，得2×3－x ＝－2 011，即6－x ＝－2 011，解得 x ＝2 01721.⎩⎨⎧x ＝2，y ＝1 22.⎩⎨⎧x ＝2，y ＝－1 23.⎩⎨⎧x ＝3，y ＝－1 24.⎩⎨⎧x ＝4，y ＝125. (1) F(243)＝(423＋342＋234)÷111＝9 F(617)＝(167＋716＋671)÷111＝14 (2) ∵ s ，t 都是“相异数”，∴ F(s)＝(302＋10x ＋230＋x ＋100x ＋23)÷111＝x ＋5，F(t)＝(510＋y ＋100y ＋51＋105＋10y)÷111＝y ＋6.∵ F(s)＋F(t)＝18，∴ x ＋5＋y ＋6＝x ＋y ＋11＝18.∴ x ＋y ＝7.∵ 1≤x ≤9，1≤y ≤9，x ，y 都是正整数，∴ ⎩⎨⎧x ＝1，y ＝6或⎩⎨⎧x ＝2，y ＝5或⎩⎨⎧x ＝3，y ＝4或⎩⎨⎧x ＝4，y ＝3或⎩⎨⎧x ＝5，y ＝2或⎩⎨⎧x ＝6，y ＝1.∵ s ，t 是“相异数”，∴ x ≠2，x ≠3，y ≠1，y ≠5.∴ 满足条件的有⎩⎨⎧x ＝1，y ＝6或⎩⎨⎧x ＝4，y ＝3或⎩⎨⎧x ＝5，y ＝2.∴ ⎩⎨⎧F （s ）＝6，F （t ）＝12或⎩⎨⎧F （s ）＝9，F （t ）＝9或⎩⎨⎧F （s ）＝10，F （t ）＝8.∴ k ＝F （s ）F （t ）＝612＝12或k＝F （s ）F （t ）＝99＝1或k ＝F （s ）F （t ）＝108＝54.∴ k 的最大值为542. 分式方程一、 1. A 2. C 3. C 4. D 5. C 6. D 7. C8. D 9. C10. A二、11. x＝3 12. x＝1 13. x＝2 14. x＝9 15.x＝－8316. x＝2 17. x＝3 18. x＝7619. x＝－2 20.－2 21. 3 22. 1 23. k<3且k≠1 24. m<6且m≠2三、25. x＝1326.两边同时乘(x－2)，得 2x－5＝3x－3－3(x－2)；去括号，得2x－5＝3x－3－3x＋6；移项，得2x－3x＋3x ＝6－3＋5；合并同类项，得2x＝8；系数化为1，得x＝4.检验：当x＝4时，x－2≠0，∴ x＝4是原分式方程的解27.方程两边都乘(x－1)，得2＝1＋x－1，解得x＝2.检验：当x＝2时，x－1≠0，∴ x＝2是原方程的解28.方程两边同乘(x－3)(x＋3)，得(x＋3)2－4(x－3)＝(x－3)(x＋3)，解得x＝－15.检验：当x＝－15时，(x －3)(x＋3)≠0，∴ x＝－15是原分式方程的解29.原方程可化为1x－2＋2＝x－1x－2，方程两边都乘(x－2)，得 1＋2(x－2)＝x－1，解得x＝2.检验：当x＝2时，x－2＝0，∴ x＝2是原方程的增根，因此原方程无解30.原方程可化为x＋1x－1－4（x＋1）（x－1）＝1，方程两边同乘(x＋1)(x－1)，得(x＋1)2－4＝(x＋1)(x－1)，解得x＝1.检验：当x＝1时，(x＋1)(x－1)＝0，∴ x＝1是原方程的增根，因此原分式方程无解31.原方程可化为3x（x－1）＋1＝xx－1，方程两边同乘x(x－1)，得3＋x(x－1)＝x2，解得x＝3.检验：当x＝3时，x(x－1)＝6≠0，∴ x＝3是原方程的根32.原方程可化为3x（x－3）－1x－3＝1，方程两边都乘x(x－3)，得3－x＝x(x－3)，即x2－2x－3＝0，∴ (x－3)(x ＋1)＝0，解得x1＝3，x2＝－1.经检验，x＝3是原方程的增根，x＝－1是原方程的根，∴原方程的根为x＝－1。

沪科版九年级数学上册第22章综合素质评价附答案

沪科版九年级数学上册第22章综合素质评价一、选择题(每题4分，共40分)1．下列四组图形中，不是相似图形的是()2．【教材P69练习T2改编】已知线段a，b，c，d是成比例线段，其中a＝2 cm，b＝4 cm，c＝5 cm，则d等于()A．1 cm B．10 cmC．52cm D．85cm3．【教材P71练习T4改编】如图，直线a，b，c被直线l1，l2所截，交点分别为点A，C，E和点B，D，F.已知a∥b∥c，且AC＝3，CE＝4，则BDBF的值是()A．3 4B．4 3C．3 7D．4 74．【教材P68例3改编】若点C是线段AB的黄金分割点，AB＝8 cm，AC＞BC，则AC的长为()A．5－12cm B．2(5－1)cmC．4(5－1)cm D．6(5－1)cm5．在△ABC和△DEF中，AB＝AC，DE＝DF，根据下列条件，能判断△ABC和△DEF 相似的是()A．ABDE＝ACDF B．ABDE＝BCEFC．∠A＝∠E D．∠B＝∠D6．如图，为估算河的宽度(河两岸平行)，在河对岸选定一个目标点A，在近岸取点B，C，D，使得AB⊥BC，CD⊥BC，点E在BC上，并且点A，E，D在同一条直线上，若测得BE＝20 m，CE＝10 m，CD＝20 m，则河的宽度AB等于()A．60 m B．40 mC．30 m D．20 m7．【2021·兰州】如图，小明探究课本中“制作视力表”的相关内容：当测试距离为5 m时，标准视力表中最大的“E”字高度为72.7 mm，当测试距离为3 m时，最大的“E”字高度为()A．4.36 mm B．29.08 mmC．43.62 mm D．121.17 mm8．【2020·云南】如图，平行四边形ABCD的对角线AC，BD相交于点O，E是CD的中点．则△DEO与△BCD的面积的比等于()A．12B．14C．16D．189．【2020·河北】在如图所示的网格中，以点O为位似中心，四边形ABCD的位似图形是()A．四边形NPMQB．四边形NPMRC．四边形NHMQD．四边形NHMR10．【2020·遵义】如图，△ABO的顶点A在函数y＝kx(x>0)的图象上，∠ABO＝90°，过AO边的三等分点M，N分别作x轴的平行线交AB于点P，Q.若四边形MNQP的面积为3，则k的值为()A．9B．12C．15D．18二、填空题(每题5分，共20分)11．【教材P 69练习T 3改编】若x y ＝34，则x ＋y y ＝________.12．【2020·郴州】如图，在平面直角坐标系中，将△AOB 以点O 为位似中心，23为相似比作位似变换，得到△A 1OB 1，已知A (2，3)，则点A 1的坐标是__________．13．【2021·南充】如图，在△ABC 中，D 为BC 上一点，BC ＝3AB ＝3BD ，则AD ∶AC 的值为________．14．【2021·扬州】如图，在△ABC 中，AC ＝BC ，矩形DEFG 的顶点D ，E 在AB上，点F ，G 分别在BC ，AC 上．若CF ＝4，BF ＝3，且DE ＝2EF ，则EF 的长为________．三、(每题8分，共16分)15．若x 2＝y 3＝z5≠0，且3x ＋2y －z ＝14，求x ，y ，z 的值．16．(1)根据下列条件，判断△ABC 与△A ′B ′C ′是否相似，并说明理由．AB ＝4 cm ，BC ＝6 cm ，AC ＝8 cm ； A ′B ′＝12 cm ，B ′C ′＝18 cm ，A ′C ′＝21 cm.(2)若(1)中两三角形不相似，那么要使它们相似，不改变AC的长，A′C′的长应改为多少？四、(每题8分，共16分)17．如图，在△ABC中，AB＝8，BC＝4，CA＝6，CD∥AB，BD是∠ABC的平分线，BD交AC于点E，求AE的长．18．【教材P91习题T8改编】如图，在▱ABCD中，AE∶EB＝2∶3，DE交AC于点F.(1)求△AEF与△CDF的周长之比；(2)若AF＝2，求FC的长．五、(每题10分，共20分)19．为测量旗杆的高度，小宇的测量方法如下：如图，将直角三角形硬纸板DEF 的斜边DF与地面保持平行，并使边DE与旗杆顶点A在同一直线上，测得DE＝0.5 m，EF＝0.25 m，目测点D到地面的距离DG＝1.6 m，到旗杆的水平距离DC＝18 m．按此方法，计算旗杆的高度．20．如图，已知△ABC的三个顶点的坐标分别为A(0，－3)，B(3，－2)，C(2，－4)(正方形网格中每个小正方形的边长是1个单位)．(1)画出△ABC向上平移6个单位后得到的△A1B1C1；(2)以点C为位似中心，在网格中画出△A2B2C，使△A2B2C与△ABC位似，且△A2B2C与△ABC的相似比为2∶1，并直接写出点A2的坐标．21．【2020·杭州】如图，在△ABC中，点D，E，F分别在AB，BC，AC边上，DE∥AC，EF∥AB.(1)求证：△BDE∽△EFC.(2)设AFFC＝12，①若BC＝12，求线段BE的长；②若△EFC的面积是20，求△ABC的面积．七、(12分)22．如图，在矩形ABCD中，AB＝12 cm，BC＝6 cm，点P沿AB边从点A开始向点B以2 cm/s的速度移动，点Q沿DA边从点D开始向点A以1 cm/s的速度移动．如果P，Q同时出发，用t(s)表示移动的时间(0≤t≤6)，那么：(1)当t为何值时，△QAP是等腰直角三角形？(2)根据四边形QAPC面积的计算结果，你能得出什么结论？(3)当t为何值时，以点Q，A，P为顶点的三角形与△ABC相似？23．【2020·南京】如图，在△ABC和△A′B′C′中，D，D′分别是AB，A′B′上一点，AD AB＝A′D′A′B′.(1)当CDC′D′＝ACA′C′＝ABA′B′时，求证：△ABC∽△A′B′C′.证明的途径可以用下面的框图表示，请填写其中的空格．(2)当CDC′D′＝ACA′C′＝BCB′C′时，判断△ABC与△A′B′C′是否相似，并说明理由．答案一、1．D2．B3．C4．C5．B6．B7．C8．B9．A 10．D提示：∵NQ∥MP∥OB，∴△ANQ∽△AMP∽△AOB.∵M，N是OA边的三等分点，∴ANAM＝12，ANAO＝13.∴S△ANQS△AMP＝14.∵四边形MNQP的面积为3，∴S△ANQ3＋S△ANQ＝14.∴S△ANQ＝1.∵1S△AOB＝⎝⎛⎭⎪⎫ANAO2＝19，∴S△AOB＝9.∴k＝2S△AOB＝18.二、11．7412．⎝⎛⎭⎪⎫43，213．3314．125三、15．解：设x2＝y3＝z5＝k(k≠0)，则x＝2k，y＝3k，z＝5k.∵3x＋2y－z＝14，∴6k＋6k－5k＝14，解得k＝2.∴x＝4，y＝6，z＝10.16．解：(1)△ABC与△A′B′C′不相似．理由如下：∵ABA′B′＝412＝13，BCB′C′＝618＝13，ACA′C′＝821，∴ABA′B′＝BCB′C′≠ACA′C′.∴△ABC与△A′B′C′不相似．(2)当A′C′＝24 cm时，两三角形相似．四、17．解：∵BD是∠ABC的平分线，∴∠ABD＝∠CBD.∵AB∥CD，∴∠D＝∠ABD.∴∠D＝∠CBD.∴BC＝CD.∵BC＝4，∴CD＝4.又∵∠AEB＝∠CED，∴△ABE∽△CDE.∴ABCD＝AECE，即84＝AECE.∴CE＝12AE.又∵AC＝6＝AE＋CE，∴AE＝4.18．解：(1)∵四边形ABCD是平行四边形，∴AB＝CD，AB∥CD.∴△AEF∽△CDF.∵AE∶EB＝2∶3，∴AE∶AB＝2∶5.∴△AEF的周长△CDF的周长＝AECD＝AEAB＝25.(2)∵△AEF∽△CDF，∴AFFC＝AECD＝25.∴FC＝52AF＝5.五、19．解：由题意得∠DEF＝∠ACD＝90°.∵∠ADC＝∠FDE，∴△ACD∽△FED.∴DECD＝EFAC.∵DE＝0.5 m，EF＝0.25 m，DC＝18 m，∴0.518＝0.25AC.∴AC＝9 m.∵DG＝1.6 m，∴BC＝1.6 m.∴AB＝10.6 m.答：旗杆的高度为10.6 m.20．解：(1)如图，△A1B1C1就是所要画的三角形．(2)如图，△A2B2C就是所要画的三角形，点A2的坐标为(－2，－2)．六、21．(1)证明：∵DE∥AC，∴∠DEB＝∠FCE.∵EF∥AB，∴∠DBE＝∠FEC.∴△BDE∽△EFC.(2)解：①∵EF∥AB，∴BEEC＝AFFC＝12.∵EC＝BC－BE＝12－BE，∴BE12－BE＝12，解得BE＝4.②∵AFFC＝12，∴FCAC＝23.∴△EFC ∽△BAC . ∴S △EFC S △ABC ＝⎝ ⎛⎭⎪⎫FC AC 2＝⎝ ⎛⎭⎪⎫232＝49. ∴S △ABC ＝94S △EFC ＝94×20＝45.七、22．解：(1)由题意知AP ＝2t cm ，DQ ＝t cm ，QA ＝(6－t )cm.当QA ＝AP 时，△QAP 是等腰直角三角形，∴6－t ＝2t ，解得t ＝2.∴当t ＝2时，△QAP 是等腰直角三角形．(2)S 四边形QAPC ＝S △QAC ＋S △APC ＝12AQ ·AB ＋12AP ·BC ＝(36－6t )＋6t ＝36(cm 2)．由计算结果发现：在P ，Q 两点移动的过程中，四边形QAPC 的面积始终保持不变．(3)分两种情况：①当AQ AB ＝AP BC 时，△QAP ∽△ABC ，则6－t 12＝2t 6，解得t ＝1.2；②当QA BC ＝AP AB 时，△P AQ ∽△ABC ，则6－t 6＝2t 12，解得t ＝3.∴当t ＝1.2或t ＝3时，以点Q ，A ，P 为顶点的三角形与△ABC 相似．八、23．解：(1)CD C ′D ′＝AC A ′C ′＝AD A ′D ′；∠A ＝∠A ′(2)△ABC 与△A ′B ′C ′相似．理由如下：如图，过点D ，D ′分别作DE ∥BC ，D ′E ′∥B ′C ′，DE 交AC 于点E ，D ′E ′交A ′C ′于点E ′.∴△ADE∽△ABC.∴ADAB＝DEBC＝AEAC.同理，A′D′A′B′＝D′E′B′C′＝A′E′A′C′.∵ADAB＝A′D′A′B′，∴DEBC＝D′E′B′C′.∴DED′E′＝BCB′C′.同理，AEAC＝A′E′A′C′.∴AC－AEAC＝A′C′－A′E′A′C′，即ECAC＝E′C′A′C′.∴ECE′C′＝ACA′C′.∵CDC′D′＝ACA′C′＝BCB′C′，∴CDC′D′＝DED′E′＝ECE′C′.∴△DCE∽△D′C′E′.∴∠CED＝∠C′E′D′.∵DE∥BC，∴∠CED＋∠ACB＝180°.同理，∠C′E′D′＋∠A′C′B′＝180°. ∴∠ACB＝∠A′C′B′.又∵ACA′C′＝CBC′B′，∴△ABC∽△A′B′C′.。

沪教版九年级数学暑假同步讲义第13讲解直角三角形的应用(解析版)

仰角视线水平线视线俯角铅垂线解直角三角形的应用是九年级数学上学期第二章第四小节的内容．本小节的学习重点在于理解仰角、俯角、方向角、坡度、坡角等概念，并能利用其解决实际问题．1、仰角与俯角在测量过程中，常常会遇到仰角和俯角．如图，当我们进行测量时，在视线与水平线所成的角中，视线在水平线上方的角叫做仰角，视线在水平线下方的角叫做俯角．解直角三角形的应用内容分析知识结构模块一：仰角与俯角知识精讲步同级年九2 / 24ABCDE F123【例1】如图，90C DEB ∠=∠=︒，FB // AC ，从A 看D 的仰角是______；从B 看D 的俯角是______；从A 看B 的______角是______；从D 看B 的______角是______．【答案】2∠；3∠；仰；1∠；仰；3∠．【解析】考查仰角、俯角的基本定义．【例2】升国旗时，某同学站在离旗杆底部24米处行注目礼．当国旗升至旗杆顶端时，该同学视线的仰角为30°．若双眼离地面1.5米，则旗杆的高度为______米．（用含根号的式子表示）【答案】2338+．【解析解：如图所示，AB 为旗杆，CD 为某同学．则24==CA DE ，5.1==AE CD ，30BDE ∠=︒，在BDE Rt △中，DE BEBDE =∠tan ，∴2433BE=， ∴38=BE ，∴2338+=+=EB AE AB ．【总结】本题主要考查锐角三角比的实际应用以及对仰角的理解．【例3】如图，两建筑物水平距离为a 米，从点A 测得点C 的俯角为α，测得点D 的俯角例题解析ABC D 为β，则较低建筑物CD 的高为（）A ．a 米B ．（tan a α）米C ．tan a α米D ．(tan tan )a αβ-米【答案】D【解析】过C 作CE ⊥AB ，垂足为E ．由题意有：a BD CE ==，α=∠ACE ，β=∠ADB 在ACE Rt △中，CEAEACE =∠tan ， ∴αtan a AE =在ABD Rt △中，BD ABADB =∠tan ， ∴βtan a AB =∴()βαβαtan tan tan tan -=-=-==a a a AE AB BE DC【总结】本题主要考查锐角三角比的实际应用以及对俯角的理解．【例4】如图，河对岸有一座铁塔AB ，若在河这边C 、D 处分别用测角仪器测得顶部A 的仰角为30°、45°，已知CD = 30米，求铁塔的高．（结果保留根号）【答案】15315+．【解析】解：由题意可得：︒=∠30ACB ，︒=∠45ADB ．设x AB =，则x BD =，在ABC Rt △中，BCAB ACB =∠tan ，∴3330=+x x ，解得：15315-=x ．【总结】本题主要考查锐角三角比的实际应用以及对仰角的理解．【例5】如图，热气球的探测器显示，从热气球看一栋高楼顶部的仰角为60°，看这栋高楼底部的俯角为30°，热气球与高楼的水平距离为120m ，请问：这栋高楼有多高？（结AB CDE步同级年九4 / 24ABCDAB CDE果精确到0.1m ）【答案】277.1米．【解析】解：由题意可得：︒=∠60BAD ，︒=∠30CAD ，120=AD在ABD Rt △中，AD BDBAD =∠tan ，∴1203BD=，∴3120=BD ．在ACD Rt △中，ADCDCAD =∠tan ，∴12033CD=，∴340=CD ． ∴1.27731603403120≈=+=+=CD BD BC【总结】本题主要考查锐角三角比的实际应用以及对仰角、俯角的理解和运用．【例6】如图，某幢大楼顶部有一块广告牌CD ，甲、乙两人分别在相距8米的A 、B 两处测得点D 和点C 的仰角为45°和60°，且A 、B 、E 三点在一条直线上，若BE = 15米，求这块广告牌的高度．（取3 1.73≈，计算结果保留整数）【答案】3【解析】解：由题意可得：︒=∠60CBE ，︒=∠45ADE ，在CBE Rt △中，BE CECBE =∠tan ，∴153CE=，∴315=CE 在AED Rt △中，AEDEDAE =∠tan ，∴1581+=DE，∴23=DE ． ∴323315≈-=-=ED EC CD ．【总结】本题主要考查锐角三角比的实际应用以及对仰角的理解和运用．模块二：方向角北北偏东30°南偏西45°北偏西70°南偏东50°30°70° 45° 50°1、方向角指北或指南方向线与目标方向线所成的小于90°的角叫做方向角．如图：北偏东30°，北偏西70°，南偏东50°，南偏西45°．【例7】如果由点A 测得点B 在北偏东15°的方向，则由B 测点A 的方向为（）A ．北偏东15°B ．北偏西75°C ．南偏西15°D ．南偏东75°【答案】B【解析】考查方向角的定义．【例8】如图，小明从A 地沿北偏东30°方向走1003米到B 地，再从B 地向正南方向走200米到C 地，此时小明离A 地_____米．【答案】100．【解析】解：由题意可知：︒=∠30ABD知识精讲例题解析A BC南西D步同级年九6 / 24在ADB Rt △中，ABADABD =∠cos ， ∴310033BD =，∴150=BD ，35022=-=DB AB AD ． ∴50150200=-=-=BD BC CD ．∴10022=+=CD AD AC ．【总结】本题主要考查对方位角的准确理解和运用．【例9】如图，一艘轮船由海平面上A 地出发向南偏西40°的方向行驶40海里到达B 地，再由B 地向北偏西20°的方向行驶40海里到达C 地，则A 、C 两地相距（） A ．30海里 B ．40海里C ．50海里D ．60海里【答案】B【解析】解：∵AB BC =，︒=∠60ABC ∴ABC △为等边三角形．∴40=AC ．【总结】本题主要考查利用方位角解决实际问题．【例10】在位于O 处某海防哨所的北偏东60°相距6海里的A 处，有一艘快艇正向正南方向航行，经过一段时间快艇到达哨所东南方向的B 处，则A 、B 间的距离是______海里．（精确到0.12 1.4143 1.732）【答案】5.5．【解析】解：由题意可知：6=OA ，︒=∠30AOC ，︒=∠45BOC在AOC Rt △中，AOACAOC =∠sin ，北北 ABC∴216=AC ，∴3CA =，3322=-=AC AO OC ． ∴33==CO BC ．∴5.5333≈+=+=BC AC AB ．【总结】本题主要考查利用方位角解决实际问题．【例11】如图，一艘海轮位于灯塔P 的北偏东65°方向，距离灯塔80海里的A 处，它沿正南方向航行一段时间后，到达位于灯塔P 的南偏东34°方向上的B 处，请问，此时，海轮所在的B 处距离灯塔P 有多远？（精确到0.01海里，cos250.91︒≈，sin340.559︒≈）【答案】130.23．【解析】解：在APC Rt △中，APPCAPC =∠cos ， ∴8091.0PC=，∴8.72=PC在BPC Rt △中，BPPCCBP =∠sin ，∴BP8.72559.0=，∴23.130=PB ．【总结】本题主要考查利用方位角解决实际问题．【例12】如图，A 、B 为湖滨的两个景点，C 为湖心一个景点．景点B 在景点C 的正东方向，从景点A 看，景点B 在北偏东75°方向，景点C 在北偏东30°方向．一游客自景点A 驾船以20米/分的速度行驶了10分到达景点C ，之后又以同样的速度驶向景点B ，该游客从景点C 到景点B 需用多长时间？（tan75 3.732︒≈，精确到1分）【答案】27分．【解析】过A 作AD ⊥BC 的延长线于D ．由题意可得：︒=∠75BAD ，︒=∠30DAC ， 2002010=⨯=AC ．在ADC Rt △中，ACDC CAD =∠cos ，东南西北ABP C∴20023AD=，∴3100=AD ，100=DC 在ABD Rt △中，DABDBAD =∠tan ，∴3100732.3BD=，∴32.373=DB∴3824.64610032.373≈-=-=CD BD BC∴2731.27203824.646≈==t ．【总结】本题主要考查利用方位角解决实际问题．【例13】如图，某船以36海里/时的速度向正东方向航行，在点A 测得某岛C 在北偏东60°方向上，航行半小时后到达点B ，测得该岛在北偏东30°方向上，已知该岛周围16海里内有暗礁．（1）试说明点B 是否在暗礁区域外？（2）若继续向东航行有无触礁危险？请说明理由．【答案】（1）B 在暗礁区外；（2）有危险．【解析】解：（1）由题意可得：︒=∠30CAB ，︒=∠60CBD ，182136=⨯=AB ．∴︒=︒-︒=∠-∠=∠303060CAB CBD ACB ，∴ACB CAB ∠=∠∴1618>==BC AB∴B 在暗礁区外．（2）在BDC Rt △中，BCDCBCD =∠cos ， ∴1823CD=，∴16188.1539<≈=CD∴若继续向东航行有触礁危险．【总结】本题主要考查利用方位角解决实际问题，注意在触礁问题中的最小距离指的是垂直距离．【例14】如图，AC 是某市环城路的一段，AE 、BF 、CD 都是南北方向的街道，其与环城路AC 的交叉路口分别是A 、B 、C ．经测量，花卉世界D 位于点A 的北偏东45°方向、点B 的北偏东30°方向上，AB = 2千米，15DAC ∠=︒．（1）求B 、D 之间的距离；（2）求C 、D 之间的距离．【答案】（1）2；（2）332．【解析】解：(1)由题意得：︒=∠45EAD ， ︒=∠30DBF ．∵FB AE ∥∴︒=∠=∠60EAB FBC∴︒=∠30DBCABCDE F环城路和平路文化路中山路G∵15DAC ∠=︒ ∴︒=∠15ADB ∴DAB ADB ∠=∠∴2==AB BD(2)∵CD AE ∥ ∴︒=∠=∠45ADC EAD ∴︒=∠30BDC过C 作CG ⊥BD ，垂足为G 在GDC Rt △中，DCDGBDC =∠cos ， ∴CD123=，∴332=CD ．【总结】本题主要考查利用方位角解决实际问题，要注意认真分析题意．αh l1、坡度（坡比）、坡角在修路、挖河、开渠等设计图纸上，都需要注明斜坡的倾斜程度．如图，坡面的铅垂高度h 和水平宽度l 的比叫做坡面的坡度（或坡比），记作i ，即hi l=．坡度通常写成1 : m 的形式，如1:1.5i =．坡面与水平面的夹角叫做坡角，记作α．坡度i 与坡角α之间的关系：tan hi l α==．【例15】某人沿着坡度为3 : 4的斜坡前进了10米，则他所在的位置比原来的位置升高______米．【答案】6．【解析】考查坡度的定义．【例16】某铁路路基的横断面是等腰梯形，其上底为10米，下底为13.6米，高1.2米，则腰面坡角的正切值为______．【答案】32．【解析】考查等腰梯形双高的辅助线．【例17】如图，坡角为30°的斜坡上两树间的水平距离AC 为2米，则两树间的坡面距离AB 为（）模块三：坡度（坡比）知识精讲例题解析AB CDABC A．4米BCD．【答案】C【解析】考查坡角的定义．【例18】如图，燕尾槽的横断面中，槽口的形状是等腰梯形，其外口宽AD = 15毫米，槽的深度为12毫米，B∠的正切值为43，则它的里口宽BC = ______．【答案】33毫米．【解析】考查等腰梯形双高的辅助线．【例19】河堤横断面是梯形，上底为4米，堤高为6米，斜坡AD的坡度为1 : 3，斜坡CB的坡角为45°，则河堤横断面的面积为______平方米．【答案】96．【解析】考查坡角的基本定义．【例20】如图，一个大坝的横断面是一个梯形ABCD，其中坝顶AB= 3米，经测量背水坡AD = 20米，坝高10米，迎水坡BC的坡度i = 1 : 0.6，求迎水坡BC的坡角C∠的余切值和坝底宽CD．【答案】53；3109+．【解析】过A、B作AE⊥CD，BF⊥CD．A BCDE FAB CD由题意可得：356.01tan ==C ，10==BF AE ， ∴5316.0cot ==C ．在BCF Rt △中，CFBFC =∠tan ， ∴CF1035=，∴6=CF ．在ADE Rt △中，31022=-=AE AD DE ，∴931063310+=++=++=FC EF DE CD ．【总结】本题主要考查坡脚和坡比的概念．【例21】如图，某村开挖一条长1600米的水渠，渠道的横断面为等腰梯形，渠道深0.8米，下底宽1.2米，坡度为1 : 1．求一共挖土多少立方米？【答案】2560．【解析】()6.18.02.18.221=⨯+⨯=ABCD S 梯形，256016006.1=⨯=V ．【总结】考查等腰梯形双高辅助线的做法和坡度的基本定义．【例22】如图，小杰发现垂直地面的旗杆AB 的影子落在地面和斜坡上，影长分别为BC 和CD ，经测量得BC =10米，CD =10米，斜坡CD 的坡度为1:3i =，且此时测得垂直于地面的1米长标杆在地面上影长为2米，求旗杆AB 的长度．3.2≈）【答案】13．【解析】解：延长AD 和BC 交于点E ，过D 作DF ⊥BE ．ABCDEF由题意可知：31tan =∠DCF ，21tan =E ．在DCF Rt △中，CF DF DCF =∠tan ，∴CF DF =31．设x DF =，x CF 3=，则()101032222==+=+=x x x FC FD DC ，∴10=x ． ∴10=DF ，103=CF ．在DEF Rt △中，EFDF E =∠tan ， ∴EF1021=，∴102=EF 在ABC Rt △中，EBABE =∠tan ，∴1021031021++=AB ，∴1351025≈+=AB ．【总结】本题主要考查利用坡脚和坡比的概念以及锐角三角比的相关概念解决实际问题．【例23】如图，斜坡AP 的坡度为1:2.4，坡长AP 为26米，在坡顶A 处的同一水平面上有一座古塔BC ，在斜坡底P 处测得该塔的塔顶B 的仰角为45°，在坡顶A 处测得该塔的塔顶B 的仰角为76°．求：（1）坡顶A 到地面PQ 的距离；（2）古塔BC 的高度．（结果精确到1米）（参考数据：sin760.97︒≈，cos760.24︒≈，tan76 4.01︒≈）【答案】（1）10；（2）19．【解析】解：延长BC 交PQ 于点E ，过A 作AD ⊥PQ由题意可知：︒=∠76BAC ，︒=∠45BPE1254.2:1tan ==∠APD ．在APD Rt △中，PD DA APD =∠tan ，∴PD DA =125．设x DA 5=，x PD 12=，则()()26131252222==+=+=x x x PD AD PA ，∴2=x ．∴10=DA ，24=PD ．在BAC Rt △中，AC BC BAC =∠tan ，∴ACBC=01.4 设x CA =，x BC 01.4=，在PBE Rt △中，EPEB BPE =∠tan ， ∴241001.41++=x x ，∴65.4=x ．∴1901.4≈=x BC ．【总结】本题主要考查利用坡脚和坡比的概念以及锐角三角比的相关概念解决实际问题．步同级年九16/ 24ACE【习题1】某飞机在离地面1200米的上空测得地面控制点的俯角为60°，此时飞机与该地面控制点之间的距离是______米．【答案】3800．【解析】考查俯角的定义．【习题2】一船在海上点B处沿南偏东10°方向航行到点C处，这时在小岛A测得点C 在南偏西80°方向，则=ACB∠______．【答案】90°【解析】考查方向角的定义．【习题3】某人沿着有一定坡度的坡面前进了10米，此时他与水平地面的垂直距离为25米，则这个坡面的坡度为______．【答案】1:2【解析】考查坡度的定义．【习题4】如图，已知楼房AB高50米，铁塔塔基距楼房房基间的水平距离BD = 50米，塔高DC为150503+米，下列结论中，正确的是（）A．由楼顶望塔顶仰角为60°随堂检测DABCNM B ．由楼顶望塔基俯角为60° C ．由楼顶望塔顶仰角为30°D ．由楼顶望塔基俯角为30°【答案】C ．【解析】解：由图可知：50====AE DE DB AB ， ∴3350503350150=-+=-=ED CD EC ．在ACE Rt △中，33503350tan ===∠AE CE CAE ，∴︒=∠30CAE ．∴由楼顶望塔顶仰角为30°．【总结】本题主要考查利用已知条件解直角三角形，再利用锐角三角比的值求出角的度数．【习题5】 A 港在B 地的正南103千米处，一艘轮船由A 港开出向西航行，某人第一次在B 处望见该船在南偏西30°，半小时后，有望见该船在南偏西60°，则该船速度为______．【答案】40h km /．【解析】解：在ACB Rt △中，AB AC CBA =∠tan ，∴33310=CA ，解得：10=CA ．在ADB Rt △中，ABAD DBA =∠tan ，∴3310=DA ，解得：30=DA ．∴201030=-=-=AC AD CD ，∴402120=÷=v ．【总结】本题主要考查利用方位角解决实际问题．【习题6】如图，一架飞机在高度为5千米的点A 时，测得前方的山顶D 的俯角为30°，水平向前飞行2千米到达点B 时，又测得山顶D 的俯角为45°，求这座山的高度DN ．（结果可保留根号）【答案】43【解析】解：由题意可得：5==CN AM ，2=AB ，︒=∠30CAD ，︒=∠45CBD ．设x CD =，则x BC =．在ACD Rt △中，tan DC CAD AC ∠=，∴233+=x x，解得：13+=x ， ∴()34135-=+-=-=CD CN DN ．【总结】本题主要考查利用仰角和俯角的有关概念解决实际问题．【习题7】小岛B 正好在深水港口A 的东南方向，一艘集装箱货船从港口A 出发，沿正东方向以每小时30千米的速度行驶，40分钟后在C 处测得小岛B 在它的南偏东15°方向，求小岛B 离深水港口A 的距离．(精确到0.1千米)1.412.45≈，sin150.26︒≈，cos150.97︒≈，tan150.27︒≈）【答案】38.6千米．【解析】解：由题意可得：203230=⨯=AC ， ︒=∠45CAB ，︒=∠30B ．过C 点作CD ⊥AB ．在ACD Rt △中，AC DC CAD =∠sin ，∴2022CD=，解得：210=CD ，∴210==CD AD ．在BCD Rt △中，BDDC B =tan ，∴BD 21033=，解得：610=BD ． ∴6.38610210≈+=+=BD AD AB ．【总结】本题主要考查利用方位角解决实际问题．【习题8】如图，以水库大坝横断面是梯形ABCD ，坝顶宽6米，坝高23米，斜坡AB的坡度1:3AB i =，斜坡CD 的坡度1:2.5CD i =．（1）求斜坡AB 和坝底AD 的长度；（2）若要把坝宽增加3米，同时背水坡AB 的坡度AB i 由原来的1 : 3变为1 : 5，请求出大坝【答案】（1）1023，132.5；（2）【解析】解：由题意可得： 6=BC ，23==CF BE ，31tan =A ，525.21tan ==D ．在ABE Rt △中，AE BE A =tan ，∴AE2331=，解得：69=AE ． ∴102369232222=+=+=AE BE AB ．在CDF Rt △中，DF CF D =tan ，∴DF 2352=，解得：2115=DF ．∴5.1322115669=++=++=FD EF AE AD ．（2）由（1）可得：66369=-=-=ME AE AM ．在HGM Rt △中，HM GM H =tan ，∴HM2351=，∴115=HM ． ∴4966115=-=-=AM HM AH ．∴()()598234932121=⋅+=⋅+=GM AH GB S GHAB 梯形．【总结】本题主要考查利用坡度来解决实际问题，注意对题目中条件的认真分析．步同级年九20 / 24【作业1】身高相同的三个小朋友甲、乙、丙放风筝，他们放出的线长分别为300米，250 米，200米，线与地面所成的角度分别为30°，45°，60°（假设风筝线是拉直的），则三人所放的风筝（）A ．甲的最高B ．乙的最低C ．丙的最低D ．乙的最高【答案】D ．【解析】由仰角的定义和解直角三角形可得：甲的风筝离地面150米，乙的风筝离地面 2125米，丙的风筝离地面3100米．∵150********>>∴乙的风筝最高．【总结】本题主要考查方位角的概念以及特殊角的锐角三角比的值．【作业2】小明在东西方向是沿江大道A 处，测得江中灯塔P 在北偏东60°方向上，在A 处正东400米的B 处，测得江中灯塔P 在北偏东30°方向上，则灯塔P 到沿江大道的距离为______米．【答案】3200．【解析】解：由题意可知：︒=∠30PAB ，︒=∠120PBA ． ∴︒=∠30APB ∴APB PAB ∠=∠ ∴400==PB AB过P 作PC ⊥AB ，垂足为C 在PBC Rt △中，PBPCPBC =∠sin ， ∴40023PC=∴3200=PC ．【总结】本题主要考查方位角的概念及运用．【作业3】某人从地面沿着坡度1:3i =的山坡走了100米，这时他离地面的高度是课后作业______米．【答案】50【解析】考查坡度的定义和解直角三角形．【作业4】如图，一渔船上的渔民在A 处看见灯塔M 在北偏东60°的方向，这艘渔船以 28海里/时的速度向正东航行，半小时到达B 处，在B 处看见灯塔M 在北偏东15°的方向，此时灯塔M 与渔船的距离是（）A ．14海里B．C ．7海里D．【答案】D【解析】解：由题意有：︒=∠30MAB ，︒=∠105ABM ，142128=⨯=AB ．∴︒=∠45M ．过B 作BC ⊥AM ，垂足为C在ABC Rt △中，721==AB BC ；在MBC Rt △中，MBBCM =sin ， ∴722MB=．∴27=MB ．【总结】本题主要考查利用方位角结合锐角三角比解决实际问题．【作业5】如图，在同一地面上有甲、乙两幢楼AB 、CD ，甲楼AB 高10米，从甲楼AB 的楼顶测得乙楼CD 的楼顶C 的仰角为30°，从乙楼CD 的楼顶C 拉下的节日庆典条幅 CE 与地面所成的角为60°，这时条幅与地面的固定点E 到甲楼B 的距离为24米，求条幅CE 的长度．【答案】24310+米．【解析】解：由题意可知：︒=∠30CAF ，︒=∠60CED 设x CE 2=，则x ED =，x CD 3= 在ACF Rt △中，AFCFCAF =∠tan ， ∴xx +-=2410333， ∴1235+=x ．∴243102+==x CE ．【总结】本题主要考查利用仰角和俯角的相关概念结合锐角三角比解决实际问题．【作业6】如图，水坝的横截面是梯形ABCD ，上底AD =4米，坝高3AM DN ==米，斜坡AB的坡比1i =，斜坡DC 的坡比21:1i =．（1）求坝底BC 的长；（结果保留根号）（2）为了增加水坝的抗洪能力，在原来的水坝上增加高度，使得水坝的上底2EF =米，求水坝增加的高度．（精确到0.11.73≈）【答案】（1）733+；（2）0.7米．【解析】解：（1）在MBA Rt △中，MBAM B =tan ，∴BM 331=，∴33=MB ．在DNC Rt △中，NCDNC =tan ， ∴NC31=，∴3=NC ．∴7333433+=++=++=NC MN BM BC ．(2)在EGB Rt △中，BG EGB =tan ，∴BG EG =31，在FCH Rt △中，HC FH C =tan ，∴HCFH=1，设x FH EG ==，则x BG 3=，x CH =，∴73323+=++=++=++=x x HC EF BG HC GH BG BC ． ∴32+=x ．∴7.013332≈-=-+=∆h ．【总结】本题主要考查利用坡度和坡比的相关概念结合锐角三角比解决实际问题．【作业7】如图，某人在建筑物AB 的顶部测得一烟囱CD 的顶端C 的仰角为45°，测得点C 在湖中的倒影C 1的俯角为60°，已知AB = 20米，求烟囱CD 的高．【答案】40320+米．【解析】解：由题意可得：︒=∠45CAE ，︒=∠601EBC ．AB CDNM过A 作AE ⊥CD ，垂足为E ．设x CE =，则x AE =． ∵C 和C 1关于BD 对称， ∴201+==x D C CD ．在1AEC Rt △中，AEEC EAC 11tan =∠， ∴xx 403+=，∴20320+=x ．∴4032020+=+=x CD ．【总结】本题主要考查利用俯角的相关概念结合锐角三角比解决实际问题，注意认真分析．【作业8】如图，一水渠的横断面是等腰梯形，已知其迎水斜坡AD 和BC 的坡度为1： 0.6，现在测得放水前的水面宽EF 为1.2米，当水闸放水后，水渠内水面宽GH 为2.1米，求放水后水面上升的高度．【答案】放水后水面上升的高度为0.75米．【解析】解：由题意可知：四边形GEFH356.0:1tan ==∠MGE ．过E 作EM ⊥GH ，过F 作FN ⊥GH由等腰梯形的性质可得：45.0==NH GM ．在GME Rt △中，GM EMMGE =∠tan ，∴45.035EM=，∴75.0=EM ．∴放水后水面上升的高度为0.75米．【总结】本题主要考查利用坡度和坡比的相关概念结合锐角三角比解决实际问题．。

沪科版九年级数学上册《反比例函数的几何综合问题大题专练》重难点培优

2021-2022学年九年级数学上册尖子生同步培优题典【沪科版】专题21.16反比例函数的几何综合问题大题专练（重难点培优）姓名：__________________ 班级：______________ 得分：_________________注意事项：本试卷试题共25题．答卷前，考生务必用0.5毫米黑色签字笔将自己的姓名、班级等信息填写在试卷规定的位置．一．解答题（共25小题）1．（2021•江川区模拟）如图，一次函数y1＝ax+b与反比例函数y2=kx的图象相交于A（2，8），B（8，2）两点，连接AO，BO，延长AO交反比例函数图象于点C．（1）求一次函数y1的表达式与反比例函数y2的表达式；（2）当y1＜y2，时，直接写出自变量x的取值范围为；（3）点P是x轴上一点，当S△PAC=45S△AOB时，请直接写出点P的坐标为．2．（2021•靖江市模拟）如图，平面直角坐标系中，一次函数y1＝ax+b（a≠0）的图象与反比例函数y2=k x（k≠0）的图象交于点A（1，2）和B（﹣2，m）．（1）求一次函数和反比例函数的表达式；（2）请直接写出y1＞y2时x的取值范围；（3）过点B作BE∥x轴，AD⊥BE于点D，点C是直线BE上一点，若AD＝3CD，求点C的坐标．3．（2017秋•黄埔区期末）已知反比例函数y=w+3x的图象的一支位于第一象限．（1）判断该函数图象的另一支所在的象限，并求w的取值范围；（2）点A在该反比例函数位于第一象限的图象上，点B与点A关于x轴对称，点C与点A关于原点O 对称，若△ABC的面积为4，求w的值．4．（2020春•慈溪市期末）如图，一次函数y＝kx+b（k≠0）与反比例函数y=mx（x＞0）的图象交于点A，B，与x轴交于点C，与y轴交于点D，其中点A（1，3）和点B（3，n）．（1）求一次函数的表达式．（2）求证：BC＝AD．（3）根据图象回答：当x为何值时，kx+b−mx＞0（请直接写出答案）．5．（2020春•海陵区期末）如图，A、B是反比例函数y=kx的图象上关于原点O对称的两点，点C是y轴负半轴上一点，直线AC与x轴交于点D，且点C是线段AD的中点，连接BD．（1）求证：BD⊥OD；（2）若点C的坐标是（0，﹣2），且△ABD的面积为5，求k的值和B点坐标．6．（2020春•扬中市期末）如图，在平面直角坐标系中，点A（3，2）在反比例函数y=kx（x＞0）的图象上，点B在OA的延长线上，BC⊥x轴，垂足为C，BC与反比例函数的图象相交于点D，连接AC，AD．（1）求该反比例函数的解析式；（2）当点B（6，4）时，求S△ABD；（3）若S△ACD=52，则线段BD＝．7．（2020春•洪泽区期末）如图，一次函数y＝kx+1与反比例函数y=mx的图象有公共点A（1，2）．直线l⊥x轴于点N（3，0），与一次函数和反比例函数的图象分别交于点B，C，请根据上述条件，解答下列问题：求：（1）k，m的值；（2）一次函数y＝kx+1图象与x轴交点D的坐标；（3）△ABC的面积．8．（2019秋•沈河区校级期中）如图，平面直角坐标系中，直线y1＝kx+b分别与x，y轴交于点A，B，与双曲线y2=mx分别交于点C，D（点C在第一象限，点D在第三象限），作CE⊥x轴于点E，tan∠BAO=12，OA＝4，OE＝2．（1）求反比例函数的解析式；（2）请直接写出使y1＞y2的x取值范围；（3）在y轴上是否存在一点P，使S△ABP＝S△CEP？若存在，请直接写出点P的坐标；若不存在，请说明理由．9．（2021•东莞市校级一模）如图，在平面直角坐标系xOy中，矩形OABC的边OA、OC分别在x轴、y轴上，EF垂直平分对角线AC，垂足为D．点E、点F分别在BC、OA上，连接CF、AE，反比例函数y= kx的图象恰好经过点D，交线段AE于点G，点D的坐标为（4，2）．（1）求证：四边形AECF为菱形；（2）求直线AE的解析式；（3）求G的坐标．10．（2021•广州模拟）如图，直线AB：y＝kx+b与x轴、y轴分别相交于点A（1，0）和点B（0，2），以线段AB为边在第一象限作正方形ABCD．（1）求直线AB的解析式；（2）求点D的坐标；（3）若双曲线y=kx（k＞0）与正方形的边CD始终有一个交点，求k的取值范围．11．（2020春•偃师市期末）如图，一次函数y=43x+b的图象与y轴交于点B（0，2），与反比例函数y=kx（x＜0）的图象交于点D．以BD为对角线作矩形ABCD，使顶点A、C落在x轴上（点A在点C的右边），BD与AC交于点E．（1）求一次函数的解析式；（2）求点D的坐标和反比例函数的解析式；（3）求点A的坐标．12．（2020春•瑞安市期末）如图，菱形ABCD放置在平面直角坐标系中，已知点A（﹣3，0），B（2，0），点D在y轴正半轴上，反比例函数的图象经过点C．（1）求反比例函数的表达式．（2）将菱形ABCD向上平移，使点B恰好落在双曲线上，此时A，B，C，D的对应点分别为A′，B′，C′，D′，且C′D′与双曲线交于点E，求点E的坐标．13．（2019春•东海县期末）如图，一次函数y＝2x+b的图象经过点A（﹣1，0），并与反比例函数y=k1 x（x＞0）的图象交于B（m，4）（1）求k1的值；（2）以AB为一边，在AB的左侧作正方形ABCD，求C点坐标；（3）将正方形ABCD沿着x轴的正方向，向右平移n个单位长度，得到正方形A1B1C1D1，线段A1B1的中点为点E，若点C1和点E同时落在反比例函数y=k2x的图象上，求n的值．14．（2021•东莞市模拟）如图，点A（1，6）和B（n，2）是一次函数y1＝kx+b的图象与反比例函数y2=m x（x＞0）的图象的两个交点．（1）求一次函数与反比例函数的表达式；（2）设点P是y轴上的一个动点，当△PAB的周长最小时，求点P的坐标；（3）从下面A，B两题中任选一题作答．A．在（2）的条件下，设点D是坐标平面内一个动点，当以点A，B，P，D为顶点的四边形是平行四边形时，请直接写出符合条件的所有点D的坐标．B．设直线AB交y轴于点C，点M是坐标平面内一个动点，点Q在y轴上运动，以点A，C，Q，M为顶点的四边形能构成菱形吗？若能，请直接写出点Q的坐标；若不能，说明理由．15．（2021•郑州模拟）如图，在平面直角坐标系中，一次函数y＝mx+5（m≠0）的图象与反比例函数y=k x（k≠0）在第一象限的图象交于A（1，n）和B（4，1）两点，过点A作y轴的垂线，垂足为M．（1）求一次函数和反比例函数的表达式．（2）求△OAM的面积S．（3）在y轴上求一点P，使PA+PB的值最小并求出此时点P的坐标．16．（2020秋•禅城区期末）如图，直线AB与双曲线y=12x在第一象限内交于点P，点P的横坐标为6，直线AB与x轴、y轴分别交于A、B两点，且∠BAO＝45°；（1）求直线AB的解析式；（2）C为线段AB上一点，过C作CD∥y轴交双曲线y=12x于D点，连接DP，当△CDP是等腰直角三角形时，求点C的坐标．17．（2020春•温州期末）如图，点A，B分别在反比例函数y=kx（k≠0），y=4x在第一象限的图象上，点C是y轴正半轴上一点，连接AB，OB，AC．已知四边形ABOC是平行四边形，且A，B两点的纵坐标之比为9：4．（1）求k的值．（2）当▱ABOC是菱形时，求AB的长．18．（2020春•东阳市期末）如图，四边形OBAC是矩形，OC＝2，OB＝6，反比例函数y=kx的图象过点A．（1）求k的值．（2）点P为反比例图象上的一点，作PD⊥直线AC，PE⊥x轴，当四边形PDCE是正方形时，求点P 的坐标．（3）点G为坐标平面上的一点，在反比例函数的图象上是否存在一点Q，使得以A、B、Q、G为顶点组成的平行四边形面积为14？若存在，请求出点G的坐标；若不存在，请说明理由．19．（2019春•海陵区校级期末）如图，在直角坐标系xOy中，矩形ABCD的DC边在x轴上，D点坐标为（﹣6，0）边AB、AD的长分别为3、8，E是BC的中点，反比例函数y=kx的图象经过点E，与AD边交于点F．（1）求k的值及经过A、E两点的一次函数的表达式；（2）若x轴上有一点P，使PE+PF的值最小，试求出点P的坐标；（3）在（2）的条件下，连接EF、PE、PF，在直线AE上找一点Q，使得S△QEF＝S△PEF直接写出符合条件的Q点坐标．20．（2021•芜湖模拟）如图，在平面直角坐标系中，反比例函数y=kx（x＞0）的图象上有一点D（m，43），过点D作CD⊥x轴于点C，将点C向左平移2个单位长度得到点B，过点B作y轴的平行线交反比例函数的图象于点A，AB＝4．（1）点A的坐标为（用含m的式子表示）；（2）求反比例函数的解析式；（3）设直线AD的解析式为y＝ax+b（a，b为常数且a≠0）．则不等式kx−（ax+b）＞0的解集是．21．（2021•济南二模）如图，一次函数y＝mx+1的图象与反比例函数y=kx的图象相交于A、B两点，点C在x轴正半轴上，点D（1，﹣2），连接OA、OD、DC、AC，四边形OACD为菱形．（1）求一次函数与反比例函数的解析式；（2）根据图象，直接写出反比例函数的值小于2时，x的取值范围；（3）设点P是直线AB上一动点，且S△OAP=12S菱形OACD，求点P的坐标．22．（2020秋•昌图县期末）如图，一次函数y1＝kx+b的图象与反比例函数y2=6x的图象交于A（2，m），B（n，1）两点，连接OA，OB．（1）求这个一次函数的表达式；（2）求△OAB的面积；（3）问：在直角坐标系中，是否存在一点P，使以O，A，B，P为顶点的四边形是平行四边形？若存在，直接写出点P的坐标；若不存在，请说明理由．23．（2021春•连云港期末）如图，在平面直角坐标系中，A（6，0）、B（0，4）是矩形OACB的两个顶点，双曲线y=kx（k≠0，x＞0）经过AC的中点D，点E是矩形OACB与双曲线y=kx的另一个交点，（1）点D的坐标为，点E的坐标为；（2）动点P在第一象限内，且满足S△PBO=89S△ODE．①若点P在这个反比例函数的图象上，求点P的坐标；②连接PO、PE，当PO﹣PE的值最大时，求点P的坐标；③若点Q是平面内一点，使得以A、C、P、Q为顶点的四边形是菱形，请你直接写出满足条件的所有点Q的坐标．24．（2020•绵阳）如图，在平面直角坐标系xOy中，一次函数的图象与反比例函数y=kx（k＜0）的图象在第二象限交于A（﹣3，m），B（n，2）两点．（1）当m＝1时，求一次函数的解析式；（2）若点E在x轴上，满足∠AEB＝90°，且AE＝2﹣m，求反比例函数的解析式．25．（2020秋•丹东期末）如图，反比例函数y=kx（k≠0）的图象与一次函数y＝mx﹣2相交于A（6，1），B（n，﹣3），直线AB与x轴，y轴分别交于点C，D．（1）求k，m的值；（2）求出B点坐标，再直接写出不等式mx﹣2＜kx的解集；（3）点M在函数y=kx（k≠0）的图象上，点N在x轴上，若以C、D、M、N为顶点的四边形是平行四边形，请你直接写出N点坐标．。

沪教版九年级数学暑假同步讲义第12讲解直角三角形(解析版)

解直角三角形是九年级上学期第二章第二节的内容，通过本节的学习，需要掌握直角三角形中，除直角外其余五个元素之间的关系，并熟练运用锐角三角比的意义解直角三角形．难点在于，若一个三角形不是直角三角形，要有意识把它化归为解直角三角形的问题．1、解直角三角形在直角三角形中，由已知元素求出所有未知元素的过程，叫做解直角三角形．在t R ABC ∆中，如果=90C ∠︒，那么它的三条边和两个锐角之间有以下的关系：（1）三边之间的关系：222a b c +=（2）锐角之间的关系：90A B ∠+∠=︒（3）边角之间的关系： sin cos a A B c ==，cos sin bA B c ==tan cot a A B b ==，cot tan b A B a== 解直角三角形内容分析知识结构知识精讲模块一：解直角三角形的基本类型步同级年九2 / 20【例1】在ABC ∆中，已知90C ∠=︒，37B ∠=︒，c = 8，求这个直角三角形的其他边和角（sin370.6︒≈，cos370.8︒≈，tan370.75︒≈，cot370.25︒≈）．【答案】53A ∠=︒， 4.8b =， 6.4a =．【解析】解：90903753A B ∠=︒-∠=︒-︒=︒；在Rt ABC △中，sin b B c =，则0.68b=，解得： 4.8b =；在Rt ABC △中，cos a B c =，则0.88a=，解得： 6.4a =．【总结】已知斜边和一锐角度数时，求直角边时，用锐角的正弦或余弦．【例2】在ABC ∆中，90C ∠=︒，43A ∠=︒，b = 9，解这个直角三角形（sin430.68︒≈，cos430.73︒≈，tan430.93︒≈，cot 43 1.07︒≈）．【答案】47B ∠=︒，8.37a =，12.33c =．【解析】解：90904347B A ∠=︒-∠=︒-︒=︒；在Rt ABC △中，tan a A b =，则0.939a=，解得：8.37a =；在Rt ABC △中，9cos A c=，则0.88a=，解得：12.33c =．【总结】已知直角边和一锐角度数时，求直角边时用锐角的正切或余切，求斜边时用锐角的正弦或余弦．【例3】在ABC ∆中，已知90C ∠=︒，c = 8，a = 6，求这个直角三角形的其他边和角（利用计算器计算）．【答案】27b =，48A ∠=︒，42B ∠=︒．【解析】解：22228627b c a =-=-=．在Rt ABC △中，sin a A c =，则3sin 4A =．利用计算器解得：48A ∠=︒，90904842B A ∠=︒-∠=︒-︒=︒．【总结】已知直角三角形的两条边，利用勾股定理求另一条边，利用锐角三角比确定锐角的度数．【例4】在ABC ∆中，已知90C ∠=︒，a = 7，b = 9，解这个直角三角形（利用计算器计算）．【答案】130c =，38A ∠=︒，52B ∠=︒．例题解析【解析】解：222279130c a b =+=+=，在Rt ABC △中，tan a A b =，则7tan 9A =，利用计算器可得：38A ∠=︒，∴90903852B A ∠=︒-∠=︒-︒=︒．【总结】已知直角三角形的两条边，利用勾股定理求另一条边，利用锐角三角比确定锐角的度数．【例5】 Rt ABC ∆中，90C ∠=︒，AB = 4，AC = 22，BC = ______，A ∠= ______．【答案】22BC =，45A ∠=︒．【解析】解：()222242222BC AB AC =-=-=．在Rt ABC △中，cos AC A AB =，则2cos 2A =，∴45A ∠=︒．【总结】已知直角三角形的两条边，利用勾股定理求另一条边，利用锐角三角比确定锐角的度数．【例6】在ABC ∆中，::1:3:2AC BC AB =，则A ∠= ______．【答案】60°．【解析】解：设AC x =，3BC x =，2AB x =，∵222AC BC AB +=，∴ABC ∆为直角三角形．师生总结解直角三角形的基本类型有哪些？并简述解法．步同级年九4 / 20在Rt ABC △中，cos AC A AB =，则1cos 2A =，∴60A ∠=︒．【总结】当已知直角三角形的三边比为32时，则这个直角三角形中的最小角为30°．【例7】 Rt ABC ∆中，90C ∠=︒，60B ∠=︒，AC + BC = 2，则AB 的长是______．【答案】32．【解析】解：在Rt ABC △中，cos BC B AB =，又60B ∠=︒，则1cos 2B =．设BC x =，则2AB x =，223AC AB BC x =-．∵AC + BC = 2， 32x x +=．解得：31x =， ∴2232AB x ==．【总结】当直角三角形中含有30°的锐角时，则三边比为32．【例8】在直角三角形中，90C ∠=︒，30A B ∠-∠=︒，a –b =2，a 、b 、c 是A ∠、B ∠、C ∠所对的边，解这个直角三角形．【答案】60A ∠=︒，30B ∠=︒，33a =+31b =，232c =．【解析】∵在Rt ABC △中，90C ∠=︒， ∴+90A B ∠∠=︒；又∵30A B ∠-∠=︒， ∴60A ∠=︒，30B ∠=︒；在Rt ABC △中，tan b B a =3ba=，即3a b =； ∵a –b =2， 32b b -=， ∴31b =．∴333a b ==2232c b ==．【总结】当直角三角形中含有30°的锐角时，则三边比为32．【例9】如图，Rt ABC ∆中，90C ∠=︒，BC = 3，AC = 4，以B 为圆心，4为半径作圆弧交AC 边于点F ，交AB 于点E ，连接CE ，求ACE ∠的正切值．【答案】316．【解析】解：过点E 作EG ⊥AC ，交AC 于点G ．∵GE BC ∥，∴AE AG GEAB AC BC ==，∴1543AG GE==，∴45AG =，35GE =，A BCDE∴416455CG AC AG =-=-=．在Rt CEG △中，335tan 16165GE ACE CG ∠===．【总结】当所求锐角三角比的锐角不在直角三角形中时，要构造包含该锐角的直角三角形求锐角三角比．【例10】如图，在Rt ABC ∆中，90C ∠=︒，D 是BC 中点，DE ⊥AB ，垂足为E ，tan B =12，AE = 7，求DE 的长．【答案】73．【解析】解：在Rt BED ∆中，1tan 2ED B BE ==，设DE x =，则2BE x =，()222225BD DE BE x x x =+=+=． ∵D 是BC 中点，∴5DC x =．在Rt ABC ∆中，1tan 2AC B BC ==，则1225AC x=，解得：5AC x =．在Rt ABC ∆中，222AB AC BC =+，则()()()22227525x x x +=+，解得：73x =．即DE 的长为73．【总结】当同一个锐角在不同的直角三角形中时，可多次运用此锐角的三角比，得到不同的线段的比值．【例11】在Rt ABC ∆中，90C ∠=︒，a 、b 、c 分别是A ∠、B ∠、C ∠的对边，解下列直角三角形：（1）60B ∠=︒，232AC BC -=-；模块二：解直角三角形的运用例题解析（2）10BC =，ABC S ∆=【答案】（1）30A ∠=︒，2BC =，AC =4AB =；（2）60A ∠=︒，30B ∠=︒，ACAB = 【解析】解：（1）9030A B ∠=︒-∠=︒．在Rt ABC ∆中，tan ACB BC ==BC x =，则AC ；∵2AC BC -=2x -=，∴2x =． ∴2BC =，AC ==24AB x ==．（2）∵ABC S ∆=12BC AC ⋅⋅，∴1102AC ⋅⋅=AC =在Rt ABC ∆中，3cot 10AC A AB ===，则60A ∠=︒． ∴906030B ∠=︒-︒=︒，2AB AC = 【总结】利用特殊角30°以及60°的特殊角的锐角三角比的值解直角三角形．【例12】如图，在菱形ABCD 中，AE ⊥BC 于点E ，EC = 1，cos B =513，则这个菱形的面积是______．【答案】3916．【解析】解：在Rt ABE ∆中，cos B =513BE AB =，设5BE x =，则13AB x =． AB CDEABCD'D ∴()()222213512AE AB EB x x x =-=-，∴1358EC x x x =-=．∵EC = 1，∴81x =，解得：18x =．∴39121316ABCD S AE BC x x =⋅=⋅=四边形．【总结】本题主要考查锐角三角比的直接运用．【例13】如图，已知正方形ABCD 的边长为2，如果将线段BD 绕着点B 旋转后，点D落在CB 的延长线上的'D 处，则tan 'BAD ∠等于（）A ．1B 2C 2D ．22【答案】B【解析】解：∵线段BD 绕着点B 旋转后，点D 落在CB 的延长线上的'D 处． ∴'22BD BD ==在'Rt ABD △中，'22tan '=2D B BAD AB ∠==．【总结】本题一方面考查锐角三角比的意义，另一方面考查图形旋转的性质．【例14】如图，在Rt ABC ∆中，90C ∠=︒，AD 是BC 边上的中线．（1）求证：tan =2tan ADC ABC ∠∠；（2）若2BD =30B ∠=︒，求AD 的长．【答案】（1）证明略；（2）423．【解析】（1）证明：在Rt ABC ∆中，tan CAABC BC∠=；在Rt ADC ∆中，tan CAADC DC∠=． ∵AD 是BC 边上的中线，∴2BC CD =， ∴2CA CABC CD⨯=． ∴tan =2tan ADC ABC ∠∠．（2）∵2BD =，AD 是BC 边上的中线， ∴222BC BD ==步同级年九8 / 20ABCD在Rt ABC ∆中，tan30AC BC ︒=322=，解得：263AC =在Rt ADC ∆中，()2222242263AD CD CA ⎛⎫++ ⎪⎝⎭．【总结】本题一方面考查锐角三角比的意义，一方面考查特殊角的锐角三角比的值．【例15】 ABC ∆中，=90C ∠︒，85AC =角平分线16153AD =解这个直角三角形．【答案】30B ∠=︒，60CAB ∠=︒，165AB =815BC = 【解析】解：在Rt ADC ∆中，853cos 16153AC CAD AD ∠===，∴30CAD ∠=︒，∵AD 平分CAB ∠， ∴60CAB ∠=︒．∴9030B CAB ∠=︒-∠=︒，2165AB AC == 在Rt ABC ∆中，tan AC B BC =385=，∴815BC =【总结】通过直角三角形中边之间的关系得到角度．【例16】如图，四边形ABCD 中，45A ∠=︒，90C ∠=︒，75ABD ∠=︒，30DBC ∠=︒，AB = 2a ，求BC 的长． 2a ．【解析】解：过B 作BE AD ⊥，垂足为E ． ∵45A ∠=︒，∴45ABE ∠=︒．∵75ABD ∠=︒，∴30EBD ∠=︒．在Rt ABE ∆中，sin EB A AB =22EBa=，∴2EB a ；在Rt DBE ∆中，cos EB DBE DB ∠=32a=，∴263DB a =．在Rt DCB ∆中，cos CB DBC DB∠=3263CB a =，∴2CB a =．【总结】将题目中的特殊角构造到直角三角形中．【例17】如图，在Rt ABC ∆中，90A ∠=︒，AC = 2，AB = 4，ACD B ∠=∠，求cos DCB ∠．【答案】45．【解析】解：过点D 作DE BC ⊥，交BC 边于点E ．在Rt ABC ∆中，22222425BC AC AB =++ ∵ACD B ∠=∠，A A ∠=∠，∴ACD ABC △∽△．∴AC AD DCAB AC BC ==，即24225AD ==∴1AD =，5CD =．∵B B ∠=∠，BED BAC ∠=∠，∴BED BAC △∽△． ∴BE BD AB BC =，即425BE ，∴655BE =．∴64255555EC BC BE =-=在Rt DCE △中，4545cos 55CE DCB CD ∠===．【总结】当所求锐角三角比的锐角不在直角三角形中时，要构造包含该锐角的直角三角形求锐角三角比．【例18】如图，在ABC ∆中，AB = AC ，BD ⊥AC ，D 为垂足，且2sin 7DBC ∠=，求BC AC的值．【答案】47．【解析】解：过点A 作AE BC ⊥，交BC 边于点E ． ∵90C DBC ∠+∠=︒，90C EAC ∠+∠=︒， ∴DBC EAC ∠=∠．∴2sin sin 7DBC EAC ∠=∠=，在Rt ACE △中，sin EC EAC AC ∠=，∴27EC AC =．∵AB AC =，AE BC ⊥， ∴2BC EC =．∴224277BC CE AC AC ==⨯=．【总结】善于发现题目中的条件得到相等的角，然后运用角度相等的锐角三角比值也相等的思路去解题．【例19】在ABC ∆中，已知D 为AB 中点，135ACB ∠=︒，AC ⊥CD ，求sin A 的值．步同级年九10 / 205．【解析】解：过点D 作DE CD ⊥，交BC 边于点E ． ∵135ACB ∠=︒，∴45DCE ∠=︒． ∵DE CD ⊥，AC ⊥CD ， ∴AC DE ∥， ∴DB EDAB AC=． ∵D 为AB 中点，∴12ED AC =．设ED x =，则CD x =，2AC x =．在Rt ACD △中，225AD AC CD x =+，∴5sin 5CD A AD x=== 【总结】1、本题还有一种辅助线的方法，如图．2、添辅助线的原则是：①将特殊角构造到直角三角形中； ②添加辅助线之后要能包含基本图形．【例20】在Rt ABC ∆中，90C ∠=︒，AC = BC ，AD 是BC 上的中线，求cos BAD ∠与sin BAD ∠的值．3101010．【解析】解：过点D 作DE AB ⊥，交AB 于点E ．设2DB x =，则2CD x =，4AC x =．在Rt ABC △中，2242AB AC BC x =+=，在Rt ADC △中，2225AD AC DC x =+，在Rt BDE △中，sin DE B BD =22DEx =，∴2DE x =，在Rt BDE △中，cos BE B BD =22BEx=，∴2BE x =，∴42222AE AB BE x x x =-==在Rt ADE △中，323cos 101025AE x BAD AD x ∠==，210sin 25DE x BAD AD x ∠=== 【总结】当所求锐角三角比的锐角不在直角三角形中时，要构造包含该锐角的直角三角形求锐角三角比．【例21】若等腰三角形两腰上的高的和等于底边上的高，求底角的余切值． 15．【解析】已知：如图，等腰ABC △中，AB AC =，CD AB ⊥，BE AC ⊥，AF BC ⊥．且满足CD BE AF +=，求cot ABC ∠的值．解：∵A A ∠=∠，AB AC =，ADC AEB ∠=∠，∴ADC AEB △≌△． ∴DC BE =． ∵CD BE AF +=， ∴2CD AF =． ∵1122BC AF AB CD ⋅⋅=⋅⋅， ∴2BA BC =．设2BC x =，则4AB x =，BF x =在Rt ABF △中，()2222415AF AB BF x x x -=-，15cot 15BF ABC AF x ∠== 【总结】本题是一道文字题，要根据题意先画出图形，然后再根据条件进行求解．【例22】在ABC ∆中，BC = 6，63AC =30A ∠=︒，求AB 的长．【答案】6或12．【解析】解：过点C 作CD AB ⊥，交AB 于点D ．在Rt ACD △中，sin CDA AC =，∴1263=，∴33CD =cos ADA AC=363=，∴6AD =．在Rt BCD △中，()22226333BD CB CD =--，∴11936AB AD B D =-=-=，229312AB AD B D =+=+=．【总结】本题主要考查对题意的理解，要注意两种情况的讨论．【例23】在四边形ABCD 中，AB = 8，BC = 1，30BAD ∠=︒，60ABC ∠=︒，四边形ABCD 的面积为53AD 的长．【答案】3【解析】解：延长AD 和BC 相交于点E ．步同级年九12 / 20∵30BAD ∠=︒，60ABC ∠=︒，∴90E ∠=︒．在Rt AEB △中，sin BE A AB =，∴128BE=，∴4BE =，3EC BE BC =-=；∵cos AE A AB =，∴328AE=，∴43AE =． ∵四边形ABCD 的面积为53，∴1144335322AEB EDC ABCD S S S DE =-=⋅⋅-⋅⋅=△△四边形，∴23DE =．∴432323AD AE DE =-=-=．【总结】当看到30°和60°这些特殊角时，要想办法把它们构造到一个直角三角形中．【例24】如图，在四边形ABCD 中，90ABC ADC ∠=∠=︒，120BCD ∠=︒，AD = 2，13AB =+，求CD 的长度．【答案】2．【解析】解：延长AD 和BC 交于点E ． ∵120BCD ∠=︒，∴60DCE ∠=．∵90ADC ∠=︒，∴30E ∠=， ∴60BAE ∠=．在Rt ABE △中，cos AB A AE =，∴1132AE +=．∴223AE =+． ∴223223DE AE AD =-=+-=．在Rt CDE △中，tan DE DCE CD ∠=，∴233CD=，∴2CD =．【总结】若题目中含有120°或者150°这些角时，要想到它们的邻补角也是特殊角．【习题1】在t R ABC ∆中，90C ∠=︒，下列条件中不能解直角三角形的是（）随堂检测AB CDCBAA ．已知c 和bB ．已知a 和A ∠C ．已知A ∠和B ∠D ．已知a 和b【答案】C【解析】两角只能确定三角形的形状，不能确定三角形的大小．【习题2】等腰三角形底边长为10厘米，周长为36厘米，则底角的余弦等于（）A ．513B ．1213C ．1013D ．512【答案】A【解析】等腰△ABC 中，AB AC =，10BC =，△ABC 的周长为36，求cos B ． ∵AB AC =，10BC =，△ABC 的周长为36， ∴13AB AC ==．过A 作AD BC ⊥，则5BD =，在Rt ABD △中，5cos 12BE B AB ==．【总结】本题主要考查等腰三角形的性质和锐角三角比的意义．【习题3】如图，在ABC ∆中，高CH 是边AB 的一半，且=75B ∠︒，求A ∠的度数（tan 75︒）．【答案】30°．【解析】在Rt BCH △中，tan 2CHB HB== 设HB x =，则(2CH x =+．∵高CH 是边AB 的一半，∴(4AB x =+．∴((43AH AB HB x x x =-=+-=+，在Rt ACH △中，2tan x CH A HA ===30A ∠=︒．【总结】本题主要考查特殊角的锐角三角比的值．【习题4】等腰三角形ABC 的周长为4+AB = AC ，30B ∠=︒，求三角形的三边长．【答案】2AB AC ==，BC =【解析】过点A 作AD BC ⊥，交BC 边于点D ．设AD x =，则2AB x =，BD =．步同级年九14 / 20ABCD FG∵等腰三角形ABC 的周长为423+ ∴2223423x x x ++=+，解得：1x =．∴2AB AC ==，23BC =【总结】本题主要考查等腰三角形的性质和特殊角的锐角三角比的值．【习题5】如图，90C ∠=︒，30A ∠=︒，AC = 6，点G 是的重心，GF // BC ，求GF的长． 233【解析】在Rt ABC △中， ∵30A ∠=︒， ∴3tan CB A AC ==∵AC = 6，∴33CB =∵点G 是的重心，GF // BC ， ∴13GF DG BC DB ==，∴12333GF BC = 【总结】本题一方面考查了重心定理，一方面考查了特殊角的锐角三角比的值．【习题6】如图，在ABC ∆中，6AB =45B ∠=︒，60C ∠=︒，求AC 、BC 的长．【答案】2，13【解析】解：过点A 作AD BC ⊥，交BC 边于点D ．在Rt ABD △中，sin ADB AB =26=，∴3AD =， ∴3BD AD == 在Rt ACD △中，sin AD C AC =33=2AC =．∴()2222231CD AC AD =-=-， ∴13BC CD BD =+=A CD EDCBA【总结】本题主要是考查通过做高，将特殊角放到直角三角形中，再利用特殊角的锐角三角比进行求值．【习题7】如图，在ABC ∆中，90C ∠=︒，tan A =12，DE 是AB 的垂直平分线， BC = 2，求：（1）sin AED ∠的值；（2）CE 的长．【答案】（1；（2）32．【解析】（1）在Rt ABC ∆中，tan BC A AC =，∴122AC=， ∴4AC =，∴AB =∴sin AC B AB === ∵90A AED ∠+∠=︒，90A B ∠+∠=︒，∴B AED ∠=∠．∴sin sin AED B ∠=（2）∵D 为AB 的中点，∴AD = 在Rt AED ∆中，tan EDA AD=，∴12=∴DE =，∴52AE ==， ∴53422AC AB AE =-=-=．【总结】当两个锐角相等时，它们的锐角三角比的值也相等．【习题8】在ABC ∆中，BC = 15，AB : AC =7 : 8，1cos2C =，求BC 边上的高．【答案】．【解析】过点A 作AD BC ⊥，交BC 边于点D ．设7AB x =，则8AC x =．在Rt ACD △中，cos CD C AC =， ∴128CDx =．∴4CD x =，∴154BD x =-．∵2222AB DB AC DC -=-，∴()()()()2222715484x x x x --=-．解得：13x =，25x =（舍去）．步同级年九16 / 20∴()()228443123AD x x x =-==．【总结】本题通过添高将已知的锐角放入直角三角形中，利用锐角三角比的值求解．【作业1】已知等边三角形一边上的中线长为a ，则此三角形的边长为______．【答案】233a ．【解析】解：△ABC 是等边三角形，AD 是BC 边上的中线，AD =a ，求AB 的长． ∵AB =AC ， ∴AD ⊥BC ，在Rt ABD △中，sin AD B AB =， ∴32aAB=，∴233AB a =．【总结】本题是一道基础题，主要考查60°角的正弦．【作业2】在Rt ABC ∆中，90C ∠=︒，a 、b 、c 分别是A ∠、B ∠、C ∠的对边，解下列直角三角形：（1）23BC =，3sin 2A =；（2）a = 5，53b =；（3）斜边上中线23CD =，AC = 6．【答案】（1）60A ∠=︒，30B ∠=︒，4AB =，2AC =；（2）30A ∠=︒，60B ∠=︒，10AB =；（3）30A ∠=︒，60B ∠=︒，43AB =，23BC =．【解析】解：（1）∵3sin 2A =，∴60A ∠=︒，∴906030B ∠=︒-︒=︒．在Rt ABC △中，cot ACA BC=， ∴3323AC = ． ∴2AC =． ∴24AB AC ==．（2）在Rt ABC △中，53cot 35b A a ===， ∴30A ∠=︒，课后作业∴903060B ∠=︒-︒=︒， ∴210c a ==．（3）∵斜边上中线CD =∴2AB CD ==在Rt ABC △中，cos AC A AB === ∴30A ∠=︒．∴903060B ∠=︒-︒=︒，12BC AB == 【总结】本题主要考查特殊角的锐角三角比的值以及运用．【作业3】在ABC ∆中，AB = AC ，BC 边上的高为8，三角形的周长为32，则sin C的值是______．【答案】45．【解析】过A 作AD ⊥BC ，则AD =8． ∵AB = AC ，三角形的周长为32， ∴232AB BC +=．∵AB = AC ，AD ⊥BC ， ∴2BC BD =，∴16AB BD +=，∴16DB BA =-．∵在Rt ABD △中，222AB AD DB =+， ∴()222816AB AB =+-． ∴10AB =，6BD =． ∴在Rt ABD △中，84sin 105AD B AB ===，∴4sin sin 5C B ==．【总结】本题比较基础，解题时注意运用等腰三角形的性质．【作业4】在ABC ∆中，=30A ∠︒，60C B ∠-∠=︒，若BC = a ，求AB 的长．．【解析】过点C 作CD ⊥AB ． ∵180A B C ∠+∠+∠=︒，=30A ∠︒，∴150B C ∠+∠=︒， ∵60C B ∠-∠=︒， ∴105C ∠=︒，45B ∠=︒．在Rt CBD △中，sin CD B CB =CD a =，∴CD =，∴BD CD ==．在Rt CAD △中，tan CD A AD =，2AD=，∴AD =，∴AB AD BD =+．【总结】当已知的特殊角不在直角三角形中时，要构造包含该特殊角的直角三角形．步同级年九18 / 20【作业5】已知在梯形ABCD 中，AD // BC ，AB = 15，CD = 13，AD = 8，B ∠是锐角，4sin 5B =，求BC 的长．【答案】12或22．【解析】过点A 、点D 分别作AE ⊥BC ，DF ⊥BC ，垂足分别为E 、F ．在Rt ABE △中，sin AEB AB=， ∴4515AE =，∴12AE =， ∴222215129BE AB AE =-=-． ∵四边形ADFE 是矩形，∴12DF AE ==．∴在Rt DCF △中，222213125CF CD DF -=-，∴117512BC BF CF =-=-=或217522BC BF CF =+=+=．【总结】本题有两种情况，要注意分类讨论．【作业6】已知在ABC ∆中，AB =23，AC = 2，BC 3BC 的长．【答案】4或2．【解析】解：如图，过A 作AD ⊥BC ，则3AD 在Rt ABD △中， ()()22222333BD AB AD =--=，在Rt ACD △中，()2222231CD AC AD =-=-，∴1312BC BD CD =-=-=或314BC BD CD =+=+=．【总结】当已知三角形两条边的长和第三边的高时，通常都有两种情况，锐角三角形和钝角三角形．【作业7】如图，在ABC ∆中，AD ⊥BC ，垂足为D ，AD = DC = 4，tan B =43．求：（1）ABC ∆的面积；（2）sin BAC ∠的值．【答案】(1)14；（27210【解析】解：（1）在Rt ABD △中，tan ADB DB=，∴443BD=，∴3BD =， ∴11741422ABC S BC AD =⋅⋅=⨯⨯=△．（2）过点C 作CE ⊥AB ，垂足为点E ．在Rt ABD △中，2222435AB AD BD =++． ∵12ABC AB CE S ⋅⋅=△， ∴15142CE ⨯⨯=， ∴285CE =．在Rt ACD △中， 22224442AC AD CD =+=+=在Rt AEC △中， 2875sin 21042EC BAC AC ∠==．【总结】本题主要考查锐角三角比的意义．【作业8】如图，在四边形ABCD 中，135ABC ∠=︒，120BCD ∠=︒，6AB =53BC =，CD = 6，求AD ．【答案】219【解析】解：过点A 作AH ∥BC 交CD 于H ，过点B 、C 分别作BE ⊥AH ，CF ⊥AH ，垂足分别为点E 、F ，过点A 作AG ⊥DC ，交DC 延长线交于点G ． ∵135ABC ∠=︒，120BCD ∠=︒，AH ∥BC ， ∴45BAE ∠=︒，60CHF ∠=︒．在Rt ABE △中，2sin 2BE BAE AB ∠==，又6AB = ∴3BE =，∴3AE BE =．∵四边形BEFC 为矩形， ∴3CF BE ==．在Rt CFH △中，tan 3CHF ∠，∴1FH =，∴22CH FH ==， ∴35316AH AE EF FH =++==，在Rt AGH △中，3sin AG AHG AH ∠=∴33AG =132GH AH ==．∴321CG GH CH =-=-=，∴7DG CG CD =+=．在Rt AGD △中，AD =．【总结】本题的综合性比较强，做题时注意辅助线的添加，依据还是构造包含特殊角的直角三角形．。

沪科版九年级数学中考复习探究说理专题(含答案)

沪科版九年级数学中考复习探究说理专题（含答案）一、选择题1. (·呼和浩特)函数y ＝x 2＋1|x|的大致图象是( )ABCD2. (·兰州)如图①，在矩形ABCD 中，动点E 从点A 出发，沿AB →BC 方向运动，当点E 到达点C 时停止运动，过点E 作FE ⊥AE ，交CD 于点F ，设点E 的运动路程为x ，FC ＝y ，图②表示的是y 与x 的函数关系的大致图象，当点E 在BC 上运动时，FC 的最大长度是25，则矩形ABCD 的面积是( )A. 235B. 5C. 6D. 254第2题第3题3. (·达州)函数y ＝⎩⎨⎧－12x（x>0），3x（x<0）的图象如图所示，P 是y 轴负半轴上一动点，过点P 作y 轴的垂线交图象于A ，B 两点，连接OA ，OB.下列结论：① 若点M 1(x 1，y 1)，M 2(x 2，y 2)在图象上，且x 1<x 2<0，则y 1<y 2；② 当点P 的坐标为(0，－3)时，△AOB 是等腰三角形；③ 无论点P 在什么位置，始终有S △AOB ＝7.5，AP ＝4BP ；④ 当点P 移动到使∠AOB ＝90°的位置时，点A 的坐标为(26，－6)．其中正确的个数为( )A. 1B. 2C. 3D. 44. (·贵港)如图，在正方形ABCD 中，O 是对角线AC 与BD 的交点，M 是BC 边上的动点(点M 不与点B ，C 重合)，CN ⊥DM ，CN 与AB 交于点N ，连接OM ，ON ，MN.下列五个结论：① △CNB ≌△DMC ；② △CON ≌△DOM ；③ △OMN ∽△OAD ；④ AN 2＋CM 2＝MN 2；⑤ 若AB ＝2，则S △OMN 的最小值是12.其中正确的个数是( )第4题A. 2B. 3C. 4D. 5 二、填空题5. (·扬州)若关于x 的方程－2x ＋m 2 017－x ＋4 020＝0存在整数解，则正整数m 的所有可能取值的和为________．6. (·连云港)如图，等边三角形OAB 与反比例函数 y ＝kx(k>0，x>0)的图象交于A ，B 两点，将△OAB 沿直线OB 翻折，得到△OCB ，点A 的对应点为C ，线段CB 交x 轴于点D ，则BD DC 的值为________．(可直接使用 sin 15°＝6－24)第6题第7题7. (·桂林)如图，在矩形ABCD 中，对角线AC ，BD 交于点O ，过点A 作EA ⊥CA 交DB 的延长线于点E.若AB ＝3，BC ＝4，则AOAE的值为________．8. (·绵阳)将形状、大小完全相同的两个等腰三角形按如图所示方式放置，点D 在AB 边上，△DEF 绕点D 旋转，腰DF 和底边DE 分别交△CAB 的两腰CA ，CB 于M ，N 两点．若CA ＝5，AB ＝6，AD ∶AB ＝1∶3，则MD ＋12MA ·DN的最小值为________．第8题三、解答题9. (·南通)某学习小组在研究函数y ＝16x 3－2x 的图象与性质时，已列表、描点并画出了图象的一部分.(1) 请补全函数图象；(2) 方程16x 3－2x ＝－2实数根的个数为________；(3) 观察图象，写出该函数的两条性质．第9题10. (·烟台)【操作发现】(1) 如图①，△ABC 为等边三角形，先将三角尺中的60°角与∠ACB 重合，再将三角尺绕点C 按顺时针方向旋转(旋转角大于0°且小于30°)．旋转后三角尺的一直角边与AB 交于点D.在三角尺斜边上取一点F ，使CF ＝CD ，线段AB 上取点E ，使∠DCE ＝30°，连接AF ，EF.① 求∠EAF 的度数．② DE 与EF 相等吗？请说明理由．【类比探究】(2) 如图②，△ABC 为等腰直角三角形，∠ACB ＝90°，先将三角尺的90°角与∠ACB 重合，再将三角尺绕点C 按顺时针方向旋转(旋转角大于0°且小于45°)．旋转后三角尺的一直角边与AB 交于点D.在三角尺另一直角边上取一点F ，使CF ＝CD ，线段AB 上取点E ，使∠DCE ＝45°，连接AF ，EF.求：① ∠EAF 的度数；② 线段AE, ED ，DB 之间的数量关系．第10题11. (·成都)问题背景：如图①，在等腰三角形ABC中，AB ＝AC ，∠BAC ＝120°，作AD ⊥BC 于点D ，则D 为BC 的中点，∠BAD ＝12∠BAC ＝60°，于是BC AB ＝2BDAB＝ 3.迁移应用：如图②，△ABC 和△ADE 都是等腰三角形，∠BAC ＝∠DAE ＝120°，D ，E ，C 三点在同一条直线上，连接BD.① 求证：△ADB ≌△AEC ；② 请直接写出线段AD ，BD ，CD 之间的等量关系式．拓展延伸：如图③，在菱形ABCD 中，∠ABC ＝120°，在∠ABC 内作射线BM ，作点C 关于BM 的对称点E ，连接AE 并延长交BM 于点F ，连接CE ，CF.① 求证：△CEF 是等边三角形； ② 若AE ＝5，CE ＝2，求BF 的长．第11题12. (·无锡)如图，在矩形ABCD中，AB＝4，AD＝m，动点P从点D出发，在边DA上以每秒1个单位长度的速度向点A运动，连接CP，作点D关于直线PC的对称点E，设点P的运动时间为t秒．(1) 若m＝6，求当P，E，B三点在同一直线上时对应的t的值．(2) 已知m满足如下条件：在动点P从点D到点A的整个运动过程中，有且只有一个时刻t，使点E到直线BC的距离等于3，求m的取值范围．第12题13.(·盐城)如图，在平面直角坐标系中，直线y＝12x ＋2与x轴交于点A，与y轴交于点C，抛物线y＝－12x2＋bx＋c经过A，C两点，与x轴的另一交点为B.(1) 求抛物线的函数解析式．(2) D为直线AC上方抛物线上一动点．①连接BC，CD，设直线BD交线段AC于点E，△CDE 的面积为S1，△BCE的面积为S2，求S1S2的最大值．②过点D作DF⊥AC，垂足为F，连接CD，是否存在点D，使得△CDF中的某个角恰好等于∠CAB的2倍？若存在，求点D的横坐标；若不存在，请说明理由．第13题答案一、 1. B 2. B 3. C 4. D二、 5. 15 点拨：原方程可化为m 2 017－x ＝2x －4 020，根据二次根式的非负性以及积的符号性质，得⎩⎨⎧2 017－x ≥0，2x －4 020≥0，解得2 010≤x ≤2 017，∴ 整数x 可取 2 010、2 011、2 012、2 013、2 014、2 015、2 016、2 017.将上述x 的值分别代入等式“m 2 017－x ＝2x －4 020”验证，正整数m 只能取3和12，∴ 正整数m 的所有可能取值的和为15. 6.3－12 7.7248. 2 3 三、 9. (1) 略 (2) 3 点拨：在题图的坐标系内，作出直线y ＝－2的图象，由图象知，函数y ＝16x 3－2x 的图象和直线 y ＝－2有三个交点，∴ 方程16x 3－2x ＝－2实数根的个数为3. (3) 答案不唯一，如① 此函数在实数范围内既没有最大值，也没有最小值；② 此函数在x<－2和x>2时，y 随x 的增大而增大；③ 此函数图象过原点；④ 此函数图象关于原点对称10. (1) ① ∵ △ABC 是等边三角形，∴ AC ＝BC ，∠BAC ＝∠B ＝60°.∵ ∠DCF ＝60°，∴ ∠ACF ＝∠BCD.在△ACF 和△BCD 中，⎩⎪⎨⎪⎧AC ＝BC ，∠ACF ＝∠BCD ，CF ＝CD ，∴ △ACF ≌△BCD.∴ ∠CAF ＝∠B ＝60°.∴ ∠EAF ＝∠BAC ＋∠CAF ＝120°② DE ＝EF 理由：∵ ∠DCF ＝60°，∠DCE ＝30°，∴ ∠FCE ＝60°－30°＝30°.∴ ∠DCE ＝∠FCE.在△DCE 和△FCE中，⎩⎪⎨⎪⎧CD ＝CF ，∠DCE ＝∠FCE ，CE ＝CE ，∴ △DCE ≌△FCE.∴ DE ＝EF.(2) ① ∵ △ABC 是等腰直角三角形，∠ACB ＝90°，∴ AC ＝BC ，∠BAC ＝∠B ＝45°.∵ ∠DCF ＝90°，∴ ∠ACF ＝∠BCD.在△ACF 和△BCD中，⎩⎪⎨⎪⎧AC ＝BC ，∠ACF ＝∠BCD ，CF ＝CD ，∴ △ACF ≌△BCD.∴ ∠CAF ＝∠B ＝45°，AF ＝BD.∴ ∠EAF ＝∠BAC ＋∠CAF ＝90° ② AE 2＋DB 2＝DE 2∵ ∠DCF ＝90°，∠DCE ＝45°，∴ ∠FCE ＝90°－45°＝45°.∴ ∠DCE ＝∠FCE.在△DCE 和△FCE中，⎩⎪⎨⎪⎧CD ＝CF ，∠DCE ＝∠FCE ，CE ＝CE ，∴ △DCE ≌△FCE.∴DE ＝EF.∵ 在Rt △AEF 中，AE 2＋AF 2＝EF 2，又∵ AF ＝DB ，EF ＝DE ，∴ AE 2＋DB 2＝DE 211. 迁移应用：① ∵ ∠BAC ＝∠DAE ＝120°，∴ ∠DAB ＝∠EAC.在△DAB 和△EAC 中，⎩⎪⎨⎪⎧DA ＝EA ，∠DAB ＝∠EAC ，AB ＝AC ， ∴ △DAB≌△EAC ② CD ＝3AD ＋BD 点拨：如图①，过点A 作AH ⊥CD 于点H.∵ ∠DAE ＝120°，且△DAE 为等腰三角形，∴ ∠ADE ＝12(180°－∠DAE)＝30°.∵ △DAB ≌△EAC ，∴ BD＝CE.在Rt △ADH 中，DH ＝AD ·cos 30°＝32AD.∵ AD ＝AE ，AH ⊥DE ，∴ DH ＝HE.∴ CD ＝DE ＋EC ＝2DH ＋BD ＝3AD ＋BD. 拓展延伸：① 如图②，连接BE ，过点B 作BG ⊥AE 于点G.∵ E 是点C 关于BM 的对称点，∴ BM 垂直平分CE.∴ FE ＝FC ，BE ＝BC.∴ △CEF 和△BEC 都是等腰三角形．∵ 四边形ABCD 是菱形，∴ AB ＝BC.∴ AB ＝BE.又∵ BG ⊥AE ，∴ ∠ABG ＝∠EBG.同理，∠EBF ＝∠CBF.∴ ∠GBF ＝∠EBG ＋∠EBF ＝12∠ABC ＝60°.∴ ∠GFB ＝30°.∴ ∠EFC ＝60°.又∵ FE ＝FC ，∴ △CEF 是等边三角形 ② ∵ AB ＝EB ，BG ⊥AE ，AE ＝5，∴ GE ＝GA ＝52.∵ CE ＝2，△CEF 是等边三角形，∴EF ＝2.∴ GF ＝GE ＋EF ＝92.在Rt △GBF 中，∵ ∠GFB ＝30°，∴ GF ＝3BG.∴ BF ＝2BG ＝2×GF3＝2×923＝3 3 第11题12. (1) 当B ，E ，P 三点共线时，如图①.∵ 点D ，E 关于CP 对称，四边形ABCD 是矩形，AB ＝4，∴ CD ＝CE ＝4，PD ＝PE ，∠PEC ＝∠PDC ＝90°.∵ 点P 的运动速度是1个单位长度/秒，运动时间是t 秒，∴ DP ＝PE ＝t.∵ B ，E ，P 三点共线，∠PEC ＝90°，∴ ∠BEC ＝90°.∴ 在Rt △BEC 中，BE ＝BC 2－CE 2＝62－42＝2 5.∴ BP ＝25＋t.在Rt △BAP 中，AB ＝4，BP ＝25＋t ，AP ＝6－t ，由勾股定理，得(25＋t)2＝42＋(6－t)2，解得t ＝6－2 5 (2) ① 当点E 在BC 上方时，如图②.过点E 作EF ⊥CD 于点F ，则CF ＝3.∵ CE ＝4，CF ＝3，EF ⊥CD ，∴ EF ＝CE 2－CF 2＝7.延长FC 到点G ，使得CG ＝CE ，连接EG ，则△EFG 是直角三角形．∵ CE ＝CG ＝4，∴ ∠EGC ＝∠CEG.∵ ∠ECF 是△ECG的外角，∴ ∠ECF ＝2∠EGC.∵ D ，E 关于CP 对称，∴ ∠DCP ＝∠ECP.∴ ∠DCP ＝∠EGC.∵ EF ＝7，FG ＝3＋4＝7，∴ tan ∠EGC ＝tan ∠DCP ＝77.∵ CD ＝4，tan ∠DCP ＝77，∴ PD ＝477.当点A 与点P 重合，即AD 的长为477时，点E到BC 的距离等于3，∴ m 的最小值是477.② 当点E 在BC 下方时，如图③.过点E 作EG ⊥DC 交DC 的延长线于点G ，连接EC.∵ 点D ，E 关于CP 对称，CD ＝4，E 到BC 的距离等于3，∴ CE ＝4，CG ＝3，DG ＝7，∴ EG ＝CE 2－CG 2＝7.在△DEG 中，EG ＝7，DG ＝7，∴ tan ∠EDG ＝77.∵ ∠ADC ＝90°，∴ ∠CPD ＝∠EDG.∴ tan ∠CPD ＝77.∵ CD ＝4，∴ PD ＝47.当点A 与点P 重合，即AD 的长为47时，点E 到BC 的距离等于3，∴ m 的最大值是47.∵ 由于动点P 从点D 开始运动，到A 点的整个过程中，有且只有一个时刻t ，使点E 到直线BC 的距离等于3，∴ m 的取值范围是477≤m<47第12题13. (1) ∵ 直线y ＝12x ＋2与x 轴交于点A ，与y 轴交于点C ，∴ A(－4，0)，C(0，2)．∵ 抛物线y ＝－12x 2＋bx＋c 经过A ，C两点，∴ ⎩⎪⎨⎪⎧0＝－12×16－4b ＋c ，2＝c ，解得⎩⎪⎨⎪⎧b ＝－32，c ＝2.∴ 抛物线的函数解析式为y ＝－12x 2－32x ＋2(2) ① 如图①，在y ＝－12x 2－32x ＋2中，令y ＝0，则－12x2－32x ＋2＝0，解得x 1＝－4，x 2＝1.∴ B(1，0)．过点D 作DM ⊥x 轴交AC 于点M ，过点B 作BN ⊥x 轴交于AC 于点N.∴ DM ∥BN.∴ △DME ∽△BNE.∴S 1S 2＝DE BE ＝DM BN.设D ⎝⎛⎭⎫a ，－12a 2－32a ＋2，∴ M ⎝⎛⎭⎫a ，12a ＋2.∵ B(1，0)，∴N ⎝⎛⎭⎫1，52.∴ S 1S 2＝DM BN＝－12a 2－2a 52＝－15(a ＋2)2＋45.∴ 当a ＝－2时，S 1S 2的最大值是45 ② ∵ A(－4，0)，B(1，0)，C(0，2)，∴ OA ＝4，OB ＝1，OC ＝2,OC OA ＝24＝12，OB OC ＝12.又∵ ∠AOC ＝∠COB ＝90°，∴ △AOC ∽△COB.∴ ∠ACO ＝∠ABC.情况1：∵ tan ∠BAC ＝OC OA ＝12≠1，∴ ∠BAC ≠45°.∴ ∠DFC ≠2∠CAB ；情况2：当∠DCF ＝2∠CAB 时，如图②，作点C 关于x 轴的对称点G ，连接AG ，则∠CAB ＝∠GAB ，G(0，－2)，∴ ∠CAG ＝2∠CAB.设直线AG 的函数解析式为y ＝kx ＋d(k ≠0)，把A(－4，0)，G(0，－2)代入，得⎩⎨⎧0＝－4k ＋b ，－2＝b ，解得⎩⎪⎨⎪⎧k ＝－12，b ＝－2.∴ 直线AG 的函数解析式为y ＝－12x －2.过点C 作CD ∥AG 交第二象限内的抛物线于点D ，则∠DCF ＝∠CAG ＝2∠CAB ，且直线CD 的函数解析式为y ＝－12x ＋2.解方程－12x ＋2＝－12x 2－32x ＋2，得x 1＝0(不合题意，舍去)，x 2＝－2，∴ 点D 的横坐标为－2；情况3：当∠CDF ＝2∠CAB 时，如图③，在x 轴上取一点P ，使PA ＝PC.∴ ∠CAB ＝∠ACP.∴ ∠CPO ＝∠CAB ＋∠ACP ＝2∠CAB.设OP ＝m ，则CP ＝AP ＝4－m.在Rt △OCP 中，由勾股定理，得OP 2＋OC 2＝CP 2，∴ m 2＋22＝(4－m)2，解得m ＝32，即OP ＝32.∴ tan ∠CDF ＝tan ∠CPO ＝CO OP ＝232＝43.∴ CF DF ＝43.过点F 作QK ∥x 轴交y 轴于点K ，过点D 作DQ ∥y 轴交QK 于点Q ，则∠Q ＝∠FKC ＝90°，∠CFK ＋∠FCK ＝90°，KC OC ＝KF OA ，∴ KC 2＝FK4，即FK ＝2KC.∵DF ⊥AC ，∴ ∠CFK ＋∠DFQ ＝90°.∴ ∠FCK ＝∠DFQ.又∵ ∠Q ＝∠FKC ，∴ △FKC ∽△DQF.∴ KC QF ＝FK DQ ＝FC DF ＝43.设QF ＝3n ，则KC ＝4n ，FK ＝8n ，DQ ＝6n ，OK ＝2－4n.∴ D(－11n ，2＋2n)．代入y ＝－12x 2－32x ＋2，得2＋2n ＝－12×(－11n)2－32×(－11n)＋2，解得n 1＝0(不合题意，舍去)，n 2＝29121.∴ －11n ＝29121，解得n ＝－2911，即点D 的横坐标为－2911.综上所述，点D 的横坐标为－2或－2911第13题。

沪教版九年级数学上册同步精品讲义

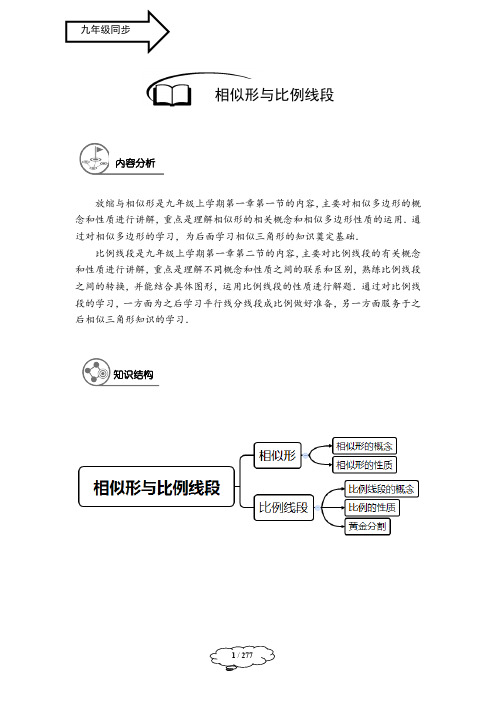
例题解析
【例 1】相似的图形，它们的形状
相同，它们的大小
（选填“一定”或“不一定”或“一定不”）
【难度】★
【答案】一定，不一定．
【解析】相似图形是形状相同的两个图形，由其定义可得出结论．
【总结】考查相似图形的概念，注意全等图形是特殊的相似图形．
相同．
【例 2】在下边的方格图中，分别画出 ABC 和四边形 ABCD 的一个相似图形．
x
y
y
2
3
3
1 3
；
（2）由
a 4
b 5
，可得
a
4 5
b
，原式=
2
4
4 5 b
b b
b
13 ；
5
（3）由
2x
5y
0
，可得
x
5 2
y
，原式=
3
5 2
y
y
:
4
5 2
y
3y
17
:14
．
【总结】考查比例性质运用中的基本计算，确定单位“1”再准确计算．
【例 15】（1）已知： a b 2 ，求 2a 4b 的值；
4
6cm ．
【解析】（1）由题意可知 ab 62 ，由此 ab 6 ， ab 1 6 1 35 ；
ab
66
（2）由题意可知 b2 9 4 36 ，可解得 b 6 ；
（3） a 、 b 都为线段，因此其比例中项只能是线段，取正值，即为 6 16 4 6cm
【总结】考查比例中项的定义，注意线段比例中项和数字比例中项的区别．
矩形 EMNH 的面积 S 与 x 的函数关系式．
【难度】★★★
【答案】 S 2x2 10x 0 x 5 ．

沪科版数学九年级上册综合训练50题含答案

沪科版数学九年级上册综合训练50题含答案（填空、解答题）一、填空题1．如图，小明抛投一个沙包，沙包被抛出后距离地面的高度h （米）和飞行时间t （秒）近似满足函数关系式()216510h t =--+，则沙包在飞行过程中距离地面的最大高度是________米．2．如图，在△ABC 中，点D ，E 分别在AB ，AC 上，DE ∥BC ，若AD =1，AB =4，则DEBC=_____．14DE AD AB，3．点B 是线段AC 的黄金分割点，且AB BC <．若4AC =，则BC 的长为______．4．如图，抛物线2y ax bx c =++与x 轴相交于A ，B ()10t +，两点，与y 轴相交于点C ，点D 在该抛物线上，且坐标为()t c ，，则点A 的横坐标是_______．【答案】1-【分析】先求出点C 的坐标为()0c ，，进而得到点C 与点D 关于抛物线对称轴对称，据此求出抛物线对称轴即可求出点A 的坐标．【详解】解：∥抛物线2y ax bx c =++与y 轴相交于点C ， ∥点C 的坐标为()0c ，，5．如图，点P 在反比例函数ky x=的图象上，P A ∥x 轴于点A ，PB ∥y 轴于点B ，且△APB 的面积为2，则k 等于______．6．若抛物线2(2)2y x m x m =---的顶点在y 轴上，则m =_______．【答案】2【分析】根据题意可知抛物线对称轴为0x =，然后可求得m 的值．【详解】解：∥抛物线2(2)2y x m x m =---的顶点在y 轴上，7．如图，无人机与亮亮的水平距离是15米，当他抬头仰视无人机时，仰角恰好为30°，若亮亮身高1.70米，则无人机距离地面的高度为____米．（结果带根号即可）【答案】()1.7##(1.7+【分析】根据特殊角三角函数值求出AB的长，再由矩形的判定和性质，得出BE的【点睛】本题考查了矩形的判定和性质以及利用特殊三角函数值求边长，理解题意，作出相应辅助线，利用三角函数求解是解题关键.8．抛物线y ＝a(x －h)2＋k 经过(－1，0)，(5，0)两点，则关于x 的一元二次方程－a(x+h －2)2－k ＝0的解是__________．【答案】x 1=3，x 2=－3【分析】将(－1，0)，(5，0)代入到二次函数解析式中，即可得出两个等式，然后对照一元二次方程与两个等式的关系即可得出结论．【详解】解：将(－1，0)，(5，0)代入到解析式中，得 0＝a(-1－h)2＋k∥ 0= a(5－h)2＋k∥将∥变形，得-a(1＋h)2-k=0∥ 将∥变形，得-a(-5＋h)2-k=0∥∥关于x 的一元二次方程－a(x+h －2)2－k ＝0的解应满足x+h －2=1＋h 或x+h －2=-5＋h解得：x 1=3，x 2=－3 故答案为x 1=3，x 2=－3．【点睛】此题考查的是根据二次函数与x 轴的交点坐标，求一元二次方程的解，掌握二次函数与x 轴的交点坐标与一元二次方程的解的关系是解决此题的关键．9．关于x 的函数()()2211y a x a =+-+（a 为实数）的函数上两点()12,A y 、2(3,)B y -，则1y ________2y （填>、＜、＝号）【答案】<【分析】根据二次函数的对称性，可利用对称性，找出点A 的对称点'A ，再利用二次函数的增减性可判断y 值的大小．【详解】解：∵该函数的解析式为：()()2211y a x a =+-+∴对称轴为：1x =∴点()12,A y 关于对称轴的对称点坐标()1'0A y ， ∵210a +>∴该二次函数开口向上，在对称轴左边y 随x 的增大而减小 ∥0＞-3 ∴12y y < 故答案为：12y y <【点睛】本题考查了二次函数图象上点的坐标特征和二次函数的性质，掌握二次函数图象的增减性是解题的关键． 10．如果反比例函数my x=过A(2，-3)，则m=_______．11．某校有航模组设计制作的火箭，它的升空高度()h m 与飞行时间()t s 满足函数关系式2261h t t =-++，则该火箭升高的最大高度是________m ．【答案】170【分析】直接利用配方法将二次函数写成顶点式，进而求出即可．【详解】由题意可得： h =-t 2+26t +1 =-（t 2-26t ）+1 =-（t -13）2+170，故火箭点火后13秒降落伞将打开，这时火箭的最大高度是170米，故答案为170．【点睛】此题主要考查了二次函数的应用，正确配方求出是解题关键，难度不大． 12．若反比例函数ky x=的图象经过点(3，2)，则此函数在每一个象限内随的增大而_______．【答案】减小．【详解】试题分析：图象经过点（3，2），先求出k 值，再根据反比例函数的性质解答．试题解析：∥图象经过点（3，2），13．如图，DE 与ABC 的边AB ，AC 分别相交于D ，E 两点，且DE BC ∥．若2,3DE cm BC cm ==，23AE cm =，则AC ＝________cm ．14．如图，正比例函数2y x =-与反比例函数()80y x x=-<的图象有一个交点A ，直线BC OA ∥，交反比例函数的图象于点B ，交y 轴于点C ，若2BC OA =，则直线BC 的解析式为______．【答案】26y x =--##62y x =--的横坐标，根据定义求得点B 的横坐标，然后求得点B 的坐标，将点B 的坐标代入15．如图是二次函数2y ax bx c =++的图象的一部分，图象过点()3,0A -，对称轴是直线1x =-，给出五个结论：①24b ac >；②20a b -=；③0c <；④0a b c ++=；⑤0a b c -+<．其中正确的是________（把你认为正确的序号都填上，答案格式如：“1234”）．16．已知线段AB=2cm，点C是线段AB的黄金分割点，则线段AC等于__________cm【点睛】本题考查的是黄金分割，掌握黄金比值是解题的关键． 17．如图，AB ，CD 都与x 轴垂直，垂足分别为B ，D ，点C 在双曲线ky x=上．若∥AOC =90°，8AOB S =△，:2:1OA OC =，则k 的值是____．CODS =CODS =122k =4k =，18．函数22y x x =-()03x ≤≤有最大值，也有最小值，则最小值是___________．【答案】1-【分析】把函数22y x x =-变成顶点式，()211y x =--，结合x 的范围，即可求得．【详解】把函数22y x x =-变成顶点式， ()211y x =--，对称轴为1x =，开口向上，在03x ≤≤，对称轴1x =取最小值，最小值：1y =-，故答案为：1-．【点睛】本题考查了二次函数得图像和性质，解决本题的关键是把二次函数化为顶点式．19．如图，两根竖直的电线杆AB 长为12，CD 长为4，AD 交BC 于点E ，则点E 到地面的距离EF 的长是__________．故答案为3．【点睛】此题主要考查了相似三角形的判定与性质，正确找出相似比是解题的关键．20．在ABC中，D为AB边上一点，E为AC边上一点，ADE与ABC相似，已知3AB=，1AD=，AC=AE=__________．时，ADE ABC，∥AB AC3223时，AED ABC，∥AE AD1AE21．如图，在平面直角坐标系中，O为坐标原点，正方形OABC的顶点A在y轴的负半轴上，点C在x轴的正半轴上，经过点A、B的抛物线y＝a（x﹣2）2+c（a＞0）的顶点为E．若∥ABE为等腰直角三角形，则a的值为__．22．如图，一次函数的图象y x b=-+与反比例函数的图象ayx=交于A(2,﹣4)，B(m, 2)两点.当x满足条件______________时，一次函数的值大于反比例函数值.23．已知函数y=x 2﹣4x+3，则函数值y 随x 的增大而减小的x 的取值范围是______．24．已知点P 是线段AB 的黄金分割点，且AP PB >，若1AB =．则AP =_____．解：点25．已知二次函数y ＝2x 2－6x ＋1，当0≤x ≤5时，y 的取值范围是______________．26．如图，有一斜坡OA ，已知斜坡上一点A 的坐标为()2A ，过点A 作AB x⊥轴，垂足为点B ，将∥AOB 以坐标原点0为位似中心缩小为原图形的12，得到∥COD ，则OC 的长度是______________，此时斜坡OA 的坡度为________________．轴，将AOB 以坐标原点()227．已知1(1,)A y -、2(0,)B y 、3(3,)C y 是二次函数2(2)1y a x =-+（0a ＞）图像上的三点，则1y ，2y ，3y 之间的大小关系为 _____（用“＞”连接）．【答案】123y y y ＞＞【分析】由二次函数2(2)1y a x =-+（0a ＞），得到对称轴为直线2x =，根据2(1)2032----＞＞，从而判定123y y y ＞＞．【详解】∥二次函数2(2)1y a x =-+（0a ＞）， ∥对称轴为直线2x =，∥2(1)2032----＞＞， ∥123y y y ＞＞．故答案为：123y y y ＞＞．【点睛】本题考查了抛物线的对称性和增减性，函数值的大小比较，熟练掌握抛物线的性质，特别是增减性是解题的关键．28．已知Rt∥ABC 中，AC =3，BC = 4，过直角顶点C 作CA 1∥AB ，垂足为A 1，再过A 1作A 1C 1∥BC ，垂足为C 1，过C 1作C 1A 2∥AB ，垂足为A 2，再过A 2作A 2C 2∥BC ，垂足为C 2，…，这样一直做下去，得到了一组线段CA 1，A 1C 1，C 1A 2，…，则CA 1=______，8999C A A C =_______【答案】29．在平面直角坐标系中两点P （x ，y ），Q （x ，y ′），其中y ′＝00yx y x >⎧⎨-≤⎩（）（），则称Q 点是P 点的可控点．若P （x ，y ）满足y ＝－x 2＋16，其中（－5≤x ≤a ）时，可控点Q（x，y′）满足－16≤y′≤16，则a的取值范围为____．【点睛】本题考查了二次函数图象应用问题，解决此类问题：首先根据题意，大致画出函数图象，依据图象确定数值的取值范围．二、解答题30．已知反比例函数y ＝2kx-的图象经过点A （3，﹣2）．（1）求k 的值．（2）点C （x 1，y 1），B （x 2，y 2）均在反比例函数y ＝2kx-的图象上，若0＜x 1＜x 2，直接写出y 1，y 2的大小关系． 8k ；（2））将点A 的坐标代入反比例函数的解析式即可得；）根据反比例函数的增减性即可得．2k y x得：2-8k ；）由（1）得：反比例函数的解析式为6x ，在每一象限内，11,),(C x y 12y y ∴<．【点睛】本题考查了反比例函数的图象与性质，熟练掌握待定系数法是解题关键．31．（1）已知一次函数的图象经过点（0，1）和（1，3），求这个函数的表达式．（2）已知y 是x 的反比例函数，且当=2x 时，=3y ，求当x ＝﹣3时y 的值．【答案】（1）21y x =+；（2）=2y -.【分析】（1）根据待定系数法将（0，1）和（1，3）代入所设的一次函数解析式中，即可求得函数的表达式；（2）由待定系数法，先求出反比例函数的解析式，再将x ＝﹣3代入解析式，可求出y 的值.【详解】解：（1）设这个函数的表达式是y kx b =+ ∥因为函数的图象经过点（0，1）和（1，3）∥13b k b =⎧⎨+=⎩，解得：21k b =⎧⎨=⎩32．如图：已知∥ABC 为等腰直角三角形，∥ACB =90°，延长BA 至E ，延长AB 至F ，∥ECF =135° 求证：∥EAC ∥∥CBF【答案】见解析【分析】利用有两组角对应相等的两个三角形相似来证明∥EAC ∥∥CBF ．【详解】解：∥∥ABC 为等腰直角三角形，∥ACB =90°， ∥∥CAB =∥CBA =45°，∥∥E +∥ECA =45°（三角形外角定理）．又∥ECF =135°，∥∥ECA +∥BCF =∥ECF -∥ACB =45°， ∥∥E =∥BCF ；同理，∥ECA =∥F ， ∥∥EAC ∥∥CBF ．33．已知关于x 的二次函数()220y ax ax c a =++≠，且3c a =-．(1)若1a =-，求该二次函数的解析式和顶点坐标；(2)在（1）的条件下，求出下表中k 、n 的值，并在以下平面直角坐标系中，用描点法画出该二次函数的图象；根据图象回答：当02x ≤≤时，直接写出y 的最小值． (3)当30x -≤≤时，y 有最小值-4，若将该二次函数的图象向右平移()1m m >个单位长度，平移后得到的图象所对应的函数'y 在30x -≤≤的范围内有最小值-3，求函数y ax m =+的解析式．【答案】(1)223y x x =--+，顶点坐标为()1,4- (2)3k =，0n =，图见解析，最小值为5- (3)2y x =+【分析】（1）利用待定系数法带入=1x -，4y =结合3c a =-即可求得函数解析数，把二次数解析式整理为顶点式即可求得顶点坐标．（2）由（1）函数解析式分别代入当0x =和1x =时即可求得k 、n 的值，根据描点法画函数图象步骤即可．（3）根据题意把函数整理为顶点式，即可知对称轴为直线=1x -，由=1x -在30x -≤≤范围内，即最值为顶点坐标的纵坐标，即可求出平移前的函数解析式，根据平移的性质即可求得答案．【详解】（1）解：3c a =-，22223y ax ax c ax ax a =++=+-，把=1x -，4y =代入上述函数得，423a a a =--，解得1a =-，3c ∴=，∴二次函数的解析式为223y x x =--+，()222232131(1)4y x x x x x =--+=-++++=-++，所以顶点坐标为()1,4-．（2）（2）由（1）得223y x x =--+，当0x =时3k =，当1x =时，1230n =--+=，图象如图所示，由图，02x ≤≤时，y 随x 的增大而减小，∴当2x =时，y 最小，最小值为222235y =--⨯+=-．（3）∥3c a =-则2223(1)4y ax ax a a x a =-+=+-， ∥抛物线对称轴为直线=1x -，顶点坐标为()1,4a --，由题意可得当30x -≤≤时，函数最小值为44a -=-， ∥1a =，()214y x =+-，二次函数的图象向右平移()1m m >个单位长度后得()2'14y x m =+--，抛物线对称轴为直线1x m =-， ∥1m >，10m ->， ∥对称轴在y 轴右侧，∥当0x =时，22'(1)4(1)4y x m m =+--=--为最小值，()2143m --=-，∥0m =（舍）或2m =， ∴1a =，2m =，∥这个函数表达式：2y x =+．【点睛】本题考查了待定系数法求函数解析式、用描点法画二次函数的图象、二次函数的性质、函数图象的平移，解题的关键在于熟练掌握待定系数法、描点法画函数图象及二次函数的图象及性质和函数图象的平移等知识．34．如图，某研究性学习小组在一次综合实践活动中发现如下问题：在楼底的B 处测得河对岸大厦上悬挂的条幅底端D 的仰角为33︒，在楼顶A 处测得条幅顶端C 的仰角为50︒．若楼AB 高度为21米，条幅CD 长度为43米，请你帮助他们求出大厦的高度CE ．（参考数据：sin330.54︒≈，cos330.84︒≈，tan330.65︒≈，sin500.77︒=，cos500.64︒=，tan50 1.20︒=）【答案】大厦的高度CE 为69m【分析】首先过点A 作AF∥CE 于点F ，易得四边形ABEF 是矩形，然后设BE=xm ，可得在Rt∥BDE 中，DE=0．65x （m ），在Rt∥ACF 中，CF=1．2x （m ），继而可得方程430.65 1.221x x +=+，解此方程即可求得答案．【详解】过点A 作AF CE ⊥，垂足为F ．∥90AFE ∠=︒∥AB BE ⊥，CE BE ⊥， ∥90ABE CEB ∠=∠=︒ ∥四边形ABEF 是矩形35．某种植户计划将一片荒山改良后种植沃柑，经市场调查得知，当种植沃柑的面积x不超过15亩时，每亩可获得利润y=1900元；超过15亩时，每亩获得利润y（元）与种植面积x（亩）之间的函数关系:y=kx+b，并且当x=20时，y=1800；当x=25时，y=1700．（1）请求出y与x的函数关系式，并写出自变量的取值范围；（2）设种植户种植x亩沃柑所获得的总利润为w元，由于受条件限制，种植沃柑面积x不超过50亩，求该种植户种植多少亩获得的总利润最大，并求总利润w（元）的最大值．【答案】（1）y=﹣20x+2200（15＜x≤110）；（2）当种植50亩时获利最大，总利润的最大值为60000元【分析】（1）根据题意设y=kx+b，再运用待定系数法求解可得；（2）根据总利润=每亩利润×亩数，分0＜x≤15和15＜x≤110两种情况分别求解可得．【详解】解：（1）y=kx+b，将x=20、y=1800和x=25、y=1700代入得：201800251700k b k b +=⎧⎨+=⎩解得：202200k b =-⎧⎨=⎩∥y=﹣20x+2200 ∥-20x+2200≥0，解得：x≤110，∥自变量的取值范围是：15＜x≤110；（2）当0＜x≤15时，W=1900x ， ∥当x=15时，W 最大=28500（元）；当15＜x≤110时，W=（﹣20x+2200）x=﹣20x 2+2200x=﹣20（x ﹣55）2+60500 ∥x≤50∥当x=50时，W 最大=60000（元）；所以，当种植50亩时获利最大，总利润的最大值为60000元．【点睛】本题主要考查二次函数的应用，熟练掌握待定系数法和由题意依据相等关系列出函数解析式是解题的关键．36．二次函数2y ax bx c =++（a ，b ，c 为实数，且0a ≠）的图象经过点()1,1--，()3,3．(1)求ca的值； (2)若12a >，点()3,A m -在该二次函数图象上，求证：3m >； (3)设(),0t 是该函数图象与x 轴的一个交点，且满足34t <<，求a 的取值范围．37．如图，直线3y x =-交x 轴于点B ，交y 轴于点A ，抛物线24y ax x c =++经过点A ，B ，点C 为抛物线的顶点．(1)求抛物线的解析式及点C 的坐标；(2)将抛物线24y ax x c =++向下平移m 个单位长度． ∥当03x ≤≤时，用含m 的式子表示y 的取值范围；∥点C 的对应点为C '，连接AC '，BC '，若2ABC S '=△，求m 的值．令0x =，则=3y -，令0y =，则3x =()()0,3,3,0A B ∴-代入24y ax x c =++得09123a cc =++⎧⎨=-⎩ 解得13a c =-⎧⎨=-⎩∴2=+43y x x --()221x =--+点C 为抛物线的顶点 ∥()2,1C （2）解：将抛物线2=+43y x x --向下平移m 个单位长度，则平移后的解析式为243y x x m =-+--()221x m =--+-，顶点坐标为()2,1m -，对称轴为2x =∥当03x ≤≤时，最大值为1y m =-，2032->-，根据离对称轴越远的点，函数值越小，∴最小值为0x =时，3y m =-- 31m y m ∴--≤≤-，∥依题意，C '()2,1m -()()0,3,3,0A B -设直线AB 的解析式为y kx b =+303b k b =-⎧⎨=+⎩解得13k b =⎧⎨=-⎩ ∴直线AB 的解析式为3y x =-ABC S'=ABC S '=△2m ⨯-38．如图1，A 、B 、C 是表示某特产公司三个连锁门市，三个门市之间有AB 、BC 、AC 公路相连，点C 、B 分别位于点A 正东和北偏东60°的方向，六位同学分别利用不同途径获得A 、C 两点的距离如表：他们又调查了各门市该种特产的库存情况，绘制了下列尚不完整的统计图2，3．(1)求表中AC长度的平均数(2)求C处特产的吨数，并补充完整图2，图3．(3)用（1）中AC长度的平均数作为AC的长度，测得点C位于点B的东南方向，因市场原因，需将A、C两门市的库存全部都调往B处，若运送1吨特产1千米需0.5元，1.7 1.4）．求运送特产所需的总费用．BAD ∠=∥2AB x =∥3x x +解得x =20∥AB =40，39．如图，一次函数5y x =-+的图像与反比例函数()0ky k x=≠在第一象限内的图像交于()1,A n 和()4,B m 两点．()1求反比例函数的表达式；()2在第一象限内，当()50k x k x-+<≠的值时，写出自变量x 的取值范围；()3求AOB面积．40．【问题情境】如图1，在等腰直角三角形ABC 中，90ACB ∠=︒，F 是AC 边上一动点（点F 不与点A ，C 重合），以CF 为边在ABC 外作正方形CDEF ，连接AD ，BF ．(1)【探究展示】∥猜想：图1中，线段BF ，AD 的数量关系是__________，位置关系是__________．∥如图2，将图1中的正方形CDEF 绕点C 顺时针旋转α，BF 交AC 于点H ，交AD 于点O ，∥中的结论是否仍然成立？请说明理由．(2)【拓展延伸】如图3，将【问题情境】中的等腰直角三角形ABC 改为直角三角形ABC ，90ACB ∠=︒，正方形CDEF 改为矩形CDEF ，连接BF 并延长，交AC 于点H ，交AD 于点O ，连接BD ，AF ．若4AC =，3BC =，43CD =，1CF =，求22BD AF +的值．解：∥BF =AD ，BF ∥AD ；延长BF 交AD 于点G ，∥等腰直角三角形ABC 中，90ACB ∠=︒， ∥AC =BC ，在正方形CDEF 中，CD =CF ，∥FCD =90°， ∥∥BCF =∥ACD ， ∥∥BCF ∥∥ACD ， ∥BF =AD ，∥CBF =∥CAD ， ∥∥CAD +∥ADC =90°， ∥∥CBF +∥ADC =90°， ∥∥BGD =90°，即BF ∥AD ，故答案为BF =AD ，BF ∥AD ；∥∥中的结论仍然成立，理由如下：等腰直角三角形ABC 中，90ACB ∠=︒， ∥AC =BC ，在正方形CDEF 中，CD =CF ，∥FCD =90°， ∥∥BCF =∥ACD ， ∥∥BCF ∥∥ACD ， ∥BF =AD ，∥CBF =∥CAD ，∥∥CBH +∥CHB =90°，∥CHB =∥AHO ， ∥∥CAD +∥AHO =90°， ∥∥AOH =90°，即BF ∥AD ，故∥中的结论仍然成立； (2)如图，连接DF ，41．在平面直角坐标系xOy中，反比例函数myx=的图象经过点（1，-6）．（1）求m的值；（2）横、纵坐标都是整数的点叫做整点．记直线12y x b=+与反比例函数myx=的图象围成的区域为W（不含边界）．若区域W内恰有1个整点，结合函数图象，直接写出b 的取值范围．92b942b <<-22．42．如图在平面直角坐标系中，∥OAB 的顶点坐标分别是O(0，0)，A(2，4)，B(6，0).(1)以原点O 为位似中心，在点O 的异侧画出∥OAB 的位似图形∥OA 1B 1，使它与∥OAB 的相似比是1：2. (2)写出点A 1、B 1的坐标.(3)若∥OAB关于点O的位似图形∥OA2B2中，点A的对应点A2的坐标为(﹣3，﹣6)，则∥OA2B2与∥OAB的相似比为______.【答案】(1)见解析；(2)A1(﹣1，﹣2)，B1(﹣3，0)；(3)3：2.【分析】(1)由以原点O为位似中心，在点O的异侧画出∥OAB的位似图形∥OA1B1，使它与∥OAB的相似比是1：2，可求得各对应点的坐标，继而画出位似图形；(2)由(1)，可求得点A1、B1的坐标；(3)根据位似图形的性质，即可求得∥OA2B2与∥OAB的相似比.【详解】解：(1)如图：(2)A1(﹣1，﹣2)，B1(﹣3，0)；(3)∥A(2，4)，点A的对应点A2的坐标为(﹣3，﹣6)，∥∥OA2B2与∥OAB的相似比为：3：2.故答案为：3：2.【点睛】此题主要考查位似，解题的关键是熟知位似得性质及作图方法.43．如图1，正比例函数y＝kx的图象与反比例函数y＝mx（x＞0）的图象都经过点A（2，2）．（1）分别求这两个函数的表达式；（2）如图2，将直线OA向下平移n个单位长度后与y轴交于点B，与x轴交于点C，与反比例函数图象在第一象限内的交点为D，连接OD，tan∥COD＝14．∥求n的值．∥连接AB，AD，求∥ABD的面积．2244．如图，矩形ABCD中，AB=6，BC=8，E为AB上一点，且AE=2，M为AD上一动点（不与A、D重合），AM=x，连结EM并延长交CD的延长线于F，过M作MG⊥EF交直线BC于点G，连结EG、FG．（1）如图1，若M是AD的中点，求证：①⊥AEM⊥⊥DFM；②⊥EFG是等腰三角形；（2）如图2，当x为何值时，点G与点C重合？（3）当x=3时，求⊥EFG的面积．在∥AEM和∥DFM中，，∥，∥，∥∥AME+∥NMG=∥NMG+∥NGM=90°，∥∥AME=∥MGN，∥∥AEM∥∥NMG，∥====，∥MN=2AE=4，由勾股定理得：EM===，∥GM=2EM=2，∥AB∥CD，∥∥DMF∥∥NGM，∥=，解得：MF=，∥EF=EM+MF=，∥∥EFG的面积=EF•GM=．45．抛物线y＝ax2＋bx﹣2与x轴交于点A和B（﹣1，0），与y轴交于点C，直线y＝﹣12x＋m过A，C两点，点P是抛物线上的一个动点．（1）求抛物线的解析式；（2）如图，若点P在直线AC的上方，当S△P AC＝3时，求点P的坐标；（3）点M为抛物线上的一点，tan∥ACM＝25时，求点M的坐标．151PHA PHC S S ＋＝12∥2CEF ，＝2ECF ∠25CA ＝， EN ∥y 轴交46．某物流公司要把3000吨货物从M市运到W市．（每日的运输量为固定值）（1）从运输开始，每天运输的货物吨数y（单位：吨）与运输时间x（单位：天）之间有怎样的函数关系式？（2）因受到沿线道路改扩建工程影响，实际每天的运输量比原计划少20%，以致推迟1天完成运输任务，求原计划完成运输任务的天数．∥y＝（x＞0）（1﹣20%）＝，47．在平面直角坐标系中，点O为坐标原点，抛物线y=﹣x2+（k﹣1）x+k（k＞0）交x轴的负半轴于点A，交x轴的正半轴于点B，交y轴的正半轴于点C，且AB=4．（1）如图1，求k的值；（2）如图2，点D在第一象限的抛物线上，点E在线段BC上，DE//y轴，若DE=，求点D的坐标；（3）如图3，在（2）的条件下，F为抛物线顶点，点P在第四象限的抛物线上，FP 交直线DE于点Q，点G与点D关于y轴对称，若GQ=DP，求点P的坐标．48．【特例发现】如图1，在∥ABC中，AG∥BC于点G，以A为直角顶点，分别以AB，AC为直角边，向∥ABC外作等腰Rt∥ABE和等腰Rt∥ACF，过点E、F作射线GA 的垂线，垂足分别为P、Q．求证：EP=FQ．【延伸拓展】如图2，在∥ABC中，AG∥BC于点G，以A为直角顶点，分别以AB，AC为直角边，向∥ABC外作Rt∥ABE和Rt∥ACF，射线GA交EF于点H．若AB=kAE，AC=kAF，请思考HE与HF之间的数量关系，并直接写出你的结论．【深入探究】如图3，在∥ABC中，G是BC边上任意一点，以A为顶点，向∥ABC外作任意∥ABE和∥ACF，射线GA交EF于点H．若∥EAB=∥AGB，∥F AC=∥AGC，AB=kAE，AC=kAF，上一问的结论还成立吗？并证明你的结论．【应用推广】在上一问的条件下，设大小恒定的角∥IHJ分别与∥AEF的两边AE、AF 分别交于点M、N，若∥ABC为腰长等于4的等腰三角形，其中∥BAC=120°，且∥IHJ=∥AGB=θ=60°，k=2；求证：当∥IHJ在旋转过程中，∥EMH、∥HMN和∥FNH均相似，并直接写出线段MN 的最小值（请在答题卡的备用图中补全作图）．【答案】(1)证明参见解析；(2)HE=HF；(3)成立，证明参见解析；(4)证明参见解析，。

2020年最新沪科版数学九年级上册章节整合提升试题及答案(全册)

最新沪科版数学九年级上册21章解码专训一：函数中的决策问题名师点金：函数中的决策问题通常包括三类：利用一次函数进行决策，利用二次函数进行决策，利用反比例函数作决策．其解题思路一般是先建立函数模型，将实际问题转化为函数问题，然后利用函数的图象和性质去分析、解决问题．利用一次函数作决策题型1购买方案1．(2015·临沂)新农村社区改造中，有一部分楼盘要对外销售．某楼盘共23层，销售价格如下：第八层楼房售价为 4 000元/米2，从第八层起每上升一层，每平方米的售价提高50元；反之，楼层每下降一层，每平方米的售价降低30元，已知该楼盘每套楼房面积均为120米2.若购买者一次性付清所有房款，开发商有两种优惠方案：方案一：降价8%，另外每套楼房赠送a元装修基金；方案二：降价10%，没有其他赠送．(1)请写出售价y(元/米2)与楼层x(1≤x≤23，x取整数)之间的函数表达式；(2)老王要购买第十六层的一套楼房，若他一次性付清购买房款，请帮他计算哪种优惠方案更合算．题型2生产方案2．(2015·无锡)某工厂以80元/箱的价格购进60箱原材料，准备由甲，乙两车间全部用于生产A产品，甲车间用每箱原材料可生产出A产品12千克，需耗水4吨；乙车间通过节能改造，用每箱原材料可生产出的A产品比甲车间少2千克，但耗水量是甲车间的一半．已知A产品售价为30元/千克，水价为5元/吨．如果要求这两车间生产这批产品的总耗水量不得超过200吨，那么该厂如何分配两车间的生产任务，才能使这次生产所能获取的利润w最大？最大利润是多少？(注：利润＝产品总售价－购买原材料成本－水费)题型3运输方案3．(2015·荆州)荆州素有“鱼米之乡”的美称，某渔业公司组织20辆汽车装运鲢鱼、草鱼、青鱼共120吨去外地销售．按计划20辆汽车都要装运，每辆汽车只能装运同一种鱼，且必须装满．根据下表提供的信息，解答以下问题：鲢鱼草鱼青鱼每辆汽车装鱼量(吨) 8 6 5每吨鱼获利(万元) 0.25 0.3 0.2(1)设装运鲢鱼的车辆为x辆，装运草鱼的车辆为y辆，求y与x之间的函数表达式；(2)如果装运每种鱼的车辆不少于2辆，那么怎样安排车辆能使此次销售获利最大？并求出最大利润．利用二次函数作决策题型1几何问题中的决策4．如图，有长为24 m的围栏，一面利用墙(墙的最大可用长度a为10 m)，围成中间隔有一道栅栏的长方形鸡舍．设鸡舍的宽AB为x m，面积为S m2.(1)求S与x的函数表达式；(2)如果围成面积为45 m2的鸡舍，AB的长是多少米？(3)能围成面积比45 m2更大的鸡舍吗？如果能，请求出最大面积；如果不能，请说明理由．(第4题)5．如图，△ABC是边长为 3 cm的等边三角形，动点P，Q同时从A，B两点出发，分别沿AB，BC方向匀速移动，它们的速度都是 1 cm/s，当点P运动到B时，P，Q两点停止运动，设P点运动时间为t(s)．(1)当t为何值时，△PBQ是直角三角形？(2)设四边形APQC的面积为y cm2，求y关于t的函数表达式，当t取何值时，四边形APQC的面积最小？并求出最小值．(第5题)题型2实际问题中的决策6．(2014·资阳)某商家计划从厂家采购空调和冰箱两种产品共20台，空调的采购单价y1(元/台)与采购数量x1(台)满足y1＝－20x1＋1 500(0＜x1≤20，x1为整数)；冰箱的采购单价y2(元/台)与采购数量x2(台)满足y2＝－10x2＋1 300(0＜x2≤20，x2为整数)．(1)经商家与厂家协商，采购空调的数量不少于冰箱数量的119倍，且空调采购单价不低于 1 200元/台，问该商家共有几种进货方案？(2)该商家分别以 1 760元/台和1 700元/台的销售单价售出空调和冰箱，且全部售完．在(1)的条件下，问采购空调多少台时总利润最大？并求最大利润．7．某宾馆有50个房间供游客住宿．当每个房间每天的定价为180元时，房间会全部住满；当每个房间每天的定价每增加10元时，就会有一个房间空闲．宾馆需对游客居住的每个房间每天支出20元的各种费用．根据规定，每个房间每天的定价不得高于340元．设每个房间每天的定价增加x元(x为10的整数倍)．(1)设一天订住的房间数为y，直接写出y与x之间的函数表达式及自变量x 的取值范围；(2)设宾馆一天获得的利润为W元，求W与x之间的函数表达式；(3)一天订住多少个房间时，宾馆获得的利润最大？最大利润是多少元？利用反比例函数作决策8．某市政府计划建设一项水利工程，工程需要运送的土石方总量为106立方米，某运输公司承担了该项工程中运送土石方的任务．(1)该运输公司平均每天的工作量v(单位：立方米/天)与完成运送任务所需的时间t(单位：天)之间有怎样的函数关系？(2)这个运输公司共有100辆卡车，若每天一共可运送土石方104立方米，则公司完成全部运输任务需要多少时间？(3)当公司以问题(2)中的速度工作40天后，由于工程进度的需要，剩下的所有运输任务必须在50天内完成，则公司至少需要再增加多少辆卡车才能按时完成任务？解码专训二：函数与几何的综合应用名师点金：初中阶段函数与几何的综合应用非常广泛，解决这类问题的关键是要学会数形结合，一方面抓住几何图形的特征，灵活运用点的坐标与线段长度之间的相互转化，以及图象特征，从而解决与一次函数、反比例函数和二次函数有关的问题，另一方面已知函数的表达式可求出点的坐标，进而解决有关几何问题．与三角形的综合1．如图，在坐标系xOy中，△ABC是等腰直角三角形，∠BAC＝90°，A(1，0)，B(0，2)，抛物线y＝12x2＋bx－2过点C.求抛物线对应的函数表达式．(第1题)2．(2015·枣庄)如图，一次函数y＝kx＋b与反比例函数y＝6x(x>0)的图象交于A(m，6)，B(3，n)两点．(1)求一次函数的表达式；(2)根据图象直接写出使kx＋b<6x成立的x的取值范围；(3)求△AOB的面积．(第2题)与四边形的综合题型1与平行四边形的综合3．如图，过反比例函数y＝6x(x＞0)的图象上一点A作x轴的平行线，交双曲线y＝－3x(x＜0)于点B，过B作BC∥OA交双曲线y＝－3x(x＜0)于点D，交x轴于点C，连接AD交y轴于点E，若OC＝3，求OE的长．(第3题)题型2与矩形的综合(第4题)4．(2015·烟台)如图，矩形OABC的顶点A，C的坐标分别是(4，0)和(0，2)，反比例函数y＝kx(x>0)的图象过对角线的交点P并且与AB，BC分别交于D，E两点，连接OD，OE，DE，则△ODE的面积为________．5．(2015·德州)如图，在平面直角坐标系中，矩形OABC的对角线OB，AC 相交于点D，且BE∥AC，AE∥OB.(1)求证：四边形AEBD是菱形；(2)如果OA＝3，OC＝2，求出经过点E的双曲线的函数表达式．(第5题) 题型3与菱形的综合(第6题)6．二次函数y＝23x2的图象如图所示，点A0位于坐标原点，点A1，A2，A3，…，A n在y轴的正半轴上，点B1，B2，B3，…，B n，在二次函数位于第一象限的图象上，点C1，C2，C3，…，C n在二次函数位于第二象限的图象上．四边形A0B1A1C1，四边形A1B2A2C2，四边形A2B3A3C3，…，四边形A n－1B n A n C n都是菱形，∠A0B1A1＝∠A1B2A2＝∠A2B3A3＝…＝∠A n－1B n A n＝60°，菱形A n－1B n A n C n的周长为________．7．(2015·武威)如图，在平面直角坐标系中，菱形ABCD的顶点C与原点O重合，点B在y轴的正半轴上，点A在函数y＝kx(k>0，x>0)的图象上，点D的坐标为(4，3)．(1)求k的值；(2)若将菱形ABCD沿x轴正方向平移，当菱形的顶点D落在函数y＝kx(k>0，x>0)的图象上时，求菱形ABCD沿x轴正方向平移的距离．(第7题)题型4与正方形的综合8．如图，在平面直角坐标系中，点O为坐标原点，正方形OABC的边OA，OC分别在x轴、y轴上，点B的坐标为(2，2)，反比例函数y＝kx(x＞0，k≠0)的图象经过线段BC的中点D.(1)求k的值；(2)若点P(x，y)在该反比例函数的图象上运动(不与点D重合)，过点P作PR⊥y轴于点R，作PQ⊥BC所在直线于点Q，记四边形CQPR的面积为S，求S关于x的表达式并写出x的取值范围．(第8题)9．(中考·孝感)如图所示，已知正方形ABCD的边长为1，点E在边BC上，若∠AEF＝90°，且EF交正方形外角的平分线CF于点F.(1)图甲中，若点E是边BC的中点，我们可以构造两个三角形全等来证明AE＝EF，请叙述你的一个构造方案，并指出是哪两个三角形全等(不要求证明)；(2)如图乙，若点E在线段BC上滑动(不与点B，C重合)．①AE＝EF是否总成立？请给出证明；②在如图乙所示的平面直角坐标系中，当点E滑动到某处时，点F恰好落在抛物线y＝－x2＋x＋1上，求此时点F的坐标．(第9题)解码专训三：探究二次函数中存在性问题名师点金：存在性问题是近年来中考的热点，这类问题的知识覆盖面广，综合性强，题型构思精巧，解题方法灵活，求解时常常要猜想或者假设问题的某种关系或结论存在，再经过分析、归纳、演算、推理找出最后的答案．常见的类型有：探索特殊几何图形的存在性问题，探索周长有关的存在性问题，探索面积有关的存在性问题．探索与特殊几何图形有关的存在性问题1．(中考·扬州)已知抛物线y＝ax2＋bx＋c经过A(－1，0)，B(3，0)，C(0，3)三点，直线l是抛物线的对称轴．(1)求抛物线对应的函数表达式；(2)设点P是直线l上的一个动点，当△PAC的周长最小时，求点P的坐标；(3)在直线l上是否存在点M，使△MAC为等腰三角形？若存在，直接写出所有符合条件的点M的坐标；若不存在，请说明理由．(第1题)探索与周长有关的存在性问题2．如图，在直角坐标系中，点A的坐标为(－2，0)，OB＝OA，且∠AOB ＝120°.(1)求点B的坐标；(2)求经过A，O，B三点的抛物线对应的函数表达式；(3)在(2)中抛物线的对称轴上是否存在点C，使△BOC的周长最小？若存在，求出点C的坐标；若不存在，请说明理由．(第2题)探索与面积有关的存在性问题3．如图，已知抛物线y＝x2＋bx＋c经过A(1，0)，B(0，2)两点，顶点为D.(1)求抛物线对应的函数表达式；(2)将抛物线沿y轴平移后经过点C(3，1)，求平移后所得抛物线对应的函数表达式；(3)设(2)中平移后的抛物线与y轴的交点为B1，顶点为D1，在此抛物线上是否存在点N，使△NBB1的面积是△NDD1面积的2倍？若存在，求出点N的坐标；若不存在，请说明理由．(第3题)解码专训四：二次函数与反比例函数中常见的热门考点名师点金：二次函数与反比例函数是中考的必考内容，难度高，综合性强，既可以与代数知识结合，又可以与几何知识结合．在中考中，反比例函数常与几何知识考查体现k的几何意义，而二次函数常以实际应用题或综合题的形式出现，重点考查最值或存在性问题．二次函数的图象与性质1．对于二次函数y＝(x－1)2＋2的图象，下列说法正确的是()A．开口向下B．对称轴是直线x＝－1C．顶点坐标是(1，2)D．与x轴有两个交点2．(2015·安顺)如图，为二次函数y＝ax2＋bx＋c(a≠0)的图象，则下列说法：①a＞0；②2a＋b＝0；③a＋b＋c＞0；④当－1＜x＜3时，y＞0.其中正确的个数为()A．1B．2C．3D．4(第2题)(第4题)3．抛物线y＝2x2－x＋1的顶点坐标是________，当________时，y随x的增大而增大．4．如图，已知抛物线y＝x2＋bx＋c经过点(0，－3)，请你确定一个b的值，使抛物线与x轴的一个交点在(1，0)和(3，0)之间，你所确定的b的值是________．用待定系数法求二次函数的表达式5．已知一个二次函数的图象的顶点为(8，9)，且经过点(0，1)，则二次函数表达式为________．6．(2014·咸宁)科学家为了推测最适合某种珍奇植物生长的温度，将这种植物分别放在不同温度的环境中，经过一定时间后，测试出这种植物高度的增长情况，部分数据如下表：温度t/℃－4 －2 0 1 4植物高度增长量l/mm41 49 49 46 25 科学家经过猜想、推测出l与t之间是二次函数关系．由此可以推测最适合这种植物生长的温度为______℃.7．如图，抛物线y＝ax2－5ax＋4经过△ABC的三个顶点，点A，C分别在x轴、y轴上，且BC∥x轴，AC＝BC，求抛物线对应的函数表达式．(第7题)二次函数与一元二次方程或不等式的关系8．抛物线y＝－9x2＋3x＋12与坐标轴的交点个数是()A．3B．2C．1D．09．二次函数y＝ax2＋bx＋c的x与y的部分对应值如下表．利用二次函数图象可知，当函数值y＜0时，x的取值范围是()x －3 －2 －1 0 1 2 3 4 5y 12 5 0 －3 －4 －3 0 5 12A.x＜0或x＞2B．0＜x＜2C．x＜－1或x＞3 D．－1＜x＜310．已知二次函数y＝ax2＋bx＋c(a≠0)的图象如图所示，则下列结论中错误的是()(第10题)A．a－b＋c＝0B．x＝3是方程ax2＋bx＋c＝0的一个根C．a＋b＋c＞0D．当x＜1时，y随x的增大而减小11．已知关于x的二次函数y＝x2－(2m－1)x＋m2＋3m＋4.(1)探究m取不同值时，该二次函数的图象与x轴的交点的个数；(2)设该二次函数的图象与x轴的交点分别为A(x1，0)，B(x2，0)，且x12＋x22＝5，与y轴的交点为C，它的顶点为M，求直线CM的函数表达式．二次函数的应用12．(2015·滨州)一种进价为每件40元的T恤，若销售单价为60元，则每周可卖出300件．为提高利润，欲对该T恤进行涨价销售．经过调查发现：每涨价1元，每周要少卖出10件．请确定该T恤涨价后每周的销售利润y(元)与销售单价x(元)之间的函数表达式，并求销售单价定为多少元时，每周的销售利润最大．13．在平面直角坐标系中，现将一块等腰直角三角板ABC放在第二象限，一直角边靠在两坐标轴上，且有点A(0，2)，点C(－1，0)，如图所示，抛物线y ＝ax2＋ax－2经过点B.(1)求点B的坐标；(2)求抛物线对应的函数表达式；(3)在抛物线上是否还存在点P(点B除外)，使△ACP仍然是以AC为直角边的等腰直角三角形？若存在，求出所有点P的坐标；若不存在，请说明理由．(第13题)反比例函数的图象与性质14．(2015·海南)点A(－1，1)是反比例函数y＝m＋1x的图象上一点，则m的值为()A．－1B．－2C．0D．115．对于反比例函数y＝4x，下列说法正确的是()A．图象经过点(2，－2)B．图象位于第二、四象限C．y随x的增大而增大D．当x>0时，y随x的增大而减小。

沪教版九年级一模冲刺复习讲义第5讲几何计算与说理(解析版)

【例1】已知90ABC ∠=︒，AB = 2，BC = 3，AD // BC ，P 为线段BD 上的动点，点Q 在射线AB 上，且满足：PQ ADPC AB=（如图1所示）．（1）当AD = 2，且点Q 与点B 重合时（如图2所示），求线段PC 的长；（2）在图1中，联结AP ．当32AD =，且点Q 在线段AB 上时，设点B 、Q 之间的距离为x ，APQ PBCS y S ∆∆=，其中APQ S ∆表示APQ ∆的面积，PBC S ∆表示PBC ∆的面积，求y 关于x 的函数解析式，并写出函数定义域；（3）当AD < AB ，且点Q 在线段AB 的延长线上时（如图3所示），求QPC ∠的大小．【分析】（1）如图2，当AD = 2时，AD = AB ，由PQ ADPC AB=，可知PQ = PC ；由AD // BC 、 AD = AB 又可知45ABD PCB PBC ∠=∠=∠=︒，再由BC = 3可得PC 的长；（2）要求y 与x 的函数关系式，而y 与APQ S ∆和PBC S ∆有关，观察这两个三角形可发现， AQ 可用x 表示，BC 已知，所以APQ PBCS y S ∆∆=的值就是点P 到AB 和BC 的距离之比，故可过P 点分别向AB 和BC 作垂线段PF 和PE ，易得34PF PF AD PE BF AB ===，从而可表达y 与x 的函数关系式；对于定义域，要分析点Q 的运动范围（在线段AB 上）及限制条件（PQ AD PC AB =），可得x 的最小值为0，当点P 在点D 处时，x 取得最大值，即得定义域；几何计算与说理例题解析E A D PCBQ 图1DAPCB （Q ）图2图3CADPBQ FM N2 / 14（3）要求QPC ∠的大小，而题中与QPC ∠有关的条件是“PQ ADPC AB=”，由（2）知若过点P 向AB 和BC 作垂线PN 和PM ，可得PN AD PM AB =，所以PN PQPM PC=，既而可得 Rt PCM ∆∽Rt PQN ∆，易得90QPC ∠=︒．【解答】（1）∵AD // BC ，∴ADB DBC ∠=∠．∵AD = AB = 2，∴ABD ADB ∠=∠．∴DBC ADB ∠=∠． ∵90ABC ∠=︒，∴45PBC ∠=︒．∵PQ AD PC AB =，AD = AB ，点Q 与点B 重合，∴PB = PQ = PC ． ∴45PCB PBC ∠=∠=︒． ∴90BPC ∠=︒．在Rt BPC ∆中，32cos 3cos452PC BC C ==⨯︒=．（2）过点P 作PE BC ⊥，PF AB ⊥，垂足分别为E 、F ． ∴90PFB FBE BEP ∠=∠=∠=︒．∴四边形FBEP 是矩形． ∴PF // BC ，PE = BF ． ∵AD // BC ，∴PF // AD ，∴PF ADBF AB=． ∵32AD =，AB = 2，∴34PF PE =． ∵2AQ AB QB x =-=-，BC = 3，∴22APQ x S PF ∆-=，32PBC S PE ∆=． ∴24APQ PBCS x S ∆∆-=，即24xy -= ．函数的定义域是708x ≤≤．（3）过点P 作PM BC ⊥，PN AB ⊥，垂足分别为M 、N ．易得四边形PNBM 为矩形，∴PN // BC ，PM = BN ，90MPN ∠=︒．∵AD // BC ，∴PN // AD ．∴PN AD BN AB =．∴PN ADPM AB =． ∵PQ AD PC AB =，∴PN PQPM PC=．又∵90PMC PNQ ∠=∠=︒，∴Rt PCM ∆∽Rt PQN ∆． ∴CPM QPN ∠=∠．∵90MPN ∠=︒，∴90CPM QPM QPN QPM MPN ∠+∠=∠+∠=∠=︒，即90QPC ∠=︒．【例2】在Rt ABC ∆中，∠ACB = 90°，BC = 30，AB = 50．点P 是AB 边上任意一点，直线PE ⊥AB ，与边AC 或BC 相交于E ．点M 在线段AP 上，点N 在线段BP 上，EM = EN ，12sin 13EMP ∠=．（1）如图1，当点E 与点C 重合时，求CM 的长；（2）如图2，当点E 在边AC 上时，点E 不与点A 、C 重合，设AP = x ，BN = y ，求y 关于x 的函数关系式，并写出函数的定义域；（3）若AME ∆∽ENB ∆（AME ∆的顶点A 、M 、E 分别与ENB ∆的顶点E 、N 、B 对应），求AP 的长．【分析】（1）当点E 与点C 重合时，易得EP 的长，再由12sin 13EMP ∠=可得CM 的长；（2）可以根据Rt AEP ∆∽Rt ABC ∆或者tan A =34得EP =43x ，再由12sin 13EMP ∠=可求得PM 和PN 的长，从而可得y 与x 的函数关系式；关于定义域，x 的最小值为0，最大值在点E 与C 重合时取得，由于不能重合，故0 < x < 32；（3）分两种情况进行讨论：当E 在AC 上或E 在BC 上；当E 在AC 上时，AM 、EN 、 EM 、NB 均可由x 表示，从而由比例关系求得AP 的长；当E 在BC 上时，重新画图，寻找解题思路．【解答】（1）∵∠ACB = 90°，PE ⊥AB ，点E 与点C 重合∴1122ABC S AC BC AB CP =⋅⋅=⋅⋅∵AE = 40，BC = 30，AB = 50， ∴CP = 24，又∵sin ∠EMP CP CM ==1312， ∴CM = 26；（2）在Rt AEP ∆与Rt ABC ∆中，∵ ∠EAP =∠BAC ，∴ Rt AEP ∆∽Rt ABC ∆， ∴ACBC AP EP =，即4030=x EP ，∴ EP =43x ， C AM P NBC(E)EAM P NB图1图24 / 14∵sin ∠EMP =1312，∴tan ∠EMP =512=MP EP ，即512=MPx43，∴ MP =165x = PN ， ∴BN =AB -AP -PN = 50-x -165x = 50-1621x ， ∴y = 50-1621x （0 < x < 32）；（3）①当E 在线段AC 上时，由（2）知，1213=EP EM ，即121343=x EM ，∴EM =1613x = EN ，∵AME ∆∽ENB ∆，又AM = AP -MP = x -165x =1611x ， ∴ NB ME EN AM =，即x x 16131611=x x1621501613-，解得：x = 22 ；②当E 在线段BC 上时，∵AME ∆∽ENB ∆，∴ ∠AEM =∠EBN ，由外角定理，∠AEC =∠EAB +∠EBN =∠EAB +∠AEM =∠EMP ， ∴Rt ACE ∆∽Rt EPM ∆，∴PM EP CE AC =，∴CE =350… 设AP = z ，∴ PB = 50-z ， ∵Rt BEP ∆∽Rt BAC ∆，∴BC BA PB BE =，即z BE -50=3050，∴BE =35(50-z )， ∴CE = BC -BE = 30-35(50-z )… 联立，，得：350=30-35(50-z )，解得：z = 42 ．综上：AP =22或42．图一DOEC BAABC DE O 【例3】如图，在半径为2的扇形AOB 中，∠AOB = 90°，点C 是AB 上的一个动点（不与点A 、B 重合），OD ⊥BC ，OE ⊥AC ，垂足分别为D 、E ．（1）若BC = 1，求OD 的长；（2）在DOE ∆中是否存在长度保持不变的边？如果存在，请指出并求其长度；如果不存在，请说明理由；（3）设BD = x ，DOE ∆的面积为y ，求y 关于x 的函数关系式，并写出它的定义域．【分析】（1）根据垂径定理可得OD 的长；（2）对于DOE ∆，很明显OD 、OE 的长会随着点C 的运动而发生变化；联结DE 后发现，点D 、E 为BC 和AC 的中点，则DE 是ABC ∆的中位线，故其长度不变，为AB 的一半；（3）DOE ∆中，DE 已知，OD 可用x 表达，这样还没有办法表达DOE ∆的面积，则需要继续挖掘关于DOE ∆的有效条件；由于OD ⊥BC ，OE ⊥AC ，若联结OC ，易得BOD COD ∠=∠，COE AOE ∠=∠，所以45DOE ∠=︒；再过点D 作OE 的垂线，则垂线段的长度和OE 的的长度均可用x 表达，从而可求得y 关于x 的函数关系式；定义域显然为：02x <<【解答】（1）∵OD ⊥BC ，BC = 1，∴1122BD BC ==．在Rt OBD 中，22221152()2OD OB BD =--；（2）存在．DE 的长保持不变．连接DE （如图一）． ∵OD ⊥BC ，OE ⊥AC ，∴D 、E 分别是BC 、AC 的中点， ∴12DE BA =．在Rt AOB ∆中，222AB OB OA =+， ∴222222AB +． ∴2DE6 / 14图二DOF E C BA（3）连接OC ，过点D 作DF OE ⊥于点F （如图二）． ∵OD ⊥BC ，OE ⊥AC ，OA OB OC ==， ∴BOD COD ∠=∠，EOC EOA ∠=∠，∵90AOB BOD COD EOC EOA ∠=∠+∠+∠+∠=， ∴45DOE EOC DOC ∠=∠+∠=． ∵OD ⊥BC ，BD = x ，2OB =， ∴2224DO OB BD x =-=- ∵DF OE ⊥，45DOE ∠=，∴224DF OF x =-． ∴222222(4)4EF DE DF x =--⋅-=．∴2211222()(4)422y OF EF DF x x =⋅+⋅=⋅--，即2244x x x y -+-(02)x <<．A BCDPQM 【例4】在矩形ABCD 中，点P 是边AD 上的动点，联结BP ，线段BP 的垂直平分线交边BC 于点Q ，垂足为点M ，联结QP （如图）．已知AD = 13，AB = 5，设AP = x ，BQ = y ．（1）求y 关于x 的函数解析式，并写出x 的取值范围；（2）当以AP 长为半径的⊙P 和以QC 长为半径的⊙Q 外切时，求x 的值；（3）点E 在边CD 上，过点E 作直线QP 的垂线，垂足为F ，如果EF = EC = 4，求x 的值．【分析】（1） AP = x ，BQ = y ，要求y 关于x 的函数解析式，而AP 、BQ 在不同的三角形中，则容易想到ABP ∆∽MQB ∆，从而根据线段的比例关系求得y 与x 的关系式；当Q 点与点C 重合时，x 取得最小值；当点P 运动到D 点时，x 取得最大值；（2）由两圆外切可得AP QC PQ BQ +==，可解得x ；（3）先根据题意将图形画出，如图，由EF = EC ，可得12∠=∠，又34∠=∠，35∠=∠，可得15∠=∠，所以CEQ ∆∽ABP ∆，再根据线段的对应成比例可求得x 的值．【解答】（1）在Rt ABP ∆中，222225BP AP AB x =+=+，∵MQ 是线段BP 的垂直平分线，∴BQ = PQ ，BM =12BP ，∠BMQ = 90°，∴∠MBQ +∠BQM = 90°，∵∠ABP +∠MBQ = 90°，∴∠ABP =∠BQM ，又∵∠A =∠BMQ = 90°， ∴ABP ∆∽MQB ∆， ∴BP AP BQ BM =，即12BP x y BP =，化简得：()22112522y BP x x x ==+．当点Q 与点C 重合时，BQ = PQ = 13，在Rt PQD ∆中，222PQ QD PD =+，即()22213513x =+-，解得：x = 1；又∵13AP AD ≤=，∴113x ≤≤．∴()21252y x x =+（113x ≤≤）．8 / 14ABCDPQN（2）当⊙P 与⊙Q 相外切时，如图所示：设切点为N ，则PQ = PN + QN = AP +（BC -BQ ） =()1313x y x y +-=+-；∵PQ = BQ ，∴13x y y +-=，即2130y x --=；将()21252y x x =+代入上式，可解得：x =2513，故当x =2513时，以AP 长为半径的⊙P 和以QC 长为半径的⊙Q 外切；（3）按题意画出图形，如图所示，联结QE ， ∵EF = EC ，EF PQ ⊥，EC QC ⊥ ∴12∠=∠， ∵PQ = BQ ， ∴34∠=∠，而1234∠+∠=∠+∠， ∴13∠=∠．又∵矩形ABCD ，∴AD // BC ， ∴35∠=∠，∴15∠=∠，又∵90C A ∠=∠=︒， ∴CEQ ∆∽ABP ∆， ∴CQ EC AP AB =，即1345y x -=，化简得：4565x y +=，将()21252y x x=+代入上式，解得：65102613x ±=，故当65102613x ±=时，EF = EC = 4．ABCD PQMF E12 34 5A BCDEF OPQ 【例5】已知：如图，AB 是半圆O 的直径，弦CD // AB ，动点P 、Q 分别在线段OC 、CD上，且DQ = OP ，AP 的延长线与射线OQ 相交于点E 、与弦CD 相交于点F （点F 与点C 、D 不重合），AB = 20，cos ∠AOC =45．设OP = x ，CPF ∆的面积为y ．（1）求证：AP = OQ ；（2）求y 关于x 的函数关系式，并写出它的定义域；（3）当OPE ∆是直角三角形时，求线段OP 的长．【分析】（1）要证AP = OQ ，分析条件中与这两条线段有关的条件为“DQ = OP ”，故想到联结 OD ，证明AOP ∆≌ODQ ∆，即可得证；（2）要表达CPF ∆的面积，由CD // AB 可得PFC ∆∽PAO ∆，只需表达出PAO ∆的面积，根据2AOPy CP S OP ∆⎛⎫= ⎪⎝⎭即可求y 关于x 的函数关系式；（3）根据直角三角形分别对三个内角分别为90°的情况进行分类讨论．【解答】（1）联结OD ，易得：AO = OD ；∵CD // AB ，∴AOC C ODQ ∠=∠=∠， ∴AOP ∆≌ODQ ∆，∴AP = OQ ；（2）作PH OA ⊥，∴4455OH OP x ==，35PH x =，∴132AOP S AO PH x ∆==；又∵PFC ∆∽PAO ∆， ∴2210AOPy CP x S OP x ∆-⎛⎫⎛⎫== ⎪ ⎪⎝⎭⎝⎭，即：2360300x x y x -+=（501013x <<）．（3）当90POE ∠=︒时，25cos 2OC CQ QCO ==∠，72OP DQ CD CQ ==-=（舍）；当90OPE ∠=︒时，cos 8OP AO COA =∠=；当90OEP ∠=︒时，AOQ DQO APO ∠=∠=∠，∴AOC AEO ∠=∠，即OEP COA ∠=∠，此种情况不存在； ∴线段OP 的长为8．ABCDEF OPQ H10 / 14A BCD E F G【例6】如图所示，梯形ABCD 中，AB // DC ，90B ∠=︒，AD = 15，AB = 16，BC = 12，点E 是边AB 上的动点，点F 是射线CD 上一点，射线ED 和射线AF 交于点G ，且AGE DAB ∠=∠．（1）求线段CD 的长；（2）如果AEG ∆是以EG 为腰的等腰三角形，求线段AE 的长；（3）如果点F 在边CD 上（不与点C 、点D 重合），设 AE = x ，DF = y ，求y 关于x 的函数解析式，并写出x 的取值范围．【分析】（1）过点D 作线段AB 的垂线段，即可求得CD 的长；（2）由AGE DAB ∠=∠可得AEG ∆∽DEA ∆，所以DEA ∆是以AE 为腰的等腰三角形，分两种情况进行讨论：AE = AD 或AE = DE ；（3）由AE = x 可表达DE 的长，根据AEG ∆∽DEA ∆可表达EG 的长，再根据DF DGAE EG=可表达DF 的长，即得y 与x 的函数关系式；对于x 的取值范围，从两点出发：F 在边 CD 上，y 的值大于0．【解答】（1）过点D 作DH AB ⊥，垂足为点H ；在Rt DAH ∆中，90AHD ∠=︒，AD = 15，DH = 12； ∴229AH AD DH =-=；又∵AB = 16，∴7CD BH AB AH ==-=；（2）∵AEG DEA ∠=∠，又AGE DAE ∠=∠，∴AEG ∆∽DEA ∆；由AEG ∆是以EG 为腰的等腰三角形，可得DEA ∆是以AE 为腰的等腰三角形；○1若AE = AD ，∵AD = 15 ∴AE = 15； ○2若AE = DE ，过点E 作EQ AD ⊥，垂足为Q ，∴11522AQ AD ==；在Rt DAH ∆中，90AHD ∠=︒，3cos 5AH DAH AD ∠==；在Rt AEQ ∆中，90AQE ∠=︒，3cos 5AQ QAE AE ∠==；∴252AE =；综上所述：当AEG ∆是以EG 为腰的等腰三角形时，线段AE 的长为15或252；（3）在Rt DHE ∆中，90DHE ∠=︒，DE = ∵AEG ∆∽DEA ∆，∴AE EGDE AE =，∴2EG∴2DG ；∵DF // AE ，∴DF DGAE EG=，即()2222129x x y x x +--=； ∴22518x y x -=，x 的取值范围为2592x <<．12 / 14ABCDEP【作业1】如图，在Rt ABC ∆中，90ACB ∠=︒．半径为1的A 与边AB 相交于点D ，与边AC 相交于点E ，连结DE 并延长，与线段BC 的延长线交于点P ．（1）当30B ∠=︒时，连结AP ，若AEP ∆与BDP ∆相似，求CE 的长；（2）若CE = 2，BD = BC ，求BPD ∠的正切值；（3）若1tan 3BPD ∠=，设CE = x ，ABC ∆的周长为y ，求y 关于x 的函数关系式．【分析】（1）∠B = 30°可得∠BAC = 60°，从而得到∠EPC = 30°，BDP ∆为等腰三角形，根据AEP ∆与BDP ∆相似可得，AE = EP ，即得AC 的长；（2）过点D 作DQ ⊥AC 于点Q ，设AQ = a ，BD = x ，可利用AD AQAB AC=表达出a 与x 的关系，则在在Rt ADQ ∆中，DQ 可用x 表示，再根据DQ ADBC AB=可求得x 的值，即BD 和BC 的长度；要求BPD ∠的正切值，由于CE 已知，则要求CP 的长度，过点C 作 CF // DP ，由于AD = AE 可得AF = AC ，从而得到BF 的长，根据BFC ∆∽BDP ∆，可求得CP 的长，即得BPD ∠的正切值；（3）过D 点作DQ ⊥AC 于点Q ，设AQ = a ，由1tan 3BPD ∠=可表达DQ ，在Rt ADQ ∆ 中，根据勾股定理可求得a 的值；在根据ADQ ∆∽ABC ∆，CE = x 可表达AB 、BC ，从而可求得y 关于x 的函数关系式．【解答】（1）解：∵∠B = 30°，∠ACB = 90°，∴∠BAC = 60°， ∵AD = AE ，∴∠AED = 60°=∠CEP ， ∴∠EPC = 30° ∴BDP ∆为等腰三角形 ∵AEP ∆与BDP ∆相似∴∠EAP =∠EP A =∠DBP =∠DPB = 30°， ∴AE = EP = 1， ∴在Rt ECP ∆中，EC =12EP =12；课后作业（2）过点D 作DQ ⊥AC 于点Q ，且设AQ = a ，BD = x ， ∵AE = 1，EC = 2，∴3QC a =-； ∵∠ACB = 90°，∴ADQ ∆∽ABC ∆，∴AD AQ AB AC = 即113a x =+，∴31a x =+, ∵在Rt ADQ ∆中，2222328111x x DQ AD AQ x x +-⎛⎫=-=-=⎪++⎝⎭，∵DQ ADBC AB=，∴228111x x x x x +-+=+，解之得：x = 4，即BC = 4；过点C 作CF // DP ，∴ADE ∆∽AFC ∆，∴AE AD AC AF =，即AF = AC ，即DF = EC = 2， ∴BF = DF = 2；∵BFC ∆∽BDP ∆， ∴2142BF BC BD BP ===，即：BC = CP = 4， ∴tan ∠BPD =2142EC CP ==；（3）过D 点作DQ ⊥AC 于点Q ，则DQE ∆∽PCE ∆，设AQ = a ，则1QE a =-， ∴QE DQ EC CP =，且1tan 3BPD ∠=，∴()31DQ a =-． ∵在Rt ADQ ∆中，据勾股定理得：222AD AQ DQ =+，即：()222131a a =+-⎡⎤⎣⎦，解之得1a =（舍去），45a = ∵ADQ ∆∽ABC ∆，∴445155AD DQ AQ AB BC AC x x====++， ∴554x AB +=，334xBC +=， ∴ABC ∆的周长553313344x xy AB BC AC x x ++=++=+++=+，即：33y x =+，其中x > 0．ABCDE PFQ14 / 14ABCDEFG P 【作业2】如图，已知在平行四边形ABCD 中，AB = 5，BC = 8，cosB =45，点P 是边BC 上的动点，以CP 为半径的圆C 与边AD 交于点E 、F （点F 在点E 的右侧），射线CE 与射线BA 交于点G ．（1）当圆C 经过点A 时，求CP 的长；（2）联结AP ，当AP //CG 时，求弦EF 的长；（3）当AGE ∆是等腰三角形时，求圆C 的半径长．【分析】（1）当圆C 经过点A 时，CP = AC ，过点A 作BC 的垂线段AH 即可求AC ；（2）当AP //CG 时，易得四边形APCE 22AH PH CP +，可求得CP 的长，既而可以求得EF ；（3）AEG DEC ∆∆∽，再进行分类讨论等腰的情况，即可求出圆C 的长．【解答】（1）作AH ⊥BC 于H ．∴BH = 4，AH = 3，∴CH = 4．∴225AC AH CH =+， ∴CP = AC = 5；（2）∵AP //CG ，∴APCE 为平行四边形，又∵CE = CP ，∴APCE 为菱形．设CP = x ，则AP = CP 22AH PH CP +． ()294x x +-=，解得：258x =，∴74EF =；（3）设AE t =，则()294CE t =+- ∵AEG DEC ∆∆∽，∴58t AG t =-，()2948t GE t t =+--分情况讨论：① AE = AG ，解得：3t =；② AE = GE ，解得：398t =，E 在F 点右边，舍去；③ AG = GE ，解得：0t =或8t =，均不可能，舍去．当AE = 3时，10CE故当AGE ∆是等腰三角形时，圆C 10。

沪教版九年级(下)学期同步讲义第4讲创新题型(解析版)

【例1】定义[x ]为不超过x 的最大整数，如[3.6] = 3，[ 3.6-] = 4-．对于任意实数x ，下列式子错误的是（） A ．[x ] = x （x 为整数） B ．0[]1x x ≤-<C ．[][][]x y x y +≤+D ．[][]n x n x +=+（n 为整数）【答案】C ．【解析】由反例[][3.8 2.7] 6.56+==，[3.8][2.7]325+=+=可知C 错误．【总结】本题考查取整函数[x ]的定义及应用．【例2】在平面直角坐标系xOy 中，对于点P （x ，y ）和Q （x ，'y ），给出如下定义：若创新题型知识结构模块一：定义应用例题解析2 / 17()()0'0y x y y x ⎧≥⎪=⎨-<⎪⎩，则称点Q 为点P 的“可控变点”．如果点（1-，2-）为点M 的可控变点，则点M 的坐标为___________．【答案】（-1，2）【解析】由题意得，当0<x 时，'=-y y ，且x 不变，所以当1x =-，时'2=y ，即点M 坐标为（1-，2）．【总结】把握好“可控变点”的定义，找出'y 与y 两者之间存在的关系．【例3】定义一种新运算：2x y x y x +*=，如2212122+⨯*==，则()()421**-=______．【答案】0．【解析】先计算()4224224+⨯*==，再计算()()2122102+-⨯*-==．【总结】根据运算法则进行运算，注意运算顺序．【例4】已知1m x =+，2n x =-+，若规定()()11m n m n y m n m n ⎧+-≥⎪=⎨-+<⎪⎩，则y 的最小值为（）A ．0B ．1C ．1-D ．2【答案】B ．【解析】把1m x =+，2n x =-+代入，得到1221222⎧⎛⎫≥ ⎪⎪⎪⎝⎭=⎨⎛⎫⎪-+< ⎪⎪⎝⎭⎩x x y x x ，当12≥x 时，1≥y ；当12<x 时，1>y ．所以y 的最小值是1，故选B ．【总结】考查分段函数求最值的问题．【例5】（2015学年·浦东新区二模·第17题）定义运算“*”：规定x y ax by *=+（其中a 、 b 为常数），若113*=，()111*-=，12*=______．【答案】4．【解析】把113*=，()111*-=代入运算法则，得31+=⎧⎨-=⎩a b a b ，解得：21=⎧⎨=⎩a b ，所以12*=2×1+1×2=4．【总结】根据新运算，求出a 、b 的值是解答本题的关键．【例6】（2015学年·宝山区、嘉定区二模·第17题）对于实数m 、n ，定义一种运算“*”为：m n mn n *=+．如果关于x 的方程()14x a x **=-有两个相等的实数根，那么满足条件的实数a 的值是______．【答案】0．【解析】根据运算法则，()*=+a x ax x ，()()*+=+++x ax x x ax x ax x ，整理得()()211104++++=a x a x ，此方程有两个相等的实数根，则()()210110+≠⎧⎪⎨=+-+=⎪⎩a a a ，解得：1201a a ==-，（舍），所以a=0．【总结】由运算法则整理得一元二次方程的一般形式，再结合一元二次方程根的判别式进行求解，注意二次项系数不能为零．【例7】（2014学年·宝山区、嘉定区二模·第17题）我们把两个三角形的外心之间的距离叫做外心距．如图，在Rt ABC ∆和Rt ACD ∆中，90ACB ACD ∠=∠=︒，点D 在边BC 的延长线上，如果BC = DC = 3，那么ABC ∆和ACD ∆的外心距是______．【答案】3．【解析】直角三角形的外心为斜边的中点，所以ABC ∆和ACD ∆ 的外心分别为AB 和AD 的中点，这两个三角形的外心距即∆ABD 的中位线，长度是132=BD ．【总结】本题考查的知识点有直角三角形的外心、三角形的中位线．【例8】（2014学年·虹口区二模·第17题）定义[a ，b ，c ]为函数2y ax bx c =++的“特征数”．如：函数232y x x =+-的“特征数”是[1，3，2-]，函数4y x =-+的“特征数”是[0，1-，4]．如果将“特征数”是[2，0，4]的函数图像向下平移3个单位，得到一个新函数图像，那么这个新函数的解析式是__________________．【答案】221=+y x ．CABD4 / 17【解析】由题意得“特征数”是[2，0，4]的函数解析式为224=+y x ，向下平移3个单位可得新函数的解析式为：221=+y x ．【总结】特征数[a ，b ，c ]即为二次函数的三个系数，已知特征数则可求得二次函数的解析式，再根据抛物线的平移法则“上加下减、左加右减”进行解题．【例9】（2015学年·闸北区二模·第17题）在平面直角坐标系xOy 中，C 的半径为r ，点P 是与圆心C 不重合的点，给出如下定义：若点'P 为射线CP 上一点，满足2'CP CP r =，则称点'P 为点P 关于C 的反演点．如图为点P 及其关于C 的反演点'P 的示意图．请写出点M （12，0）关于以原点O 为圆心，以1为半径的O 的反演点'M 的坐标．【答案】（2，0）．【解析】由反演点的定义可得2'=OM OM r ，即21'12=OM ，解得：'2=OM ，又点'M 在x 轴上，所以点'M 的坐标为（2，0）．【总结】掌握“反演点”的定义中，两点之间存在的关系．【例10】（2014学年·普陀区二模·第17题）如图1，对于平面上不大于90°的MON ∠，我们给出如下定义：如果点P 在MON ∠的内部，作PE OM ⊥，PF ON ⊥，垂足分别为点E 、F ，那么称PE + PF 的值为点P 相对于MON ∠的“点角距离”，记为 d （P ，MON ∠）．如图2，在平面直角坐标系xOy 中，点P 在第一象限内，且点P 的横坐标比纵坐标大1，对于xOy ∠，满足d （P ，xOy ∠）= 5，点P 的坐标是__________．【答案】（3，2）．【解析】过点P 分别作PA ⊥x 轴，PB ⊥y 轴， ∵点P 在第一象限内且横坐标比纵坐标大1， ∴设PA =a ，则PB =a +1，xyP' CPO ENF OPM 图1yx-11-11O图2∵d （P ，xOy ∠）= 5，可得：PA +PB =5，即a +a +1=5，解得：a =2，所以点P 的坐标为（3,2）．【总结】本次考查“点角距离”的定义，利用定义求解相关点的坐标．【例11】一组数1，1，2，x ，5，y ，…，满足“从第三个数起，每个数都等于它前面的两个数之和”，那么这组数中y 表示的数为______．【答案】8．【解析】由题得，x =1+2=3，y =3+5=8．【总结】本题难度不大，运算也比较简单．【例12】四个数a 、b 、c 、d 排列成a b c d，我们称之为二阶行列式．规定它的运算法则为：a b ad bc c d=-．若331233x x x x +-=-+，则x =______．【答案】1．【解析】由运算法则得()()22333333+-=+---+x x x x x x ，整理得：1212=x ，解得：x =1．【总结】由运算法则整理，再解关于x 的方程即可．模块二：阅读理解例题解析6 / 17D CBA【例13】对于两个不相等的实数a 、b ，我们规定符号{max a ，}b 表示a 、b 中的较大值，如：{max 2，}44=，按照这个规定，方程{max x ，}21x x x+-=的解为（） A ．12B ．22-C ．1212-D ．12+1-【答案】D ．【解析】当x >0时，{}max x x x -=，，解方程21+=x x x，得：12=±x 所以12=x 当x <0时，{}max x x x -=-，，解方程21x x x+-=，得：121==-x x ，所以1=-x ；综上，12=+x 1-，故选D ．【总结】本题注意分类讨论，根据定义进行取值，再解关于x 的方程．【例14】（2014学年·奉贤区二模·第17题）我们把三角形中最大内角与最小内角的度数差称为该三角形的“内角正度值”．如果等腰三角形的腰长为2，“内角正度值”为45°，那么该三角形的面积等于______．【答案】1或2．【解析】设最小角为x ，则最大角为45x +，当顶角为45x +，则45180x x x +++=，解得：45x =，此三角形为等腰直角三角形，∴此三角形的面积=12222⨯=；当顶角为x 时，则4545180x x x ++++=，解得：30x =．如图，2==AB AC ，30A ∠=，作CD ⊥AB ，在Rt ADC ，∵30A ∠=，∴112==CD AC ， ∴此三角形的面积=12112⨯=．综上所述，该三角形的面积等于1或2．【总结】本题注意分类讨论．根据“内角正度值”的定义求出三角形各内角的度数，再进行面积的求解．DCBA【例15】（2013学年·松江区二模·第17题）如果三角形有一边上的中线长恰好等于这边的长，那么称这个三角形为“有趣三角形”，这条中线称为“有趣中线”．已知Rt ABC ∆，90C ∠=︒，较短的一条直角边边长为1，如果Rt ABC ∆是“有趣三角形”，那么这个三角形“有趣中线”长等于．【解析】“有趣中线”有三种情况：若“有趣中线”为斜边AB 上的中线，直角三角形的斜边中点到三顶点距离相等，不合题意；若“有趣中线”为BC 边上的中线，根据斜边大于直角边，矛盾，不成立；若“有趣中线”为另一直角边AC 上的中线，如图所示，BC =1，设2BD x =，则CD x =．在Rt BCD 中，勾股定理得1+()222=x x ，解得：x，所以BD =2x．【总结】本题考查“有趣中线”的定义，注意分类讨论．【例16】（2015学年·崇明县二模·第17题）如果一个平行四边形一个内角的平分线分它的一边为1 : 2的两部分，那么称这样的平行四边形为“协调平行四边形”，称该边为“协调边”．当“协调边”为3时，它的周长为______．【答案】8或10．【解析】由题意可知，存在两种情况：（1）一组邻边长分别为3和1，周长=8；（2）一组邻边长分别为3和2，周长=10．【总结】本题考查“协调平行四边形”的定义及平行四边形的性质．【例17】（2015学年·虹口区二模·第17题）设正n 边形的半径为R ，边心距为r ，如果我们将Rr的值称为正n 边形的“接近度”，那么正六边形的“接近度”是______（结果保留根号）．8 / 1723【解析】设正六边形的边长为a ，则半径为R=a ，边心距为3，所以R r23【总结】本题考查“接近度”的定义及正六边形的性质．【例18】（2013学年·静安区二模·第16题）将关于x 的一元二次方程20x px q ++=变形为2x px q =--，就可将2x 表示为关于x 的一次多项式，从而达到“降次”的目的，我们称这样的方法为“降次法”．已知210x x --=，可用“降次法”求得431x x --的值是____________．【答案】1．【解析】由210x x --=，得21=+x x ，代入431x x --=()221311+--=-=x x x x ．【总结】本题运用“降次”及“整体代入”的思想进行解题．【例19】（2014学年·金山区二模·第17题）在平面直角坐标系中，我们把半径相等且外切、连心线与直线y = x 平行的两个圆，称之为“孪生圆”；已知圆A 的圆心为（2-，3）2，那么圆A 的所有“孪生圆”的圆心坐标为_________．【答案】（0，5）或（-4，1）．【解析】由题意得，连心线所在直线为5=+y x ，因为两圆外切，设另一圆心为圆B ，所以圆心距22=AB (),5+B x x ，所以22(2)(2)22+++=AB x x 解得：10=x ，24=-x ，所以圆心B 的坐标为（0,5）或（-4,1）．【总结】本题考查了“孪生圆”的定义、一次函数的图像以及圆与圆的位置关系．【例20】（2013学年·黄浦区二模·第17题）当两个圆有两个公共点，且其中一个圆的圆心在另一圆的圆内时，我们称此两圆的位置关系为“内相交”．如果1O 、2O 半径分别3和1，且两圆“内相交”，那么两圆的圆心距d 的取值范围是___________．【答案】23<<d ．【解析】两个圆有两个公共点即两圆相交，可得24<<d ，当小圆的圆心恰好在大圆上时，3=d ，所以内相交的圆心距d 取值范围是23<<d ．【总结】本题考查圆与圆的位置关系及“内相交”的定义．10 / 17【例21】观察下列各数：1，43，97，1615，…，按你发现的规律计算这列数的第6个数为（）A ．2531B ．3635C ．47D ．6263【答案】C ．【解析】根据题意，可知规律为221n n -，故第6个数为：3663，化简为47，故选C ．【总结】本题考查针对给定的一列数字找规律．【例22】按一定规律排列的一列数：12，22，32，52，82，132，…．若x 、y 、z 表示这列数中的连续三个数，猜测x 、y 、z 满足的解析式是____________．【答案】=xy z ．【解析】由给出的这一列数字，可得出规律：从第三个数字开始，每个数等于它两个数的乘积，所以=xy z ．【总结】本题考查针对给定的一列数字找规律．【例23】在平面直角坐标系中，有三个点A （1，1-）、B （1-，1-）、C （0，1），点P（0，2）关于点A 的对称点为1P ，1P 关于点B 的对称点为2P ，2P 关于点C 的对称点为3P ，按此规律，继续以点A 、B 、C 为对称中心重复前面的操作，依次得到点4P ，5P ，6P ，…，则点2017P 的坐标为（）A ．（0，0）B ．（0，2）C ．（2，4-）D ．（4-，2）【答案】C ．【解析】由题意得1P （2，-4）、2P （-4，2）、3P （4，0）、4P （-2，-2）、 5P （0，0），6P （0，2），每6个数形成一个周期，2017÷6=336……1，所以2017P 的坐标和1P 的坐标相同，故选C ．模块三：规律探究例题解析DCAB【总结】本题考查了点的对称问题及周期问题的处理．【例24】如图，正方形ABCD 的边长为2，其面积标记为1S ，以CD 为斜边作等腰直角三角形，以该等腰直角三角形的一条直角边为边向外作正方形，其面积标记为2S ，…，按照此规律继续下去，则2017S 的值为_____________．【答案】20141()2．【解析】由题意得1S =2×2=4=22，2S =1222⨯=，3S =111⨯==20，…… 由以上规律，可知2017S =2-201420141()2=．【总结】本题考查了找规律在几何图形中的应用．【习题1】定义：如果二次函数2111y a x b x c =++（10a ≠，1a 、1b 、1c 是常数）与2222y a x b x c =++（20a ≠，2a 、2b 、2c 是常数）满足120a a +=，12b b =，120c c +=，那么称这两个函数互为“旋转函数”．若函数2423y x mx =-+-与22y x nx n =-+互为“旋转函数”，则()2017m n +=________．【答案】-1．【解析】由“旋转函数”的定义得42320⎧=-⎪⎨⎪-+=⎩m nn ，解得：32=-⎧⎨=⎩m n ，所以()2017m n +=（-1）2017=-1．【总结】本题考查“旋转函数”的定义．随堂检测12 / 17DCBA【习题2】（2013学年·虹口区二模·第17题）如果三角形有一边上的中线长恰好等于这边的长，那么称这个三角形为“好玩三角形”．在Rt ABC ∆中，90C ∠=︒，若Rt ABC ∆是“好玩三角形”，则tan A =_______． 323【解析】由于直角三角形斜边上的中线等于斜边的一半，因此斜边上的中线不满足；故只能是直角边上的中线等于此直角边的长，如图所示，设BD =2x ，CD =x ，则3=BC x ，在Rt ABC 中，AC =2x ，3=BC x ．当∠A 为较小锐角时，3tan A 当∠A 为较大锐角时，23tan A =．【总结】本题考查“好玩三角形”的定义，注意分类讨论．【习题3】（2013学年·杨浦区二模·第17题）我们把四边形两条对角线中点的连线段称为“奇异中位线”．现有两个全等三角形，边长分别为3cm 、4cm 、5cm ．将这两个三角形相等的边重合拼成凸四边形，如果凸四边形的“奇异中位线”的长不为0，那么“奇异中位线”的长是______cm ．【答案】710．【解析】如图，将两个全等的直角ABC 与DEF 的斜边AC 与DF 重合，拼成凸四边形ABCE ，AC 与BE 交于点O ，M 为AC 的中点．∵△ABC ≌△DEF ，易证AO ⊥BE ．在Rt AOB 中，AO =AB •cos ∠BAO =95，因为1522==AM AC ，所以5972510=-=-=OM AM OA ．即奇异中位线的长是710．【总结】本题考查了“奇异中位线”的定义，注意根据题目要求画出合适的图形．【习题4】（2014学年·崇明县二模·第17题）如果一个二次函数的二次项系数为1，那么这OPP'BOA图1 图2个函数可以表示为2y x px q =++，我们将[p ，q ]称为这个函数的特征数．例如二次函数242y x x =-+的特征数是[4-，2]．请根据以上的信息探究下面的问题：如果一个二次函数的特征数是[2，3]，将这个函数的图像先向左平移2个单位，再向下平移3个单位，那么此时得到的图像所对应的函数的特征数为______．【答案】[6，8]．【解析】特征数是[2，3]的二次函数为223=++y x x ，即2(1)2=++y x ，将其向左平移2个单位，再向下平移3个单位后得到的二次函数为2(3)1=+-y x ，即268=++y x x ，所以特征数为[6，8]．【总结】本题考查了“特征数”的定义及二次函数图像的平移．【习题5】（2014学年·黄浦区二模·第18题）如图1，点P 是以r 为半径的圆O 外一点，点'P 在线段OP 上，若满足2'OP OP r =，则称点'P 是点P 关于圆O 的反演点．如图2，在Rt ABO ∆中，90B ∠=︒，AB = 2，BO = 4，圆O 的半径为2，如果点'A 、'B 分别是点A 、B 关于圆O 的反演点，那么''A B 的长是______． 5．【解析】由反演点的定义，可知：2'=OA OA r ，2'=OB OB r ，则'=OA OA 'OB OB ，即''=OA OB OB OA ，又∠=∠O O ，可证''OA B ∽OBA ， ∴'''=OB A B OA AB 225''=A B ，解得：''A B 5．【总结】本题考查了“反演点”的定义，以及相似三角形的判定与性质．【习题6】正方形111A B C O ，2221A B C C ，3332A B C C ，…，按如图所示的方式放置．点1A ，2A ，3A ，…和点1C ，2C ，3C ，…，分别在直线y kx b =+（0k >）和x 轴上，已知点14 / 171B （1，1），2B （3，2），则点6B 的坐标是__________，点n B 的坐标是__________．【答案】（63，32），1(212)n n --，．【解析】由1A （0，1）、2A （1，2），可求得直线解析式为1=+y x ．可求得3A （3，4）、3B （7，4），4A （7，8）、 4B （15，8），5A （15，16）、5B （31，16）， 6A （31，32）、6B （63，32）， ……，按照此规律可得n B 1(212)n n --，．【总结】本题考查了一次函数与几何图形背景下找出点坐标的规律．【作业1】（2014学年·浦东新区二模·第17题）对于函数()2y ax b =+，我们称[a ，b ]为这个函数的特征数．如果一个函数()2y ax b =+的特征数为[2，5-]，那么这个函数图像与x 轴的交点坐标为_______．【答案】（52，0）．【解析】特征数为[2，5-]的函数为()225=-y x ，令0=y ，解得52=x ，所以函数图像与x 轴的交点坐标为（52，0）．【总结】本题考查了“特征数”的定义，以及二次函数的图像．【作业2】（2013学年·金山区二模·第17题）如果一个三角形的一边长等于另一边长的两倍，我们把这样的三角形成为“倍边三角形”，如果一个直角三角形是倍边三角形，那课后作业xyOABC Oxy 么这个直角三角形的较小的锐角的正切值为． 3或12．【解析】当斜边长等于直角边长的两倍时，最小角为303；当直角边长等于另一直角边长的两倍时，最小角的正切值为12．【总结】本题考查了“倍边三角形”的定义，以及锐角三角比的求值．【作业3】已知抛物线p ：2y ax bx c =++的顶点为C ，与x 轴相交于A 、B 两点（点A 在点B 左侧），点C 关于x 轴的对称点为'C ，我们称以点A 为顶点且过点'C ，对称轴与y 轴平行的抛物线为抛物线p 的“梦之星”抛物线，直线'AC 为抛物线p 的“梦之星”直线．若一条抛物线的“梦之星”抛物线和“梦之星”直线分别是221y x x =++和22y x =+，则这条抛物线的解析式为________________．【答案】223=--y x x ．【解析】由221y x x =++=2(1)+x 可求得：A （-1，0）．由22122++=+x x x ，可求得：1=±x ，所以点'C （1，4），点'C 关于x 轴的对称点为C （1，-4）．那么所求的抛物线顶点为C （1，-4）且经过点A （-1，0），可求得：2(1)4=--y x 即223=--y x x ．【总结】本题考查了“梦之星”抛物线和“梦之星”直线的定义，以及二次函数的图像与性质求解函数的解析式．【作业4】（2013学年·徐汇区二模·第17题）如图，我们把一个半圆与抛物线的一部分围成的封闭图形称为“果圆”．已知点A 、B 、C 、D 分别是“果圆”与坐标轴的交点，抛物线的解析式为223y x x =--，AB 为半圆的直径，则这个“果圆”被y 轴截得的弦16 / 17ABC D E F GHCD 的长为__________．【答案】33+【解析】抛物线223y x x =--与x 轴交点为A （-1，0）、B （3，0），与y 轴交点为D （0，-3）．半圆圆心为E （1，0）， ∴CE =2，勾股定理，得：OC 3=CD 33 【总结】本题考查了二次函数的图像以及圆的基本性质．【作业5】（2014学年·杨浦区二模·第17题）对于平面直角坐标系 xOy 中的点P （a ，b ），若点'P 的坐标为（ba k+，ka b +）（其中k 为常数，且0k ≠），则称点'P 为点P 的“k属派生点”．例如：P （1，4）的“2属派生点”为'P （412+，214⨯+），即'P （3，6）．若点P 的“k 属派生点”'P 的坐标为（3，3），请写出一个符合条件的点P 的坐标：____________．【答案】（2，1）．【解析】由题意得33⎧+⎪=⎨⎪+=⎩b a k ka b ，整理得：33+=⎧⎨+=⎩ka b k ka b ，所以1=k ，只要满足3+=a b 即可，可取点P （2，1）．【总结】本题考查了“派生点”的定义，关键是求出k 的值，答案不唯一．【作业6】如图，正方形ABCD 的边长为1，以对角线AC 为边作第二个正方形ACEF ，再以对角线AE 为边作第三个正方形AEGH ，…，如此下去，第n 个正方形的边长为__________． 12-n ．【解析】第一个正方形的边长为1第三个正方形的边长为2，依次规律，第n1 ．【总结】本题考查了几何图形背景下线段长度上存在的规律．。

沪科版九年级上册第9-10周培优资料 - -

九年级上册数学培优(第9-10周)比例的基本性质一、1.比例性质：（1）基本性质⇔=dcb a （2）合比性质 ⇔=dc ba（3）等比性质⇒∙∙∙===nn b a b a b a b a 332211 2.若线段c b a ,,之间有c b b a ::=，那么b 叫做线段c a ,的，得等式为3.黄金分割比例：练习1.如果的值求且k c b a k acb bc a c ,0,b a ≠++=+=+=+2.如果的值。

求k k ac bc b a b a c ,=+=+=+ 3.=-+≠==yzy x z y x 则若,0542 4.=-+=-+=-+c b a ba c a cbc b a 2::4,342求已知5.已知5===f e c d b a ，则的值fd b ec a 4242+-+-为 6.在比例尺为1:40000的工程示意图上，南宁地铁一号线长度约为54.5cm 。

则它的实际长度约为 km 。

7. 若等于的比例中项，则和是且c b c a b b a :,3:4:= 8.已知线段AB=1，点C 是线段AB 的黄金分割点，则AC •BC=平行线分线段成比例定理一、 1.定理如图，1l ∥2l ∥3l ,则有：=BC AB =ABBC =AC AB =AC BCDFACDEAB==2.推论：平行于三角形一边的直线截其他两边所得的对应线段成比例。

如图：DE ∥BC ，ACBDAE AD ==⇒“A ”字型 “X ”字型第3页第4页二、练习1.如图，AB=a ,BC=b, DF=a ,则DE=的长。

求：，于交的中点，是，于中，如图，在AF cm DC cm BD cm AB F AB BC EF BC E D BC AD ABC ,4,6,8.7===⊥⊥∆8. 如图，在△ABC 中，DE ∥BC,EF ∥CD,求证：AD 是AB 和AF 的比例中项。

9.如图，E 为正方形ABCD 的BC 边延长线上一点，AE 交CD 于F ，FN ∥AD 交DE 于N ，EDENBE CE =求证：10.已知D ，E 为BC 上两点，分别过点D ，E 作AB ，AC 的平行线，它们相交于点F ，连接AF ，并延长交BC 于点G ,求证：EGCEDG BD =.。

沪科版九年级下学期中考数学培优拔高强化训练(较难)含答案

沪科版九年级数学培优拔高强化训练（较难）一、选择题（本大题共10小题，共40.0分）1、当1≤x≤2时，ax+2>0，则a的取值范围是()A. a>−1B. a>−2C. a>0D. a>−1且a≠02、如图，已知关于x的函数y=k(x−1)和y=kx(k≠0)，它们在同一坐标系内的图象大致是() A. B. C. D.3、一次函数y=43x−b与y=43x−1的图象之间的距离等于3，则b的值为()A. −2或4B. 2或−4C. 4或−6D. −4或64、如图，AB为半圆O的直径，AD、BC分别切⊙O于A，B两点，CD切⊙O于点E，连接OD、OC，下列结论：①∠DOC=90°，②AD+BC=CD，③S△AOD：S△BOC=AD2：AO2，④OD：OC=DE：OE，⑤OD2= DE⋅CD，正确的有()A. 2个B. 3个C. 4个D. 5个第4题图5、如图，抛物线y=ax2+bx+c(a≠0)的对称轴为x=−1，与x轴的一个交点在(−3,0)和(−2,0)之间，其部分图象如图所示，则下列结论：第5题图第6题图①b2−4ac>0 ②2a=b③点(−72,y1)、(−32,y2)、(54,y3)是该抛物线上的点，则y1<y2<y3④3b+2c<0⑤t(at+b)≤a−b(t为任意实数) 其中正确结论的个数是()A. 2B. 3C. 4D. 56、如图，P为反比例函数y=kx(k>0)在第一象限内图象上的一点，过点P分别作x轴，y轴的垂线交一次函数y=−x−4的图象于点A、B.若∠AOB=135°，则k的值是()A. 2B. 4C. 6D. 87、如果函数y=2x2−3ax+1，在自变量x的值满足1≤x≤3的情况下，与其对应的函数值y的最小值为−23，则a的值为()A. 263B. 3√2 C. 8√33或143D. 1438、如图，在矩形纸片ABCD中，AB=4，BC=6，点E是BC的中点，连接AE，将△ABE沿AE折叠，点B落在点F处，则cos∠DAF=()A. 45B. 1213C. 724D. 24259、如图，在菱形ABCD中，tan∠ABC=43，P为AB上一点，以PB为边向外作菱形PMNB，连结DM，取DM中点E，连结AE，PE，则AEPE的值为()A. 23B. √33C. 12D. 3410、如图，P是正方形ABCD内一点，∠APB=135°，BP=1，AP=√7，则PC的值()A. √5B. 3C. 2√2D. 2二、填空题（本大题共4小题，共20.0分）11如图，函数y =1x (x >0)和y =3x (x >0)的图象分别是l 1和l 2.设点P 在l 2上，PA//y 轴，交l 1于点A ，PB//x 轴，交l 1于点B ，则△PAB 的面积为______ ．12、如图，正方形ABCD 中，BE =EF =FC ，CG =2GD ，BG 分别交AE ，AF 于M ，N.下列结论：①AF ⊥BG ；②BN =43NF ；③BMMG =38；④S 四边形CGNF =12S 四边形ANGD .其中正确的结论的序号是______．13、如图，在矩形ABCD 中，将∠ABC 绕点A 按逆时针方向旋转一定角度后，BC 的对应边交CD 边于点G.连接、若AD =7，CG =4，，则=''B BC C (结果保留根号)．14、如图，边长为10的等边三角形ABC 中，E 是对称轴AD 上的一个动点，连接EC ，将线段EC 绕点C 逆时针旋转60°得到FC ，连接DF.则在点E 运动过程中，DF 的最小值是．三、计算题（本大题共1小题，共4分）15、计算|tan60°−tan45°|+√cos230°−2 cos30°+1 ．四、解答题（本大题共8小题，共86分）16、（10分）如图，某人在山坡坡脚A处测得电视塔尖点C的仰角为60°，沿山坡向上走到P处再测得点C的仰角为45°，已知OA=200米，山坡坡度i=1：2，且O、A、B在同一条直线上．(1)求电视塔OC的高度；(2)求此人所在位置点P的铅直高度PB.(测倾器高度忽略不计，结果保留根号形式)17、（10分）如图，在平面直角坐标系中，△ABC的三个顶点坐标分别为A(2,1)，B(1,−2)，C(3,−1)，P(m,n)是△ABC的边AB上一点．(1)画出△A1B1C1，使△A1B1C1与△ABC关于点O成中心对称，并写出点A、P的对应点A1、P1的坐标；(2)以原点O为位似中心，位似比为1:2，在y轴的左侧，画出将△A1B1C1放大后的△A2B2C2，并分别写出点A1、P1的对应点A2、P2的坐标；(3)求sin∠B2A2C2的值．18、（10分）如图，在平面直角坐标系中，正方形OABC的顶点O与坐标原点重合，点C的坐标为(0,3)，点A在x轴的负半轴上，点D、M分别在边AB、OA上，且AD=2DB，AM=2MO，一次函数y=kx+b的的图象经过点D，与BC的交点为N．图象过点D和M，反比例函数y=mx(1)求反比例函数和一次函数的表达式；(2)若点P在直线DM上，且使△OPM的面积与四边形OMNC的面积相等，求点P的坐标．19、（10分）如图，直角△ABC中，∠BAC=90°，D在BC上，连接AD，作BF⊥AD分别交AD于E，AC 于F．(1)如图1，若BD=BA，求证：△ABE≌△DBE；(2)如图2，若BD=4DC，取AB的中点G，连接CG交AD于M，求证：①GM=2MC；②AG2=AF⋅AC．20、（10分）如图，AB是⊙O的直径，C为⊙O上一点，经过点C的直线与AB的延长线交于点D，连接AC，BC，∠BCD=∠CAB.E是⊙O上一点，弧CB=弧CE，连接AE并延长与DC的延长线交于点F．(1)求证：DC是⊙O的切线；(2)若⊙O的半径为3，sinD=3，求线段AF的长．521、（12分）农经公司以30元/千克的价格收购一批农产品进行销售，为了得到日销售量p(千克)与销售价格x(元/千克)之间的关系，经过市场调查获得部分数据如下表：销售价格x(元/千克) 30 35 40 45 50日销售量p(千克) 600 450 300 150 0(1)x之间的函数表达式；(2)农经公司应该如何确定这批农产品的销售价格，才能使日销售利润最大？(3)若农经公司每销售1千克这种农产品需支出a元(a>0)的相关费用，当40≤x≤45时，农经公司的日获利的最大值为2430元，求a的值．(日获利=日销售利润−日支出费用)22、（12分）将一副三角尺如图拼接：含30°角的三角尺(△ABC)的长直角边与含45°角的三角尺(△ACD)的斜边恰好重合．已知AB=2√3，P是AC上的一个动点．(1)当点P运动到∠ABC的平分线上时，连接DP，求DP的长；(2)当点P在运动过程中出现PD=BC时，求此时∠PDA的度数；(3)当点P运动到什么位置时，以D，P，B，Q为顶点的平行四边形的顶点Q恰好在边BC上？求出此时▱DPBQ 的面积．23、（12分）如图，直线y=−23x+c与x轴交于点A(3,0)，与y轴交于点B，抛物线y=−43x2+bx+c经过点A，B．(1)求点B的坐标和抛物线的解析式；(2)M(m,0)为x轴上一动点，过点M且垂直于x轴的直线与直线AB及抛物线分别交于点P，N．①点M在线段OA上运动，若以B，P，N为顶点的三角形与△APM相似，求点M的坐标；②点M在x轴上自由运动，若三个点M，P，N中恰有一点是其它两点所连线段的中点(三点重合除外)，则称M，P，N三点为“共谐点”.请直接写出使得M，P，N三点成为“共谐点”的m的值．参考答案一、选择题（本大题共10小题，共40.0分）1-5ADDDC, 6-10 DDDCB二、填空题（本大题共4小题，共20.0分）11、23，12、①③，13、√745，14、2.5三、计算题（本大题共1小题，共4分）15、计算|tan60°−tan45°|+√cos230°−2 cos30°+1 ．解：原式=|tan60°−tan45°|+|cos30°−1|=tan60°−tan45°+1−cos30° =√3−1+1−√32=√32．四、解答题（本大题共7小题，共86分）16、（10分）解：(1)作PE⊥OB于点E，PF⊥CO于点F，在Rt△AOC中，AO=100，∠CAO=60°，∴CO=AO⋅tan60°=200√3(米)；(2)设PE=x米，∵tan∠PAB=PE，AE=PEAE =12，∴AE=2x．在Rt△PCF中，∠CPF=45°，CF=200√3−x，PF=OA+AE=200+2x，∵PF=CF，∴200+2x=200√3−x，解得x=200√3−2003．答：电视塔OC的高度是100√3米，所在位置点P的铅直高度是200√3−2003米．17（10分）(1)如图2，A1(−2,−1)，P1(−m,−n)；(2)如图2，A2(−4,−2)，P2(−2m,−2n)；(3)|B2A2|=2√10，|A2C2|=2√5，|C2B2|=2√5，等腰直角三角形B2A2C2,∠B2A2C2=45°，sin∠B2A2C2=sin45°=√22．18、（10分）解：(1)∵正方形OABC的顶点C(0,3)，∴OA=AB=BC=OC=3，∠OAB=∠B=∠BCO=90°，∵AD=2DB，∴AD=23AB=2，∴D(−3,2)，把D坐标代入y=mx得：m=−6，∴反比例解析式为y =−6x ，∵AM =2MO ，∴MO =13OA =1，即M(−1,0)，把M 与D 坐标代入y =kx +b 中得：{−k +b =0−3k +b =2，解得：k =b =−1，则直线DM 解析式为y =−x −1； (2)把y =3代入y =−6x 得：x =−2，∴N(−2,3)，即NC =2，设P(x,y)，∵△OPM 的面积与四边形OMNC 的面积相等， ∴12(OM +NC)⋅OC =12OM|y|，即|y|=9，解得：y =±9，当y =9时，x =−10，当y =−9时，x =8，则P 坐标为(−10,9)或(8,−9)． 19、（10分）证明：(1)在Rt △ABE 和Rt △DBE 中，{BA =BDBE =BE ，∴△ABE ≌△DBE ；(2)①过G 作GH//AD 交BC 于H ， ∵AG =BG ，∴BH =DH ，∵BD =4DC ，设DC =1，BD =4， ∴BH =DH =2，∵GH//AD ， ∴GM MC =HD DC=21，∴GM =2MC ； ②过C 作CN ⊥AC 交AD 的延长线于N ，则CN//AG ， ∴△AGM ∽△NCM ，∴AGNC =GMMC ，由①知GM =2MC ，∴2NC =AG ，∵∠BAC =∠AEB =90°， ∴∠ABF =∠CAN =90°−∠BAE ，∴△ACN ∽△BAF ， ∴AFCN =ABAC ，∵AB =2AG ，∴AFCN =2AG AC，∴2CN ⋅AG =AF ⋅AC ，∴AG 2=AF ⋅AC ．20、（10分）(1)证明：连接OC ，BC ， ∵AB 是⊙O 的直径，∴∠ACB =90°，即∠1+∠3=90°． ∵OA =OC ，∴∠1=∠2，∵∠DCB =∠BAC =∠1，∴∠DCB +∠3=90°， ∴OC ⊥DF ，∴DF 是⊙O 的切线；(2)解：在Rt △OCD 中，OC =3，sinD =35，∴OD =5，AD =8，∵ĈE =B ̂C ， ∴∠2=∠4，∴∠1=∠4，∴OC//AF ，∴△DOC ∽△DAF ， ∴OCAF =ODAD ，∴3AF=58，∴AF =245．21、（12分）解：(1)假设p 与x 成一次函数关系，设函数关系式为p =kx +b ，则{30k +b =60040k +b =300，解得：k =−30，b =1500，∴p =−30x +1500，检验：当x =35，p =450；当x =45，p =150；当x =50，p =0，符合一次函数解析式，∴所求的函数关系为p=−30x+1500；(2)设日销售利润w=p(x−30)=(−30x+1500)(x−30)即w=−30x2+2400x−45000，∴当x=−24002×(−30)=40时，w有最大值3000元，故这批农产品的销售价格定为40元，才能使日销售利润最大；(3)日获利w=p(x−30−a)=(−30x+1500)(x−30−a)，即w=−30x2+(2400+30a)x−(1500a+45000)，对称轴为x=−2400+30a2×(−30)=40+12a，①若a>10，则当x=45时，w有最大值，即w=2250−150a<2430(不合题意)；②若0<a<10，则当x=40+12a时，w有最大值，将x=40+12a代入，可得w=30(14a2−10a+100)，当w=2430时，2430=30(14a2−10a+100)，解得a1=2，a2=38(舍去)，综上所述，a的值为2．22、（12分）解：在Rt△ABC中，AB=2√3，∠BAC=30°，∴BC=√3，AC=3．(1)如图(1)，作DF⊥AC．∵Rt△ACD中，AD=CD，∴DF=AF=CF=32．∵BP平分∠ABC，∴∠PBA=30°，∵∠PBA=∠PAB=30°，∴PA=PB，设PA=x，PC=3−x，根据勾股定理：BC2+PC2=PB2，可以得出x=2，∴CP=1，∴PF=12，∴DP=√PF2+DF2=√102．(2)当P点位置如图(2)所示时，根据(1)中结论，DF =32，∠ADF =45°，又∵PD =BC =√3，∴PF =√PD 2−DF 2=√32，又∵在直角三角形中，较短的直角边与斜边之比为1：2，则较小的角为30°， ∴∠PDF =30°．∴∠PDA =∠ADF −∠PDF =15°．当P 点位置如图(3)所示时，同(2)可得∠PDF =30°．∴∠PDA =∠ADF +∠PDF =75°．故∠PDA 的度数为15°或75°；(3)当点P 运动到边AC 中点(如图4)，即CP =32时，以D ，P ，B ，Q 为顶点的平行四边形的顶点Q 恰好在边BC 上． ∵四边形DPBQ 为平行四边形，∴BC//DP ，∵∠ACB =90°，∴∠DPC =90°，即DP ⊥AC ．而在Rt △ABC 中，AB =2√3，BC =√3， ∴根据勾股定理得：AC =3，∵△DAC 为等腰直角三角形， ∴DP =CP =12AC =32，∵BC//DP ，∴PC 是平行四边形DPBQ 的高，∴S 平行四边形DPBQ =DP ⋅CP =94． 23、（12分）解：(1)∵y =−23x +c 与x 轴交于点A(3,0)，与y 轴交于点B ， ∴0=−2+c ，解得c =2，∴B(0,2)，∵抛物线y =−43x 2+bx +c 经过点A ，B ，∴{−12+3b +c =0c =2，解得{b =103c =2，∴抛物线解析式为y=−43x2+103x+2；(2)①由(1)可知直线解析式为y=−23x+2，∵M(m,0)为x轴上一动点，过点M且垂直于x轴的直线与直线AB及抛物线分别交于点P，N，∴P(m,−23m+2)，N(m,−43m2+103m+2)，∴PM=−23m+2，AM=3−m，PN=−43m2+103m+2−(−23m+2)=−43m2+4m，∵△BPN和△APM相似，且∠BPN=∠APM，∴∠BNP=∠AMP=90°或∠NBP=∠AMP=90°，当∠BNP=90°时，则有BN⊥MN，∴N点的纵坐标为2，∴−43m2+103m+2=2，解得m=0(舍去)或m=2.5，∴M(2.5,0)；当∠NBP=90°时，过点N作NC⊥y轴于点C，则∠NBC+∠BNC=90°，NC=m，BC=−43m2+103m+2−2=−43m2+103m，∵∠NBP=90°，∴∠NBC+∠ABO=90°，∴∠ABO=∠BNC，∴Rt△NCB∽Rt△BOA，∴NCOB =CBOA，∴m2=−43m2+103m3，解得m=0(舍去)或m=118，∴M(118,0)；综上可知当以B，P，N为顶点的三角形与△APM相似时，点M的坐标为(2.5,0)或(118,0)；②由①可知M(m,0)，P(m,−23m+2)，N(m,−43m2+103m+2)，∵M，P，N三点为“共谐点”，∴有P为线段MN的中点、M为线段PN的中点或N为线段PM的中点，当P为线段MN的中点时，则有2(−23m+2)=−43m2+103m+2，解得m=3(三点重合，舍去)或m=12；当M为线段PN的中点时，则有−23m+2+(−43m2+103m+2)=0，解得m=3(舍去)或m=−1；当N 为线段PM 的中点时，则有−23m +2=2(−43m 2+103m +2)，解得m =3(舍去)或m =−14；综上可知当M ，P ，N 三点成为“共谐点”时m 的值为12或−1或−14．。

1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

九年级数学综合培优讲义
1．如图，若将左图正方形剪成四块，恰能拼成右图的矩形，设a=1，则b=（）
A．B．C．D．
【解答】解：依题意得（a+b）2=b（b+a+b），
而a=1，
∴b2﹣b﹣1=0，
∴b=，而b不能为负，
∴b=．
故选B．
2．如图，已知⊙O是正方形ABCD的外接圆，点E是弧AD上任意一点，则∠BEC 的度数为（）
A．30°B．45°C．60°D．90°
【解答】解：连接OB，OC，
∵⊙O是正方形ABCD的外接圆，
∴∠BOC=90°，
∴∠BEC=∠BOC=45°．
故选B．
3．已知：如图，在半径为4的⊙O中，AB，CD是两条直径，M为OB的中点，CM的延长线交⊙O于点E，且EM＞MC，连接DE，DE=．
（1）求证：AM•MB=EM•MC；
（2）求EM的长．
【解答】证明：（1）∵AB、CE是⊙O内的两条相交弦，
∴AM•MB=EM•MC；
（2）∵M是OB中点，圆半径R=4，
∴OM=MB=2，
∴AM=6，
∵CD是直径，
∴∠CED=90°，
∴CE2=CD2﹣DE2，
∴CE==7，
设EM=x，6×2=x•（7﹣x），
解得x=3或x=4，
∵EM＞MC，
∴EM=4．
4．农民购买农机设备政府会给予一定额度的补贴，其中购买Ⅰ、Ⅱ型农机设备的金额与政府补贴的金额存在表所示的函数对应关系：
（1）分别求出y 1和y 2的函数解析式；（2）张大伯打算共用10万元购买Ⅰ、Ⅱ两型农机设备．请你帮助张大伯设计一个能获得最大补贴金额的方案，并求出按此方案能获得的最大补贴金额．
【解答】解：（1）由题意可得，
0.4=1×k ，得k=0.4，
即y 1与x 的函数关系式为y 1=0.4x ，
，解得，，
即y 2
与x 的函数关系式为y 2=；
（2）设购买Ⅱ型农机设备投资t 万元，购买Ⅰ型农机设备投资（10﹣t ）万元，共获补贴Q 万元，
Q=y 1+y 2=0.4（10﹣t ）﹣=，
∴当t=3时，Q 取得最大值，此时Q=
，10﹣t=10﹣3=7，答：投资7万元购买Ⅰ型农机设备，投资3万元购买Ⅱ型农机设备，共获最大补贴万元．
5、如图，为了测量出楼房AC 的高度，从距离楼底C 处603米的点D(点D 与楼底C 在同一水平面上)出发，沿斜面坡度为i ＝1∶3的斜坡DB 前进30米到达点B ，在点B 处测得楼顶A 的仰角为53°，求楼房AC 的高度．(参考数据：sin 53°≈0.8，cos 53°≈0.6，tan 53°
≈43
，计算结果用根号表示，不取近似值)
解：如图作BN ⊥CD 于N ，BM ⊥AC 于M.在Rt △BDN 中，BD ＝30，BN ∶ND ＝1∶3，∴BN ＝15，DN ＝153，∵∠C ＝∠CMB ＝∠CNB ＝90°，∴四边形CMBN 是矩形，∴CM ＝BN ＝15，
BM ＝CN ＝603－153＝453，在Rt △ABM 中，tan ∠ABM ＝AM BM ＝43
，∴AM ＝603，∴AC ＝AM ＋CM ＝15＋60 3
6．AB 是⊙O 的直径，点E 是半圆上一动点（点E 与点A 、B 都不重合），点C 是BE 延长线上的一点，且CD ⊥AB ，垂足为D ，CD 与AE 交于点H ，点H 与点A 不重合．
（1）求证：△AHD ∽△CBD ；
（2）连HO ，若CD=AB=2，求HD +HO 的值．
【解答】（1）证明：AB 是⊙O 的直径
∴∠AEB=90°，则∠ABC +∠BAE=90°，
又∵CD ⊥AB ，
∴∠BAE +∠AHD=90°，
∴∠AHD=∠ABC ，
又∵∠ADH=∠CDB=90°，
∴△AHD ∽△CBD ．
（2）解：设OD=x，则BD=1﹣x，AD=1+x，
∵Rt△AHD∽Rt△CBD，
则HD：BD=AD：CD，
即HD：（1﹣x）=（1+x）：2，
即HD=，
在Rt△HOD中，由勾股定理得：
OH==，
所以HD+HO=+=1；
②当点E移动到使D与O重合的位置时，这时HD与HO重合，由Rt△AHO∽Rt △CBO，利用对应边的比例式为方程，可以算出HD=HO=，即HD+HO=1；
③当D在OA段时BD=1+x，AD=1﹣x，证明同①∵Rt△AHD∽Rt△CBD，
则HD：BD=AD：CD，
即HD：（1﹣x）=（1+x）：2，
即HD=，
在Rt△HOD中，由勾股定理得：
OH==，
所以HD+HO=+=1．
7、如图，⊙O是△ABC的外接圆，AD是⊙O的直径，AD与BC相交于点M，且BM=MC，过点D作BC的平行线，分别与AB、AC的延长线相交于点E、F．（1）求证：EF与⊙O相切；
（2）若BC=2，MD=，求CE的长．
【解答】（1）证明：∵AD是⊙O的直径，AD与BC相交于点M，且BM=MC，∴AD⊥BC，
∵EF∥BC，
∴AD⊥EF，
∴EF与⊙O相切；
（2）解：连接OB，
在△OBM中，BM2+OM2=OB，即（）+（OB﹣）=OB2，OB=2
∴OM=MD=，
∵BC∥EF，
∴△ABC∽△AEF
∴=，
∴EF===，
∵tan∠CAM===，
∴∠CAM=30°，
作CN⊥EF，
∵AD⊥EF，
∴CN∥AD，
∴∠FCN=∠CAM=30°，
∵BC∥EF，
∴四边形MDNC是矩形，
∴CN=MD=，
∴NF=CN•tan30°=×=，
∴EN=EF﹣NF=﹣=，
∴EC==．
8、我们知道，三角形三个内角平分线的交点叫做三角形的内心，已知点I为△ABC的内心．
（1）如图1，连接AI并延长交BC于点D，若AB=AC=3，BC=2，求ID的长；（2）如图2，过点I作直线交AB于点M，交AC于点N．
①若MN⊥AI，求证：MI2=BM•CN；
②如图3，AI交BC于点D，若∠BAC=60°，AI=4，求+的值．
【解答】解：（1）如图1中，作IE⊥AB于E．设ID=x．
∵AB=AC=3，AI平分∠BAC，
∴AD⊥BC，BD=CD=1，
在Rt△ABD中，AD===2，
∵∠EBI=∠DBI，∠BEI=∠BDI=90°，BI=BI，
∴△BEI≌△BDI，
∴ID=IE=x，BD=BE=1，AE=2，
在Rt△AEI中，∵AE2+EI2=AI2，
∴22+x2=（2﹣x）2，
∴x=，
∴ID=．
（2）如图2中，连接BI、CI．
∵I是内心，
∴∠MAI=∠NAI，
∵AI⊥MN，
∴∠AIM=∠AIN=90°，
∵AI=AI，
∴△AMI≌△ANI（ASA），
∴∠AMN=∠ANM，
∴∠BMI=∠CNI，
设∠BAI=∠CAI=α，∠ACI=∠BCI=β，∴∠NIC=90°﹣α﹣β，
∵∠ABC=180°﹣2α﹣2β，
∴∠MBI=90°﹣α﹣β，
∴∠MBI=∠NIC，
∴△BMI∽△INC，
∴=，
∴NI2=BM•CN，
∵NI=MI，
∴MI2=BM•CN．
（3）过点N作NG∥AD交MA的延长线于G．
∴∠ANG=∠AGN=30°，
∴AN=AG，NG=AN，
∵AI∥NG，
∴=，
∴=，
∴+=．。