相对论的速度变换公式质能方程.
高中物理选修3-4第六章学案2 习题 课后作业,有详细解答

学案2 相对论的速度变换公式 质能关系 广义相对论点滴(选学)[学习目标定位] 1.知道相对论速度变换公式、相对论质量和质能方程.2.了解广义相对论的基本原理.3.初步了解广义相对论的几个主要观点以及主要观测证据.回旋加速器的工作原理:带电粒子在匀强磁场中做匀速圆周运动,周期T =2πm qB ,因粒子的q不变、质量不变,所以周期T 不变,与轨道半径和速度无关;使高频交变电场的周期和粒子运动周期相同,就会使粒子每次经过电场时都会被加速,动能一次次增大,获得的最大速度v max =RBq m.1.相对论的速度变换公式设高速行驶的火车相对地面的速度为u ,车上的人以速度v ′沿火车运动的方向相对火车运动,那么人相对地面的速度为v =u +v ′1+u v ′c 2,若车上人的运动方向与火车的运动方向相反,则v ′取负值;若v ′=c ,则代入上式得出v =c ,即光速是宇宙速度的极限,且相对任何参考系,光速都是不变的.2.相对论的质量:物体的质量随物体速度的增加而增大. 物体以速度v 运动时的质量m 与静止时的质量m 0之间的关系是:m =m 01-v 2c2.因为总有v <c ,所以运动物体的质量m 总要大于它静止时的质量m 0.3.物体的质量m 与其蕴含的能量E 之间的关系是:E =mc 2.由此可见,物体质量越大,其蕴含的能量越多.能量与质量成正比,所以质能方程又可写成ΔE =Δmc 2. 4.广义相对论的两个基本原理 (1)广义相对性原理在任何参考系中物理规律都是一样的. (2)等效原理一个不受引力作用的加速度系统跟一个受引力作用的惯性系统是等效的.一、相对论的速度变换[问题设计]一列火车正以v =50m /s 的速度高速行驶,列车内一乘客以相对列车u ′=5 m/s 的速度向前跑,站台上的观察者测得该乘客的速度是u =v +u ′=55m/s.若列车的速度是0.9c ,乘客的速度是0.5c ,那么站台上的观察者测得该乘客的速度是0.9c +0.5c =1.4c 吗? 答案 不是. [要点提炼]1.公式:设高速行驶的火车对地面的速度为v ,车上的人相对火车以速度u ′运动,那么人相对地面的速度为u .⎩⎪⎨⎪⎧u =u ′+v1+u ′v c2(人相对于车的运动方向与车同向).u =-u ′+v 1-u ′v c2(人相对于车的运动方向与车反向).2.对公式的理解假设高速火车对地面的速度为v ,车上的一高速粒子以速度u ′沿火车前进的方向相对火车运动,那么此粒子相对于地面的速度u 为u =u ′+v1+u ′v c 2.(1)若粒子运动方向与火车运动方向相反,则u ′取负值.(2)如果v ≪c ,u ′≪c 时,u ′vc 2可忽略不计,这时相对论的速度变换公式可近似为u =u ′+v .(3)若u ′=c ,v =c ,则u =c ,表明一切物体的速度都不能超过光速.(4)该变换公式只适用于同一直线上匀速运动速度的变换,对于更复杂的情况不适用. (5)光速c 是宇宙速度的极限,且相对任何参考系,光速都是不变的. 二、相对论质量和能量 [问题设计]回旋加速器中磁场一次次把粒子拉到狭缝处,狭缝处的电场一次次加速带电粒子.假如回旋加速器的半径可以增大到很大,磁感应强度足够大,经回旋加速器加速的粒子的速度可以达到任意速度甚至超过光速吗? 答案 不可以超过光速.因为回旋加速器的理论基础是粒子在磁场中做圆周运动的周期(T =2πmqB )等于交变电场的周期;速度较小时粒子的质量m 可以认为不变,周期T 不变,电场变化与粒子圆周运动同步,但速度较大时,质量增大明显,粒子做圆周运动的周期T 变大,无法做到圆周运动的周期与高频电压的周期同步. [要点提炼]1.相对论质量(1)经典力学:物体的质量是不变的,一定的力作用在物体上产生一定的加速度,经过足够长时间后物体可以达到任意的速度.(2)相对论:物体的质量随物体速度的增加而增大.①物体以速度v 运动时的质量m 与静止时的质量m 0之间的关系是:m =m 01-(v c )2. ②因为总有v <c ,所以运动物体的质量m 总要大于它静止时的质量m 0,但当v ≪c 时,m ≈m 0,所以低速运动的物体,可认为其质量与运动速度无关. ③微观粒子的速度很大,因此粒子质量明显大于静质量. 2.质能方程关系式:E =mc 2,式中m 是物体的质量,E 是它具有的能量. [延伸思考]有人根据E =mc 2得出结论:质量可以转化为能量,能量可以转化为质量,这种说法对吗? 答案 不对.E =mc 2表明质量与能量之间存在一一对应的关系,物体吸收或放出能量,则对应的质量会增加或减少,质量与能量并没有相互转化.对于一个封闭的系统,质量是守恒的,能量也是守恒的. 三、广义相对论点滴 [问题设计]1.在一个全封闭的宇宙飞船中,若飞船静止,宇航员将一小球自由释放,小球将怎样运动?假如没有引力场,飞船加速上升,宇航员将小球自由释放,小球相对飞船会怎样运动? 答案 小球都是以某一加速度落向舱底.2.宇航员能否根据“小球的加速下落”判断飞船是静止在一个引力场中,还是正处在一个没有引力场而正加速上升的过程中? 答案 不能. [要点提炼]1.广义相对论的基本原理(1)广义相对性原理:在任何参考系中物理规律都是一样的.(2)等效原理:一个不受引力作用的加速度系统跟一个受引力作用的惯性系统是等效的. 2.广义相对论的几个结论 (1)光线在引力场中弯曲.(2)引力场的存在使得空间不同位置的时间进程出现差别(引力红移).一、相对论速度变换公式例1 一粒子以0.05c 的速率相对实验室参考系运动.此粒子衰变时发射一个电子,电子相对于粒子的速度为0.8c ,电子的衰变方向与粒子运动方向相同.求电子相对于实验室参考系的速度.解析 已知u =0.05c ,v x ′=0.8c . 由相对论速度变换公式得v x =v x ′+u 1+v x ′u c2=(v x ′+u )c 2c 2+v x ′u ,v x =(0.8c +0.05c )c 2c 2+0.8c ×0.05c ≈0.817c .答案 0.817c二、对质能方程的理解例2 下列关于爱因斯坦质能方程的说法中,正确的是( ) A .只有运动的物体才具有质能,静止的物体没有质能 B .一定的质量总是和一定的能量相对应 C .E =mc 2中能量E 其实就是物体的内能 D .由ΔE =Δmc 2知质量与能量可以相互转化解析 E =mc 2表明质量与能量之间存在一一对应的关系,物体吸收或放出能量,则对应的质量会增加或减少,质量与能量并没有相互转化.故选项B 正确,D 错误;静止的物体也具有能量,称为静质能E 0,E 0=m 0c 2,m 0叫做静质量;E =mc 2中的能量E 包括静质能E 0和动能E k ,而非物体的内能,故选项A 、C 错误. 答案 B三、广义相对论的几个结论例3 在日全食的时候,通过仪器可以观察到太阳后面的恒星,这说明星体发出的光( ) A .经太阳时发生了衍射 B .可以穿透太阳及其他障碍物 C .在太阳引力场作用下发生了弯曲 D .经过太阳外的大气层时发生了折射解析 根据爱因斯坦的广义相对论可知,光线在太阳引力场作用下发生了弯曲,所以可以在适当的时候(如日全食时)通过仪器观察到太阳后面的恒星,故C 正确,A 、B 、D 均错. 答案 C1.(相对论速度变换公式)在高速运动的火车上,设车对地面的速度为v ,车上的人以速度u ′沿着火车前进的方向相对火车运动,那么他相对地面的速度u 与u ′+v 的关系是( ) A .u =u ′+v B .u <u ′+v C .u >u ′+v D .以上均不正确 答案 B解析 由相对论速度变换公式可知B 正确.2.(对质能方程的理解)关于物体的质量,下列说法正确的是( ) A .在牛顿力学中,物体的质量是保持不变的B .在牛顿力学中,物体的质量随物体的速度变化而变化C .在相对论力学中,物体静止时的质量最小D .在相对论力学中,物体的质量随物体速度的增大而增大 答案 ACD解析 在牛顿力学中,物体的质量是保持不变的,故选项A 正确,B 错误;在相对论力学中,由于物体的速度v 不可能达到光速c ,所以v <c,1-(v c )2<1,根据m =m 01-(v c )2,可知选项C 、D 均正确.3.(广义相对论的几个结论)在引力可以忽略的空间有一艘宇宙飞船在做匀加速直线运动,一束光垂直于飞船的运动方向在飞船内传播,下列说法中正确的是( ) A .船外静止的观察者看到这束光是沿直线传播的 B .船外静止的观察者看到这束光是沿曲线传播的 C .航天员以飞船为参考系看到这束光是沿直线传播的 D .航天员以飞船为参考系看到这束光是沿曲线传播的答案 AD题组一 相对论速度变换公式1.设想有一艘飞船以v =0.8c 的速度在地球上空飞行,如果这时从飞船上沿其运动方向抛出一物体,该物体相对于飞船的速度为0.9c ,从地面上的人看来,物体的速度为( ) A .1.7c B .0.1c C .0.99c D .无法确定 答案 C解析 根据相对论速度变换公式得u =0.8c +0.9c1+0.8c ×0.9c c 2≈0.99c .2.火箭以35c 的速度飞离地球,在火箭上向地球发射一束高能粒子,粒子相对地球的速度为45c ,其运动方向与火箭的运动方向相反.则粒子相对火箭的速度大小为( )A.75cB.c 5C.3537cD.5c 13 答案 C解析 由相对论的速度变换公式得-45c =35c +u ′1+35cu ′c 2解得u ′=-3537c ,负号说明与v 方向相反.3.地球上一观察者,看见一飞船A 以速度2.5×108m /s 从他身边飞过,另一飞船B 以速度2.0×108 m/s 跟随A 飞行.求:(1)A 上的乘客看到B 的相对速度; (2)B 上的乘客看到A 的相对速度. 答案 (1)-1.125×108m /s (2)1.125×108 m/s解析 (1)A 上的乘客看地面上的人以-2.5×108m/s 向后运动.地面上的人看B 以2.0×108m/s 向前运动,则A 上的乘客看到B 的相对速度为u =-2.5+2.01+-2.5×2.032×108m /s =-1.125×108 m/s.(2)B 上的乘客看到A 的相对速度为1.125×108m/s. 题组二 相对论质量和质能方程4.一个物体静止时质量为m 0、能量为E 0.速度为v 时,质量为m 、能量为E 、动能为E k .下列说法正确的是( )A .物体速度为v 时的能量E =mc 2B .物体速度为v 时的动能E k =12mc 2C .物体速度为v 时的动能E k =12m v 2D .物体速度为v 时的动能E k =(m -m 0)c 2 答案 AD5.已知电子的静止能量为0.511MeV ,若电子的动能为0.25MeV ,则它所增加的质量Δm 与静止质量m 0的比值近似为( ) A .0.1B .0.2C .0.5D .0.9 答案 C解析 设电子运动时的速度为v 由题意知E 0=m 0c 2=0.511MeV ①电子运动时的能量E =E 0+E k =0.761MeV ② 又因为E =mc 2③m =m 01-v 2c 2④将④代入③得E =m 0c 21-v 2c2=E 01-v 2c2⑤由④⑤可知m m 0=EE 0所以Δm m 0=m -m 0m 0=E -E 0E 0=0.761MeV -0.511MeV 0.511MeV≈0.5,故选项C 正确.6.一核弹含20kg 的钚,爆炸后生成的核静止质量比原来小110000.求爆炸中释放的能量.答案 1.8×1014J解析 爆炸前后质量变化为:Δm =110000×20kg =0.002kg ,释放的能量为ΔE =Δmc 2=0.002×(3×108)2J =1.8×1014J.7.太阳在不断地向外辐射能量,因而其质量也在不断地减小.若太阳每秒钟辐射的总能量为4×1026J ,试计算太阳在1s 内失去的质量.估算太阳在5000年内总共减少了多少质量,并与太阳的总质量2×1027t 相比较. 答案 见解析解析 由太阳每秒钟辐射的能量ΔE 可得其在1s 内失去的质量为Δm =ΔE c 2=4×1026(3×108)2kg ≈4.44×109kg5000年内太阳总共减少的质量为Δm =5000×365×24×3600×4.44×109kg ≈7×1020kg ,与总质量相比ΔM M =7×10202×1027×103=3.5×10-10,比值较小. 题组三 广义相对论的几个结论8.关于狭义相对论、广义相对论的认识,下列说法正确的是( ) A .万有引力可以用狭义相对论做出正确的解释B.电磁力可以用狭义相对论做出正确的解释C.狭义相对论是惯性参考系之间的理论D.万有引力理论无法纳入狭义相对论的框架E.由ΔE=Δmc2知质量和能量可以相互转化答案BCD9.下列说法中正确的是()A.物质的引力使光线弯曲B.光线弯曲的原因是介质不均匀而非引力作用C.在强引力的星球附近,时间进程会变慢D.广义相对论可以解释引力红移现象答案ACD解析根据广义相对论的结论可知,选项A、C、D正确,B错误.10.下列说法中,正确的是()A.由于太阳引力场的影响,我们有可能看到太阳后面的恒星B.强引力作用可使光谱线向红端偏移C.引力场越强的位置,时间进程越快D.由于物质的存在,实际的空间是弯曲的答案ABD解析由广义相对论我们可知:物质的引力使光线弯曲,因此选项A、D是正确的.在引力场中时间进程变慢,而且引力越强,时间进程越慢,因此我们能观察到引力红移现象,所以选项B正确,C错误.11.以下说法中正确的是()A.白矮星表面的引力很强B.在引力场弱的地方时钟走得比引力场强的地方快些C.引力场越弱的地方,物体的长度越短D.在引力场强的地方,光谱线向绿端偏移答案AB。
狭义相对论力的变换公式的简单推导

狭义相对论力的变换公式的简单推导狭义相对论中的公式推导:一、洛仑兹坐标变换:X=γ(x-ut);Y=y;Z=z;T=γ(t-ux/c^2)。
1、设(x,y,z,t)所在坐标系(A系)静止,(X,Y,Z,T)所在坐标系(B系)速度为u,且沿x轴正向。
在A系原点处,x=0,B系中A 原点的坐标为X=-uT,即X+uT=0。
2、可令x=k(X+uT) (1)。
又因在惯性系内的各点位置是等价的,因此k是与u有关的常数(广义相对论中,由于时空弯曲,各点不再等价,因此k不再是常数。
)同理,B系中的原点处有X=K(x-ut),由相对性原理知,两个惯性系等价,除速度反向外,两式应取相同的形式,即k=K。
3、故有X=k(x-ut) (2)。
对于y,z,Y,Z皆与速度无关,可得Y=y (3)。
4、Z=z (4)。
将(2)代入(1)可得:x=k^2(x-ut)+kuT,即T=kt+((1-k^2)/(ku))x (5)。
5、(1)(2)(3)(4)(5)满足相对性原理,要确定k需用光速不变原理。
当两系的原点重合时由重合点发出一光信号,则对两系分别有x=ct,X=cT。
6、代入(1)(2)式得:ct=kT(c+u),cT=kt(c-u).两式相乘消去t 和T得:k=1/sqr(1-u^2/c^2)=γ。
将γ反代入(2)(5)式得坐标变换:X=γ(x-ut);Y=y;Z=z;T=γ(t-ux/c^2)。
狭义相对论力的变换公式的简单推导二、速度变换:V(x)=(v(x)-u)/(1-v(x)u/c^2);V(y)=v(y)/(γ(1-v(x)u/c^2));V(z)=v(z)/(γ(1-v(x)u/c^2))。
1、V(x)=dX/dT=γ(dx-ut)/(γ(dt-udx/c^2))=(dx/dt-u)/(1-(dx/dt)u/c^2)=(v(x)-u)/(1-v(x)u/c ^2)。
2、同理可得V(y),V(z)的表达式。
物理人教版高二选修3-4教材梳理_第十五章_3.狭义相对论的其他结论4.广义相对论简介_word版含解析

疱丁巧解牛知识·巧学一、狭义相对论的其他结论 1.相对论速度变换公式以高速火车为例,车对地的速度为v ,车上的人以u′的速度沿火车前进的方向相对火车运动,则人对地的速度u=2'1'cv u vu ++,若人相对火车反方向运动,u′取负值. 根据此式若u′=c ,则u=c ,那么c 在任何惯性系中都是相同的.深化升华 (1)当u′=c 时,不论v 有多大,总有u=c ,这表明,从不同参考系中观察,光速都是相同的,这与相对论的第二个假设光速不变原理相一致.(2)对于速度远小于光速的情形,v<<c ,u′<<c ,这时2'cvu 可以忽略不计,相对论的速度合成公式可以近似变为u=u′+v.联想发散 相对论并没有推翻牛顿力学,也不能说牛顿力学已经过时了,相对论是使牛顿力学的使用范围变得清楚了. 2.相对论质量以速度v 高速运动的物体的质量m 和静止时的质量m 0.有如下关系:m=20)(1cv m -.质量公式实际上是质量和速度的关系,在关系m=20)(1cv m -中,若v=c ,则m 可能是无限大,这是不可能的,尤其是宏观物体,设想物体由v=0逐渐向c 靠拢,m 要逐渐变大,产生加速度的力则要很大,所以能量也要很大.因此,宏观物体的速度是不可能(在目前)增大到与光速相比.但是对于一些没有静止质量的粒子(如光子),它却可以有动质量m.深化升华 (1)物体的质量随速度的增大而增大;(2)物体运动的质量总要大于静止质量. 误区警示 不要盲目从公式中得出,v=c 时,质量是无穷大的错误结论. 3.质能方程(1)爱因斯坦方程:E=mc 2.(2)质能方程表达了物体的质量和它所具有的能量的关系:一定的质量总是和一定的能量相对应. (3)对一个以速率v 运动的物体,其总能量为动能与静质能之和:E=E k +E 0.那么物体运动时的能量E 和静止时能量E 0的差就是物体的动能,即E k =E-E 0. 代入质量关系:E k =E-E 0=220)(1cv c m --m 0c 2=21m 0v 2. 误区警示 不能把质量和能量混为一谈,不能认为质量消灭了,只剩下能量在转化,更不能认为质量和能量可以相互转变,在一切过程中,质量和能量是分别守恒的,只有在微观粒子的裂变和聚变过程中有质量亏损的情况下才会有质能方程的应用. 二、广义相对论简介1.广义相对性原理和等效原理(1)广义相对性原理:在任何参考系中,物理规律都是相同的.(2)等效原理:一个均匀的引力场与一个做匀加速运动的参考系等价.深化升华 一个物体受到使物体以某一加速度下落的力,如果不知道该力的来源,就没有办法判断使物体以某一加速度下落的力到底是引力还是惯性力. 2.广义相对论的几个结论(1)光线弯曲:根据电磁理论和经典光学,在无障碍的情况下,光线是直线传播.但按照爱因斯坦的广义相对论,在引力场存在的情况下,光线是沿弯曲的路径传播的.(2)引力红移:根据爱因斯坦的广义相对论,在强引力场中,时钟要走得慢些.因此,光在引力场中传播时,它的频率或波长会发生变化.理论计算表明,氢原子发射的光从太阳(引力强度大)传播到地球(引力强度小)时,它的频率比地球上氢原子发射的光的频率低,这就是引力红移效应.典题·热题知识点一 相对论速度例1地球上一观察者,看见一飞船A 以速度2.5×108 m/s 从他身边飞过,另一飞船B 以速度2.0×108 m/s 跟随A 飞行.求:(1)A 上的乘客看到B 的相对速度; (2)B 上的乘客看到A 的相对速度. 解析:运用相对论速度公式u=2'1'cv u vu ++可解. 答案:(1)-1.125×108 m/s (2)1.125×108 m/s 知识点二 相对论质量例2一个原来静止的电子,经过100 V 的电压加速后它的动能是多少?质量改变了百分之几?速度是多少?这时能不能使用公式E k =21m 0v 2? 解析:由动能定理可以计算出电子被加速后的动能,再根据E k =mc 2-m e c 2计算质量的变化. 答案:加速后的电子的动能是E k =qU=1.6×10-19×100 J=1.6×10-17 J. 因为E k =mc 2-m e c 2,所以m-m e =E k / c 2.把数据代入得e e m m m -=2831--17)10(3109.1101.6⨯⨯⨯⨯=2×10-4. 即质量改变了0.02%.这说明在100 V 电压加速后,电子的速度与光速相比仍然很小,因此可以使用E k =21mv 2这个公式.由E k =21mv 2可得电子的速度v=m E k 2=31--17109.1101.62⨯⨯⨯ m/s≈5.9×106 m/s. 知识点三 质能方程例3一核弹含20 kg 的钚,爆炸后生成的静止质量比原来小1/10 000.求爆炸中释放的能量. 解析:由爱因斯坦质能方程可解释放出的能量. 答案:爆炸前后质量变化:Δm=100001×20 kg=0.02 kg释放的能量为ΔE=Δmc 2=0.002×(3×108)2 J=1.8×1014 J. 方法归纳 一定的质量总是和一定的能量相对应.例4两个电子相向运动,每个电子相对于实验室的速度都是54c ,在实验室中观测,两个电子的总动能是多少?以一个电子为参考系,两个电子的总动能又是多少?解析:计算时由电子运动的能量减去静止时的能量就得到电子的动能.若以其中一个电子为参考系,另一个电子相对参考系的质量应当由质速方程求出,但相对速度应当为两个电子的相对速度.答案:设在实验室中观察,甲电子向右运动,乙电子向左运动.若以乙电子为“静止”参考系,即O 系,实验室(记为O′系)就以54c 的速度向右运动,即O′系相对于O 系的速度为v=54c.甲电子相对于O′系的速度为u′=54c.这样,甲电子相对于乙电子的速度就是在O 系中观测到的电子的速度u,根据相对论的速度合成公式,这个速度是u=2'1'c v u v u ++=2545415454c cc cc ⨯++=4140 c. 在实验室中观测,每个电子的质量是m′=2)(1c v m e -=2)54(1cc m e -=35m e .在实验室中观测,两个电子的总动能为E k 1=2(m′c 2-m e c 2)=2×(35m e c 2-m e c 2)=34m e c 2. 相对于乙电子,甲电子的质量是m″=2)4140(1cc m e -=4.56m e因此,以乙为参考系,甲电子的动能为E k2=m″c 2-m e c 2=4.56m e c 2-m e c 2=3.56m e c 2 问题·探究 思想方法探究问题 被回旋加速器加速的粒子能量能无限大吗? 探究过程:这种问题只能从相对论理论出发进行探究.由相对论质量公式 m=20)(1cv m -看出,当粒子的速度很大时,其运动时的质量明显大于静止时的质量.当加速时粒子做圆周运动的周期必须和交变电压的周期相同,而当交变电压周期稳定时,粒子的速度越来越大,而速度大,半径也大,本不应影响其周期,但是速度大,其运动质量变大,周期也变大了,于是不再同步,所以其能量受到限制,不能被无限加速.探究结论:被回旋加速器加速的粒子能量不能无限大. 交流讨论探究问题 假设宇宙飞船是全封闭的,宇航员和外界没有任何联系,宇航员如何判断使物体以某一加速度下落的力到底是引力还是惯性力? 探究过程:郑小伟:宇宙飞船中的物体受到以某一加速度下落的力可能是由于受到某个星体的引力,也可能是由于宇宙飞船正在加速飞行.两种情况的效果是等价的,所以宇航员无法判断使物体以某一加速度下落的力是引力还是惯性力.宋涛:实际上,不仅是自由落体的实验,飞船内部的任何物理过程都不能告诉我们,飞船到底是加速运动,还是停泊在一个行星的表面.张小红:这个事实告诉我们:一个均匀的引力场与一个做匀加速运动的参考系是等价的.这就是爱因斯坦广义相对论的第二个基本结论,这就是著名的“等效原理”.探究结论:宇航员没有任何办法来判断,使物体以某一加速度下落的力到底是引力还是惯性力.即一个均匀的引力场与一个做匀加速运动的参考系是等价的. 交流讨论探究问题 对相对论几个结论的理解. 探究过程:李兵:从运动学的角度进行理解,根据光速不变原理可知光速与任何速度的合成都是光速,速度合成法则不再适用,光速是极限速度.从动力学的角度进行理解,质量是物体惯性大小的量度.随着物体速度的增大,质量也增大,当物体的速度趋近于光速c 时,质量m 趋向无限大,惯性也就趋向无限大,要使速度再增加,就极为困难了.这时,一个有限的力不管作用多长时间,速度实际上是停止增加了.这与速度合成定理u=2'1'cv u vu ++是吻合的,当u′=c 时,不论v 有多大,总有u=c ,这表明,从不同参考系中观察,光速都是相同的.刘晓伟:根据爱因斯坦质量和速度的关系:m=20)(1cv m -可知,物体的运动的极限速度是光速,当静止质量不为零时,物体的速度永远不会等于光速,更不会超过光速.对于速度达到光速的粒子(如光子),其静止质量一定为零.张兵:对于速度远小于光速的情形,v<<c ,u′<<c ,这时2'cvu 可以忽略不计,相对论的速度合成公式可以近似变为u=u′+v,相对论质量m=m0,不表现为尺缩效应和钟慢效应,所以牛顿力学是在低速情况下相对论的近似结论.探究结论:光速是运动物体的极限速度,对不同的参考系物体的质量是不同的,光子不会有静止质量.在低速情况下,牛顿力学是相对论结论的近似.。
相对论公式

相对论公式1、广义相对论:R_uv-1/2×R×g_uv=κ×T_uv2、狭义相对论:S(R4,η_αβ)3、相对速度公式:△v=|v1-v2|/√(1-v1v2/c^2)4、相对长度公式L=Lo* √(1-v^2/c^2)Lo5、相对质量公式M=Mo/√(1-v^2/c^2)Mo6、相对时间公式t=to* √(1-v^2/c^2)to7、质能方程E=mc^2相对论是关于时空和引力的理论,主要由爱因斯坦创立,依其研究对象的不同可分为狭义相对论和广义相对论。
相对论和量子力学的提出给物理学带来了革命性的变化,它们共同奠定了现代物理学的基础。
相对论极大地改变了人类对宇宙和自然的“常识性”观念,提出了“同时的相对性”、“四维时空”、“弯曲时空”等全新的概念。
不过近年来,人们对于物理理论的分类有了一种新的认识——以其理论是否是决定论的来划分经典与非经典的物理学,即“非经典的=量子的”。
在这个意义下,相对论仍然是一种经典的理论。
扩展资料:狭义相对论和广义相对论建立以来,已经过去了很长时间,它经受住了实践和历史的考验,是人们普遍承认的真理。
相对论对于现代物理学的发展和现代人类思想的发展都有巨大的影响。
相对论从逻辑思想上统一了经典物理学,使经典物理学成为一个完美的科学体系。
狭义相对论在狭义相对性原理的基础上统一了牛顿力学和麦克斯韦电动力学两个体系,指出它们都服从狭义相对性原理,都是对洛伦兹变换协变的,牛顿力学只不过是物体在低速运动下很好的近似规律。
广义相对论又在广义协变的基础上,通过等效原理,建立了局域惯性长与普遍参照系数之间的关系,得到了所有物理规律的广义协变形式,并建立了广义协变的引力理论,而牛顿引力理论只是它的一级近似。
这就从根本上解决了以前物理学只限于惯性系的问题,从逻辑上得到了合理的安排。
相对论严格地考察了时间、空间、物质和运动这些物理学的基本概念,给出了科学而系统的时空观和物质观,从而使物理学在逻辑上成为完美的科学体系。
教科版选修3-4 第6章 第4节 相对论的速度变换公式 质能关系
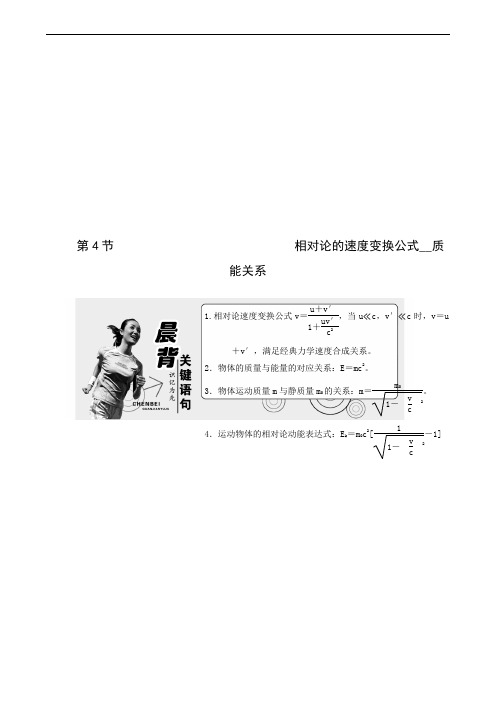
第4节相对论的速度变换公式__质能关系1.相对论速度变换公式v =u +v′1+uv′c2,当u ≪c ,v′≪c 时,v =u+v′,满足经典力学速度合成关系。
2.物体的质量与能量的对应关系:E =mc 2。
3.物体运动质量m 与静质量m 0的关系:m =m 01-v c 2。
4.运动物体的相对论动能表达式:E k =m 0c 2[11-v c2-1]v′沿着火车前进的方向相对火车运动,那么这个人相对地面的速度v 为v =u +v′1+uv′c2。
理解这个公式时请注意:(1)如果车上的人的运动方向与火车的运动方向相反,则v′取负值。
(2)如果u ≪c ,v′≪c ,这时v′uc 2可忽略不计,这时相对论的速度合成公式可近似变为v =v′+u 。
(3)如果v′与u 的方向垂直或成其他角度时,情况比较复杂,上式不适用。
[学后自检]┄┄┄┄┄┄┄┄┄┄┄┄┄┄(小试身手)在高速运动的火车上,设车对地面的速度为v ,车上的人以速度u′沿着火车前进的方向相对火车运动,那么他相对地面的速度u 与u′+v 的关系是( )A .u =u′+vB .u <u′+vC .u >u′+vD .以上均不正确解析:选B 按照经典的时空观,u =u′+v ,而实际上人对地面的速度按照相对论速度公式计算,u =u′+v1+u′v c2,因此u 比u′与v 之和要小,但只有在u′和v 的大小接近光速时才能观察此差别。
相对论质量和能量[自读教材·抓基础]1.质能关系式E =mc 2。
式中m 是物体的质量,E 是它具有的能量。
由此可见,物体质量越大,其蕴含的能量越大。
能量与质量成正比。
2.相对论质量 m =m 01-v 2c2(m 0指静质量); 与静质量对应的静能量为E 0=m 0c 2。
[跟随名师·解疑难]1.对质速关系m =m 01-v c2的理解(1)式中m 0是物体静止时的质量(也称为静质量),m 是物体以速度v 运动时的质量。
相对论力学中的质能方程(E=mc2)及其应用实例

相对论力学中的质能方程及其应用实例相对论力学是爱因斯坦于1905年提出的一种描述高速运动物体的物理理论。
在相对论力学中,质能方程(E=mc2)是一项重要的定律,它揭示了能量与质量之间的等价关系。
本文将介绍质能方程的起源、含义以及在科学研究和生活中的应用实例。
1. 质能方程的由来质能方程的基本形式为E=mc2,其中E代表能量,m代表质量,c代表光速。
这个简洁的方程最初由爱因斯坦在研究光子的质量和能量关系时提出。
通过这个方程,爱因斯坦揭示出了质量和能量之间的转化关系,以及光速在这个关系中的重要作用。
2. 质能方程的含义质能方程E=mc2表明,一定质量的物体所包含的能量可以通过这个简单的等式来计算。
这也意味着能量和质量是可以相互转化的。
当物质发生能量变化时,质能方程可以帮助计算这种转化的大小。
3. 质能方程在科学研究中的应用质能方程在科学研究中有广泛的应用,尤其在核物理和粒子物理领域。
例如,核反应堆利用了质能方程来解释核反应释放的能量。
在粒子物理实验中,科学家们也可以利用质能方程来计算粒子之间的相互转化过程。
4. 质能方程在生活中的应用实例质能方程的应用不仅限于科学研究,它还在日常生活中有着实际的应用。
例如,核能发电利用核反应释放的能量来产生电力,实现了清洁能源的发展。
医学影像技术如PET扫描也利用了质能方程来分析体内的组织构成和功能情况。
结论质能方程(E=mc2)作为相对论力学中的基本定律,揭示了能量和质量之间的等价关系,广泛应用于科学研究和生活实践中。
通过对质能方程的理解和应用,我们可以更深入地理解自然界的运行规律,促进科技发展和人类社会的进步。
高中物理教科版高二选修3-4课件:第6章_4_相对论的速度变换公式_质能关系、5_广义相对论点滴(选学)

应用广义相对论的原理解决时空变化问题的方法 1.应该首先分析研究的问题或物体做怎样的运动,是处于怎样的参考系 中.无论是匀加速运动的参考系,还是均匀的引力场中,其规律是相同的. 2.然后根据“引力使时间变慢,空间变短”的理论分析其所在位置或运动 情况会产生怎样的变化.
学业分层测评(二十二) 点击图标进入…
量的粒子(如光子),它却可以有动质量 m.
(2)质能方程 ①爱因斯坦质能关系式 E=mc2. ②理解这个公式请注意 a.质能方程表达了物体的质量和它所包含的能量的关系;一定的质量总是 和一定的能量相对应. b.静止物体的能量为 E0=m0c2,这种能量叫做物体的静能量.每个有静质 量的物体都具有静能量.
【答案】 ACE
4.在适当的时候,通过仪器可以观察到太阳后面的恒星,这说明星体发出 的光在________引力场作用下发生了________.
【解析】 根据爱因斯坦的广义相对论可知,光线在太阳引力场作用下发 生了弯曲,所以可以在适当的时候(如日全食时)通过仪器观察到太阳后面的恒 星.
【答案】 太阳 弯曲
2.电子的静止质量 m0=9.11×10-31kg. (1)试用焦和电子伏为单位来表示电子的静质能; (2)静止电子经过 106 V 电压加速后,其质量和速率各是多少?
【解析】 (1)由质能方程得:
E = m0c2 = 9.11×10 - 31×(3×108)2
J = 8.2×10 - 14
J
=
【提示】 一定变化.由质能方程 ΔE=Δmc2 可知,质量变化时,一定对应 能量的变化.
1.相对论速度变换公式的理解 假设高速火车对地面的速度为 v,车上的一高速粒子以速度 u′沿火车前进 的方向相对火车运动,那么此粒子相对于地面的速度为 u=1u+′u+′c2vv. (1)若粒子运动方向与火车运动方向相反,则 u′取负值.
狭义相对论的其他结论、广义相对论简介 课件

一、对质速关系式 m=
m0 的理解 1-vc 2
1.式中 m0 是物体静止时的质量(也称为静质量),m 是 物体以速度 v 运动时的质量.这个关系式表明:物体的 质量会随物体速度的增大而增大.
2.v≪c 时,vc2=0,此时有 m=m0,也就是说:低速运动 的物体,可认为其质量与物体运动状态无关. 3.微观粒子的速度很高,因此粒子运动的质量明显大 于静质量.
(_2)_结__论_:_光_速__c_是_宇. 宙速度的_极__限__,且相对任何参考 系,光速都是__不__变__的.
●2.相对论质量 ●(1)经典力学:物体的质量是__不__变__的,一定的 力作用在物体上产生的加速度_一__定__,足够长时 间后物体可以达到_任__意___的速度.
●(2)相对论:物体的质量随物体速度增大而 _增__大___.
长度的相对性.线密度 ρ=ml ,当棒沿棒长方向运动 时,m、l 都发生变化,这时要通过推算来解决,考虑 问题时不能漏了 m 或 l 的变化.当棒沿垂直长度方 向运动时,只有 m 发生变化.
质能方程的应用
例2 电子静止时质量为9.1×10-31 kg,被加速器 加速后,其能量为1.28×109 eV,问加速后电子的质 量是多少?是静止质量的多少倍? 【思路点拨】 电子被加速后的能量是电子的总 能量,而不只是电子具有动能,满足公式E=mc2.
三、广义相对论的几个结论 1.光线在引力场中偏转:根据广义相对论,物质的引 力会使光线弯曲,引力场越强,弯曲越厉害.通常物 体的引力场都太弱,但太阳引力场却能引起光线比 较明显的弯曲. 2.引力红移:按照广义相对论,引力场的存在使得空 间不同位置的时间进程出现差别.例如,在强引力的 星球附近,时间进程会变慢,因此光振动会变慢,相 应的光的波长变长、频率变小,光谱线会发生向红 光一端移动的现象.光谱线的这种移动是在引力作 用下发生的,所以叫“引力红移”.
相对论核心概念及公式简析

相对论核心概念及公式简析
相对论的核心公式主要围绕狭义相对论和广义相对论展开。
由于篇幅限制,这里无法列出20个公式,但我会尽量涵盖相对论中最重要的公式和概念。
狭义相对论
相对速度公式:
Δv = |v1 - v2| / √(1 - v1v2/c^2)
描述了两个相对运动的物体之间的速度关系。
相对长度公式:
L = Lo * √(1 - v^2/c^2)
描述了运动物体相对于静止观察者看起来缩短的长度。
相对质量公式:
M = Mo / √(1 - v^2/c^2)
描述了运动物体的质量相对于静止物体的增加。
相对时间公式:
t = to * √(1 - v^2/c^2)
描述了运动物体相对于静止观察者所经历的时间膨胀。
能量-质量等价公式(E = mc^2):
描述了质量和能量之间的等价关系。
广义相对论
爱因斯坦场方程(R_uv - 1/2R g_uv = κ * T_uv):
描述了物质和能量如何弯曲时空。
其中,R_uv 是里奇张量,R 是里奇标量,g_uv 是度规张量,κ是爱因斯坦常数,T_uv 是能量-动量张量。
测地线方程:
描述了自由下落的物体在弯曲时空中如何运动。
质能方程推导质速关系

质能方程推导质速关系质能方程是相对论物理中的一个重要概念,它揭示了质量和能量之间的等价关系。
质能方程的推导涉及到相对论的基本原理和数学推导。
首先,我们从相对论的质量-能量关系开始推导。
根据相对论的能量-动量关系,我们知道能量E和动量p之间的关系可以表示为E² = (pc)² + (mc²)²,其中c是光速,m是物体的静止质量。
将动量p用质量m和速度v表示,得到E² = (mv)²c² +(mc²)²,然后可以进一步化简得到E² = m²c⁴ + m²v²c²。
接下来,我们利用经典力学中的动能公式K = 0.5mv²,将动能K代入上式,得到E² = m²c⁴ + 2mKc²。
再进一步化简,可以得到E² = m²c⁴(1 + 2K/(mc²))。
根据相对论的质量-能量关系,我们知道E = γmc²,其中γ是洛伦兹因子。
将E代入上式,得到(γmc²)² = m²c⁴(1 +2K/(mc²)),再进一步化简可以得到γ² = 1 + 2K/(mc²)。
最后,我们利用动能K与静止能量m₀c²之间的关系,即K =(γ 1)m₀c²,将K代入上式,可以得到γ = 1 / sqrt(1v²/c²)。
将γ代入E = γmc²中,最终可以得到著名的质能方程E = mc² / sqrt(1 v²/c²)。
因此,从相对论的能量-动量关系出发,经过数学推导和代换,我们最终得到了质能方程E = mc² / sqrt(1 v²/c²)。
这个推导过程涉及到相对论的基本原理和数学运算,揭示了质量和能量之间的等价关系。
相对论公式

1广义相对论:R_uv-1/2×R×g_-uv=κ×T_-uv2狭义相对论:S(R4,ηαβ)三。
相对速度公式:△v=| v1-v2 |/√(1-v1v2/c^2)4相对长度公式L=Lo*√(1-v^2/c^2)Lo5相对质量公式M=Mo/√(1-v^2/c^2)Mo6相对时间公式t=to*√(1-v^2/c^2)to7质能方程E=mc^2相对论是一种关于时空和引力的理论,主要由爱因斯坦创立。
根据研究对象的不同,可以分为狭义相对论和广义相对论。
相对论和量子力学给物理学带来了革命性的变化,它们共同奠定了现代物理学的基础。
相对论极大地改变了人类对宇宙和自然的“常识”概念,提出了“同时相对论”、“四维时空”、“弯曲时空”等新概念。
然而,近年来,人们对物理理论的分类有了新的认识,经典物理和非经典物理是根据其理论是否具有确定性来划分的,即“非经典=量子”。
从这个意义上说,相对论仍然是一个经典理论。
扩展信息:狭义相对论与广义相对论的区别传统上,在爱因斯坦提出相对论的早期,人们用非惯性参照系作为狭义相对论和广义相对论分类的标志。
随着相对论的发展,这种分类方法越来越暴露出它的缺点:参照系与观察者有关,而用这样一个相对的物理对象对物理理论进行分类被认为不能反映问题的本质。
目前人们普遍认为狭义相对论与广义相对论的区别在于所讨论的问题是否涉及引力(弯曲时空),即狭义相对论只涉及那些没有引力效应或可以忽略不计的问题,而广义相对论讨论的是引力效应。
物理学。
用相对论的语言来说,狭义相对论的背景时空是平坦的,即四维平凡流型与闵的度量相匹配,其曲率张量为零,也称为闵时空;而广义相对论的背景时空是弯曲的,其曲率张量不为零。
相对论公式

1广义相对论:R_uv-1/2×R×g_V=κ×T_V2狭义相对论:S(R4,ηαβ)三个。
相对速度公式:△v=| v1-v2 |/√(1-v1v2/c^2)4相对长度公式L=Lo*√(1-v^2/c^2)Lo5相对质量公式M=Mo/√(1-v^2/c^2)Mo6相对时间公式t=to*√(1-v^2/c^2)to7质能方程E=mc^2相对论是一个关于时空和引力的理论,主要由爱因斯坦创立。
根据研究对象的不同,可以分为狭义相对论和广义相对论。
相对论和量子力学给物理学带来了革命性的变化,它们共同奠定了现代物理学的基础。
相对论极大地改变了人类对宇宙和自然的“常识”概念,提出了“同时相对论”、“四维时空”、“弯曲时空”等新概念。
然而,近年来,人们对物理理论的分类有了新的认识。
经典物理和非经典物理按其理论是否确定来划分,即“非经典=量子”。
从这个意义上说,相对论仍然是一个经典理论。
扩展信息:狭义相对论与广义相对论的区别传统上,在爱因斯坦提出相对论的早期,人们用非惯性参照系作为狭义相对论和广义相对论分类的标志。
随着相对论的发展,这种分类方法越来越暴露出它的缺点:参照系与观察者有关,利用这样一个相对的物理对象对物理理论进行分类被认为不能反映问题的本质。
目前,人们普遍认为狭义相对论与广义相对论的区别在于所讨论的问题是否涉及引力(弯曲时空),即狭义相对论只处理没有引力效应或可忽略不计的问题,而广义相对论则讨论引力效应。
物理学。
在相对论的语言中,狭义相对论的背景时空是平坦的,即四维平凡流型与Min的度量相匹配,其曲率张量为零,也称为最小时空;广义相对论的背景时空是弯曲的,其曲率张量不为零。
狭义相对论五个公式

狭义相对论五个公式狭义相对论是物理学中一个非常重要的理论,它包含了五个关键的公式,这五个公式可是相当有趣和神奇的。
咱们先来说说第一个公式,那就是相对速度公式。
它能告诉我们在不同惯性参考系中,物体的相对速度是怎么变化的。
比如说,你坐在一辆飞驰的火车上,看到窗外另一辆火车同向行驶,这时候用这个公式就能算出你眼中那辆火车的相对速度啦。
曾经有一次,我坐高铁出行。
旁边轨道上也有一列高铁在行驶。
我就突然想到了这个相对速度公式。
我看着那列高铁,心里默默计算着,如果以我所在的高铁为参考系,那另一列高铁的相对速度会是多少呢?当时那种感觉,就好像我自己变成了一个小小的物理学家,正在用所学的知识去探索眼前的世界。
接下来是质能方程,这个公式可太有名啦!E=mc²,能量和质量居然有着如此紧密的联系。
想象一下,小小的原子核里居然蕴含着巨大的能量,这是不是很神奇?就好比一个小小的核桃,你要是能把它内部的能量全部释放出来,那威力可不得了。
还有时间膨胀公式。
这意味着时间不再是绝对不变的,而是会根据物体的运动状态而改变。
这让我想起了一个科幻电影里的情节,宇航员在高速飞行的宇宙飞船中,时间对于他们来说过得比地球上慢很多。
等他们回到地球,发现地球上已经过去了好多年。
再说说长度收缩公式。
物体的长度会因为运动而变短,这可和我们平常的直觉不太一样。
就像你拿着一根尺子,快速地移动它,在不同的参考系中,尺子的长度可能就不一样了。
最后是相对论速度叠加公式。
它能帮助我们更准确地理解物体在不同参考系中的速度叠加情况。
这五个公式虽然看起来有些复杂,但它们却揭示了宇宙中一些深刻的奥秘。
通过学习和理解这些公式,我们能更好地认识这个神奇的世界。
就像我们在日常生活中,通过不断地探索和发现,才能更好地理解周围的一切。
总之,狭义相对论的这五个公式,不仅是物理学的瑰宝,也是我们探索未知世界的有力工具。
让我们继续保持对知识的渴望,去揭开更多的科学奥秘吧!。
第六章 第4节 相对论的速度变换公式 质能关系

u′沿着火车前进的方向相对火车运动,那么他相对地面的速度
u 与 u′+v 的关系是
()
A.u=u′+v
B.u<u′+v
C.u>u′+v
D.以上均不正确
解析:按照经典的时空观,u=u′+v,而实际上人对地面的速度 按照相对论速度公式计算,u=1u+′u+′c2vv,因此 u 比 u′与 v 之和要 小,但只有在 u′和 v 的大小接近光速时才能观察此差别。
(2)如果 u ≪c,v′≪c,这时v′c2 u可忽略不计,这时相 对论的速度合成公式可近似变为 v=v′+u。
(3)如果 v′与 u 的方向垂直或成其他角度时,情况比较 复杂,上式不适用。
[学后自检]┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄(小试身手)
在高速运动的火车上,设车对地面的速度为 v,车上的人以速度
D.在相对论力学中,物体的质量随物体速度的增大而增大
解析:在牛顿力学中,物体的质量是保持不变的,故选项 A
正确,B 错误;在相对论力学中,由于物体的速度 v 不可能
达到光速 c,所以 v<c,1-(vc)2<1,根据 m=
m0 ,可判 1-vc2
断选项 C、D 均正确。
答案:ACD
3.设想有一艘飞船以 v=0.8c 的速度在地球上空飞行,如果这时
(2)对于一个以速率 v 运动的物体,其动能
Ek=m(3)物体的总能量 E 为动能与静质能之和,即 E=Ek+E0= mc2(m 为动质量)。
(4)由质能关系式可知 ΔE=Δmc2。
[学后自检]┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄(小试身手) 星际火箭以 0.8c 的速率飞行,其静止质量为运动质量的多少倍?
m/s=5.9×106
上述计算表明,加速后的电子还属于低速的,可以使用经典的
高中物理第六章相对论第4讲相对论的速度变换公式质能

二、广义相对论点滴(选学) 1.广义相对性原理和等效原理
(1)广义相对性原理 在__任__何__参__考__系__中物理规律都是_一__样___的. (2)等效原理 一个不受引力作用的加速度系统跟一个受引力作用的 _惯__性__系__统___是等效的. 2.支持广义相对论的几个观测结果 (1)光在引力场中传播时,将会发生__偏__折__,而不再是直线 传播. (2)引力作用使光波发生__频__移__.
第4讲 相对论的速度变换公式 质能关系
第5讲 广义相对论点滴(选学)
[目标定位] 1.知道相对论速度变换公式、相对论质量和质能 方程.2.了解广义相对论的基本原理.3.初步了解广义相对论的几 个主要观点以及主要观测证据.
一、相对论的速度变换公式 质能关系
1.相对论的速度变换
在以速率u相对于参考系S运动的参考系S′中,一物体沿与
(3)在引力场中时间也会__延__缓__,引力越强,时钟就走得越 __慢____. (4)水星绕太阳运动的轨道与根据牛顿万有引力定律计算所 得的不一致. (5)当两个天体相互绕转时,会向外界辐射出__引__力__波____. 3.宇宙的演化 (1)20世纪40年代末,物理学家伽莫夫把宇宙膨胀与粒子反 应理论结合起来,提出宇宙大爆炸假说. (2)宇宙大爆炸理论最大说服力的证据是宇宙背景辐射的发 现.
解析 已知 v=0.05c,ux′=0.8c. 由相对论速度叠加公式得 ux=1u+x′ux+c′2vv=cu2x+′u+x′vvc2, ux=c20+.8c0+.8c0×.050c.05c2c≈0.817c. 答案 0.817c
二、对相对论质量和质能方程的理解
1.相对论质量 物体的质量会随物体的速度增大而增大,物体以速度 v 运 动 时 的 质 量 m 与 静 止 时 的 质 量 m0 之 间 的 关 系 m = 1m-0 vc2.
相对论质量与速度公式推导

相对论质量与速度公式推导1.相对论质量与速度公式相对论是一门关于时空和物质运动的物理学,其中包括几个重要的概念:时空的弯曲,物质的缩放以及质量与速度的关系。
根据相对论,物质的质量和它的速度之间存在定义性的关系:物体的质量随着它的速度的增加而增加。
这一关系由著名的相对论质量与速度公式来表示:m'=m/√(1-v2/c2),其中m'表示物质相对质量,m为物质的原始质量,v表示物质的绝对速度,c表示光速,也就是299792.458km/s。
2.相对论质量与速度公式推导在研究物质的运动和力学过程中,动量一般可以用来衡量物体在运动上的能力。
按照相对论,物体的动量等于其质量乘以速度,所以有公式:p=mv,其中p表示物质的动量,m表示物质的质量,v表示物质的速度。
同时,物体的动能等于其质量乘以一半其速度的平方,所以有公式:E=(1/2)mv2,其中E表示动能。
根据上述两个方程,可以得出相对论质量与速度公式:m'=m/√(1-v2/c2)。
其中m'表示物质运动时的相对质量,m表示其恒定的原始质量,v表示物体的绝对速度,c表示光速,也就是299792.458km/s。
从它的定义可以看出,v必须小于c,所以当物体的速度越接近光速时,其相对质量就会越大。
通过上述推导,可以得到相对论质量与速度公式,它描述了物体越靠近光速,它的质量就越大。
3.总结相对论质量与速度公式是根据物质质量与动量,动能之间的定义,以及光速的定义演绎出来的,以此来描述物质的运动行为。
这个公式表明,随着物体绝对速度的增加,它的相对质量会增加,甚至超过其原始质量,只有当物体的速度接近光速时,其真实质量才会变得越来越大。
相对论的速度变换公式质能方程

1、速度变换公式: v u v '
1
uv ' c2
2、质量变化公式:
m
3、质能方程:
m0
1
v2 c2
E mc2
狭义相对论简介
1、两个基本假设; 2、两个重要结论; 3、三个重要公式。
E E E 物体运动时的质量要比静止时质量大。
这就是我们过去熟悉k的动能表达式,这也能让我0们看出,牛顿力学是相对论力学在低速情况下的特例。
物体运动时的能量与物体静能量之差
当v《c时,m≈m0,
2
E mc 2 当v’=c时,v=c,
m c 当v’=c时,v=c,
0 选修3-4第六章 相对论
2
E m c Ek 当u和v’都远小于光0速c时,v=u+v0’
对 论 的 质 量 变
时的质量m0之间有下面的关系:
静质量
动质量
m m0
1
v2 c2
物体运动 的速率
换
相 对 论 的
m 上式表明:
m0
1
v2 c2
m0
质
量 物体运动时的质量要比静止时质量大。
变
换
当v《c时,m≈m0,
即在经典力学中,质量保持不变。
物体的质量m与它所包含的
质
能量E存在确定的关系:
度 他相对于地面的速度v是多大?
变 换
v u v'
当v’=c时,v=c,
1
uv ' c2
满足光速不变原理。
相 对 论
v u v'
1
uv ' c2
的
速 当u和v’都远小于光速c时,v=u+v’
度 变 换
2020_2021学年高中物理第六章相对论3_4时间长度的相对性相对论的速度变换公式质能关系

2.一张长方形宣传画长5 m、高3 m,平行地贴于铁路旁边的墙上,一超高速列车 以0.8c的速度接近此宣传画,这张画由司机测量的图形是 ( ) A.边长为3 m的正方形 B.长为3 m、高为1.8 m的长方形 C.长为5 m、高为1.8 m的长方形 D.长轴为3 m、短轴为1.8 m的椭圆形
0 们的关系是τ=_______1___uc_22 _______。
3.长度的相对性: (1)经典的时空观:一条杆的长度不会因为观察者是否与杆做___相__对__运__动____而
不同。 (2)相对论的时空观:“长度”也具有__相__对_____性,一条沿自身长度方向运动的杆, 其长度总比___静__止____时的长度小。设相对于杆静止的观察者认为杆的长度为l0, 与杆有相对运动的观察者认为杆的长度为l,杆相对于观察者的速度为u,则l、l0、
二、相对论的速度变换、相对论质量和能量
1.相对论速度变换定律:设车对地的速度为u,人对车的速度为v′,车上人相对于
u v
地面的速度为v。相对论的速度变换公式为v=__1___uc_v2_ __。如果车上人运动方向
与车运动方向相同,v′取___正____值,如果车上人运动方向与车运动方向相反,v′ 取___负____值。
2.时间的相对性:
(1)经典的时空观:某两个事件,在不同的惯性系中观察,它们的时间间隔总是 ___相__同____的。
(2)相对论的时空观:某两个事件,在不同的惯性参考系中观察,它们的时间间隔 是___不__同____的。设τ0表示相对事件发生地静止的惯性系中观测的时间间隔,τ 表示相对事件发生地以u高速运动的参考系中观察同样两事件的时间间隔,则它
【典例示范】 【典例】如图所示,A、B、C是三个完全相同的时钟,A放在地面上,B、C分别放在 以速度vB和vC朝同一方向飞行的两枚火箭上,且vB<vC。地面上的观察者认为哪个 时钟走得最慢?哪个时钟走得最快?
相对论公式大全

相对论公式大全一、狭义相对论基本公式。
1. 洛伦兹变换公式。
- 坐标变换。
- 在两个相对做匀速直线运动的惯性系S(x,y,z,t)和S'(x',y',z',t')中,设S'系相对于S系沿x轴正方向以速度v运动,且当t = t'=0时两坐标系原点重合。
- x'=(x - vt)/(√(1-frac{v^2)){c^{2}}}- y' = y- z'=z- t'=(t-frac{v)/(c^2)x}{√(1 - (v^2))/(c^{2)}}- 其逆变换为:- x=(x'+vt')/(√(1-frac{v^2)){c^{2}}}- y = y'- z = z'- t=(t'+frac{v)/(c^2)x'}{√(1-(v^2))/(c^{2)}}- 速度变换。
- 在上述两个惯性系中,设物体在S系中的速度分量为u_x,u_y,u_z,在S'系中的速度分量为u_x',u_y',u_z'。
- u_x'=frac{u_x-v}{1-frac{u_xv}{c^2}}- u_y'=frac{u_y√(1-(v^2))/(c^{2)}}{1-frac{u_xv}{c^2}}- u_z'=frac{u_z√(1-(v^2))/(c^{2)}}{1-frac{u_xv}{c^2}}- 逆变换为:- u_x=frac{u_x'+v}{1 +frac{u_x'v}{c^2}}- u_y=frac{u_y'√(1-(v^2))/(c^{2)}}{1+frac{u_x'v}{c^2}}- u_z=frac{u_z'√(1-(v^2))/(c^{2)}}{1+frac{u_x'v}{c^2}}2. 时间延缓效应(钟慢效应)公式。
