浙大2000年-2002年数学分析考研试题及解答
2000年全国硕士研究生入学统一考试数学一、二、三、四试题完整版附答案解析及评分标准

x y2
f12)
1 y2
f2
1 y
(xf21
x y2
f
22
)
1 x2
g
y x3
g
2000 年 • 第 2 页
f1
1 y2
f2 ' xyf11
x y3
f22
1 x2
g
y x3
g .
„„5 分
五、(本题满分 6 分)
计算曲线积分 I
L
xdy ydx 4x2 y2
,其中
L
是以点(1,0)为中心,R
三、(本题满分 5 分)
1
求
lim(
x0
2
ex
4
sin x
x) .
1 ex
1
4
3
解:因
lim
x0
(
2
ex
4
sin x
2e
) lim (
x
x0
x e
4
x
sin x) 1 x
,
1 ex
e x 1
1
1
2 ex
lim (
x0
4
sin x) x
2 ex
lim (
x0
4
sin x) 2 1 1, x
(5) 设二维随机变量 X ,Y 服从二维正态分布,则随机变量 X Y 与 X Y 不相关
的充分必要条件为
(B)
(A) E(X)=E(Y)
(B) E X 2 E X 2 E Y 2 E Y 2
(C) E X 2 E Y 2
(D) E X 2 E X 2 E Y 2 E Y 2
为半径的圆周(R>1).取逆时
2002考研数学一试题及答案解析

2002年全国硕士研究生入学统一考试数学一试题一、填空题(本题共5小题,每小题3分,满分15分.把答案填在题中横线上.) (1)⎰∞+exx dx2ln =.(2)已知函数()y y x =由方程0162=-++x xy e y 确定,则(0)y ''=. (3)微分方程02='+''y y y 满足初始条件0011,'2x x yy ====的特解是.(4)已知实二次型323121232221321444)(),,(x x x x x x x x x a x x x f +++++=经正交变换x Py =可化成标准型216y f =,则a =.(5)设随机变量X 服从正态分布2(,)(0)N μσσ>,且二次方程042=++X y y 无实根的概率为12,则μ= .二、选择题(本题共5小题,每小题3分,满分15分.每小题给出的四个选项中,只有一项符合题目要求,把所选项前的字母填在题后的括号内.)(1)考虑二元函数),(y x f 的下面4条性质: ①),(y x f 在点),(00y x 处连续; ②),(y x f 在点),(00y x 处的两个偏导数连续; ③),(y x f 在点),(00y x 处可微;④),(y x f 在点),(00y x 处的两个偏导数存在.若用“P Q ⇒”表示可由性质P 推出性质Q ,则有(A ) ②⇒③⇒①. (B ) ③⇒②⇒①. (C ) ③⇒④⇒①.(D ) ③⇒①⇒④.(2)设0(1,2,3,)n u n ≠=,且lim1n nnu →∞=,则级数11111(1)()n n n n u u ∞+=+-+∑ (A ) 发散. (B ) 绝对收敛.(C ) 条件收敛.(D ) 收敛性根据所给条件不能判定.(3)设函数()y f x =在(0,)+∞内有界且可导,则 (A ) 当0)(lim =+∞→x f x 时,必有0)(lim ='+∞→x f x .(B ) 当)(lim x f x '+∞→存在时,必有0)(lim ='+∞→x f x .(C ) 当0lim ()0x f x +→=时,必有0lim ()0x f x +→'=. (D ) 当0lim ()x f x +→'存在时,必有0lim ()0x f x +→'=.(4)设有三张不同平面的方程123i i i i a x a y a z b ++=,3,2,1=i ,它们所组成的线性方程组的系数矩阵与增广矩阵的秩都为2,则这三张平面可能的位置关系为(5)设1X 和2X 是任意两个相互独立的连续型随机变量,它们的概率密度分别为1()f x 和2()f x ,分布函数分别为1()F x 和2()F x ,则(A ) 1()f x +2()f x 必为某一随机变量的概率密度. (B ) 1()f x 2()f x 必为某一随机变量的概率密度. (C ) 1()F x +2()F x 必为某一随机变量的分布函数. (D ) 1()F x 2()F x 必为某一随机变量的分布函数.三、(本题满分6分) 设函数)(x f 在0x =的某邻域内具有一阶连续导数,且(0)0,(0)0f f '≠≠,若()(2)(0)af h bf h f +-在0→h 时是比h 高阶的无穷小,试确定b a ,的值.四、(本题满分7分) 已知两曲线)(x f y =与⎰-=x t dt e yarctan 02在点(0,0)处的切线相同,写出此切线方程,并求极限)2(lim nnf n ∞→.五、(本题满分7分) 计算二重积分dxdy e Dy x⎰⎰},max{22,其中}10,10|),{(≤≤≤≤=y x y x D .六、(本题满分8分)设函数)(x f 在(,)-∞+∞内具有一阶连续导数,L 是上半平面(y >0)内的有向分段光滑曲线,其起点为(b a ,),终点为(d c ,).记2221[1()][()1],L xI y f xy dx y f xy dy y y=++-⎰(1)证明曲线积分I 与路径L 无关; (2)当cd ab =时,求I 的值.七、(本题满分7分)(1)验证函数333369()1()3!6!9!(3)!n x x y x x n =++++++-∞<<+∞满足微分方程x e y y y =+'+'';(2)利用(1)的结果求幂级数30(3)!nn x n ∞=∑的和函数.八、(本题满分7分)设有一小山,取它的底面所在的平面为xOy 坐标面,其底部所占的区域为2{(,)|D x y x =275}y xy +-≤,小山的高度函数为),(y x h xy y x +--=2275.(1)设),(00y x M 为区域D 上一点,问),(y x h 在该点沿平面上什么方向的方向导数最大?若记此方向导数的最大值为),(00y x g ,试写出),(00y x g 的表达式.(2)现欲利用此小山开展攀岩活动,为此需要在山脚下寻找一上山坡最大的点作为攀登的起点.也就是说,要在D 的边界线2275x y xy +-=上找出使(1)中),(y x g 达到最大值的点.试确定攀登起点的位置.九、(本题满分6分)已知四阶方阵),,,(4321αααα=A ,4321,,,αααα均为4维列向量,其中432,,ααα线性无关,3212ααα-=,如果4321ααααβ+++=,求线性方程组β=Ax 的通解.十、(本题满分8分) 设,A B 为同阶方阵,(1)若,A B 相似,证明,A B 的特征多项式相等. (2)举一个二阶方阵的例子说明(1)的逆命题不成立. (3)当,A B 均为实对称矩阵时,证明(1)的逆命题成立.十一、(本题满分7分) 设维随机变量X 的概率密度为10,cos ,()220,x x f x π⎧≤≤⎪=⎨⎪⎩其他.对X 独立地重复观察4次,用Y 表示观察值大于3π的次数,求2Y 的数学期望.十二、(本题满分7分)其中1(0)2θθ<<是未知参数,利用总体X 的如下样本值3,1,3,0,3,1,2,3,求θ的矩估计值和最大似然估计值.2002年考研数学一试题答案与解析一、填空题 (1)【分析】 原式2ln 11.ln ln eed x x x+∞+∞==-=⎰(2)【分析】 方程两边对x 两次求导得'6'620,y e y xy y x +++=① 2'''6''12'20.y y e y e y xy y ++++=②以0x =代入原方程得0y =,以0x y ==代入①得'0,y =,再以'0x y y ===代入②得''(0) 2.y =-(3)【分析】 这是二阶的可降阶微分方程.令'()y P y =(以y 为自变量),则'''.dy dP dPy P dx dx dy=== 代入方程得20dP yPP dy +=,即0dP y P dy+=(或0P =,但其不满足初始条件01'2x y ==). 分离变量得0,dP dy P y+= 积分得ln ln ',P y C +=即1C P y=(0P =对应10C =); 由0x =时11,',2y P y ===得11.2C =于是又由01x y==得21,C =所求特解为y =(4)【分析】 因为二次型Tx Ax 经正交变换化为标准型时,标准形中平方项的系数就是二次型矩阵A 的特征值,所以6,0,0是A 的特征值.又因iiia λ=∑∑,故600, 2.a a a a ++=++⇒=(5)【分析】 设事件A 表示“二次方程042=++X y y 无实根”,则{1640}{A X X =-<=>4}.依题意,有1(){4}.2P A P X =>=而 4{4}1{4}1(),P X P X μΦσ->=-≤=-即414141(),(),0. 4.22μμμΦΦμσσσ----===⇒=二、选择题(1)【分析】 这是讨论函数(,)f x y 的连续性,可偏导性,可微性及偏导数的连续性之间的关系.我们知道,(,)f x y 的两个偏导数连续是可微的充分条件,若(,)f x y 可微则必连续,故选(A ).(2)【分析】 由1lim 101n n un n →+∞=>⇒充分大时即,N n N ∃>时10n u >,且1lim 0,n nu →+∞=不妨认为,0,n n u ∀>因而所考虑级数是交错级数,但不能保证1nu 的单调性. 按定义考察部分和111111111111(1)()(1)(1)nn nk k k n k k k k k k k S u u u u +++===++=-+=-+-∑∑∑1111111(1)11(1)1(1)(),k n nn l k l k l n n u u u u u ++==+--=-+-=+→→+∞∑∑⇒原级数收敛.再考察取绝对值后的级数1111()n nn u u ∞=++∑.注意111112,11n n n n u u n n n u u n n++++=+⋅→+ 11n n ∞=∑发散⇒1111()n n n u u ∞=++∑发散.因此选(C ).(3)【分析】 证明(B )对:反证法.假设lim ()0x f x a →+∞'=≠,则由拉格朗日中值定理,(2)()'()()f x f x f x x ξ-=→∞→+∞(当x →+∞时,ξ→+∞,因为2x x ξ<<);但这与(2)()(2)()2f x f x f x f x M -≤+≤矛盾(()).f x M ≤(4)【分析】 因为()()23r A r A ==<,说明方程组有无穷多解,所以三个平面有公共交点且不唯一,因此应选(B ).(A )表示方程组有唯一解,其充要条件是()() 3.r A r A ==(C )中三个平面没有公共交点,即方程组无解,又因三个平面中任两个都不行,故()2r A =和()3r A =,且A 中任两个平行向量都线性无关.类似地,(D )中有两个平面平行,故()2r A =,()3r A =,且A 中有两个平行向量共线.(5)【分析】 首先可以否定选项(A )与(C ),因121212[()()]()()21,()()112 1.f x f x dx f x dx f x dx F F +∞+∞+∞-∞-∞-∞+=+=≠+∞++∞=+=≠⎰⎰⎰对于选项(B ),若121,21,1,01,()()0,0,x x f x f x -<<-<<⎧⎧==⎨⎨⎩⎩其他,其他,则对任何(,),x ∈-∞+∞ 12()()0f x f x ≡,12()()01,f x f x dx +∞-∞=≠⎰因此也应否定(C ),综上分析,用排除法应选(D ).进一步分析可知,若令12max(,)X X X =,而~(),1,2,i i X f x i =则X 的分布函数()F x 恰是12()().F x F x1212(){max(,)}{,}F x P X X x P X x X x =≤=≤≤1212{}{}()().P X x P X x F x F x =≤≤=三、【解】 用洛必达法则.由题设条件知lim[()(2)(0)](1)(0).h af h bf h f a b f →+-=+-由于(0)0f '≠,故必有10.a b +-=(2)'(0)0,a b f =+=及(0)0f '≠,则有20a b +=. 综上,得2, 1.a b ==-四、【解】 由已知条件得(0)0,f =22arctan arctan 02'(0)()'1,1xx t xx x e f e dt x --=====+⎰故所求切线方程为y x =.由导数定义及数列极限与函数极限的关系可得五、【分析与求解】 D 是正方形区域如图.因在D 上被积函数分块表示2222,,max{,}(,),,,x x y x y x y D y x y ⎧≥⎪=∈⎨≤⎪⎩于是要用分块积分法,用y x =将D 分成两块:1212,{},{}.D D D D D y x D D y x ==≤=≥⇒I 222212max{,}max{,}xy xy D D e dxdy e dxdy =+⎰⎰⎰⎰2221212x y x D D D e dxdy e dxdy e dxdy =+=⎰⎰⎰⎰⎰⎰(D 关于y x =对称)2102xx dx e dy =⎰⎰(选择积分顺序)221102 1.x xxe dx e e ===-⎰六、【分析与求解】(1)易知Pdx Qdy +∃原函数,2211()()()()()x Pdx Qdy dx yf xy dx xf xy dy dy ydx xdy f xy ydx xdy y y y+=++-=-++ 0()()()[()].xy x xd f xy d xy d f t dt y y =+=+⎰⇒在0y >上Pdx Qdy +∃原函数,即0(,)()xy xu x y f t dt y =+⎰. ⇒积分I 在0y >与路径无关.(2)因找到了原函数,立即可得(,)(,)(,).c d a b c a I u x y d b==-七、【证明】 与书上解答略有不同,参见数三2002第七题(1)因为幂级数3693()13!6!9!(3)!n x x x x y x n =++++++的收敛域是()x -∞<+∞,因而可在()x -∞<+∞上逐项求导数,得25831'()2!5!8!(31)!n x x x x y x n -=+++++-,4732''()4!7!(32)!n x x x y x x n -=+++++-,所以2'''12!!n x x x y y y x e n ++=+++++=()x -∞<+∞.(2)与'''xy y y e ++=相应的齐次微分方程为'''0y y y ++=,其特征方程为210λλ++=,特征根为1,2122λ=-±. 因此齐次微分方程的通解为212(cossin )22x Y eC x C x -=+. 设非齐次微分方程的特解为xy Ae *=,将y *代入方程'''xy y y e ++=可得13A =,即有13x y e *=.于是,方程通解为2121(cossin )223xx y Y y eC x C x e -*=+=++. 当0x =时,有112121(0)1,23,0.311'(0)0.223y C C C y C ⎧==+⎪⎪⇒==⎨⎪==-++⎪⎩于是幂级数30(3)!n n x n ∞=∑的和函数为221()33x x y x e x e -=+()x -∞<+∞八、【分析与求解】(1)由梯度向量的重要性质:函数),(y x h 在点M 处沿该点的梯度方向0000(,)(,)0000(,){,}{2,2}x y x y h h h x y x y y x x y∂∂==-+-+∂∂grad方向导数取最大值即00(,)(,)x y h x y grad 的模,00(,)g x y ⇒=(2)按题意,即求(,)g x y 求在条件22750x y xy +--=下的最大值点⇔22222(,)(2)(2)558g x y y x x y x y xy =-+-=+-在条件22750x y xy +--=下的最大值点.这是求解条件最值问题,用拉格朗日乘子法.令拉格朗日函数 2222(,,)558(75),L x y x y xy x y xy λλ=+-++--则有 22108(2)0,108(2)0,750.L x y x y x L y x y x yL x y xy λλλ⎧∂=-+-=⎪∂⎪∂⎪=-+-=⎨∂⎪⎪∂=+--=⎪∂⎩解此方程组:将①式与②式相加得()(2)0.x y x y λ++=⇒=-或 2.λ=-若y x =-,则由③式得2375x =即5, 5.x y =±=若2,λ=-由①或②均得y x =,代入③式得275x=即x y =±=±于是得可能的条件极值点1234(5,5),(5,5),(M M M M ----现比较222(,)(,)558f x y g x y x y xy ==+-在这些点的函数值:1234()()450,()()150.f M f M f M f M ==== 因为实际问题存在最大值,而最大值又只可能在1234,,,M M M M 中取到.因此2(,)g x y 在12,M M 取到在D 的边界上的最大值,即12,M M 可作为攀登的起点.九、【解】 由432,,ααα线性无关及3212ααα-=知,向量组的秩1234(,,,)3r αααα=,即矩阵A 的秩为3.因此0Ax =的基础解系中只包含一个向量.那么由123412312(,,,)2010ααααααα⎡⎤⎢⎥-⎢⎥=-+=⎢⎥⎢⎥⎣⎦知,0Ax =的基础解系是(1,2,1,0).T- 再由123412341111(,,,)1111A βαααααααα⎡⎤⎡⎤⎢⎥⎢⎥⎢⎥⎢⎥=+++==⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦知,(1,1,1,1)T 是β=Ax 的一个特解.故β=Ax 的通解是1121,1101k ⎡⎤⎡⎤⎢⎥⎢⎥-⎢⎥⎢⎥+⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦其中k 为任意常数.十、【解】(1)若,A B 相似,那么存在可逆矩阵P ,使1,P AP B -=故 111E B E P AP P EP P AP λλλ----=-=-11().P E A P P E A P E A λλλ--=-=-=-(2)令0100,,0000A B ⎡⎤⎡⎤==⎢⎥⎢⎥⎣⎦⎣⎦那么2.E A E B λλλ-==- 但,A B 不相似.否则,存在可逆矩阵P ,使10P AP B -==.从而100A P P -==,矛盾,亦可从()1,()0r A r B ==而知A 与B 不相似.(3)由,A B 均为实对称矩阵知,,A B 均相似于对角阵,若,A B 的特征多项式相等,记特征多项式的根为1,,,n λλ则有A 相似于1,n λλ⎡⎤⎢⎥⎢⎥⎢⎥⎣⎦B 也相似于1.n λλ⎡⎤⎢⎥⎢⎥⎢⎥⎣⎦即存在可逆矩阵,P Q ,使111.n P AP Q BQ λλ--⎡⎤⎢⎥==⎢⎥⎢⎥⎣⎦ 于是111()().PQ A PQ B ---=由1PQ -为可逆矩阵知,A 与B 相似.十一、【解】 由于311{}cos ,3222x P X dx πππ>==⎰依题意,Y 服从二项分布1(4,)2B ,则有2222111()()4(4) 5.222EY DY EY npq np =+=+=⨯⨯+⨯= 十二、【解】 22012(1)23(12)34,EX θθθθθθ=⨯+⨯-+⨯+⨯-=-1(3).4EX θ=- θ的矩估计量为1ˆ(3),4X θ=-根据给定的样本观察值计算1(31303123)8x =+++++++ 2.=因此θ的矩估计值11ˆ(3).44x θ=-= 对于给定的样本值似然函数为624()4(1)(12),ln ()ln 46ln 2ln(1)4ln(12),L L θθθθθθθθ=--=++-+-2ln ()62824286.112(1)(12)d L d θθθθθθθθθθ-+=--=---- 令ln ()0d L d θθ=,得方程2121430θθ-+=,解得θ=1,2θ=>不合题意). 于是θ的最大似然估计值为ˆθ=。
2000年-年考研数学一历年真题完整版(word版)

2000年全国硕士研究生入学统一考试数学(一)试卷一、填空题(本题共5小题,每小题3分,满分15分.把答案填在题中横线上)(1)⎰=_____________.(2)曲面2222321x y z ++=在点(1,2,2)--的法线方程为_____________. (3)微分方程30xy y '''+=的通解为_____________.(4)已知方程组12312112323120x a x a x ⎡⎤⎡⎤⎡⎤⎢⎥⎢⎥⎢⎥+=⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥-⎣⎦⎣⎦⎣⎦无解,则a = _____________. (5)设两个相互独立的事件A 和B 都不发生的概率为19,A 发生B 不发生的概率与B 发生A 不发生的概率相等,则()P A =_____________.二、选择题(本题共5小题,每小题3分,满分15分.每小题给出的四个选项中,只有一个符合题目要求,把所选项前的字母填在题后的括号内)(1)设()f x 、()g x 是恒大于零的可导函数,且()()()()0f x g x f x g x ''-<,则当a x b <<时,有 (A)()()()()f x g b f b g x > (B)()()()()f x g a f a g x >(C)()()()()f x g x f b g b >(D)()()()()f x g x f a g a >(2)设22221:(0),S x y z a z S ++=≥为S 在第一卦限中的部分,则有 (A)14SS xdS xdS =⎰⎰⎰⎰(B)14SS ydS xdS =⎰⎰⎰⎰(C)14SS zdS xdS =⎰⎰⎰⎰(D)14SS xyzdS xyzdS =⎰⎰⎰⎰(3)设级数1nn u∞=∑收敛,则必收敛的级数为(A)1(1)nn n un ∞=-∑(B)21nn u∞=∑(C)2121()n n n uu ∞-=-∑(D)11()nn n uu ∞+=+∑(4)设n 维列向量组1,,()m m n <αα线性无关,则n 维列向量组1,,m ββ线性无关的充分必要条件为(A)向量组1,,m αα可由向量组1,,m ββ线性表示 (B)向量组1,,m ββ可由向量组1,,m αα线性表示(C)向量组1,,m αα与向量组1,,m ββ等价(D)矩阵1(,,)m =A αα与矩阵1(,,)m =B ββ等价(5)设二维随机变量(,)X Y 服从二维正态分布,则随机变量X Y ξ=+与 X Y η=-不相关的充分必要条件为(A)()()E X E Y =(B)2222()[()]()[()]E X E X E Y E Y -=-(C)22()()E X E Y =(D)2222()[()]()[()]E X E X E Y E Y +=+三、(本题满分6分)求142e sin lim().1exx xxx→∞+++四、(本题满分5分)设(,)()x x z f xy g y y =+,其中f 具有二阶连续偏导数,g 具有二阶连续导数,求2.zx y∂∂∂五、(本题满分6分)计算曲线积分224L xdy ydxI x y -=+⎰,其中L 是以点(1,0)为中心,R 为半径的圆周(1),R >取逆时针方向.六、(本题满分7分)设对于半空间0x >内任意的光滑有向封闭曲面,S 都有2()()e 0,x Sx f x d y d zx y f xd z d x z d x d y --=⎰⎰其中函数()f x 在(0,)+∞内具有连续的一阶导数,且0lim ()1,x f x +→=求()f x .七、(本题满分6分) 求幂级数113(2)nn nn x n ∞=+-∑的收敛区间,并讨论该区间端点处的收敛性.八、(本题满分7分)设有一半径为R 的球体0,P 是此球的表面上的一个定点,球体上任一点的密度与该点到0P 距离的平方成正比(比例常数0k >),求球体的重心位置.九、(本题满分6分)设函数()f x 在[0,]π上连续,且()0,()cos 0.f x dx f x xdx ππ==⎰⎰试证:在(0,)π内至少存在两个不同的点12,,ξξ使12()()0.f f ξξ==十、(本题满分6分)设矩阵A 的伴随矩阵*10000100,10100308⎡⎤⎢⎥⎢⎥=⎢⎥⎢⎥-⎣⎦A 且113--=+ABA BA E ,其中E 为4阶单位矩阵,求矩阵B .十一、(本题满分8分)某适应性生产线每年1月份进行熟练工与非熟练工的人数统计,然后将16熟练工支援其他生产部门,其缺额由招收新的非熟练工补齐.新、老非熟练工经过培训及实践至年终考核有25成为熟练工.设第n 年1月份统计的熟练工与非熟练工所占百分比分别为n x 和,n y 记成向量.n n x y ⎛⎫⎪⎝⎭(1)求11n n x y ++⎛⎫ ⎪⎝⎭与n n x y ⎛⎫ ⎪⎝⎭的关系式并写成矩阵形式:11.n n n n x x y y ++⎛⎫⎛⎫= ⎪ ⎪⎝⎭⎝⎭A(2)验证1241,11-⎛⎫⎛⎫== ⎪⎪⎝⎭⎝⎭ηη是A 的两个线性无关的特征向量,并求出相应的特征值. (3)当111212x y ⎛⎫⎪⎛⎫= ⎪ ⎪ ⎪⎝⎭ ⎪⎝⎭时,求11.n n x y ++⎛⎫ ⎪⎝⎭十二、(本题满分8分)某流水线上每个产品不合格的概率为(01)p p <<,各产品合格与否相对独立,当出现1个不合格产品时即停机检修.设开机后第1次停机时已生产了的产品个数为X ,求X 的数学期望()E X 和方差()D X .十三、(本题满分6分)设某种元件的使用寿命X 的概率密度为2()2e (;)0x x f x x θθθθ-->⎧=⎨≤⎩,其中0θ>为未知参数.又设12,,,n x x x 是X 的一组样本观测值,求参数θ的最大似然估计值.2001年全国硕士研究生入学统一考试数学(一)试卷一、填空题(本题共5小题,每小题3分,满分15分.把答案填在题中横线上)(1)设e (sin cos )(,xy a x b x a b =+为任意常数)为某二阶常系数线性齐次微分方程的通解,则该方程为_____________.(2)222z y x r ++=,则(1,2,2)div(grad )r -= _____________.(3)交换二次积分的积分次序:⎰⎰--0112),(y dx y x f dy =_____________.(4)设24+-=A A E O ,则1(2)--A E = _____________.(5)()2D X =,则根据车贝晓夫不等式有估计≤≥-}2)({X E X P _____________.二、选择题(本题共5小题,每小题3分,满分15分.每小题给出的四个选项中,只有一个符合题目要求,把所选项前的字母填在题后的括号内)(1)设函数)(x f 在定义域内可导,)(x f y =的图形如右图所示,则)(x f y '=的图形为(A) (B)(C) (D)(2)设),(y x f 在点(0,0)的附近有定义,且1)0,0(,3)0,0(='='y x f f 则 (A)(0,0)|3dz dx dy =+(B)曲面),(y x f z =在(0,0,(0,0))f 处的法向量为{3,1,1}(C)曲线(,)0z f x y y ==在(0,0,(0,0))f 处的切向量为{1,0,3}(D)曲线(,)0z f x y y ==在(0,0,(0,0))f 处的切向量为{3,0,1}(3)设0)0(=f 则)(x f 在x =0处可导⇔(A)20(1cos )lim h f h h→-存在(B) 0(1e )lim h h f h→-存在(C)2(sin )limh f h h h→-存在(D)hh f h f h )()2(lim-→存在(4)设111140001111000,11110000111100⎛⎫⎛⎫⎪⎪⎪⎪== ⎪ ⎪ ⎪⎪⎝⎭⎝⎭A B ,则A 与B (A)合同且相似 (B)合同但不相似 (C)不合同但相似(D)不合同且不相似(5)将一枚硬币重复掷n 次,以X 和Y 分别表示正面向上和反面向上的次数, 则X 和Y 相关系数为(A) -1 (B)0(C)12(D)1三、(本题满分6分)求2arctan e exxdx ⎰.四、(本题满分6分)设函数),(y x f z =在点(1,1)可微,且3)1,1(,2)1,1(,1)1,1(='='=y x f f f ,)),(,()(x x f x f x =ϕ,求13)(=x x dxd ϕ.五、(本题满分8分)设()f x = 21a r c t a n 010x x x x x +≠=,将)(x f 展开成x 的幂级数,并求∑∞=--1241)1(n n n的和.六、(本题满分7分) 计算222222()(2)(3)LI y z d x z x d y x y d z =-+-+-⎰,其中L 是平面 2=++z y x 与柱面1=+y x 的交线,从Z 轴正向看去,L 为逆时针方向.七、(本题满分7分)设)(x f 在(1,1)-内具有二阶连续导数且0)(≠''x f .证明:(1)对于)1,0()0,1( -∈∀x ,存在惟一的)1,0()(∈x θ,使 )(x f =)0(f +))((x x f x θ'成立. (2)5.0)(lim 0=→x x θ.八、(本题满分8分)设有一高度为t t h )((为时间)的雪堆在融化过程,其侧面满足方程)()(2)(22t h y x t h z +-=(设长度单位为厘米,时间单位为小时),已知体积减少的速率与侧面积成正比(系数为0.9),问高度为130厘米的雪堆全部融化需多少时间?九、(本题满分6分)设12,,,s ααα为线性方程组=AX O 的一个基础解系,1112221223121,,,s s t t t t t t =+=+=+βααβααβαα,其中21,t t 为实常数,试问21,t t 满足什么条件时12,,,s βββ也为=AX O 的一个基础解系?十、(本题满分8分)已知三阶矩阵A 和三维向量x ,使得2,,A A x x x 线性无关,且满足3232=-A A A x x x . (1)记2(,,),=P A A x x x 求B 使1-=A PBP . (2)计算行列式+A E .十一、(本题满分7分)设某班车起点站上客人数X 服从参数为(0)λλ>的泊松分布,每位乘客在中途下车的概率为(01),p p <<且中途下车与否相互独立.Y 为中途下车的人数,求:(1)在发车时有n 个乘客的条件下,中途有m 人下车的概率. (2)二维随机变量(,)X Y 的概率分布.十二、(本题满分7分)设2~(,)X N μσ抽取简单随机样本122,,,(2),n X X X n ≥样本均值∑==ni i X n X 2121,∑=+-+=ni i n i X X X Y 12)2(,求().E Y2002年全国硕士研究生入学统一考试数学(一)试卷一、填空题(本题共5小题,每小题3分,满分15分.把答案填在题中横线上) (1)⎰∞+exx dx2ln = _____________. (2)已知2e 610yxy x ++-=,则(0)y ''=_____________.(3)02='+''y y y 满足初始条件1(0)1,(0)2y y '==的特解是_____________. (4)已知实二次型323121232221321444)(),,(x x x x x x x x x a x x x f +++++=经正交变换可化为标准型216y f =,则a =_____________.(5)设随机变量),(~2σμN X ,且二次方程042=++X y y 无实根的概率为0.5,则μ=_____________.二、选择题(本题共5小题,每小题3分,满分15分.每小题给出的四个选项中,只有一个符合题目要求,把所选项前的字母填在题后的括号内)(1)考虑二元函数),(y x f 的四条性质:①),(y x f 在点),(00y x 处连续, ②),(y x f 在点),(00y x 处的一阶偏导数连续, ③),(y x f 在点),(00y x 处可微, ④),(y x f 在点),(00y x 处的一阶偏导数存在. 则有:(A)②⇒③⇒① (B)③⇒②⇒① (C)③⇒④⇒①(D)③⇒①⇒④(2)设0≠n u ,且1lim=∞→n n u n ,则级数)11()1(11+++-∑n n n u u 为(A)发散(B)绝对收敛(C)条件收敛(D)收敛性不能判定.(3)设函数)(x f 在+R 上有界且可导,则 (A)当0)(lim =+∞→x f x 时,必有0)(lim ='+∞→x f x(B)当)(lim x f x '+∞→存在时,必有0)(lim ='+∞→x f x(C) 当0)(lim 0=+→x f x 时,必有0)(lim 0='+→x f x (D) 当)(lim 0x f x '+→存在时,必有0)(lim 0='+→x f x .(4)设有三张不同平面,其方程为i i i i d z c y b x a =++(3,2,1=i )它们所组成的线性方程组的系数矩阵与增广矩阵的秩都为2,则这三张平面可能的位置关系为(5)设X 和Y 是相互独立的连续型随机变量,它们的密度函数分别为)(x f X 和)(y f Y ,分布函数分别为)(x F X 和)(y F Y ,则(A))(x f X +)(y f Y 必为密度函数 (B) )(x f X )(y f Y 必为密度函数(C))(x F X +)(y F Y 必为某一随机变量的分布函数 (D) )(x F X )(y F Y 必为某一随机变量的分布函数.三、(本题满分6分)设函数)(x f 在0x =的某邻域具有一阶连续导数,且0)0()0(≠'f f ,当0→h 时,若)()0()2()(h o f h bf h af =-+,试求b a ,的值.四、(本题满分7分) 已知两曲线)(x f y =与2arctan 0ex t y dt -=⎰在点(0,0)处的切线相同.求此切线的方程,并求极限)2(lim nnf n ∞→.五、(本题满分7分) 计算二重积分22max{,}ex y Ddxdy ⎰⎰,其中}10,10|),{(≤≤≤≤=y x y x D .六、(本题满分8分)设函数)(x f 在R 上具有一阶连续导数,L 是上半平面(y >0)内的有向分段光滑曲线,起点为(b a ,),终点为(d c ,).记dy xy f y y x dx xy f y y I ]1)([)](1[1222-++=⎰, (1)证明曲线积分I 与路径L 无关.(2)当cd ab =时,求I 的值.七、(本题满分7分)(1)验证函数∑∞==03)!3()(n n n x x y (+∞<<∞-x )满足微分方程e xy y y '''++=.(2)求幂级数∑∞==03)!3()(n nn x x y 的和函数.八、(本题满分7分)设有一小山,取它的底面所在的平面为xoy 面,其底部所占的区域为}75|),{(22≤-+=xy y x y x D ,小山的高度函数为),(y x h xy y x +--=2275.(1)设),(00y x M 为区域D 上一点,问),(y x h 在该点沿平面上何方向的方向导数最大?若此方向的方向导数为),(00y x g ,写出),(00y x g 的表达式.(2)现欲利用此小山开展攀岩活动,为此需要在山脚下寻找一山坡最大的点作为攀登的起点.也就是说要在D 的边界线上找出使(1)中),(y x g 达到最大值的点.试确定攀登起点的位置.九、(本题满分6分)已知四阶方阵1234(,,,)=A αααα, 1234,,,αααα均为四维列向量,其中234,,ααα线性无关,1232=-ααα.若1234=+++βαααα,求线性方程组x =A β的通解.十、(本题满分8分) 设,A B 为同阶方阵,(1)若,A B 相似,证明,A B 的特征多项式相等. (2)举一个二阶方阵的例子说明(1)的逆命题不成立. (3)当,A B 为实对称矩阵时,证明(1)的逆命题成立.十一、(本题满分7分)设维随机变量X 的概率密度为()f x =1c o s 0220 xx x≤≤其它对X 独立地重复观察4次,用Y 表示观察值大于3π的次数,求2Y 的数学期望.十二、(本题满分7分) 设总体的概率分布为其中θ(02θ<<)是未知参数,利用总体X 的如下样本值 3,1,3,0,3,1,2,3.求θ的矩估计和最大似然估计值.2003年全国硕士研究生入学统一考试数学(一)试卷一、填空题(本题共6小题,每小题4分,满分24分.把答案填在题中横线上)(1))1ln(12)(cos lim x x x +→ = .(2)曲面22y x z +=与平面042=-+z y x 平行的切平面的方程是 . (3)设)(cos 02ππ≤≤-=∑∞=x nx ax n n,则2a = .(4)从2R 的基1211,01⎛⎫⎛⎫== ⎪⎪-⎝⎭⎝⎭αα到基1211,12⎛⎫⎛⎫== ⎪ ⎪⎝⎭⎝⎭ββ的过渡矩阵为 . (5)设二维随机变量(,)X Y 的概率密度为(,)f x y =60x01x y ≤≤≤其它,则=≤+}1{Y X P .(6)已知一批零件的长度X (单位:cm)服从正态分布)1,(μN ,从中随机地抽取16个零件,得到长度的平均值为40 (cm),则μ的置信度为0.95的置信区间是 .(注:标准正态分布函数值.)95.0)645.1(,975.0)96.1(=Φ=Φ二、选择题(本题共6小题,每小题4分,满分24分.每小题给出的四个选项中,只有一个符合题目要求,把所选项前的字母填在题后的括号内)(1)设函数()f x 在),(+∞-∞内连续,其导函数的图形如图所示,则()f x 有(A)一个极小值点和两个极大值点(B)两个极小值点和一个极大值点(C)两个极小值点和两个极大值点(D)三个极小值点和一个极大值点(2)设}{},{},{n n n c b a 均为非负数列,且0lim =∞→n n a ,1lim =∞→n n b ,∞=∞→n n c lim ,则必有(A)n n b a <对任意n 成立(B)n n c b <对任意n 成立(C)极限n n n c a ∞→lim 不存在(D)极限n n n c b ∞→lim 不存在(3)已知函数(,)f x y 在点(0,0)的某个邻域内连续,且1)(),(lim2220,0=+-→→y x xyy x f y x ,则(A)点(0,0)不是(,)f x y 的极值点 (B)点(0,0)是(,)f x y 的极大值点 (C)点(0,0)是(,)f x y 的极小值点(D)根据所给条件无法判断点(0,0)是否为(,)f x y 的极值点 (4)设向量组I:12,,,r ααα可由向量组II:12,,,s βββ线性表示,则(A)当s r <时,向量组II 必线性相关 (B)当s r >时,向量组II 必线性相关 (C)当s r <时,向量组I 必线性相关(D)当s r >时,向量组I 必线性相关(5)设有齐次线性方程组0x =A 和0x =B ,其中,A B 均为n m ⨯矩阵,现有4个命题: ① 若0x =A 的解均是0x =B 的解,则秩()≥A 秩()B ② 若秩()≥A 秩()B ,则0x =A 的解均是0x =B 的解 ③ 若0x =A 与0x =B 同解,则秩()=A 秩()B ④ 若秩()=A 秩()B , 则0x =A 与0x =B 同解 以上命题中正确的是 (A)①②(B)①③(C)②④(D)③④(6)设随机变量21),1)((~XY n n t X =>,则 (A)2~()Y n χ (B)2~(1)Y n χ-(C)~(,1)Y F n(D)~(1,)Y F n三、(本题满分10分)过坐标原点作曲线ln y x =的切线,该切线与曲线ln y x =及x 轴围成平面图形D . (1)求D 的面积A .(2)求D 绕直线e x =旋转一周所得旋转体的体积V .四、(本题满分12分)将函数x x x f 2121arctan )(+-=展开成x 的幂级数,并求级数∑∞=+-012)1(n nn 的和.五 、(本题满分10分)已知平面区域}0,0),{(ππ≤≤≤≤=y x y x D ,L 为D 的正向边界.试证: (1)sin sin sin sin e e e e y x y x LLx dy y dx x dy y dx ---=-⎰⎰.(2)sin sin 2e e 2.y x Lx dy y dx π--≥⎰六 、(本题满分10分)某建筑工程打地基时,需用汽锤将桩打进土层.汽锤每次击打,都将克服土层对桩的阻力而作功.设土层对桩的阻力的大小与桩被打进地下的深度成正比(比例系数为.0k k >).汽锤第一次击打将桩打进地下a m.根据设计方案,要求汽锤每次击打桩时所作的功与前一次击打时所作的功之比为常数(01)r r <<.问(1)汽锤击打桩3次后,可将桩打进地下多深?(2)若击打次数不限,汽锤至多能将桩打进地下多深? (注:m 表示长度单位米.)七 、(本题满分12分)设函数()y y x =在),(+∞-∞内具有二阶导数,且)(,0y x x y =≠'是()y y x =的反函数.(1)试将()x x y =所满足的微分方程0))(sin (322=++dy dx x y dy x d 变换为()y y x =满足的微分方程.(2)求变换后的微分方程满足初始条件23)0(,0)0(='=y y 的解.八 、(本题满分12分) 设函数()f x 连续且恒大于零,⎰⎰⎰⎰⎰+++=Ω)(22)(222)()()(t D t d y xf dvz y xf t F σ,⎰⎰⎰-+=t t D dxx f d y x f t G 12)(22)()()(σ,其中}),,{()(2222t z y x z y x t ≤++=Ω,}.),{()(222t y x y x t D ≤+=(1)讨论()F t 在区间),0(+∞内的单调性. (2)证明当0t >时,).(2)(t G t F π>九 、(本题满分10分)设矩阵322232223⎡⎤⎢⎥=⎢⎥⎢⎥⎣⎦A ,010101001⎡⎤⎢⎥=⎢⎥⎢⎥⎣⎦P ,1*-=B P A P ,求2+B E 的特征值与特征向量,其中*A 为A 的伴随矩阵,E 为3阶单位矩阵.十 、(本题满分8分)已知平面上三条不同直线的方程分别为:1l 032=++c by ax ,:2l 032=++a cy bx , :3l 032=++b ay cx .试证这三条直线交于一点的充分必要条件为.0=++c b a十一 、(本题满分10分)已知甲、乙两箱中装有同种产品,其中甲箱中装有3件合格品和3件次品,乙箱中仅装有3件合格品. 从甲箱中任取3件产品放入乙箱后,求:(1)乙箱中次品件数的数学期望.(2)从乙箱中任取一件产品是次品的概率.十二 、(本题满分8分) 设总体X 的概率密度为()f x =2()2e 0x θ--x x θ>≤其中0>θ是未知参数. 从总体X 中抽取简单随机样本n X X X ,,,21 ,记).,,,min(ˆ21nX X X =θ (1)求总体X 的分布函数()F x .(2)求统计量θˆ的分布函数)(ˆx F θ. (3)如果用θˆ作为θ的估计量,讨论它是否具有无偏性.2004年全国硕士研究生入学统一考试数学(一)试卷一、填空题(本题共6小题,每小题4分,满分24分.把答案填在题中横线上) (1)曲线ln y x =上与直线1=+y x 垂直的切线方程为__________ .(2)已知(e )e x xf x -'=,且(1)0f =,则()f x =__________ .(3)设L 为正向圆周222=+y x 在第一象限中的部分,则曲线积分⎰-Lydx xdy 2的值为__________.(4)欧拉方程)0(024222>=++x y dx dyx dxy d x 的通解为__________ . (5)设矩阵210120001⎡⎤⎢⎥=⎢⎥⎢⎥⎣⎦A ,矩阵B 满足**2=+ABA BA E ,其中*A 为A 的伴随矩阵,E 是单位矩阵,则B =__________ .(6)设随机变量X 服从参数为λ的指数分布,则}{DX X P >= __________ .二、选择题(本题共8小题,每小题4分,满分32分.每小题给出的四个选项中,只有一个符合题目要求,把所选项前的字母填在题后的括号内)(7)把+→0x 时的无穷小量dt t dt t dt t xx x⎰⎰⎰===302sin ,tan ,cos 2γβα,使排在后面的是前一个的高阶无穷小,则正确的排列次序是(A)γβα,, (B)βγα,, (C)γαβ,,(D)αγβ,,(8)设函数()f x 连续,且,0)0(>'f 则存在0>δ,使得 (A)()f x 在(0,)δ内单调增加(B)()f x 在)0,(δ-内单调减少(C)对任意的),0(δ∈x 有()(0)f x f >(D)对任意的)0,(δ-∈x 有()(0)f x f >(9)设∑∞=1n na为正项级数,下列结论中正确的是(A)若n n na ∞→lim =0,则级数∑∞=1n na收敛(B)若存在非零常数λ,使得λ=∞→n n na lim ,则级数∑∞=1n na发散(C)若级数∑∞=1n na收敛,则0lim 2=∞→n n a n(D)若级数∑∞=1n na发散, 则存在非零常数λ,使得λ=∞→n n na lim(10)设()f x 为连续函数,⎰⎰=ttydx x f dy t F 1)()(,则)2(F '等于(A)2(2)f(B)(2)f (C)(2)f -(D) 0(11)设A 是3阶方阵,将A 的第1列与第2列交换得B ,再把B 的第2列加到第3列得C ,则满足=AQ C 的可逆矩阵Q 为(A)⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡101001010(B)⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡100101010 (C)⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡110001010(D)⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡100001110 (12)设,A B 为满足=AB O 的任意两个非零矩阵,则必有 (A)A 的列向量组线性相关,B 的行向量组线性相关 (B)A 的列向量组线性相关,B 的列向量组线性相关 (C)A 的行向量组线性相关,B 的行向量组线性相关 (D)A 的行向量组线性相关,B 的列向量组线性相关(13)设随机变量X 服从正态分布(0,1),N 对给定的)10(<<αα,数αu 满足αα=>}{u X P ,若α=<}{x X P ,则x 等于(A)2αu(B)21α-u(C)21α-u(D) α-1u(14)设随机变量)1(,,,21>n X X X n 独立同分布,且其方差为.02>σ 令∑==ni i X n Y 11,则(A)21Cov(,)X Y nσ=(B)21Cov(,)X Y σ= (C)212)(σnn Y X D +=+(D)211)(σnn Y X D +=-三、解答题(本题共9小题,满分94分.解答应写出文字说明、证明过程或演算步骤) (15)(本题满分12分)设2e e a b <<<,证明2224ln ln ()eb a b a ->-. (16)(本题满分11分)某种飞机在机场降落时,为了减少滑行距离,在触地的瞬间,飞机尾部张开减速伞,以增大阻力,使飞机迅速减速并停下.现有一质量为9000kg 的飞机,着陆时的水平速度为700km/h 经测试,减速伞打开后,飞机所受的总阻力与飞机的速度成正比(比例系数为).100.66⨯=k 问从着陆点算起,飞机滑行的最长距离是多少?(注:kg 表示千克,km/h 表示千米/小时) (17)(本题满分12分) 计算曲面积分,)1(322233dxdy z dzdx y dydz x I ⎰⎰∑-++=其中∑是曲面)0(122≥--=z y x z 的上侧.(18)(本题满分11分)设有方程10n x nx +-=,其中n 为正整数.证明此方程存在惟一正实根n x ,并证明当1α>时,级数1n n x α∞=∑收敛.(19)(本题满分12分)设(,)z z x y =是由2226102180x xy y yz z -+--+=确定的函数,求(,)z z x y =的极值点和极值.(20)(本题满分9分) 设有齐次线性方程组121212(1)0,2(2)20,(2),()0,n n n a x x x x a x x n nx nx n a x ++++=⎧⎪++++=⎪≥⎨⎪⎪++++=⎩试问a 取何值时,该方程组有非零解,并求出其通解.(21)(本题满分9分)设矩阵12314315a -⎡⎤⎢⎥=--⎢⎥⎢⎥⎣⎦A 的特征方程有一个二重根,求a 的值,并讨论A 是否可相似对角化. (22)(本题满分9分)设,A B 为随机事件,且111(),(|),(|)432P A P B A P A B ===,令 ;,,0,1不发生发生A A X ⎩⎨⎧= .,,0,1不发生发生B B Y ⎩⎨⎧= 求:(1)二维随机变量(,)X Y 的概率分布. (2)X 和Y 的相关系数.XY ρ(23)(本题满分9分)设总体X 的分布函数为,1,1,0,11),(≤>⎪⎩⎪⎨⎧-=x x x x F ββ其中未知参数n X X X ,,,,121 >β为来自总体X 的简单随机样本,求:(1)β的矩估计量. (2)β的最大似然估计量.2005年全国硕士研究生入学统一考试数学(一)试卷一、填空题(本题共6小题,每小题4分,满分24分.把答案填在题中横线上)(1)曲线122+=x x y 的斜渐近线方程为 _____________.(2)微分方程x x y y x ln 2=+'满足91)1(-=y 的解为____________.(3)设函数181261),,(222z y x z y x u +++=,单位向量}1,1,1{31=n ,则)3,2,1(n u∂∂=.________.(4)设Ω是由锥面22y x z +=与半球面222y x R z --=围成的空间区域,∑是Ω的整个边界的外侧,则⎰⎰∑=++zdxdy ydzdx xdydz ____________.(5)设123,,ααα均为3维列向量,记矩阵123(,,)=A ααα,123123123(,24,39)=++++++B ααααααααα,如果1=A ,那么=B .(6)从数1,2,3,4中任取一个数,记为X , 再从X ,,2,1 中任取一个数,记为Y , 则}2{=Y P =____________.二、选择题(本题共8小题,每小题4分,满分32分.每小题给出的四个选项中,只有一项符合题目要求,把所选项前的字母填在题后的括号内)(7)设函数n nn xx f 31lim )(+=∞→,则()f x 在),(+∞-∞内(A)处处可导 (B)恰有一个不可导点 (C)恰有两个不可导点(D)至少有三个不可导点(8)设()F x 是连续函数()f x 的一个原函数,""N M ⇔表示"M 的充分必要条件是",N 则必有 (A)()F x 是偶函数()f x ⇔是奇函数 (B)()F x 是奇函数()f x ⇔是偶函数 (C)()F x 是周期函数()f x ⇔是周期函数(D)()F x 是单调函数()f x ⇔是单调函数(9)设函数⎰+-+-++=yx yx dt t y x y x y x u )()()(),(ψϕϕ, 其中函数ϕ具有二阶导数,ψ 具有一阶导数,则必有(A)2222y ux u ∂∂-=∂∂(B)2222yu x u ∂∂=∂∂(C)222yu y x u ∂∂=∂∂∂(D)222x uy x u ∂∂=∂∂∂ (10)设有三元方程ln e 1xzxy z y -+=,根据隐函数存在定理,存在点(0,1,1)的一个邻域,在此邻域内该方程(A)只能确定一个具有连续偏导数的隐函数(,)z z x y =(B)可确定两个具有连续偏导数的隐函数(,)x x y z =和(,)z z x y = (C)可确定两个具有连续偏导数的隐函数(,)y y x z =和(,)z z x y = (D)可确定两个具有连续偏导数的隐函数(,)x x y z =和(,)y y x z =(11)设21,λλ是矩阵A 的两个不同的特征值,对应的特征向量分别为12,αα,则1α,12()+A αα线性无关的充分必要条件是(A)01≠λ (B)02≠λ(C)01=λ(D)02=λ(12)设A 为(2)n n ≥阶可逆矩阵,交换A 的第1行与第2行得矩阵**.,B A B 分别为,A B 的伴随矩阵,则(A)交换*A 的第1列与第2列得*B (B)交换*A 的第1行与第2行得*B (C)交换*A 的第1列与第2列得*-B(D)交换*A 的第1行与第2行得*-B(13)设二维随机变量(,)X Y 的概率分布为已知随机事件}0{=X 与}1{=+Y X 相互独立,则(A)0.2,0.3a b == (B)0.4,0.1a b == (C)0.3,0.2a b ==(D)0.1,0.4a b ==(14)设)2(,,,21≥n X X X n 为来自总体(0,1)N 的简单随机样本,X 为样本均值,2S 为样本方差,则(A))1,0(~N X n(B)22~()nS n χ(C))1(~)1(--n t SXn (D)2122(1)~(1,1)nii n X F n X=--∑三 、解答题(本题共9小题,满分94分.解答应写出文字说明、证明过程或演算步骤) (15)(本题满分11分) 设}0,0,2),{(22≥≥≤+=y x y x y x D ,]1[22y x ++表示不超过221y x ++的最大整数. 计算二重积分⎰⎰++Ddxdy y xxy .]1[22(16)(本题满分12分) 求幂级数∑∞=--+-121))12(11()1(n n n x n n 的收敛区间与和函数()f x .(17)(本题满分11分)如图,曲线C 的方程为()y f x =,点(3,2)是它的一个拐点,直线1l 与2l 分别是曲线C 在点(0,0)与(3,2)处的切线,其交点为(2,4).设函数()f x 具有三阶连续导数,计算定积分⎰'''+32.)()(dx x f x x(18)(本题满分12分)已知函数()f x 在[0,1]上连续,在(0,1)内可导,且(0)0,(1)1f f ==. 证明: (1)存在),1,0(∈ξ 使得ξξ-=1)(f .(2)存在两个不同的点)1,0(,∈ζη,使得.1)()(=''ζηf f (19)(本题满分12分)设函数)(y ϕ具有连续导数,在围绕原点的任意分段光滑简单闭曲线L 上,曲线积分24()22Ly dx xydyx y φ++⎰的值恒为同一常数.(1)证明:对右半平面0x >内的任意分段光滑简单闭曲线,C 有24()202Cy dx xydyx yφ+=+⎰.(2)求函数)(y ϕ的表达式. (20)(本题满分9分)已知二次型21232221321)1(22)1()1(),,(x x a x x a x a x x x f +++-+-=的秩为2. (1)求a 的值;(2)求正交变换x y =Q ,把),,(321x x x f 化成标准形. (3)求方程),,(321x x x f =0的解. (21)(本题满分9分)已知3阶矩阵A 的第一行是c b a c b a ,,),,,(不全为零,矩阵12324636k ⎡⎤⎢⎥=⎢⎥⎢⎥⎣⎦B (k 为常数),且=AB O ,求线性方程组0x =A 的通解.(22)(本题满分9分)设二维随机变量(,)X Y 的概率密度为(,)f x y =1001,02x y x <<<<其它 求:(1)(,)X Y 的边缘概率密度)(),(y f x f Y X . (2)Y X Z -=2的概率密度).(z f Z (23)(本题满分9分)设)2(,,,21>n X X X n 为来自总体(0,1)N 的简单随机样本,X 为样本均值,记.,,2,1,n i X X Y i i =-=求:(1)i Y 的方差n i DY i ,,2,1, =. (2)1Y 与n Y 的协方差1Cov(,).n Y Y2006年全国硕士研究生入学统一考试数学(一)试卷一、填空题(本题共6小题,每小题4分,满分24分.把答案填在题中横线上)(1)0ln(1)lim1cos x x x x→+=-. (2)微分方程(1)y x y x-'=的通解是 .(3)设∑是锥面z (01z ≤≤)的下侧,则23(1)xdydz ydzdx z dxdy ∑++-=⎰⎰ .(4)点(2,1,0)到平面3450x y z ++=的距离z = . (5)设矩阵2112⎛⎫=⎪-⎝⎭A ,E 为2阶单位矩阵,矩阵B 满足2=+BA B E ,则B = .(6)设随机变量X 与Y 相互独立,且均服从区间[0,3]上的均匀分布,则{}max{,}1P X Y ≤= .二、选择题(本题共8小题,每小题4分,满分32分. 每小题给出的四个选项中,只有一项符合题目要求,把所选项前的字母填在题后的括号内)(7)设函数()y f x =具有二阶导数,且()0,()0f x f x '''>>,x ∆为自变量x 在0x 处的增量,y ∆与dy 分别为()f x 在点0x 处对应的增量与微分,若0x ∆>,则(A)0dx y <<∆ (B)0y dy <∆< (C)0y dy ∆<<(D)0dy y <∆<(8)设(,)f x y 为连续函数,则140(cos ,sin )d f r r rdr πθθθ⎰⎰等于(A)(,)xf x y dy ⎰⎰(B)(,)f x y dy ⎰⎰(C)(,)yf x y dx ⎰⎰(C)(,)f x y dx ⎰⎰(9)若级数1nn a∞=∑收敛,则级数(A)1nn a∞=∑收敛 (B)1(1)nn n a ∞=-∑收敛(C)11n n n a a ∞+=∑收敛(D)112n n n a a ∞+=+∑收敛 (10)设(,)f x y 与(,)x y ϕ均为可微函数,且1(,)0y x y ϕ≠.已知00(,)x y 是(,)f x y 在约束条件(,)0x y ϕ=下的一个极值点,下列选项正确的是(A)若00(,)0x f x y '=,则00(,)0y f x y '= (B)若00(,)0x f x y '=,则00(,)0y f x y '≠ (C)若00(,)0x f x y '≠,则00(,)0y f x y '=(D)若00(,)0x f x y '≠,则00(,)0y f x y '≠(11)设12,,,,s ααα均为n 维列向量,A 是m n ⨯矩阵,下列选项正确的是 (A)若12,,,,s ααα线性相关,则12,,,,s A αA αA α线性相关 (B)若12,,,,s ααα线性相关,则12,,,,s A αA αA α线性无关(C)若12,,,,s ααα线性无关,则12,,,,s A αA αA α线性相关 (D)若12,,,,s ααα线性无关,则12,,,,s A αA αA α线性无关.(12)设A 为3阶矩阵,将A 的第2行加到第1行得B ,再将B 的第1列的-1倍加到第2列得C ,记110010001⎛⎫ ⎪= ⎪ ⎪⎝⎭P ,则(A)1-=C P AP (B)1-=C PAP(C)T =C P AP(D)T =C PAP(13)设,A B 为随机事件,且()0,(|)1P B P A B >=,则必有(A)()()P A B P A > (B)()()P A B P B >(C)()()P AB P A =(D)()()P AB P B =(14)设随机变量X 服从正态分布211(,)N μσ,Y 服从正态分布222(,)N μσ, 且12{||1}{||1},P X P Y μμ-<>-<则(A)12σσ<(B)12σσ>(C)12μμ<(D)12μμ>三、解答题(本题共9小题,满分94分.解答应写出文字说明、证明过程或演算步骤) (15)(本题满分10分) 设区域D=(){}22,1,0x y xy x +≤≥,计算二重积分2211DxyI dxdy x y+=++⎰⎰. (16)(本题满分12分)设数列{}n x 满足()110,sin 1,2,...n x x x n ππ+<<==. 求:(1)证明lim n x x →∞存在,并求之.(2)计算211lim n x n x n x x +→∞⎛⎫ ⎪⎝⎭. (17)(本题满分12分) 将函数()22xf x x x=+-展开成x 的幂级数. (18)(本题满分12分)设函数()()0,,f u +∞在内具有二阶导数且z f=满足等式22220z zx y∂∂+=∂∂.(1)验证()()0f u f u u'''+=. (2)若()()10,11,f f '==求函数()f u 的表达式. (19)(本题满分12分) 设在上半平面(){},0D x y y =>内,数(),f x y 是有连续偏导数,且对任意的0t >都有()()2,,f tx ty t f x y =.证明: 对L 内的任意分段光滑的有向简单闭曲线L ,都有(,)(,)0Lyf x y dx xf x y dy -=⎰.(20)(本题满分9分) 已知非齐次线性方程组1234123412341435131x x x x x x x x ax x x bx +++=-⎧⎪++-=-⎨⎪++-=⎩ 有3个线性无关的解,(1)证明方程组系数矩阵A 的秩()2r =A . (2)求,a b 的值及方程组的通解.(21)(本题满分9分)设3阶实对称矩阵A 的各行元素之和均为3,向量()()121,2,1,0,1,1TT=--=-αα是线性方程组0x =A 的两个解.(1)求A 的特征值与特征向量.(2)求正交矩阵Q 和对角矩阵A ,使得T=Q AQ A . (22)(本题满分9分)随机变量x 的概率密度为()()21,1021,02,,40,令其它x x f x x y x F x y ⎧-<<⎪⎪⎪=≤<=⎨⎪⎪⎪⎩为二维随机变量(,)X Y 的分布函数.(1)求Y 的概率密度()Y f y . (2)1,42F ⎛⎫-⎪⎝⎭. (23)(本题满分9分)设总体X 的概率密度为(,0)F X = 10θθ- 0112x x <<≤<其它,其中θ是未知参数(01)θ<<,12n ,...,X X X 为来自总体X 的简单随机样本,记N 为样本值12,...,n x x x 中小于1的个数,求θ的最大似然估计.2007年全国硕士研究生入学统一考试数学(一)试卷一、选择题(本题共10小题,每小题4分,满分40分,在每小题给的四个选项中,只有一项符合题目要求,把所选项前的字母填在题后括号内)(1)当0x +→时,(A)1-(B)1(D)1-(2)曲线1ln(1e )x y x=++,渐近线的条数为 (A)0 (B)1 (C)2(D)3(3)如图,连续函数()y f x =在区间[3,2],[2,3]--上的图形分别是直径为1的上、下半圆周,在区间[2,0],[0,2]-的图形分别是直径为2的上、下半圆周,设()()xF x f t dt =⎰.则下列结论正确的是(A)3(3)(2)4F F =-- (B)5(3)(2)4F F =(C)3(3)(2)4F F =(D)5(3)(2)4F F =--(4)设函数()f x 在0x =处连续,下列命题错误的是(A)若0()limx f x x→存在,则(0)0f =(B)若0()()limx f x f x x→+- 存在,则(0)0f =(C)若0()lim x f x x→ 存在,则(0)0f '=(D)若0()()lim x f x f x x→-- 存在,则(0)0f '=(5)设函数()f x 在(0, +∞)上具有二阶导数,且"()0f x >, 令()1,2,,,n u f n n ==则下列结论正确的是(A)若12u u >,则{n u }必收敛(B)若12u u >,则{n u }必发散(C)若12u u <,则{n u }必收敛(D)若12u u <,则{n u }必发散(6)设曲线:(,)1L f x y =((,)f x y 具有一阶连续偏导数),过第2象限内的点M 和第Ⅳ象限内的点,N Γ为L 上从点M 到N 的一段弧,则下列小于零的是(A)(,)x y dx Γ⎰(B)(,)f x y dy Γ⎰(C)(,)f x y ds Γ⎰(D)'(,)'(,)x y f x y dx f x y dy Γ+⎰(7)设向量组123,,ααα线性无关,则下列向量组线形相关的是 (A),,122331---αααααα (B),,122331+++αααααα (C)1223312,2,2---αααααα(D)1223312,2,2+++αααααα(8)设矩阵211121112--⎛⎫ ⎪=-- ⎪ ⎪--⎝⎭A ,100010000⎛⎫ ⎪= ⎪⎪⎝⎭B ,则A 与B(A)合同,且相似(B)合同,但不相似(C)不合同,但相似(D)既不合同,也不相似(9)某人向同一目标独立重复射击,每次射击命中目标的概率为()01p p <<,则此人第4次射击恰好第2次命中目标的概率为(A)23(1)p p -(B)26(1)p p -(C)223(1)p p -(D)226(1)p p -(10)设随即变量(,)X Y 服从二维正态分布,且X 与Y 不相关,()X f x ,()Y f y 分别表示,X Y 的概率密度,则在Y y =的条件下,X 的条件概率密度|(|)XYf x y 为(A)()X f x(B)()Y f y(C)()X f x ()Y f y (D)()()X Y f x f y二、填空题(11-16小题,每小题4分,共24分,请将答案写在答题纸指定位置上) (11)31211e x dx x⎰=_______. (12)设(,)f u v 为二元可微函数,(,)yxz f x y =,则zx∂∂=______. (13)二阶常系数非齐次线性方程2''4'32e xy y y -+=的通解为y =____________. (14)设曲面:||||||1x y z ++=∑,则(||)x y ds ∑+⎰⎰=_____________.(15)设矩阵01000010********⎛⎫⎪⎪= ⎪⎪⎝⎭A ,则3A 的秩为________.(16)在区间(0,1)中随机地取两个数,则这两个数之差的绝对值小于12的概率为________.三、解答题(17-24小题,共86分.请将解答写在答题纸指定的位置上.解答应写出文字说明、证明过程或演算步骤)(17)(本题满分11分)求函数 2222(,)2f x y x y x y =+-在区域22{(,)|4,0}D x y x y y =+≤≥上的最大值和最小值. (18)(本题满分10分)计算曲面积分23,I xzdydz zydzdx xydxdy ∑=++⎰⎰其中 ∑为曲面221(01)4y z x z =--≤≤的上侧.(19)(本题满分11分)设函数(),()f x g x 在[,]a b 上连续,在(,)a b 内具有二阶导数且存在相等的最大值,()(),()()f a g a f b g b ==,证明:存在(,)a b ξ∈,使得 ()()f g ξξ''''=. (20)(本题满分10分) 设幂级数nn n a x∞=∑ 在(,)-∞+∞内收敛,其和函数()y x 满足240,(0)0,(0) 1.y xy y y y ''''--===(1)证明:22,1,2,.1n n a a n n +==+(2)求()y x 的表达式. (21)(本题满分11分)设线性方程组1231232123020,40x x x x x ax x x a x ++=⎧⎪++=⎨⎪++=⎩与方程12321,x x x a ++=-有公共解,求a 的值及所有公共解. (22)(本题满分11分)设3阶实对称矩阵A 的特征向量值12311,2, 2.(1,1,1)T λλλ===-=-α是A 的属于特征值1λ的一个特征向量,记534,=-+B A A E 其中E 为3阶单位矩阵.(1)验证1α是矩阵B 的特征向量,并求B 的全部特征值与特征向量. (2)求矩阵B .(23)(本题满分11分)设二维随机变量(,)X Y 的概率密度为2,01,01(,)0,x y x y f x y --<<<<⎧=⎨⎩其他 (1)求{2}.P X Y >(2)求Z X Y =+的概率密度.(24)(本题满分11分) 设总体X 的概率密度为1,021(;),12(1)0,x f x x θθθθθ⎧<<⎪⎪⎪=≤<⎨-⎪⎪⎪⎩其他12,,n X X X 是来自总体x 的简单随机样本,X 是样本均值(1)求参数θ的矩估计量ˆθ. (2)判断24X 是否为2θ的无偏估计量,并说明理由.。
最新2003年浙江大学数学分析试题答案

2003年浙江大学数学分析试题答案2003年浙江大学数学分析试题答案一、,,0N ∃>∀ε当N n >时,ε<->>∀m n a a N n N m ,, 证明:该数列一定是有界数列,有界数列必有收敛子列}{kn a ,a a k n k =∞→lim ,所以,ε2<-+-≤-a a a a a a k k n n n n二 、,,0N ∃>∀ε当N x >时,ε<-)()(x g x f ,,0,01>∃>∀δε当1'''δ<-x x 时,ε<-)''()'(x f x f对上述,0>ε当N x x >'','时,且1'''δ<-x xε3)''()'()''()''()'()'()''()'(<-+-+-≤-x f x f x f x g x g x f x g x g当N x x <'','时,由闭区间上的连续函数一定一致收敛,所以,0,02>∃>∀δε2'''δ<-x x 时ε<-)''()'(x g x g ,当'''x N x <<时,由闭区间上的连续函数一定一致收敛,在 ],['','22δδ+-∈N N x x 时,ε<-)''()'(x g x g ,取},m in{21δδδ=即可。
三、由,0)('',0)('<>x f a f 得,0)('<x f 所以)(x f 递减, 又2))((''21))((')()(a x f a x a f a f x f -+-+=ξ,所以-∞=+∞→)(lim x f x ,且0)(>a f ,所以)(x f 必有零点,又)(x f 递减,所以有且仅有一个零点。
2000年浙江大学804数学分析考研真题【圣才出品】

2000年浙江大学804数学分析考研真题浙江大学2000年攻读硕士学位研究生入学试题考试科目:数学分析(804)一、(10分)()i 求极限10(1)lim x x e x x →-+; ()ii 设01,x a x b ==,21,2,3,2n n n x x x n ---==.求lim n n x →∞.二、(10分) ()i 设(0)f K '=,试证明00()()lim a b f b f a K b a -+→→-=-;()ii 设()f x 在[],a b 上连续,()f x ''在(),a b 内存在,试证明存在(),a b ξ∈,使得2()()()2()()24a b b a f b f a f f ξ+-''+-=.三、(15分)()i 求数项级数12n n n ∞=∑的和;()ii 试证明函数11()x n S x n ∞==∑在()1,+∞上连续.四、(15分)()i 设方程组0sin sin 0x y u v x u y v +++=⎧⎨+=⎩,确定了可微函数(,)(,)u u x y v v x y =⎧⎨=⎩,试求,,v v du x y ∂∂∂∂; ()ii 设2)()y x y F y dx x =,求(1)F '.五、(30分) ()i 计算积分20sin 1cos x x I dx x π=+⎰;()ii 求以曲面22x y z e --=为顶,平面0z =为底,柱面221x y +=为侧面的曲顶柱体的体积V ;()iii 设S 表示半球面221)z x y =+≤的上侧,求第二类曲面积分222()(2)(2)S J x y z dydz x y z dzdx x z y dxdy=++-++⎰⎰.六、(20分)()i 将函数(),()f x x x ππ=-≤≤展开成Fourier 级数;()ii 求级数211n n ∞=∑的和;()iii 计算广义积分10ln(1)x dx x -⎰.。
浙江大学2002年考研题解
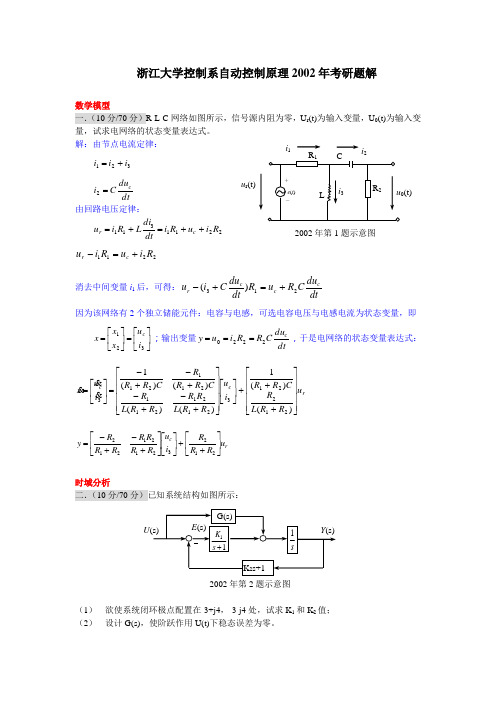
浙江大学控制系自动控制原理2002年考研题解数学模型 一.(10分/70分)R-L-C 网络如图所示,信号源内阻为零,U r (t)为输入变量,U 0(t)为输入变量,试求电网络的状态变量表达式。
解:由节点电流定律: 321i i i +=dtduC i c =2由回路电压定律:2211311R i u R i dtdi LR i u c r ++=+= 2211R i u R i u c r +=-消去中间变量i 1后,可得:dtduC R u R dt du Ci u c c c r 213)(+=+- 因为该网络有2个独立储能元件:电容与电感,可选电容电压与电感电流为状态变量,即⎥⎦⎤⎢⎣⎡=⎥⎦⎤⎢⎣⎡=321i u x x x c ;输出变量dt duC R R i u y c 2220===,于是电网络的状态变量表达式:r c c u R R L R C R R i u R R L R R R R L R C R R R C R R i ux⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡+++⎥⎦⎤⎢⎣⎡⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡+-+-+-+-=⎥⎦⎤⎢⎣⎡=)()(1)()()()(12122132121211211213r c u R R R i u R R R R R R R y ⎥⎦⎤⎢⎣⎡++⎥⎦⎤⎢⎣⎡⎥⎦⎤⎢⎣⎡+-+-=21232121212时域分析 二.(10分/70分)已知系统结构如图所示:(1) 欲使系统闭环极点配置在-3+j4,-3-j4处,试求K 1和K 2值; (2) 设计G(s),使阶跃作用U(t)下稳态误差为零。
u r (t)2002年第1题示意图解:(1)确定K 1和K 2值利用梅逊公式,求系统的闭环传递函数:ss G s p )()(1=;)1()(12+=s s K s p信号流图的特征式及余子式:)1()1(1)(21+++=∆s s s K K s ;1)()(21=∆=∆s s系统的闭环传递函数:)1()1()()1()()(2112211s K K s s K s G s p p S U s Y +++++=∆∆+∆= 故,系统的特征方程:0)1()(1212=+++=∆K s K K s s由题意,欲使系统闭环极点配置在-3+j4,-3-j4处,即希望系统的特征方程: 0256)43)(43(2=++=-+++s s j s j s 即可求得:251=K ;2.02=K(2)因为:)()1()1()()1()1()()()1()()(21122s U s K K s s K s G s s K s U s Y s K s U s E ++++++-=+-=按题意稳态误差为零,故令:E(s)=0,则应有:)1()()1)(1(])()1)[(1()1()1(2121221s K K s G s s K K s G s s K s K K s s ++++=+++=+++ 故得:)()1)(1()1(2s G s s K s s ++=+因而求得:s ss K s s G s s K s s 2.011)()1)(1()1(22+=+=++=+根轨迹三.(10分/70分) 系统的开环传递函数为 )22)(3()()(2+++=s s s s Ks H s G ,绘制根轨迹图,并列出详细步骤。
数学分析与高等代数考研真题详解--浙江大学卷

∴(αT Aβ )2 = (α TCTCβ )2 = (Cα ,Cβ )2 ≤ (Cα ,Cα )(Cβ ,Cβ ) = (αTCTCα )(β TCTCβ ) = (α T Aα )(β T Aβ )
由于上述不等式,等号成立时候当且仅当,存在数 k1, k2 ,使
k1Cα + k2Cβ = 0 ,即 k1α + k2β = 0 ,即α , β 线性相关
2
浙江大学
1999 年招收硕士研究生入学考试《高等代数》试题及解答
3
1999 年招收硕士研究生入学考试《高等代数》试题解答
一:证明:充分性:若 f ( x) 能表示成一个整数多项式的平方,显然 f ( x) 在有理数域上可
约
必要性:由于 f ( x) 在有理数域上可约,在存在整数系数多项式 g ( x), h ( x) 有
所以 Α 是一个线性变换,
由于 A 和 − A 无公共特征根,即根据 (1) 的结论就有
AX = X (− A) 只有零解,即 AX + XA = 0 只有零解,从而 Α 可逆,即
八:证明:(1) 设 A 的特征多项式为 f (λ ) , B 的特征多项式为 g (λ ) ,由于 A, B 无公共特
( 征值,从而 f (λ ), g (λ )) = 1,所以 f ( B) 可逆,由于 AX = XB ,故对于 ∀n ∈ ∗ ,均有
An X = XBn ,就有 f ( A) X = Xf ( B) ,所以 Xf ( B) = 0 ⇒ X = 0 ,
⎡⎣En − αα T ⎤⎦−1 = ⎡⎣En + αα T ⎤⎦
三:证明: (1) 由于存在 m 阶可逆矩阵 P1 和 n 阶可逆矩阵 P2 ,有 A = P1 [Em 0] P2 ,即
2002考研数二真题及解析

2002年全国硕士研究生入学统一考试数学二试题一、填空题(本题共5小题,每小题3分,满分15分,把答案填在题中横线上)(1) 设函数tan 21,0arcsin()2,xx e x x f x ae x ⎧->⎪⎪=⎨⎪⎪≤⎩在0x =处连续,则a = .(2) 位于曲线(0)xy xe x -=≤<+∞下方,x 轴上方的无界图形的面积是_______.(3) 微分方程20yy y '''+=满足初始条件011,2x x yy =='==的特解是_________.(4) 1limn n →∞=_____ . (5) 矩阵022222222--⎡⎤⎢⎥-⎢⎥⎢⎥--⎣⎦的非零特征值是_________.二、选择题(本题共5小题,每小题3分,共15分,在每小题给出的四个选项中,只有一项符合题目要求,把所选项前的字母填在题后的括号内.)(1) 设函数()f u 可导,2()y f x =当自变量x 在1x =-处取得增量0.1x ∆=-时,相应的函数增量y ∆ 的线性主部为0.1,则(1)f '=( )(A)-1 (B)0.1 (C)1 (D)0.5 (2) 设函数()f x 连续,则下列函数中,必为偶函数的是( )(A)20()xf t dt ⎰ (B)20()xf t dt ⎰(C)[()()]xt f t f t dt --⎰(D)0[()()]xt f t f t dt +-⎰(3) 设()y x =是二阶常系数微分方程3xy py qy e '''++= 满足初始条(0)(0)0y y '==的特解,则当0x →,函数2ln(1)()x y x +的极限( )(A)不存在 (B)等于1 (C)等于2 (D)等于3 (4) 设函数()y f x =在(0,)+∞内有界且可导,则( )(A)当lim ()0x f x →+∞=时,必有lim ()0x f x →+∞'=.(B)当lim ()x f x →+∞'存在时,必有lim ()0x f x →+∞'=.(C)当0lim ()0x f x +→=时,必有0lim ()0x f x +→'=. (D)当0lim ()x f x +→'存在时,必有0lim ()0x f x +→'=. (5) 设向量组123,,ααα线性无关,向量1β 可由123,,ααα线性表示,而向量2β 不能由123,,ααα线性表示,则对于任意常数k ,必有( )(A)123,,ααα , 12k ββ+线性无关; (B)123,,ααα , 12k ββ+线性相关; (C)123,,ααα,12k ββ+线性无关; (D)123,,ααα,12k ββ+线性相关三、(本题满分6分)已知曲线的极坐标方程是1cos r θ=- ,求该曲线上对应于6πθ=处的切线与法线的直角坐标方程.四、(本题满分7分)设2232,102(),01(1)xx x x x f x xe x e ⎧+-≤<⎪⎪=⎨⎪≤≤⎪+⎩求函数1()()xF x f t dt -=⎰的表达式.五、(本题满分7分)已知函数()f x 在(0,)+∞内可导()0f x >,lim ()1x f x →+∞= , 且满足110()lim()()hx h f x hx e f x →+=,求()f x .六、(本题满分8分)求微分方程(2)0xdy x y dx +-=的一个解()y y x =,使得由曲线()y y x =, 与直线1,2x x ==以及x 轴所围成的平面图形绕x 轴旋转一周的旋转体体积最小.七、(本题满分7分)某闸门的性状与大小如图所示,其中直线l 为对 称轴,闸门的上部为矩形ABCD ,下部由二次抛物线 与线段AB 所围成,当水面与闸门的上端相平时,欲使 闸门矩形部分承受的水压力与闸门下部承受的水压力之 比为5:4,闸门矩形部分的高h 应为多少m (米)?八、(本题满分8分)设1103,1,2,)n x x n +<<==,证明数列{}n x 的极限存在,并求此极限.九、(本题满分8分)设0a b <<,证明不等式222ln ln a b a a b b a -<<+-十、(本题满分8分)设函数 ()f x 在0x =的某邻域内具有二阶连续导数,且(0)0,(0)0,f f '≠≠(0)0.f ''≠ 证明:存在惟一的一组实数123,,λλλ,使得当0h →时,123()(2)(3)(0)f h f h f h f λλλ++-是比2h 高阶的无穷小.十一、(本题满分6分)已知,A B 为3 阶矩阵,且满足124A B B E -=-,其中E 是3阶单位矩阵. (1) 证明:矩阵2A E -可逆;(2) 若120120002B -⎡⎤⎢⎥=⎢⎥⎢⎥⎣⎦,求矩阵.A十二、(本题满6分)已知4阶方阵1234(,,,),A αααα=1234,,,αααα均为4维列向量,其中234,,ααα线性无关,1232ααα=-.如果1234βαααα=+++,求线性方程组Ax β=的通解.D1m2002年全国硕士研究生入学统一考试数学二试题解析一、填空题(1)【答案】 -2【详解】如果分段函数()f x 连续,则()f x 在0点处的左右极限相等,从而确定a 的值. 当0x →+时,tan 1tan xex x ---;arcsin22x x,所以有 tan 00001tan lim ()lim lim lim 2arcsin222x x x x x e x xf x x x x++++→→→→---==-==; 20lim ()lim (0)xx x f x ae a f --→→=== 如果()f x 在0x =处连续,必有(0)(0)(0),f f f +-== 即 2.a =-(2)【答案】 1 【详解】面积00x x x xS xe dx xde xe e dx +∞+∞----+∞⎡⎤==-=--⎣⎦⎰⎰⎰lim 00x xx x b b xe e xe e ----→+∞+∞⎡⎤⎡⎤=--=--⎣⎦⎣⎦lim 11b bb be e --→+∞⎡⎤=---=⎣⎦ 其中 1lim limlim 0bb bb b b b bee e -→+∞→+∞→+∞==洛.(3)【答案】y =【详解】方法1:这是属于缺x 的(,)y f y y '''=类型. 命,dp dp dy dpy p y p dx dy dx dy'''====. 原方程20yy y '''+=化为20dpypp dy+=,得 0p =或0dpyp dy+= 0p =,即0dy dx =,不满足初始条件1'02y x ==,弃之;所以0p ≠所以,0dp yp dy +=,分离变量得dy dp y p =-,解之得1.C p y = 即1.C dy dx y= 由初始条件11,'2yy x x ====,可将1C 先定出来:1111,212C C ==. 于是得12dy dx y=解之得,22,y x C y =+=.以01x y ==代入,得1=,所以应取“+”号且21C =.于是特解是y =方法2:将20y y'''+=改写为()0yy ''=,从而得1yy C '=. 以初始条件1(0)1,(0)2y y '==代入,有1112C ⨯=,所以得12yy '=. 即21yy '=,改写为2()1y '=. 解得2,y x C =+y =1=""+且21C =. 于是特解y =(4)【答案】π【详解】利用定积分的概念将被积函数化为定积分求极限.因为1lim ...n n →∞ 11limnn i nππ→∞==11lim ()ni n i i f x nππ→∞==∆∑ 其中(),(1,2,,)i f x x i n nπ=∆==,所以根据定积分的定义,有1lim n n →∞+1cos 2x dx πππππ===⎰⎰(5)【答案】4【详解】记022222222A --⎡⎤⎢⎥=-⎢⎥⎢⎥--⎣⎦,则02222222222222222E A λλλλλλλ--⎛⎫⎛⎫⎛⎫ ⎪ ⎪ ⎪-=--=-- ⎪ ⎪ ⎪ ⎪ ⎪ ⎪---⎝⎭⎝⎭⎝⎭(对应元素相减)两边取行列式,E A λ-22222222λλλ=---22230222λλλλ+-行行222011222λλλλ -把第行的公因子提出来0122011222λλλ-⨯ -行行11111(1)22λλλ+⋅⋅--按第行展开(其中11(1)+-指数中的1和1分别是λ所在的行数和列数)2(22)λλ=--2(4)λλ=-令0E A λ-=,解得1230,4λλλ===,故4λ=是矩阵的非零特征值.(另一个特征值是0λ=(二重))二、选择题 (1)【答案】(D)【详解】在可导条件下,0()x x dyy x o x dx=∆=∆+∆,当00x x dy dx=≠时x x dy x dx=⋅∆称为y ∆的线性主部.而2()2dy x f x x x dx '⋅∆=∆,以1,0.1x x =-∆=-代入得(1)0.2dyx f dx'⋅∆=⨯,由题设它等于0.1,于是(1)0.5f '=,应选(D).(2)【答案】(D)【详解】对与(D),令0()[()()]xF x t f t f t dt =+-⎰,则0()[()()]xF x t f t f t dt --=+-⎰,令t u =-,则dt du =-,所以()[()()]()[()()]xxF x t f t f t dt u f u f u du --=+-=--+-⎰⎰[()()](),xu f u f u du F x =-+=⎰所以(D)为偶函数.同理证得(A)、(C)为奇函数,而(B)不确定,如()1f t t =+.故应选(D).(3)【答案】(C)【详解】由3xy py qy e '''++=,且(0)(0)0y y '==,可知(0)1y ''=方法1:因为当20x →时,22ln(1)x x +,所以20ln(1)lim ()x x y x →+=2000222lim lim lim 2()()()1x x x x x y x y x y x →→→==='''=, 故选(C).方法2:由于(0)(0)0,(0)1y y y '''===. 将函数()y x 按麦克劳林公式展开22()00()2x y x o x =+++,代入2ln(1)()x y x +,有222000222ln(1)1lim lim lim 211()()()22x x x x x o x y x x o x x→→→+==++=.(4) 【详解】方法1:排斥法.令21()sin f x x x =,则()f x 在(0,)+∞有界,2221()sin 2cos f x x x x'=-+, lim ()0x f x →+∞=,但lim ()x f x →+∞'不存在,故(A)不成立;0lim ()0x f x +→=,但 0lim ()10x f x +→'=≠,(C)和(D)不成立,故选(B). 方法2:证明(B)正确. 设lim ()x f x →+∞'存在,记lim ()x f x A →+∞'=,证明0A =.用反证法,若0A >,则对于02Aε=>,存在0X >,使当x X >时,()2A f x A ε'-<=,即3()2222A A A AA f x A '=-<<+=由此可知,()f x '有界且大于2A.在区间[,]x X 上应用拉格朗日中值定理,有()()()()()()2Af x f X f x X f X x X ξ'=+->+-从而lim ()x f x →+∞=+∞,与题设()f x 有界矛盾.类似可证当0A <时亦有矛盾. 故0A =.(5)【答案】A【详解】方法1:对任意常数k ,向量组123,,ααα,12k ββ+线性无关. 用反证法,若123,,ααα,12k ββ+线性相关,因已知123,,ααα线性无关,故12k ββ+可由123,,ααα线性表出. 即存在常数123,,λλλ,使得 12112233k ββλαλαλα+=++又已知1β可由123,,ααα线性表出,即存在常数123,,l l l ,使得1112233l l l βααα=++代入上式,得121122332112233()k k l l l ββαααβλαλαλα+=+++=++⇒2111222333()()()kl kl kl βλαλαλα=-+-+-与2β不能由123,,ααα线性表出矛盾.故向量组123,,ααα,12k ββ+线性无关,选(A) 方法2:用排除法B 选项:取0k =,向量组123,,ααα,12k ββ+即123,,ααα,2β线性相关不成立,否则因为123,,ααα,2β线性相关,又123,,ααα线性无关,故2β可由123,,ααα线性表出.即存在常数123,,λλλ,使得 2112233βλαλαλα=++与已知矛盾,排除(B).C 选项:取0k =,向量组123,,ααα,12k ββ+,即123,,ααα,1β线性无关不成立,因为1β可由123,,ααα线性表出,123,,ααα,1β线性相关,排除(C).D 选项:0k ≠时,123,,ααα,12k ββ+线性相关不成立.若123,,ααα,12k ββ+线性相关,因已知123,,ααα线性无关,故12k ββ+可由123,,ααα线性表出.即存在常数123,,λλλ,使得 12112233k ββλαλαλα+=++. 又已知1β可由123,,ααα线性表出,即存在常数123,,l l l ,使得1112233l l l βααα=++代入上式,得121122332112233()k l l l k ββαααβλαλαλα+=+++=++ ⇒2111222333()()()k l l l βλαλαλα=-+-+-因为0k ≠,故3311222123l l l kkkλλλβααα---=++与2β不能由123,,ααα线性表出矛盾.故123,,ααα,12k ββ+线性相关不成立,排除(D). 故选(A).三【详解】由极坐标到直角坐标的变换公式cos sin x r y r θθ=⎧⎨=⎩,化极坐标曲线1cos r θ=-为直角坐标的参数方程为(1cos )cos (1cos )sin x y θθθθ=-⎧⎨=-⎩, 即 2c o s c o ss i nc o s s i n x y θθθθθ⎧=-⎨=-⎩ 曲线上6πθ=的点对应的直角坐标为31,2424-- 22666cos sin cos 1.sin 2cos sin dy dy d dx dxd ππθθπθθθθθθθθθ===+-===-+于是得切线的直角坐标方程为13()24y x -=--,即504x y -=.(这是由直线的点斜式得到的,直线的点斜式方程为00()y y k x x -=-,由导数的几何意义知在6πθ=时斜率为1,且该点的直角坐标为31,42), 法线方程为113(()),24124y x --=---即1044x y +-+=.(这是由直线的点斜式方程及在同一点切线斜率与法线斜率为负倒数的关系而得) 四【详解】当10x -≤<时1()()x F x f t dt -=⎰223131(2)()122x x t t dt t t -=+=+-⎰3211.22x x =+-当01x ≤<时,011()()()()x xF x f t dt f t dt f t dt --==+⎰⎰⎰232001()12(1)tx t te t t dt e =++-+⎰0112(1)x t td e =--+⎰010211x t tx t dt e e =--+++⎰01211tx x t x e dt e e --=--+++⎰1ln(1)021t x x x e e -=---++1ln ln 2211x xx x e e e =--++++ 所以3211,1022()1ln ln 2,01112xx x x x x F x e x x e e ⎧+--≤<⎪⎪=⎨⎪-+-≤<⎪++⎩当当五【详解】因为11()ln h ()()()f x hx hf x f x hx ef x ⎛⎫+ ⎪⎝⎭⎛⎫+= ⎪⎝⎭,又 001()1limln lim (ln ()ln ())()h h f x hx f x hx f x h f x h →→⎛⎫+=+- ⎪⎝⎭, 0x ≠ 0ln ()ln ()lim()h f x hx f x x hx→+-=⨯()(ln ())()xf x f x x f x ''=⨯=从而得到 1()1()0()lim ()xf x hf x x h f x hx e ef x '→⎛⎫+= ⎪⎝⎭由题设于是推得()1(ln ())()xf x f x x f x x ''==,即21(ln ())f x x'= 解此微分方程,得 11ln ()f x C x=-+,改写成 1()x f x Ce -=再由条件lim ()1x f x C →+∞==,于是得1().xf x e -=六【详解】这是一阶线性微分方程21y y x'-=-,由通解公式(如果一个一阶线性方程为()()y p x y q x '+=那么通解为()()[()]p x dx p x dxy e q x e dx C -⎰⎰=+⎰)有 22[]dx dx x x y e e dx C -⎰⎰=-+⎰221[]x dx C x =-+⎰221(),12x C x Cx x x=+=+≤≤由曲线2y x Cx =+与1,2x x ==及x 轴围成的图形绕x 轴旋转一周的旋转体的体积为2222131157()()523V x Cx dx C C ππ=+=++⎰ (旋转体的体积公式:设有连续曲线:()()y f x a x b Γ=≤≤,()0f x ≥与直线,x a x b ==及x 轴围成平面图形.该图形绕x 轴旋转一周产生旋转体的体积为2()ba V f x dx π=⎰)取C 使V 最小,由求最值的方法知先求函数的驻点,即0dVdC=的点, 6215()052dV C dC π=+= 解得75.124C =- 又()0V C ''>,故75124C =-为V 的惟一极小值点,也是最小值点,于是所求曲线为275.124y x x =-七【详解】方法1:建立坐标系如下图,由于底部是二次抛物线我们设此抛物线为2y px q =+,由坐标轴的建立知此抛物线过(0,0),(1,1)点,把这两点代入抛物线的方程,得220011p q p q⎧=⨯+⎨=⨯+⎩,所以0,1q p ==. 即底部的二次抛物线是2y x =,11x -≤≤.细横条为面积微元,按所建立的坐标系及抛物线的方程,得到面积微元2dA xdy =,因此压力微元2(1)dp gx h y dy ρ=+- (这是由压力的公式得到的:压力=压强⨯面积)平板ABCD 上所受的总压力为1112(1)hP gx h y dy ρ+=+-⎰其中以1x =代入,计算得21P gh ρ=.抛物板AOB 上所受的总压力为1202(1),P gx h y dy ρ=+-⎰其中由抛物线方程知x =2124()315P g h ρ=+,由题意12:5:4P P =,即251244()315h h =+ 解之得2h =(米)(13h =-舍去),即闸门矩形部分的高应为2m .D八【详解】由103x <<知1x 及13x -()均为正数,故211130(3).22x x x <≤+-= (2()2a b ab +≤,a b 为正数)假设302k x <≤,则再一次用不等式2()2a b ab +≤,得113(3).22k k k x x x +≤+-=由数学归纳法知,对任意正整数2n ≥有302n x <≤.另一方面,1n n n x x x +-20.≤=≥所以{}n x 单调增加.单调增加数列{}n x 有上界,所以lim n n x →∞存在,记为.a由1n x +=两边取极限,于是由极限的运算性质得a =即2230,a a -=解得32a =或0a =,但因10x >且单调增,故0a ≠,所以 3lim 2n n x →∞=.九【详解】左、右两个不等式分别考虑. 先证左边不等式, 方法1:由所证的形式想到用拉格朗日中值定理.ln ln 1(ln ),0.x b ax a b b aξξξ=-'==<<<-而22112a b a bξ>>+中第二个不等式来自不等式222a b ab +>(当0a b <<时),这样就证明了要证明的左边.方法2:用单调性证,将b 改写为x 并移项,命222()()ln ln a x a x x a a xϕ-=--+,有()0a ϕ=. 22222124()()()a ax x a x x a x a x ϕ-'=-+++222222()4()0()()x a ax x a x a x a x --=+>++(当0a x <<),所以,当0x a >>时()x ϕ单调递增. 所以()()0x a ϕϕ>=,故()0b ϕ>, 即222()()ln ln 0a b a b b a a b ϕ-=-->+⇒22ln ln 2b a ab a a b->-+再证右边不等式,用单调性证,将b 改写为x 并移项,命()ln ln ),x x a x aψ=---有()0a ψ=,及21()0,x x ψ'==<所以当0x a >>时,()0x ψ<,再以x b =代入,得ln ln ),b a b a-<-即ln ln b a b a -<-右边证毕.十【详解】从题目结论出发,要证存在唯一的一组123,,λλλ,使得1232()(2)(3)(0)lim0h f h f h f h f L h λλλ→++-==由极限的四则运算法则知,分子极限应为0,即[]1230lim ()(2)(3)(0)h f h f h f h f λλλ→++=由于()f x 在0x =连续,于是上式变形为123(0)()(0).f f λλλ++= 由(0)0,f ≠知123 1.λλλ++= (1)由洛必达法则,1232()(2)(3)(0)limh f h f h f h f L hλλλ→++-=1230()2(2)3(3)lim 2h f h f h f h hλλλ→'''++= (2) 由极限的四则运算法则知分子的极限应是0,即1230lim(()2(2)3(3))0h f h f h f h λλλ→'''++=由于()f x '在0x =连续,于是上式变形为123(23)(0)0f λλλ'++=,由(0)0,f '≠知123230λλλ++= (3)对(2)再用洛必达法则,和()f x ''在0x =连续1231230()4(2)9(3)1lim(49)(0)22h f h f h f h L f λλλλλλ→''''''++''==++ 由(0)0f ''≠,故应有123490λλλ++= (4)将(1)、(3)、(4)联立解之,由于系数行列式11112320,149=≠ 由克莱姆法则知,存在唯一的一组解满足题设要求,证毕.十一【详解】(1) 由题设条件124A B B E -=-,两边左乘A ,得124AA B AB A -=-,即24B AB A =-24AB B A ⇒-=所以 (2)A E B -2AB B =-4488A A E E ==-+4(2)8A E E =-+,⇒(2)4(2)8A E B A E E ---=⇒(2)(2)48A E B A E E E ---⋅=⇒(2)(4)8A E B E E --=⇒1(2)(4)8A EB E E --=根据可逆矩阵的定义知2A E -可逆,且11(2)(4)8A EB E --=-.(2) 由(1)结果知11(2)(4)8A EB E --=-,根据逆矩阵的性质111()kA k A ---=,其中k为不等于零的常数,有1112(4)8(4)8A E B E B E --⎡⎤-=-=-⎢⎥⎣⎦故 18(4)2A B E E -=-+又 1204003204120040120002004002B E ---⎡⎤⎡⎤⎡⎤⎢⎥⎢⎥⎢⎥-=-=-⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥-⎣⎦⎣⎦⎣⎦(对应元素相减) 因为若()()1A E E A - →初等行变换,对[]4B E E -进行初等行变换,[]3201004120010002001B E E ⎡--⎤⎢⎥-=-⎢⎥⎢⎥-⎣⎦13120010320100002001⎡-⎤⎢⎥→--⎢⎥⎢⎥-⎣⎦、行互换2131200100801300011002+⨯⎡⎤⎢⎥-⎢⎥→-⎢⎥⎢⎥-⎢⎥⎣⎦行行12()8010120130100880011002⨯-⎡⎤⎢⎥-⎢⎥⎢⎥→--⎢⎥⎢⎥⎢⎥-⎢⎥⎣⎦行12211044100130100880011002+⨯⎡⎤-⎢⎥⎢⎥⎢⎥→--⎢⎥⎢⎥⎢⎥-⎢⎥⎣⎦行行 故11104413(4)0881002B E -⎡⎤-⎢⎥⎢⎥⎢⎥-=--⎢⎥⎢⎥⎢⎥-⎢⎥⎣⎦,代入18(4)2A B E E -=-+中,则 18(4)2A B E E -=-+110442138028821002⎡⎤-⎢⎥⎡⎤⎢⎥⎢⎥⎢⎥=--+⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦⎢⎥-⎢⎥⎣⎦(常数与矩阵相乘,矩阵的每一个元素都需要乘以该常数)220213020042-⎡⎤⎡⎤⎢⎥⎢⎥=--+⎢⎥⎢⎥⎢⎥⎢⎥-⎣⎦⎣⎦020110002⎡⎤⎢⎥=--⎢⎥⎢⎥-⎣⎦(对应元素相加)十二【详解】方法1:记[]1234,,,A αααα=,由234,,ααα线性无关,及123420,αααα=-+即1α可以由234,,ααα线性表出,故1234,,,αααα线性相关,及1234βαααα=+++即β可由1234,,,αααα线性表出,知[][][][]12341234123,,,,,,,(),,3r A r r r A r βααααβααααααα=====系数矩阵的秩与增广矩阵的秩相等,故Ax β=有解.对应齐次方程组0Ax =,其系数矩阵的秩为3,故其基础解系中含有4-3(未知量的个数-系数矩阵的秩)个线性无关的解向量,故其通解可以写成k ξ,η*是Ax β=的一个特解,根据非齐次线性方程组的解的结构定理,知Ax β=的通解为k ξη*+,其中k ξ是对应齐次方程组0Ax =的通解,η*是Ax β=的一个特解,因123420,αααα=-+故[]123412341220,,,010αααααααα⎡⎤⎢⎥-⎢⎥-+-==⎢⎥⎢⎥⎣⎦,故[]1,2,1,0Tξ=-是0Ax =的一个非零解向量,因为0Ax =的基础解系中只含有一个解向量,故[]1,2,1,0Tξ=-是0Ax =的基础解系.又[]1234123411,,,11βαααααααα⎡⎤⎢⎥⎢⎥=+++=⎢⎥⎢⎥⎣⎦,即1111A β⎡⎤⎢⎥⎢⎥=⎢⎥⎢⎥⎣⎦故[]1,1,1,1Tη*=是Ax β=的一个特解,根据非齐次线性方程组的解的结构定理,方程组的通解为[][]1,2,1,01,1,1,1T Tk -+.(其中k 是任意常数) 方法2:令[]1234,,,Tx x x x x =,则线性非齐次方程为[]1234,,,Ax x αααα=[]12123434,,,x x x x αααα⎡⎤⎢⎥⎢⎥=⎢⎥⎢⎥⎣⎦11223344x x x x ααααβ=+++=已知1234βαααα=+++,故11223344x x x x αααα+++=1234αααα+++将1232ααα=-代入上式,得23122334423234(2)(2)x x x x αααααααααα-+++=-+++⇒21312233442323424223x x x x x αααααααααααα-+++=-+++=+⇒12231334424(2)30x x x x x αααααα+-++--= ⇒12213344(23)()(1)0x x x x x ααα+-+-++-=由已知234,,ααα线性无关,根据线性无关的定义,不存在不全为零的常数使得2233440k k k ααα++=,上式成立当且仅当1213423010x x x x x +=⎧⎪-+=⎨⎪-=⎩ 其系数矩阵为210010100001⎛⎫⎪- ⎪ ⎪⎝⎭,因为3阶子式10001010001=≠,其秩为3,故其齐次线性方程组的基础解系中存在1个(4-3)线性无关的解向量,取自由未知量3x k =,则方程组有解431321,,,23x x k x x k x k =====-+故方程组Ax β=有通解123410232310101x k x k k x k x ⎡⎤⎡⎤⎡⎤⎡⎤⎢⎥⎢⎥⎢⎥⎢⎥-+-⎢⎥⎢⎥⎢⎥⎢⎥==+⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦⎣⎦⎣⎦.(其中k 是任意常数)。
2000年考研数学试题详解及评分参考

……2 分
即 f (x) ( 1 1) f (x) 1 e2x , x 0 .按一阶线性非齐次微分方程通解公式,有
x
x
f
(
x)
e
(1
1 x
)dx
[
1
e2x
e
(
1 x
1)
dx
dx
C]ex[ Nhomakorabea1 e2x.xexdx C] ex (ex C) .
……5 分
f22
1 x2
g y x3
g .
……5 分
五、(本题满分 6 分)
计算曲线积分 I xdy ydx ,其中 L 是以点 (1, 0) 为中心,R 为半径的圆周 (R 1) .
L 4x2 y2
取逆时针方向.
解: P
y 4x2
y2
,Q
x 4x2
y2
P
0,
……4 分
即得
L
xdy ydx 4x2 y2
C
xdy ydx 4x2 y2
2 0
1 2
2
2
d
.
……6 分
六、(本题满分 7 分) 设对于半空间 x 0 内任意的光滑有向封闭曲面 S ,都有
2000 年 • 第 4 页
郝海龙:考研数学复习大全·配套光盘·2000 年数学试题详解及评分参考
所以 zdS 4 xdS ,故选 (C).
S
S1
(3) 设级数 un 收敛,则必收敛的级数为 n 1
(A) 1n un
n 1
浙江大学2000年研究生数学分析试题参考答案

浙江大学2000年研究生数学分析试题一.(共10分)(1)求极限1(1)lim xx e x x→-+解:原式=12(1)ln(1)2(1)lim(1)xx x xe x x x x ++-+→+=(2)设2101,,,2,3,,lim 2n n n nn x x x a x b x n x --→∞-==== 求解:)(21211-----=-n n n n x x x x ,这可以构造成为一个压缩映象,则数列收敛,以下求解就按照}{1--n n x x 这个数列来进行即可。
二.(共10分)1.设K ab a f b f K f b a =--=+-→→)()(lim,)0(0试证明‘证: K ab a f f f b f ab a f b f b a b a ==--+-=--+-+-→→→→ )()0()0()(lim )()(lim2.设()f x 在[,]a b 上连续,()f x ''在(,)a b 内存在,试证明存在(,)a b ξ∈,使得)(4)()2(2)()(2ξf a b b a f a f b f ''-=+-+分析:考虑函数)()()(2x f x f x F b a -+=+即可三.(共15分)1.求数项级数∑∞=12n nn的和S分析:S=2S-S2.试证明∑∞==11)(n xnx s 在),1(∞上的连续函数四.(共15分) 1.设方程组⎩⎨⎧=+=+++0sin sin 0v y u x v u y x ,确定了可微函数⎩⎨⎧==),(),(y x v v y x u u ,试求yvx v du ∂∂∂∂,,分析:用隐函数组的方法求解; 2.设2)()d yx y F y x x=,求)1(F '分析:dt dx dx y F tty t y yxyx yxyx ⎰⎰⎰-=+=1cos cos 0cos 0cos 232222)(五.(共30分) 1.计算定积分2sin cos 1cos x x I dx xπ=+⎰分析:令t=cosx ,I=0。
浙大2000年-2002年数学分析考研试题及解答

浙江大学2000年数学分析考研试题及解答一、(1)求极限()11limtt t et →+-;解 ()111ln(1)ln(1)1011limlimlimt t tttt t t t eeeee ttt++-→→→+---==1ln(1)10ln(1)11lim ln(1)1t tt t e t e t t t+-→+--=+- 20000ln(1)111ln(1)1lim lim lim lim 22(1)2t t t t t t t t e t t e e e e t t t t t →→→→+--+--+=====-+; 或()1ln(1)11ln(1)21ln(1)()1(1)limlimlim1t tt ttt t t t e t eeet t t tt++→→→+-+--+==20ln(1)1lim t t t t e t→-++=2011(1)1lim 2t t t e t →-++=20lim 2(1)2t t e e t t →-==-+。
(2)设01,x a x b ==,211()2n n n x x x --=-,求nn xlim ∞→.解 由条件,得 12111211()()22n n n n n n n x x x x x x x ------+=-+=+, 反复使用此结果1111011()()()()22n n n n x x x x b a ---+=+=+, ,2,1=n ;于是 21212221100()()()n n n n n x x x x x x x x ++-=+-++++-22111()()()()()22n n a b a b a b a -=++-++++-2111()222()()1331()2n b a a b a a b a +---=+-→+-=--,)(∞→n ; 22212122100()()()n n n n n x x x x x x x x ---=+-++-++212211()()()()()22n n a b a b a b a --=+-++-++211()222()()1331()2na b a b a a b a ---=-++→-++=--,)(∞→n , 当2a b =时,lim 0nn x →∞=;当2a b ≠时,lim n n x →∞不存在。
最新浙江大学数学分析试题及解答汇总

2005年浙江大学数学分析试题及解答浙江大学2005年数学分析解答一 (10分)计算定积分20sin x e xdx π⎰解:2sin xe xdx π⎰=()011cos 22x e x dx π⎡⎤-⎢⎥⎣⎦⎰ ()01x e dx e ππ=-⎰ 由分部积分法0cos 2xe xdx π=⎰()1e π-+20sin 2x e xdx π=⎰()1e π-04cos 2x e xdx π-⎰所以0cos 2x e xdx π=⎰()115e π-,所以20sin x e xdx π⎰=()215e π- 解毕 二 (10分)设()f x 在[0,1]上Riemann可积,且1()2f x dx =⎰,计算 11lim 4ln[1()]nn i if n n →∞=+∑解:因为()f x 在[0,1]上Riemann 可积,所以0,()M f x M ∃>≤,所以1()0if n n→ 因为0ln(1)lim 1x x x →+=,所以114ln[1()]n i i f n n =+∑与114()ni i f n n =∑等价且极限值相等由Riemann 积分的定义:11lim 4ln[1()]nn i if n n →∞=+∑=410()f x dx =⎰解毕三 (15分)设,,a b c 为实数,且1,0b c >-≠试确定,,a b c 的值,使得30sin limln(1)x x b ax xc t dtt →-=+⎰解:若0b ≠,显然30sin lim0ln(1)x x b ax xt dtt →-=+⎰,这与0c ≠矛盾,所以0b =计算300sin limln(1)x x ax xt dtt →-+⎰,利用洛必达法则:33000sin cos lim lim ln(1)ln(1)x x x ax x a xt x dt t x→→--=++⎰,易有30ln(1)lim0x x x→+=,若1a ≠, 33000sin cos limlim ln(1)ln(1)x x x ax x a x t x dt t x →→--==∞++⎰,矛盾,所以1a =.计算301cos lim ln(1)x xx x→-+,继续利用洛必达法则:33001cos cos limlim ln(1)ln(1)x x x x x x x x x →→--=++24003321cos sin 2sin cos lim lim 3631(1)x x x x x x x x x x x x x →→-++==-++332243343cos sin 1lim(612)(1)6(63)(1)2(1)x x x x c x x x x x x x →-===-+--++ 解毕 四 (15分)设()f x 在[,]a b 上连续,且对每一个[],x a b ∈,存在[],y a b ∈,使得1()()2f y f x ≤,证明:在存在[,],a b ξ∈使得()0f ξ=证明:反证法,由于()f x 在[,]a b 上连续,由闭区间上连续函数的性质,不妨假设0()m f x M <<<对于任选的一点1x ,存在2,x 使得211()()2f x f x ≤, 存在3,x 使得321211()()()22f x f x f x ≤≤所以1111[,],()()0,()22n n n n Mx a b f x f x n --∈≤≤→→∞即lim ()0n n f x →∞=,但对所有的x, 0()m f x M <<<,矛盾.所以[,]a b 存在零点 证毕五 (20分)(1)设()f x 在[,)a +∞上连续,且()af x dx +∞⎰收敛。
2002年考研数学三真题及答案解析

e(x ) , 若x ,
f (x; ) 0,
若x
而 X1, X 2 , , X n 是来自总体 X 的简单随机样本,则未知参数 的矩估计量为
二、选择题(本题共 5 小题,每小题 3 分,共 15 分,在每小题给出的四个选项中,只有一项 符合题目要求,把所选项前的字母填在题后的括号内.)
(1) 设函数 f (x) 在闭区间[a,b] 上有定义,在开区间 (a,b) 内可导,则 ( )
2002 年全国硕士研究生入学统一考试数学三试题
一、填空题(本题共 5 小题,每小题 3 分,满分 15 分,把答案填在题中横线上)
n
(1)
设常数 a
1 2
,则
lim
n
ln
n 2na 1
n(1 2a)
.
1
y
1
1
(2) 交换积分次序: 4 dy
0
y
f (x, y)dx
2 1
dy
2 f (x, y)dx
y y y ex
(2)利用(1)的结果求幂级数
x3n 的和函数.
n0 3n!
八、(本题满分 6 分)
设函数 f (x), g(x) 在[a,b] 上连续,且 g(x) 0 .利用闭区间上连续函数性质,证明存在
b
b
一点 [a,b],使 f (x)g(x)dx f ( ) g(x)dx .
求该设备每次开机无故障工作的时间Y 的分布函数 F ( y) .
2002 年全国硕士研究生入学统一考试数学三试题解析
一、填空题
(1)【答案】 1 1 2a
【详解】“ln”里面为“1”型,通过凑成重要极限形式来求极限,
n
n(12a) 1
2002考研数学一真题及答案解析

2002年全国硕士研究生入学统一考试数学一试题一、填空题(本题共5小题,每小题3分,满分15分.把答案填在题中横线上.) (1)⎰∞+exx dx2ln =.(2)已知函数()y y x =由方程0162=-++x xy e y 确定,则(0)y ''=. (3)微分方程02='+''y y y 满足初始条件0011,'2x x yy ====的特解是.(4)已知实二次型323121232221321444)(),,(x x x x x x x x x a x x x f +++++=经正交变换x Py =可化成标准型216y f =,则a =.(5)设随机变量X 服从正态分布2(,)(0)N μσσ>,且二次方程042=++X y y 无实根的概率为12,则μ= .二、选择题(本题共5小题,每小题3分,满分15分.每小题给出的四个选项中,只有一项符合题目要求,把所选项前的字母填在题后的括号内.)(1)考虑二元函数),(y x f 的下面4条性质: ①),(y x f 在点),(00y x 处连续; ②),(y x f 在点),(00y x 处的两个偏导数连续; ③),(y x f 在点),(00y x 处可微;④),(y x f 在点),(00y x 处的两个偏导数存在.若用“P Q ⇒”表示可由性质P 推出性质Q ,则有(A ) ②⇒③⇒①. (B ) ③⇒②⇒①. (C ) ③⇒④⇒①.(D ) ③⇒①⇒④.(2)设0(1,2,3,)n u n ≠=L ,且lim1n nnu →∞=,则级数11111(1)()n n n n u u ∞+=+-+∑ (A ) 发散. (B ) 绝对收敛.(C ) 条件收敛.(D ) 收敛性根据所给条件不能判定.(3)设函数()y f x =在(0,)+∞内有界且可导,则 (A ) 当0)(lim =+∞→x f x 时,必有0)(lim ='+∞→x f x .(B ) 当)(lim x f x '+∞→存在时,必有0)(lim ='+∞→x f x .(C ) 当0lim ()0x f x +→=时,必有0lim ()0x f x +→'=. (D ) 当0lim ()x f x +→'存在时,必有0lim ()0x f x +→'=.(4)设有三张不同平面的方程123i i i i a x a y a z b ++=,3,2,1=i ,它们所组成的线性方程组的系数矩阵与增广矩阵的秩都为2,则这三张平面可能的位置关系为(5)设1X 和2X 是任意两个相互独立的连续型随机变量,它们的概率密度分别为1()f x 和2()f x ,分布函数分别为1()F x 和2()F x ,则(A ) 1()f x +2()f x 必为某一随机变量的概率密度. (B ) 1()f x 2()f x 必为某一随机变量的概率密度. (C ) 1()F x +2()F x 必为某一随机变量的分布函数. (D ) 1()F x 2()F x 必为某一随机变量的分布函数.三、(本题满分6分) 设函数)(x f 在0x =的某邻域内具有一阶连续导数,且(0)0,(0)0f f '≠≠,若()(2)(0)af h bf h f +-在0→h 时是比h 高阶的无穷小,试确定b a ,的值.四、(本题满分7分) 已知两曲线)(x f y =与⎰-=x t dt e yarctan 02在点(0,0)处的切线相同,写出此切线方程,并求极限)2(lim nnf n ∞→.五、(本题满分7分) 计算二重积分dxdy e Dy x⎰⎰},max{22,其中}10,10|),{(≤≤≤≤=y x y x D .六、(本题满分8分)设函数)(x f 在(,)-∞+∞内具有一阶连续导数,L 是上半平面(y >0)内的有向分段光滑曲线,其起点为(b a ,),终点为(d c ,).记2221[1()][()1],L xI y f xy dx y f xy dy y y=++-⎰(1)证明曲线积分I 与路径L 无关; (2)当cd ab =时,求I 的值.七、(本题满分7分)(1)验证函数333369()1()3!6!9!(3)!nx x y x x n =++++++-∞<<+∞L L 满足微分方程x e y y y =+'+'';(2)利用(1)的结果求幂级数30(3)!nn x n ∞=∑的和函数.八、(本题满分7分)设有一小山,取它的底面所在的平面为xOy 坐标面,其底部所占的区域为2{(,)|D x y x =275}y xy +-≤,小山的高度函数为),(y x h xy y x +--=2275.(1)设),(00y x M 为区域D 上一点,问),(y x h 在该点沿平面上什么方向的方向导数最大?若记此方向导数的最大值为),(00y x g ,试写出),(00y x g 的表达式.(2)现欲利用此小山开展攀岩活动,为此需要在山脚下寻找一上山坡最大的点作为攀登的起点.也就是说,要在D 的边界线2275x y xy +-=上找出使(1)中),(y x g 达到最大值的点.试确定攀登起点的位置.九、(本题满分6分)已知四阶方阵),,,(4321αααα=A ,4321,,,αααα均为4维列向量,其中432,,ααα线性无关,3212ααα-=,如果4321ααααβ+++=,求线性方程组β=Ax 的通解.十、(本题满分8分) 设,A B 为同阶方阵,(1)若,A B 相似,证明,A B 的特征多项式相等. (2)举一个二阶方阵的例子说明(1)的逆命题不成立. (3)当,A B 均为实对称矩阵时,证明(1)的逆命题成立.十一、(本题满分7分) 设维随机变量X 的概率密度为10,cos ,()220,x x f x π⎧≤≤⎪=⎨⎪⎩其他.对X 独立地重复观察4次,用Y 表示观察值大于3π的次数,求2Y 的数学期望.十二、(本题满分7分)其中1(0)2θθ<<是未知参数,利用总体X 的如下样本值3,1,3,0,3,1,2,3,求θ的矩估计值和最大似然估计值.2002年考研数学一试题答案与解析一、填空题 (1)【分析】 原式2ln 11.ln ln eed x x x+∞+∞==-=⎰(2)【分析】 方程两边对x 两次求导得'6'620,y e y xy y x +++=① 2'''6''12'20.y y e y e y xy y ++++=②以0x =代入原方程得0y =,以0x y ==代入①得'0,y =,再以'0x y y ===代入②得''(0) 2.y =-(3)【分析】 这是二阶的可降阶微分方程.令'()y P y =(以y 为自变量),则'''.dy dP dPy P dx dx dy=== 代入方程得20dP yPP dy +=,即0dP y P dy+=(或0P =,但其不满足初始条件01'2x y ==). 分离变量得0,dP dy P y+= 积分得ln ln ',P y C +=即1C P y=(0P =对应10C =); 由0x =时11,',2y P y ===得11.2C =于是又由01x y==得21,C =所求特解为y =(4)【分析】 因为二次型Tx Ax 经正交变换化为标准型时,标准形中平方项的系数就是二次型矩阵A 的特征值,所以6,0,0是A 的特征值.又因iiia λ=∑∑,故600, 2.a a a a ++=++⇒=(5)【分析】 设事件A 表示“二次方程042=++X y y 无实根”,则{1640}{A X X =-<=>4}.依题意,有1(){4}.2P A P X =>=而 4{4}1{4}1(),P X P X μΦσ->=-≤=-即414141(),(),0. 4.22μμμΦΦμσσσ----===⇒=二、选择题(1)【分析】 这是讨论函数(,)f x y 的连续性,可偏导性,可微性及偏导数的连续性之间的关系.我们知道,(,)f x y 的两个偏导数连续是可微的充分条件,若(,)f x y 可微则必连续,故选(A ).(2)【分析】 由1lim 101n n un n →+∞=>⇒充分大时即,N n N ∃>时10n u >,且1lim 0,n nu →+∞=不妨认为,0,n n u ∀>因而所考虑级数是交错级数,但不能保证1nu 的单调性. 按定义考察部分和111111111111(1)()(1)(1)nn nk k k n k k k k k k k S u u u u +++===++=-+=-+-∑∑∑1111111(1)11(1)1(1)(),k n nn l k l k l n n u u u u u ++==+--=-+-=+→→+∞∑∑⇒原级数收敛.再考察取绝对值后的级数1111()n nn u u ∞=++∑.注意111112,11n n n n u u n n n u u n n++++=+⋅→+ 11n n ∞=∑发散⇒1111()n n n u u ∞=++∑发散.因此选(C ).(3)【分析】 证明(B )对:反证法.假设lim ()0x f x a →+∞'=≠,则由拉格朗日中值定理,(2)()'()()f x f x f x x ξ-=→∞→+∞(当x →+∞时,ξ→+∞,因为2x x ξ<<);但这与(2)()(2)()2f x f x f x f x M -≤+≤矛盾(()).f x M ≤(4)【分析】 因为()()23r A r A ==<,说明方程组有无穷多解,所以三个平面有公共交点且不唯一,因此应选(B ).(A )表示方程组有唯一解,其充要条件是()() 3.r A r A ==(C )中三个平面没有公共交点,即方程组无解,又因三个平面中任两个都不行,故()2r A =和()3r A =,且A 中任两个平行向量都线性无关.类似地,(D )中有两个平面平行,故()2r A =,()3r A =,且A 中有两个平行向量共线.(5)【分析】 首先可以否定选项(A )与(C ),因121212[()()]()()21,()()112 1.f x f x dx f x dx f x dx F F +∞+∞+∞-∞-∞-∞+=+=≠+∞++∞=+=≠⎰⎰⎰对于选项(B ),若121,21,1,01,()()0,0,x x f x f x -<<-<<⎧⎧==⎨⎨⎩⎩其他,其他,则对任何(,),x ∈-∞+∞ 12()()0f x f x ≡,12()()01,f x f x dx +∞-∞=≠⎰因此也应否定(C ),综上分析,用排除法应选(D ).进一步分析可知,若令12max(,)X X X =,而~(),1,2,i i X f x i =则X 的分布函数()F x 恰是12()().F x F x1212(){max(,)}{,}F x P X X x P X x X x =≤=≤≤1212{}{}()().P X x P X x F x F x =≤≤=三、【解】 用洛必达法则.由题设条件知lim[()(2)(0)](1)(0).h af h bf h f a b f →+-=+-由于(0)0f '≠,故必有10.a b +-=(2)'(0)0,a b f =+=及(0)0f '≠,则有20a b +=. 综上,得2, 1.a b ==-四、【解】 由已知条件得(0)0,f =22arctan arctan 02'(0)()'1,1xx t xx x e f e dt x --=====+⎰故所求切线方程为y x =.由导数定义及数列极限与函数极限的关系可得五、【分析与求解】 D 是正方形区域如图.因在D 上被积函数分块表示2222,,max{,}(,),,,x x y x y x y D y x y ⎧≥⎪=∈⎨≤⎪⎩于是要用分块积分法,用y x =将D 分成两块:1212,{},{}.D D D D D y x D D y x ==≤=≥U I I⇒I 222212max{,}max{,}xy xy D D e dxdy e dxdy =+⎰⎰⎰⎰2221212x y x D D D e dxdy e dxdy e dxdy =+=⎰⎰⎰⎰⎰⎰(D 关于y x =对称)2102xx dx e dy =⎰⎰(选择积分顺序)221102 1.x xxe dx e e ===-⎰六、【分析与求解】(1)易知Pdx Qdy +∃原函数,2211()()()()()x Pdx Qdy dx yf xy dx xf xy dy dy ydx xdy f xy ydx xdy y y y+=++-=-++ 0()()()[()].xy x xd f xy d xy d f t dt y y =+=+⎰⇒在0y >上Pdx Qdy +∃原函数,即0(,)()xy xu x y f t dt y =+⎰. ⇒积分I 在0y >与路径无关.(2)因找到了原函数,立即可得(,)(,)(,).c d a b c a I u x y d b==-七、【证明】 与书上解答略有不同,参见数三2002第七题(1)因为幂级数3693()13!6!9!(3)!nx x x x y x n =++++++L L的收敛域是()x -∞<+∞,因而可在()x -∞<+∞上逐项求导数,得25831'()2!5!8!(31)!n x x x x y x n -=+++++-L L ,4732''()4!7!(32)!n x x x y x x n -=+++++-L L ,所以2'''12!!nx x x y y y x e n ++=+++++=L L ()x -∞<+∞.(2)与'''xy y y e ++=相应的齐次微分方程为'''0y y y ++=,其特征方程为210λλ++=,特征根为1,2122λ=-±.因此齐次微分方程的通解为212(cossin )22x Y eC x C x -=+. 设非齐次微分方程的特解为xy Ae *=,将y *代入方程'''xy y y e ++=可得13A =,即有13x y e *=.于是,方程通解为2121(cossin )223xx y Y y eC x C x e -*=+=++. 当0x =时,有112121(0)1,23,0.311'(0)0.223y C C C y C ⎧==+⎪⎪⇒==⎨⎪==-++⎪⎩于是幂级数30(3)!n n x n ∞=∑的和函数为221()33x x y x e x e -=+()x -∞<+∞八、【分析与求解】(1)由梯度向量的重要性质:函数),(y x h 在点M 处沿该点的梯度方向0000(,)(,)0000(,){,}{2,2}x y x y h h h x y x y y x x y∂∂==-+-+∂∂grad方向导数取最大值即00(,)(,)x y h x y grad 的模,00(,)g x y ⇒=(2)按题意,即求(,)g x y 求在条件22750x y xy +--=下的最大值点⇔22222(,)(2)(2)558g x y y x x y x y xy =-+-=+-在条件22750x y xy +--=下的最大值点. 这是求解条件最值问题,用拉格朗日乘子法.令拉格朗日函数2222(,,)558(75),L x y x y xy x y xy λλ=+-++--则有22108(2)0,108(2)0,750.Lx y x y x Ly x y x y L x y xy λλλ⎧∂=-+-=⎪∂⎪∂⎪=-+-=⎨∂⎪⎪∂=+--=⎪∂⎩ 解此方程组:将①式与②式相加得()(2)0.x y x y λ++=⇒=-或 2.λ=-若y x =-,则由③式得2375x =即5, 5.x y =±=m 若2,λ=-由①或②均得y x =,代入③式得275x =即x y =±=±于是得可能的条件极值点1234(5,5),(5,5),(M M M M ----现比较222(,)(,)558f x y g x y x y xy ==+-在这些点的函数值:1234()()450,()()150.f M f M f M f M ====因为实际问题存在最大值,而最大值又只可能在1234,,,M M M M 中取到.因此2(,)g x y 在12,M M 取到在D 的边界上的最大值,即12,M M 可作为攀登的起点.九、【解】由432,,ααα线性无关及3212ααα-=知,向量组的秩1234(,,,)3r αααα=,即矩阵A 的秩为3.因此0Ax =的基础解系中只包含一个向量.那么由123412312(,,,)2010ααααααα⎡⎤⎢⎥-⎢⎥=-+=⎢⎥⎢⎥⎣⎦知,0Ax =的基础解系是(1,2,1,0).T-再由123412341111(,,,)1111A βαααααααα⎡⎤⎡⎤⎢⎥⎢⎥⎢⎥⎢⎥=+++==⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦知,(1,1,1,1)T是β=Ax 的一个特解.故β=Ax 的通解是1121,1101k ⎡⎤⎡⎤⎢⎥⎢⎥-⎢⎥⎢⎥+⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦其中k 为任意常数.十、【解】 (1)若,A B 相似,那么存在可逆矩阵P ,使1,P AP B -=故111E B E P AP P EP P AP λλλ----=-=-11().P E A P P E A P E A λλλ--=-=-=-(2)令0100,,0000A B ⎡⎤⎡⎤==⎢⎥⎢⎥⎣⎦⎣⎦那么2.E A E B λλλ-==- 但,A B 不相似.否则,存在可逆矩阵P ,使10P AP B -==.从而100A P P -==,矛盾,亦可从()1,()0r A r B ==而知A 与B 不相似.(3)由,A B 均为实对称矩阵知,,A B 均相似于对角阵,若,A B 的特征多项式相等,记特征多项式的根为1,,,n λλL 则有A 相似于1,n λλ⎡⎤⎢⎥⎢⎥⎢⎥⎣⎦O B也相似于1.n λλ⎡⎤⎢⎥⎢⎥⎢⎥⎣⎦O 即存在可逆矩阵,P Q ,使111.n P AP Q BQ λλ--⎡⎤⎢⎥==⎢⎥⎢⎥⎣⎦O 于是111()().PQ A PQ B ---=由1PQ -为可逆矩阵知,A 与B 相似.十一、【解】 由于311{}cos ,3222x P X dx πππ>==⎰依题意,Y 服从二项分布1(4,)2B ,则有2222111()()4(4) 5.222EY DY EY npq np =+=+=⨯⨯+⨯=十二、【解】 22012(1)23(12)34,EX θθθθθθ=⨯+⨯-+⨯+⨯-=-1(3).4EX θ=- θ的矩估计量为1ˆ(3),4X θ=-根据给定的样本观察值计算1(31303123)8x =+++++++ 2.=因此θ的矩估计值11ˆ(3).44x θ=-= 对于给定的样本值似然函数为624()4(1)(12),ln ()ln 46ln 2ln(1)4ln(12),L L θθθθθθθθ=--=++-+-2ln ()62824286.112(1)(12)d L d θθθθθθθθθθ-+=--=----令ln ()0d L d θθ=,得方程2121430θθ-+=,解得θ=1,2θ=>不合题意). 于是θ的最大似然估计值为ˆθ=。
(NEW)浙江大学819数学分析历年考研真题汇编(含部分答案)

正数 ,使得 中任何两点 满足
时,必属于某个开区间
.
六、(15分) 用球面坐标 .
变换方程
七、(10分) 计算
八、(15分) 求
其中
.
. 在条件
九、(15分) 利用公式
下的最大最小值, 计算积分
的值.(说明计算过程中每一步的合理性)
十、(20分) 设 为 中光滑区域, 为其边界, 在
上
有连续二阶导数.证明:
求曲面积分
,其中 是曲面
的上侧.
五、(15分) 设二元函数 .
试比较
与
给出一个使等式 之.
在正方形区域
上连续,记
的大小并证明之; 成立的充分条件并证明
六、(15分) 设 是在 上可积且在 处连续的函数,记 .
证明:
.
2000年浙江大学804数学分析考研真题
浙江大学2000年攻读硕士学位研究生入学试题
.
其中 为沿边界 外法线方向的导数, 为边界上的面积元, .
的坐标为
,函数
.
证明: 在
上成立.
设
是以 为中心 为半径的球,
上 满足 ,则
为其边界.若在
.
2003年浙江大学431数学分析考研真题
浙江大学2003年攻读硕士学位研究生入学试题 考试科目:数学分析(431) 考生注意: 1.本试卷满分为150 分,全部考试时间总计180 分钟; 2.答案必须写在答题纸上,写在试题纸上或草稿纸上均无效。
浙江大学2002年攻读硕士学位研究生入学试题
考试科目:数学分析
一、(30分) 用“ 语言”证明
;
给出一个一元函数 ,在有理点都不连续,在无理点都连续, 并证明之;
浙江大学99-06年研究生数学分析试题-12页word资料

浙江大学2019年研究生数学分析试题一.求极限)(ln )1(∞→-n nn n Limn 二.在xy 平面上求一点,使它到三条直线0,0==y x 及0162=-+y x 的距离平方和最小三.计算二重积分⎰⎰Dxydxdy ,其中D 由曲线 y x y x +=+22 所围城的区域四.设)(x f 在0>x 时连续,3)1(=f ,并且⎰⎰⎰+=xy xy dt t f y dt t f x dt t f 111)()()(,)0,0(>>y x ,试求函数)(x f五.设函数),()(b a t f 在连续,若有数列)),(,(,b a y x a y a x n n n n ∈→→使)()()()(∞→=∞→=n B y Limf n A x Limf n n 及,则对A ,B 之间的任意数μ,可找到数列a x n →,使得μ=)(n z Limf六.设∑===<≤nk k n k a s n k a a 1,....,2,1,0令,证明不等式n nnk kk s n ns a a -≥-∑=11 七.设函数f 在nab v a f f f b a n n vn -=+=>δδ),(,0],[记上连续,且,试证明:)}()(ln 1exp{∞→-=⎰n dx x f a b ba并利用上述等式证明下式r dx r x r ln 2)cos 21ln(21202=+-⎰ππ )1(>r 八.从调和级数 +++++n131211中去掉所有在分母的十进表示中含数码9的项,证明由此所得余下的级数必定是收敛的浙江大学2000年研究生数学分析试题一.(共10分)(1)求极限10(1)limxx e x x →-+(2)设2101,,,2,3,,lim 2n n n nn x x x a x b x n x --→∞-====求二.(共10分)1.设Kab a f b f K f b a =--=+-→→)()(lim ,)0(00试证明‘2.设()f x 在[,]a b 上连续,()f x ''在(,)a b 内存在,试证明存在(,)a b ξ∈,使得)(4)()2(2)()(2ξf a b b a f a f b f ''-=+-+三.(共15分)1.求数项级数∑∞=12n nn的和S2.试证明∑∞==11)(n xn x s 在),1(∞上的连续函数四.(共15分)1.设方程组⎩⎨⎧=+=+++0sin sin 0v y u x v u y x ,确定了可微函数⎩⎨⎧==),(),(y x v v y x u u ,试求y vx v du ∂∂∂∂,, 2.设2)()d yx y F y x x =,求)1(F '五.(共30分)1.计算定积分2sin cos 1cos x xI dx x π=+⎰2.求以曲面22y xez --=为顶,以平面0=z 为底,以柱面122=+y x 为侧面的曲顶柱体的体积V 3.设∑+表示半球面)1(12222≤+--=y x y x z 的上侧,求第二类曲面积分⎰⎰∑++-++=+dxdy y z x dzdx z y x dydz z y x J 222)2()2()(六.(共20分)1.将函数x x f =)( )(ππ≤≤-x 展开成Fourier 级数2.求级数∑∞=121n n 的和 3.计算广义积分⎰-10)1ln(dx xx浙江大学2000年研究生数学分析试题一.(共10分)(1)求极限10(1)limxx e x x →-+解:原式=12(1)ln(1)2(1)lim(1)xx x xe x x x x ++-+→+=(2)设2101,,,2,3,,lim 2n n n nn x x x a x b x n x --→∞-====求解:)(21211-----=-n n n n x x x x ,这可以构造成为一个压缩映象,则数列收敛,以下求解就按照}{1--n n x x 这个数列来进行即可。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
浙江大学2000年数学分析考研试题及解答一、(1)求极限()11limtt t et→+-;解 ()111ln(1)ln(1)111limlimlimt t ttt t t t t eeeee ttt++-→→→+---==1ln(1)1ln(1)11limln(1)1t tt t e t e t tt+-→+--=+-200ln(1)111ln(1)1limlimlim lim22(1)2t t t t t t tt e t te e e e tttt t →→→→+--+--+=====-+;或()1ln(1)11ln(1)21ln(1)()1(1)limlimlim1t tt ttt t t t e t ee et t tt t ++→→→+-+--+==2ln(1)1lim t tt te t→-++=211(1)1lim2t t te t→-++=2lim2(1)2t t e e t t →-==-+。
(2)设01,x a x b ==,211()2n n n x x x --=-,求n n x lim∞→.解 由条件,得 12111211()()22n n n n n n n x x x x x x x ------+=-+=+,反复使用此结果1111011()()()()22n n n n x x x x b a ---+=+=+, ,2,1=n ;于是 21212221100()()()n n n n n x x x x x x x x ++-=+-++++-22111()()()()()22n n a b a b a b a -=++-++++- 2111()222()()1331()2n b a a b a a b a +---=+-→+-=--,)(∞→n ;22212122100()()()n n n n n x x x x x x x x ---=+-++-++212211()()()()()22n n a b a b a b a --=+-++-++ 211()222()()1331()2na b a b a a b a ---=-++→-++=--,)(∞→n , 当2a b =时,lim 0n n x →∞=;当2a b ≠时,lim n n x →∞不存在。
二、(1)设()f x 在0x =可导,0,0,()n n a b n -+→→→∞,证明: ()()l i m(0)n n n n nf b f a f b a →∞-'=-. 证明 由0()(0)lim(0)0x f x f f x →-'=-,得对任意0ε>,存在0δ> ,当0||x δ<<时,成立()(0)|(0)|f x f f xε-'-<;因为0,0n n a b -+→→,对上述0ε>及确定的0δ>,存在正整数0δ>,当n N >时, 便有0,0n n a b δδ-<<<<,()(0)|(0)|n nf a f f a ε-'-<,()(0)|(0)|n nf b f f b ε-'-<,于是|()(0)(0)|()n n n f a f f a a ε'--<-,|()(0)(0)|n n n f b f f b b ε'--<, 从而|()()(0)()|n n n n f b f a f b a '---|()(0)(0)||()(0)(0)|n n n n f b f f b f a f f a ''≤--+-++ ()n n b a ε<-,即得()()|(0)|()n n n n f b f a f b a ε-'-<-,故有()()lim(0)n n n n nf b f a f b a →∞-'=- .(2)设函数()f x 在[,]a b 上连续, 在(,)a b 内二阶可导, 则存在(,)a b ξ∈, 使得2()()2()()24a b b a f b f f a f ξ+-⎛⎫''-+= ⎪⎝⎭.证明 :由于()2()()()222a b a b a b f b f f a f b f f f a +⎡+⎤⎡+⎤⎛⎫⎛⎫⎛⎫-+=---⎪ ⎪ ⎪⎢⎥⎢⎥⎝⎭⎝⎭⎝⎭⎣⎦⎣⎦. 作辅助函数()(),,22b a a b F x f x f x x a -+⎛⎫⎡⎤=+-∈ ⎪⎢⎥⎝⎭⎣⎦, 于是 ()()2()22a b a b F F a f b f f a ++⎛⎫⎛⎫-=-+ ⎪ ⎪⎝⎭⎝⎭. 在,2a b a +⎡⎤⎢⎥⎣⎦上对)(x F 运用拉格朗日中值定理, 1,2a b a ξ+⎛⎫∃∈ ⎪⎝⎭ , 使得 11()()222a b b a b a F F a f f ξξ+⎡-⎤-⎛⎫⎛⎫''-=+-⋅⎪ ⎪⎢⎥⎝⎭⎝⎭⎣⎦.再在11,2b a ξξ-⎡⎤+⎢⎥⎣⎦上对()f x '运用拉格朗日中值定理, 11,(,)2b a a b ξξξ-⎛⎫∃∈+⊂ ⎪⎝⎭, 使得2()()2()()24a b b a f b f f a f ξ+-⎛⎫''-+= ⎪⎝⎭.三、(1)求幂级数∑∞=1n nnx的和,求级数12n n n ∞=∑的和。
解 由于,由于1lim =∞→nn n ,所以∑∞=1n nnx的收敛半径1=R ;为了求出它的和,对幂级数xxn n-=∑∞=110,)1|(|<x逐项求导数,就有211)1(1x nxn n -=∑∞=-,因而∑∞=1n nnx211)1(x x nxx n n -==∑∞=-,)1|(|<x 。
在上式中取12x =,就得221=∑∞=n nn 。
(2)、证明 黎曼ζ函数∑∞==11)(n xnx ζ在),1(+∞内是连续的,并在这区间内有任意阶连续导函数。
(这种性质,也称为无穷次可微。
)证明令xxnnnx u -==1)(,显然xxn nnx u -==1)(,n nx u xn ln )(--=',2)(ln )(n n x u x n -='',kxkk n n n x u )(ln )1()]([)(--=,,3,2,1=k都在),1(+∞上连续;对任何1>δ,当x δ≥时,1|()|n u x nδ≤,1|()|ln nu x n nδ'≤,()1|[()]|(ln )k kn u x n nδ≤,而11(ln )kn n n δ∞=∑收敛,所以1()n n u x ∞=∑,)(1x u n n∑∞=',)(1)]([k n n x u ∑∞=, ( ,3,2,1=k )都在),[+∞δ上一致收敛,故∑∞==11)(n xnx ζ在),[+∞δ内是连续的,并在这区间内有任意阶连续导函数。
由于1>δ是任意的,所以∑∞==11)(n xnx ζ在),1(+∞内是连续的,并在这区间内有任意阶连续导函数。
显然11xn n∞=∑在),1(+∞内非一致收敛,∑∞==11)(n xn x ζ在),1(+∞内不一致连续。
假若∑∞==11)(n xnx ζ在),1(+∞内一致连续,则有1lim ()x x A ζ+→=存在且有限,在11()Nxn x nζ=>∑中令1x +→,取极限,得11Nn A n=>∑,(1,2,3,)N = ,矛盾。
四、(1)设方程组0,sin sin 0x y u v x u y v +++=⎧⎨+=⎩确定了可微函数(,),(,)u u x y v v x y =⎧⎨=⎩试求,,u vdu x y ∂∂∂∂ 。
解 由0,sin cos sin cos 0dx dy du dv udx x udu vdy y vdv +++=⎧⎨+++=⎩解出d u ,dv ;就可得. (2)设2cos()()yx y F y dx x=,求(1)F ' 。
解2222sin()sin()sin()()||x y x yx x y x y x y F y dx xxx=-'=+2321sin()sin()()sin()2yy y F y x y dx yy'=-+-,1(1)sin 12F '=-.五、若)(x f 在[0,1]上连续,证明⎰=π)(sin dx x xf ⎰ππ)(sin 2dx x f ;由此计算 2sin 1cos x x dx xπ+⎰.证:作变量替换x t -=π,有(sin )()(sin())()xf x dx t f t d t πππππ=---⎰⎰(sin )(sin )f x dx xf x dx πππ=-⎰⎰.解上述方程,就得到所证结论.利用此公式可得2sin 1cos x x I dx xπ=+⎰02()sin()()1cos ()y y dy y ππ-π-=-+π-⎰222()s i n s i n s i n1c o s 1c o s1c o sy y x x x d y d x dx yx x ππππ-==π-+++⎰⎰⎰2sin 1cos x dx I xπ=π-+⎰于是2sin 1cos x x I dx xπ=+⎰2sin 21cos x dx xππ=+⎰=201cos 21cos d x xππ-+⎰=[]0arctan(cos )2x ππ-=42π.(2)求以22x yz e--=为顶,以0z =为底,以柱面122=+yx 为侧面的曲顶柱体的体积V 。
解 设22{(,):1}D x y x y =+≤,则22x yDV edxdy--=⎰⎰22121112()(1)2rrd redr ee πθππ---==⋅-=-⎰⎰。
(3)求曲面积分222()(2)(2)Sx y z dydz xy z dzdx x z y dxdy ++-++⎰⎰,其中S是半球面221)z x y =+≤的上侧。
解 记22{(,,):1,0}x y z x y z ∑=+≤=,(取下侧)222{(,,):1,0}V x y z x y z z =++≤≥,则V S ∂=+∑,由高斯公式知,222()(2)(2)Sx y z dydz x y z dzdx x z y dxdy ++-++⎰⎰S +∑∑=-⎰⎰⎰⎰222()Vzx y dxdydz =++⎰⎰⎰22212x y xy dxdy +≤+⎰⎰222()0Vx y z dxdydz =+++⎰⎰⎰21222000sin d d r r dr ππθϕϕ=⎰⎰⎰122155ππ=⋅⋅=。
