自由度计算题
自由度计算例题63435
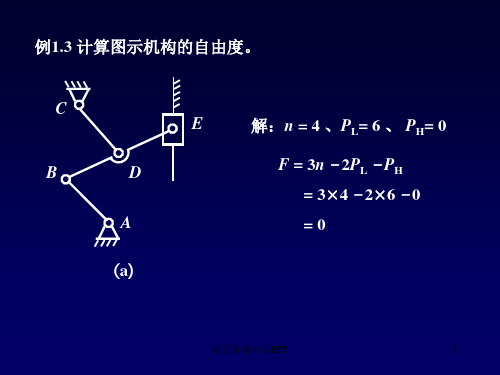
C
E
解:n = 4 、PL= 6 、 PH= 0
B
D
F = 3n–2PL–PH = 3×4–2×6–0
A
=0
(a)
语言资格考试PPT
1
A
D
E
解:n = 5 、PL= 7 、 PH= 0
G
F = 3n–2PL–PH
B
C
F
(b)
= 3×5–2×7–0
=1
语言资格考试PPT
(若存在复合铰链、局部自由度或虚约束请指明)
复合铰链:J 局部自由度:D 虚约束:M(N )
F =3n -2PL-PH = 3×9 -2×12 - 2 =1
语言资格考试PPT
8
2020
5
B A
(3)
局部自由度:B、C
D
虚约束:E(F )
C
F = 3n–2PL–PH
= 3×3–2×3–2
E
=1
F
语言资格考试PPT
6
J
I H
F
E
B
A
(4)
复合铰链:D
K
局部自由度:H
虚约束:F(G )
G D
F = 3n–2PL–PH = 3×8–2×11–1 =1
C
语言资格考试PPT
7
提高题:求机构自由度。
E
=1
A
F
语言资格考试PPT
4
例1.6 计算Байду номын сангаас列机构的自由度(若存在复合铰链、局部自由度或 虚约束请指明)
局部自由度:C
虚约束:D(E )
F = 3n - 2PL - PH = 3×3 - 2×3 - 2 = 1
机械原理计算自由度习题附答案
.
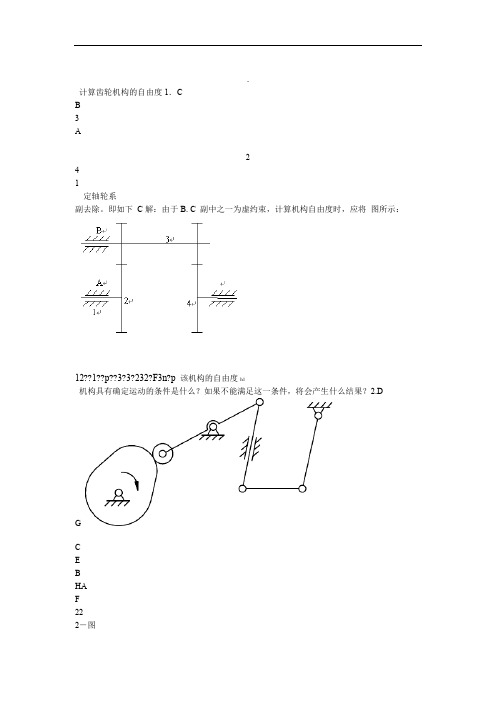
计算齿轮机构的自由度1.C
B
3
A
2
4
1
定轴轮系
副去除。
即如下C解:由于B. C 副中之一为虚约束,计算机构自由度时,应将图所示:
12??1??p??3?3?232?F3n?p该机构的自由度h1
机构具有确定运动的条件是什么?如果不能满足这一条件,将会产生什么结果?2.D
G
C
E
B
HA
F
22
2-图
B处有一个局部自由度,应去除。
机构在滚子?3n?2p?p?3?F5?2?7?1?0该机构的自由度h1.当自由度F=1时,该机构才能运动,如果不能满足这一条件,该机构无法运动。
该机构当修改为下图机构,则机构可动:
N=4, PL=5, Ph=1。
F?3?4?2?5?1?1自由度
3. 计算机构的自由度.
1)由于机构具有虚约束, 机构可转化为下图机构。
F?3?4?2?5?1?1自由度
2)由于机构具有虚约束, 机构可转化为下图机构。
F?3?1?2?1?1自由度
3)由于机构具有虚约束, 机构可转化为下图机构。
F?3?3?2?4?1自由度。
自由度计算例题

自由度计算例题在机械设计、力学分析以及各种工程领域中,自由度的计算是一项重要且基础的任务。
它帮助我们理解和预测物体或系统在特定条件下的运动可能性。
下面,我们通过几个具体的例题来深入探讨自由度的计算。
首先,来看一个简单的平面机构。
假设有一个平面四连杆机构,由四个杆件通过转动副连接而成。
我们要计算这个机构的自由度。
根据平面机构自由度的计算公式:F = 3n 2PL PH ,其中 F 表示自由度,n 表示活动构件的数目,PL 表示低副的数目,PH 表示高副的数目。
在这个四连杆机构中,活动构件的数目 n 为 3(因为机架不算活动构件),低副的数目 PL 为 4(四个转动副),高副数目 PH 为 0 。
将这些值代入公式,得到:F = 3×3 2×4 0 = 9 8 = 1 。
这意味着这个平面四连杆机构只有一个自由度,其运动是确定的。
再看一个稍微复杂一些的例子。
假设有一个平面凸轮机构,由一个凸轮和一个从动件组成,它们通过高副接触。
在这个例子中,活动构件的数目 n 为 2 ,低副的数目 PL 为 1(一个转动副或移动副),高副的数目 PH 为 1 。
代入公式可得:F = 3×2 2×1 1 = 6 2 1 = 3 。
这说明该平面凸轮机构有 3 个自由度。
接下来,考虑一个空间机构的例子。
假设有一个空间四连杆机构,由四个杆件通过球铰连接。
对于空间机构,自由度的计算公式为:F = 6n 5PL 6PH 。
这里,活动构件数目 n 为 3 ,低副数目 PL 为 4 (四个球铰相当于4 个低副),高副数目 PH 为 0 。
计算可得:F = 6×3 5×4 0 = 18 20 =-2 。
自由度为负数,这表明该机构的运动是受到约束的,无法自由运动。
再看一个包含复合铰链的例子。
假设有一个机构,其中三个杆件在同一处通过转动副连接。
在这种情况下,这个连接点处应视为两个复合铰链。
机械原理计算自由度习题及答案

1. 计算齿轮机构的自由度.
解:由于B. C 副中之一为虚约束,计算机构自由度时,应将 C 副去除。
即如下
图所示:
该机构的自由度1213233231=⨯-⨯-⨯=--=h p p n F
2. .机构具有确定运动的条件是什么?如果不能满足这一条件,将会产生什么结果?
机构在滚子B 处有一个局部自由度,应去除。
该机构的自由度0
17253231=-⨯-⨯=--=h p p n F 定轴轮系
A
B C
1 2
3 4 图2-22
A B
C
D
G
E
H F
当自由度F=1时,该机构才能运动, 如果不能满足这一条件,该机构无法运动。
该机构当修改为下图机构,则机构可动:
N=4, PL=5, Ph=1;
F=⨯-⨯-=
自由度342511
3. 计算机构的自由度.
1)由于机构具有虚约束, 机构可转化为下图机构。
F=⨯-⨯-=
自由度342511
2)由于机构具有虚约束, 机构可转化为下图机构。
F=⨯-⨯=
自由度31211
3)由于机构具有虚约束, 机构可转化为下图机构。
F=⨯-⨯=
自由度33241
(注:专业文档是经验性极强的领域,无法思考和涵盖全面,素材和资料部分来自网络,供参考。
可复制、编制,期待你的好评与关注)。
机械设计自由度计算121题

1 1
2 2
3 3
4
活动构件数3 低副数4 高副数0 自由度数 3X3-2X4-0=1
虚约束
56 7
4 2 2
3 31
11 4
活动构件数5 低副数7 高副数1 自由度数 3X5-2X7-1=0
5
活动构件数8 低副数11 高副数1 自由度数3X8-2X11-1X1=1
1 11 22
虚约束
8
活动构件数9个
4
9 11
10 低副数12个
虚约束
复合铰
局部自由度 1 1
12
8
11
97
14
10
2 2
1 6
4
9 10 13
5
56
33
4
7
8
虚约束
活动构件数10个 低副数14个 高副数1个 自由度数3X10-2X14-1=1
2 2
1
1
5 5
44 1 3
3
2
活动构件数5个 低副数5个 高副数2个 自由度数3X5-2X5-2=3
复合铰
复合铰
虚约束
3 4
3
1
12 12
2
2 11 1
活动构件数3个 低副数4个 高副数1个 自由度数3X3-2X4-1=0
活动构件数2个 低副数2个 高副数1个 自由度数3X2-2X2-1=1
4
45 35
21
2
3
6
1
7
活动构件数5个 低副数7个 高副数0个 自由度数3X5-2X7-0=1
虚约束
7 8
5
5
4
复合铰
虚约束
2 2
4 4
结构力学自由度的计算例题及解析

1. 对于一个简单的平面桁架结构,若共有6个节点和10根构件,那么其自由度为多少?- A. 6- B. 8- C. 10- D. 122. 在一个平面梁结构中,每个支座具有多少个约束?- A. 1- B. 2- C. 3- D. 43. 计算一个刚性连接的平面框架结构的自由度时,若结构有8个节点和12根构件,自由度公式为:自由度 = 3n - 2j,其中n是节点数,j是构件数。
该结构的自由度是多少?- A. 4- B. 6- C. 8- D. 104. 一个平面结构中,假设有4个节点,6根构件,所有构件都在一个平面上,计算其自由度时需考虑:- A. 3自由度每节点,减去2自由度每构件- B. 2自由度每节点,减去1自由度每构件- C. 2自由度每节点,减去2自由度每构件- D. 3自由度每节点,减去1自由度每构件5. 对于一个三维空间的桁架结构,若有10个节点和20根构件,其自由度计算应使用的公式是:- A. 自由度 = 6n - 3j- B. 自由度 = 3n - 2j- C. 自由度 = 3n - 3j- D. 自由度 = 6n - 6j6. 在平面框架结构中,如果节点数为5,构件数为8,计算其自由度时,正确的自由度为: - A. 6- B. 8- C. 10- D. 127. 对于一个有10个节点和15根构件的平面结构,其自由度为:- A. 15- B. 18- D. 248. 一个简单的平面框架结构中有6个节点,8根构件,计算自由度时,如果框架是完全支撑的,结果是:- A. 3- B. 6- C. 9- D. 129. 对于一个空间框架结构,其中有5个节点和12根构件,计算自由度时所用的公式为: - A. 自由度 = 6n - 3j- B. 自由度 = 3n - 2j- C. 自由度 = 6n - 2j- D. 自由度 = 3n - 3j10. 若一个平面结构中节点数为7,构件数为10,且结构为刚性框架,计算其自由度时,结果为:- A. 5- B. 7- C. 9- D. 11。
机械原理自由度计算题典型例题

选择题:一个平面机构由4个构件组成,其中有5个低副,则该机构的自由度数为:A. 0B. 1(正确答案)C. 2D. 3一个空间机构有6个活动构件,8个低副和1个高副,该机构的自由度数为:A. 1B. 2(正确答案)C. 3D. 4平面连杆机构中,若各构件均在同一平面内运动,且有一个构件被固定,该机构属于:A. 自由度为1的机构B. 自由度为2的机构(正确答案)C. 自由度为3的机构D. 无法确定自由度一个机械系统由5个活动构件组成,包含7个转动副和2个移动副,该系统的自由度数为:A. 1(正确答案)B. 2C. 3D. 4在计算平面机构自由度时,若机构中存在复合铰链,每增加一个复合铰链,将:A. 增加一个约束,自由度减少1(正确答案)B. 减少一个约束,自由度增加1C. 自由度不变D. 无法确定对自由度的影响一个机构由3个构件通过4个转动副连接而成,其中一个构件被固定,该机构的自由度数为:A. 0(正确答案)B. 1C. 2D. 3空间机构中,若包含n个活动构件,p个低副,q个高副,则该机构的自由度F计算公式为:A. F = 3n - 2p - q(正确答案)B. F = 2n - 3p - qC. F = n - p - qD. F = p + q - n平面四杆机构中,若固定其中一个构件,则该机构的自由度数为:A. 0B. 1(正确答案)C. 2D. 3在计算机构自由度时,局部自由度对机构自由度的影响是:A. 使自由度增加B. 使自由度减少C. 不影响机构自由度(正确答案)D. 无法确定对自由度的影响。
单自由度计算例题
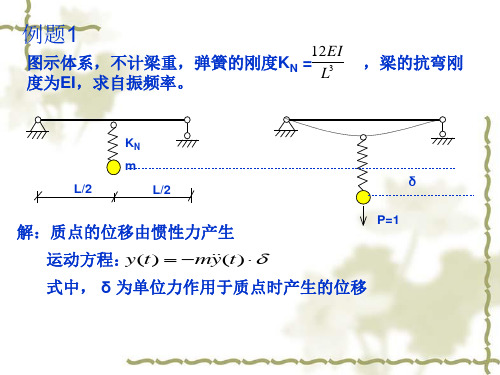
EI
m
KN=3EI/L3
KN
L
L
EI
KN
P=1 L
KN
2
1
KN
1/L
P sin t
m
yt
P=1
L
1
KN
2
3L/4
L
P=1
KN
1/L
L
P=1
KN
KN
5/4
2
=39L3/24EI
yt myt P sint
4、 EI=常数
EA m
A
L
P=1
EA
求自由振动频率,EA=6EI/L2
L
L m
A EA
P=1
=
6EI L3
,不计
梁的自重,θ= 89 EI 。求B点的最大动力位移反应
4mL3
m A
P sinθt
B
C
D
KN
L/3
L/3
L/3
1)求B点的柔度δ
P=1
P=1
2L/9
MP图
11
267 1458
L3 EI
24 L3 1P 1458 EI
P=1
X 基本体系
X=1
M1 图
❖ 求柔度δ
P=1
18L/89
M图
4L3
267 EI
P=1
2L/9
M图
2)求动力荷载为1时在质点出产生的位移
P=1
2L/9
2L/9
MP图
P=1 75L /801
171L /801
M图
* 7L3
534 EI
X=1
M图
P=1
2L /9
自由度计算习题

1 指出图示机构中的复合铰链、局部自由度和虚约束,并计算机构自由度。
解:第2、3、4三个构件构成2个回转付。
(这是复合铰链)构件6、7构成一个回转付。
加上A、B、D三处三个回转付总共6个回转付。
构件4和机架,3和5各构成一个移动付。
构件7和机架,6和5各构成一个移动付共有4个移动付。
共计有10个低付,没有高付。
∴共有8个构件,其中7个活动件。
n=7由计算自由度的公式:F=3n-2-=3*7-2*10-0=1∴该机构的自由度为1。
即只要一个原动件,机构即可有确定的运动。
2 求机构的自由度,并判断机构是否有确定的相对运动。
解:构件3、4、5构成2个回转付共7个回转付,2个移动付。
=7+2=9一个高付PH=1。
(凸轮与滚子从动件接触处)n=7∴F=3n-2- =3*7-2*9-1=2该机构自由度为2∴必须要有二个主动件,机构才能有确定的运动。
3、计算图示机构的自由度,并判断机构是否具有确定的运动。
(作业)(如有复合铰链、虚约束、局部自由度须指出)4、计算如图所示机构的自由度(若有复合铰链、局部自由度、虚约束必须明确指出)(作业)5. 在图示机构中, 已知 ω110= rad/s , l l l AB BC BD ===01. m 。
用图解法求 v D以及全部瞬心。
(本题10分)(作业)(1) 求 v DQ r r rv v v C B C B 22=+,v l B AB ==⨯=ω110011. m/sr r rv v v C C C C 2323=+, v C 30=∴=+r r rv v v C C B C B 232作 速 度 多 边 形, 利 用 影 像 法 求 d ,v v D B =≈21414. m/s(瞬心。
略)。
双杆机构名称自由度计算例题

双杆机构名称自由度计算例题
1.构件数n为7,低副p为9,高副pn 为1,局部自由度为1,虚约束为0. E处为局部自由度,c处为复合铰链
F=3n-2p-pn=3*7-2*9-1=2(与原动件数目一致,运动确定)
2.B处有复合铰链,有2个转动副。
无局部自由度。
B点左侧所有构件和运动副带入的约束为虚约束,属于与运动无关的对称部分。
n=5,PL=7,PH=0,F=3n-2PL-PH=3x5-2x7-
1x0=1。
运动链有确定运动,因为原动件数=自由度数。
3.A处为复合铰链,因为有3个构件在此处组成成转动副,所以应算2个转动副。
B处为局部自由度,假设将滚子同构件CB 固结。
无虚约束。
n=6,PL=8,PH=1,F=3n-2PL-PH=3x6-2x8-1=1运动链有确定运动,因为原动件数=自由度数。
4. 没有复合铰链、局部自由度、虚约束。
n=4PL=5PH=1,F=3n-2PL-PH=3x4-2x5-1=1
运动链有确定运动,因为原动件数=自由度数。
自由度计算

题4图 压榨机机构
机构的自由度与确定运动条件
计算机构自由度典型例题分析
典型例题一:计算图示某包装机送纸机构的自由度, 并判断该机构是否有确定运动。
解法2: 复合铰链:D包含2个转动副 (杆4和7)
局部自由度:F’=2 虚约束:杆8及转动副F、I引 入1个虚约束。
计算自由度前直接去除虚约 束和局部自由度: n=6 p5=7 p4=3 F=3n-2p5-p4=1
计算机构自由度典型例题分析
机构的自由度与确定运动条件
典型例题二:计 算 图 示 机 构 的 自 由 度, 如 有 复 合 铰 链、 局 部 自 由 度 和 虚 约 束,需 明 确 指 出。 画 箭 头 的 构 件 为 原 动 件。
局部自由度 复合铰链
复合铰链
1图
(b )
平面机构自由度计算例题及答案

平面机构自由度计算例题及答案在机械原理中,平面机构自由度的计算是一个重要的知识点。
通过计算机构的自由度,可以判断机构的运动可能性和确定性,为机构的设计和分析提供重要依据。
下面我们通过几个例题来详细讲解平面机构自由度的计算方法。
例题 1:如图所示的平面机构,由 4 个杆件组成,其中杆件 1 为机架,杆件2 和杆件 3 通过转动副连接,杆件 3 和杆件 4 通过移动副连接。
试计算该机构的自由度。
分析:首先,我们需要确定机构中的运动副类型和数量。
在这个机构中,有 2 个转动副(分别在杆件 2 和杆件 3 的连接处,以及杆件 1 和杆件 2 的连接处)和 1 个移动副(在杆件 3 和杆件 4 的连接处)。
接下来,我们根据自由度的计算公式 F = 3n 2PL PH 进行计算。
其中,n 为活动构件的数目,PL 为低副的数目,PH 为高副的数目。
在这个机构中,活动构件的数目 n = 3(杆件 2、3、4),低副的数目 PL = 3(2 个转动副和 1 个移动副),高副的数目 PH = 0。
将这些值代入公式,得到:F = 3×3 2×3 0 = 9 6 = 3所以,该机构的自由度为 3。
例题 2:考虑一个平面机构,由 5 个杆件组成,杆件 1 固定不动,杆件 2 与杆件 1 通过转动副连接,杆件 2 与杆件 3 通过移动副连接,杆件 3 与杆件 4 通过转动副连接,杆件 4 与杆件 5 通过移动副连接。
计算该机构的自由度。
分析:首先明确运动副类型及数量。
此机构有 3 个转动副(分别在杆件 1 和杆件 2、杆件 3 和杆件 4 、杆件 4 和杆件 5 的连接处),2 个移动副(分别在杆件 2 和杆件 3、杆件 4 和杆件 5 的连接处)。
然后计算活动构件数目 n = 4(杆件 2、3、4、5),低副数目 PL = 5(3 个转动副和 2 个移动副),高副数目 PH = 0。
将数值代入自由度计算公式:F = 3×4 2×5 0 = 12 10 = 2所以该机构的自由度为 2。
平面机构自由度计算例题及答案

平面机构自由度计算例题及答案在机械原理的学习中,平面机构自由度的计算是一个非常重要的知识点。
它能够帮助我们判断机构是否具有确定的运动,以及机构的运动是否受到合理的约束。
下面,我们通过几个具体的例题来深入理解平面机构自由度的计算方法。
例题 1如下图所示的平面机构,其中构件 1 为机架,构件 2 与构件 1 以转动副连接,构件 3 与构件 2 以移动副连接,构件 4 与构件 3 以转动副连接,构件 5 与构件 4 以转动副连接。
试计算该机构的自由度。
!平面机构示例 1(解题思路首先,我们需要确定活动构件的数量。
在这个机构中,活动构件有构件 2、3、4、5,共 4 个。
然后,计算低副的数量。
转动副有 4 个(构件 2 与构件 1 之间、构件 4 与构件 3 之间、构件 5 与构件 4 之间),移动副有 1 个(构件 3与构件 2 之间),所以低副总数为 5 个。
接下来,计算高副的数量。
在这个机构中没有高副。
最后,根据自由度的计算公式:F = 3n 2PL PH (其中 F 为自由度,n 为活动构件数,PL 为低副数,PH 为高副数),代入数值计算。
n = 4,PL = 5,PH = 0F = 3×4 2×5 0= 12 10 0= 2答案该平面机构的自由度为 2。
例题 2如下图所示的平面机构,构件 1 为机架,构件 2 与构件 1 以转动副连接,构件 3 与构件 2 以转动副连接,构件 4 与构件 3 以转动副连接,同时构件 4 与构件 1 以移动副连接。
计算该机构的自由度。
!平面机构示例 2(解题思路活动构件有构件 2、3、4,共 3 个。
低副方面,转动副有 3 个(构件 2 与构件 1 之间、构件 3 与构件 2之间、构件 4 与构件 3 之间),移动副有 1 个(构件 4 与构件 1 之间),低副总数为 4 个。
高副数量为 0。
n = 3,PL = 4,PH = 0F = 3×3 2×4 0= 9 8 0= 1答案该平面机构的自由度为 1。
机械原理计算自由度习题及答案

1. 计算齿轮机构的自由度.
解:由于B. C 副中之一为虚约束,计算机构自由度时,应将 C 副去除。
即如下图所示: 该机构的自由度1213233231=⨯-⨯-⨯=--=h p p n F
2. .机构具有确定运动的条件是什么?如果不能满足这一条件,将会产生什么结果?
机构在滚子B 处有一个局部自由度,应去除。
该机构的自由度017253231=-⨯-⨯=--=h p p n F
当自由度F=1时,该机构才能运动, 如果不能满足这一条件,该机构无法运动。
该机构当修改为下图机构,则机构可动:
N=4, PL=5, Ph=1;
自由度342511F =⨯-⨯-=
3. 计算机构的自由度.
1) 由于机构具有虚约束, 机构可转化为下图机构。
自由度342511F
=⨯-⨯-= 2) 由于机构具有虚约束, 机构可转化为下图机构。
自由度31211F =⨯-⨯= 3) 由于机构具有虚约束, 机构可转化为下图机构。
图2-
22
定轴轮系 A
B C
1 2
3 4
F=⨯-⨯=自由度33241。
自由度计算例题

自由度计算例题在统计学中,自由度(degrees of freedom)是指用于衡量一个估计值或统计量的可自由变动的样本数量。
它是衡量样本数据中信息的度量。
自由度的计算方式因统计问题的不同而异。
下面我们来看一个自由度计算的例题:假设有一个实验,需要将一批样本分成两组,分别为甲组和乙组。
我们需要研究两组样本在某个特定因素上的差异。
首先,我们需要确定一些基本信息。
设甲组的样本数量为n1,乙组的样本数量为n2。
那么,甲组的自由度为n1-1,乙组的自由度为n2-1。
接下来,我们需要考虑合并两组样本的情况。
当我们将两组样本进行合并时,合并后的总样本数量为n1 + n2。
对于这种情况,总的自由度为(n1 + n2)-1。
此外,在某些情况下,我们还需要考虑到样本之间的相关性。
假设两组样本是相关的,那么在计算自由度时需要考虑到相关样本的数量。
具体计算方式根据实际情况而定。
以下是一个示例:假设甲组的样本数量为10,乙组的样本数量为8。
我们需要计算出甲组和乙组的自由度以及合并后总的自由度。
甲组的自由度 = 10 - 1 = 9乙组的自由度 = 8 - 1 = 7合并后总的自由度 = (10 + 8) - 1 = 17通过以上计算,我们得出了甲组、乙组以及合并后所得到的总的自由度。
自由度是统计学中一个重要的概念,它可以帮助我们更准确地评估样本数据的差异和变动情况。
在实际的统计分析中,我们需要根据具体情况灵活地计算自由度,以获得更可靠的结果。
总结起来,自由度是用于衡量样本数据中信息的度量,其计算方式根据不同统计问题的需求而异。
在计算自由度时,我们需要考虑到样本的数量、样本之间的相关性等因素,以获得准确的计算结果。
通过对自由度的合理计算,我们可以更准确地评估样本数据的变异程度,进而进行统计推断、假设检验等相关分析。
机构自由度计算题
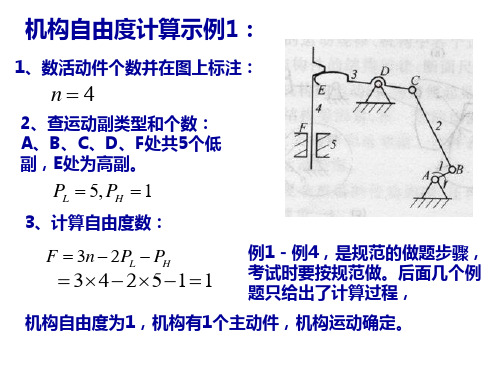
机构自由度计算示例1:
1、数活动件个数并在图上标注:
n4
2、查运动副类型和个数: A、B、C、D、F处共5个低 副,E处为高副。
首先检查处理复合铰链、局部自由度和虚约束。 1 2
1
3
5
2
4
局部自由度 5
3 4
7
6
6
局部自由度
8
n6
PL 8, PH 1
F 3n 2PL PH 36 2811
n8
PL 11, PH 1
F 3n 2PL PH 38 2111 1
复合铰链 复合铰链
F 3n 2PL PH
33 240 1
机构自由度为1,机构有1个主动 件,机构运动确定。
考试时做题,按以上步骤。
例4 计算滚子从动件凸轮机构的 自由度。 解:滚子是局部自由度,数构件 时不计算,机构中有2个活动构 件。 A、D处是低副,B处是高副
n=2, PL=2, PH=1 F=3×2-2×2-1=1 机构运动确定。
Hale Waihona Puke 例1-7 计算大筛机自由度 解:C处是复合铰链,F处滚轮是局部自由度,E处有虚约束。 7个构件,A、B、D、 E、O各有一个低副, C处两个低副,G处两 个低副,共9个低副。
n=7,PL=9,PH=1 F=3n-2 PL-PH= 3×7-2×9-1=2 自由度为2,机构有2个主动件,机构运动确定。
首先检查处理复合铰链、局部自由度和虚约束。
自由度计算题

1.试计算下列平衡体系的自由度数:(1) 298.15 K、101 325Pa下固体NaCl与其水溶液平衡;(2) I2(s) ? I2(g);(3) NaCl(s)与含有HCl的NaCl饱和溶液。
(答案:①0,②1,③3)解:(1) C = 2, P= 2 又T, p已指定∴F= C -P + n = 2- 2 + 0 = 0(2) C=1, P=2则F= C - P + n = 1- 2 + 2 = 1(3) C=3, P =2∴F= C -P + n =3- 2 + 2 = 32.固体NH4HS和任意量的H2S及NH3气体混合物组成的体系按下列反应达到平衡:NH4HS(s) ≒NH3(g)+H2S(g)(1) 求该体系组元数和自由度数;(2) 若将NH4HS放在一抽空容器内分解,平衡时,其组元数和自由度数又为多少?(答案:①2,2,②1,1)解:(1) C =3- 1=2, 即体系组元数为2P=2体系的自由度数F= C -P + n = 2 – 2 + 2 = 2体系平衡时的组元数C = 3 – 1 –1 = 1P=2体系的自由度数 F= C -P + n = 1- 2 + 2 = 13.已知Na2CO3(s)和H2O(l)可形成的水合物有三种:Na2CO3·H2O(s),Na2CO3·7H2O(s)和Na2CO3·10H2O(s)试问:(1) 在101 325 Pa下,与Na2CO3水溶液及冰平衡共存的含水盐最多可有几种?(2) 在293.15 K时,与水蒸气平衡共存的含水盐最多可有几种?(答案:①1,②2)解:(1) 设最多有x种含水盐,则K = 2 + x,R = x∴C = K-R = 2 + x- x = 2又P= 2 + x,n = 1∴由相律F = C -P + n得:F= 2- (2+x) +1 = 1- x而F≥0 ∴x≤1,即最多只能有一种含水盐与之共存。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
1.试计算下列平衡体系的自由度数:
(1) 298.15 K、101 325Pa下固体NaCl与其水溶液平衡;
(2) I2(s) ? I2(g);
(3) NaCl(s)与含有HCl的NaCl饱和溶液。
(答案:①0,②1,③3)
解:(1) C = 2, P= 2 又T, p已指定
∴F= C -P + n = 2- 2 + 0 = 0
(2) C=1, P=2
则F= C - P + n = 1- 2 + 2 = 1
(3) C=3, P =2
∴F= C -P + n =3- 2 + 2 = 3
2.固体NH4HS和任意量的H2S及NH3气体混合物组成的体系按下列反应达到平衡: NH4HS(s) ≒NH3(g)+H2S(g)
(1) 求该体系组元数和自由度数;
(2) 若将NH4HS放在一抽空容器内分解,平衡时,其组元数和自由度数又为多少?
(答案:①2,2,②1,1)
解:(1) C =3- 1=2, 即体系组元数为2
P=2
体系的自由度数F= C -P + n = 2 – 2 + 2 = 2
体系平衡时的组元数C = 3 – 1 – 1 = 1
P=2
体系的自由度数 F= C -P + n = 1- 2 + 2 = 1
3.已知Na2CO3(s)和H2O(l)可形成的水合物有三种:Na2CO3·H2O(s),Na2CO3·7H2O(s)和Na2CO3·10H2O(s)试问:
(1) 在101 325 Pa下,与Na2CO3水溶液及冰平衡共存的含水盐最多可有几种?
(2) 在293.15 K时,与水蒸气平衡共存的含水盐最多可有几种? (答案:①1,②2)解:(1) 设最多有x种含水盐,则K = 2 + x,R = x
∴C = K-R = 2 + x- x = 2
又P= 2 + x,n = 1
∴由相律F = C -P + n得:F= 2- (2+x) +1 = 1- x
而F≥0 ∴x≤1,即最多只能有一种含水盐与之共存。
****(2) 同上理K = 2 + x,R = x
∴C = K-R = 2 + x- x = 2,而P= 1 + x,n = 1
∴F= 2- (1+x) +1 = 2- x
而f≥0 ∴x≤2,即最多有两种含水盐与水蒸汽平衡共存。
