树(第五章)
智慧树劳动教育第五章答案

智慧树劳动教育第五章答案
1、判断题:
学生的身份并不当然的限制郭懿作为一个普通的劳动者加入劳动力的群体。
()
选项:A:错B:对
答案: 【对】
2、判断题:
广东省的实习协议可以根据实习的性质和需要,约定意外伤害保险的投保人、投保额度、损害赔偿、实习报酬、保密等其他事项。
()
选项:A:错B:对
答案: 【对】
3、多选题:
求职中可能遇到的陷阱有()。
选项:A:骗入传销组织B:押金、保证金、诚意金C:信息泄露D:培训贷款
答案: 【骗入传销组织;押金、保证金、诚意金;信息泄露;培训贷款】
4、判断题:
三方协议的法律性质虽然属于民事协议,但是由它引起的争议也需要经过劳动仲裁再进入法院的一审和二审程序。
()
选项:A:对B:错
答案: 【错】
5、多选题:
劳动合同法的新规定有()。
选项:
A:试用期期限与合同期限挂钩
B:禁止重复约定试用期
C:试用期期间解除劳动合同
D:试用期期间的工资
E:禁止约定试用期的情形
答案: 【试用期期限与合同期限挂钩;禁止重复约定试用期;试用期期间解除劳动合同;试用期期间的工资;禁止约定试用期的情形】。
第五章-树-练习-答案
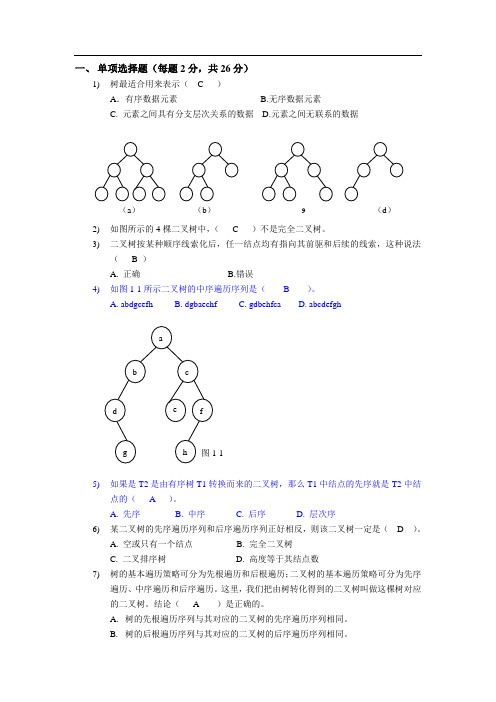
一、 单项选择题(每题2分,共26分)1) 树最适合用来表示( C )A .有序数据元素 B.无序数据元素C. 元素之间具有分支层次关系的数据D.元素之间无联系的数据2) 如图所示的4棵二叉树中,( C )不是完全二叉树。
3) 二叉树按某种顺序线索化后,任一结点均有指向其前驱和后续的线索,这种说法( B )A. 正确B.错误4) 如图1-1所示二叉树的中序遍历序列是( B )。
A. abdgcefhB. dgbaechfC. gdbehfcaD. abcdefgh5) 如果是T2是由有序树T1转换而来的二叉树,那么T1中结点的先序就是T2中结点的( A )。
A. 先序B. 中序C. 后序D. 层次序6) 某二叉树的先序遍历序列和后序遍历序列正好相反,则该二叉树一定是( D )。
A. 空或只有一个结点B. 完全二叉树C. 二叉排序树D. 高度等于其结点数7) 树的基本遍历策略可分为先根遍历和后根遍历;二叉树的基本遍历策略可分为先序遍历、中序遍历和后序遍历。
这里,我们把由树转化得到的二叉树叫做这棵树对应的二叉树。
结论( A )是正确的。
A. 树的先根遍历序列与其对应的二叉树的先序遍历序列相同。
B. 树的后根遍历序列与其对应的二叉树的后序遍历序列相同。
(a ) (b ) 9 (d )C. 树的先根遍历序列与其对应的二叉树的中序遍历序列相同。
D. 以上都不对8) 如图所示的T2是由森林T1转换而来的二叉树,那么森里T1有( C )个叶子结点。
A. 4B. 5C. 6D. 79) 深度为5的二叉树至多有( C )个结点。
A. 16B. 32C. 31D. 1010) 在一非空二叉树的中序遍历序列中,根结点的右边( A )。
A. 只有右子树上的所有结点B. 只有右子树的部分结点C. 只有左子树上的部分结点D. 只有左子树上的所有结点11) 设n ,m 为一棵二叉树上的两个结点,在中序遍历时,n 在m 前的条件是( C )。
2022智慧树国家安全教育第五章答案

2022智慧树国家安全教育第五章答案1、28.公民和组织发现间谍行为,应当及时向()?报告;向公安机关等其他国家机关、组织报告的,相关国家机关、组织应当立即移送国家安全机关处理。
[单选题] *A.国家安全机关或者公安机关B.公安机关C.司法机关D.国家安全机关(正确答案)2、9. 党的十九大报告指出,有效维护国家安全,要严密防范和坚持打击各种()。
*A.渗透颠覆破坏活动(正确答案)B.暴力恐怖活动(正确答案)C.黑恶势力活动D.民族分裂活动、宗教极端活动。
(正确答案)3、79、坚持党对国家安全工作的(),各级党委要发挥好在本地区、本部门安全工作中的领导作用。
[单选题] *A、绝对领导(正确答案)B、统一领导C、高度领导D、全面领导4、7、坚持中国共产党对国家安全工作的领导,建立()的国家安全领导体制。
[单选题] *A、集中统一、高效权威(正确答案)B、统分结合、协调高效C、高效权威、反应灵敏D、高效权威、集中统一5、92. 宣扬恐怖主义、极端主义、煽动实施恐怖活动罪的行为表现有()。
*A.制作、散发宣扬恐怖主义、极端主义图书、音频视频资料及其他物品(正确答案)B.通过讲授、发布信息等方式宣扬恐怖主义、极端主义(正确答案)C.煽动实施恐怖活动(正确答案)D.强迫他人在公共场合穿戴恐怖主义、极端主义服饰和标志6、12、社会监督渠道畅通。
开通网络投诉举报平台,设立统一的投诉举报电话,建成覆盖市、县的投诉举报业务系统,实现网络24小时畅通,电话在受理时间内接通率≥90%,按法定时限回复率、有效处置率均达()。
[单选题] *A、90%B、95%C、80%D、100%(正确答案)7、26. 第一届全国人民代表大会第一次会议通过《中华人民共和国宪法》的时间()[单选题] *A 1951年B 1952年C 1953年D 1954年(正确答案)8、58、以下哪些说法是正确的(A,C,D)*A、民间借贷属于高风险事件,法律规定高于同期利率4倍以上的民间借贷,是不受法律保护的。
树据结构 第5章答案(已核 )

第5章习题答案一、选择1.以下说法错误的是 ( )A.树形结构的特点是一个结点可以有多个直接前趋B.线性结构中的一个结点至多只有一个直接后继C.树形结构可以表达(组织)更复杂的数据D.树(及一切树形结构)是一种"分支层次"结构2,以下说法错误的是 ( BC )A.二叉树可以是空集B.二叉树的任一结点都有两棵子树(是“最多有”两棵子树)C.二叉树与树具有相同的树形结构(二叉树的孩子必有左右之分,只有一个孩子时也要分出左右,而树即使是有序树, 只有一个孩子时部分左右)D.二叉树中任一结点的两棵子树有次序之分3、以下说法错误的是( )A.完全二叉树上结点之间的父子关系可由它们编号之间的关系来表达B.在三叉链表上,二叉树的求双亲运算很容易实现C.在二叉链表上,求根,求左、右孩子等很容易实现D.在二叉链表上,求双亲运算的时间性能很好4、以下说法错误的是 ( )A.一般在哈夫曼树中,权值越大的叶子离根结点越近B.哈夫曼树中没有度数为1的分支结点C.若初始森林中共有n裸二叉树,最终求得的哈夫曼树共有2n-1个结点D.若初始森林中共有n裸二叉树,进行2n-1次合并后才能剩下一棵最终的哈夫树5.深度为6的二叉树最多有( )个结点 ( )A.64B.63C.32D.316.将含有83个结点的完全二叉树从根结点开始编号,根为1号,后面按从上到下、从左到右的顺序对结点编号,那么编号为41的双结点编号为 ( )A.42B.40C.21D.207.设二叉树有n个结点,则其深度为( )A.n-1B.nC.5floor(log2n)D.无法确定注:完全二叉树才能确定其深度。
8.设深度为k的二叉树上只有度为0 和度为2 的节点,则这类二叉树上所含结点总数最少()个A.k+1B.2kC.2k-1D.2k+1注:单支数含结点个数最少,但题目规定该二叉树中不存在度为1的结点。
所以,在单支树的基础上把结点补齐,使之度数为2 或 0,结果就是有2k-1个结点。
数据结构 第五章树答案

第五章 树(答案)一、选择题1、二叉树的第i 层最多有( )个结点。
A .2i B. 2i C. 2i-1 D.2i -12.对于一棵满二叉树,高度为h ,共有n 个结点,其中有m 个叶子结点,则( )A .n=h+m B.h+m=2n C.m=h-1 D.n=2h -1 3.在一棵二叉树中,共有16个度为2的结点,则其共有( )个叶子结点。
A .15 B.16 C.17 D.184. 一棵完全二叉树中根结点的编号为1,而且编号为23的结点有左孩子但没有右孩子,则此树中共有( )个结点。
A .24 B.45 C.46 D.47 5.下述编码那一组不是前缀码( )A .00,01,10,11 B.0,1,00,11 C.0,10,110,111 D.1,01,001,000 6.某二叉树的中序序列和后序序列相同,则这棵二叉树必然是( )A .空树B .空树或任一结点均无左孩子的非空二叉树C .空树或任一结点均无右孩子的非空二叉树D .空树或仅有一个结点的二叉树7.设n,m 为一棵二叉树上的两个结点,在中序遍历时,n 在m 前的条件是( )A .n 在m 的右边 B.n 是m 的祖先C .n 在m 的左边 D.n 是m 的子孙8、假定中根遍历二叉树的定义如下:若二叉树为非空二叉树,则中根遍历根的右子树;访问根结点;中根遍历根的左子树。
按此定义遍历下图所示的二叉树,遍历的结果为: A 、 DBEAFHGC A B 、 C GHFADBE B C C 、 E BDAFHGC E D FD 、 FHGCADBE GH9、文中出现的字母为A 、B 、C 、D 和E ,每个字母在电文中出现的次数分别为9、27、3、5和11。
按哈夫曼编码(构造时左小右大),则字母C 的编码应是:A 、10B 、0110C 、1110D 、1100 10、设树T 的度为4,其中度为1,2,3和4的结点个数分别为4,2,1,1 则T 中的叶子数为( )A .5B .6C .7D .8 11.算术表达式a+b*(c+d/e )转为后缀表达式后为( )A .ab+cde/*B .abcde/+*+C .abcde/*++D .12. 设有一表示算术表达式的二叉树(见下图),它所表示的算术表达式是( )A. A*B+C/(D*E)+(F-G)B. (A*B+C)/(D*E)+(F-G)C. (A*B+C)/(D*E+(F-G ))D. A*B+C/D*E+F-G13.已知一算术表达式的中缀形式为 A+B*C-D/E ,后缀形式为ABC*+DE/-,其前缀形式为( ) A .-A+B*C/DE B. -A+B*CD/E C .-+*ABC/DE D. -+A*BC/DE14.若一棵二叉树具有10个度为2的结点,5个度为1的结点,则度为0的结点个数是( )A .9B .11C .15D .不确定15.树的后根遍历序列等同于该树对应的二叉树的( ).A. 先序序列B. 中序序列C. 后序序列16.已知一棵二叉树的前序遍历结果为ABCDEF,中序遍历结果为CBAEDF,则后序遍历的结果为( )。
果树栽培学 第五章 果树整形修剪

4.辅养枝:
• 又称控制枝。是整形过程中留下的临时性 枝。 • 具有利用空间,促进生长,缓和树势,提 早结果的作用。
5.树冠:
• 树冠是果树的主体部分。树冠的体积、形状、结构等,对于合理利用 空间和光能、确保果树生长结果和果实品质、以及提高劳动生产率等, 都有重要影响。 • ①树冠体积:由冠高和冠径决定,影响树冠形成快慢和光能利用。在 一定限度内,缩小树体体积,已成为果园现代化的主要方向。 • ②树高、冠径和间隔:主要考虑劳动效率、光能利用、树种特性和抗 灾能力等。提倡树高3—4m,冠厚2.5—3.5m,冠径3m。 • ③树冠形状:分为自然形、扁形(篱架形、树篱形)和水平形(棚架 形、盘状形、匍匐形)三类。在解决密植与光能利用、密植与操作的 矛盾中,以扁形最好,自然形其次,水平形再次。 • ④树冠结构和叶幕配置: • a.叶片水平排列,叶面积指数1;均匀垂直排列,叶面积指数3;丛状 均匀排列,叶面积指数9; • b.树冠结构:层性,单位枝群(主枝、侧枝及枝组)圆锥形或三角形, 叶丛枝的叶片丛生性,都是合理的结构。
(三)树篱形:
• 其特点是株间树冠相接,果树群体成为树 篱。是矮化密植的主要树形。 • 1.自然树篱形:有长方形、三角形、梯形和 半圆形。常用于柑橘类。 • 2.扁纺锤形:常用于苹果、梨。 • 3.自然扇形:常用于苹果、梨。
(四)篱架形:
• 其特点是需设置篱架,以固定植株和枝梢, 整形较方便。常用于蔓性果树。 • 1.棕榈叶形; • 2.双层栅篱形; • 3.Y形。
五、其他树形
• 1.棚架形:主要用于蔓性果树。 • 2.丛状形:其特点是无主干,着地分枝成丛 状。主要适用于灌木果树。 • 3.匍匐形:将果树倾斜匍匐于地表,有利于 冬季埋土防寒。 • 4.无骨干形:全树只有1—2个枝组(大型枝 组),不设骨干枝,枝组不断回缩更新。 用于桃、苹果的草地果园。
第五章图论树

条边,要使G成为树,G中只应留下5条边,故应删去
10条边,选C。
4。最小生成树 在带权图G中所生成的总权数最小的生成树称为
最小生成树。 5。最小生成树的求法
选取权数最大的边所在的回路,去掉其中权数 最大的边,如此做下去,直到求出生成树为止。这 样求出的生成树一定是最小生成树。
还有一种方法称为克鲁斯特尔算法。先去掉所有 的边,然后从权数最小的边的开始,从小到大逐步选 取,如果所选取的边和已选取的边构成了回路,则不 选取这条边重新选取,直到连接完所有的结点。这样 求出的树就是最小生成树。
3。任何非平凡树中至少有2片树叶。
二、生成树
1。生成树 若图G的生成子图是一棵树,则称此树是G的生
成树。
2。树的补 图G中不属于生成树T的边的集合称为树T的补。
3。生成树的求法 一般可用破圈法做,即把图G中的回路去掉一
条边,使它不再是回路。如此做下去,直到恰好把
所有的回路都破坏掉,就得到了生成树。
用破圈法一共要去掉
条边。
e 1v
[例题]
设G=<V,E>是有p个结点,s条边的连通图,则从G
中删去
条边,才能确定G的一棵生成树。
解:设要删去k条边,s k v 1, k s 1 v
[例题]
设G是有6个结点的完全图,从G中删去 C 条
边则能得到树。
A) 6
B) 9
C) 10
D) 15
解:∵G是有6个结点的完全图,∴G中共有6×5/2=15
a
1e 2
d
T=<{a,b,c,d,e},{(c,b),(b,e),(e,a),(e,d)}>。 3 b
c
1
[例题]
第五章园林树木的养护管理PPT课件

2、客土栽培
3、培土(壅土、压土与掺沙)
厚度:5~10cm
5—2 园林树木的土壤管理 经营者提供商品或者服务有欺诈行为的,应当按照消费者的要求增加赔偿其受到的损失,增加赔偿的金额为消费者购买商品的价款或接受服务的费用
三、树木生长地的土壤改良及管理
4、改良土壤 (1)松土透气、控制杂草
①松土除草的范围:
6、不提倡夏季施肥,但夏季树体表现缺肥时要即时补肥。
7、树木生长正常不考虑施肥,每2~4年施基肥一次。
经营者提供商品或者服务有欺诈行为 的,应 当按照 消费者 的要求 增加赔 偿其受 到的损 失,增 加赔偿 的金额 为消费 者购买 商品的 价款或 接受服 务的费 用
5—5
园林树木的病虫害防治
原则:防重于治,治要及时扑灭 一、病害的种类及病原生物的类型:分两大类
多用于施基肥,深度20~50cm,常用方法有:
(1)环状沟施:
(2)放射状沟施(辐射状沟施):
(3)穴状施:
(4)条状沟施:
2、施追肥:
(1)根施法:
(2)根外施肥: ① 叶面喷肥 ②树干注射
经营者提供商品或者服务有欺诈行为 的,应 当按照 消费者 的要求 增加赔 偿其受 到的损 失,增 加赔偿 的金额 为消费 者购买 商品的 价款或 接受服 务的费 用
5—2 园林树木的土壤管理 经营者提供商品或者服务有欺诈行为的,应当按照消费者的要求增加赔偿其受到的损失,增加赔偿的金额为消费者购买商品的价款或接受服务的费用
一、树木栽植前土壤类型的鉴别
园林树木生长地的土壤类型大致可分为以下几种类型:
1、荒山荒地 2、平原肥土 3、水边低湿地 4、煤灰土或建筑垃圾土 5、市政工程施工后的场地 6、人工土层 7、沿海地区的土壤 8、酸性红壤 9、工矿污染地 10、紧实土壤 11、盐碱土 12、重黏土 13、砂砾土
《数据结构与算法设计》第5章 树

5.2.2 二叉树的性质
➢ 满二叉树和完全二叉树
满二叉树是指深度为h且节点数取得最大值2h-1的二叉树。 如果一棵深度为h的二叉树,除第h层外,其他每层的节点数 都达到最大,且最后一层的节点自左而右连续分布,这样的二 叉树称为完全二叉树。
5.2.2 二叉树的性质
5.2.2 二叉树的性质
性质6 对含有n个节点的完全二叉树自上而下、同一层从左往右 对节点编号0,1,2,…,n-1,则节点之间存在以下关系: (1)若i=0,则节点i是根节点,无双亲;若i>0,则其双亲节 点的编号为i/2-1; (2)若2×i +1≤n,则i的左孩子编号为2×i+1; (3)若2×i+2≤n,则i的右孩子编号为2×i+2; (4)若i>1且为偶数,则节点i是其双亲的右孩子,且有编号为 i-1的左兄弟; (5)若i<n-1且为奇数,则节点i是其双亲的左孩子,且有编号 为i+1的右兄弟。
5.3.3 二叉树的二叉链表类模板定义
//根据二叉树的先序遍历序列和中序遍历序列创建以r为根的二叉树
void CreateBinaryTree(BTNode<DataType> * &r, DataType pre[], DataType
in[], int preStart, int preEnd, int inStart, int inEnd); int Height(BTNode<DataType> *r); //求以r为根的二叉树高度 //求以r为根的二叉树中叶子节点数目
5.1.2 树的术语
(9)节点的层次:从根节点开始,根为第一层,根的孩子为 第二层,根的孩子的孩子为第三层,依次类推,树中任一节 点所在的层次是其双亲节点所在的层次数加1。 (10)堂兄弟:双亲在同一层的节点互为堂兄弟。
智慧树创新创业第五章答案

智慧树创新创业第五章答案1、()是当前我国调整劳动关系的主要依据。
[单选题]A、宪法B、劳动法律C、劳动规章D、国务院劳动行政法规(正确答案)2、下列关于现代企业计划职能的重要作用,说法不正确的是()。
[单选题]A、使决策目标具体化B、有利于提高企业的工作效率C、为控制提供标准D、有利于员工快速适应工作(正确答案)3、关于背景调查应遵循的原则,下列说法错误的是()。
[单选题]A、只调查与工作相关的情况B、要评估调查材料的可靠程度C、重视客观内容的调查核实D、视应聘考者性格方面的主观评价内容(正确答案)4、下列说法中,属于世界500强企业关于优秀员工的核心标准的是()。
[单选题]A、不把自己当员工,要把自己当老板B、不随便提出自认为好的建议,以免影响上司决策C、不把细节作为关注点,而是增强执行力D、不找任何借口,要自动自发地工作(正确答案)5、团队成员怎样发现创造性解决问题的方法,如何长期保持高效率以及在外部环境变化时改变程序和规范,属于()。
[单选题]A、团队历练B、团队磨合C、团队学习(正确答案)D、团队规范6、关于职业化,正确的说法是()。
[单选题]A、职业化是企业管理者对被管理者的要求,已经完全脱离了市场的影响B、职业化是新型劳动观的核心内容,对新型劳动观提出了更高标准和要求(正确答案)C、职业化要求抛弃主观性因素干扰,不宜作为精神力量存在于职场D、把职责的要求体现在个人履行职业的自律上的做法是职业化的异化7、()就是通过各种资料信息来考察和选拔人才的方法。
[单选题]A、笔试筛选法B、面试筛选法C、小组筛选法D、材料筛选法(正确答案)8、符合“中国商业诚信公约”规定的做法是()。
[单选题]A、宣传和树立“以商为本”的经营理念B、建立和强化商品进货的免检、免验制度C、倡导科学消费、积极消费、扩大消费等先进的消费方式D、对售出商品实行商品质量先行负责制(正确答案)9、()要求企业和部门在提供信息时,从实际出发,实事求是,并尽可能突出重点,抓住问题的要害。
第五章 优树选择

120
110
95%
100
置 信 90 区 间 80 树 高 ( 70 )
60
m
50
40 FZ10 FZ23 FZ7 WC14 WC2 WC27 WC5 XL17 XL4 FZ16 FZ29 WC11 WC17 WC24 WC3 WC8 XL20
图5-8
种源
6年生水曲柳家系间树高分布图
六、选优过程
第五章 优树选择
主要内容
一、人工选择特点和选择类型 二、优树的选择和利用 三、优树标准和选优林分 四、优树评选 五、种源选择和优树选择的结合
重点掌握:优树选择的方法和标准的制定。
有关概念
优树(superior ,plus tree):又称正号树,是指在相似 环境条件,如相同立地条件、相同林龄、采取相同营林措 施的天然林或人工林中,在生长量、材性及抗性适应性上 表现优良的个体。
0.50~0.60
31~35: 0.46~0.59
0.46~0.57
36~40: 0.42~0.53
0.43~0.54
41~45: 0.33~0.45
0.40~0.55
46~55: 0.32~0.43
0.39~0.52
56~65: 0.31~0.41
0.38~0.50
形质指标
形率0.65,弯曲度-完全通直,高径比>80%,冠径比<27, 枝下高>0.45,枝径比<0.25等,木材纹理-完全通直。
(三)综合评定
1.连续选择法 就是依次先对某一性状进行选择,再对第二个性状选择, 然后对第三个性状选择,直至达到目的。
2.独立标准法 对所选择的各项性状,都规定一个最低的标准。只要有一 个性状不够标准,不管其他性状如何优越,都不能入选。
第5章 树和二叉树

B A
C
D
E
F
G
H
I
J
K
L
T1
T2
M
2015年10月20日
T3
树的其它表示方式
A D K L F C G E B H M J I
A
A B E K L F C G
B C D
嵌套集合
E
D H M
F
G
H
I
J
I J
K
L
M
凹入表示
(A(B(E(K,L),F),C(G),D(H(M),I,J)))
广义表
2015年10月20日
北京林业大学信息学院
2015年10月20日
二叉树的链式存储
PARENT
lchild
data
rchild
DATA
lchild
data
parent rchild
LCHILD
RCHILD
北京林业大学信息学院
2015年10月20日
二叉链表
A A ^ B D lchild data rchild
B
C
E
G
F
二叉树的五种不同形态
2015年10月20日
练习
具有3个结点的二叉树可能有几种不同形态?普通树呢? 5种/2种
2015年10月20日
二叉树的抽象数据类型定义
ADT BinaryTree{ 数据对象D: D是具有相同特性的数据元素的集合。 数据关系R: 若D=Φ,则R= Φ ; 若D≠Φ,则R= {H};存在二元关系: ① root 唯一 //关于根的说明 ② Dj∩Dk= Φ //关于子树不相交的说明 ③ …… //关于数据元素的说明 ④ …… //关于左子树和右子树的说明 //至少有20个 基本操作 P: }ADT BinaryTree
数据结构 树 考试习题

第五章树11.不含任何结点的空树( )A)是一棵树 B)是一棵二叉树C)既不是树也不是二叉树 D)是一棵树也是一棵二叉树12.二叉树是非线性数据结构,所以( )A)它不能用顺序存储结构存储; B)它不能用链式存储结构存储;C)顺序存储结构和链式存储结构都能存储; D)顺序存储结构和链式存储结构都不能使用13.把一棵树转换为二叉树后,这棵二叉树的形态是( )A)唯一的 B)有多种C)有多种,但根结点都没有左孩子 D)有多种,但根结点都没有右孩子9. 11 , 8 , 6 , 2 , 5 的叶子结点生成一棵哈夫曼树,它的带权路径长度为()A) 24 B) 72 C) 48 D) 5310.一棵含18个结点的二叉树的高度至少为( )A) 3 B) 4 C) 6 D) 511.下面的二叉树中,( C )不是完全二叉树。
10. 设结点x和结点y是二叉树T中的任意两个结点,若在前序序列中x在y之前,而在中序序列中x在y之后,则x和y的关系是()A)x是y的左兄弟 B)x是y的右兄弟C)y是x的祖先 D)y是x的孩子11.设二叉树根结点的层次为1,所有含有15个结点的二叉树中,最小高度是()A) 6 B) 5 C) 4 D) 37.下列陈述中正确的是()A)二叉树是度为2的有序树B)二叉树中结点只有一个孩子时无左右之分C)二叉树中必有度为2的结点D)二叉树中最多只有两棵子树,并且有左右之分8. 树最适合用来表示()A)有序数据元素 B)无序数据元素C)元素之间具有分支层次关系的数据 D)元素之间无联系的元素9. 3个结点有()不同形态的二叉树A) 2 B) 3 C) 4 D) 56.二叉树是非线性数据结构,( )A)它不能用顺序存储结构存储; B)它不能用链式存储结构存储;C)顺序存储结构和链式存储结构都能存储;D)顺序存储结构和链式存储结构都不能使用7.二叉树上叶结点数等于( )A ) 分支结点数加1B ) 单分支结点数加1C ) 双分支结点数加1D ) 双分支结点数减18.如将一棵有n个结点的完全二叉树按顺序存放方式,存放在下标编号为0, 1,…, n-1的一维数组中,设某结点下标为k(k>0),则其双亲结点的下标是( )A ) (k-1)/2B ) (k+1)/2C ) k/2D ) k-18. 树最适合用来表示()。
第五章整形修剪

二、整形修剪的时期
(一)休眠期修剪(冬剪)
(二)生长期修剪(夏剪)
三、修剪技术
1.短截:剪去枝条的一段,保留一定长度和
一定数量的芽,称短截。
修枝剪(圆口弹簧剪)
2.疏剪:
是指将枝条从着生基部剪除的方法称疏剪,
也叫疏删、疏枝。
疏剪大枝
三 锯 法3.回缩 Nhomakorabea回缩常用于多年生骨干枝的复壮。
第五章 树木的整形修剪
修剪:是对园林树木的某些器官,如茎、枝、
阵、花、巢、芽、根等进行剪截或删除的措 施。
整形:是对植株施行一定的修剪措施而形成
某种树体结构形态的方法。
一、整形修剪的意义
1.保证树木的健康
2.培育良好的树形 3.调节树体各个部分的均衡关系 4.保障人身和财产安全
式。
2.自然开心形
3.多领导干形
4.中央领导干形
5.丛球形
6.棚架形
4、辅助修剪
摘心
抹芽 环割 刻伤 折裂等等
四、整形技术
(一)自然式整形
(二)人工式整形
(三)混合式整形:
根据园林绿化的要求,对自然树形加以或多
或少的人工改造而形成的树形。 常见的有杯形、自然开心形、多领导干形、 中央领导干形、丛球形、棚架形等。
杯型:即所谓“三股、六杈、十二枝”的形
第五章习题

三、填空题
9. n个结点的各棵树中,其深度最小的那棵树的深度 是 2 。它共有 n-1 个叶子结点和 1 个非叶子结点, 其中,深度最大的那棵树的深度是 n ,它共有 1 个 叶子结点和 n-1 个非叶子结点。
10.先根遍历树林正好等同于 先序 遍历对应的二叉树,后 根遍历树林正好等同于按 中序 遍历对应的二叉树。 11.若一个二叉树的叶子结点是某子树的中序遍历序列中的 前序 最后一个结点,则它必是该子树的______序列中的最后一个 结点。
C,E,F,G,
二、判断题
× 1.二叉树是度为2的有序树。
× 2. 完全二叉树一定存在度为1的结点。 √
√
3.深度为K的二叉树中结点总数≤2k-1。 4. 一个树的叶结点,在前序遍历和后序遍历 下,皆以相同的相对位置出现。 但是,如果我们还知道该树的根结点是哪一个, 则可以确定这棵二叉树。 一个栈。
C A
10.深度为h的满m叉树的第k层有( )个结 点。(1=<k=<h) A.mk-1 B.mk-1 C.mh-1 D.mh-1
一、选择题
11.高度为 K的二叉树最大的结点数为( A.2k B.2k-1 C.2k -1 D.2k-1-1 12. 一棵树高为K的完全二叉树至少有( A.2k –1 B. 2k-1 –1 C. 2k-1 D. 2k )。
第五章 树和二叉树
习题讨论
、选择题
1.已知一算术表达式的中缀形式为 A+B*C-D/E,后缀形式 为ABC*+DE/-,其前缀形式为( ) A.-A+B*C/DE B. -A+B*CD/E C.-+*ABC/DE D. -+A*BC/DE
D
C
2. 设有一表示算术表达式的二叉树(见下图),它所表示的算 术表达式是( ) A. A*B+C/(D*E)+(F-G) / B. (A*B+C)/(D*E)+(F-G) + + C * C. (A*B+C)/(D*E+(F-G)) * D E F G D. A*B+C/D*E+F-G A B
第五章二叉树-.ppt

1
2
3
4
5
6
7
图5.9 满二叉树
则称这样的二叉树为完全二叉树,图5.10(b)、 (c)是2棵非完全二叉树。满二叉树是完全二叉树的 特例。
1
2
3
45
6
(a)完全二叉树
1
2
3
4
5
7
(b)非完全二叉树
图5.10 完全二叉树
1
2
3
6
7
( c)非完全二叉树
完全二叉树的特点是:
(1)所有的叶结点都出现在第k层或k-1层。
n0,度为2的结点数为n2,则n0=n2+1。
设二叉树中度为1的结点数为n1,二叉树中总结点数 为N,因为二叉树中所有结点均小于或等于2,所以
有:N=n0+n1+n2
(5-1)
再看二叉树中的分支数,除根结点外,其余结点都
有一个进入分支,设B为二叉树中的分支总数,
则有:N=B+1。
由于这些分支都是由度为1和2的结点射出的,所有有: B=n1+2*n2 N=B+1=n1+2×n2+1 (5-2)
5.1 树的定义和基本术语
定义:树(Tree)是n(n>=0)个结点的有限集T,T为 空时称为空树,否则它满足如下两个条件:
(1)有且仅有一个特定的称为根(Root)的结点;
(2)其余的结点可分为m(m>=0)个互
不相交的子集T1,T2,T3…Tm,其中每 个子集又是一棵树,并称其为子树
(Subtree)。
第五章 二叉树
树型结构是一类重要的非线性结构。树型结 构是结点之间有分支,并且具有层次关系的结构, 它非常类似于自然界中的树。树结构在客观世界 国是大量存在的,例如家谱、行政组织机构都可 用树形象地表示。树在计算机领域中也有着广泛 的应用,例如在编译程序中,用树来表示源程序 的语法结构;在数据库系统中,可用树来组织信 息;在分析算法的行为时,可用树来描述其执行 过程。等等。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
6章树和二叉树6.1 已知一棵树边的集合为{<I,M>, <I,N>, <E,I>, <B,E>, <B,D>, <A,B>, <G,J>, <G,K>, <C,G>, <C,F>, <A,C>},请画出这棵树,并回答下列问题:(1) 哪个是根结点?(2) 哪些是叶子结点?(3) 哪个是结点G的双亲?(4) 哪些是结点G的祖先?(5) 哪些是结点G的孩子?(6) 哪些是结点E的子孙?(7) 那些是结点E的子孙?(8) 结点B和N的层次号分别是什么?(9) 树的深度是多少?(10) 以结点C为根的子树的深度是多少?6.2 一棵度为2的树与一棵二叉树有何区别?解:二叉树是颗有序树,但度为2的树则未必有序。
6.3 试分别画出具有3个结点的树和3个结点的二叉树的所有不同形态。
6.4 一棵深度为H 的满k 叉树有如下性质:第H 层上的结点都是叶子结点,其余各层上每个结点都有k 棵非空子树。
如果按层次顺序从1开始对全部结点编号,问: (1) 各层的结点数目是多少?(2) 编号为p 的结点的父结点(若存在)的编号是多少? (3) 编号为p 的结点的第i 个儿子结点(若存在)的编号是多少?(4) 编号为p 的结点有右兄弟的条件是什么?其右兄弟的编号是多少?解:(1)11--k k H(2)如果p 是其双亲的最小的孩子(右孩子),则p 减去根结点的一个结点,应是k 的整数倍,该整数即为所在的组数,每一组为一棵满k 叉树,正好应为双亲结点的编号。
如果p 是其双亲的最大的孩子(左孩子),则p+k-1为其最小的弟弟,再减去一个根结点,除以k ,即为其双亲结点的编号。
综合来说,对于p 是左孩子的情况,i=(p+k-2)/k ;对于p 是右孩子的情况,i=(p-1)/k如果左孩子的编号为p ,则其右孩子编号必为p+k-1,所以,其双亲结点的编号为⎥⎦⎥⎢⎣⎢-+=k k p i 2 向下取整,如1.5向下取整为1(3)结点p 的右孩子的编号为kp+1,左孩子的编号为kp+1-k+1=k(p-1)+2,第i 个孩子的编号为k(p-1)+2+i-1=kp-k+i+1。
(4)当(p-1)%k != 0时,结点p 有右兄弟,其右兄弟的编号为p+1。
6.5 已知一棵度为k 的树中有1n 个度为1的结点,2n 个度为2的结点,…,k n 个度为k 的结点,问该树中有多少个叶子结点?解:根据树的定义,在一颗树中,除树根结点外,每个结点有且仅有一个前驱结点,也就是说,每个结点与指向它的一个分支一一对应,所以除树根结点之外的结点树等于所有结点的分支数,即度数,从而可得树中的结点数等于所有结点的度数加1。
总结点数为k kn n n n +++++ (321321)而度为0的结点数就应为总结点数减去度不为0的结点数的总和,即∑=-+=++++-+++++=ki i k k n i n n n n kn n n n n 13213210)1(1)...( (321)6.6 已知在一棵含有n 个结点的树中,只有度为k 的分支结点和度为0的叶子结点。
试求该树含有的叶子节点数目。
解:利用上题结论易得结果。
设度为k 的结点个数为k n ,则总结点数为k n n k +=1。
叶子结点的数目应等于总结点数减去度不为0的结点的数目,即kn n n n n k 10--=-= 6.7 一棵含有n 个结点的k 叉树,可能达到的最大深度和最小深度各为多少?解:能达到最大深度的树是单支树,其深度为n 。
满k 叉树的深度最小,其深度为⎡⎤)1)1((log +-k n k (证明见徐孝凯著数据结构实用教程P166)6.8 证明:一棵满k 叉树上的叶子结点数0n 和非叶子结点数1n 之间满足以下关系:()1110+-=n k n解:一棵满k 叉树的最后一层(深度为h)的结点数(叶子结点数)为10-=h kn ,其总结点数为11--k k h ,则非叶子结点数00011111n k kn n k k n h ---=---=,从而得1)1(10+-=n k n 6.9 试分别推导含有n 个结点和含0n 个叶子结点的完全三叉树的深度H 。
解:(1) 根据完全三叉树的定义 11111--≤<---k k n k k H H 132131-≤<--H H n)12(3312+<≤+n n H)12(log 1)12(log 33++<≤+n H n)12(log 3+=n H(2) 设总的结点数为n ,非叶子结点数为1n 注意到每个非叶子结点的度均为3,则 n n =+131由 n n n =+1021230-=n n 0303log 1)3(log n n H +== 6.10 对于那些所有非叶子结点均含有左右子数的二叉树: (1) 试问:有n 个叶子结点的树中共有多少个结点?(2) 试证明:()1211=∑=--ni l i,其中n 为叶子结点的个数,i l 表示第i 个叶子结点所在的层次(设根节点所在层次为1)。
解:(1)总结点数为121n +,其中1n 为非叶子结点数,则叶子结点数为11+=n n ,所以总结点数为12-n 。
(2)用归纳法证明。
i=1,说明二叉树只有一个叶子结点,则整棵树只有一个根结点,11=l ,12)1(1=--l ,结论成立。
设有n 个叶子结点时也成立,即12...2...22)1()1()1()1(21=++++++-------n p l l l l ,现假设增加一个叶子结点,这意味着在某叶子结点p 上新生两个叶子结点,而结点p 则成为非叶子结点,可见,总结点数增2,叶子结点数增1。
此时,所有叶子结点是原结点除去p ,然后加上两个深度为1+p l 的新叶子结点,由此,)11()11()1()1()1()1()1(222...22...221121-+--+-+---------+++++++++-p p n p p l l l lll l12...2...22)1()1()1()1(21=+++++=+-------n p l l l l则当i=n+1时,也成立,由此即得到证明。
6.11 在二叉树的顺序存储结构中,实际上隐含着双亲的信息,因此可和三叉链表对应。
假设每个指针域占4个字节,每个信息域占k 个字节。
试问:对于一棵有n 个结点的二叉树,且在顺序存储结构中最后一个节点的下标为m ,在什么条件下顺序存储结构比三叉链表更节省空间?解:采用三叉链表结构,需要n(k+12)个字节的存储空间。
采用顺序存储结构,需要mk 个字节的存储空间,则当mk<n(k+12)时,即nm nk -<12时,采用顺序存储比采用三叉链表更节省空间。
6.12 对题6.3所得各种形态的二叉树,分别写出前序、中序和后序遍历的序列。
6.13 假设n 和m 为二叉树中两结点,用1、0或#(分别表示肯定、恰恰相反或不一定)填写下表:注:如果(1)离a和b最近的共同祖先p存在,且(2)a在p的左子树中,b在p的右子树中,则称a在b的左方(即b在a的右方)。
6.14 找出所有满足下列条件的二叉树:(a) 它们在先序遍历和中序遍历时,得到的节点访问序列相同;(b) 它们在后序遍历和中序遍历时,得到的结点访问序列相同;(c) 它们在先序遍历和后序遍历时,得到的节点访问序列相同。
解:(a) 不含左子树的二叉树。
(b) 不含右子树的二叉树。
(c) 即不含左子树,也不含右子树的二叉树。
6.15 解:6.16 解:1 2 3 4 5 6 7 8 9 10 11 12 13 146.17 解:其错误在于中序遍历应先访问其左子树,可做如下修改:BiTree InSucc(BiTree q){// 一直q是指向中序线索二叉树上某个结点的指针,// 本函数返回指向*q的后继的指针。
r=q->rchild;if(!r->ltag)while(!r->ltag) r=r->lchild;return r;} // InSucc6.18 解:如果p是根结点,则其后继为空。
否则需查找p的双亲结点。
从p结点开始中序线索遍历,如果某结点的左指针域等于p,说明该结点是p的双亲结点,且p是它的左孩子;如果某结点的右指针域等于p,说明该结点是p的双亲结点,且p是它的右孩子;如此即可确定访问次序。
若是右孩子,其后继是双亲结点;若是左孩子,其后继是其兄弟最左下的子孙,如果兄弟不存在,其后继是其双亲结点。
6.19 分别画出和下列树对应的各个二叉树:解:6.20 解:(1) 先序:1 2 3 4 5 6 8 7 9 10 11 12 13 15 14(2) 中序:3 4 8 6 7 5 2 1 10 9 11 15 14 13 12(3) 后序:8 7 6 5 4 3 2 10 15 14 13 12 11 9 16.23 解:树的先根序列为GFKDAIEBCHJ,后根序列为DIAEKFCJHBG,可以先转化成二叉树,再通过二叉树转换成树。
注意二叉树的先根序列与等价树的先根序列相同,二叉树的中序序列对应着树的后根序列。
GFKDAIEBCHJ为所求二叉树的先序序列,DIAEKFCJHBG为二叉树的中序序列。
通过观察先序序列,G为二叉树的根结点,再由中序序列,G的左子树序列为DIAEKFCJHB,右子为空。
可以表示成如下形式:G(DIAEKFCJHB,NULL)对于子树先序序列为FKDAIEBCHJ,中序序列为DIAEKFCJHB,显然子树根为F。
再由中序序列可以看到,F的左子树是DIAEK,右子树为CJHB。
进一步表示成:G(F(DIAEK,CJHB),NULL)对于DIAEK(中序表示),先序为KDAIE,K为根,左子为DIAE,右子为空;对于CJHB,B为根,左子为CJH,右子为空。
进一步表示成:G(F(K(DIAE,NULL),B(CJH,NULL)),NULL)G(F(K(D(NULL,IAE),NULL),B(C(NULL,JH),NULL)),NULL)G(F(K(D(NULL,A(I,E)),NULL),B(C(NULL,H(J,NULL)),NULL)) ,NULL)由此画出二叉树,进而画出树。
6.24 解:本题应注意下列转换:树森林二叉树先根先序先序后根中序中序6.25 解;用归纳法证明。
当n=2时,要使其成为最优二叉树,必须使两个结点都成为叶子结点。
设n=k时成立,则当n=k+1时,要使其成为最优,必须用k个结点的哈夫曼树与第k+1个结点组成一个新的最优二叉树,所以n=k+1时也成立。
