《多边形的面积》单元知识结构图
五年级数学上册人教版第六单元《多边形的面积》(单元解读)

第六单元多边形的面积单元解读一、链接课标《义务教育数学课程标准(2022年版)》指出在小学阶段“图形与几何”领域所对应的核心素养侧重于空间观念,几何直观,量感和推理意识。
学生要结合生活情境认识平面图形及特征,会计算图形的周长和面积,并解决一定的实际问题。
多边形的面积是图形与几何领域测量中的重要内容。
通过本单元的教学,要引导学生探索并掌握平行四边形、三角形和梯形的面积公式,会计算组合图形的面积,在观察、实验、猜想、验证等活动中,渗透平移、旋转、转化等数学思想方法,发展合情推理能力,促进学生空间观念的进一步发展、感受几何直观和符号意识的作用,渗透估测意识、策略,了解解决问题方法的多样性,培养学生的应用意识和创新意识。
二、单元目标学生已经在生活中积累了有关图形认识和图形测量的经验,同时已经研究了长方形、正方形、三角形的特征以及长方形、正方形的面积计算。
在研究本单元中,教师应引导学生紧密联系生活实际,从已有的认知基础和生活经验出发,让学生在数、剪、拼、摆等操作活动中,完成对新知的构建。
引导学生利用转化的数学思想,在操作中研究新知是本单元教学的重要环节。
通过实际操作活动,发展学生的空间观念,培养动手操作能力,为接下来研究圆的面积作好铺垫。
根据学情及教材内容制定了教学目标:1.理解并掌握各种图形的面积计算公式。
2.引导学生运用转化的方式来探索规律,认识新旧知识之间的联系。
3.会拼、摆、拆分各种组合图形,并正确计算组合图形的面积。
4.通过实验、操作、拼摆、割补等方法,使学生经历计算公式的推导过程,进一步发展学生的思维。
5.应用面积的计算公式,使学生运用转化的方法解决实际问题,发展学生的空间观念。
沟通知识与生活的联系,激发学生的学习兴趣,培养学生探究意识和创新能力,发展学生的空间观念。
三、单元教学重点、难点:教学重点:掌握平行四边形、三角形和梯形的面积计算公式,并能正确运用。
教学难点:通过探索活动,能够掌握平行四边形、三角形和梯形的面积计算公式推导的过程。
第六单元 多边形的面积 —组合图形的面积

我的收获
计算组合图形的面积,一般是把它 们分割或添补成基本图形,如长方形、 正方形、三角形、梯形等,再计算它们 的面积之和或差。
这是我们学校将要开辟的一块草坪,如下图。 你能算出它的面积吗?
人教新课标五年级数学上册
长方形面积=长×宽 S=ab
正方形面积=边长×边长 S=a2
猜一猜,里面 都有哪些平面 图形?
平行四边形的面积=底×高 S=ah
三角形的面积=底×高÷2 S=ah ÷2
梯形的面积=(上底+下底) × 高÷2 S=(a+b) ×h ÷2
这些都是简单的、基本的图形。
由几个简单的图形组合而成的图形叫组合图形。
3m
7m
7m
7m
分割法
4m
6m 3m
7m
添补法
2m
5m
右图表示的是一间房子
侧面墙的形状。它的面
积是多少平方米?
5m
可以把它看成一个正方 形和一个三角形的组合 。
2m
5m
我的方法是:
5m
侧面墙的面积=(正方形面积)+( 三角形面积) 5×5+5×2÷2
=25+5 =30( m2 ) 答:它的面积是30平方米
它们分别是由哪些图形组成的?
这些都叫做什么图形呢? 组合图形
小华家新买了新房,计划在客厅和餐
厅铺木地板(平面图如下)。请大家帮他 出一下主意如何才能求出他家的地面面积?
4m
6m
四人一小组讨论: 可以把这个组合图形 转化成哪几个简单图 形,可以边说边画。
7m
3m
4m4mຫໍສະໝຸດ 4m6m6m
《多边形的面积》单元整体设计解读

《多边形的面积》单元整体设计解读多边形的面积是几何学中的一个重要概念,是研究多边形性质和解决与多边形相关问题的基础知识。
在初中数学中,多边形的面积通常在七年级上学期或八年级上学期进行学习。
本文将对多边形的面积单元整体设计进行解读。
一、设计目标本单元的设计目标主要有以下几点:1.掌握计算各类多边形的面积的方法。
2.理解面积的概念和计算面积的意义。
3.培养学生观察、分析和解决实际问题的能力。
4.培养学生合作学习和信息技术应用的能力。
二、设计内容本单元的主要内容包括以下几个方面:1.熟悉多边形的概念和分类。
2.掌握计算正方形、长方形和平行四边形的面积公式及应用。
3.掌握计算三角形的面积公式及应用。
4.认识圆和圆的面积计算方法。
5.解决多边形面积计算问题和实际问题。
三、设计步骤1.知识导入:通过图示和实际物体引入多边形面积的概念,并进行讨论。
3.计算三角形的面积:介绍计算三角形的面积公式(底乘以高除以2),并进行实例分析。
5.复习和巩固:进行一些小组练习,包括计算各类多边形的面积和解决实际问题。
6.拓展和应用:进行一些开放性问题,引导学生应用所学知识解决实际生活和数学问题。
7.总结和评价:学生对本单元的学习进行总结,给予评价和反馈。
四、教学方法在本单元的教学中,可以运用多种教学方法,以提高学生的学习效果和兴趣,具体包括:1.讲解法:通过清晰简洁的语言,向学生讲解多边形面积的概念和计算方法。
2.演示法:通过示范具体的计算步骤和实例,让学生能够观察和模仿,提高计算的准确性和效率。
3.合作学习法:组织学生进行小组讨论和合作学习,在解决问题的过程中培养学生的合作与交流能力。
4.情境教学法:设计一些与实际生活相关的问题,让学生在实际情境中应用已学知识解决问题,提高学生的问题解决能力和应用能力。
5.案例分析法:介绍一些实际问题案例,引导学生分析问题和提出解决方法,培养学生的观察和分析能力。
五、评价方式在本单元的评价中,可以采用多种评价方式,综合考察学生的知识掌握程度、思维能力和实际应用能力,具体包括:1.口头回答:通过学生口头回答问题的方式,考察学生对面积概念和计算方法的理解和掌握情况。
《多边形的面积复习》PPT课件

(
).
3.一个平行四边形的底是14厘米,高是9厘米,它的面积是
(
);与它等底等高的三角形面积是(
).
4.一个梯形的上底是3米,下底2米,高2米,这个梯形的面积是
(
)平方米;与它等上、下底之和等高的平行四边形的面
积是(
).
5.工地上有一堆钢管,横截面是一个梯形,已知最上面一层有2根,
最下面一层有12根,共堆了11层,这堆钢管共有( )根。
()
3.长是a,宽是b的长方形,底是a,高是b的平行
四边形,底是2a,高是b的三角形,这三个图形的
面积必相等。( )
4.只要知道梯形的两底之和的长度和它的高,就
可以求出它的面积。( )
5.两个周长相等的等边三角形,面积必相等。
()
6.梯形的面积比平行四边形的面积小。( )
7.梯形的上底一定比下底短。(
6.一个三角形比与它等底等高的平行四边的面积少30平方厘米,
则这个三角形的面积是( )。
7.一个三角形的面积是4.5平方分米,底是5分米,高是( )分米。
8.一个等边三角形的周长是18厘米,高是3.6厘米,它的面积是( )
平方厘米。
二、判定题
1.两个面积相等的三角形,一定能拼成一
个平行四边形.(
)
):
个三角形的面积是( )。
A.21 B. 30 C.14
1.在推导平行四边形面积计算公式时,可把平行四边形通过割补平移转化为(
)
形去
推导,推导三角形面积计算公式时,可把两个完全一样的三角形拼成一个(
)形
去推
导,推导梯形面积计算公式时,可把两个完全一样的梯形拼成一个(
)形进行推导。
《多边形的面积——比较图形的面积》数学教学PPT课件(3篇)

可以用尺量出它的长和宽,再求面积。
可以把它放在一个边长为1厘米的小正方形的方格纸 里,数一数它有多少个面积为1cm2的正方形小方格, 就可以知道它的面积有多大……
同学们说得都对,那么现在请看这里有几个平面图形,今天我们就 来比较它们的面积。
二、自主探究 说说你们是怎样比较面积的大小的? 1号和3号图的面积相等,我们用数方格的方法。
多边形的面积
比较图形的面积
课堂导入-新知探究-课堂练习-课堂小结-课堂作业
1.借助方格纸,能直接判断图形面积的大小。 2.通过交流,知道比较图形面积大小的基本方法。 3.体验图形形状的变化与面积大小变化的关系。
你还记得吗?我们已经学过哪些平面图形?
观察并比较下面各图形的面积大小有什么关系?
小组合作学习探索研究: 1.将剪好的三角形或四边形拼一拼, 摆一摆。 2.找出两个面积相等的图形,与同伴 说一说你是怎样找到的?
我们还发现了图8和图10的面积也相等。
||| ||| ||
像上面这样分割、移补后,图形的面积没有改变,这就是 数学上的“出入相补”原理。
通过以上交流我们发现10个图形它们的形状不完 全相同,但我们发现许多面积相等的图形,那么 图形形状的变化和图形面积大小变化有什么样的 关系呢?
图形形状不同,它们的面积可能相等。
填空。 两个形状和大小完全相同的图形,面积(一定 ) 相等;两个面积相等的图形,形状(不一定 ) 相同。
一个长方形,长8厘米,宽6厘米,在这个长方形的一边剪 去一个最大的正方形后,剩余部分的周长和面积各是多少?
8﹣6=2(厘米) 周长: (2+6)×2
=8×2 =16(厘米) 面积:2×6=12(平方厘米)
2.通过比较、观察、归纳等活动,体验图形形状变化和面 积大小变化的关系。
北师大版小学数学五年级上册第四单元《多边形的面积》

(每个小方格的边长表示1cm)
4.先测量,再计算下列图形的面积,并与同伴交流。
(3+8)×6÷2=33(根)
梯形的面积=(上底+下底)×高÷2 用字母表示是S=(a+b)×h÷2或
S=
1 2
(a+b)×h
剪一剪,将图形A剪成两个部分,使它们能拼成图 形B。如果想拼成图形C,可以怎样剪? B A C
这节课,我们学习了比较多边形的 面积大小,比较多边形面积的方法有多 种,有
。
北师大版 五年级上册 第四单元 多边形的面积
认识底和高
高
高
与同伴说一说什么是梯形、平行四边形和三角形 的高,再认一认。
上底
3.平行四边形花圃的面积是25m2,图中长边对应的 高是多少米?
25÷10=2.5(m)
4.在方格纸上画3个等底等高的平行四边形。(每 个小方格的边长表示1cm)
⑴你是怎么画的?与同伴交流。 ⑵它们的面积一样吗?说一说你的理由。
5.一块平行四边形街头广告牌,底是8.5m,高是 5.4m。要粉刷这块广告牌,每平方米要用油漆
1 2
上底
高 下底
下底
平行四边形的面积 =底×高 =(上底+下底)×高 梯形的面积 =(上底+下底)×高÷2
S=(a+b)×h÷2 平行四边形的面积 =底×高 =(上底+下底)×(高÷2)
上底
高÷2 下底 上底
梯形的面积 =(上底+下底)×高÷2
20m 40m
80m
(20+80)×40÷2=2000(m2)
5m 6m
3m
5m
5m
6m 6m
3m
长方形的面积: 6×5=30
高 底 长
宽
五年级上册数学北师大版《多边形的面积复习课》课件

( 3 )长8厘米宽2米的长方形 ( 6 )底4厘米高4厘米平行四边形 ( 5 )上底4厘米下底12厘米高2厘米梯形
二、选择题
(1)小明用同样长的两根铁丝围成了甲乙两个图形, 比较他们的面积,那么( )。
A.甲比乙大 B.乙比甲大 C. 一样大 D.无法比较
甲
乙
(2)右图中,直线a与直线b相互平行。比较三
操作题 请你在图中画一个梯形和三角形,使它们的面积和 图中平行四边形的面积相等。
3、已知一个等腰梯形菜地的面积为56平方米,高为8米,上底为5 米,腰长为9米。如果用篱笆围这块菜地,需要围多少米?
小结
1、你心中关于面积的问题解决了吗?
数学就是研究千变万化中不变的关系。
———约翰尼斯·开普勒
拓展练习
北师大版小学数学五年级上册
多边形的面积复习课(一)
知识结构图
正方形面积=边长×边长
知识结构图
三角形=底×高 2
长方形面积=长×宽
平行四边形=底×高 梯形面积=(上底+下底)×高 2
面积是16平方厘米的图形
(1)底4厘米高4厘米三角形
( 4 )底8厘米高4厘米三角形
( 2 )边长为4厘米的正方形
如图(单位长:1cm)梯形的面积是( )。如果在这个梯形 中截出一个最大的平行四边形,这个平行四边形的面积是( );如 果在这个梯形中截出一个最大的三角形,这个三角形的面积是 ( )。
10
10
18
角形ABC和三角形BCD的面积大小关系。( )
A、SABC > SBCD C、SABC = SBCD
B、SABC< SBCD D、无法比较
aA
D
bB
C
第四单元《多边形的面积》推导过程和典型题目
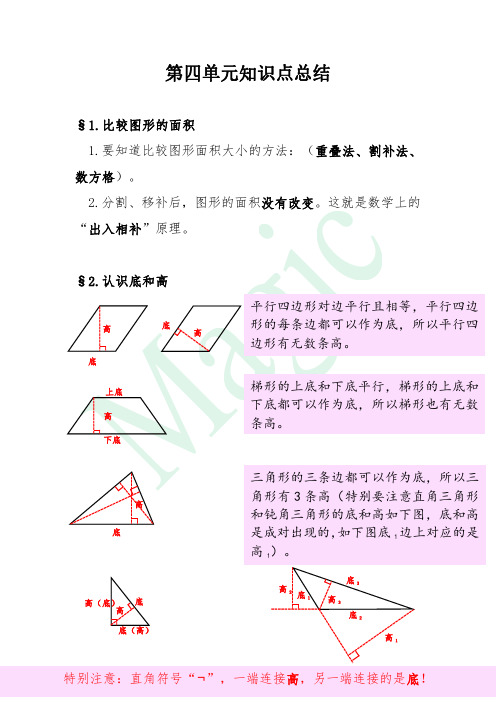
第四单元知识点总结§1.比较图形的面积1.要知道比较图形面积大小的方法:(重叠法、割补法、数方格)。
2.分割、移补后,图形的面积没有改变。
这就是数学上的“出入相补”原理。
§2.认识底和高平行四边形对边平行且相等,平行四边形的每条边都可以作为底,所以平行四边形有无数条高。
底高高底高下底上底梯形的上底和下底平行,梯形的上底和下底都可以作为底,所以梯形也有无数条高。
高底三角形的三条边都可以作为底,所以三角形有3条高(特别要注意直角三角形和钝角三角形的底和高如下图,底和高是成对出现的,如下图底1边上对应的是高1)。
高1底2底3底1高2高3高底底(高)高(底)特别注意:直角符号“¬”,一端连接高,另一端连接的是底!§3.探索活动:平行四边形的面积如果已知平行四边形的面积和高,可以推出底=S 平÷高;如果已知平行四边形的面积和底,可以推出高=S 平÷底。
§4.探索活动:三角形的面积方法一:如果已知三角形的面积和高,可以推出底=2×S △÷高;如果已知三角形的面积和底,可以推出高=2×S △÷底。
通过割补,平行四边形转化成面积相等的长方形。
长方形的长相当于平行四边形的底,长方形的宽相当于平行四边形的高,长方形的面积=长×宽,所以平行四边形的面积=底×高。
如果用S 表示平行四边形的面积,用a 和h 分别表示平行四边形的底和高,那么,平行四边形的面积公式可以写成:S=ah 用两个完全一样的三角形,可以拼成一个平行四边形,一个三角形的面积是平行四边形面积的一半。
平行四边形的底和高与原三角形的底和高一样,平行四边形的面积=底×高,所以一个三角形的面积=底×高÷2。
如果用S 表示三角形的面积,用a 和h 分别表示三角形的底和高,那么,三角形的面积公式可以写成:S=ah÷2。
