2011-2012-2实验7排队论问题的编程实现
七下排队问题知识点总结

七下排队问题知识点总结一、解决排队问题的方法1. 冒泡排序冒泡排序是一种简单的排序算法,它重复地走访过要排序的数列,一次比较两个元素,如果它们的顺序错误就进行交换。
重复进行下去,直到没有再输人交换,有了问题解决排队问题的方法,可以更有效地解决排队问题。
2. 快速排序快速排序是对冒泡排序的一种改进。
它通过一趟排序将要排序的数据分割成独立的两部分,其中一部分的所有数据都比另一部分的数据小。
然后按照此方法对这两部分数据进行快速排序,以此达到整个数据变成有序序列的效果。
可以应用到排队问题的解决中。
3. 插入排序插入排序是一种简单直观的排序算法。
它的工作原理是通过构建有序序列,对于未排序数据,在已排序序列中从后向前扫描,找到相应位置并插入。
通过这种方法可以在排队问题中找到更好的解决方法。
4. 选择排序选择排序是一种简单直观的排序算法。
它的工作原理是通过构建有序序列,在待排序的数据元素中选择最小(或最大)的一个元素,存放在序列的起始位置,然后,从剩余的未排序元素中继续寻找最小(大)元素,然后放到已排序序列的末尾,以此类推,直到所有元素均排序完毕。
可以应用在排队问题的解决中。
5. 归并排序归并排序是一种分治算法,它是建立在归并操作上的一种有效的排序算法。
它是一种稳定的排序算法,它也是采用分治法的一个非常典型的应用。
可以应用在排队问题的解决中。
二、排队问题的应用排队问题在日常生活中是非常普遍的,比如排队买票、排队上车、排队结账等等。
对于这些问题的解决,可以采用上述的排队算法,通过一定的规则和方法来进行排队,以达到快速、有效地解决排队问题。
1. 排队买票当人们在购买车票、电影票、演唱会门票等时,需要排队等候购买,此时可以采用排队算法,通过合理的规则来进行排队,以避免拥堵和混乱。
2. 排队上车在公交车站、地铁站等处,人们需要排队上车,如果采用合理的排队算法,可以有效地避免拥堵和混乱,提高上车效率。
3. 排队结账在超市、商场等处,人们在购物后需要排队结账,如果采用合理的排队算法,可以提高结账效率,让顾客更快地完成购物。
排队论问题实验报告(3篇)

第1篇一、实验背景排队论是运筹学的一个重要分支,主要研究在服务系统中顾客的等待时间和服务效率等问题。
在现实生活中,排队现象无处不在,如银行、医院、超市、餐厅等。
通过对排队问题的研究,可以帮助我们优化服务系统,提高顾客满意度,降低运营成本。
本实验旨在通过模拟排队系统,探究排队论在实际问题中的应用。
二、实验目的1. 理解排队论的基本概念和原理。
2. 掌握排队模型的建立方法。
3. 熟悉排队系统参数的估计和调整。
4. 分析排队系统的性能指标,如平均等待时间、服务效率等。
5. 培养运用排队论解决实际问题的能力。
三、实验内容1. 建立排队模型本实验以银行排队系统为例,建立M/M/1排队模型。
该模型假设顾客到达服从泊松分布,服务时间服从负指数分布,服务台数量为1。
2. 参数估计根据实际数据,估计排队系统参数。
假设顾客到达率为λ=2(人/分钟),服务时间为μ=5(分钟/人)。
3. 模拟排队系统使用计算机模拟排队系统,记录顾客到达、等待、服务、离开等过程。
4. 性能分析分析排队系统的性能指标,如平均等待时间、服务效率、顾客满意度等。
四、实验步骤1. 初始化参数设置顾客到达率λ、服务时间μ、服务台数量n。
2. 生成顾客到达序列根据泊松分布生成顾客到达序列。
3. 模拟排队过程(1)当服务台空闲时,允许顾客进入队列。
(2)当顾客进入队列后,开始计时,等待服务。
(3)当服务台服务完毕,顾客离开,开始下一个顾客的服务。
4. 统计性能指标记录顾客等待时间、服务时间、顾客满意度等数据。
5. 分析结果根据实验数据,分析排队系统的性能,并提出优化建议。
五、实验结果与分析1. 平均等待时间根据模拟结果,平均等待时间为2.5分钟。
2. 服务效率服务效率为80%,即每分钟处理0.8个顾客。
3. 顾客满意度根据模拟结果,顾客满意度为85%。
4. 优化建议(1)增加服务台数量,提高服务效率。
(2)优化顾客到达率,降低顾客等待时间。
(3)调整服务时间,缩短顾客等待时间。
排队论使用lingo编写
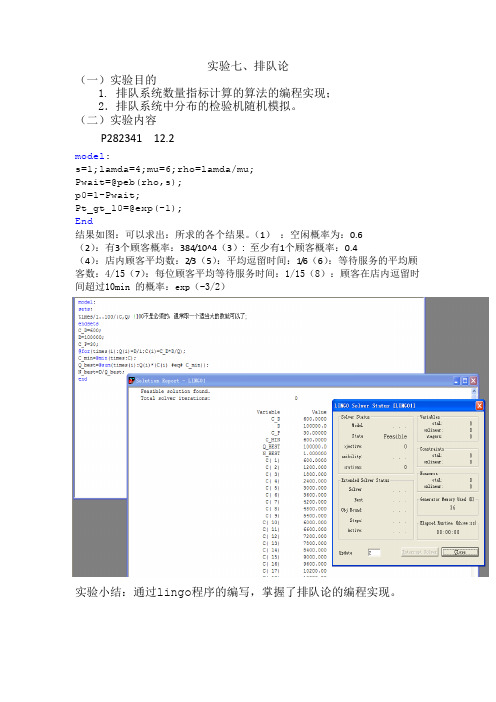
p0=1-Pwait;
Pt_gt_1可以求出:所求的各个结果。(1):空闲概率为:0.6
(2):有3个顾客概率:384/10^4(3):至少有1个顾客概率:0.4
(4):店内顾客平均数:2/3(5):平均逗留时间:1/6(6):等待服务的平均顾客数:4/15(7):每位顾客平均等待服务时间:1/15(8):顾客在店内逗留时间超过10min的概率:exp(-3/2)
实验七排队论一实验目的排队系统数量指标计算的算法的编程实现
实验七、排队论
(一)实验目的
1.排队系统数量指标计算的算法的编程实现;
2.排队系统中分布的检验机随机模拟。
(二)实验内容
P282341 12.2
model:
s=1;lamda=4;mu=6;rho=lamda/mu;
Pwait=@peb(rho,s);
排队论方法讲解

排
队 论 方 法
1. 基本概念
1.排队过程的一般模型 顾客服务过程分为四个步骤:
进入排队系统(输入) 等候服务 接受服务 离开系统(输出)
顾客接受服务后立即离开系统,因此输出 过程可以不用考虑,则
讲
解
输入过程 排队系统排队规则 服务机构
排
队 论
①输入过程: I.顾客总体 (顾客源)
排
队 论
1.5.2 指数分布
当顾客流为泊松流时,用T表示两顾客相 继到达的时间间隔,则T是一个随机变量, 其分布函数为
FT (t ) P{T t} 1 P(T t ) 1 P0 (t )
t t 又P ( t ) e , 则 F ( t ) 1 e , 0 T
k 0 n
讲
解
(全概公式、独立性 ) Pn k (t ) Pk (t , t t )
k 0 n
Pn (t )(1 t ) Pn 1 (t )t o(t )
排 队 论
Pn (t , t t ) Pn (t ) o(t ) Pn (t ) Pn 1 (t ) t t
讲
解
排
队 论
(1) 无后效性:在不相交的时间区 间内,顾客到达数相互独立,即在 [t,t+△t]时段内到达的顾客数,与 时刻t之前到达的顾客数无关; (2)平稳性:对于充分小的△t,在 [t,t+△t]内有1个顾客到达的概率, 只与△t有关,而与t无关,且 P1 (t , t t ) t o(t ),
t
实际中,多数问题都属于稳态情 况,且通常在经过某一时段后即可 到达稳态,而不需要t→∞
排
队 论
排队模拟系统课程设计

排队模拟系统课程设计一、课程目标知识目标:1. 学生能理解排队模拟系统的基本概念,掌握其数学模型及相关参数。
2. 学生能运用所学知识分析并解决生活中的排队问题。
3. 学生了解计算机编程在排队模拟系统中的应用。
技能目标:1. 学生能运用数学知识构建简单的排队模型。
2. 学生能通过编程实现排队模拟系统的运行。
3. 学生能运用数据分析方法评估排队模拟系统的效果。
情感态度价值观目标:1. 培养学生运用数学和计算机知识解决实际问题的兴趣和信心。
2. 增强学生的团队协作意识和沟通能力。
3. 提高学生对生活中排队现象的关注和思考,培养良好的社会公德意识。
课程性质:本课程为信息技术与数学跨学科课程,结合计算机编程和数学建模,培养学生解决实际问题的能力。
学生特点:学生具备一定的数学基础和编程技能,对新鲜事物充满好奇,善于合作和探究。
教学要求:注重理论与实践相结合,引导学生主动参与,鼓励学生创新思维,提高解决问题的能力。
通过课程学习,将目标分解为具体的学习成果,便于后续教学设计和评估。
二、教学内容1. 排队论基本概念:介绍排队系统的组成,排队论的基本参数(到达率、服务率、排队规则等)。
教材章节:第五章第一节2. 排队模型建立:分析不同排队模型的数学表达式,如M/M/1、M/M/c等。
教材章节:第五章第二节3. 计算机编程实现:运用Python等编程语言,实现排队模拟系统的编写。
教材章节:第七章4. 数据分析方法:介绍数据分析方法,如排队长度、等待时间、系统利用率等指标的统计和分析。
教材章节:第六章5. 实际案例分析与讨论:结合生活中的排队现象,运用所学知识进行案例分析,提出优化方案。
教材章节:第八章教学安排与进度:第一课时:排队论基本概念及排队模型的介绍第二课时:计算机编程实现排队模拟系统第三课时:数据分析方法及案例讨论第四课时:学生展示与点评,总结提升教学内容确保科学性和系统性,结合教材章节和实际案例,引导学生从理论到实践,逐步掌握排队模拟系统的相关知识。
算法分析与设计实验报告

排序问题求解实验日志实验题目:排序问题求解实验目的:1)以排序(分类)问题为例,掌握分治法的基本设计策略。
2)熟练掌握一般插入排序算法的实现;3)熟练掌握快速排序算法的实现;4) 理解常见的算法经验分析方法;实验要求:1.生成实验数据.要求:编写一个函数datagenetare,生成2000个在区间[1,10000]上的随机整数,并将这些数输出到外部文件data.txt中。
这些数作为后面算法的实验数据。
2.实现直接插入排序算法.3.实现快速排序算法.实验主要步骤:#include<stdlib.h>#include<stdio.h>#include<time.h>#include<math.h>#define RAND_MAX 10000#define Max 1000intI_Change_count = 0; //插入排序比较计数器intI_Move_count = 0; //插入排序移动计数器intS_Change_count =0; //选择排序比较计数器intS_Move_count = 0; //选择排序移动计数器intQ_Change_count = 0; //快速排序比较计数器intQ_Move_count = 0; //快速排序移动计数器void main(){longnum;long Array[Max],Brray[Max],Crray[Max];//分别用来保存随机数作为两个排序的对象intA_Length;int Low = 0;int High;time_t t;voidInsertSort(long Array[],intA_Length);//void SelectSort(long Brray[],intA_Length);voidQuickSort(long Crray[],intLow,int High);srand((unsigned) time(&t));/*用时间初始化随机函数*/intT,i;printf("输入你想要比较的数的个数,本算法是按照2的次方来计算的:");scanf("%d",&T);A_Length = (int)pow(2.,T);if(A_Length> 1000){exit(0); //如果比较次数大于100000,退出程序}High = A_Length - 1;printf("比较的个数为:%d\n",A_Length);printf("=======================原序列=========================\n");for(i=0;i<A_Length;i++){Array[i]=rand()%1000000;//产生1000000内的第一个随机数Brray[i]=Array[i];Crray[i]=Array[i];printf("%ld\t",Array[i]);}printf("\n\n");printf("=======================插入排序后的序列=========================\n");InsertSort(Array,A_Length);for(i=0;i<A_Length;i++){printf("%ld\t",Array[i]);}printf("\n=======================插入排序的时间复杂度=========================");printf("\n插入排序:比较次数=%d,移动次数=%d,时间复杂度=%d\n\n",I_Change_count,I_Move_count,I_Change_count+I_Move_count);/*printf("=======================选择排序后的序列=========================\n");SelectSort(Brray,A_Length);for(int i=0;i<A_Length;i++){printf("%ld\t",Brray[i]);}printf("\n=======================选择排序的时间复杂度=========================");printf("\n选择排序:比较次数=%d,移动次数=%d,时间复杂度=%d\n\n",S_Change_count,S_Move_count,S_Change_count+S_Move_count);*/printf("=======================快速排序后的序列=========================\n");QuickSort(Crray,Low,High);for( i=0;i<A_Length;i++){printf("%ld\t",Crray[i]);}printf("\n=======================快速排序的时间复杂度=========================");printf("\n插入排序:比较次数=%d,移动次数=%d,时间复杂度=%d\n",Q_Change_count,Q_Move_count,Q_Change_count+Q_Move_count);}voidInsertSort(long Array[],intA_Length){inti,j;long signal;for(i = 1;i <A_Length;i++) //依次插入Array[1],…,Array[n-1]if(Array[i]<Array[i-1]||(I_Change_count++&&0))//比较失败时,比较计数器自加{I_Change_count ++; //比较成功时因为“||”后面的不执行所以比较计数器得自加signal = Array[i];j=i-1; //signal是哨兵,且是Array[i]的副本do{ //从右向左在有序区Array[1..i-1]中查找Array[i]的插入位置I_Change_count ++; //比较成功时直接执行所以比较计数器放在此处Array[j+1]=Array[j];//将关键字大于Array[i]的记录后移I_Move_count ++;j--;}while(signal < Array[j]);//当signal≥Array[j]时终止I_Change_count ++;//比较失败时,循环跳出比较计数器自加一次Array[j+1]=signal; //Array[i]插入到正确的位置上}//endif}voidSelectSort(long Brray[],intA_Length){inti,j,k;long signal;for(i=0;i<A_Length;i++){k = i;for(j=i+1;j<A_Length;j++){S_Change_count ++; //因为不管比较成不成功都要比较A_Length-j次//所以将比较计数器放在比较前if(Brray[j] <Brray[k])k = j;}if(k != i){signal = Brray[i];Brray[i] = Brray[k];Brray[k] = signal;S_Move_count ++; //每次交换当做移动一次,因为其他赋值都是为了完成算法而写的//我们认为两者的交换只要一次就实现}}}voidQuickSort(long Crray[],intLow,int High){intC_Low = Low,C_High = High;long signal = Crray[Low];if(Low >= High) return ;while(C_Low != C_High){while(C_Low<C_High&&Crray[C_High] >= signal)C_High --;Crray[C_Low] = Crray[C_High];while(C_Low<C_High&&Crray[C_Low] <= signal)C_Low ++;Crray[C_High] = Crray[C_Low];Q_Change_count ++;}Crray[C_Low] = signal;Q_Move_count ++;QuickSort(Crray,Low,C_Low-1);QuickSort(Crray,C_Low+1,High);}实验结果:输入7共有128个数排序,运行结果如下心得体会:通过本次实验更加深刻的了解的快速排序和直接插入排序算法,通过编写程序实现排序,掌握分治法的基本策略,明白了算法时间复杂度的分析,同一个要求,使用不同的算法,所需时间和空间不同,因此根据不同的实验要求,编写合适的算法是非常重要的,有利于缩短运行时间。
队列c语言代码

队列c语言代码队列是一种线性数据结构,它具有先进先出(FIFO)的特点。
在队列中,元素被添加到队列的尾部,被移除时则从队列的头部开始移除。
以下是一个简单的队列实现的C语言代码:```c#include <stdio.h>#include <stdlib.h>#define MAX_SIZE 10int queue[MAX_SIZE];int front = -1;int rear = -1;void enqueue(int x){if(rear == MAX_SIZE - 1){printf('队列已满,无法插入元素');return;}if(front == -1){front = 0;}rear++;queue[rear] = x;void dequeue(){if(front == -1 || front > rear){ printf('队列为空,无法删除元素');return;}front++;}int get_front(){if(front == -1 || front > rear){ printf('队列为空');return -1;}return queue[front];}int get_rear(){if(front == -1 || front > rear){ printf('队列为空');return -1;return queue[rear];}void display(){if(front == -1 || front > rear){ printf('队列为空');return;}for(int i=front; i<=rear; i++){ printf('%d ', queue[i]);}printf('');}int main(){enqueue(1);enqueue(2);enqueue(3);enqueue(4);display();dequeue();display();printf('%d', get_front());printf('%d', get_rear());return 0;}```在这个队列实现中,我们使用了一个数组来存储元素。
排队论详解及案例

cmLiu@shufe
Operations Research
9.2 几个常用的概率分布
9.2.1 经验分布 9.2.2 泊松分布 9.2.3 负指数分布 9.2.4 爱尔朗分布
cmLiu@shufe
Operations Research
9.2.1 经验分布
主要指标
平均间隔时间 = 总时间 到达顾客总数
Operations Research
9.1.3 排队论研究的基本问题
(3)系统优化问题的研究 研究排队系统的目的就是通过对该系统概率规律的研究, 实现系统的优化。系统的优化包括最优设计和最优运营问 题。前者属于静态问题,它是在输入和服务参数给定的情 况下,确定系统的设计参数,以使服务设施达到最大效益 或者服务机构实现最为经济。后者属于动态问题,它是指 对于一个给定的系统,在系统运行的参数可以随着时间或 状态变化的情况下,考虑如何运营使某个目标函数达到最 优。
cmLiu@shufe
Operations Research
9.1.1 排队系统的描述和组成
一般的排队过程可以这样描述:顾客由顾客源出发,到达 服务机构(服务台、服务员)前,按排队规则排队等待接 受服务,服务机构按服务规则给顾客服务,顾客接受完服 务后就离开。
cmLiu@shufe
Operations Research
9.1.1 排队系统的描述和组成
尽管排队系统是多种多样的,但所有的排队系统都是由输入过程、排 队规则、服务机构及服务规则三个基本部分组成的。 (1)输入过程 描述顾客来源以及顾客到达排队系统的规律。 一般从以下几个方面对输入过程进行描述:顾客源中顾客的数量是 有限还是无限;顾客到达的方式是单个到达还是成批到达;顾客的到 达是否相互独立(以前到达的顾客对以后达到的顾客没有影响,则称 顾客的达到是相互独立的,否则就是有关联的);顾客相继到达的间 隔时间分布是确定型的还是随机型的(如果是随机分布,需要知道单 位时间内的顾客到达数或者顾客相继到达时间间隔的概率分布);输 入的过程是平稳的还是非平稳的(若相继到达的间隔时间分布参数 (如期望值、方差等)都是与时间无关的,则称输入过程是平稳的, 否则称为非平稳)。 本章主要讨论顾客的到达是相互独立的、输入过程是平稳的情形。
实验排队论问题的编程实现

实验排队论问题的编程实现Prepared on 21 November 2021实验7 排队论问题的编程实现专业班级信息112 学号 0218 姓名高廷旺报告日期 .实验类型:●验证性实验○综合性实验○设计性实验实验目的:熟练排队论问题的求解算法。
实验内容:排队论基本问题的求解算法。
实验原理对于几种基本排队模型:M/M/1、M/M/1/N、M/M/1/m/m、M/M/c 等能够根据稳态情形的指标公式,求出相应的数量指标。
实验步骤1 要求上机实验前先编写出程序代码2 编辑录入程序3 调试程序并记录调试过程中出现的问题及修改程序的过程4 经反复调试后,运行程序并验证程序运行是否正确。
5 记录运行时的输入和输出。
预习编写程序代码:实验报告:根据实验情况和结果撰写并递交实验报告。
实验总结:排队问题用lingo求解简单明了,容易编程。
加深了对linggo 中for语句,还有关系式表达的认识。
挺有成就感。
很棒。
参考程序例题 1 M/M/1 模型某维修中心在周末现只安排一名员工为顾客提供服务,新来维修的顾客到达后,若已有顾客正在接受服务,则需要排队等待,假设来维修的顾客到达过程为Poisson流,平均每小时5人,维修时间服从负指数分布,平均需要6min,试求该系统的主要数量指标。
例题 2 M/M/c 模型设打印室有 3 名打字员,平均每个文件的打印时间为 10 min,而文件的到达率为每小时16 件,试求该打印室的主要数量指标。
例题 3 混合制排队 M/M/1/N 模型某理发店只有 1 名理发员,因场所有限,店里最多可容纳 5 名顾客,假设来理发的顾客按Poisson过程到达,平均到达率为 6 人/h,理发时间服从负指数分布,平均12 min可为1名顾客理发,求该系统的各项参数指标。
例题 4 闭合式排队 M/M/1/K/1 模型设有 1 名工人负责照管 8 台自动机床,当机床需要加料、发生故障或刀具磨损时就自动停车,等待工人照管。
排队问题的三种方法

排队问题的三种方法排队问题是一类经典的图论问题,通常涉及到在一条流水线上安排生产任务或者服务请求,使得所有任务或者请求都能够及时完成,本文将介绍三种解决排队问题的方法。
方法一:贪心算法贪心算法是一种简单的算法思想,通过每次选择最优解来得到全局最优解。
在排队问题中,贪心算法可以通过不断尝试最坏情况来得到最优解。
具体来说,我们可以从最后一个待安排的任务开始,依次将当前任务和已经安排的任务进行交换,直到任务队列为空。
这种方法能够保证所有的任务都能够及时完成,但是可能会出现任务队列为空的情况,也就是没有任务可以安排。
方法二:动态规划算法动态规划算法是一种通过构建状态转移方程来求解问题的方法,通常适用于问题的规模较大或者最优解不是唯一的情况。
在排队问题中,我们可以将任务队列看作是状态,任务等待时间和执行任务的时间看作是状态转移方程。
具体来说,我们可以从最后一个待安排的任务开始,依次计算出当前任务需要等待的时间和已经安排的任务需要执行的时间,然后将当前任务和已经安排的任务进行交换,直到任务队列为空。
这种方法可以得到最优解,但是需要计算大量的状态转移方程。
方法三:图论算法图论算法是一种通过构建图来分析问题的方法,通常适用于问题的规模较大或者最优解不是唯一的情况。
在排队问题中,我们可以将任务队列看作是一个图,任务之间的等待关系看作是边,然后通过最小生成树或者贪心算法来得到最优解。
具体来说,我们可以从最后一个待安排的任务开始,依次将当前任务和已经安排的任务进行交换,直到任务队列为空。
这种方法可以得到最优解,但是需要计算大量的边。
以上三种方法是解决排队问题的常见方法,贪心算法适用于没有最优解的情况,动态规划算法适用于有多个最优解的情况,图论算法适用于问题规模较大的情况。
此外,排队问题的拓展应用还有很多,例如排队论、排队系统、排队论模型等。
计算机仿真排队系统实验报告(附代码)

计算机仿真实验报告第一题1•作业内容应用排队系统流程图,用C语言编制仿真程序,求解以下问题。
修理店只有一个修理工,来修理的顾客到达次数服从泊松分布,平均4人/h;修理时间服从指数分布,平均需6min。
试求(随机数发生器采用float Icgrand(int stream)种子stream 为自己学号的最后两位。
):①修理店空闲的概率;②店内有三个顾客的概率;③店内至少有一个顾客的概率;④在店内顾客的平均数;⑤顾客在店内的平均逗留时间;⑥顾客必须在店内消耗15分钟以上的概率。
统计量实现算法:①修理店空闲的概率;p1=1-area_server_status/sim_timearea_server_status: 总服务时间(即修理工在这段仿真时间里非空闲时间)sim_time: 总仿真时间用1减去非空闲概率,即为空闲概率。
②店内有三个顾客的概率;p2=Three_people_time/sim_time增加变量Three_people_time,即有三个顾客在店内的时间。
三个顾客在店里,也就是说一个顾客在理发,两个人在排队,此时,无论是来一个新的客人或者离开一个客人,都会破坏这种三个人的状态,所以我们每次要统计的,就是这种三个人的状态持续的时间。
因此,用到的是time_si nce_last_eve nt 这个变量,该变量用于统计两种状态(事件,包括离开和到来)之间的事件。
因此,在每次计算完time_s in ce_last_eve nt之后,考察队伍中的人数是否为2,若为2,则把该段time_since_last_event 加到Three_people_time中。
仿真结束时,用Three_people_time/总仿真时间,即为店内有三个顾客的概率。
③店内至少有一个顾客的概率;p3=p3=1-idle_time/sim_time增加变量idle_time,即店里空闲的概率(没有顾客),用1减去一个顾客都没有的概率,就是至少有一个顾客的概率。
(C#数据结构)解决队列的编程问题

2
3
数据结构(C#语言版 语言版) 数据结构 语言版
解决队列的编程问题
用顺序栈解决堆栈的编程问题——对顺序队列进行操作 对顺序队列进行操作 用顺序栈解决堆栈的编程问题
5.求队列的长度:GetLength() 求队列的长度:
循环顺序队列的长度应该是:(rear-front+m构(C#语言版 语言版) 数据结构 语言版
解决队列的编程问题
用顺序栈解决堆栈的编程问题——对顺序队列进行操作 对顺序队列进行操作 用顺序栈解决堆栈的编程问题
4.取队头元素:GetFront() 取队头元素:
取队头元素操作与出队操作相似,只是取队头元素操作不改变原有队列, 不删除取出的队头元素。要执行取队头操作,需要执行下面的步骤: 步骤 1 操作 检查顺序队列中是否含有元素,如果没有,提示队列 为空;否则执行下面的步骤 设置front的值为(front + 1) % maxsize,即使front 指向所取元素的位置 返回队头指示器front所在位置的元素
数据结构(C#语言版 语言版) 数据结构 语言版
解决队列的编程问题
认识队列——分析队列的逻辑结构 分析队列的逻辑结构 认识队列
1. 队列的定义
队列(Queue)是一种特殊的线性表,是一种只允许在表的一端进行插入操作而 在另一端进行删除操作的线性表 。 把进行插入操作的表尾称为队尾(Rear),把进行删除操作的头部称为队头 (Front)。 当队列中没有数据元素时称为空队列(Empty Queue)。 。
6.循环顺序队列是否为满:IsFull() 循环顺序队列是否为满:
一种是当队列还没有一个元素出队,队头指示器front的值为-1而队尾指示器 rear的值为maxsize-1 。 另一种情况是队尾指示器rear落后于队头指示器front,而且满足条件: (rear+1) % maxsize == front。采用条件(rear+1) % maxsize == front作为 “队列满”的条件,实际上此时队列还有一个空位置,就是front所指示的位 置
排队论系统仿真

于零,即
dPn (t ) 0, 对一切n 。 dt 因为稳态和时间无关,所以将符号简化,用 Pn 代替 Pn(t),于是
Pn n 1 n 2 0 P0 n n 1 1
i 0 n i 1
——平均服务率,即单位时间内接受服务的顾客数;
C——并列服务台的个数;
——服务强度。
通常,排队论研究的相关问题可大体分成统计问题和最优化问题两大类。 统计问题是排队系统建模中的一个组成部分,它主要研究对现实数据的处理 问题, 在输入数据的基础上, 首先要研究顾客相继到达的间隔时间是否独立同分
布,如果是独立同分布,还要研究分布类型以及有关参数的确定问题.类似地, 对服务时间也要进行相应的研究。 排队系统的优化问题涉及到系统的设计、控制以及有效性评价等方面的内 容。 排队论本身不是一种最优化方法,它是一种分析工具。常见的系统最优设计 问题是在系统设置之前, 根据已有的顾客输入与服务过程等资料对系统的前景进 行估计或预测,依此确定系统的参数。 系统最优控制问题是根据顾客输入的变化而对现有服务系统进行的适度调 整,即根据系统的实际情形,制定一个合理的控制策略,并据此确定系统运行的 最佳参数。作为一种分析工具,处理排队问题的过程可以概括为以下四步: (1)确定排队问题的各个变量,建立它们之间的相互关系; (2)根据已知的统计数据, 运用适当的统计检验方法以确定相关的概率分布; (3)根据所得到的概率分布,确定整个系统的运行特征; (4)根据服务系统的运行特征,按照一定的目的,改进系统的功能。
P0 (t ) e t
T 小于等于 t 的概率 P(T≤t)表示为 F(t) (累积分布函数) ,有
F (t ) 1 et
2011-2012-2实验7 排队论问题的编程实现

实验7 排队论问题的编程实现专业班级信息112 学号18 姓名高廷旺报告日期.实验类型:●验证性实验○综合性实验○设计性实验实验目的:熟练排队论问题的求解算法。
实验内容:排队论基本问题的求解算法。
实验原理对于几种基本排队模型:M/M/1、M/M/1/N、M/M/1/m/m、M/M/c等能够根据稳态情形的指标公式,求出相应的数量指标。
实验步骤1 要求上机实验前先编写出程序代码2 编辑录入程序3 调试程序并记录调试过程中出现的问题及修改程序的过程4 经反复调试后,运行程序并验证程序运行是否正确。
5 记录运行时的输入和输出。
预习编写程序代码:实验报告:根据实验情况和结果撰写并递交实验报告。
实验总结:排队问题用lingo求解简单明了,容易编程。
加深了对linggo中for语句,还有关系式表达的认识。
挺有成就感。
很棒。
参考程序例题1 M/M/1 模型某维修中心在周末现只安排一名员工为顾客提供服务,新来维修的顾客到达后,若已有顾客正在接受服务,则需要排队等待,假设来维修的顾客到达过程为Poisson流,平均每小时5人,维修时间服从负指数分布,平均需要6min,试求该系统的主要数量指标。
例题 2 M/M/c 模型设打印室有3 名打字员,平均每个文件的打印时间为10 min,而文件的到达率为每小时16 件,试求该打印室的主要数量指标。
例题3 混合制排队M/M/1/N 模型某理发店只有 1 名理发员,因场所有限,店里最多可容纳 5 名顾客,假设来理发的顾客按Poisson过程到达,平均到达率为6 人/h,理发时间服从负指数分布,平均12 min可为1名顾客理发,求该系统的各项参数指标。
例题4 闭合式排队M/M/1/K/1 模型设有1 名工人负责照管8 台自动机床,当机床需要加料、发生故障或刀具磨损时就自动停车,等待工人照管。
设平均每台机床两次停车的时间间隔为1h,停车时需要工人照管的平均时间是6min,并均服从负指数分布,求该系统的各项指标。
数学建模中的排队论问题

数学建模中的排队论问题数学建模是运用数学方法来解决实际问题的一种学科,而排队论则是数学建模中的一个重要问题。
排队论是研究人们在排队等待时所产生的等待时间、服务时间、队列长度等问题的数学理论。
在各个领域中,排队论都有广泛的应用,例如交通运输、生产调度、服务管理等。
排队论的基本概念包括顾客、服务台、队列、到达率、服务率等。
顾客是指等待服务的个体,可以是人、机器或其他物体。
服务台是为顾客提供服务的地方,可以是柜台、服务窗口或机器设备。
队列是顾客排队等待的区域。
到达率是指单位时间内到达队列的顾客数量。
服务率则是指单位时间内服务台完成服务的顾客数量。
排队论的目标是通过数学模型来分析和优化排队系统,以提高效率和服务质量。
常用的排队论模型有M/M/1, M/M/c, M/M/∞等,其中M表示到达率和服务率满足泊松分布,1表示一个服务台,c表示多个服务台,∞表示无穷多个服务台。
在现实生活中,排队论的应用非常广泛。
以交通运输为例,交通流量大的道路上常常出现拥堵现象。
排队论可以用来研究交通信号灯的时序控制,从而减少交通阻塞和等待时间。
排队论还可以应用于生产调度问题,如工厂的生产线、餐馆的点餐队列等,通过优化排队系统可以提高生产效率和顾客满意度。
除了基本的排队论模型,还有许多扩展模型用于解决更复杂的实际问题。
例如,考虑到顾客的不满意程度,可以引入优先级排队模型。
考虑到服务台设备可能发生故障,可以引入可靠性排队模型。
排队论也可以与优化算法相结合,寻找最佳的服务策略和资源配置。
在数学建模中,解决排队论问题通常需要进行数学推导、建立数学模型、进行仿真实验以及进行实际数据的拟合和验证。
通过数学建模的方法,可以对排队系统的性能进行全面评估,从而提出改进方案和决策策略。
综上所述,数学建模中的排队论问题在实际应用中具有重要的意义。
通过研究排队论,可以优化排队系统,提高效率和服务质量。
随着科技的进步和数据的丰富,排队论的研究将在各个领域中得到更广泛的应用和发展。
c排队叫号系统课程设计

c 排队叫号系统课程设计一、课程目标知识目标:1. 学生能理解排队叫号系统的基本原理和流程。
2. 学生能掌握利用编程实现排队叫号系统的关键步骤。
3. 学生了解并掌握队列数据结构在排队叫号系统中的应用。
技能目标:1. 学生能运用所学知识设计和编写简单的排队叫号系统程序。
2. 学生能通过实际操作,分析并解决排队叫号系统中出现的问题。
3. 学生能运用团队协作、沟通与表达技巧,完成项目任务。
情感态度价值观目标:1. 学生培养对计算机科学的兴趣和热情,激发学习编程的积极性。
2. 学生通过项目实践,认识到编程在解决实际问题中的价值,增强自信心。
3. 学生在团队协作中学会尊重他人、关心同伴,培养良好的团队精神和沟通能力。
本课程针对高年级学生,结合教材内容,注重理论与实践相结合,培养学生运用编程知识解决实际问题的能力。
课程设计充分考虑学生的认知水平、学习兴趣和个性特点,旨在提高学生的编程技能、团队协作能力和创新思维。
通过本课程的学习,使学生能够明确学习目标,达成具体的学习成果。
二、教学内容1. 排队叫号系统基本原理:介绍排队叫号系统的概念、作用和基本组成部分,引导学生理解其实际应用场景。
2. 队列数据结构:讲解队列的基本概念、操作方法,以及队列在排队叫号系统中的应用。
3. 编程实现排队叫号系统:结合教材相关章节,教授如何使用编程语言(如Python)设计和实现排队叫号系统。
- 系统设计:分析系统需求,设计系统功能模块。
- 编程实践:编写代码实现排队、叫号、查询等功能。
4. 排队叫号系统优化:探讨如何提高系统效率,降低等待时间,如优先级队列、多队列处理等策略。
5. 项目实践与展示:分组进行项目实践,每组完成一个排队叫号系统的设计和实现,并进行展示和交流。
教学内容根据课程目标和教材章节进行合理安排,注重科学性和系统性。
教学进度分为五个阶段,每个阶段对应具体的教学内容,确保学生能够逐步掌握排队叫号系统的设计与实现。
通过项目实践,培养学生将理论知识应用于实际问题的能力。
排队论算法matlab代码

%按负指数分布产生各顾客达到时间间隔
events(1,:) = exprnd(arr_mean,1,arr_num);
%各顾客的到达时刻等于时间间隔的累积和
events(1,:) = cumsum(events(1,:));
%按负指数分布产生各顾客服务时间
out=[Ws,Wq,Wb,Ls,Lq,p];
演示代码
clear
clc
%*****************************************
%初始化顾客源
%*****************************************
%总仿真时间
Total_time = 10;
leave_time=sort(leave_time);%离开事1; %更新队长
end
end
LL=[LL,L]; %记录队长序列
步骤:
(1)确定问题是否属于排队论领域
(2)确定修理工个数s
(3)确定机器源数m
(4)找到时间终止点T
(5)带入模型即可
function out=MMSmteam(s,m,mu1,mu2,T)
%M/M/S/m排队模型
%s——修理工个数
%m——机器源数
%T——时间终止点
%mu1——机器离开-到达时间服从指数分布
%队列最大长度
N = 10000000000;
%到达率与服务率
lambda = 10;
mu = 6;
%平均到达时间与平均服务时间
arr_mean = 1/lambda;
ser_mean = 1/mu;
排队论代码

1.排队论import java.util.Arrays;import java.util.Random;import java.util.Scanner;class MM1{/** MM1所具有的函数有以下几个:* MM1:构造函数,知道langda和miu以及number仿真总人数就可以进行仿真* Produce:通过负指数分布landa的值产生到达人群的时间间隔,计算得出时间点(泊松分布是产生人群,与到达人群是无关的)* Leave:通过负指数分布miu的值计算服务时间,队列时间以及等待时间* Print_need:打印出所需要的平均逗留时间,平均队列时间,平均服务时间与平均队长(这是仿真模型,打印出来的是仿真结果)* Print_people:打印出编号为x的人的到达时间,队列时间,服务时间与离开时间* Print_time:打印出时间为T时的队列人数,此时的平均服务时间,到达该窗口的累计人数,当前窗口人数*/double in;//in为langda,一秒钟到来了几个人double out;//out为miu,人离开的速率,完成速率double[ ] arrive_time;//到达时间间隔double[ ] arrivetime;//顾客到达时间double[ ] serve_time;//服务时间double[ ] leave_time;//离开时间double[ ] wait_time;//等待(在服务窗的总时间)时间double[ ] queue_time;//排队时间MM1(double in,double out,int number){arrive_time=new double[number];//到达时间间隔arrivetime=new double[number];//顾客到达时间serve_time=new double[number];//服务时间leave_time=new double[number];//顾客离开时间wait_time=new double[number];//等待时间,(在服务窗的总时间)queue_time=new double[number];//排队时间this.in=in;this.out=out;}void Produce(int number){for(int i=0;i<number;i++){Random random=new java.util.Random();// 定义随机类double result=random.nextDouble();// 返回0到1之间的小数arrive_time[i]=Math.log(result)*-1/in;//负指数分布函数产生到达时间间隔}arrivetime[0]=arrive_time[0];for(int i=1;i<number;i++){arrivetime[i]=arrivetime[i-1]+arrive_time[i];//通过到达时间间隔计算出到达时间}}void Leave(int number){for(int i=0;i<number;i++){Random random=new java.util.Random();// 定义随机类double result=random.nextDouble();// 返回0到1之间的小数if(result<0) result*=-1;serve_time[i]=Math.log(result)*-1/out;}leave_time[0]=serve_time[0]+arrivetime[0];/** 离开时间的计算方法:* 如果前面那个人的离开时间大于我,我的离开时间等于他的离开时间加上我的服务时间* 如果前面那个人的离开时间小于我,我的离开时间等于我的到达时间加上我的服务时间*/for(int i=1;i<number;i++){if(leave_time[i-1]<arrivetime[i])leave_time[i]=arrivetime[i]+serve_time[i];elseleave_time[i]=leave_time[i-1]+serve_time[i];}for(int i=0;i<number;i++){queue_time[i]=leave_time[i]-arrivetime[i]-serve_time[i];//队列时间的计算wait_time[i]=leave_time[i]-arrivetime[i];//等待时间的计算}}void Print_people_x(int x)//x是编号{System.out.println("第"+x+"个人的数据如下:");System.out.println("到达时间:"+arrivetime[x]);System.out.println("队列时间:"+queue_time[x]);System.out.println("服务时间:"+serve_time[x]);System.out.println("离开时间:"+leave_time[x]);}void Print_need(int x)//x是规模{double[] line_wait;//当前队长(包括正在服务的)double sum_wait=0,sum_queue=0,sum_serve=0,sum_line=0;for(int i=0;i<x;i++){sum_wait+=wait_time[i];sum_queue+=queue_time[i];sum_serve+=serve_time[i];}sum_wait/=x;sum_queue/=x;sum_serve/=x;System.out.println("平均逗留时间为:"+sum_wait);System.out.println("平均队列时间为:"+sum_queue);System.out.println("平均服务时间为:"+sum_serve);double last_time=leave_time[x-1];line_wait=new double[(int)last_time+1];int time=0;for(time=0;time<last_time;time++){for(int i=0;i<x;i++){if(time>arrivetime[i]&&time<leave_time[i]){line_wait[time]++;}}sum_line+=line_wait[time];}sum_line/=time;System.out.println("平均队长为:"+sum_line);}void Print_time(double time,int number){int queue_people=0;int arrive_people=0;int leave_people=0;double servertime=0;for(int i=0;i<number;i++){if(arrivetime[i]<time&&leave_time[i]>time)queue_people++;if(arrivetime[i]<time)arrive_people++;if(leave_time[i]<time)leave_people++;}servertime=(time-arrive_time[0])/(leave_people+1);System.out.println("第"+time+"时间的数据如下:");System.out.println("此时队列人数有:"+queue_people);System.out.println("此时的平均服务时间"+servertime);System.out.println("到达该窗口累计人数:"+arrive_people);System.out.println("离开此窗口的累计人数:"+leave_people);}}class MMN extends MM1{int N;MMN(double in, double out, int number,int N) {super(in, out, number);this.N=N;// TODO Auto-generated constructor stub}void Leave(int number){for(int i=0;i<number;i++){Random random=new java.util.Random();// 定义随机类double result=random.nextDouble();// 返回0到1之间的小数if(result<0) result*=-1;serve_time[i]=Math.log(result)*-1/out;}double[]leave_x=new double[N];for(int i=0;i<N;i++){leave_time[i]=serve_time[i]+arrivetime[i];leave_x[i]=leave_time[i];}for(int i=N;i<number;i++){Arrays.sort(leave_x);if(leave_x[0]<arrivetime[i])//到达时间比最小的都大时{leave_time[i]=arrivetime[i]+serve_time[i];leave_x[0]=leave_time[i];}else if(leave_x[0]>arrivetime[i]){leave_time[i]=leave_x[0]+serve_time[i];leave_x[0]=leave_time[i];}}for(int i=0;i<number;i++){queue_time[i]=leave_time[i]-arrivetime[i]-serve_time[i];wait_time[i]=leave_time[i]-arrivetime[i];}}}public class Queue {public static void main(String[] args) {// TODO Auto-generated method stubint number=10000;int flag=0;while(flag!=5){System.out.println("济民宝宝为郭阳小姐姐服务:");System.out.println("本系统提供如下服务:");System.out.println("1.提供Print_need的测试样例,输入1回车可见(具体代码见Queue类的注释1部分)");System.out.println("2.提供Print_time的测试样例,输入2回车可见(具体代码见Queue类的注释2部分)");System.out.println("3.提供Print_people的测试样例,输入3回车可见(具体代码见Queue类的注释3部分)");System.out.println("4.提供排队论仿真模型(可自行输入输出),输入4回车可见(具体代码见Queue类的注释4部分)");System.out.println("5.结束");Scanner in =new Scanner(System.in);flag=in.nextInt();/** 注释1* 函数的具体功能见MM1类的注释* 包含MM1和MM3的Print_need*/if(flag==1){System.out.println("这是一个测试类:测试数据集为10000,langda=0.2,miu=0.5的MM1模型");MM1 test1=new MM1(0.2,0.5,number);test1.Produce(number);test1.Leave(number);test1.Print_need(number);System.out.println("\n--------------OvO华丽的分割线QAQ-------------\n");System.out.println("这是一个测试类:测试数据集为10000,langda=0.2,miu=0.5的MM3模型");MMN test2=new MMN(0.2,0.5,number,3);test2.Produce(number);test2.Leave(number);test2.Print_need(number);}/** 注释2* 包含MM1和MM3的Print_time*/if(flag==2){System.out.println("这是一个测试类:测试数据集为10000,langda=0.2,miu=0.5的MM1模型");MM1 test1=new MM1(0.2,0.5,number);double time=100.0;test1.Produce(number);test1.Leave(number);test1.Print_time(time, number);System.out.println("\n--------------OvO华丽的分割线QAQ-------------\n");System.out.println("这是一个测试类:测试数据集为10000,langda=0.2,miu=0.5的MM3模型");MMN test2=new MMN(0.2,0.5,number,3);test2.Produce(number);test2.Leave(number);test2.Print_time(time, number);}/** 注释3* 包含MM1和MM3的Print_people*/if(flag==3){System.out.println("这是一个测试类:测试数据集为10000,langda=0.2,miu=0.5的MM1模型");MM1 test1=new MM1(0.2,0.5,number);double time=100.0;test1.Produce(number);test1.Leave(number);test1.Print_people_x(100);System.out.println("\n--------------OvO华丽的分割线QAQ-------------\n");System.out.println("这是一个测试类:测试数据集为10000,langda=0.2,miu=0.5的MM3模型");MMN test2=new MMN(0.2,0.5,number,3);test2.Produce(number);test2.Leave(number);test2.Print_time(time, number);test2.Print_people_x(100);}/** 注释4* 自选输入输出*/if(flag==4){System.out.println("请选择你想模拟的是MM1还是MMN");System.out.println("MM1的话输入1换行,MMN的话输入2换行");Scanner one=new Scanner(System.in);int flag_one=one.nextInt();System.out.println("请输入langda:");double langda=one.nextDouble();System.out.println("请输入miu:");double miu=one.nextDouble();System.out.println("请输入仿真数量集:");number=one.nextInt();System.out.println("请输入你想仿真的方法:");System.out.println("1.Print_need,输入1回车");System.out.println("2.Print_people,输入2回车");System.out.println("3.Print_time,输入3回车");int method=one.nextInt();if(flag_one==1){MM1 test1=new MM1(langda,miu,number);test1.Produce(number);test1.Leave(number);switch(method){case 1:test1.Print_need(number);break;case 2:System.out.println("请输入你想print_people的编号(不能大于你给的数据集):");int people=one.nextInt();test1.Print_people_x(people);break;case 3:System.out.println("请输入你想print_time的时间(不能大于你给的数据集的最后一个人的离开时间):");double time_one=one.nextDouble();test1.Print_time(time_one, number);break;}System.out.println("\n--------------OvO华丽的分割线QAQ-------------\n");}else if(flag_one==2){System.out.println("请输入你想输入的窗口数");int window_number=one.nextInt();MMN test1=new MMN(langda,miu,number,window_number);test1.Produce(number);test1.Leave(number);switch(method){case 1:test1.Print_need(number);break;case 2:System.out.println("请输入你想print_people的编号(不能大于你给的数据集):");int people=one.nextInt();test1.Print_people_x(people);break;case 3:System.out.println("请输入你想print_time的时间(不能大于你给的数据集的最后一个人的离开时间):");double time_one=one.nextDouble();test1.Print_time(time_one, number);break;}}}System.out.println("5秒后返回主菜单");for(int i=0;i<3;i++)System.out.println();//清屏try {Thread.sleep(5000);} catch (InterruptedException e) {// TODO Auto-generated catch blocke.printStackTrace();}}}}2.生物群的竞争排斥模型function dx=fun(t,x,r1,r2,n1,n2,s1,s2)r1=0.3;r2=4.7;n1=419059;n2=419059;s1=1;s2=1;dx=[r1*x(1)*(1-x(1)/n1-s1*x(2)/n2);r2*x(2)*(1-s2*x(1)/n1-x(2)/n2)];h=10;%所取时间点间隔ts=[0:h:60];%时间区间x0=[0,2.3];%初始条件opt=odeset('reltol',1e-6,'abstol',1e-9);%相对误差1e-6,绝对误差1e-9[t,x]=ode45(@fun,ts,x0,opt);%使用5级4阶龙格—库塔公式计算plot(t,x(:,1),'r',t,x(:,2),'b','LineWidth',2),grid;pause;plot(x(:,1),x(:,2),'LineWidth',2),grid %作相轨线。
排队问题程序

function[maxque,mwait_t,mstay_t,queue_l,use_rate]=MM1queue(mean_arr,mean_lea,peo_num)status=zeros(3,peo_num);%用一个3行矩阵表示每个顾客的状态;%到达时间间隔,服务时间,等待时间;status(1,=exprnd(mean_arr,1,peo_num);%随机生成各顾客的到达间隔;status(2,=exprnd(mean_lea,1,peo_num);%随机生成各顾客的服务时间;for i=2:peo_numif status(1,i)<=status(2,i-1)+status(3,i-1)status(3,i)=status(2,i-1)+status(3,i-1)-status(1,i);elsestatus(3,i)=0;end;%对状态进行更新;end;arr_time=cumsum(status(1,);status(1,:)=arr_time;lea_time=sum(status);stairs([0 arr_time],0:peo_num);%绘出各顾客的到达时间图;hold on;stairs([0 lea_time],0:peo_num,'r');%绘出各顾客的离去时间图;legend('Arrive curve','leave curve',0)hold offfigure;plot(1:peo_num,status(3,:),'r:',1:peo_num,status(2,:)+status(3,:),'k-');%绘出每个顾客的等待时间和停留时间;legend('Wait Time','Stay Time',0);n1=1;n2=1;mstay_t=(sum(status(2,:))+sum(status(3,:)))/peo_num;mwait_t=mean(status(3,:));%求平均停留时间和等待时间;queue_num=zeros(1,2*peo_num+1);queue_time=zeros(1,2*peo_num+1);n3=1;%while循环求每个时间队列的长度;while n1<=peo_numif arr_time(n1)<lea_time(n2)queue_num(1,n3)=n1-n2+1;queue_time(1,n3)=arr_time(n1);n1=n1+1;elsequeue_num(1,n3)=n1-n2-1;queue_time(1,n3)=lea_time(n2);n2=n2+1;end;end;while n2<=peo_numn3=n3+1;queue_num(1,n3)=peo_num-n2;queue_time(1,n3)=lea_time(n2);n2=n2+1;end;figure;stairs(queue_time,queue_num,'k');%绘出队列长度的时间变化曲线, stairs 是Matlab的函数legend('Queue Length Curve',0);temp=diff(queue_time);overtime=max(queue_time);queue_l=sum(temp.*queue_num(22*peo_num+1)))/overtime;use_rate=sum(temp(find(queue_num)))/overtime;maxque=max(queue_num); % 最大队长%然后在Matlab命令窗口中输入命令即可,如:[maxque,mwait_t,mstay_t,queue_l,use_rate]=mm1queue(0.5,0.4,200),其中0.5表示平均来到时间间隔,%0.4表示平均离开时间,200为人数注意以下几点:1.首先因为M/M/1中,各个实体的到达时间和服务时间相互独立,所以才能首先把每个实体的这两个时间,根据所给的参数产生模拟的随机数来。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
实验7 排队论问题的编程实现
成绩
专业班级 信息112学号18姓名 高廷旺 报告日期 实验类型: 实验目的: 实验内容: 实验原理 态情形的指标公式, 实验步骤 要求上机实验前先编写出程序代码 编辑录入程序
调试程序并记录调试过程中出现的问题及修改程序的过程
经反复调试后,运行程序并验证程序运行是否正确。
记录运行时的输入和输出。
•验证性实验 o 综合性实验 o
设计性实验 熟练排队论问题的求解算法 。
排队论基本问题的求解算法。
对于几种基本排队模型: M/M/1、M/M/1/N 、M/M/1/m/m 、M/M/c 等能够根据稳 求岀相应的数量指标。
1 2 3 4
5 预习编写程序代码: 实验报告:根据实验情况和结果撰写并递交实验报告。
实验总结:排队问题用lingo 求解简单明了, 还有关系式表达的认识。
挺有成就感。
很棒。
参考程序 例题1 M/M/1 模型
某维修中心在周末现只安排一名员工为顾客提供服务, 正在接受服务,则需要排队等待,假设来维修的顾 5人,维修时间服从负指数分布, 平均需要6min ,试求该系统的主要数量指标。
例题 2 M/M/C 模型 设打印室有3名打字员,平均每个文件的打印时间为 16件,试求该打印室的主要数量指标。
例题3混合制排队 M/M/1/N 模型 某理发店只有 1名理发员,因场所有限,店里最多可容纳 5名顾客,假设来理发的顾客 按Poisson 过程到达,平均到达率为 6人/h ,理发时间服从负指数分布,平均 12 min 可 为1名顾客理发,求该系统的各项参数指标。
例题4闭合式排队 M/M/1/K/1 模型 设有1名工人负责照管 8台自动机床,当机床需要加料、 发生故障或刀具磨损时就自动停车, 等待工人照管。
设平均每台机床两次停车的时间间隔为 1h ,停车时需要工人照管的平均时间是 6min ,并均服从负指数分布,求该系统的各项指标。
参考程序 ______________ 例题1等待制M/M/1 模型 sx=1;
rx=5; tx=6/60; lq=rx*tx; twait= @p eb(lq,sx); 容易编程。
加深了对 linggo 中for 语句, 新来维修的顾客到达后,若已有顾客 客到达过程为Po isso n 流,平均每小时 10 min ,而文件的到达率为每小时 例题2等待制 M/M/C 模型
sx=3; rx=16; tx=10/60; lq=rx*tx;
twait= @p eb(lq,sx);
wq=twait*tx/(sx-lq); wq=twait*tx/(sx-lq);
lq=rx*wq; lq=rx*wq;
ws=wq+tx; ws=wq+tx;
ls=ws*rx; ls=ws*rx;
Feasible soluti on found. No feasible soluti on found.
Total solver iterati ons: Total solver iterati ons:
0 0
Variable Value Variable Value
SX 1.000000 SX 3.000000
RX 5.000000 RX 16.00000
TX 0.1000000 TX 0.1666667
LQ 0.5000000 LQ 2.666667
TWAIT 0.5000000 TWAIT 0.7975078
WQ 0.1000000 WQ 0.3987539
WS 0.2000000 WS 0.5654206
LS 1.000000 LS 9.046729
Row Slack or Sur plus Row Slack or Surp lus
1 0.000000 1 0.000000
2 0.000000 2 0.000000
3 0.000000 3 0.000000
4 0.000000 4 0.000000
5 0.000000 5 0.000000
6 0.000000 6 0.000000
7 0.000000 7 -3.713396
8 0.000000 8 0.000000
9 0.000000 对运算结果进行解释,得到该系统的主要数量 指标 (1) (2) 系统平均队长 I 系统平均等待队长
Ls = 1(人) Lq = 0.5( 9 0.000000
对运算结果进行解释,得到该系统的主要数量 指标
(1) 现有的平均文件数 (2) 等待打印的平均文件数
Ls= 9.047()
Lq =
顾客平均逗留时间 顾客平均等待时间 (3)
(4) (5 )系统繁忙频率 P WAIT = 0.5 Ws = 0.2( Wq = 0.1( h) h)
6.380()
(3)
(4) (5) 文件平均停留时间 打印平均等待时间 打印室不空闲概率 Ws = 0.565() Wq = 0.399() P wait =0.798
例题3混合制排队 M/M/1/N 模型 sets : ttq/1...10/: P; en dsets ; s=1;k=5;r=6;t=12/60; p 0*r=1/t* p(1); (叶 1/t)* p(1)=p0* 叶s/t* p(2); @for (ttq(i)|i #gt# 1 #and# i #lt# k; ((叶 s/t)* p(i)=p( i-1)* r+s/t* p(i+1) p(k-1)*r=s/t* p(k); p0+ @sum(ttq(i)|i #le# k; p(1))=1; plost=p(k);q=1- p(k);re=q*r; ls= @sum(state(i)|i
#le# k;i* p( i));
lq=ls-re*t; ws=ls/re; wq=ws-t; Feasible soluti on found. Total solver iterati ons: Variable Value 1.000000
5.000000
6.000000
0. 2000000
PO
0.100 7057
例题4闭合式排队
M/M/1/K/1 模型
S=1;K=8;R=1;T=0.1; Ls=@p fs(K*T*R,S,K); Re=R*(K-Ls); P=(K-Ls)/K; Lq=Ls-Re*T; Ws=Ls/Re;Wq=Ws-T; P work=Re/S*T;
Feasible soluti on found. Total solver iterati ons:
Variable Value
LS RE LQ WS WQ 1.000000
8.000000
1.000000
0.1000000
1.383184
6.616816
0.8271020
0.7215028
0.2090408
0.1090408
PWORK 0.6616816
P LOST 0.2505881 Row Slack or Surp lus
Q 0.7494119 1 0.000000
R_E 4.496471 2 0.000000
L_Q 3.021172 3 0.000000
W_S 0.6718985 4 0.000000
W_Q 0.4718985 5 0.000000
P( 1) 0.1208469 6 0.000000
P( 2) 0.1450163 7 0.000000
P( 3) 0.1740195 8 0.000000
P( 4) 0.2088234 9 0.000000
P( 5) 0.2505881 10 0.000000
P( 6) 0.000000 11 0.000000
对运算结果进行解释,得到该系统的主要数量P( 7) 0.000000 指标
(1 )机床的平均队长L s= 1.383()
P( 8) 0.000000 (2 )平均等待队长L q= 0.722()
(3 )机床平均逗留时间W s= 0.209()
(4)平均等待时间W q= 0.109()
P( 9) 0.000000
(5 )机床正常工作概率P = 82.71%
P( 10) 0.000000 (6 )工人的劳动强度Pwork =0.662
对运算结果进行解释,得到该系统的主要数量
指标
(1) 理发店的空闲率P0= 10.1%
(2)顾客损失率P lost =25.1%
(3)每小时进入理发店的平均顾客数R e=
4.496()
(4)店内平均顾客数L s= 3.021()
(5)顾客平均逗留时间W s= 0.672()
(6)等待理发平均顾客数(等待队长)L q
=2.122()
(7)顾客平均等待时间W q= 0.472()
实验总结:排队问题用lingo 求解简单明了,容易编程,但不同模型的排队问题,需要编写不同的程序,如果大量的问题求解,较废时间。
