排队论模型及实例完整版本共50页
合集下载
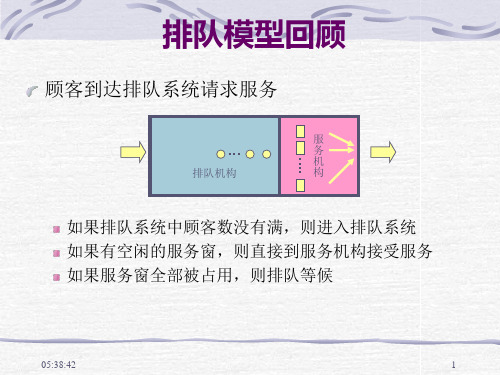
排队论模型及实例

排队论模型及实例
排队论模型是用来模拟和研究特定场景下客户服务时间的工具。
它可
以用来分析系统效率,估算客户服务时间,确定服务可被提供的时间量,
以及改善服务系统的性能。
排队论模型由不同的参数组成,包括服务水平、服务时间、排队时间和系统的平均人数等。
实例:
假设一家小吃店每天提供三个收银台服务,每小时的服务水平为 1.2,服务时间为3分钟,排队等候的平均时间为6分钟,这个时段的客户人数
为15人,那么可以用排队论模型来模拟这家小吃店的情况,估算客户在
这家小吃店排队等候的服务时间。
带优先权排队论模型简介应用案例

0.325 hour
0.033 hour
0.889 hour
0.048 hour
文档仅供参考,如有不当之处,请联系改正。
案例求解 3
即
W1
=W
= Wq
+
1 m
=
Lq l
+
1 m
=
P0(l m)s r s!(1- r)2 l
+
1 m
其中
r= l sm
åé s-1 (l / m)n (l / m)s 1 ù
➢ 非强占性优先权(Nonpreemptive Priorities)——虽然一种高优先级
旳顾客到达,也不能强制让一种正在接受服务旳低优先级顾客返回排队。
➢ 强占性优先权(Preemptive Priorities)——若有高优先级旳顾客到达,
服务员即中断对低优先级顾客旳服务,并立即开始为高优先级顾客服务。
N
l = å li
i=1
r= l m
k
å 【注:】这里假设了 li < sm,
i=1
从而使其能到达稳定状态。
文档仅供参考,如有不当之处,请联系改正。
计算公式 2
抢占性优先权(基于M/M/1)
1/ m
Wk = Bk-1Bk
for k=0,1,2,…,N
文档仅供参考,如有不当之处,请联系改正。
案例求解 3
文档仅供参考,如有不当之处,请联系改正。
案ቤተ መጻሕፍቲ ባይዱ求解 3
W1-1/μ W2-1/μ W3-1/μ
Preemptive Priorities
s=1
s=2
0.024 hour
0.154 hour
排队论模型专业知识课件

排队等待旳顾客数,其期望记为
(队长)=等待服务旳顾客数+正被服务旳顾客数,所以
越大,
;排队长度则仅指在队列中
. 系统中旳顾客数
阐明服务效率越低。
(2)等待时间:是指从顾客到达时间算起到他开始接受
顾客到达时刻算起到他接受服务完毕为止所需要旳时间,
逗留时间=等待时间+服务时间 (3)忙期:是指服务台连续繁忙旳时间,即顾客从到达空闲服务台算起到服务台再次变为空闲时止旳这段时间。这是服务台最关心数量指标,它直接关系到服务员工作强度,与忙期相相应旳是闲期,这是指服务台连续保持空闲旳时间长度;显然,在排队系统中忙期与闲期,是交替出现旳。
从而在生灭过程中取
(9.5)
记 ,称为服务强度 当 时,模型不稳( 时达不到统计) 当 <1时,模型稳定,有稳定解 (3)X(t)旳分布律 由(9.12),(1.15)式得此模型旳微分差分方程组 (9.6) 当 时,稳态解满足
1.生灭过程旳定义 设有一种系统,具有有限个状态,其状态集s={0,1,2…k}或有可数个状态,状态集s={0,1,2…},令X(t)为系统在时刻t所处旳状态,若在某一时刻t系统旳状态数为n,假如对△t>0有。 (1)到达(生):在(t,t+△t)内系统出现一种新旳到达旳概率为
服务时止旳这段时间,其期望值记
;逗留时间则指从
即是顾客在系统中所花费旳总时间,其期望值记
。
排队系统除了上述三个主要数量指标外,另外服务台旳利用率(即服务员忙碌旳时间在总时间中所占百分比)在排队论旳研究中也是很主要旳指标。
(二)排队模型旳符号表达与几种主要排队模型 1.排队模型旳符号一般表达法 一般表达法 A/B/C/D/E/F A:顾客来到时间间隔旳分布类型 B:服务时间旳分布类型 C:服务员个数 D:系统容量 E:顾客源个数 F:服务规则 先来先服务旳等待排队模型主要由三参数法即A/B/C例“M/M/1/k/
(队长)=等待服务旳顾客数+正被服务旳顾客数,所以
越大,
;排队长度则仅指在队列中
. 系统中旳顾客数
阐明服务效率越低。
(2)等待时间:是指从顾客到达时间算起到他开始接受
顾客到达时刻算起到他接受服务完毕为止所需要旳时间,
逗留时间=等待时间+服务时间 (3)忙期:是指服务台连续繁忙旳时间,即顾客从到达空闲服务台算起到服务台再次变为空闲时止旳这段时间。这是服务台最关心数量指标,它直接关系到服务员工作强度,与忙期相相应旳是闲期,这是指服务台连续保持空闲旳时间长度;显然,在排队系统中忙期与闲期,是交替出现旳。
从而在生灭过程中取
(9.5)
记 ,称为服务强度 当 时,模型不稳( 时达不到统计) 当 <1时,模型稳定,有稳定解 (3)X(t)旳分布律 由(9.12),(1.15)式得此模型旳微分差分方程组 (9.6) 当 时,稳态解满足
1.生灭过程旳定义 设有一种系统,具有有限个状态,其状态集s={0,1,2…k}或有可数个状态,状态集s={0,1,2…},令X(t)为系统在时刻t所处旳状态,若在某一时刻t系统旳状态数为n,假如对△t>0有。 (1)到达(生):在(t,t+△t)内系统出现一种新旳到达旳概率为
服务时止旳这段时间,其期望值记
;逗留时间则指从
即是顾客在系统中所花费旳总时间,其期望值记
。
排队系统除了上述三个主要数量指标外,另外服务台旳利用率(即服务员忙碌旳时间在总时间中所占百分比)在排队论旳研究中也是很主要旳指标。
(二)排队模型旳符号表达与几种主要排队模型 1.排队模型旳符号一般表达法 一般表达法 A/B/C/D/E/F A:顾客来到时间间隔旳分布类型 B:服务时间旳分布类型 C:服务员个数 D:系统容量 E:顾客源个数 F:服务规则 先来先服务旳等待排队模型主要由三参数法即A/B/C例“M/M/1/k/
排队论课件MM排队模型
t 0
j是正在忙的服务窗个数
j=i,im 系统顾客数少于等于服务窗数时,所有顾客都在 接受服务 j=m,i>m 系统顾客数大于 服务窗个数时,所有服务窗都在 服务,正在接受服务的顾客数=服务窗个数
04:37:02
9
第三章 单服务窗排队模型
第一节 损失制M/M/1/1 第二节 等待制M/M/1 第三节 混合制M/M/1/m 第四节 可变服务率的M/M/1 第五节 可变输入率的M/M/1 第六节 具有不耐烦顾客的M/M/1 第七节 单服务窗闭合式M/M/1/m/m 第八节 有差错服务的M/M/1
04:37:02
8
增长率和消亡率的分析
由此,M/M/…型排队模型,在状态时的增长率和消亡率为:
i lim pi ,i 1 (t ) t pi ,i 1 (t ) t lim
t 0(t )
t 0
i lim
t 0
t j t 0(t ) lim j t 0 t
04:37:02
10
第一节 单服务窗损失制排队模型 M/M/1/1
04:37:02
11Байду номын сангаас
排队模型分析
M/M/1/1 t 顾客到达间隔时间为负指数分布,参数为, a(t ) e t 服务窗服务时间为负指数分布,参数为, b(t ) e
损失的顾客
0 1
系统最大顾客数1决定了系统状态为{0,1}
队列长度有限
D= 等待制
队列最大长度
04:37:02
3
M/M/…的排队模型
考虑整个排队系统中顾客数的变化
有顾客到达,系统中顾客数加1 有顾客服务完毕,系统中顾客数减1 总之,顾客的到达和离开致使系统顾客数有变化
j是正在忙的服务窗个数
j=i,im 系统顾客数少于等于服务窗数时,所有顾客都在 接受服务 j=m,i>m 系统顾客数大于 服务窗个数时,所有服务窗都在 服务,正在接受服务的顾客数=服务窗个数
04:37:02
9
第三章 单服务窗排队模型
第一节 损失制M/M/1/1 第二节 等待制M/M/1 第三节 混合制M/M/1/m 第四节 可变服务率的M/M/1 第五节 可变输入率的M/M/1 第六节 具有不耐烦顾客的M/M/1 第七节 单服务窗闭合式M/M/1/m/m 第八节 有差错服务的M/M/1
04:37:02
8
增长率和消亡率的分析
由此,M/M/…型排队模型,在状态时的增长率和消亡率为:
i lim pi ,i 1 (t ) t pi ,i 1 (t ) t lim
t 0(t )
t 0
i lim
t 0
t j t 0(t ) lim j t 0 t
04:37:02
10
第一节 单服务窗损失制排队模型 M/M/1/1
04:37:02
11Байду номын сангаас
排队模型分析
M/M/1/1 t 顾客到达间隔时间为负指数分布,参数为, a(t ) e t 服务窗服务时间为负指数分布,参数为, b(t ) e
损失的顾客
0 1
系统最大顾客数1决定了系统状态为{0,1}
队列长度有限
D= 等待制
队列最大长度
04:37:02
3
M/M/…的排队模型
考虑整个排队系统中顾客数的变化
有顾客到达,系统中顾客数加1 有顾客服务完毕,系统中顾客数减1 总之,顾客的到达和离开致使系统顾客数有变化
排队论举例

经满员 就离去? 就离去? Lq Wq = = 1.39 = 0.48h = 28.86 min 2.89 λe
(5) 在可能到来的顾客中,有百分之几不等待就离开? 在可能到来的顾客中,有百分之几不等待就离开?
1 ρ 1 0.75 N P7 = ρ = × 0.757 = 3.71% 1 ρ N +1 1 0.758
= 1 . 89 + 1/0.4 = 4.39 分钟
例 题 解 析 售票处的空闲的概率为0 售票处的空闲的概率为0.0748
平均等待时间 平均逗留时间 95( 队长 L s=3.95(人)
89分钟 分钟, W q=1.89分钟, 39分钟 W s=4.39分钟 70( L q=1.70(人)
例 题 解 析
Ls = m
λ ( + λ )(1 P0 ) Lq = Ls (1 P0 ) = m λ 1 Ls m Ws = = (1 P0 ) m (1 P0 ) λ 1 = Lq Wq = Ws (1 P0 )
某车间有5台机器 台机器, 例3 某车间有 台机器,每台机器的连续运转时间服从负指数 分布。平均连续运转时间15分钟 有一个修理工, 分钟, 分布。平均连续运转时间 分钟,有一个修理工,修理时间 服从负指数分布,平均每次12分钟 分钟。 服从负指数分布,平均每次 分钟。求: (1) 修理工空闲时间
(1 P0 )
解:(1) ∵ m=5,λ=1/15,μ=1/12,ρ=4/5=0.8 m! i P0 = ∑ ρ i = 0 ( m i )!
m 1
5! 5! 5! 5! 5! 2 3 4 5 = 1 + × 0.8 + × 0.8 + × 0.8 + × 0.8 + × 0.8 3! 2! 1! 0! 4!
排队论模型

j , j s ,
j s, (因为最多只有条线路在通话 s ) j s.
于是我们得到
dPj (t ) dt j 1Pj 1 (t ) ( j j ) Pj (t ) j 1Pj 1 (t ), j 1,2,, (9)
(10)
解上面的微分方程组得到
P0 (t ) e
t
(t ) t , Pi (t ) e , i 1,2,. i!
i
我们称呼叫次数{N(t):t>=0}所满足的这个规律 为泊松(Poisson)过程.我们知道, 均值 E ( N (t )) t , 方差 D( N (t )) t. 下面我们给出相邻呼叫的时间间隔的分布. 由假设,任何连续两次呼叫的时间间隔是独 立同分布的随机变量.以T表示,则
j 1,2,, s 对j=0或者s,类似讨论,我们可以得到
dP0 (t ) dPs (t ) P (t ) P0 (t ), Ps 1 (t ) sPs (t ). (5) 1 dt dt
1, j i, 若t 0时, 系统处于 i , 则初始条件为Pj (0) E : 0, j i.
电话总机的设臵问题
一.呼叫发生与通话时间的概率描述
令N(t)为时间[0,t)内总机收到的通话要求次数.模 型假设: 1.在互不重叠的时间间隔内,总机收到的呼叫次 数是相互独立的随机变量.
2.以Pi (t ) Pi ( N (t t ) N (t ) i ), i 0,1,2, 表 示 在[t , t )间 隔内呼 叫次 数 为的 事件 的 概 率假 设这 一 , i , 概 率仅 与 时 间间 隔t有 关,与 时间 的 起 点无 关 t .
3.2 排队论模型

从上表知方案乙的总费用最省。 例7.2.3 要购置计算机,有两种方案.甲方案是购进 一大型计算机,乙方案是购置n台小型计算机.每台小型 计算机是大型计算机处理能力的1/ n 倍.设要求上机的题 目是参数为 的最简单流,大型计算机与小型计算机计 算题目的时间是负指数分布,大型计算机的参数是 试 从平均逗留时间、等待时间看,应该选择哪一个方案. 解 设 按甲方案,购大型计算机. 平均等待时问 平均逗留时间 按乙方案,购n台小型计算机,每台小计算机的题目
两个或
时间区间内1个顾客被服务完的概率为 两个以上顾客被服务完的概率为 且 与系统的 顾客数无关,与微小时问区间的起点无关. 对任意给定的 微小增量 假设 时 先考虑j=i十1的情况, 当 P{ 时间内恰好到达1个顾客而没 有顾客被服务完或恰好有k个顾客到 达并且k -1个顾客被服务完,
=p{ 时间内恰好到达1个顾客而没有顾客被服务完} 十{ 时间内到达k个顾客而服务完k -1个顾客,
这两组关系式,可以作这样直观解释:当系统内有顾 客时,平均等待队长Lq应该是平均队长L减1,当系统内 没有顾客时,平均等待队长Lq与平均队长L相等,所以
单位时间内平均进入系统的顾客为 个. 每个顾客在系 统内平均逗留W单位时间.因此系统内平均有 W个顾客 同样理由,系统内平均有 Wq个顾客在等待服务.
表12-9
为病人完成手术时间v(小时) 出现次数fv 0.0—0.2 0.2—0.4 0.4—0.6 0.6—0.8 0.8—1.0 1.0—1.2 1.2以上 合计 38 25 17 9 6 5 0 100
• (1)算出每小时病人平均到达率= ∑n fn =2.1 (人/小时) • 100 • 每次手术平均时间= ∑v fv =0.4 (小时/人) • 100 • • 每小时完成手术人数(平均服务率)= 1/0.4 =2.5 (人/小时)
排队论

P n (t t ) P n (t ) P n1 (t ) P n1 (t ) ( ) P n (t ) t
P 0 (t t ) P 1 (t ) t P 0 (t )(1 t )
P 0 (t t ) P 0 (t ) P 1 (t ) P 0 (t ) t
P X (t t ) X (t ) 0 1 t o t
顾客到达的时间间隔 T1 , T2 , T3 ,..., Tn ,... 独立同指 数分布Exp( ),即
1 e , t 0; FT (t ) P(T t ) t 0. 0,
●顾客排队逗留时间 顾客到达时间间隔 Z ~ E( ) ,服务时间 T ~ E( ) , 顾客排队逗留时间 Y ~ E( ) 顾客平均逗留时间
W EY 1 L
●顾客平均等待时间
Wq W ( )
1 L 1
例1. 某医院某科室有一位医生值班,每小时平均有 4个病人,医生每小时平均可诊治5个病人。如果要 满足99%以上的病人有座位,至少应设多少个座位? 如果每小时可诊治6个病人,可减少多少个座位? 病人平均等待时间是多少?
排队论模型及应用
一、背景 例子 顾客在超市排队付款,汽车过收费站 a. 增加收银台,则增加投资,有可能发生空闲 浪费; b. 减少收银台,顾客排队时间太长。 选择最优收银台数 二、随机服务系统 顾客等待服务接受服务顾客离开
三、M/M/s模型假设
顾客到达规律(到达人数) M 组成部分 服务时间(时间长短) M 排队规则(怎么排队)
1 Pn 1 P0 1 P0 1 P0 1 1 n 0 n 0
P 0 (t t ) P 1 (t ) t P 0 (t )(1 t )
P 0 (t t ) P 0 (t ) P 1 (t ) P 0 (t ) t
P X (t t ) X (t ) 0 1 t o t
顾客到达的时间间隔 T1 , T2 , T3 ,..., Tn ,... 独立同指 数分布Exp( ),即
1 e , t 0; FT (t ) P(T t ) t 0. 0,
●顾客排队逗留时间 顾客到达时间间隔 Z ~ E( ) ,服务时间 T ~ E( ) , 顾客排队逗留时间 Y ~ E( ) 顾客平均逗留时间
W EY 1 L
●顾客平均等待时间
Wq W ( )
1 L 1
例1. 某医院某科室有一位医生值班,每小时平均有 4个病人,医生每小时平均可诊治5个病人。如果要 满足99%以上的病人有座位,至少应设多少个座位? 如果每小时可诊治6个病人,可减少多少个座位? 病人平均等待时间是多少?
排队论模型及应用
一、背景 例子 顾客在超市排队付款,汽车过收费站 a. 增加收银台,则增加投资,有可能发生空闲 浪费; b. 减少收银台,顾客排队时间太长。 选择最优收银台数 二、随机服务系统 顾客等待服务接受服务顾客离开
三、M/M/s模型假设
顾客到达规律(到达人数) M 组成部分 服务时间(时间长短) M 排队规则(怎么排队)
1 Pn 1 P0 1 P0 1 P0 1 1 n 0 n 0
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
42、只有在人群中间,才能认识自 己。——德国
43、重复别人所说的话,只需要教育; 而要挑战别人所说的话,则需要头脑。—— 玛丽·佩蒂博恩·普尔
44、卓越的人一大优点是:在不利与艰 难的遭遇里百折不饶。——贝多芬
45、自己的饭量自己知道。——苏联
排队论模型及实例完整版本
•
46、寓形宇内复几时,曷不委心任去 留。
•
47、采菊东篱下,悠然见南山。
•
48、啸傲东轩下,聊复得此生。
பைடு நூலகம்
•
49、勤学如春起之苗,不见其增,日 有所长 。
•
50、环堵萧然,不蔽风日;短褐穿结 ,箪瓢 屡空, 晏如也 。
41、学问是异常珍贵的东西,从任何源泉吸 收都不可耻。——阿卜·日·法拉兹
43、重复别人所说的话,只需要教育; 而要挑战别人所说的话,则需要头脑。—— 玛丽·佩蒂博恩·普尔
44、卓越的人一大优点是:在不利与艰 难的遭遇里百折不饶。——贝多芬
45、自己的饭量自己知道。——苏联
排队论模型及实例完整版本
•
46、寓形宇内复几时,曷不委心任去 留。
•
47、采菊东篱下,悠然见南山。
•
48、啸傲东轩下,聊复得此生。
பைடு நூலகம்
•
49、勤学如春起之苗,不见其增,日 有所长 。
•
50、环堵萧然,不蔽风日;短褐穿结 ,箪瓢 屡空, 晏如也 。
41、学问是异常珍贵的东西,从任何源泉吸 收都不可耻。——阿卜·日·法拉兹
