初中数学——用“倍半角模型”解题事半功倍
半角模型十五个结论及证明

半角模型十五个结论及证明《探索半角模型的十五个结论及证明》嗨,大家好!今天我要和大家一起探索一个超有趣的数学知识——半角模型的十五个结论及证明。
这就像是一场奇妙的数学冒险,跟我来呀!一、什么是半角模型呢?半角模型呀,就像是一个神秘的数学宝藏,藏在各种几何图形里。
想象一下,我们有一个正方形或者等腰直角三角形,然后在这个图形里出现了一个角,这个角是另外一个大角的一半,这就形成了半角模型。
比如说,在正方形里,一个角是45度,它就是直角90度的一半呢。
这时候啊,就会有好多神奇的结论冒出来。
二、结论一:线段相等我给大家举个例子哈。
在正方形ABCD中,∠EAF = 45度(E、F分别在BC、CD 上)。
我们能发现BE + DF = EF。
这是为啥呢?我们可以把△ADF绕着点A顺时针旋转90度,这样AD就和AB重合了。
旋转后的点F变成了F'。
那这个时候呀,我们就会发现△AEF和△AEF'是全等的。
为啥呢?因为AF = AF',∠EAF = ∠EAF' = 45度,AE是公共边啊。
就像两个一模一样的小积木,那EF就等于EF'了,而EF'就是BE + DF呀。
你们说神奇不神奇?这就好比是把分散的力量集中起来了,原本分开的BE和DF,通过旋转这个魔法,就变成了和EF相等的线段。
三、结论二:三角形面积关系还有一个有趣的结论呢。
三角形AEF的面积等于三角形ABE的面积加上三角形ADF的面积。
这又怎么理解呢?我们刚刚把△ADF旋转到了△ABF'的位置。
那三角形AEF的面积就等于三角形AEF'的面积啦。
而三角形AEF'的面积就是三角形ABE的面积加上三角形ABF'(也就是原来的三角形ADF)的面积。
这就好像是把两个小地块合并起来就等于一个大地块的面积一样。
四、结论三:角平分线如果我们延长CB到G,使得BG = DF,连接AG。
我们会发现AG是∠EAG的角平分线呢。
倍半角模型知识精讲

倍半角模型知识精讲一、二倍角模型处理方法1. 作二倍角的平分线,构成等腰三角形.例:如图,在△ABC中,∠ABC=2∠C,作∠ABC的平分线交AC于点D,则∠DBC=∠C,DB=DC,即△DBC是等腰三角形.2. 延长二倍角的一边,使其等于二倍角的另一边,构成两个等腰三角形.例:如图,在△ABC中,∠B=2∠C,延长CB到点D,使得BD=AB,连接AD,则△ABD、△ADC都是等腰三角形.例题:如图,在△ABC中,∠C=2∠A,AC=2BC,求证:∠B=90º.【解答】见解析【证法一】如图1,作∠C的平分线CE交AB于点E,过点E作ED⊥AC于点D.则∠ACE=∠A,AE=CE,∵AE=EC,ED⊥AC,∴CD=AC,又∵AC=2BC,∴CD=CB,∴△CDE≌△CBE,∴∠B=∠CDE=90º;【证法二】如图2,延长AC到点D,使得CD=CB,连接BD,取AC的中点E,连接BE. 由题意可得EC=CD=BC,∠DBE=90º,∵CD=CB,∠D=∠CBD,∴∠ACB=2∠D,∵∠ACB=2∠A,∠A=∠D,∴AB=BD,又∵AE=DC,∴△ABE≌△DBC,∴∠ABE=∠DBC,∴∠ABC=∠EBD=90º.【证法三】如图3,作∠C的平分线CD,延长CB到点E,使得CE=AC,∴AC=BC+BE. ∵AC=2BC,∴BC=BE,在△ACD与△ECD中,AC=EC,∠ACD=∠ECD,CD=CD,∴△ACD≌△ECD,∴∠A=∠E,又∵∠DCB=∠DCA=∠A,∴∠E=∠DCB,∴DC=DE,∴∠ABC=90º.二、倍半角综合1. 由“倍”造“半”已知倍角求半角,将倍角所在的直角三角形相应的直角边顺势延长即可.如图,若,则()2. 由“半”造“倍”已知半角求倍角,将半角所在的直角三角形相应的直角边截取线段即可.如图,在Rt△ABC(∠A<45º)的直角边AC上取点D,当BD=AD时,则∠BDC=2∠A,设,则,在Rt△BCD中,由勾股定理可得,解得,故有.三、一些特殊的角度1. 由特殊角30º求tan15º的值如图,先构造一个含有30º角的直角三角形,设BC=1,,AB=2,再延长CA至D,使得AD=AB=2,连接BD,构造等腰△ABD,则∠D=∠BAC=15º,.2. 由特殊角45º求tan22.5º的值由图可得,.3. “345”三角形(1)如图1,Rt△ABC三边比为3:4:5,Rt△BCD三边比为,若,则;(2)如图2,Rt△ABC三边比为3:4:5,Rt△BCD三边比为,若,则;(3)如图3,Rt△ABC三边比为3:4:5,Rt△BCD三边比为,若,则.。
《用“倍半角模型”解题事半功倍》

用“倍半角模型”解题事半功倍段广猛(江苏省爲邮市赞化学校)首先,一个问题如果是确左性的,那么就注泄是可解的•英次,因果法是一种重要的思考问题的方式,"由因导果、执果索因”是分析问题、解决问题的重要途径.下而笔者借助平时教学中遇到过的一些问题,通过常规解法及“倍半角”解法,两相对比,让大家体会“倍半角” 解题模型的优势.一、“倍半角模型”(一)问题的提出:首先介绍一下,什么是“倍半角模型” ?如图1,在RtAABC中,记ZA二卩,贝lj tan卩二(不妨b0 设a<b),当冬b确左时,tan0及Zp都随之确定,那么2P及2卩角也是确左的,从而ta〒及tan2p的值也是确定的,既然是确立的,注立是可解的,那么如何求解呢?P(二)由“倍0”到“半:2如图2、延长CA至D,使AD二AB二c,连结BD,构造岀等B pB腰/\血,贝IJZD二ZDBA二一‘从而构造出角一‘而且此一角2 2 2P a恰好在RtADBC中,故可求出tan- = ---------------2 b +c上而这个过程不妨称为“由倍到半”的过程,简单易懂,但结论作用却很大,可以实现已知一个角的三角函数值,轻易求出这个角的一半所对应的三角函数值,从而此半角所在的直角三角形三边之比就可以确建下来,用于计算.(三)由“半卩”到“倍2卩":如图3,作斜边AB的垂直平分线交AC于点E,连结BE 构造出等腰△ABE,则ZA=ZEBA=p, ZBEC二2p,从而构造岀角2p 而且此2卩角恰好在Rt/kEBC中,设CE二x,贝IJAE二BE二b-x,在RtAEBC 2 22 b2-a2中,由勾股左理得x + “ = (b—x)>解之得x = ------------------- 故可2b C LCA图2图ia lab求岀二十"(此公式不需要记忆).上而这个过程不妨称为“由半到倍”的过程,计算稍显复杂,但结论作用却很大,可以实现已知一个角的三角函数值,轻易求出这个角的2倍所对应的三角函数值,从而此倍角所在的直角三角形三边之比就可以确定下来,用于计算.通过上而两个过程,可以看岀,一般情况下,“由倍到半”容易,“由半到倍”稍复杂些,而且都是通过构造等腰三角形得出已知角的“半角”与“倍角”的,操作容易,作用极大.作者简介:段广猛(1989年一〉,男,江苏宿迁人,中学一级教师.任教于商邮市赞化学校•理学颁七,毕业于苏州大学数学系.主要从事数学教仃与中学教学研尤。
人教版中考数学压轴题解题模型----几何图形之半角模型(含解析汇报)

几何图形之半角模型主题半角模型教学内容教学目标1.掌握正方形的定义,弄清正方形与平行四边形、菱形、矩形的关系。
2.掌握正方形的性质定理1和性质定理2。
3.正确运用正方形的性质解题。
4.通过四边形的从属关系渗透集合思想。
5.通过理解四种四边形内在联系,培养学生辩证观点。
知识结构正方形的性质因为正方形是特殊的平行四边形,还是特殊的矩形,特殊的菱形,所以它具有这些图形性质的综合,因此正方形有以下性质(由学生和老师一起总结)。
正方形性质定理1:正方形的四个角都是直角,四条边相等。
正方形性质定理2:正方形的两条对角线相等并且互相垂直平分,每一条对角线平分一组对角。
说明:定理2包括了平行四边形,矩形,菱形对角线的性质,一个题设同时有四个结论,这是该定理的特点,在应用时需要哪个结论就用哪个结论,并非把结论写全。
小结:(1)正方形与矩形,菱形,平行四边形的关系如上图(2)正方形的性质:①正方形对边平行。
②正方形四边相等。
③正方形四个角都是直角。
④正方形对角线相等,互相垂直平分,每条对角线平分一组对角。
典型例题精讲例1.如图,折叠正方形纸片ABCD ,先折出折痕BD ,再折叠使AD 边与对角线BD 重合,得折痕DG ,使2AD =,求AG .【解析】:作GM ⊥BD ,垂足为M . 由题意可知∠ADG=GDM , 则△ADG ≌△MDG . ∴DM=DA=2. AC=GM 又易知:GM=BM .而BM=BD-DM=22-2=2(2-1), ∴AG=BM=2(2-1).例2 .如图,P 为正方形ABCD 内一点,10PA PB ==,并且P 点到CD 边的距离也等于10,求正方形ABCD 的面积?【解析】:过P 作EF AB ⊥于F 交DC 于E .设PF x =,则10EF x =+,1(10)2BF x =+.由222PB PF BF =+. 可得:222110(10)4x x =++. 故6x =.216256ABCD S ==.例 3. 如图,E 、F 分别为正方形ABCD 的边BC 、CD 上的一点,AM EF ⊥,•垂足为M ,AM AB =,则有EF BE DF =+,为什么?【解析】:要说明EF=BE+DF ,只需说明BE=EM ,DF=FM 即可,而连结AE 、AF .只要能说明△ABE ≌△AME ,△ADF ≌△AMF 即可. 理由:连结AE 、AF .由AB=AM ,AB ⊥BC ,AM ⊥EF ,AE 公用, ∴△ABE ≌△AME . ∴BE=ME .同理可得,△ADF ≌△AMF .∴DF=MF .∴EF=ME+MF=BE+DF .例4.如下图E 、F 分别在正方形ABCD 的边BC 、CD 上,且45EAF ︒∠=,试说明EF BE DF =+。
2025年中考数学总复习第二部分重难专题突破专题5“倍半角”模型解决旋转变换问题

∠BAD=∠EAF.∴ ∠EAG=∠EAF.又∵ AE=AE,∴
△AEG≌△AEF.∴ EG=EF.∵ EG=BE+BG,∴ EF
=BE+DF.
(3) 如图③,在四边形ABCD中,AD=AB,∠ABC与∠D互补,点E,
1
F分别在射线CB,DC上,且∠EAF= ∠BAD.当BC=4,CD=7,CF=1
的半角模型是90°含45°,120°含60°.
(1) 如图①,在正方形ABCD中,E,F分别是边AB,BC上的点,且
∠EDF=45°,探究线段EF,AE,FC之间的数量关系.
小明的探究思路如下:如图①,延长BC到点M,使CM=AE,连接
DM,先证明△ADE≌△CDM,再证明△DEF≌△DMF.小亮发现
2
时,△CEF的周长为 13 .
解:(3)解析:如图②,在DF上截取DM=BE,连接AM.
∵ ∠ABC与∠D互补,
∴ ∠D+∠ABC=∠ABE+∠ABC=180°.
∴ ∠D=∠ABE.∵ AD=AB,∴ △ADM≌△ABE.
∴ AM=AE,∠DAM=∠BAE.
∵ ∠EAF=∠BAE+∠BAF=∠DAM+∠BAF= ∠BAD,
∵ ∠EAF= ∠BAD,∴ ∠GAF=∠DAG+∠DAF=∠BAE+∠DAF
=∠BAD-∠EAF=∠EAF.∴ ∠EAF=∠GAF.
=,
在△AEF和△AGF中,ቐ∠=∠,
=,
∴ △AEF≌△AGF.∴ EF=GF.
∵ GF=DG+DF=BE+DF,∴ EF=BE+DF.
解:(2) EF=BE+DF.如图①,延长EB到点G,使
BG=DF,连接AG.∵ ∠ABC+∠D=180°,∠ABG+
2022年中考数学几何模型之半角模型与倍角模型(讲+练)(解析版)

专题04 半角模型与倍角模型模型一、正方形中含半角模型如图,在正方形ABCD中,点E,F分别在边BC,CD上,∠EAF=45°,连接EF,过点A作AG⊥于EF 于点G,则:EF=BE+DF,AG=AD.例.如图,正方形ABCD的边长为4,点E,F分别在AB,AD上,若CE=5,且∠ECF=45°,则CF的长为4.【答案】4【解答】解:如图,延长FD到G,使DG=BE;连接CG、EF;∵四边形ABCD为正方形,在△BCE与△DCG中,,∴△BCE≌△DCG(SAS),∴CG=CE,∠DCG=∠BCE,∴∠GCF=45°,在△GCF与△ECF中,,∴△GCF≌△ECF(SAS),∴GF=EF,∵CE=5,CB=4,∴BE=3,∴AE=1,设AF=x,则DF=4﹣x,GF=1+(4﹣x)=5﹣x,∴EF==,∴(5﹣x)2=1+x2,∴x=,即AF=,∴DF=4﹣=,∴CF===4,故答案为:4.【变式训练1】已知四边形ABCD 是正方形,一个等腰直角三角板的一个锐角顶点与A 点重合,将此三角板绕A 点旋转时,两边分别交直线BC ,CD 于M ,N .(1)如图1,当M ,N 分别在边BC ,CD 上时,求证:BM +DN =MN(2)如图2,当M ,N 分别在边BC ,CD 的延长线上时,请直接写出线段BM ,DN ,MN 之间的数量关系(3)如图3,直线AN 与BC 交于P 点,MN =10,CN =6,MC =8,求CP 的长.【答案】(1)见解析;(2)BM DN MN -=;(3)3【详解】(1)证明:如图,延长CB 到G 使BG DN =,连接AG ,∵四边形ABCD 是正方形,∵AB AD =,90ABG ADN BAD ∠=∠=∠=︒,在ABG 与ADN △中,AB AD ABG ADN BG DN =⎧⎪∠=∠⎨⎪=⎩, ()AGB AND SAS ∴△≌△,AG AN ∴=,GAB DAN ∠=∠,45MAN ∠=︒,90BAD ∠=︒,∵45DAN BAM BAD MAN ∠+∠=∠-∠=︒,45GAM GAB BAM DAN BAM ∴∠=∠+∠=∠+∠=︒,GAM NAM ∴∠=∠,在AMN 与AMG 中,AM AM GAM NAM AN AG =⎧⎪∠=∠⎨⎪=⎩, ()AMN AMG SAS ∴△≌△,MN GM ∴=,又∵BM GB GM +=,BG DN =,BM DN MN ∴+=;(2)BM DN MN -=,理由如下:如图,在BM 上取一点G ,使得BG DN =,连接AG ,∵四边形ABCD 是正方形,∵AB AD =,90ABG ADN BAD ∠=∠=∠=︒,在ABG 与ADN △中,AB AD ABG ADN GB DN =⎧⎪∠=∠⎨⎪=⎩, ()AGB AND SAS ∴△≌△,AG AN ∴=,GAB DAN ∠=∠,∵GAB GAD DAN GAD ∠+∠=∠+∠,∵90GAN BAD ∠=∠=︒,又45MAN ∠=︒,45GAM GAN MAN MAN ∴∠=∠-∠=︒=∠,在AMN 与AMG 中,AM AM GAM NAM AN AG =⎧⎪∠=∠⎨⎪=⎩, ()AMN AMG SAS ∴△≌△,MN GM ∴=,又∵BM BG GM -=,BG DN =,∵BM DN MN -=,故答案为:BM DN MN -=;(3)如图,在DN 上取一点G ,使得DG BM =,连接AG ,∵四边形ABCD 是正方形,∵AB AD BC CD ===,90ABM ADG BAD ∠=∠=∠=︒,//AB CD ,在ABM 与ADG 中,AB AD ABM ADG BM DG =⎧⎪∠=∠⎨⎪=⎩, ()ABM ADG SAS ∴△≌△,AM AG ∴=,MAB GAD ∠=∠,∵MAB BAG GAD BAG ∠+∠=∠+∠,∵90MAG BAD ∠=∠=︒,又45MAN ∠=︒,45GAN MAG MAN MAN ∴∠=∠-∠=︒=∠,在AMN 与AGN 中,AM AG MAN GAN AN AN =⎧⎪∠=∠⎨⎪=⎩, ()AMN AGN SAS ∴△≌△,10MN GN ∴==,设DG BM x ==,∵6CN =,8MC =,∵1064DC DG GN CN x x =+-=+-=+,8BC MC BM x =-=-,∵DC BC =,∵48x x +=-,解得:2x =,∵6AB BC CD CN ====,∵//AB CD ,∵BAP CNP ∠=∠,在ABP △与NCP 中,APB NPC BAP CNP AB CN ∠=∠⎧⎪∠=∠⎨⎪=⎩, ()ABP NCP AAS ∴△≌△,132CP BP BC ∴===, ∵CP 的长为3.【变式训练2】如图,在四边形ABCD 中,AB =AD ,BC =CD ,∠ABC =∠ADC =90°,∠MAN =∠BAD .(1)如图1,将∠MAN 绕着A 点旋转,它的两边分别交边BC 、CD 于M 、N ,试判断这一过程中线段BM 、DN 和MN 之间有怎样的数量关系?直接写出结论,不用证明;(2)如图2,将∠MAN 绕着A 点旋转,它的两边分别交边BC 、CD 的延长线于M 、N ,试判断这一过程中线段BM 、DN 和MN 之间有怎样的数量关系?并证明你的结论;(3)如图3,将∠MAN 绕着A 点旋转,它的两边分别交边BC 、CD 的反向延长线于M 、N ,试判断这一过程中线段BM 、DN 和MN 之间有怎样的数量关系?直接写出结论,不用证明.【答案】见解析 【详解】解:(1)证明:延长MB 到G ,使BG =DN ,连接AG .∵∵ABG =∵ABC =∵ADC =90°,AB =AD ,∵∵ABG ∵∵ADN .∵AG =AN ,BG =DN ,∵1=∵4.∵∵1+∵2=∵4+∵2=∵MAN =∵BAD .∵∵GAM =∵MAN .又AM=AM,∵∵AMG∵∵AMN.∵MG=MN.∵MG=BM+BG.∵MN=BM+DN.(2)MN=BM﹣DN.证明:在BM上截取BG,使BG=DN,连接AG.∵∵ABC=∵ADC=90°,AD=AB,∵∵ADN∵∵ABG,∵AN=AG,∵NAD=∵GAB,∵∵MAN=∵NAD+∵BAM=∵DAB,∵∵MAG=∵BAD,∵∵MAN=∵MAG,∵∵MAN∵∵MAG,∵MN=MG,∵MN=BM﹣DN.(3)MN=DN﹣BM.模型二、等腰直角三角形角含半角模型如图,在△ABC中,AB=AC,∠BAC=90°,点D,E在BC上,且∠DAE=45°,则:BD2+CE2=DE2.例.如图,已知∵ABC中,∵BAC=90°,AB=AC,D,E是B C边上的点,将∵ABD绕点A旋转,得到∵AC D′,当∵DAE=45°时,求证:DE=D′E;在(1)的条件下,猜想:BD2,DE2,CE2有怎样的数量关系?请写出,并说明理由.【答案】见解析【详解】解析:因为∵ABD绕点A旋转,得到△ACD′∵AD=AD′,∵DAD’=∵BAC=90°∵∵DAE=45°,∵∵EAD’=∵DAD’-∵DAE=45°∵在∵AED和∵AED′中,AE=AE,∵EAD=∵AED’,AD=AD’∵∵AED∵∵AED’,∵DE=D’E由(1)得∵AED∵∵AED’,ED=ED’在∵ABC中,AB=AC,∵BAC=90°,∵∵B=∵ACB=45°∵∵ABD绕点A旋转,得到∵ACD’,∵BD=CD’,∵B=∵ACD’=45°∵∵BCD’=∵ACB+∵ACD’=45°+45°=90°【变式训练1】在等腰Rt△ABC中,CA=CB,∠ACB=90º,O为AB的中点,∠EOF=45º,交CA于F,交BC的延长线于E.(1)求证:EF=CE+AF;(2)如图2,当E在BC上,F在CA的反向延长线上时,探究线段AF、CE、EF之间的数量关系,并证明.【答案】(1)见解析;(2)AF-EF=CE.【解析】(1)连接CO,过点O作OG⊥OF交BE于点G,如图所示:由题意可得△AOF≌△COG,∴OF=OG,∴△EOF≌△EOG,∴EF=EG,∴EF=EG=EC+CG=EC+AF;(2)AF-EF=CE.【变式训练2】如图所示,等腰直角∵ABC 中,∵ACB =90°,E 、F 为AB 上两点(E 左F 右),且∵ECF =45°,求证:222AE BF EF +=.【答案】见解析【详解】解:222AE BF EF +=,理由如下:如图,将∵BCF 绕点C 旋转得∵ACF ′,使∵BCF 的BC 与AC 边重合,即∵ACF ′∵∵BCF ,∵在∵ABC 中,∵ACB =90°,AC =BC ,∵∵CAF ′=∵B =45°,∵∵EAF ′=90°,∵∵ECF =45°,∵∵ACE +∵BCF =45°,∵∵ACF ′=∵BCF ,∵∵ECF ′=45°,在∵ECF 和∵ECF ′中45CE CE ECF ECF CF CF =⎧⎪∠=∠='︒⎨='⎪⎩∵∵ECF ∵∵ECF ′(SAS ),∵EF =EF ′,在Rt ∵AEF ′中,222AE F A F E ''+=,∵222AE BF EF +=.【变式训练3】如图,∵ABC 是边长为3的等边三角形,∵BDC 是等腰三角形,∵BDC =120º,以D 为顶点作一个60º的角,使其两边分别交AB 于M ,交AC 于N ,连接MN ,则∵AMN 的周长是多少?【答案】6【详解】∵∵BDC 是等腰三角形,且∵BDC =120º,∵∵BCD =∵DBC =30º,∵∵ABC 是边长为3的等边三角形,∵∵ABC =∵BAC =∵BCA =60º,∵DBA =∵DCA =90º,如图,延长AB 至点F ,使BF =CN.连接DF,在∵BDF与∵CND中,∵∵BDF=∵CDN,DF=DN,∵∵MDN=60º,∵∵BDM+∵CDN=60º,∵∵BDM+∵BDF=60º,在∵DMN与∵DMF中,∵MN=MF,∵∵AMN的周长是:AM+AN+MN=AM+MB+BF+AN=AB+AC=6.模型三、二倍角模型(1)作二倍角的平分线,构成等腰三角形.(2)延长二倍角的一边,使其等于二倍角的另一边,构成两个等腰三角形.例.已知及的值(利用倍半角模型解题).,.【解析】由图1,由图2可得.【变式训练1】如图,在正方形ABCD中,E为AD边上的中点,过点A作AF⊥BE交CD边于点F,M是AD边上一点,且BM=DM+CD.(1)求证:点F是CD边上的中点;(2)求证:∠MBC=2∠ABE.【答案】(1)见解析;(2)见解析【解析】(1)∵四边形ABCD是正方形,∴AD=DC=AB=BC,∠C=∠D=∠BAD=90º,AB∥CD,∵AF⊥BE,∴∠AOE=90º,∴∠EAF+∠AEB=90º,∠EAF+∠BAF=90º,∴∠AEB=∠BAF,∵AB∥CD,∴∠BAF=∠AFD,∴∠AEB=∠AFD,∵∠BAD=∠D,AB=AD,∴△BAE≌△ADF,∴AE=DF,∵点E是边AD的中点,∴点F是CD边上的中点;(2)延长AD至点G,使得MG=MB,连接FG、FB,如图所示:∵BM=DM+CD,∴DG=DC=BC,∵∠GDF=∠C=90º,DF=CF,∴△FDG≌△FCB,∴∠DFG=∠CFB,∴点B、F、G共线,∵点E为AD边上的中点,点F是CD边上的中点,AD=CD,∴AE=CF,∵AB=BC,∠C=∠BAD=90º,AE=CF,∴△ABE≌△CBF,∴∠ABE=∠CBF,∵AG∥BC,∴∠AGB=∠CBF=∠ABE,∴∠MBC=∠AMB=2∠AGB=2∠GBC=2∠ABE,∴∠MBC=2∠ABE.【变式训练2】如图,在△ABC中,∠BAC=90º,AB=3,AC=4,点D是BC的中点,将△ABD沿AD 翻折得到△AED,连接CE,求线段CE的长.【解析】如图,连接BE交AD于点O,作AH⊥BC于点H.在Rt△ABC中,∵AC=4,AB=3,∴BC=5,∵CD=DB,∴AD=DC=DB=,,∵AE=AB,DE=DB=DC,∴AD垂直平分线段BE,△BCE是直角三角形,,∴BE=2OB=,在Rt△BCE.课后训练1.如图,在△ABC中,∠ACB=90º,D是AB边上的一点,M是CD的中点,若∠AMD=∠BMD.求证:∠CDA=2∠ACD.【答案】见解析【解析】证明:过点A作AG∥DC交BM延长线于点H交BC的延长线于点G,连接HC,如图所示:由题意可得∠BMD=∠AHB,∠AMD=∠HAM,∠HAC=∠ACD,即,∵CM=DM,∴HG=AH,即点H是AG的中点,∵AC⊥BC,∴,∴∠HCA=∠HAC=∠ACD,∴∠HCM=∠HCA+∠ACD=∠ACD+∠ACD=2∠ACD,∵∠HAM=∠AMD,∠AMD=∠BMD,∠BMD=∠AHB,∠BMD=∠HMC,∴HM=AM,∵MD=MC,∠AMD=∠HMC,AM=HM,∴△AMD≌△HMC,∴∠ADM=∠HCM=2∠ACD.2.在△ABC中,∠C=90º,AC=8,AB=10,点P在AC上,AP=2BP与AB、AC.的半径为1【解析】过点O作OD⊥AB于点D,OE⊥AC于点E,延长CA至点F,使得AF=AB=10,连接OA、BF,如图所示:由题意可得OD=OE,AO平分∠EAO,∠F=BAC,∴tan∠EAO=tan∠F=,设的半径为,由BC=PC=6,∴△PBC为等腰直角三角形,∴EP=OE=,EA=+2,,解得1.3.如图,在四边形ABCD中,AB=AD,∠B+∠D=180º,E、F分别是边BC、CD上的点,且∠EAF=∠BAD,求证:EF=BE+FD.【答案】见解析【解析】如图,将△ADF顺时针旋转得到△ABG,使得AD与AB重合.∵旋转,∴△ADF≌△ABG,∴∠FAG=∠BAD,AF=AG,DF=GB,∵∠EAF=∠BAD,∴∠EAF=∠EAG,又∵AE=AE,∴△EAG≌△EAF,∴GE=EF,∵GE=GB+BE=DF+BE,∴EF=BE+FD.4.已知,在正方形ABCD中,∠MAN=45º,∠MAN绕点A顺时针旋转,它的两边分别交CB、DC(或它们的延长线)于点M、N,当∠MAN绕点A旋转到BM=DN时(如图1),易证BM+DN=MN.(1)当∠MAN绕点A旋转到BM≠DN时(如图2),线段BM、DN、和MN之间有怎样的数量关系?猜想一下,并加以证明;(2)当∠MAN绕点A旋转到如图3的位置时,线段BM、DN和MN之间又有怎样的数量关系?请直接写出你的猜想.【解答】(1)猜想:BM+DN=MN;(2)猜想:DN-BM=MN【解析】(1)猜想:BM+DN=MN.证明:如图,将△AND绕点A顺时针旋转90º,得到△ABE,则E、B、M共线,∴∠EAM=90º-∠NAM=90º-45º=45º,∵∠NAM=45º,在△AEM与△ANM中,∴ME=MN,∵ME=BE+BM=DN+BM,∴DN+BM=MN;(2)猜想:DN-BM=MN.证明:在线段DN上截取DQ=BM,如图所示.在△ADQ与△ABM中,,∴∠DAQ=∠BAM,∴∠QAN=∠MAN,在△AMN与△AQN中,∴MN=QN,∴DN-BM=MN.5.如图,在平面直角坐标系中,且.(1)求证:△ABC是等边三角形;(2)如图2,A、B两点在轴上、轴上的位置不变,在线段AB上有两动点M、N,满足∠MON=45º,试猜想线段BM、AN、MN之间的数量关系,并证明你的结论.【解答】(1)见解析;(2)【解析】(1),且,∴,,∴OA =OB =OC =4,∵∠AOB =∠BOC =90º,∴∠BCA =∠CBO =∠OBA =∠BAC =45º,∴BA =BC 且∠CBA =90º,即△ABC 是等腰直角三角形;(2)猜想:.∵OA =OB =4,∴∠AOB =90º,如图,将△BOM 绕点O 顺时针旋转90º得到△AOD , ∴AD =BM ,DO =MO ,∠OAD =∠OBM =45º,且∠DOM =∠AOB =90º,∴∠AOD =∠BOM , ∵∠MON =45º,∠AOB =90º,∴∠BOM +∠AON =45º,∴∠AOD +∠AON =45º,即∠DON =∠MON =45º,∴△DON ≌△MON ,∴DN =MN ,∵∠OAD =∠OBM =∠BAO =45º,即∠NAD =90º,.6.已知正方形ABCD ,45MAN ∠=︒,MAN ∠绕点A 顺时针旋转,它的两边分别交CB 、DC 于点M 、N ,AH MN ⊥于点H .(1)如图①,当BM DN =时,可以通过证明≌ADN ABM ,得到AH 与AB 的数量关系,这个数量关系是___________;(2)如图②,当BM DN ≠时,(1)中发现的AH 与AB 的数量关系还成立吗?说明理由;(3)如图③,已知AMN 中,45MAN ∠=︒,AH MN ⊥于点H ,3MH =,7=NH ,求AH 的长.【答案】(1)AB AH =;(2)AB AH =成立,理由见解析;(3)AH =【详解】解:(1)∵正方形ABCD ,∵AB =AD ,∵B =∵D =∵BAD =90°,在Rt ∵ABM 和Rt ∵ADN 中,AB AD B D BM DN ⎧⎪∠∠⎨⎪⎩===,∵Rt ∵ABM ∵Rt ∵ADN (SAS ),∵∵BAM =∵DAN ,AM =AN , ∵∵MAN =45°,∵∵BAM +∵DAN =45°,∵∵BAM =∵DAN =22.5°,∵∵MAN =45°,AM =AN ,AH ∵MN ,∵∵MAH =∵NAH =22.5°,∵∵BAM =∵MAH ,在Rt ∵ABM 和Rt ∵AHM 中,BAM MAH B AHM AM AM ∠∠⎧⎪∠∠⎨⎪⎩===,∵Rt ∵ABM ∵Rt ∵AHM (AAS ),∵AB =AH ,故答案为:AB =AH ;(2)AB =AH 成立,理由如下:延长CB 至E ,使BE =DN ,如图:∵四边形ABCD 是正方形,∵AB =AD ,∵D =∵ABE =90°,在Rt ∵AEB 和Rt ∵AND 中,AB AD ABE D BE DN ⎧⎪∠∠⎨⎪⎩=== ∵Rt ∵AEB ∵Rt ∵AND (SAS ),∵AE =AN ,∵EAB =∵NAD ,∵∵DAN +∵BAM =45°,∵∵EAB +∵BAM =45°,∵∵EAM =45°,∵∵EAM =∵NAM =45°,在∵AEM 和∵ANM 中,AE AN EAM MAN AM AM ⎧⎪∠∠⎨⎪⎩===,∵∵AEM ∵∵ANM (SAS ),∵AB ,AH 是∵AEM 和∵ANM 对应边上的高,∵AB =AH .(3)分别沿AM ,AN 翻折∵AMH 和∵ANH ,得到∵ABM 和∵AND ,分别延长BM 和DN 交于点C ,如图:∵沿AM ,AN 翻折∵AMH 和∵ANH ,得到∵ABM 和∵AND ,∵AB =AH =AD ,∵BAD =2∵MAN =90°,∵B =∵AHM =90°=∵AHN =∵D , ∵四边形ABCD 是正方形,∵AH =AB =BC =CD =AD .由折叠可得BM =MH =3,NH =DN =7,设AH =AB =BC =CD =x ,在Rt ∵MCN 中,由勾股定理,得MN 2=MC 2+NC 2,∵()()()2227+3=37x x -+-,解得5x =5x =,∵AH =。
2025年中考数学总复习第二部分重难专题突破专题4等腰三角形中的“倍半角”问题

2
3
= =
.
3. 如图①,在△ABC中,∠ABC=2∠C,AD⊥BC于点D,M是BC
的中点.
1
求证:DM= AB;
2
(1)
解:(1) 证明:如图①,取AC的中点H,连
接HM,DH.∵ M是BC的中点,H是AC的中
点,∴ MH∥AB,MH= AB.∴ ∠HMC=
∠ABC.又∵ ∠ABC=2∠C,∴ ∠HMC=2∠C.
∵ AD⊥BC,H是AC的中点,∴ DH=HC.∴
∠HDC=∠C.∴ ∠HMC=2∠HDC.∵ ∠HMC
如图②,延长BA至点D,使AD=AC,连接CD,则∠D
=∠ACD=20°,且AD=AB.易证CA平分∠PCD.过点A分
别作CD,CP的垂线,垂足分别为G,H,则AG=
AH.∵∠ACP=20°,∠BAC=40°,∴ ∠APH=20°+40°
=60°.∵ 易证BC=2AG,∴ BC=2AH.∴
2sin∠APH=2sin60°= 3.
2
3.
变式训练
1.
如图,在等边三角形ABC中,P为AB上一点,∠A=2∠ACP,则
=
2 .
解析:在等边三角形ABC中,AC=BC,∠A=60°.∵
∠A=2∠ACP,∴ ∠ACP=30°.在△ACP中,∠APC
=180°-30°-60°=90°.∴
BC,∴
=2.
=sin30°= .∵
=2∠BAD,∴ ∠C=∠EAD.∴ ∠ADE=∠C+∠DAC=∠EAD+
∠DAC=∠EAC.∴ ∠E=∠ADE=∠EAC.∴ AC=CE=3a.∵ ∠E=
中考数学解题的基本模型半角模型
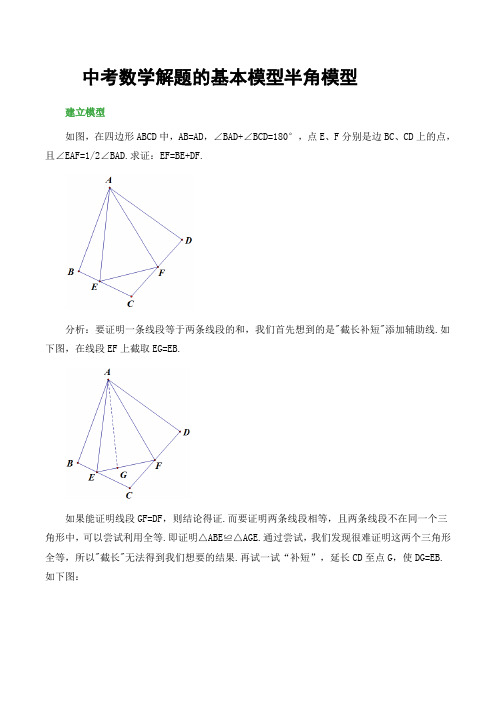
中考数学解题的基本模型半角模型建立模型如图,在四边形ABCD中,AB=AD,∠BAD+∠BCD=180°,点E、F分别是边BC、CD上的点,且∠EAF=1/2∠BAD.求证:EF=BE+DF.分析:要证明一条线段等于两条线段的和,我们首先想到的是"截长补短"添加辅助线.如下图,在线段EF上截取EG=EB.如果能证明线段GF=DF,则结论得证.而要证明两条线段相等,且两条线段不在同一个三角形中,可以尝试利用全等.即证明△ABE≌△AGE.通过尝试,我们发现很难证明这两个三角形全等,所以"截长"无法得到我们想要的结果.再试一试“补短”,延长CD至点G,使DG=EB.如下图:此时若能证明FG=FE,则FE=FG=FD+DG=FD+BE.结论得证.而要证明FE=FG,只需证明△AEF≌AGF即可.证明:延长FD至点G,使DG=BE.易证△ABE≌△ADG(SAS),∴AE=AG,∠BAE=∠DAG.∴∠EAF=1/2∠BAD=∠BAE+∠FAD=∠DAG+∠FAD=∠GAF又∵AF=AF,∴△EAF≌△GAF.∴EF=GF=DF+DG=DF+BE反思:1、本题中的辅助线:延长DG=BE,也可以通过旋转来实现(实际上就是将三角形ABE绕点A逆时针旋转∠BAD的度数).需要指出的是,如果用旋转,需说明C、D、G三点共线(证明∠ADG+∠ADC=180°即可).2、题中有三个非常重要的元素:(1)∠EAF=1/2∠BAD(半角模型名称的由来);(2)AB=AD. 共端点的两条线段相等,这点尤为关键,它为下一步的旋转提供了条件.当题中出现一个角等于另一角的一半,且共端点的线段相等时,常采用旋转,将分散的条件集中起来,为下一步的证明做好铺垫. (3)对角互补.由于对角互补的存在,通过旋转,两边的两个三角形可拼成一个大三角形,进而可证明三角形全等.一、半角结构之90°与45°先来看一道题目:如图,在正方形ABCD中,点E,F分别在BC,CD上,∠EAF=45°.求证:EF=BE+DF.证明:证明:∵四边形ABCD是正方形∴AB=AD且∠ABE+∠ADF=180°将△ABE绕点A逆时针旋转90°得到△ADG,此时点C、D、G三点共线.∴∠BAE=∠DAG,AE=AG. ∵∠EAF=45°∴∠BAE+∠DAF=∠DAG+∠DAF=∠GAF=45°∴∠EAF=∠GAF. 又∵AF=AF.∴△EAF≌△GAF.∴EF=GF=DF+DG=DF+BE.模型应用1:如图,在正方形ABCD中,点E,F分别在边BC,CD上,∠EAF=45°.BE=2cm,DF=3cm.求正方形的边长.分析:根据上题的结论可知EF=BE+DF=5.设正方形的边长为x,那么CE=x-2,CF=x-3.在Rt△CEF中,根据勾股定理得,CE^2+CF^2=EF^2,即(x-2)^2+(x-3)^2=5^2,解得,x=6.所以正方形的边长为6以上的半角结构主要发生在四边形中,再次回顾半角结构中的重要元素:(1)半角(2)邻边相等(3)对角互补. 半角模型中经常通过旋转将分散的条件集中起来,进而通过三角形的全等进行证明.在三角形中同样存在半角模型,下面以一道题为例来说明三角形中的半角模型.如图,在△ABC中,∠BAC=90°,AB=AC.点D,E是BC边上两点且∠DAE=45°求证:BD^2+CE^2=DE^2分析:看到这个结论,相信大部分同学首先想到的是勾股定理,但DE,BD,CE不在同一个三角形中.所以要想办法将他们集中在一个三角形里面,根据题中条件AB=AC,共端点的两条线段相等,可以尝试旋转.证明:因为AB=AC,且∠BAC=90°.将△ABD绕点A逆时针旋转90°得到△ACG,连接EG. 如下图:由旋转的性质可知,△ABD≌△ACG.∴AD=AG,∠BAD=∠CAG,∠ABD=∠ACG=45°.∵∠DAE=45°,∴∠BAD+∠EAC=∠CAG+∠EAC=45°∴∠DAE=∠GAE∴△DAE≌△GAE(SAS)∴DE=GE在Rt△GCE中CE^2+CG^2=GE^2∵BD=CG,DE=CG∴BD^2+CE^2=DE^2反思:对于本题,我们通过旋转将分散的条件集中起来,进而得到结论。
倍半角,镜面相似,2020贵阳中考压轴题分析

倍半角,镜面相似,2020贵阳中考压轴题分析
传播知识,传播力量!
贵阳市是贵州的省会,贵州有9个地级行政区,2020年的中考有三各个地方考卷一样(贵阳,安顺,六盘水),其他地方各自为战。
今天做的是贵阳中考:
选择题:
结合图形来看,主要应用二函对称性
开口无所谓:
填空题:
本题为静态几何求长度
所用的策略是倍半角构造之先转移再构造!
关键把∠A转移到∠BFC
再倍半构造即
倍半角处理策略,依山势建城堡,含例题分析
解答题几何:
看着也就最后一题有难度
(1)略
(2)其实和(3)是连续性的,甚至可以得到一般性结论,即△ABO不轮转多少度,△PQB恒为等直的结论。
联结O'A 可发现模型:
(交互式)镜面相似模型
简单证明:
证毕!
(3)就根据等直很好算了!
感谢支持:分享、转发、右下角点“在看赞”
“知识”这个东西非常的神奇,你把它分享出去,它不但不会减少,反而会增加,所分享知识应当是快乐的,也能够让自己提升,这就是我每天分享知识的信念。
2022年中考数学几何模型提升专题08 倍半角模型

专题08倍半角模型【模型解读】半角向外构等腰,倍角向内构等腰.【必备知识】等腰三角形与“倍半角”在等腰ABC △中,AB AC =,则2CAD B ∠=∠【模型建立】 (一)向外构造等腰,得到“半”角 如图,在直角三角形中,若tan a b θ=,则tan 2a b cθ=+已知“倍角”求“半角”,只需将该倍角所在的直角三角形相应的直角边顺势延长,“等腰现,半角出”(二)向内构造等腰得到“倍”角如图,在Rt △的直角边上取点,向内构造等腰,设x ,在粉色Rt △中,由勾股定理可以解出x ,从而得到tan 2θ已知“半角”求“倍角”,只需在该半角所在的直角三角形相应的直角边截取线段,“等腰现,倍角出”; 可以看出:由“倍”造“半”,极其容易,只需口算;由“半”造“倍”,相对麻烦,需要方程;【特殊“半角”】(一)15°角问题:如何计算tan15°的值呢?由15°容易联想到30°,它们之间存在着“倍半”关系;如图,先构造一个含30°角的Rt △ABC,设1,BC CA AB ===2,再延长CA 至D 使AD=AB=2,连接BD ,构造出等腰△ABD ,则115,2D BAC ︒∠=∠=故在Rt △DBC 中,有tan152BC DC ︒===(二)22.5°角 构造可得tan 22.5BC DC ︒==1= 而tan 67.51,tan 22.5DC BC︒︒==与tan67.5°互为倒数. ba x1D(三)“345”三角形①如图,Rt △ABC 三边比为3:4:5,Rt △BCE 三边比为1:即若3tan ,4BAC ∠=11tan tan 23E BAC ∠=∠=②如图,Rt △ABC 三边比为3:4:5,Rt △ACF 三边比为1:2即若4tan ,3ABC ∠=11tan tan 22F ABC ∠=∠=121D54B54F③如图,Rt △ABC 三边比为3:4:5,Rt △BCD 三边比为7:24:25,即若3tan ,4A ∠=则tan 24tan 27BDC A ∠=∠=记住这些常用的数据以及来龙去脉,对于解题来说,百利而无一害.【模型实例】1.如图,在正方形ABCD 中,1AB =,点E 、F 分别在边BC 和CD 上,AE AF =,60EAF ∠=︒,则CF 的长是 .2.如图,在正方形纸片ABCD 中,E 是CD 的中点,将正方形纸片折叠,点B 落在线段AE 上的点G 处,折痕为AF ,若4AD cm =,则CF 的长为 cm .3.如图,ABC ∆中,点E 在边AC 上,EB EA =,2A CBE ∠=∠,CD 垂直于BE 的延长线于点D ,8BD =,11AC =,则边BC 的长为 .x43B4.如图,点A 在反比例函数(0)k y x x=<上,过点A 作AB x ⊥轴于点B ,C 为x 轴正半轴上一点,连接AC 交y 轴于点D ,3tan 4ACB ∠=,AO 平分CAB ∠,此时,8ABC S ∆=,则k 的值为 .5.如图,正方形ABCD 的边长为4,点E 是CD 的中点,AF 平分BAE ∠交BC 于点F ,将ADE ∆绕点A 顺时针旋转90︒得ABG ∆,则CF 的长为 .6.如图,AB 是O 的直径,C ,P 是AB 上两点,13AB =,5AC =,如图,若点P 是AB 的中点,求PA 的长;7.如图,在Rt ABC ∆中,90ACB ∠=︒,6AC =,8BC =,AD 平分BAC ∠,AD 交BC 于点D ,ED AD ⊥交AB 于点E ,ADE ∆的外接圆O 交AC 于点F ,连接EF .(1)求证:BC 是O 的切线;(2)求O 的半径r 及3∠的正切值.8.如图,BM 是以AB 为直径的O 的切线,B 为切点,BC 平分ABM ∠,弦CD 交AB 于点E ,DE OE =.(1)求证:ACB ∆是等腰直角三角形;(2)求证:2OA OE DC =;(3)求tan ACD ∠的值.9.如图,在Rt ABC ∆中,90ABC ∠=︒,以CB 为半径作C ,交AC 于点D ,交AC 的延长线于点E ,连接BD ,BE .(1)求证:ABD AEB ∆∆∽;(2)当43AB BC =时,求tan E ; (3)在(2)的条件下,作BAC ∠的平分线,与BE 交于点F ,若2AF =,求C 的半径.10.如图,AB 为O 的直径,C 为O 上一点,D 是弧BC 的中点,BC 与AD 、OD 分别交于点E 、F .(1)求证://DO AC ;(2)求证:2DE DA DC ⋅=;(3)若1tan 2CAD ∠=,求sin CDA ∠的值.11.如图,在平面直角坐标系中,直线122y x =-+与x 轴交于点A ,与y 轴交于点B ,抛物线212y x bx c =-++经过A ,B 两点且与x 轴的负半轴交于点C .(1)求该抛物线的解析式;(2)若点D 为直线AB 上方抛物线上的一个动点,当2ABD BAC ∠=∠时,求点D 的坐标;12.二次函数24(0)y ax bx a =++≠的图象经过点(4,0)A -,(1,0)B ,与y 轴交于点C ,点P 为第二象限内抛物线上一点,连接BP 、AC ,交于点Q ,过点P 作PD x ⊥轴于点D .(1)求二次函数的表达式;(2)连接BC ,当2DPB BCO ∠=∠时,求直线BP 的表达式;13.如图,在平面直角坐标系中,直线122y x =+与x 轴交于点A ,与y 轴交于点C ,抛物线212y x bx c =-++经过A 、C 两点,与x 轴的另一交点为点B .(1)求抛物线的函数表达式;(2)点D 为直线AC 上方抛物线上一动点,过点D 作DF AC ⊥,垂足为点F ,连接CD ,是否存在点D ,使得CDF ∆中的某个角恰好等于BAC ∠的2倍?若存在,求点D 的横坐标;若不存在,请说明理由.14.如图,抛物线26y ax x c =++交x 轴于A ,B 两点,交y 轴于点C ,直线5y x =-经过点B ,C .(1)求抛物线的解析式;(2)过点A 的直线交直线BC 于点M ,连接AC ,当直线AM 与直线BC 的夹角等于ACB ∠的2倍时,请直接写出点M 的坐标.15.如图,抛物线2y x bx c =++交x 轴于A 、B 两点,其中点A 坐标为(1,0),与y 轴交于点(0,3)C -.(1)求抛物线的函数表达式;(2)如图①,连接AC,点P在抛物线上,且满足2PAB ACO∠=∠.求点P的坐标;16.在平面直角坐标系中,直线122y x=-与x轴交于点B,与y轴交于点C,二次函数212y x bx c=++的图象经过B,C两点,且与x轴的负半轴交于点A,动点D在直线BC下方的二次函数图象上.(1)求二次函数的表达式;(2)如图,过点D作DM BC⊥于点M,是否存在点D,使得CDM∆中的某个角恰好等于ABC∠的2倍?若存在,直接写出点D的横坐标;若不存在,请说明理由.专题08倍半角模型【模型解读】半角向外构等腰,倍角向内构等腰.【必备知识】等腰三角形与“倍半角”在等腰ABC △中,AB AC =,则2CAD B ∠=∠【模型建立】 (一)向外构造等腰,得到“半”角 如图,在直角三角形中,若tan a b θ=,则tan 2a b cθ=+已知“倍角”求“半角”,只需将该倍角所在的直角三角形相应的直角边顺势延长,“等腰现,半角出”(二)向内构造等腰得到“倍”角如图,在Rt △的直角边上取点,向内构造等腰,设x ,在粉色Rt △中,由勾股定理可以解出x ,从而得到tan 2θ已知“半角”求“倍角”,只需在该半角所在的直角三角形相应的直角边截取线段,“等腰现,倍角出”;可以看出:由“倍”造“半”,极其容易,只需口算;由“半”造“倍”,相对麻烦,需要方程;【特殊“半角”】(一)15°角问题:如何计算tan15°的值呢?由15°容易联想到30°,它们之间存在着“倍半”关系;如图,先构造一个含30°角的Rt△ABC,设1,BC CA AB===2,再延长CA至D使AD=AB=2,连接BD,构造出等腰△ABD,则115,2D BAC︒∠=∠=故在Rt△DBC中,有tan152BCDC︒===(二)22.5°角构造可得tan22.5BCDC︒==1=而tan67.51,tan22.5DCBC︒︒==与tan67.5°互为倒数.bax1D(三)“345”三角形①如图,Rt △ABC 三边比为3:4:5,Rt △BCE三边比为1:即若3tan ,4BAC ∠=11tan tan 23E BAC ∠=∠=②如图,Rt △ABC 三边比为3:4:5,Rt △ACF 三边比为1:2:即若4tan ,3ABC ∠=11tan tan 22F ABC ∠=∠=121D54B③如图,Rt△ABC三边比为3:4:5,Rt△BCD三边比为7:24:25,即若3 tan,4A∠=则tan24tan27 BDC A∠=∠=记住这些常用的数据以及来龙去脉,对于解题来说,百利而无一害.【模型实例】1.如图,在正方形ABCD中,1AB=,点E、F分别在边BC和CD上,AE AF=,60EAF∠=︒,则CF1.54Fx43B【解答】解:四边形ABCD 是正方形,90B D BAD ∴∠=∠=∠=︒,1AB BC CD AD ====,在Rt ABE ∆和Rt ADF ∆中, AE AFAB AD=⎧⎨=⎩, Rt ABE Rt ADF(HL)∴∆≅∆,BAE DAF ∴∠=∠,60EAF ∠=︒, 30BAE DAF ∴∠+∠=︒, 15DAF ∴∠=︒,在AD 上取一点G ,使15GFA DAF ∠=∠=︒,如图所示,AG FG ∴=,30DGF ∠=︒, 1122DF FG AG ∴==,DG ,设DF x =,则DG ,2AG FG x ==, AG DG AD +=,21x ∴=,解得:2x =2DF ∴=,1(21CF CD DF ∴=-=-=;1-.2.如图,在正方形纸片ABCD 中,E 是CD 的中点,将正方形纸片折叠,点B 落在线段AE上的点G 处,折痕为AF ,若4AD cm =,则CF 的长为 (6- cm .【解答】解:设BF x =,则FG x =,4CF x =-.在Rt ADE ∆中,利用勾股定理可得AE =.根据折叠的性质可知4AG AB ==,所以4GE =.在Rt GEF ∆中,利用勾股定理可得2224)EF x =+, 在Rt FCE ∆中,利用勾股定理可得222(4)2EF x =-+,所以22224)(4)2x x +=-+,解得2x =.则46FC x =-=-故答案为:(6-.3.如图,ABC ∆中,点E 在边AC 上,EB EA =,2A CBE ∠=∠,CD 垂直于BE 的延长线于点D ,8BD =,11AC =,则边BC 的长为【解答】解:延长BD 到F ,使得DF BD =, CD BF ⊥,BCF ∴∆是等腰三角形, BC CF ∴=,过点C 作//CH AB ,交BF 于点H 22ABD CHD CBD F ∴∠=∠=∠=∠, HF HC ∴=, //CH AB ,ABE CHE ∴∠=∠,BAE ECH ∠=∠, EH CE ∴=,EA EB =,AC BH ∴=,8BD =,11AC =,3DH BH BD AC BD ∴=-=-=, 835HF HC ∴==-=,在Rt CDH ∆,∴由勾股定理可知:4CD =,在Rt BCD ∆中,BC ∴==,故答案为:4.如图,点A 在反比例函数(0)ky x x=<上,过点A 作AB x ⊥轴于点B ,C 为x 轴正半轴上一点,连接AC 交y 轴于点D ,3tan 4ACB ∠=,AO 平分CAB ∠,此时,8ABC S ∆=,则k 的值为 6- .【解答】解:设点A 纵坐标为m ,则点A 坐标为(km,)m ,作OE 垂直于AC 于点E , AB m ∴=, 3tan 4AB ACB BC ∠==, 4433BC AB m ∴==, 21128223ABC S AB BC mBC m ∆∴=⋅===,解得m =或m =-),AB ∴=,BC =,AC OE OB =,1111()82222ABC ABO AOC S S S AB BO AC OE BO AB AC BO ∆∆∆∴=+=⋅+⋅=+=⨯=,解得BO =∴点A 坐标为(,6k ∴==-.故答案为:6-.5.如图,正方形ABCD 的边长为4,点E 是CD 的中点,AF 平分BAE ∠交BC 于点F ,将ADE ∆绕点A 顺时针旋转90︒得ABG ∆,则CF 的长为 6-【解答】解:正方形ABCD 的边长为4,点E 是CD 的中点,2DE ∴=,AE ∴=ADE ∆绕点A 顺时针旋转90︒得ABG ∆,AG AE ∴==,2BG DE ==,34∠=∠,90GAE ∠=︒,90ABG D ∠=∠=︒,而90ABC ∠=︒,∴点G 在CB 的延长线上,AF 平分BAE ∠交BC 于点F , 12∴∠=∠,2413∴∠+∠=∠+∠,即GAF DAF ∠=∠, DAF AFG ∠=∠, GA GF ∴=,GF GA AE ∴===426CF CG GF ∴=-=+-=-故答案为6-6.如图,AB 是O 的直径,C ,P 是AB 上两点,13AB =,5AC =.如图,若点P 是AB 的中点,求PA 的长【解答】解:如图所示,连接PB ,AB 是O 的直径且P 是AB 的中点,45PAB PBA ∴∠=∠=︒,90APB ∠=︒,又在等腰三角形APB ∆中有13AB =,PA ∴. 7.如图,在Rt ABC ∆中,90ACB ∠=︒,6AC =,8BC =,AD 平分BAC ∠,AD 交BC 于点D ,ED AD ⊥交AB 于点E ,ADE ∆的外接圆O 交AC 于点F ,连接EF . (1)求证:BC 是O 的切线; (2)求O 的半径r 及3∠的正切值.【解答】(1)证明:ED AD ⊥, 90EDA ∴∠=︒,AE 是O 的直径, AE ∴的中点是圆心O ,连接OD ,则OA OD =, 1ODA ∴∠=∠,AD 平分BAC ∠,21ODA ∴∠=∠=∠,//OD AC ∴,90BDO ACB ∴∠=∠=︒, BC ∴是O 的切线;(2)解:在Rt ABC ∆中,由勾股定理得,10AB ===, //OD AC , BDO BCA ∴∆∆∽,∴OD OB AC AB =,即10610r r-=, 154r ∴=,在Rt BDO ∆中,5BD =, 853CD BC BD ∴=-=-=,在Rt ACD ∆中,31tan 262CD AC ∠===, 32∠=∠,1tan 3tan 22∴∠=∠=.8.如图,BM 是以AB 为直径的O 的切线,B 为切点,BC 平分ABM ∠,弦CD 交AB 于点E ,DE OE =.(1)求证:ACB ∆是等腰直角三角形; (2)求证:2OA OE DC =; (3)求tan ACD ∠的值.【解答】证明:(1)BM 是以AB 为直径的O 的切线,90ABM ∴∠=︒, BC 平分ABM ∠,1452ABC ABM ∴∠=∠=︒AB 是直径90ACB ∴∠=︒,45CAB CBA ∴∠=∠=︒ AC BC ∴=ACB ∴∆是等腰直角三角形;(2)如图,连接OD ,OCDE EO =,DO CO =EDO EOD ∴∠=∠,EDO OCD ∠=∠ EDO EDO ∴∠=∠,EOD OCD ∠=∠EDO ODC ∴∆∆∽∴OD DEDC DO=2OD DE DC ∴=2OA DE DC EO DC ∴==(3)如图,连接BD ,AD ,DO ,作BAF DBA ∠=∠,交BD 于点F ,DO BO =ODB OBD ∴∠=∠,2AOD ODB EDO ∴∠=∠=∠,453CAB CDB EDO ODB ODB ∠=∠=︒=∠+∠=∠,15ODB OBD ∴∠=︒=∠ 15BAF DBA ∠=∠=︒AF BF ∴=,30AFD ∠=︒ AB 是直径90ADB ∴∠=︒2AF AD ∴=,DF =2BD DF BF AD ∴=++tan tan 2AD ACD ABD BD ∴∠=∠===-9.如图,在Rt ABC ∆中,90ABC ∠=︒,以CB 为半径作C ,交AC 于点D ,交AC 的延长线于点E ,连接BD ,BE . (1)求证:ABD AEB ∆∆∽; (2)当43AB BC =时,求tan E ; (3)在(2)的条件下,作BAC ∠的平分线,与BE 交于点F ,若2AF =,求C 的半径.【解答】解:(1)90ABC ∠=︒, 90ABD DBC ∴∠=︒-∠,由题意知:DE 是直径, 90DBE ∴∠=︒, 90E BDE ∴∠=︒-∠, BC CD =, DBC BDE ∴∠=∠,ABD E ∴∠=∠, A A ∠=∠, ABD AEB ∴∆∆∽;(2):4:3AB BC =,∴设4AB =,3BC =,5AC ∴==, 3BC CD ==,532AD AC CD ∴=-=-=,由(1)可知:ABD AEB ∆∆∽,∴AB AD BDAE AB BE==,2AB AD AE ∴=, 242AE ∴=,8AE ∴=,在Rt DBE ∆中 41tan 82BD AB E BE AE ====;(3)过点F 作FM AE ⊥于点M , :4:3AB BC =,∴设4AB x =,3BC x =,∴由(2)可知;8AE x =,2AD x =,6DE AE AD x ∴=-=,AF 平分BAC ∠,∴BF ABEF AE =, ∴4182BF x EF x ==, 1tan 2E =,cos E ∴=,sin E =,∴BE DE =,BE ∴=,23EF BE ∴==,sin MF E EF ∴=, 85MF x ∴=,1tan 2E =, 1625ME MF x ∴==, 245AM AE ME x ∴=-=,222AF AM MF =+,222484()()55x x ∴=+,x ∴C ∴的半径为:3x =.另解:由上述知1tan 3FMFAM AM∠==, BC DC CE ==,35BC AC =, ::2:3:3AD DC CE ∴=,1tan 2FME ME∠==, 设FM a =,则3AM a =,2ME a =, 5AE a ∴=,31588DC AE a ∴==,由勾股定理可知:AF =,2AF =,a ∴=DC ∴=10.如图,AB 为O 的直径,C 为O 上一点,D 是弧BC 的中点,BC 与AD 、OD 分别交于点E 、F . (1)求证://DO AC ; (2)求证:2DE DA DC ⋅=; (3)若1tan 2CAD ∠=,求sin CDA ∠的值.【解答】解:(1)因为点D 是弧BC 的中点, 所以CAD BAD ∠=∠,即2CAB BAD ∠=∠, 而2BOD BAD ∠=∠, 所以CAB BOD ∠=∠, 所以//DO AC ; (2)CD BD =,CAD DCB ∴∠=∠, DCE DAC ∴∆∆∽,2CD DE DA ∴=⋅;(3)1tan 2CAD ∠=,连接BD ,则BD CD =,DBC CAD ∠=∠,在Rt BDE ∆中,1tan 2DE DE DBE BD CD ∠===, 设:DE a =,则2CD a =, 而2CD DE DA =⋅,则4AD a =, 3AE a ∴=,∴3AEDE=, 而AEC DEF ∆∆∽,即AEC ∆和DEF ∆的相似比为3, 设:EF k =,则3CE k =,8BC k =, 1tan 2CAD ∠=, 6AC k ∴=,10AB k =,3sin 5CDA ∴∠=.11.如图,在平面直角坐标系中,直线122y x =-+与x 轴交于点A ,与y 轴交于点B ,抛物线212y x bx c =-++经过A ,B 两点且与x 轴的负半轴交于点C .(1)求该抛物线的解析式;(2)若点D 为直线AB 上方抛物线上的一个动点,当2ABD BAC ∠=∠时,求点D 的坐标;【解答】解:(1)在122y x =-+中,令0y =,得4x =,令0x =,得2y =(4,0)A ∴,(0,2)B把(4,0)A ,(0,2)B ,代入212y x bx c =-++,得2116402c b c =⎧⎪⎨-⨯++=⎪⎩,解得322b c ⎧=⎪⎨⎪=⎩ ∴抛物线的解析式为213222y x x =-++ (2)如图,过点B 作x 轴得平行线交抛物线于点E ,过点D 作BE 的垂线,垂足为F//BE x 轴,BAC ABE ∴∠=∠ 2ABD BAC ∠=∠,2ABD ABE ∴∠=∠即2DBE ABE ABE ∠+∠=∠DBE ABE ∴∠=∠DBE BAC ∴∠=∠设D 点的坐标为213(,2)22x x x -++,则BF x =,21322DF x x =-+tan DF DBE BF ∠=,tan BO BAC AO∠= ∴DF BO BF AO=,即2132224x xx -+= 解得10x =(舍去),22x = 当2x =时,2132322x x -++=∴点D 的坐标为(2,3)12.二次函数24(0)y ax bx a =++≠的图象经过点(4,0)A -,(1,0)B ,与y 轴交于点C ,点P 为第二象限内抛物线上一点,连接BP 、AC ,交于点Q ,过点P 作PD x ⊥轴于点D . (1)求二次函数的表达式;(2)连接BC ,当2DPB BCO ∠=∠时,求直线BP 的表达式;【解答】解:(1)二次函数24(0)y ax bx a =++≠的图象经过点(4,0)A -,(1,0)B , ∴2(4)(4)4040a b a b ⎧⋅-+⋅-+=⎨++=⎩,解得:13a b =-⎧⎨=-⎩,∴该二次函数的表达式为234y x x =--+;(2)如图,设BP 与y 轴交于点E , //PD y 轴, DPB OEB ∴∠=∠, 2DPB BCO ∠=∠, 2OEB BCO ∴∠=∠, ECB EBC ∴∠=∠,BE CE ∴=,令0x =,得4y =, (0,4)C ∴,4OC =,设OE a =,则4CE a =-, 4BE a ∴=-,在Rt BOE ∆中,由勾股定理得:222BE OE OB =+,222(4)1a a ∴-=+, 解得:158a =, 15(0,)8E ∴, 设BE 所在直线表达式为(0)y kx e k =+≠, ∴150810k e k e ⎧⋅+=⎪⎨⎪⋅+=⎩, 解得:158158k e ⎧=-⎪⎪⎨⎪=⎪⎩,∴直线BP 的表达式为151588y x =-+; 13.如图,在平面直角坐标系中,直线122y x =+与x 轴交于点A ,与y 轴交于点C ,抛物线212y x bx c =-++经过A 、C 两点,与x 轴的另一交点为点B .(1)求抛物线的函数表达式;(2)点D 为直线AC 上方抛物线上一动点,过点D 作DF AC ⊥,垂足为点F ,连接CD ,是否存在点D ,使得CDF ∆中的某个角恰好等于BAC ∠的2倍?若存在,求点D 的横坐标;若不存在,请说明理由.【解答】解:(1)根据题意得(4,0)A -,(0,2)C , 抛物线212y x bx c =-++经过A 、C 两点,∴1016422b c c ⎧=-⨯-+⎪⎨⎪=⎩, ∴322b c ⎧=-⎪⎨⎪=⎩, 213222y x x ∴=--+;(2)(4,0)A -,(1,0)B ,(0,2)C ,AC ∴=,BC ,5AB =,222AC BC AB ∴+=,ABC ∴∆是以ACB ∠为直角的直角三角形,取AB 的中点P ,3(2P ∴-,0),52PA PC PB ∴===, 2CPO BAC ∴∠=∠, 4tan tan(2)3CPO BAC ∴∠=∠=, 过D 作x 轴的平行线交y 轴于R ,交AC 的延长线于G , 情况一:如图,2DCF BAC DGC CDG ∴∠=∠=∠+∠, CDG BAC ∴∠=∠, 1tan tan 2CDG BAC ∴∠=∠=, 即12RC DR =, 令213(,2)22D a a a --+,DR a ∴=-,21322RC a a =--,∴2131222a aa --=-, 10a ∴=(舍去),22a =-, 2D x ∴=-,情况二,2FDC BAC ∴∠=∠, 4tan 3FDC ∴∠=, 设4FC k =,3DF k ∴=,5DC k =,31tan 2k DGC FG ∠==, 6FG k ∴=,2CG k ∴=,35DG k =,25RC k ∴=,45RG k =, 4511535DR k k k =-=, ∴21155132522kDR a RC a ak -==--,10a ∴=(舍去),22911a =-, 点D 的横坐标为2-或2911-.14.如图,抛物线26y ax x c =++交x 轴于A ,B 两点,交y 轴于点C ,直线5y x =-经过点B ,C .(1)求抛物线的解析式;(2)过点A 的直线交直线BC 于点M .连接AC ,当直线AM 与直线BC 的夹角等于ACB ∠的2倍时,请直接写出点M 的坐标.【解答】解:(1)当0x =时,55y x =-=-,则(0,5)C -, 当0y =时,50x -=,解得5x =,则(5,0)B ,把(5,0)B ,(0,5)C -代入26y ax x c =++得253005a c c ++=⎧⎨=-⎩,解得15a c =-⎧⎨=-⎩,∴抛物线解析式为265y x x =-+-;(2)作AN BC ⊥于N ,NH x ⊥轴于H ,作AC 的垂直平分线交BC 于1M ,交AC 于E ,如图, 11M A M C =,11ACM CAM ∴∠=∠, 12AM B ACB ∴∠=∠,ANB ∆为等腰直角三角形, 2AH BH NH ∴===,(3,2)N ∴-,易得AC 的解析式为55y x =-,E 点坐标为1(2,5)2-,设直线1EM 的解析式为15y x b =-+,把1(2E ,5)2-代入得15102b -+=-,解得125b =-,∴直线1EM 的解析式为11255y x =--, 解方程组511255y x y x =-⎧⎪⎨=--⎪⎩得136176x y ⎧=⎪⎪⎨⎪=-⎪⎩,则113(6M ,17)6-;在直线BC 上作点1M 关于N 点的对称点2M ,如图2,则212AM C AM B ACB ∠=∠=∠,设2(,5)M x x -, 13632x +=, 236x ∴=, 223(6M ∴,7)6-, 综上所述,点M 的坐标为13(6,17)6-或23(6,7)6-.15.如图,抛物线2y x bx c =++交x 轴于A 、B 两点,其中点A 坐标为(1,0),与y 轴交于点(0,3)C -.(1)求抛物线的函数表达式;(2)如图,连接AC ,点P 在抛物线上,且满足2PAB ACO ∠=∠.求点P 的坐标;【解答】解:(1)抛物线2y x bx c =++经过点(1,0)A ,(0,3)C - ∴10003b c c ++=⎧⎨++=-⎩解得:23b c =⎧⎨=-⎩ ∴抛物线的函数表达式为223yx x =+-(2)①若点P 在x 轴下方,如图1,延长AP 到H ,使AH AB =,过点B 作BI x ⊥轴,连接BH ,作BH 中点G ,连接并延长AG 交BI 于点F ,过点H 作HI BI ⊥于点I 当2230x x +-=,解得:13x =-,21x = (3,0)B ∴- (1,0)A ,(0,3)C -1OA ∴=,3OC =,AC ==4AB = Rt AOC ∴∆中,sin OA ACO AC ∠==,cos OC ACO AC ∠==AB AH =,G 为BH 中点AG BH ∴⊥,BG GH =BAG HAG ∴∠=∠,即2PAB BAG ∠=∠2PAB ACO ∠=∠ BAG ACO ∴∠=∠Rt ABG ∴∆中,90AGB ∠=︒,sin BG BAG AB ∠=BG ∴==2BH BG ∴= HBI ABG ABG BAG ∠+∠=∠+∠=︒ HBI BAG ACO ∴∠=∠=∠Rt BHI ∴∆中,90BIH ∠=︒,sin HI HBI BH ∠=cos BI HBI BH ∠==45HI ∴==,125BI = 411355H x ∴=-+=-,125H y =-,即11(5H -,12)5-设直线AH 解析式为y kx a =+ ∴0111255k a k a +=⎧⎪⎨-+=-⎪⎩解得:3434k a ⎧=⎪⎪⎨⎪=-⎪⎩ ∴直线33:44AH y x =-2334423y x y x x ⎧=-⎪⎨⎪=+-⎩解得:1110x y =⎧⎨=⎩(即点)A ,22943916x y ⎧=-⎪⎪⎨⎪=-⎪⎩9(4P ∴-,39)16-;②若点P 在x 轴上方,如图2,在AP 上截取AH AH '=,则H '与H 关于x 轴对称 11(5H '∴-,12)5设直线AH '解析式为y k x a ''=+ ∴0111255k a k a ''+=⎧⎪⎨''-+=⎪⎩解得:3434k a ⎧'=-⎪⎪⎨⎪'=⎪⎩ ∴直线33:44AH y x '=-+2334423y x y x x ⎧=-+⎪⎨⎪=+-⎩解得:1110x y =⎧⎨=⎩(即点)A ,221545716x y ⎧=-⎪⎪⎨⎪=⎪⎩15(4P ∴-,57)16. 综上所述,点P 的坐标为15(4-或9(4-,39)16-.解法二:在y 轴上取一点T ,是的AT CT =,则ACT TAC ∠=∠, 2ATO TAC ACT ACT ∴∠=∠+∠=∠,设OT t =,则3AT CT t ==-, 在Rt AOT ∆中,则有2221(3)t t +=-, 43t ∴=,即43OT =, ①当P 在y 轴的正半轴上时,过点A 作1AK AT ⊥交y 轴于1K , 由OAT ∆∽△1OK A 得到OK OAOA OT=, 134OK ∴=, 13(0,)4K ∴,∴直线1AK 的解析式为3344y x =-+, 由2334423y x y x x ⎧=-+⎪⎨⎪=+-⎩,解得10x y =⎧⎨=⎩或1545716x y ⎧=-⎪⎪⎨⎪=⎪⎩,即115(4P -,57)16. 当2K 在y 轴的负半轴上时,根据对称性可知23(0,)4K -,∴直线2AK 的解析式为3344y x =-, 由2334423y x y x x ⎧=-⎪⎨⎪=+-⎩,解得10x y =⎧⎨=⎩或943916x y ⎧=-⎪⎪⎨⎪=-⎪⎩,即29(4P -,39)16-.16.在平面直角坐标系中,直线122y x =-与x 轴交于点B ,与y 轴交于点C ,二次函数212y x bx c =++的图象经过B ,C 两点,且与x 轴的负半轴交于点A ,动点D 在直线BC 下方的二次函数图象上. (1)求二次函数的表达式;(2)如图过点D 作DM BC ⊥于点M ,是否存在点D ,使得CDM ∆中的某个角恰好等于ABC ∠的2倍?若存在,直接写出点D 的横坐标;若不存在,请说明理由.【解答】解:(1)把0x =代122y x =-得2y =-, (0,2)C ∴-.把0y =代122y x =-得4x =, (4,0)B ∴,设抛物线的解析式为1(4)()2y x x m =--,将(0,2)C -代入得:22m =-,解得:1m =-,(1,0)A ∴-.∴抛物线的解析式1(4)(1)2y x x =-+,即213222y x x =--. (2)如图所示:过点D 作DR y ⊥垂足为R ,DR 交BC 与点G .(1,0)A -,(4,0)B ,(0,2)C -,AC ∴BC =,5AB =,222AC BC AB ∴+=, ABC ∴∆为直角三角形.取AB 的中点E ,连接CE ,则CE BE =, 2OEC ABC ∴∠=∠. 4tan 3OC OEC OE ∴∠==. 当2MCD ABC ∠=∠时,则1tan tan 2CDR ABC ∠=∠=.设213(,2)22D x x x --,则DR x =,21322CR x x =-+.∴2131222x xx -+=,解得:0x =(舍去)或2x =. ∴点D 的横坐标为2.当2CDM ABC ∠=∠时,设3MD k =,4CM k =,5CD k =. 1tan 2MGD ∠=, 6GM k ∴=,GD =, 2GC MG CM k ∴=-=,GR ∴=,CR =.RD ∴==.∴21322x x CR DR x -+==21129022x x -+=,解得:0x =(舍去)或2911x =. ∴点D 的横坐标为2911. 综上所述,当点D 的横坐标为2或2911.。
【模型导学】细解倍角含半角模型,举例说明其应用

【模型导学】细解倍角含半角模型,举例说明其应用“倍角含半角模型”(也称半角模型),是中考中最常见的题型之一。
因为其内容丰富,变换灵活,所以具有一定的难度。
虽然网络上对于“倍角含半角模型”的文章比较多,但仅仅是对某一具体的模型挖掘的比较透彻——尤其是对“90°含45°模型”挖掘的比较透彻,但对于“倍角含半角模型”的一般情况研究的不多,且对于“倍角含半角模型”和“对角互补模型”之间的关系研究不多。
方法是利器,思想是灵魂。
本文尝试运用“从特殊到一般的思想”和“从一般到特殊思想”来研究下“倍角含半角模型”。
重点研究“倍角含半角模型”的由来及应对策略,以期建立通法通解,并揭示“倍角含半角模型”与“对角互补模型”的关系。
关于“90°含45°半角模型”及“对角互补模型”的相关内容,请大家自己百度,不是本文重点讲述内容。
基本模型一:等腰三角形顶角之半角例1、如图1,已知正△ABC中,BD=CE=2,∠DAE=30°,求DE;解析:如图2,∵△ABC为正三角形,且BD=CE=2,易想到三线合一,作BC边上的高AF,则FB=FD。
设FD=FE=x,则FB=FC=x+2,AB=AC=2x+4,AF=√3(x+2).如果能够建立关于x的方程,即可求解。
显然,此时还不能构造方程——思路受阻!观察到题目中∠DAE=30°还没有用到,显然,∠BAD=∠DAF=∠FAE=∠EAC=15°。
如图3,作DM⊥AB于M,则易证△MAD≌△FAD,则DM=DF。
因为BD=2,∠B=60°,则易知BM=1,则DM=DF=FE=√3,则DE=2√3。
例2、如图4,已知正△ABC中,BD=1,CE=3,∠DAE=30°,求DE;解析:这道题目,由于BD≠EC,大家可以尝试一下,仿照例1的方法好像已经行不同了。
那么我们必须寻找别的思路。
如图5,把△ABD以AD所在直线为对称轴折叠到△ADM的位置,连接ME。
初中数学解题方法:倍半角+解形
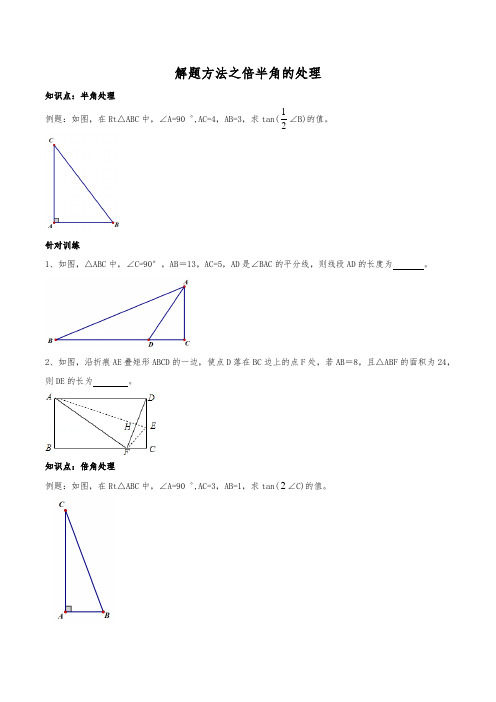
解题方法之倍半角的处理知识点:半角处理例题:如图,在Rt △ABC 中,∠A=90゜,AC=4,AB=3,求tan(21∠B)的值。
针对训练1、如图,△ABC 中,∠C=90°,AB =13,AC=5,AD 是∠BAC 的平分线,则线段AD 的长度为 。
2、如图,沿折痕AE 叠矩形ABCD 的一边,使点D 落在BC 边上的点F 处,若AB =8,且△ABF 的面积为24,则DE 的长为 。
知识点:倍角处理例题:如图,在Rt △ABC 中,∠A=90゜,AC=3,AB=1,求tan(2∠C)的值。
针对训练:如图,点A 、B 、C 在⊙O 上,cos ∠ACB =54,那么tan ∠O 的值为 。
知识点:倍半角与特殊角例题:分别求015tan ,075tan ,05.22tan ,05.67tan ,015cos ,075cos ,015sin ,075sin 的值。
针对训练:在Rt △ABC 中,∠CAB =90°,点D 是边AB 的中点,连接CD ,点E 在边BC 上,且AE ⊥CD 交CD 于点F .当∠ACB =75°时,则的值为 .解题方法之“解形”“解形”:解一个形状固定的三角形的线段,面积,三角函数等等相关属性“解形”分类“SSS”形已知三角形三边,求解三角形的一些属性。
例题:如图,在△ABC中,AC=5,AB=7,BC=8,求①S△ABC;②sin∠A;③∠C针对训练:如图,△BAC放置在正方形网格中,则tan∠BAC的值是。
“SAS”形已知三角形的两边及夹角,求解三角形的一些属性。
方法:锐角特角内部作高,钝角特角外部作高例题:如图,在△ABC中,AB=2,BC=4,∠B=60°,求①S△ABC;②AC;③sin∠C针对训练:已知:如图,△ABC 中,AB =3,∠ABC =120°,BC=2,求AC 的长.“ASA ”形已知两角及其夹边,求解三角形的一些属性。
初中数学半角模型

初中数学半角模型
初中数学半角模型是什么?半角模型是一种通过图形方式表示数学问题的方法。
在半角模型中,我们将数学问题转化为一条直线或一条线段。
这样做的好处是可以更加直观地理解问题,更容易找到解决问题的方法。
在初中数学中,半角模型常用于解决比例、百分数、几何等问题。
例如,我们可以使用半角模型来解决以下问题:某个物品原价为200元,现在打8折出售,售价是多少?我们可以用线段表示原价和折后价,然后通过数学计算找到答案。
另外,半角模型也可以用于解决方程、不等式等问题。
例如,我们可以使用半角模型来解决以下问题:已知一组数的平均值是25,其中最小的数是15,最大的数是35,这组数中共有几个数?我们可以用一条线段表示这组数的范围,然后通过数学计算找到答案。
总之,初中数学半角模型是一种非常实用的工具,能够帮助我们更好地理解和解决数学问题。
- 1 -。
数学中考复习——半角模型

中考复习专题之半角模型
——奏响思维“直通车”之歌
学习目标:
1.在解题过程中提炼解题策略、经验、方法、技巧。
2.在学习过程中树立模型意识,充分关注模型、提炼模型、运用模型、深化模型、实际应用。
3.通过导师引领,小组合作,提高学习效率。
学习过程:
一、提炼模型
正方形ABCD,E、F分别为BC、CD上的点,∠EAF=45°,求证:①EF=BE+DF ②∠AEF=∠AEB,∠AFD=∠AFE; ③△ECF的周长为正方形边长的2倍;④点A到EF的距离等于正方形边长。
解题策略:
二、运用模型
⑤若点E、F分别在CB、DC的延长线上,∠EAF=45°,那么线段EF、
DF、BE之间有怎样的数量关系?
三、深化模型
⑥连接BD交AE于点M,交AF于点N,那么线段DN,MN,BM之间有怎样的数量关系?
变形训练:如图,在Rt△ABD中,AB=AD,M、N是斜边BD上两点,
且∠MAN=45°,你能直接写出BM、MN、DN之间的数量关系吗?
四、中考链接°
此问题的方法是,延长FD到点G,使DG=BE,连结AG,先证明
△ABE≌△ADG,再证明△AEF≌△AGF.可得出结论,他的结论是。
探索延伸:如图2,若在四边形ABCD中,AB=AD,∠B+∠D=180°,E,F分别是BC,CD上的。
(完整版)初中数学——用“倍半角模型”解题事半功倍

用“倍半角模型”解题事半功倍
本文中题目几乎都是在平时教学中学生遇到过的习题,这里笔者介绍一个“倍半角模型”,对每道例题采用“常规解法”及“倍半角解法”,两相比较,让大家体会“倍半角模型”的优势.当然笔者还是强烈建议学生首先会“常规解法”,然后再研究“倍半角解法”,两相结合,能力自会提升,趣味更会无穷!分两部分呈现给大伙!摘要:通过平时教学中遇到过的一些问题,提供其常规解法及“倍半角模型”解法,两相对比,让读者体会“倍半角模型”解题的优势.另外,本文中体现出来的“基于确定性思想的因果关系分析法”是我们解题解决问题的一种重要思考方式与方法.
关键字:一题多解;倍半角模型;确定性思想;因果分析法
首先,一个问题如果是确定性的,那么就注定是可解的.其次,因果法是一种重要的思考问题的方式,“由因导果、执果索因”是分析问题、解决问题的重要途径.下面笔者借助平时教学中遇到过的一些问题,通过常规解法及“倍半角”解法,两相对比,让大家体会“倍半角”解题模型的优势.。
专题1-6 二倍角的解题策略:倍半角模型与绝配角(原卷版)

专题1-6二倍角的解题策略:倍半角模型与绝配角导语:见到2倍角的条件,首先想到“导”,将图形中的角度都推导出来,挖掘出隐藏边的信息,再观察角度的位置,结合其他条件,这里做题的经验,总结了六个字:翻、延、倍、分、导、造目录知识点梳理.............................................................................................................................................................策略一:向外构造等腰(大角减半).........................................................................................................策略二:向内构造等腰(小角加倍或大角减半).....................................................................................策略三:沿直角边翻折半角(小角加倍).................................................................................................策略四:邻二倍角的处理.............................................................................................................................【经典例题讲解】.........................................................................................................................................【一题多解1】围绕2倍角条件,解法围绕“翻” “延” 倍”“分”................................................................【一题多解2】常规法与倍半角处理对比..................................................................................................策略五:绝配角模型.....................................................................................................................................题型一向外构造等腰三角形(大角减半).....................................................................................................2023·深圳南山区联考二模............................................................................................................................2023·山西·统考中考真题..............................................................................................................................题型二向内构造等腰(小角加倍或大角减半) (10)题型三沿直角边翻折半角(小角加倍).........................................................................................................2023·深圳宝安区二模..............................................................................................................................2023·深圳中学联考二模.........................................................................................................................题型四邻二倍角的处理.....................................................................................................................................题型五绝配角.....................................................................................................................................................题型六坐标系中的二倍角问题.........................................................................................................................宿迁·中考........................................................................................................................................................盐城·中考........................................................................................................................................................河南·中考........................................................................................................................................................2023.内蒙古赤峰.统考中考真题 (21)江苏苏州·统考中考真题................................................................................................................................内蒙古鄂尔多斯.统考中考真题....................................................................................................................2022.内蒙古呼和浩特.统考中考真题..........................................................................................................2023.湖北黄冈.统考中考真题......................................................................................................................题型七 其它构造方式. (24)知识点梳理策略一:向外构造等腰(大角减半)已知条件:如图,在△ABC 中,∠ABC =2∠ACB辅助线作法:延长CB 到D ,使BD =BA ,连接AD 结论:AD =AC ,△BDA ∽△ADC策略二:向内构造等腰(小角加倍或大角减半)已知条件:如图,在△ABC 中,∠ABC =2∠B辅助线作法:法一:作∠ABC 的平分线交AC 于点D ,结论:∠DBC =∠C ,DB =DC法二:在BC 上取一点E ,使AE =CE ,则∠AEB =2∠C =∠B (作AC 中垂线得到点E )总结:策略一和策略二都是当2倍角和1倍角共边时对应的构造方法,下面我们再来看看不在同一个三角形中时该如何处理ACACACB D ADBC策略三:沿直角边翻折半角(小角加倍)已知条件:如图,在Rt △ABC 中,∠ACB =90°,点D 为边BC 上一点,连接AD ,∠B =2∠CAD辅助线作法:沿AC 翻折△ACD 得到△ACE结论:AD =AE ,∠DAE =∠B ,BA =BE ,△ADE ∽△BAE策略四:邻二倍角的处理已知条件:如图,在Rt △ABC 中,∠C =90°,点D 为边BC 上一点,∠BAD =2∠CAD辅助线作法:法一:向外构造等腰(导角得相似)延长AD 到E ,使AE =AB ,连接BE ,结论:BD =BE ,∠DBE =∠BAD ,△BDE ∽△ABE法二:作平行线,把二倍角转到同一个三角形中,延长AD 到F ,使CE ∥AB ,则∠F =∠BAD【经典例题讲解】例题1如图,在正方形ABCD 中,AB =1,点E 、F 分别在边BC 和CD 上,AE =AF ,∠EAF =60°,则CF 的长是( )AB C D EA.B.C1-D .23例题2如图,正方形ABCD 的边长为4,点E 是CD 的中点,AF 平分∠BAE ,交BC 于点F ,将△ADE 绕点A 顺时针旋转90°得△ABG ,则CF 的长为 .例题3 如图,面积为24的□ABCD 中,对角线BD 平分∠ABC ,过点D 作DE ⊥BD 交BC 的延长线于点E ,DE =6,则sin ∠DCE 的值为( )例题4 如图,在Rt △ABC 中,∠ACB =90°,AB =10,BC =6,CD ∥AB ,∠ABC 的平分线BD 交AC 于点E ,则DE =_________.总结:具体问题具体对待,并非哪一种方法绝对简单,需根据问题特征选取较为合适的方法.【一题多解1】围绕2倍角条件,解法围绕“翻” “延” 倍”“分”如图,在△ABC 中,∠ABC =2∠ACB ,AB =3,BC =5,求线段AC 的长.(5种解法)M 图17-1-2ABDC EFFEO CD B A图17-1-1图17-2-1图17-2-2AB C DEAB DCG EF图17-2-2AB C DE图17-3-1B ACDE【一题多解2】常规法与倍半角处理对比如图,AB 为⊙O 的直径,BC 、CD 是⊙O 的切线,切点分别为点B 、D ,点E 为线段OB 上的一个动点,连接OD 、CE 、DE ,已知AB =2,BC =2,当CE +DE 的值最小时,则CEDE的值为( )(3种解法)A .910B .23CD 如图,AB 为⊙O 的直径,D 是弧BC 的中点,BC 与AD 、OD 分别交于点E 、F .(1)求证:DO //AC ;(2)求证:2D E D A D C×=(3)若tan 12CAD Ð=,求sin ∠CDA 的值。
倍半角模型经典例题

倍半角模型经典例题倍半角模型是一种数学模型,用于解决涉及倍角和半角的问题。
以下是一些倍半角模型的经典例题:已知sin(x)=1/2,求sin(3x)和sin(x/3)。
已知cos(x)=1/2,求cos(3x)和cos(x/3)。
已知tan(x)=1,求tan(3x)和tan(x/3)。
已知sin(x)=√3/2,求sin(3x)和sin(x/3)。
已知cos(x)=-√3/2,求cos(3x)和cos(x/3)。
已知tan(x)=√3,求tan(3x)和tan(x/3)。
已知sin(x)=1/4,求sin(3x)和sin(x/3)。
已知cos(x)=-1/4,求cos(3x)和cos(x/3)。
已知tan(x)=-1,求tan(3x)和tan(x/3)。
已知sin(x)=-1/4,求sin(3x)和sin(x/3)。
已知sin(x)=1/2,求sin(2x)和sin(x/2)。
已知cos(x)=1/2,求cos(2x)和cos(x/2)。
已知tan(x)=1,求tan(2x)和tan(x/2)。
已知sin(x)=√3/2,求sin(2x)和sin(x/2)。
已知cos(x)=-√3/2,求cos(2x)和cos(x/2)。
已知tan(x)=√3,求tan(2x)和tan(x/2)。
已知sin(x)=1/4,求sin(2x)和sin(x/2)。
已知cos(x)=-1/4,求cos(2x)和cos(x/2)。
已知tan(x)=-1,求tan(2x)和tan(x/2)。
已知sin(x)=-1/4,求sin(2x)和sin(x/2)。
已知cos(x)=-√3/4,求cos(2x)和cos(x/2)。
已知tan(x)=-√3,求tan(2x)和tan(x/2)。
已知sin(x)=-√3/4,求sin(2x)和sin(x/2)。
已知cos(x)=-1/4,求cos(2x)和cos(x/2)。
已知tan(x)=-√3,求tan(2x)和tan(x/2)。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
用“倍半角模型”解题事半功倍
本文中题目几乎都是在平时教学中学生遇到过的习题,这里笔者介绍一个“倍半角模型”,对每道例题采用“常规解法”及“倍半角解法”,两相比较,让大家体会“倍半角模型”的优势.当然笔者还是强烈建议学生首先会“常规解法”,然后再研究“倍半角解法”,两相结合,能力自会提升,趣味更会无穷!分两部分呈现给大伙!摘要:通过平时教学中遇到过的一些问题,提供其常规解法及“倍半角模型”解法,两相对比,让读者体会“倍半角模型”解题的优势.另外,本文中体现出来的“基于确定性思想的因果关系分析法”是我们解题解决问题的一种重要思考方式与方法.
关键字:一题多解;倍半角模型;确定性思想;因果分析法
首先,一个问题如果是确定性的,那么就注定是可解的.其次,因果法是一种重要的思考问题的方式,“由因导果、执果索因”是分析问题、解决问题的重要途径.下面笔者借助平时教学中遇到过的一些问题,通过常规解法及“倍半角”解法,两相对比,让大家体会“倍半角”解题模型的优势.。
