按行按列展开
3 行列式行列式的按行(列)展开

则根据归纳假设得证: Dn ( x 2 x1 )( x 3 x1 )( x n x1 ) ( x i x j )
( x i x j ).
n i j 1
n i j 2
作
业
P26 4(4), 9 补充: 利用范德蒙德行列式计算4阶行列式
1 1 1 1 16 8 2 4 D 81 27 3 9 256 64 4 16
D = ai 1 Ai 1 + ai 2 Ai 2 + = a1 j A1 j + a2 j A2 j + + ain Ain + anj Anj .
i , j 1,2,
, n
推论 行列式中任一行或列的元素与另一行对应元 素的代数余子式乘积之和为零。 ai 1 Aj 1 ai 2 Aj 2 ain Ajn 0, i j
1 1
例2 求解方程
1 x 0. x2
2 3 4 9
解
方程左端
D 3 x 2 4 x 18 9 x 2 x 2 12
x 2 5 x 6,
由 x 2 5 x 6 0 解得
x 2 或 x 3.
推论
行列式中任一行或列的元素与另一行 或列对应元素的代数余子式乘积之和 为零。即
a11 A11 a12 A12 a13 A13 a1 j A1 j
j 1
3
定理4 三阶行列式等于它的任一行或列的各元素 与其代数余子式乘积之和,即
D ai 1 Ai 1 ai 2 Ai 2 ai 3 Ai 3
a1 j A1 j a2 j A2 j a3 j A3 j ( j 1,2, 3)
1.3行列式按行列展开定理
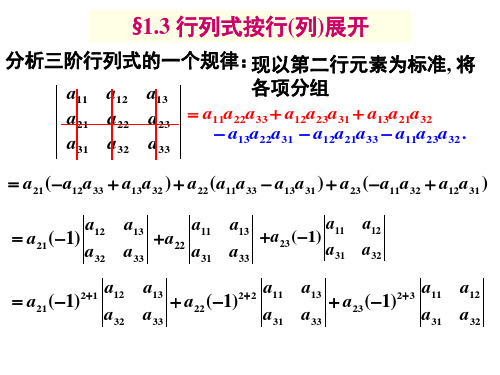
= a21 ( − a12 a33 + a13 a32 ) + a22 (a11a33 − a13 a31 ) + a23 ( − a11a32 + a12 a31 )
= a21 ( −1) a12 a32
2+1
a13 a33
a11 + a22 a31
a11 a12 a13 + a23 ( −1) a31 a32 a33
0 Dn = 0 M 0
x2 − x1 x2 ( x2 − x1 ) M n x2 − 2 ( x2 − x1 )
x3 − x1 x3 ( x3 − x1 )
L L
xn − x1 xn ( xn − x1 )
M M n n x3 − 2 ( x3 − x1 ) L xn − 2 ( xn − x1 )
( j = 1, 2,L , n )
往证 D = ai 1 Ai 1 + ai 2 Ai 2 + L + ain Ain (∗) 证明思路: 证明思路 式两端所含项数相同, ① (*)式两端所含项数相同 并且各项互不相同 式两端所含项数相同 并且各项互不相同; 每一项都是D中的项 并且带有相同的符号. 中的项, ② 右端 aij Aij 每一项都是 中的项 并且带有相同的符号 a11 L a1 j −1 a1 j +1 L a1n
M M ij = M M M ai −11 L ai −1 j −1 ai +11 L ai +1 j −1 M a n1 M L anj −1 ai −1 j + 1 L ai −1 n ai + 1 j + 1 L ai + 1 n M anj +1 L M ann
行列式依行(列)展开

适用于小规模行列
式
行列式依行(列)展开适用于小规模 的行列式计算,对于大规模的行 列式计算可能效率较低。
不适用于特殊行列
式
对于一些特殊类型的行列式,如 奇异值分解的行列式,行列式依 行(列)展开可能不适用。
注意计算复杂度
行列式依行(列)展开的计算复杂度 较高,对于大规模的行列式计算 需要采用更高效的算法。
05
行列式依行(列)展开的注 意事项
计算精度问题
保持计算精度
在行列式展开过程中,需要注 意保持计算精度,避免因为舍
入误差导致结果不准确。
选择合适的数学软件
使用数学软件进行行列式展开 时,应选择具有高精度运算能
力的软件,如Matlab、 Python的NumPy库等。
避免大数运算
在行列式展开过程中,尽量避 免大数运算,以免造成精度损
在矩阵运算中的应用
矩阵的逆运算
行列式依行(列)展开可以用于计算矩阵的逆,通过求行列式和代 数余子式来计算逆矩阵。
矩阵的行列式
行列式依行(列)展开是计算矩阵行列式的基础,通过展开可以求 得矩阵的行列式值。
矩阵的秩
行列式依行(列)展开可以用于计算矩阵的秩,通过展开可以判断 矩阵是否可逆,从而确定其秩。
其中,$A_{11}$是第一行第一列元素的代数余子 式,$A_{21}$是第二行第一列元素的代数余子式 ,$A_{31}$是第三行第一列元素的代数余子式。
其中,$A_{11}$是第一行第一列元素的代数余子 式,$A_{21}$是第二行第一列元素的代数余子式 ,$A_{31}$是第三行第一列元素的代数余子式, $A_{41}$是第四行第一列元素的代数余子式。
失。
符号使用规范
统一符号体系
§6 行列式按行(列)展开

i 1,2,, n i 1,2,, n
a1 n
证
a11
a12
D a i 1 0 0 0 a i 2 0 0 0 a in a n1
即有 D a11 M11 .
A11 1
11
又
从而
M 11 M 11 ,
D a11 A11 .
在证一般情形, 此时
© 2009, Henan Polytechnic University §6 行列式按行(列)展开
6 6
第一章 行列式
a11 a1 j a1n 0 D 0 aij ij an1 anj ann
© 2009, Henan Polytechnic University §6 行列式按行(列)展开
1515
第一章 行列式
例2
3
1
1 3 1 3 5
2 4 1 3 1 1 0 5 1 3 1 3 1 1 0 0
1616
5 1 D 2 0 1 5
c1 2c3 11
第一章 行列式
在n阶行列式中, 把元素a ij所在的第i行和第j列划去后,
留下来的n-1阶行列式叫做元素 a ij的余子式,记作 M ij . 记
Aij 1
i j
M ij,
叫做元素 a ij 的代数余子式.
a11 a 21 例如 D a 31 a 41
A23 1
2 3
© 2009, Henan Polytechnic University §6 行列式按行(列)展开
8 8
第一章 第3节 按行(列)展开定理 (1)

克莱姆法则亦可叙述为 如果线性方程组的系数行列式|A|≠ 则方 定理 : 如果线性方程组的系数行列式 ≠0,则方 程组一定有解,且解是唯一的 程组一定有解 且解是唯一的。 且解是唯一 定义:当方程组右边的常数项全部为零时, 定义:当方程组右边的常数项全部为零时,方程 组变为齐次线性方程组 组变为齐次线性方程组
了解定理的证明
证:写成矩阵方程A ⋅ x = b → x = A ⋅ b
A可逆
x1 A11 A21 L An1 b1 x A A22 L An2 b2 1 12 2 = M det A M M M M xn A1n A2n L Ann bn
−1
1 ∴ xj = (b1A1 j + b2 A2 j + L+ bnAnj ) det A = det Aj (b) det A (1 ≤ j ≤ n)
练习: 练习 解线性方程组
2 x1 + x2 − 5 x3 + x4 = 8, x − 3x − 6 x4 = 9, 1 2 2 x2 − x3 + 2 x4 = −5, x1 + 4 x2 − 7 x3 + 6 x4 = 0.
当系数矩阵可逆时,有惟一解: 系数矩阵可逆时 惟一解:
xj =
det Aj (b) det A
(1 ≤ j ≤ n)
T
其中Aj (b):A的第j列换成b = (b1 , b2 ,L, bn ) 后的矩阵
a11 a12 L a1n a21 a22 L a2n A= M M M an1 an2 L ann
定理: 定理
如果齐次线性方程组的系数行列式不等于零, 如果齐次线性方程组的系数行列式不等于零
矩阵按行按列展开公式(一)

矩阵按行按列展开公式(一)矩阵按行按列展开公式什么是矩阵按行按列展开公式矩阵按行按列展开公式指的是将一个矩阵按照行或列的方式展开成一个一维的向量。
这种展开方式在线性代数、矩阵计算、矩阵求导等领域有着重要应用。
矩阵按行展开公式矩阵按行展开公式表示将一个矩阵按照行的方式展开成一个一维的向量。
展开的顺序是从矩阵的第一行开始,按照从左到右的顺序展开,直到最后一行结束。
矩阵按行展开公式可以用下面的数学公式表示:A=[a11a12⋯a1n a21a22⋯a2n ⋮⋮⋱⋮a m1a m2⋯a mn]→[a11,a12,⋯,a1n,a21,a22,⋯,a2n,⋯,a m1,a m2,⋯,a mn]其中,A表示待展开的矩阵,a ij表示矩阵中的元素。
矩阵按列展开公式矩阵按列展开公式表示将一个矩阵按照列的方式展开成一个一维的向量。
展开的顺序是从矩阵的第一列开始,按照从上到下的顺序展开,直到最后一列结束。
矩阵按列展开公式可以用下面的数学公式表示:A=[a11a12⋯a1n a21a22⋯a2n ⋮⋮⋱⋮a m1a m2⋯a mn]→[a11,a21,⋯,a m1,a12,a22,⋯,a m2,⋯,a1n,a2n,⋯,a mn]其中,A表示待展开的矩阵,a ij表示矩阵中的元素。
矩阵按行按列展开公式的应用举例例子1:按行展开考虑一个3x3的矩阵A:A=[123 456 789]按行展开后的结果为:A row=[1,2,3,4,5,6,7,8,9]例子2:按列展开考虑一个3x3的矩阵A:A=[123 456 789]按列展开后的结果为:A column=[1,4,7,2,5,8,3,6,9]总结矩阵按行按列展开公式是将一个矩阵按照行或列的方式展开成一个一维的向量的数学公式。
按行展开从矩阵的第一行开始,按照从左到右的顺序展开;按列展开从矩阵的第一列开始,按照从上到下的顺序展开。
这种展开方式在矩阵计算和求导等领域有着重要应用。
行列式的展开法则

03. 行列式的展开法则 一、按一行(列)展开法则定义3.1 (,)i j 元素或(,)i j 位置的余子式ij M 、代数余子式(1)i j ij ij A M +=- 例3.1 3111112121313111112121313||ij a a M a M a M a A a A a A =-+=++. 定理3.1 1)按一行展开法则 1122||(1,2,,)A i i i i in in a A a A a A i n =+++= ; 2)按一列展开法则 1122||(1,2,,)A j j j j nj nj a A a A a A j n =+++= . 按第一行的展开公式就是n 阶行列式(2)n ≥的降阶定义. 例3.2 计算下列n 阶行列式1)xy x yyx; 2)111111121n n----; 3)121111n n na a xD a xa x---=-.解 1)按1c 展开得原式1111111(1)(1)n n n n n n n xA yA xxy y x y -+-+=+=+-=+-. 2)原式121(1)(12)2n n nn n c c c c n n n A c -++++++++=按展开. 3)法1 按1r 展开得()112112121223121211(,,,)(,,)(,,).()n n n n n n n n n n n n n n n D a a a a x D a a a x a x D a a a x a x a x a D a a --------=+=++==++++=法2 在n D 中,元素(21)i a i n ≤≤-的余子式为11111(1)11i n i i x x M x x x x-----==---.将n D 按1c 展开得11211211(1)ni n n n i i n n i D a M a x a x a x a +---==-=++++∑ .法3 1121212112121101,1,,210i i nn n n n n n na a x a r xr D i n n a x a x a a x a x a x a --------+-+=-+++-++++12121n n n n a x a x a x a ---=++++ . ()11111(1)(1)(1)1n n n n n A M ++-=-=--=法4 按n r 展开得111212121.n n n nn n n n n n n n n n D a A xA a xD a a x xD a x a x a x a ------=+=+=++==++++定理3.2 当i j ≠时, 11220i j i j in jn a A a A a A +++= ;11220i j i j ni nj a A a A a A +++= . 注 1122||A i j i j in jn ij a A a A a A +++= δ, 1122||A i j i j ni nj ij a A a A a A +++= δ,其中1,;0,ij i j i j=⎧=⎨≠⎩当当δ为克罗内克(Kronecker )符号.例3.3 1)二元(实)函数1,;(,)0,.x y f x y x y =⎧=⎨≠⎩当当 显然(,)xy f x y =δ.2)diag(1,1,,1)[]ij n n ⨯= δ.例3.4 设四阶行列式1212211220211234D =. 1)求代数余子式12A ; 2)求1121314123A A A A +++; 3)求41424344A A A A +++.行列式的完全展开定义、公理化定义、降阶定义可以互相推证. 以降阶定义为原始定义做理论推导时,可以引入仿克罗内克符号1,;0,.ij i j i j <⎧=⎨>⎩当当ρ 例3.5 1)若正整数i j ≠,则1.ij ji +=ρρ2)仿克罗内克符号有缺项定位功能. 在序列124567,,,,,a a a a a a 中,(17,3)i a i i ≤≤≠位于第3i i -ρ位. 在序列12467,,,,a a a a a中,(17,3,5)i a i i ≤≤≠位于第35i i i --ρρ位.3)仿克罗内克符号有描述逆序功能.s t j j 构成逆序01s t t s j j j j ⇔=⇔=ρρ,121()t sn j j s t nj j j ≤<≤=∑τρ.例3.6 n 阶范德蒙(Vandermonde )矩阵1[]i j n n a -⨯的行列式122131121(,,,)()()()(,,)().n n n j i i j nV a a a a a a a a a V a a a a ≤<≤=---=-∏例3.7 填空11112345_____49162582764125----=----.例3.8 设0abcd ≠,求证222211(,,,)11a a bcd b b acdV a b c d c c abd d d abc=-.例3.9 计算n 阶三对角行列式111n a b ab a b ab D a b aba b++=++ .二、按多行(列)展开法则定义3.2 矩阵A m n ⨯的k l ⨯子矩阵1212A k l i i i j j j ⎛⎫ ⎪⎝⎭ 及其余子阵,k 阶子方阵、k 阶子式;n 阶方阵或其行列式中k 阶子式的n k -阶余子式M 、代数余子式1212()()(1)k k i i i j j j A M +++++++=- ,k 阶(顺序)主子阵、k 阶(顺序)主子式. 主子式的代数余子式就是余子式.例3.10 设55[]A ij a ⨯=.1)25135A ⎛⎫⎪⎝⎭是A 的一个23⨯子矩阵,13424A ⎛⎫⎪⎝⎭为其余子阵;2)1325A ⎛⎫⎪⎝⎭是A 的一个2阶子方阵,1325A ⎛⎫ ⎪⎝⎭是A 的一个2阶子式,245134A ⎛⎫⎪⎝⎭为对应余子式,而对应代数余子式为(13)(25)245245(1)134134A A +++⎛⎫⎛⎫-=- ⎪ ⎪⎝⎭⎝⎭;3)235235A ⎛⎫ ⎪⎝⎭是A 的一个3阶主子阵,235235A ⎛⎫⎪⎝⎭是A 的一个3阶主子式,其代数余子式就是余子式1414A ⎛⎫⎪⎝⎭,是A 的一个2阶主子式;4)A 共有五个顺序主子阵(式).定理3.3 按多行(列)展开法则——拉普拉斯(Laplace )定理1122C C ||A k k nnN A N A N A =+++ .例3.11 计算四阶行列式1234500112365112D -=--.例3.12 计算六阶行列式111000234000310161111101112411243161139D =---.例3.13 计算六阶行列式120000350000635475124583240064270034D -=-.例3.14 计算叉形行列式1)11211n n n nna b a b D c d c d =;2)112111nn n nna b a b D e c d c d +=.。
行列式的展开法则

03. 行列式的展开法则 一、按一行(列)展开法则定义3.1 (,)i j 元素或(,)i j 位置的余子式ij M 、代数余子式(1)i j ij ij A M +=- 例3.1 3111112121313111112121313||ij a a M a M a M a A a A a A =-+=++. 定理3.1 1)按一行展开法则1122||(1,2,,)A i i i i in in a A a A a A i n =+++=L L ; 2)按一列展开法则1122||(1,2,,)A j j j j nj nj a A a A a A j n =+++=L L . 按第一行的展开公式就是n 阶行列式(2)n ≥的降阶定义. 例3.2 计算下列n 阶行列式1)xy x y yxO O; 2)111111121n n----O OL ; 3)121111n n n a a x D a x a x---=-M O O .解 1)按1c 展开得原式1111111(1)(1)n n n n n nn xA yA xx y y x y -+-+=+=+-=+-.2)原式121(1)(12)2n n nn n c c c c n n n A c -++++++++=L L 按展开. 3)法1 按1r 展开得法2 在n D 中,元素(21)i a i n ≤≤-的余子式为11111(1)11i n i i x xM x x xx-----==---O OO O. 将n D 按1c 展开得11211211(1)ni n n n i i n n i D a M a x a x a x a +---==-=++++∑L .法3 1121212112121101,1,,210i i nn n n n n n na a x a r xr D i n n a x a x a a x a x a x a --------+-+=-+++-++++M O OL L L12121n n n n a x a x a x a ---=++++L . ()11111(1)(1)(1)1n n n n n A M ++-=-=--=法4 按n r 展开得 定理3.2 当i j ≠时,11220i j i j in jn a A a A a A +++=L ;11220i j i j ni nj a A a A a A +++=L . 注 1122||A i j i j in jn ij a A a A a A +++=L δ, 1122||A i j i j ni nj ij a A a A a A +++=L δ,其中为克罗内克(Kronecker )符号.例3.3 1)二元(实)函数显然(,)xy f x y =δ. 2)diag(1,1,,1)[]ij n n ⨯=L δ.例3.4 设四阶行列式1212211220211234D =.1)求代数余子式12A ; 2)求1121314123A A A A +++; 3)求41424344A A A A +++.行列式的完全展开定义、公理化定义、降阶定义可以互相推证. 以降阶定义为原始定义做理论推导时,可以引入仿克罗内克符号例3.5 1)若正整数i j ≠,则2)仿克罗内克符号有缺项定位功能. 在序列 中,(17,3)i a i i ≤≤≠位于第3i i -ρ位. 在序列 中,(17,3,5)i a i i ≤≤≠位于第35i i i --ρρ位.3)仿克罗内克符号有描述逆序功能.s t j j 构成逆序01s t t s j j j j ⇔=⇔=ρρ,121()t sn j j s t nj j j ≤<≤=∑L τρ.例3.6 n 阶范德蒙(Vandermonde )矩阵1[]i j n n a -⨯的行列式例3.7 填空11112345_____49162582764125----=----.例3.8 设0abcd ≠,求证222211(,,,)11a a bcdbb acdV a b c d c c abd d d abc=-.例3.9 计算n 阶三对角行列式111n a b ab a b ab D a b aba b++=++O OO .二、按多行(列)展开法则定义3.2 矩阵A m n ⨯的k l ⨯子矩阵1212A k l i i i j j j ⎛⎫⎪⎝⎭L L 及其余子阵,k 阶子方阵、k 阶子式;n 阶方阵或其行列式中k 阶子式的n k -阶余子式M 、代数余子式1212()()(1)k k i i i j j j A M +++++++=-L L ,k 阶(顺序)主子阵、k 阶(顺序)主子式. 主子式的代数余子式就是余子式.例3.10 设55[]A ij a ⨯=.1)25135A ⎛⎫⎪⎝⎭是A 的一个23⨯子矩阵,13424A ⎛⎫⎪⎝⎭为其余子阵; 2)1325A ⎛⎫⎪⎝⎭是A 的一个2阶子方阵,1325A ⎛⎫ ⎪⎝⎭是A 的一个2阶子式,245134A ⎛⎫ ⎪⎝⎭为对应余子式,而对应代数余子式为(13)(25)245245(1)134134A A +++⎛⎫⎛⎫-=- ⎪ ⎪⎝⎭⎝⎭;3)235235A ⎛⎫⎪⎝⎭是A 的一个3阶主子阵,235235A ⎛⎫ ⎪⎝⎭是A 的一个3阶主子式,其代数余子式就是余子式1414A ⎛⎫⎪⎝⎭,是A 的一个2阶主子式;4)A 共有五个顺序主子阵(式).定理3.3 按多行(列)展开法则——拉普拉斯(Laplace )定理1122C C ||A k k nnN A N A N A =+++L .例3.11 计算四阶行列式1234500112365112D -=--.例3.12 计算六阶行列式111000234000310161111101112411243161139D =---.例3.13 计算六阶行列式120000350000635475124583240064270034D -=-.例3.14 计算叉形行列式1)11211n n n nna b a b D c d c d =ONN O;2)112111nn n nna b a b D e c d c d +=ONN O.。
行列式按行列展开定理讲解学习

行列式按行列展开定理行列式按行列展开定理一、 余子式的定义:在n 阶行列式中,把(i.j )元ij a 所在的第i 行,第j 列去掉之后,留下来的n-1阶行列式称作ij a 的余子式,记作ij M二、 代数余子式:在n 阶行列式的ij a 余子式ij M 加上符号(1)i j +-,称作ij a 的代数余子式ij A : (1)i j ij ij A M +=-三、 引理1:一个n 阶行列式,如果其中的第i 行所有元素除了(i,j )元ija 外都为0,则这个行列式等于ij a 与它的代数余子式乘积:ij ij D a A =⋅四、 行列式按行(列)展开法则:定理3:行列式等于它的任一行(列)的各个元素与其对应的代数余子式的乘积之和:1122i i i i in in D a A a A a A =⋅+⋅+⋅⋅⋅+⋅1122j j j j nj nj D a A a A a A =⋅+⋅+⋅⋅⋅+⋅ (i j ≠)推论:行列式某一行(列)的元素与对应的另一行(列)元素的代数余子式乘积之和等于0:1122i j i j in jn D a A a A a A =⋅+⋅+⋅⋅⋅+⋅1122i j i j ni nj D a A a A a A =⋅+⋅+⋅⋅⋅+⋅ (i j ≠)五、 克拉默法则:如果含有n 个未知数的n 个线性方程组:11112211n n a x a x a x b ++⋅⋅⋅+=21122222n n a x a x a x b ++⋅⋅⋅+=31132233n n a x a x a x b ++⋅⋅⋅+=………………………………………………………………………………………………………1122n n nn n n a x a x a x b ++⋅⋅⋅+=其系数行列式不等于0,即:1111............0...nn nna a D a a =≠ 那么,方程组有惟一解:11D x D =,22D x D =,…n N D x D= 1111,1122,11,1......................j nj j n n n j nn a b a a b a D a b a a +++=① 定理4:如果含n 个未知数的n 个线性方程组的系数行列式不等于0,则方程一定有解,且解是惟一的。
行列式按一行(列)展开

证明过程
• 利用归纳假设和余子式的性质,证明$D_{n+1}$ 可以按第$n+1$行(或第$n+1$列)展开。
证明过程
3. 结论
通过数学归纳法,证明了行列式可以按任意一行(或列)展开。
04
Байду номын сангаас行列式按一行(列)展开的 实例
实例一:二阶行列式
定义
01
二阶行列式表示为$|begin{matrix} a & b c & d
行列式按一行(列)展 开
目录
• 行列式按一行(列)展开的定义 • 行列式按一行(列)展开的公式 • 行列式按一行(列)展开的证明
目录
• 行列式按一行(列)展开的实例 • 行列式按一行(列)展开的应用
01
行列式按一行(列)展开的 定义
定义与性质
定义
行列式按某一行(或列)展开,是指 将该行列式拆分成若干个二阶子行列 式之和。
• 应用:用于计算高维向量的外积和混合积,以及解决线性方程组等数学问题。
05
行列式按一行(列)展开的 应用
在线性代数中的应用
计算行列式的值
行列式按一行或一列展开,可以方便地计算行列式的 值。
矩阵的逆运算
行列式按一行或一列展开,可以用于计算矩阵的逆运 算。
线性方程组的求解
行列式按一行或一列展开,可以用于求解线性方程组。
数值分析
行列式按一行或一列展开,可以用于数值分析中的矩阵运算和数值逼近。
THANKS
感谢观看
3. 将上述求和结果作 为分子,分母保持不 变,得到按选定行 (或列)展开后的行 列式。
02
行列式按一行(列)展开的 公式
展开公式
线性代数03-行列式按行(列)展开

1
3 4 c1 2c3 11
1
3 1
2 0 1 1 c4 c3
0010
1 5 3 3
5 5 3 0
511 (1)33 11 1 1
5 5 0
r2 r1
5 11 6 2 0 5 5 0
(1)13 6 2 40. 5 5
说明
定理3叫做行列式按行(列)展开法则, 利用这个法则降阶并结合行列式的性质, 可以简化行列式的计算.
思考 任意一个行列式是否都可以用较低阶的行列式表示?
在n 阶行列式中,把元素 aij 所在的第 i 行和第 j 列划去后,
留下来的n-1阶行列式叫做元素 aij 的余子式,记作Mij .
把 Aij 1 i j Mij 元素 aij 的代数余子式.
例如
a11 a12 a13 a14
D a21 a22 a23 a24 a31 a32 a33 a34
a41 a42 a43 a44
a11 a12 a14 M23 a31 a32 a34
a41 a42 a44
A23 1 23 M23 M23
结论 行标和列标是行列式中元素的唯一标识,有且仅有一 个余子式和一个代数余子式与行列式中每一个元素对应.
说明
(1)对于给定的 n 阶行列式 D det(aij ) ,元素
证明 我们以3阶行列式为例.
a11 a12 a13 a11 A11 a12 A12 a13 A13 a21 a22 a23
a31 a32 a33
把第1行的元素换成第2行的对应元素,则
a21 a22 a23
a21 A11 a22 A12 a23 A13 a21 a22 a23 0.
行列式按行按列展开

... a1n ... ... ... 0 . ... ... ... ann
把D转化为(1)的情形
· · · · · , 把 D 的第 i 行依次与第 i 1 行,第 i 2 行,·
第2行,第1行交换;再将第 j 列依次与第 j 1 列, 第 j 2 列,· · · · · · , 第2列,第1列交换,这样共经过
an ( 1)n 1 1 0 x 1 0 x 0 0 0 0 0 0 0 0 x 1
Dn x 0 an 1
x
an 2 a2
于是,得递推公式
Dn xDn1 an
而由递推公式,得
继续递推公式,得
Dn1 xDn 2 an1 D1 x a1
(1) ( j2 j3 ... jn ) a2 j2 a3 j3 ...anjn 恰是 M 11 的一般项。
D a11 M11
a11 (1)11 M11
a11 A11
13
(2) 设 D 的第 i 行除了 aij 外都是 0 。
a11 ... a1 j ... D 0 ... an1 ... ... ... aij ... ... ... anj
... ... ... an 2 ... ann
12
由行列式定义,D 中仅含下面形式的项
D
a11 (1) (1 j2 j3 ... jn ) a2 j2 a3 j3 ...anjn
其中 所以,
1 j2 j3 ... jn
(1) (1 j2 j3 ... jn ) a11a2 j2 a3 j3 ...anjn
... ai 1, j 1 ... ai 1,n
(1)i j aij Mij aij Aij
线性代数1.6行列式按行(列)展开

感谢您的观看
THANKS
某一行(列)的元素与另一行(列)的对应元素的代数余子式乘积之和等于零。即
$D = a_{i1}A_{ j1} + a_{i2}A_{ j2} + ldots + a_{in}A_{ jn} = 0$,其中 $i neq j$。
行列式等于它的任一行(列)的各元素与其对应的代数余子式乘积之和。即
$D = a_{i1}A_{i1} + a_{i2}A_{i2} + ldots + a_{in}A_{in}$ 或 $D = a_{1j}A_{1j} + a_{2j}A_{2j} + ldots + a_{nj}A_{nj}$。
行列式按行(列)展开的性质二
行列式中某一行(列)的所有元素都 乘以同一数 $k$,等于用数 $k$ 乘此 行列式。即:$D_1 = kD$。
行列式中如果有两行(列)元素成比 例,则此行列式等于零。
行列式按行(列)展开的性质三
若行列式中某一行(列)的所有元素 都是两数之和,则这个行列式可以拆 分为两个行列式的和,这两个行列式 分别由这两组数构成。
01
02
行列式是一个数值,由方阵中所 有元素的代数和计算得出。
03
行列式具有交换性质,即交换行 列式中两行(列)的位置,行列 式的值变号。
04
行列式按行(列)展开的意义
行列式按行(列)展开是计算行列式的 一种重要方法,特别是当行列式的阶数 较高时,直接计算往往比较困难,而按 行(列)展开可以简化计算过程。
行列式按行展开的步骤
01
1. 选择要展开的行(或列)。
02 2. 划去该元素所在的行和列,得到余子式。
03
行列式按行(列)展开

D=
a11 a12 a13 a14 a21 a22 a23 a24 0 0 a33 0 a41 a42 a43 a44
= ( −1)
3+3
a11 a12
a14
a33 a21 a22 a24 . a41 a42 a44
§6
行列式按行( 行列式按行(列)展开
定理3 行列式等于它的任一行(列)的各元素与其对应的 定理3 代数余子式乘积之和, 即 D= ai1 Ai1+ ai2 Ai2 +· · · + ain Ain 或 D= a1j A1j+ a2j A2j+· · · + anj Anj
§6
行列式按行( 行列式按行(列)展开
1 1 x3 ⋮
n x3 − 2
把每列的公因子(xi-x1)提出,就有
⋯ ⋯ ⋯ 1 xn ⋮
n xn − 2
x2 Dn = ( x 2 − x1 )( x3 − x1 ) ⋯ ( xn − x1 ) ⋮
n x2 − 2
= ( x2 − x1 )( x3 − x1 ) ⋯ ( x n − x1 ) =
1 xn
(1)
n n x1n−1 x2 −1 ⋯ xn −1
∏ 其中记号“
”表示全体同类因子的乘积.
§6
行列式按行( 行列式按行(列)展开
1 1
证 用数学归纳法.
D2 = = x2 − x2 =
x1 x2
2≥i > j ≥1
∏ (x − x ),
i j
所以当n=2时(1) 式成立. 现在假设(1) 式对于n-1阶范德蒙德行列式成 立, 要证(1) 式对于n阶范德蒙德行列式也成立.
§6
行列式按行(列)展开

b
0 M M M
0 a M + b(−1)1+2n M M M 0 c
2( n−1)
b O a c N b d O d N
M c d 0 0 L L L L 0 d 14442 443 4 4 4
2( n−1)
c 0 L L L L 0 1 442 443 4 4 4 4
上页
下页
返回
= adD2( n−1) − bc(−1)2n−1+1 D2( n−1)
上式右端行列式中有两行对应元素相等, 当 i ≠ j 时,上式右端行列式中有两行对应元素相等, 故行列式为 0 ,即得
= an − an−2 = an−2 (a2 − 1).
上页
下页
返回
由定理3 可得下列推论: 由定理 可得下列推论: 行列式任一行( 推论 行列式任一行(列)的元素与另一行 的对应元素的代数余子式乘积之和等于零。 (列)的对应元素的代数余子式乘积之和等于零。 即
ai1 Aj1 + ai 2 Aj 2 + L+ ain Ajn = 0, i ≠ j,
A32 = (−1)3+2 M32 = − M32 .
上页 下页 返回
阶行列式, 引理 一个 n 阶行列式,如果其中第 i 行所有 元素除 aij 外都为 0 ,那么这个行列式等于aij 与它 的代数余子式的乘积, 的代数余子式的乘积,即
D = aij Aij
证 先证aij 位于第 1 行、第 1 列的情形,此时 列的情形,
阶行列式中, 在 n 阶行列式中,把元素 aij 所在的第 i 行和 列的元素划去, 第 j 列的元素划去,留下来的 n-1 阶行列式叫做 元素 aij 的余子式,记作 Mij ; 余子式, 记 Aij =(-1)i+j Mij , - Aij 称为元素 aij 的代数余子式。 代数余子式。
行列式按行(列)展开定理

证 由定理1,行列式等于某一行的元素分别与它们 代数余子式的乘积之和.
10
a11
a12
a1n
ai1
ai2
a in
在行列式 D
ak1
ak 2
a kn
an1
3 1 1 2
5 1
例2 计算行列式 D
20
3 4 .
1 1
1 5 3 3 14
3 1 1 2
解
5 D
1
20
3 4 1 1
1 5 3 3
c1 2 c3 c4 c3
5 1 1 1 11 1 3 1
0 010 5 5 3 0
15
5 11
5 11
(1)33 11
1
1 r2 r1 6
2
0
5 5 0
的代数余子式.
a11 a12 a13 a14
例如
a21 a22 a23 a24 D
a31 a32 a33 a34
a41 a42 a43 a44
3
a11 a12 a14
M23 a31 a32 a34 a23 的余子式.
a41 a42 a44
A23
1
M 2 3 23
M23
a23 的代数余子式.
an
0
b 0
0
0
0 b
0
0
00
b
[(a1 a2 an ) b](b)n1
32
例9 x1 a a a
a x2 a a
D a
a
x3
行列式性质,按行展开

a11 L = bi 1 L an1
a12 L a1n L L L
a11
a12 L a1n L ci 2 L an 2 L L L L L cin L ann
L bi 2 L bin + ci 1 L L L L an1 an 2 L ann
性质5 将行列式的某一行 列)的所有元素乘以数 后 将行列式的某一行(列 的所有元素乘以数 的所有元素乘以数k后
1
2 0
3 1
4 2 .
【例1】 计算 D = 】
1
3 −1 −1 0 1 2 0 −5
【解】 D = a14 A14 + a24 A24 + a34 A34 + a44 A44
1 2 3 1 0 1 1+ 4 + 2 × ( −1) 2 + 4 3 − 1 − 1 = 4 × ( −1) 3 − 1 − 1 1 2 0 1 2 0 1 2 3 + ( −5) × ( −1)4 + 4 1 0 1 3 −1 −1
【解】
1 −1 0
2
1
1
0
(1) + (3) 0 −1 −1 2 0 −1 −1 2 − D=− − 2×(1) + (4) 0 1 −1 2 −1 2 −1 0 0 3 1 −4
2 1 1 0
1 0
0 0
2
1
−1
0
2
( 2) + ( 3 ) 3 × ( 2) + ( 4) −
−1 −1
0 0
0 −1
加到另一行( 加到另一行(列)的相应元素上,行列式的值不变. 的相应元素上,行列式的值不变
1 a 1
行列式的展开法则

03. 行列式的展开法则 一、按一行(列)展开法则定义3.1 (,)i j 元素或(,)i j 位置的余子式ij M 、代数余子式(1)i j ij ij A M +=- 例3.1 3111112121313111112121313||ij a a M a M a M a A a A a A =-+=++. 定理3.1 1)按一行展开法则1122||(1,2,,)A i i i i in in a A a A a A i n =+++=L L ; 2)按一列展开法则1122||(1,2,,)A j j j j nj nj a A a A a A j n =+++=L L . 按第一行的展开公式就是n 阶行列式(2)n ≥的降阶定义. 例3.2 计算下列n 阶行列式1)xy x y yxO O; 2)111111121n n----O OL ; 3)121111n n n a a x D a x a x---=-M O O .解 1)按1c 展开得原式1111111(1)(1)n n n n n nn xA yA xx y y x y -+-+=+=+-=+-.2)原式121(1)(12)2n n nn n c c c c n n n A c -++++++++=L L 按展开. 3)法1 按1r 展开得()112112121223121211(,,,)(,,)(,,).()n n n n n n n n n n n n n n n D a a a a x D a a a x a x D a a a x a x a x a D a a --------=+=++==++++=L L L LL法2 在n D 中,元素(21)i a i n ≤≤-的余子式为11111(1)11i n i i x xM x x xx-----==---O OO O. 将n D 按1c 展开得11211211(1)ni n n n i i n n i D a M a x a x a x a +---==-=++++∑L .法3 1121212112121101,1,,210i i nn n n n n n na a x a r xr D i n n a x a x a a x a x a x a --------+-+=-+++-++++M O OL L L12121n n n n a x a x a x a ---=++++L . ()11111(1)(1)(1)1n n n n n A M ++-=-=--=法4 按n r 展开得111212121.n n n nn n n n n n n n n n D a A xA a xD a a x xD a x a x a x a ------=+=+=++==++++L L定理3.2 当i j ≠时,11220i j i j in jn a A a A a A +++=L ;11220i j i j ni nj a A a A a A +++=L . 注 1122||A i j i j in jn ij a A a A a A +++=L δ, 1122||A i j i j ni nj ij a A a A a A +++=L δ,其中1,;0,ij i j i j=⎧=⎨≠⎩当当δ为克罗内克(Kronecker )符号.例3.3 1)二元(实)函数1,;(,)0,.x y f x y x y =⎧=⎨≠⎩当当 显然(,)xy f x y =δ.2)diag(1,1,,1)[]ij n n ⨯=L δ.例3.4 设四阶行列式1212211220211234D =.1)求代数余子式12A ; 2)求1121314123A A A A +++; 3)求41424344A A A A +++.行列式的完全展开定义、公理化定义、降阶定义可以互相推证. 以降阶定义为原始定义做理论推导时,可以引入仿克罗内克符号1,;0,.ij i j i j <⎧=⎨>⎩当当ρ 例3.5 1)若正整数i j ≠,则1.ij ji +=ρρ2)仿克罗内克符号有缺项定位功能. 在序列124567,,,,,a a a a a a 中,(17,3)i a i i ≤≤≠位于第3i i -ρ位. 在序列12467,,,,a a a a a中,(17,3,5)i a i i ≤≤≠位于第35i i i --ρρ位.3)仿克罗内克符号有描述逆序功能.s t j j 构成逆序01s t t s j j j j ⇔=⇔=ρρ,121()t sn j j s t nj j j ≤<≤=∑L τρ.例3.6 n 阶范德蒙(Vandermonde )矩阵1[]i j n n a -⨯的行列式122131121(,,,)()()()(,,)().n n n j i i j nV a a a a a a a a a V a a a a ≤<≤=---=-∏L L L例3.7 填空11112345_____49162582764125----=----.例3.8 设0abcd ≠,求证222211(,,,)11a a bcdbb acdV a b c d c c abd d d abc=-.例3.9 计算n 阶三对角行列式111n a b ab a b abD a b aba b++=++O O O. 二、按多行(列)展开法则定义3.2 矩阵A m n ⨯的k l ⨯子矩阵1212A k l i i i j j j ⎛⎫⎪⎝⎭L L 及其余子阵,k 阶子方阵、k 阶子式;n 阶方阵或其行列式中k 阶子式的n k -阶余子式M 、代数余子式1212()()(1)k k i i i j j j A M +++++++=-L L ,k 阶(顺序)主子阵、k 阶(顺序)主子式. 主子式的代数余子式就是余子式.例3.10 设55[]A ij a ⨯=.1)25135A ⎛⎫⎪⎝⎭是A 的一个23⨯子矩阵,13424A ⎛⎫⎪⎝⎭为其余子阵; 2)1325A ⎛⎫⎪⎝⎭是A 的一个2阶子方阵,1325A ⎛⎫ ⎪⎝⎭是A 的一个2阶子式,245134A ⎛⎫ ⎪⎝⎭为对应余子式,而对应代数余子式为(13)(25)245245(1)134134A A +++⎛⎫⎛⎫-=- ⎪ ⎪⎝⎭⎝⎭;3)235235A ⎛⎫⎪⎝⎭是A 的一个3阶主子阵,235235A ⎛⎫ ⎪⎝⎭是A 的一个3阶主子式,其代数余子式就是余子式1414A ⎛⎫⎪⎝⎭,是A 的一个2阶主子式;4)A 共有五个顺序主子阵(式).定理3.3 按多行(列)展开法则——拉普拉斯(Laplace )定理1122C C ||A k k nnN A N A N A =+++L .例3.11 计算四阶行列式1234500112365112D -=--.例3.12 计算六阶行列式111000234000310161111101112411243161139D =---.例3.13 计算六阶行列式12000035000635475124583240064270034D -=-. 例3.14 计算叉形行列式1)11211n n n nna b a b D c d c d =ONN O;2)112111nn n nna b a b D e c d c d +=ON N O.。
第三节 按行(列)展开定理

性质五:行列式某一行 (列)的所有元素的 k 倍加到另一行 (列) 性质五:
的对应元素上, 的值不变。 的对应元素上,行列式 的值不变。
余子式与 余子式与代数余子式
a11 ⋮ a i −11 ∆= a12 ⋮ ⋯ a1 j −1 ⋮
a1 j ⋮
a1 j +1 ⋮
行列式相等。 即:行列式和它的转置 行列式相等。
),行列式的值改变符 性质二: 互换行列式的两行( 性质二: 互换行列式的两行(列 ),行列式的值改变行列式有两行(列) 完全相同,则此行列式 的值为零。 完全相同, 的值为零。
性质三: 性质三:
行列式的某一行( 式的外面。 行列式的某一行(列) 的公因子可以提到行列 式的外面。
b a a a b a a a = b 2a + b a a 2a + b b a 2a + b a b
2a + b a a
2a + b b a 1 0 b−a 0
2a + b a b 0 0 b−a
1 = ( 2a + b ) a a
1 b a
1 a b
= ( 2a + b ) a a
b−a = ( 2a + b ) 0
n
按第一例元素的展开式
= a11 A11 + a 21 A21 + ⋯ + a n1 An1 = ∑ a i 1 Ai 1
i =1
n
b 例题 1:计算行列式 a a
a b a
a a 的值。 的值。 b
分析: 行列式的特点是每列元 素之和都是 2a + b, 分析: 所以将第二行、第三行 都加到第一行上,得 都加到第一行上, 所以将第二行、
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
例3
计算(1) 计算
1 2 3 4
D4 = 3
解
2 3 4 1 4 1 2
.
4 1 2 3 1 2 3 4
2 3 4 1 4 1 2
D4 = 3
.
4 1 2 3 34 将 D4的第2、、行都加到第1行,并从第1行中 提取公因子10,得
用提取公因子法计算
1 1 1 1 2 3 4 1 D = 10 3 4 1 2 4 1 2 3
定理 (拉普拉斯定理 )设n阶方阵A = (aij ), 在 det A中 任选定k行(1 ≤ k ≤ n),由这k行的所有k阶子式与之对应 的代数余子式乘积之和等与 det A
例1 计算行列式 a 0 L 1
0 a M 0 0 0 O M
1 0 L a
例2 计算行列式 a11 a12 a21 a22 a31 a32
第i行 第 j行
a i 1 A j 1 + L + a in A jn
相同
当 i ≠ j 时,
a i 1 A j 1 + a i 2 A j 2 + L + a in A jn = 0 ,
( i ≠ j ).
同理 a1i A1 j + a 2 i A2 j + L + a ni Anj = 0, ( i ≠ j ).
D ,当 i = j , 2. ∑ aki Akj = Dδ ij = 0 ,当 i ≠ j ; k =1
n
D ,当 i = j , ∑ aik Ajk = Dδ ij = 0 ,当 i ≠ j; k =1
n
1 ,当 i = j, 其中 δ ij = 0 ,当 i ≠ j .
D = a i 1 Ai 1 + a i 2 Ai 2 + L + a in Ain
证
a11 L a12 L
(i = 1,2,L, n )
L L a1n L
D = ai1 + 0 + L+ 0 0 + ai 2 + L+ 0 L 0 + L+ 0 + ain L L L L an1 an2 ann L
−3 1:求 例1:求行列式 5 2
6 1
4 3 中元素2和 − 2的代数余子式
−2 1
4 3+ 1 6 A 31 = ( −1) = 14 1 3
A 32 = ( −1)
3+ 2
−3 4 = − ( −29) 5 3
引理 一个 n 阶行列式,如果其中第 i 行所有 阶行列式, 外都为零, 元素除 a ij外都为零,那末这行列式等于 a ij 与它的 代数余子式的乘积, 代数余子式的乘积,即 D = a ij Aij .
= ( 4 − 1 )( 3 − 1 )( 2 − 1 )( 4 − 2 )( 3 − 2 )( 4 − 3 ) = 12
例4 计算下列行列式
3.按行按列第二展开定理 3.按行按列第二展开定理 Def1:k阶子式N n阶行列式中任选k行k列,位于交叉处 的元素按原位置所构成的k阶行列式 Def2:k阶子式的余子式M 阶子式所在的行、 划去k阶子式所在的行、列 后余下的元素按原位置构成的n-k阶行列式 Def3:k阶子式的代数余子式为 ( −1)i1 + i2 +Lik + j1 + j2 +L jk M 其中 i1i2 L ik为k阶子式所在的行号 , j1 j2 L jk为k阶 子式所在的列号
ri − ri − 1
Dn
i = n,n −1,L2
=
1 0 0
1 x 2 − x1 x 2 (x 2 − x1 )
1 x 3 − x1 x 3 (x 3 − x1 )
L L L
1 x n − x1 xn (xn − x1 )
M M M M n 0 xn − 2 (x 2 − x1 ) xn− 2 (x 3 − x1 ) L xn − 2 (xn − x1 ) 2 3
a11 a12 L a1n L L L L = ai1 0 L 0 L L L L an1 an2 L ann
a11 a12 L a1n L L L L + 0 ai 2 L 0 L L L L an1 an2 L ann
a11 a12 L a1n L L L L + L+ 0 0 L ain = a i 1 Ai 1 + a i 2 Ai 2 + L + a in Ain L L L L (i = 1,2,L, n ) an1 an2 L ann
例如
a11 a12 a21 a22 a31 a32
a13 a22 a23 = a11 a32 a33
a23 a33
− a12
a21 a23 a31 a33
+ a13
a21 a31
a23 a33
= a11 (a22a33 − a23a32 ) + a12 (a23a31 − a21a33 ) + a13 (a21a32 − a22a31 )
= a11a22a33 + a12a23a31 + a13a21a32 − a11a23a32 − a12a21a33 − a13a22a31,
1
x
3
例1 1) 已知行列式D= x 2 0 中,(1,2)元素的代数 5 −1 4 余子式A12 = 8, 求D 2)已知四阶行列式D中第三列元素依此为1,2,0,-1, 3,-2,4,5,求 对应的余子式分别为3,-2,4,5,求D的值
a 11 M a i1 = M a j1 M a n1 L L L L a1n M a in M , a jn M a nn
a j 1 A j 1 + L + a jn A jn
把 a jk 换成 a ik ( k = 1,L, n), 可得
a 11 M a i1 = M a i1 M a n1 L L L L a1n M a in M , a in M a nn
1 1+ x 1 1
x−1 −1 −1 −1
2 1 0 0 0 1 (3) 0 0 0 2 1 0 0 1 2 1 0 0 1 2 1 0 0 1 2
例3
证明范德蒙德(Vandermonde)行列式 行列式 证明范德蒙德
1 x1 1 x2
2 x2
L L L
1
2 x n = ∏ ( x i − x j ). n ≥ i > j ≥1 M
行列式任一行( 的元素与另一行( 推论 行列式任一行(列)的元素与另一行(列) 的对应元素的代数余子式乘积之和等于零, 的对应元素的代数余子式乘积之和等于零,即
a i 1 A j 1 + a i 2 A j 2 + L + a in A jn = 0 , i ≠ j .
行展开, 证 把行列式 D = det(a ij ) 按第 j 行展开,有
∴ Dn = ( x 2 − x1 )( x 3 − x1 )L( x n − x1 ) =
n≥ i > j ≥ 2
∏ ( xi − x j )
n ≥ i > j ≥1
∏ ( x i − x j ).
例
计算 1 1
1
1
1 2 3 4 D4 = 1 4 9 16 = 1 8 27 64
∏j≥1 ( x i − x j ) 4≥ i >
M , D1 = det(a ij ) = M M , D2 = det(bij ) = M bn1 L bnn a k 1 L a kk
证明
D = D1 D2 .
三、小结
1. 行列式按行(列)展开法则是把高阶行列 行列式按行( 式的计算化为低阶行列式计算的重要工具. 式的计算化为低阶行列式计算的重要工具
例2
3 设行列式D = 1
−5 1
2 0
1 −5 ,求 3
−1 3 1 2 − 4 −1 − 3
A11 +A12 +A13 +A 14 及M 11 +M 21 +M 31 +M 41
行列式计算方法: 行列式计算方法:
一 般 行 列 式 :按 行 ( 列 )展 开 ;化 成 上 ( 下 )三 角 形 行(列)和相同 带 形 爪形 逐行加减 特殊行列式 按行( 列)展开 加边法 数学归纳法 递推法
1 2 = 10 1 − 3 − 2 −1
c j − c1
1
0
0
0
2 1 2 −1 = 10 j =2, 3பைடு நூலகம்4 3 1 − 2 −1 4 − 3 − 2 −1
2 −1 0 − 1 = 160 − 3 0 −1
1 −1 c2 − c3 − 2 − 1 = 20 1
1 (2) 1 1 1+ x
−1 −1 x−1 −1
a11 D= a 21 0 a 41
a12 a 22 0 a 42
a13 a 23 a 33 a 43
a14
0
0
a 33 a13
0 a14
a 24 = ( −1)3−1 a11 a12 a 21 a 22 0 a 41 a 42 a
44
a 23 a 43
a 24 a 44 a14 a 24 a44
a 33 a 3−1+ 3−1 13 = ( −1) a 23 a 43
1 2 0 M 0
1 0 3 M 0
L L L O L
1 0 n 1 0 = n! 1 − ∑ . j j=2 M n
关于代数余子式的重要性质
