第八届奥林匹克全国数学大赛初二的题
初二数学竞赛试题7套整理版(含答案)

初二数学竞赛试题7套整理版(含答案)初二数学竞赛试题7套整理版(含答案)第一套试题1. 某数与它的四分之一之和的和是28,求这个数是多少?解:设这个数为x,根据题意可得方程 x + (1/4)x + x = 28,化简得9/4x = 28,解得 x = 44.2. 有一个矩形,长是宽的3倍,如果长再加上宽再加上1的和等于50,求矩形的长和宽各是多少?解:设矩形的宽为x,则长为3x,根据题意可得方程 3x + x + 1 = 50,化简得 4x + 1 = 50,解得 x = 12,所以长为3 * 12 = 36,宽为12.3. 某个数的三次方减去它自身等于608,求这个数是多少?解:设这个数为x,根据题意可得方程 x^3 - x = 608,化简得 x^3 - x - 608 = 0,因此需求解该方程的解x.4. 甲数和乙数之和是300,甲数比乙数大30,求甲数和乙数各是多少?解:设甲数为x,乙数为y,根据题意可得方程 x + y = 300,x - y = 30,联立这两个方程可以解得甲数x和乙数y.5. 家长购买某品牌的饮料,每瓶售价为5元,如果购买10瓶,优惠50%,那么需要支付的价格是多少?解:购买10瓶优惠50%,相当于购买5瓶的价格,所以需要支付 5 * 10 * (1 - 50%) = 25元.第二套试题1. 学校图书馆购买300本新书,若图书馆中已有书籍500本,现将这些书按每排放10本的方式摆放,共需要多少排?解:新书300本加上原有书籍500本,共计800本书,每排放10本,所以需要 800 / 10 = 80排.2. 小明每天早上跑步30分钟,下午骑自行车25分钟,晚上游泳40分钟,求他一天中运动的总时长是多少分钟?解:小明一天早上跑步30分钟,下午骑自行车25分钟,晚上游泳40分钟,总时长为 30 + 25 + 40 = 95分钟.3. 甲、乙两人开始一起钓鱼,甲每分钟能钓2条鱼,乙每分钟能钓1条鱼,如果他们一起钓了45分钟,那么他们一共钓到了多少条鱼?解:甲每分钟能钓2条鱼,乙每分钟能钓1条鱼,他们一起钓了45分钟,所以甲和乙一共钓到了 2 * 45 + 1 * 45 = 135 条鱼.4. 某商品原价100元,现在打8折,过了一段时间后再降价,降到原价的85%,现在这个商品的售价是多少?解:原价100元,打8折后为 100 * (1 - 80%) = 80元,再降到原价的85%为 80 * 85% = 68元.5. 某人的年收入为12000元,每月生活费占月收入的1/5,那么这个人每月的生活费用是多少元?解:年收入12000元,月收入为 12000 / 12 = 1000元,生活费占收入的1/5,所以生活费用为 1000 * 1/5 = 200元.第三套试题1. 甲、乙两个人合作修一个房子,甲一个人修需要8天,乙一个人修需要12天,问他们一起修需要多少天?解:甲一个人修需要8天,乙一个人修需要12天,他们一起修需要的时间为 1/(1/8 + 1/12) = 4.8天.2. 甲购买一本书花费了原价的3/4,折后价格为60元,问这本书的原价是多少?解:折后价格为60元,花费原价的3/4,所以原价为 60 / (3/4) = 80元.3. 甲、乙两人比赛,甲第一轮跑步用时1分钟,第二轮用时50秒,第三轮用时40秒;乙第一轮跑步用时55秒,第二轮用时45秒,第三轮用时35秒,问谁的平均速度更快?解:甲第一轮跑步用时1分钟,第二轮用时50秒,第三轮用时40秒,平均速度为 (60 + 50 + 40) / 3 = 50 秒/轮;乙第一轮跑步用时55秒,第二轮用时45秒,第三轮用时35秒,平均速度为 (55 + 45 + 35) / 3 = 45 秒/轮;所以甲的平均速度更快.4. 一只小狗每小时能跑5公里,一只小猫每小时能跑8公里,如果它们从同一地点同时出发并分别向东和西跑,4小时后它们相距了多少公里?解:小狗每小时能跑5公里,4小时后跑了5 * 4 = 20公里,小猫每小时能跑8公里,4小时后跑了8 * 4 = 32公里,所以它们相距了 32 -20 = 12 公里.5. 三个连续的偶数相加的和是60,求这三个数分别是多少?解:设第一个偶数为x,那么第二个偶数为x + 2,第三个偶数为x+ 4,根据题意可得方程 x + (x + 2) + (x + 4) = 60,求解该方程可得x及其对应的三个连续偶数.第四套试题1. 一个数的2倍加上5等于13,求这个数是多少?解:设这个数为x,根据题意可得方程 2x + 5 = 13,解得 x = 4.2. 甲乙两数相差22,乙数的2倍与甲数的3倍之和等于70,求甲、乙两数各是多少?解:设甲数为x,乙数为y,根据题意可得方程 y - x = 22,2y + 3x= 70,联立这两个方程可以解得甲数x和乙数y.3. 一辆汽车以每小时80千米的速度行驶,行驶了1小时20分钟后停下来休息,求这段时间内汽车行驶的路程?解:汽车以每小时80千米的速度行驶,1小时20分钟共1.33 小时,所以汽车行驶的路程为 80 * 1.33 = 106.4 千米.4. 甲、乙两个人一起做一件工作,甲单独完成需要4小时,乙单独完成需要6小时,他们一起完成这件工作需要多少小时?解:甲单独完成需要4小时,乙单独完成需要6小时,他们一起完成需要的时间为 1/(1/4 + 1/6) = 2.4小时.5. 一个数加上它的四分之一之和的和是28,求这个数是多少?解:设这个数为x,根据题意可得方程 x + (1/4)x + x = 28,化简得9/4x = 28,解得 x = 44.第五套试题1. 一条宽10米的路,两边分别种植了向阳向每排7棵树或9棵树,每棵树之间距离相等,而且与路两边相邻树之间距离也相等,问道路中间最宽的地方有多宽?解:分别种植7棵树和9棵树,每棵树之间距离相等,所以道路中间最宽的地方为两排树之间的距离.2. 一个数与4的乘积减去2等于18,求这个数是多少?解:设这个数为x,根据题意可得方程 4x - 2 = 18,解得 x = 5.3. 甲、乙、丙三人合作种田,甲一个人种地需要10天,乙一个人种地需要12天,丙一个人种地需要15天,问他们三个人一起种地需要多少天?解:甲一个人种地需要10天,乙一个人种地需要12天,丙一个人种地需要15天,他们一起种地需要的时间为 1/(1/10 + 1/12 + 1/15) =4.8天.4. 某人共有100元,买了一本书花掉了原价的3/5,剩下的钱还能买另一本原价为80元的书吗?解:100元买了一本书花掉了原价的3/5,剩下的钱为 100 * (1 - 3/5) = 40元,剩下的钱不足以购买另一本80元的书.5. 一团面粉重800克,其中水分为15%,求这团面粉中水分的重量是多少克?解:面粉重800克,其中水分为15%,所以水分的重量为800 * 15% = 120克.第六套试题1. 一个数与它的五分之一之和的和是40,求这个数是多少?解:设这个数为x,根据题意可得方程 x + (1/5)x + x = 40,化简得7/5x = 40,解得 x = 28.57.2. 甲、乙两个人分别完成一项工作需要的时间比为2:5,如果他们一起完成这项工作需要3小时,求乙单独完成这项工作需要多少时间?解:甲、乙两个人分别完成一项工作需要的时间比为2:5,设甲单独完成需要的时间为x,乙单独完成需要的时间为y,根据题意可得方程 2x + 5x = 3,解得 y = 7.5.3. 有两个相交的圆,圆心之间的距离为8,两圆的半径分别为5和3,求两圆相交的弦的长度是多少?解:两个圆的半径分别为5和3,圆心之间的距离为8,利用勾股定理可以求得两圆相交的弦的长度.4. 甲乙两个人一起做一件工作,甲单独完成需要10小时,乙单独完成需要15小时,他们一起完成这件工作需要多少小时?解:甲单独完成需要10小时,乙单独完成需要15小时,他们一起完成需要的时间为 1/(1/10 + 1/15) = 6小时.5. 甲给乙20元,乙给丙30元,丙给甲10元,这三个人一共交易了多少元?解:甲给乙20元,乙给丙30元,丙给甲10元,所以一共交易了20 + 30 + 10 = 60元.第七套试题1. 某数比它的2/3小12,求这个数是多少?解:设这个数为x,根据题意可得方程 x - (2/3)x = 12,化简得 1/3x = 12,解得 x = 36.2. 甲、乙两个人一起修一条路,甲单独修需要8小时,乙单独修需要12小时,也有可能甲的速度是乙的倍数,问他们一起修需要多少小时?解:甲单独修需要8小时,乙单独修需要12小时,他们一起修需要的时间为 1/(1/8 + 1/12) = 4.8小时.3. 某品牌的衣服原价为200元,现在打折8折,过了一段时间后再降价,降到原价的85%,现在这件衣服的售价是多少?解:原价200元,打8折后为 200 * (1 - 80%) = 160元,再降到原价的85%为 160 * 85% = 136元.4. 甲、乙两个人一起做工,甲一个小时能做1/3的工作量,乙一个小时能做1/4的工作量,问他们一起做一份工作需要多少时间?解:甲一个小时能做1/3的工作量,乙一个小时能做1/4的工作量,他们一起做一份工作需要的时间为 1/(1/3 + 1/4) = 12/7小时.5. 某人的年收入为12000元,每月花销占收入的1/4,那么这个人每月的花销是多少元?解:年收入12000元,。
全国奥林匹克数学初二竞赛题

全国奥林匹克数学初二竞赛题
全国奥林匹克数学初二竞赛题
一、数学逻辑
1、已知函数f(x)的定义域为[a,b],若f(a)=8,f(b)=15,求f(c)的值。
2、若函数f(x)的定义域为[a,b],其图像对称轴的方程若为y=kx-k,求a,b的值。
3、已知椭圆的两个焦点F1,F2在x轴上,以及它们到圆心的距离为a,求椭圆方程。
二、不等式
4、设a,b,c分别为正实数,求使a,b,c满足不等式x^2+2ax+2bx+c=0
的有界解集。
5、若x^2+2ax+2bx+c>0,其中a,b,c均为正实数,求对应的x的取值范围。
6、已知x,y,a,b均为正实数,求使x^2+2ax+2bx+y^2+2ay+2by=c的有
界解集。
三、函数
7、已知f(x)的定义域为[2,30],求f(x)的最大值以及f(x)的最小值。
8、已知直线上有m,n两点,求m到n的最短距离以及对应的方程(以
y=mx+b的形式表示)。
9、已知椭圆上有m,n两点,求m到n的最短距离以及对应的方程(以ax^2+by^2+cx+dy+k=0的形式表示)。
四、应用题
10、已知某商品的销售总额为50万,还知该商品的单位成本为100元,求该商品的最大利润。
11、若有两段距离分别为a,b共需要t小时,若要同时全程行驶,求所
需的最大时间。
12、已知f(x)的定义域为[1,50],求f(x)的单调递增区间及它们的
端点值。
初二数学竞赛试题及答案

初二数学竞赛试题及答案一、选择题(每题4分,共40分)1. 下列哪个数是无理数?A. 0.5B. √2C. 0.33333…D. 3答案:B2. 一个等腰三角形的底边长为6,腰长为5,那么这个三角形的面积是多少?A. 12B. 15C. 18D. 20答案:B3. 如果一个数的平方等于它本身,那么这个数可能是:A. 0B. 1C. -1D. 以上都是答案:D4. 一个两位数,十位上的数字比个位上的数字大3,这个两位数可能是:A. 23B. 47C. 52D. 69答案:B5. 下列哪个分数是最简分数?A. 3/6B. 4/8C. 5/10D. 7/14答案:A6. 一个圆的直径是10厘米,那么这个圆的面积是多少平方厘米?A. 25πB. 50πC. 100πD. 200π答案:C7. 一个数的相反数是-5,那么这个数是:A. 5C. 0D. 10答案:A8. 一个数的绝对值是5,那么这个数可能是:A. 5B. -5C. 0D. 以上都是答案:D9. 一个等差数列的前三项分别是2,5,8,那么这个数列的第五项是多少?A. 11B. 12C. 13答案:A10. 下列哪个图形是轴对称图形?A. 平行四边形B. 梯形C. 等腰三角形D. 不规则多边形答案:C二、填空题(每题4分,共20分)11. 一个等腰直角三角形的斜边长为10厘米,那么这个三角形的面积是______平方厘米。
答案:2512. 如果一个数的立方等于8,那么这个数是______。
答案:213. 一个数的平方根是3,那么这个数是______。
答案:914. 一个数的倒数是1/4,那么这个数是______。
答案:415. 一个圆的周长是31.4厘米,那么这个圆的半径是______厘米。
答案:5三、解答题(每题10分,共40分)16. 已知一个等腰三角形的底边长为8,腰长为10,求这个三角形的高。
解:根据勾股定理,设高为h,则有:h^2 + (8/2)^2 = 10^2h^2 + 16 = 100h^2 = 84h = √84 = 2√21答:这个三角形的高是2√21。
数学竞赛8年级真题试卷【含答案】

数学竞赛8年级真题试卷【含答案】专业课原理概述部分一、选择题(每题1分,共5分)1. 若函数f(x) = x² 2x + 1,则f(1)的值为?A. 0B. 1C. 2D. 32. 下列哪个数是无理数?A. √9B. √16C. √3D. √13. 若a > b,则下列哪个选项是正确的?A. a c > b cB. a + c < b + cC. ac < bcD. a/c > b/c (c ≠ 0)4. 下列哪个方程的解集是实数集?A. x² + 1 = 0B. x² 2x + 1 = 0C. x² + x + 1 = 0D. x² x + 1 = 05. 若一组数据的平均数为10,则这组数据的和为?A. 5B. 10C. 20D. 50二、判断题(每题1分,共5分)1. 若a > b,则a² > b²。
()2. 两个负数相乘的结果是正数。
()3. 任何实数的平方都是非负数。
()4. 若a、b、c是等差数列,则a²、b²、c²也是等差数列。
()5. 两个无理数的和一定是无理数。
()三、填空题(每题1分,共5分)1. 若a + b = 5,a b = 3,则a = ______,b = ______。
2. 若x² 5x + 6 = 0,则x = ______或x = ______。
3. 若一组数据的方差为4,则这组数据的平均数为______。
4. 若等差数列{an}的前n项和为Sn = 2n² + 3n,则a1 = ______,d = ______。
5. 若函数f(x) = 2x + 3,则f(2) = ______。
四、简答题(每题2分,共10分)1. 解释什么是无理数。
2. 什么是等差数列?给出一个等差数列的例子。
3. 解释函数的定义。
初二数学奥林匹克竞赛题及答案
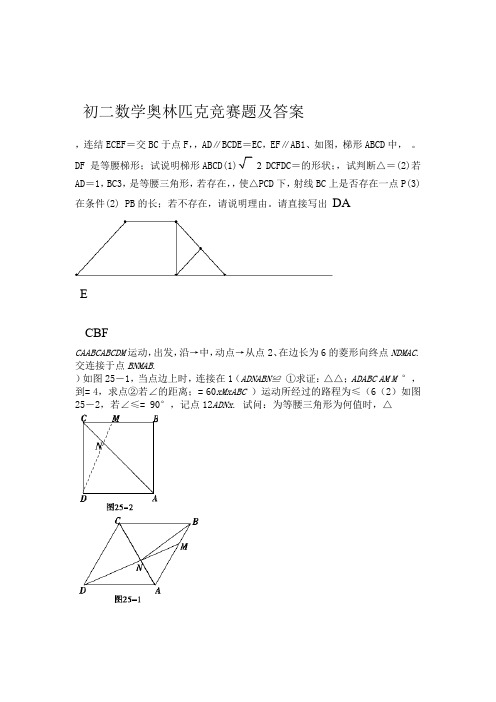
初二数学奥林匹克竞赛题及答案,连结ECEF=交BC于点F,,AD∥BCDE=EC,EF∥AB1、如图,梯形ABCD中,。
DF 是等腰梯形;试说明梯形ABCD(1)2 DCFDC=的形状;,试判断△=(2)若AD=1,BC3,是等腰三角形,若存在,,使△PCD下,射线BC上是否存在一点P(3)在条件(2) PB的长;若不存在,请说明理由。
请直接写出DAECBFCAABCABCDM运动,出发,沿→中,动点→从点2、在边长为6的菱形向终点NDMAC. 交连接于点BNMAB.)如图25-1,当点边上时,连接在1(ADNABN≌①求证:△△;ADABC AM M°,到= 4,求点②若∠的距离;= 60xMxABC )运动所经过的路程为≤(6(2)如图25-2,若∠≤= 90°,记点12ADNx. 试问:为等腰三角形为何值时,△ONOMMOONOMM,的方向运动到左转弯继续运动到,点=沿,使3、对于点、OMOMON ⊥.,这一过程称为且点完成一次“左转弯运动”点关于PPBABCDPPAPP,左转弯运动到正方形左转弯运动到和点,,点关于关于2211PDCPPPPA左转弯运动到,,关于左转弯运动到关于左转弯运动到…….,关于53344P 1)请你在图中用直尺和圆规在图中确定点的位置;(1ADP之间有怎样的关系?并说明理由。
BPA、P,判断△ABP与△2()连接111ABDAD y、在第二象限,为轴建立直角坐标系,并且已知点(3)以为原点、直线AB PPPP三点的坐标.)1,请你推断:、、,(),两点的坐标为(04、1201020094O1PNMCD1图2图4、如图1和2,在20×20的等个距网格(每格的宽和高均是1AABC与单位长)中,Rt△从点M1重合的位置开始,以每秒点当个单位长的速度先向下平移,BC边与网的底部重合时,继续C 同样的速度向右平移,当点ABCP停止△重合时,Rt与点x秒,△设运动时间为移动.yQAC.的面积为CABABC的位置时,请你在网格中画出Rt1,当Rt△△向下平移到(1)如图111QNCAB Rt△关于直线成轴对称的图形;111xyABC的函数关系式,向下平移的过程中,请你求出2,在Rt△与(2)如图yx取得最大值和最小值?最大值和最小值分别是多并说明当分别取何值时,少?yxABC取得最大值和)在Rt△取何值时,向右平移的过程中,请你说明当(3 最小值?最大值和最值分别是多少?为什么?BCEF点作∥的平分线交于O点,过O5、如图①,△ABC中,AB=AC,∠B、∠C F.AC 于E、交AB、之间有怎样的关系,并说、CF EF与BE猜想:(1)图中有几个等腰三角形? 明理由.如果有,AB≠AC,其他条件不变,图中还有等腰三角形吗?(2)如图②,若?间的关系还存在吗BE、CF问中分别指出它们.在第(1)EF与,过O与三角形外角平分线CO交于ABC中∠B的平分线BO(3)如图③,若△CFBE、F于.这时图中还有等腰三角形吗?EF与BC点作OE∥交AB于E,交ACO理你的?说明系关又如何由。
初二奥林匹克数学竞赛试题

22008年初中数学联赛(初二组)试卷一、选择题(本大题满分56分,每小题8分)1、已知a 、b 、c 是三角形的三边,则a 4+b 4c 4 -2 a 2c 2-2 b 2c 2-2 a 2c 2的值是( )A.恒正 B. 恒负 C.可正可负 D.非负 2、已知a +b +c =0, a1+b1+c1=-4,那么,(a1)2+(b1)2+(c1)2的值是( ) A.3 B. 8 C. 16 D.203、已知:a 1-│a │=1,那么代数式a1+│a │的值是( )A.25B.-25C.-5D. 54、已知│a │=5,b 2=9时,且ab >0则a +b 的值为( ),A. 8B.-2C.-8或8D.-2或25、已知a 、b 、c 是正整数,a >b ,且a 2-a b -a c +bc =7,则a -c 的值为( )A.-1B.-1或-7C.1D.1或7 6、已知△ABC 的一个角是400,且∠A =∠B ,那么∠C 的外角的大小是( )A. 1400B. 800或1000C. 1000或 1400D. 800 或14007、如图,已知FA =FB,FC =FD,下列结论中:①∠A ②DE =CE ;③连接FE ,则FE 平分∠F ,正确的是( ) A. ①② B.②③ C.①③ D.①②③二、填空题(本大题满分40分,每小题8分)1、若x 2+x y +y =14,y 2+x y +x =28,则 x +y 的值为 .2、(3+1)2001-2(3+1)2000-2(3+1)1999+2008= .3、已知x 、y 是实数,43+x +y 2-6y+9=0,若axy-3x=y ,则a= . 4、a 、b 、c 为△ABC 的三边,且3a 3+6a 2b-3a 2c-6abc=0,则△ABC 的形状为 .5、已知x1+y1=5,则yxy x yxy x +++-2252= .1 2三、计算(本大题满分20分,)要求写出必要的步骤.(1)2115141021151410+++--+2) 18612⨯+(1+3)(1-3)四、(本大题满分12分,)如图,在△ABC 中,AD 若AB=5,AC=3,求AD五、(本大题满分12分)如图,在△ABC 中,AB=AC ∠BAC=80°O 为△ABC 内一点,且∠OBC=10°,∠OCA=20°,求∠BAO 的度数.。
初二数学奥林匹克竞赛题及答案

F EA DC B 初二数学奥林匹克竞赛题及答案1、如图,梯形ABCD 中,AD ∥BC,DE =EC ,EF ∥AB 交BC 于点F,EF =EC ,连结DF 。
(1)试说明梯形ABCD 是等腰梯形;(2)若AD =1,BC =3,DC 2DCF 的形状;(3)在条件(2)下,射线BC 上是否存在一点P ,使△PCD 是等腰三角形,若存在,请直接写出PB 的长;若不存在,请说明理由。
2、在边长为6的菱形ABCD 中,动点M 从点A 出发,沿A →B →C 向终点C 运动,连接DM 交AC 于点N .(1)如图25-1,当点M 在AB 边上时,连接BN 。
①求证:△ABN ≌△ADN ; ②若∠ABC = 60°,AM = 4,求点M 到AD 的距离; (2)如图25-2,若∠ABC = 90°,记点M 运动所经过的路程为x (6≤x ≤12)试问:x 为何值时,△ADN 为等腰三角形。
3、对于点O 、M ,点M 沿MO 的方向运动到O 左转弯继续运动到N ,使OM =ON ,且OM ⊥ON ,这一过程称为M 点关于O 点完成一次“左转弯运动”.正方形ABCD 和点P ,P 点关于A 左转弯运动到P 1,P 1关于B 左转弯运动到P 2,P 2关于C 左转弯运动到P 3,P 3关于D 左转弯运动到P 4,P 4关于A 左转弯运动到P 5,……. (1)请你在图中用直尺和圆规在图中确定点P 1的位置;(2)连接P 1A 、P 1B ,判断 △ABP 1与△ADP 之间有怎样的关系?并说明理由。
(3)以D 为原点、直线AD 为y 轴建立直角坐标系,并且已知点B 在第二象限,A 、P 两点的坐标为(0,4)、(1,1),请你推断:P 4、P 2009、P 2010三点的坐标.4、如图1和2,在20×20的等PBAON距网格(每格的宽和高均是1个单位长)中,Rt△ABC从点A与点M重合的位置开始,以每秒1个单位长的速度先向下平移,当BC边与网的底部重合时,继续同样的速度向右平移,当点C与点P重合时,Rt△ABC停止移动。
第八届奥林匹克全国数学大赛初二试题

第八届 全国数学大赛初二试题(时间:120分钟 满分:140分)题号 一 二三总分 1718 19 20 得分一、选择 题(每小题5分,共40分)1、已知a ,b ,c 为△ABC 三边,且满足a 2c 2-b 2c 2=a 4-b 4,则它的形状为( )A .直角三角形B .等腰三角形C .等腰直角三角形D .等腰三角形或直角三角形2、已知方程组⎩⎨⎧=+=+4535y ax y x 与⎩⎨⎧=-=+5235y x by x 有相同的解,则b a ,的值为( )A .⎩⎨⎧==21b aB .⎩⎨⎧-=-=64b aC .⎩⎨⎧=-=26b aD .⎩⎨⎧==114b a3、甲是乙现在的年龄时,乙l0岁;乙是甲现在的年龄时,甲25岁,那么( ). A .甲比乙大5岁 B .甲比乙大10岁 C .乙比甲大10岁 D .乙比甲大5岁4、化简)2(2)2(2234++-n n n 得( ). A .8121-+n B .12+-n C .87 D .475、如果式子aa ---11)1( 根号外的因式移入根号内,化简的结果为( )A .a -1B .1-aC .1--aD .a --1 6、如图,已知△ABC 中,AB =AC ,∠BAC =90°,直角EPF 的 顶点P 是BC 中点,两边PE 、PF 分别交AB 、AC 于点C 、F , 给出以下四个结论:①AE =CF ; ②△EPF 是等腰直角三角形; ③S 四边形AEPF =21S △ABC ;④EF =AP .当∠EPF 在△ABC 内绕顶点P 旋转时(点E 不与A 、B 重合),上述结论中始终正确的有( )A .1个B .2个C .3个D .4个.7、在实验课上,小明用弹簧称将铁块A 悬于盛有水的水槽中,然后匀速向上提起(不考虑水的阻力),直至铁块完全露出水面一定高度,则下图能反映弹簧称的读数y (单位N )与铁块被提起的高度x (单位cm )之间的函数关系的大致图象是( )A .B .C .D .8、若p 为质数,35p +仍为质数,则57p +为( ).A.质数B.可为质数也可为合数C.合数D.既不是质数也不是合数二、填空题(每小题5分,共40分)9、若关于x 的方程)2(2015)1(--=-x n x m 有无数个解,则m 2015+n 2015= . 10、已知3=xy ,那么yx y xy x +的值为 .11、某数的平方根是22b a +和1364+-b a ,那么这个数是 . 12、设43239-的整数部分为a ,小数部分为b ,则ba b a -+++41111= . 13、直角三角形有一条直角边为11,另外两条边长是自然数,则周长为__________.14、如图,已知直线l :y =33x ,过点A (0,1)作y 轴的垂线交直线l 于点B ,过点B 作直线l 的垂线交y 轴于点A 1;过点A 1作y 轴的垂线交直线l 于点B 1,过点B 1作直线l 的垂线交y 轴于点A 2;……按此作法继续下去,则点A 2015的坐标为 .15.如上图,在四边形ABCD 中,∠A =60°,∠B =∠D =90°,BC =2, CD =3,则AB =16、小明、小强、小华三人参加奥林匹克杯数学大赛,他们是来自北京、上海、成都的选手,并分别获得一、二、三等奖。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第八届奥林匹克全国数学大赛初二的题题目一:第八届奥林匹克全国数学大赛初二组
一、选择题(共20题,每题4分,共80分)
1. 在一个等差数列中,首项为3,公差为5,第5项为23,则这个等差
数列的前n项和Sn为__________。
2. 已知一组数的平均值是18,如果将其中一个数3改成2,则新的平
均值为____。
3. 若一个正整数除以8余2,除以10余6,求这个数除以40的余数是
多少?
4. 若直线y=3x+2与圆的方程为$x^2+y^2-2x-4y-11=0$,求这个圆与y
轴的交点坐标。
5. 若正方形的边长为a,则其对角线的长度为______。
6. 若两条直线的斜率之和为5,斜率之积为-6,则这两条直线的方程分
别是______。
7. 若甲乙两个数的和是100,乙丙两个数的和是80,乙数比丙数多10,求甲数是多少?
8. 若一个正整数除以5余3,除以6余4,求这个数除以30的余数是多少?
9. 设A、B、C三个整数满足A<B<C,如果A、B、C是一个等差数列,则这个等差数列的公差为______。
10. 若集合A={1, 2, 3},集合B={2, 3, 4},则集合A与集合B的并集为______。
二、填空题(共5题,每题6分,共30分)
1. 在一个等差数列中,首项为2,公差为4,若前n项的和为56,则这个等差数列的第n项为______。
2. 设矩形的长是宽的3倍,周长为72,这个矩形的长和宽的分别是
______。
3. 若$ax^2+bx+c$的图像与x轴两交点均为负数,则a、b、c的关系式为______。
4. 若直线y=2x-7与直线y=kx-2平行,则k的值为______。
5. 设一个正整数的个、十位数字和为12,将该数字的个、十位数字对调后,新数字比原数字增大36,该正整数为______。
三、解答题(共5题,每题10分,共50分)
1. 设$\log_5{x}=a,\log_3{x}=b$,求$\log_{75}{x}$的值。
2. 若正方体三个相邻顶点上的数字之和为15,求该正方体的体积。
3. 判断函数$y=2x^2-3x+1$的单调性,并画出该函数的图像。
4. 已知$\frac{1}{a}+\frac{1}{b}=\frac{2}{5}$,求$\frac{2a+3b}{5a}$的值。
5. 一条长为12米的绳子上有7只蚂蚁在爬行,每只蚂蚁匀速爬行,蚂蚁每次都随机选择一方向爬行的距离,每次爬行的距离在0到12米之间,已知蚂蚁爬行的总距离是有限的,求蚂蚁爬行的总距离可能的最小值和最大值。
四、证明题(共2题,每题15分,共30分)
1. 证明:如果两个整数互质,那么它们的乘积也是它们的最小公倍数。
2. 设由0、1两个数字组成的6位数有多少个?请按照正确的计算步骤
给出计算过程。
