2.6 稳定流动的能量方程
工程热力学(王修彦)

.
Ma2 1 dcf dA cf A
b )M a 1 c f c d c f 与 d A 同 号 ,c f A
当Ma > 1时, dcf>0 →dA>0 ,采用渐扩喷管;
.
c )M a 1 c f c c f d A 0
截面上Ma=1,cf=c,称临界截面(minimum cross-sectional area)[也称喉部(throat)截面],临界截面上速度达当地音速 (velocity of sound)
4) cf cr 21p0v01(cr)1
21p0v012111
21p0v0
21RgT0
ccr RgTcr
. 与上式是否矛盾?
3.背压pb对流速的影响
a)收缩喷管:
p b p c r p 2 p bc f 2 c 2M a 2 1
p b p c r p 2 p c rc f 2 c 2M a 2 1
工程热力学课件
华北电力大学
工程热物理教研室制作 2015年1月
.
第八章 气体和蒸汽的流动 (Gas and Steam Flow)
.
工程中有许多流动问题需考虑宏观动能和位能,特别 是喷管(nozzle; jet)、扩压管(diffuser)及节流阀(throttle valve)内流动过程的能量转换情况。
c c r R g T c r 1 .4 2 8 4.2 7 1 4 9 2 .0 0 m s 1 7
o r 2 h 0 h cr 2 c p T 0 T cr
2 1 0 4.8 0 9 4 2 4 4 .2 1 4 9 2 .0 0 m /s 8 7
A cf
.
2
p2 T2 qm2 cf2 2
气体绝热节流膨胀制冷

1、绝热节流过程节流是高压流体气体、液体或气液混合物)在稳定流动中,遇到缩口或调节阀门等阻力元件时由于局部阻力产生,压力显著下降的过程。
节流膨胀过程由于没有外功输出,而且工程上节流过程进行得很快,流体与外界的热交换量可忽略,近似作为绝热过程来处理。
根据稳定流动能量方程:δq=dh+δw(2.1)得出绝热节流前后流体的比焓值不变,由于节流时流体内部存在摩擦阻力损耗,所以它是一个典型的不可逆过程,节流后的熵必定增大。
绝热节流后,流体的温度如何变化对不同特性的流体而言是不同的。
对于任何处于气液两相区的单一物质,节流后温度总是降低的。
这是由于在两相区饱和温度和饱和压力是一一对应的,饱和温度随压力的降低而降低。
对于理想气体,焓是温度的单值函数,所以绝热节流后焓值不变,温度也不变。
对于实际气体,焓是温度和压力的函数,经过绝热节流后,温度降低、升高和不变3种情况都可能出现。
这一温度变化现象称为焦耳-汤姆逊效应,简称J-T效应。
2、实际气体的节流效应实际气体节流时,温度随微小压降而产生的变化定义为微分节流效应,也称为焦耳-汤姆逊系数:αh=(ɑT/ɑp)2.2)αh>0表示节流后温度降低,αh<0表示节流后温度升高。
当压降(P2-P1)为一有限数值时,整个节流过程产生的温度变化叫做积分节流效应:ΔTh=T2-T1=ƒp2p1αhdp(2.3)理论上,可以使用热力学基本关系式推算出αh的表达式进行分析。
有焓的特性可知:dh=cpdT-[T(αv/aT)p-v]dp(2.4)由于焓值不变,dh=0,将上式移项整理可得:αh=(αT/αp)h=1/cp[T(αv/αT)p-v](2.5)由式(2.3)可知,微分节流效应的正负取决于T(αv/aT)p和v的差值。
若这一差值大于0,则αh>0节流时温度降低;若等于0则αh=0,节流时温度不变;若小于0则αh<0,节流时温度升高。
从物理实质出发,可以用气体节流过程中的能量转化关系来解释着三种情况的出现,由于节流前后气体的焓值不变,所以节流前后内能的变化等于进出推动功的差值:u2-u1=p1v1-p2v2气体的内能包括内动能和内位能两部分,而气体温度是降低、升高、还是不变,仅取决于气体内动能是减小、增大、还是不变。
工程热力学 第七章 气体与蒸汽的流动.

出口截面积。
解:(1)确定滞止参数
根据初态参数,在h-s图上确定进
口状态点1,为过热蒸汽,cr 0.546。
过1点作定熵线,截取线段 01 的
长度为 h0 h1 c2f 1 / 2 5kJ / kg,点0 即为滞止点,查得:p0 2.01106 Pa,h0 3025kJ / kg 。
流经截面1-1和2-2的质量
流量为 qm1 、qm2 ,流速为c f 1 、 cf 2。 质量守恒:qm1 qm2 qm const
A1cf 1 A2c f 2 Acf const
v1
v2
v
dA dcf dv 0 A cf v
上式适用于任何工质和任何过程(可逆和不可逆)。
(2)确定临界参数
pcr cr p0 2.01106 Pa
定压线与定熵线的交点即为临界
状态点,查得:hcr 2865kJ / kg , vcr 0.219m3/kg。
(3)确定出口参数
p2 pb 0.1106 Pa
定压线与定熵线的交点即为出口
状态点2,查得:h2 2420kJ / kg,v2 1.55m3/kg。
(2)尺寸计算
●渐缩喷管
A2 qmv2 / c f 2
●缩放喷管
Acr qmvcr / c f ,cr
扩张段的长度:
A2 qmv2 / c f 2
l d2 dmin
2 tan( / 2)
—顶锥角,取10°-12°。
4、计算步骤 ■设计性计算
根据已知条件,选择喷管外形并确定几何尺寸。 ■校核性计算
稳定流动系统的能量方程

稳定流动系统能量方程是热力学中的一个基本方程,描述了流体在流动过程中的能量转换。
其数学表达为:
∑(P/ρ) + ∑gz + ∑(V^2/2g) + Q/W = 常数
其中P为压力,ρ为密度,g为重力加速度,z为高度,V 为速度,Q为热量或热量流,W为功或功率。
这个方程的含义是:在稳态条件下,液体或气体在管道或管道网络中流动过程中,系统的压力、重力势能、动能和内能之和保持恒定。
其中,压力能、重力势能和动能的单位都是焦耳,内能的单位是热量单位(例如卡路里或焦耳)。
方程的右侧的常数部分是常数热量值,通常可以忽略。
工程传热学-第七章 气体流动

qm
Ac f v
const
A1c f 1 v1
A2 c f 2 v2
dA dc f dv 0 A cf v
2、能量方程式
开口系统稳定流动能量方程:
1 2 q dh d (c f ) gdz w s 2
dz 0
w s 0
1 2 2 q h2 h1 (c f 2 c f 1 ) 2
c f ,cr ccr kpcr vcr
c f ,cr p 2k cr p0 v0 1 k 1 p0
k 1 k
按临界流速等于当地音速的关系,可以推得 对理想气体、定熵流动时:
cr
pcr 2 p0 k 1
dc f dA 2 Ma 1 A cf
当Ma>1时,超音速,dcf>0 dA>0,应该渐放。 因而当气体流速由小于 声速增加到大于声速时,整 个喷管应该由渐缩形的前段 和渐放形的后段组合而成,如图所示。这种 喷管称为拉法尔喷管或称缩放喷管。显然在 缩放形喷管的喉部即其最小截面积处,气体 的流速正好等于声速。
5.过程方程式
pv const
Tv
k 1
1 k k
k
dv dp k 0 v p
dv dT ( k 1) 0 v T
1 k dp dT 0 k p T
const
Tp
const
k 1 k
p2 T2 T1 p 1
pB / p0 cr pB / p0 cr
出口p2 pB 出口p2 pcr
其他计算和设计计算类似。
工程热力学-第三章热力学第一定律-稳定流动能量方程的应用

qm1h1 qm2h2 qm3h3
THANK YOU
,
q
内部贮能增量 0
wC wt h2 h1 q
02
2.3 换热器(heat exchanger)
流入:
qm1
h1
1 2
cf21
gz1
qm2
h3
1 2
cf23
gz3
流出:
qm1
h2
1 2
cf22
gz2
qm2
h4
若忽略位能差
h1
h2
1 2
(cf22
cf21)
02
2.7 混合
qm1、h1
qm2、h2 qm3、h3
流入:
qm1
h1
1 2
cf21
gz1
qm2
h3
1 2
cf23
gz3
流出:
qm3
h3
1 2
cf23
gz3
内增: 0 忽略动能差、位能差
第三章 热力学第一定律 之
稳定流动能量方程 的应用
CONTENTS
01. 常见设备及过程 02. 应用分析
01. 常见设备及过程
01
常见设备及过程
1.蒸汽轮机、气轮机 2.压气机,水泵类 3.换热器(锅炉、加热器等) 4. 管内流动 5. 绝热节流 6. 喷管 7. 混合
02. 应用分析
工程热力学第二章

8
∫ pdv
q = ∫ Tds
条件
7
准静态或可逆
4、示功图与示热图 p W T Q
二、储存能
1、内部储存能——热力学能 储存于系统内部的能量, ,与系统内工质粒子的微 储存于系统内部的能量 观运动和粒子的空间位置有关。 观运动和粒子的空间位置有关。 分子动能( 分子动能(移动、 移动、转动、 转动、振动) 振动)T 分子位能( 分子位能(相互作用) 相互作用)V 核能 化学能
对推进功的说明
1、与宏观流动 与宏观流动有关 流动有关, 有关,流动停止, 流动停止,推进功不存在 2、作用过程中, 作用过程中,工质仅发生位置 工质仅发生位置变化 位置变化, 变化,无状 态变化 3、w推=p v与所处状态有关, 与所处状态有关,是状态量 4、并非工质本身的能量( 并非工质本身的能量(动能、 动能、位能) 位能)变化引 起,而由外界做出, 而由外界做出,流动工质所携带的能量 流动工质所携带的能量 可解为: 可理解为:由于工质的进出, 由于工质的进出,外界与系统之间 所传递的一种机械功 所传递的一种机械功, 机械功,表现为流动工质进出系 统使所携带 统使所携带和所 携带和所传递 和所传递的一种 传递的一种能量 的一种能量
15 16
三、焓
内能+流动功 焓的定义式 焓的定义式: 定义式:焓=内能+ 对于m 对于m千克工质: 千克工质: H = U + pV 对于1 对于1千克工质: 千克工质: h=u+ p v 焓的物理意义: 焓的物理意义: --对 --对流动工质 流动工质( 工质(开口系统 开口系统) 系统),表示沿流动方向传递 的总能量中, 的总能量中,取决于热力状态 取决于热力状态的那部分能量 热力状态的那部分能量. 的那部分能量. --对 --对不流动工质 不流动工质( 闭口系统) 焓只是一个复合状 工质(闭口系统 系统),焓只是一个复合状 态参数 思考: 思考:特别的对理想气体 h=f(T h=f(T) f(T) 17
工程热力学课后题答案--沈维道-童钧耕-版

P301P564P939P13313P19318P23526P26330P28134P39635P301.闭与外界无物质交换,系统内质量保持恒定,那么系统内质量保持恒定的热力系一定是闭口系统吗?不一定,稳定流动系统内质量也保持恒定。
2.有人认为开口系统内系统与外界有物质交换,而物质又与能量不可分割,所以开口系统不可能是绝热系。
对不对,为什么?不对,绝热系的绝热是指热能单独通过系统边界进行传递(传热量),随物质进出的热能(准确地说是热力学能)不在其中。
3.平衡状态与稳定状态有何区别和联系?平衡状态一定是稳定状态,稳定状态则不一定是平衡状态。
4.倘使容器中气体的压力没有改变,试问安装在该容器上的压力表的读数会改变吗?绝对压力计算公式p =p b +p g (p > p b ), p = p b -p v (p < p b )中,当地大气压是否必定是环境大气压?当地大气压p b 改变,压力表读数就会改变。
当地大气压p b 不一定是环境大气压。
5.温度计测温的基本原理是什么?热力学第零定律6.经验温标的缺点是什么?为什么?不同测温物质的测温结果有较大的误差,因为测温结果依赖于测温物质的性质。
7.促使系统状态变化的原因是什么?举例说明。
有势差(温度差、压力差、浓度差、电位差等等)存在。
8.分别以图1-20所示的参加公路自行车赛的运动员、运动手枪中的压缩空气、杯子里的热水和正在运行的电视机为研究对象,说明这些是什么系统。
参加公路自行车赛的运动员是开口系统、运动手枪中的压缩空气是闭口绝热系统、杯子里的热水是开口系统(闭口系统——忽略蒸发时)、正在运行的电视机是闭口系统。
4题图9.家用电热水器是利用电加热水的家用设备,通常其表面散热可忽略。
取正在使用的家用电热水器为控制体(但不包括电加热器),这是什么系统?把电加热器包括在研究对象内,这是什么系统?什么情况下能构成孤立系统?不包括电加热器为开口(不绝热)系统(a 图)。
热工基础-2-(2)热力学第一定律

节流的特点: 节流的特点:
①绝热: 绝热: 在节流过程中,工质与 在节流过程中 工质与
外界交换的热量可以忽 略不计,故节流又称 故节流又称绝热 略不计 故节流又称绝热 节流。 节流。 ②简化为稳定流动 : 进、出口截面必须取在离节流孔一定距离的稳 定状态处。 定状态处。
③不可逆:缩孔附近的工质有摩擦和涡流。 不可逆:缩孔附近的工质有摩擦和涡流。 动能差、位能差忽略。 ④无功量交换 ,动能差、位能差忽略。 用能量方程得: 机): 叶轮式机械(动力机、压气机):
在工质流经叶轮式动力机时,压力降低, 在工质流经叶轮式动力机时,压力降低,体积 膨胀,对外作功。 膨胀,对外作功。 通常工质进、出口的动能差 位能差、 动能差、 通常工质进、出口的动能差、位能差、系统向 外散热量(绝热)均可忽略不计 不计。 外散热量(绝热)均可忽略不计。
h1 = h2
结论: 结论: 节流前后工质的焓相等。 节流前后工质的焓相等。
例题:空气在活塞式压气机(包括进气、 例题:空气在活塞式压气机(包括进气、压缩和 排气三个工作过程)中被压缩,压缩前: 排气三个工作过程)中被压缩,压缩前: /kg;压缩后: p1=0.1MPa,v1=0.86m3/kg;压缩后: /kg;设压缩中每kg kg空气的 p2=0.8MPa, v2=0.18m3/kg;设压缩中每kg空气的 热力学能增加150kJ 同时放出热50kJ, 150kJ, 50kJ,求 热力学能增加150kJ,同时放出热50kJ,求: (1)压缩过程中对每kg空气所作的功; (1)压缩过程中对每kg空气所作的功; 压缩过程中对每kg空气所作的功 (2)每生产1kg压缩空气所需的功; (2)每生产1kg压缩空气所需的功; 每生产1kg压缩空气所需的功 (3)若该机每分钟生产15kg压缩空气, (3)若该机每分钟生产15kg压缩空气,问用多大 若该机每分钟生产15kg压缩空气 功率的电动机带动该机? 功率的电动机带动该机?
第八章稳定流动基本方程

速度变化与管道截面积变化之间的关系
dA dc 2 Ma 1 A c
马赫数与喷管选型
当Ma<1时 dc>0 ,则 dA<0 渐缩型喷管 当Ma>1时 dc>0, 则 dA>0 渐扩型喷管 当Ma<1 →Ma>1时,则dA<0→dA>0 缩放型喷管(拉伐尔喷管) 缩放型喷管喉部Ma=1,c=a处于临界状态 当气体在喷管中充分膨胀时,声速沿着气流 方向逐渐降低.
rc
cr
喷管中气体流量的计算
适用于任何性质的气体
可逆, 不可逆过程
A2c2 qm v2
rc nim
c A
rc
v
xam m
q
气体在喷管中有摩擦流动
气体在喷管中有摩擦流动是不可逆过程,有 能量损耗,工程上用以描述这种情况的有速 度系数,喷管效率和能量损失系数三种方式. 喷管的速度系数φ:喷管出口气体实际流 速与出口气体理想流速之比.
q m v 2 4 0.0896 A 4.67 10 4 m 2 467 mm 2 c2 767 .46
例题2
利用节流测量管道中湿蒸汽的干度.
h
p1
p2
1
2
t2
x1
s
作业
思考题:200页8,9,10,11,12,13.
作业题:8-2,8-4,8-7,8-9,8-11,8-13,8-14,815.
滞止焓 滞止温度 滞止压力 滞止比体积
1 2 h c pT c 2
0
c T 0T p c2
T p 0 p T RrT 0 0 v 0 p
0 k k 1
2
或
T v 0 v 0 T
工程热力学-02热力学第一定律

由可逆过程 δq du pdv, h u pv ,有 δq d(h-pv) pdv dh d( pv) pdv
即 δq dh vdp 可逆过程中热力学第一定律另一主要形式。
2020年8月4日
第二章 热力学第一定律
15
2-5 轴功
由稳定流动能量方程式,可得轴功与其他形式能量间的关系为:
2020年8月4日
第二章 热力学第一定律
10
2-3 开口系统能量方程式
质量守恒: dm δm1 δm2
dm
d
δm1
d
δm2
d
qm1 qm2
该式称为连续性方程式,它说明单位时间内开口系统中工质质 量增加的数量等于流入和流出系统的质量流量之差。
2020年8月4日
第二章 热力学第一定律
11
推动功: 在进出口边界上推动工质流入或流出系统所消耗的功量。
z1)
ws
2020年8月4日
第二章 热力学第一定律
14
焓 h u pv H U pV 状态参数
对1kg流动工质,其稳定状态稳定流动能量方程式:
q
(h2
h1)
1 2
(cf22
cf21)
g
(
z2
z1)
ws
• 焓并不能看作是工质储存的能量,可近似看成随工质 流动一起转移的能量。
• 热力学能是工质内部储存能量的唯一形式。
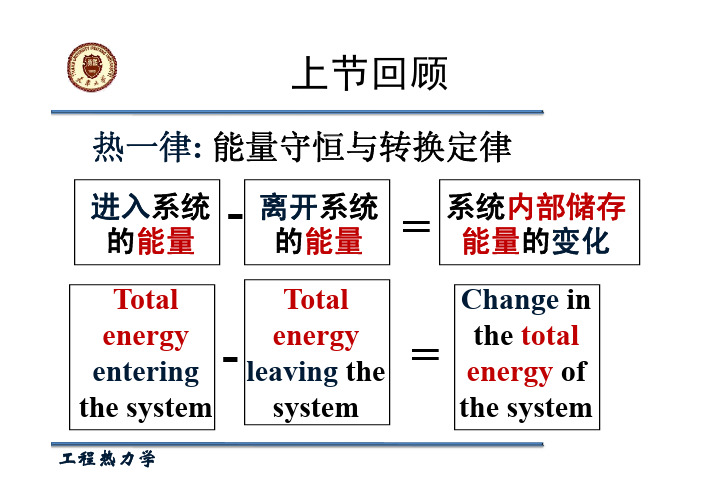
自然界中物质所具有的能量,既不能创造也不能消灭,而只能从一 种能量形态转换为另一种能量形态,转换中能量的总量守恒。
对任何系统,各项能量之间的平衡关系一般可表示为: 进入系统的能量 - 离开系统的能量 =系统储存能量的变化
热力学第一定律: 热能作为一种能量形态,可以和其它能量形态相互转换,转
工程热力学思考题答案整理版

⒉ 有人认为,开口系统中系统与外界有物质交换,而物质又与能量不可分割,所以开口系不可能是绝热系。
这种观点对不对,为什么?答:不对。
“绝热系”指的是过程中与外界无热量交换的系统。
热量是指过程中系统与外界间以热的方式交换的能量,是过程量,过程一旦结束就无所谓“热量”。
物质并不“拥有”热量。
一个系统能否绝热与其边界是否对物质流开放无关。
⒊ 平衡状态与稳定状态,平衡状态与均匀状态有何区别和联系?答:“平衡状态”与“稳定状态”的概念均指系统的状态不随时间而变化,这是它们的共同点;但平衡状态要求的是在没有外界作用下保持不变;而平衡状态则一般指在外界作用下保持不变,这是它们的区别所在。
⒋ 倘使容器中气体的压力没有改变,试问安装在该容器上的压力表的读数会改变吗?在绝对压力计算公式)( )( b v b b e b P P P P P P P P P P <-=>+=;中,当地大气压是否必定是环境大气压?答:可能会的。
因为压力表上的读数为表压力,是工质真实压力与环境介质压力之差。
环境介质压力,譬如大气压力,是地面以上空气柱的重量所造成的,它随着各地的纬度、高度和气候条件不同而有所变化,因此,即使工质的绝对压力不变,表压力和真空度仍有可能变化。
“当地大气压”并非就是环境大气压。
准确地说,计算式中的P b 应是“当地环境介质”的压力,而不是随便任何其它意义上的“大气压力”,或被视为不变的“环境大气压力”。
⒌ 温度计测温的基本原理是什么?答:温度计对温度的测量建立在热力学第零定律原理之上。
它利用了“温度是相互热平衡的系统所具有的一种同一热力性质”,这一性质就是“温度”的概念。
⒍ 经验温标的缺点是什么?为什么?答:由选定的任意一种测温物质的某种物理性质,采用任意一种温度标定规则所得到的温标称为经验温标。
由于经验温标依赖于测温物质的性质,当选用不同测温物质制作温度计、采用不同的物理性质作为温度的标志来测量温度时,除选定的基准点外,在其它温度上,不同的温度计对同一温度可能会给出不同测定值(尽管差值可能是微小的),因而任何一种经验温标都不能作为度量温度的标准。
第五讲:热力学第一定律2-稳定系统能量方程
mu '− m0u0 − (m − m0 )h = 0
工程热力学
u ' = h(m − m0 ) + m0u0 m
四种可取系统 3)
Energy balance for steady-flow systems
稳定流动条件
1、
•
•
•
mout = min = m
•
2、 Q = Const
δmin
uin
1 2
ci2n
gzin
3、
•
W net
= Const
•
=Ws
轴功Shaft work δQ
4、 每截面状态不变 dEC,V / δτ = 0
焓变
冷流体吸热量:q ' = Δ h = h2' − h1' > 0
工程热力学
例4:绝热节流Throttling Valves
管道阀门 制冷
空调
膨胀阀、毛细管
h1
h2
工程热力学
绝热节流过程,前后h不 变,但h不是处处相等
练习题
储气罐原有气体m0,u0
h
输气管状态不变,h
经τ时间充气,关阀 储气罐中气体m
可理解为:由于工质的进出,外界与系统之
间所传递的一种机械功,表现为流动工质进 出系统使所携带和所传递的一种能量
工程热力学
开口系能量方程的推导
uin pvin
δmin
gzin
1 2
ci2n
δQ
δQ + δmin(u + c2/2 + gz)in
δWnet
δmout uout
pvout gzout
《工程热力学》学习资料 (4)

由连续性方程,可得气体流量为:
qm
Acf v
为了计算方便,一般取喷管出口截面进行计算
即
qm
A2cf2
已经得出计算公式
v2
流速公式
1
由c绝f 2热方程2 得k k出1 p0v0v[21v(0 pp02pp)02(kk1)
k]
qm A2
2 k p0 [( p2 )2 k ( p2 )(k1) k ]
k 1 v0 p0
p0
33
7.3喷管的计算
三、流量的计算
qm A2
2 p0 [( p2 )2 k ( p2 )(k1) k ]
1 v0 p0
p0
分析: 当初参数p0、v0及出口截面A2保持恒定时
流量 qm 随p2/p0而变化
当 p2 1 qm 0 p0
当 p2 0 qm 0 p0
可见p2/p0从1到0, qm 有一个极大值。
34
7.3喷管的计算
三、流量的计算
(1)截面积不变,改变进出口的压差-力学条件;
(2)固定压差,改变进出口截面面积-几何条件。
本节目的:找到流速和截面变化的关系 17
7.2促使流速改变的条件
一、工质状态参数的变化规律
1、p与cf的关系:要流动,需要有动力(压差)
由
q
(h2
h1 )
c
2 f
2
2
c
2 f1
g(z2
z1 )
wi
对可逆过程:
c f, cr
cf22
12pk0vk0 1p0v20[11(Rppg02T)0(k
1)
k]
即临界流速取决于进口状态,当p0、v0或T0较高时临界流速的数
流体稳定流动时的能量衡算柏努利方程(最全)word资料

四、流体稳定流动时的能量衡算——柏努利方程1.流体流动时所具有的机械能(1)位能:由于流体几何位置的高低而决定的能量。
位能是一个相对值,其大小随所选基准水平面的位置而定。
m kg 流体的位能mgz = J; 1kg 流体的位能zg = J/kg1N 流体的位能z = J/N(2)动能:由于流体有一定流速而具有的能量。
m kg 流体的动能221mu = J; 1kg 流体的动能22u =J/kg 1N 流体的动能gu 22= J/N(3)静压能:流体克服截面上的压力而作的功,即由于流体有一定静压力而具有的能量。
m kg 流体的静压能ρm p=J; 1kg 流体的静压能ρp=J/kg1N 流体的静压能gpρ=J/N m kg 流体的总机械能为: ρmpmu mgz ++221 J; 1kg 流体的总机械能为: ρpu zg ++22 J/kg1N 流体的总机械能为: gpg u z ρ++22 J/N (4)外加能量:1kg 流体从输送机械所获得的机械能。
用功W 表示,单位为J/kg 。
1N 流体的外加能量gW H 功功=J/N(5)损失能量(阻力损失):1kg 流体克服两截面间各项阻力所消耗的能量。
用∑损h表示,单位为J/kg 。
1N 流体的损失能量ghH ∑=损损 J/N2.流体稳定流动时的能量衡算——柏努利方程 如图所示,按照能量守恒及转化定律,输入系统的总机械能必须等于由系统中输出的总能量。
以单位质量(1Kg )流体为衡算基准:∑+++=+++损功h pu g z W p u g z ρρ22222211 J/kg 实际流体的柏努利方程式3.柏努利方程的分析及讨论(1)若输送无黏性、流动时不产生摩擦阻力的理想流体时,0=∑损h且 0=功W常数=++=++ρρ2222121122pu g z p u g z 理想流体的柏努利方程式理想流体进行稳定流动时,在管路任一截面的流体总机械能是一个常数,流体在不同截面间各种机械能的形式可以互相转化。
稳定流动能量方程

稳定流动能量方程
稳定流动过程的能量方程式可以写为:q=Δh+1/2Δc2+gΔZ+ws。
扩展资料:
流体的稳定流动是指流体在各个截面上的状态对外热交换、功交换都不随时间改变并且同时期流过任何截面上的流量均相等。
稳定流动是指能量转换设备处于稳定工况时,流道中任何位置上流体的状态及流速、流量等都不随时间变化而始终保持稳定。
一般能量转换装置经常是在稳定工况下工作的。
例如蒸汽动力装置或燃气动力装置经常需要保持稳定的输出功率,压气机输出的气体经常需要保持稳定的状态及流量;制冷装置从冷藏库吸热的功率经常需保持稳定的数值等。
在这种稳定工况下,系统所进行的能量转换过程维持稳定,不随时间而变。
热工基础热力学第一定律稳定流动系统能量方程

2-4 热力学第一定律及其解析式 热力学第一定律是人类从长期实践经验中总结
得到的自然界最重要、最普遍的基本定律,适用于
一切工质和一切热力过程。对于不同的具体问题, 可以表达为不同的数学表达式。
22
热工基础
第二章 热力学第一定律
1. 闭口系能量方程
对如图所示的闭口系: 根据能量守恒原理: 加入系统的热量-系统对外做的功 =系统总储能增量 即 Q-W= ΔE 或 Q = ΔE+W
第二章 热力学第一定律
热工基础
第二章 热力学第一定律
2-1 热力学第一定律的实质
实质:
是能量守恒及转换定律在热现象上的应用。
两种表述:
表述Ⅰ: 热量与其它形式的能量相互转换时, 总量保持不变。 对于一个循环,则 Q W
表述Ⅱ:第一类永动机是不可能制成的。
1
热工基础
第二章 热力学第一定律
显然过程中:
ds>0→q>0,吸热 ds<0→q<0,放热 ds=0→q=0,绝热
对可逆过程,熵变是判断系统工质与外界有无热 量交换及热流方向的判据。
18
热工基础
第二章 热力学第一定律
(2) 可逆过程热量在T-s 图上的表示 由 q=T· ds(微元面积) (过程线下面积) q Tds
针对工程上形形色色的热工设备和热力过程,常常将它
们抽象简化为不同的系统,不同的系统与外界之间的能量关 系不同,因此其相应的热力学第一定律表达式(能量方程) 也不同,但其本质都是相同的。
根据能量守恒原理,热力学第一定律的一般表 达式为:
系统收入能量-系统支出能量
=系统总储存能的增量
2
热工基础
2-2 系统的储存能 内部储存能
