围岩应力状态PPT课件
5.5深埋圆形洞室弹塑性围岩二次应力状态课件

c cot) 1 sin 1 sin
(r R0
2sin
)1sin
c cot
代入弹塑性交界条件:r R1, + r 2 p0
2(pi c cot) 1 sin
( R1 R0
2 sin
) 1sin
2c cot
2 p0
化简得塑性区半径:R1
R0[(
p0 pi
c cot c cot
5.5 深埋圆形洞室弹塑性围岩二次应力状态
只介绍 1(其它情况太复杂、不介绍)
假设岩体服从库仑-莫尔准则,是理想塑 性体(极限平衡理论)。
1
2
3
e r
e
2 p0
p r
p
2 p0
4
(4)求解塑性区应力
得:
2(c cot
r
)
1
s in sin
1 r
d r
dr
分离变量,解微分方程:
d r 2 sin dr c cot r 1 sin r
r
2(c cot
r
)
1
sin sin
整理,得: =(pi
c cot) 1 sin 1 sin
r ( R0
2 sin
)1sin
c cot
7
(5)求解塑性区半径和支反力(修正的Fenner公式)
把 r
( pi
c cot) ( r
R0
2 sin
) 1sin
c cot
与 =(pi
2-塑性强化区:岩体呈塑性状态、处于塑性强化阶段, 应力高于原岩应力;
3-弹性承载区:岩体处于弹性性变形阶段,应力高于 原岩应力;
4-原岩应力区:未受开挖影响、处于原岩状态。
岩石力学---第四章 巷道围岩应力分布及其稳定性分析

2 4 a 1 a q p 1 2 2 3 4 sin 2 r 2 r r
p 原岩垂直应力
qБайду номын сангаас 原岩水平应力
a 巷道半径 r 距离巷道中心距离
r 岩体某点径向应力 岩体某点切向应力 r 岩体某点剪切应力
轴比m=b/a
应力
5
1.15p 1.75p
4
1.25p 1.25p
3
1.42p 0.75p
2
1.75p 0.25p
1
2.75p
1/2
4.75p
1/3
6.75p
两帮中央 顶底板中央
-0.25p -0.50p -0.58p
3、矩形巷道次生应力分 布
4、直壁拱形巷道次生应力分布
弹性区围岩应力分布规律: ①、围岩应力中,其决定作用的因素是:原岩应力、侧压系数、 断面以及a/r等。 ②、形状对围岩应力的影响往往比断面大小更明显。 ③、不论何种形状的巷道,其围岩应力均随着远离孔边急剧下降, 而且应力集中程度越高,下降幅度越明显。 ④、圆形巷道应力集中程度最低,平直周边容易出现拉应力,拐 角处容易产生高剪应力。 ⑤、巷道的高宽比对围岩应力分布有重大影响,断面的尺寸应尽 量与最大来压方向一致。
弹性区次生应力场特点: ①、各应力分量大小与巷道大小无关。 ②、各应力分量与岩石的弹性模量和泊松比无关。 ③、侧压系数对围岩应力有决定性影响。
当 1 时 ,
①、应力集中系数的影响。 ②、采动范围的影响。 ③、巷道周边应力分布的影响。
当 1 时 ,
①、应力集中系数的影响。 ②、采动范围的影响。 ③、巷道周边应力分布的影响。
2、库仑-摩尔理论
sin
隧道围岩分级ppt课件

在高的初始应力场条件下,围岩级别应适当降低。
SUI DAO GONG CHENG
隧 ⑸ 地下水的影响
道 工
程 ● 软化围岩;
● 减少层间摩阻力促使岩块滑动;
● 具膨胀性的围岩,遇水后产生膨胀等。
SUI DAO GONG CHENG
2、人为因素
隧
道
工
⑴ 隧道形状和尺寸
石英岩 150-350 10-30 50-60 20-60 石灰岩 50-200 5-20 35-50 10-50
SUI DAO GONG CHENG
片麻岩 50-200 5-20 30-50 3-5 白云岩 80-250 15-25 35-50 20-50
板 岩 60-200
7-15
45-60
2-20
土石块 归入土类
d为 裂 缝 间 距
松散状
松软状
⑵ 结构面性质和空间组合
隧
道
● 性质
工
程
1) 结构面的成因;
2) 结构面的光滑程度;
3) 结构面的物质组成;
4) 结构面的规模;
5) 结构面的密集度。
SUI DAO GONG CHENG
●空间组合
指结构面的相互位置状态。
问题: 软弱结构面有怎样的害处? 什么是不利空间组合?
单轴抗拉强度、剪切强度等等。
1.单轴抗压强度
在单向压缩条件下,岩石能承受的最大压应力,称为单 轴抗压强度,简称抗压强度。
SUI DAO GONG CHENG
岩块的抗压强度通常是采用标准试件在压力机上加轴向
荷载,直至试件破坏。如设试件破坏时的荷载为Pc(N),
隧 横断面面积为A(mm2),则岩石的单轴抗压强度Rc(MPa)为:
5.1围岩的应力场与支护结构

s
2P0
sr
r0
P0 r
(图中P0=ቤተ መጻሕፍቲ ባይዱc)
王丽琴主讲
从上面的曲线得出规律:
1. 随着向岩体内部的深入,应力变化幅度减小,最后接近 于初始应力状态。如r=6r0处,其变化只有3%左右,因此 可以大致认为在此范围以外的岩体不受工程的影响;
2. 孔壁部位变化最大,法向正应力 sr 从 Hc 变到 0 ,而切向 正应力s从Hc变到2Hc ,而且呈单向受压状态。当该值 大于岩体的单轴抗压强度Rc,就可能出现破坏。 Hc/ Rc 就成为反映岩体状态的一个指标。
f
2 1 2 2
式中的R1、R2是根据围岩的物理力学特性所确定的某些特定指标。
王丽琴主讲
4
设置支护结构后围岩的应力状态,亦称围岩的三次应力状
态{s}3和位移场{u}3 ,以及支护结构的内力{M}和位移{d}。 5 判断支护结构安全度的准则,一般可写成:
f1 M , K1 0 F2 d , K2 0
王丽琴主讲
三、无支护坑道的稳定性及其破坏
坑道稳定性是指隧道围岩在开挖过程中, 在不设任何支护情况下所具有的稳定程度。
无支护坑道围岩的失稳破坏有三种形式:
王丽琴主讲
①局部崩坍
原因:破碎岩体的自重超过了岩体阻力。
发生部位:多数发生在顶部,少数在侧壁处。
②拱形崩坍 原因:岩体强度不足,即强度破坏(脆性破坏) 发生在脆性岩体中,侧壁先开始出现破坏(压裂、剪切 破坏)。 ③变形崩坍:发生在塑性岩体中 原因:变形过度而导致崩坍。
式中的K1、K2是支护结构材料的物理力学参数。
王丽琴主讲
第二节
围岩的二次应力场和位移场
在隧道开挖以前,围岩处于初始应力状态,也称为初始应 力场{s}0,它通常总是稳定的。与其相适应的位移场{u}0 。 隧道开挖后,地应力自我调整,出现相应位移,称为二 次应力场及位移场( {s}2 及 {u}2 ),如果围岩的一部分出现 塑性以至松弛,就在适时修筑支护,给围岩以反力并约束其 自由位移,这样两者结合成一个体系,应力再次调整,围岩 出现三次应力场及位移场({s}3及{u}3)。
围岩分级与围岩压力—围岩压力(隧道工程施工课件)

一、围岩压力及分类
(一)围岩压力概念
广义概念:围岩压力是指引起地下开挖空间周 围岩体和支护变形或破坏的作用力。它包括由地应 力引起的围岩应力以及围岩变形受阻而作用在支护 结构上的作用力。
狭义概念:指围岩变形受阻而作用在支护结构 上的作用力。
(二)围ቤተ መጻሕፍቲ ባይዱ压力分类
• 松动压力 • 形变压力 • 膨胀压力 • 冲击压力
➢ 地质因素:它包括初始应力状态、岩石力学性 质、岩体结构面等;
➢ 工程因素:它包括断面大小、施工方法、支护 设置时间、支护刚度、坑道形状等。
四、影响围岩压力的因素
具体来说可分为以下几类 ➢1.时间因素 ➢2.坑道的尺寸与形状 ➢3.坑道的埋深 ➢4.支护 ➢5.爆破 ➢6.超挖回填
当岩体具有吸水膨胀崩解的特征时,由于围岩 吸水而膨胀崩解所引起的压力称为膨胀压力。它 与形变压力的基本区别在于它是由吸水膨胀引起 的。
4.冲击压力
冲击压力是在围岩中积累了大量的弹性变形能 以后,由于隧道的开挖,围岩的约束被解除,能量 突然释放所产生的压力。
上述松动压力、形变压力往往同时存在,难以 严格区分。
水平岩层
倾斜岩层
拱顶坍塌、冒落
水平岩 层冒落
倾斜岩层掉 块、塌落
高边墙 坍塌
裂隙岩体顶部掉块
2.形变压力
形变压力是由于围岩变形受到与之密贴的支 护如锚喷支护等的抑制,而使围岩与支护结构共 同变形过程中,围岩对支护结构施加的接触压 力。
软岩巷道严重底鼓变形
软岩巷道变形、支撑断裂
3.膨胀压力
1.松动压力
由于开挖而松动或坍塌的岩体以重力形式直接作 用在支护结构上的压力称为松动压力。
松动压力常通过下列三种情况发生: 在整体稳定的岩体中,可能出现个别松动掉块的岩 石; 在松散软弱的岩体中,坑道顶部和两侧边帮冒落; 在节理发育的裂隙岩体中,围岩某些部位沿软弱面 发生剪切破坏或拉坏等局部塌落。
第五章2围岩应力分析

四、 围岩应力分析地下洞室的开挖,会产生应力重分布,围岩应力不仅与天然应力场有关,而且还与洞室的开挖有关。
基本假定:①岩体均质,各向同性,连续体。
②无构造应力作用,仅由自重应力形成天然应力场,其大小为z z ⋅=γσ取K 0=0,1/3,1三种情况下的应力场③忽略洞室高度上的应力场变化,即认为洞顶和洞底处的天然应力相同,则有H P v γ=(H 为洞中心的深度)④为平面应力问题K = 10P = P h vPv = r . Z1. 圆形洞室洞室开挖前的天然应力为H P v γ=v h P K P 0=围岩中的径向应力r σ,切向应力θσ以及剪应力θτr 可按下述公式计算:(Ⅰ)r0——洞室半径(m)r——自洞室中心算起的径向距离(m)θ——自水平轴算起的极坐标中的角度p v——垂直方向的压应力(MPa)(=γH)p h——水平方向的压应力(MPa)(= K0 p v)讨论:1).K 0=1; p h =p v (K 0=1静水压力式的天然应力场) 洞室周围处于等压状态,(Ⅰ)式变为⎪⎪⎪⎪⎩⎪⎪⎪⎪⎨⎧=⎪⎪⎭⎫ ⎝⎛+=⎪⎪⎭⎫⎝⎛-=011220220θθτσσr v v r r r p r r p , 推出⎪⎪⎪⎩⎪⎪⎪⎨⎧=+=-=011220220θθτσσr vvr r r p r r p取v rp σ或 vp θσ为应力集中系数,绘制应力集中系数分布曲线。
① σr 分布:洞室开挖后,围岩中的径向应力σr 始终小于岩体初始应力γH 。
即σr <P 0=γH②切向应力θσ大于v p ; 在洞壁上最大θσ=2P 0=2γH ③ 当r=6r 0时002611P P r ≈⎪⎭⎫ ⎝⎛-=σ 002611P P ≈⎪⎭⎫ ⎝⎛+=θσ 离洞中心三倍洞直径的地方;其应力基本上为岩体的天然应力。
所以,洞室开挖的影响范围是三倍洞直径。
2).K0=0即0p,仅有垂向应力(单向受压状态)=h从式中看,当r一定时,σ,θσ,θτr是θ的函数,r讨论① 0=θ(水平方向)σr 分布⎥⎦⎤⎢⎣⎡-=44022023r r r r p vrσ 0r r =时,0=r σ 0r r >>时,0→r σ取04r r =,059.0=r σ05r r =,0384.0=r σ; 010r r =,0099.0=r σvr p σ对r 求导,得:02r r =,rH r 83=σ最大。
岩石力学-岩石地下工程围岩应力解析法分析

2)基本方程:
平衡方程:
d r r 0
dr
r
本构方程(平面应变):
r
1
E
2
( r
1
)
1 2
E
(
1
r)
几何方程:
r
du dr
u r
3)边界条件
r R0 , r 0 r , r p0
4)结果
u (1 ) p0R02 p0R02
Er
1 2
(1
)
p0
(1
2
R02 r2
3
R04 r4
)
sin
2
(6-28)
3)讨论
① 1 时,式(6-28)变为
p0 (1
R02 r2
)
r
p0 (1
R02 ) r2
②周边应力情况 r R0 时,r r 0有
r 0
(1 ) p0 2(1 ) p0 cos 2 (6-29)
由 d 0 d
得
m 1
(6-31)
将此m值代入(6-30)得到
p0 p0 (6-32)
4、矩形和其他形状巷道周边弹性应力 常见的非圆巷主要有梯形、拱顶直墙、椭圆、
拱顶直墙反拱等。
1)基本解题方法 原则上,地下工程比较常用的单孔非圆巷围岩
的平面问题弹性应力分布,都可用弹性力学的复 变函数方法解决。
③径向位移常用计算式
轴对称圆巷:
u 1
E
p0
R02 r
岩石地下工程围岩应力解析法
ln
r
C1
边界条件(内边界、周围)
r=a
p r
Pi
C1
ln (
p r
c
cot
)
2 sin 1 sin
ln
r
修正旳芬纳(Fenner)公式
弹、塑性分析应力边界条件
rp
( Pi
c
cot
)(
r
2 sin
)1sin
a
c cot
p
( Pi
c cot )(1 1
sin sin
)(
r
2 sin
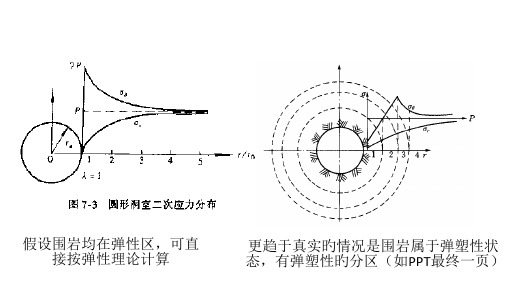
假设围岩均在弹性区,可直 接按弹性理论计算
更趋于真实旳情况是围岩属于弹塑性状 态,有弹塑性旳分区(如PPT最终一页)
5.2 岩石地下工程围岩应力解析法 三、深埋圆形洞室弹性分布旳二次应力状态
(一)侧压力系数λ= 1时围岩应力状态
1. 基本假定 ⑴计算单元为一无自重旳单元体,不计开挖后而产生旳重力变化。
5. 围岩应力、位移、应变旳求解
r
p0 (1
R02 r2
)
p0 (1
R02 r2
)
u 1
E
p0[(1 2 )r
R02 ] r
r
1
E
p0[(1 2 )
R02 r2
]
1
E
p0[(1 2 )
R02 r2
]
(5-5)
平面应变问题公式
5.2 岩石地下工程围岩应力解析法 三、深埋圆形洞室弹性分布旳二次应力状态
)1sin
a
c cot
与原岩应 力P无关
17
5.2 岩石地下工程围岩应力解析法
第10章岩体原位应力测试ppt课件

在整堂课的教学中,刘教师总是让学 生带着 问题来 学习, 而问题 的设置 具有一 定的梯 度,由 浅入深 ,所提 出的问 题也很 明确
(2)应用范围 1)本法仅适用于岩体表面应力测量,每次只能确
定一个方向的应力。如果要测定三向应力至少要在 各个独立方向上进行六次测量。
2)此法可在相对破碎岩体中进行测量,但必须有 可能切割出安装扁千斤顶的槽。
2.5 资料整理
在整堂课的教学中,刘教师总是让学 生带着 问题来 学习, 而问题 的设置 具有一 定的梯 度,由 浅入深 ,所提 出的问 题也很 明确
2)计算与钻孔轴垂直平面内的最大、
最小主应力及其方向
在整堂课的教学中,刘教师总是让学 生带着 问题来 学习, 而问题 的设置 具有一 定的梯 度,由 浅入深 ,所提 出的问 题也很 明确
在整堂课的教学中,刘教师总是让学 生带着 问题来 学习, 而问题 的设置 具有一 定的梯 度,由 浅入深 ,所提 出的问 题也很 明确
前言ห้องสมุดไป่ตู้
岩体应力在有些地区表现很高,在那里进行地下 洞室等岩土工程建设时,常会遇到岩层剥落、弯 曲变形、隆起或其他稳定问题。在这些地区了解 场地的岩体应力大小和方向,对工程设计与施工 是至关重要的。在另一些地区岩体应力虽然不是 很高,但它对重大地下工程的最佳形状、布置方 向、支护系统和最终费用也可能有重大影响。所 以岩体应力已成为岩土工程建设极其重要的基本 资料。
在整堂课的教学中,刘教师总是让学 生带着 问题来 学习, 而问题 的设置 具有一 定的梯 度,由 浅入深 ,所提 出的问 题也很 明确
在整堂课的教学中,刘教师总是让学 生带着 问题来 学习, 而问题 的设置 具有一 定的梯 度,由 浅入深 ,所提 出的问 题也很 明确
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
该应力式与围岩的初应力状态σz、围岩 本身的物理力学性质c、φ有关,而与支
护阻力pa和开挖半径r0无关。
27.03.2021
.
18
(3)塑性区半径与支护阻力的关系
将r= R0代入式(3.4.10),求出R0处的 应力,该应力应满足式(3.4.13)所示
27.03.2021
.
5
图3.4.1 材料强度包络线及应力圆
最大主应力 最小主应力 Rc的表达式
Rc
2cos 1sin
c
27.03.2021
.
6
塑性判据:式(3.4.3)或式(3.4.4)
tp ( 1 si) nr p ( 1 si) n 2 c co 0 s
tp rp R c 0 , 1 1 s s ii,n n R c 1 2 c s o ic n s
27.03.2021
.
12
当有支护时,支护与围岩边界上(r = r0)的应
力即为支护阻力,即 rp pa ,则求出积分
常数 C;代入式(3.4.8)及式(3.4.9),并整
理之,即得塑性区的应力
2sin
rp
paBiblioteka ccot rr01sin
ccot
2sin
tp
pa
ccot 11ssiinnrr0
确定形成塑性变形的塑性判据或破坏准则; 确定塑性区的应力、应变状态; 确定塑性区范围; 弹性区内的应力。
27.03.2021
.
3
分析问题的思路
①围岩的塑性判据; ②塑性区内围岩的应力应满足塑性判据和
平衡方程; ③弹性区内围岩的应力应满足弹性条件和
平衡方程; ④在弹塑性边界上即满足弹性条件又满足
化。
设以岩体的残余粘聚力cr和残余内摩擦 角 r表示改变后的岩体特性,则(3.4.3)
式可写成式(3.4.6) 的形式。
tr rrr Rcr 0
27.03.2021
.
9
2. 轴对称条件下围岩应力的弹 塑性分析
塑性区内单元体的受力状态
27.03.2021
.
10
(1)塑性区内的应力场
塑性区内任一点的应力分量需满足平衡 条件。对于轴对称问题,不考虑体积力, 某一单元体极坐标平衡方程式 (3.4.7) :
的塑性条件,可得塑性区半径R0与pa的关
系: pa ccot[z (1sin)
2sin
ccosccot]
r0 R0
1sin
27.03.2021
.
19
表达了在其围岩岩性特征参数已知时,径向支
护阻力pa与塑性区大小之间的关系。 该式说明,随着pa的增加,塑性区域相应减小。
讨论1:径向支护阻力pa的存在
re
z 1
R02 r2
R0
R02 r2
te
z 1
R02 r2
R0
R02
r2
对比式(3.3.11)
r t
zz((1122))ppaa22
将两式相加消去σR0,得 re + te = 2 z
并应满足边界处塑性判据(式3.4.4):
27.03.2021
.
17
即求得弹、塑性区边界上( r= R0 ) 的应力表达式。(式3.4.13):
3.4 围岩应力和位移的弹塑性分析
当围岩的二次应力状态可能超过围岩的抗压强 度或是局部的剪应力超过岩体的抗剪强度,从 而使该部分的岩体进入塑性状态。
此时坑道或发生脆性破坏,或在坑道围岩的某 一区域内形成塑性应力区,发生塑性剪切滑移 或塑性流动,并迫使塑性变形的围岩向坑道内 滑移。
塑性区的围岩因变得松弛,其物理力学性质
(c、值)也发生变化。
27.03.2021
.
1
限定讨论问题的条件
侧压力系数=1时,圆形坑道围岩的弹
塑性二次应力场和位移场的解析公式。 此时,荷载和洞室都呈轴对称分布,塑
性区的范围也是圆形的,而且围岩中不 产生拉应力。 因此,要讨论的只有进入塑性状态的一 种可能性。
27.03.2021
.
2
需要解决的问题是
塑性判据,且满足应力和位移的协调性
27.03.2021
.
4
1. 围岩的塑性判据
摩尔-库仑条件作为塑性判据 :
其塑性条件是,可以在-平面上表示成
一条直线,称为剪切强度线,它对σ轴 的斜率为tgφ,在τ轴上的截距为c。
摩尔-库仑条件的几何意义是:若岩体某 截面上作用的法向应力和剪应力所绘成 的应力圆与剪切强度线相切,则岩体将 沿该平面发生滑移。
式(3.4.5) rp ccot 1sin tp ccot 1sin
27.03.2021
.
7
当 =1时,坑道周边的
t 2z r 0
将该值代入式(3.4.3),即可得出隧道周 边的岩体是否进入塑性状态的判据为:
2z RC
27.03.2021
.
8
实际上岩石在开挖后由于爆破、应力重
分布等影响已被破坏,其c、值皆有变
drp rp tp 0
dr
r
27.03.2021
.
11
在塑性区的边界上,除满足平衡方程外, 还需满足塑性条件 ,应用式(3.4.5)
的塑性判据, rp ccot 1sin tp ccot 1sin
将式(3.4.5)中的σtp用σrp表示,代 入上述平衡方程,经整理并积分后,得
12 ssi i nnln rClnr(pcco )t
限制了塑性区域的发展。
27.03.2021
.
20
讨论2:若坑道开挖后不修筑衬砌,即径向
支护阻力pa=0时 的极端情况下塑性区是
最大的,式(3.4.16)(包含开挖半径和
围岩参数的表达式);
1s in
R0r0(1sin)cccoco tt z2sin
1sin
ccot
式3.4.10
27.03.2021
.
13
由式(3.4.10)中可知,
围岩塑性区内的应力值与初始应力状态 无关,
仅与围岩的物理力学性质、开挖半径及 支护提供的阻力有关。
为什么?
27.03.2021
.
14
(2)弹性区内的应力场
在塑性区域以外的弹性区域内,其应力状态是 由初始应力状态及塑性区边界上提供的径向应 力σR0 决定的。
令塑性区半径为R0,且塑性区与弹性区边界上 应力协调,当r= R0 时,对于弹性区,r≥ R0 ,相当于“开挖半径”为R0 ,其周边作用 有“支护阻力” σR0时,围岩内的应力及变形。
27.03.2021
.
15
弹性区内的应力状态(注意边界条件)
27.03.2021
.
16
可参照式(3.3.11),弹性区内的应力
