中考复习图形的认识与三角形一

合集下载

中考数学复习第4章图形的认识与三角形第15讲等腰三角形与直角三角形课件

1 为圆心，大于 2 AC的长为半径画弧，两弧相交于点M，N，作直线MN，
交BC于点D，连接AD，则∠BAD的度数为( A ) A．65° B．60° C．55° D．45°
A 由作图知，MN是AC的垂直平分线，∴∠DAC＝∠C＝30°.又 ∵∠BAC＝180°－∠B－∠C＝180°－55°－30°＝95°，∴∠BAD＝ ∠BAC－∠DAC＝95°－30°＝65°.
1 ∴∠CDE＝∠CED＝ 2
∠BCD＝30°.
∴∠DBC＝∠DEC. ∴DB＝DE(等角对等边)．
变式运用► [2017·蓬江区质检]如图，在△ABC中，AB＝AC，点D，E， F分别在AB，BC，AC边上，且BE＝CF，BD＝CE. (1)求证：△DEF是等腰三角形； (2)当∠A＝40°时，求∠DEF的度数．解：(1)证明：∵AB＝AC， ∴∠ABC＝∠ACB. 在△DBE和△ECF中，
第四章
图形的认识与三角形
第 15讲
等腰三角形与直角三角形
考点梳理过关
考点1 等腰三角形的性质及判定 6年1考等腰三角形的两腰①相等(定义赋予) 等腰三角形的两个底角相等，即“②等边对等角” 性质
提示►(1)在一个三角形中，等腰三角形顶角的平分线、底边上的中线、如果一个角的平分线与该底边上的高相互重合，即“③三线合一” 角对边上的中线重合，那么这个三角形是等腰三角形；(2)在一个三角形中，等腰三角形是轴对称图形，有④一条对称如果一个角的平分线与该轴角对边上的高重合，那么有两⑤边相等的三角形是等腰三角形(定义这个三角形是等腰三角形赋予) 有两个⑥角相等的三角形是等腰三角形，即“⑦等角对等边”
判定
考点2
等边三角形的性质及判定 6年1考
考点3

山东潍坊市2018年中考数学复习第4章图形的初步认识与三角形第14讲图形的初步认识

六年真题全练
命题点1 角的运算
通过近六年潍坊市的中考题可以看出角的运算不是潍坊中考命题的重点，一般情况下不会单独出题，多数情况下是在做题的过程中用到角的运算． 1．[2016·潍坊，20(2)，3分]链接第26讲六年真题全练第2 题．
命题点2 平行线的性质与判定
通过近六年潍坊市的中考题可以看出平行线的性质与判定是潍坊市中考命题的重点，一般情况下不会单独出题，经常是在做题的过程中用到平行线的性质和判定． 2．[2017·潍坊，5,3分]如图，∠BCD＝90°，AB∥DE，则∠α 与∠β 满足( B )
第四章图形的初步认识与三角形第14讲图形的初步认识
考点梳理过关
考点1 线
线段线段有① 两个端点；两点之间，② 线段最短
直线
把线段向两个方向无限延伸，就得到直线，直线有③ 端点；经过两点，有且只有④ 一条直线
0
个
射线
将线段向一个方向无限延伸就得到射线，射线有⑤ 点
一
个端
(1)概念：在同一平面内两条⑥ 不相交的直线叫做平行线；
技法点拨►本题主要考查平行线的性质．判断“三线八角”时关键是“截线”，有平行线时要联想同位角、内错角和同旁内角．涉及的相关问题有：如图，若AB∥CD，试探究∠A，∠C，∠AEC之间的关系．
变式运用►1.[2017·凉山中考]如图，AB∥CD，则下列式子一定成立的是( D)
A．∠1＝∠3
B．∠2＝∠3
公理公认的真命题称为公理
经过证明并且作为推理依据的真命题称为定理．如果一个定理定理的逆命题是真命题，那么这个逆命题就叫做原定理的逆定
理．任何命题都有逆命题，但一个定理不一定有逆定理
证明
推理的过程，叫做证明．用反证法证明命题的第一步是⑧ 设命题的结论不成立

全国2020年中考数学试题精选50题图形的初步认识与三角形含解析

2020年全国中考数学试题精选50题：图形的初步认识与三角形一、单选题1.（2020·玉林）如图是A，B，C三岛的平面图，C岛在A岛的北偏东35°方向，B岛在A岛的北偏东80°方向，C岛在B岛的北偏西55°方向，则A，B，C三岛组成一个（）A. 等腰直角三角形B. 等腰三角形 C. 直角三角形 D. 等边三角形2.（2020·玉林）一个三角形木架三边长分别是75cm，100cm，120cm，现要再做一个与其相似的三角形木架，而只有长为60cm和120cm的两根木条.要求以其中一根为一边，从另一根截下两段作为另两边（允许有余料），则不同的截法有（）A. 一种B. 两种 C. 三种 D. 四种3.（2020·玉林）已知：点D，E分别是△ABC的边AB，AC的中点，如图所示.求证：DE∥BC，且DE＝BC.证明：延长DE到点F，使EF＝DE，连接FC，DC，AF，又AE＝EC，则四边形ADCF是平行四边形，接着以下是排序错误的证明过程：①∴DF BC；②∴CF AD.即CF BD；③∴四边形DBCF是平行四边形；④∴DE∥BC，且DE＝BC.则正确的证明顺序应是（）A. ②→③→①→④B. ②→①→③→④C . ①→③→④→② D. ①→③→②→④4.（2020·河池）如图，在中，CE平分∠BCD，交AB于点E，EA=3，EB=5，ED=4.则CE的长是（）A. 5B. 6C. 4D. 55.（2020·河池）观察下列作图痕迹，所作CD为△ABC的边AB上的中线是（）A. B. C.D.6.（2020·河池）在Rt△ABC中，∠C=90°，BC=5，AC=12，则sinB的值是（）A. B.C.D.7.（2020·河池）如图，AB是O的直径，CD是弦，AE⊥CD于点E，BF⊥CD于点F.若BF=FE=2，DC=1，则AC的长是（）A. B.C.D.8.（2020·铁岭）一个零件的形状如图所示，，则的度数是（）A. 70°B. 80°C. 90°D. 100°9.（2020·铁岭）如图，矩形的顶点在反比例函数的图象上，点和点在边上，，连接轴，则的值为（）A. B.3 C. 4D.10.（2020·盘锦）我国古代数学著作《九章算术》记载了一道有趣的问题.原文是：今有池方一丈，葭生其中央，出水一尺，引葭赴岸，适与岸齐.问水深、葭长各几何.译为：有一个水池，水面是一个边长为10尺的正方形，在水池正中央有一根芦苇，它高出水面1尺，如果把这根芦苇拉向水池一边的中点，它的顶端恰好到达池边的水面，水的深度与这根芦苇的长度分别是多少？设芦苇的长度是尺.根据题意，可列方程为（）A. B. C.D.11.（2020·盘锦）如图，在中，，，以为直径的⊙O交于点，点为线段上的一点，，连接并延长交的延长线于点，连接交⊙O于点，若，则的长是（）A. B.C.D.12.（2020·锦州）如图，在菱形中，P是对角线上一动点，过点P作于点E.于点F.若菱形的周长为20，面积为24，则的值为（）A. 4B.C.6 D.13.（2020·锦州）如图，在中，，，平分，则的度数是（）A. B.C.D.14.（2020·丹东）如图，在四边形中，，，，，分别以和为圆心，以大于的长为半径作弧，两弧相交于点和，直线与延长线交于点，连接，则的内切圆半径是（）A. 4B.C. 2D.15.（2020·丹东）如图，是的角平分线，过点作交延长线于点，若，，则的度数为（）C. 125°D. 135°16.（2020·朝阳）如图，在平面直角坐标系中，一次函数的图象与x轴、y轴分别相交于点B，点A，以线段AB为边作正方形，且点C在反比例函数的图象上，则k的值为（）A. -12B. -42 C. 42D. -2117.（2020·朝阳）如图，四边形是矩形，点D是BC边上的动点（点D与点B、点C不重合），则的值为（）A. 1B.C. 2D. 无法确定18.（2020·雅安）如图，内接于圆，，过点C的切线交的延长线于点．则（）A. B.C.D.19.（2020·雅安）如图，在中，，若，则的长为（）C.D.20.（2020·绵阳）下列四个图形中，不能作为正方体的展开图的是（）A. B. C.D.21.（2020·绵阳）在螳螂的示意图中，AB∥DE，△ABC是等腰三角形，∠ABC＝124°，∠CDE＝72°，则∠ACD＝（）A. 16°B. 28°C. 44°D. 45°22.（2020·绵阳）如图，在四边形ABCD中，∠A＝∠C＝90°，DF∥BC，∠ABC的平分线BE交DF于点G，GH⊥DF，点E恰好为DH的中点，若AE＝3，CD＝2，则GH＝（）A. 1B. 2C. 3D. 423.（2020·眉山）如图，四边形的外接圆为⊙O，，，，则的度数为（）A. B.C.D.24.（2020·眉山）一副三角板如图所示摆放，则与的数量关系为（）A. B. C.D.25.（2020·凉山州）如图，等边三角形ABC和正方形ADEF都内接于，则（）A. B.C.D.26.（2020·凉山州）点C是线段AB的中点，点D是线段AC的三等分点．若线段，则线段BD的长为（）A. 10cmB. 8cmC. 8cm或10cm D. 2cm或4cm27.（2020·淄博）如图，若△ABC≌△ADE，则下列结论中一定成立的是（）A. AC＝DEB. ∠BAD＝∠CAE C. AB＝AE D. ∠ABC＝∠AED28.（2020·淄博）如图1，点P从△ABC的顶点B出发，沿B→C→A匀速运动到点A，图2是点P运动时，线段BP的长度y随时间x变化的关系图象，其中M是曲线部分的最低点，则△ABC的面积是（）A. 12B.24 C. 36 D. 48 29.（2020·淄博）如图，在直角坐标系中，以坐标原点O（0，0），A（0，4），B（3，0）为顶点的Rt△AOB，其两个锐角对应的外角角平分线相交于点P，且点P恰好在反比例函数y＝的图象上，则k的值为（）A. 36B.48 C.49 D. 64 30.（2020·淄博）如图，在四边形ABCD中，CD∥AB，AC⊥BC，若∠B＝50°，则∠DCA等于（）A. 30°B.35° C. 40°D. 45°二、填空题31.（2020·徐州）在中，若，，则的面积的最大值为________.32.（2020·徐州）如图，在中，，，.若以所在直线为轴，把旋转一周，得到一个圆锥，则这个圆锥的侧面积等于________.33.（2020·徐州）如图，在中，，、、分别为、、的中点，若，则________.34.（2020·徐州）如图，，在上截取.过点作，交于点，以点为圆心，为半径画弧，交于点；过点作，交于点，以点为圆心，为半径画弧，交于点；按此规律，所得线段的长等于________.35.（2020·河池）如图，菱形ABCD的周长为16，AC，BD交于点O，点E在BC上，OE∥AB，则OE的长是________.36.（2020·铁岭）如图，以为边，在的同侧分别作正五边形和等边，连接，则的度数是________.37.（2020·铁岭）如图，在中，，以为圆心，以适当的长为半径作弧，交于点，交于点，分别以为圆心，以大于的长为半径作弧，两弧在的内部相交于点，作射线，交于点，点在边上，，连接，则的周长为________.38.（2020·铁岭）一张菱形纸片的边长为，高等于边长的一半，将菱形纸片沿直线折叠，使点与点重合，直线交直线于点，则的长为________ .39.（2020·盘锦）如图，直线，的顶点和分别落在直线和上，若，，则的度数是________.40.（2020·盘锦）如图，菱形的边长为4，，分别以点和点为圆心，大于的长为半径作弧，两弧相交于两点，直线交于点，连接，则的长为________.三、综合题41.（2020·徐州）如图，，，. ，与交于点.（1）求证：；（2）求的度数.42.（2020·玉林）如图，四边形ABCD中，对角线AC与BD交于点O，且OA＝OB＝OC＝OD＝AB.（1）求证：四边形ABCD是正方形；（2）若H是边AB上一点（H与A，B不重合），连接DH，将线段DH绕点H顺时针旋转90°，得到线段HE，过点E分别作BC及AB延长线的垂线，垂足分别为F，G.设四边形BGEF的面积为s1，以HB，BC为邻边的矩形的面积为s2，且s1＝s2.当AB＝2时，求AH的长.43.（2020·玉林）如图，AB是⊙O的直径，点D在直径AB上（D与A，B不重合），CD⊥AB，且CD＝AB，连接CB，与⊙O交于点F，在CD上取一点E，使EF＝EC.（1）求证：EF是⊙O的切线；（2）若D是OA的中点，AB＝4，求CF的长.44.（2020·河池）如图（1）如图（1），已知CE与AB交于点E，AC=BC，∠1=∠2.求证：.（2）如图（2），已知CD的延长线与AB交于点E，AD=BC，∠3=∠4.探究AE与BE的数量关系，并说明理由.45.（2020·铁岭）在等腰和等腰中，，，将绕点逆时针旋转，连接，点为线段的中点，连接.（1）如图1，当点旋转到边上时，请直接写出线段与的位置关系和数量关系；（2）如图2，当点旋转到边上时，（1）中的结论是否成立？若成立，请写出证明过程，若不成立，请说明理由.（3）若，在绕点逆时针旋转的过程中，当时，请直接写出线段的长.46.（2020·铁岭）如图，四边形内接于是直径，，连接，过点的直线与的延长线相交于点，且.（1）求证：直线是的切线；（2）若，，求的长.47.（2020·盘锦）如图，是的直径，是的弦，交于点，连接，过点作，垂足为，.（1）求证：；（2）点在的延长线上，连接.①求证：与相切；②当时，直接写出的长.48.（2020·盘锦）如图，两点的坐标分别为，将线段绕点逆时针旋转90°得到线段，过点作，垂足为，反比例函数的图象经过点.（1）直接写出点的坐标，并求反比例函数的解析式；（2）点在反比例函数的图象上，当的面积为3时，求点的坐标.49.（2020·锦州）已知和都是等腰直角三角形，.（1）如图1：连，求证：；（2）若将绕点O顺时针旋转，①如图2，当点N恰好在边上时，求证：；②当点在同一条直线上时，若，请直接写出线段的长.50.（2020·阜新）如图，正方形和正方形（其中），的延长线与直线交于点H.（1）如图1，当点G在上时，求证：，；（2）将正方形绕点C旋转一周.①如图2，当点E在直线右侧时，求证：；②当时，若，，请直接写出线段的长答案解析部分一、单选题1.【答案】 C【解析】【解答】解：如图，过点C作CD∥AE交AB于点D，∴∠DCA＝∠EAC＝35°，∵AE∥BF，∴CD∥BF，∴∠BCD＝∠CBF＝55°，∴∠ACB＝∠ACD+∠BCD＝35°+55°＝90°，∴△ABC是直角三角形.故答案为：C.【分析】如图，过点C作CD∥AE交AB于点D，可得∠DCA＝∠EAC＝35°，根据AE∥BF，可得CD∥BF，可得∠BCD＝∠CBF＝55°，进而得△ABC是直角三角形.2.【答案】 B【解析】【解答】解：长120cm的木条与三角形木架的最长边相等，则长120cm的木条不能作为一边，设从120cm的木条上截下两段长分别为xcm，ycm（x+y≤120），由于长60cm的木条不能与75cm的一边对应，否则x、y有大于120cm，当长60cm的木条与100cm的一边对应，则，解得：x＝45，y＝72；当长60cm的木条与120cm的一边对应，则，解得：x＝37.5，y＝50.答：有两种不同的截法：把120cm的木条截成45cm、72cm两段或把120cm的木条截成37.5cm、50cm两段. 故答案为：B.【分析】分类讨论：长120cm的木条与三角形木架的最长边相等，则长120cm的木条不能作为一边，设从120cm的一根上截下的两段长分别为xcm，ycm（x+y≤120），易得长60cm的木条不能与75cm的一边对应，所以当长60cm的木条与100cm的一边对应时有；当长60cm的木条与120cm的一边对应时有，然后分别利用比例的性质计算出两种情况下得x和y的值.3.【答案】 A【解析】【解答】证明：延长DE到点F，使EF＝DE，连接FC，DC，AF，∵点D，E分别是△ABC的边AB，AC的中点，∴AD＝BD，AE＝EC，∴四边形ADCF是平行四边形，∴CF AD.即CF BD，∴四边形DBCF是平行四边形，∴DF BC，∴DE∥BC，且DE＝BC.∴正确的证明顺序是②→③→①→④，故答案为：A.【分析】证出四边形ADCF是平行四边形，得出CF AD.即CF BD，则四边形DBCF是平行四边形，得出DF BC，即可得出结论.4.【答案】 C【解析】【解答】解：∵CE平分∠BCD，∴∠BCE=∠DCE，∵四边形ABCD是平行四边形，∴AB=CD，AD=BC，AB∥CD，∴∠BEC=∠DCE，∴∠BEC=∠BCE，∴BC=BE=5，∴AD=5，∵EA=3，ED=4，在△AED中，，即，∴∠AED=90°，∴CD=AB=3+5=8，∠EDC=90°，在Rt△EDC中，.故答案为：C.【分析】利用平行四边形的性质，可证得AB=CD，AD=BC，AB∥CD，再利用角平分线的定义及平行线的性质可以推出∠BEC=∠BCE，利用等角对等边，就可求出BC的长，即可得到AD的长；再利用勾股定理的逆定理证明△ADE是直角三角形，由此可证△DEC是直角三角形，利用勾股定理求出CE的长。

中考数学复习第四章图形的初步认识与三角形第17讲等腰三角形与直角三角形

12
【思路点拨】本题考查等腰三角形的性质．根据等腰三角形的性质和三角形的内角和即可得到结论．
第一部分教材同步复习
13
1.(2017海南)已知△ABC的三边长分别为4,4,6，在△ABC所在平面
内画一条直线，将△ABC分割成两个三角形，使其中的一个是等腰三角形，则这样
的直线最多可画__________条． A．3
第一部分教材同步复习
6
(2)在 Rt△ABC 中，∠ACB＝90°，∠A＝30°，BC＝1，则 AB 边上的中线长为
A．1
B．2
(A )
C．1.5
D． 3
(3)已知直角三角形中 30°角所对的直角边为 2 cm，则斜边的长为
(B )
A．2 cm
B．4 cm
C．6 cm
D．8 cm
第一部分教材同步复习
周长：c＝a＋b＋c；
周长、面积
面积：SRt△ABC＝12ab＝12ch(其中
a，b
为两个直角边，c
为斜边，h
为斜边上
的高)
第一部分教材同步复习
知识点四等腰直角三角形的判定与性质
【回顾】
(1)等腰直角三角形的直角边为 2，则斜边的长为
A． 2
B．2 2
C．1
D．2
1 (2)等腰直角三角形的斜边长 2，则它的面积为___2_______.
第一部分教材同步复习
8
(1)有一个角为⑤___9_0_°_____的三角形是直角三角形；
判 (2)勾股定理逆定理：如果三角形的三边长 a，b，c 满足 a2＋b2＝c2，那么定这个三角形是直角三角形；
(3)一条边的中线等于这条边的一半的三角形是直角三角形；

河北省中考数学系统复习第四单元图形的初步认识与三角形方法技巧训练(一)与角平分线有关的基本模型

如图5，BO是∠ABC的平分线，过点O作OE⊥AB于点E，过点O作OF⊥BC于点F，则OE＝OF，△BEO≌△BFO.
②角平分线的两端过角的顶点取相等的两条线段构造全等三角形
如图6，BO是∠ABC的平分线，在BA，BC上取线段BE＝BF，则△BEO≌△BFO.
解题通法：遇到角平分线时，我们通常过角平分线上的一点向两边作垂线或在角平分线的两端取相等的线段构造全等三角形．
与角平分线有关的图形与辅助线
1．角平分线＋平行线→等腰三角形
如图4，BD是∠ABC的平分线，点O是BD上一点，OE∥BC交AB于点E，则△BOE是等腰三角形．
解题通法：遇到角平分线及平行线，除了可以得到角度的关系，还可以得到一个等腰三角形．
图4 图5 图6 图7
2．与角平分线有关的辅助线
①过角平分线上的点作角两边的垂线
方法技巧训练(一) 与角平分线有关的基本模型
三角形中角平分线的夹角的计算
类型1 两个内角平分线的夹角
如图1，在△ABC中，∠ABC，∠ACB的平分线BE，CF相交于点G，则∠BGC＝90°＋ ∠A.
图1 图2 图3
解题通法：三角形两内角的平分线的夹角等于90°与第三个内角的一半的和．
类型2 一个内角平分线和一个外角平分线的夹角
A．10 cmB．28 cmC．20 cmD．18 cm
3.如图，矩形ABCD中，AB＝4 cm，BC＝8 cm，如果将该矩形沿对角线BD折叠，那么图中阴影部分的面积(B)
A．8 cm2B．10 cm2C．15 cm2D．20 cm2
4．(2018·某某)如图，∠B＝∠C＝90°，M是BC的中点，DM平分∠ADC，且∠ADC＝110°，则∠MAB＝(B)
A．30° B．35° C．45° D．60°

2020年中考数学第一轮复习第十七讲三角形与全等三角形知识点+真题学生版(后含答案)

2020年中考数学第一轮复习教案第三章图形的认识与三角形第十七讲三角形与全等三角形【中考真题考点例析】考点一：三角形三边关系例1 （温州）下列各组数可能是一个三角形的边长的是（）A．1，2，4 B．4，5，9 C．4，6，8 D．5，5，11对应练习1－1（长沙）如果一个三角形的两边长分别为2和4，则第三边长可能是（）A．2 B．4 C．6 D．8考点二：三角形内角、外角的应用例2 （2019青岛中考）如图，BD 是△ABC 的角平分线，AE⊥ BD ，垂足为F ．若∠ABC＝35°，∠ C＝50°，则∠CDE 的度数为（）A. 35°B. 40°C. 45°D. 50°对应练习2－1（2019年威海）把一块含有45°角的直角三角板与两条长边平行的直尺如图放置（直角顶点在直尺的一条长边上），若∠1＝23°，则∠2＝°对应练习2－2（2019年枣庄）将一副直角三角板按如图所示的位置放置，使含30°角的三角板的一条直角边和含45°角的三角板的一条直角边放在同一条直线上，则∠α的度数是（）.A.45°B. 60°C. 75°D. 85°考点三：三角形全等的判定和性质例3 （2019年山东滨州）如图，在△OAB和△OCD中，OA=OB，OC=OD，OA>OC ，∠AOB=∠COD=40°，连接AC，BD交于点M，连接OM，下列结论：①AC=BD；②∠AMB=40°；③OM平分∠BOC；④MO平分∠BMC．其中正确的个数为（）A．4 B．3 C．2 D．1对应练习3－1 （天门）如图，已知△ABC ≌△ADE ，AB 与ED 交于点M ，BC 与ED ，AD 分别交于点F ，N ．请写出图中两对全等三角形（△ABC ≌△ADE 除外），并选择其中的一对加以证明．对应练习3－2 （宜宾）如图：已知D 、E 分别在AB 、AC 上，AB=AC ，∠B=∠C ，求证：BE=CD ．考点四：全等三角形开放性问题例4 （云南）如图，点B 在AE 上，点D 在AC 上，AB=AD ．请你添加一个适当的条件，使△ABC ≌△ADE （只能添加一个）．（1）你添加的条件是．（2）添加条件后，请说明△ABC ≌△ADE 的理由．对应练习4－1 （昭通）如图，AF=DC ，BC ∥EF ，只需补充一个条件，就得△ABC ≌△DEF ．第十七讲三角形与全等三角形参考答案【中考真题考点例析】考点一：三角形三边关系例1答案：C 对应练习1－1答案：B 考点二：三角形内角、外角的应用例2答案：C 对应练习2－1答案：68 对应练习2－2 答案：C 考点三：三角形全等的判定和性质MOCD B例3 答案：B 对应练习3－1 答案：△AEM ≌△ACN ，△BMF ≌△DNF ，△ABN ≌△ADM ．选择△AEM ≌△ACN ，证明：∵△ADE ≌△ABC ，∴AE=AC ，∠E=∠C ，∠EAD=∠CAB ，∴∠EAM=∠CAN ，∵在△AEM 和△ACN 中，∠E ＝∠CAE ＝AC∠EAM ＝∠CAN∴△AEM ≌△ACN （ASA ）．对应练习3－2 答案：证明：在△ABE 和△ACD 中，⎪⎩⎪⎨⎧)公共角A(＝∠A ∠)已知AC(＝ AB )已知C(＝∠B ∠ ∴△ABE ≌△ACD （ASA ），∴BE=CD （全等三角形的对应边相等）．考点四：全等三角形开放性问题例4 答案：解：（1）∵AB=AD ，∠A=∠A ，∴若利用“AAS ”，可以添加∠C=∠E ，若利用“ASA ”，可以添加∠ABC=∠ADE ，或∠EBC=∠CDE ，若利用“SAS ”，可以添加AC=AE ，或BE=DC ，综上所述，可以添加的条件为∠C=∠E （或∠ABC=∠ADE 或∠EBC=∠CDE 或AC=AE 或BE=DC ）；故答案为：∠C=∠E ；（2）选∠C=∠E 为条件．理由如下：∵在△ABC 和△ADE 中，⎪⎩⎪⎨⎧AD ＝AB E＝∠C ∠A ＝∠A ∠ ∴△ABC ≌△ADE （AAS ）．对应练习4－1 答案：BC=EF ，解析：∵AF=DC ，∴AF+FC=CD+FC ，即AC=DF ，∵BC ∥EF ，∴∠EFC=∠BCF ，∵在△ABC 和△DEF 中，⎪⎩⎪⎨⎧DF ＝AC BCF＝∠EFC ∠BC ＝EF ∴△ABC ≌△DEF （SAS ）．故答案为：BC=EF ．【聚焦中考真题】一、选择题 1.（湘西州）如图，一副分别含有30°和45°角的两个直角三角板，拼成如下图形，其中∠C=90°，∠B=45°，∠E=30°，则∠BFD 的度数是（）A ．15°B ．25°C ．30°D ．10°2．（鄂州）一副三角板有两个直角三角形，如图叠放在一起，则∠α的度数是（）A ．165°B ．120°C ．150°D ．135°3．（泉州）在△ABC 中，∠A=20°，∠B=60°，则△ABC 的形状是（）A ．等边三角形B ．锐角三角形C ．直角三角形D ．钝角三角形4．（宜昌）下列每组数分别表示三根木棒的长度，将它们首尾连接后，能摆成三角形的一组是（）A ．1，2，6B ．2，2，4C ．1，2，3D ．2，3，45．（衡阳）如图，∠1=100°，∠C=70°，则∠A 的大小是（）A ．10°B ．20°C ．30°D ．80°6．（河北）如图1，M 是铁丝AD 的中点，将该铁丝首尾相接折成△ABC ，且∠B=30°，∠C=100°，如图2．则下列说法正确的是（）A ．点M 在AB 上B ．点M 在BC 的中点处C ．点M 在BC 上，且距点B 较近，距点C 较远D ．点M 在BC 上，且距点C 较近，距点B 较远7．（铁岭）如图，在△ABC 和△DEC 中，已知AB=DE ，还需添加两个条件才能使△ABC ≌△DEC ，不能添加的一组条件是（）A．BC=EC，∠B=∠E B．BC=EC，AC=DCC．BC=DC，∠A=∠D D．∠B=∠E，∠A=∠D8．（台州）已知△A1B1C1△A2B2C2的周长相等，现有两个判断：①若A1B1=A2B2，A1C1=A2C2，则△A1B1C1≌△A2B2C2；②若∠A1=∠A2，∠B1=∠B2，则△A1B1C1≌△A2B2C2，对于上述的两个判断，下列说法正确的是（）A．①正确，②错误B．①错误，②正确C．①，②都错误D．①，②都正确9．（邵阳）如图所示，点E是矩形ABCD的边AD延长线上的一点，且AD=DE，连结BE交CD 于点O，连结AO，下列结论不正确的是（）A．△AOB≌△BOC B．△BOC≌△EOD C．△AOD≌△EOD D．△AOD≌△BOC10．（河北）一个正方形和两个等边三角形的位置如图所示，若∠3=50°，则∠1+∠2=（）A．90°B．100°C．130°D．180°11．（陕西）如图，在四边形ABCD中，AB=AD，CB=CD，若连接AC、BD相交于点O，则图中全等三角形共有（）A．1对B．2对C．3对D．4对二、填空题12.（威海）将一副直角三角板如图摆放，点C在EF上，AC经过点D．已知∠A=∠EDF=90°，AB=AC．∠E=30°，∠BCE=40°，则∠CDF= ．13．（黔东南州）在△ABC中，三个内角∠A、∠B、∠C满足∠B-∠A=∠C-∠B，则∠B= 度．14．（柳州）如图，△ABC≌△DEF，请根据图中提供的信息，写出x= ．15．（巴中）如图，已知点B、C、F、E在同一直线上，∠1=∠2，BC=EF，要使△ABC≌△DEF，还需添加一个条件，这个条件可以是．（只需写出一个）16．（郴州）如图，点D、E分别在线段AB，AC上，AE=AD，不添加新的线段和字母，要使△ABE≌△ACD，需添加的一个条件是（只写一个条件即可）．17.（达州）如图，在△ABC中，∠A=m°，∠ABC和∠ACD的平分线交于点A1，得∠A1；∠A1BC和∠A1CD的平分线交于点A2，得∠A2；…∠A2012BC和∠A2012CD的平分线交于点A2013，则∠A2013= 度．三、解答题18．（聊城）如图，四边形ABCD中，∠A=∠BCD=90°，BC=CD，CE⊥AD，垂足为E，求证：AE=CE．19．（菏泽）如图，在△ABC中，AB=CB，∠ABC=90°，D为AB延长线上一点，点E在BC边上，且BE=BD，连结AE、DE、DC．（1）求证：△ABE≌△CBD；（2）若∠CAE=30°，求∠BDC的度数．20．（临沂）如图，在△ABC中，AD是BC边上的中线，E是AD的中点，过点A作BC的平行线交BE的延长线于点F，连接CF．（1）求证：AF=DC；（2）若AB⊥AC，试判断四边形ADCF的形状，并证明你的结论．21．（东营）（1）如图（1），已知：在△ABC中，∠BAC=90°，AB=AC，直线m经过点A，BD⊥直线m，CE⊥直线m，垂足分别为点D、E．证明：DE=BD+CE．（2）如图（2），将（1）中的条件改为：在△ABC中，AB=AC，D、A、E三点都在直线m上，并且有∠BDA=∠AEC=∠BAC=α，其中α为任意锐角或钝角．请问结论DE=BD+CE是否成立？如成立，请你给出证明；若不成立，请说明理由．（3）拓展与应用：如图（3），D、E是D、A、E三点所在直线m上的两动点（D、A、E三点互不重合），点F为∠BAC平分线上的一点，且△ABF和△ACF均为等边三角形，连接BD、CE，若∠BDA=∠AEC=∠BAC，试判断△DEF的形状．22．（烟台）已知，点P是直角三角形ABC斜边AB上一动点（不与A，B重合），分别过A，B向直线CP作垂线，垂足分别为E，F，Q为斜边AB的中点．（1）如图1，当点P与点Q重合时，AE与BF的位置关系是，QE与QF 的数量关系式；（2）如图2，当点P在线段AB上不与点Q重合时，试判断QE与QF的数量关系，并给予证明；（3）如图3，当点P在线段BA（或AB）的延长线上时，此时（2）中的结论是否成立？请画出图形并给予证明．23．（玉林）如图，AB=AE，∠1=∠2，∠C=∠D．求证：△ABC≌△AED．24．（湛江）如图，点B、F、C、E在一条直线上，FB=CE，AB∥ED，AC∥FD，求证：AC=DF．25.（荆州）如图，△ABC与△CDE均是等腰直角三角形，∠ACB=∠DCE=90°，D在AB上，连结BE．请找出一对全等三角形，并说明理由．26．（十堰）如图，点D，E在△ABC的边BC上，AB=AC，BD=CE．求证：AD=AE．27.（佛山）课本指出：公认的真命题称为公理，除了公理外，其他的真命题（如推论、定理等）的正确性都需要通过推理的方法证实．（1）叙述三角形全等的判定方法中的推论AAS；（2）证明推论AAS．要求：叙述推论用文字表达；用图形中的符号表达已知、求证，并证明，证明对各步骤要注明依据．28．（内江）已知，如图，△ABC和△ECD都是等腰直角三角形，∠ACD=∠DCE=90°，D为AB边上一点．求证：BD=AE．29．（舟山）如图，△ABC与△DCB中，AC与BD交于点E，且∠A=∠D，AB=DC．（1）求证：△ABE≌DCE；（2）当∠AEB=50°，求∠EBC的度数？30．（荆门）如图1，在△ABC中，AB=AC，点D是BC的中点，点E在AD上．（1）求证：BE=CE；（2）如图2，若BE的延长线交AC于点F，且BF⊥AC，垂足为F，∠BAC=45°，原题设其它条件不变．求证：△AEF≌△BCF．31．（随州）如图，点F 、B 、E 、C 在同一直线上，并且BF=CE ，∠ABC=∠DEF ．能否由上面的已知条件证明△ABC ≌△DEF ？如果能，请给出证明；如果不能，请从下列三个条件中选择一个合适的条件，添加到已知条件中，使△ABC ≌△DEF ，并给出证明．提供的三个条件是：①AB=DE ；②AC=DF ；③AC ∥DF ．第十七讲三角形与全等三角形参考答案【聚焦中考真题】一、选择题1-5 AADDC 6-10 CCDAB 11 C二、填空题12答案：25°13答案：6014答案：2015答案：CA=FD16答案：∠B=∠C17答案：20152m解：∵A1B 平分∠ABC ，A1C 平分∠ACD ，∴∠A1=21∠A ，∠A2=21∠A1=221∠A ，… ∴∠A2 015=201521∠A=20152m 。

中考数学总复习第四单元图形的初步认识与三角形特殊三角形课件

课前双基巩固
考点四勾股定理及其逆定理
勾股定理如果直角三角形两直角边分别为 a,b,斜边为 c,那么
a2+b 2=c 2
勾股定理的逆定理如果三角形的三边 a,b,c 满足 a 2+b 2=c 2 ,那么这个三角形是直角三角形
逆定理
用途 (1)判断某三角形是不是直角三角形 ;(2)证明两条线段垂直 ;(3)解决生活中的实际问题
A.16 cm
B.17 cm
(B)
C.20 cm
D.16 cm 或 20 cm
课前双基巩固
3.下列四组线段中 ,能构成直角三角形的是 ( D )
A.a= 1,b= 2,c= 3
B.a= 2,b= 3,c= 4
C.a= 2,b= 4,c= 5
D.a= 3,b= 4,c= 5
4.如图 18-1,线段 AC 的垂直平分线交线段 AB 于点 D,∠A=50°,则∠BDC= ( B )
形,此时三角形的周长为 3+ 3+ 2= 8.
综上,三角形的周长为 11 或 8.
课前双基巩固
7.如图 18-2 所示,在△ABC 中,AB=AC,BD⊥AC,垂足为 D,∠A
= 40°,则 ∠DBC=
.
[答案 ] 20° [解析 ] ∵在△ABC 中,AB=AC,∠= 70°. 又∵BD⊥AC,∴∠ DBC= 90°-∠ACB= 90°-70°= 20°.
课前双基巩固
例 1 (2)[2018·
成都] 等腰三角形的一个底角为 50°,则它的顶角的度数为 80° .
[ 方法模型] 在等腰三角形中进行边或角的计算时,往往要分类讨论:当等腰三角形的边不确定时,要利用三边关系确定腰或底;当等腰三角形的角不确定时,要利用三角形的内角和来确定顶角和底角.

2020年中考数学第一轮复习第十九讲解直角三角形知识点+真题

2020年中考数学第一轮复习教案第三章图形的认识与三角形第十九讲解直角三角形【基础知识回顾】一、锐角三角函数定义：在Rt△ABC中，∠C=900, ∠A、∠B、∠C的对边分别为a、b、c，则∠A的正弦可表示为：sinA= ，∠A的余弦可表示为cosA= ∠A的正切：tanA= ，它们统称为∠A的锐角三角函数注意：1、sinA、∠cosA、tanA表示的是一个整体，是两条线段的比，没有单位，这些比值只与有关，与直角三角形的无关2、取值范围<sinA< ，cosA< ，tanA>注意：1、三个特殊角的三角函数值都是根据定义应用直角三角形性质算出来的，要在理解的基础上结合表格进行记忆2、正弦和正切值随着角度的增大而余弦值随着角度的增大而3、几个特殊关系：⑴sinA+cos2A= ,tanA=sin A（）⑵若∠A+∠B=900，则sinA= ，tanA·tanB=三、解直角三角形：1、定义：由直角三角形中除直角外的个已知元素，求出另外个未知元素的过程叫解直角三角形2、解直角三角形的依据：Rt∠ABC中，∠C=900 三边分别为a、b、c⑴三边关系：⑵两锐角关系⑶边角之间的关系：sinA cosA tanAsinB cosB tanB注意：解直角三角形中已知的两个元素应至少有一个是当没有直角三角形时应注意构造直角三角形，再利用相应的边角关系解决3、解直角三角形应用中的有关概念⑴仰角和俯角：如图：在图上标上仰角俯角 ⑵坡度坡角：如图：斜坡AB 的垂直度h 和水平宽度l 的比叫做坡度，用i 表示，即i= 坡面与水平面得夹角为用字母α表示，则i=tanα=hl。

⑶方位角：是指南北方向线与目标方向所成的小于900的水平角如图：OA 表示 OB 表示 OC 表示OD 表示（也可称东南方向）3、利用解直角三角形知识解决实际问题的一般步骤：⑴把实际问题抓化为数学问题（画出平面图形，转化为解直角三角形的问题）⑵根据条件特点，选取合适的锐角三角函数去解直角三角形 ⑶解出数学问题答案，从而得到实际问题的答案注意：在解直角三角形实际应用中，先构造符合题意的三角形，解题的关键是弄清在哪个直角三角形中用多少度角的哪种锐角三角函数解决【中考真题考点例析】考点一：锐角三角函数的概念例1 （2019年威海）如图，一个人从山脚下的A 点出发，沿山坡小路AB 走到山顶B 点。

2024年中考第一轮复习相似三角形课件

么这四条线段 a,b,c,d 叫做成比例线段,简称比例线段
（续表）
如果点 P 把线段 AB 分成两条线段 AP 和 PB(AP>BP),使
黄金分割
④ PA2=PB·AB ,那么称线段 AB 被点 P 黄金分割,点 P 叫做线段 AB
的黄金分割点,线段 AP 与 AB 的比叫做黄金比,黄金比
AP
=⑤
①∠B=∠ACD;②∠ADC=∠ACB;

③
=

;④AC2=AD·AB.

A.1 个
B.2 个
C.3 个
D.4 个
图20-7
10.如图20-8,点F在平行四边形ABCD的边AB上,射线CF交DA的延长线于点E,在
不添加辅助线的情况下,与△AEF相似的三角形有 2
图20-8
个.
■ 知识梳理
与△ OCD 的面积分别是 S1 和 S2,△ OAB 和△ OCD 的周长分别是 C1 和 C2,则下列等式一
定成立的是

3
A. =

2

3
C. 1 =
2
2
(
)

3
B. =

2

3
D. 1 =
2
2
图20-9
【方法点析】相似三角形主要应用在以下几方面:①求角的度数;②求或证明比
值关系;③证线段等积式;④求面积或面积比.相似三角形的对应边成比例是求线
■ 知识梳理
1.比例的性质

(1)基本性质:

=

⇒ad=①

bc
.

(2)比例中项:如果三个数 a,b,c 满足比例式 = ⇔② b2=ac ,则 b 就叫做 a,c 的比例

三角形基本知识、全等三角形中考复习

第16讲三角形的基本知识及全等三角形考点1 三角形的概念及其分类⎧⎪⎪⎪⎪⎪⎪⎪⎪⎧⎪⎧⎨⎪⎪⎪⎪⎪⎨⎪⎪⎪⎪⎪⎪⎩⎪⎨⎪⎧⎪⎪⎪⎪⎧⎨⎪⎪⎪⎨⎪⎪⎪⎪⎩⎩⎪⎩⎩概念：由不在同一直线上的三条线段连接所得到的图形叫做三角形.角三角形按角分类角三角形角三角形分类不等边三角形底与腰不相等的等腰三角形按边分类等腰三角形三角形①②③④⑤ 考点2 与三角形有关的线段【易错提示】“SSA”和“AAA”不能判定三角形全等.1.判断给定的三条线段能否组成三角形，只需判断两条较短线段的和是否大于最长线段即可.2.“截长法”和“补短法”是证明和差关系的重要方法，无论用哪一种方法都是要将线段的和差关系转化为证明线段相等的问题，因此添加辅助线构造全等三角形是通向结论的桥梁.命题点1 三角形中的线段例1 不一定在三角形内部的线段是( )A.三角形的角平分线B.三角形的中线C.三角形的高D.三角形的中位线【思路点拨】不管是哪种类型的三角形，三角形的角平分线、中线和中位线都在三角形内部，但是锐角三角形的三条高在三角形内部，直角三角形的一条高在三角形内部，其余两条高与直角边重合，钝角三角形的一条高在三角形内部，其余两条高在三角形外部.方法归纳：解答本题的关键是熟练掌握三角形高、角平分线和中线的画法.1.(2013·温州)下列各组数可能是一个三角形的边长的是( )A.1,2,4B.4,5,9C.4,6,8D.5,5,112.如图，在长方形网格中，每个小长方形的长为2，宽为1，A、B两点在网格格点上，若点C也在网格格点上，以A、B、C为顶点的三角形面积为2，则满足条件的点C个数是( )A.2B.3C.4D.53.三角形的下列线段中能将三角形的面积分成相等的两部分的是( )A.中线B.角平分线C.高D.中位线命题点2 三角形中的角例2 (2013·海南改编)如图，AB∥CD，AE＝AF，CE交AB于点F，∠C＝110°，求∠A的度数.【思路点拨】根据“两直线平行，同位角相等”求出∠EFB的度数，进而求出∠AFE，根据“等边对等角”求出∠E的度数，根据三角形内角和定理求出∠A的度数.【解答】方法归纳：当问题中含有平行线时，可利用平行线的性质将其转化为其他角；当该角是一个三角形的外角或内角时，根据三角形外角的性质和三角形内角和定理进行计算.1.(2013·龙岩)如图，AB∥CD，BC与AD相交于点M，N是射线CD上的一点.若∠B＝65°，∠MDN＝135°，则∠AMB＝ .2.(2014·邵阳)如图，在△ABC中，∠B＝46°，∠C＝54°,AD平分∠BAC，交BC于D，DE ∥AB，交AC于E，则∠ADE的大小是( )A.45°B.54°C.40°D.50°3.(2014·威海)如图，在△ABC中，∠ABC＝50°，∠ACB＝60°，点E在BC的延长线上，∠ABC的平分线BC与∠ACE的平分线CD相交于点D，连接AD.下列结论不正确的是( ) A.∠BAC＝70° B.∠DOC＝90° C.∠BDC＝35° D.∠DAC＝55°命题点3 三角形的中位线例3 (2014·湘潭)如图，AB是池塘两端，设计一方法测量AB的距离，取点C，连接AC、BC，再取它们的中点D、E，测得DE=15米，则AB=( )A.7.5米B.15米C.22.5米D.30米【思路点拨】因为DE是△ABC的中位线，利用中位线定义求AB的长.方法归纳：解答本题的关键是要依据题目条件，活用中位线定理的结论.1.(2014·泸州)如图，等边△ABC中，点D、E分别为边AB、AC的中点，则∠DEC的度数为( )A.30°B.60°C.120°D.150°2.如图，D是△ABC内一点，BD⊥CD,AD=6,BD=4,CD=3.E、F、G、H分别是AB、AC、CD、BD 的中点，则四边形EFGH的周长是( )A.7B.9C.10D.113.如图，在△ABC中，点D、E、F分别是AB、AC、BC的中点，若△ABC的周长为12 cm，则△DEF的周长是 cm.命题点4 全等三角形的性质与判定例4 (2014·福州)如图，点E，F在BC上，BE=CF，AB=DC，∠B=∠C.求证：∠A=∠D.【思路点拨】∠A与∠D分别在△ABF和△DEC中，直接证明△ABF和△DCE全等即可. 【解答】方法归纳：证明两条边或两个角相等时，若两条边或两个角分别在两个三角形当中，通常证明这两条边或两个角所在的三角形全等.1.(2014·南充)如图，AD、BC相交于O，OA=OC,∠OBD=∠ODB.求证：AB=CD.2.(2014·宜宾)如图，已知：在△AFD和△CEB中，点A、E、F、C在同一直线上，AE=CF，∠B=∠D，AD∥BC.求证：AD=BC.1.小华在电话中问小明：“已知一个三角形三边长分别是4，9，12，如何求这个三角形的面积？”小明提示说：“可通过作最长边上的高来求解.”小华根据小明的提示作出的图形正确的是( )2.(2013·襄阳)如图，在△ABC中，D是BC延长线上一点，∠B＝40°，∠ACD＝120°，则∠A等于( )A.60°B.70°C.80°D.90°3.(2014·枣庄)如图，AB∥CD，AE交CD于C，∠A=34°，∠DEC=90°，则∠D的度数为( )A.17°B.34°C.56°D.124°4.(2013·河池)一个三角形的周长是36 cm，则以这个三角形各边中点为顶点的三角形的周长是( )A.6 cmB.12 cmC.18 cmD.36 cm5.(2014·益阳)如图，平行四边形ABCD中，E,F是对角线BD上的两点，如果添加一个条件使△ABE≌△CDF，则添加的条件不能是( )A.AE=CFB.BE=FDC.BF=DED.∠1=∠26.(2014·广州)△ABC中，已知∠A=60°,∠B=80°,则∠C的外角的度数 .7.(2014·长沙)如图，点B，E，C，F在一条直线上，AB∥DE，AB=DE，BE=CF，AC=6，则DF= .8.(2014·温州)如图，直线AB，CD被BC所截，若AB∥CD，∠1=45°，∠2=35°，则∠3= 度.9.(2013·娄底)如图，AB=AC，要使△ABE≌△ACD，应添加的条件是 .(添加一个条件即可)10.(2014·连云港)如图，AB∥CD，∠1=62°，FG平分∠EFD，则∠2= .11.(2013·威海)将一副直角三角板如图摆放,点C在EF上,AC经过点D,已知∠A=∠EDF=90°,AB=AC,∠E=30°,∠BCE=40°,则∠CDF= .12.(2014·威海)如图，有一直角三角形纸片ABC，边BC＝6，AB＝10，∠ACB＝90°，将该直角三角形纸片沿DE折叠，使点A与点C重合，则四边形DBCE的周长为 .13.(2014·十堰)如图，点D在AB上，点E在AC上，AB=AC，AD=AE.求证：∠B=∠C.14.(2014·武汉)如图，AC和BD相交于点O，OA=OC，OB=OD.求证：DC∥AB.15.(2014·宜昌)如图，在Rt△ABC中，∠ACB=90°,∠B=30°,AD平分∠CAB.(1)求∠CAD的度数；(2)延长AC至E，使CE=AC,求证:DA=DE.16.(2014·杭州)在△ABC中，AB=AC，点E,F分别在AB,AC上，AE=AF，BF与CE相交于点P，求证：PB=PC，并请直接写出图中其他相等的线段.17.(2014·泰安)如图，∠ACB=90°，D为AB的中点，连接DC并延长到E，使CE=13CD,过点B作BF∥DE，与AE的延长线交于点F.若AB=6，则BF的长为( )A.6B.7C.8D.1018.(2013·达州改编)如图，在△ABC中，∠A=m°，∠ABC和∠ACD的平分线交于点A1，得∠A1；∠A1BC和∠A1CD的平分线交于点A2，得∠A2；…∠A2 014BC和∠A2 014CD的平分线交于点A2 015，则∠A2 015= 度.19.(2014·苏州)如图，在Rt△ABC中，∠ACB=90°,点D，F分别在AB，AC上，CF=CB.连接CD，将线段CD绕点C按顺时针方向旋转90°后得CE，连接EF.(1)求证：△BCD≌△FCE;(2)若EF∥CD，求∠BDC的度数.。

浙江省2017中考数学总复习第一篇考点梳理;即时训练第四章图形的认识与三角形第15课时全等三角形课件

(1)证明：∵五边形 ABCDE 是正五边形， ∴ AB＝ BC，∠ ABM＝∠ BCN. 又 BM＝ CN，∴△ ABM≌△ BCN. (2)解： ∵∠ APN 是△ ABP 的一个外角， ∴ ∠ APN ＝ ∠ BAM ＋ ∠ ABN ＝ ∠ CBN ＋ ∠ ABN ＝（ 5－ 2）× 180° ∠ ABC＝＝ 108° . 5
考点一全等三角形的概念Fra bibliotek性质1．概念：能够重合的两个三角形叫做全等三角形．温馨提示：记两个三角形全等时，通常把表示对应顶点的字母写在对应的位置上 . 如右图，△ ABC 和△ DBC 全等，点 A 和点 D，点 B 和点 B，点 C 和点 C 是对应顶点，记作△ ABC≌△ DBC．
如图，已知△ ABC 三个内角的平分线交于点 O，点 D 在 CA 的延长线上，且 DC＝ BC， AD＝ AO，若∠ BAC ＝ 80° ，则∠ BCA 的度数为．
【解析】 ∵∠ BAC＝ 80° ， ∴∠ BAD ＝ 100° ， ∠ BAO ＝ 40° ， ∴∠ DAO＝ 140° .∵ AD＝ AO， ∴∠ D＝ 20° .∵△ ABC 三个内角的平分线交于点 O， ∴∠ ACO＝∠ BCO.在△ COD 和△ COB 中，CD＝ CB，∠ OCD＝∠ OCB，OC 是公共边， ∴△ COD≌△ COB ， ∴∠ D ＝ ∠ CBO. ∴∠ CBO ＝ 20° ， ∴∠ ABC＝ 40° ，∴∠ BCA＝ 60° . 【答案】 60°
第15课时
全等三角形
1．(2016· 金华 )如图，已知∠ ABC＝∠ BAD，添加下列条件还不能判定△ ABC≌△ BAD 的是 ( A )
A． AC＝ BD C．∠ C＝∠ D

2014中考数学复习课件14三角形及性质-第一轮复习第四单元三角形

A `
E B
30° D
F
C
第 15 题 3
考点直角三角形的性质和判定如图，∠BAM=30° ，其中 AB=2 3 ，点 P 是 AM 上的动点，连接 BP，当 AP= 时， 3或 4 △ABP 是直角三角形。
30°
30°
考点直角三角形的性质和判定
（ 2013 哈尔滨 19）在△ ABC 中， AB= 2 2 ， BC=1， ∠ ABC=45° ，以 AB 为一边作等腰直角三角形 ABD，使 ∠ABD=90° ，连接 CD，则线段 CD 的长为 5或 13 ．
3．(2013· 湘西州)如图，一副分别含有 30° 和 45° 角的两个直角三角板，拼在一起，其中∠C＝90° ，∠B＝ 45° ， ∠E＝30° ，则∠BFD 的度数是( A A．15° C．30° B．25° D．10° )
解析： ∵∠ E＝ 30° ， ∴∠C DF ＝ 60° .∵∠C DF 是 △ BDF 的外角，∴∠BFD＝ ∠C DF－∠B＝ 60° － 45° ＝ 15° .故选 A.
2014中考复习第一轮
第14讲
三角形及性质
第14讲
三角形及性质
│考点随堂练│
考点一三角形定义及其分类 1.定义：三条线段首尾顺次连接所成的图形叫三角形
2.按边分为：
三角形底边和腰不相等的等腰三角形等腰三角形等边三角形
不等边三角形三边互不相等
3.按角分为：
三角形锐角三角形斜三角形钝角三角形
直角三角形
考点二
一般三角形的性质
1．三角形的两边之和大于第三边，两边之差小于第三边． 2．三角形的内角和是180° 3.三角形的外角等于与它不相邻的两个内角的和，三角形的外角大于任何一个和它不相邻的内角． 4．如果三角形的三条边固定，那么三角形的形状和大小就完全确定了，三角形的这个特征，叫做三角形的稳定性．

初中等角三角形综合知识归纳

初中等角三角形综合知识归纳导读：我根据大家的需要整理了一份关于《初中等角三角形综合知识归纳》的内容，具体内容：几何可以说占了初中数学的半壁江山，囊括了包括等角三角形在内的无数重点知识、难点知识、无数的中考考点。

为此，以下是我分享给大家的初中等角三角形综合知识，希望可以帮到你!初中等角三...几何可以说占了初中数学的半壁江山，囊括了包括等角三角形在内的无数重点知识、难点知识、无数的中考考点。

为此，以下是我分享给大家的初中等角三角形综合知识，希望可以帮到你!初中等角三角形综合知识第一章图形的初步认识考点一、线段垂直平分线，角的平分线，垂线1、线段垂直平分线的性质定理及逆定理垂直于一条线段并且平分这条线段的直线是这条线段的垂直平分线。

线段垂直平分线的性质定理：线段垂直平分线上的点和这条线段两个端点的距离相等。

逆定理：和一条线段两个端点距离相等的点，在这条线段的垂直平分线上。

2、角的平分线及其性质一条射线把一个角分成两个相等的角，这条射线叫做这个角的平分线。

角的平分线有下面的性质定理：(1)角平分线上的点到这个角的两边的距离相等。

(2)到一个角的两边距离相等的点在这个角的平分线上。

3垂线的性质：性质1：过一点有且只有一条直线与已知直线垂直。

性质2：直线外一点与直线上各点连接的所有线段中，垂线段最短。

简称：垂线段最短。

考点二、平行线1、平行线的概念在同一个平面内，不相交的两条直线叫做平行线。

同一平面内，两条直线的位置关系只有两种：相交或平行。

4、平行线的性质(1)两直线平行，同位角相等;(2)两直线平行，内错角相等;(3)两直线平行，同旁内角互补。

考点三、投影与视图1、投影投影的定义：用光线照射物体，在地面上或墙壁上得到的影子，叫做物体的投影。

平行投影：由平行光线(如太阳光线)形成的投影称为平行投影。

中心投影：由同一点发出的光线所形成的投影称为中心投影。

2、视图当我们从某一角度观察一个实物时，所看到的图像叫做物体的一个视图。

人教版九年级数学中考总复习《直角三角形与勾股定理》课件20张 (共20张PPT)

考点精讲
【例】（2016广东）如图1-4-5-1，
Rt△ABC中，∠B=30°，∠ACB=90°， CD⊥AB交AB于点D，以CD为较短的直角边向△CDB的同侧作Rt△DEC，满足∠E= 30°，∠DCE=90°，再用同样的方法作 Rt△FGC，∠FCG=90°，继续用同样的方法作Rt△HIC， ∠HCI=90°. 若AC=a，求CI的长.
课堂巩固训练
1. 将一副直角三角板按如图1-4-5-11放置，若∠AOD=20°，
则∠BOC的大小为
（B）
A. 140°
B. 160°
C. 170° D. 150°
2. 如图1-4-5-12，在Rt△ABC中，∠B=90°，∠A=30°，DE垂
思路点拨：在Rt△ACD中，利用30°角的性质和勾股定理求出 CD的长；同理在Rt△ECD中求出FC的长，在Rt△FCG中求出CH 的长；最后在Rt△HCI中，利用30°角的性质和勾股定理求出 CI的长. 解：在Rt△ACB中，∠B=30°，∠ACB=90°， ∴∠A=90°-30°=60°. ∵CD⊥AB， ∴∠ADC=90°. ∴ቤተ መጻሕፍቲ ባይዱACD=30°.
•1、多少白发翁，蹉跎悔歧路。寄语少年人，莫将少年误。 •2、三人行，必有我师焉；择其善者而从之，其不善者而改之。2021/10/312021/10/312021/10/3110/31/2021 8:14:06 PM •3、一年之计，莫如树谷；十年之计，莫如树木；终身之计，莫如树人4、智力教育就是要扩大人的求知范围 •5、教育是一个逐步发现自己无知的过程。 •6、要经常培养开阔的胸襟，要经常培养知识上诚实的习惯，而且要经常学习向自己的思想负责任。2021年10月 2021/10/312021/10/312021/10/3110/31/2021

2022年中考训练专题九图形的初步认识与三角形(含答案)

专题九图形的初步认识与三角形一、单选题1.（2022最新·衢州）过直线l外一点P作直线l的平行线，下列尺规作图中错误的是（）A. B. C. D.2.（2022最新·衢州）如图，把一张矩形纸片ABCD按所示方法进行两次折叠，得到等腰直角三角形BEF，若BC=1，则AB的长度为（）A. B. C.D.3.（2022最新·台州）把一张宽为1cm的长方形纸片ABCD折叠成如图所示的阴影图案，顶点A，D互相重合，中间空白部分是以E为直角顶点，腰长为2cm的等腰直角三角形，则纸片的长AD（单位:cm）为（）A. 7+3B. 7+4C. 8+3D. 8+44.（2022最新·绍兴）将如图的七巧板的其中几块，拼成一个多边形，为中心对称图形的是( )A. B. C. D.5.（2022最新·绍兴）如图，等腰三角形ABC中，∠ABC=90°，BA=BC，将BC绕点B顺时针旋转θ(0°<θ<90°)，得到BP，连结CP，过点A作AH⊥CP 交CP的延长线于点H，连结AP，则∠PAH的度数（）A. 随着θ的增大而增大B. 随着θ的增大而减小C. 不变D. 随着θ的增大，先增大后减小6.（2022最新·宁波）如图，在Rt△ABC中，∠ACB=90°，CD为中线，延长CB 至点E，使BE=BC，连结DE，F为DE中点，连结BF.若AC=8，BC=6，则BF的长为（）D. 47.（2022最新·宁波）△BDE和△FGH是两个全等的等边三角形，将它们按如图的方式放置在等边三角形ABC内.若求五边形DECHF的周长，则只需知道（）A. △ABC的周长B. △AFH的周长C. 四边形FBGH的周长 D. 四边形ADEC的周长8.（2022最新·金华·丽水）如图，工人师傅用角尺画出工件边缘AB的垂线a和b，得到a∥b，理由是（）A. 连结直线外一点与直线上各点的所有线段中，垂线段最短B. 在同一平面内，垂直于同一条直线的两条直线互相平行C. 在同一平面内，过一点有一条而且仅有一条直线垂直于已知直线D. 经过直线外一点，有且只有一条直线与这条直线平行9.（2019·衢州）如图，取两根等宽的纸条折叠穿插，拉紧，可得边长为2的正六边形。

湖南省2019年、2020年数学中考试题分类(9)——图形初步认识与三角形(含解析)

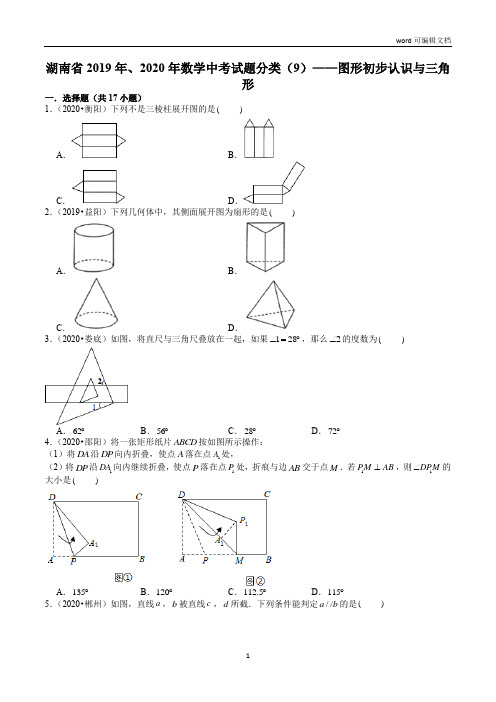
湖南省2019年、2020年数学中考试题分类（9）——图形初步认识与三角形一．选择题（共17小题）1．（2020•衡阳）下列不是三棱柱展开图的是( )A ．B ．C ．D ．2．（2019•益阳）下列几何体中，其侧面展开图为扇形的是( )A ．B ．C ．D ．3．（2020•娄底）如图，将直尺与三角尺叠放在一起，如果128∠=︒，那么2∠的度数为( )A ．62︒B ．56︒C ．28︒D ．72︒4．（2020•邵阳）将一张矩形纸片ABCD 按如图所示操作：（1）将DA 沿DP 向内折叠，使点A 落在点1A 处，（2）将DP 沿1DA 向内继续折叠，使点P 落在点1P 处，折痕与边AB 交于点M ．若1PM AB ⊥，则1DPM ∠的大小是( )A ．135︒B ．120︒C ．112.5︒D ．115︒5．（2020•郴州）如图，直线a ，b 被直线c ，d 所截．下列条件能判定//a b 的是( )A ．13∠=∠B ．24180∠+∠=︒C ．45∠=∠D ．12∠=∠6．（2020•岳阳）如图，DA AB ⊥，CD DA ⊥，56B ∠=︒，则C ∠的度数是( )A ．154︒B ．144︒C ．134︒D ．124︒7．（2020•怀化）如图，已知直线a ，b 被直线c 所截，且//a b ，若40α∠=︒，则β∠的度数为( )A ．140︒B ．50︒C ．60︒D ．40︒8．（2020•常德）如图，已知//AB DE ，130∠=︒，235∠=︒，则BCE ∠的度数为( )A ．70︒B ．65︒C ．35︒D ．5︒9．（2019•岳阳）如图，已知BE 平分ABC ∠，且//BE DC ，若50ABC ∠=︒，则C ∠的度数是( )A ．20︒B ．25︒C ．30︒D ．50︒10．（2019•衡阳）如图，已知//AB CD ，AF 交CD 于点E ，且BE AF ⊥，40BED ∠=︒，则A ∠的度数是( )A ．40︒B ．50︒C ．80︒D ．90︒11．（2019•长沙）如图，平行线AB ，CD 被直线AE 所截，180∠=︒，则2∠的度数是( )A ．80︒B ．90︒C ．100︒D ．110︒12．（2020•永州）如图，已知AB DC =，ABC DCB ∠=∠，能直接判断ABC DCB ∆≅∆的方法是( )A ．SASB ．AASC ．SSSD ．ASA13．（2020•益阳）如图，在ABC ∆中，AC 的垂直平分线交AB 于点D ，CD 平分ACB ∠，若50A ∠=︒，则B ∠的度数为( )A ．25︒B ．30︒C ．35︒D ．40︒14．（2020•怀化）在Rt ABC ∆中，90B ∠=︒，AD 平分BAC ∠，交BC 于点D ，DE AC ⊥，垂足为点E ，若3BD =，则DE 的长为( )A ．3B ．32C ．2D ．6 15．如图，ACD ∠是ABC ∆的外角，若110ACD ∠=︒，50B ∠=︒，则(A ∠= )A ．40︒B ．50︒C ．55︒D ．60︒16．如图，在ABC ∆中，90C ∠=︒，8AC =，13DC AD =，BD 平分ABC ∠，则点D 到AB 的距离等于( )A ．4B ．3C ．2D ．117．（2019•益阳）已知M 、N 是线段AB 上的两点，2AM MN ==，1NB =，以点A 为圆心，AN 长为半径画弧；再以点B 为圆心，BM 长为半径画弧，两弧交于点C ，连接AC ，BC ，则ABC ∆一定是( )A ．锐角三角形B ．直角三角形C ．钝角三角形D ．等腰三角形二．填空题（共20小题）18．（2020•永州）已知直线//a b ，用一块含30︒角的直角三角板按图中所示的方式放置，若125∠=︒，则2∠= ．19．（2020•益阳）如图，//AB CD ，AB AE ⊥，42CAE ∠=︒，则ACD ∠的度数为．20．（2020•湘西州）如图，直线//AE BC ，BA AC ⊥，若54ABC ∠=︒，则EAC ∠= 度．21．（2020•衡阳）一副三角板如图摆放，且//AB CD ，则1∠的度数为．22．（2019•娄底）如图，//AB CD ，//AC BD ，128∠=︒，则2∠的度数为．23．（2019•益阳）如图，直线//AB CD ，OA OB ⊥，若1142∠=︒，则2∠= 度．24．（2019•张家界）已知直线//a b ，将一块含30︒角的直角三角板ABC 按如图所示方式放置(30)BAC ∠=︒，并且顶点A ，C 分别落在直线a ，b 上，若118∠=︒，则2∠的度数是．25．（2020•娄底）由4个直角边长分别为a ，b 的直角三角形围成的“赵爽弦图”如图所示，根据大正方形的面积2c 等于小正方形的面积2()a b -与4个直角三角形的面积2ab 的和证明了勾股定理222a b c +=，还可以用来证明结论：若0a >、0b >且22a b +为定值，则当a b 时，ab 取得最大值．26．（2020•岳阳）如图，在Rt ABC ∆中，CD 是斜边AB 上的中线，20A ∠=︒，则BCD ∠= ︒．27．（2020•株洲）如图所示，点D 、E 分别是ABC ∆的边AB 、AC 的中点，连接BE ，过点C 作//CF BE ，交DE 的延长线于点F ，若3EF =，则DE 的长为．28．（2020•湘潭）如图，点P 是AOC ∠的角平分线上一点，PD OA ⊥，垂足为点D ，且3PD =，点M 是射线OC 上一动点，则PM 的最小值为．29．（2020•怀化）如图，在ABC ∆和ADC ∆中，AB AD =，BC DC =，130B ∠=︒，则D ∠= ︒．30．（2019•永州）已知60AOB ∠=︒，OC 是AOB ∠的平分线，点D 为OC 上一点，过D 作直线DE OA ⊥，垂足为点E ，且直线DE 交OB 于点F ，如图所示．若2DE =，则DF = ．31．（2019•永州）如图，已知点F 是ABC ∆的重心，连接BF 并延长，交AC 于点E ，连接CF 并延长，交AB于点D ，过点F 作//FG BC ，交AC 于点G ．设三角形EFG ，四边形FBCG 的面积分别为1S ，2S ，则12:S S = ．32．（2019•邵阳）公元3世纪初，中国古代数学家赵爽注《周髀算经》时，创造了“赵爽弦图”．如图，设勾6a =，弦10c =，则小正方形ABCD 的面积是．33．（2019•邵阳）如图，已知AD AE =，请你添加一个条件，使得ADC AEB ∆≅∆，你添加的条件是．（不添加任何字母和辅助线）34．（2019•株洲）如图所示，在平面直角坐标系xOy 中，在直线1x =处放置反光镜Ⅰ，在y 轴处放置一个有缺口的挡板Ⅱ，缺口为线段AB ，其中点(0,1)A ，点B 在点A 上方，且1AB =，在直线1x =-处放置一个挡板Ⅲ，从点O 发出的光线经反光镜Ⅰ反射后，通过缺口AB 照射在挡板Ⅲ上，则落在挡板Ⅲ上的光线的长度为．35．（2019•株洲）如图所示，在Rt ABC ∆中，90ACB ∠=︒，CM 是斜边AB 上的中线，E 、F 分别为MB 、BC 的中点，若1EF =，则AB = ．36．（2019•怀化）若等腰三角形的一个底角为72︒，则这个等腰三角形的顶角为．37．（2019•长沙）如图，要测量池塘两岸相对的A ，B 两点间的距离，可以在池塘外选一点C ，连接AC ，BC ，分别取AC ，BC 的中点D ，E ，测得50DE m =，则AB 的长是 m ．三．解答题（共3小题）38．（2020•衡阳）如图，在ABC ∆中，B C ∠=∠，过BC 的中点D 作DE AB ⊥，DF AC ⊥，垂足分别为点E 、F ．（1）求证：DE DF =；（2）若40BDE ∠=︒，求BAC ∠的度数．39．（2020•常德）已知D 是Rt ABC ∆斜边AB 的中点，90ACB ∠=︒，30ABC ∠=︒，过点D 作Rt DEF ∆使90DEF ∠=︒，30DFE ∠=︒，连接CE 并延长CE 到P ，使EP CE =，连接BE ，FP ，BP ，设BC 与DE 交于M ，PB 与EF 交于N ．（1）如图1，当D ，B ，F 共线时，求证：①EB EP =；②30EFP ∠=︒；（2）如图2，当D ，B ，F 不共线时，连接BF ，求证：30BFD EFP ∠+∠=︒．40．（2019•益阳）已知，如图，AB AE=，//∠=︒，求证：ABC EADD∆≅∆．ECBAB DE，70∠=︒，110湖南省2019年、2020年数学中考试题分类（9）——图形初步认识与三角形一．选择题（共17小题）1．（2020•衡阳）下列不是三棱柱展开图的是()A．B．C．D．【解答】解：A、C、D中间三个长方形能围成三棱柱的侧面，上、下两个三角形围成三棱柱的上、下两底面，故均能围成三棱柱，均是三棱柱的表面展开图．B围成三棱柱时，两个三角形重合为同一底面，而另一底面没有．故B不能围成三棱柱．故选：B．2．（2019•益阳）下列几何体中，其侧面展开图为扇形的是()A．B．C．D．【解答】解：A、圆柱的侧面展开图是矩形，故A错误；B、三棱柱的侧面展开图是矩形，故B错误；C、圆锥的侧面展开图是扇形，故C正确；D、三棱锥的侧面展开图是三个三角形组成的图形，故D错误．故选：C．3．（2020•娄底）如图，将直尺与三角尺叠放在一起，如果128∠的度数为()∠=︒，那么2A．62︒B．56︒C．28︒D．72︒【解答】解：如图，标注字母，由题意可得：90BAC ∠=︒，162DAC BAC ∠=∠-∠=︒，//EF AD ，262DAC ∴∠=∠=︒，故选：A ．4．（2020•邵阳）将一张矩形纸片ABCD 按如图所示操作：（1）将DA 沿DP 向内折叠，使点A 落在点1A 处，（2）将DP 沿1DA 向内继续折叠，使点P 落在点1P 处，折痕与边AB 交于点M ．若1PM AB ⊥，则1DPM ∠的大小是( )A ．135︒B ．120︒C ．112.5︒D ．115︒【解答】解：折叠，且190PMA ∠=︒， 145DMP DMA ∴∠=∠=︒，即45ADM ∠=︒，折叠，1122.52MDP ADP PDM ADM ∴∠=∠=∠=∠=︒， ∴在△1DPM 中，11804522.5112.5DPM ∠=︒-︒-︒=︒，故选：C ．5．（2020•郴州）如图，直线a ，b 被直线c ，d 所截．下列条件能判定//a b 的是( )A ．13∠=∠B ．24180∠+∠=︒C ．45∠=∠D ．12∠=∠ 【解答】解：A 、当13∠=∠时，//c d ，故此选项不合题意； B 、当24180∠+∠=︒时，//c d ，故此选项不合题意； C 、当45∠=∠时，//c d ，故此选项不合题意； D 、当12∠=∠时，//a b ，故此选项符合题意；故选：D ． 6．（2020•岳阳）如图，DA AB ⊥，CD DA ⊥，56B ∠=︒，则C ∠的度数是( )A ．154︒B ．144︒C ．134︒D ．124︒ 【解答】解：DA AB ⊥，CD DA ⊥， 90A D ∴∠=∠=︒， 180A D ∴∠+∠=︒， //AB CD ∴，180B C ∴∠+∠=︒， 56B ∠=︒，180124C B ∴∠=︒-∠=︒，故选：D ． 7．（2020•怀化）如图，已知直线a ，b 被直线c 所截，且//a b ，若40α∠=︒，则β∠的度数为( )A ．140︒B ．50︒C ．60︒D ．40︒【解答】解：40α∠=︒， 140α∴∠=∠=︒， //a b ，140β∴∠=∠=︒．故选：D ．8．（2020•常德）如图，已知//AB DE ，130∠=︒，235∠=︒，则BCE ∠的度数为( )A ．70︒B ．65︒C ．35︒D ．5︒【解答】解：作//CF AB ， //AB DE ， //CF DE ∴，////AB DE CF ∴，1BCF ∴∠=∠，2FCE ∠=∠， 130∠=︒，235∠=︒，30BCF ∴∠=︒，35FCE ∠=︒， 65BCE ∴∠=︒，故选：B ．9．（2019•岳阳）如图，已知BE 平分ABC ∠，且//BE DC ，若50ABC ∠=︒，则C ∠的度数是( )A ．20︒B ．25︒C ．30︒D ．50︒ 【解答】解：BE 平分ABC ∠，50ABC ∠=︒， 25ABE EBC ∴∠=∠=︒， //BE DC ，25EBC C ∴∠=∠=︒．故选：B ． 10．（2019•衡阳）如图，已知//AB CD ，AF 交CD 于点E ，且BE AF ⊥，40BED ∠=︒，则A ∠的度数是( )A ．40︒B ．50︒C ．80︒D ．90︒ 【解答】解：BE AF ⊥，40BED ∠=︒， 9050FED BED ∴∠=︒-∠=︒， //AB CD ，50A FED ∴∠=∠=︒．故选：B ． 11．（2019•长沙）如图，平行线AB ，CD 被直线AE 所截，180∠=︒，则2∠的度数是( )A ．80︒B ．90︒C ．100︒D ．110︒【解答】解：180∠=︒， 3100∴∠=︒，//AB CD，23100∴∠=∠=︒．故选：C．12．（2020•永州）如图，已知AB DC=，ABC DCB∠=∠，能直接判断ABC DCB∆≅∆的方法是()A．SAS B．AAS C．SSS D．ASA【解答】解：AB DC=，ABC DCB∠=∠，BC CB=，()ABC DCB SAS∴∆≅∆，故选：A．13．（2020•益阳）如图，在ABC∆中，AC的垂直平分线交AB于点D，CD平分ACB∠，若50A∠=︒，则B∠的度数为()A．25︒B．30︒C．35︒D．40︒【解答】解：DE垂直平分AC，AD CD∴=，A ACD∴∠=∠又CD平分ACB∠，2100ACB ACD∴∠=∠=︒，1801805010030B A ACB∴∠=︒-∠-∠=︒-︒-︒=︒，故选：B．14．（2020•怀化）在Rt ABC∆中，90B∠=︒，AD平分BAC∠，交BC于点D，DE AC⊥，垂足为点E，若3BD=，则DE的长为()A．3B．32C．2D．6【解答】解：90B∠=︒，DB AB∴⊥，又AD平分BAC∠，DE AC⊥，3DE BD∴==，故选：A．15．如图，ACD ∠是ABC ∆的外角，若110ACD ∠=︒，50B ∠=︒，则(A ∠= )A ．40︒B ．50︒C ．55︒D ．60︒【解答】解：ACD ∠是ABC ∆的外角， ACD B A ∴∠=∠+∠， A ACD B ∴∠=∠-∠，110ACD ∠=︒，50B ∠=︒， 60A ∴∠=︒，故选：D ．16．如图，在ABC ∆中，90C ∠=︒，8AC =，13DC AD =，BD 平分ABC ∠，则点D 到AB 的距离等于( )A ．4B ．3C ．2D ．1【解答】解：如图，过点D 作DE AB ⊥于E ，8AC =，13DC AD =，18213CD ∴=⨯=+，90C ∠=︒，BD 平分ABC ∠， 2DE CD ∴==，即点D 到AB 的距离为2．故选：C ．17．（2019•益阳）已知M 、N 是线段AB 上的两点，2AM MN ==，1NB =，以点A 为圆心，AN 长为半径画弧；再以点B 为圆心，BM 长为半径画弧，两弧交于点C ，连接AC ，BC ，则ABC ∆一定是( ) A ．锐角三角形 B ．直角三角形 C ．钝角三角形 D ．等腰三角形【解答】解：如图所示，4AC AN ==，3BC BM ==，2215AB =++=， 222AC BC AB ∴+=，ABC ∴∆是直角三角形，且90ACB ∠=︒，故选：B ．二．填空题（共20小题） 18．（2020•永州）已知直线//a b ，用一块含30︒角的直角三角板按图中所示的方式放置，若125∠=︒，则2∠= 35︒ ．【解答】解：过点B 作//EF a ． //a b ，////EF a b ∴．1ABF ∴∠=∠，2FBC ∠=∠．ABC ∆是含30︒角的直角三角形， 60ABC ∴∠=︒．60ABF CBF ∠+∠=︒， 2602535∴∠=︒-=︒．故答案为：35︒．19．（2020•益阳）如图，//AB CD ，AB AE ⊥，42CAE ∠=︒，则ACD ∠的度数为 132︒ ．【解答】解：AB AE ⊥，42CAE ∠=︒， 904248BAC ∴∠=︒-︒=︒， //AB CD ，180BAC ACD ∴∠+∠=︒， 132ACD ∴∠=︒．故答案为：132︒． 20．（2020•湘西州）如图，直线//AE BC ，BA AC ⊥，若54ABC ∠=︒，则EAC ∠= 36 度．【解答】解：BA AC ⊥， 90BAC ∴∠=︒， 54ABC ∠=︒，905436C ∴∠=︒-︒=︒， //AE BC ，36EAC C ∴∠=∠=︒，故答案为：36． 21．（2020•衡阳）一副三角板如图摆放，且//AB CD ，则1∠的度数为 105︒ ．【解答】解：如图，//AB CD ，45D ∠=︒， 245D ∴∠=∠=︒．123∠=∠+∠，360∠=︒，1234560105∴∠=∠+∠=︒+︒=︒．故答案是：105︒．22．（2019•娄底）如图，//AB CD ，//AC BD ，128∠=︒，则2∠的度数为 28︒ ．【解答】解：//AC BD ，1A ∴∠=∠， //AB CD ， 2A ∴∠=∠，2128∴∠=∠=︒，故答案为：28︒． 23．（2019•益阳）如图，直线//AB CD ，OA OB ⊥，若1142∠=︒，则2∠= 52 度．【解答】解：//AB CD ，32∴∠=∠， OA OB ⊥， 90O ∴∠=︒，13142O ∠=∠+∠=︒，211429052O ∴∠=∠-∠=︒-︒=︒，故答案为：52． 24．（2019•张家界）已知直线//a b ，将一块含30︒角的直角三角板ABC 按如图所示方式放置(30)BAC ∠=︒，并且顶点A ，C 分别落在直线a ，b 上，若118∠=︒，则2∠的度数是 48︒ ．【解答】解：//a b ，21183048CAB ∴∠=∠+∠=︒+︒=︒，故答案为：48︒ 25．（2020•娄底）由4个直角边长分别为a ，b 的直角三角形围成的“赵爽弦图”如图所示，根据大正方形的面积2c 等于小正方形的面积2()a b -与4个直角三角形的面积2ab 的和证明了勾股定理222a b c +=，还可以用来证明结论：若0a >、0b >且22a b +为定值，则当a = b 时，ab 取得最大值．【解答】解：如图，作斜边c 上高h ，2()0a b -，2220a b ab ∴+-，又222a b c +=，22a b +为定值，22c ab ∴， ab ∴最大值为22c ，a ，b 为直角边的直角三角形面积1122a b c h ==，∴22c c h =， 2c h ∴=，等腰直角三角形斜边上的高是斜边的一半，∴当a b =时，2ch =，故答案为：=． 26．（2020•岳阳）如图，在Rt ABC ∆中，CD 是斜边AB 上的中线，20A ∠=︒，则BCD ∠= 70 ︒．【解答】解：在Rt ABC ∆中，CD 是斜边AB 上的中线，20A ∠=︒，则70B ∠=︒，90ACB∠=︒，CD是斜边AB上的中线，BD CD AD∴==，70BCD B∴∠=∠=︒，故答案为70．27．（2020•株洲）如图所示，点D、E分别是ABC∆的边AB、AC的中点，连接BE，过点C作//CF BE，交DE的延长线于点F，若3EF=，则DE的长为32．【解答】解：D、E分别是ABC∆的边AB、AC的中点，DE∴为ABC∆的中位线，//DE BC ∴，12DE BC=，//CF BE，∴四边形BCFE为平行四边形，3BC EF∴==，∴1322 DE BC==．故答案为：32．28．（2020•湘潭）如图，点P是AOC∠的角平分线上一点，PD OA⊥，垂足为点D，且3PD=，点M是射线OC上一动点，则PM的最小值为3．【解答】解：根据垂线段最短可知：当PM OC⊥时，PM最小，当PM OC⊥时，又OP平分AOC∠，PD OA⊥，3PD=，3PM PD∴==，故答案为：3．29．（2020•怀化）如图，在ABC∆和ADC∆中，AB AD=，BC DC=，130B∠=︒，则D∠=130︒．【解答】证明：在ADC∆和ABC∆中，AD ABAC ACCD CB=⎧⎪=⎨⎪=⎩，()ABC ADC SSS∴∆≅∆，D B∴∠=∠，130B∠=︒，130D∴∠=︒，故答案为：130．30．（2019•永州）已知60AOB∠=︒，OC是AOB∠的平分线，点D为OC上一点，过D作直线DE OA⊥，垂足为点E，且直线DE交OB于点F，如图所示．若2DE=，则DF=4．【解答】解：过点D作DM OB⊥，垂足为M，如图所示．OC是AOB∠的平分线，2DM DE∴==．在Rt OEF∆中，90OEF∠=︒，60EOF∠=︒，30OFE∴∠=︒，即30DFM∠=︒．在Rt DMF∆中，90DMF∠=︒，30DFM∠=︒，24DF DM∴==．故答案为：4．31．（2019•永州）如图，已知点F是ABC∆的重心，连接BF并延长，交AC于点E，连接CF并延长，交AB 于点D，过点F作//FG BC，交AC于点G．设三角形EFG，四边形FBCG的面积分别为1S，2S，则12:S S= 18．【解答】解：点F是ABC∆的重心，2BF EF∴=，3BE EF∴=，//FG BC，EFG EBC∴∆∆∽，∴13EFBE=，2111()39EBCSS∆==，121:8S S∴=；故答案为：18．32．（2019•邵阳）公元3世纪初，中国古代数学家赵爽注《周髀算经》时，创造了“赵爽弦图”．如图，设勾6a=，弦10c=，则小正方形ABCD的面积是4．【解答】解：勾6a=，弦10c=，∴股221068=-=，∴小正方形的边长862=-=，∴小正方形的面积224==故答案是：433．（2019•邵阳）如图，已知AD AE=，请你添加一个条件，使得ADC AEB∆≅∆，你添加的条件是AB AC=或ADC AEB∠=∠或ABE ACD∠=∠．（不添加任何字母和辅助线）【解答】解：A A∠=∠，AD AE=，∴可以添加AB AC=，此时满足SAS；添加条件ADC AEB∠=∠，此时满足ASA；添加条件ABE ACD∠=∠，此时满足AAS，故答案为AB AC=或ADC AEB∠=∠或ABE ACD∠=∠；34．（2019•株洲）如图所示，在平面直角坐标系xOy中，在直线1x=处放置反光镜Ⅰ，在y轴处放置一个有缺口的挡板Ⅱ，缺口为线段AB，其中点(0,1)A，点B在点A上方，且1AB=，在直线1x=-处放置一个挡板Ⅲ，从点O发出的光线经反光镜Ⅰ反射后，通过缺口AB照射在挡板Ⅲ上，则落在挡板Ⅲ上的光线的长度为 1.5．【解答】解：当光线沿O 、G 、B 、C 传输时，过点B 作BF GH ⊥于点F ，过点C 作CE GH ⊥于点E ，方法一：GOB ∆为等腰三角形， G ∴(1,1)，B 为CG 中点，C ∴(1,3)-，同理(1,1.5)D -，3 1.5 1.5CD ∴=-=方法二：OGH CGE α∠=∠=，设GH a =，则2GF a =-，则tan tan OGH CGE ∠=∠，即：OH BF GH GF=，即：112a a=-，解得：1a =，则45α=︒，2GE CE ∴==，123C y =+=，当光线反射过点A 时，同理可得： 1.5D y =，落在挡板Ⅲ上的光线的长度3 1.5 1.5CD ==-=，故答案为1.5．35．（2019•株洲）如图所示，在Rt ABC ∆中，90ACB ∠=︒，CM 是斜边AB 上的中线，E 、F 分别为MB 、BC 的中点，若1EF =，则AB = 4 ．【解答】解：E 、F 分别为MB 、BC 的中点，22CM EF ∴==，90ACB ∠=︒，CM 是斜边AB 上的中线，24AB CM ∴==，故答案为：4．36．（2019•怀化）若等腰三角形的一个底角为72︒，则这个等腰三角形的顶角为 36︒ ．【解答】解：等腰三角形的一个底角为72︒，∴等腰三角形的顶角180727236=︒-︒-︒=︒，故答案为：36︒．37．（2019•长沙）如图，要测量池塘两岸相对的A ，B 两点间的距离，可以在池塘外选一点C ，连接AC ，BC ，分别取AC ，BC 的中点D ，E ，测得50DE m =，则AB 的长是 100 m ．【解答】解：点D ，E 分别是AC ，BC 的中点，DE ∴是ABC ∆的中位线，2250100AB DE ∴==⨯=米．故答案为：100．三．解答题（共3小题）38．（2020•衡阳）如图，在ABC ∆中，B C ∠=∠，过BC 的中点D 作DE AB ⊥，DF AC ⊥，垂足分别为点E 、F ．（1）求证：DE DF =；（2）若40BDE ∠=︒，求BAC ∠的度数．【解答】（1）证明：DE AB ⊥，DF AC ⊥，90BED CFD ∴∠=∠=︒，D 是BC 的中点，BD CD ∴=，在BED ∆与CFD ∆中，BED CFD B CBD CD ∠=∠⎧⎪∠=∠⎨⎪=⎩， ()BED CFD AAS ∴∆≅∆，DE DF ∴=；（2）解：40BDE ∠=︒，50B ∴∠=︒，50C ∴∠=︒，80BAC ∴∠=︒．39．（2020•常德）已知D 是Rt ABC ∆斜边AB 的中点，90ACB ∠=︒，30ABC ∠=︒，过点D 作Rt DEF ∆使90DEF ∠=︒，30DFE ∠=︒，连接CE 并延长CE 到P ，使EP CE =，连接BE ，FP ，BP ，设BC 与DE 交于M ，PB 与EF 交于N ．（1）如图1，当D ，B ，F 共线时，求证：①EB EP =；②30EFP ∠=︒；（2）如图2，当D ，B ，F 不共线时，连接BF ，求证：30BFD EFP ∠+∠=︒．【解答】证明（1）①90ACB ∠=︒，30ABC ∠=︒，903060A ∴∠=︒-︒=︒，同理60EDF ∠=︒，60A EDF ∴∠=∠=︒，//AC DE ∴，90DMB ACB ∴∠=∠=︒，D 是Rt ABC ∆斜边AB 的中点，//AC DM ，∴12BM BD BC AB ==，即M 是BC 的中点，EP CE =，即E 是PC 的中点，//ED BP ∴，90CBP DMB ∴∠=∠=︒，CBP ∴∆是直角三角形，12BE PC EP ∴==； ②30ABC DFE ∠=∠=︒，//BC EF ∴，由①知：90CBP ∠=︒，BP EF ∴⊥，EB EP =，EF ∴是线段BP 的垂直平分线，PF BF ∴=，30PFE BFE ∴∠=∠=︒；（2）如图2，延长DE 到Q ，使EQ DE =，连接CD ，PQ ，FQ ，EC EP=，DEC QEP ∠=∠， ()QEP DEC SAS ∴∆≅∆，则PQ DC DB ==，QE DE =，90DEF ∠=︒EF ∴是DQ 的垂直平分线，QF DF ∴=，CD AD =，60ACD A ∴∠=∠=︒，60ADC ∴∠=︒，120CDB ∴∠=︒，120120(60)6060FDB FDC EDC EDC EQP FQP ∴∠=︒-∠=︒-︒+∠=︒-∠=︒-∠=∠， ()FQP FDB SAS ∴∆≅∆，QFP BFD ∴∠=∠，EF 是DQ 的垂直平分线，30QFE EFD ∴∠=∠=︒，30QFP EFP ∴∠+∠=︒，30BFD EFP ∴∠+∠=︒．40．（2019•益阳）已知，如图，AB AE =，//AB DE ，70ECB ∠=︒，110D ∠=︒，求证：ABC EAD ∆≅∆．【解答】证明：由70ECB ∠=︒得110ACB ∠=︒ 又110D ∠=︒ACB D ∴∠=∠//AB DECAB E ∴∠=∠在ABC ∆和EAD ∆中，ACB D CAB E AB AE ∠=∠⎧⎪∠=∠⎨⎪=⎩，()ABC EAD AAS ∴∆≅∆．。

2018—2020年江苏省数学中考试题分类(11)——图形的初步认识与三角形(含解析)

2018—2020年江苏省数学中考试题分类（11）——图形的初步认识与三角形一．选择题（共19小题）1．（2020•泰州）把如图所示的纸片沿着虚线折叠，可以得到的几何体是()A．三棱柱B．四棱柱C．三棱锥D．四棱锥2．（2019•连云港）一个几何体的侧面展开图如图所示，则该几何体的底面是() A．B．C．D．3．（2018•常州）下列图形中，哪一个是圆锥的侧面展开图？()A．B．C．D．4．（2020•宿迁）如图，直线a，b被直线c所截，//∠的度数为()a b，150∠=︒，则2A．40︒B．50︒C．130︒D．150︒5．（2020•南通）如图，已知//∠=︒，则C∠的度数是()EAB CD，54A∠=︒，18A．36︒B．34︒C．32︒D．30︒6．（2020•常州）如图，直线a、b被直线c所截，//∠的度数是()a b，1140∠=︒，则2A ．30︒B ．40︒C ．50︒D ．60︒ 7．（2019•南通）如图，//AB CD ，AE 平分CAB ∠交CD 于点E ，若70C ∠=︒，则AED ∠度数为( )A ．110︒B ．125︒C ．135︒D ．140︒ 8．（2019•常州）如图，在线段PA 、PB 、PC 、PD 中，长度最小的是( )A ．线段PAB ．线段PBC ．线段PCD ．线段PD 9．（2019•苏州）如图，已知直线//a b ，直线c 与直线a ，b 分别交于点A ，B ．若154∠=︒，则2∠等于( )A ．126︒B ．134︒C ．136︒D ．144︒ 10．（2019•宿迁）一副三角板如图摆放（直角顶点C 重合），边AB 与CE 交于点F ，//DE BC ，则BFC ∠等于( )A ．105︒B ．100︒C ．75︒D ．60︒ 11．（2020•南通）如图，在ABC ∆中，2AB =，60ABC ∠=︒，45ACB ∠=︒，D 是BC 的中点，直线l 经过点D ，AE l ⊥，BF l ⊥，垂足分别为E ，F ，则AE BF +的最大值为( )A ．6B ．22C ．23D ．32 12．（2020•宿迁）在ABC ∆中，1AB =，5BC =，下列选项中，可以作为AC 长度的是( ) A ．2 B ．4 C ．5 D ．6 13．（2020•常州）如图，AB 是O 的弦，点C 是优弧AB 上的动点(C 不与A 、B 重合），CH AB ⊥，垂足为H ，点M 是BC 的中点．若O 的半径是3，则MH 长的最大值是( )A ．3B ．4C ．5D ．6 14．（2020•徐州）若一个三角形的两边长分别为3cm 、6cm ，则它的第三边的长可能是( ) A ．2cm B ．3cm C ．6cm D ．9cm 15．（2019•无锡）如图，在正方形网格（每个小正方形的边长都是1)中，若将ABC ∆沿A D -的方向平移AD 长，得(DEF B ∆、C 的对应点分别为E 、)F ，则BE 长为( )A ．1B ．2C ．5D ．3 16．（2019•徐州）下列长度的三条线段，能组成三角形的是( ) A ．2，2，4 B ．5，6，12 C ．5，7，2 D ．6，8，10 17．（2019•泰州）如图所示的网格由边长相同的小正方形组成，点A 、B 、C 、D 、E 、F 、G 在小正方形的顶点上，则ABC ∆的重心是( )A ．点DB ．点EC ．点FD ．点G 18．（2019•扬州）已知n 是正整数，若一个三角形的三边长分别是2n +、8n +、3n ，则满足条件的n 的值有( ) A ．4个 B ．5个 C ．6个 D ．7个 19．（2019•盐城）如图，点D 、E 分别是ABC ∆边BA 、BC 的中点，3AC =，则DE 的长为( )A ．2B ．43C ．3D ．32二．填空题（共18小题） 20．（2019•常州）如果35α∠=︒，那么α∠的余角等于 ︒． 21．（2019•苏州）“七巧板”是我们祖先的一项卓越创造，可以拼出许多有趣的图形，被誉为“东方魔板”．图①是由边长为10cm 的正方形薄板分为7块制作成的“七巧板”，图②是用该“七巧板”拼成的一个“家”的图形．该“七巧板”中7块图形之一的正方形边长为 cm （结果保留根号）．22．（2019•扬州）如图，在ABC ∆中，5AB =，4AC =，若进行以下操作，在边BC 上从左到右依次取点1D 、2D 、3D 、4D 、⋯；过点1D 作AB 、AC 的平行线分别交AC 、AB 于点1E 、1F ；过点2D 作AB 、AC 的平行线分别交AC 、AB 于点2E 、2F ；过点3D 作AB 、AC 的平行线分别交AC 、AB 于点3E 、3F ⋯，则1122201920191122201920194()5()D E D E D E D F D F D F ++⋯++++⋯+= ．23．（2019•扬州）将一个矩形纸片折叠成如图所示的图形，若26ABC ∠=︒，则ACD ∠= ︒．24．（2020•宿迁）如图，在ABC ∆中，AB AC =，BAC ∠的平分线AD 交BC 于点D ，E 为AB 的中点，若12BC =，8AD =，则DE 的长为．25．（2020•常州）如图，在ABC ∆中，45B ∠=︒，62AB =，D 、E 分别是AB 、AC 的中点，连接DE ，在直线DE 和直线BC 上分别取点F 、G ，连接BF 、DG ．若3BF DG =，且直线BF 与直线DG 互相垂直，则BG 的长为．26．（2020•徐州）如图，30MON ∠=︒，在OM 上截取13OA =．过点1A 作11A B OM ⊥，交ON 于点1B ，以点1B 为圆心，1B O 为半径画弧，交OM 于点2A ；过点2A 作22A B OM ⊥，交ON 于点2B ，以点2B 为圆心，2B O 为半径画弧，交OM 于点3A ；按此规律，所得线段2020A B 的长等于．27．（2020•徐州）如图，在Rt ABC ∆中，90ABC ∠=︒，D 、E 、F 分别为AB 、BC 、CA 的中点，若5BF =，则DE = ．28．（2020•常州）如图，在ABC ∆中，BC 的垂直平分线分别交BC 、AB 于点E 、F ．若AFC ∆是等边三角形，则B ∠= ︒．29．（2020•扬州）《九章算术》是中国传统数学的重要著作之一，奠定了中国传统数学的基本框架．如图所示是其中记载的一道“折竹”问题：“今有竹高一丈，末折抵地，去根三尺，问折者高几何？”题意是：一根竹子原高1丈(1丈10=尺），中部有一处折断，竹梢触地面处离竹根3尺，试问折断处离地面多高？答：折断处离地面尺高．30．（2020•南京）如图，线段AB 、BC 的垂直平分线1l 、2l 相交于点O ，若139∠=︒，则AOC ∠= ．31．（2020•苏州）如图，在ABC ∆中，已知2AB =，AD BC ⊥，垂足为D ，2BD CD =．若E 是AD 的中点，则EC = ．32．（2020•泰州）如图，将分别含有30︒、45︒角的一副三角板重叠，使直角顶点重合，若两直角重叠形成的角为65︒，则图中角α的度数为．33．（2019•南通）如图，ABC ∆中，AB BC =，90ABC ∠=︒，F 为AB 延长线上一点，点E 在BC 上，且AE CF =，若25BAE ∠=︒，则ACF ∠= 度．34．（2019•镇江）如图，直线//a b ，ABC ∆的顶点C 在直线b 上，边AB 与直线b 相交于点D ．若BCD ∆是等边三角形，20A ∠=︒，则1∠= ︒．35．（2019•苏州）如图，扇形OAB 中，90AOB ∠=︒．P 为弧AB 上的一点，过点P 作PC OA ⊥，垂足为C ，PC 与AB 交于点D ．若2PD =，1CD =，则该扇形的半径长为．36．（2019•南京）在ABC ∆中，4AB =，60C ∠=︒，A B ∠>∠，则BC 的长的取值范围是． 37．（2019•南京）无盖圆柱形杯子的展开图如图所示．将一根长为20cm 的细木筷斜放在该杯子内，木筷露在杯子外面的部分至少有 cm ．三．解答题（共8小题） 38．（2020•镇江）如图，AC 是四边形ABCD 的对角线，1B ∠=∠，点E 、F 分别在AB 、BC 上，BE CD =，BF CA =，连接EF ．（1）求证：2D ∠=∠；（2）若//EF AC ，78D ∠=︒，求BAC ∠的度数．39．（2020•常州）已知：如图，点A 、B 、C 、D 在一条直线上，//EA FB ，EA FB =，AB CD =．（1）求证：E F ∠=∠；（2）若40A ∠=︒，80D ∠=︒，求E ∠的度数．40．（2020•盐城）以下虚线框中为一个合作学习小组在一次数学实验中的过程记录，请阅读后完成虚线框下方的问题1~4．（Ⅰ）在Rt ABC ∆中，90C ∠=︒，22AB =AC2.8 2.7 2.6 2.3 2 1.5 0.4BC 0.4 0.8 1.2 1.6 2 2.4 2.8AC BC +3.2 3.5 3.8 3.9 4 3.9 3.2 （Ⅱ）根据学习函数的经验，选取上表中BC 和AC BC +的数据进行分析：①BC x =，AC BC y +=，以(,)x y 为坐标，在图①所示的坐标系中描出对应的点： ②连线：观察思考（Ⅲ）结合表中的数据以及所画的图象，猜想．当x ＝____时，y 最大；（Ⅳ）进一步精想：若Rt ABC ∆中，90C ∠=︒，斜边2(AB a a =为常数，0)a >，则BC ＝____时，AC BC +最大．推理证明（Ⅴ）对（Ⅳ）中的猜想进行证明．问题1，在图①中完善（Ⅱ）的描点过程，并依次连线；问题2，补全观察思考中的两个猜想：（Ⅲ）；（Ⅳ）；问题3，证明上述（Ⅴ）中的猜想；问题4，图②中折线B E F G A --------是一个感光元件的截面设计草图，其中点A ，B 间的距离是4厘米，1AG BE ==厘米．90E F G ∠=∠=∠=︒．平行光线从AB 区域射入，60BNE ∠=︒，线段FM 、FN 为感光区域，当EF 的长度为多少时，感光区域长度之和最大，并求出最大值．41．（2020•徐州）如图，AC BC ⊥，DC EC ⊥，AC BC =，DC EC =，AE 与BD 交于点F ．（1）求证：AE BD =；（2）求AFD ∠的度数．42．（2020•泰州）如图，在O 中，点P 为AB 的中点，弦AD 、PC 互相垂直，垂足为M ，BC 分别与AD 、PD 相交于点E 、N ，连接BD 、MN ．（1）求证：N 为BE 的中点．（2）若O 的半径为8，AB 的度数为90︒，求线段MN 的长．43．（2020•苏州）问题1：如图①，在四边形ABCD 中，90B C ∠=∠=︒，P 是BC 上一点，PA PD =，90APD ∠=︒．求证：AB CD BC +=．问题2：如图②，在四边形ABCD 中，45B C ∠=∠=︒，P 是BC 上一点，PA PD =，90APD ∠=︒．求AB CDBC+的值．44．（2020•无锡）如图，已知//AB CD ，AB CD =，BE CF =．求证：（1）ABF DCE ∆≅∆；（2）//AF DE ．45．（2020•南京）如图，点D 在AB 上，点E 在AC 上，AB AC =，B C ∠=∠，求证：BD CE =．2018—2020年江苏省数学中考试题分类（11）——图形的初步认识与三角形一．选择题（共19小题）1．（2020•泰州）把如图所示的纸片沿着虚线折叠，可以得到的几何体是()A．三棱柱B．四棱柱C．三棱锥D．四棱锥【解答】解：观察展开图可知，几何体是三棱柱．故选：A．2．（2019•连云港）一个几何体的侧面展开图如图所示，则该几何体的底面是()A．B．C．D．【解答】解：由题意可知，该几何体为四棱锥，所以它的底面是四边形．故选：B．3．（2018•常州）下列图形中，哪一个是圆锥的侧面展开图？()A．B．C．D．【解答】解：圆锥的侧面展开图是光滑的曲面，没有棱，只是扇形．故选：B．4．（2020•宿迁）如图，直线a，b被直线c所截，//∠的度数为()a b，150∠=︒，则2A．40︒B．50︒C．130︒D．150︒【解答】解：//a b，∴∠=∠=︒．2150故选：B．5．（2020•南通）如图，已知//∠=︒，则C∠的度数是()EAAB CD，54∠=︒，18A．36︒B．34︒C．32︒D．30︒【解答】解：（方法一）过点E作//EF AB，则//EF CD，如图1所示．EF AB，//∴∠=∠=︒，AEF A54∠=∠-∠=︒-︒=︒．541836CEF AEF AEC又//EF CD，∴∠=∠=︒．C CEF36（方法二）设AE与CD交于点O，如图2所示．AB CD，//DOE A∴∠=∠=︒．54又DOE C E∠=∠+∠，C DOE E∴∠=∠-∠=︒-︒=︒．541836故选：A．6．（2020•常州）如图，直线a、b被直线c所截，//∠的度数是()∠=︒，则2a b，1140A．30︒B．40︒C．50︒D．60︒【解答】解：13180∠=︒，∠+∠=︒，1140∴∠=︒-∠=︒-︒=︒3180118014040a b，//∴∠=∠=︒．2340故选：B ． 7．（2019•南通）如图，//AB CD ，AE 平分CAB ∠交CD 于点E ，若70C ∠=︒，则AED ∠度数为( )A ．110︒B ．125︒C ．135︒D ．140︒ 【解答】解：//AB CD ， 180C CAB ∴∠+∠=︒， 70C ∠=︒， 110CAB ∴∠=︒， AE 平分CAB ∠，1552CAE CBA ∴∠=∠=︒，7055125AED C CAE ∴∠=∠+∠=︒+︒=︒，故选：B ． 8．（2019•常州）如图，在线段PA 、PB 、PC 、PD 中，长度最小的是( )A ．线段PAB ．线段PBC ．线段PCD ．线段PD 【解答】解：由直线外一点到直线上所有点的连线中，垂线段最短，可知答案为B ．故选：B ． 9．（2019•苏州）如图，已知直线//a b ，直线c 与直线a ，b 分别交于点A ，B ．若154∠=︒，则2∠等于( )A ．126︒B ．134︒C ．136︒D ．144︒【解答】解：如图所示： //a b ，154∠=︒， 1354∴∠=∠=︒，218054126∴∠=︒-︒=︒．故选：A ．10．（2019•宿迁）一副三角板如图摆放（直角顶点C 重合），边AB 与CE 交于点F ，//DE BC ，则BFC ∠等于( )A ．105︒B ．100︒C ．75︒D ．60︒ 【解答】解：由题意知45E ∠=︒，30B ∠=︒， //DE CB ，45BCF E ∴∠=∠=︒，在CFB ∆中，1801803045105BFC B BCF ∠=︒-∠-∠=︒-︒-︒=︒，故选：A ． 11．（2020•南通）如图，在ABC ∆中，2AB =，60ABC ∠=︒，45ACB ∠=︒，D 是BC 的中点，直线l 经过点D ，AE l ⊥，BF l ⊥，垂足分别为E ，F ，则AE BF +的最大值为( )A ．6B ．22C ．23D ．32 【解答】解：如图，过点C 作CK l ⊥于点K ，过点A 作AH BC ⊥于点H ，在Rt AHB ∆中，60ABC ∠=︒，2AB =， 1BH ∴=，3AH =，在Rt AHC ∆中，45ACB ∠=︒，2222(3)(3)6AC AH CH ∴=+=+=，点D 为BC 中点， BD CD ∴=，在BFD ∆与CKD ∆中，90BFD CKD BDF CDKBD CD ∠=∠=︒⎧⎪∠=∠⎨⎪=⎩， ()BFD CKD AAS ∴∆≅∆， BF CK ∴=，延长AE ，过点C 作CN AE ⊥于点N ，可得AE BF AE CK AE EN AN +=+=+=，在Rt ACN ∆中，AN AC <，当直线l AC ⊥时，最大值为6，综上所述，AE BF +的最大值为6．故选：A ． 12．（2020•宿迁）在ABC ∆中，1AB =，5BC =，下列选项中，可以作为AC 长度的是( ) A ．2 B ．4 C ．5 D ．6 【解答】解：在ABC ∆中，1AB =，5BC =， ∴5151AC -<<+，51251-<<+，451>+，551>+，651>+， AC ∴的长度可以是2，故选项A 正确，选项B 、C 、D 不正确；故选：A ． 13．（2020•常州）如图，AB 是O 的弦，点C 是优弧AB 上的动点(C 不与A 、B 重合），CH AB ⊥，垂足为H ，点M 是BC 的中点．若O 的半径是3，则MH 长的最大值是( )A ．3B ．4C ．5D ．6 【解答】解：CH AB ⊥，垂足为H ， 90CHB ∴∠=︒，点M 是BC 的中点．12MH BC ∴=，BC 的最大值是直径的长，O 的半径是3， MH ∴的最大值为3，故选：A ． 14．（2020•徐州）若一个三角形的两边长分别为3cm 、6cm ，则它的第三边的长可能是( ) A ．2cm B ．3cm C ．6cm D ．9cm 【解答】解：设第三边长为xcm ，根据三角形的三边关系可得： 6363x -<<+，解得：39x <<，故选：C ． 15．（2019•无锡）如图，在正方形网格（每个小正方形的边长都是1)中，若将ABC ∆沿A D -的方向平移AD 长，得(DEF B ∆、C 的对应点分别为E 、)F ，则BE 长为( )A ．1B ．2C ．5D ．3【解答】解：如图所示：22125BE =+=．故选：C ．16．（2019•徐州）下列长度的三条线段，能组成三角形的是( ) A ．2，2，4 B ．5，6，12 C ．5，7，2 D ．6，8，10 【解答】解：224+=，2∴，2，4不能组成三角形，故选项A 错误， 5612+<，5∴，6，12不能组成三角形，故选项B 错误， 527+=，5∴，7，2不能组成三角形，故选项C 错误， 6810+>，6∴，8，10能组成三角形，故选项D 正确，故选：D ． 17．（2019•泰州）如图所示的网格由边长相同的小正方形组成，点A 、B 、C 、D 、E 、F 、G 在小正方形的顶点上，则ABC ∆的重心是( )A ．点DB ．点EC ．点FD ．点G 【解答】解：根据题意可知，直线CD 经过ABC ∆的AB 边上的中线，直线AD 经过ABC ∆的BC 边上的中线， ∴点D 是ABC ∆重心．故选：A ． 18．（2019•扬州）已知n 是正整数，若一个三角形的三边长分别是2n +、8n +、3n ，则满足条件的n 的值有( ) A ．4个 B ．5个 C ．6个 D ．7个【解答】解：①若283n n n +<+，则 28383n n nn n +++>⎧⎨+⎩，解得104n n <⎧⎨⎩，即410n <，∴正整数n 有6个：4，5，6，7，8，9； ②若238n n n +<+，则 23838n n n n n ++>+⎧⎨+⎩，解得24n n >⎧⎨⎩，即24n <，∴正整数n 有2个：3和4；③若328n n n +<+，则不等式组无解；综上所述，满足条件的n 的值有7个，故选：D ． 19．（2019•盐城）如图，点D 、E 分别是ABC ∆边BA 、BC 的中点，3AC =，则DE 的长为( )A ．2B ．43 C ．3 D ．32【解答】解：点D 、E 分别是ABC ∆的边BA 、BC 的中点， DE ∴是ABC ∆的中位线，11.52DE AC ∴==．故选：D ．二．填空题（共18小题） 20．（2019•常州）如果35α∠=︒，那么α∠的余角等于 55 ︒．【解答】解：35α∠=︒， α∴∠的余角等于903555︒-︒=︒ 故答案为：55． 21．（2019•苏州）“七巧板”是我们祖先的一项卓越创造，可以拼出许多有趣的图形，被誉为“东方魔板”．图①是由边长为10cm 的正方形薄板分为7块制作成的“七巧板”，图②是用该“七巧板”拼成的一个“家”的图形．该“七巧板”中7块图形之一的正方形边长为 522cm （结果保留根号）．【解答】解：21010100()cm ⨯= 10052)8cm = 答：该“七巧板”中7块图形之一的正方形边长为522．故答案为：522． 22．（2019•扬州）如图，在ABC ∆中，5AB =，4AC =，若进行以下操作，在边BC 上从左到右依次取点1D 、2D 、3D 、4D 、⋯；过点1D 作AB 、AC 的平行线分别交AC 、AB 于点1E 、1F ；过点2D 作AB 、AC 的平行线分别交AC 、AB 于点2E 、2F ；过点3D 作AB 、AC 的平行线分别交AC 、AB 于点3E 、3F ⋯，则1122201920191122201920194()5()D E D E D E D F D F D F ++⋯++++⋯+= 40380 ．【解答】解：11//D F AC ，11//D E AB ， ∴111D F BF AC AB =，即1111D F AB DE AC AB -=， 5AB =，4BC =， 11114520D E DF ∴+=，同理22224520D E D F +=，⋯，20192019201920194520D E D F +=，1122201920191122201920194()5()20201940380D E D E D E D F D F D F ∴++⋯++++⋯+=⨯=；故答案为40380． 23．（2019•扬州）将一个矩形纸片折叠成如图所示的图形，若26ABC ∠=︒，则ACD ∠= 128 ︒．【解答】解：延长DC ，由题意可得：26ABC BCE BCA ∠=∠=∠=︒，则1802626128ACD ∠=︒-︒-︒=︒．故答案为：128．24．（2020•宿迁）如图，在ABC ∆中，AB AC =，BAC ∠的平分线AD 交BC 于点D ，E 为AB 的中点，若12BC =，8AD =，则DE 的长为 5 ．【解答】解：AB AC =，AD 平分BAC ∠， AD BC ∴⊥，6BD CD ==， 90ADB ∴∠=︒，22228610AB AD BD ∴=+=+=，AE EB =，152DE AB ∴==，故答案为5． 25．（2020•常州）如图，在ABC ∆中，45B ∠=︒，62AB =，D 、E 分别是AB 、AC 的中点，连接DE ，在直线DE 和直线BC 上分别取点F 、G ，连接BF 、DG ．若3BF DG =，且直线BF 与直线DG 互相垂直，则BG 的长为 4或2 ．【解答】解：如图，过点B 作BT BF ⊥交ED 的延长线于T ，过点B 作BH DT ⊥于H ．DG BF ⊥，BT BF ⊥，//DG BT∴， AD DB =，AE EC =， //DE BC ∴，∴四边形DGBT 是平行四边形，BG DT ∴=，DG BT =，45BDH ABC ∠=∠=︒， 32AD DB ==， 3BH DH ∴==，90TBF BHF ∠=∠=︒，90TBH FBH ∴∠+∠=︒，90FBH F ∠+∠=︒， TBH F ∴∠=∠，1tan tan 3BT DG F TBH BF BF ∴∠=∠===，∴13TH BH =， 1TH ∴=，134DT TH DH ∴=+=+=， 4BG ∴=．当点F 在ED 的延长线上时，同法可得312DT BG ==-=．故答案为4或2．26．（2020•徐州）如图，30MON ∠=︒，在OM 上截取13OA =．过点1A 作11A B OM ⊥，交ON 于点1B ，以点1B 为圆心，1B O 为半径画弧，交OM 于点2A ；过点2A 作22A B OM ⊥，交ON 于点2B ，以点2B 为圆心，2B O 为半径画弧，交OM 于点3A ；按此规律，所得线段2020A B 的长等于 192 ．【解答】解：111B O B A =，112B A OA ⊥， 112OA A A ∴=，22B A OM ⊥，11B A OM ⊥， 1122//B A B A ∴，112212B A A B ∴=，22112A B A B ∴=，同法可得233221122A B A B A B ==，⋯，由此规律可得192020112A B A B =， 1113tan3031A B OA =︒=⨯=， 1920202A B ∴=，故答案为192． 27．（2020•徐州）如图，在Rt ABC ∆中，90ABC ∠=︒，D 、E 、F 分别为AB 、BC 、CA 的中点，若5BF =，则DE = 5 ．【解答】解：如图，在Rt ABC ∆中，90ABC ∠=︒，F 为CA 的中点，5BF =， 210AC BF ∴==．又D 、E 分别为AB 、BC 的中点， DE ∴是Rt ABC ∆的中位线，152DE AC ∴==．故答案是：5．28．（2020•常州）如图，在ABC ∆中，BC 的垂直平分线分别交BC 、AB 于点E 、F ．若AFC ∆是等边三角形，则B ∠= 30 ︒．【解答】解：EF 垂直平分BC ，BF CF ∴=， B BCF ∴∠=∠，ACF ∆为等边三角形， 60AFC ∴∠=︒，30B BCF ∴∠=∠=︒．故答案为：30． 29．（2020•扬州）《九章算术》是中国传统数学的重要著作之一，奠定了中国传统数学的基本框架．如图所示是其中记载的一道“折竹”问题：“今有竹高一丈，末折抵地，去根三尺，问折者高几何？”题意是：一根竹子原高1丈(1丈10=尺），中部有一处折断，竹梢触地面处离竹根3尺，试问折断处离地面多高？答：折断处离地面 4.55 尺高．【解答】解：设折断处离地面x 尺，根据题意可得：2223(10)x x +=-，解得： 4.55x =．答：折断处离地面4.55尺．故答案为：4.55． 30．（2020•南京）如图，线段AB 、BC 的垂直平分线1l 、2l 相交于点O ，若139∠=︒，则AOC ∠= 78︒ ．【解答】解：解法一：连接BO ，并延长BO 到P ，线段AB 、BC 的垂直平分线1l 、2l 相交于点O ，AO OB OC ∴==，90BDO BEO ∠=∠=︒，180DOE ABC ∴∠+∠=︒，1180DOE ∠+∠=︒，139ABC ∴∠=∠=︒，OA OB OC ==，A ABO ∴∠=∠，OBC C ∠=∠，AOP A ABO ∠=∠+∠，COP C OBC ∠=∠+∠，23978AOC AOP COP A ABC C ∴∠=∠+∠=∠+∠+∠=⨯︒=︒；解法二：连接OB ，线段AB 、BC 的垂直平分线1l 、2l 相交于点O ，AO OB OC ∴==，AOD BOD ∴∠=∠，BOE COE ∠=∠，1180DOE ∠+∠=︒，139∠=︒，141DOE ∴∠=︒，即141BOD BOE ∠+∠=︒，141AOD COE ∴∠+∠=︒，360()()78AOC BOD BOE AOD COE ∴∠=︒-∠+∠-∠+∠=︒；故答案为：78︒．31．（2020•苏州）如图，在ABC ∆中，已知2AB =，AD BC ⊥，垂足为D ，2BD CD =．若E 是AD 的中点，则EC = 1 ．【解答】解：设AE ED x ==，CD y =，2BD y ∴=，AD BC ⊥，90ADB ADC ∴∠=∠=︒，在Rt ABD ∆中，22244AB x y ∴=+，221x y ∴+=，在Rt CDE ∆中，2221EC x y ∴=+=0EC >1EC ∴=．另解：依据AD BC ⊥，2BD CD =，E 是AD 的中点，即可得判定CDE BDA ∆∆∽，且相似比为1:2， ∴12CE AB =，即1CE =．故答案为：132．（2020•泰州）如图，将分别含有30︒、45︒角的一副三角板重叠，使直角顶点重合，若两直角重叠形成的角为65︒，则图中角α的度数为 140︒ ．【解答】解：如图，30B ∠=︒，65DCB ∠=︒，306595DFB B DCB ∴∠=∠+∠=︒+︒=︒，4595140D DFB α∴∠=∠+∠=︒+︒=︒，故答案为：140︒．33．（2019•南通）如图，ABC ∆中，AB BC =，90ABC ∠=︒，F 为AB 延长线上一点，点E 在BC 上，且AE CF =，若25BAE ∠=︒，则ACF ∠= 70 度．【解答】解：在Rt ABE ∆与Rt CBF ∆中，AE CF AB BC =⎧⎨=⎩， Rt ABE Rt CBF(HL)∴∆≅∆．25BAE BCF ∴∠=∠=︒；AB BC =，90ABC ∠=︒，45ACB ∴∠=︒，254570ACF ∴∠=︒+︒=︒；故答案为：70．34．（2019•镇江）如图，直线//a b ，ABC ∆的顶点C 在直线b 上，边AB 与直线b 相交于点D ．若BCD ∆是等边三角形，20A ∠=︒，则1∠= 40 ︒．【解答】解：BCD ∆是等边三角形，60BDC ∴∠=︒，//a b ，260BDC ∴∠=∠=︒，由三角形的外角性质和对顶角相等可知，1240A ∠=∠-∠=︒，故答案为：40．35．（2019•苏州）如图，扇形OAB 中，90AOB ∠=︒．P 为弧AB 上的一点，过点P 作PC OA ⊥，垂足为C ，PC 与AB 交于点D ．若2PD =，1CD =，则该扇形的半径长为 5 ．【解答】解：连接OP ，如图所示．OA OB =，90AOB ∠=︒，45OAB ∴∠=︒．PC OA ⊥，ACD ∴∆为等腰直角三角形，1AC CD ∴==．设该扇形的半径长为r ，则1OC r =-，在Rt POC ∆中，90PCO ∠=︒，3PC PD CD =+=，222OP OC PC ∴=+，即22(1)9r r =-+，解得：5r =．故答案为：5．36．（2019•南京）在ABC ∆中，4AB =，60C ∠=︒，A B ∠>∠，则BC 的长的取值范围是 8343BC< ．【解答】解：作ABC ∆的外接圆，如图所示：BAC ABC ∠>∠，4AB =，当90BAC ∠=︒时，BC 是直径最长，60C ∠=︒，30ABC ∴∠=︒，2BC AC ∴=，34AB AC ==，433AC ∴=， 833BC ∴=；当BAC ABC ∠=∠时，ABC ∆是等边三角形，4BC AC AB ===，BAC ABC ∠>∠，BC ∴长的取值范围是8343BC <；故答案为：8343BC <． 37．（2019•南京）无盖圆柱形杯子的展开图如图所示．将一根长为20cm 的细木筷斜放在该杯子内，木筷露在杯子外面的部分至少有 5 cm ．【解答】解：由题意可得：杯子内的筷子长度为：2212915+=，则筷子露在杯子外面的筷子长度为：20155()cm -=．故答案为：5．三．解答题（共8小题）38．（2020•镇江）如图，AC 是四边形ABCD 的对角线，1B ∠=∠，点E 、F 分别在AB 、BC 上，BE CD =，BF CA =，连接EF ．（1）求证：2D ∠=∠；（2）若//EF AC ，78D ∠=︒，求BAC ∠的度数．【解答】证明：（1）在BEF ∆和CDA ∆中，1BE CD B BF CA =⎧⎪∠=∠⎨⎪=⎩，()BEF CDA SAS ∴∆≅∆，2D ∴∠=∠；（2）2D ∠=∠，78D ∠=︒，278D ∴∠=∠=︒，//EF AC ，278BAC ∴∠=∠=︒．39．（2020•常州）已知：如图，点A 、B 、C 、D 在一条直线上，//EA FB ，EA FB =，AB CD =．（1）求证：E F ∠=∠；（2）若40A ∠=︒，80D ∠=︒，求E ∠的度数．【解答】证明：（1）//EA FB ，A FBD ∴∠=∠，AB CD =，AB BC CD BC ∴+=+，即AC BD =，在EAC ∆与FBD ∆中，EA FB A FBD AC BD =⎧⎪∠=∠⎨⎪=⎩，()EAC FBD SAS ∴∆≅∆，E F ∴∠=∠；（2）EAC FBD ∆≅∆，80ECA D ∴∠=∠=︒，40A ∠=︒，180408060E ∴∠=︒-︒-︒=︒，答：E ∠的度数为60︒．40．（2020•盐城）以下虚线框中为一个合作学习小组在一次数学实验中的过程记录，请阅读后完成虚线框下方的问题1~4．（Ⅰ）在Rt ABC ∆中，90C ∠=︒，22AB =，在探究三边关系时，通过画图，度量和计算，收集到一组数据如下表：（单位：厘米）AC2.8 2.7 2.6 2.3 2 1.5 0.4 BC0.4 0.8 1.2 1.6 2 2.4 2.8 AC BC +3.2 3.5 3.8 3.9 4 3.9 3.2 （Ⅱ）根据学习函数的经验，选取上表中BC 和AC BC +的数据进行分析：①BC x =，AC BC y +=，以(,)x y 为坐标，在图①所示的坐标系中描出对应的点：②连线：观察思考（Ⅲ）结合表中的数据以及所画的图象，猜想．当x ＝____时，y 最大；（Ⅳ）进一步精想：若Rt ABC ∆中，90C ∠=︒，斜边2(AB a a =为常数，0)a >，则BC ＝____时，AC BC +最大．推理证明（Ⅴ）对（Ⅳ）中的猜想进行证明．问题1，在图①中完善（Ⅱ）的描点过程，并依次连线；问题2，补全观察思考中的两个猜想：（Ⅲ） 2 ；（Ⅳ）；问题3，证明上述（Ⅴ）中的猜想；问题4，图②中折线B E F G A --------是一个感光元件的截面设计草图，其中点A ，B 间的距离是4厘米，1AG BE ==厘米．90E F G ∠=∠=∠=︒．平行光线从AB 区域射入，60BNE ∠=︒，线段FM 、FN 为感光区域，当EF 的长度为多少时，感光区域长度之和最大，并求出最大值．【解答】解：问题1：函数图象如图所示：问题2:（Ⅲ）观察图象可知，2x =时，y 有最大值．（Ⅳ）猜想：2BC a =．故答案为：2，2BC a =．问题3：设BC x =，AC BC y +=，在Rt ABC ∆中，90C ∠=︒22224AC AB BC a x ∴=-=-，224y x a x ∴=+-，224y x a x ∴-=-，222224y xy x a x ∴-+=-，2222240x xy y a ∴-+-=，关于x 的一元二次方程有实数根，∴△222442(4)0y y a =-⨯⨯-，228y a ∴，0y >，0a >，22y a ∴，当22y a =时，2224240x ax a -+=2(22)0x a ∴-=，122x x a ∴==，∴当2BC a =时，y 有最大值．问题4：延长AM 交EF 的延长线于C ，过点A 作AH EF ⊥于H ，过点B 作BK GF ⊥于K 交AH 于Q ．在Rt BNE ∆中，90E ∠=︒，60BNE ∠=︒，1BE cm =，tan BE BNE EN∴∠=， 3)NE cm ∴=， //AM BN ，60C ∴∠=︒，90GFE ∠=︒，30CMF ∴∠=︒，30AMG ∴∠=︒，90G ∠=︒，1AG cm =，30AMG ∠=︒，∴在Rt AGM ∆中，tan AG AMG GM ∠=， 3()GM cm ∴=，90G GFH ∠=∠=︒，90AHF ∠=︒，∴四边形AGFH 为矩形，AH FG ∴=，90GFH E ∠=∠=︒，90BKF ∠=︒∴四边形BKFE 是矩形，BK FE ∴=，3434332FN FM EF FG EN GM BK AH BQ AQ KQ QH BQ AQ +=+--=+--=+++-=++-，在Rt ABQ ∆中，4AB cm =，由问题3可知，当22BQ AQ cm ==时，AQ BQ +的值最大，此时(122)EF cm =+，22BQ AQ ∴==时，FN FM +的最大值为43(422)cm +-，此时(122)EF cm =+． 41．（2020•徐州）如图，AC BC ⊥，DC EC ⊥，AC BC =，DC EC =，AE 与BD 交于点F ．（1）求证：AE BD =；（2）求AFD ∠的度数．【解答】解：（1）AC BC ⊥，DC EC ⊥，90ACB DCE ∴∠=∠=︒，ACE BCD ∴∠=∠，在ACE ∆和BCD ∆中，AC BC ACE BCD CE CD =⎧⎪∠=∠⎨⎪=⎩，()ACE BCD SAS ∴∆≅∆，AE BD ∴=；（2）设BC 与AE 交于点N ，90ACB ∠=︒，90A ANC ∴∠+∠=︒，ACE BCD ∆≅∆，A B ∴∠=∠，ANC BNF ∠=∠，90B BNF A ANC ∴∠+∠=∠+∠=︒，90AFD B BNF ∴∠=∠+∠=︒．42．（2020•泰州）如图，在O中，点P为AB的中点，弦AD、PC互相垂直，垂足为M，BC分别与AD、PD相交于点E、N，连接BD、MN．（1）求证：N为BE的中点．（2）若O的半径为8，AB的度数为90︒，求线段MN的长．【解答】（1）证明：AD PC⊥，∴∠=︒，EMC90点P为AB的中点，=，∴PA PBADP BCP∴∠=∠，∠=∠，CEM DEN∴∠=∠=︒=∠，DNE EMC DNB90=，PA PB∴∠=∠，BDP ADP∴∠=∠，DEN DBNDE DB∴=，∴=，EN BN∴为BE的中点；N（2）解：连接OA，OB，AB，AC，AB的度数为90︒，∴∠=︒，90AOB==，8OA OB∴=AB82由（1）同理得：AM EM=，EN BN=，∆的中位线，MN∴是AEB1422MN AB ∴==． 43．（2020•苏州）问题1：如图①，在四边形ABCD 中，90B C ∠=∠=︒，P 是BC 上一点，PA PD =，90APD ∠=︒．求证：AB CD BC +=．问题2：如图②，在四边形ABCD 中，45B C ∠=∠=︒，P 是BC 上一点，PA PD =，90APD ∠=︒．求AB CD BC+的值．【解答】证明：（1）90B APD ∠=∠=︒，90BAP APB ∴∠+∠=︒，90APB DPC ∠+∠=︒，BAP DPC ∴∠=∠，又PA PD =，90B C ∠=∠=︒，()BAP CPD AAS ∴∆≅∆，BP CD ∴=，AB PC =，BC BP PC AB CD ∴=+=+；（2）如图2，过点A 作AE BC ⊥于E ，过点D 作DF BC ⊥于F ，由（1）可知，EF AE DF =+，45B C ∠=∠=︒，AE BC ⊥，DF BC ⊥，45B BAE ∴∠=∠=︒，45C CDF ∠=∠=︒，BE AE ∴=，CF DF =，2AB AE =，2CD DF =，2()BC BE EF CF AE DF ∴=++=+， ∴2()2AB CD AE DF BC ++==． 44．（2020•无锡）如图，已知//AB CD ，AB CD =，BE CF =．求证：（1）ABF DCE ∆≅∆；（2）//AF DE ．【解答】证明：（1）//AB CD ， B C ∴∠=∠，BE CF =，BE EF CF EF ∴-=-，即BF CE =，在ABF ∆和DCE ∆中，AB DC B C BF CE =⎧⎪∠=∠⎨⎪=⎩，()ABF DCE SAS ∴∆≅∆；（2）ABF DCE ∆≅∆，AFB DEC ∴∠=∠，AFE DEF ∴∠=∠，//AF DE ∴．45．（2020•南京）如图，点D 在AB 上，点E 在AC 上，AB AC =，B C ∠=∠，求证：BD CE =．【解答】证明：在ABE ∆与ACD ∆中A A AB AC B C ∠=∠⎧⎪=⎨⎪∠=∠⎩，()ABE ACD ASA ∴∆≅∆．AD AE ∴=．BD CE ∴=．。