异面直线的判定练习题及答案
异面直线所成的角专题训练

异面直线所成的角专题训练1.在正方体ABCD-A1B1C1D1中,异面直线AC和XXX所成的角为多少度?答案:90度。
2.在正方体ABCD-A1B1C1D1中,AB的中点M,DD1的中点N,则异面直线B1M与CN所成的角是多少度?答案:60度。
3.在正方体ABCD-A1B1C1D1中,E为线段AC的中点,则异面直线DE与B1C所成角的大小为多少度?答案:无法确定,题目中缺少信息。
4.在三棱锥ABC-A1B1C1中,底面为正三角形,侧棱垂直于底面,AB=4,AA1=6.若E是棱BB1上的点,且BE=B1E,则异面直线A1E与AC1所成角的余弦值为多少?答案:1/3.5.在三棱锥P-ABC中,△ABC为等边三角形,△PAC为等腰直角三角形,PA=PC=4,平面PAC⊥平面ABC,D为AB的中点,则异面直线AC与PD所成角的余弦值为多少?答案:-1/2.6.在棱长为1的正方体ABCD-A1B1C1D1中,M和N分别为A1B1和BB1的中点,直线AM与CN所成角的余弦值是多少?答案:-3/5.7.在直三棱柱ABC-A1B1C1中,AC⊥BC,且CA=CC1=10,则直线B1C与直线AB1所成角的余弦值为多少?答案:5/13.8.在直三棱柱ABC-A1B1C1中,AA1=2,A1B1=2,AB⊥BC,点M是AC1的中点,则异面直线MB与AA1所成角的余弦值为多少?答案:-1/3.9.正三棱锥A-PBC的侧棱两两垂直,D,E分别为棱PA,BC的中点,则异面直线PC与DE所成角的余弦值为多少?答案:-3/5.10.在正方体ABCD-A1B1C1D1中,点E为BC的中点,点F为B1C1的中点,则异面直线AF与C1D所成角的大小为多少度?答案:无法确定,题目中缺少信息。
中,ABCD是正方形,E是AD的中点,F是BC的中点,异面直线EF与AC所成的角的正弦值为(。
)A.12B.13C.23D.110.在正方体ABCD A1B1C1D1中,E是AD的中点,F是BC的中点,异面直线EF与直线AC所成的角的正切值为(。
专题10:异面直线问题高考真题(原卷版)

专题10:异面直线问题高考真题(原卷版)一、单选题1.2018年全国普通高等学校招生统一考试理数(全国卷II )在长方体1111ABCD A B C D -中,1AB BC ==,13AA =,则异面直线1AD 与1DB 所成角的余弦值为A .15B .5C .5D .222.2017年全国普通高等学校招生统一考试理科数学(新课标2卷) 已知直三棱柱111C C AB -A B 中,C 120∠AB =,2AB =,1C CC 1B ==,则异面直线1AB 与1C B 所成角的余弦值为( )A .3B .15C .10D .3 3.2016年全国普通高等学校招生统一考试理科数学(新课标1卷) 平面过正方体ABCD —A 1B 1C 1D 1的顶点A ,,,,则m ,n 所成角的正弦值为 A . B . C . D .4.2014年全国普通高等学校招生统一考试理科数学(全国Ⅱ卷)直三棱柱ABC -A 1B 1C 1中,∠BCA =90°,M ,N 分别是A 1B 1,A 1C 1的中点,BC =CA =CC 1,则BM 与AN 所成角的余弦值为( )A .110 B .25 C 30D 25.2018年全国普通高等学校招生统一考试文数(全国卷II ) 在正方体1111ABCD A B C D -中,E 为棱1CC 的中点,则异面直线AE 与CD 所成角的正切值为A .22 B .32 C 5 D .72二、解答题6.2015年全国普通高等学校招生统一考试理科数学(新课标Ⅰ)如图,四边形ABCD为菱形,∠ABC=120°,E,F是平面ABCD同一侧的两点,BE⊥平面ABCD,DF⊥平面ABCD,BE=2DF,AE⊥EC.(1)证明:平面AEC⊥平面AFC;(2)求直线AE与直线CF所成角的余弦值.。
异面直线所成的角测试题(含答案).docx
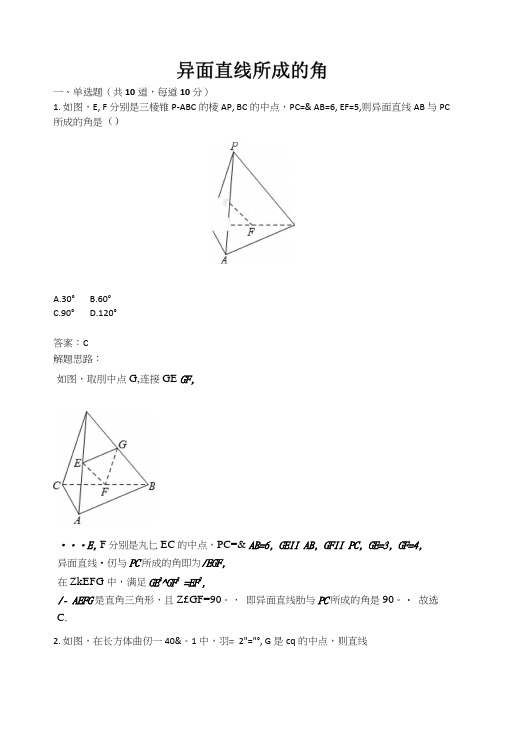
一、单选题(共10道,每道10分)1.如图,E, F分别是三棱锥P-ABC的棱AP, BC的中点,PC=& AB=6, EF=5,则异面直线AB 与PC 所成的角是()A.30°B.60°C.90°D.120°答案:C解题思路:如图,取刖中点G,连接GE GF,•・・E, F分别是丸匕EC的中点,PC=& AB=6, GEII AB, GFII PC, GE=3, GF=4,异面直线•仞与PC所成的角即为/EGF,在ZkEFG 中,满足GE2^GF2 =EF2,/- AEFG是直角三角形,且Z£GF=90。
,即异面直线肋与PC所成的角是90。
・故选C.2.如图,在长方体曲仞一40&。
1中,羽= 2"="°, G是cq的中点,则直线4G与EG所成角的大小是()A.30°B.45°C.60°D.120°答案:C解题思路:如图,取44]的中点E,连接EG, BE,易证,EG,・・・直线4G与PG所成的角可转化为EG与BG所成的角,即ZBGE,T AA X— 2AB = 2AD , G是CQ 的中点,/. /\BGE是等边三角形,••厶GE=6g即直线赵C芍BG所成的角是60。
・故选C.试题难度:三颗星知识点:界面直线及其所成的角3.如图,在正方体曲CD-40iCi£)i屮,点p在线段上运动,则异面直线CP与牌所成的角&的取值范围是()A.O。
<^<90°B 0° GW 90°C.0。
W0W 60°D 0°60°答案:D解题思路:如图,连接川C, CD1,则码II CD,,异面直线CP与码所成的角即为CP与C®所成的角, 即e=ZPCD\,•・• △zpc是等边三角形,・•・当点P和点加重合时,扫60。
异面直线专题复习附答案

2014~2015学年度第一学期综合训练(二)异面直线一、选择题——对异面直线的理解1.没有公共点的两条直线的位置关系是( )(A)平行 (B)异面 (C)平行或异面 (D)不能确定 2.分别在两相交平面内的两条直线的位置关系是( )(A)异面 (B)平行 (C)平行或异面 (D)平行或异面或相交 3.两条异面直线指的是( ) (A)(B)某一平面内的一条直线和这个平面外的一条直线(C)(D)4.a 、b 是异面直线,b 、c 也是异面直线,那么a 、c 的位置是( )(A)异面 (B)异面或平行 (C)异面或相交 (D)相交、平行或异面 5.说出正方体中各对线段的位置关系:(1) AB 和CC 1; (2)A 1C 和BD 1; (3)A 1A 和CB 1;(4)A 1C 1和CB 1; (5)A 1B 1和DC ; (6)BD 1和DC.6.在棱长为1的正方体ABCD —A 1B 1C 1D 1中,M 和N 分别为A 1B 1和BB 1的中点,那么直线AM 与CN 所成角的余弦值是()32((()()55A B C D二、求异面直线所成角例 S 是正三角形ABC 所在平面外的一点,如图SA =SB =SC ,且∠ASB =∠BSC =∠CSA =2π,M 、N 分别是AB 和SC 的中点.求异面直线SM 与BN 所成的角的余弦值.练习、 如图,在直三棱柱ABC -A 1B 1C 1中,∠BCA =90°,M 、N 分别是A 1B 1和A 1C 1的中点,若BC =CA =CC 1,求BM 与AN 所成的角.B M AN CS B 1(第5题)A 1ABC 1D 1C D B 1(第6题)A 1AB C 1 D 1 CD M N ANMA 1 C 1B 1课后巩固: 一、选择题1.正方体ABCD —A 1B 1C 1D 1中,直线BC 1与AC(A)相交且垂直 (B)相交但不垂直 (C)异面且垂直 (D)异面但不垂直 2.设a 、b 、c 是空间中的三条直线,下面给出四个命题:①如果a ⊥b 、b ⊥c ,则a ∥c ;②如果a 和b 相交,b 和c 相交,则a 和c 也相交;③如果a 、b 是异面直线,c 、b 是异面直线,则a 、c 也是异面直线; ④如果a 和b 共面,b 和c 共面,则a 和c 也共面 在上述四个命题中,真命题的个数是()(A)4 (B)3 (C)2 (D)1 (E)0 3.如果直线l 和n 是异面直线,那么和直线l 、n 都垂直的直线(A)不一定存在 (B)总共只有一条(C)总共可能有一条,也可能有两条 (D)有无穷多条 4.如图,四面体S-ABC 的各棱长都相等,如果E 、F 分别为SC 、AB 的中点,那么异面直线EF 与SA 所成的角等于(A)90° (B)60° (C)45° (D)30°5.如图,A 1B 1C 1—ABC 是直三棱柱(三侧面为矩形),∠BCA=90°, 点D 1、F 1 分别是A 1B 1、A 1C 1BC=CA=CC 1,则BD 1与AF 1所成角的余弦值是()105(()2A B二.如图,四面体ABCD 中,AC ⊥BD,且AC =4,BD =3,M 、N 分别是AB 、CD 的中点,求MN 和BD所成角的正切值三.如图,四面体ABCD 中,AB ⊥BC ,AB ⊥BD ,BC ⊥CD ,且AB =BC =6,BD =8,E 是AD 中点,求BE 与CD 所成角的余弦值四.如图,正三棱柱的九条棱都相等,三个侧面都是正方体,M 、N 分别是BC 和A 1C 1MN 与CC 1所成角的余弦值。
考点练习(必修二):异面直线的判定(附答案)

异面直线的判定1. 如图,正方体ABCD-A1B1C1D1中,判断下列直线的位置关系:①直线A1B与直线D1C的位置关系是________;②直线A1B与直线B1C的位置关系是________;③直线D1D与直线D1C的位置关系是________;④直线AB与直线B1C的位置关系是________.2. 若a、b是异面直线,b、c是异面直线,则()A.a∥c B.a、c是异面直线C.a、c相交D.a、c平行或相交或异面3. 若a,b,c是空间3条直线,a∥b,a与c相交,则b与c的位置关系是()A.异面B.相交C.平行D.异面或相交4. 若直线a、b、c满足a∥b,a、c异面,则b与c()A.一定是异面直线B.一定是相交直线C.不可能是平行直线D.不可能是相交直线5. 如下图所示,点P,Q,R,S分别在正方体的4条棱上,且是所在棱的中点,则直线PQ 与RS是异面直线的一个图是________.6. 在长方体ABCD-A1B1C1D1中,与棱AA1垂直且异面的棱有________.7. 如下图所示是一个正方体的平面展开图,则在正方体中,AB与CD的位置关系为()A.相交B.平行C.异面而且垂直D.异面但不垂直8. 若P是两条异面直线l,m外的任意一点,则()A.过点P有且仅有一条直线与l,m都平行B.过点P有且仅有一条直线与l,m都垂直C.过点P有且仅有一条直线与l,m都相交D.过点P有且仅有一条直线与l,m都异面9. 如右图所示,正方体ABCD-A1B1C1D1中,M,N分别是A1B1,B1C1的中点.问:(1)AM和CN是否是异面直线?说明理由.(2)D1B和CC1是否是异面直线?说明理由.参考答案1. 【自主解答】根据题目条件知道直线A1B与直线D1C在平面A1BCD1中,且没有交点,则两直线“平行”,所以①应该填“平行”;点A1、B、B1在一个平面A1BB1内,而C不在平面A1BB1内,则直线A1B与直线B1C“异面”.同理,直线AB与直线B1C“异面”.所以②④都应该填“异面”;直线D1D与直线D1C相交于D1点,所以③应该填“相交”.【答案】①平行②异面③相交④异面2. D 若a、b是异面直线,b、c是异面直线,那么a、c可以平行,可以相交,可以异面.3. 答案:D4. C 若a∥b,a、c是异面直线,那么b与c不可能平行,否则由公理4知a∥c.5. 答案:③6.【解析】如图,与棱AA1垂直且异面的棱有DC,BC,D1C1,B1C1.【答案】DC,BC,D1C1,B1C17. 答案:D8. 答案:B9. 解:(1)不是异面直线.理由:∵M,N分别是A1B1,B1C1的中点,∴MN∥A1C1.又A1A D1D,而D1D C1C,∴A1A C1C.∴四边形A1ACC1为平行四边形.∴A1C1∥AC,得到MN∥AC.∴A,M,N,C在同一个平面内,故AM和CN不是异面直线.(2)是异面直线.证明如下:假设D1B与CC1在同一个平面D1CC1内,则B∈平面CC1D1,C∈平面CC1D1,∴BC⊂平面CC1D1.而BC⊥平面CC1D1,BC⊄平面CC1D1,∴假设不成立,故D1B与CC1是异面直线.。
异面直线的判定练习题及答案

5.平行六面体 ABCD-A 1B 1C 1D 1中,求证:CD 所在的直线与 BC i 所在的直线是异面直线.异面直线的判定 1•已知空间四边形 ABCD , E 、H 分别是AB 、AD 的中点, 三等分点(如图),求证:(1) 对角线AC 、BD 是异面直线;(2) 直线EF 和HG 必交于一点,且交点在 AC 上.F 、G 分别是边BC 、DC 的 2.A 是厶BCD 平面外的一点,E 、F 分别是BC 、AD 的中点,(1)求证:直线EF 与BD 是异面直线;3.已知:平面 af 平面3 =a b? a, b A a=A c? B 且c // a ,求证: b 、c 是异面直线.4.已知不共面的三条直线 与BC 是异面直线.a 、b 、c 相交于点 P , A € a , B € a , C € b , D € c ,求证:ADD C小结:常用方法是反证法(1)利用反证法证明对角线AC、BD是共面直线,推出矛盾,从而证明是异面直(2)说明直线EF和HG必交于一点,然后证明这点在平面ADC内.又在平面ABC内,必在它们的交线AC 上.:⑴假设对角线AC、BD在同一平面a内,则A、B、C、D都在平面a内,这与ABCD是空间四边形矛盾,:.AC、BD是异面直线.(2)T E、H分别是AB、AD的中点所以EH平行且等于1/2BD,又F、G分另堤BC、DC的三等分点,EG平行等于2/3BD,. •: EH// FG,且EH v FG.:FE与GH 相交设交点为0,又0在GH 上, GH在平面ADC内,•:O在平面ADC内.同理,0在平面ABC内.从而0在平面ADC与平面ABC的交线AC 上.2. (1)假设EF与BD不是异面直线,则EF与BD共面,得到A、B、C、D在同一平面内,矛盾.(1)证明:用反证法•设EF与BD不是异面直线,_则EF与BD共面,从而DF与BE共面,即AD与BC共面,所以A、B、C、D在同一平面内,这与A是厶BCD平面外的一点相矛盾.故直线EF与BD是异面直线.3证明b、c是异面直线,比较困难,考虑使用反证法,即若b与c不是异面直线,则b// c或b与C相交,证明b// c或b与c相交都是不可能的, 从而证明b、c是异面直线证明:用反证法:若b与c不是异面直线,则b// c或b与c相交(1)若b// c. :a//c,•: a//b 这与a H b=A矛盾;(2)若b,c相交于B,则B E B,又a H b=A:.A E AB? 3 即b? B这与b np =AF盾:-b,c是异面直线.4证明:法一:(反证法)假设AD和BC共面,所确定的平面为a那么点P、A、B、C、D都在平面a内,•:直线a b、c都在平面a内,与已知条件a b、c不共面矛盾,假设不成立,:AD和BC是异面直线.法二:(直接证法):a n c=P •:它们确定一个平面,设为a由已知C?平面a, B E平面a,AD?平面a, B?AD,:・AD和BC是异面直线.5证明:用反证法,假设CD1所在的直线与BC1所在的直线不是异面直线.设直线CD1与BC1共面aV C, D1E CD1, B, C1E BC1, •: C, D1, B, C1E a •/ CC1 / BB1,:.CC1, BB1 确定平面BB1C1C, :. C, B, C1 E 平面BB1C1C.T不共线的三点C, B, C1只有一个平面,•:平面a与平面BB1C1C重合••:D1E平面BB1C1C,矛盾.因此,假设错误,即CD1所在的直线与BC1所在的直线是异面直线。
异面直线的判定(含答案)

异面直线的判定一、单选题(共9道,每道11分)1.在三棱锥的六条棱中任选两条,则这两条棱所在直线互为异面直线的概率是( )A. B.C. D.答案:B解题思路:试题难度:三颗星知识点:异面直线的判定2.下列四个命题:①分别在两个平面内的两条直线是异面直线;②和两条异面直线都垂直的直线有且只有一条;③和两条异面直线都相交的两条直线必异面;④若a和b是异面直线,b和c是异面直线,则a和c也是异面直线.其中真命题有( )A.3个B.2个C.1D.0个答案:D解题思路:试题难度:三颗星知识点:异面直线的判定3.设A为空间一点,是两条直线,α,β是两个平面,有下列四个命题:①若,,则可能为异面直线;②若,,则;③已知为异面直线,,,,,则α∥β;④若α⊥β,,则.其中正确命题的序号是( )A.①③B.②④C.②③D.①④答案:A解题思路:试题难度:三颗星知识点:直线与平面垂直的判定4.如图,正方体的所有面对角线中,与面对角线成异面直线的有( )A.7条B.6条C.5条D.4条答案:C解题思路:试题难度:三颗星知识点:异面直线的判定5.如图,在四棱锥P-ABCD中,已知底面ABCD是矩形,则各棱所在直线中互为异面直线的共有( )A.4对B.6对C.8对D.12对答案:C解题思路:试题难度:三颗星知识点:异面直线的判定6.如图是正方体纸盒的平面展开图,则直线AB,CD在原正方体中的位置关系是( )A.平行B.垂直C.相交成60°D.异面且成60°角答案:D解题思路:试题难度:三颗星知识点:表面展开图7.如图,已知正方体的棱长为a,则下列结论不正确的是( )A.异面直线与所成的角为60°B.直线与垂直C.直线与平行D.三棱锥的体积为答案:C解题思路:试题难度:三颗星知识点:异面直线的判定8.如图,在正四棱柱中,E,F分别是的中点,则下列结论不成立的是( )A.EF与垂直B.EF与BD垂直C.EF与CD异面D.EF与异面答案:D解题思路:试题难度:三颗星知识点:异面直线的判定9.如图,在正方体中,O是底面正方形ABCD的中心,M是的中点,N是上的动点,则直线NO,AM的位置关系是( )A.平行B.相交C.异面垂直D.异面不垂直答案:C解题思路:试题难度:三颗星知识点:异面直线的判定。
专题10:异面直线问题高考真题(解析版)

专题10:异面直线问题高考真题(解析版)一、单选题1.2018年全国普通高等学校招生统一考试理数(全国卷II )在长方体1111ABCD A B C D -中,1AB BC ==,1AA =1AD 与1DB 所成角的余弦值为A .15BCD.2【答案】C 【解析】分析:先建立空间直角坐标系,设立各点坐标,利用向量数量积求向量夹角,再根据向量夹角与线线角相等或互补关系求结果.详解:以D 为坐标原点,DA,DC,DD 1为x,y,z轴建立空间直角坐标系,则11(0,0,0),(1,0,0),(1,1D A B D ,所以11(1,0,3),(1,1AD DB =-=,因为1111111cos ,2ADDB AD DB AD DB ⋅-===⨯,所以异面直线1AD 与1DB 所成角,选C. 点睛:利用法向量求解空间线面角的关键在于“四破”:第一,破“建系关”,构建恰当的空间直角坐标系;第二,破“求坐标关”,准确求解相关点的坐标;第三,破“求法向量关”,求出平面的法向量;第四,破“应用公式关”. 2.2017年全国普通高等学校招生统一考试理科数学(新课标2卷)已知直三棱柱111C C AB -A B 中,C 120∠AB=,2AB =,1C CC 1B ==,则异面直线1AB 与1C B 所成角的余弦值为() A .B C D 【答案】C 【解析】如图所示,补成直四棱柱1111ABCD A B C D -,则所求角为21111,2,21221cos603,5BC D BC BD C D AB ∠==+-⨯⨯⨯︒===,易得22211C D BD BC =+,因此111210cos 55BC BC D C D ∠===,故选C .平移法是求异面直线所成角的常用方法,其基本思路是通过平移直线,把异面问题化归为共面问题来解决,具体步骤如下:①平移:平移异面直线中的一条或两条,作出异面直线所成的角; ②认定:证明作出的角就是所求异面直线所成的角; ③计算:求该角的值,常利用解三角形;④取舍:由异面直线所成的角的取值范围是(0,]2π,当所作的角为钝角时,应取它的补角作为两条异面直线所成的角.求异面直线所成的角要特别注意异面直线之间所成角的范围.3.2016年全国普通高等学校招生统一考试理科数学(新课标1卷) 平面过正方体ABCD —A 1B 1C 1D 1的顶点A ,,,,则m ,n 所成角的正弦值为A .B .C .D .【答案】A 【解析】试题分析:如图,设平面平面=,平面 平面=,因为平面,所以,则所成的角等于所成的角.延长,过作,连接,则为,同理为,而,则所成的角即为所成的角,即为,故所成角的正弦值为,选A.【考点】平面的截面问题,面面平行的性质定理,异面直线所成的角.【名师点睛】求解本题的关键是作出异面直线所成的角,求异面直线所成角的步骤是:平移定角、连线成形、解形求角、得钝求补.4.2014年全国普通高等学校招生统一考试理科数学(全国Ⅱ卷)直三棱柱ABC -A 1B 1C 1中,∠BCA =90°,M ,N 分别是A 1B 1,A 1C 1的中点,BC =CA =CC 1,则BM 与AN 所成角的余弦值为( ) A .110B .25C 30D .22【答案】C 【解析】以C 为原点,直线CA 为x 轴,直线CB 为y 轴,直线1CC 为z 轴,则设CA=CB=1,则(0,1,0)B ,11(,,1)22M ,A (1,0,0),1(,0,1)2N ,故11(,,1)22BM =-,1(,0,1)2AN =-,所以cos ,BM AN BM AN BM AN⋅〈〉==⋅3465=⋅30C. 考点:本小题主要考查利用空间向量求线线角,考查空间向量的基本运算,考查空间想象能力等数学基本能力,考查分析问题与解决问题的能力.5.2018年全国普通高等学校招生统一考试文数(全国卷II )在正方体1111ABCD A B C D -中,E 为棱1CC 的中点,则异面直线AE 与CD 所成角的正切值为A .22B .32C .52D .72【答案】C 【分析】利用正方体1111ABCD A B C D -中,//CD AB ,将问题转化为求共面直线AB 与AE 所成角的正切值,在ABE ∆中进行计算即可. 【详解】在正方体1111ABCD A B C D -中,//CD AB ,所以异面直线AE 与CD 所成角为EAB ∠,设正方体边长为2a ,则由E 为棱1CC 的中点,可得CE a =,所以5BE a =,则55tan 22BE a EAB AB a ∠===.故选C.【点睛】求异面直线所成角主要有以下两种方法:(1)几何法:①平移两直线中的一条或两条,到一个平面中;②利用边角关系,找到(或构造)所求角所在的三角形;③求出三边或三边比例关系,用余弦定理求角; (2)向量法:①求两直线的方向向量;②求两向量夹角的余弦;③因为直线夹角为锐角,所以②对应的余弦取绝对值即为直线所成角的余弦值.二、解答题6.2015年全国普通高等学校招生统一考试理科数学(新课标Ⅰ)如图,四边形ABCD 为菱形,∠ABC =120°,E ,F 是平面ABCD 同一侧的两点,BE ⊥平面ABCD ,DF ⊥平面ABCD ,BE =2DF ,AE ⊥EC .(1)证明:平面AEC⊥平面AFC;(2)求直线AE与直线CF所成角的余弦值.【答案】(1)见解析;(2).【解析】试题分析:(Ⅰ)连接BD,设BD∩AC=G,连接EG,FG,EF,在菱形ABCD 中,不妨设GB=1易证EG⊥AC,通过计算可证EG⊥FG,根据线面垂直判定定理可知EG⊥平面AFC,由面面垂直判定定理知平面AFC⊥平面AEC;(Ⅱ)以G为坐标原点,分别以的方向为轴,y轴正方向,为单位长度,建立空间直角坐标系G-xyz,利用向量法可求出异面直线AE与CF所成角的余弦值.试题解析:(Ⅰ)连接BD,设BD∩AC=G,连接EG,FG,EF,在菱形ABCD中,不妨设GB=1,由∠ABC=120°,可得AG=GC=.由BE⊥平面ABCD,AB=BC可知,AE=EC,又∵AE⊥EC,∴EG=,EG⊥AC,在Rt△EBG中,可得BE=,故DF=.在Rt△FDG中,可得FG=.在直角梯形BDFE中,由BD=2,BE=,DF=可得EF=,∴,∴EG⊥FG,∵AC∩FG=G,∴EG⊥平面AFC,∵EG面AEC,∴平面AFC⊥平面AEC.(Ⅱ)如图,以G为坐标原点,分别以的方向为轴,y轴正方向,为单位长度,建立空间直角坐标系G-xyz,由(Ⅰ)可得A(0,-,0),E(1,0,),F(-1,0,),C(0,,0),∴=(1,,),=(-1,-,).…10分故.所以直线AE与CF所成的角的余弦值为.考点:空间垂直判定与性质;异面直线所成角的计算;空间想象能力,推理论证能力。
最新异面直线练习1含答案

异面直线练习1一、选择题1.和两条异面直线都相交的两条直线的位置关系是() A.异面B.相交C.平行D.异面或相交解析:如图,在正方体ABCD-A′B′C′D′中,AB与B′C′为两条异面直线,则BB′与AC′两条直线都与AB、B′C′相交,BB′与AC′异面,而BB′、BC′都与AB、B′C′相交,BB′、BC′却相交.答案:D2.已知a、b是异面直线,直线c∥直线a,则c与b () A.一定是异面直线B.一定是相交直线C.不可能是平行直线D.不可能是相交直线解析:c与b不可能是平行直线,否则与条件矛盾.答案:C3.如图,α∩β=l,A、B∈α,C∈β,C∉l,直线AB∩l=M,则平面ABC 与β的交线是() A.直线AC B.直线ABC.直线BC D.直线CM解析:通过直线AB 与点C 的平面,为面ABC ,M ∈AB .∴M ∈面ABC ,而C ∈面ABC ,又∵M ∈β,C ∈β.∴面ABC 和β的交线必通过点C 和点M .答案:D4.(2012年重庆)设四面体的六条棱的长分别为1,1,1,1,2和a ,且长为a 的棱与长为2的棱异面,则a 的取值范围是( )A .(0,2)B .(0,3)C .(1,2)D .(1,3)解析:构造四面体ABCD ,使AB =a ,CD =2, AD =AC =BC =BD =1,取CD 的中点E , 则AE =BE =22,∴22+22>a,0<a <2, 故选A. 答案:A5.(2012年大同调研)直三棱柱ABC -A 1B 1C 1中,若∠BAC =90°,AB =AC =AA 1,则异面直线BA 1与AC 1所成的角等于( )A .30°B .45°C .60°D .90°解析:分别取AB 、AA 1、A 1C 1的中点D 、E 、F ,则BA 1∥DE ,AC 1∥EF ,所以异面直线BA1与AC1所成的角为∠DEF(或其补角),设AB=AC=AA1=2,则DE=EF=2,DF=6,由余弦定理得,∠DEF=120°.答案:C6.过正方体ABCD-A1B1C1D1的顶点A作直线l,使l与棱AB,AD,AA1所成的角都相等,这样的直线l可以作A.1条B.2条C.3条D.4条解析:如图所示.AC1,AC2,AC3,AC4即为所求.答案:D二、填空题7.在三棱锥P-ABC中,P A⊥底面ABC,AC⊥BC,P A=AC=BC,则直线PC与AB所成角的大小是________.解析:分别取P A,AC,CB的中点F,D,E,连接FD,DE,EF,AE,则∠FDE是直线PC与AB所成角或其补角.设P A=AC=BC=2a,在△FDE中,易求得FD=2a,DE=2a,FE=AF2+AE2=6a,根据余弦定理,得cos∠FDE=2a2+2a2-6a22×2a×2a=-12,所以∠FDE=120°.所以PC与AB所成角的大小是60°.答案:60°8.已知a、b为不垂直的异面直线,α是一个平面,则a、b在α上的射影可能是:①两条平行直线;②两条互相垂直的直线;③同一条直线;④一条直线及其外一点.则在上面的结论中,正确结论的编号是________(写出所有正确结论的编号).解析:①、②、④对应的情况如下:用反证法证明③不可能.答案:①②④9.(2012年南京一模)在图中,G、H、M、N分别是正三棱柱的顶点或所在棱的中点,则表示直线GH、MN是异面直线的图形有________.(填上所有正确答案的序号)解析:图①中,直线GH ∥MN ;图②中,G 、H 、N 三点共面,但M ∉面GHN , 因此直线GH 与MN 异面; 图③中,连接MG ,GM ∥HN ; 因此GH 与MN 共面;图④中,G 、M 、N 共面,但H ∉面GMN , ∴GH 与MN 异面.所以图②、④中GH 与MN 异面. 答案:②④ 三、解答题 10.如图所示,空间四边形ABCD 中,E 、F 、G 分别在AB 、BC 、CD 上,且满足AE ∶EB =CF ∶FB =2∶1,CG ∶GD =3∶1,过E 、F 、G 的平面交AD 于H ,连接EH .(1)求AH ∶HD ;(2)求证:EH 、FG 、BD 三线共点. 解:(1)∵AE EB =CFFB =2,∴EF ∥AC .∴EF ∥平面ACD .而EF ⊂平面EFGH ,且平面EFGH ∩平面ACD =GH , ∴EF ∥GH .而EF ∥AC , ∴AC ∥GH .∴AH HD =CGGD =3,即AH ∶HD =3∶1.(2)证明:∵EF ∥GH ,且EF AC =13,GH AC =14, ∴EF ≠GH .∴四边形EFGH 为梯形.令EH ∩FG =P ,则P ∈EH ,而EH ⊂平面ABD ,所以P ∈面ABD ,P ∈FG ,FG ⊂平面BCD ,所以P ∈面BCD ,而平面ABD ∩平面BCD =BD ,∴P ∈BD .∴EH 、FG 、BD 三线共点.11.如图所示,在空间四边形ABCD 中,已知AD =1,BC =3,且AD ⊥BC ,对角线BD =132,AC =32,求AC 和BD 所成的角的大小.解:如图所示,分别取AD ,CD ,AB ,DB 的中点E ,F ,G ,H , 连接EF ,FH ,HG ,GE ,GF , 则由三角形中位线定理知EF ∥AC 且EF =12AC =34,GE ∥BD 且GE =12BD =134, GH ∥AD ,GH =12AD =12, HF ∥BC ,HF =12BC =32,从而可知GE与EF所成的锐角(或直角)即为BD和AC所成的角,GH和HF 所成的锐角(或直角)即为AD与BC所成的角.∵AD⊥BC,∴∠GHF=90°∴GF2=GH2+HF2=1.在△EFG中,EG2+EF2=1=GF2,∴∠GEF=90°,即AC与BD所成的角为90°.12.正方体ABCD-A1B1C1D1中.(1)求AC与A1D所成角的大小;(2)若E、F分别为AB、AD的中点,求A1C1与EF所成角的大小.解:(1)如图所示,连接AB1,B1C,由ABCD-A1B1C1D1是正方体,易知A1D∥B1C,从而B1C与AC所成的角就是AC与A1D所成的角.∵AB1=AC=B1C,∴∠B1CA=60°.即A1D与AC所成的角为60°.(2)如图所示,连接AC、BD,在正方体ABCD-A1B1C1D中,AC⊥BD,AC∥A1C1,∵E、F分别为AB、AD的中点,∴EF∥BD,∴EF⊥AC.∴EF⊥A1C1.即A1C1与EF所成的角为90°.[热点预测]13.(1)在底面为正方形的长方体上任意选择4个顶点,则以这4个顶点为顶点构成的几何形体可能是:①矩形;②不是矩形的平行四边形;③有三个面为直角三角形,一个面为等腰三角形的四面体;④每个面都是等腰三角形的四面体;⑤每个面都是直角三角形的四面体.则其中正确结论的序号是()A.①③④⑤B.①②④⑤C.①②③⑤D.①②③④(2)如图是正四面体的平面展开图,G、H、M、N分别为DE、BE、EF、EC 的中点,在这个正四面体中,①GH与EF平行;②BD与MN为异面直线;③GH与MN成60°角;④DE与MN垂直.以上四个命题中,正确命题的序号是________.解析:(1)由长方体的性质知①正确,②不正确;对于③,长方体ABCD-A1B1C1D1中的四面体A1-ABD符合条件,③正确;对于④,长方体ABCD-A1B1C1D1中的四面体A1-BC1D符合条件,④正确;对于⑤,长方体ABCD-A1B1C1D1中的四面体A1-ABC符合条件.(2)还原成正四面体知GH与EF为异面直线,BD与MN为异面直线,GH 与MN成60°角,DE⊥MN.答案:(1)A(2)②③④。
异面直线--选择题-经典(含解析)

异面直线—经典一.选择题(共27小题)1.如图,正三棱锥A﹣BCD中,E在棱AB上,F在棱CD 上.并且(0<λ<+∞),设α为异面直线EF与AC所成的角,β为异面直线EF与BD所成的角,则α+β的值是()A.B.C.D.与λ的值有关2.(2012•陕西)如图,在空间直角坐标系中有直三棱柱ABC﹣A1B1C1,CA=CC1=2CB,则直线BC1与直线AB1夹角的余弦值为()A.B.C.D.3.(2010•江西)过正方体ABCD﹣A1B1C1D1的顶点A作直线L,使L与棱AB,AD,AA1所成的角都相等,这样的直线L可以作()A. 1条B. 2条C. 3条D. 4条4.(2008•四川)一个正方体的展开图如图所示,B,C,D为原正方体的顶点,A为原正方体一条棱的中点.在原来的正方体中,CD与AB所成角的余弦值为()A.B.C.D.5.(2007•福建)如图,在正方体ABCD﹣A1B1C1D1中,E、F、G、H分别为AA1、AB、BB1、BC1的中点,则异面直线EF与GH所成的角等于()A. 45°B. 60°C. 90°D. 120°6.(2004•天津)如图,在棱长为2的正方体ABCD﹣A1B1C1D1中,O是底面ABCD的中心,E、F分别是CC1、AD的中点,那么异面直线OE和FD 1所成的角的余弦值等于()A.B.C.D.7.(2003•北京)如图,在正三角形ABC中,D,E,F分别为各边的中点,G,H,I,J分别为AF,AD,BE、DE 的中点.将△ABC沿DE,EF,DF折成三棱锥以后,GH与IJ所成角的度数为()A. 90°B. 60°C. 45°D. 0°8.(2002•天津)正六棱柱ABCDEF﹣A1B1C1D1E1F1的底面边长为1,侧棱长为,则这个棱柱侧面对角线E1D 与BC1所成的角是()A. 90°B. 60°C. 45°D. 30°9.点P在正方形ABCD所在平面外,PD⊥平面ABCD,PD=AD,则PA与BD所成角的度数为() A. 30°B. 45°C. 60°D. 90°10.如图,在棱长为2的正方体ABCD﹣A1B1C1D1中,O为底面的中心,E是CC1的中点,那么异面直线A1D与EO所成角的余弦值为()A.B.C.D. 0A. 30°B. 45°C. 60°D. 90°12.如图所示,棱长都相等的棱锥A﹣BCD中,E、F分别在棱AB、CD 上,使(λ>0)设f(λ)=αλ+βλ,αλ表示EF与AC所成的角的度数,βλ表示EF与BD所成角的度数,则()13.在等边三角形ABC中,M、N、P分别为AB、AC、BC的中点,沿MN将△AMN折起,使得面AMN与面MNCB 所在二面角的余弦值为,则直线AM与NP所成角的大小为()A. 90°B . 60°C.D.14.在矩形ABCD中,AB=1,BC=2,沿对角线AC折成直二面角,则折后异面直线AB与CD所成的角为()A.arccos B.arcsinC.arccosD.arccos15.如图的正方体ABCD﹣A1B1C1D1中,异面直线A1B与B1C所成的角是()A.30°B. 45°C.60°D. 90°16.如图,正方体AC1中,E、F分别是DD1、BD的中点,则直线AD1与EF所成的角余弦值是().A.B.C.D.17.正方体ABCD﹣A1B1C1D1中,E为CC1中点,则异面直线BC1与AE所成角的余弦值为()A.B.C.D.18.如图正方体ABCD﹣A1B1C1D1中,M是正方形ABCD的中心,则直线A1D与直线B1M所成角大小为()A.300B.450C.600D.90019.正方体AC1中M是棱D1D的中点,O是正方形ABCD的中心,则异面直线OA1与AM所成的角是() A. 90°B. 60°C. 45°D.均不对20.长方体ABCD﹣A1B1C1D1中AB=AA1=2,AD=1,E为CC1的中点,则异面直线BC1与AE所成角的余弦值为()A.B.C.D.21.将正方形ABCD沿对角线BD折起,使平面ABD⊥平面CBD,E是CD的中点,则异面直线AE、BC所成角的正切值为()A.B.C. 2 D.22.如图,在正方体ABCD﹣A1B1C1D1中,点P是CD上的动点,则直线B1P与直线BC1所成的角等于()A. 30°B. 45°C. 60°D. 90°23.正方体ABCD﹣A1B1C1D1中,E、F分别是AA1与CC1的中点,则直线ED与D1F所成角的余弦值是() A.B.C.D.24.已知异面直线a与b所成的角为50°,P为空间一点,则过点P与a、b所成的角都是300的直线有且仅有() A. 1条B. 2条C. 3条D. 4条25.已知三棱柱ABC﹣A1B1C1,底面是正三角形,侧棱和底面垂直,直线B1C和平面ACC1A1成角为30°,则异面直线BC1和AB1所成的角为()A.B.C.D.26.如图,在正方形ABCD中,PB=BC,PB⊥平面ABCD,则PC与BD所成的角是()A. 90°B. 45°C. 60°D. 30°27.在正四棱锥P﹣ABCD中,PA=AB,E、N、F分别为棱AB、棱BC和棱PC的中点,则异面直线PE与FN所成角为()A.arccos B. 30°C.arccosD. 60°高中数学异面直线专题参考答案与试题解析一.选择题(共27小题)1.重复题目如图,正三棱锥A﹣BCD中,E在棱AB上,F在棱CD上.并且(0<λ<+∞),设α为异面直线EF与AC所成的角,β为异面直线EF与BD所成的角,则α+β的值是()A.B.C.D.与λ的值有关考点:异面直线及其所成的角。
异面直线的判断与所成的角

异面直线的判断与所成的角一.选择题(共10 小题)1.异面直线是指()A.空间中两条不相交的直线B.平面的一条直线与平面外的一条直线C.分别位于两个不同平面的两条直线D.不同在任何一个平面的两条直线2.已知:空间四边形ABCD如图所示,E、F分别是AB、AD的中点,G、H分别是BC, CD上的点,且•,则直线FH与直线EG()A.平行B.相交C.异面D.垂直3.在下列图形中,G、H、M、N 分别是正三棱柱的顶点或所在棱的中点,则表示直线GH、MN 是异面直线的图形有()A. 1 个B. 2 个C. 3 个D. 4 个4•在长方体ABCD- A i BiGD i的十二条棱中,与面对角线AC垂直且异面的棱的条数是()A. 2B. 4C. 6D. 85.正方体ABCD- A i B i C i D i中,与对角线A i B成45°勺棱有()条.A. 4B. 8C. i2D. 26.如图所示,在三棱锥P- ABC的六条棱所在的直线中,异面直线共有()A. 2 对B. 3 对C. 4 对D. 6对7.将正方体的纸盒展开如图,直线AB、CD在原正方体的位置关系是()A.平行B.垂直C.相交成60。
角D.异面且成60。
角8.如果两条异面直线称为“一对”,那么在正方体的十二条棱中共有异面直线()A. i2 对B. 24 对C. 36 对D. 48 对9.如图,点P、Q、R、S分别在正方体的四条棱上,并且是所在棱的中点,则直线PQ与RS是异面直线的一个图是()A. B. C. D.10.一个正方体纸盒展开后如图所示,在原正方体纸盒中有下列结论:①AB丄EF;②AB与CM成60°角;③EF与MN是异面直线;④MN //CD,其中正确的是()A.①②B•③④ C.②③ D.①③二.填空题(共5小题)11.如图所示,在棱长为2的正方体ABCD- A i B i C i D i中,0是底面ABCD的中心,E、F分别是CG, AD的中点,那么异面直线0E和FD所成角的余弦值等于___________ .12.在正四棱锥P-ABCD中,PA=2,直线PA与平面ABCD所成角为60°, E为PC的中点,则异面直线PA与BE所成角的大小为________ .13 .在棱长为1的正方体ABCD- A'B'C'D中,异面直线A'D与AB所成角的大小是 _________ .14.__________________________________________________________________如图是正方体的展开图,其中直线AB与CD在原正方体中所成角的大小是__________________ .15.空间四边形ABCD中,对角线AC=10, BD=6, M、N分别是AB、CD的中点,且MN=7,则异面直线AC与BD所成的角为_________ .异面直线的判断与所成的角参考答案与试题解析一.选择题(共10 小题)1.异面直线是指()A.空间中两条不相交的直线B.平面的一条直线与平面外的一条直线C.分别位于两个不同平面的两条直线D.不同在任何一个平面的两条直线【分析】依据异面直线的定义,逐一分析研究各个选项的正确性,可以通过举反例的方法进行排除.【解答】解:A不正确,因为空间中两条不相交的直线可能平行.B 不正确,因为平面的一条直线与平面外的一条直线可能平行,也可能相交.C不正确,因为分别位于两个不同平面的两条直线可能平行,也可能相交.D 正确,这就是异面直线的定义.故选D.【点评】本题考查异面直线的定义,用举反例的方法判断一个命题是假命题,是一种简单有效的方法.2.已知:空间四边形ABCD如图所示,E、F分别是AB、AD的中点,G、H分别是BC, CD上的点,且•,则直线FH与直线EG()A.平行B.相交C.异面D.垂直【分析】由已知EF为三角形ABD的中位线,从而EF// BD且EF=BD由•,得在四边形EFHG 中,EF/ HG,即卩E, F,G,H四点共面,且EF^HG,由此能得出结论.【解答】解::•••四边形ABCD是空间四边形,E、F分别是AB、AD的中点,••• EF为三角形ABD的中位线••• EF/ BD且EF=BD又T .,•••△ CHG^^CDB 且HG// BD, HG=BD•••在四边形EFHG中, EF// HG即E, F, G, H四点共面,且EF M HG,•四边形EFGH是梯形,•直线FH与直线EG相交,故选B.【点评】本题考查的知识点是平行线分线段成比例定理,是基础题,根据已知条件,判断出EF// HG且EF M HG,是解答本题的关键.3.在下列图形中,G、H、M、N 分别是正三棱柱的顶点或所在棱的中点,则表示直线GH、MN 是异面直线的图形有()A. 1 个B. 2 个C. 3 个D. 4 个【分析】利用G、H、M、N分别是正三棱柱的顶点或所在棱的中点,线面的关系可判断GH、MN 是异面直线的图形.【解答】解:由题意:G、H、M、N分别是正三棱柱的顶点或所在棱的中点,对于图1:G,M 是中点,上下面平行,故得GH、MN 平行;对于图2:过N点作GH的平行线,可得GH与MN相交.GH与MN不平行;且GH与MN 不在同一平面,故得直线GH、MN 是异面直线;对于3: GH与MN不在同一平面,GH与MN不平行,延长必相交.故得直线GH、MN不是异面直线;对于4:取GH的中点为E,可得GENM是平行四边形.故得GH MN平行;图2,图3中直线GH、MN是异面直线;故选:B.【点评】本题考查了两条直线在空间图形中的位置的判断.利用了正三棱柱的特征和中点的性质.属于基础题.4•在长方体ABCD- A i BiGD i的十二条棱中,与面对角线AC垂直且异面的棱的条数是()A. 2 B. 4 C. 6 D. 8【分析】作出图形,列举出与面对角线AC垂直且异面的棱.【解答】解:如图,在长方体ABCD- A i B i C i D i的十二条棱中,与面对角线AC垂直且异面的棱有:BB和DD,•••与面对角线AC垂直且异面的棱的条数是2.故选:A.【点评】本题考查满足条件的棱的条数的求法,考查长方体的结构特征等基础知识,考查数形结合思想,是基础题.5.正方体ABC— A i B i C i D i 中,与对角线A i B成45°勺棱有()条.A. 4B. 8C. 12D. 2【分析】根据线线角的定义在正方体中逐一寻找判断即可.【解答】解:如图所示:在正方形ABBA i 中,AA i、AB、BBi、A i B i 与A i B均成45°角,根据线线角的定义知,DD i、CG、DC、D i C i都与A i B成45°角, 所以满足条件的棱有8 条,故选:B.【点评】本题考查空间中异面直线所成角的定义及其求法,属基础题.6.如图所示,在三棱锥P- ABC的六条棱所在的直线中,异面直线共有()A. 2 对B. 3 对C. 4 对D. 6对【分析】画出三棱锥,找出它的棱所在直线的异面直线即可.【解答】解:如图所示,三棱锥P-ABC中,棱PA与BC是异面直线,棱PB与AC是异面直线,棱PC与AB是异面直线;共3 对.故选:B.【点评】本题考查了空间中的异面直线的判定问题,解题时应结合图形进行解答,是基础题.7.将正方体的纸盒展开如图,直线AB、CD在原正方体的位置关系是()A.平行B.垂直C.相交成60。
异面直线练习

练习一1.选择题(1)“a,b是异面直线”是指①a∩b=Φ且a不平行于b;②a⊂平面α,b⊂平面β且a∩b=Φ③a⊂平面α,b⊄平面α④不存在平面α,能使a⊂α且b⊂α成立上述结论中,正确的是()(A)①②(B)①③(C)①④(D)③④(2)长方体的一条对角线与长方体的棱所组成的异面直线有()(A)2对(B)3对(C)6对(D)12对(3)两条直线a,b分别和异面直线c,d都相交,则直线a,b的位置关系是()(A)一定是异面直线(B)一定是相交直线(C)可能是平行直线(D)可能是异面直线,也可能是相交直线(4)一条直线和两条异面直线中的一条平行,则它和另一条的位置关系是()(A)平行(B)相交(C)异面(D)相交或异面2.画图表示两条异面直线(至少要画两种不同的图形)3.命题“平面内一点和平面外一点的连线和平面内不过该点的直线是异面直线”(1)改写为符号叙述(2)试证明该命题.4.用以上结论证明空间四边形对边是异面直线.练习二1.判断下列命题的真假,真的打“√”,假的打“×”(1)平行于同一直线的两条直线平行 ( ) (2)垂直于同一直线的两条直线平行 ( ) (3)过直线外一点,有且只有一条直线与已知直线平行 ( ) (4)与已知直线平行且距离等于定长的直线只有两条 ( ) (5)若一个角的两边分别与另一个角的两边平行,那么这两个角相等( )(6)若两条相交直线和另两条相交直线分别平行,那么这两组直线所成的锐角(或直角)相等 ( ) 2.填空题(1)三条直线a ,b ,c 中,a //b ,b 与c 相交,那么a 与c 的位置关系是 . (2)空间四边形ABCD 各边中点分别为M 、N 、P 、Q ,则四边形MNPQ 是 四边形 3.如图AB //CD ,AB ∩α=E ,CD ∩α= F ,画出AD 与平面α的交点,写出画法,并说明理由.4.将一张长方形的纸片ABCD 对折一次,EF 为折痕,再打开竖直在桌面上,如图所示连结AD 、BC ,求证:⊿ADE ≌⊿BCF5.正方体ABCD —A 1B 1C 1D 1中,M 、N 分别是棱AA 1、CC 1的中点, (1)判断四边形DMB 1N 的形状 (2)求四边形DMB 1N 的面积练习三1.选择题(1)分别在两个平面内的两条直线间的位置关系是( )A 、B 、C 、D 、E 、F 、CBFEADB 1A 1 C 1D 1N MABCD(A )异面 (B )平行 (C )相交 (D )以上都有可能(2)异面直线a ,b 满足a ⊂α,b ⊂β,α∩β=l ,则l 与a ,b 的位置关系一定是( ) (A )l 与a ,b 都相交(B )l 至少与a ,b 中的一条相交 (C )l 至多与a ,b 中的一条相交(D )l 至少与a ,b 中的一条平行(3)两异面直线所成的角的范围是( )(A )(0°,90°)(B )[0°,90°) (C )(0°,90°] (D )[0°,90°] 2.判断下列命题的真假,真的打“√”,假的打“×”(1)两条直线和第三条直线成等角,则这两条直线平行 ( ) (2)和两条异面直线都垂直的直线是这两条异面直线的公垂线 ( ) (3)平行移动两条异面直线中的任一条,它们所成的角不变 ( ) (4)四边相等且四个角也相等的四边形是正方形 ( ) 3.如图所示,ABCD —A 1B 1C 1D 1是边长为a 的正方体,计算下列问题: (1)A 1D 1与B 1B 所成角的大小; (2)A 1D 1与AC 所成角的大小; (3)AD 1与B 1C 所成角的大小; (4)A 1C 与AB 所成角的正切值; (5)A 1D 1与B 1B 的距离; (6)A 1C 1与BD 的距离; (7)A 1D 1与AB 1的距离;(8)若E 、F 、G 、H 为对应棱的中点,求EF 、EH 所成的角.4.E 、F 分别是空间四边形ABCD 的边AB 、CD 的中点,且EF =5,BC =6,AD =8,求异面直线AD 与EF 所成角的正弦值.练习四1.判断题(对的打“√”,错的打“×”) (1)垂直于两条异面直线的直线有且只有一条( )(2)两线段AB 、CD 不在同一平面内,如果AC =BD ,AD =BC ,则AB ⊥CD ( ) (3)在正方体中,相邻两侧面的一对异面的对角线所成的角为60º( ) ABC DGEFHA 1B 1 D 1C 1BCFEAD(4)四边形的一边不可能既和它的邻边垂直,又和它的对边垂直 ( )2.右图是正方体平面展开图,在这个正方体中 ① BM 与ED 平行; ② CN 与BE 是异面直线; ③ CN 与BM 成60º角; ④ DM 与BN 垂直.以上四个命题中,正确命题的序号是 ( )(A )①②③(B )②④(C )③④(D )②③④3.在空间四边形ABCD 中,E 、F 、G 、H 分别为AB 、BC 、CD 、DA 的中点 (1)若AC ⊥BD 时,求证:EFGH 为矩形;(2)若BD =2,AC =6,求EG 2+HF 2;(3)若AC 、BD 成30º角,AC =6,BD =4,求四边形EF GH 的面积;(4)若AB =BC =CD =DA =AC =BD =2,求AC 与BD 间的距离.EA FB C MN DBACDEFGHABCD。
异面直线典型例题

典型例题一例1 假设b a //,A c b = ,则a ,c 的位置关系是〔 〕.A .异面直线B .相交直线C .平行直线D .相交直线或异面直线 分析:判断两条直线的位置关系,可以通过观察满足已知条件的模型或图形而得出正确结论.解:如下图,在正方体1111D C B A ABCD -中,设a B A =11,b AB =,则b a //. 假设设c B B =1,则a 与c 相交.假设设c BC =,则a 与c 异面.故选D .说明:利用具体模型或图形解决问题的方法既直观又易于理解.一般以正方体、四面体等为具体模型.例如,a ,b 相交,b ,c 相交,则a ,c 的位置关系是相交、平行或异面.类似地;a ,b 异面,b ,c 异面,则a ,c 的位置关系是平行、相交或异面.这些都可以用正方体模型来判断.典型例题二例2 已知直线a 和点A ,α∉A ,求证:过点A 有且只有一条直线和a 平行. 分析:“有且只有”的含义说明既有又惟一,因而这里要证明的有两个方面,即存在性和惟一性.存在性,即证明满足条件的对象是存在的,它常用构造法〔即找到满足条件的对象来证明〕;惟一性,即证明满足条件的对象只有..一个,换句话说,说是不存在第二个满足条件的对象.因此,这是否认性...命题,常用反证法. 证明:〔1〕存在性.∵ a A ∉,∴ a 和A 可确定一个平面α,由平面几何知识知,在α内存在着过点A 和a 平行的直线. 〔2〕惟一性假设在空间过点A 有两条直线b 和c 满足a b //和a c //.根据公理4,必有c b //与A c b = 矛盾,∴ 过点A 有一条且只有一条直线和a 平行.说明:对于证明“有且只有”这类问题,一定要注意证明它的存在性和惟一性.典型例题三例3 如下图,设E ,F ,G ,H 分别是空间四边形ABCD 的边AB ,BC ,CD ,DA 上的点,且λ==AD AH AB AE ,μ==CDCGCB CF ,求证: 〔1〕当μλ=时,四边形EFGH 是平行四边形; 〔2〕当μλ≠时,四边形EFGH 是梯形. 分析:只需利用空间等角定理证明FG EH //即可.证明:连结BD , 在ABD ∆中,λ==ADAHAB AE ,∴ BD EH //,且BD EH λ=.在CBD ∆中,μ==CDCGCB CF ,∴ BD FG //,且BD FG μ=. ∴ FG EH //,∴ 顶点E ,F ,G ,H 在由EH 和FG 确定的平面内. 〔1〕当μλ=时,FG EH =,故四边形EFGH 为平行四边形; 〔2〕当μλ≠时,FG EH ≠,故四边形EFGH 是梯形. 说明:显然,课本第11页的例题就是此题〔2〕的特殊情况. 特别地,当21==μλ时,E ,F ,G ,H 是空间四边形各边中点,以它们为顶点的四边形是平行四边形.如果再加上条件BD AC =,这时,平行四边形EFGH 是菱形.典型例题四例4 已知b a 、是两条异面直线,直线a 上的两点B A 、的距离为6,直线b 上的两点D C 、的距离为8,BD AC 、的中点分别为N M 、且5=MN ,求异面直线b a 、所成的角.分析:解题的关键在于依据异面直线所成角的定义构造成和异面直线b a 、平行的两条相交直线,然后把它们归纳到某一三角形中求解.解:如图,连结BC ,并取BC 的中点O ,连结ON OM 、,∵ON OM 、分别是ABC ∆和BCD ∆的中位线, ∴AB OM //,CD ON //,即 a OM //,b ON //.∴ON OM 、所成的锐角或直角是异面直线b a 、所成的角. 又∵ 6=AB ,8=CD , ∴3=OM ,4=ON .在OMN ∆中,又∵5=MN ,∴222MN ON M =+,∴90=∠MON .故异面直线b a 、所成的角是90.说明:在求两条异面直线所成的角时,一般要依据已知条件,找出与两条异面直线分别平行并且相交于一点的两条直线.但是,异面直线所成角的定义中的点O 一般是在图形中存在着的,需要认真观察分析图形的性质,从而找出这一点和过这一点与两异面直线平行的直线,以得到两条异面直线所成的角,在求这个角的大小时,一般是根据平面图形中解三角形的知识求解的.典型例题五例5 已知四面体ABC S -的所有棱长均为a .求: 〔1〕异面直线AB SC 、的公垂线段EF 及EF 的长; 〔2〕异面直线EF 和SA 所成的角.分析:依异面直线的公垂线的概念求作异面直线AB SC 、的公垂线段,进而求出其距离;对于异面直线所成的角可采取平移构造法求解.解:〔1〕如图,分别取AB SC 、的中点F E 、,连结CF SF 、.由已知,得SAB ∆≌CAB ∆. ∴CF SF =,E 是SC 的中点, ∴SC EF ⊥.同理可证AB EF ⊥∴EF 是AB SC 、的公垂线段.在SEF Rt ∆中,a SF 23=,a SE 21=.∴22SE SF EF -=a a a 22414322=-. 〔2〕取AC 的中点G ,连结EG ,则SA EG //.∴EF 和GE 所成的锐角或直角就是异面直线EF 和SA 所成的角. 连结FG ,在EFG ∆中,a EG 21=,a GF 21=,a EF 22=. 由余弦定理,得22222124142412cos 222222=⋅⋅-+=⋅⋅-+=∠a a aa a EF EG GF EF EG GEF . ∴45=∠GEF .故异面直线EF 和SA 所成的角为45.说明:对于立体几何问题要注意转化为平面问题来解决,同时要将转化过程简要地写出来,然后再求值.典型例题六例6 如下图,两个三角形ABC ∆和'''C B A ∆的对应顶点的连线'AA 、'BB 、'CC 交于同一点O ,且32'''===O C CO O B BO O A AO . (1)证明:''//B A AB ,''//C A AC ,''//C B BC ; (2)求'''C B A ABCS S ∆∆的值.分析:证两线平等当然可用平面几何的方法.而求面积之比则需证两个三角形相似,由于三角形是平面图形,故也可用平面几何的方法证明.证明:(1)当ABC ∆和'''C B A ∆在O 点两侧时,如图甲 ∵'AA 与'BB 相交于O 点,且OB BOO A AO ''=, ∴''//B A AB 〔因为'AA 、'BB 共面〕. 同理''//C A AC ,''//C B BC .(2)∵''//B A AB ,且''//C A AC ,AB 和''B A ,AC 和''C A 的方向相反,∴'''C A B BAC ∠=∠,同理'''C B A ABC ∠=∠.因此,ABC ∆∽'''C B A ∆.又32'''==O A AO B A AB ,∴94322'''=⎪⎭⎫⎝⎛=∆∆C B A ABC S S . 当ABC ∆和'''C B A ∆在O 点的同侧时,如图乙所示,同理可得(1)(2).说明:此题ABC ∆与'''C B A ∆是否共面并不重要,因为等角定理对各种位置已作说明.典型例题七例7 S 是矩形ABCD 所在平面外一点,BC SA ⊥,CD SB ⊥,SA 与CD 成︒60角,SD 与BC 成︒30角,a SA =,求:(1)直线SA 与CD 的距离; (2)求直线SB 与AD 的距离.分析:要求出SA 与CD 、SB 与AD 的距离,必须找到它们的公垂线段,公垂线段的长度即为异面直线间的距离.解:如下图,在矩形ABCD 中,AD BC //. ∵BC SA ⊥,∴AD SA ⊥.又AD CD ⊥,∴AD 是异面直线SA 、CD 的公垂线段, 其长度为异面直线SA 、CD 的距离.在SAD Rt ∆中,∵SDA ∠是SD 与BC 所成的角, ∴︒=∠30SDA .又a SA =,∴a AD 3=.(2)在矩形ABCD 中,CD AB //,AD SB ⊥, ∴AB SB ⊥,又AD AB ⊥,∴AB 是直线SB 、AD 的公垂线段,其长度为异面直线SB 、AD 的距离. 在SAB Rt ∆中,SAB ∠是异面直线SA 与CD 所成的角,∴︒=∠60SAB . 又a SA =,∴260cos a a AB =︒=, ∴直线SB 与AD 的距离为2a . 说明:(1)求异面直线之间距离的步骤是:①找〔作〕线段;②证线段是公垂线段;③求公垂线段的长度.(2)求异面直线间的距离的问题,高考中一般会给出公垂线段.典型例题八例8 a 、b 、c 是三条直线,假设a 与b 异面,b 与c 异面,判断a 与c 的位置关系,并画图说明.分析:这是一道考查异面直线概念及空间直线位置关系的问题,同时也考查了图形语言的表达能力.解:直线a 与c 的位置关系有以下三种情形如图:∴直线a 与c 的位置关系可能平行〔图中的(1)〕;可能相交〔如图中的(2)〕; 可能异面〔图中的(3)〕.说明:此题也考查了空间想象能力和逻辑划分、分类讨论的能力.典型例题九例9 如果两条异面直线称作“一对”,那么在正方体的十二条棱中,共有几对异面直线〔 〕.A .12对B .24对C .36对D .48对分析:一般地,立体几何中的计数问题,是由所数的量的性质,确定一规律,然后按此规律进行计数.正方体的各棱具有相同的位置关系.所以以一条棱为基量,考察与其异面的几对,问题可解.解:如图,正方体中与AB 异面有C C 1,D D 1,11C B ,11D A ,∵各棱具有相同的位置关系,且正方体有12条棱,排除两棱的重复计算成本, ∴异面直线共有242412=⨯对. 说明:分析清楚几何体特点是防止重复计数的关键.计数问题必须防止盲目乱数,做到“不重不漏”.典型例题十例10 如图,已知不共面的直线a ,b ,c 相交于O 点,M 、P 是直线a 上两点,N 、Q 分别是b ,c 上一点.求证:MN 和PQ 是异面直线.证法1:假设MN 和PQ 不是异面直线, 则MN 与PQ 在同一平面内,设为α∵a P M ∈、,α∈P M 、 ∴α⊂a .又a O ∈,∴α∈O .∵α∈N 且b O ∈,b N ∈, ∴α⊂b . 同理:α⊂C∴a ,b ,c 共面于α,与已知a ,b ,c 不共面相矛盾, ∴MN 、PQ 是异面直线.证法2:∵O c a = ,∴直线a ,c 确定一平面设为β. ∵a P ∈,c Q ∈,∴β∈P ,β∈Q , ∴β⊂PQ 且β∈M ,PQ M ∉. 又a ,b ,c 不共面,b N ∈,∴β∉N , ∴MN 与PQ 为异面直线.说明:证明两条直线异面的方法有两种. (1)用定义证明〔即定义法〕:此时需借反证法,假设两条直线不异面,根据空间两条直线的位置关系,这两条直线一定共面,即这两条直线可能相交也可能平行,然后,推导出矛盾即可.(2)用定理证明〔即定理法〕:用该法证明时,必须阐述出定理满足的条件:α⊂a ,α∉A ,a B ∉,然后可以推导出直线a 与AB 是异面直线.典型例题十一例11 已知平面α与平面β相交于直线l ,A ,B 为直线l 上的两点.在α内作直线AC ,在β内作直线BD .求证AC 和BD 是异面直线.已知:平面α 平面β=l ,l A ∈,l B ∈,α⊂AC ,β⊂BD ,如图.求证:AC 、BD 是异面直线.证明:假设AC ,BD 不是异面直线,则它们必共面. ∴A 、B 、C 、D 在同一平面内.即A 、B 、C 所确定的平面α与A 、B 、D 确定的平面β重合 这与平面α 平面β=l 矛盾∴AC 、BD 是异面直线.说明:证明两条直线为异面直线,用反证法往往比较简单.典型例题十二例12 已知空间四边形ABCD ,求证它的对角线AC 和BD 是异面直线. 证法一:〔反证法〕如图假设AC 和BD 不是异面直线,则AC 和BD 在同一平面内.∴A 、B 、C 、D 在同一平面内,即四边形ABCD 是平面四边形, 这与已知条件矛盾,所以假设不成立. 因此AC 和BD 是异面直线. 证法二:〔定理法〕过BC 和CD 作一平面α,则对角线BD 在平面α内.对角线AC 与平面α交于BD 外的一点C ,即点C 不在直线BD 上, 且A 点在平面α外.∴根据异面直线判定定理知:AC 和BD 是异面直线.说明:判定两条直线是异面直线的证明问题常用这两种方法,即(1)反证法,(2)用判定定理.典型例题十三例13 已知空间四边形ABCD ,AC AB ≠,AE 是ABC ∆的BC 边上的高,DF 是BCD ∆的BC 边上的中线,求证:AE 和DF 是异面直线.证法一:〔定理法〕如图由题设条件可知点E 、F 不重合,设BCD ∆所在平面α.∴⇒⎪⎪⎩⎪⎪⎨⎧∉∈∉⊂DFE E A DF αααAE 和DF 是异面直线. 证法二:〔反证法〕假设AE 和DF 不是异面直线,则AE 和DF 共面,设过AE 、DF 的平面为β. (1)假设E 、F 重合,则E 是BC 的中点,这与题设AC AB ≠相矛盾. (2)假设E 、F 不重合,∵EF B ∈,EF C ∈,β⊂EF ,∴β⊂BC . ∵β∈A ,β∈D ,∴A 、B 、C 、D 四点共面,这与题设ABCD 是空间四边形相矛盾. 综上,假设不成立.故AE 和DF 是异面直线.说明:反证法不仅应用于有关数学问题的证明,在其他方面也有广泛的应用. 首先看一个有趣的实际问题:“三十六口缸,九条船来装,只准装单,不准装双,你说怎么装?” 对于这个问题,同学们可试验做一做. 也许你在试验几次后却无法成功时,觉得这种装法的可能性是不存在的.那么你怎样才能清楚地从理论上解释这种装法是不可能呢?用反证法可以轻易地解决这个问题.假设这种装法是可行的,每条船装缸数为单数,则9个单数之和仍为单数,与36这个双数矛盾.只须两句话就解决了这个问题.典型例题十四例14 已知E 、1E 分别是正方体1111D C B A ABCD -的棱AD 、11D A 的中点. 求证:111C E B BEC ∠=∠.分析:欲证两个角相等,可通过等角定理或其推论来实现. 证明:如图,连结1EE∵1E ,E 分别为11D A ,AD 中点, ∴11E A AE ,∴EA E A 11为平行四边形. ∴A A 1E E 1. 又∵A A 1B B 1,∴EE 1B B 1,∴四边形11EBB E 是平行四边形.∴EB B E //11.同理EC C E //11.又111B E C ∠与CEB ∠方向相同. ∴CEB B E C ∠=∠111.说明:有关证明角相等问题,一般采用下面三种途径:(1)利用等角定理及其推论;(2)利用证三角形相似;(3)利用证三角形全等.本例是通过第一种途径来实现.请同学们再利用第三种途径给予证明.典型例题十五例15 由四个全等的等边三角形的封面几何体称为正四面体,如图,正四面体ABCD 中,E 、F 分别是棱BC 、AD 的中点,CF 与DE 是一对异面直线,在图形中适当的选取一点作出异面直线CF 、DE 的平行线,找出异面直线CF 与DE 成的角.分析1:选取平面ACD ,该平面有以下两个特点,(1)该平面包含直线CF ,(2)该平面与DE 相交于点D ,伸展平面ACD ,在该平面中,过点D 作CF DM //交AC 的延长线于M ,连结EM .可以看出:DE 与DM 所成的角,即为异面直线DE 与CF 所成的角.如图.分析2:选取平面BCF ,该平面有以下两个特点:(1)该平面包含直线CF ,(2)该平面与DE 相交于点E .在平面BCF 中,过点E 作CF 的平行线交BF 于点N ,连结ND ,可以看出:EN 与ED 所成的角,即为异面直线FC 与ED 所成的角.如图.分析3:选取平面ADE ,该平面有如下两个特点:(1)该平面包含直线DE ,(2)该平面与CF 相交于点F .在平面ADE 中,过点F 作DE FG //,与AE 相交于点G ,连结CG ,可以看出:FG 与FC 所成的角,即为异面直线CF 与DE 所成的角.分析4:选取平面BCD ,该平面有如下特点:(1)该平面包含直线DE ,(2)该平面与CF 相交于点C ,伸展平面BCD ,在该平面内过点C 作DE CK //与BD 的延长线交于点K ,且BD DK =,连结FK ,则CF 与CK 所成的角,即为异面直线CF 与DE 所成的角.如图.说明:(1)两条异面直线所成的角是非常重要的知识点,是每年高考的必考内容,要求牢固掌握两条异面直线所成的角的定义和两条异面直线互相垂直的概念,两条异面直线所成的角是刻划两条异面直线相对位置的一个量,是通过转化为相交直线成角来解决的,这里我们要注意:两条异面直线所成的角θ的范围是︒≤<︒900θ,当︒=90θ时,这两条异面直线互相垂直.求两条异面直线所成角的关键是作出这两条异面直线所成的角,作两条异面直线所成的角的方法是:将其中一条平移到某个位置使其与另一条相交或是将两条异面直线同时平移到某个位置使它们相交,然后在同一平面内求相交直线所成的角.值得注意的是:平移后相交所得的角必须容易算出,因此平移时要求选择恰当位置.一般提倡像思考2,那样作角,因为此角在几何体内部,易求.(2)本例题多方位、多角度思考问题,思路开阔、运用知识灵活,对我们解决异面直线所成角问题大有裨益,要认真理解.典型例题十六例16 如图,等腰直角三角形ABC 中,︒=∠90A ,2=BC ,AC DA ⊥,AB DA ⊥,假设1=DA ,且E 为DA 的中点.求异面直线BE 与CD 所成角的余弦值.分析:根据异面直线所成角的定义,我们可以选择适当的点,分别引BE 与DC 的平行线,换句话说,平移BE 〔或CD 〕.设想平移CD ,沿着DA 的方向,使D 移向E ,则C 移向AC 的中点F ,这样BE 与CD 所成的角即为BEF ∠或其补角,解EFB ∆即可获解.解:取AC 的中点F ,连结EF ,在ACD ∆中,E 、F 分别是AD 、AC 的中点, ∴CD EF //,∴BEF ∠即为所求的异面直线BE 与CD 所成的角或其补角.在EAB Rt ∆中,1=AB ,2121==AD AE ,∴25=BE . 在AEF Rt ∆中,1=AC ,21=AE ,∴22=EF . 在ABF Rt ∆中,1=AB ,21=AE ,∴25=BF . 在等腰三角形EBF 中,1010254221cos ===∠BE EF FEB , ∴异面直线BE 与CD 所成角的余弦值为1010. 说明:求角或求角的三角函数值的一般步骤是:①找〔或作出〕角,适合题意,②求角或求角的三角函数值,往往是化归成一个三角形的内角,通过解三角形求得.典型例题十七例17 在正四面体ABCD 中,已知E 是棱BC 的中点,求异面直线AE 和BD 所成角的余弦值.分析:可在平面BCD 内过E 作BD 平行线,可在AEF ∆中求得所成角的余弦值.解:如图,取CD 的中点F ,连结EF ,AF ,∵E 为BC 的中点,∴EF 为CBD ∆的中位线,∴BD EF //,∴AE 与EF 所成的锐角或直角就是异面直线AE 和BD 所成的角.设正四面体的棱长为a ,由正三角形的性质知, a AF AE 23==,a EF 21=.在AEF ∆中, 6321cos ==∠AE EF AEF ,即异面直线AE 和BD 所成角的余弦值为63. 说明:此题是利用三角形中位线到达平移的目的.这种作异面直线所成角的方法称为中位线平移法.典型例题十八例18 在正方体1111D C B A ABCD -中,求正方体对角线1BD 和面对角线AC 所成角的大小.解:如图.取D D 1上中点N ,则有:DN N D =1,连结BD .令O AC BD = ,则DO BO =,连结NO ,NA ,NC∵N ,O 分别为D D 1,BD 的中点,∴NO 121BD , ∴NOA ∠(或NOC ∠)是异面直线1BD 和AC 所成的角.在NAD Rt ∆及NCD Rt ∆中,∵CD AD =,ND ND =,∴NAD Rt ∆≌NCD Rt ∆,∴NC NA =,∴ANC ∆为等腰三角形.又O 为AC 中点,∴AC NO ⊥,∴异面直线1BD 和AC 所成角为︒90.说明:(1)由于异面直线所成角最大为直角,所以,在把异面直线平移得到的两个夹角中,必须选取其中较小的角为异面直线的所成角.(2)实际上,正方体的体对角线与任意一条面对角线所成角均为直角.典型例题十九例19 在正方体1111D C B A ABCD -中,E 、F 分别为1BB 、1CC 的中点,求AE 、BF 所成角的余弦值.分析1:可平移BF 至1EC ,可得到角1AEC ,再解三角形即可.但要注意到1AEC ∠为钝角.解法1:如图,连结1EC ,则BF EC //1,由AE 与1EC 所成的锐角或直角,就是AE 与BF 所成的角,连1AC ,令正方体的棱长为a ,有a EC AE 251==,a AC 31=在1AEC ∆中,515612122cos 22122121-=-=-=-=∠AE AC AE AC AE AEC , ∴1AEC ∠的补角为异面直线AE 与BF 所成角. ∴AE 、BF 所成角的余弦值是51. 分析2:连结DB 、FD ,可得DFB ∠即为异面直线AE 和BF 所成的角.进而求其余弦值.解法2:连结DB 、FD ,可证得AE FD //.(∵EF AD )DFB ∠(或其补角)即为异面直线AE 、BF 所成的角.a BF DF 25==,a BD 2=. 由余弦定理,有 ()5125245452525222525cos 222=-+=⋅⋅-⎪⎪⎭⎫ ⎝⎛+⎪⎪⎭⎫ ⎝⎛=∠a a aa a DFB , ∴AE 、BF 所成角的余弦值是51. 说明:异面直线所成角的范围是]90,0(︒︒,当求得某角的余弦值为负值时,则此角的补角是异面直线所成角.典型例题二十例20 在空间四边形ABCD 中:CD AB =,BD AC =,E ,F 分别是AD ,BC 的中点.求证:线段EF 是异面直线AD ,BC 的公垂线.证明:如图.连结AF 、DF 、BE 、CE .在ABD ∆和ACD ∆中,CD AB =,BD AC =,AD 公用∴ABD ∆≌ACD ∆.又E 是AD 中点,∴CE BE =.在BEC ∆中,F 是BC 的中点,∴BC EF ⊥.同理AD EF ⊥,∴EF 是异面直线AD 、BC 的公垂线.说明:证明某一条直线是两条异面直线的公垂线,须证明以下两点:(1)与两条异面直线都垂直;(2)与两条异面直线都相交.典型例题二十一例21 如图,空间四边形ABCD 中,四边AB 、BC 、CD 、DA 和对角线AC 、BD 都等于a ,E 、F 分别为AB 、CD 的中点.(1)求证:EF 是异面直线AB 、CD 的公垂线.(2)求异面直线AB 和CD 的距离.分析:要证明EF 是异面直线AB 与CD 的公垂线,必须说明两个方面的问题,一个方面EF 与AB 、CD 都相交,另一个方面AB 、CD 与EF 都垂直.(1)证明:连结AF 、BF ,由已知BCD ∆和ACD ∆均为正三角形,E 、F 分别为AB 、CD 的中点,∴BF AF =,AB EF ⊥.同理CD EF ⊥,又EF 与AB 、CD 都相交,∴EF 为异面直线AB 、CD 的公垂线.(2)解:∵空间四边形各边及对角线AC 、BD 的长均为a , ∴a BF AF 23==,而a AE 21=, ∴在AEF Rt ∆中,a AE AF EF 2222=-=. ∴异面直线AB 和CD 之间的距离为a 22. 说明:(1)求线段的长度一般地要把该线段放到一个三角形中去求解,尤其是放到特殊三角形中去求解,如直角三角形、等腰三角形等.(2)满足条件的该空间四边形其实质是空间正四面体,该问题实质上是求正四面体对棱之间的距离.典型例题二十二例22 已知a 、b 是异面直线,直线c //直线a ,那么c 与b 〔 〕.A .一定是异面直线B .一定是相交直线C .不可能是平行直线D .不可能是相交直线解:由已知a 、b 是异面直线,直线c //直线a ,所以直线c 直线b ,否则假设b c //,则有b a //与已知矛盾.所以c b .∴应选C .说明:此题考察两直线位置关系和公理4的应用及异面直线定义.典型例题二十三例23 两条异面直线指的是〔 〕.A .在空间内不相交的两条直线B .分别位于两个不同平面内的两条直线C .某平面内的一条直线和这个平面外的一条直线D .不在同一平面内的两条直线解:对于A,在空间内不相交的两条直线也可能是平行,应排除A .对于B ,分别位于两个不同平面内的两条直线可能是异面直线,也可能是相交直线或平行直线,应排除B .对于C ,某平面内的一条直线和这个平面外的一条直线可能是异面直线,也可能是平行直线,应排除C .∴应选D .说明:此题主要考查对异面直线定义的掌握,特别是对“不同在任何一个平面内的两条直线”含义的理解.典型例题二十四例24 如图,在棱长为1的正方体1111D C B A ABCD -中,M 、N 分别为11B A 和1BB 的中点,那么直线AM 与CN 所成的角的余弦值是〔 〕.A .23B .1010C .53D .52 解:在平面11A ABB 中,过N 点作AM NP //,交AB 于P ,连结PC ,如图,PNC ∠(或其补角)就是AM 与CN 所成的角.设AB 的中点为Q ,则P 是BQ 中点.可求得45=NP ,417=CP ,25=NC . 在PNC ∆中,由余弦定理得522cos 222=⋅-+=∠PN NC PC PN NC PNC . ∴应选D .说明:作出平行线PN ,进而在PNC ∆中利用余弦定理求出直线AM 与CN 所成角的余弦值.典型例题二十五例25 如图,1111D C B A ABCD -是正方体,4111111B A F D E B ==,则1BE 与1DF 所成的角的余弦值是〔 〕.A .1715B .21C .178D .23解:过A 点在平面11A ABB 内作1//DF AF ,再过1E 在平面11A ABB 内作FA E E //1, 则E BE 1∠(或其补角)即是1BE 与1DF 所成的角.由已知4111111B A F D E B ==, 1111D C B A ABCD -是正方体,所以可求得a BE 4171=(a 为正方体的棱长), 又E E AF DF 11==,而11BE DF =,∴a E E 4171=,显然a EB 21=. 在E BE 1∆中,由余弦定理,得171541722141722cos 2211221211=⎪⎪⎭⎫ ⎝⎛⎪⎭⎫ ⎝⎛-⎪⎪⎭⎫ ⎝⎛=⋅-+=∠a a a E E BE EB E E BE E BE . ∴应选A .说明:(1)解答此题的关键是作平行线AF 、E E 1.进而在E BE 1∆中解出E BE 1∠的余弦值;(2)考查历届高考试题,求异面直线所成角的题常以正方体和正四面体为载体,在正方体和正四面体中命题. 典型例题二十六例26 在棱长都相等的四面体BCD A -中,E 、F 分别是棱AD 、BC 的中点,连结AF 、CE ,如下图,求异面直线AF 、CE 所成角的余弦值.解:连结DF ,取DF 的中点G ,连结EG ,CG ,又E 是AD 的中点,故AF EG //,所以GEC ∠是异面直线AF 、CE 所成角. ∵AF 是正三角形ABC 的高, ∴AB AF 23=,∴AB EG 43=. 在FCG Rt ∆中,AB AB FD FG 43232121=⋅==,AB CF 21=,则 AB AB AB FC FG CG 4721432222=⎪⎭⎫ ⎝⎛+⎪⎪⎭⎫ ⎝⎛=+=. 在EGC ∆中,AB CE 23=,AB EG 43=,AB CG 47=, 用余弦定理可得32cos =∠GEC . ∴异面直线AF 、CE 所成角的余弦值是32. 说明:求两条异面直线所成角或求所成角的函数值,关键是作出异面直线所成的角.作两条异面直线所成角的方法一般是:将其中一条平移到某个位置使其也另一条相交也或者将两条异面直线同时平移到某个位置使它们相交,使得这个角在某一个平面的三角形内,进而求出.但要注意:平移后相交所得的角必须容易算出,因此平移时应选择恰当的位置.。
异面直线的判定-高中数学知识点讲解(含答案)

异面直线的判定(北京习题集)(教师版)一.选择题(共8小题)1.(2017秋•东城区期末)在正方体1111ABCD A B C D -中,与棱AD 所在直线异面的棱的条数是( ) A .2B .4C .6D .82.(2017秋•海淀区校级月考)在四面体ABCD 中,截面PQMN 是正方形,则下列结论错误的是( )A .AC BD =B .PM 与BD 异面C .//AC 截面PQMND .AC BD ⊥3.(2015秋•石景山区期末)将正方体的纸盒展开如图,直线AB 、CD 在原正方体的位置关系是( )A .平行B .垂直C .相交成60︒角D .异面且成60︒角4.(2016秋•西城区校级期中)四棱锥P ABCD -的底面为菱形,侧棱PC 与底面垂直,则侧棱PA 与菱形对角线BD 的关系是( ) A .平行B .相交不垂直C .异面垂直D .相交垂直5.(2014•海淀区校级模拟)如图,点P 、Q 、R 、S 分别在正方体的四条棱上,并且是所在棱的中点,则直线PQ与RS 是异面直线的一个图是( )A .B .C .D .6.(2009秋•朝阳区期末)如图,在正方体1111A B C D ABCD -各棱所在的直线中,与直线AB 异面的有( )A .2B .4C .6D .87.(2008•崇文区一模)如图,在正方体1111ABCD A B C D -中,O 是底面正方形ABCD 的中心,M 是1D D 的中点,N 是11A B 上的动点,则直线NO 、AM 的位置关系是( )A .平行B .相交C .异面垂直D .异面不垂直8.(2005秋•西城区校级期末)下列命题中正确的是( ) A .空间三点可以确定一个平面 B .垂直于同一条直线的两条直线平行 C .四边相等的四边形是菱形D .既不相交也不平行的两条直线是异面直线异面直线的判定(北京习题集)(教师版)参考答案与试题解析一.选择题(共8小题)1.(2017秋•东城区期末)在正方体1111ABCD A B C D -中,与棱AD 所在直线异面的棱的条数是( ) A .2B .4C .6D .8【分析】根据异面直线的定义,在12棱中,分别找到与AD 既不相交也不平行的棱即可. 【解答】解:由图象知与AD 异面的直线有 11A B ,1BB ,1CC ,11C D 有4条,故选:B .【点评】本题考查空间中直线的位置关系:异面直线,以及识图、读图能力,属简单题.2.(2017秋•海淀区校级月考)在四面体ABCD 中,截面PQMN 是正方形,则下列结论错误的是( )A .AC BD =B .PM 与BD 异面C .//AC 截面PQMND .AC BD ⊥【分析】利用线面平行与垂直的判定定理和性质定理、正方形的性质、异面直线所成的角即可判定. 【解答】解:在四面体ABCD 中,截面PQMN 是正方形, //PQ MN ∴,PQ ⊂/平面ACD ,MN ⊂平面ACD , //PQ ∴平面ACD .平面ACB ⋂平面ACD AC =,//PQ AC ∴,可得//AC 平面PQMN .故C 选项结论正确.同理可得//BD 平面PQMN ,//BD PN .PN PQ ⊥,AC BD ∴⊥.故选项D 结论正确. 由//BD PN ,MPN ∴∠是异面直线PM 与BD 所成的角,PM ∴与BD 异面.故选项B 结论正确.由上面可知://BD PN ,//PQ AC .PN AN BD AD =,MN DNAC AD=. 而AN DN ≠,PN MN =,BD AC ∴≠.故选项A 结论错误. 故选:A .【点评】本题考查了线面平行与垂直的判定定理和性质定理、正方形的性质、异面直线所成的角,属于中档题. 3.(2015秋•石景山区期末)将正方体的纸盒展开如图,直线AB 、CD 在原正方体的位置关系是( )A .平行B .垂直C .相交成60︒角D .异面且成60︒角【分析】以AB 所在平面为底面,将右侧正方形折起为右边的平面,因为//DE AB ,所以CDE ∠即为直线AB ,CD 所成的角,在CDE ∆中求解即可.【解答】解:如图,直线AB ,CD 异面.因为//DE AB , 所以CDE ∠即为直线AB ,CD 所成的角, 因为CDE ∆为等边三角形,故60CDE ∠=︒ 故选:D .【点评】本题以图形的折叠为载体,考查平面图形向空间图形的转化,考查折叠问题、异面直线的判断及异面直线所成的角,考查空间想象能力和运算能力.4.(2016秋•西城区校级期中)四棱锥P ABCD -的底面为菱形,侧棱PC 与底面垂直,则侧棱PA 与菱形对角线BD 的关系是( ) A .平行B .相交不垂直C .异面垂直D .相交垂直【分析】利用线面垂直的判定与性质定理、菱形的性质即可判断出关系.【解答】解:PC⊥底面ABCD,BD⊂平面ABCD,∴⊥,PC BD又底面ABCD为菱形,=.∴⊥,又PC AC CBD AC∴⊥平面PAC,BD∴⊥,BD PA又PA,BD异面,所以侧棱PA与BD的关系是异面垂直,故选:C.【点评】本题考查了线面垂直的判定与性质定理、菱形的性质,考查了推理能力与计算能力,属于中档题.5.(2014•海淀区校级模拟)如图,点P、Q、R、S分别在正方体的四条棱上,并且是所在棱的中点,则直线PQ与RS是异面直线的一个图是()A.B.C.D.【分析】利用一面直线的定义和正方体的性质,逐一分析各个选项中的2条直线的位置关系,把满足条件的选项找出来.【解答】解:A中的PQ与RS是两条平行且相等的线段,故选项A不满足条件.B中的PQ与RS是两条平行且相等的线段,故选项B也不满足条件.D 中,由于PR 平行且等于12SQ ,故四边形SRPQ 为梯形,故PQ 与RS 是两条相交直线,它们和棱交与同一个点,故选项D 不满足条件. C 中的PQ 与RS 是两条既不平行,又不相交的直线,故选项C 满足条件.故选:C .【点评】本题主要考查异面直线的定义,正方体的性质,判断2条直线的位置关系,属于基础题.6.(2009秋•朝阳区期末)如图,在正方体1111A B C D ABCD -各棱所在的直线中,与直线AB 异面的有( )A .2B .4C .6D .8【分析】根据判断异面直线的方法:过平面外一点和平面内一点与平面内不经过该点的直线是异面直线,判断出正方体中与直线AB 异面的直线.【解答】解:与直线AB 异面的有:1D D ,1C C ,11A D ,11B C 故选:B .【点评】判断两条直线异面,一般利用判定定理:过平面外一点和平面内一点与平面内不经过该点的直线是异面直线;证明两条直线是异面直线常用反证法.7.(2008•崇文区一模)如图,在正方体1111ABCD A B C D -中,O 是底面正方形ABCD 的中心,M 是1D D 的中点,N 是11A B 上的动点,则直线NO 、AM 的位置关系是( )A .平行B .相交C .异面垂直D .异面不垂直【分析】N 是11A B 上的动点,O 是底面正方形ABCD 的中心,确定平面11A B O ,判定MA 与平面11A B O 的关系,即可判定直线NO 、AM 的位置关系.【解答】解:在正方体1111ABCD A B C D -中,O 是底面正方形ABCD 的中心,M 是1D D 的中点,N 是11A B 上的动点,连接1A O ,1B O ,不难证明AM ⊥平面11A B O ,所以直线NO AM ⊥,因为它们不相交.故选:C.【点评】本题考查异面直线的判定,考查空间想象能力,逻辑思维能力,是基础题.8.(2005秋•西城区校级期末)下列命题中正确的是()A.空间三点可以确定一个平面B.垂直于同一条直线的两条直线平行C.四边相等的四边形是菱形D.既不相交也不平行的两条直线是异面直线【分析】根据空间不共线的三点可以确定一个平面,得到A错;根据在空间中,垂直于同一条直线的两条直线平行、相交、异面都有可能,得到B错;根据在平面内,四边相等的四边形是菱形但在空间中,四边相等的四边形有可能是空间四边形,得到C错;根据既不相交也不平行的两条直线是异面直线,是异面直线的定义,得到D对.【解答】解:对于A,空间不共线的三点可以确定一个平面,所以A错;对于B,在空间中,垂直于同一条直线的两条直线平行、相交、异面都有可能,所以B错;对于C,在平面内,四边相等的四边形是菱形但在空间中,四边相等的四边形有可能是空间四边形,故C错;对于既不相交也不平行的两条直线是异面直线,是异面直线的定义,故D对.故选:D.【点评】题主要考查了平面的基本性质及推论、确定平面的条件及空间想象的能力,属于基础题.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
异面直线的判定
1.已知空间四边形ABCD,E、H分别是AB、AD的中点,F、G分别是边BC、DC的三等分点(如图),求证:(1)对角线AC、BD是异面直线;
(2)直线EF和HG必交于一点,且交点在AC上.
¥
是△BCD平面外的一点,E、F分别是BC、AD的中点,
(1)求证:直线EF与BD是异面直线;
3.已知:平面α∩平面β=a,b⊂α,b∩a=A,c⊂β且c∥a,求证:b、c是异面直线.
,
4.已知不共面的三条直线a、b、c相交于点P,A∈a,B∈a,C∈b,D∈c,求证:AD与
BC是异面直线.
{
5.平行六面体ABCD-A1B1C1D1中,求证:CD1所在的直线与BC1所在的直线是异面直线.
%
小结:常用方法是反证法
(1)利用反证法证明对角线AC、BD是共面直线,推出矛盾,从而证明是异面直
(2)说明直线EF和HG必交于一点,然后证明这点在平面ADC内.又在平面ABC内,必在它们的交线AC上.
:(1)假设对角线AC、BD在同一平面α内,
则A、B、C、D都在平面α内,这与ABCD是空间四边形矛盾,∴AC、BD是异面直线.
(2)∵E、H分别是AB、AD的中点所以EH平行且等于1/2BD, 又F、G分别是BC、DC的三等分点,
EG平行等于2/3BD,.∴EH∥FG,且EH<FG.∴FE与GH相交
设交点为O,又O在GH上,GH在平面ADC内,∴O在平面ADC内.
同理,O在平面ABC内.从而O在平面ADC与平面ABC的交线AC上.
2.(1)假设EF与BD不是异面直线,则EF与BD共面,得到A、B、C、D在同一平面内,矛盾.
3.(1)证明:用反证法.设EF与BD不是异面直线,
4.则EF与BD共面,从而DF与BE共面,即AD与BC共面,
5.所以A、B、C、D在同一平面内,这与A是△BCD平面外的一点相矛盾.
6.故直线EF与BD是异面直线.
7.3.证明b、c是异面直线,比较困难,考虑使用反证法,即若b与c不是异面直线,则b∥c或b与c相交,证明b∥c或b与c相交都是不可能的,从而证明b、c是异面直线证明:用反证法:
8.若b与c不是异面直线,则b∥c或b与c相交
9.(1)若b∥c.∵a∥c,∴a∥b这与a∩b=A矛盾;
10.(2)若b,c相交于B,则B∈β,又a∩b=A,
11.∴A∈β∴AB⊂β,即b⊂β这与b∩β=A矛盾
12.∴b,c是异面直线.
4.证明:法一:(反证法)假设AD和BC共面,所确定的平面为α,
5.那么点P、A、B、C、D都在平面α内,∴直线a、b、c都在平面α内,与已知条件a、b、c不共面矛盾,
6.假设不成立,∴AD和BC是异面直线.
7.法二:(直接证法)∵a∩c=P,∴它们确定一个平面,
8.设为α,由已知C∉平面α,B∈平面α,AD⊂平面α,B∉AD,∴AD和BC是异面直线.
9.证明:用反证法,
10.假设CD1所在的直线与BC1所在的直线不是异面直线.
11.设直线CD1与BC1共面α.
12.∵C,D1∈CD1,B,C1∈BC1,∴C,D1,B,C1∈α∵CC1∥BB1,∴CC1,BB1确定平面BB1C1C,∴C,B,C1∈平面BB1C1C.
13.∵不共线的三点C,B,C1只有一个平面,∴平面α与平面BB1C1C重合.∴D1∈平面BB1C1C,矛盾.
14.因此,假设错误,即CD1所在的直线与BC1所在的直线是异面直线
{。
