天津大学研究生课程-数理方程试题
天津大学《线性代数(专)》期末考试必备通关指导

线性代数(专)复习题(特别提示:该课程有答疑视频,请参照视频与复习资料进行复习)一、单项选择题1、设111111111aA aa+⎛⎫⎪=+⎪⎪+⎝⎭的秩为3,则下列答案正确的是( A )。
A.3a≠-且0a≠ B.3a=-或0a= C.3a≠- D.0a≠2、设1200470000410072A⎛⎫⎪⎪=⎪⎪⎪⎝⎭,则1A-=( B )。
A.7200410000210074-⎛⎫⎪- ⎪⎪-⎪⎪-⎝⎭B.7200410000210074-⎛⎫⎪-⎪⎪-⎪⎪-⎝⎭C.7200410000210074-⎛⎫⎪-⎪⎪-⎪⎪-⎝⎭D.7200410000410072-⎛⎫⎪- ⎪⎪-⎪⎪-⎝⎭3、设3阶方阵A的3个特征值为23 4-,,,则A*的3个特征值为( C )。
A.111234-,, B.23 4-,, C.12 86--,, D.128 6-,,4、设1200470000250013A⎛⎫⎪⎪=⎪⎪⎪⎝⎭,则1A-=( C )。
A.7200410000350012-⎛⎫⎪- ⎪⎪-⎪⎪-⎝⎭B.7200410000350012-⎛⎫⎪-⎪⎪-⎪⎪-⎝⎭C. 7200410000350012-⎛⎫ ⎪- ⎪ ⎪- ⎪ ⎪-⎝⎭D.7200410000350012-⎛⎫ ⎪- ⎪ ⎪- ⎪ ⎪-⎝⎭5、设4元齐次线性方程组0AX =,()1r A =,则其基础解系含有解向量的个数为( B )。
6、设3阶方阵2A =则13A -=( C )。
A. 32B. 6C. 272D. 54 7、设5元齐次线性方程组0AX =,如果()1r A =则基础解系含有( B )个向量。
A. 5B. 4C. 3D. 18、行列式123024147D ==( D )。
A. 2-B. 14C. 2D. 09、设3阶111111x A x x ⎛⎫ ⎪= ⎪ ⎪⎝⎭的秩为1,则x =( B )。
A. 2-B. 1C. 21-或D.21-或10、设3阶方阵111111a A a a ⎛⎫ ⎪= ⎪ ⎪⎝⎭的秩为2,则a =( A )。
001011[线性代数] 天津大学考试题库及答案
![001011[线性代数] 天津大学考试题库及答案](https://img.taocdn.com/s3/m/da1dba5f6137ee06eff918ae.png)
线性代数复习题(特别提示:该课程可以参照答疑视频进行复习)一、单项选择题1、设3阶方阵A的3个特征值为24 5-,,,则A*的3个特征值为( D)。
A. 24 5-,,B.111245-,, C. 2010 8-,,D.20 108--,,2、设1200470000250013A⎛⎫⎪⎪=⎪⎪⎪⎝⎭,则1A-=( C )。
A.7200410000350012-⎛⎫⎪- ⎪⎪-⎪⎪-⎝⎭B.7200410000350012-⎛⎫⎪-⎪⎪-⎪⎪-⎝⎭C.7200410000350012-⎛⎫⎪-⎪⎪-⎪⎪-⎝⎭D.7200410000350012-⎛⎫⎪- ⎪⎪-⎪⎪-⎝⎭3、设1300250000210074A⎛⎫⎪⎪=⎪⎪⎪⎝⎭,则1A-=( C )。
A.5300210000410072-⎛⎫⎪- ⎪⎪-⎪⎪-⎝⎭B.5300210000410072-⎛⎫⎪-⎪⎪-⎪⎪-⎝⎭C.5300210000410072-⎛⎫⎪-⎪⎪-⎪⎪-⎝⎭D.5300210000410072-⎛⎫⎪- ⎪⎪-⎪⎪-⎝⎭4、设n 阶方阵,,A B C 则()TABC =( B )。
A. T T T A B CB.T T T C B AC.T T T B A CD.T T T A C B 5、设3阶方阵A 的3个特征值为1 24-,,,则A *的3个特征值为( A )。
A. 8 4 2--,, B.8 4 2-,, C.1 2 4-,, D.111 24-,, 6、设111111111a A a a +⎛⎫ ⎪=+ ⎪ ⎪+⎝⎭的秩为2,则下列答案正确的是( A )。
A. 3a =-B. 0a =C. 3a =-或0a =D. 3a ≠-且0a ≠ 7、设五元齐次线性方程组0AX =,若()1r A =,则其基础解系含有解向量的个数为( D )。
A. 1B. 2C. 3D. 48、设111111a A a a ⎛⎫ ⎪= ⎪ ⎪⎝⎭的秩为1,则a =( D )。
天津大学高等代数考研真题(含参考书信息)

天津大学高等代数考研真题(含参考书信息)
天津大学没有指定考研参考书目,官方仅提供考研大纲,这对于备考的研友来讲提出了更高要求。
天津考研网签约硕博团队结合近年考研大纲及考试实际变动总结得出,往年考研参考书对于考研必考仍旧具有重要参考价值。
以下是天津考研网小编为研友汇总的天津大学高等代数详细考研参考书目:
1、北京大学数学系主编《高等代数》
《高等代数》是第四版,基本上保持了第三版的内容,增加了两个附录及一份总习题。
增加的两个附录是:代数基本定理的一个比较简单的证明,若尔当标准形的几何理论。
后者把过去用近世代数中模论方法的经典证明更新为仅用线性代数知识来完成。
《高等代数》主要内容是:多项式、行列式、线性方程组、矩阵、二次型、线性空间、线性变换、A-矩阵、欧几里得空间、双线性函数与辛空间、总习题,附录包括关于连加号、整数的可除性理论、代数基本定理的证明、若尔当标准形的几何理论。
2、天津大学数学专业(602数学分析+836高等代数)考研真题复习宝典
由天津考研网签约的天津大学在读本硕博团队搜集整理精心编制成套,严格依照天津大学最新考研大纲及考研参考书目整理,目前为市面上最全面的资料,基础阶段使用本科笔记配合指定教材复习,梳理知识点,切实感受天大课题氛围;强化阶段使用考研辅导班笔记总结分析总结天大授课重点;冲刺阶段使用历年试题等试题资料进行测试,通过试题答案可以检验做题效果,同时可以分析出题思路及重点。
此资料由天津考研网整理提供,转载请注明出处,更多考研资料请登录网站下载正版!。
天大1999年硕士研究生入学考试试题

天津大学研究生院一九九九年招收硕士生入学试题考试科目:运筹学基础 页数:5一、(27%)填空1、 某工程公司拟从四个项目中选择若干项目,若令x i= 1,第i 个项目被选中(i=1,2,3,4)0,第i 个项目为被选中(i=1,2,3,4)请用x i 的线性表达式表示下列要求:(1)从1,2,3项目中至少选择一个:(2)只有项目2被选中,项目4才能被选中2、 考虑线形规划问题maxz=5x 1+12x 2+4x 3x 1+2x 2+x 3≤5s.t. 2x 1-x 2+3x 3=2x 1,x 2,x 3≥0用单纯型法求解,得其终表如下:其中x 4位松弛变量,x 5为人工变量。
(1)上述模型的对偶模型为(2)对偶模型的最优解为(3)当两种资源分别单独增加一个单位时,目标函数值分别增加 和。
(4)最优基的逆矩阵B -1= (5)如果原问题增加一个变量,则对偶问题的可行域将可能变大还是变小?3、 用表上作业法求解某运输问题,若已计算出某空格的检验数为-2,则其经济意义是,若从该空格出发进行调整,该调整量为2,则调后可使总运费下降。
4、 动态规划中的Bellman 最优性原理是5、 某施工网络图(PERT )的关键路线如下图,箭线上数字为工序时间ij t ,下面数字为工序方差σij 2。
①11.460.78−−−→②15.380.64−−−→③10.510.39−−−→④121.00−−→⑤ 此工程的期望完工期T E =,工程在48天内完工的概率为(只列表达式)6、 设报童每日的售报量Q 是随机变量,其概率分布为P(Q),报童每售出一份报赚k 元,若报纸当天未售出,每份赔h 元,则报童每天最佳的(期望损失最小的)报纸订购(批发)量Q*的确定方法是现若知k=2.5,h=1.25,P(Q)如下表所示,则报童每日订购份最佳。
7、矩阵对象的研究对象是对策问题。
它在纯策略意义下有解得充要条件是:该解是点二、 (13%)用表上作业法求解下面的平衡运输问题 Minz=11m n i j CijXij ==∑∑1n j Xij =∑=a i , i=1,……,ms.t. 1m i Xij =∑=b j , j=1,……,nXij ≥0, i=1,……,m, j=1,……,n时,计算某方案的空格[i,j]检验数σij 可采用位势法,其主要步骤如下:(1)建立线形方程组U i +V j =C ij ,其中C ij 为所有有数个的运价,U i ,V j 分别称发地i 和收地j 的位势。
数理方程-天津大学2010~2011研究生课程考试试卷

天津大学2010~2011研究生课程考试试卷一、填空题(每空2分,共30分)1、数学物理方程中需求解的定解问题是由 和 组成。
2、导热杆的绝热端为第 类边界条件。
3、设)(x P n 为n 阶Legendre 正交多项式,则=⎰-dx x P x P m n )()(11 。
4、拟线性偏微分方程是指方程关于未知函数的 是线性的。
5、方程⎩⎨⎧='==+''0)0()0(0)()(X X x X x X λ的固有值是 ,固有函数系是 。
6、在区域Ω内具有二阶连续偏导数的函数u ,且满足 ,则称u 是Ω内的调和函数。
7、线性偏微分方程的类型及标准型只依赖于它的 部分。
8、初始位移2)(x e x -=φ,初始速度x x sin )(=ψ的无界弦做自由振动,其振动规律=),(t x u 。
9已知 kt e t f at sin )(=,则f 的Laplace 变换=)(p L 。
10、已知)(t φ的Fourier 变换是)(~ωφ,则t a ωωφcos )(~关于ω的Fourier 逆变换是=),(t x u 。
11、若一个定解问题的解存在、 且 ,则称该问题是适定的。
12、设长为l 的均匀细杆侧面绝热,内部无热源,0=x 端的温度保持l x C o =,0端在温度为C o 0的介质中自由冷却。
已知初始温度为)(x φ,则杆的温度变化用定解问题描述为 。
二、简答题(共22分)1、(12分)判断下列二阶线性偏微分方程所属类型,并将其化为标准型。
(1) 032=-+yy xy xx u u u ;(2) 0,0>=+y u yu yy xx 。
2、(10分) 定义卷积τττd t f f t f t f t f )()()(*)()(2121-==⎰+∞∞-,证明: (1) 卷积满足交换律,即:)(*)()(*)(1221t f t f t f t f =。
(2) 卷积具有时移特性,即:())(*)()(*)(2121212211t t t f t t t f t f t t f t t f --=--=--三、计算题(每小题12分,共48分)1、长为l 两端固定的均匀弦做自由微小横振动。
天津大学研究生院2000-2005年招收硕士生入学试题429概要
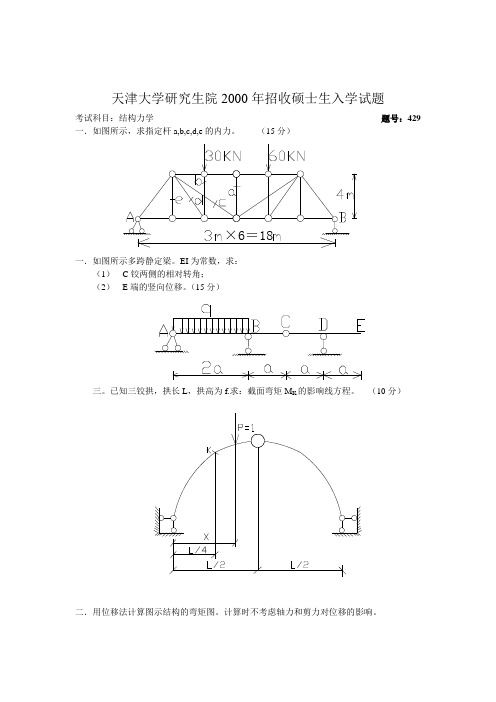
天津大学研究生院2000年招收硕士生入学试题考试科目:结构力学题号:429 一.如图所示,求指定杆a,b,c,d,e的内力。
(15分)×6=18一.如图所示多跨静定梁。
EI为常数,求:(1)C铰两侧的相对转角;(2)E端的竖向位移。
(15分)三。
已知三铰拱,拱长L,拱高为f.求:截面弯矩M K的影响线方程。
(10分)二.用位移法计算图示结构的弯矩图。
计算时不考虑轴力和剪力对位移的影响。
两段固定等截面直杆在均匀荷载作用下的固端剪力和固端弯矩为:212AB ql m =-212AB ql m = 2AB ql Q = 2AB ql Q =- 三.用力法求杆件AB 的轴力。
其中,AB 杆的拉伸刚度为EA 。
其余各杆弯曲刚度为EI.除AB 外,其余各杆计算时均不考虑轴力和剪力对位移的影响。
(20分)四.图示简支刚架,质点质量均为m.,杆的自重不计。
动力荷载()sin t P P t θ=,不考虑阻尼,EI 为常数。
1. 建立运动方程2. 求出结构的自振频率3. 求出质量处的最大动位移。
(20分)θ天津大学研究生院2001年招收硕士生入学试题考试科目:结构力学题号:429 一.是非题(将判断结果填入括弧,以O表示正确,以×表示错误)本大题共4小题,合计14分1.(本小题3分)弹性体系虚功的特点是:(1)在作功过程中,力的数值保持不变;(2)作功的力与相应的位移无因果关系,位移由其他力系或其他因素所产生。
()2.(本小题3分)力法只能用于线性变形体系。
()3.(本小题4分)结构的温度变化及单位荷载作用下的内力如图a,b所示,梁截面为矩形,h=0.6m,材料线膨胀系数为α,则C,D两点的相对水平位移为400α。
()°°°°°°4.(本小题4分)图示珩架各杆EA相同,C点受水平荷载P作用,则AB杆内力/2N=.( )AB二.选择题(将选中答案的字母填入括弧内)本大题共4个小题,合计16分。
2020-2021年天津大学工程分析与计算力学考研真题、考研参考书、复试线、招生人数

2020-2021年天津大学工程分析与计算力学考研真题、考研参考书、复试线、招生人数育明教育506大印老师联合名校导师及考研状元联合整理2019年9月20日星期日【温馨解析】院校选择也很重要,选择适合自己的院校是成功的关键,但是考生信息有限,很难选择适合自己的院校,在这里,大家可以直接联系我,我免费给大家做规划和咨询。
育明教育从2006年开始办学,校长是北京外国语大学夏教授,北京总部负责人是北京大学政管院博士,主打专业课一对一辅导。
到现在已经有十年的时间,在我们育明教育,每年都有成功学员积累的一些经验可供各位考生参考。
育明教育整合利用历届育明优秀学员的成功经验与高分资料,为每一位学员构建考研成功的基础保障。
我们的辅导包括前期的报考指导,中期的核心参考书的讲解、专题(真题、出题老师论文专著、最新时事)讲解、模拟考(答题技巧框架、创新点的讲解)。
后期还会有教务老师时事根据上课情况,对考生进行查缺补漏,进行答题技巧的辅导。
在我们育明教育,前期咨询师、后期教务与辅导老师三方对您的上课负责,所以每年我们的通过率一直都是有保证的。
目录一、2019-2020年考研真题、考研参考书笔记二、2020-2021年院校考研复习技巧三、2020-2021年考研专业课答题技巧内容一、2019-2020年考研真题、考研参考书笔记一、研究方向:1.(压电材料性能模型及计算仿真)2.(生物及新材料科学中新的数学模型及计算方法)3.(工程计算软件编制原理与技术)4.(有限元边界元新方法及其在工程中的应用)5.(纳细观复合有限元方法研究及CAE技术应用)二、专业特点:本学科主要开展工程分析与计算力学中具有重要意义的基础理论与计算方法的研究,解决科学与工程领域中的重大计算问题,着重研究计算方法的构造、理论分析及实现。
同时,分析和提高计算的可靠性、有效性和精确性。
研究各类数值软件的开发技术。
注重交叉学科的发展。
现有教师6名(其中博士生导师2名),副教授6名。
天津大学硕士研究生工程数学课后答案全版

+
a xn−1 n−1
++
a2 x2
+
a1 (x
−1).
由上可知,(x −1, x2 , x3 ,, xn )是W的一个基,故 dimW = n.
6. (1“) ⇒ ”:因为T是线性的,故有T (0) = 0.于是,若T (x) = 0,则由T −1存在知T是单射,从而有x = 0. “ ⇐ ”:要证T −1存在,只需证明T是单射:
+
dE22 ,即σ
E20
=
0
b
0
d )T ,
a 0 b 0
∴ A =0
a
0
b
.
c 0 d 0
0
c
0
d
4
习题二
A
一、判断题
1.√;2.×;3.√;4.√;5.×;6.√;7.×;8.×;9.√;10.√;11.×;12.×.
二、填空题
2 0 0 2 0 0 1. x ;2. n ;3. λ, (λ −1)2 , λ + i, λ − i ;4. λ −1, λ +1 ;5. 0 0 −4 ;6. 0 2 0 ;7. O ;
f : x x2 ,取A =[−2, 0], B =[−1, 3],则A ∩ B =[−1, 0]. 于是f ( A ∩ B) = f ([−1, 0]) = [0, 1], 而
f (A) ∩ f (B) = [0, 4] ∩[0, 9] = [0, 4]. 从而有
.
[ ] [ ] 2. 证(1) ∀n ∈ N ,有 −2 + 1 , 2 − 1
, ∃k ∈ N
,使得
x
>
天津大学工程数学基础2017级试题

一.判断(10分)1.设是K上的线性空间,算子则是的子空间.()2.线性无关.()3.对L e g e n d r e 多项式,有.()4.,则可对角化.()5.设是H e r mi t e插值余项,则节点为的二重零点.()6.C o t e s 系数只与求积节点的个数有关而与被积函数和积分区间无关.()7.设是上的任意方阵范数,则.()8.,则.()9.若为G a u s s型求积公式,则.()10.若正规矩阵,其特征值均为实数,则为酉矩阵.()二、填空(10分)1.已知,则.2.,则.3.设是S e i d e l迭代矩阵,则的所有特征值中绝对值最小的为.4.若为插值型求积公式,,是n次L a g r a n g e插值基函数,令则.5.设酉矩阵,且则的不变因子.三.(8分)设,求的有理标准形.题号12345678910平时成绩成绩得分四.(8分)求解初值问题五.(8分)已知线性方程组为(1)写出S e i d e l迭代格式,(2)判断迭代格式收敛性.六.(8分)由下列插值条件1.631.731.952.282.5314.09416.84418.47520.96323.135用三次N e w t o n插值多项式计算的近似值(结果保留至小数点后第3位)七.(10分)用算法求积分的近似值,并将计算结果列于下表(计算结果保留至小数点后第5位)01234八.(10分)用L e g e n d r e 多项式求函数在上的三次最佳平方逼近,并求(结果保留到小数点后第5位,取)九.(8分)写出用标准R u n g e-K u t t a方法解下列初值问题的计算公式.十.(10分)证明1.内积空间中的任何正交系都是线性无关的.2.,则。
天津大学考研真题答案

高等代数问题解答 终于完成了,来张美图犒劳自己一下吧.
这个贝壳漂亮吧?
◇※☆■◇◇※☆■◇
5
高等代数资源博客
高等代数问题解答
高等代数资源博客 November 21, 2010
1 声明
您现在看到的这份文件来自.本站原创的内容,采用创作共用组 织(Creative Commons)的“公共领域”(Public Domain)许可。即放弃一切权利,全 归公共领域。但涉及到其他版权人的摘录、转载、投稿、翻译等类内容不在此列。 本文的内容仅供学习参考之用,作者不对内容的正确性作任何承诺,作者不对因使用本 文而造成的一切后果承担任何责任. 关于如何使用本文的建议:首先保证自己认真做了一遍题目,否则请不要查看本文.记 住: 别人做是别人的,自己做才是自己的 . 作者水平有限,错误不可避免,欢迎您来信指教:www52gdorg@.
即A的特征值只能为−1, −2, −3.由A的阶数为偶数知|A| > 0.(因为行列式为所有特征值的 1 1 乘积).A−1 的特征值只能为−1, − 2 , −3 .而A∗ = |A|A−1 .易知A∗ 实对称.从而A∗ 的特征值都 是负的. 1
高等代问题解答
2.设V 是数域P 上的线性空间,V = W1 ⊕ W2 . A1 , A2 分别为W1 , W2 上的线性变换.定义 法则A 如下: A (α1 + α2 ) = 2A1 (α1 ) − 3A2 (α2 ), ∀α1 ∈ W1 , α2 ∈ W2 1)求证A 是V 上的线性变换; 2)求证W1 是A −子空间; 3)若dim W1 = n1 , dim W2 = n2 , detA1 = d1 , detA2 = d2 ,求detA . 证明:1)∀α1 , β1 ∈ W1 , α2 , β2 ∈ W2 , ∀k ∈ P,则 A [(α1 + α2 ) + (β1 + β2 )] = A [(α1 + β1 ) + (α2 + β2 )] = 2A1 (α1 + β1 ) − 3A2 (α2 + β2 ) = 2A1 (α1 ) + 2A1 (β1 ) − 3A2 (α2 ) − 3A2 (β2 ) = A (α1 + α2 ) + A (β1 + β2 ) A [k (α1 + α2 )] = A (kα1 + kα2 ) = 2A1 (kα1 ) − 3α = k (2A1 (α1 ) − 3A2 (α2 )) = 2A (α1 + α2 ) 故结论成立. 2)∀α1 ∈ W1 ,则 于是 A (α1 ) = 2A1 (α1 ) − 3A2 (0) = 2A1 (α1 ) ∈ W1 故结论成立. 3)设 α1 , · · · , αn1 与 β1 , · · · , βn2 分别为W1 , W2 的基,则它们合起来为V 的基.设 A1 (α1 , · · · , αn1 ) = (α1 , · · · , αn1 )A1 A1 (β1 , · · · , βn2 ) = (β1 , · · · , βn2 )A2 则 A (α1 , · · · , αn1 , β1 , · · · , βn2 ) = (α1 , · · · , αn1 , β1 , · · · , βn2 ) 于是 detA = 2A1 −3A2 = |2A1 || − 3A2 | = 2n1 d1 (−3)n2 d2 . ( 2A1 ) −3A2 α1 = α1 + 0, α1 ∈ W1 , 0 ∈ W2
天大2005年硕士研究生入学试题及答案

天津大学招收2005年硕士学位研究生入学考试试题参考答案一、 填空1、-M 基变量2、偏差 小 目标(软)3、s t v Vv V ∈∈ 正4、ij i mi jijjmi iu p up EMV EPPI )(max max )(*11θθ∑∑==--(先)或ij i mi ij jmi i u p u p )(min min )(11θθ∑∑==+-5、******max min (,)min max (,)(,)x y y y x x E x y E x y E x y ==6、分布函数; 1()X F R -=二 对偶问题1234123124min 128161224222430,1,2,3,4iW y y y y y y y y y y y i =+++++≥⎧⎪++≥⎨⎪≥=⎩⎩⎨⎧=++=++∴>>3422242,0,042132121y y y y y y x x 其对偶问题取严格等式 (*) 1414(1)(4)0,0y y ∴== 第,两种资源有剩余,即原问题约束、取严格不等式对应对偶问题变量代入(*)式,2432=+y y ,322=y 23,8123==∴y y []140812**********=⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎣⎡=∴W**14z w ∴==由121122844162x x x x x +==⎧⎧⇒⎨⎨==⎩⎩ 综上,原问题最优解[]14,24*==Z x T对偶问题最优解14,08123*=⎥⎦⎤⎢⎣⎡=W y T三 设标准袋生产1x ,高档袋生产2x (1)21910max x x Z +=⎪⎪⎪⎪⎪⎪⎩⎪⎪⎪⎪⎪⎪⎨⎧≥≤+≤+≤+≤+0,135411017083260065216301072121212121x x x x x x x x x x1j j B j C C B P σ-=-[]375.434375.025.19375.0875.10100903133-=⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡----=-=∴-p B C σ )6,,1(0 =≤j j σ∴是终表∴最优生产计划[]1801200252540=x ,即普通袋540个,高档袋252个∴最大利润Z []7668252540910*=⎥⎦⎤⎢⎣⎡= (美元) 345601200182412018x x x x ====因为松弛变量,,,所以第,种资源有剩余,分别为,。
天津大学数学考研试卷真题

天津大学数学考研试卷真题天津大学数学考研试卷真题一直是备考者们关注的焦点。
这些试题不仅考察了考生们对数学知识的掌握程度,还考察了他们的思维能力和解题能力。
在这篇文章中,我们将探讨一些天津大学数学考研试卷真题,并分析其中的一些难点和解题技巧。
首先,我们来看一道典型的数学分析题。
试题如下:设函数$f(x)=\frac{1}{3}x^3-3x^2+9x-7$,则函数$f(x)$的最小值为多少?这道题考察了对函数极值的求解。
我们可以通过求导数的方法来解决。
首先,我们对函数$f(x)$求导,得到$f'(x)=x^2-6x+9$。
然后,令$f'(x)=0$,解得$x=3$。
接着,我们求得$f''(x)=2x-6$,将$x=3$代入,得到$f''(3)=0$。
由于$f''(3)=0$,我们无法通过二阶导数判断极值的性质。
因此,我们需要进一步分析。
我们可以观察到函数$f(x)$的导函数$f'(x)$是一个二次函数,并且开口向上。
这意味着函数$f(x)$在$x=3$处取得了极小值。
我们可以进一步求得$f(3)=\frac{1}{3}(3)^3-3(3)^2+9(3)-7=2$。
因此,函数$f(x)$的最小值为2。
接下来,我们来看一道线性代数的题目。
试题如下:设矩阵$A=\begin{bmatrix} 2 & 1 \\ 1 & 2 \end{bmatrix}$,求矩阵$A$的特征值和特征向量。
这道题考察了对矩阵特征值和特征向量的求解。
我们可以通过求解矩阵$A$的特征方程来解决。
首先,我们设矩阵$A$的特征值为$\lambda$,则有$\det(A-\lambda I)=0$,其中$I$为单位矩阵。
代入矩阵$A$的元素,得到$(2-\lambda)(2-\lambda)-1=0$。
解这个方程,我们可以得到两个特征值$\lambda_1=1$和$\lambda_2=3$。
2023年天津考研数学三试题及答案-完整版

【导语】国庆佳节喜洋洋,红红灯笼家家亮;好运挽着开⼼到,幸福挤着媚眼笑;点燃蜡烛许个愿,祖国明天更辉煌;烟花豪放笑飞扬,普天同贺国庆到,节⽇快乐!以下是⽆忧考为您整理的《⼩学⽣⼗⼀国庆节祝福寄语》,供⼤家赏阅。
【篇⼀】⼩学⽣⼗⼀国庆节祝福寄语 1、国庆到,送你⼀张吉祥信⽤卡:存⼊耕耘,提取收获;存⼊微笑,提取快乐;存⼊努⼒,提取成功;存⼊善良,提取好运;存⼊运动,提取健康;存⼊真⼼,提取友情。
随你提取福运佳,信⽤额度⽆限⼤,愿你⼼情乐哈哈,⼀⽣绽放幸福花!祝⼤家国庆快乐! 2、买了两瓶浪漫,从⼼灵的深处切下⼏许关怀,作为礼物送给你,祝国庆快乐! 3、⼀万个思念,在空⽓中凝固。
扬起风吹向你,带着我的祝福,寂寞我不在乎,你快乐我就满⾜,想你是我的幸福!国庆佳节,盼望与你相聚! 4、如果有选择的话,我想当⼀只猫,可以在阳光下撒娇,我⼀定是⼀只懒猫!可是我⼀定会上,因为我想在在你的怀⾥撒娇。
国庆节快乐! 5、国庆国庆普天同庆,祝福你和嫂⼦在这个和平幸福的年代⾥节⽇快乐,⾝体健康,幸福永远。
6、⽤祝福的短信来编织⼀件彩⾐,将彩⾐在全国飞舞,让我们的温暖和喜悦,在国庆节传递开来吧,收到信息后请转发! 7、快乐是溪流欢快流淌,幸福是云朵⾃由倘徉,吉祥是蝴蝶轻舞飞扬,如意是美景活⾊⽣⾹。
该遗忘的烦恼遗忘,该记住的美好珍藏,能改变的风貌改善,能接受的依靠抓牢。
国庆佳节翩翩来到,短信送上朋友关照,祝你天天开⼼美妙,幸福⽆限快乐逍遥! 8、国庆佳节喜洋洋,休闲放松快乐享,朋友祝福不能忘,祝你幸福⼜健康,⼯作顺⼼创辉煌,愿你平安再吉祥,⽣活美好更富强。
提前祝国庆节快乐! 9、真挚的友情如同美酒,浓浓如醇,芳⾹四溢;美好的祝福恰似美景,沁⼊⼼⽥,赏⼼悦⽬。
朋友,国庆佳节,让快乐和美好天天陪伴着你! 10、骄傲的是,祖国华诞之际,我们变强⼤了,经济在⾼速腾飞,⽣活在⽇益提⾼,和平在周围环绕,安居乐业,国泰民安,国庆节,我们有美好的理由欢笑! 11、让幸福变成巧克⼒,只要吃了你就会甜蜜,让开⼼变成⽅便⾯,简简单单就能来到你⾝边,国庆节⾥,祝哥哥有⼀份好⼼情。
天津大学数学考试题及答案

天津大学数学考试题及答案一、选择题(每题3分,共30分)1. 下列哪个选项是最小的正整数?A. 0B. 1C. -1D. 2答案:B2. 函数f(x) = x^2 + 3x + 2的顶点坐标是:A. (-1, 1)B. (-2, -2)C. (1, 4)D. (2, 2)答案:A3. 已知集合A = {1, 2, 3},B = {2, 3, 4},求A∪B:A. {1, 2, 3}B. {1, 2, 3, 4}C. {2, 3}D. {1, 4}答案:B4. 若sinα = 0.6,则cosα的值是:A. 0.8B. -0.8C. -0.6D. 0.6答案:A5. 极限lim (x->2) [(x^2 - 4)/(x - 2)]的值是:A. 0B. 4C. 2D. 不存在答案:B6. 微分方程dy/dx = x^2 - y^2的解是:A. y = x^2B. y = x + CC. y = C/xD. y = C * e^x答案:B7. 曲线y = x^3在点(1, 1)处的切线斜率是:A. 3B. 2C. 1D. 0答案:A8. 定积分∫[0, 1] x dx的值是:A. 1/2B. 1/3C. 1/4D. 1/6答案:B9. 方程x^2 - 5x + 6 = 0的根是:A. 2, 3B. -2, 3C. 1, 6D. -1, 6答案:A10. 已知|z| = 5,且z的实部为3,则z的虚部可以是:A. 4iB. -4iC. 2iD. -2i答案:B和D二、填空题(每题4分,共20分)11. 圆的方程为(x - 2)^2 + (y - 3)^2 = 9,则该圆的半径为_________。
答案:312. 若函数f(x) = 2x^3 - 6x^2 + 3x在x = 1处取得极小值,则f(1) = _______。
答案:-113. 已知向量a = (3, 4),b = (-2, 1),则向量a与向量b的夹角θ满足cosθ = __________。
001012[概率论与数理统计] 天津大学考试参考资料答案
![001012[概率论与数理统计] 天津大学考试参考资料答案](https://img.taocdn.com/s3/m/65be0a5065ce0508773213ab.png)
概率论与数理统计复习题(特别提示:该课程有答疑录像,请参照答疑视频进行复习)填空题:1.一箱中有6个球,其中有红色球2个,白色球4个,从中任取出3个球,X 表示取出的3只球中的红球数,求: (1)X 的分布律; (2)X 的分布函数()F x ; (3)期望()E X ; (4)方差()D X 。
参考的答案: (1)X 的分布律为:34361{0}5C P X C ===,1224363{1}5C C P X C ===, 2124361{2}5C C P X C === (2)X 的分布函数为0,01,015()4,1251,2x x F x x x <⎧⎪⎪≤<⎪=⎨⎪≤<⎪⎪≥⎩(3)()=1E X(4)27()=5E X ,2()=5D X2.某城市有两种报纸:晚报和日报。
居民中订阅日报的有35%,同时订阅晚报及日报的有20%,则“只订阅日报”的事件发生的概率为 。
参考的答案:0.153.从正态总体~(17,4)X N 中随机抽取一个容量为16的简单随机样本,X 为样本均值,则{1617}P X <<= 。
((0.5)0.6915Φ= (2)0.9772Φ=). 参考的答案:0.19154.设123ˆˆˆ,,θθθ都是总体分布中参数θ的无偏估计量,令123ˆˆˆˆ23a θθθθ=-+, 当a = 时,ˆθ也是θ的无偏估计量。
参考的答案:05.设随机变量X 的分布律为111{1},{0},{1}442P X P X P X =-=====;Y 的分布律为21{0},{1},P Y P Y ====且X 与Y 独立, 令Z X Y =+,则Z 的分布律为6.设,A B 为随机事件,且()0.5,()0.6,()0.8,P A P B P B A ===则()P A B ⋃= 。
参考的答案:0.77.设随机变量(,)X Y 的联合概率密度为23,02,01(,),20,xy x y f x y ⎧≤≤≤≤⎪=⎨⎪⎩其它则()E XY = 。
天津大学研究生课程-数理方程试题

一. 判断题(每题2分).1. 2u u x y x y x∂∂+=∂∂∂是非线性偏微分方程.( ) 2. 绝对可积函数一定可做Fourier 积分变化.( )3. ()(1) 1.n n F x n Legendre F =是次正交多项式, 则 ( )4. (,)0xy f x y =的解是调和函数.( )5. **12u u 已知,是线性偏微分方程(,)xx yy u u f x y +=的解,则**12u u -是0u ∆= 的解.( )二. 填空题(每题2分).1. ()sin t xx yy u u u xt -+= 是____________型偏微分方程.2. 内部无热源的半径为R 的圆形薄板,内部稳态温度分布,当边界上温度为()t φ时,试建立方程的定解问题________________________.3. 2x 的Legendre 正交多项式的分解形式为__________________.4.某无界弦做自由振动,此弦的初始位移为()x φ,初始速度为()a x φ-,则弦振动规律为______________________________.5. []()____________.at m L e t s =三.求解定解问题(12分)200sin ;0,0;0.t xx xx x x l t u a u A t u u u ω===-====四.用积分变换方法求解以下微分方程(每题12分,共24分)(1) 001,0,0;1,1.xy x y u x y u y u ===>>=+= (2) 00230, 1.tt t y y y e y y =='''+-='==五.某半无界弦的端点是自由的,初始位移为零,初始速度为cos x ,求弦的自由振动规律。
(12分)六.设有长为a ,宽为b 的矩形薄板,两侧面绝热,有三边的温度为零,另一边的温度分布为x ,内部没有热源,求稳定状态时板内的温度分布。
天大1999年硕士研究生入学考试试题

天津大学研究生院一九九九年招收硕士生入学试题考试科目:运筹学基础 页数:5 一、(27%)填空 1、 某工程公司拟从四个项目中选择若干项目,若令x i = 1,第i 个项目被选中(i=1,2,3,4) 0,第i 个项目为被选中(i=1,2,3,4) 请用x i 的线性表达式表示下列要求: (1)从1,2,3项目中至少选择一个:(2)只有项目2被选中,项目4才能被选中2、 考虑线形规划问题maxz=5x 1+12x 2+4x 3 x 1+2x 2+x 3≤5 s.t. 2x 1-x 2+3x 3=2 x 1,x 2,x 3≥0用单纯型法求解,得其终表如下:其中x 45(1)上述模型的对偶模型为 (2)对偶模型的最优解为(3)当两种资源分别单独增加一个单位时,目标函数值分别增加 和。
(4)最优基的逆矩阵B -1=(5)如果原问题增加一个变量,则对偶问题的可行域将可能变大还是变小?3、 用表上作业法求解某运输问题,若已计算出某空格的检验数为-2,则其经济意义是,若从该空格出发进行调整,该调整量为2,则调后可使总运费下降。
4、动态规划中的Bellman最优性原理是5、 某施工网络图(PERT )的关键路线如下图,箭线上数字为工序时间ij t ,下面数字为工序方差σij2。
①11.460.78−−−→②15.380.64−−−→③10.510.39−−−→④121.00−−→⑤ 此工程的期望完工期T E =,工程在48天内完工的概率为(只列表达式)。
6、 设报童每日的售报量Q 是随机变量,其概率分布为P(Q),报童每售出一份报赚k 元,若报纸当天未售出,每份赔h 元,则报童每天最佳的(期望损失最小的)报纸订购(批发)量Q*的确定方法是现若知k=2.5,h=1.25,P(Q)如下表所示,则报童每日订购份最佳。
7、矩阵对象的研究对象是对策问题。
它在纯策略意义下有解得充要条件是:该解是二、 (13%)用表上作业法求解下面的平衡运输问题Minz=11mni j C ij X ij ==∑∑1nj X i j =∑=a i , i=1,……,ms.t.1mi X ij =∑=b j , j=1,……,nX i j ≥0, i=1,……,m, j=1,……,n时,计算某方案的空格[i,j]检验数σij 可采用位势法,其主要步骤如下:(1)建立线形方程组U i +V j =C ij ,其中C ij 为所有有数个的运价,U i ,V j 分别称发地i 和收地j 的位势。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
一. 判断题(每题2分).
1. 2u u x y x y x
∂∂+=∂∂∂是非线性偏微分方程.( ) 2. 绝对可积函数一定可做Fourier 积分变化.( )
3. ()(1) 1.n n F x n Legendre F =是次正交多项式, 则 ( )
4. (,)0xy f x y =的解是调和函数.( )
5. **12u u 已知,是线性偏微分方程(,)xx yy u u f x y +=的解,则**12u u -是0u ∆= 的解.( )
二. 填空题(每题2分).
1. ()sin t xx yy u u u xt -+= 是____________型偏微分方程.
2. 内部无热源的半径为R 的圆形薄板,内部稳态温度分布,当边界上温度为()t φ时,试建立方程的定解问题________________________.
3. 2x 的Legendre 正交多项式的分解形式为__________________.
4.某无界弦做自由振动,此弦的初始位移为()x φ,初始速度为()a x φ-,则弦振动规律为______________________________.
5. []()____________.at m L e t s =
三.求解定解问题(12分)
200sin ;
0,0;0.
t xx x
x x x l t u a u A t u u u ω===-====
四.用积分变换方法求解以下微分方程(每题12分,共24分)
(1) 001,0,0;
1,1.
xy x y u x y u y u ===>>=+= (2) 00230, 1.t
t t y y y e y y =='''+-='==
五.某半无界弦的端点是自由的,初始位移为零,初始速度为cos x ,求弦的自由振动规律。
(12分)
六.设有长为a ,宽为b 的矩形薄板,两侧面绝热,有三边的温度为零,另一边的温度分布为x ,内部没有热源,求稳定状态时板内的温度分布。
(12分)
七.判断下列方程所属类型并求其标准形式(8分) 0xx yy yu xu +=
八.叙述并证明Laplace变换的微分性质和卷积性质。
(12分)。
