光波在介质界面上的反射和折射 菲涅耳公式
合集下载
Fresnel(菲涅尔)公式
d=z=
2π
λ0
n12 sin2 i1 − n22 ；(3)波矢常数： k2 sin i2 > k2 。
应用：近场光学
15
1.3 反射率和透射率
W1
=
I1σ
cos i1
=
n1 2
ε0 μ0
A1 2 cos i1
W1′ =
I1′σ
cos i1
=
n1 2
ε0 μ0
A1′ 2 cos i1
W2
=
I2σ
cos i2
2.4
2.2
n =1.33 1
n =1
2.0
2
r
r
s
p
1.8
t
t
s
p
1.6
1.4
1.2
i
c
1.0
0.8
0.6
0.4
0.2
i
B
0.0
-0.2 0
10
20
30
40
50
60
i
1
12
全内反射的应用： 1、导波光学 Waveguide / Optical fiber
n 1
n <n , n <n 12 32
n 2
1
Stocks 公式：
A
Ar
Att'
Ar
Arr
Art
At
Atr'
At
Arr + Att′ = A 可知： Art + Atr′ = 0
r2 + tt′ = 1 r + r′ = 0
2
1.2 振幅反射(透射)比 相位跃变(相移) 1、透射比与相位跃变
精选折射和反射定律菲涅耳公式讲义(ppt)
(13)
2、公式的另外两种形式
rsE Eri0 0ss n n1 1c co oiiss n n2 2c co ottss
(8)
ts
Er0s Ei0s
n1c2 on1 iscno2 cisots
n1 n2
rp
Er0p Ei0p
n n1 1cco ottss n n2 2ccrpo oiissEEri00(pp12)cco将onss1它ii 们 cc变oon形ss2tt
H ip 界面
ki θi
θr kr
Ers
Hrp
1
O
2
θt kt
Ets
n
H tp
图2
在界面上电场切向分 量连续：
n(E 2E 1)0
Ei0sEr0sEt0s (5)
在界面上磁场的切向分
量连续： n(H 2H 1)0
规定：电场和磁场
的s分量垂直于纸面，
向外为正，向内为负。 H i0 p co i H s r0 p co r s H t0 p co t (s 6)
rsE Eri0 0ss n n1 1c co oiiss n n2 2c co ottss
(8)
ts
Er0s Ei0s
n1c2 on1 iscno2 cisots
(9)
rp
Er0p Ei0p
n1cotsn2cois n1cotsn2cois
(12)
tp
Er0p Ei0p
n1co2n1tscno2cisois
Ei0sEr0sEt0s (5)
rsE Eri0 0ss n n1 1c co oiiss n n2 2c co ottss
(8)
ts
一、 菲涅耳公式(Fresnel formula)
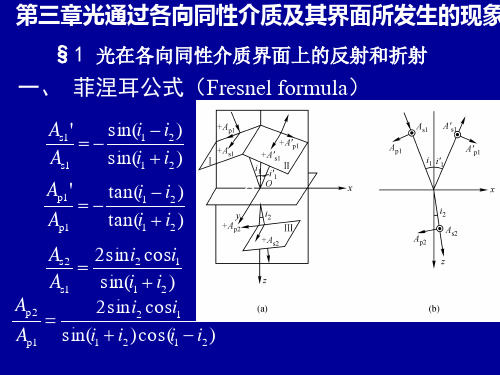
1
4
紫光的散射强度大约是红光的10倍。
4． 偏振性
O z
y p B’
y D A’ B
AP z
x
D’ 实验 自然光入射到散射物质中，观察到：
正侧方（z）线偏振 斜方向（C）部分偏振 对着x方向（x）自然光
解释 用电偶极子次级辐射可解释 实验现象
分解成 +
被微粒散射时，各方向上的振幅可看成以上 两个分振动的合成。 退偏振 线偏振光照射某些气体或液体，从侧向 观察时，散射光变成部分偏振的，称为退偏 振。其机理是介质分子本身是各向异性的。
2．正交棱镜法
研究色散，目的是寻找 n f ( )的函数形式。 正交棱镜装置
三棱镜P1→AH（光谱） P1 P2→A’H’（光谱） n f ( ) ——弯曲光谱的形状。
3．正常色散与反常色散（Normal dispersion and abnormal dispersion）
正常色散曲线的信息
dut余虹一菲涅耳公式fresnelformula第三章光通过各向同性介质及其界面所发生的现象1光在各向同性介质界面上的反射和折射布儒斯特角线偏振光四用反射和折射法获得偏振光布儒斯特定律玻璃片堆要提高反射线偏振光的强度可利用玻璃片堆的多次反射
第三章光通过各向同性介质及其界面所发生的现象 §1 光在各向同性介质界面上的反射和折射 一、 菲涅耳公式（Fresnel formula）
dI Idx dI a Idx I dI d I I 0 a dx a 为吸收系数 I I 0 e a d ，
0
d
a AC ，式中A是一个与浓度无关 稀溶液：
的常量，C为溶液的浓度。
§ 3 光的色散（Dispersion of Light） 1．色散的特点
基础光学第4章光波在界面的反射和折射规律课件
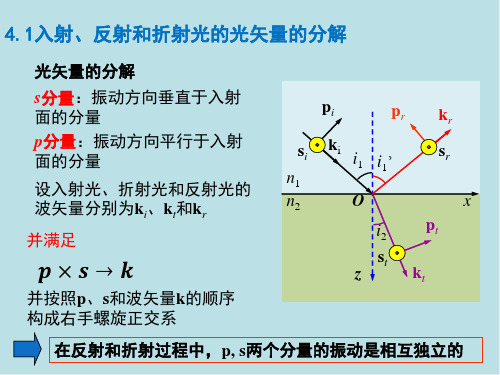
无论 n1 n2 或 n1 n2
透射光1’和2’振动方
向相同。即无半波损失。
只要光线2存在，光线1
和2的振动方向总是相
反的，即1和2的光程之
间存在半波损失。
光在多层透明介质界面的反射和折射
n1 < n2< n3 或n3 < n2< n1
时，光线1和2之间的光程
没有半波损失。
当折射率不按顺序排列时，
p
s
n2 n1
t p ts
2n1
n2 n1
入射
反射
约定
n1 < n2 n1 > n2
rp
rs
tp
ts
+
+
+
+
+
约定
实际
实际
+
反射
入射
n1
n2
约定
实际
透射
(a) n1 < n2
n1 < n2 时反射光与入射光振动方向相反
n1 > n2 时反射光与入射光振动方向相同
在任何情况下，透射光的方向和入射光相同
中的多次反射，分别求光从空气（折射率为1.0）正入射到玻
璃上表面，以及光从玻璃下表面射出时的振幅反射率、光强
反射率、振幅透射率和光强透射率。
【解】 正入射： i1 i2 0
n n
2n1
rp 2 1 rs ， t p ts
n2 n1
n2 n1
2
n2 n1
在反射和折射过程中，p, s两个分量的振动是相互独立的
4.2 菲涅尔反射和折射公式
n cos i1 n1 cos i2
菲涅尔方程式
菲涅尔方程式
菲涅耳方程式（Fresnel Equations）是用来描述光在两种介质界面上反射和透射的现象和规律的方程式。
它由奥古斯汀·菲涅耳（Augustin-Jean Fresnel）在19世纪提出，并成为光学领域中的重要理论工具。
菲涅耳方程式分为反射方程和透射方程，分别描述了光在界面上的反射和折射（透射）行为。
这些方程式基于电磁波的传播和边界条件，可以通过麦克斯韦方程和边界条件进行推导。
反射方程描述了入射光波在介质界面上的反射行为。
对于垂直入射的光，反射系数（反射光强与入射光强之比）可以通过下述菲涅耳反射方程计算：
r = (n1 - n2) / (n1 + n2)
其中，n1和n2分别是两种介质的折射率，r是反射系数。
透射方程描述了入射光波通过介质界面的折射行为。
同样对于垂直入射的光，透射系数（透射光强与入射光强之比）可以通过下述菲涅耳透射方程计算：
t = 2n1 / (n1 + n2)
其中，n1和n2分别是两种介质的折射率，t是透射系数。
需要注意的是，菲涅耳方程式仅适用于垂直入射的光，并且忽略了光在界面上的散射和吸收行为。
在实际应用中，还需要考虑光的入射角度、极化状态和表面特性等因素，并结合其他衍射、干涉等现象来对界面上的光行为进行更全面的描述。
菲涅耳方程式在材料科学、光学器件设计和表面反射控制等领域中具有广泛的应用，并能解释和预测光在界面上的反射和透射现象。
光波在介质界面上的反射和折射
(3) 应用
3、全反射 、
• 设光波从光密介质射向光疏介质(n 设光波从光密介质射向光疏介质 1>n2)， ， 折射角θ 大于入射角θ 折射角 2 大于入射角 1 。 当 sinθ1 ＝ n2/n1 时 ， θ2 这时折射角沿界面掠过。 为 90o ， 这时折射角沿界面掠过 。 若入射角再 增大， 增大，使sinθ1>n2/n1 ，这时不能定义实数的折 射角。 的入射角θ 称为临界角， 射角 。 使 θ2=90o 的入射角 1 称为临界角 ， 记作 θc即 即
2、反射系数和透射系数
rp =
E0 rp E0ip
n2 cosθ1 − n1 cosθ2 tan(θ1 − θ2 ) = = n2 cosθ1 + n1 cosθ2 tan(θ1 + θ2 )
2n1 cos θ1 2 cos θ1 sinθ 2 = = n2 cos θ1 + n1 cos θ 2 sin(θ1 +θ 2) cos(θ1 −θ 2)
8
2、Fresnel公式－p波 Fresnel公式－ 公式
1、基本关系
e z × ( E0i + E0 r ) = e z × E0t e z × ( H 0i + H 0 r ) = e z × H 0t
H 0ip + H 0 rp＝H t 0 p E0ip cos θi − E0 rp cos θ r＝Et 0 p cos θ t
n2 θ c = arcsin n1
当 θ1≥θc时， 没有折射光， 入射光全部返回 时 没有折射光， 介质1，这个现象为全反射。 介质 ，这个现象为全反射。
16
4、全反射 (1) 定义
当透射波传播方向和法线夹角等于90度时发生的物理现 当透射波传播方向和法线夹角等于90度时发生的物理现 90 发生全反射的最小角度称为临界角( 象。发生全反射的最小角度称为临界角(θc)。
2.10光在电介质表面的反射和折射菲涅尔公式(修正版)
p s
W1'p WW11'sp W1s
Rp Rs
p s
W2 p
WW12ps W1s
cos i2
ccoossii12 cos i1
Tp
Ts
(4) 能量守恒公式：
W1'p W2 p W1p ，W1's W2s W1s
p p 1 ，s s 1
E2s均为复数 E1ss1
E1P E1'
A1P exp(i1p ), E1s
A1' exp(i1' ) E1' p
p1'
A1sEe1x'sps1(' i1s
)
E1' p E2
A1' p exp(i1' p ), A2 exp(i2 )
E1's
A1's
（2）当 i1 iB 时，i1 i2 900
rp
tan( i1 tan( i1
i2 ) i2 )
tan(i1 i2) 0 ，tan(i1 i2 ) 0
rp 0 ，是负的实数
rp rp rp exp(i )
'p(out) ，有相位突变 p(out) 的相位突变如图所示
Rp
cos i2 cos i1
TP
1
，Rs
cos i2 cos i1
Ts
1
rp
2 n2 cos i2 n1 cos i1
tp
2
1
，rs
2 n2 cos i2 n1 cos i1
菲涅尔反射折射公式
菲涅尔反射折射公式菲涅尔反射折射公式啊，这可是物理学中相当重要的一部分内容呢！咱先来说说啥是菲涅尔反射折射公式。
简单来讲，它就是用来描述光线在不同介质界面上反射和折射时，能量分配情况的一组公式。
这就好比光线是个调皮的小孩子，在不同的“游乐场”（介质）之间穿梭时，它的行为是有规律可循的，而菲涅尔反射折射公式就是这个规律。
比如说，当一束光从空气斜射到玻璃表面时，一部分光会被反射回去，一部分光会折射进玻璃。
那到底反射多少，折射多少呢？这就得靠菲涅尔反射折射公式来算一算啦。
我还记得有一次，在给学生们讲解这个知识点的时候，发生了一件特别有趣的事儿。
那是一个阳光明媚的上午，教室里的光线特别好。
我拿着一块玻璃砖和一个激光笔，准备给学生们做个直观的实验。
我把激光笔的光斜着照在玻璃砖上，然后让学生们观察反射光和折射光的情况。
可是，当我打开激光笔的时候，那束光居然没按照我预想的那样照在玻璃砖上，而是照到了旁边的墙上！全班同学都哄堂大笑，我也有点不好意思。
不过我马上调整了一下，重新让光准确地照在了玻璃砖上。
同学们认真地观察着，眼睛里充满了好奇和探索的欲望。
菲涅尔反射折射公式中的一些参数，像入射角、折射角，还有介质的折射率，它们相互作用，决定了光线的行为。
折射率这个概念也挺有意思，不同的介质有不同的折射率，就像不同的人有不同的性格一样。
比如水的折射率和玻璃的折射率就不一样，所以光在进入水和进入玻璃时的表现也不同。
在实际应用中，菲涅尔反射折射公式可有着大用处呢！比如说在光学仪器的设计中，像照相机的镜头、望远镜的镜片，都得考虑光线的反射和折射，这时候菲涅尔反射折射公式就能派上用场，帮助工程师们设计出更好的产品。
还有在我们日常生活里，你有没有注意过，有时候从水面上看水底的东西，会觉得位置比实际的浅？这其实就是因为光的折射，而菲涅尔反射折射公式就可以解释这个现象。
总之啊，菲涅尔反射折射公式虽然看起来有点复杂，但它其实就像一把钥匙，能帮我们打开了解光的行为的神秘大门。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
ki sini kr sin r ki sini kt sin t
( ki k r ) r 0 ( ki k t ) r 0
(123) (124)
n1 n2 O
kr ki kt
r
B
分界面
(121) (122)
i
t
A C
2.1 反射定律和折射定律 又因为 k n / c ，可将上二式改写为
H ip cos1 H rp cos1 H tp cos 2 (132)
利用
H E ，上式变为
(Eis Ers )n1cos1 Ets n2 cos 2 (133)
3. 菲涅耳公式 再利用折射定律，并由（131）式和（133）式消去 Ets，经整理可得
Ers sin ( 2 1 ) Eis sin ( 2 1 )
sin (1 2 ) rs =sin (1 2 )
(134)
(Eis Ers )n1cos1 Ets n2 cos 2 (133)
3. 菲涅耳公式 利用类似方法，可以推出 p 分量的反射系数和透射系 数表示式， 这就是著名的菲涅耳公式：
O
kr
2
Ers k t
1.s 分量和 p 分量
E p1
H s1
z
1 Hs
E p2 H s2
y
o
E p1
x
2. 反射系数和透射系数 假设介质中的电场矢量为
El E0l e－i(l t－kl r ) l i, r, t ( 127)
其 s 分量和 p 分量表示式为
Elm E0lm e－i(l t－kl r ) m s, p （ 128）
2. 反射系数和透射系数 则定义 s 分量、p 分量的反射系数、透射系数分别为
E0 rm rm E0im E0tm tm E0im
(129) (130)
Elm E0lm e－i(l t－kl r )
m s, p
（ 128）
3. 菲涅耳公式 假设界面上的入射光、反射光和折射光同相位, 根据 电磁场的边界条件及 s 分量、P 分量的正方向规定， 可得 Eis Ers Ets (131) 和
1 2
i r
O
kr
x
界面
t kt
2.1 反射定律和折射定律 r 是界面上任意点的矢径，在上图所示的坐标情况 下，有
r ix jy
z ki n12源自i rOkr
x
界面
t kt
2.1 反射定律和折射定律 根据电磁场的边界条件，可得
i r t
( ki k r ) r 0 ( ki k t ) r 0 (120) (121) (122)
kr
n1 n2 kt O ki 分界面
r
B
i t
A C
1.s 分量和 p 分量 通常把垂直于入射面振动的分量叫做 s 分量，把平 行于入射面振动的分量叫做 p 分量。为讨论方便起 见，规定 s 分量和 p 分量的正方向如图所示。
Erp Ers k i n1 n2 Erp Ers Erp
1 2
Eis Ers Ets
(131)
(Eis Ers )n1cos1 Ets n2 cos 2 (133)
3. 菲涅耳公式 将 （128）式代入上式，利用（121）式关系，并根据 反射系数定义，得到
sin (1 2 ) rs =sin (1 2 )
Elm E0lm e－i(l t－kl r )
代入边值关系 n Ei Er n Et ，该式总是成立，故
i r t
( ki k r ) r 0 ( ki k t ) r 0 (120) (121) (122)
2.1 反射定律和折射定律 进一步，根据图所示的几何关系，可得可由（121） 式和（122）式得到
Ers sin ( 2 1 ) Eis sin ( 2 1 )
(ki kr ) r 0 (121)
(134)
m s, p
（ 128）
E0 rm rm E0 im
(129)
3. 菲涅耳公式 由 （134）式和（133）式消去 Ers，经运算整理得
2n1 cos 1 ts =n1 cos 1 n2 cos 2 (135)
ni sini nr sin r ni sini nt sin t
(125) (126)
这就是介质界面上的反射定律和折射定律，折射定 律又称为斯涅耳（Snell）定律。
2. 2 菲涅耳公式 (Fresnel formula ) 光的电磁理论除了给出描述光在界面上传播方向的 反射定律和折射定律外，还给出入射光、反射光和 折射光之间的振幅、相位关系。
2.1 反射定律和折射定律 (Reflection law and refraction
law)
现假设二介质为均匀、透明、各向同性，分界面为 无穷大的平面，入射、反射和折射光均为平面光波, 其电场表示式为
El E0l e－i (l t－kl r ) l i, r, t (119)
ki z n
①入射光、反射光和折射光具有相同的频率； ②入射光、反射光和折射光均在入射面内，ki、kr 和 kt 波矢关系如图所示。
反射定律和折射定律（三种光传播方向的关系）
El E0l e－i (l t－kl r ) l i, r, t (119)
Ei Ai exp i ki r i t Er Ar exp i k r r r t Et At exp i k t r t t
光波在介质界面上的反射和折射 (The reflection and refraction of light wave in the interface of medium )
由光的电磁理论可知，光在介质界面上的反射和折 射，实质上是光与介质相互作用的结果，因而进行 一般的理论分析非常复杂。在这里，采用简化的处 理方法，不考虑光与介质的微观作用，只根据麦克 斯韦方程组和电磁场的边界条件进行讨论。
( ki k r ) r 0 ( ki k t ) r 0
(123) (124)
n1 n2 O
kr ki kt
r
B
分界面
(121) (122)
i
t
A C
2.1 反射定律和折射定律 又因为 k n / c ，可将上二式改写为
H ip cos1 H rp cos1 H tp cos 2 (132)
利用
H E ，上式变为
(Eis Ers )n1cos1 Ets n2 cos 2 (133)
3. 菲涅耳公式 再利用折射定律，并由（131）式和（133）式消去 Ets，经整理可得
Ers sin ( 2 1 ) Eis sin ( 2 1 )
sin (1 2 ) rs =sin (1 2 )
(134)
(Eis Ers )n1cos1 Ets n2 cos 2 (133)
3. 菲涅耳公式 利用类似方法，可以推出 p 分量的反射系数和透射系 数表示式， 这就是著名的菲涅耳公式：
O
kr
2
Ers k t
1.s 分量和 p 分量
E p1
H s1
z
1 Hs
E p2 H s2
y
o
E p1
x
2. 反射系数和透射系数 假设介质中的电场矢量为
El E0l e－i(l t－kl r ) l i, r, t ( 127)
其 s 分量和 p 分量表示式为
Elm E0lm e－i(l t－kl r ) m s, p （ 128）
2. 反射系数和透射系数 则定义 s 分量、p 分量的反射系数、透射系数分别为
E0 rm rm E0im E0tm tm E0im
(129) (130)
Elm E0lm e－i(l t－kl r )
m s, p
（ 128）
3. 菲涅耳公式 假设界面上的入射光、反射光和折射光同相位, 根据 电磁场的边界条件及 s 分量、P 分量的正方向规定， 可得 Eis Ers Ets (131) 和
1 2
i r
O
kr
x
界面
t kt
2.1 反射定律和折射定律 r 是界面上任意点的矢径，在上图所示的坐标情况 下，有
r ix jy
z ki n12源自i rOkr
x
界面
t kt
2.1 反射定律和折射定律 根据电磁场的边界条件，可得
i r t
( ki k r ) r 0 ( ki k t ) r 0 (120) (121) (122)
kr
n1 n2 kt O ki 分界面
r
B
i t
A C
1.s 分量和 p 分量 通常把垂直于入射面振动的分量叫做 s 分量，把平 行于入射面振动的分量叫做 p 分量。为讨论方便起 见，规定 s 分量和 p 分量的正方向如图所示。
Erp Ers k i n1 n2 Erp Ers Erp
1 2
Eis Ers Ets
(131)
(Eis Ers )n1cos1 Ets n2 cos 2 (133)
3. 菲涅耳公式 将 （128）式代入上式，利用（121）式关系，并根据 反射系数定义，得到
sin (1 2 ) rs =sin (1 2 )
Elm E0lm e－i(l t－kl r )
代入边值关系 n Ei Er n Et ，该式总是成立，故
i r t
( ki k r ) r 0 ( ki k t ) r 0 (120) (121) (122)
2.1 反射定律和折射定律 进一步，根据图所示的几何关系，可得可由（121） 式和（122）式得到
Ers sin ( 2 1 ) Eis sin ( 2 1 )
(ki kr ) r 0 (121)
(134)
m s, p
（ 128）
E0 rm rm E0 im
(129)
3. 菲涅耳公式 由 （134）式和（133）式消去 Ers，经运算整理得
2n1 cos 1 ts =n1 cos 1 n2 cos 2 (135)
ni sini nr sin r ni sini nt sin t
(125) (126)
这就是介质界面上的反射定律和折射定律，折射定 律又称为斯涅耳（Snell）定律。
2. 2 菲涅耳公式 (Fresnel formula ) 光的电磁理论除了给出描述光在界面上传播方向的 反射定律和折射定律外，还给出入射光、反射光和 折射光之间的振幅、相位关系。
2.1 反射定律和折射定律 (Reflection law and refraction
law)
现假设二介质为均匀、透明、各向同性，分界面为 无穷大的平面，入射、反射和折射光均为平面光波, 其电场表示式为
El E0l e－i (l t－kl r ) l i, r, t (119)
ki z n
①入射光、反射光和折射光具有相同的频率； ②入射光、反射光和折射光均在入射面内，ki、kr 和 kt 波矢关系如图所示。
反射定律和折射定律（三种光传播方向的关系）
El E0l e－i (l t－kl r ) l i, r, t (119)
Ei Ai exp i ki r i t Er Ar exp i k r r r t Et At exp i k t r t t
光波在介质界面上的反射和折射 (The reflection and refraction of light wave in the interface of medium )
由光的电磁理论可知，光在介质界面上的反射和折 射，实质上是光与介质相互作用的结果，因而进行 一般的理论分析非常复杂。在这里，采用简化的处 理方法，不考虑光与介质的微观作用，只根据麦克 斯韦方程组和电磁场的边界条件进行讨论。