第十二章 非正弦周期电流电路和信号的频谱
合集下载
谐波计算
§12 –3 3
有效值、 有效值、平均值和平均功率
前已指出，任一周期电流i 有效值I 前已指出，任一周期电流i的有效值I已经定义
1 T 2 I= i dt ∫0 T
•当然可以用非正弦周期函数直接进行上述定义的 当然可以用非正弦周期函数直接进行上述定义的 积分求有效值。 积分求有效值。这里主要是寻找有效值和各次谐 波有效值之间的关系。 波有效值之间的关系。
第十二章 非正弦周期电流电路和信号的 频谱
§12 –1 §12 –2 §12 –3 §12 –4 非正弦周期信号 周期函数分解为傅利叶级数 有效值、 有效值、平均值和平均功率 非正弦周期电流电路的计算
§12 –2 周期函数分解为傅利叶级数 2
周期电流、电压、 周期电流、电压、信号等都可以用一个周期 函数表示， 函数表示，即：
§12 –1 1
非正弦周期信号
图（a）脉冲波形
图（b）方波电压
图
12－ 12－1
非正弦周期电流、 非正弦周期电流、电压波形
§12 –1 1
非正弦周期信号
图（c） 锯齿波 图 12－ 12－1
图（d）磁化电流
非正弦周期电流、 非正弦周期电流、电压波形
§12 –1 1
非正弦周期信号
图（e）半波整流波形 图 12－ 12－1 非正弦周期电流、 非正弦周期电流、电压波形
f (t ) = f (t + kT)
式中， 为周期函数 为周期函数f 的周期。 式中，T为周期函数f（t）的周期。 k＝0，1，2，… ＝
§12 –2 周期函数分解为傅利叶级数 2
如果给定的周期函数满足狄里赫利条件， 如果给定的周期函数满足狄里赫利条件，它就能 展开成一个收敛的傅立叶级数， 展开成一个收敛的傅立叶级数，即
电子技术(电工学Ⅱ)(第3版)课件：非正弦周期电流电路
返回主目录
5 非正弦周期电流电路
二、教学要求： 1. 通过学习，理解用傅里叶级数将非正弦周 期信号分解为谐波的方法 ； 2. 理解和掌握非正弦周期电流电路中的有效 值、平均值和平均功率的计算 ； 3.了解线性电路在非正弦激励下的计算方法。
返回主目录
5.1非正弦周期量的分解
非正弦周期信号
u
Um
u
u
2 2
5.2.2 平均值 非正弦周期电流、电压的平均值分别为
I av
1 T
T
idt
0
U av
1 T
T
udt
0
返回主目录
5.2效非值正、弦平周均期值电和流平电均路功中率的有 5.2.3 非正弦周期电流电路的平均功率 设某无源二端网络端口处的电压、电流取关联的参 考方向，并设其电压、电流为：
u U0 Ukm sinkt ku k 1
例5-2设二端网络的端口电压、电流为关联的参考方 向，已知：
u 10 141.4sint 50 sin3t 60V
i sin t 700 0.3sin 3t 600 A
求二端网络的平均功率P。
解： P U 0 I 0 U1I1 cos1 U 3 I3 cos3
U0I0
返回主目录
5.3线性电路在非正弦激 励下的计算
例5-3如图所示电路，已知R=100Ω，C=1μF。激励源
uS为矩形波。已知Um=11V，T=1mS，求输出电压 uO 。
11
0
0.5
1
t ms
返回主目录
5.3线性电路在非正弦激 励下的计算
解：由已知条件可得基波角频率
1
2
T
1
2
10
3
5 非正弦周期电流电路
二、教学要求： 1. 通过学习，理解用傅里叶级数将非正弦周 期信号分解为谐波的方法 ； 2. 理解和掌握非正弦周期电流电路中的有效 值、平均值和平均功率的计算 ； 3.了解线性电路在非正弦激励下的计算方法。
返回主目录
5.1非正弦周期量的分解
非正弦周期信号
u
Um
u
u
2 2
5.2.2 平均值 非正弦周期电流、电压的平均值分别为
I av
1 T
T
idt
0
U av
1 T
T
udt
0
返回主目录
5.2效非值正、弦平周均期值电和流平电均路功中率的有 5.2.3 非正弦周期电流电路的平均功率 设某无源二端网络端口处的电压、电流取关联的参 考方向，并设其电压、电流为：
u U0 Ukm sinkt ku k 1
例5-2设二端网络的端口电压、电流为关联的参考方 向，已知：
u 10 141.4sint 50 sin3t 60V
i sin t 700 0.3sin 3t 600 A
求二端网络的平均功率P。
解： P U 0 I 0 U1I1 cos1 U 3 I3 cos3
U0I0
返回主目录
5.3线性电路在非正弦激 励下的计算
例5-3如图所示电路，已知R=100Ω，C=1μF。激励源
uS为矩形波。已知Um=11V，T=1mS，求输出电压 uO 。
11
0
0.5
1
t ms
返回主目录
5.3线性电路在非正弦激 励下的计算
解：由已知条件可得基波角频率
1
2
T
1
2
10
3
非正弦周期信号的频谱
频谱分析在通信、电力、自动控制等领域 都有广泛的应用，其分析结果可以为相关 领域的发展提供支持和指导。
02
非正弦周期信号的基本概念
非正弦周期信号的定义
01
非正弦周期信号是指在一个周期 内，信号的波形不是正弦波形的 周期信号。
02
与正弦周期信号相比，非正弦周 期信号的波形更加复杂，包含多 种频率成分。
05
非正弦周期信号频谱分析的应 用
在通信领域的应用
调制与解调
在通信系统中，非正弦周期信号 常被用作调制信号，通过频谱分 析可以了解信号的频率成分，进
而实现信号的调制与解调。
信道特性分析
通过分析信道对非正弦周期信号的 频谱影响，可以评估信道的传输特 性，为信道均衡和信号恢复提供依 据。
干扰识别与抑制
高精度算法
02
发展更高精度的频谱分析算法，以应对复杂和微弱信号的挑战，
提高分析的灵敏度和分辨率。
多域联合分析
03
结合时域、频域和其他变换域的分析方法，提供更全面、深入
的信号特征提取和理解。
对未来技术的展望
实时分析技术
开发能够实时处理和分析非正弦周期信号的技术，以满足实时监 测和控制的需求。
自适应分析技术
频谱的奇对称性
如果非正弦周期信号的波形具有奇对称性（即波形关于原 点对称），则其频谱具有奇对称性。在这种情况下，正负 频率分量的幅度相等，相位相同。
频谱的非对称性
对于不具有偶对称性或奇对称性的非正弦周期信号，其频 谱可能呈现出非对称性。这意味着正负频率分量的幅度和 相位关系可能不遵循简单的对称规律。
在通信系统中，干扰信号往往具有 特定的频谱特征。通过频谱分析， 可以识别干扰信号并采取相应的抑 制措施。
非正弦周期电流的电路.pptx
k p
第39页/共46页
一、非正弦周期函数的平均值
若 u(wt) = U0 + U km sin(kwt + k ) k =1
正弦量的平均值为0
则其平均值为： (直流分量)
U AV
=
1
2
2
0 u(wt)dwt = U0
第40页/共46页
二、非正弦周期函数的有效值
若 u(wt) = U0 + U km sin(kwt + k ) k =1
is3
=
100 sin 3
3106 t
μA
Z (3w1) = 374 .5 89.19
U 3 = IS 3 Z (3w1)
= 33.3 10 6 374 .5 89.19 2
= 12.47 89.2 mV 2
第25页/共46页
4. 五次谐波 作用
20Ω
R
is3
C L u3
is5
直流分量+基波+三次谐波
第10页/共46页
三次谐波
频谱图
时域
U
Um
T
t
4U m
=U0
U0
3
w 3w
频域
U0
5w
5w
U = 4Um (sinwt + 1 sin 3wt + 1 sin 5wt +)
3
5
时域 周期性函数
第11页/共46页
频域 离散谱线
§5.3 非正弦周期交流电路的分析 和计算 要点
f (wt) = A0 + Bkm sin kwt + Ckm cos kwt
k =1
k =1
第39页/共46页
一、非正弦周期函数的平均值
若 u(wt) = U0 + U km sin(kwt + k ) k =1
正弦量的平均值为0
则其平均值为： (直流分量)
U AV
=
1
2
2
0 u(wt)dwt = U0
第40页/共46页
二、非正弦周期函数的有效值
若 u(wt) = U0 + U km sin(kwt + k ) k =1
is3
=
100 sin 3
3106 t
μA
Z (3w1) = 374 .5 89.19
U 3 = IS 3 Z (3w1)
= 33.3 10 6 374 .5 89.19 2
= 12.47 89.2 mV 2
第25页/共46页
4. 五次谐波 作用
20Ω
R
is3
C L u3
is5
直流分量+基波+三次谐波
第10页/共46页
三次谐波
频谱图
时域
U
Um
T
t
4U m
=U0
U0
3
w 3w
频域
U0
5w
5w
U = 4Um (sinwt + 1 sin 3wt + 1 sin 5wt +)
3
5
时域 周期性函数
第11页/共46页
频域 离散谱线
§5.3 非正弦周期交流电路的分析 和计算 要点
f (wt) = A0 + Bkm sin kwt + Ckm cos kwt
k =1
k =1
非正弦周期电流电路和信号的频谱
S UI
§13－4 非正弦周期电流电路的计算
① 把给定的非正弦周期电压或电流分解为傅里叶级数，高 次谐波取到哪一项，要根据所需准确度的高低而定；
② 分别求出电源电压或电流的恒定分量及各次谐波分量单
独作用时的响应。a. 恒定分量（直流）求解，电容看作开路， 电感看作短路；b. 各次谐波分量用相量法进行求解，但须注意 感抗、容抗与频率有关； ③ 应用叠加定理，把步骤 ② 所计算出的结果化为时域表达 式后进行相加，最终响应是用时间函数表示的。 例13－2：下图所示电路中， 输入电源为 uS [10 141.4 cos(1t )
3. 非正弦周期电流电路的计算和平均功率；
4. 谐波分析法。
§13-1 非正弦周期信号
实际的交流发电机发出的电压波形或多或少有些差别，严格 来讲是非正弦的。如果电路存在非线性元件，即使电流电压是正 弦形，电路中也会产生非正弦电流。 非正弦电流可分为周期与非周期两种。
非正弦周期电压、电流或信号作用下线性电路的分析和计算
U0 I 0 U1I1 cos1 U 2 I 2 cos2 U k I k cosk
其中 U k U km , I k I km , k uk ik , k 1, 2 , 2 2
平均功率等于恒定分量构成的功率和各次谐波平均功率的 代数和。 (3) 非正弦周期电流电路的视在功率：
47.13cos(31t ) 28.28cos(51t ) 20.20cos(71t ) 15.7 cos(91t ) ] V
R 3 , 1 9.45 , 求电流 i 和电阻吸收的平均功率。 1C
解：电流相量的一般表达式, U Sm k I m k R j 1 k1C
第十二章 非正弦周期电流电路
由傅立叶级数演变出一种从时间域到频率域的变换——傅立叶 变换，是信号分析与处理的极其重要的数学工具。通过傅立叶变 换，可以将随时间变化的函数（信号）变换为幅值随频率变化的 信号，可以方便地分析不同频率下信号的特点和贡献幅值大小。
前边已经讲到过一种变换——相量，是将正弦函数变换到复 频域的相量的一种数学变换。再后边还要讲到拉普拉斯变换， 也是一种数学上的变换，是专门解决动态电路问题的，拉普拉 斯变换可以将一个高阶微分方程变换为一个代数方程，可以避 免求解微分方程的困难。
4Em
3
频率为5ω1的5次谐波成分幅值为：
4Em
5
2019/5/30
15
§12-3有效值、平均值和平均功率
一、有效值
定义：非正弦周期电流 i(t)的有效值定义为： I 1 T i2 t dt
T0 如果将i(t)的傅立叶级数展开为如下表达式：
f t I0 I1m cost 1 I2m cos2t 2
代替原函数，但工程上只要达到要求的精度，取前若干项也就
2019/5/30
7
可以了。
2、傅氏级数另一种表达式：
将 an cos nt bn sin nt 合并（进行和差化积）可得：
f t fT t A0 A1m cost 1 A2m cos2t 2
bk
4kEm。所以可得：
f
t
4Em
sin 1t
1 3
s
in
31t
1 5
sin51t
若只取前3项，合成的波形如下图(a) ：
2019/5/30
13
若取到前5项， 即取到9次谐波， 合 Nhomakorabea的波形如 下图(b)：
第十二章 非正弦周期电流电路
IS 0
is1
is3
华东理工大学 上 页 下
页
§12-3 有效值、平均值和平均功率
一. 有效值
根据周期量有效值的定义, 为其方均根值:
I
1 T
0
T
[it ] dt U
2
1 T
0
T
[u t ]2 dt
it I 0 I km cos(k1t k )
k 1
P U 0 I 0 U k I k cos k
k 1
（三角函数的正交性）
U 0 I 0 U 1 I1 cos1 U 2 I 2 cos 2 U k I k cos k
Um Im 式中 : U k , Ik , k uk ik , k 1,2, 华东理工大学 2 2
0
ui
t
+ uo
③非正弦激励下的线性电路
0
－
+
0
t
ui
t
uo
0
t
页
－ 华东理工大学 上 页 下
§12-2 周期函数分解为傅里叶级数 (谐波分析) 一. 数学分析
设非正弦周期电流i(t)=i(t+T) ,当满足狄里赫利条件 ( ① i(t)在一周期内连续or有有限多个第一类间断点; ② i(t)在一周期内有有限多个极大值与极小值 )时, 可展成收敛的傅里叶级数：
I av
1 T i dt 0 T
例：正弦电流的平均值 为 1 T 2 I av 0 I m cost dt I M 0.898 I M 0.637 I T 恒定分量（直流分量） 磁电系仪表：
电磁系仪表： 全波整流仪表：
is1
is3
华东理工大学 上 页 下
页
§12-3 有效值、平均值和平均功率
一. 有效值
根据周期量有效值的定义, 为其方均根值:
I
1 T
0
T
[it ] dt U
2
1 T
0
T
[u t ]2 dt
it I 0 I km cos(k1t k )
k 1
P U 0 I 0 U k I k cos k
k 1
（三角函数的正交性）
U 0 I 0 U 1 I1 cos1 U 2 I 2 cos 2 U k I k cos k
Um Im 式中 : U k , Ik , k uk ik , k 1,2, 华东理工大学 2 2
0
ui
t
+ uo
③非正弦激励下的线性电路
0
－
+
0
t
ui
t
uo
0
t
页
－ 华东理工大学 上 页 下
§12-2 周期函数分解为傅里叶级数 (谐波分析) 一. 数学分析
设非正弦周期电流i(t)=i(t+T) ,当满足狄里赫利条件 ( ① i(t)在一周期内连续or有有限多个第一类间断点; ② i(t)在一周期内有有限多个极大值与极小值 )时, 可展成收敛的傅里叶级数：
I av
1 T i dt 0 T
例：正弦电流的平均值 为 1 T 2 I av 0 I m cost dt I M 0.898 I M 0.637 I T 恒定分量（直流分量） 磁电系仪表：
电磁系仪表： 全波整流仪表：
12.非正弦周期电流电路和信号的频谱
（2）分别求出电源电压或电流的恒定分量及各次谐波分量 单独作用时的响应。 对恒定分量（ω=0），求解时把电容（C）看作开路，
即：1/ωC = ；电感（L）看作短路，即：ωL=0。
对各次谐波分量可以用相量法求解，但要注意感抗、容 抗与频率的关系，即：
X Lk
k1 L，X Ck
1
k 1C
(3)并把计算结果转换为时域形式;
一．有效值 任一周期电流 i 的有效值定义为：
I
1 T
T
0
i 2dt
设一非正弦周期电流 i 可以分解为傅里叶级数：
i I0 Ikm cos(k1t k )
k 1
代入有效值公式，则得此电流的有效值为：
I
1 T
T
0
[
I0
Ikm
k 1
cos(k1t
k
)]2 dt
上式中 i 的展开式平方后将含有下列各项：
(4)应用叠加定理，把步骤（3）计算出的结果进 行叠加，求得所需响应。
注意：将表示不同频率正弦电流相量或电压相量 直接相加是没有意义的。
二．举例
i
R
+
例12-2 图示电路中,
us
C
R 3, 1 9.45,输 入 电 源 为: 1C
us 10 141.40cos(1 t ) 47.13cos(31t ) 28.28cos(51t ) 20.20cos(71t) 15.71cos(91t) V
k 1
还可以写成另一种形式:
f (t ) A0 A1m cos(1t 1 ) A2m cos(21t 21 )
Akm cos(k1t k )
A0 Akm cos(k1t k )
k 1
即：1/ωC = ；电感（L）看作短路，即：ωL=0。
对各次谐波分量可以用相量法求解，但要注意感抗、容 抗与频率的关系，即：
X Lk
k1 L，X Ck
1
k 1C
(3)并把计算结果转换为时域形式;
一．有效值 任一周期电流 i 的有效值定义为：
I
1 T
T
0
i 2dt
设一非正弦周期电流 i 可以分解为傅里叶级数：
i I0 Ikm cos(k1t k )
k 1
代入有效值公式，则得此电流的有效值为：
I
1 T
T
0
[
I0
Ikm
k 1
cos(k1t
k
)]2 dt
上式中 i 的展开式平方后将含有下列各项：
(4)应用叠加定理，把步骤（3）计算出的结果进 行叠加，求得所需响应。
注意：将表示不同频率正弦电流相量或电压相量 直接相加是没有意义的。
二．举例
i
R
+
例12-2 图示电路中,
us
C
R 3, 1 9.45,输 入 电 源 为: 1C
us 10 141.40cos(1 t ) 47.13cos(31t ) 28.28cos(51t ) 20.20cos(71t) 15.71cos(91t) V
k 1
还可以写成另一种形式:
f (t ) A0 A1m cos(1t 1 ) A2m cos(21t 21 )
Akm cos(k1t k )
A0 Akm cos(k1t k )
k 1
非正弦周期信号
在计算每个正弦激励单独作用引起的电压和电流时， 仍然可以使用相量法先计算出电压电流相量，然后得到 电压电流的瞬时值uk(t)和ik(t)。
2021/6/16
24
例10-27 图(a)所示电路中，已知
电压源电压 u S (t)2c0o 1st0 (1 0 )0 V 电流源电流 iS (t)2co 2s0 t (5 0)0 A
2021/6/16
2
12.1 非正弦周期信号 学习目标：掌握谐波的概念，理解非正弦周期信号与
各次谐波之间的关系。
12.1.1 非正弦周期信号的产生 1.电路中含有非线性元件（如二极管半波整流电路）
输入正弦波
D R
输出半波整流
2021/6/16
3
2.实验室中的信号发生器或示波器中的水平扫描电压
示波器
奇谐波函数：特点是波形的后半周与前半周具有镜像 对称性，也称为奇次对称性，奇谐波函 数的傅里叶级数表达式中只含有奇次谐 波。
偶谐波函数：特点是波形的前、后半周变化相同。也 称为偶次对称性，偶谐波函数的傅里叶 级数表达式中一般只包含偶次谐波。
零次谐波： 非正弦周期波中的直流分量称为零次谐 波。偶次谐波中一般包含零次谐波。
cos35cos15示三种非正弦周期信号的傅里叶级数分别例1028图1056a所示幅度a10v周期t628ms周期方波电压信号ucos20cos2a5v直流电压源作用时由于0在直流稳态条件下电感相当于短路所以rads根据相应的相量模型可以计算出相应的相量电压分量45183201010104510cosrads根据相应的相量模型可以计算出相应的相量电压分量7110cos6717147520301010rads根据相应的相量模型计算出相应的相量电压分量7810cos2578176610107810cos257110cos674510cos注意
2021/6/16
24
例10-27 图(a)所示电路中，已知
电压源电压 u S (t)2c0o 1st0 (1 0 )0 V 电流源电流 iS (t)2co 2s0 t (5 0)0 A
2021/6/16
2
12.1 非正弦周期信号 学习目标：掌握谐波的概念，理解非正弦周期信号与
各次谐波之间的关系。
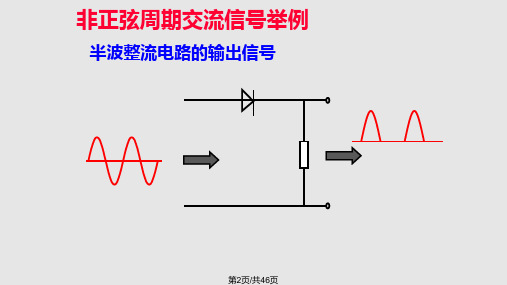
12.1.1 非正弦周期信号的产生 1.电路中含有非线性元件（如二极管半波整流电路）
输入正弦波
D R
输出半波整流
2021/6/16
3
2.实验室中的信号发生器或示波器中的水平扫描电压
示波器
奇谐波函数：特点是波形的后半周与前半周具有镜像 对称性，也称为奇次对称性，奇谐波函 数的傅里叶级数表达式中只含有奇次谐 波。
偶谐波函数：特点是波形的前、后半周变化相同。也 称为偶次对称性，偶谐波函数的傅里叶 级数表达式中一般只包含偶次谐波。
零次谐波： 非正弦周期波中的直流分量称为零次谐 波。偶次谐波中一般包含零次谐波。
cos35cos15示三种非正弦周期信号的傅里叶级数分别例1028图1056a所示幅度a10v周期t628ms周期方波电压信号ucos20cos2a5v直流电压源作用时由于0在直流稳态条件下电感相当于短路所以rads根据相应的相量模型可以计算出相应的相量电压分量45183201010104510cosrads根据相应的相量模型可以计算出相应的相量电压分量7110cos6717147520301010rads根据相应的相量模型计算出相应的相量电压分量7810cos2578176610107810cos257110cos674510cos注意
第十二章 非正弦周期电流电路和信号的频谱
k
)
其中:
A
0
： 恒定分量 (直流分量)
： 一次谐波。
A 1 m cos( t 1 )
也称为基波分量。
A km cos( k 1 t k )
k 2 ,3 , 4 ,
称为高次谐波（如2次谐波、3次谐波等等）。
二、 频谱(图):
(1) 幅度频谱： (2) 相位频谱：
A km k 1
(sin t
1 3
sin 3 t )
f(t) A
O
t
O
t
f1 ( t )
f 1 (t) 4 A /
4A
sin t
f 3 ( t) A
f3 (t )
4A
(sin t
1 3
sin 3 t
1 5
sin 5 t )
O
t
O
t
f (t ) f3 (t )
电容对低频电流有抑制作用, 电感对低频电流起分流作用。
12-6
付里叶级数的指数形式
一、 付里叶级数的指数形式：
付里叶级数的指数形式：
f (t )
其中：
ck 1 T
k
cke
jk 1 t
T
f (t )e
jk 1 t
dt
0
二、 说明：
因为： 且：
A km cos( k 1 t k ) 1 2 A km e
P
k 1
U k I k cos k Leabharlann pk ok
p
k o
k
第十二章 非正弦周期电流电路和信号的频谱
PP 0 P 1P 3
I R I R I R I R 1945.3 (W )
2 0 2 1 2 3 2
17
例2 已知：R=20Ω，ωL1=0.625 Ω, ωL2=5Ω,
1/ωc=45Ω,
Us(t)=100+276cosωt+100cos(3ωt+40o)V 求:电流表读数和电压表读数以及R上消耗的平均功率
第十二章 非正弦周期电流电路和信号的频谱 $ 12-1非正弦周期信号
1、正弦周期信号：f（t）=Acos（ωt+φ）
2、非正弦周期信号：按非正弦规律作周期变动的电 源和信号
3 、非正弦周期电流电路：线性电路中若有多个不同频率
的正弦激励电源，或者线性电路中含有非正弦周期电源， 则电路进入稳态后的电流和电压响应将是非正弦周期函数， 称这种电路为非正弦周期电流电路。
22
习题：
12-3 12-5
12-6
12-9
12-10
12-6 R=10,L=0.0318,C=318.9uF,θ3= -99.420，P=515.4W 12-10 A读数=9.35A,
dis U 2 M 50 cos(10t 110 0 ) 75 cos( 30t 60 0 ) dt
u -
+
R L
i I0 i1 i3 2 2 18.55 cos( t 21.8 ) o 16 2 6.4 cos(3 t 20.19 )( A)
o
2）求I、P：
I I I I
2 0 2 1
2 3
22 18.552 6.42 19.725 ( A)
19
3）3次谐波 （k 3） 100 （3） US 40O V 2
第十二章 非正弦周期电流电路和信号的频谱
帕斯瓦尔定理 P = U 0 I 0 + ∑ Pk
k =1
∞
功率叠加原理（只限于非正弦） 功率叠加原理（只限于非正弦） 同频率电压电流作用的平均功率和 因为不同频率电压电流乘积积分为0 正交）， 因为不同频率电压电流乘积积分为0（正交）， 不产生平均功率
12－ §12－4 非正弦周期电流电路 的计算
(2)利用叠加定理计算单个谐波（正弦） (2)利用叠加定理计算单个谐波（正弦）作用下的 利用叠加定理计算单个谐波 响应（相量法）； 响应（相量法）； (3)求和 求和。 (3)求和。
§12－2周期函数分解 12－ 为傅里叶级数
1 、任何周期信号f (t) = f (t + kT )可分解为一组 正交基的线性组和。 正交基的线性组和。
测 u 的直流分量 u 的平均值 刻度×1.11即可测正弦有效值 刻度×1.11即可测正弦有效值 故万用表只能测正弦波有效值，非正弦波不可用 故万用表只能测正弦波有效值，非正弦波不可用。
4、平均功率
∞ 1 T 1 T P = ∫ pdt = ∫ uidt = U 0 I 0 + ∑ I kU k cos k T 0 T 0 k =1
由时域可得到的信号信息： 由时域可得到的信号信息： 波形形状：平缓、陡峭、突变等； ① 波形形状：平缓、陡峭、突变等； 变化快慢：周期（基频率），持续时间； ），持续时间 ② 变化快慢：周期（基频率），持续时间； 对称关系： 偶等。 ③ 对称关系：奇、偶等。
）：每个频率点是一个 ) 频域表示）： c 频谱 Akm ( kω 1 （频域表示）：每个频率点是一个
另外还有峰值(最大值),峰峰值 另外还有峰值(最大值),峰峰值V p p (波峰和波谷的差) ), 波峰和波谷的差)
非正弦周期电流电路
单元四非正弦周期电流电路一、非正弦周期信号二、非正弦周期量的有效值、平均值及三、非正弦周期电流电路的平均功率四、非正弦周期电流电路的计算一、非正弦周期信号1.非正弦周期信号：随时间周期性地按非正弦规律变化的信号。
2.非正弦周期函数的分解傅里叶级数：若周期为T ，角频率ω=2π/T 的周期函数，满足狄里赫利条件，则的可展开为∑∞=++=++++++++=1022110)sin cos ( sin cos 2sin 2cos sin cos )(k k k k k t k b t k a a t k b t k a t b t a t b t a a t f ωωωωωωωω ∵)t k (sin A sin cos k k ψ+=+ωωωt k b t k a k k ∴+++++=)2sin()sin()(22m 11m 0θωθωt A t A A t f 直流分量基波二次谐波∑∞=++=10)sin(k k k t k A A ψω（K=1、2、3、4…）几种非正弦周期函数的傅里叶级数名称波形傅里叶级数有效值平均值梯形波f (t) =απmA4(sinαsinωt +91sin3αsin3ωt+251sin5αsin5ωt +…+2k1sinkαsinkωt +…)（式中α =Td2π，k为奇数）A mπα-341A m(1－πα)三角波f (t) =2mA8π(sinωt－91sin3ωt+251sin5ωt +…+221kk)1(--sinkωt +…)（k为奇数）3A m2A m名称波形傅里叶级数有效值平均值矩形波f (t) =πmA4(sinωt+31sin3ωt+51sin5ωt +k1sinkωt +…)（k为奇数）A m A m半波整流波f (t) =πmA2(21+4πcosωt+311⨯cos2ωt －531⨯cos4ωt+751⨯cos6ωt －…)2A mπmA全波整流波f (t) =πmA4(21+311⨯cos2ωt－531⨯cos4ωt +751⨯cos6ωt－…)2A mπmA2名称波形傅里叶级数有效值平均值锯齿波f (t) = A m [21－π1(sinωt+21sin2ωt+31sin3ωt +…) ]3A m2A m矩形脉冲波f (t) =A m [ α+π2(sinαπcosωt+21sin2απcos2ωt+31sin3απcos3ωt +…) ]αA mαA m3.几种波形具有对称性的周期函数的傅里叶级数1. 奇函数的傅里叶级数奇函数：f (t )=－f (－t )；奇函数的波形对称于坐标系的原点。
第十二章 非正弦周期电流电路和信号的频谱
概述
非正弦周期交流信号的特点：
不是正弦波 按周期规律变化
12.1 非正弦周期信号
生产实践和科学实验中，通常会遇到按非正弦规律变动的电源和 信号。例如： 实际的交流发电机发出的电压波形； 收音机、电视机收到的信号电压或电流；
自动控制、电子计算机等技术领域中用到的脉冲信号；
电路中存在非线性元件时；
离散谱线
例：电路如图，已知 us 10cos5t (V ) , is 2 cos4t ( A) ，求 i0
+
。
1Ω
1F
us 1H -
is
i0
解：us 单独作用时电路相量 模型如图。
1 5
j1L j5
I m
+
U mS
1Ω
j
1 j j 0.2 1C 10 0o (V ) U
ωt
直流分量
基波
t
三次谐波
t
五次谐波 七次谐波
t
直流分量+基波
直流分量 基波
直流分量+基波+三次谐波
三次谐波
频谱图
U
Um
T
时域
4U m U0
频域
U0 3
t
U0 5
3
5
1 1 U (sint sin 3t sin 5t ) 3 5
时域 频域
4U m
周期性函数
0
Ckm
1
2
0
f ( t ) cos k td ( t )
f (t ) 的
求出A0、Bkm、Ckm便可得到原函数 展开式。
例 周期性方波的分解
非正弦周期信号的频谱
减小的。
2006-1-1
！
5
非正弦周期信号的频谱(5)
• 图9.7 幅值频谱和相位频谱
• 采用PSpice进行仿真，仿真用电路图如图9.8所示。其中电压源使用VPLUSE 模型，图中表格分别给出了T = 2τ、T = 4τ和T = 8τ时的参数值。
2006-1-1
！
6
非正弦周期信号的频谱(6)
• 采用瞬时仿真，其中还提供了傅立叶分析，参数设置为：Print Step = 0.01s，Final Time = 12s，Step Ceiling = 0.01；选中Enable Fourier，Center Frequency = 0.5Hz，Output Vars = V(1)。对于T = 2τ时，其仿真结果如图9.9所示。对于进行傅立叶分析，可在图9.9界面上点击 按钮，分析结果如图9.10所示。
3 j
0.4
1 j2
• 那么对其进行傅立叶反变换，得到输出电压的 t− e−3 t) ε(t)
2006-1-1
！
15
2006-1-1
！
11
傅立叶变换在电路分析中 的应用 (5)
例9.3 如图9.14所示，一个矩形脉冲v(t)，幅值V = 5，脉冲宽度τ = 2。请求其傅 立叶变换。
v(t) V
τ 2
τ 2
ωt
θ(ω)
(b)
π
−4π−3π−2π −π O π 2π 3π 4π ω
−π
图9.14 矩形脉冲
图9.15 矩形脉冲的幅值频谱
)e
jk1t
dt
2
2 T
2Ve jk1t dt 2
2V
k
sin
k1
2
2006-1-1
！
5
非正弦周期信号的频谱(5)
• 图9.7 幅值频谱和相位频谱
• 采用PSpice进行仿真，仿真用电路图如图9.8所示。其中电压源使用VPLUSE 模型，图中表格分别给出了T = 2τ、T = 4τ和T = 8τ时的参数值。
2006-1-1
！
6
非正弦周期信号的频谱(6)
• 采用瞬时仿真，其中还提供了傅立叶分析，参数设置为：Print Step = 0.01s，Final Time = 12s，Step Ceiling = 0.01；选中Enable Fourier，Center Frequency = 0.5Hz，Output Vars = V(1)。对于T = 2τ时，其仿真结果如图9.9所示。对于进行傅立叶分析，可在图9.9界面上点击 按钮，分析结果如图9.10所示。
3 j
0.4
1 j2
• 那么对其进行傅立叶反变换，得到输出电压的 t− e−3 t) ε(t)
2006-1-1
！
15
2006-1-1
！
11
傅立叶变换在电路分析中 的应用 (5)
例9.3 如图9.14所示，一个矩形脉冲v(t)，幅值V = 5，脉冲宽度τ = 2。请求其傅 立叶变换。
v(t) V
τ 2
τ 2
ωt
θ(ω)
(b)
π
−4π−3π−2π −π O π 2π 3π 4π ω
−π
图9.14 矩形脉冲
图9.15 矩形脉冲的幅值频谱
)e
jk1t
dt
2
2 T
2Ve jk1t dt 2
2V
k
sin
k1
2
电路PPT课件第12章 非正弦周期电流电路和信号的频
iS
iS
Im 2
2Im(s
in t
1s 3
in3t
Im
1s in5t )
5
T/2 T
t
代入已知数据：
Im 15μ 7A, T6.28μs
直流分量
I0
Im15 778 .5μA 22
基波最大值
I1m2Im2 3.1 1 .547 10A 0
三次谐波最大值 I3m1 3I1m33 .3A
s
inptd(t)
0
k p
2. 非正弦周期函数的有效值
若 i(t)I0 Iks ik n t(k) k1
则有效值:
I
1 T
T
0
i2td(t)
1
T
T
0
I0
k1
Ik
sinkt
k
2
d(t)
利用三角函数的正交性得：
ak
2
2
0
iS
(t)c
o
sktd(t)
2Im
1 s inkt
k
0
0
i s 的展开式为：
i S I 2 m 2 I m (sti 1 3 n s3 it n 5 1 s5 it n )
周期性方波波形分解
直流分量
t
三次谐波
t
基波
t
五次谐波 七次谐波
P U 0 I 0 U 1 I 1 c1 o U 2 I s 2 c2 o s
结论 平均功率＝直流分量的功率＋各次谐波的平均功率
ch12非正弦周期交流电路和信号的频谱
∞
Akm—ω曲线称为 的幅值频谱； 曲线称为f(t)的幅值频谱 的幅值频谱； ψk —ω曲线称为 的相位频谱。 曲线称为f(t)的相位频谱 的相位频谱。
谐波的初相位
图为一锯齿波f(t)， 例12-1 图为一锯齿波 ，试将它表示为傅立叶级 并分析其频谱。 数，并分析其频谱。 E
0 T
t
7
解： f ( t ) = E t ( 0 ≤ t ≤ T ) T 1 TE E a0 = ∫ tdt = T 0 T 2
k =1 ∞
∞
2 2 2 = I 0 + I1 + I 2 + ⋯ = I 0 + ∑ I 2 2 k k =1
16
二、平均值
非正弦周期电压或电流的平均值定义为其绝对值 的平均值。 的平均值。 1 T I av = ∫ i dt T 0 正弦电流的平均值为： 正弦电流的平均值为：
1 T I av = ∫ I m cosωt dt =0.637 I m T 0
k =1
13
周期函数为奇谐波函数， 周期函数为奇谐波函数，即f(t) = − f(t+T/2) ， 奇谐波函数 u 波形特点:关于镜象对称， 波形特点 关于镜象对称， 关于镜象对称 即任意相差半周期的函数值 大小相等，符号相反。 大小相等，符号相反。 0 a2k= b2k =0 (偶次谐波与直 偶次谐波与直 流分量为零)。 流分量为零 。 奇谐波函数 展开式为
注意： 注意： 1）测量 非正弦周期电流或电压的有效值要用电磁 非正弦周期电流或电压的有效值要用电磁 ） 系或电动系仪表， 系或电动系仪表， 2）测量非正弦周期量的平均值要用全波整流磁电 ）测量非正弦周期量的平均值要用全波整流磁电 系仪表。 系仪表。 17
相关主题
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
f(t)
Em
T/2 T
t
0
π 2π
ω1t
-Em
解: f（t）在第一个周期内的表达式为
f (t) Em f (t) Em
利用公式求系数为:
0 t T 2
T t T 2
a0
1 T
T
0
f (t )dt
0
ak
1
2
0
f (t )cos(k1t )d (1t )
1
0
Em
cos(k1t )d(1t
)
2
1C
-
us 10 141.40cos(1 t ) 47.13cos(31t ) 28.28cos(51t )
20.20cos(71t) 15.71cos(91t) V
求电流 i 和电阻吸收的平均功率P 。
解：电路中的非正弦周期电压已分解为傅立叶级数形式。
•
电流相量一般表达式为：
•
I (k)
最后按时域形式迭加为：
i 10.08 2 cos(1t 72.39) 7.66 2 cos(31t 46.4)
5.58 2 cos(51t 32.21) 4.34 2 cos(71t 24.23)
3.49 2 cos(91t 19.29) A
P P0 P1 P3 P9 669.80W
最后，把所得分量按时域形式叠加，得到电路在非正弦 周期激励下的稳态电流和电压。
这种方法称为谐波分析法。实质上是把非正弦周期电流 电路的计算化为一系列正弦电流电路的计算。
12.2 周期函数分解为傅里叶级数
一．傅氏级数
周期电流、电压、信号等都可以用一个周期函数表 示，即
f(t)=f(t+kT)
式中 T为周期函数f(t)的周期，k=0,1,2,…。
k 1
还可以写成另一种形式:
f (t ) A0 A1m cos(1t 1 ) A2m cos(21t 21 )
Akm cos(k1t k )
A0 Akm cos(k1t k )
k 1
两种形式系数之间的关系如下:
A0 a0 Akm ak2 bk2
ak Akm cos k bk Akm sin k
I av
1 T
T
0
i dt
即非正弦周期电流的平均值等于此电流绝对值的平均值。
按上式可求得正弦电流的平均值为：
I av
1 T
T
0
Im
cos(t )dt
4Im T
T
4 0
cos
(t
)dt
4Im
T
T
[sin(t )]04
0.637Im
0.898I
它相当于正弦电流经全波整流后的平均值，因为取电流的 绝对值相当于把负半周的值变为对应的正值。
cos
(
4
1t
)
V
•
设负载两端的第k次谐波为U (k ) ，用结点电压法有：
L
＋
1 1
jk1 L
R
•
jk1C U (k)
1•
U jk1L s(k)
us －
C
R
•
•
U (k)
1 R
U s(k)
jk1C
jk1 L
1
令k=0, 2, 4, •••, 并代入数据,可分别求得:
U 0 100V U ( 2) 2.5V U (4) 0.12V
例12-3 图示电路中L=5H，C=10µF，负载电阻R=2KΩ，电源us
为正弦全波整流波形，设ω1=314rad/s，Um=157V。求 负载两端电压的各谐波分量。
L +
us Um
us
CR
-
0
π 2π
ω1t
解: 将给定的 us 分解为傅立叶级数,得
us
4
157
1 2
1 3
cos
(
2
1
t
)
1 15
k
当k为偶数时: 当k为奇数时: 由此求得:
cos(kπ)=1, cos(kπ)= -1,
bk=0 bk=4Em/kπ
f
(t)
4Em
sin(1 t)
1 3
s in(31t )
1 5
sin(51t)
频谱图:
Akm
4Em
4Em
3
4Em
5
0 ω1
3ω1
5ω1
kω1
当函数为偶函数（纵轴对称）时，有 bk=0
三．滤波器
利用电感和电容元件的感抗和容抗对各次谐波的反应 不同，组成含有电感和电容的各种不同电路，将其接在输 入和输出之间，让某些所需频率分量顺利通过而抑制某些 不需要的频率分量，这种电路为滤波器。
低通滤波器：使低频电流分量顺利通过，抑制高频电流分量。 高通滤波器：使高频电流分量顺利通过，抑制低频电流分量。
k
arctan(
bk ak
)
f (t ) A0 A1m cos(1t 1 ) A2m cos(21t 21 ) Akm cos(k1t k )
A0 Akm cos(k1t k )
k 1
傅里叶级数是一个无穷三角级数。展开式中:
A0 —为周期函数f(t)的恒定分量（或直流分量）；
低通
高通
例：图示电路中，激励 u1(t) = u11(1)+u12( 2)，包含 1、 2 两个频率分量，且 1< 2 ，要求响应 u2(t) 只含 有 1 频率电压，如何实现？
+
C3
L1
u1(t) _
u2(t)
+
u1(t) _
可由下列滤波电路实现：
+ C2 R u2(t)
_
ω2
1 L1C 2
高次谐波取到哪一项为止，要根据所需准确度的高低 而定。
（2）分别求出电源电压或电流的恒定分量及各次谐波分量 单独作用时的响应。
对恒定分量（ω=0），求解时把电容（C）看作开路，
即： 1/ωC= ；电感（L）看作短路，即：ωL=0。
对各次谐波分量可以用相量法求解，但要注意感抗、容 抗与频率的关系，即：
幅度频谱：表示各谐波分量的振幅的频谱为幅度频谱。 相位频谱：把各次谐波的初相用相应线段依次排列的频谱
为相位频谱。
例
Akm
0 ω1 2ω1 3ω1 4ω1 5ω1 6ω1
kω1
由于各谐波的角频率是ω1的整数倍，所以这种频谱 是离散的，又称为线频谱。
例12-1 求图示周期性矩形信号的傅立叶级数展开式及其频谱.
并联谐振，开路
ω1
1 L1(C2 C3 )
串联谐振，短路
例：电路如图所示，已知ω=1000rad/s，C=1μF，R=1Ω，
us(t ) 12 15 2 cos(t) 16 2 cos(2t)V
在稳态时，uR(t)中不含基波，而二次谐波与电源二次谐波 电压相同，求：
(1t )
1
f (t )cos(k1t )d(1t )
bk
2 T
T
0
f (t )sin(k1t)dt
2 T
T
2 T 2
f (t )sin(k1t )dt
1
2
0
f
(t
)
sin(k1t
)d
(1t
)
1
f (t )sin(k1t )d(1t )
上述计算式中k=1, 2, 3, …
二．频谱
用长度与各次谐波振幅大小相对应的线段，按频率的高 低顺序把它们依次排列起来，所得到的图形，称为f(t)的频 谱图。
U s(k) 1
R j
k 1C
根据迭加定理，按k=0，1，2，…的顺序，依次求解如下：
k 0, 直流分量U0 10V , I0 0, P0 0
•
k 1, U s(1) 1000V
•
1000
I (1)
A 10.0872.39 A
3 j9.45
P(1)
I
2 (1)
R
305.02W
•
k 3, U s(3) 33.330V
X Lk
k1 L，X Ck
1
k 1C
(3)并把计算结果转换为时域形式;
(4)应用叠加定理，把步骤（3）计算出的结果进 行叠加，求得所需响应。
注意：将表示不同频率正弦电流相量或电压相量 直接相加是没有意义的。
二．举例
i
R
+
例12-2 图示电路中,
us
C
R 3, 1 9.45,输 入 电 源 为:
a0
ak cos(k1t ) bk sin(k1t )
k 1
上式中的系数，可由下列公式计算：
a0
1 T
T
0
f (t )dt
1 T
T
2 T 2
f (t )dt
ak
2 T
T
0
f (t )cos(k1t )dt
2 T
T
2 T 2
f (t )cos(k1t )dt
1
2
0
f
(t )cos(k1t
)d
第十二章 非正弦周期电流电路和信号的频谱
重点
1. 周期函数分解为傅立叶级数和信号的频谱; 2. 周期量的有效值、平均值； 3. 非正弦电流电路的计算和平均功率; 4. 滤波器的概念。
12.1 非正弦周期信号 12.2 周期函数分解为傅立叶级数 12.3 有效值、平均值和平均功率 12.4 非正弦周期电流电路的计算
Em
cos(k1t
)d (1t
)
2Em
0
cos(k1t )d (1t )
Em
T/2 T
t
0
π 2π
ω1t
-Em
解: f（t）在第一个周期内的表达式为
f (t) Em f (t) Em
利用公式求系数为:
0 t T 2
T t T 2
a0
1 T
T
0
f (t )dt
0
ak
1
2
0
f (t )cos(k1t )d (1t )
1
0
Em
cos(k1t )d(1t
)
2
1C
-
us 10 141.40cos(1 t ) 47.13cos(31t ) 28.28cos(51t )
20.20cos(71t) 15.71cos(91t) V
求电流 i 和电阻吸收的平均功率P 。
解：电路中的非正弦周期电压已分解为傅立叶级数形式。
•
电流相量一般表达式为：
•
I (k)
最后按时域形式迭加为：
i 10.08 2 cos(1t 72.39) 7.66 2 cos(31t 46.4)
5.58 2 cos(51t 32.21) 4.34 2 cos(71t 24.23)
3.49 2 cos(91t 19.29) A
P P0 P1 P3 P9 669.80W
最后，把所得分量按时域形式叠加，得到电路在非正弦 周期激励下的稳态电流和电压。
这种方法称为谐波分析法。实质上是把非正弦周期电流 电路的计算化为一系列正弦电流电路的计算。
12.2 周期函数分解为傅里叶级数
一．傅氏级数
周期电流、电压、信号等都可以用一个周期函数表 示，即
f(t)=f(t+kT)
式中 T为周期函数f(t)的周期，k=0,1,2,…。
k 1
还可以写成另一种形式:
f (t ) A0 A1m cos(1t 1 ) A2m cos(21t 21 )
Akm cos(k1t k )
A0 Akm cos(k1t k )
k 1
两种形式系数之间的关系如下:
A0 a0 Akm ak2 bk2
ak Akm cos k bk Akm sin k
I av
1 T
T
0
i dt
即非正弦周期电流的平均值等于此电流绝对值的平均值。
按上式可求得正弦电流的平均值为：
I av
1 T
T
0
Im
cos(t )dt
4Im T
T
4 0
cos
(t
)dt
4Im
T
T
[sin(t )]04
0.637Im
0.898I
它相当于正弦电流经全波整流后的平均值，因为取电流的 绝对值相当于把负半周的值变为对应的正值。
cos
(
4
1t
)
V
•
设负载两端的第k次谐波为U (k ) ，用结点电压法有：
L
＋
1 1
jk1 L
R
•
jk1C U (k)
1•
U jk1L s(k)
us －
C
R
•
•
U (k)
1 R
U s(k)
jk1C
jk1 L
1
令k=0, 2, 4, •••, 并代入数据,可分别求得:
U 0 100V U ( 2) 2.5V U (4) 0.12V
例12-3 图示电路中L=5H，C=10µF，负载电阻R=2KΩ，电源us
为正弦全波整流波形，设ω1=314rad/s，Um=157V。求 负载两端电压的各谐波分量。
L +
us Um
us
CR
-
0
π 2π
ω1t
解: 将给定的 us 分解为傅立叶级数,得
us
4
157
1 2
1 3
cos
(
2
1
t
)
1 15
k
当k为偶数时: 当k为奇数时: 由此求得:
cos(kπ)=1, cos(kπ)= -1,
bk=0 bk=4Em/kπ
f
(t)
4Em
sin(1 t)
1 3
s in(31t )
1 5
sin(51t)
频谱图:
Akm
4Em
4Em
3
4Em
5
0 ω1
3ω1
5ω1
kω1
当函数为偶函数（纵轴对称）时，有 bk=0
三．滤波器
利用电感和电容元件的感抗和容抗对各次谐波的反应 不同，组成含有电感和电容的各种不同电路，将其接在输 入和输出之间，让某些所需频率分量顺利通过而抑制某些 不需要的频率分量，这种电路为滤波器。
低通滤波器：使低频电流分量顺利通过，抑制高频电流分量。 高通滤波器：使高频电流分量顺利通过，抑制低频电流分量。
k
arctan(
bk ak
)
f (t ) A0 A1m cos(1t 1 ) A2m cos(21t 21 ) Akm cos(k1t k )
A0 Akm cos(k1t k )
k 1
傅里叶级数是一个无穷三角级数。展开式中:
A0 —为周期函数f(t)的恒定分量（或直流分量）；
低通
高通
例：图示电路中，激励 u1(t) = u11(1)+u12( 2)，包含 1、 2 两个频率分量，且 1< 2 ，要求响应 u2(t) 只含 有 1 频率电压，如何实现？
+
C3
L1
u1(t) _
u2(t)
+
u1(t) _
可由下列滤波电路实现：
+ C2 R u2(t)
_
ω2
1 L1C 2
高次谐波取到哪一项为止，要根据所需准确度的高低 而定。
（2）分别求出电源电压或电流的恒定分量及各次谐波分量 单独作用时的响应。
对恒定分量（ω=0），求解时把电容（C）看作开路，
即： 1/ωC= ；电感（L）看作短路，即：ωL=0。
对各次谐波分量可以用相量法求解，但要注意感抗、容 抗与频率的关系，即：
幅度频谱：表示各谐波分量的振幅的频谱为幅度频谱。 相位频谱：把各次谐波的初相用相应线段依次排列的频谱
为相位频谱。
例
Akm
0 ω1 2ω1 3ω1 4ω1 5ω1 6ω1
kω1
由于各谐波的角频率是ω1的整数倍，所以这种频谱 是离散的，又称为线频谱。
例12-1 求图示周期性矩形信号的傅立叶级数展开式及其频谱.
并联谐振，开路
ω1
1 L1(C2 C3 )
串联谐振，短路
例：电路如图所示，已知ω=1000rad/s，C=1μF，R=1Ω，
us(t ) 12 15 2 cos(t) 16 2 cos(2t)V
在稳态时，uR(t)中不含基波，而二次谐波与电源二次谐波 电压相同，求：
(1t )
1
f (t )cos(k1t )d(1t )
bk
2 T
T
0
f (t )sin(k1t)dt
2 T
T
2 T 2
f (t )sin(k1t )dt
1
2
0
f
(t
)
sin(k1t
)d
(1t
)
1
f (t )sin(k1t )d(1t )
上述计算式中k=1, 2, 3, …
二．频谱
用长度与各次谐波振幅大小相对应的线段，按频率的高 低顺序把它们依次排列起来，所得到的图形，称为f(t)的频 谱图。
U s(k) 1
R j
k 1C
根据迭加定理，按k=0，1，2，…的顺序，依次求解如下：
k 0, 直流分量U0 10V , I0 0, P0 0
•
k 1, U s(1) 1000V
•
1000
I (1)
A 10.0872.39 A
3 j9.45
P(1)
I
2 (1)
R
305.02W
•
k 3, U s(3) 33.330V
X Lk
k1 L，X Ck
1
k 1C
(3)并把计算结果转换为时域形式;
(4)应用叠加定理，把步骤（3）计算出的结果进 行叠加，求得所需响应。
注意：将表示不同频率正弦电流相量或电压相量 直接相加是没有意义的。
二．举例
i
R
+
例12-2 图示电路中,
us
C
R 3, 1 9.45,输 入 电 源 为:
a0
ak cos(k1t ) bk sin(k1t )
k 1
上式中的系数，可由下列公式计算：
a0
1 T
T
0
f (t )dt
1 T
T
2 T 2
f (t )dt
ak
2 T
T
0
f (t )cos(k1t )dt
2 T
T
2 T 2
f (t )cos(k1t )dt
1
2
0
f
(t )cos(k1t
)d
第十二章 非正弦周期电流电路和信号的频谱
重点
1. 周期函数分解为傅立叶级数和信号的频谱; 2. 周期量的有效值、平均值； 3. 非正弦电流电路的计算和平均功率; 4. 滤波器的概念。
12.1 非正弦周期信号 12.2 周期函数分解为傅立叶级数 12.3 有效值、平均值和平均功率 12.4 非正弦周期电流电路的计算
Em
cos(k1t
)d (1t
)
2Em
0
cos(k1t )d (1t )