范德瓦耳斯
§4-6 真实气体的范德瓦耳斯方程

a V
2
)( V
M M
mol
b)
M
mol
RT
对于压强不是很高(低于500大气压),温 度不是太低的实际气体,范德瓦尔斯方程是很 好的近似公式。
范德瓦尔斯方程是经验方程,各种气体的常 数a、b可由实验测量。
太原理工大学物理系
§4-6 真实气体的范德瓦耳斯方程 理想气体微观模型: 1)分子无大小 2)分子间无作用力(碰撞时除外) 1873年荷兰物理学家范德瓦耳斯对理想气体 的两个基本假设进行了修正,得出了描述真实 气体行为的范德瓦耳斯方程。 一、分子固有体积修正 把分子当作有一定体积的刚性球,分子的 活动空间减小。 太原理工大学物理系
设1mol气体的占有体积 V m
气体分子能自由活动的体积 V m b
1mol气体的状态方程
p (V m b ) RT
可以证明:b等于1mol气体固有体积的4倍。 二、分子吸引力修正 由于分子可活动的范围减小,分子和容器 壁的碰撞增加,压强就该增大。 太原理工大学物理系
分子实际作用于器壁的由实验可测的压强
p RT Vm b p in
其中
p in
a V
2 m
a 是一个与气体种类、气体温度有关的常数 三、范德瓦耳斯方程 1mol气体的范德瓦耳斯方程 a ( p 2 )( V m b ) RT Vm 太原理工大学物理系
质量为M气体的范德瓦耳斯方程
(p M M
2 2 mol
范德瓦耳斯气体相变

范德瓦耳斯气体相变范德瓦耳斯气体相变是一种物理现象,涉及到气体在特定条件下的相变过程。
下面将从几个方面详细阐述这一现象:1、范德瓦耳斯方程的提出范德瓦耳斯方程是描述气体相变的重要理论工具。
该方程考虑了分子间的相互作用,引入了范德瓦耳斯状态方程来修正理想气体方程,以更准确地描述气体的行为。
范德瓦耳斯方程能够描述气体的压缩性和热容,从而为气体相变的研究提供了基础。
2、气体相变的特征当气体受到低温或高压的影响时,气体分子间的平均距离会发生变化。
由于分子间的相互作用,气体逐渐变得不均匀,并最终发生相变。
在相变过程中,气体的性质会发生显著变化,如密度、热容和分子运动速度等。
这些特征的变化使得气体相变成为一个值得研究的物理现象。
3、范德瓦耳斯气体相变的实验验证为了验证范德瓦耳斯气体相变的存在和理论预测的准确性,科学家们进行了大量的实验研究。
通过测量气体在不同温度和压力下的性质,并与范德瓦耳斯方程的理论预测进行比较,可以得出气体相变的实验证据。
这些实验不仅证实了范德瓦耳斯方程的正确性,也为气体相变的研究提供了宝贵的数据。
4、范德瓦耳斯气体相变的应用范德瓦耳斯气体相变在多个领域中都有实际应用。
例如,在石油工业中,人们利用气体相变来提高石油的采收率。
通过调整温度和压力条件,使油藏中的气体从液态转变为气态,从而增加油藏的流动性,提高石油的开采效率。
此外,在制冷技术、化学反应和材料科学等领域,范德瓦耳斯气体相变也有着广泛的应用。
5、未来研究展望尽管范德瓦耳斯气体相变已经得到了广泛的研究和应用,但仍有许多未知领域值得探索。
随着科学技术的不断进步,未来可以进一步深入研究气体相变的机制、影响因素以及潜在的应用前景。
此外,通过探索更精确的模型和理论工具,有望更深入地理解气体的行为和性质,为相关领域的发展提供更多支持。
综上所述,范德瓦耳斯气体相变是一种重要的物理现象,涉及到气体在特定条件下的相变过程。
这一现象不仅在理论上具有重要意义,而且在实践应用中也具有广泛的价值。
波义耳定律范德瓦耳斯定律

波义耳定律范德瓦耳斯定律1、玻意耳定律:温度T不变,压强P是体积V的反比例函数,表示等温过程的P-V图象称为等温线.2、范德瓦耳斯方程:“对应态定律”,用临界参数π=p/pc,φ=V/Vc,θ=T/Tc 表示物质的状态,建立了一个适用于任何流体的普遍方程:π+ 3/φ2(3φ+1)=8θ.理论通过对物质聚集态的全面描述,给予了气体实验以极大的帮助.荷兰物理学家[范德瓦耳斯]把经验数据、分子模型、热力学和分子运动论结合起来,提出一个状态方程,它十分简单,有适度的准确性,而且从分子角度考虑十分容易理解. 范德瓦耳斯家庭出身较为贫寒,直到1862年才有机会上大学,当时他已二十五岁.他靠当中学教师维持生计,到1873年才最后完成莱顿大学的学位论文.荷兰的学位论文通常内容很充实,但范德瓦耳斯的论文总共只有一个主要工作.他改进了气体的状态方程,把分子间的作用力和分子的有限体积放进方程中去.他论证了,分子间距离较远时,它们间必定存在吸引力,这一作用附加到容器壁施加的压强上去.他进一步提供论据,假设附加产生的压强反比于气体比容的平方.还有,由于分子占有体积,它们可利用的空间必须减少,或者说得更明白些,减少的总体积就正比于分子在相互接触时所占有的体积.于是一摩尔真实气体的状态方程变成|>[tex](p + frac{a}{{V^2 }})(V - b) = RT[/tex]. 这简单方程包含两个常数,即a和b,对于每一种物质它们可由实验确定.R是普适气体数学. 特定情况下T恒定时的曲线,称做等温线(示意图略).它们分为两种类型:在高温时,等温线与p=常数的线只有一个相交点;在低温时有三个交点.把两族曲线分开的那条等温线有一个切线为水平线的拐点.这条等温线称为临界等温线,而拐点称为临界点.在高温限度内等温线与理想气体的线重合起来.低温时,等温线在一确定的体积间隔内,实际上为一条直线所取代,它相应于液体和蒸气同时存在.事实上,温度或压力固定时,一真实物质可以全部是液体或者全部是蒸气,也可部分液体部分蒸气.等温线的水平部分就表征了这一情况.水平线应位于何处?麦克斯韦用热力学证明了判据应是:由水平线和范德瓦耳斯等温线所确定的两个回线应有的相同面积. 仅仅只有两个经验常数的范德瓦耳斯方程就能够以很好的近似提供大量的数据,这是十分令人惊讶的. |>在临界点上,[tex]V_c = 3b[/tex],[tex]p_c = a/27b^2[/tex],[tex]T_c = 8a/27bR[/tex].于是把[tex]p/p_c = pi[/tex],[tex]V/V_c = phi[/tex]和[tex]T/T_c = theta[/tex]作为变量,方程中的常数就可以消去.这时范德瓦耳斯方程变成|>[tex](pi + frac{3}{{phi ^2 }})(3phi - 1) = 8theta[/tex]. 上式表达了对应态的规律.它曾推广应用于系统探究工作,特别是在有名望的莱顿实验室里更是如此. 在今天,人们已不大欣赏范德瓦耳斯工作的重要性了.现在,我们对[分子]了解得很多,因而他的结果就显得原始,甚至有点幼稚,但是当时[麦克斯韦]和[玻耳兹曼]却对它们产生极深的印象.玻耳兹曼在有关分子运动论的论著中,用很大一部分篇幅专门叙述范德瓦耳斯的工作,并称他为“在气体违背波义耳定律方面做出成绩的牛顿”,恰如麦克斯韦把[安培]称为“电学中的[牛顿]”一样.范德瓦耳斯将有生之年用于改进他的论文,这里我并非在嘲讽他,因为他的论文确实包含了极为丰富而重要的新思想.分子运动论逐步形成了一门有严密体系的精确科学.与此同时实验也越做越精,人们发现绝大多数气体的行为与理想气体的性质不符.1847年勒尼奥(Henri Victor Regnault,1810—1878)做了大量实验,证明除了氢以外,没有一种气体严格遵守波意耳定律,这些气体的膨胀系数都会随压强增大而变大.1852 年焦耳和W.汤姆生合作做了多孔塞实验.发现实际气体在膨胀过程中内能会发生变化,证明分子之间有作用力存在.1863 年安德纽斯的CO2 等温线(图2—6)说明CO2 气体存在一个临界温度31.3℃,高于这个温度无论如何也无法使气体液化.1871 年J.汤姆生(James Thomson,1822—1892)对气液两态问题提出了新的见解,他对安德纽斯的实验结果做了补充,认为在临界温度以下气液两态应有连续性的过渡,并且提出一个“~”形的等温线.不过他既没作定量计算也没有用分子理论加以解释.荷兰物理学家范德瓦耳斯(Johannes Diderik Van der Waals,1837—1923)1873 年在博士论文《论气态和液态的连续性》中考虑了分子体积和分子间吸力的影响,推出了著名的物态方程:(p+a/V2)(V-b)=RT后来人们称之为范德瓦耳斯方程.他还导出了b 是分子体积的4 倍.这个方程不仅能解释安德纽斯的实验结果及J.汤姆生的见解,而且能从常数a、b 值计算出临界参数,这对“永久气体”液化的理论起了指导作用.这篇论文是用荷兰文发表的,起初影响不大,后由于麦克斯韦注意到了他的论文,并于次年(1874 年)在有国际影响的《自然》杂志上对该文作了热情的述评,于是迅速为世人注意.1910 年范德瓦耳斯由于气体和液体状态方程的工作而获诺贝尔物理奖.1881 年范德瓦耳斯进一步提出“对应态定律”,用临界参数π=p/pc,φ=V/Vc,θ=T/Tc 表示物质的状态,建立了一个适用于任何流体的普遍方程:π+ 3/φ2(3φ+1)=8θ.尽管这个方程并不十分精确,但对实际工作例如对于早期尝试进行氢、氦的液化仍有一定的指导意义.范德瓦耳斯之所以能取得如此突出的成就,并在这一领域产生巨大影响,主要是由于他对分子运动比前人有更明确的概念,他继承并发展了波意耳、伯努利、克劳修斯等人的研究成果,并注意到安德鲁斯等人已经从实验发现了气液连续的物态变化,这些实验结果为他的工作提供了实践基础.。
范德瓦尔斯方程

荷兰物理学家范德瓦耳斯(Johannes Diderik Van der Waals,1837—1923)改进了气体的状态方程,把分子间的作用力和分子的有限体积放进方程中去。他论证了,分子间距离较远时,它们间必定存在吸引力,这一作用附加到容器壁施加的压强上去。他进一步提供论据,假设附加产生的压强反比于气体比容的平方。还有,由于分子占有体积,它们可利用的空间必须减少,或者说得更明白些,减少的总体积就正比于分子在相互接触时所占有的体积。于是一摩尔真实气体的状态方程变成(p+an2/V2)(V-nb)=RT。 这简单方程包含两个常数,即a和b,对于每一种物质它们可由实验确定。R是普适气体数学。1873 年在博士论文《论气态和液态的连续性》中考虑了分子体积和分子间吸力的影响,推出了著名的物态方程:(p+a/V2)(V-b)=RT 后来人们称之为范德瓦耳斯方程。他还导出了b 是分子体积的4 倍。这个方程不仅能解释安德纽斯的实验结果及J.汤姆生的见解,而且能从常数a、b 值计算出临界参数,这对“永久气体”液化的理论起了指导作用。
范德华方程是范德瓦耳斯方程的另一种翻译,简称范氏方程,是荷兰物理学家范德瓦耳斯(van der Waals,又译“范德华”、“凡德瓦耳”)于1873年提出的一种实际气体状态方程。范氏方程是对理想气体状态方程的一种改进,特点在于将被理想气体模型所忽略的的气体分子自身大小和分子之间的相互作用力考虑进来,以便更好地描述气体的宏观物理性质。
式中A* 为每个分子的亥姆霍兹自由能。由此得到,引力使压强减小的量正比于1/v2。记该比例常数为a,可得...这便是范氏方程。(注:由于笔者自身水平有限,“。。。”处笔者这样的:先由范德瓦耳斯提出假设,再通过计算证明假设的成立,因此当初方程的产生并不是由于数学推导,而是一种经验性的假设,通过计算,符合事实,便成为一个结论。更简单的理解是:根据理想气体状态方程pV=nRT,由于真是气体压强和体积的测定相对于真实气体存在误差,因此要对压强和体积进行修正。体积上的修正很容易理解,就是理想气体体积减去分子占有体积就是真实气体运动所占有的体积,而对于压强的修正,理解是这样的:分子间的吸引力会对气体对外表现出的压强产生减弱,因此在真实气体的基础上加上由于吸引减弱的压力才是理想气体表现出的压力。而这个分子间的吸引力的大小,是与分子的密度有关的。而在分子间吸引力相同的情况下,分子密度越大,吸引力对压力的削减也越强,因此在压强出的修正方面,是加上分子密度平方的正比。
范德瓦尔斯方程与真实气体状态试验

范德瓦耳斯(Van der Walls)方程与真实气体状态实验在近代工程技术和科学研究中,经常需要处理高压或低温条件下的气体问题,例如在现代化的大型蒸汽涡轮机中,为了提高效率,都采用高压下的高温蒸汽作为工作物质;又如化学工程中的气体合成,以及许多尖端材料和产品的加工制造,也都需要在高压的条件下进行。
所以学习真实气体的物态方程及其压力、体积、温度关系的测绘方法十分必要并有意义。
实验原理:一般气体,在密度不太高,压力不太大(与大气压比较)和温度不太低(与室温比较)的实验范围内,遵守玻意耳定律、盖•吕萨克定律和查理定律。
我们把在任何情况下都遵守上述三条实验定律的气体称为理想气体。
对于质量为m,摩尔质量为M 的理想气体的物态方程为RT M m PV = (1)但真实气体只是在温度不太低,压力不太高的条件下,才能遵守理想气体的状态方程。
理想气体的等温线是等轴双曲线,而真实气体的等温线,并非都是等轴双曲线。
研究真实气体的等温线,就可了解真实气体偏离理想气体定律的情况,从而对真实气体的性质得到进一步的认识。
因此,理想气体状态方程应用到真实气体,必须考虑到真实气体的特征,予以必要的修正。
上世纪以来,许多物理学家先后提出了各种不同的修正意见,建立了各种不同形式的气体状态方程,其中形式较为简单,物理意义比较清楚的就是范德瓦耳斯方程。
范德瓦耳斯方程为RT b V V a P ννν=−+))((22 (2)式中是考虑到气体分子本身体积的修正量,对于给定的气体,是一个恒量,可由实验来测定,一般约等于1摩尔气体分子本身体积的四倍。
另一常数是由气体分子间的引力引起,决定于气体的性质,可由实验来测定。
对于一定量气体,其摩尔数b b a M m =ν。
图1:CO 2实验等温线 图2: 范德瓦耳斯三次方程图范德瓦耳斯方程等温线与真实气体的实验等温线作比较(见图1),二者都有一条临界等温线。
在临界等温线以上,二者比较接近;在温度很高时,二者之间没有区别,在临界等温线以下,却有显著的区别。
范德瓦尔斯力引发的神秘现象

范德瓦尔斯力引发的神秘现象上世纪初,荷兰物理学家范德瓦尔斯发现了一种奇妙的力量,即范德瓦尔斯力。
这种力量可以让分子之间产生相互作用,使得物体可以凝聚为固体或液体状态。
范德瓦尔斯力虽然非常微弱,但是却在自然界中起到了至关重要的作用。
除了对物理科学的重要贡献,范德瓦尔斯力还引发了一系列神秘的现象。
下面我们来一一地探讨这些现象。
1. 亲密接触引发的反弹大家都知道,当两个物体之间有范德瓦尔斯力时,它们会吸引在一起。
但是,当这两个物体脱离接触后,会发生什么呢?实验证明,在亲密接触的物体分离后,它们会发生反弹,就好像它们之间有一种弹性相似的反作用力。
这种现象被称为“臭氧力”,它是由范德瓦尔斯力造成的。
因此,我们可以看到类似于静电的效应。
这个现象虽然看似简单,但是科学家们还不完全理解它的本质。
2. 滚珠和平衡范德瓦尔斯力还会影响两个表面之间的摩擦力。
例如,在玻璃球上涂抹一层透明胶水,然后将球放置在地面上,就可以看到它不断地滚动,而且不会停下来。
这是因为范德瓦尔斯力使得球在地面上产生了微小的变形,这种变形又会影响摩擦因数。
因此,球表面一旦接触到地面,就会受到一些复杂的范德瓦尔斯力的影响,并且会在表面上发生数学上的运动,而不是摩擦阻力。
3. 阴离子效应物理学家还发现,气体分子中的一些物质,例如臭氧、镭等,具有高反应能力,这是由于它们带有负电的特殊性质。
这些分子不仅具有较高反应速度,在破坏性方面也比普通分子更加强大。
科学家们称之为“阴离子效应”,这种现象表现为在气体分子之间形成了一个电荷场,以吸引或排斥某些分子的特殊能力,进而影响了范德瓦尔斯力。
这种效应被认为是许多自然现象的关键因素之一。
4. 外形狭小的物体受到的影响未来的科学家将继续探索范德瓦尔斯力的奥秘,因为它仍有许多未知的方面。
其中之一是范德瓦尔斯力如何影响外形狭小的物体。
例如,科学家们已经研究了如何在提高光学性能的同时缩小微小的光学器件。
范德瓦尔斯力被用来在器件的表面上制造出细微的纹理和凹陷,从而修正光动力学的问题,使设备具有更高的效率和精度。
范德瓦耳斯和他的状态方程

范德瓦耳斯和他的状态方程顾韶晖宁波工程学院化学工程与工艺精化071班摘要:在物理学发展史上,范德瓦耳斯对气一液流体系统做了开创性的研究工作,建立了人类历史上第一个既能反映气、液各相性质,又能描述相变和临界现象的状态方程。
范德瓦耳斯的理论成就和研究方法对热力学、统计力学和低温物理学的发展产生了重要而深远的影响。
关键词:范德瓦耳斯,状态方程前言状态方程是描述热力学系统平衡态的独立参量与温度之间的函数关系式,是物理学的一个重要研究内容。
人类对状态方程的研究可以追溯到很早的年代。
早在1662年和1679年,英国化学家玻意耳(Boyle R)和法国物理学家马略特(Mariotte)就分别提出了描述理想气体性质的状态方程。
两个世纪后,范德瓦耳斯在克劳修斯热力学理论的启发下,通过考虑分子体积和分子间引力的影响,导出了描述实际气体性质的状态方程,即著名的范德瓦耳斯方程。
范德瓦耳斯方程在历史上具有莫大的重要性,它是人类历史上第一个既能描述气、液各相性质,又能显示出相变的状态方程。
由于它形式简单,物理意义清楚,成为热力学和统计物理学的重要应用对象。
范德瓦耳斯也是第一个定量研究分子间相互作用的物理学家,他所使用的研究方法实际上就是后来所说的平均场方法,这一方法对铁磁、超导、超流等众多物理系统相变和临界现象的研究,对热力学和统计物理论的发展产生了重大影响[1]。
1 范德瓦耳斯的生平及科学成就范德瓦耳斯(Johannes Diderik van der Waals),荷兰人,1837年1月23日生于荷兰莱顿一个普通工人家庭。
范德瓦耳斯早年家境不甚宽裕,在出生地完成了他的初等教育后,便做了一名小学教师。
按照荷兰当时的法律,要进一步接受他所喜爱的自然科学的教育,就必须首先通过希腊文和拉丁文的考试。
范德瓦耳斯在这方面的基础不够好,未能获得参加考试的资格。
尽管如此,范德瓦耳斯并未放弃自己的努力。
在1862-1865年期间,他利用业余时间在莱顿大学继续学业,并获得了数学和物理的教学资格。
范德瓦尔斯结合

范德瓦尔斯力类型
(1)极性分子间的结合 极性分子具有电偶极矩,极性分子间的作用力是库仑力, 为了使系统的能量最低,两个分子靠近的两个原子一定 是异性的。 (2)极性分子与非极性分子的结合 极性分子的电偶极矩具有长程作用,它使附近的非极性 分子产生极化。使非极性分子也成为一个电偶极子。极 性分子的偶极矩与非极性分子的诱导偶极矩的吸引力叫 诱导力。显然诱导力也是库仑力。
(3)非极性分子的结合 非极性分子在低温下能形成晶体,其结合力是分子间 瞬时电偶极矩(某一瞬时由于正、负电中心不重合而使 原子呈现出瞬时偶极矩)的一种相互作用。这种作用是 较弱的。 在离子键、共价键、金属键等结合类型中,原子中的价 电子态在成键时都发生了变化,而范德瓦耳斯键则发生 在分子与分子之间,与前面几种结合键类型相比,形成 晶体时各原子结构(电子结构)基本保持稳定。
对于He,Ne,Ar,Kr以及一些有机分子,电子形成了闭 合壳层,因而电子被紧紧地束缚住。对于这种物质在适 当条件下,也能形成晶体。可以认为这些电子和分子是 球对称的,没有极性的,因此,分子间不存在固有电偶 极矩的相互作用。由于电子在核外不停地绕核运动,在 某一瞬间,电子必定处于某一位置上,电荷的分布不均 匀,多少会产生某种“瞬间”的电偶极矩,即出现“瞬 间”的正负电荷中心不重合。这种涨落着的偶极矩间存 在的吸引力倾向于把惰性气体原子和一些有机分子结合 在一起形成分子晶体。
从上面的讨论还可以看出,如果组成固体的粒子是具有 固有偶极矩的有极性分子,则分子间的相互作用力除上 述作用力之外,还可以存在固有偶极矩间的相互作用。 因为有极性分子存在固有偶极矩,无极性分子可以被有 极性分子的电场极化而产生诱导偶极矩,故有极性分子 与无极性分子之间也存在相互作用。
分子晶体:具有饱和电子结构的原子或分子,依靠范德 瓦尔斯力相结合成的晶体,最简单的分子晶体是由于惰 性元素形成的单原子分子等。惰性元素最外层电子为8个, 具有球对称的稳定封闭结构,是面心立方结构。 分子晶体的基本特性:结合力弱、熔点低、硬度小(大 分子晶体的基本特性 部分有机化合物晶体和惰性气体等在低温下形成的晶体 均属分子晶体)。从导电性的角度,分子晶体均为绝缘 体,因为所有电子均局域在分子内,参与分子内的键合。 范德瓦尔斯力在其他晶体中也存在,但是与使晶体结合 的离子键、共价键和金属键相比,范德瓦尔斯力太弱, 可以忽略不如有满壳层结构的惰性元 素)之间或价电子已用于形成共价键的饱和分子之间结 合成晶体时,原来原子的电子组态不能发生很大变化。 而是靠偶极矩的相互作用而结合的,这种力通常称为范 德瓦尔斯力。 范德瓦尔斯力通过分子间作用力(分子键)成键; 通过电偶极矩(极性分子之间)、诱导偶极矩(极性 分子和非极性分子之间)、瞬时偶极矩(非极性分子 之间)之间的相互作用而结合;没有方向性和饱和性。
范德瓦耳斯结合
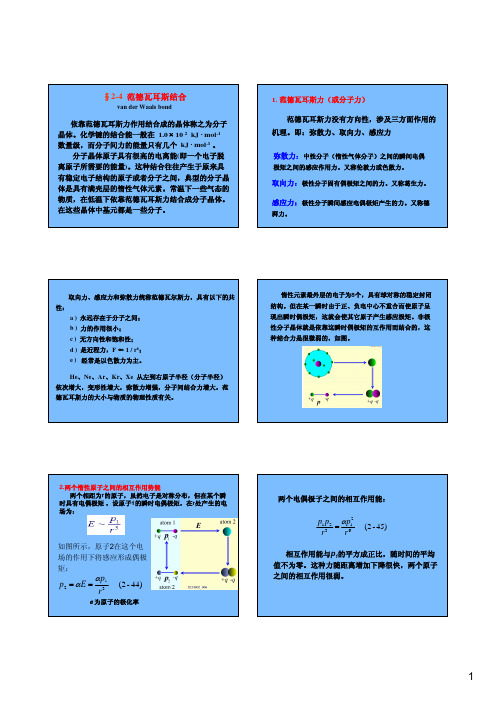
2.两个惰性原子之间的相互作用势能两个相距为r 的原子,虽然电子是对称分布,但在某个瞬时具有电偶极矩,设原子1的瞬时电偶极矩,在r 处产生的电场为:α为原子的极化率如图所示,原子2在这个电场的作用下将感应形成偶极矩:44)-(2 321r pE p αα==范德瓦尔斯力引起的吸引能都与分子间距r 的6次方成反比,也称为范德瓦耳斯相互作用能,写为:a 、b 为两个参数。
排斥能的经验公式为:12)(r b r u =排斥因此两分子间的相互作用能可以表示为:6)(r ar u −=吸引126)(rbr a r u +−=(2-46)3.范德瓦耳斯相互作用能我们作出(2-47)式的函数曲线图,看式中的参数ε、σ所代表的意义。
εσ4)()( r U x f rx ==;令61211)(xx x f −=则(2-47)式子可以写为:47)-(2 4)(6126⎥⎥⎦⎤⎢⎢⎣⎡⎟⎠⎞⎜⎝⎛−⎟⎠⎞⎜⎝⎛∈=r r r u σσ引入新的参量:εand σ,两个原子的相互作用势能可以表示为:4.勒纳-琼斯(Lennard -Jones )势12.12 0612 ,0)(61713==∴=+−=−−x x x dxx df 即:曲线极小值对应于:U(r)/4εr/σ1.12作出(2-47)式的函数曲线如图所示:常数所代表的意义:参数σ反映了排斥力的作用范围,单位是Å(埃);ε反映吸引力的强弱,单位是erg (尔格)。
忽略惰性气体的动能,由N 个惰性气体原子组成的分子晶体的总相互作用势能为:⎥⎥⎦⎤⎢⎢⎣⎡⎟⎠⎞⎜⎝⎛−⎟⎠⎞⎜⎝⎛=6612122)(r A r A N r U σσε(2-48)A 12、A 6是与晶体结构有关的晶格求和常数。
对于面心立方结构:A 12=….≈12.13;A 6=…. ≈14.45求解A 12、A 6的方法看后面的例题。
根据势能函数的最小值可以确定晶格常数、结合能和体变模量。
范德瓦尔斯方程

分子力示意图
1. 分子力 当 r<r0时,斥力; 当 r>r0时,引力; 当 r= r0时,分子力=0 r0:平衡距离 当 r>s 时,分子力0
s :有效作用距离 1
实际气体的分子模型:
有引力的刚性球
d:分子的有效直径
2. 范德瓦耳斯方程
V=
m M
Vm
)
对氮气,常温和压强低于 5107 Pa范围
a = 0.84 105 Pa L2/mol2 , b = 0.0305 L/mo4l
3. 范德瓦耳斯气体等温线
临界等温线
BE :过饱和蒸汽 引入凝结核心 - 液化BC 云室
CF: 过热液体 引入汽化核心 — 汽化
范德瓦耳斯气体等温线
气泡室
FE: 实际不可实现
BC: 虚线实际气体 5
气泡室的外形和高速粒子径迹的照片
6
无悔无愧于昨天,丰硕殷实 的今天,充满希望的明天。
1mol 气体 p RT Vm
考虑分子本身的体积
p RT Vm b
理论上 ,b 约为 1mol 气体分子本身体积的 4 倍
b
4N
A
4 3
(1010 2
)3
106
m3
1(cm3)
p增大,容积与 b 可比拟时,b 的修正必须考虑2
分子间引力引起的修正
器壁受到的压强要比没考 虑引力时要小
p
RT vm b
pin
气体内压强的产生
内压强pin :表面层分子受到指向气体内部的单
位面积的作用力。
pm
n2
1 VБайду номын сангаас2
范德瓦尔斯方程

分子力示意图
1. 分子力 当 r<r0时,斥力; 当 r>r0时,引力; 当 r= r0时,分子力=0 r0:平衡距离 当 r>s 时,分子力0
s :有效作用距离 1
实际气体的分子模型:
有引力的刚性球
d:分子的有效直径
2. 范德瓦耳斯方程
1mol 气体 p RT Vm
考虑分子本身的体积
p RT Vm b
理论上 ,b 约为 1mol 气体分子本身体积的 4 倍
b
4NA
4 3
(1010 2
)3
106
m3
1(cm3 )
p增大,容积与 b 可比拟时,b 的修正必须考虑2
分子间引力引起的修正
器壁受到的压强要比没考 虑引力时要小
p
RT vm b
pin
气体内压强的产生
内压强pin :表面层分子受到指向气体内部的单
位面积的作用力。
pm
n2
ቤተ መጻሕፍቲ ባይዱ
1 Vm2
a 或 pin Vm2
a:反映分子之间引力的常量
3
1mol 气体的范德瓦耳斯方程
(
p
a Vm2
)(Vm
b)
RT
质量为 m 的气体的范德瓦耳斯方程
(
p
m2 M2
a V2
)(V
m b) M
m M
RT
(其中
V=
m M
Vm
)
对氮气,常温和压强低于 5107 Pa范围
12-10 实际气体的范德瓦耳斯方程
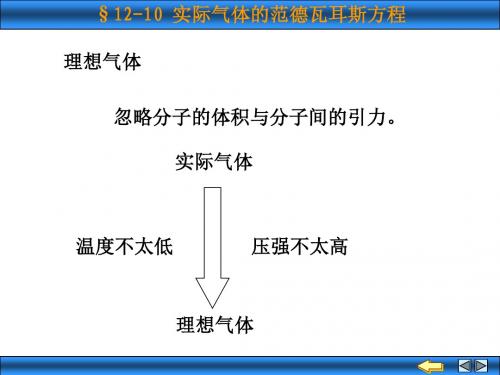
1 2 pi n 2 V p pi V b RT
f
范德瓦耳斯方程 §12-10 实际气体的范德瓦耳斯方程
3 范德瓦耳斯方程
令
a pi 2 V
其中 a 为反映分子间引力的一个常量。 修正后1mol 理想气体的状态方程可写成:
a p 2 V b RT V
p(V b) RT
b N Ad
3
d:两个分子中心的最小间距
范德瓦耳斯方程 §12-10 实际气体的范德瓦耳斯方程
2 对压强的修改
对于实际气体,分子间的引力不可忽略,因此气体 分子在对器壁的碰撞时,由于受到内部气体分子的吸 引而减弱对器壁的碰撞,压强将小于同种条件的理想 R 气体的压强,引入压强修正。 气体分子相当于一个指向 内部的压强pi . f
§12-10 实际气体的范德瓦耳斯方程 理想气体
忽略分子的体积与分子间的引力。
实际气体
温度不太低
压强不太高
理想气体
§12-10 实际气体的范德瓦耳斯方程
一 真实气体的等温线
在非常温或非常压的情况下,气体就不能看成理想气体。
P(101325Pa) D p
液
C
气
72.3
48.1C
理想气体 V
液汽 共存 45
理论上把完全遵守此方程的气体称为范德瓦尔斯气体。
汽
31.1C 21C 13C
V/(m3.kg-1)
CO2的实验等温线
B 0
A 2.1710-3
瓦耳斯方程
1 对体积的修正 1mol 理想气体的状态方程可写成
pV RT
分子有大小时,则每个分子活动 的自由空间为:V - b
范德华方程

范德华方程范德华方程范德华方程是范德瓦耳斯方程的另一种翻译,简称范氏方程,是荷兰物理学家范德瓦耳斯(van der Waals,又译“范德华”、“凡德瓦耳”)于1873年提出的一种实际气体状态方程。
1范德华方程范德华方程是范德瓦耳斯方程的另一种翻译,简称范氏方程,是荷兰物理学家范德瓦耳斯(van der Waals,又译“范德华”、“凡德瓦耳”)于1873年提出的一种实际气体状态方程。
范氏方程是对理想气体状态方程的一种改进,特点在于将被理想气体模型所忽略的的气体分子自身大小和分子之间的相互作用力考虑进来,以便更好地描述气体的宏观物理性质。
2适用范围范氏方程对气-液临界温度以上流体性质的描写优于理想气体方程。
对温度稍低于临界温度的液体和低压气体也有较合理的描述。
但是,当描述对象处于状态参量空间(P,V,T)中气液相变区(即正在发生气液转变)时,对于固定的温度,气相的压强恒为所在温度下的饱和蒸气压,即不再随体积V(严格地说应该是单位质量气体占用的体积,即比容)变化而变化,所以这种情况下范氏方程不再适用。
3与理想气体方程模拟结果的比较3.1低压状况在气体压强不太高的情况下,以下事实成立:排斥体积b 的影响相对V 而言极小,可以忽略;以二氧化碳(CO2)为例,在标准状况(0°C,1标准大气压)下,一摩尔CO2体积V 为22414 cm³,而相应的b= 43 cm³,比V 小3个数量级;分子间的距离足够大,a/V² 项完全可以视为0;譬如在一大气压下二氧化碳气体的a/V² 值只有7‰。
所以此时理想气体方程是范氏方程(也是对实际气体行为的)的一个良好近似。
分别用理想气体方程和范德瓦耳斯方程模拟的二氧化碳气体70°C时的p-V等温线3.2中高压状况随着气体压力的增加,范氏方程和理想气体方程结果的差别会变得十分明显(左图为CO2分别用理想气体方程和范德瓦耳斯方程模拟的p-V等温线,温度70°C):在压强为5000~15000kPa(50~150标准大气压)的中压区,由于体积被“压小”导致分子间距靠近,分子间的引力(表现为a/V² 项)变得不可忽略。
§4-6-真实气体的范德瓦耳斯方程(推荐文档)

设1mol气体的占有体积 Vm
气体分子能自由活动的体积 Vm b
1mol气体的状态方程
p(Vm b) RT
可以证明:b等于1mol气体固有体积的4倍。
二、分子吸引力修正
由于分子可活动的范围减小,分子和容器 壁的碰撞增加,压强就该增大。
太原理工大学物理系
分子实际
b
pin
pin
a Vm2
a 是一个与气体种类、气体温度有关的常数
三、范德瓦耳斯方程
1mol气体的范德瓦耳斯方程
a ( p Vm2 )(Vm b) RT
太原理工大学物理系
质量为M气体的范德瓦耳斯方程
(p
M2
M
2 mol
a V2
)(V
M M mol
b)
M M mol
§4-6 真实气体的范德瓦耳斯方程 理想气体微观模型: 1)分子无大小 2)分子间无作用力(碰撞时除外)
1873年荷兰物理学家范德瓦耳斯对理想气体 的两个基本假设进行了修正,得出了描述真实 气体行为的范德瓦耳斯方程。 一、分子固有体积修正
把分子当作有一定体积的刚性球,分子的 活动空间减小。
太原理工大学物理系
RT
对于压强不是很高(低于500大气压),温 度不是太低的实际气体,范德瓦尔斯方程是很 好的近似公式。
范德瓦尔斯方程是经验方程,各种气体的常 数a、b可由实验测量。
太原理工大学物理系
范德瓦耳斯结合

原子呈现出瞬时偶极矩
—— 惰性元素具有球对称,结合时排列最紧密以使势能 最低
—— Ne、Ar、Kr、Xe的晶体都是面心立方 —— 透明的绝缘体,熔点特低 —— 分别为24K、84K、117K和161K
A12 ( r
)12
A6 ( r
)6
]
—— 1/2因子: 相互作用能为两个原子共有
—— A12和A6: 与晶格结构有关的求和项
晶体总的势能
U(r)
1 2
N
(4
)[
A12
(
r
)12
A6
(
r
)6
]
—— 非极性分子晶体的晶格常数、结合能和体变模量
晶格常数
平衡状态体变模量 晶体的结合能
两个惰性原子之间的相互作用势能
—— 两个相距为r的原子,原子中电子是对称分布 —— 偶极矩作用
设原子1的瞬时电偶极矩
在r处产生的电场
原子1的电场
原子2在电场的作用下感应偶极矩 —— 原子的极化率
两个电偶极子之间的相互作用能
—— 作用能与p1的平方成正比,对时间的平均值不为零 —— 力随距离增加下降很快,两原子之间相互作用很弱
两个原子的相互作用势能u源自r)A r6B r12
—— B/r12: 重叠排斥势能,A和B为经验参数,都是正数
两原子相互作用势能
引入新的参量
相互作用势能 u(r) 4[( )12 ( )6 ]
r
r
—— 勒纳-琼斯(Lennard-Jones)势
晶体总的势能 — N 个原子
U
(r)
§4、5分子力,范德瓦尔斯气体

以质心间距离r 为横坐标,分子间作用力 F(r)
为纵坐标,画出两分子间互作用力曲线。
分子作用力曲线
设分子是球形的, 分子间的互作用 是球对称的中心 力场。
质心间距离r 为横坐标,分子间作用力 F(r)为纵坐标。
r = r0 时分子力为零,相当于两分子刚好“接触”。
r<r0 时,两分子受到“挤压”过程中产生强斥力,这时 F(r)>0,且随r0减少而剧烈增大。
一般来说在气体内部,气体分子受到其它分子的吸引 力的合力为零。 但是在容器内紧靠容器壁有一个界面层。
界面层的厚度等于分子作用力半径。
界面层中所有分子都大小不等地受到作用球内气体分 子对它的吸引力的合力的作用,合力的方向都指向气体 内部。 气体内部分子在越过界面 层向器壁运动,以及与器
合力 为零
壁碰撞以后返回穿过界面分子力的合力方向
dr 若令分子间距离r 趋向无穷远时的势能为零,则
E p ( p) F (r )dr
r
F
dE p
和分子作用力曲线所对应的互作用势能曲线
注意:
E p (r ) ~ r
E p ( p) F (r )dr
r
在平衡位置 r = r0 处,分子力 F(r) = 0,势 能有极小值 ,极小值是负的。
△k与向内的拉力成正比,而拉力与分子数密度n 成正
比,设比例系数为K, 则
△k = K n
单位时间内与单位面积碰撞的分子数也与n成正 强 △p = a / V m2
范德瓦耳斯方程
将
△p = a /Vm2 代入
得到
a ( p 2 )(Vm b) RT Vm
§4 .分子力
真实气体的等温线
范德瓦耳斯常量的 量纲分析

a=AaNA b=AbNA d , 式中的Aa和Ab均为无量 纲量,显然两式中的诸分别为 2 4 -2 dima=dim(pv )=L N dimf, dimNA=N-1, dimd=L, t t dim=dim(fr )=L dimf, 3 -1 dimb=L N . 由此可确定a和b的表述式。
4 -2 dima=L N dimf -1 2 -( t -4) t =(N ) [L ](L dimf )
2 -( t -4) =(dimNA) [(dimd) ]
(dim) 2 -( t -4) =dim[NA d ]. 2 -( t -4) 故得a=AaNA d .
3 -1 dimb=L N
-1 3 =(N )(L ) 3 =(dimNA)(dimd) 3 =dim(NAd ). 3 故得b=AbNAd .
注意:其实b与无关。
由此可见,范德 瓦耳斯常量的表述 式为 2 -( t -4) a=AaNA d , 3 b=AbNAd .
范德瓦耳斯 常量的 量纲分析
由于范德瓦耳斯常量 a 和 b 分别反映出分子间引 力和分子本身所占有体积 (本质上也就是分子间斥 力)对一摩尔范德瓦耳斯 气体的修正,所以它们都 应该与分子的运动无关。
因此可以预期, a 和 b 都与分子质量和分子平均 速率无关,只能与一摩尔 气体分子的总数(即阿伏 伽德罗常量)NA、分子的 有效直径 d 和分子间引力 常量 有关,故均可设
范德瓦尔斯等温线

范德瓦尔斯等温线范德瓦耳斯等温线1范德瓦耳斯等温线2麦克斯韦构图法3范德瓦耳斯等温线中各线段状态的讨论4临界点1. 范德瓦耳斯等温线(van der waals isothermal)023=-++-p ab V p a V p RT pb V m m m范德瓦耳斯方程是能统一描述气相、液相及气液相变的方程。
范德瓦耳斯等温线十分相似于安德鲁斯等温线.只要以一段水平直线段代替范德瓦耳等温线中的弯曲线段,则曲线就是安德鲁斯等温线。
p2. 麦克斯韦构图法(Maxwellian construction) e-d-c-b-a-c-e 可逆循环=由a-c-b-a (正循环)+ e-d-c-e (逆循环)edceacba S S W -=0>W 违背热力学第二定律0<W 违背热力学第二定律。
0=W edceacba S S =麦克斯韦构图法:等面积法则3. 范德瓦耳斯等温线中各线段状态的讨论Ø不稳定的 d-c-b0m T p V ⎛⎫∂> ⎪∂⎝⎭不稳定Ø处于亚稳态的过冷蒸汽及过热液体0<⎪⎪⎭⎫ ⎝⎛∂∂T m V p 稳定d-c-b 段a-b 段; e-d 段e-d :过冷蒸汽(过饱和蒸汽)a-b:过热液体 过冷、过热的状态都是亚热态。
亚稳态对于小的扰动是稳定的,但对于足够大的扰动都是不稳定的,最终它们必将成为最稳定的两相共存态4. 临界点在临界点所发生的气液相变与在低于临界温度时的相变完全不同,它有很多特殊性质1. 临界点状态参量的确定临界压强 p c 、临界摩尔体积V c,m 、临界温度T c 。
临界点同时兼有极大及极小的特征,同时满足下述两个条件: 0=⎪⎪⎭⎫ ⎝⎛∂∂T m V p 022=⎪⎪⎭⎫ ⎝⎛∂∂Tm V p 连续相变:无潜热的吸放,也无两相共存,没有过冷过热现象(二级相变)RT V ab pb V a pV mm m =--+20=⎪⎪⎭⎫ ⎝⎛∂∂T mV p 322m m V ab V a p -=0624,3,22=+-=⎪⎪⎭⎫ ⎝⎛∂∂m c m c Tm V ab V a V p 227b a p c =Rb a T c 278=,3c m V b=667.238,==m c c c V p RT 临界系数(critical coefficient)实验测出各种气体的临界系数均不同,而且相差甚大例如:二氧化碳K 19.304=cT 136,mol m 1001.94--⋅⨯=m c V 25m N 1080.73-⋅⨯=c p 由此算出临界系数为3.64例如:水的136,25mol m 1025.56,m N 1043.220,K 30.647---⋅⨯=⋅⨯==m c c c V p T 所算出的临界系数为4.34 范德瓦耳斯方程是有很大近似性的,它仅适用于温度不是太低,压强不是太高的气体。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
范德瓦尔斯
范德瓦尔斯(Johannes Diderik van der Waals)
1837年11月23日生于荷兰的莱顿,父亲名叫雅各布.范德瓦尔斯,母亲名叫伊丽莎白·范登伯格(Elisa bethvandenBurg)。
范德瓦尔斯在家乡结束了初等教育后,成为一名中学教员。
虽然他因不懂古典语言而未能参加大学人学考试,但在1862—1865年期间,他利用业余时间在莱顿大学继续学习,并获得了数学和物理学的教师证书。
1864年,范德瓦尔斯任德文特一所中学的教师。
1866年到海牙,先当该城一所中学的教师,后任该校校长。
新的立法取消了理工科大学生人学前必须受古典语言教育的规定,使范德瓦尔斯能够参加大学考试。
1873年他以《论气态和液态的连续性》这篇论文取得了博士学位,使他立刻进入了第一流物理学家的行列。
在这篇论文中,他提出了包括气态和液态的“物态方程”,论证了气液态混合物不仅以连续的方式互相转化,而且事实上它们具有相同的本质。
关于范德瓦尔斯第一篇论文中提出的这个结论的重要性,在J.C.麦克斯韦的《自然》一书中有这样的评价:“毫无疑问,范德瓦尔斯的名字将很快出现在第一流的分子科学家的名单中”,“可以肯定,不止一个科学家正在注意学习他的论文所用的…低地荷兰语‟”(麦克斯韦可能想说“低地德语”,但这是不对的,因为荷兰语有权自成为一种语言)。
后来,他就这个课题和与此有关的课题又写了大量论文,发表在《荷兰皇家科学院学报》和《荷兰年鉴》上,并被译成多种文字。
1876年颁布了新的高等教育法,将阿姆斯特丹古老的雅典语学
院扩充成综合大学,范德瓦尔斯被任命为该校第一名物理学教授。
他和同事范托夫(Van… tHoff)、遗传学家休戈·德弗里斯(Hugodevries)使该校声誉大增。
尽管各处向他发出盛情的邀请,但他一直忠实地留在该校,直到退休。
范德瓦尔斯对他论文的课题发生兴趣的直接原因,是克劳修斯的论文中将热看成是一种运动现象,使他想对安德鲁斯1869年证明气体存在临界温度时所作的实验寻找一种解释。
范德瓦尔斯天才地发现,必须考虑分子的体积和分子间的作用力(现在一般称为范德瓦尔斯力),“才能建立气体和液体的压强、体积、温度之间的关系。
范德瓦尔斯经过艰苦的努力,于1880年发表了第二项重大发现,当时他称之为“对应态定律”。
这个定律指出:如果压强表示成临界压强的单调函数,体积表示成临界体积的单调函数,温度表示成临界温度的单调函数,、就可得到适用于所有物质的物态方程的普遍形式,因为在这个方程中,a,b,产这三个常数可用特殊物质的临界值来表示,因此在方程中消失。
正是由于在这个定律的指导下进行实验,J.杜瓦才在1898年制成了液态氢,翁纳斯在1908年制成了液态氦。
翁纳斯因研究低温和制成液态氦而荣获1910的诺贝尔物理学奖。
他在1910年写道:“我们一直把范德瓦尔斯的研究看成是实验取得成功的关键,莱顿的低温实验室是在他的理论影响下发展起来的。
十年后,即1890年,关于“二元溶液理论”的第一篇论文在《荷兰年鉴》上刊出,这是范德瓦尔斯的又一项重大成就。
他把物态方程和热力学第二定律结合起来,创造了一种图示法,以吉布斯在“非均匀物质的平衡”这篇论文中首次提出的形式用一个面表示他的数学公式。
为纪念吉布斯,他把这个面称为“w面”,因为吉布斯用希腊字母w作为自由能的符号,他认为自
由能对平衡有着重大意义。
二元混合物理论引起了一系列实验,首先是库恩的实验。
他发现,临界现象的特征完全可由理论预言。
还应当提到范德瓦尔斯关于毛细现象的热力学理论,其基本形式是在1893年首次提出的。
该理论认为,在液体和蒸气之间的边界层存在着密度的逐渐变化,尽管变化是很快的。
这个观点和吉布斯的不同,吉布斯假设从液体到蒸气,密度是突变的。
拉普拉斯早年建立了毛细现象的理论,范德瓦尔斯却认为分子永远在作高速运动。
在临界温度附近所作的关于这个现象的实验支持了范德瓦尔斯的观点。
范德瓦尔斯获得了许多荣誉,特别应提到的是;他是剑桥大学的荣誉博士,莫斯科帝国自然科学学会名誉会员,爱尔兰皇家科学院名誉院士,美国哲学协会名誉会员,法国研究院通讯院士,柏林皇家科学院通讯院士,比利时皇家科学院名誉院士,伦敦化学协会外籍会员,美国国家科学院外籍院士,罗马科学院外籍院士。
范德瓦尔斯的主要爱好是散步和朗诵,特别是在乡郊散步。
1923年8月8日他在阿姆斯特丹逝世。
