2-4 范德瓦尔斯结合
固体物理学-晶体结合类型

同时,由于距离增大,价电子与原子实之间的势能相对于 自由原子时要高。但由于自由电子屏蔽作用的存在,势能的 升高相对于动能的降低要小,二者能量之差就是金属结合的 主要来源。
12
I . 固体结合类型
------共价结合和共价晶体
13
共价键(氢分子为例)
•共价结合是靠两个原子各贡献一个电子,形成共价键。这样一对为两个 原子所共有的自旋相反配对的电子结构称为共价键。
•这对自旋相反的电子在两原子核之间的区域会形成较大的电子云密度, 同时受到两个原子核较强的库仑吸引作用,这就是共价键产生的物理根 源。
这种相互作用一定包括吸引和排斥两种类型。吸引力使粒子 聚集一起,排斥力使粒子之间保持一定间距,维持固体形态。 两种作用并存,粒子处于平衡状态,从而结合形成稳定的晶体 结构。这种维系原子结合在一起的作用力或称为“键”。
粒子之间的作用力应全部归结于静电相互作用,磁力和万有 引力忽略不计。粒子间的吸引作用可以归结为异性电荷间的库 仑吸引力;而排斥作用可以归结为同性电荷之间的库仑斥力以 及由泡利原理引起的排斥力。
4
根据键的特征,固体结合类型主要有以下几种:1. 金属 性结合;2. 共价结合;3. 离子性结合;4.范德瓦尔斯结合。 与结合力类型相对应,晶体可大致分为四种基本类型: 1. 金属晶体; 2. 共价晶体;3.离子晶体;4.分子晶体。
值得指出的是,以上这些类型之间的区分不是严格的, 某些固体的结合往往具有混合的特点或过渡的性质。
§2.6 范德瓦尔斯结合

式中
aj 是参考原子i与其它任一原子 的距离r 同最近邻原子间 与其它任一原子j的距离 a j是参考原子 与其它任一原子 的距离 ij同最近邻原子间
j
A12 = ∑ ' 12 j a j
1
'1 , A6 = ∑ 6
N
的比值( )。试计算面心立方的A 距R的比值( aj = rij R )。试计算面心立方的 6和A12。 的比值 (1)只计及最近邻原子; (2)计及最近邻和次近邻原子。 (1)只计及最近邻原子; (2)计及最近邻和次近邻原子。 只计及最近邻原子 计及最近邻和次近邻原子 (1)面心立方 最近邻原子有12个 面心立方, 解: (1)面心立方,最近邻原子有 个,
r近 = R,
a1 = a2 = ⋅ ⋅ ⋅ = a12 = 1
上页 下页 返回 结束
A12 =
1 1 = 12 × 12 = 12 ∑ 12 1 j =1 a j
12
第二章 晶体的结合 12 1 1 A6 = ∑ 6 = 12 × 6 = 12 1 j =1 a j
(2)计及最近邻和次近邻 次近邻有 个。 计及最近邻和次近邻,次近邻有 计及最近邻和次近邻 次近邻有6个
上页
下页
返回
结束
第二章 晶体的结合 个惰性气体原子构成的分子晶体, 例1:由N个惰性气体原子构成的分子晶体,其总互作用势 个惰性气体原子构成的分子晶体 能可表示为
12 6 σ σ U( R) = 2Nε A − A6 12 R R
3. 晶体的结合能
dU dR =0
R0
2A R0 = 12 A 6
1/ 6
σ
U 0 = U ( R0 ) = −2源自ε A62 A12N
2.3-范德瓦尔斯结合、晶体结合的规律性

I 族的碱金属和 VII 族的卤族元素负电性 差别最大,它们之间形成最典型的离子晶体
随着元素之间负电性差别的减小,离子性结 合逐渐过渡到共价结合,从 I-Ⅶ 族的碱金属 卤化物到Ⅲ-Ⅴ族化合物,这种变化十分明显
从晶格结构来看, 碱金属卤化物具有 NaCl 或 CsCl 的典型离子晶格结构, 而Ⅲ-Ⅴ族化合物 具有类似于金刚石结构的闪锌矿结构;
同的,但具有基本相同的变化趋势
在具有 Z 个价电子的原子中, 一个价电子受到带正电
的原子实的库仑吸引作用, 其它 (Z-1) 个价电子对
它的平均作用可以看作起着屏蔽原子实的作用
假使屏蔽作用是完全的, 价电子将只受到 +e 电荷的吸引力
实际上,由于许多价电子属于同一壳层,它们的 相互屏蔽只是部分的,因此,作用在价电子上的 有效电荷在 +e 和 +Ze 之间,随 Z 增大而加强
证明: (1) 一对正负离子的平均吸引势为 e2
R
平均排斥势为 2B
Rn
晶体的内能或总的互作用势能为
U
N
e2
R
2B
Rn
由平衡条件dU 0 得到 NhomakorabeadR R0
B
e2
2n
Rn1 0
带回到内能表达式有
U
(R0
)
Ne2
R0
1
1 n
考虑到 2ln 2 并采用国际单位制, 则可写成
U
(R0
)
2Ne2 ln 2
3. 化合物晶体的结合规律
不同元素的组合形成合金或化合物晶体
不同金属元素之间依靠金属性结合形成合金固溶体
由于金属性结合的特点,它们和一般化合物不同, 所 包含不同元素的比例不是严格限定的, 而可以有一 定的变化范围, 甚至可以按任意比例形成合金 这个特点对于合金在技术上的广泛应用具有重要意义
晶体的结合

第二章 晶体的结合组成晶体的原子能够保持中性稳定的周期性排列,说明原子之间有着强烈的相互作用力。
晶体粒子之间的相互作用力包括两种类型:吸引力和排斥力。
当原子受到压缩时,这种作用表现为斥力;当晶体受到拉伸时,这种作用表现为引力。
当斥力和引力平衡时,晶体保持一定的体积和外形。
因此,晶体结构取决于组成晶体的原子的性质及相互作用。
从能量的观点来看,一块晶体处于稳定状态时,它的总能量0E (原子的动能和相互作用势能的总和)比组成这晶体的原子处于自由状态时的总能量N E 低。
两者之差被定义为晶体的结合能W :即0N W E E =-。
结合能就是把晶体分离成自由原子所需要的能量。
对于晶体中原子相互作用的研究,实际上是量子力学的多粒子问题。
由于问题的复杂性,只能采取多种近似的方法进行处理。
本章首先介绍晶体结合类型的物理本质,然后利用经典理论重点讨论离子晶体和分子晶体的结合能。
§2-1晶体的结合类型与原子电负性对原子结合成晶体起主要作用的是各原子的最外层的电子。
按原子间相互作用的性质,可把晶体分为离子晶体、共价晶体、金属晶体、分子晶体和氢键晶体等等。
2.1.1晶体的结合类型 1.离子晶体离子晶体是由正、负离子所组成,依赖离子之间的静电相互作用结合成晶体。
最典型的离子晶体是碱金属元素和卤族元素之间形成的化合物,它们的晶体结构也比较简单,分别属于NaCl 或CsCl 两种典型结构。
在NaCl 晶体中,Na +和Cl -离子相间排列,每一种离子都是以异性离子为最近邻,总的库仑作用的效果是吸引的。
同时,由于Na +和Cl -离子都具有满电子壳层结构,当两个离子相互接近电子云发生重叠时,除静电相互作用外,由于泡利不相容原理,它们之间将产生很强的排斥作用,晶体正是依靠库仑吸引和排斥相平衡结合成稳定的结构。
由于离子具有满壳层电子结构,其电荷分布近似于球对称,所以离子键是没有方向性的,是晶格配位数较高的结构。
这种离子键是相当强的,其结合能的数量级约为800kJ/mol ,离子间的吸引能的数量级约为几eV ,因此一般离子晶体的熔点较高,硬度较大。
清华大学考研专业课839固体物理考试范围及历年真题汇编

第二卷固体物理知识点(参考黄昆的书,学有余力也建议学习韦丹固体物理,各有特色)第一章晶体结构1.1 晶格的相关概念及几种不同晶格1.2 理解原胞概念1.3 晶面晶向的标定1.4 倒易点阵的定义及相关性质1.5 立方体、正四面体、正六角柱的对称操作1.6 五种旋转对称的推导1.7 十四种布拉伐格子,结合材料科学基础,弄清楚。
1.8 表1-2记住,材科基会考第二章固体的结合2.1 离子性结合的特点,推导马德隆常数,系统内能的表示,求平衡距离和体变模量2.2 共价结合的特点2.3 金属性结合的特点,排斥作用来源2.4 范德瓦尔斯结合的特点,Lennard-Jones 势的相关推导第三章晶格振动与晶体的热学性质3.1 了解简谐近似、简正坐标、振动模的概念3.2 格波、声子概念,一维单原子链的色散关系等计算,q 的范围,长波极限特点3.3 一维双原子链相关推导,q 的取值范围,声学波光学波的概念,长波极限的特点3.4 声学波,光学波的数量判断,q 的分布密度,第一布里渊区的概念,画法3.5 了解LST 关系3.6 确定色散关系的几种方法及其原理3.8 爱因斯坦模型和德拜模型的假设、结果、适用范围、缺陷及全部推导过程3.9 不同条件下推导晶格振动模式密度3.10 热膨胀产生原因3.11晶格热传导原理,热导率的影响因素,N、U过程,不同温度下晶格热导原理第四章能带理论4.1 布洛赫定理内容,简约波矢概念4.2 一维周期长中求带隙大小,解释其成因4.3 三维周期场的布里渊区和能带,SC、BCC、FCC的简约布里渊区及相关数据。
结合2015年十一题和课后4.8弄懂图4-114.5 紧束缚近似的概念,该近似下求SC、BCC、FCC的能带函数E(k)4.7 不同维度下求能态密度,近自由电子的等能面,费米面,费米半径的相关计算第五章晶体中电子在电场和磁场中的运动5.1 波包概念,E、F、v、a、m*的相关公式及计算5.2 恒定电场下电子的运动过程,振荡频率5.3 导体、半导体、绝缘体的能带特点5.4 了解廊道能级概念5.5 回旋共振的应用5.6 德·哈斯-范·阿尔芬效应的原理及作用第六章金属电子论(可参考材科学习辅导第九章:功能材料基础)6.1 电子热容量公式(掌握大致证明过程),电子热容量与晶格热容量大小比较及原理6.3 了解定态导电过程中的玻尔兹曼方程6.4 了解弛豫时间的概念及电导率公式6.5 了解对各向同性散射过程中弛豫时间表达式的理解6.6 晶格散射的 U 过程和 N 过程,弛豫时间公式中包含的两个重要结论第七章至第十一章:出现频率极低,搞懂相关真题,学有余力关注其中一些概念即可。
固体物理基础第2章 固体的结合

2-1 亲和能
亲和能: 中性原子 + (-e) → 负离子 中性原子吸收一个电子成为负离子所放出的能量
3 2 1 电子亲和能 / eV 0 -1 -2 -3 -4
Be
Mg Ca Zn
He
Ne
Ar
Kr
C
Si
V
Cu
Ge
F
Cl
Br
电离能均为正值(吸收能量),亲和能有正有负 与电离能的变化规律有何区别?
2-1 晶体结合能的普遍规律
原子间相互作用势能
A B u( r ) m n r r
r :两原子间的距离 A、B、m、n>0
A m r
吸引能
B n r
f (r )
排斥能
两原子间的相互作用力
du( r ) dr
2-1 晶体结合能的普遍规律
假设相距无穷远的两个自由原子间的相互作用能为零,相互作用力为零。
u( r )
(a)互作用势能和原子间距的关系 (b)互作用力和原子间距的关系
r
(a ) f (r )
rr r0 , f (r ) 0 ,
斥力 引力
r r0 , f (r ) 0, u(r )min
(b)
r r0 , f (r ) 0 ,
r0
rm
df d 2u ( ) ( 2 ) rm 0 r dr dr r
溴
2-1 元素周期性规律
随着原子序数的递增
引起了
最外层电子数 1→8 (K层电子数 1→2) 原子半径: 化合价: 大→小(除稀有气体) +1→+7 -4→-1
核外电子排布呈周期性变化
决定了
(稀有气体元素为零)
范德瓦尔斯异质结构建模型

范德瓦尔斯异质结构建模型全文共四篇示例,供读者参考第一篇示例:范德瓦尔斯异质结构是一种新型的材料结构,由两种或多种不同的原子层堆叠而成。
它的特性在于在层间和层内的相互作用相对较弱,因此具有许多独特的物理性质。
范德瓦尔斯异质结构最初是由荷兰物理学家范德瓦尔斯提出的,其特点是由非共价键相互作用而形成的。
范德瓦尔斯异质结构在电子学、光电子学、热电子学等领域有着广泛的应用。
它的独特结构和性质为我们提供了一种全新的材料设计思路。
在范德瓦尔斯异质结构中,通过合理设计原子层的排列和选择不同的原材料,可以实现许多优异的电子和光学性能,比如量子点、量子阱、异质结构等。
范德瓦尔斯异质结构的建模是研究这种新型材料的关键。
建模可以帮助我们更深入地了解其内部结构和物理性质,从而为材料的设计和性能优化提供指导。
下面我们将介绍一种常用的范德瓦尔斯异质结构建模方法。
范德瓦尔斯异质结构建模的方法之一是第一性原理计算。
该方法基于量子力学原理,通过求解薛定谔方程来描述材料的电子结构和性质。
通过第一性原理计算,可以计算出材料的能带结构、电子密度分布、原子间相互作用等关键参数,进而预测材料的电子输运性质、光学性能等。
第一性原理计算是一种基于数学和物理的理论方法,需要借助计算机进行大量的计算。
首先需要确定材料的晶体结构,然后建立晶体结构模型,确定原子的位置和化学键的类型。
接着通过求解薛定谔方程,计算出材料的波函数和能带结构。
最后根据得到的结果,分析材料的性质和行为。
除了第一性原理计算外,还可以通过分子动力学模拟、密度泛函理论等方法进行范德瓦尔斯异质结构的建模。
这些方法可以帮助我们更全面地了解材料的结构和性质,为材料的设计和性能优化提供依据。
第二篇示例:范德瓦尔斯异质结构是一种常见的纳米材料,具有多种应用价值,因此其建模研究具有重要意义。
近年来,科学家们通过理论模拟和实验研究,不断探索范德瓦尔斯异质结构的性质和应用,取得了一系列突破性进展。
固体物理第二章 固体的结合

(四)范德瓦耳斯结合
1879年范德瓦耳斯(Van der Waals)提出在实际气体 分子中,两个中性分子(或原子)间存在着“分子力”, 即范德瓦耳斯力。由范德瓦耳斯力的作用所组成的晶体称 为分子晶体。
范德瓦耳斯结合往往产生于原来具有稳固电子结构的 原子或分子之间,如:具有满壳层结构的惰性气体元素, 或价电子已用于形成共价键的饱和分子。
18
固体物理
固体物理学
共价键与离子键间的混合键
完全离子结合(如NaCl):正负离子通过库仑相互 作用结合在一起, Na+和Cl-的电子云几乎没有重叠。
19
固体物理
固体物理学
完全共价结合(如金刚石):相邻两个C原子各出一个 未配对的自旋相反的电子归这两个原子所共有,在这两个原 子上找到电子的概率相等,即这两个C原子对共价键的贡献
15
固体物理
固体物理学
1
1 2
(j2s
j2 px
j2 py
j2 pz
)
2
1 2
(j2s
j2 px
j2 py
j2 pz
)
3
1 2
(j2s
j2 px
j2 py
j2 pz
)
4
1 2
(j2
s
j2 px
j2 py
j2pz )
“杂化轨道”
原来在2s和2p轨道上的4个电子,分别处于 1 , 2 , 3 , 4
21
固体物理
固体物理学
1. 有效离子电荷 q*
以 GaAs 为例:GaAs的离子实分别为带+3q 和+5q 的离 子Ga3+和As5+,每一对Ga 和As 共有8个价电子。 (1) 若为完全的共价结合,共价键上的每对电子均分在两 个近邻原子上,则:Ga-1As+1。 (2) 若为完全的离子结合(设Ga原子的3个价电子转移到As 原子),则:Ga3+As3-。 (3) 实际介于二者之间,引入有效离子电荷q*,(以电子 电荷为单位)Ga原子的q*肯定介于-1和+3之间。
2.4 分子力结合
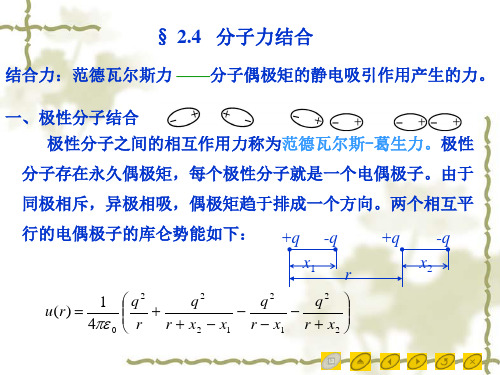
2、 非极性分子晶体的结合能 惰性气体分子间的相互作用是瞬时偶极矩与瞬时感应 偶极矩间的作用,可以类似于极性分子与非极性分子的吸引 势,则惰性气体分子间的吸引势为: A
-
r6
排斥势的计算较复杂,一般由实验得出与r12成反比,即 1 排斥能 r 12 A B u( r ) 6 12 因此一对分子间的互作用势能为:
1 ' A6 6
N j
aj
A6 , A12 是仅与晶体结构有关的常数。
3、平衡时体积弹性模量和晶体的结合能 (1)、晶体的结合能
dU dR 0
R0
2 A12 R0 A 6
1/ 6
U 0 U ( R0 )
2 A6
2 A12
N
平衡时最近邻原子 间距离
q 2 x2 x1 p1 p2 3 2 0 r 2 0 r 3
可见极性分子之间的吸引势与r3成反比。 二、极性分子与非极性分子的结合 非极性分子被极性分子的电场极化而产生诱导偶极矩。诱 导偶极矩与极性分子永久偶极矩间的相互作用力称为范德瓦尔
斯---德拜力。
极性分子与非极性分子的库仑势: 设p1是极性分子的偶极矩,则在偶极矩延长线上的电场为: p1 E 2 0 r 3
2
x1, x2 , x2 x1 r
2 2 2 x2 x1 x2 x1 x1 x1 x2 x2 q 11 1 1 4 0 r r r r r r r
18
2
1 12 6 12.094 64
1 12 6 12.75 8
1 1 1 A6 2 6 12 6 6 1 ( 2 )6 j 1 a j
2.1离子性结合解析

定义为晶体的结合能,这里记作W。
粒子(原子、分子或离子)从自由状态结合成晶体
的过程中要释放出能量;反之,稳定的晶体分离为 各个自由粒子必须吸收能量。
结合能愈大,形成的晶体愈稳定。
结合能W的数学描述
定义:E0为晶体能量;EN为组成该晶体的N 个原子处于自由状态的总能量,则结合能W 可表示为:
(
j i
b )] n aj
(2)记作B
离子晶体总相互作用能
q B U N [ n] 4 0 r r
2
所以,只有当
?
n ? W U ( r0 ) B ? r0 ?
(1)马德隆常数α的确定 (Madelung constant)
以第i个离子为参考离子,设最近邻距离为r,
则
即可得到:
rij a j r
N N
q2 b q2 N 1 1 U N ( n ) N[ ( ) n 4 r r 4 r a r j i j i 0 ij ij 0 j
(1)马德隆常数(记作α) 同号为负,异号为正
K E A H N 最近邻 4个 a j 1 次近邻 4个 a j 2 G M F L 解:设最近邻距离为r, A为中心参考离子,我们 选取不同的中性离子组来 计算,作以比较。 第一种选法 选取中性离子组EFGH来计算α; 贡献因子1/2 贡献因子1/4
异号 同号
rij a j r
4 11 2 4 1 2 1 4 1.2929
Na 基本特点:以离子而不是以原子为结合单元,
NaCl,CsCl等碱金属和卤素形成的化合物。
Cl
即靠正负离子间的静电库仑作用相互结合,原 子间以离子键相互作用。 硬度较大,导电性也很弱等。
范德瓦尔斯结合剖析

矩为p1,r处电场应正比于p1/r3,原子2感应到的瞬时 电偶极矩为p2, 则r处电场应正比于
p2
E
p1
r3
(为原子极化率)
相互作用能
U
p1 p2 r3
p12
r6
,可知U随r增加而迅速下
降,表明这种相互作用很弱。
两个氦原子之间由于电子运动产生瞬时偶极子的 相关作用
(a)吸引态
氦原子
(b)排斥态
A12
(
r0
)12
A6
(
r0
)6
2NA62
4 A12
8.6N
K的表达式
2U
U
K (V V 2 )V0
V 2 2Nr3
2N
A12
(
r
)12
A6 ( r
)6
K
4A12 3
(
A6 A12
5
)2
75 3
惰性气体的林纳德-琼斯势参数
Ne
Ar
Kr
Xe
ε(ev) 0.0031 0.0104 0.0140 0.0200
第1近邻:12个 aj=1
第2 近邻:6个
aj= 2
第3 近邻:24个 aj= 3
A6 1216 6 ( 2 )6 24 ( 3)6 13.639
A12 12112 6 ( 2 )12 24 ( 3)12 12.127
若晶胞再选大些,则数据将更准确些, 通常对于面心立方结构:A6=14.45392, A12=12.13188。
构均为面心立方晶格。
公式:
A12
N ji
1 a1j2 , A6
N ji
1
a
6 j
范德瓦耳斯结合
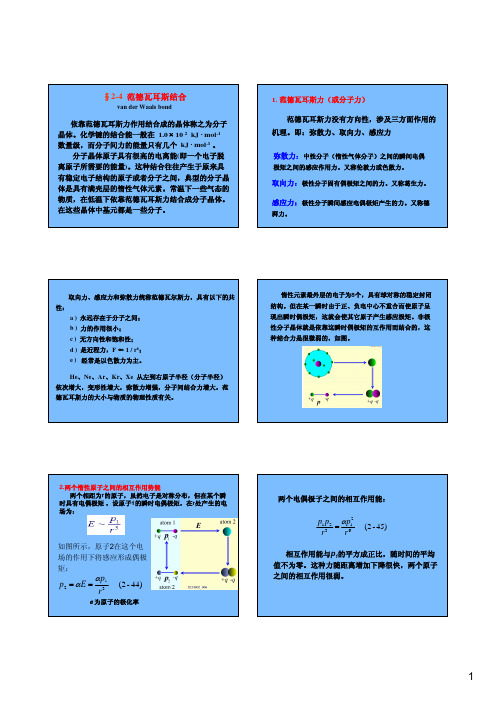
2.两个惰性原子之间的相互作用势能两个相距为r 的原子,虽然电子是对称分布,但在某个瞬时具有电偶极矩,设原子1的瞬时电偶极矩,在r 处产生的电场为:α为原子的极化率如图所示,原子2在这个电场的作用下将感应形成偶极矩:44)-(2 321r pE p αα==范德瓦尔斯力引起的吸引能都与分子间距r 的6次方成反比,也称为范德瓦耳斯相互作用能,写为:a 、b 为两个参数。
排斥能的经验公式为:12)(r b r u =排斥因此两分子间的相互作用能可以表示为:6)(r ar u −=吸引126)(rbr a r u +−=(2-46)3.范德瓦耳斯相互作用能我们作出(2-47)式的函数曲线图,看式中的参数ε、σ所代表的意义。
εσ4)()( r U x f rx ==;令61211)(xx x f −=则(2-47)式子可以写为:47)-(2 4)(6126⎥⎥⎦⎤⎢⎢⎣⎡⎟⎠⎞⎜⎝⎛−⎟⎠⎞⎜⎝⎛∈=r r r u σσ引入新的参量:εand σ,两个原子的相互作用势能可以表示为:4.勒纳-琼斯(Lennard -Jones )势12.12 0612 ,0)(61713==∴=+−=−−x x x dxx df 即:曲线极小值对应于:U(r)/4εr/σ1.12作出(2-47)式的函数曲线如图所示:常数所代表的意义:参数σ反映了排斥力的作用范围,单位是Å(埃);ε反映吸引力的强弱,单位是erg (尔格)。
忽略惰性气体的动能,由N 个惰性气体原子组成的分子晶体的总相互作用势能为:⎥⎥⎦⎤⎢⎢⎣⎡⎟⎠⎞⎜⎝⎛−⎟⎠⎞⎜⎝⎛=6612122)(r A r A N r U σσε(2-48)A 12、A 6是与晶体结构有关的晶格求和常数。
对于面心立方结构:A 12=….≈12.13;A 6=…. ≈14.45求解A 12、A 6的方法看后面的例题。
根据势能函数的最小值可以确定晶格常数、结合能和体变模量。
晶体的结合

对比下表各个周期,可看出以下两个特性:
(1)周期表由上到下,负电性逐渐弱;
(2)周期表越往下,一个周期内负电性的差别也越小。 负
IA Li IIA Be 1.5 Mg 1.2 Ca 1.0 B IIIB
电
IVB C 2.5 Si 1.8
性
VB N VIB O 3.5 S 2.5 Se 2.4 VIIB F
2.对金属导电现象的解释:
金属的导电可理解为金属的自由电子在外加电场的影 响下,沿外加电场的电势梯度定向流动,形成电流。 一般情况下金属是良导体,可认为没有电阻存在。但 实验事实告诉我们,随温度的上升金属的电导率下降。 金属的电导率主要取决于自由价电子数和电子迁移率 (即电子运动的速度)。σ= neμ。在金属中的自由 价电子的数目是较多的且基本上不随温度而变,所以 当温度升高的时候,金属电导率的变化主要取决于电 子运动速度。因为晶格中的原子和离子不是静止的, 它们在晶格的格点上作一定的振动,且随温度升高这 种振动会加剧,正是这种振动对电子的流动起着阻碍 作用,温度升高,阻碍作用加大,电子迁移率下降, 电导率自然也下降了。
★共价晶体的基本特性:高力学强度、高熔点、
高沸点和低挥发性;低温时电导率很低,温度增 加或加入杂质时电导率增大(如半导体硅、锗 等)。 ★ 共价晶体的特点及与键性的相关性: 共价键晶体结构稳定没有可移动的电子,所以 不导电,熔点从低到高范围较宽,但纯共价晶体 的熔点一般都是很高的,硬度很大(同共价晶体 的结合力很强相联系,如金刚石的高强度)。
共价键的方向性:共价键形成时,在可能的范围 内,一定采用电子云密度最大的方向(增大电子 云的重叠,使共价键稳固,相应的结合能大。)
所以当某个原子在几个方向与其它原子形成几个 共价键时,由于方向性的影响,键有一定趋向,故产生 键与键之间的特定夹角,这一特性对于分析原子晶体的 几何结构是有帮助的。 1.NH3中有三个共价键(饱和性),相互夹角接近90° (方向性)
范德瓦尔斯层间耦合

范德瓦尔斯层间耦合范德瓦尔斯层间耦合(Van der Waals interlayer coupling)是指在二维材料中,由于范德瓦尔斯力的作用,不同层之间发生的相互作用。
范德瓦尔斯力是一种虚拟的力,由于电子云的重叠而产生,与两个物体的距离的6次方成反比。
在二维材料中,范德瓦尔斯力成为了不同层之间的主要相互作用力,影响了材料的结构和性质。
范德瓦尔斯层间耦合的重要性在于它可以改变二维材料的电子结构和磁性。
通过调节不同层之间的距离和相对方向,可以调控材料的能带结构和带隙大小。
例如,在二维铁磁材料中,通过调节不同层之间的范德瓦尔斯耦合强度,可以实现磁性相变。
另外,范德瓦尔斯层间耦合还可以改变二维材料的光学性质。
通过调节不同层之间的距离和相对方向,可以调控材料的吸收谱和发射谱,从而实现光学器件的调控。
范德瓦尔斯层间耦合的研究不仅对于理论物理学有重要意义,也对于实际应用有很大潜力。
范德瓦尔斯层间耦合可以用于设计新型的二维材料和器件。
例如,通过在不同层之间插入特定的分子或原子,可以实现材料的功能化和多功能性。
另外,范德瓦尔斯层间耦合还可以用于设计新型的自旋电子器件。
通过调节不同层之间的范德瓦尔斯耦合强度和方向,可以实现自旋的控制和传输,从而实现自旋逻辑门和自旋存储器。
范德瓦尔斯层间耦合的研究还面临一些挑战。
首先,范德瓦尔斯层间耦合的强度很小,通常只有几meV。
因此,在实验上实现范德瓦尔斯层间耦合的调控是一项技术上的挑战。
其次,范德瓦尔斯层间耦合的理论模型还不完善,需要进一步的研究和发展。
最后,范德瓦尔斯层间耦合的机制还不清楚,需要通过实验和理论的相结合来揭示。
总的来说,范德瓦尔斯层间耦合在二维材料中起着重要作用,影响了材料的结构和性质。
通过调节不同层之间的距离和相对方向,可以调控材料的电子结构、磁性和光学性质。
范德瓦尔斯层间耦合的研究不仅对于理论物理学有重要意义,也有很大的应用潜力。
然而,范德瓦尔斯层间耦合的研究还面临一些挑战,需要进一步的实验和理论研究来解决。
2.3共价结合 金属结合 范德瓦尔斯结合 电负性

“杂化轨道”
2.特征
共价键结合比较强:原子晶体具有高力学强度、高熔点、 高沸点和低挥发性的特点,导电率和导热率低。原子晶体一般 属于半导体或绝缘体。 §2-3 金属性结合 1.结构 结合力:金属键 第Ⅰ族、第Ⅱ族及过渡元素晶体都是典型的金属晶体。 金属晶体多采取配位数为12的密堆积,少数金属为体心立 方结构,配位数为8。
非极性分子被极性分子的电场极化而产生的诱导偶极矩与
极性分子永久偶极矩间的相互作用力称为范德瓦尔斯---德拜 力。 非极性分子的瞬时偶极矩间相互作用力称为范德瓦尔斯伦敦力。
1.结构 具有饱和电结构的原子或分子+范德瓦尔斯--伦敦力。惰性
气体分子He、Ne、Ar、Kr、Xe在低温下形成非极性分子晶体。
dU dR 0
R0
2A R0 12 A 6
1/ 6
U 0 U ( R0 )
2 A6
2 A12
N
平衡时最近邻原 子间距离
平衡时总的互作 用势能
2 U0 A6 平均每个原子的能量u0为:u0 N 2A12
晶体的结合能: E
b
U 0 2 A
12 6 U ( R ) 2 N A12 A6 R R
式中
A12
'
j
N
1
a 12 j
'1 , A6 a 6 j
N j
a j是参考原子i与其它任一原子j的距离rij同最近邻原子间
距R的比值( a j rij R )。试计算面心立方的A6和A12。 (1)只计及最近邻原子; (2)计及最近邻和次近邻原子。 解: (1)面心立方,最近邻原子有12个,
晶体的结合类型

2.晶体的结合类型
2.4分子结合
单原子分子或共价分子由范德瓦尔斯力凝聚而成的晶体 葛生力
- + + -
+
极性分子
-
+ -
+ + + -
2
例:两原子的相互作用能可由 u ( r ) m n 得到,如果m=2, r r n=10. 且两原子形成一稳定的分子,其核间距为0.3nm, 平稳时
能量为-4eV.求:1). 解:1)
α,β; 2). 使此原子分裂时的临界间距。 (1) (2)
5 2 19 2 u ( r ) r 4.5 10 eV m 由(1)、(2)得 0 0 4 8 r0 5.9 10 96 eVm10 5 d 2u ( r ) 2 3 10 11 2) 4 0 2 12 dr rm rm rm
V R
2U U R 2U R U 2 R ( 2) ( ) V R V VR V R V 2 V
2U R 2 U 2 R ( ) 2 V R V 2 R
平衡时 =0
晶体平衡时体积弹性模量:
R0 2U 1 2U K ( 2 ) R R0 ( 2 ) R R0 9 NR0 R 9V0 R
极性分子与非极性分 子之间的相互作用如图 所示。
极性分子与非极性分子间的相互作用
在偶极子延长线上的电场为 设 p1是极性分子的电矩 ,
2 p1 E 4 r 3
非极性分子的感生电偶极矩与E成正比,即
范德瓦尔斯分子相互作用势能大物

范德瓦尔斯分子相互作用势能大物范德瓦尔斯相互作用是描述分子之间非化学键相互作用的一种力。
这种相互作用是由于偶极矩的不同或者永久偶极矩引起的。
相对于化学键的共价键、离子键和金属键,范德瓦尔斯相互作用非常弱,但是它在分子间距很远的情况下开始发挥作用。
在生物体系中,范德瓦尔斯相互作用起着至关重要的作用,对于蛋白质折叠、分子间识别、药物和受体的相互作用等具有重要的意义。
吸引项由一个常数C6和分子之间的距离r的幂次-6组成。
这一项表示当分子之间距离适当时,它们之间存在吸引力。
这个吸引力是由于分子中的电子云会在彼此靠近时发生重叠,导致周围电子的电荷分布发生变化,从而引发电偶极矩的产生。
排斥项由一个常数C12和分子之间的距离r的幂次-12组成。
这一项表示当分子之间距离过近时,它们之间存在排斥力。
这个排斥力是由于两个分子的电子云之间的静电排斥力造成的,这是由于两个电子云中的电子靠近时会导致电子之间的排斥。
在低能量区域,吸引力项主导范德瓦尔斯相互作用,而在高能量区域,排斥力项起主导作用。
通过调整C6和C12的值,可以控制分子之间的相互作用强度。
范德瓦尔斯相互作用的重要性不仅表现在分子之间的相互吸引、排斥和结合上,还在于决定分子的结构和性质。
例如,蛋白质的三维结构往往是由范德瓦尔斯相互作用稳定的,而药物和受体之间的相互作用也是通过范德瓦尔斯力来实现的。
此外,范德瓦尔斯相互作用还可以通过一些方法来增强或减弱。
例如,通过增加溶液中的离子浓度,可以屏蔽范德瓦尔斯相互作用,从而使得分子更容易分散。
另外,通过在分子结构中引入极性基团,也可以增强分子间的范德瓦尔斯相互作用。
总而言之,范德瓦尔斯相互作用是不可或缺的一种力,它在分子间的相互作用、结构稳定性和物性上都发挥着重要作用。
通过深入理解范德瓦尔斯相互作用,我们可以更好地理解分子结构和性质,并在研究和应用中更好地利用这种相互作用。
范德瓦尔斯方程推导

范德瓦尔斯方程推导范德瓦尔斯方程(也称为理想气体方程)是描述气体状态的一个基本方程,它是由荷兰物理学家约翰内斯·范德瓦尔斯于1873年提出的。
这个方程可以用来计算气体的压力、温度和体积之间的关系。
范德瓦尔斯方程的推导是基于分子动理论和统计物理学的基本原理。
在1827年,法国科学家克劳修斯·克拉贡在研究气体状态方程时提出了最早的分子动理论,认为气体的压力和体积与分子的碰撞有关。
首先,我们假设气体分子之间不存在相互作用力,这意味着气体是完全理想的。
在这种情况下,气体分子是一个粒子系统,遵循玻尔兹曼分布。
根据统计物理学的理论,玻尔兹曼分布可以表达为:f(v) = Ae^(-mv^2/(2kT))其中,f(v)是分子速度的概率密度函数,v是分子的速度,m是分子的质量,k是玻尔兹曼常数,T是气体的温度。
我们希望得到气体的状态方程,即压力P与温度T、体积V之间的关系。
根据理想气体的定义,我们可以使用分子动力学的原理来推导范德瓦尔斯方程。
首先,我们考虑气体分子在一个边长为L的立方体容器中运动。
由于完全理想气体没有相互作用力,所以分子之间的碰撞可以视为完全弹性碰撞。
在一个时间间隔dt内,分子在x,y,z三个方向上所接到的动量变化可以表示为:dpx = -2mvxdtdpy = -2mvydtdpz = -2mvzdt根据力学定律,动量的变化等于所受到的力乘以时间间隔,因此可以得到:Fxdx = -2mvxdtFydy = -2mvydtFzdz = -2mvzdt其中,Fx、Fy、Fz是分子所受到的力。
根据理想气体状态方程P = F/A,我们可以将上式转化为:Pdx = -2mvxdtPdy = -2mvydtPdz = -2mvzdt现在我们考虑在立方体容器中,具有不同速度的分子产生的压力总和。
根据速度分布函数f(v),可以得到在v到v+dv之间的速度范围内,分子对于x方向产生的压力为:P(x) = ∫[v=v1 to v2] Pdx = ∫[v=v1 to v2] -2mvxdt =∫[v=v1 to v2] -2mvxx/(v) dv同样的,我们可以得到分子对于y和z方向产生的压力分别为:P(y) = ∫[v=v1 to v2] -2mvy yy/(v) dvP(z) = ∫[v=v1 to v2] -2mvz zz/(v) dv将上述三个方向的压力相加,我们可以得到分子在整个容器内产生的总压力P:P = P(x) + P(y) + P(z)= ∫[v=v1 to v2] (-2mvxx/(v) + -2mvy yy/(v) + -2mvzzz/(v)) dv由于我们假设了理想气体分子之间没有相互作用力,所以分子在x、y、z三个方向上的速度分布函数相同,即v1和v2可以相等。
范德瓦尔斯气体的绝热自由膨胀

范德瓦尔斯气体的绝热自由膨胀咱们今天聊聊一个挺有意思的物理现象——范德瓦尔斯气体的绝热自由膨胀。
你听说过这个吗?名字一听就觉得有点高深莫测,实话说,刚开始接触这个概念时,我也觉得它离我们日常生活有点远。
不过,你看,物理本来就得跟我们生活紧密结合才能不那么枯燥,是吧?所以今天我们就轻松点,来聊聊这个有点像“魔法”一样的过程。
放心,咱们不是要挑战什么高深的理论,只是想搞明白这背后的小故事。
什么叫做“绝热自由膨胀”呢?好家伙,一听这名字就感觉很复杂,实际上它说的就是气体在不跟外界交换热量的情况下,自己在一个容器里膨胀开来。
想象一下,你拿一个气球,吹得满满的,然后戳破它,气体就会迅速散开,膨胀,空气迅速充满周围的空间。
听起来是不是很简单?但实际上,这个“绝热”这一点就让它跟平常我们理解的膨胀有些不同了。
要明白这一点,咱们得先搞清楚一个核心概念——温度。
在我们的常规认知中,气体膨胀的时候温度应该下降,尤其是那种“自由膨胀”——气体无拘无束地迅速扩展,能量和温度都应该有所变化。
可问题是,如果气体的膨胀是绝热的(也就是说,没有热量进出),它怎么可能在膨胀的过程中改变温度呢?哎,这就是范德瓦尔斯气体的特别之处。
它不像理想气体那么简单,理想气体会按照很简单的公式来运行,而范德瓦尔斯气体的行为就更复杂了。
它不仅考虑了气体分子之间的相互作用力,还考虑了气体分子的体积。
所以,当它膨胀时,除了温度的变化,还会有一些额外的因素在起作用。
说到这里,可能你会有点儿疑惑:咱们不就是讨论气体膨胀吗,怎么一会儿聊温度变化,一会儿又聊分子间的相互作用?这不都没什么关系吗?其实不然!想象一下,如果是理想气体,咱们就简单地按照理想气体方程来算,它的膨胀就是一个完美的过程——没有能量损失,没有相互作用,一切都井井有条。
但是范德瓦尔斯气体不同,它的分子间有吸引力,尤其是在气体膨胀的过程中,分子之间的这种吸引力会让气体不那么“乖乖地”膨胀,反而会导致一些额外的“乱象”。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
例如: —— 惰性元素具有球对称,结合时排列最紧密以使势能最低 —— Ne、Ar、Kr、Xe的晶体都是面心立方 —— 透明的绝缘体,熔点特低 —— 分别为24K、84K、117K和161K
固体物理(Solid Physics) 重庆交通大学
范德瓦尔斯力的本质
1.葛生力(Keesom,亦称静电力)
葛生力:极性分子的永久偶极矩间的静电相互作 用。 最初,人们对范德瓦耳斯键的本质的认识来源于 葛生力(由Keesom1912年提出而得名)。 显然这种静电吸引力大小与偶极矩取向有关。
固体物理(Solid Physics) 重庆交通大学
有金属键的特点。(石墨是一种良导体,可做电
极等) Ⅲ.层与层之间以范德瓦尔斯键结合。(结合力 弱,所以石墨质地疏松,在层与层之间可插入其 它物质,制成石墨插层化合物。)
——石墨是共价键、金属键和分子键的混合键。
固体物理(Solid Physics)
重庆交通大学
2.SiO2、P2O5、B2O3等是形成玻璃的主要形
晶体总的势能
1 12 6 U ( r ) N ( 4 )[ A12 ( ) A6 ( ) ] 2 r r
—— 非极性分子晶体的晶格常数、结合能和体变模量
dU 0 晶格常数 dr r r0
d 2U 平衡状态体变模量 K (V ) 2 V0 dV
晶体的结合能 W U ( r0 )
—— 原子的极化率
2 p p p 两个电偶极子之间的相互作用能 E 1 2 1 6 3 r r
—— 作用能与p1的平方成正比,对时间的平均值不为零 —— 力随距离增加下降很快,两个原子之间的相互作用很弱 两个原子的相互作用势能
A B u( r ) 6 12 间作用力(分子键)成键;通过电偶极
矩(极性分子之间)、诱导偶极矩(极性分子和非极性 分子之间)、瞬时偶极矩(非极性分子之间)之间的相 互作用而结合; (2)没有方向性和饱和性。
固体物理(Solid Physics)
重庆交通大学
分子晶体的基本特性:
——结合力弱、熔点低、硬度小(大部分有机化合物晶体和、 惰性气体等在低温下形成的晶体均属分子晶体)。
对伦敦力或色散力,可以采用量子力学进行具体计算。
固体物理(Solid Physics) 重庆交通大学
范德瓦尔斯力的特性
范德瓦尔斯力是普遍存在于原子或分子间的 一种力,即使其偶极矩为零,这种力依然存 在(如色散力)。 它是吸引力,力的大小与r-7成正比,作用范 围在几个Å。
固体物理(Solid Physics)
重庆交通大学
两个惰性原子之间的相互作用势能
—— 两个相距为r的原子,原子中电子是对称分布 —— 偶极矩作用 设原子1的瞬时电偶极矩 在r处产生的电场
p1
p1 原子1的电场 E ~ 3 r
固体物理(Solid Physics) 重庆交通大学
p1 E~ 3 r
原子2在电场的作用下感应偶极矩
p2 E
固体物理(Solid Physics)
重庆交通大学
3.伦敦力(London,色散力)
惰性气体分子的电子云分布是球对称的,其偶极矩P为
零(非极性分子),其相互间作用力应为零,但实验表 明在惰性气体分子(非极性分子)之间仍然存在着相互 作用力。 这种作用力的产生按前面的思路都得不到解释,故此, 除葛生力(静电力)、德拜力(诱导力)外,分子间相 互作用应存在第三种力,1930年London应用量子力 学证实这种力的存在,称为伦敦力或色散力。
对于大多数晶体而言,它们的 键并不单纯属于某一种,而具 有某种综合性。换言之,许多 晶体存在混合键。
1.石墨: Ⅰ.C原子的三个价电子同最 近邻的三个C原子组成共价键,
三个共价键几乎在同一平面上, 构成层状结构。
固体物理(Solid Physics) 重庆交通大学
Ⅱ.第四个价电子则自由的在整个层内活动,具
固体物理(Solid Physics)
重庆交通大学
2.德拜力(Debye,亦称诱导力)
Keesom所考虑的只是极性分子间的永久偶极矩的相互 作用,但某一个分子的电荷分布不可避免地要受到其它 分子电场的影响,由此产生诱导偶极矩。 由两个分子诱导偶极矩间的相互作用而产生诱导力或德
拜力。
所以不难理解极性分子与非极性分子之间也存在作用力, 即来源于非极性分子,且可被极性分子的电场极化而产 生诱导偶极矩。(1912年由Debye提出)
—— 非极性分子晶体依靠瞬时偶极矩的相互作用而结合 —— 作用力非常微弱
—— 1873年范德瓦耳斯(Van der Waals) 提出在实际气体分 子中,两个中性分子间存在着“分子力”
固体物理(Solid Physics) 重庆交通大学
原子呈现出瞬时偶极矩
固体物理(Solid Physics)
重庆交通大学
固体物理(Solid Physics)
重庆交通大学
这种力的本质可以用非极性分子的瞬间偶极矩的相互作 用来简要说明。
非极性分子(如惰性气体分子)其核外电子云分布是球 对称的,既不具有永久性偶极矩。 但按照量子理论的观点,这所表明的是在原子核周围电
子出现的几率是相同的,则在某一段时间内偶极矩平均 值为零。但在某一瞬间,电子云在核外分布可能存在不 均匀性,因而非极性分子可以具有一个瞬间偶极矩。 非极性分子可以通过瞬间偶极矩的相互作用或相互极化 而产生吸引力。
—— 勒纳-琼斯(Lennard-Jones)势 晶体总的势能 — N 个原子
1 12 6 U ( r ) N ( 4 )[ A12 ( ) A6 ( ) ] 2 r r
—— 1/2因子: 相互作用能为两个原子共有 —— A12和A6: 与晶格结构有关的求和项
固体物理(Solid Physics) 重庆交通大学
固 体 物 理
Solid Physics 王 念
重庆交通大学 土木建筑学院材料科学与工程系
第二章 固体的结合
离子性结合 共价结合 金属性结合 范德瓦尔斯结合 元素和化合物晶体结合的规律性
§ 2-4 范德瓦耳斯结合
VIII 族元素在低温时结合成的晶体 —— 非极性分子晶体
分子晶体的作用力
—— 惰性元素最外层8个电子,具有球对称的稳定封闭结构 —— 某一瞬时正负电中心不重合使原子呈现出瞬时偶极矩 —— 使其它原子产生感应极矩
—— B/r12: 重叠排斥势能,A和B为经验参数,都是正数
固体物理(Solid Physics)
A B 两原子相互作用势能 u( r ) 6 12 r r 引入新的参量 and 4 6 A, 4 12 B
6 u ( r ) 4 [( ) ( ) ] 相互作用势能 r r 12
成体,Stanworth发现均具有混合型键。其中
SiO2有共价键──离子键;P2O5有共价键──离子 键;B2O3有共价键──离子键。形成玻璃必须为
混合键。
3.大部分合金都具有金属键──共价键的混合键
型,同时键的性质可随成分变化,故可通过改变
成分改变键性比例,从而改进材料性能等。(键 的计算、设计即电子结构的计算、设计→材料设 计。)
固体物理(Solid Physics) 重庆交通大学
*氢键与氢键晶体
氢键:一个氢原子同时与两个电子亲和能大、
原子半径较小的原子(如F、O、N等)等结 合而形成的特殊化学键。
——有方向性和饱和性。 典型的氢键晶体有:冰晶体、 KH 2 PO4 晶 体(铁电材料)。
固体物理(Solid Physics) 重庆交通大学
固体氟化氢:
F
F
H H F H
F H F
H的唯一外层电子与F形成共价键后,因氢原子 核暴露,故还可以与负电性较大的F通过库伦力 而结合; 若有第三个负离子要与H核结合,则受到已与H
核结合的2个F的斥力,所以氢键有方向性和饱
和性。
固体物理(Solid Physics) 重庆交通大学
* 混合键与混合键型晶体
