奇数阶魔方阵
奇数幻方
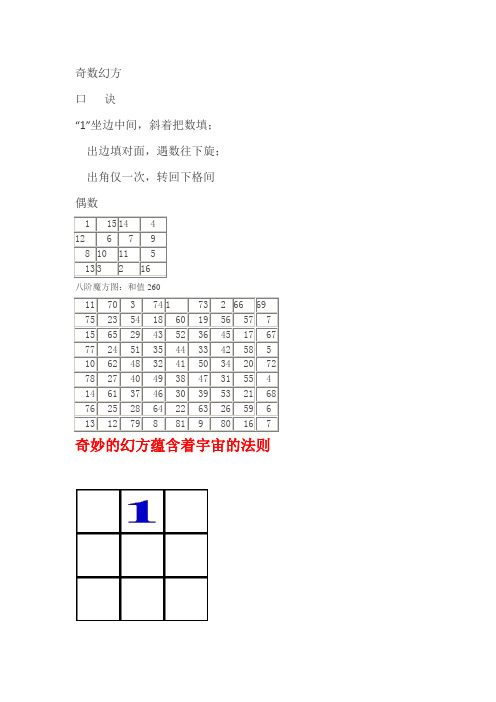
奇数幻方口诀“1”坐边中间,斜着把数填;出边填对面,遇数往下旋;出角仅一次,转回下格间偶数八阶魔方图:和值260一、幻方及其起源在《射雕英雄传》中郭靖、黄蓉二人被裘千仞追到黑龙潭,躲进瑛姑的小屋。
瑛姑出了一道题:数字1~9填到三行三列的表格中,要求每行、每列、及两条对角线上的和都相等。
这道题难倒了瑛姑十几年,被黄蓉一下子就答出来了。
4 9 23 5 78 1 6这就是一个最简单的3阶平面幻方(三阶幻方,幻和为15,中间数字必填5)。
幻方又称为魔方,方阵或厅平方,它最早起源于我国。
公元13世纪的宋朝数学家杨辉已经编制出3-10阶幻方,记载在他1275年写的《续古摘厅算法》一书中。
杨辉称之为纵横图。
我国的纵横图通过东南亚国家,印度、阿拉伯传到西方。
由于纵横图具有十分奇幻的特性,西方把纵横图叫作Magic Square,翻译成中文就是“幻方”或“魔方”。
在一个由若干个排列整齐的数组成的正方形中,图中任意一横行、一纵行及对角线的几个数之和都相等,具有这种性质的图表,称为“幻方”。
幻方图中任意一横行、一纵行及对角线的几个数之和都相等的这种性质,称为幻方法则。
关于幻方的起源,我国有“河图”和“洛书”之说。
相传在远古时期,伏羲氏取得天下,把国家治理得井井有条,感动了上天,于是黄河中跃出一匹龙马,背上驮着一张图,作为礼物献给他,这就是“河图”,也是最早的幻方。
伏羲氏凭借着“河图”而演绎出了八卦,后来大禹治洪水时,洛水中浮出一只大乌龟,它的背上有图有字,人们称之为“洛书”。
“洛书”所画的图中共有黑、白圆圈45 个。
把这些连在一起的小圆和数目表示出来,得到九个。
这九个数就可以组成一个纵横图,人们发现,这个图案每一列,每一行及对角线,加起来的数字和都是一样的。
也有人认为"洛书"是外星人遗物;而"河图"则是描述了宇宙生物(包括外星人)的基因排序规则,幻方是外星人向地球人的自我介绍。
魔方阵算法及C语言实现

魔方阵算法及C语言实现1 魔方阵概念魔方阵是指由1,2,3……n2填充的,每一行、每一列、对角线之和均相等的方阵,阶数n = 3,4,5…。
魔方阵也称为幻方阵。
例如三阶魔方阵为:魔方阵有什么的规律呢?魔方阵分为奇幻方和偶幻方。
而偶幻方又分为是4的倍数(如4,8,12……)和不是4的倍数(如6,10,14……)两种。
下面分别进行介绍。
2 奇魔方的算法2.1 奇魔方的规律与算法奇魔方(阶数n = 2 * m + 1,m =1,2,3……)规律如下:1.数字1位于方阵中的第一行中间一列;2.数字a(1 < a ≤ n2)所在行数比a-1行数少1,若a-1的行数为1,则a的行数为n;3.数字a(1 < a ≤ n2)所在列数比a-1列数大1,若a-1的列数为n,则a的列数为1;4.如果a-1是n的倍数,则a(1 < a ≤ n2)的行数比a-1行数大1,列数与a-1相同。
2.2 奇魔方算法的C语言实现1 #include <stdio.h> 2// Author: / 3// N为魔方阶数 4#define N 115 6int main()7{8int a[N][N]; 9int i;10 int col,row;1112 col = (N-1)/2;13 row = 0;1415a[row][col] = 1;1617for(i = 2; i <= N*N; i++)18 {19if((i-1)%N == 0 )20 {21 row++;22 }23else24 {25// if row = 0, then row = N-1, or row = row - 126 row--;27 row = (row+N)%N;2829// if col = N, then col = 0, or col = col + 130 col ++;31 col %= N;32 }33 a[row][col] = i;34 }35for(row = 0;row<N;row++)36 {37for(col = 0;col < N; col ++)38{39 printf("%6d",a[row][col]);40 }41printf("\n");42 }43return0;44 }3 偶魔方的算法偶魔方的情况比较特殊,分为阶数n = 4 * m(m =1,2,3……)的情况和阶数n = 4 * m + 2(m = 1,2,3……)情况两种。
数据结构课程设计之奇数魔方阵

长沙理工大学《数据结构》课程设计报告田晓辉学院计算机与通信工程专业计算机科学与技术班级计08-01 学号************学生姓名田晓辉指导教师陈倩诒课程成绩完成日期2010年7月10日课程设计成绩评定学院计算机与通信工程专业计算机科学与技术班级计08-01学号200850080110 学生姓名田晓辉指导教师陈倩诒完成日期2010年7月10日指导教师对学生在课程设计中的评价指导教师对课程设计的评定意见课程设计任务书计算机与通信工程学院计算机科学技术专业用C语言解决魔方阵的问题学生姓名:田晓辉指导老师:陈倩诒摘要本课程设计主要解决设计一个n×n的矩阵中填入1到n2的数字(n为奇数),使得每一行、每一列、每条对角线的累加和都相等的问题。
在课程设计中,系统开发平台为Windows 7,程序设计语言采用Visual C++6.0,程序运行平台为Windows 98/2000/XP/7。
在程序设计中,采用了C 语言结构化程序设计思想和过程设计方法,以功能函数为基本结构,对问题中的要求做出了准确的实现。
程序通过调试运行,初步实现了设计目标。
关键词程序设计;C++6.0;结构化;过程设计;功能函数目录1.引言 (1)1.1课程设计目的 (1)1.2课程设计内容 (1)2.设计思路与方案 (2)3.详细实现 (3)3.1数据结构与数据存储表示 (3)3.2功能函数 (3)3.3函数逻辑功能调用图 (5)3.4本程序执行流程图 (6)4.运行环境与结果 (7)4.1程序运行环境 (7)4.2程序运行结果 (7)5.结束语 (9)参考文献 (10)附录源程序代码 (11)1 引言本课程设计主要解决设计一个n×n的方阵中填入1到n2(n为奇数)的数字,使得每一行、每一列、每条对角线上各个数字累加的和都相等的问题。
1.1 课程设计目的通过这次课程设计进一步了解了二维数组的使用方法和一些基本的设计思路。
数据结构课程设计之奇数魔方阵

长沙理工大学《数据结构》课程设计报告田晓辉学院计算机与通信工程专业计算机科学与技术班级计08-01 学号************学生姓名田晓辉指导教师陈倩诒课程成绩完成日期2010年7月10日课程设计成绩评定学院计算机与通信工程专业计算机科学与技术班级计08-01学号200850080110 学生姓名田晓辉指导教师陈倩诒完成日期2010年7月10日指导教师对学生在课程设计中的评价指导教师对课程设计的评定意见课程设计任务书计算机与通信工程学院计算机科学技术专业用C语言解决魔方阵的问题学生姓名:田晓辉指导老师:陈倩诒摘要本课程设计主要解决设计一个n×n的矩阵中填入1到n2的数字(n为奇数),使得每一行、每一列、每条对角线的累加和都相等的问题。
在课程设计中,系统开发平台为Windows 7,程序设计语言采用Visual C++6.0,程序运行平台为Windows 98/2000/XP/7。
在程序设计中,采用了C 语言结构化程序设计思想和过程设计方法,以功能函数为基本结构,对问题中的要求做出了准确的实现。
程序通过调试运行,初步实现了设计目标。
关键词程序设计;C++6.0;结构化;过程设计;功能函数目录1.引言 (1)1.1课程设计目的 (1)1.2课程设计内容 (1)2.设计思路与方案 (2)3.详细实现 (3)3.1数据结构与数据存储表示 (3)3.2功能函数 (3)3.3函数逻辑功能调用图 (5)3.4本程序执行流程图 (6)4.运行环境与结果 (7)4.1程序运行环境 (7)4.2程序运行结果 (7)5.结束语 (9)参考文献 (10)附录源程序代码 (11)1 引言本课程设计主要解决设计一个n×n的方阵中填入1到n2(n为奇数)的数字,使得每一行、每一列、每条对角线上各个数字累加的和都相等的问题。
1.1 课程设计目的通过这次课程设计进一步了解了二维数组的使用方法和一些基本的设计思路。
奇数魔方阵的规律

奇数魔方阵的规律奇数魔方阵的排列规律如下:1. 将1放在第一行中间一列。
2. 从2开始直到n×n止各数依次按下列规则存放:每一个数存放的行比前一个数的行数减1,列数加1。
3. 如果上一个数的行数为1,则下一个数的行数为n(指最下一行),例如1在第一行,则2应放在最下一行,列数同样加1。
4. 当上一个数的列数为n时,下一个数的列数应为1,行数减去1。
例如2在第3行最后一列,则3应放在第二行第一列。
5. 如果按上面规则确定的位置上已有数,或上一个数是第一行第n列时,则把下一个数放在上一个数的下面。
例如按上面的规定,4应该放在第1行第2列,但该位置已经被占据,所以4就放在3的下面。
6. 如果按照上面的规则确定的放置位置超出了数字的排列范围(即行号大于n或列号大于n),则将该数放在此行最下面或最左边。
例如,如果数字9按照上述规则应该放在第3行第3列,但该位置超出了数字的排列范围,因此9将放在第3行的最下面。
7. 无论数字存放在哪个位置,只要按照上述规则进行移动,就可以保证奇数魔方阵的完整性。
这种排列规律是基于一个数学原理,即任何一个奇数都可以表示为1与若干个2、3、4、5、6、7、8、9之和的形式。
因此,按照上述规则排列的奇数魔方阵可以适用于任何一个奇数的情况。
例如,当n=7时,奇数魔方阵如下:1 3 5 7 9 11 13151****086416 17 19 21 23 25 27 28 26 24 22 20 18 16 32 34 36 38 40 42 44 45 43 41 39 37 35 33 48 50 52 54 56 58 60 59 57 55 53 51 49 47 64 66 68 70 72 74 76 77 75 73 71 69 67 65 80 82 84 86 ...。
c语言魔方阵课程设计

c语言魔方阵课程设计一、课程目标知识目标:1. 理解魔方阵的概念,掌握其基本性质和特点;2. 学会使用C语言实现魔方阵的生成、显示和验证;3. 掌握魔方阵相关算法,如:奇数阶魔方阵的生成方法、行列、对角线求和等;4. 了解魔方阵在实际应用中的价值,如:数学游戏、密码学等。
技能目标:1. 能够运用C语言编写程序,生成指定阶数的魔方阵;2. 能够分析魔方阵算法的时间复杂度和空间复杂度;3. 能够运用所学知识解决魔方阵相关实际问题,提高编程能力;4. 能够通过魔方阵编程实践,培养解决问题的策略和逻辑思维能力。
情感态度价值观目标:1. 培养学生对C语言编程的兴趣,激发学习热情;2. 培养学生合作探究、积极参与的精神,增强团队协作能力;3. 培养学生勇于克服困难、面对挑战的信心,提高自主学习能力;4. 引导学生认识到编程在生活中的应用价值,激发学生创新意识和实践能力。
课程性质:本课程为C语言编程实践课程,旨在让学生通过魔方阵编程实践,巩固C语言知识,提高编程能力。
学生特点:学生具备一定的C语言基础,对编程有兴趣,但可能缺乏实际编程经验。
教学要求:注重理论与实践相结合,强调动手实践,培养学生编程思维和解决问题的能力。
通过本课程的学习,使学生能够将所学知识运用到实际编程中,提高编程水平。
二、教学内容1. 魔方阵基本概念与性质- 魔方阵的定义与特点- 魔方阵的数学性质:行列、对角线求和等2. C语言编程基础回顾- 数据类型与变量- 控制结构:顺序、选择、循环- 数组的使用3. 魔方阵生成算法- 奇数阶魔方阵生成方法- 魔方阵生成程序的编写与调试4. 魔方阵显示与验证- 魔方阵的格式化输出- 验证魔方阵的正确性:行列、对角线求和检验5. 魔方阵编程实践- 编写生成指定阶数魔方阵的程序- 分析算法的时间复杂度和空间复杂度- 解决魔方阵相关实际问题6. 教学案例分析与讨论- 分析实际编程案例,总结编程技巧- 讨论编程中遇到的问题及解决方法7. 创新思维与实践- 探讨魔方阵在其他领域的应用- 鼓励学生进行创新编程实践,提高编程能力教学内容安排与进度:1. 基本概念与性质(1课时)2. C语言编程基础回顾(1课时)3. 魔方阵生成算法(2课时)4. 魔方阵显示与验证(1课时)5. 魔方阵编程实践(2课时)6. 教学案例分析与讨论(1课时)7. 创新思维与实践(1课时)教材章节关联:本教学内容与教材中关于数组、循环控制结构、函数等章节相关,通过魔方阵编程实践,使学生将所学理论知识应用于实际问题中,提高编程能力。
奇数阶幻方的杨辉方法

奇数阶幻方的杨辉方法从三阶幻方谈起。
三阶幻方是指将1,2,3,…,8,9这九个数排列成一个3×3方阵,使三横行、三竖列和两条对角线上的三个数之和都相等。
这个相等的和数就叫做三阶幻方的幻和。
我们很容易求得这个幻和:1289451533++++== 。
要排出一个三阶幻方,中心这个数是一个关键。
这个数有四条线通过它,为此,我们把三数之和为15的算式全部列出来: 1+5915+=,16815++= ,2+ 5815+= ,2+ 6 715+=,34815++= ,3+5715+=,24915++= ,4+ 5615+= 。
(一共八个式子,幻方的三行、三列和两条对角线也正好是八个,所以上列八个式子正好表示行、列和对角线上的组成情形。
)5这个数在上列八个式子中出现了四次,这表明中心数就是5。
中心这个数定好之后,再确定四个角上的数,每个角上的数有三条线通过它,2,4,6,8这四个数在上列八个式子中各出现了三次,由此我们可以确定四个角上的数就是2,4,6,8这四个数。
首先可以任意指定某一个角是2,那么与2构成对角线的另一端只能是8;余下的两个角就是4,6。
中心和四角这五个数确定之后,余下的四个数不难计算求得。
图1给出了三阶幻方的一个示例。
关于三阶幻方的排法,我国古代数学家杨辉给出了一个巧妙的排法:九子斜排,上下对易,左右相更,四维挺进。
参见图2。
如图2所示,它形象的表达了杨辉的方法。
这个方法可以变通一下:“上下对易,左右相更”改为上、下、左、右的各个元素各向对方移动三格,这样不仅可以省去“四维挺进”,而且最后得到的方阵是一个标准的33⨯方阵。
参见图3。
杨辉的方法不仅可以构造三阶幻方,而且还可以构造任图 1987654321176852349图2428637915图 3意奇数阶幻方。
杨辉的方法:设n 为奇数。
1.将221,2,3,,1,n n - 排成一个斜的n n ⨯方阵;2.以212n +为中心作一个n n ⨯方阵(格);3.将位于这个n n ⨯方阵外的所有元素都向方阵内平移n 格,即得。
(完整版)任意奇数阶幻方的杨辉斜排法(20210206050533)

任意奇数阶幻方的杨辉斜排法--- 对杨辉口诀的讨论 范贤荣2016.3.8关于三阶幻方的排法,我国古代数学家杨辉给出了一个巧妙的排法: “九子斜排,上下对易,左右相更,四维挺出”。
按照这个口诀,画出“上下对易,左右相更”之后,形成图 1d 的图面。
因此,必定有一个“四维挺出”的步骤。
最后得到“戴九履一,左三右七,二四爲肩,六八爲足”的三阶幻方。
见图1。
九子斜徘a上下对易 即g 对易 b左右相更四錐艇出巴d幻方即磁 -图1杨辉口诀的画法可见,杨辉口诀是在利用 5X 5的方格,斜排9个数后,按照他的步骤,仍然是画出 5X 5方格的3阶的幻方,如图1e 。
图2 菱中取方的画法现在,我们很多人用的是“取方框”画法 。
即在5X 5的方阵中,取出 3X 3方框来,如图2b 的红框。
红框外的1,是走到框内的绿方块中,红框外的9,是走到框内的蓝方块中。
因此1、9没有“对易”。
同样,3、7也没有“相更”。
因此,就没有“上下对易,左右相更”了。
所以,就不需要“四维挺出”了。
因此,现在的画法,与原来的口诀不一致了。
所以,我根据作图的次序,将杨辉的口诀,演绎成:各子斜排为菱形,中间取方当作城, 城外有子城内空,四围都往城中进。
挺进多少方可止,几阶就挺几步深。
注1: “四围”就是上下左右四边。
“都往城中进”,因此是相向而行,都到城中。
注2: “几阶就挺几步深”。
如3阶进3步,5阶进5步,7阶进7步……后续亦如此类推。
见图 2。
1斗17SS69四團都向坝挺进 九彳網排成羞理 挺进三步幻方成F面,我将2~13各奇数阶,由菱方阵演变成幻方的情况,列于后。
1*□7j3S6S.1戈子斜排咸羞延中值]取方当作城城外育子城肉空四團都向城挺进芽mA.r33h F锂进三歩幻方咸1s-1117J];&4211?ri395IS14101310152420SS1n&117*16口s17139y 1、IS14102315242-0|城外有子城内空图3 5阶菱方阵与幻方1s I15g3丄"£16104 (2317115)241a126 4337312S丹13x ja32262014 _ r27a464034234B42491124720 412283 17313工g 10IS114r r 236"w"七15四围祁向城挺讲图4 7阶菱方阵与幻方377?702162135456333D712263144B477 費8031722355151643e4081笼6-124565717+9g11右336525舉閔IS50142T-434EE5T10512聽存3536ea fin115?3典T07723' 20611253445图5 9阶菱方阵与幻方112斗2;13_324144453525b5托2(51666:57车3?27177~9655S4$3S2S1933?79695?4?3V291?9 1M的80?0*050J0302010 111101?1軒716151JI312】11 13:9282724252壮3211 1】:93?363534333 114104SJ74&15444H.*二S3栖55]1£]«80聒ir ir97£77798S8119金]?fl1101:3图6 11阶菱方阵与幻方图7 11阶幻方图8 13阶菱方阵图9 13阶幻方。
奇数阶魔方阵算法分析

奇数阶魔方阵一、提出问题所谓“奇数阶魔方阵”是指n 为不小于3的奇数的魔方阵。
这类魔方阵的形式多样,这里我们仅讨论其中的一种形式的正规魔方阵。
例如:3阶、5阶和7阶的魔方阵如图3 – 4 所示。
294753618 ,92251811321191210222013641614752315812417 ,20112494031221234341322321444423324151345363425161453735261786462927189747382819101183930 图3 – 4 3阶5阶和7阶魔方阵容易知道,这三个魔方阵的魔方常数分别是15、65和175。
现在要求给出:能让计算机自动输出类似图3 – 4 所示的n 阶奇数魔方阵的算法,其中n 为任意给定的一个不小于3的奇数。
二、简单分析决定“奇数阶魔方阵”的关键是要按要求决定其方阵中的各个数字。
观察图3 – 4中的三个奇数阶魔方阵,不难发现:1.由于是正规魔方,故所填入的n 2个不同整数依次为1、2、3、…、n 2 ;2.各行、列和对角线上的数字虽各不相同,但其和却是相同的。
这表明,其魔方常数可由公式n ( n 2 + 1 ) / 2得到。
3.数字在阵列中的次序,并没有遵从阵列单元的行、列下标的顺序,但数字“1”却始终出现在阵列第一行的正中间位置,而数字“n 2”也始终出现在阵列第n 行的正中间位置,这说明阵列中的数字排列应该是有一定规律的。
通过对两个奇数阶魔方阵的简单分析,下面几个基本问题必须得到解决:◆ 奇数阶魔方阵中的数字有些什么规律?◆ 数字“1”的位置应如何确定?三、设计准备1.奇数阶魔方阵中的数字规律通过对奇数阶魔方阵的分析,其中的数字排列有如下的规律:(1)自然数1出现在第一行的正中间;(2)若填入的数字在第一行(不在第n 列),则下一个数字在第n 行(最后一行)且列数加1(列数右移一列);(3)若填入的数字在该行的最右侧,则下一个数字就填在上一行的最左侧;(4)一般地,下一个数字在前一个数字的右上方(行数少1,列数加1);(5)若应填的地方已经有数字或在方阵之外,则下一个数字就填在前一个数字的下方。
奇数阶魔方阵

魔方阵 ①问题描述魔方阵是一个古老的智力问题,它要求在一个m ×m 的矩阵中填入1~m 2的数字(m 为奇数),使得每一行、每一列、每条对角线的累加和都相等,如图1所示。
②基本要求● 输入魔方阵的行数m ,要求m 为奇数,程序对所输入的m 作简单的判断,如m 有错,能给出适当的提示信息。
● 实现魔方阵。
● 输出魔方阵。
③实现提示本实验使用的数据结构是数组。
解魔方阵问题的方法很多,这里采用如下规则生成魔方阵。
● 由1开始填数,将1放在第0行的中间位置。
● 将魔方阵想象成上下、左右相接,每次往左上角走一步,会有下列情况:✧ 左上角超出上方边界,则在最下边相对应的位置填入下一个数字; ✧ 左上角超出左边边界,则在最右边相应的位置填入下一个数字; ✧ 如果按上述方法找到的位置已填入数据,则在同一列下一行填入下一个数字。
以3×3魔方阵为例,说明其填数过程,如图2所示。
图2 三阶魔方阵的生成过程由三阶魔方阵的生成过程可知,某一位置(x,y)的左上角的位置是(x-1,y-1),如果x-1≥0,不用调整,否则将其调整为x-1+m ;同理,如果y-1≥0,不用调整,否则将其调整为y-1+m 。
所以,位置(x,y)的左上角的位置可以用求模的方法获得,即:x=(x-1+m)%my=(y-1+m)%m如果所求的位置已经有数据了,将该数据填入同一列下一行的位置。
这里需要注意的是。
此时的x和y已经变成之前的上一行上一列了,如果想变回之前位置的下一行同一列,x需要跨越两行,y需要跨越一列,即:x=(x+2)%my=(y+1)%m④思考可以考虑使用其他方法生成魔方阵。
任何算法都有不同的实现方法,通过采用不同实现方法来重新实现算法,这要比单纯学习算法的效果好得多。
具体算法:*/最大可以求99阶魔方阵*/#include<stdio.h>#include<stdlib.h>#define MAX 100int main(){int a[MAX][MAX]={0};int i,m,x=1,y,j;printf("请输入魔方阵阶数:");scanf("%d",&m);if(m%2==0) {printf("请输入奇数\n"); system("pause"); return 0;}else a[1][(m+1)/2]=1;y=(m+1)/2;for(i=2;i<=m*m;i++){if(x-1>0&&y-1>0){x=x-1;y=y-1;if(a[x][y]==0){a[x][y]=i;}else {x=(x+2)%m;y=(y+1)%m;if(x==0) x=x+m;if(y==0) y=y+m;a[x][y]=i;}continue;}if(x-1<=0&&y-1>0){x=x-1+m;y=y-1;if(a[x][y]==0){a[x][y]=i;}else {x=(x+2)%m;y=(y+1)%m;if(x==0) x=x+m;if(y==0) y=y+m;a[x][y]=i;}continue;}if(x-1>0&&y-1<=0){x=x-1;y=y-1+m;if(a[x][y]==0){a[x][y]=i;}else {x=(x+2)%m;y=(y+1)%m;if(x==0) x=x+m;if(y==0) y=y+m;a[x][y]=i;}continue;}if(x-1<=0&&y-1<=0){x=x-1+m;y=y-1+m;if(a[x][y]==0){a[x][y]=i;}else {x=(x+2)%m;y=(y+1)%m;if(x==0) x=x+m;if(y==0) y=y+m;a[x][y]=i;}continue;}}for(i=1;i<=m;i++){for(j=1;j<=m;j++){printf("%5d",a[i][j]);}printf("\n");}system("pause");return 0;}。
魔方阵 C语言

一、幻方按照阶数可分成了三类,即奇数阶幻方、双偶阶幻方、单偶阶幻方。
二、奇数阶幻方(劳伯法)奇数阶幻方最经典的填法是罗伯法。
填写的方法是:把1(或最小的数)放在第一行正中;按以下规律排列剩下的(n×n-1)个数:(1)每一个数放在前一个数的右上一格;(2)如果这个数所要放的格已经超出了顶行那么就把它放在底行,仍然要放在右一列;(3)如果这个数所要放的格已经超出了最右列那么就把它放在最左列,仍然要放在上一行;(4)如果这个数所要放的格已经超出了顶行且超出了最右列,那么就把它放在底行且最左列;(5)如果这个数所要放的格已经有数填入,那么就把它放在前一个数的下一行同一列的格内。
例,用该填法获得的5阶幻方:三、单偶数阶幻方(斯特拉兹法)所谓单偶阶幻方就是当n不可以被4整除时的偶阶幻方,即4K+2阶幻方。
如(n=6,10,14……)的幻方。
单偶数阶幻方最经典的填法是斯特拉兹法。
填写的方法是:以10阶幻方为例。
这时,k=2。
(1)把魔方阵分为A,B,C,D四个象限,这样每一个象限肯定是奇数阶。
用罗伯法,依次在A象限,D象限,B象限,C象限按奇数阶幻方的填法填数。
(2)在A象限的中间行、中间格开始,按自左向右的方向,标出k格。
A象限的其它行则标出最左边的k格。
将这些格,和C象限相对位置上的数互换位置。
(3)在B象限所有行的中间格,自右向左,标出k-1格。
(注:6阶幻方由于k-1=0,所以不用再作B、D象限的数据交换),将这些格,和D象限相对位置上的数互换位置。
四、源代码如下,已加详细注释#include<stdio.h>#include<stdlib.h>int array[15][15];intinit(int degree) //初始化{inti;int j;for(i=0; i<=degree+1; i++)for(j=0; j<=degree+1; j++)array[i][j] = 0;return 0;}inttest_print(int x, int y, int w, int h) //测试用的,输出以(x,y)为原点,宽为w,高为h,这个区域的数值{inti;int j;for(i=y; i<=y+h-1; i++){for(j=x; j<=x+w-1; j++){printf("%2d ",array[i][j]);}printf("\n");}return 0;}intlao_bo_er(int degree, int x, int y, intnum) //劳伯法{inti;int j;int k;i = y;j = degree/2 + x;for(k=num; k<=num+degree*degree-1; k++){array[i][j] = k;if((k-num+1)%degree == 0){ //如果这个数所要放的格已经有数填入i = (i-y+1)%degree+y;}else{ //每一个数放在前一个数的右上一格i = (i-y-1+degree)%degree+y;j = (j-x+1)%degree+x;}}return 0;}intseq_range(int degree) //把数字按顺序填{inti;int j;intnum;num = 1;for(i=1; i<=degree; i++){for(j=1; j<=degree; j++){array[i][j] = num++;}}return 0;}intsi_te_la_zi(int degree, int x, int y, intnum) //斯特拉兹法{intdeg;int k;int temp;inti;int j;deg = degree/2;lao_bo_er(deg, x, y, num); //用罗伯法,依次在A象限,D象限,B象限,C象限按奇数阶幻方的填法填数lao_bo_er(deg, x+deg, y, num+2*deg*deg);lao_bo_er(deg, x, y+deg, num+3*deg*deg);lao_bo_er(deg, x+deg, y+deg, num+deg*deg);k = (degree-2)/4;for(i=1; i<=deg; i++){ //A象限和C象限对换数据for(j=1; j<=k; j++){temp = array[i][j];array[i][j] = array[i+deg][j];array[i+deg][j]=temp;}for(j=deg+deg/2+1; j>=deg+deg/2-k+3; j--){temp = array[i][j];array[i][j] = array[i+deg][j];array[i+deg][j]=temp;}}for(i=j=1; j<=deg/2+k; j++){ //B象限和D象限对换数据temp = array[i+deg/2][j];array[i+deg/2][j] = array[i+deg+deg/2][j];array[i+deg+deg/2][j]=temp;}return 0;}inthai_er_fa(int degree) //海尔法{inti;int j;int complement;intdeg;seq_range(degree);complement = degree*degree+1;deg = degree/4;for(i=0; i<deg; i++){for(j=0; j<deg; j++){ //对角线上的数字换成和它互补的数array[i*4+1][j*4+1] = complement -array[i*4+1][j*4+1];array[i*4+1][j*4+4] = complement -array[i*4+1][j*4+4];array[i*4+4][j*4+1] = complement -array[i*4+4][j*4+1];array[i*4+4][j*4+4] = complement -array[i*4+4][j*4+4];array[i*4+2][j*4+2] = complement -array[i*4+2][j*4+2];array[i*4+2][j*4+3] = complement -array[i*4+2][j*4+3];array[i*4+3][j*4+2] = complement -array[i*4+3][j*4+2];array[i*4+3][j*4+3] = complement -array[i*4+3][j*4+3];}}return 0;}int main(){int degree;printf("please input the degree\n");scanf("%d",°ree);init(degree);if(degree%2 == 1){ //奇数阶幻方lao_bo_er(degree,1,1,1);test_print(1,1,degree,degree);}else if(degree%4 == 2){ //双偶阶幻方si_te_la_zi(degree, 1, 1, 1);test_print(1,1,degree,degree);}else{ //单偶阶幻方hai_er_fa(degree);test_print(1,1,degree,degree);}return 0;}。
幻方

1)下面这些构造方法都是比较适合于编程的。
构造幻方分奇数阶幻方、4n型偶数幻方、4n+2型的偶数幻方(以下简称双偶数、单偶数)。
构造奇数阶较简单,常用的是连续摆数法。
下面的n均指阶数,在这里(y,x)表示第y横行的第x个数。
(1)在第一行的正中间(即[1,(n+1)/2])放上1 (2)若数a的位置在(y,x),则a+1的位置在:(y-1,x+1),若有这个位子且里面没数(n,x+1),若y=1且x<n (y-1,1),若x=n且y>1 (y+1,x),若x=n且y=1或(y,x)已经有数。
(y,x)已经有数的充要条件是a=n(mod n) (3)所构成的(n×n)方即为一个幻方。
我们还可以把连续摆数法推广,先定义几个概念:普通向量:正常走步的情况。
(即上面第一种情况)正常走步记作(b,a)。
中断向量:即走到(1,n)这个格子或(y,x)已经有数的情况。
记作(d,c) 下面是几个推广的情况:(1,-1)(0,1);(1,-1)(0,2);(2,1)(1,-2);(2,1)(1,-1);(2,1)(1,0);(2,1)(1,2)下面是构造双偶数阶幻方:对称法:把双偶数型的幻方分成四个正方形,在左上角正方形中每行每列各取一半打上○(实际上就是使无论从每行还是每列来看都刚好有一半有○,一半无○。
)然后向剩下的三个小方块中映象(镜像对称),于是整个方阵都布好了○。
(用电脑实行则可以选择在该布○的地方填上-1)。
接下来该填数了。
适用于电脑的方法:向所有格子内填数,(推荐x,y分别从1~n的双重计数循环):若(y,x)没有○,则填入(y-1)*n+x;若(y,x)中有○,则填入(n-y+1)*n+x+1。
适用于笔算的方法:从左上角依次1~n*n填数,遇上○则不填,这个数字还是要跳过去。
填完后,把方阵旋转180度后再从1~n*n往○里填数,没有○的地方就不填,跳过数字。
因为对称的原理,因此这回填的数刚好是上次跳过的数,这次跳过的刚好是上次填过的数。
输出魔方阵

for(j=0;j<n;j++)a[n][i]+=a[j][i];
for(i=0;i<n;i++)a[n][n]+=a[i][i];//主对角线的和
}
void main()
{
int n;
int a[M][M]={0};
printf("魔方阵的阶数n=");//n为大于2的任意整数
}
}
//三、当n为单偶数(n=4k+2)时,可把方阵分为4个2k+1的小方阵,编号如下:
//1.各小方阵按奇数阶算法依次填入A(1…[2k+1]2)、B([2k+1]2+1…2[2k+1]2)、C(…)、D(…4[2k+1]2);
//2.将A与D换:A中间格始向右取k格;A最左边的k列(除中行);
//3.将C与B互换:从C的中间列开始向左数k-1列。
MagicOdd(a,0,m,2*m*m+1,m);//C阵(右上)
MagicOdd(a,m,0,3*m*m+1,m);//D阵(左下)
for(j=k;j<m-1;j++){//从A的中间格开始向右数k格...
t=a[k][j];
a[k][j]=a[k+m][j];//...与D对应位置交换
a[k+m][j]=t;
}
void MagicSev(int a[M][M],int st,int n)//单偶4k+2阶魔方阵,起始数st
{
int m=n/2,k=m/2;//将原矩阵分为2×2的方阵
delphi 数组定义

有:a[5]={1,2,3,4,5} ;
那么在 delphi中,这个数组的赋值该怎么写??
问题补充:下面有人说的对,我就是想在声明数组的时候赋初值,至于初值的内容你们不需要知道,我想知道的只是申明的时候赋值的格式,而不是通过一个过程去实现
var
a:=array[1..5] of integer=(1,2,3,4,5)
var
MyArr: TMyArr; //再定义静态数组
--------------------------------------------------------------------------------
//4. 在非过程区可以直接赋值:
var
MyArr: array[0..2] of Integer = (11,22,33);
//8. 根据其他类型定义数组:
var
MyArr: array[Byte] of Char;
begin
MyArr[255] := #65;
ShowMessage(MyArr[255]); //A
end;
//应尽量不使用内建类型,可以新建类型:
type
TNewByte = Byte;
end;
var
Arr1: array[0..100] of MyRec;
Arr2: array[0..100] of record s: string; r: Real; b: Byte; end; //可以直接这样定义
Arr3: packed array[0..100] of MyRec; //压缩数组定义, 好像没有区别?
对于整个二维数组的元素引用时,大多采用二重循环来实现。如:给如上说明的二维数组a 进行赋
矩阵变换、矩阵求值

矩阵变换、矩阵求值对⼀个矩阵进⾏某种运算和操作,其结果还是⼀个矩阵。
对⾓阵三⾓阵矩阵的转置矩阵的旋转矩阵的翻转矩阵求逆等等1.对⾓阵对⾓阵:只有对⾓线上有⾮零元素的矩阵。
数量矩阵:对⾓线上的元素相等的对⾓矩阵。
单位矩阵:对⾓线上的元素都为1的对⾓矩阵。
(1) 提取矩阵的对⾓线元素diag(A):提取矩阵A主对⾓线元素,产⽣⼀个列向量。
diag(A,k):提取矩阵A第k条对⾓线的元素,产⽣⼀个列向量。
对⾓线如下:(2) 构造对⾓阵diag(V):以向量 V为主对⾓线元素,产⽣对⾓矩阵。
diag(V,k):以向量 V为第k条对⾓线元素,产⽣对⾓矩阵。
例⼦:先建⽴5×5矩阵A,然后将A的第⼀⾏元素乘以1,第⼆⾏乘以2,…,第五⾏乘以5。
>> A=[7,0,1,0,5;3,5,7,4,1;4,0,3,0,2;1,1,9,2,3;1,8,5,2,9]A = 7 0 1 0 53 5 74 14 0 3 0 21 1 92 31 8 52 9>> D=diag(1:5); //对⾓线元素为12345>> D*A //对⾓阵左乘⼀个矩阵时,即矩阵对⾓线的第⼀个元素,乘以该矩阵的第⼀⾏。
ans = 7 0 1 0 56 10 14 8 212 0 9 0 64 4 36 8 125 40 25 10 45要将A的各列元素分别乘以对⾓阵的对⾓线元素,如何实现?——对⾓阵右乘矩阵A 要将A的各列元素分别乘以对⾓阵的对⾓线元素,可以⽤⼀个对⾓阵右乘矩阵A。
>> A=[7,0,1,0,5;3,5,7,4,1;4,0,3,0,2;1,1,9,2,3;1,8,5,2,9]A = 7 0 1 0 53 5 74 14 0 3 0 21 1 92 31 8 52 9>> D=diag(1:5);>> A*Dans =7 0 3 0 253 10 21 16 54 0 9 0 101 2 27 8 151 16 15 8 452.三⾓阵上三⾓阵:矩阵的对⾓线以下的元素全为零的矩阵。
浅谈奇阶幻方图填写方法

浅谈奇阶幻方图填写方法一、洛书九宫数的启示洛书九宫数的排列方式:“戴九履一,左三右七,四二为肩,八六为足,五居中宫”,实际上洛书九宫图就是一个最简单的三阶幻方奇阵图。
图示如下:492357816从洛书九宫图中,我们可以得出以下基本结论:1、中间位置的数为奇数,四角位置的数为偶数。
2、对角两个数相加和为中间数的2倍。
3、处于中间位置对应两个数相加和为中间数的2倍。
上述3个结论在排列奇阵图时会用到。
二、填写奇数阶幻方图的具体方法(以七阶幻方图为例)121197494740482022173732246362423281444535292521155816222726344261831331330441039414313 38(七阶幻方全图)Ø第一步:分层七阶幻方图的49个数从外到内可以分为四层。
如下图所示:第一层第二层第三层第四层Ø第二步:确定每一层应填写的数字(数源):我们把小于中间数字的所有数称之为小数;把大于中间数字的所有数称之为大数;把小于中间数字的所有奇数称之为小奇数;把大于中间数字的所有奇数称之为大奇数;把小于中间数字的所有偶数称之为小偶数;把大于中间数字的所有偶数称之为大偶数。
对于七阶幻方图来讲:第一层的24个数应该是1——49当中最外层的24个数。
分别是:1——12和38——49。
同理:第二层的16个数应该是:13——20和30——37第三层的8个数应该是:21——24和26——29第四层的1个数应该是最中间的一个数:25如下图:小数大数第一层:1——1238——49第二层:13——2030——37第三层:21——2426——29第四层:25Ø第三步:最后一层数的填写方法:(阶数2+1)÷2如:七阶幻方图最后一层的数字:(72+1)÷2=25Ø第四步:其它各层数的填写方法:1、左边上下两角两个数的确定:最大的两个小偶数。
然后根据对角两个数相加之和等于中间数的二倍,可得另外两个角的数。
C++实例奇数阶魔方阵问题

奇数阶魔⽅阵是指由1到n2(n为奇数)个⾃然数构成的n*n的⽅阵,它的每⼀⾏,每⼀列,和对⾓线各元素之和均相等,3阶的魔⽅阵如下: 8 1 6 3 5 7 4 9 2 n阶魔⽅阵的构造⽅法为: 1> ⾸先把1放在顶⾏的正中间,然后把后继数按顺序放置在右上斜的对⾓线上; 2> 当到达顶⾏时,下⼀个数放到底⾏,好像它在顶⾏的上⾯; 3> 当到达最右列时,下⼀个数放在最左端列,好像它仅靠在右端列的右⽅; 4> 当到达的位置已经填好数时,考试⼤提⽰:或到达右上⾓的位置时,下⼀个数就放在刚填写的位置的正下⽅。
C++函数如下: /*奇数阶魔⽅阵问题*/ #include using namespace std; const int MAX=50; void main() { int matrix[MAX][MAX]; int count; int row; int column; int order; cout<<"请输⼊阶数:"; cin>>order; if(order%2==0) { cout<<"阶数必须是⼀个奇数,请重新输⼊!"< } else { row=0; column=order/2; for(count=1;count<=order*order;count++) { matrix[row][column] = count; if (count % order == 0) { row++; } else { row = (row == 0) ? order - 1 : row - 1; column = (column == order-1) ? 0 : column + 1; } } for (row = 0; row < order; row++) { for (column = 0; column < order; column++) { cout<<"\t"< } cout< } } } 程序运⾏打印出相应的n阶魔⽅阵.。
一个2n(n为奇数)阶魔方阵的简单解法

定是 15; 在直的方向, 仍然是維持每擴增兩
列, 和就增加 5 的情形。 所以, 我們最後所形
成的 Θ′, 是一個橫列方向和等於 15 , 而直
欄方向和等於 5n的矩陣。
接下來, 讓我們討論步驟 (五) 的 Θ′′。
在直欄的方向, 仍然是維持每擴增兩列,
就增加 5的情形, 所以, 直欄方向的和等於
1. 前言
魔方陣 (magic square), 又被稱做是 「幻方」, 在中國古時候的 「洛書」 中, 它則被 稱做是 「縱橫圖」[1]。 魔方陣的條件是:
將 {1, 2, · · · , n2 − 1, n2} 排 列在一個 n × n 維的矩陣中, 讓 每一橫列、 每一縱欄與兩條對角線 的數字和, 都相等。
1234 5678 9 10 11 12 13 14 15 16
1 15 14 4 12 6 7 9 ⇒ 8 10 11 5 13 3 2 16
上面所介紹的兩種解法, 只是眾多解 法中, 被認為最簡單的兩種方法, 它們 的證明過程也是相當的容易, 只要使用類 似梁培基與張航輔 在 「 4k 階全對稱幻方的 一種快速構作方法」[3] 該篇文章的證明方法 即可。
(6) 1213431343 4342421212 1213134343 434242 1212 121313 4343
替代方陣 (3)。
一個 2n ( n 為奇數) 階魔方陣的簡單解法 73
我們再將擴展後的方陣 (5) 與方陣 (6)
重疊相加, 就得到橫、 直、 對角方向的和, 皆
是
100×(100+1) 2
是 Brualdi, R. A. 所寫的 『Introductory Combainatorics』[2]。
C语言魔方阵的三种实现方法

C语⾔魔⽅阵的三种实现⽅法⽬录魔⽅阵:1.奇数阶魔⽅阵2.偶数阶魔⽅阵(n=4K)3.偶数阶魔⽅阵(n=4K+2)魔⽅阵:把1到n*n排成n⾏n列⽅阵,使⽅阵中的每⼀⾏、每⼀列以及对⾓线上的数之和都相同,即为n阶魔⽅阵。
根据魔⽅阵的规律,我将它分为三种情况。
1.奇数阶魔⽅阵规律:第⼀个数放在第⼀⾏的中间,下⼀个数放在上⼀个数的上⼀⾏下⼀列,若该位置已经有了数字即放在上个数的下⾯⼀⾏的相同列⽤C语⾔编程如下:⽰例:n=5;#include<stdio.h>#include<stdlib.h>#include<assert.h>void Magic1(){#define ROW 5#define COL ROWassert(ROW % 2 != 0); //判断n是否为奇数int arr[ROW][COL] = { 0 }; //定义⼆维数组int currow = 0;int curcol = COL / 2;arr[currow][curcol] = 1;for (int i = 2; i <= ROW * COL; i++){if (arr[(currow - 1 + ROW) % ROW][(curcol + 1) % COL] == 0) //按照规律赋值{currow = (currow - 1 + ROW) % ROW;curcol = (curcol + 1) % COL;}else{currow = (currow + 1) % ROW;}arr[currow][curcol] = i;}for (int i = 0; i < ROW; i++) //打印魔⽅阵{for (int j = 0; j < COL; j++){printf("%-3d", arr[i][j]);}printf("\n");}}int main(){Magic1();return 0;}结果:2.偶数阶魔⽅阵(n=4K)规律:按数字从⼩到⼤,即1,2,3……n顺序对魔⽅阵从左到右,从上到下进⾏填充;将魔⽅阵分成若⼲个4×4⼦⽅阵(如:8阶魔⽅阵可分成四个4×4⼦⽅阵),将⼦⽅阵对⾓线上的元素取出;将取出的元素按从⼤到⼩的顺序依次填充到n×n⽅阵的空缺处。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
魔方阵 ①问题描述
魔方阵是一个古老的智力问题,它要求在一个m ×m 的矩阵中填入1~m 2的数字(m 为奇数),使得每一行、每一列、每条对角线的累加和都相等,如图1所示。
②基本要求
● 输入魔方阵的行数m ,要求m 为奇数,程序对所输入的m 作简单的判
断,如m 有错,能给出适当的提示信息。
● 实现魔方阵。
● 输出魔方阵。
③实现提示
本实验使用的数据结构是数组。
解魔方阵问题的方法很多,这里采用如下规则生成魔方阵。
● 由1开始填数,将1放在第0行的中间位置。
● 将魔方阵想象成上下、左右相接,每次往左上角走一步,会有下列情况:
✧ 左上角超出上方边界,则在最下边相对应的位置填入下一个数字; ✧ 左上角超出左边边界,则在最右边相应的位置填入下一个数字; ✧ 如果按上述方法找到的位置已填入数据,则在同一列下一行填入下
一个数字。
以3×3魔方阵为例,说明其填数过程,如图2所示。
图2 三阶魔方阵的生成过程
由三阶魔方阵的生成过程可知,某一位置(x,y)的左上角的位置是(x-1,y-1),如果x-1≥0,不用调整,否则将其调整为x-1+m ;同理,如果y-1≥0,不用调整,否则将其调整为y-1+m 。
所以,位置(x,y)的左上角的位置可以用求模的方
法获得,即:
x=(x-1+m)%m
y=(y-1+m)%m
如果所求的位置已经有数据了,将该数据填入同一列下一行的位置。
这里需要注意的是。
此时的x和y已经变成之前的上一行上一列了,如果想变回之前位置的下一行同一列,x需要跨越两行,y需要跨越一列,即:
x=(x+2)%m
y=(y+1)%m
④思考
可以考虑使用其他方法生成魔方阵。
任何算法都有不同的实现方法,通过采用不同实现方法来重新实现算法,这要比单纯学习算法的效果好得
多。
具体算法:
*/最大可以求99阶魔方阵*/
#include<stdio.h>
#include<stdlib.h>
#define MAX 100
int main(){
int a[MAX][MAX]={0};
int i,m,x=1,y,j;
printf("请输入魔方阵阶数:");
scanf("%d",&m);
if(m%2==0) {printf("请输入奇数\n"); system("pause"); return 0;}
else a[1][(m+1)/2]=1;
y=(m+1)/2;
for(i=2;i<=m*m;i++)
{if(x-1>0&&y-1>0){
x=x-1;y=y-1;
if(a[x][y]==0)
{a[x][y]=i;}
else {x=(x+2)%m;
y=(y+1)%m;
if(x==0) x=x+m;
if(y==0) y=y+m;
a[x][y]=i;}
continue;}
if(x-1<=0&&y-1>0){
x=x-1+m;y=y-1;
if(a[x][y]==0)
{a[x][y]=i;}
else {x=(x+2)%m;
y=(y+1)%m;
if(x==0) x=x+m;
if(y==0) y=y+m;
a[x][y]=i;}
continue;
}
if(x-1>0&&y-1<=0){
x=x-1;y=y-1+m;
if(a[x][y]==0)
{a[x][y]=i;}
else {x=(x+2)%m;
y=(y+1)%m;
if(x==0) x=x+m;
if(y==0) y=y+m;
a[x][y]=i;}
continue;
}
if(x-1<=0&&y-1<=0){
x=x-1+m;y=y-1+m;
if(a[x][y]==0)
{a[x][y]=i;}
else {x=(x+2)%m;
y=(y+1)%m;
if(x==0) x=x+m;
if(y==0) y=y+m;
a[x][y]=i;}continue;
}
}
for(i=1;i<=m;i++){
for(j=1;j<=m;j++){
printf("%5d",a[i][j]);
}
printf("\n");}
system("pause");
return 0;
}。
