微积分高等数学课件完整版
合集下载
《微积分》(上下册) 教学课件 01.第1章 函数、极限、连续 高等数学第一章第9-10节
12
定义 2 设函数 f ( x)在U(x0, )内有定义,如果
y
lim f (x) f (x ),
x x0
0
y f (x)
称函数 f ( x)在点 x 连续. 0
如 f ( x) x2,
0
x0
x
lim f ( x) lim x2 4 f (2),
x2
x2
f ( x) x2在x 2点连续.
说明 y f (x)在x x0点连续 下列三条同时成立 (1) f (x0)有定义;
(2) lim f (x)存在; xx0
(3)lim x x0
f
(x)
f (x0 ).
13
例1
试证函数
f
ห้องสมุดไป่ตู้
(
x)
x
sin1 x
,
0,
处连续.
证 lim x sin 1 0,
x0
x
又 f (0) 0, lim f ( x) f (0), x0
3、反函数函数的连续性
严格单调的连续函数必有严格单调的连续反函数. 例如, y sin x在[ , ]上单调增加且连续,
22 故 y arcsinx 在[1,1]上也是单调增加且连续.
同理 y arccosx 在[1,1]上单调减少且连续;
y arctanx, y arccot x 在(,)上单调且连续.
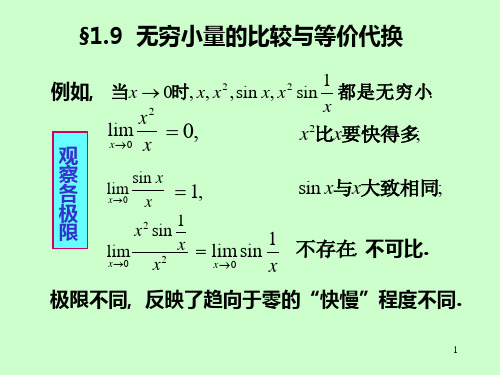
§1.9 无穷小量的比较与等价代换
例如, 当x 0时, x, x2,sin x, x2 sin 1 都是无穷小.
x2
lim 0,
观
x0 x
x x2比x要快得多;
察 各 极 限
lim sin x x0 x
定义 2 设函数 f ( x)在U(x0, )内有定义,如果
y
lim f (x) f (x ),
x x0
0
y f (x)
称函数 f ( x)在点 x 连续. 0
如 f ( x) x2,
0
x0
x
lim f ( x) lim x2 4 f (2),
x2
x2
f ( x) x2在x 2点连续.
说明 y f (x)在x x0点连续 下列三条同时成立 (1) f (x0)有定义;
(2) lim f (x)存在; xx0
(3)lim x x0
f
(x)
f (x0 ).
13
例1
试证函数
f
ห้องสมุดไป่ตู้
(
x)
x
sin1 x
,
0,
处连续.
证 lim x sin 1 0,
x0
x
又 f (0) 0, lim f ( x) f (0), x0
3、反函数函数的连续性
严格单调的连续函数必有严格单调的连续反函数. 例如, y sin x在[ , ]上单调增加且连续,
22 故 y arcsinx 在[1,1]上也是单调增加且连续.
同理 y arccosx 在[1,1]上单调减少且连续;
y arctanx, y arccot x 在(,)上单调且连续.
§1.9 无穷小量的比较与等价代换
例如, 当x 0时, x, x2,sin x, x2 sin 1 都是无穷小.
x2
lim 0,
观
x0 x
x x2比x要快得多;
察 各 极 限
lim sin x x0 x
微积分讲解ppt课件

多元函数的表示 方法
多元函数可用记号 f(x1,x2,…,xn)或z=f(x,y) 表示。
多元函数的定义 域
使多元函数有意义的自 变量组合(x1,x2,…,xn) 的集合。
多元函数的值域
多元函数所有值的集合 。
20
偏导数与全微分
偏导数的定义
设函数z=f(x,y)在点(x0,y0)的某一邻域内有定义,当y固定在y0而x在x0处有增量Δx时,相应地函数有增量 f(x0+Δx,y0)-f(x0,y0)。如果Δz与Δx之比当Δx→0时的极限存在,那么此极限值称为函数z=f(x,y)在点(x0,y0)处对 x的偏导数。
22
06
微积分在实际问题中的应用
2024/1/25
23
在物理学中的应用
运动学
描述物体的位置、速度和加速度 之间的关系,通过微积分可以精 确地计算物体的运动轨迹和速度 变化。
力学
研究物体受力作用下的运动规律 ,微积分可用于求解牛顿第二定 律中的加速度和力的关系。
电磁学
分析电场和磁场的分布和变化规 律,微积分可用于求解麦克斯韦 方程组等电磁学基本方程。
2024/1/25
9
微分法则与运算技巧
微分的基本法则
包括和差微分法则、乘积 微分法则、商微分法则等 。
微分运算技巧
换元法、分部积分法、有 理化分母等,用于简化复 杂的微分运算。
隐函数与参数方程
对于无法直接求解的隐函 数和参数方程,可通过微 分法求解其导数。
微分的应用
在几何、物理、经济等领 域中的应用,如求曲线的 切线、求速度加速度、求 边际效应等。
全微分的定义
如果函数z=f(x,y)在点(x,y)的全增量Δz=f(x+Δx,y+Δy)-f(x,y)可以表示为Δz=AΔx+BΔy+o(ρ),其中A、B不依赖 于Δx, Δy而仅与x,y有关,ρ=(Δx^2+Δy^2)^0.5,则称函数z=f(x,y)在点(x,y)处可微,AΔx+BΔy称为函数 z=f(x,y)在点(x,y)处的全微分。
大学微积分课件(PPT幻灯片版)pptx

高阶导数计算
高阶导数的计算一般采用归纳法 或莱布尼茨公式等方法进行求解。 需要注意的是,在计算过程中要 遵循求导法则和运算顺序。
应用举例
高阶导数在物理学、工程学等领 域有着广泛的应用。例如,在物 理学中,加速度是速度的一阶导 数,而速度是位移的一阶导数; 在工程学中,梁的挠度是荷载的 一阶导数等。
03 一元函数积分学
VS
几何意义
函数$y = f(x)$在点$x_0$处的导数 $f'(x_0)$在几何上表示曲线$y = f(x)$在点 $(x_0, f(x_0))$处的切线的斜率。
求导法则与技巧总结
基本求导法则
包括常数的导数、幂函数的导数、指数函数的导数、对数函数的导 数、三角函数的导数、反三角函数的导数等。
求导技巧
连续性与可微性关系
连续性
函数在某一点连续意味着函数在 该点有定义,且左右极限相等并 等于函数值。连续性是函数的基 本性质之一。
可微性
函数在某一点可微意味着函数在 该点的切线斜率存在,即函数在 该点有导数。可微性反映了函数 局部变化的快慢程度。
连续性与可微性关
系
连续不一定可微,但可微一定连 续。即函数的连续性是可微性的 必要条件,但不是充分条件。
历史发展
微积分起源于17世纪,由牛顿和莱布尼 茨独立发展。经过数百年的完善,已成 为现代数学的重要基础。
极限思想与运算规则
极限思想
极限是微积分的基本概念,表示函数在某一点或无穷远处的变 化趋势。通过极限思想,可以研究函数的局部和全局性质。
运算规则
极限的运算包括极限的四则运算、复合函数的极限、无穷小量 与无穷大量的比较等。这些规则为求解复杂函数的极限提供了 有效方法。
高等数学(微积分)ppt课件

,且f'(x0)=0,则可通过二阶导数 f''(x0)的符号来判断f(x)在x0处取得极大值还是极小值。
曲线的凹凸性与拐点
凹凸性
若函数f(x)在区间I上二阶可导,且 f''(x)>0(或<0),则称曲线y=f(x)在 I上是凹的(或凸的)。
拐点
拐点的判定
若函数f(x)在点x0处二阶可导,且 f''(x0)=0,则可通过三阶导数f'''(x0) 的符号来判断点(x0,f(x0))是否为曲线 的拐点。
THANKS
感谢观看
非线性微分方程
通过变量替换、积分等方法求解,或 利用数值方法近似求解
级数的概念与性质
级数的定义 无穷序列的部分和序列
级数的性质 加法、减法、乘法、除法、重排等性
质
级数的收敛与发散 部分和序列有极限则级数收敛,否则 发散
常见级数及其敛散性 等差级数、等比级数、调和级数、交 错级数等,通过比较法、比值法、根 值法等方法判断其敛散性
VS
极限的性质
唯一性、局部有界性、保号性、保不等式 性、迫敛性等。
极限的运算法则
极限的四则运算法则
若两个函数的极限存在,则它们的和、差、积、商(分母不为零)的极限也存在,且等于这两 个函数极限的和、差、积、商。
复合函数的极限运算法则
设函数$y=f[g(x)]$是由函数$u=g(x)$与函数$y=f(u)$复合而成,若$lim_{x
无穷小量的定义
如果函数$f(x)$当$x to x_0$(或$x to infty$)时的极限为零,那么称函数$f(x)$为当$x to x_0$(或$x to infty$)时 的无穷小量。
曲线的凹凸性与拐点
凹凸性
若函数f(x)在区间I上二阶可导,且 f''(x)>0(或<0),则称曲线y=f(x)在 I上是凹的(或凸的)。
拐点
拐点的判定
若函数f(x)在点x0处二阶可导,且 f''(x0)=0,则可通过三阶导数f'''(x0) 的符号来判断点(x0,f(x0))是否为曲线 的拐点。
THANKS
感谢观看
非线性微分方程
通过变量替换、积分等方法求解,或 利用数值方法近似求解
级数的概念与性质
级数的定义 无穷序列的部分和序列
级数的性质 加法、减法、乘法、除法、重排等性
质
级数的收敛与发散 部分和序列有极限则级数收敛,否则 发散
常见级数及其敛散性 等差级数、等比级数、调和级数、交 错级数等,通过比较法、比值法、根 值法等方法判断其敛散性
VS
极限的性质
唯一性、局部有界性、保号性、保不等式 性、迫敛性等。
极限的运算法则
极限的四则运算法则
若两个函数的极限存在,则它们的和、差、积、商(分母不为零)的极限也存在,且等于这两 个函数极限的和、差、积、商。
复合函数的极限运算法则
设函数$y=f[g(x)]$是由函数$u=g(x)$与函数$y=f(u)$复合而成,若$lim_{x
无穷小量的定义
如果函数$f(x)$当$x to x_0$(或$x to infty$)时的极限为零,那么称函数$f(x)$为当$x to x_0$(或$x to infty$)时 的无穷小量。
高等数学《微积分基本定理》课件

5.3 微积分基本定理
5.3.1 积分上限函数及其导数 5.3.2 微积分的基本定理
5.3.1 积分上限函数及其导数
1、 问题的提出
在变速直线运动中,) v(t)
物体在时间间隔
内经过的路程为 T2v(t)dt T1
另一方面这段路程可表示为 s(T2 ) s(T1 )
又由
~
b0
,得 c1 2
故a 1
例4.
证明
只要证
在
内为单调递增函数 .
F ( x) 0
证:
x
x
f (x)0
f (t)dt
x
f (x)0 t
f (t)dt
x 0
f
(t )d t
2
x
f
(
x
)
(
0
x
t
)
f (t)dt
x
0
f
(t )d t
2
0
例 5 设 f ( x)在[0,1]上连续,且 f ( x) 1.证明
b a
f
( x)dx
F
(
x
)
b a
F (b)
F (a)
★ 微积分基本定理
牛顿——莱布尼兹公式
b
a f ( x)dx
f ( )(b a) F ( )(b a) F(b) F(a)
积分中值定理
微分中值定理
通常把这一公式又叫微积分基本定理
例1 求
2 (2cos x sin x 1)dx.
所以f ( x)在[a, b]上连续
定理 2 如果 f ( x)在[a, b]上连续,则积分上限的函
数( x)
x
a
f
5.3.1 积分上限函数及其导数 5.3.2 微积分的基本定理
5.3.1 积分上限函数及其导数
1、 问题的提出
在变速直线运动中,) v(t)
物体在时间间隔
内经过的路程为 T2v(t)dt T1
另一方面这段路程可表示为 s(T2 ) s(T1 )
又由
~
b0
,得 c1 2
故a 1
例4.
证明
只要证
在
内为单调递增函数 .
F ( x) 0
证:
x
x
f (x)0
f (t)dt
x
f (x)0 t
f (t)dt
x 0
f
(t )d t
2
x
f
(
x
)
(
0
x
t
)
f (t)dt
x
0
f
(t )d t
2
0
例 5 设 f ( x)在[0,1]上连续,且 f ( x) 1.证明
b a
f
( x)dx
F
(
x
)
b a
F (b)
F (a)
★ 微积分基本定理
牛顿——莱布尼兹公式
b
a f ( x)dx
f ( )(b a) F ( )(b a) F(b) F(a)
积分中值定理
微分中值定理
通常把这一公式又叫微积分基本定理
例1 求
2 (2cos x sin x 1)dx.
所以f ( x)在[a, b]上连续
定理 2 如果 f ( x)在[a, b]上连续,则积分上限的函
数( x)
x
a
f
高等数学(微积分)课件--§7.1常数项级数的概念与性质

请利用几何级数计算: 1: ( ) 3 n 1 2 :
n 1
2
n
( 1) 2 3
n 1
n 1
3 : ( ) n2 4
n
8
例题(证明级数发散)
例 证明
证明级数 1 2 3 n 是发散的
n(n 1) 2
.
这级数的部分和为
sn 1 2 3 n
3 3
( 1)
n
8 9
n n
;
(2)
1 3
1 6
1 9
1 3n
; q 8 9 , 1 q
解
( 1 ) 因为级数是等比级数且
故原级数收敛
.
( 2 ) 因为级数
n1
1 n
是调和级数
, 它是发散的,
故由级数的性质知级数
1 3
1 6
1 9
1 3n
第七章
无穷级数
§7.1常数项级数的概念与性质 §7.2正项级数敛散性的判别 §7.3任意项级数敛散性的判别 §7.4*广义积分敛散性的判别 §7.5*幂级数 §7.6*函数的幂级数展开
1
§7.1常数项级数的概念与性质
一、常数项级数的概念 二、级数的基本性质 三、习题
2
一、常数项级数的概念
解
因为级数
n1
1 2
n
和
n1
1 3
n
都是收敛的等比级数
,
故由级数的性质知级数
1 1 1 1 1 1 2 2 n n 3 2 3 3 2 2
n 1
2
n
( 1) 2 3
n 1
n 1
3 : ( ) n2 4
n
8
例题(证明级数发散)
例 证明
证明级数 1 2 3 n 是发散的
n(n 1) 2
.
这级数的部分和为
sn 1 2 3 n
3 3
( 1)
n
8 9
n n
;
(2)
1 3
1 6
1 9
1 3n
; q 8 9 , 1 q
解
( 1 ) 因为级数是等比级数且
故原级数收敛
.
( 2 ) 因为级数
n1
1 n
是调和级数
, 它是发散的,
故由级数的性质知级数
1 3
1 6
1 9
1 3n
第七章
无穷级数
§7.1常数项级数的概念与性质 §7.2正项级数敛散性的判别 §7.3任意项级数敛散性的判别 §7.4*广义积分敛散性的判别 §7.5*幂级数 §7.6*函数的幂级数展开
1
§7.1常数项级数的概念与性质
一、常数项级数的概念 二、级数的基本性质 三、习题
2
一、常数项级数的概念
解
因为级数
n1
1 2
n
和
n1
1 3
n
都是收敛的等比级数
,
故由级数的性质知级数
1 1 1 1 1 1 2 2 n n 3 2 3 3 2 2
高等数学微积分第一章函数及其图形(共44张PPT)

如果A,B互相包含,即A B且B A,则称A与B相等,记为A=B。
如果把 y看作自变量,x 看作因变量,按照函数的定义就得到一个新的函数,这个新函数称为函数y=f(x)的反函数,记作 x=j(y)。
解: 要使函数有意义,必须x 0,且x2-4³0。
如果A,B互相包含,即A B且B A,则称A与B相等,记为A=B。
1
O
x
3.对数函数
指数函数y=ax的反函数叫做对数函数,记为
y=logax(a>0,a 1). 对数函数的定义域是区间(0,+ ).
单调性:
若a>1,则logax单调增加; 若0<a<1,则logax单调减少.
性质见书P34
y y=ax
1
O
y=logxax
a>1
4.三角函数
U(a)。 设>0,则称区间(a-, a+)为点a 的邻域,记作U(a, ),
即 U(a, ) ={x|a-<x<a+} ={x| |x-a|<}。
其中点 a 称为邻域的中心, 称为邻域的半径。
O a-
a+ x
去心邻域:
U
(a,)
={x
|0<|
x-a
|<}。
O a- a a+ x
左(右)邻域、M领域的概念见书中第七页。
bx
[a, b]={x|axb}称为闭区间。
[a, b]
Oa
bx
[a, b)={x|ax<b}及 (a, b]={x|a<xb}称为
半开区间。 [a, b)
Oa
bx
(a, b]
Oa
bx
大学微积分课件(PPT版)

微分方程是包含未知函数及其导数的等式。
微分方程的解
满足微分方程的函数称为微分方程的解。
一阶微分方程
一阶线性微分方程
形如y'=f(x)y' = f(x)y'=f(x)y=f(x)的一阶微 分方程,可以通过分离变量法求解。
一阶非线性微分方程
形如y'=f(y/x)y' = f(y/x)y'=f(y/x)的一阶微 分方程,可以通过变量代换法求解。
定积分的计算
计算方法与技巧
定积分的计算是微积分中的重要技能。常用的计算方法包括换元法、分部积分法、牛顿-莱布尼兹公 式等。通过这些方法,可以将复杂的定积分转化为易于计算的形式。
反常积分
概念与计算方法
VS
反常积分分为无穷积分和瑕积分两种 类型。对于无穷积分,需要讨论其在 有限的区间上收敛的情况;对于瑕积 分,需要讨论其在某一点附近的收敛 情况。反常积分的计算方法与定积分 的计算方法类似,但需要注意收敛的 条件。
极限与连续性
极限的定义与性质
极限的定义
极限是描述函数在某点附近的变化趋势 的一种数学工具。对于函数$f(x)$,如果 当$x$趋近于$a$时,$f(x)$的值趋近于 某个确定的常数$L$,则称$L$为函数 $f(x)$在点$a$处的极限。
极限的性质
极限具有唯一性、有界性、保序性和 局部有界性等性质。这些性质有助于 我们更好地理解极限的概念和应用。
连续函数的图像
连续函数的图像是连续不断的曲线。在微积分中,我们经常需要研究连续函数的性质和 变化规律,以便更好地解决实际问题。
03
导数与微分
导数的定义与性质
要点一
导数的定义
导数是函数在某一点的变化率,表示函数在该点的切线斜 率。
微分方程的解
满足微分方程的函数称为微分方程的解。
一阶微分方程
一阶线性微分方程
形如y'=f(x)y' = f(x)y'=f(x)y=f(x)的一阶微 分方程,可以通过分离变量法求解。
一阶非线性微分方程
形如y'=f(y/x)y' = f(y/x)y'=f(y/x)的一阶微 分方程,可以通过变量代换法求解。
定积分的计算
计算方法与技巧
定积分的计算是微积分中的重要技能。常用的计算方法包括换元法、分部积分法、牛顿-莱布尼兹公 式等。通过这些方法,可以将复杂的定积分转化为易于计算的形式。
反常积分
概念与计算方法
VS
反常积分分为无穷积分和瑕积分两种 类型。对于无穷积分,需要讨论其在 有限的区间上收敛的情况;对于瑕积 分,需要讨论其在某一点附近的收敛 情况。反常积分的计算方法与定积分 的计算方法类似,但需要注意收敛的 条件。
极限与连续性
极限的定义与性质
极限的定义
极限是描述函数在某点附近的变化趋势 的一种数学工具。对于函数$f(x)$,如果 当$x$趋近于$a$时,$f(x)$的值趋近于 某个确定的常数$L$,则称$L$为函数 $f(x)$在点$a$处的极限。
极限的性质
极限具有唯一性、有界性、保序性和 局部有界性等性质。这些性质有助于 我们更好地理解极限的概念和应用。
连续函数的图像
连续函数的图像是连续不断的曲线。在微积分中,我们经常需要研究连续函数的性质和 变化规律,以便更好地解决实际问题。
03
导数与微分
导数的定义与性质
要点一
导数的定义
导数是函数在某一点的变化率,表示函数在该点的切线斜 率。
高等数学(微积分)课件--§6.1定积分的概念与性质

y = f (x)
O a
b x
3
无限细分、无限求和
处理该类问题的基本思路: 无限细分(化曲为直)、无限求和!
y y= f (x)
O
a
b
x
4
曲边梯形的面积计算—分割
设函数在区间[a,b]上连续, y=f(x)≥0 y 分割:
任意插入n-1个分点:
a x0 x1 xn 1 xn b
T1 t0 t1 t n 1 t n T2
把[T1,T2]分成n小段[ti-1, ti] (i=1,2,…,n),每小段 时间长度∆ti= ti- ti-1 ;相应地,位移也分成n段∆si v ②取近似: ∆siv(i)∆ti (i=1,2,…,n) v vt ③求和:
浙江财经学院本科教学课程 ----经济数学(一)
微积分
第六章 定积分
§6.1定积分的概念与性质 §6.2微积分基本定理 §6.3定积分计算方法 §6.4定积分的应用 §6.5广义积分初步
1
§6.1定积分的概念与性质
一、曲边梯形的面积 二、定积分的定义 三、定积分的几何意义 四、定积分的基本性质 在本节中我们将从一些实际问题的计算里 提炼出一类关于“和式极限”计算的数学问 题,从而引申出定积分的概念,并探讨它的性 质、几何意义。
s v i ti
i 1 n
④取极限: 所求位移为
s lim
0
T1
T2
v t (其中 maxt )
i i i 1
1i n i
n
O
t 0 ... ti 1 t i ... t n
t
10
解决此类求和问题的数学模式
吉林大学微积分(高等数学) PPT课件

例如实数集R中集合 A {x 0 x 1}的 补集是
AC A {x x 0 或 x 1 }.
9
二、集合的基本运算
1. 集合的并、交、差
设 A、B 是两个集合,由所有属于A 或者属 于B 的元素组成的集合, 称为A 与 B 的并集(简称 并), 记作 A B,
即 A B {x x A 或 x B};
[a,b] {x a x b}.
oa
b
x
a 和 b 称为闭区间[a, b]的端点, a [a, b], b [a, b].
16
类似地可定义半开区间:
[a,b) { x a x b},(a,b] { x a x b}. 有限区间 [a, b]、(a, b)、(a, b]、[a, b).
a
a
a
点 a 叫做这个邻域的中心,
叫做这个邻域的半径.
x
19
去心邻域的定义:
点 a 的 邻域去掉中心a 后, 称为a 的去心
o
邻域, 记作U (a, ),即
o
U(a, ) { x 0 x a }.
开区间(a ,a) 称为a 的左 邻域, 开区间 (a, a ) 称为a 的右 邻域.
(,) {x x R} R
ob x
18
4.邻域的定义
设 是任一正数, 则开区间(a ,a ) 是 a 的一个邻域, 称为点a 的 邻域, 记作U(a, ). U(a, ) {x x a } {x a x a }.
22
按 照 定 义 , 如 果 数 集E有 界 , 则 存 在 常 数l与L(l L), 使 得 对 一 切x E, 都 有
AC A {x x 0 或 x 1 }.
9
二、集合的基本运算
1. 集合的并、交、差
设 A、B 是两个集合,由所有属于A 或者属 于B 的元素组成的集合, 称为A 与 B 的并集(简称 并), 记作 A B,
即 A B {x x A 或 x B};
[a,b] {x a x b}.
oa
b
x
a 和 b 称为闭区间[a, b]的端点, a [a, b], b [a, b].
16
类似地可定义半开区间:
[a,b) { x a x b},(a,b] { x a x b}. 有限区间 [a, b]、(a, b)、(a, b]、[a, b).
a
a
a
点 a 叫做这个邻域的中心,
叫做这个邻域的半径.
x
19
去心邻域的定义:
点 a 的 邻域去掉中心a 后, 称为a 的去心
o
邻域, 记作U (a, ),即
o
U(a, ) { x 0 x a }.
开区间(a ,a) 称为a 的左 邻域, 开区间 (a, a ) 称为a 的右 邻域.
(,) {x x R} R
ob x
18
4.邻域的定义
设 是任一正数, 则开区间(a ,a ) 是 a 的一个邻域, 称为点a 的 邻域, 记作U(a, ). U(a, ) {x x a } {x a x a }.
22
按 照 定 义 , 如 果 数 集E有 界 , 则 存 在 常 数l与L(l L), 使 得 对 一 切x E, 都 有
高等数学(微积分学)教学课件

三、两个重要极限
重要极限Ⅰ lim sin x 1 x0 x
它可以拓展为 lim sin[ f (x)] 1 f (x)0 f (x)
sin 2x
例:lim x 2x
1
1 cos x
lim
x0
x2
lim
x0
2 sin 2 x 2
4 x2 4
lim
1
sin
x 2
x0 2 x
2
2
1 2
判断:lim sin x 1
叫做因变量.
数集 D 称为这个函数的定义域.
全体函数值的集合称为函数的值域.
2. 函数的表示法
解析法(公式法):用解析表达式(或公式)表示函数关系.
y x 1
表格法:用列表的方法来表示函数关系.
x123456789 y 1 4 9 16 25 36 49 64 81
图示法:用平面直角坐标系 xoy 上的曲线来表示函数关系.
x
x
1 0
x
x
1
1
1 lim( x0 1
x
)
1 x
x
lim
x0
(1 (1
x) x
1
x) x
lim x0
(1 x) x
1 (1)
[1 (x)] x
e e1
e2
一类特殊极限
若f
(x)
a0 xm a1xm1 a2 xm2 b0 xn b1xn1 b2 xn2
am1x am bn1x bn
x 果对于定义区间的任意点 , 恒有 f (x) f (x) , 则称f (x)
为 D 内的偶函数;如果恒有 f (x) f (x) , 则称 f (x)为D
大学微积分课件(PPT幻灯片版)

i 1
例 1 比较积分值0 e dx 和0 xdx 的大小.
解 令 f ( x ) e x x,
2
x
2
x [ 2, 0]
x ( e 2 x )dx 0, 0
f ( x ) 0,
0
0
2
e dx 2xdx ,
x
于是
2
0
e dx 0 xdx .
a
x1
x i 1 i xi
x n 1 b
x
以 [ xi 1 , xi ]为底, f ( i ) 为高的小矩形面积为
Ai f ( i ) x i
曲边梯形面积的近似值 n 为
i 1
A f ( i )xi
当分割无限加细 , 记小区间的最大长度 或者 ( x )
x max{ x1 , x2 , x n }
积分上限
为
f ( i )x i a f ( x )dx I lim 0 i 1
被 积 函 数
被 积 表 达 式
b
n
积分和
积分下限
积 分 变 量
[a , b] 积分区间
注意:
(1)积分值仅与被积函数及积分区间有关, 而与积分变量的字母无关.
a f ( x )dx a f (t )dt a f (u)du
(2)定义中区间的分法和 i 的取法是任意的.
(3)当函数 f ( x ) 在区间[a , b]上的定积分存在时 ,
b
b
b
称 f ( x ) 在区间[a , b]上可积.
三、存在定理
定理 1 当函数 f ( x ) 在区间[a , b ] 上连续时
例 1 比较积分值0 e dx 和0 xdx 的大小.
解 令 f ( x ) e x x,
2
x
2
x [ 2, 0]
x ( e 2 x )dx 0, 0
f ( x ) 0,
0
0
2
e dx 2xdx ,
x
于是
2
0
e dx 0 xdx .
a
x1
x i 1 i xi
x n 1 b
x
以 [ xi 1 , xi ]为底, f ( i ) 为高的小矩形面积为
Ai f ( i ) x i
曲边梯形面积的近似值 n 为
i 1
A f ( i )xi
当分割无限加细 , 记小区间的最大长度 或者 ( x )
x max{ x1 , x2 , x n }
积分上限
为
f ( i )x i a f ( x )dx I lim 0 i 1
被 积 函 数
被 积 表 达 式
b
n
积分和
积分下限
积 分 变 量
[a , b] 积分区间
注意:
(1)积分值仅与被积函数及积分区间有关, 而与积分变量的字母无关.
a f ( x )dx a f (t )dt a f (u)du
(2)定义中区间的分法和 i 的取法是任意的.
(3)当函数 f ( x ) 在区间[a , b]上的定积分存在时 ,
b
b
b
称 f ( x ) 在区间[a , b]上可积.
三、存在定理
定理 1 当函数 f ( x ) 在区间[a , b ] 上连续时
《高等数学微积分》课件

实际应用
极值问题在经济学、物理学等领域有广泛应 用,如成本最小化、利润最大化等。
曲线的长度
曲线长度公式
利用微积分计算曲线的长度。
参数方程
通过参数方程将曲线表示为参数的函数,便于计算长度。
实际应用
在工程、地理等领域,需要计算各种曲线的长度,如河流长度、 道路长度等。
面积和体积
面积和体积公式
利用微积分计算平面图形的面积和空间图形的体积。
结合律
微积分运算还具有结合律,即函数的微积分运算顺序不影响结果。
交换律
此外,微积分运算还满足交换律,即函数的微积分运算满足交换律 。
微积分运算的法则
分部积分法
分部积分法是微积分运算中的一 种重要方法,它将两个函数的乘 积的导数转化为两个函数的导数 的乘积,从而简化了计算过程。
换元法
换元法是微积分运算中的另一种 重要方法,它通过引入新的变量 来简化计算过程。
如何提高微积分的计算能力?
总结词:掌握计算方法 总结词:细心谨慎 总结词:多做练习题
详细描述:提高微积分的计算能力需要熟练掌握各种计 算方法,如极限的计算、导数的计算和积分的计算等。 掌握这些方法可以更快更准确地完成计算。
详细描述:在微积分的计算过程中,需要细心谨慎,避 免因粗心大意而导致的错误。仔细检查每一步的计算过 程,确保准确性。
微分
微分的定义与性质
微分是函数在某一点附近的小变化量,它描述了函数在该点附近的变化趋势。微分具有一些重要的性质,如线性性、 可加性和可乘性。
微分的计算方法
包括微分的四则运算法则、复合函数的微分法则、隐函数的微分法则等。这些方法可以帮助我们快速准确地计算函数 的微分。
微分的应用
微分在许多领域都有广泛的应用,如近似计算、误差估计、优化问题等。例如,在近似计算中,微分可 以用来估计函数在某一点的近似值;在优化问题中,微分可以用来寻找函数的极值点。
《微积分》课件

微分学主要研究函数在某一点附近的 局部行为,包括切线、函数的变化率 等;积分学则研究函数在某个区间上 的整体行为,包括面积、体积等。
微积分的历史背景
01
微积分的发展可以追溯到古代数 学,如希腊数学家阿基米德在求 面积和体积时已经有了积分学的 萌芽。
02
微积分的真正奠基人是牛顿和莱 布尼茨,他们分别独立地发展出 了微积分的基本理论,为后来的 数学发展奠定了基础。
《微积分》PPT课件
contents
目录
• 微积分的定义与历史 • 微积分的基本概念 • 微积分的应用 • 微积分的解题技巧 • 微积分的重点与难点解析 • 微积分的习题与答案解析
01
微积分的定义与历史
微积分的定义
微积分是研究函数、极限和连续性的 数学分支,通过微分和积分的方法来 研究函数的性质和变化规律。
极限的运算性质与法则
1 2
极限的运算性质
极限的四则运算法则、复合函数的极限运算法则 等。
极限的法则
极限的保号性、极限的局部有界性等。
3
注意事项
理解极限的运算法则和性质是解决极限问题的关 键,需要注意运算过程中的等价变换和放缩技巧 。
导数的几何意义与运算性质
导数的几何意义
切线的斜率、函数图像的变化率等。
习题一:极限的运算
$lim_{x to infty} frac{1}{x}$
判断下列叙述是否正 确,并说明理由
$lim_{x to 0} (1 + x)^{1/x}$
习题一:极限的运算
$lim_{x to 0} frac{sin x}{x} = 1$
$lim_{x to infty} frac{1}{x} = 0$
$lim_{x to 0} (1 + x)^{1/x} = e$
微积分的历史背景
01
微积分的发展可以追溯到古代数 学,如希腊数学家阿基米德在求 面积和体积时已经有了积分学的 萌芽。
02
微积分的真正奠基人是牛顿和莱 布尼茨,他们分别独立地发展出 了微积分的基本理论,为后来的 数学发展奠定了基础。
《微积分》PPT课件
contents
目录
• 微积分的定义与历史 • 微积分的基本概念 • 微积分的应用 • 微积分的解题技巧 • 微积分的重点与难点解析 • 微积分的习题与答案解析
01
微积分的定义与历史
微积分的定义
微积分是研究函数、极限和连续性的 数学分支,通过微分和积分的方法来 研究函数的性质和变化规律。
极限的运算性质与法则
1 2
极限的运算性质
极限的四则运算法则、复合函数的极限运算法则 等。
极限的法则
极限的保号性、极限的局部有界性等。
3
注意事项
理解极限的运算法则和性质是解决极限问题的关 键,需要注意运算过程中的等价变换和放缩技巧 。
导数的几何意义与运算性质
导数的几何意义
切线的斜率、函数图像的变化率等。
习题一:极限的运算
$lim_{x to infty} frac{1}{x}$
判断下列叙述是否正 确,并说明理由
$lim_{x to 0} (1 + x)^{1/x}$
习题一:极限的运算
$lim_{x to 0} frac{sin x}{x} = 1$
$lim_{x to infty} frac{1}{x} = 0$
$lim_{x to 0} (1 + x)^{1/x} = e$
吉林大学微积分(高等数学)课件

23
定义 2 设E是R的非空子集,如果存在常数
R( R ),满足条件
(1) 对一切x E都有x ( x ),即 ( )为 的E下界(上界); 都存在x0 E , 使得 x0 ( x0 ), 则称 ( )为E的下 确 界 (上 确 界 ) . 数集E的下确界和上确界 分别记为
[a,) { x x a}
o
a
x o x
( , b) { x x b}
(,) { x x R} R
b
18
4.邻域的定义
设 是任一正数, 则开区间(a , a ) 是 a 的一个邻域, 称为点a 的 邻域, 记作 U (a, ).
高等数学
吉林大学数学学院 杨 泰 山
1
主要内容
第一章 预备知识 第二章 极限与连续函数 第三章 导数与微分 第四章 微分中值定理与导数的应用 第五章 不定积分 第六章 定积分 第七章 空间解析几何
2
第一章 预备知识
§1 实 数 集 §2 函数 §3 常用逻辑符号简介
3
§1 实 数 集
一、集合的概念与表示 二、集合的基本运算
(1) 列举法: 即把集合的全体元素一一列举.
例如 A {a1 , a2 ,, an };
(2) 描述法: 若集合M是由具有某种性质P 的元素的全体所组成, 写出其特性.
M { x x 具有性质 P }. 2 例 如 集合 B 是方程 x 1 0 的解集,
则集合 B { x x 1 0 }.
25
21
定义1 设E是R的一个非空子集,如果存在 常数l(或L),使得对一切x E都有 l x或xL, 则称数集E有下界(或有上界),常数l(或L) 称为数集E的一个下界(或上界),否则称 数集 E无下界或(无上界). 如果数集E既 有下界又有上界,则称E有界,否则称E无界
定义 2 设E是R的非空子集,如果存在常数
R( R ),满足条件
(1) 对一切x E都有x ( x ),即 ( )为 的E下界(上界); 都存在x0 E , 使得 x0 ( x0 ), 则称 ( )为E的下 确 界 (上 确 界 ) . 数集E的下确界和上确界 分别记为
[a,) { x x a}
o
a
x o x
( , b) { x x b}
(,) { x x R} R
b
18
4.邻域的定义
设 是任一正数, 则开区间(a , a ) 是 a 的一个邻域, 称为点a 的 邻域, 记作 U (a, ).
高等数学
吉林大学数学学院 杨 泰 山
1
主要内容
第一章 预备知识 第二章 极限与连续函数 第三章 导数与微分 第四章 微分中值定理与导数的应用 第五章 不定积分 第六章 定积分 第七章 空间解析几何
2
第一章 预备知识
§1 实 数 集 §2 函数 §3 常用逻辑符号简介
3
§1 实 数 集
一、集合的概念与表示 二、集合的基本运算
(1) 列举法: 即把集合的全体元素一一列举.
例如 A {a1 , a2 ,, an };
(2) 描述法: 若集合M是由具有某种性质P 的元素的全体所组成, 写出其特性.
M { x x 具有性质 P }. 2 例 如 集合 B 是方程 x 1 0 的解集,
则集合 B { x x 1 0 }.
25
21
定义1 设E是R的一个非空子集,如果存在 常数l(或L),使得对一切x E都有 l x或xL, 则称数集E有下界(或有上界),常数l(或L) 称为数集E的一个下界(或上界),否则称 数集 E无下界或(无上界). 如果数集E既 有下界又有上界,则称E有界,否则称E无界
