麦克斯韦速率分布律气体分子的平均碰撞频率和平均自
合集下载
4-4 气体分子碰撞和平均自由程
单原子
i3
刚性双原子 i 5
刚性多原子 i 6
3.能均分定理
在温度为T 的平衡态下, 物质分子的每一个
自由度都具有相同的平均动能, 其大小为 1 kT. 2
4.每个分子的平均总动能
i kT
2 5.1mol 理想气体的热力学能
i
i
E0 N 0(2 kT ) 2 RT
6.质量为M 的理想气体的热力学能
所以
Z 2 d 2vn
上式表明
平均碰撞次数与分子数密度，分子平均速 率成正比，也是与分子的直径的平方成正比．
把 Z 2 d 2vn代入
得
上式表明
vt v Zt Z
1
2 d 2n
平均自由程与分子碰撞截面、分子数密度 成反比，而与分子平均速率无关。
因为 所以
p nkT
kT
2 d 2 p
上式表明
kT
2 d 2 p
当气体的温度给定时，气体的压强越大 （即气体越密集），分子的平均自由程越短； 反之，若气体压强越小（即气体越稀薄），分 子的平均自由程越长.
4.4.3 例题分析
例1 求在标准状态下,空气分子的平均自由程、 平均速率及平均碰撞次数.（已知空气的平均摩 尔质量为 2910-3kg·mol-1, 空气分子的有效直 径为3. 5 10-10m）.
上式表明
分子间碰撞越频繁，平均自由程越小。
(1) 假设分子中只有一个分子A以平均速 率 v 运动，其余分子都静止不动。 请看动画演示
这样,凡是中心与
A分子中心的距离小
于或等于有效直径d
A
dd
的分子,都要与A分子
相碰。
麦克斯韦气体速率分布律
麦克斯韦气体速率分布律Maxwell Velocity Distribution大家知道，由气体的温度公式可以得出气体分子的方均根速率。
例如在时，氦气。
氧气。
但我们要注意的是，方均根速率仅是运动速率的一种统计平均值，并非气体分子都以方均根速率运动。
事实上，处于平衡状态下的任何一种气体，各个分子均以不同的速率、沿各个方向运动着。
有的速率大于方均根速率，有的速率小于方均根速率，它们的速率可以取零到无穷大之间的任意值。
而且由于气体分子间的相互碰撞，每个分子的速度也在不断地改变，所以在某一时刻，对某个分子来说，其速度的大小和方向完全是偶然的。
然而就大量分子整体而言，在平衡状态下，分子的速率分布遵守一个完全确定的统计性分布规律又是必然的。
下面我们介绍麦克斯韦应用统计理论和方法导出的分子速率分布规律。
气体分子按速率分布的统计规律，最早是由麦克斯韦于1859年在概率论的基础上导出的，1877年玻耳兹曼由经典统计力学中也导出该规律。
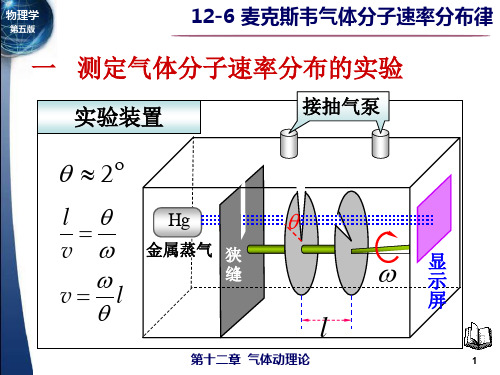
由于技术条件的限制，测定气体分子速率分布的实验，直到本世纪二十年代才实现。
1920年斯特恩（O.Stern首先测出银蒸汽分子的速率分布；1934年我国物理学家葛正权测出铋蒸汽分子的速率分布；1955年密勒（Mlier和库士（Kusch测出钍蒸汽分子的速率分布。
斯特恩实验是历史上最早验证麦克斯韦速率分布律的实验。
限于数学上的原因和本课程的要求，我们不推导这个定律，只介绍它的一些基本内容。
*麦克斯韦（J. C. Maxwell，1831—1879）英国物理学家，经典电磁理论的奠基人，气体动理论的创始人之一。
他提出了有旋电场和位移电流概念，建立了经典电磁理论，这个理论包括电磁现象的所有基本定律，并预言了以光速传播的电磁波的存在。
1873年，他的《电磁学通论》问世，这本书凝聚着杜费、富烂克林、库仑、奥斯特、安培、法拉第……的心血，这是一本划时代巨著，它与牛顿时代的《自然哲学的数学原理》并驾齐驱，它是人类探索电磁规律的一个里程碑。
大学物理第十二章气体动理论第6节 麦克斯韦气体分子速率分布律
解
m(H 2 ) m(O2 ) v p ( H 2 ) v p (O 2 )
vp (H2 ) 2 000m.s-1
2kT vp m
o
2 000
v/ ms
1
vp ( H 2 )
m( O 2 ) 32 4 v p (O 2 ) m( H 2 ) 2
vp (O2 ) 500m.s
f ( v)
dS
dN f ( v)dv dS N
v
第十二章 气体动理论
o
v v dv
概率密度
3
物理学
第五版
12-6 麦克斯韦气体分子速率分布律
f (v)dv物理意义
表示在温度为 T 的平衡状态下，速 率在 v 附近单位速率区间 的分子数占总 数的百分比 .
f (v)dv 的物理意义：
表示速率在 v v dv 区间的分 子数占总分子数的百分比.
第十二章 气体动理论
4
物理学
第五版
12-6 麦克斯韦气体分子速率分布律 麦克斯韦气体分子速率分布律 12-6
dN Nf ( v)dv 速率在 v v dv 内分子数： 速率位于 v1 v2区间的分子数： v2 N v N f (v)dv 1 速率位于 v1 v2 区间的分 f ( v)
-1
第十二章 气体动理论
17
f (v )
vp v v
2
第十二章 气体动理论
vp v 2 v
v
15
物理学
第五版
12-6 麦克斯韦气体分子速率分布律 麦克斯韦气体分子速率分布律 12-6
讨论 1 已知分子数 N ，分子质量 m ，分布函 数 f ( v) . 求 （1） 速率在 vp ~ v 间的分子 数；（2）速率在 vp ~ 间所有分子动能 之和 . 解 （ 1）
平均碰撞频率和自由程
(2)
(1)
dS V
V2 d V pdV V2 R R ln 0 V 1 T V V1
20
实际气体的性质
一. 实际气体的等温线
实际气体的等温线 可以分成四个区域
汽态区(能液化) 汽液共存区 液态区 气态区(不能液化)
CO 2 等Байду номын сангаас线
从图中的曲线可知
只有在较高温度或低的 压强时，CO2气体的性 质才和理想气体相近。
u 运动，其它分子都看作静止不动。
3
单位时间内与分子 A · 发生碰撞的分子数为 平均碰撞频率为 ·
n π d 2u
Z n π d 2u
考虑到所有分子实际上都在运动，则有 u ·
2v
Z 2 nπ d 2v
用宏观量 p 、T 表示的平均碰撞频率为
p p 2 8 RT Z 2 nπ d v 2 πd kT πM T
a ( p 2 )(v b ) RT v
任意质量气体的范德瓦尔斯方程为
m2 a m m ( p 2 2 )(V b ) RT M V M M
24
三 范德瓦尔斯等温线
从图中看出范德瓦尔斯 ·
等温线与实际气体等温 线颇为相似。
在临界等温线以上，二 · 者很接近，并且温度愈 高二者愈趋于一致。但 在临界等温线以下，二 者却有明显的区别。 尽管范德瓦尔斯方程能 · 较好地反映实际气体的
2
4
二. 分子的平均自由程
分子在连续两次碰撞之间自由运动的平均路程，称为分子 的平均自由程。
v 1 λ 2 Z 2πd n
用宏观量 p、T 表示的分子平均自由程为
k T T λ 2 2π d p p
(1)
dS V
V2 d V pdV V2 R R ln 0 V 1 T V V1
20
实际气体的性质
一. 实际气体的等温线
实际气体的等温线 可以分成四个区域
汽态区(能液化) 汽液共存区 液态区 气态区(不能液化)
CO 2 等Байду номын сангаас线
从图中的曲线可知
只有在较高温度或低的 压强时，CO2气体的性 质才和理想气体相近。
u 运动，其它分子都看作静止不动。
3
单位时间内与分子 A · 发生碰撞的分子数为 平均碰撞频率为 ·
n π d 2u
Z n π d 2u
考虑到所有分子实际上都在运动，则有 u ·
2v
Z 2 nπ d 2v
用宏观量 p 、T 表示的平均碰撞频率为
p p 2 8 RT Z 2 nπ d v 2 πd kT πM T
a ( p 2 )(v b ) RT v
任意质量气体的范德瓦尔斯方程为
m2 a m m ( p 2 2 )(V b ) RT M V M M
24
三 范德瓦尔斯等温线
从图中看出范德瓦尔斯 ·
等温线与实际气体等温 线颇为相似。
在临界等温线以上，二 · 者很接近，并且温度愈 高二者愈趋于一致。但 在临界等温线以下，二 者却有明显的区别。 尽管范德瓦尔斯方程能 · 较好地反映实际气体的
2
4
二. 分子的平均自由程
分子在连续两次碰撞之间自由运动的平均路程，称为分子 的平均自由程。
v 1 λ 2 Z 2πd n
用宏观量 p、T 表示的分子平均自由程为
k T T λ 2 2π d p p
气体动理论
1. 理想气体状态方程：处于平衡态的理想气体，质量为m 0，摩尔质量为M ，总分子数为N ，其状态参量P 、V 、T 之间满足状态方程：RT Mm PV 0=， 1131.8--⋅⋅=K mol J R ， nkT P = 式中VN n =为分子数密度， 1231038.1--⋅⨯=K J k 为玻尔兹曼常数。
4． 理想气体压强公式：)21(32322v m n n P k ==ε 5． 理想气体温度公式： k k T ε32=6．麦克斯韦速率分布律：处于平衡态的N 个分子，其速率分布在dv v v +-之间的分子数为dN ，则 dv v f NdN )(= )(v f 称为速率分布函数，)(v f 表示速率分布于v 附近单位速率区间的分子数占总分子数的百分比， 速率在v 1 --v 2 区间 的分子数占总分子数的比率为dv v f N N v v )(21⎰=∆， 归一化条件为1)(0=⎰∞dv v f 。
7． 气体分子的三种统计速率：（1） 物理量（如分子速率v ）的平均值为dv v vf v )(0⎰∞=。
（2） 最概然速率（曾用名：最可几速率）p v ，f(v)的极大值所对应的速率，用于研究分子的速率分布情况MRT M RT m kT v p 41.122≈==。
（3） 平均速率v ，用于研究分子碰撞MRT M RT m kT v 60.188≈==ππ。
（4） 方均根速率2v ，用于研究分子平均平动动能，MRT M RT m kT v 73.1332≈==。
8． 能量均分定理，理想气体的热力学能（内能）：（1） 自由度：决定一个物体在空间的位置所需要的独立坐标数目。
（2） 能量均分定理：在平衡态下，分子热运动的每一个自由度的平均动能都等于kT 21。
（3） 分子的平均总动能ε：设分子有t 个平动自由度，r 个转动自由度，s 个振动自由度，令i=t+r+2s, 则分子的平均总能量是：kT i 2=ε 单原子分子i=3， kT 23=ε ， 刚性双原子分子i=5， kT 25=ε， 刚性多原子分子（3个及3个以上），i=6，kT 26=ε。
11.4-11.6 麦克斯韦速率分布规律 麦克斯韦-波尔兹曼分布律、分子平均碰撞次数和平均自由程
1）
v
vp
Nf
(v)dv
2）
vp
1 2
mv 2
Nf
(v)dv
例 如图示两条 f (v) ~ v 曲线分别表示氢气和
氧气在同一温度下的麦克斯韦速率分布曲线， 从图
上数据求出氢气和氧气的最可几速率 .
f (v) O2
H2
vp
2RT M mol
M mol (H2 ) M mol (O2 )
469.1m / s
由公式
v2 3RT M mol
v2
38.31 300 29 103
507.1m
/
s
例 已知分子数 N ，分子质量 m ，分布函数
f (v) 求 1） 速率在vp ~ v 间的分子数； 2）速率
在 vp ~ 间所有分子动能之和 .
解：速率在v v dv 间的分子数 dN Nf (v)dv
N
dN
0
dN
f ()d
N
0N 0
8kT 8RT 1.60 RT
m
M mol
M mol
3
2dN
0
2
f
(
)d
N
0
或由w 1 m2 3 kT
2
2
可得 2 3kT
v1~v2
v2 f ()d
v1
v2 f ()d
v1
v v1~v2
v2 vf (v)dv
v1
对于v的某个函数g(v)，一般地，其平均值可以表示为
分子平均碰撞次数和平均自由程
第一节
12-6 麦克斯韦气体分子速率分布律
第十二章 气体动理论
12-6 麦克斯韦气体分子速率分布律
热运动分子之间 频繁碰撞 分子的运动路径 曲折复杂 自由程 ： 分 子两次相邻碰 撞之间自由通 过的路程 .
第十二章 气体动理论
12-6 麦克斯韦气体分子速率分布律
简化模型
(1) 分子为刚性小球 .d (2) 分子有效直径为 （分子间距平均值）. (3) 其它分子皆静止，某分子以平均速率 u 相对其它分子运动 .
第十二章 气体动理论
12-8 分子平均碰撞次数和平均自由程
碰撞时两分子质心距离的平均值称为
分子的有效直径
平均碰撞频率:分子在单位时间内与其它分子碰撞的平均次数称 碰撞频率的倒数为 相邻两次碰撞时间
分子在与其它分子的相邻两次碰撞之间所经历路程的平均值为
平均自由程
为分子的平均速率
可联系
进行估算
第十二章 气体动理论
3、理想气体的内能
1 mol 理想气体的内能 1 i E N A N Ai kT RT 2 2
( R N Ak )
理想气体的内能
m' i i E RT RT M 2 2
m' ( 为气体的摩尔数 ) M
试指出下列各式所表示的物理意义
1 3 i i m i (1) kT , (2) kT , (3) kT , (4) RT , (5) RT 2 2 2 2 M2
12-8 分子平均碰撞次数和平均自由程
平均自由程
若能找出
与
的关系，则
可求
设分子 的碰撞路径ABCD长度
设气体分子数密度
则柱内分子数为
平均碰撞频率
质心在半径为 、长度为 的圆柱 体内的分子都会与 相碰。
12-6 麦克斯韦气体分子速率分布律
第十二章 气体动理论
12-6 麦克斯韦气体分子速率分布律
热运动分子之间 频繁碰撞 分子的运动路径 曲折复杂 自由程 ： 分 子两次相邻碰 撞之间自由通 过的路程 .
第十二章 气体动理论
12-6 麦克斯韦气体分子速率分布律
简化模型
(1) 分子为刚性小球 .d (2) 分子有效直径为 （分子间距平均值）. (3) 其它分子皆静止，某分子以平均速率 u 相对其它分子运动 .
第十二章 气体动理论
12-8 分子平均碰撞次数和平均自由程
碰撞时两分子质心距离的平均值称为
分子的有效直径
平均碰撞频率:分子在单位时间内与其它分子碰撞的平均次数称 碰撞频率的倒数为 相邻两次碰撞时间
分子在与其它分子的相邻两次碰撞之间所经历路程的平均值为
平均自由程
为分子的平均速率
可联系
进行估算
第十二章 气体动理论
3、理想气体的内能
1 mol 理想气体的内能 1 i E N A N Ai kT RT 2 2
( R N Ak )
理想气体的内能
m' i i E RT RT M 2 2
m' ( 为气体的摩尔数 ) M
试指出下列各式所表示的物理意义
1 3 i i m i (1) kT , (2) kT , (3) kT , (4) RT , (5) RT 2 2 2 2 M2
12-8 分子平均碰撞次数和平均自由程
平均自由程
若能找出
与
的关系，则
可求
设分子 的碰撞路径ABCD长度
设气体分子数密度
则柱内分子数为
平均碰撞频率
质心在半径为 、长度为 的圆柱 体内的分子都会与 相碰。
6-3 气体分子速率分布率和平均自由程
100~200
200~300 300~400
0.081
0.165 0.214
400~500
500~600 600~700
0.206
0.151 0.092
700~800
800~900 900以上
0.048
0.021 0.009
第三节
气体分子速率分布律和能量分布律
N 1 由此数据为依据，以v N v 为横轴，以单位速率间隔 21.4% 内的分子数在总分子数内 所占的百分比为纵轴，作 16.5% 如图所示的锯齿形图。注 8.0% 意在速率间隔∆ν内实际包 200 400 括由v到v+∆ν内的所有速率 的分子。
f (v)
平 均 速 率
O
v
v
第三节
气体分子速率分布律和能量分布律
方均根速率：
气体分子速率平方的平均值的平方根。
v
2
N
0
v dN N
2
0
m e v f (v) 4p 2pkT
3 dN 2 2 mv 2 f (v )dv 2 2 kT RT 3kT 3 RT v N m 1.73
dN f (v )dv N
或
dN f (v ) Ndv
分子速率分布函数
第三节
气体分子速率分布律和能量分布律
速率分布函数
dN f (v ) Ndv
a、物理意义： 速率在v 附近的单位速率区间的 分子数占总分子的百分比。 b、应用: 确定分布在任一有限速率分布范围v1～v2 内的分子数占总分子数的百分比。
mv2 2 kT v 2 e
第三节
气体分子速率分布律和能量分布律
麦克斯韦分子速率分布定律(-28)
例（P247）计算在0℃时，氧气、氢气和氮气分子的 方均根速率。
说明气体 vrms v2 ～100m/s
历史上，曾因气体分子的方均根速率(或平均速率) 具有数百米每秒这一计算结果，引起一些人对早期 的气体动理论的怀疑和责难。
克劳修斯为说明这类分子碰撞问题，还提出了分子 碰撞次数和自由程的概念，它不仅解决了上述质疑， 而且使气体动理论建立在更加坚实的基础上，并向 前推进了一步。
x
v v
vf S
A
Bx
f x
粘度(又称粘性系数)
•国际单位制中，η的单位：kg m1 s1
～气体粘度与气体的性质和状态有关，可由实验测定
•微观机制(气体动理论的观点)
•气体流动时，气体分子除具有热运动的速度外， 还具有定向运动速度(即气体的流动速度)．
•由于,假定气体的温度T=C(即气体分子的热运动平 均速率为一常量)，气体分子数密度 n=C 。
用dN代表气体分子速率在 v v dv 区间内的分子
数，则
v
vdN
0
vNf (v)dv
0
f (v)vdv 4 (
m
3
)2
e
mv2 2kT
v3dv
N
N
0
2 kT 0
令 m
2kT
利用积分式：
e x2
0
x3dx
1
2 2
v 4 (
m
3
)2
ev2 v3dv 4 (
m
3
)2
1
2 kT 0
f(v)
1）最概然速率 vp
在 f (v) v的关系曲线中
，f (v)与的极大值相对应的
速率叫做最概然速率，也称 O 为最可几速率。
气体分子的平均碰撞频率和平均自由程
大学物理
气体动理论
第9讲 气体分子的平均碰撞频率 和平均自由程
一、分子的平均碰撞频率
平均碰撞频率和平均自由程
平衡态宏观性质的维持 非平衡态向平衡态过渡
依靠分子间的频繁碰撞实现
刚性球 模型
不可以像讨论压强那样 将分子看成质点
不需像讨论内能那样考 虑分子内部结构
分子的有效直径 d 约为10-10 m
无引力刚 性球模型
=
1.013×105 1.38×10−23 × 273
=
2.69 ×1025 m−3
λ = 1 = 2.14 ×10−7 m 2π d 2n
z = v = 7.95×109 s−1
λ
(约80亿次)
平均碰撞频率和平均自由程
d d
假定: 分子是直径为d 的弹性小球
分子A以平均相对速率 u 运动, 其他分子静止 由麦克斯韦速率分布可证 u = 2 v
球心轨迹为轴, d 为半径作折圆柱体
平均碰撞频率和平均自由程
d d
球心在圆柱体内的分子将与A碰撞
单位时间内有 πd 2u n 个分子与A发生碰撞
平均碰撞频率: z = 2π d 2nv
• 当温度一定时,平均自由程与压强成反比,压强越小,平 均自由程越长.
平均碰撞频率和平均自由程
例. 求氢在标准状态下一秒内分子的平均碰撞次数. (已知 分子直径d = 2×10-10m )
解:
v=
8RT =
Mπ
8×8.31× 273
2 ×10−3π
= 1.70 ×103 m ⋅ s−1
n
=
P kT
二、平均自由程平均碰撞频率平均自由程平均自由程( λ ): 分子在连续两次和其它分子发生碰撞
气体动理论
第9讲 气体分子的平均碰撞频率 和平均自由程
一、分子的平均碰撞频率
平均碰撞频率和平均自由程
平衡态宏观性质的维持 非平衡态向平衡态过渡
依靠分子间的频繁碰撞实现
刚性球 模型
不可以像讨论压强那样 将分子看成质点
不需像讨论内能那样考 虑分子内部结构
分子的有效直径 d 约为10-10 m
无引力刚 性球模型
=
1.013×105 1.38×10−23 × 273
=
2.69 ×1025 m−3
λ = 1 = 2.14 ×10−7 m 2π d 2n
z = v = 7.95×109 s−1
λ
(约80亿次)
平均碰撞频率和平均自由程
d d
假定: 分子是直径为d 的弹性小球
分子A以平均相对速率 u 运动, 其他分子静止 由麦克斯韦速率分布可证 u = 2 v
球心轨迹为轴, d 为半径作折圆柱体
平均碰撞频率和平均自由程
d d
球心在圆柱体内的分子将与A碰撞
单位时间内有 πd 2u n 个分子与A发生碰撞
平均碰撞频率: z = 2π d 2nv
• 当温度一定时,平均自由程与压强成反比,压强越小,平 均自由程越长.
平均碰撞频率和平均自由程
例. 求氢在标准状态下一秒内分子的平均碰撞次数. (已知 分子直径d = 2×10-10m )
解:
v=
8RT =
Mπ
8×8.31× 273
2 ×10−3π
= 1.70 ×103 m ⋅ s−1
n
=
P kT
二、平均自由程平均碰撞频率平均自由程平均自由程( λ ): 分子在连续两次和其它分子发生碰撞
麦克斯韦速率分布律
dN m 3 / 2 mv 2 / 2 kT 2 f ( v) 4 ( ) e v Ndv 2 π kT
23 ´ 当m 2 10 g , T 273k , V 800m / s
f (800) 10 什么含义
6
在800-800+dv速率区间，单位速 率区间分子数占总分子数之比
f (v ) d v
0 v0 2 av d v 0
0
1 3 av 0 3
3 a 3 v0
（2）设总分子数为N， 则
v
v 0
Nf (v ) d v N
2
v 0
f (v ) d v
v0 v 0
a 4 1 3 4 3 av d v v 0 ( 3 )v 0 v 0 4 v0 4 4
m 1.45 1.50 1.55 1.60 1.65 1.70 1.75 1.80 1.85 1.90 1.95
总人数1380 1.50-1.55m的人数130
30 25 20 15 10 5 0 25 26 26 26 27
1.51
1.52
1.53
1.54
1.55
1.56
50 40 30 20 10 0
N v d N v 0 N d Nv 0
i
N v 0
d Nv N
v 0
f (v ) d v
8kT 8RT 对麦氏速率分布经计算得： v πm π
v (v ) f (v ) d v
0
规律：任意v 的函数(v)对 全体分子的平均值都可以用 速率分布函数由上式求得：
6-(4-5) 能量均分定律 麦克斯韦速率分布率
6.74( K )
6 – 4
能量均分定律
理想气体内能
第六章气体动理论
一、统计规律的演示 一个小球落在哪里 有偶然性；少量小球 的分布每次都可能不 同；大量小球的分布 却是稳定的。
【演示】伽尔顿板
统计规律：大量偶然事件所显示的稳定的 规律 。
6 – 4
能量均分定律 理想气体内能 第六章气体动理论 下面列出了氧气分子在0OC时分子速率的分布情况
v
8 kT π m
f (v )
O2
v
2
3 kT mT 2 1200 K NhomakorabeaH2
o
v p1 v p 2
v
o
v p 0 v pH
v
N2 分子在不同温 度下的速率分布
同一温度下不同 气体的速率分布
6 – 5
麦克斯韦速率分布定律 讨论
第六章气体动理论
麦克斯韦速率分布中最概然速率 v p 的概念
下面哪种表述正确？ （A） v p 是气体分子中大部分分子所具有的速率. （B） v （C） v p 是麦克斯韦速率分布函数的最大值. （D） 速率大小与最概然速率相近的气体分子的比 率最大.
麦氏分布函数 f ( v ) 4 π (
其物理意义是：处于 温度为T的平衡气体，分子 速率出现在v附近、单位速 率区间内的分子数占总分 子数的百分率。
m 2 π kT
)
3 2
e
2 kT
v
2
f (v)
f (v )
dN Nd v
o
v
6 – 5
麦克斯韦速率分布定律
第六章气体动理论
分子速率分布与温度的关系： 1）存在最可几速率vp 。T增大，速率大的分子数增 多，最可几速率vp增大。 2）f(v)满足归一化条件： f (v )dv 1
第三讲 平均碰撞频率与平均自由程
4.写出旋转体中悬浮粒子的径向分布。设旋转体旋转角 速度为ω，粒子离旋转中心轴距离为r.
5.试以气体为例，用分子热运动观点对内摩擦、 热传导、扩散现象做出微观定性解释。
答案
—— 热学 ——
真实气体 范德瓦斯方程
作业
P149：1.26
预习 第二章 １、２、３、４节
—— 热学 ——
气体分子的平均自由程
1、粘滞现象
河流中水流的流速分布：
河岸
河流 u
河岸
f
u2
下层对上层的阻力
u1
f
上层对下层的作用力
—— 热学 ——
真实气体 范德瓦斯方程
各层气流的流速不同 相邻两层气流之间产生阻碍气体流动的阻力 ——称为粘性力。（这种现象称为内摩擦现象）
du -----速度梯度 dy
平均碰撞频率
z
平均自由程
平均速率
—— 热学 ——
λυ z
气体分子的平均自由程
（实际上其它分子也在运动）
平均相对速率 u 2υ 分子有效直径：d
—— 热学 ——
气体分子的平均自由程
d
u u
d
A
d
引入： 碰撞截面
d 2
结论： z 2σnυ
1
kT
λ
2σn 2πd 2 p
注：实际平均自由程可能与容器线度有关。
迁移现象产生的原因: 流速、温度、密度不均匀
无外界干预时，系统要从非平衡态自发地向平衡态 过渡。亦称输运过程。 讨论气体在非平衡态下的三种特殊过程。 即：三种迁移现象：
粘 滞 现 象 ——分子动量迁移； 热 传 导 现 象——分子能量迁移； 扩 散 现 象 ——分子密度迁移；
—— 热学 ——
5.试以气体为例，用分子热运动观点对内摩擦、 热传导、扩散现象做出微观定性解释。
答案
—— 热学 ——
真实气体 范德瓦斯方程
作业
P149：1.26
预习 第二章 １、２、３、４节
—— 热学 ——
气体分子的平均自由程
1、粘滞现象
河流中水流的流速分布：
河岸
河流 u
河岸
f
u2
下层对上层的阻力
u1
f
上层对下层的作用力
—— 热学 ——
真实气体 范德瓦斯方程
各层气流的流速不同 相邻两层气流之间产生阻碍气体流动的阻力 ——称为粘性力。（这种现象称为内摩擦现象）
du -----速度梯度 dy
平均碰撞频率
z
平均自由程
平均速率
—— 热学 ——
λυ z
气体分子的平均自由程
（实际上其它分子也在运动）
平均相对速率 u 2υ 分子有效直径：d
—— 热学 ——
气体分子的平均自由程
d
u u
d
A
d
引入： 碰撞截面
d 2
结论： z 2σnυ
1
kT
λ
2σn 2πd 2 p
注：实际平均自由程可能与容器线度有关。
迁移现象产生的原因: 流速、温度、密度不均匀
无外界干预时，系统要从非平衡态自发地向平衡态 过渡。亦称输运过程。 讨论气体在非平衡态下的三种特殊过程。 即：三种迁移现象：
粘 滞 现 象 ——分子动量迁移； 热 传 导 现 象——分子能量迁移； 扩 散 现 象 ——分子密度迁移；
—— 热学 ——
麦克斯韦气体分子速率分布律
速率区间 （m/s）
100以下 100～200 200～300 300～400 400～500 500～600 600～700 700～800 800～900
900以上
分子数出现的概率 ΔN/N
0.014 0.081 0.165 0.214 0.206 0.151 0.092 0.048 0.020 0.009
25
7-6 麦克斯韦气体分子速率分布律
第七章 气体动理论
1865年春辞去教职回到家乡系统地总结他的关于 电磁学的研究成果，完成了电磁场理论的经典巨著 《论电和磁》，并于1873年出版。1871年受聘为剑桥 大学新设立的卡文迪什实验物理学教授，负责筹建著 名的卡文迪什实验室，1874年建成后担任这个实验室 的第一任主任，直到1879年11月5日在剑桥逝世。
(v)dv
N
v1
N
表示在速率v1～v2速率区间内， 分子出现的概率。
(4)
v2
Nf (v)dv N
表示在速率v1 ～ v2速率区间内， 分子出现的个数。
v1
20
7-6 麦克斯韦气体分子速率分布律
麦克斯韦速率分布律的实验 验证
麦克斯韦在 1860 年 从理论上预言了理想气 体的速率分布律。60 年 后，也就是 1920 年斯特 恩通过实验验证了这一 规律，后来密勒和库将 实验进一步完善。
ΔN→0
v
N vdN
vf (v)dv
0N
0
14
7-6 麦克斯韦气体分子速率分布律
第七章 气体动理论
2.平均速率 v
v 0 vf (v)dv
代入麦克斯韦理想气体的速率分布函数：
v 4
m
3
/
2
麦克斯韦气体速率分布律
却进行得很慢。(演示）
克劳修斯指出：气体分子的速度虽然很大，但前
进中要与其他分子作频繁的碰撞，每碰一次，分
子运动方向就发生改变，所走的路程非常曲折。
一、平均自由程 和平均碰撞次数的定义
1、平均自由程 分子在连续两次碰撞之间
所经过的路程的平均值叫做平均自由程。(演示）
2、平均碰撞频率 Z 在单位时间内一个分子与其它分子碰撞的平均次 数，叫做分子的平均碰撞次数或平均碰撞频率。 3、二者关系
D l R 2
2、实验结果
•分子数在总分子数中所占 的比率与速率和速率间隔的 大小有关； •速率特别大和特别小的分 子数的比率非常小； •在某一速率附近的分子数 的比率最大； •改变气体的种类或气体的 温度时，上述分布情况有所 差别，但都具有上述特点。
二、麦克斯韦气体分子速率分布律
4-5 麦克斯韦气体速率分布律
4-6
4-7
玻尔兹曼能量分布律 等温气压公式(自学)
分子平均碰撞次数和平均自由程
4－5 麦克斯韦气体速率分布律
平衡态下，理想气体分子速度分布是有规律的， 这个规律叫麦克斯韦速度分布律。若不考虑分子速度 的方向，则叫麦克斯韦速率分布律。 气体分子按速率分布的统计规律最早是由麦克
间v1 ~ v2 内的分子数 占总分子数的比率。
—— 分布在有限速率区
5. Nf (v )dv
v1
v2
N ( v2 )
N ( v1 )
dN
间 v1 ~ v2 内的分子数。
—— 分布在 0 ～ ∞ 速率区
6.
0
f (v )dv 1
间内的分子数占总分子数的 比率。（ 归一化条件）
—— v2 的平均值。
克劳修斯指出：气体分子的速度虽然很大，但前
进中要与其他分子作频繁的碰撞，每碰一次，分
子运动方向就发生改变，所走的路程非常曲折。
一、平均自由程 和平均碰撞次数的定义
1、平均自由程 分子在连续两次碰撞之间
所经过的路程的平均值叫做平均自由程。(演示）
2、平均碰撞频率 Z 在单位时间内一个分子与其它分子碰撞的平均次 数，叫做分子的平均碰撞次数或平均碰撞频率。 3、二者关系
D l R 2
2、实验结果
•分子数在总分子数中所占 的比率与速率和速率间隔的 大小有关； •速率特别大和特别小的分 子数的比率非常小； •在某一速率附近的分子数 的比率最大； •改变气体的种类或气体的 温度时，上述分布情况有所 差别，但都具有上述特点。
二、麦克斯韦气体分子速率分布律
4-5 麦克斯韦气体速率分布律
4-6
4-7
玻尔兹曼能量分布律 等温气压公式(自学)
分子平均碰撞次数和平均自由程
4－5 麦克斯韦气体速率分布律
平衡态下，理想气体分子速度分布是有规律的， 这个规律叫麦克斯韦速度分布律。若不考虑分子速度 的方向，则叫麦克斯韦速率分布律。 气体分子按速率分布的统计规律最早是由麦克
间v1 ~ v2 内的分子数 占总分子数的比率。
—— 分布在有限速率区
5. Nf (v )dv
v1
v2
N ( v2 )
N ( v1 )
dN
间 v1 ~ v2 内的分子数。
—— 分布在 0 ～ ∞ 速率区
6.
0
f (v )dv 1
间内的分子数占总分子数的 比率。（ 归一化条件）
—— v2 的平均值。
5-4、5-5麦克斯韦速率分布律、平均自由程详解
v
窄条：
dN dN f ( )d d Nd N
分子速率在 v—v+dv 区间内的概率
2
1
部分：
f ( )d
设任一速率区间为: ~ 设总的气体分子数为N，在该区间内的分子数为ΔN
N N
——分布在速率 v～ v+△v速率间隔内的分子数占 总分子数的比率。 占总分子数的比率。
N ——分布在速率 v附近单位速率间隔内的分子数 vN
上页 下页 返回 退出
2. 速率分布函数 f(v) 的定义
三、麦克斯韦速率分布律
早在1859年，麦克斯韦应用统计概念和力学原理导出 在平衡态下理想气体分子速率分布函数的具体形式
m0 3 2 f ( ) 4π( ) e 2πkT
f ( )
m0 2 2 kT
2
麦克斯韦速 率分布函数
麦克斯韦速率分布曲线
O
上页 下页 返回 退出
四、气体分子速率的三种统计平均值
2 f d 0 2 12
2 3 2 3 d 0 F
12
F
3 5
上页 下页 返回 退出
（4）电子气中一个电子的平均动能为
F 1 1 1 3 2 2 2 3 2 2 t me me f ( )d me 3 d meF 0 0 2 2 2 F 10
1.6 RT
m0 2 2 kT
d
2
8kT πm0
3. 方均根速率
8RT π
m0 2 2 kT
f ( )d 0
2 2 0
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
分子碰撞频率:
在单位时间内一个分子与其他分子碰撞的次数。
大量分子的分子自由程与每秒碰撞次数服从统计 分布规律。可以求出平均自由程和平均碰撞次数。
一、平均碰撞次数
假 每个分子都是有效直径为d 的弹性小球。
定 只有某一个分子A以平均速率 v运动，
其余分子都静止。
d
v
d
v
A
d
d
v
d
v
A
d
球心在圆柱 体内的分子
d (m) 2.301010 3.101010 2.901010 3.701010
例 计算空气分子在标准状态下的平均自由程和碰 撞频率。取分子的有效直径d=3.510-10m。已知空气 的平均分子量为29。
解： 已知 T 273K , p 1.0atm 1.013105 Pa, d 3.51010 m
vp v v2
v
vp v v2
vp
2kT m
v 8kT πm
v2 3kT m
f (v)
T1 300K T2 1200K
o vp1 vp2
v
N2 分子在不同温 度下的速率分布
f (v)
O2 H2
o vp0 vpH
v
同一温度下不同 气体的速率分布
讨论
麦克斯韦速率分布中最概然速率 v p 的概念
f ()d
dN N
分子速率在 d
间隔内的分子数占
总分子数的百分比
Nf ()d dN 分子速率在 d
间隔内的分子数
2）f (v ) 的性质
f ()d 1 归一性质
0
dN 0 N
f ()d 1 几何意义
o
v1 v2 v
dN Nf (v)dv
速率位于
v1
v2
区间的分子数
N
v2
v1
N
f
(v)dv
速率位于 v1 v2 区间的分子数占总数的百分比
S
N (v1 N
v2 )
v2
v1
f
(v)dv
讨论
1）f (v ) 的意义
f
()
dN
Nd
分子速率在 附近
单位速率间隔内的分子数 占总分子数的百分比
m
M
3）方均根速率 v2
f (v)
N v2dN v2Nf (v)dv
v2 0
0
N
N
o
v
v2 3kT m
vrms
v2
3kT m
3RT M
v 1.60 kT 1.60 RT
m
M
vp
2kT m
2RT M
vp v v2
f(v)
都与 T 成正比，
与 M（或 ）成反比
• 理想气体忽略了分子间的引力
解决真实气体从修正理气模型入手
一、范德瓦耳斯气体模型
分子力：
f
f rs rt
引力 斥力
s = 9 ~15 t = 4~7
分斥 力
子
o
力
力r
引
分子间在距离较近时表现为斥力 距离较远时表现为引力
二、真实气体的状态方程 1mol理气状态方程
速率在 v v dv 间的分子数 dN Nf (v)dv
1）
v
vp
Nf
(v)dv
2）
vp
1 2
mv 2
Nf
(v)dv
例 如图示两条 f (v) ~ v 曲线分别表示氢气和
氧气在同一温度下的麦克斯韦速率分布曲线， 从图
上数据求出氢气和氧气的最可几速率 .
f (v)
vp
2kT m
v
dN f (v)dv dS N
归一化条件
表示在温度为 T 的平衡
状态下，速率在 v 附近单位
速率区间 的分子数占总数的
百分比 .
表示速率在v v dv
区间的分子数占总分子数的
百分比 .
0N
dN N
0
f
(v)dv
1
f (v)
dN f (v)dv dS
N
S
速率位于v v dv 内分子数
等宽度区间，能量越低的粒子出现的概率越大， 随着能量升高，粒子出现的概率按指数率减小。
如果E1 E2 ,则dN1 dN2
§7-7 分子的平均碰撞次数和平均自由程
气体分子 平均速率
v 1.60 RT M mol
氮气分子在270C时的平均速率为476m/s.
气体分子热运动平均速率高， 矛盾 但气体扩散过程进行得相当慢。
第三讲
麦克斯韦速率分布律 气体分子的平均碰撞频率和平均自由程
本次课内容
§7-5 麦克斯韦分子速率分布定律 §7-7 分子的平均碰撞次数和平均自由程
课本 pp241—262；练习册 第十七单元
§7-5 麦克斯韦分子速率分布定律
平衡态下，理想气体分子速度分布是有规律的， 这个规律叫麦克斯韦速度分布律。若不考虑分子速 度的方向，则叫麦克斯韦速率分布律。
v
N 为速率在 v v v 区间的分子数.
S N N
表示速率在 v v v
子数占总数的百分比 .
区间的分
分布函数 f (v) lim N 1 lim N 1 dN v0 Nv N v0 v N dv
f (v)
物理意义
dS
o v v dv
在速率区间v~v+dv中的分子数为 dN f ( v )dv dN
dN
n0eE p
kT (
m
2kT
)3
e2 Ek
kT 4v2dvdxdydz
dN
n0 (
m
2kT
)3
e2 ( Ek E p
)
kT 4v2dvdxdydz
n0 (
m
2kT
)3
2eE
kT 4v2dvdxdydz
麦克斯韦速率分布律: 1、速率分布率的实验测量 2、 分布函数及其意义 3、 麦克斯韦速率分布函数 4、 速率分布函数的应用
1.测定气体分子速率分布的实验
实验装置
接抽气泵
2
l v
Hg
金属蒸汽 狭 缝
vl
l
显 示
屏
分子速率分布图
N /(Nv)
N ：分子总数
S
o
v v v
下面哪种表述正确？
v （A） p 是气体分子中大部分分子所具有的速率. v （B） p 是速率最大的速度值. v （C） p 是麦克斯韦速率分布函数的最大值.
（D） 速率大小与最概然速率相近的气体分子的比
率最大.
例 计算在 27 C 时，氢气和氧气分子的方均
根速率 vrms .
MH 0.002kg mol1 R 8.31J K1 mol 1
克劳修斯指出：气体分子的速度虽然很大，但前 进中要与其他分子作频繁的碰撞，每碰一次，分 子运动方向就发生改变，所走的路程非常曲折。
ห้องสมุดไป่ตู้
在相同的t时间内，分子由A到
B的位移大小比它的路程小得多
A B
扩散速率
平均速率
(位移量/时间) (路程/时间)
分子自由程: 气体分子两次相邻碰撞之间自由通过的路程。
一秒钟内A与其它分子发生碰撞的平均次数 Z
平均自由程
v 1
Z
2 d 2n
与分子的有效直径的平方和分子数密度成反比
p nkT
kT 2d 2 p
当温度恒定时,平均自由程与气体压强成反比
在标准状态下，几种气体分子的平均自由程
气体 氢
氮
氧
空气
(m) 1.13 107 0.599107 0.647 107 7.0108
4 e4 4 10 0.42%
π
395
* §7-6 玻耳兹曼分布律
一、 麦克斯韦速度分布律
vz dv x dv y
dvz
v vz o
分子的速度分量限制在
vx ~ vx dvx , vy ~ vy dvy , vz ~ vz dvz
内的分子数占总分子数的百分比
vx vy
0
f
()
dΔNN
NNΔd
f ()d
oo
Δd
曲线下面积恒为1
2.麦克斯韦速率分布函数
麦氏分布函数
f (v) 4π(
m
)3
2
mv 2
e 2kT
v2
2πkT
dN 4π(
m
)3
2
mv 2
e 2kT
v2dv
N
2πkT
反映理想气体在热动 平衡条件下，各速率区间
vx vy
dN N
(
m
2kT
)3
2
e
m 2kT
(vx2
v
2 y
vz
2
)dv
xdv
y
dvz
dN F(v)
Ndvxdv ydvz
速度空间单位体积元内的分子数占总分子数的比率， 即速度概率密度（气体分子速度分布函数）
麦克斯韦速度分布函数
F
(v
x
,
v
y
,
vz
)
(
m
2kT
)3
2