关联分析与解耦控制
合集下载
第七章 解耦控制系统
pij 第一放大系数（开环增益） qij 第二放大系数（闭环增益）
2. 相对增益与相对增益矩阵
第一放大系数pij （开环增益） 指耦合系统中，除Uj到Yi通道外，其它通道 全部断开时所得到的Uj到Yi通道的静态增益; 即，调节量 Uj 改变了 Uj 所得到的 Yi 的变化 量 Yi 与 Uj 之比，其它调节量 Uk （ k≠j ）均 不变。 pij可表示为：
通过计算过程的微分分别计算出第一放大系数和 第二放大系数，从而得到相对增益矩阵。
另一种方法是增益矩阵计算法
先计算第一放大系数，再由第一放大系数直接计 算第二放大系数，从而得到相对增益矩阵。
2. 相对增益与相对增益矩阵
增益矩阵计算法
即由第一放大系数直接计算第二放大系数。
2. 相对增益与相对增益矩阵
的根所决定。即特征方程的根具有负实部， 两个关联回路是稳定的。
1. 耦合过程及其要解决的问题
通常认为，在一个多变量被控过程中，如果每一个被控
变量只受一个控制变量的影响，则称为无耦合过程，其分 析和设计方法与单变量过程控制系统完全一样。
存在耦合的多变量过程控制系统的分析与设计中需要解决 的主要问题： 1. 如何判断多变量过程的耦合程度？ 2. 如何最大限度地减少耦合程度？ 3. 在什么情况下必须进行解耦设计，如何设计？
1. 耦合过程及其要解决的问题
稳定性如何判别？
1. 耦合过程及其要解决的问题
当两个回路有关联时，则闭环稳定性由特征方程：
Q(s) [1 G11 (s)Gc1 (s)][1 G22 (s)Gc 2 (s)] G12 (s)G21 (s)Gc1 (s)Gc 2 (s) 0
式中
K 22 h11 K11 K 22 K12 K 21
解耦控制系统
2023/5/24
5
9.1.2 被控对象的典型耦合结构
对于具有相同数目的输入量和输出量的被控对象，典型的 耦合结构可分为P规范耦合和V规范耦合。
图9-3为P规范耦合对象。
2023/5/24
6
它有n个输入和n个输出，并且每一个输出变量
Yi(i=1,2,3,…,n）都受到所有输入变量Ui(i=1,2,3,…,n）的影响。 如果用pij(s)表示第j个输入量Uj与第 i个输出量Yi之间的传递函数， 则P规范耦合对象的数学描述式如下：
2023/5/24
13
对于一个耦合系统，因为每一个控制变量不只影响一 个被控变量，所以只计算在所有其他控制变量都固定 不变的情况下的开环增益是不够的。因此，特定的被 控变量Yi对选定的控制变量的响应还取决于其他控制 变量处于何种状况。
对于一个多变量系统，假设 Y是包含系统所有被
控变量Yi的列向量；U是包含所有控制变量Uj的列向量。 为了衡量系统的关联性质首先在所有其它回路均为开
从而求得耦合系统的相对增益ij。
2023/5/24
25
(2) 直接计算法 现以图9-7所示双变量耦合系统为例说明如何由第一放
大系数直接求第二放大系数。引入P矩阵，式（9-10）可写 成矩阵形式，即
Y Y 1 2 p p1 21 1p p1 2 2 2 U U 1 2 K K 1 21 1K K 1 2 2 2 U U 1 2 （9-14）
（9-13）
2023/5/24
24
从上述分析可知，第一放大系数pij是比较容易 确定的，但第二放大系数qij则要求其他回路开环增 益为较为复杂，特别是多变量系统。
事实上，由式（9-12）和式（9-13）可看出，第 二放大系数qij完全取决于各个第一放大系数pij，这 说明有可能由第一放大系数直接求第二放大系数，
第十章_解耦
第10章 解耦控制系统当再同一设备或装置上设置两套以上控制系统时，就要考虑系统间关联的问题。
其关联程度可通过计算各通道相对增益大小来判断。
如各通道相对增益都接近于1，则说明系统间关联较小；如相对增益于1差距较大，则说明系统间关联较为严重。
对于系统间关联比较小的情况，可以采用控制器参数整定，将各系统工作频率拉开的办法，以削弱系统间的关联的影响。
如果系统间关联非常严重，就需要考虑解耦的办法来加以解决。
解耦的本质是设置一个计算装置，去抵消过程中的关联，以保证各个单回路控制系统能独立地工作。
为了便于分析，下面对2×2系统的关联及其解耦方法进行研究。
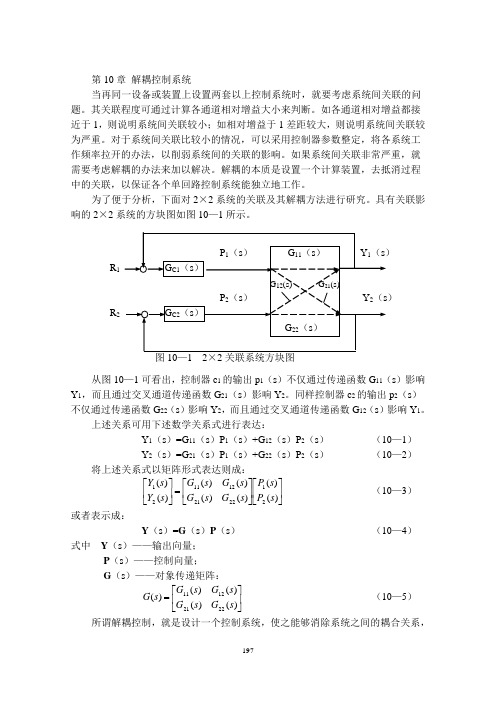
具有关联影响的2×2系统的方块图如图10—1所示。
从图10—1可看出，控制器c 1的输出p 1（s ）不仅通过传递函数G 11（s ）影响Y 1，而且通过交叉通道传递函数G 21（s ）影响Y 2。
同样控制器c 2的输出p 2（s ）不仅通过传递函数G 22（s ）影响Y 2，而且通过交叉通道传递函数G 12（s ）影响Y 1。
上述关系可用下述数学关系式进行表达：Y 1（s ）=G 11（s ）P 1（s ）+G 12（s ）P 2（s ）（10—1） Y 2（s ）=G 21（s ）P 1（s ）+G 22（s ）P 2（s ）（10—2）将上述关系式以矩阵形式表达则成：⎥⎦⎤⎢⎣⎡⎥⎦⎤⎢⎣⎡=⎥⎦⎤⎢⎣⎡)()()()()()()()(212221121121s P s P s G s G s G s G s Y s Y （10—3）或者表示成：Y （s ）=G （s ）P （s ）（10—4）式中 Y （s ）——输出向量；P （s ）——控制向量；G （s ）——对象传递矩阵：⎥⎦⎤⎢⎣⎡=)()()()()(22211211s G s G s G s G s G （10—5）所谓解耦控制，就是设计一个控制系统，使之能够消除系统之间的耦合关系，R 1） R 2图10—1 2×2关联系统方块图而使各个系统变成相互独立的控制回路。
工业过程控制工程课件10.解耦控制
C1
C2
C1 y20 C1 C2
y20 C2
C1
C2
变量配对举例（续）
6. 进行合适的变量配对 ( 假设C1 >y20 >C2 )：
u10
y20 C2 C1 C2
y10 , u20
C1 y20 C1 C2
y10
y20 C2
C1 C1
C2 y20
C1 C2
C1 y20 C1 C2 y20 C2 C1 C2
12 22
1 j 2 j
1n
2n
• • • • • •
yi
i1
i 2
ij
in
• • • • • •
yn n1
n2
nj
nn
相对增益系数的计算方法1
输入输出稳态方程
u1(s)
y1(s) y1 K11u1 K12u2
u2(s)
y2(s) y2 K21u1 K22u2
p11
多变量系统中的耦合
u1(s)
y1(s)
u2(s) ...
MIMO 过程
y2(s) ...
un(s)
yn(s)
基本问题：若采用SISO控制器，如何进行 输入输出变量之间的配对？
多回路PID 控制
相对增益的概念
第一放大系数 pij：在其它控制量 ur (r≠j)均不变的前
提下， uj 对yi 的开环增益
y1 u1
u2
K11
y1
K11u1 K12
y2
K21u1 K 22
q11
y1 u1
y2
K11
K12 K21 K 22
11
1
1 K12 K21
《过程控制系统》课程介绍与教学大纲
《过程控制系统》课程简介课程编号：06024012课程名称：过程控制系统/ Process Control System学分：2.5学时：40 （课内实验：4 上机：课外实践：）适用专业：自动化专业建议修读学期：7开课单位：测控技术与仪器系先修课程：《自动控制原理》《自动检测技术》等考核方式与成绩评定标准：考试，成绩=期末成绩（70%） +平时成绩（30%）教材与主要参考书目：《过程控制系统》（第二版）方康玲主编武汉理工大学出版社2007.2《过程控制工程》，蒋慰孙、俞金寿编著，中国石化出版社，1999《过程控制系统及工程》，翁维勤、周庆海编，化学工业出版社，1996《过程控制工程》，孙洪程等编，高等教育出版社，2006《工业生产过程控制》，何衍庆等编，化学工业出版社，2004内容概述：中文：过程控制和运动控制是自动控制技术的两个重要分支。
本课程主要介绍了过程控制的基本概念、组成以及简单过程控制、复杂过程控制系统的基本原理、系统设计技术以及应用技术等。
在介绍每一种控制策略的同时，都给出了其在不同实际场合下的具体应用实例。
英文：Process control and motion control are the two important branch of automation control technology. This course mainly introduce the basic concept of process control, constitution and the basic principle, system design technology, and application technology of process control. At the same time, concrete examples are given to introduce the different control strategy applied in practice.《过程控制系统》教学大纲课程编号：06024012课程名称：过程控制系统/ Process Control System学分：2.5学时：40 (课内实验：4 上机：课外实践： )适用专业：自动化专业建议修读学期：7一、课程性质、目的与任务本课程是自动化专业必修课。
设计串联解耦环节实现系统的解耦控制 (自动保存的)
馈。由于状态变量不一定具有物理意义，所以状态反馈往往不易实现。而输出变量则有明
显的物理意义，因而输出反馈易实现。
对于式(2.1)描述的线性系统，当将系统的控制量 取为输出 的线性函数
(2.4)
时，称之为输出反馈，其中其中 为 维参考输入向量， 为 矩阵，称为输出反馈增益矩阵。
将式(2.4)代入式(2.1)，可得到采用输出反馈后闭环系统的状态空间方程
3.
3.
3.
对于具有相同输入、输出个数的MIMO线性定常系统
(3.8)
设 为系统的输入输出个数，可采用控制规律 ，即存在输入变换阵和状态反馈矩阵对 进行解耦的充要条件是：可解耦性判别矩阵 为非奇异。且当选取 为 时，解耦控制系统的传递函数矩阵为
(3.9)
其中 ， 与 是解耦控制中两个基本特征量。对 对角线上第一个元素可提出第 个极点要求，并有
2.
设不完全能控的多输入系统为
(2.21)
经过坐标变换，即经过能控结构分解，式(2.21)可写成
(2.22)
式中， 为能控子系统，由于坐标变换不改变系统的极点，所以式(2.21)与式(2.22)系统的极点相同，它们的极点集为
(2.23)
极点 为能控极点， 为不能控极点，考虑式(2.22)系统的任意状态反馈
设计主要内容：
（1）求出系统的传递函数。
（2）设计串联解耦环节，并求出解耦后的系统传递函数。
（3）对解耦后的系统进行极点配置，并求出配置后系统的传递函数。
（4）绘制原系统及配置极点后系统的输出响应曲线图，并进行分析。
3.
3.
线性定常系统的状态空间表达式包括状态方程和输出方程，简写形式如下
(3.1)
式中， 分别为 维， 维， 维向量。式(3.1)中，上式为状态方程，下式为输出方程。状态空间表达式实际上是对MIMO系统的时域描述，而传递函数阵则是对系统的频域描述，把时域的数学模型转换成频域的数学模型，其基本方法是在零初始条件下取拉氏变换。因此，对式(3.1)在零初始条件下取拉氏变换，则有
显的物理意义，因而输出反馈易实现。
对于式(2.1)描述的线性系统，当将系统的控制量 取为输出 的线性函数
(2.4)
时，称之为输出反馈，其中其中 为 维参考输入向量， 为 矩阵，称为输出反馈增益矩阵。
将式(2.4)代入式(2.1)，可得到采用输出反馈后闭环系统的状态空间方程
3.
3.
3.
对于具有相同输入、输出个数的MIMO线性定常系统
(3.8)
设 为系统的输入输出个数，可采用控制规律 ，即存在输入变换阵和状态反馈矩阵对 进行解耦的充要条件是：可解耦性判别矩阵 为非奇异。且当选取 为 时，解耦控制系统的传递函数矩阵为
(3.9)
其中 ， 与 是解耦控制中两个基本特征量。对 对角线上第一个元素可提出第 个极点要求，并有
2.
设不完全能控的多输入系统为
(2.21)
经过坐标变换，即经过能控结构分解，式(2.21)可写成
(2.22)
式中， 为能控子系统，由于坐标变换不改变系统的极点，所以式(2.21)与式(2.22)系统的极点相同，它们的极点集为
(2.23)
极点 为能控极点， 为不能控极点，考虑式(2.22)系统的任意状态反馈
设计主要内容：
（1）求出系统的传递函数。
（2）设计串联解耦环节，并求出解耦后的系统传递函数。
（3）对解耦后的系统进行极点配置，并求出配置后系统的传递函数。
（4）绘制原系统及配置极点后系统的输出响应曲线图，并进行分析。
3.
3.
线性定常系统的状态空间表达式包括状态方程和输出方程，简写形式如下
(3.1)
式中， 分别为 维， 维， 维向量。式(3.1)中，上式为状态方程，下式为输出方程。状态空间表达式实际上是对MIMO系统的时域描述，而传递函数阵则是对系统的频域描述，把时域的数学模型转换成频域的数学模型，其基本方法是在零初始条件下取拉氏变换。因此，对式(3.1)在零初始条件下取拉氏变换，则有
第七章解耦控制系统_2023年学习资料
1.耦合过程及其要解决的问题-U1控y1,u2控y2?还是U1控y2,u2控y1?-选择控制作用Uj和y的 响条件：-1.选择u对y有直接和快速影响，同时，y对u的滞-后很小。-2.选择u,y后使控制回路间的关联程 最小。
1.耦合过程及其要解决的问题-·稳定性如何判别？
厨路1-Ys=-Y,]_GusGuU-y,o=GnGLU.o」-Ga-U:s=G:s[sp1s-Y,s-U s=Ge2s[sp2s-Y2s-Y1s=p11s5p1s十p12ssps-Y2s=pa ssp1s+p22 sp25-Pa=-Gi2sGe2s-回路2-Qs）-b-Ps=GaGas-Q5-1=-GuGas+GasG sGusGs-Gsizs-P-GaG.s+GaG.:[GaXim-CGn-Qs）=[1+G11sG1s][ TG22sGzs]-G12sG,sGeLss
1,耦合过程及其要解决的问题-·当两个回路有关联时，则闭环稳定性由特征方程：-Qs=[1+G11SGs]1 G22SGc2s]-G2sG21sG1sGe2s=0-的根所决定。即特征方程的根具有负实部，-两个关联回路 稳定的。
1.锅合过程及其要解决的问题-必通常认为，在一个多变量被控过程中，如果每一个被控-变量只受一个控制变量的影 ，则称为无耦合过程，其分-析和设计方法与单变量过程控制系统完全一样。-冬存在耦合的多变量过程控制系统的分析 设计中需要解决-的主要问题：-1.如何判断多变量过程的耦合程度？-2.如何最大限度地减少耦合程度？-3.在 么情况下必须进行解耦设计，如何设计？
2.相对赠益与相对增益矩-令某一通道在其它系统均为开环时的放大系-数与该一通道在其它系统均为闭环时的放大数之比为，称为相对增益；-相对增益入是U:相对于过程中其他调节量对-该被控量Y而言的增益（U,→Y;;-· 义为-P-第一放大系数（开环增益）-gi-第二放大系数（闭环增益）
(工业过程控制)10.解耦控制
动态解耦
在系统运行过程中，通过动态调整控制参数或策略，实现耦合的 实时解耦。
解耦控制的方法与策略
状态反馈解耦
通过引入状态反馈控制 器，对系统状态进行实 时监测和调整，实现解
耦。
输入/输出解耦
通过合理设计输入和输 出信号，降低变量之间
的耦合程度。
参数优化解耦
通过对系统参数进行优 化调整，改善耦合状况， 实现更好的解耦效果。
通过线性化模型，利用线性控制理论设计控制器，实现系统 解耦。
非线性解耦控制
针对非线性系统，采用非线性控制方法，如滑模控制、反步 法等，实现系统解耦。
状态反馈与动态补偿解耦控制
状态反馈解耦控制
通过状态反馈技术，将系统状态反馈 到控制器中，实现系统解耦。
动态补偿解耦控制
通过动态补偿器对系统进行补偿，消 除耦合项，实现系统解耦。
特点
解耦控制能够简化系统分析和设计过 程，提高系统的可维护性和可扩展性 ，同时降低系统各部分之间的相互影 响，增强系统的鲁棒性。
解耦控制的重要性
01
02
03
提高系统性能
通过解耦控制，可以减小 系统各部分之间的相互干 扰，提高系统的整体性能。
简化系统设计
解耦控制能够将复杂的系 统分解为若干个独立的子 系统，简化系统的分析和 设计过程。
调试和维护困难
耦合问题增加了系统调试和维护的难度，提高了运营成本。
解耦控制在工业过程控制中的实施
建立数学模型
01
对工业过程进行数学建模，明确各变量之间的耦合关系。
选择合适的解耦策略
02
根据耦合程度和系统特性，选择合适的解耦策略，如状态反馈、
输出反馈等。
控制器设计
03
在系统运行过程中，通过动态调整控制参数或策略，实现耦合的 实时解耦。
解耦控制的方法与策略
状态反馈解耦
通过引入状态反馈控制 器，对系统状态进行实 时监测和调整，实现解
耦。
输入/输出解耦
通过合理设计输入和输 出信号，降低变量之间
的耦合程度。
参数优化解耦
通过对系统参数进行优 化调整，改善耦合状况， 实现更好的解耦效果。
通过线性化模型，利用线性控制理论设计控制器，实现系统 解耦。
非线性解耦控制
针对非线性系统，采用非线性控制方法，如滑模控制、反步 法等，实现系统解耦。
状态反馈与动态补偿解耦控制
状态反馈解耦控制
通过状态反馈技术，将系统状态反馈 到控制器中，实现系统解耦。
动态补偿解耦控制
通过动态补偿器对系统进行补偿，消 除耦合项，实现系统解耦。
特点
解耦控制能够简化系统分析和设计过 程，提高系统的可维护性和可扩展性 ，同时降低系统各部分之间的相互影 响，增强系统的鲁棒性。
解耦控制的重要性
01
02
03
提高系统性能
通过解耦控制，可以减小 系统各部分之间的相互干 扰，提高系统的整体性能。
简化系统设计
解耦控制能够将复杂的系 统分解为若干个独立的子 系统，简化系统的分析和 设计过程。
调试和维护困难
耦合问题增加了系统调试和维护的难度，提高了运营成本。
解耦控制在工业过程控制中的实施
建立数学模型
01
对工业过程进行数学建模，明确各变量之间的耦合关系。
选择合适的解耦策略
02
根据耦合程度和系统特性，选择合适的解耦策略，如状态反馈、
输出反馈等。
控制器设计
03
宋彤过程控制工程-8 关联解耦_lt
Part II: Control System Design
Chapter 7 Control of Single-Input-Single-Output (SISO) Processes
Chapter 8 Two-Degree-of-Freedom (2DOF) Control of SISO Processes
先进控制技术研究所
8. 系统关联及解耦控制
工业生产过程中多变量输出以及各控制回路之间通 常存在着不同程度的耦合关联关系。强相关或负相关 的耦合关系会严重影响控制性能，甚至破坏闭环系统 的稳定性，因此应在控制系统设计中考虑解耦问题。
主要内容： 关联系统描述分析 相对增益阵Λ 系统耦合强度的削减方法 解耦控制设计
Chapter 9 Cascade Control System 先进控制介绍
Chapter 10 Multiloop Control of Multivariable Processes 解耦控制
Chapter 11 Decoupling Control of Multivariable Processes
P12(s)
G12(s)GC2(s) Q(s)
P21(s)
G21(s)
G12(s)
u2
G22(s)
Y1(s) Y2(s)
开环
Y(s) Y Y 1 2((s s)) G G 1 21 1((s s))
G 12(s)U 1(s) G 22(s) U 2(s)
闭环系统(Multiloop)： 由闭环回路有：
u1
Gc1(s)
G11(s) G21(s)
F1
F2
数学描述方式：对角阵
YyyH FGHF 01(s)
解耦控制decoupling
( p1 p2 ) ( p0 p2 ) ( p0 p1 ) ( p0 p2 )
2
• 如果p1 p2，则I，说明1 h， 2 p1可行
• 如果p1 p0，则11和22 0，而 21和12 1，此时应 重新匹配变量，即1 p1 ， 2 h可行 • 如果p1=(p0-p2)/2， ij=0.5，只能解耦
2
ij 在0 1之间，因为 p0 p1 p2
p0 p1 p0 p2 ( p1 p2 ) p0 p1 p1 p2 p0 p1 p0 p2 ( p0 p1 ) 1 0 Λ 回路间不耦合 0 1 0.5 0.5 Λ 耦合最严重 0.5 0.5
r1
-
Kc1 gc1
1
K11 g11
K21 g21
+
+
y1
K12 g12 r2
-
Kc2 gc2
调节器
2
K22 g22
过程
+
+
y2
二.求取相对增益的方法
1.利用相对增益定义（7-4）来计算 例7-1
PC QC
p1
PT DT
h p2 2
p0 1
压力--流量系统的数学描述：
1 2 ( p0 p2 ) h 1 ( p0 p1 ) 2 ( p1 p2 ) (7 6) 1 2 y1 h, y2 p1
(7 12) (7 13)
y2
K12 K 21 K11 K 22 (7 14)
11
p11 K11 K 22 q11 K11 K 22 K12 K 21
依此办理可得12， 21， 22。 由上例可知，只要有Kij就可推得相对增益，是否可以 有更方便的计算方法？ 假设有一个矩阵H，它与第二放大系数矩阵Q有如下关 系：
解耦控制
ij
pij q ij
pij 第一放大系数（开环增益） qij 第二放大系数（闭环增益）
过程控制 青海大学
2014-1-17
17
3.2.2
相对增益与相对增益矩阵
第一放大系数pij （开环增益） – 指耦合系统中，除Uj到Yi通道外，其它通 道全部断开时所得到的Uj到Yi通道的静态 增益; – 即，调节量 Uj 改变了 Uj 所得到的 Yi的变 化量Yi与Uj之比，其它调节量 Uk（k≠j） 均不变。 – pij可表示为：
2014-1-17
过程控制 青海大学
10
3.2.1
耦合过程及其要解决的问题
耦合程度分析方法
– 直接法
解析法
– 相对增益法
求相对增益矩阵的计算方法
2014-1-17
过程控制 青海大学
11
3.2.1
耦合过程及其要解决的问题
直接法
– 借助耦合系统的方框图，直接解析地导出各 变量之间的函数关系，从而确定过程中每个 被控量相对每个调节量的关联程度。
PC FC
u1
PT
FT
u2
图 6-8 关联严重的控制系统
2014-1-17
过程控制 青海大学
4
3.2.1
耦合过程及其要解决的问题
控制回路间的关联
控制回路间的耦合
– 单回路控制系统 – 多回路控制系统 – 各回路间的耦合
一个调节量影响多个被控变量；
R1
U1 Gc1 Gp1 Y1
Rn
Yn Gcn Un Gpn
Yi qij U j
2014-1-17
Yk const
Uj → Yi的增益 （不仅Uj → Yi通道投运，其 他通道也投运）
工学解耦控制系统
GsDs I diag1，1，，1
（6-30）
即通过解耦，使各个系统的对象特性成1:1的比例环节。 此时解耦装置D(s)为
Ds
D11 s
D21
s
D12 D22
s s
G11s G21s
G12
s
1
G22s
G22 s G21 s
G12 s
G11
s
G11sG22 s G21sG12 s
（6-31）
6.3.4设计中的有关问题 (1). 实践表明,在很多情况下采用静态解耦已能获得相当 好的效果。
对于采用前馈补偿法时，若式（6-32）中G21(s) 和 G态2项2(s相)动近态时项，相采近用，静式态（解6耦-3十3）分中简G单11和(s方)和便G。12(s)的动
(2) 一般地说，需要采用动态解耦时，宜采用超前滞后 环节即 K T1 s 1 的形式。
6.4工业应用实例
在此介绍某乙烯装置裂解炉的解耦控制。它具有四个控制器和四 个控制阀，并配上解耦装置，构成解耦控制系统可以解决问题。 在此而采用一个温度主控制器，另外引入四个偏差设定器，并使 用计算机进行解耦计算，达到了令人满意的结果。
在λ11=0.5时
0.5 0.5
0.5 0.5
图6-1所示压力和流量系统就属此情况。
在λ11=1.2时
1.2 0.2
0.2.
1.2
(2). 在相对增益阵列中所有元素为正时，称之为正耦合。 当k11与k22同号（都为正或都为负），k12与k21中一正 一负时， 都为ij 正值，且 ≤1，ij 属正耦合系统。
（6-6）
12
21
k12 k 21 k11 k 22 k12 k 21
最新过程控制作业答案
（2）写出对象的传递函数G（s），并指出其增益K和时间常数T的数值。
dH
(1)物料平衡方程为Q,-(Q2•Q3)=F-dt
增量关系式为-■=Q2-■Q3=F钊
dt
代入增量关系式，则有F土•（R2R3”h=.Q,
dt
（2）两边拉氏变换有：
FsH (s)
R2R3
故传函为：
R2R3
土R2R3K
G(S八Qi(s) _FR2R3s[_Ts1
如果进料流量波动较大试设计一个前馈串级复合控制系统已知系统中有关传递函数分别为sshktis1仃02si试画出此复合控制系统的传递函数框图并写出前馈调节器的传递函数2?气开型工艺要求一旦发生事故终止蒸汽供应3?主副控制器均为反作用厲21厲小1jr06031042104osj或者代公式得到11050604气从而得到相对第八章关联分析和解耦控制已知一耦合过程的传递函数矩阵为gilg120503g21g220406试计算该过程的相对增益矩阵说明其变量配对的合理性然后按照前馈补偿解耦方式进行解耦求取前馈补偿解耦装置的数学模型画出前馈解耦系统框图
R2+R3
第一章
概述
1.1过程ห้องสมุดไป่ตู้制系统由哪些基本单元构成？画出其基本框图。
控制器、执行机构、被控过程、检测与传动装置、报警，保护，连锁等部件
1.2按设定值的不同情况，自动控制系统有哪三类？ 定值控制系统、随机控制系统、程序控制系统
1.3简述控制系统的过渡过程单项品质指标，它们分别表征过程控制系统的什么性能?
a.衰减比和衰减率：稳定性指标；
b.最大动态偏差和超调量：动态准确性指标；
c.余差：稳态准确性指标；
d.调节时间和振荡频率：反应控制快速性指标。
dH
(1)物料平衡方程为Q,-(Q2•Q3)=F-dt
增量关系式为-■=Q2-■Q3=F钊
dt
代入增量关系式，则有F土•（R2R3”h=.Q,
dt
（2）两边拉氏变换有：
FsH (s)
R2R3
故传函为：
R2R3
土R2R3K
G(S八Qi(s) _FR2R3s[_Ts1
如果进料流量波动较大试设计一个前馈串级复合控制系统已知系统中有关传递函数分别为sshktis1仃02si试画出此复合控制系统的传递函数框图并写出前馈调节器的传递函数2?气开型工艺要求一旦发生事故终止蒸汽供应3?主副控制器均为反作用厲21厲小1jr06031042104osj或者代公式得到11050604气从而得到相对第八章关联分析和解耦控制已知一耦合过程的传递函数矩阵为gilg120503g21g220406试计算该过程的相对增益矩阵说明其变量配对的合理性然后按照前馈补偿解耦方式进行解耦求取前馈补偿解耦装置的数学模型画出前馈解耦系统框图
R2+R3
第一章
概述
1.1过程ห้องสมุดไป่ตู้制系统由哪些基本单元构成？画出其基本框图。
控制器、执行机构、被控过程、检测与传动装置、报警，保护，连锁等部件
1.2按设定值的不同情况，自动控制系统有哪三类？ 定值控制系统、随机控制系统、程序控制系统
1.3简述控制系统的过渡过程单项品质指标，它们分别表征过程控制系统的什么性能?
a.衰减比和衰减率：稳定性指标；
b.最大动态偏差和超调量：动态准确性指标；
c.余差：稳态准确性指标；
d.调节时间和振荡频率：反应控制快速性指标。
解耦控制系统
PT
FT
u2
图 6-8 关联严重的控制系统
6.5.2. 相对增益
令某一通道在其它系统均为开环时的放大系数与该一通道在 其它系统均为闭环时的放大系数之比为 λij，称为相对增益， 则 yi u j u λ ij y yi u j 上式中分子项外的下标u表示除了uj以外，其它都保持不变， 即都为开环；分母项外的下标y表示除了yi以外，其它y都保 持不变，即其它系统都为闭环系统。
u y λ y λ
1 1 2
11 21
u λ λ
12 22
2
u1
k11
y1
k21 k12 u2 k22 y2
பைடு நூலகம்
图 6-9 双输入双输出对象静态特性框
被控变量与操纵变量间 正确匹配
串接解耦控 制
控制器的参数整 定 减少控制回路
6.5.4. 串接解耦控制
串接解耦装置D(s)的作用是使G(s)•D(s) 的积 成为对角阵，这样关联就消除了。要求 G(s)D(s)之积为对角阵，对其非零元素又有三 类方法。
对角线矩阵法 单位矩阵法 前馈补偿法
6.5.5.工业应用实例
某乙烯装置裂解炉的解耦控制。它具有四组并 联的裂解炉管，每组炉管对应于8个烧嘴。每 组有燃料油的控制阀。原料油（煤油、柴油等） 经预热至590 0C后进入裂解炉管进行裂解，生 成乙烯、丙烯，丁烯、甲烷、乙烷、丙烷…… 等。为了减少炉管结焦和提高乙烯等产品收率， 需要降低裂解炉管内的油气分压，因此须按一 定的比率加入稀释蒸汽。原料油和稀释蒸汽的 比率应该控制好。
6.5. 解耦控制系统
6.5.1. 系统的关联分析
解耦控制
1
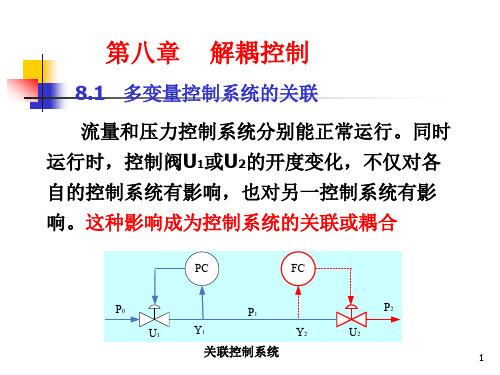
11 1
12 2
y k u k u
2
21 1
22 2
其它控制回路均为开环，控制输入不变即 U (s) 0 得 2
y
p 1 k
u 11
u2111同理y p 1
k ，p
y 2
k ，p
y 2
k
u 12
u1
12
u 21
u2
21
u 22
u1
22
2
1
2
7
q 第二增益系数 ij
输入
u j
对输出
y i
的第二增益系数指其它控制回路
v
Y 1
11
G11(s)
Y1
G 21 (s)
G12 (s)
R2
Y2
- Gc2 (s)
U2
G22 (s)
2
从图中可看出，控制器Gc1(s)的输出U1(s)不仅通过传 递函数G11(s)影响系统输出Y1(s)，而且还通过交叉通 道传递函数G21(s)影响系统的输出Y2(s)；同样，控制 器Gc2(s)的输出U2(s)不仅通过传递函数G22(s)影响系 统输出Y2(s)，而且还通过交叉通道传递函数G12(s)影 响系统的输出Y1(s)。
（7）当系统的某一个相对增益 在0.3~0.7之间或大于1.5时 ij 说明系统存在严重耦合，必须用解耦控制系统设计方法去
解除耦合。
14
8.3 典型耦合结构
1）P规范耦合 n个输入，n个输出，每一个输出均受 到所有输入的影响。
Y p U p U p U
U 1
p p p
1
11 1
12 2
1n n
第一增益系数
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
n个入（Uj）
n个出（Yi）
U1
Y1
Ui
Yi
Un
Yn
Y1 v11(U1 v12Y2 v1nYn )
Y2 v22 (U2 v21Y1 v2nYn )
Yn vnn (Un vn1Y1 v Y n,n1 n1)
9
8 关联分析与解耦控制
U1
U2
Un
v11
0
v22
0
vnn
Y1 Y2
11 12 1n
21
22
2
n
n1
n2
nn
yi
uj
21
8 关联分析与解耦控制
8.2.2 相对增益的计算
▪ 确定相对增益，关键是计算第一放大系数和 第二放大系数。
▪ 一种方法是解析法
通过计算过程的微分分别计算出第一放大系数和 第二放大系数，从而得到相对增益矩阵。
▪ 另一种方法是第二放大系数直接计算法
Y1
▪ 各回路间的耦合
➢一个调节量影响多个被控变量； Rn
Gcn
Gpn
Yn
Un
➢一个被控变量受多个调节量的影响。
3
8 关联分析与解耦控制
进料
温度变送器
塔顶温度 y1
精
馏 塔底温度 y2
塔
1
GC1
u1
2
GC2
u2
再沸器
xB
xD
r1
Qr 塔顶回流量
r2
Qs 加热蒸汽量
图8.1 精馏塔温度控制方案
4
8 关联分析与解耦控制
8 关联分析与解耦控制
est
1
8 关联分析与解耦控制
本章学习内容
❖8.1 控制回路间的关联 ❖8.2 相对增益矩阵 ❖8.3 减少和消除耦合的方法 ❖8.4 解耦控制系统设计
2
8 关联分析与解耦控制
8.1 控制回路间的关联
❖控制回路间的耦合
▪ 单回路控制系统 ▪ 多回路控制系统
R1
U1
Gc1
Gp1
▪ 两放大系数相同，其它回路存在与否对该通道
没有影响，即该通道与其他通道不存在关联；
▪ 放大系数不同，各通道间有关联。
19
8 关联分析与解耦控制
❖依相对增益判断过程（ uj→yi ）的关联程度
▪ λij =1 无静态关联
▪ λij =0 关联严重
其他回路未投入时yi不受uj影响（pij=0）
投入后却有影响（ pij≠0 ）了
▪ pij可表示为：
Y p i
ij U j Uk c onst
Uj → Yi的增益
（仅Uj → Yi通道投运， 其他通道不投运）
17
8 关联分析与解耦控制
❖第二放大系数qij
▪ 指除所观察的Uj到Yi通道之外，其它通道 均闭合且保持Yk（k≠j）不变时，Uj到Yi 通道之间的静态增益。
▪ qij可表示为：
该被控量Yi而言的增益（ Uj → Yi ）；
▪ λij定义为
p
ij
q ij ij
pij 第一放大系 数 qij 第二放大系
数
16
8 关联分析与解耦控制
❖第一放大系数pij
▪ 指耦合系统中，除Uj到Yi通道外，其它 通道全部断开时所得到的Uj到Yi通道的 静态增益;
▪ 即，除调节量Uj改变了Uj以外，其它 调节量Uk（k≠j）均不变。
❖直接法
▪ 借助耦合系统的方框图，直接解析地导出各 变量之间的函数关系，从而确定过程中每个 被控量相对每个调节量的关联程度。
▪ 注意：
yi ~ uj
分析中，考虑的是系统的静态耦合结构
12
8 关联分析与解耦控制
例8.1 试用直接法分析下图双变量耦合系 统的耦合程度。
R1
1
U1
3 s 1
Y1
5 s 1
6
8 关联分析与解耦控制
8.1 控制回路间的关联
❖P规范耦合
n个入（Uj）
n个出（Yi）
U1
Y1
Uj
Yi
Un
Yn
Y =P U
Y 1
pU 11 1
pU 12 2
pU 1n n
Y 2
pU 21 1
pU 22 2
pU 2n n
Y n
pU n1 1
pU n2 2
pU nn
n
Y1
p 11
p 12
p 1n
Yn
0 v21 v31 vn1
v12 0 v32 vn2
v1n v2n v3n 0
图8-4 V规范耦合对象方框图
10
8 关联分析与解耦控制
8.1 控制回路间的关联 ❖耦合程度分析方法
▪ 直接法
解析法
▪ 相对增益法
求相对增益矩阵的计算方法
11
8 关联分析与解耦控制
8.1.3 耦合程度分析方法
先计算第一放大系数，再由第一放大系数直接计 算第二放大系数，从而得到相对增益矩阵。
R1
Gc1(s) U1 Gp11(s)
Y1
Gp21(s)
Gp12(s)
R2
Gc2 (s) U 2 Gp22(s)
Y2
图8.2 精馏塔温度控制系统方框图
5
8 关联分析与解耦控制
8.1 控制回路间的关联 ❖被控对象的典型耦合结构
▪ 对于具有相同数目的输入量和输出量的控制 对象，典型的耦合结构可分为:
P规范耦合 V规范耦合
U1
Y
i
p ij
U
i
Yn
p n1
p nn
U
n
7
8 关联分析与解耦控制
U1
U2
Un
p11 p21 pn1 p12 p22 pn2
p1n p2n pnn
Y1 Y2
Yn
图8.3 P规范耦合对ห้องสมุดไป่ตู้方框图
8
8 关联分析与解耦控制
8.1 控制回路间的关联
❖V规范耦合
▪ λij =∞ ▪ λij >1
关联严重 有关联
其他回路投入后，uj→yi通道的增益下降
需要解耦
▪ λij <1 有关联
需要解耦
▪ λij <0 关联严重
其他回路的投入与否是系统由正反馈变成负反馈，
系统由不稳定性变为稳定，或相反
20
8 关联分析与解耦控制
❖相对增益矩阵
▪ 由相对增益ij元素构成的矩阵，即
4
s 1
R2
1
U2
5s 1 s 1
Y2
图8.5 双变量耦合系统
13
8 关联分析与解耦控制
R1
1 U1
3
Y1
5
4
R2
1 U2
1
Y2
图8.6 静态耦合结构
U R Y
1
1
1
U R Y
2
2
2
Y 3U 4U
1
1
2
Y 5U U
2
1
2
14
8 关联分析与解耦控制
13 1
Y1
14
R1
7
R2
0.9286R1
Y q i
ij U j Yk const
Uj → Yi的增益 （不仅Uj → Yi通道投运，其
他通道也投运）
18
8 关联分析与解耦控制
❖相对增益ij定义为：
p ij
Y i
q ij U
ij
j Uk const
Y i
U j Yk const
❖相对增益ij表示
▪ 其他回路投运与否对Uj → Yi增益的影响
0.1429R2
56 Y2 28 R1 7 R2 0.1786R1 0.8571R2
❖直接法分析结果
▪ Y1主要受R1影响，也受R2影响 ▪ Y2主要受R2影响，也受R1影响
15
8 关联分析与解耦控制
8.1.3 耦合程度分析方法
❖相对增益分析法
▪ 相对增益λij是Uj相对于过程中其他调节量对