第三章 可靠性概率分布
《工程机械可靠性》课件-第三章-可靠性指标及计算

可靠度计算示例: 例:设t=0时,投入工作的10000只灯泡,当t=365天时,发现有300只灯泡 坏了,求一年时的工作可靠度。
5
《工程机械可靠性》精品培训-第三章-可靠性指标及计算
第一节 可靠性概率指标
第一节 可靠性概率指标
2. 失效概率
与可靠度相对应的是不可靠度,也就是“产品在规定的条件下 和规定的时间内不能完成规定功能的概率”,记为F (Failure),为
= 0.0537
不失效概率,即可靠度R(t):
R(t) = 1− F (t) = 1− 0.0539 = 0.9463
17
《工程机械可靠性》精品培训-第三章-可靠性指标及计算
第一节 可靠性概率指标
第一节 可靠性概率指标
三、失效率: (1)定义
产品工作到 t 时刻后,单位时间内发生故障的概率。即产品 工作到t 时刻后,在单位时间内发生故障的产品数与在时刻t 时仍
t
图2-1 零件寿命试验数据直方图
10
《工程机械可靠性》精品培训-第三章-可靠性指标及计算
第一节 可靠性概率指标
1) 第i区间∆t = ti − ti−1;零件的失效频数为∆N fj , 其失效频率为:
fi
=
∆N N
fj
2) 在ti < t时间内的累计失效数为:
∑i
N fi = ∆N fj
j =1
第一节 可靠性概率指标
零件寿命试验数据
顺 区间间距 区间
序 号
∆t / h
中值
ti / h
1 0~100 50
2 100~200 150
3 200~300 250
4 300~400 350
5 400~500 450
[工学]03可靠性工程讲义第三章
![[工学]03可靠性工程讲义第三章](https://img.taocdn.com/s3/m/71eeee7b852458fb770b566a.png)
MTBF
热贮备和温贮备系统的可靠性模型
• 温储备系统的储备单元处于轻载工作状态,不处 于完全不工作状态,例如,电子管的灯丝。
• 当设备处于比较恶劣的环境时,不工作储备单元 的故障率要比轻载的故障率大得多,这时也必须 使储备单元处于轻载工作状态。例如,处于潮湿 环境中的电子设备,通电工作的故障率要比长期 储存(不工作)的失效率低。
A
˦ A
B
˦ B¡¢ ºÍ
˦
' B
若转换装置不是完全可靠,则当开关故障
率λK不为零或不能忽略时
RS (t)
e At
K
A A B
B'
e e Bt
(K A 'B )t
MTBF
1
A
1
B
(
A
A B'
K
)
两单元相同时
• 当λA=λB=λ、λ‘B=λ’,即,工作时A、B 两单元工作故障率相同时,可求得:
从设计角度,提高并联系统可靠性措施:
(1)提高单元可靠性,即减少失效率; (2)尽量增加并联数目; (3)等效地缩短任务时间t。
并联单元数与系统可靠度关系
例3-2 已知并联系统由两个服从指数分布的单元
组成,两个单元的故障率分别为1 0.0005h1 2 0.0001h1 ,工作时间t=1000h,试求系
对于单调系统任一元件的失效只会使系统失效概率增加每个元件有两种状态正常状态和失效状态且二者必居其一满足全概率公式的条件因此系统的可靠度其中表示在x正常情况下系统正常的事件相当于把x的两端短接起来表示在x失效情况下系统正常的事件相当于把x的两端断开
第三章 系统可靠性模型
可靠性中常用的概率分布

(3-4)
指数分布的累积分布函数
F(x)=1-e-x
(3-5)
——若产品在一定时间区间内的失效数服从泊松分布,则该产品的 寿命服从指数分布。
3.5 正态分布
正态分布密度函数定义为:
f (x)
1
2
exp
1 2
x
2, x来自其中: -均值, -标准差。
(3-6)
标准正态分布
例如,对于图(下左)中所示的两种分布形式(一种为 Weibull分布,另一种为正态分布),虽然它们的概率密度 函数曲线差别很小,但其累积分布函数(反映可靠性特征) 在小概率区域的差别却十分显著,如图(下右)所示。
Probability density function
Probability
0.35
当 (t) 为常数时,满足上述条件的计数过程 {N (t),t 0} 为
时齐泊松随机过程。
泊松随机过程的概率密度分布
(t) 0.5 h 1
P(m, t )
n
t/h
3.4 指数分布
指数分布的定义
指数分布的密度函数为
e x
f (x) 0
式中为常数,是指数分布的失效率。
(x 0; 0)
(3-3)
P{X k} Cnk pk (1 p)nk
(k 0,1,2,..., n)
泊松过程
泊松随机过程作为一种重要的计数过程, 可以很好地用于描述“顾客流”、“粒子流” 、“信号流”等事件的概率特性。
设 {N(t),t 0} 为一计数过程,且满足以下条件: (1) N(0)=0; (2) {N (t),t 0} 是一个独立增量过程,即任取 0 t1 t2 tm
失效率函数
可靠性中常用的概率分布
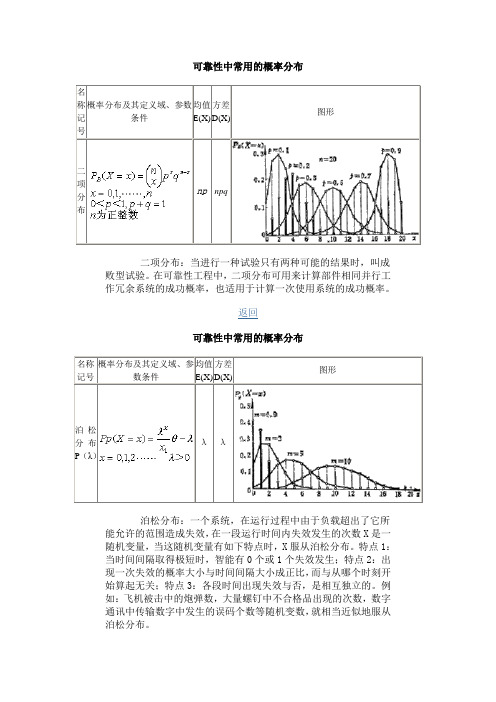
名称记号概率分布及其定义域、参数条件均值E(X)方差D(X)图形二项分布np npq二项分布:当进行一种试验只有两种可能的结果时,叫成败型试验。
在可靠性工程中,二项分布可用来计算部件相同并行工作冗余系统的成功概率,也适用于计算一次使用系统的成功概率。
返回可靠性中常用的概率分布名称记号概率分布及其定义域、参数条件均值E(X)方差D(X)图形泊松分布P(λ)λλ泊松分布:一个系统,在运行过程中由于负载超出了它所能允许的范围造成失效,在一段运行时间内失效发生的次数X是一随机变量,当这随机变量有如下特点时,X服从泊松分布。
特点1:当时间间隔取得极短时,智能有0个或1个失效发生;特点2:出现一次失效的概率大小与时间间隔大小成正比,而与从哪个时刻开始算起无关;特点3:各段时间出现失效与否,是相互独立的。
例如:飞机被击中的炮弹数,大量螺钉中不合格品出现的次数,数字通讯中传输数字中发生的误码个数等随机变数,就相当近似地服从泊松分布。
名称记号概率分布及其定义域、参数条件均值E(X)方差D(X)图形超几何分布H(n,M,N)返回可靠性中常用的概率分布名称记号概率分布及其定义域、参数条件均值E(X)方差D(X)图形指数分布e(λ)指数分布:许多电子产品的寿命分布一般服从指数分布。
有的系统的寿命分布也可用指数分布来近似。
它在可靠性研究中是最常用的一种分布形式。
指数分布是伽玛分布和威布尔分布的特殊情况,产品的失效是偶然失效时,其寿命服从指数分布。
可靠性中常用的概率分布名称记号概率分布及其定义域、参数条件均值E(X)方差D(X)图形威布尔分布(Ⅲ型极值分布)W(k,a,b)威布尔分布:在可靠性工程中被广泛应用,尤其适用于机电类产品的磨损累计失效的分布形式。
由于它可以利用概率纸很容易地推断出它的分布参数,被广泛应用与各种寿命试验的数据处理。
可靠性中常用的概率分布名称记号概率分布及其定义域、参数条件均值E(X)方差D(X)图形正态分布(高斯分布)N(μ,σ)μσ2正态分布:是在机械产品和结构工程中,研究应力分布和强度分布时,最常用的一种分布形式。
系统可靠性分析与设计

该机构对电子产品的设计
该机构对电子产品的设计
结论:
该机构对电子产品的设计
3、表决系统 n个单元中,至少要r个单元可靠时系统才可靠。
系统R如何求?
n个单元中i个可靠,n-i个失效,组合方式的种类种组合方式发生的概率为:
= 0.9883 > 0.9624 为什么,因为贮备状态的单元可靠度在投入使用之间, 可靠度是不随时间而变化即为 e t e xo 1 (开关系统)
5、混联系统
Rs1=R1R2
Rs2=1-(1-Rs1)(1-R3) Rs=Rs2R4
对于复杂混联系统,采用全概率公式或穷举法
解:取事件A表示单元1正常
Rs e
kt
(kt ) i! i 0
nk
i
例:某理想开关系统数,数据同前,求系统可靠度。 kt 3 40 10 6 7200 0.864 Rs e kt
i 0 nk
kt i
i!
2 3 0 . 864 0 . 864 0.864 =e 1 0.864 2! 3!
的“电子可靠性顾问团”(AGREE:Advisory
Group on Reliability of Electronic Equipment)
该机构对电子产品的设计、试制、生产、试验、
储存、输送、管理、使用等各方面的可靠性问题,作
了全面的调查研究。并于1957年写出了《电子设备 可靠性报告》,该报告比较完整地阐述了可靠性的理 论甚础与研究方法,60年代以后,可靠性研究逐步 完善的发展,并从电子产品扩展到机械产品,各国也 越来越重视可靠性工作。
讨论: 1、x1表示系统维持正常工作的概率,即有效度 2、上面可修复系统的极限状态矩阵如何求?
可靠性概率分布讲解

关于可靠性分布函数及其工程应用的讨论学号:*********姓名:***目录一、引言 (3)二、分布函数及其应用的讨论 (3)(一)、指数分布 (3)1.定义: (3)2.指数分布的可靠度与不可靠度函数 (4)3.图像分析 (4)4.应用 (5)(二)、正态分布 (6)1.定义: (6)2.正态分布的可靠度与不可靠度函数 (6)3.失效率函数 (6)4.图像分析 (7)5.应用 (8)(三)、对数正态分布 (9)1.定义: (9)2.对数正态分布的可靠度与不可靠度函数 (9)3.对数正态分布失效率 (9)4.图像分析 (9)5应用 (11)(四)、威布尔分布 (12)1.三参数威布尔分布的定义: (12)2.可靠度与不可靠度函数 (12)3.威布尔分布失效率 (12)4.图像分析 (12)5.应用 (15)三、小结 (16)参考文献 (17)附录 (18)一、引言可靠性是指产品在规定的条件下,规定时间内,完成规定功能的能力,是对产品无故障工作能力的度量。
可靠性作为衡量产品质量的一个重要的指标,已广泛的应用于各个工程领域。
与可靠性相反,产品丧失规定功能称为失效或故障。
工程机械系统是由零件和部件组成的,零件或部件的失效会导致系统的失效。
然而,失效的原因是多种多样的,如结构缺陷、工艺缺陷、使用不当、老化等等。
引起每种失效的原因也可能是不同的,如性能退化可能由于疲劳、蠕变、裂纹扩展、磨损或者腐蚀等导致的[1]。
实践表明,系统或零、部件的失效时间往往是不确定的,要定量描述系统或零、部件的失效时间,应当采用统计学方法。
将失效时间作为一个随机变量,用一个恰当的概率分布函数去描述它。
从数据的统计分析中找出产品寿命分布的规律,是进一步分析产品故障,预测故障发展,研究其失效机理及制定维修策略的重要手段。
可靠性分析与评估是可靠性分析中非常重要的一部分,它是指在产品的寿命周期内,根据产品的可靠性分布模型、结构,以及相关的可靠性信息,利用统计方法,对产品的可靠性指标做出估计的过程。
第3章 结构可靠性设计理论基础

可见,是lnR和lnS的表达式。 根据概率论原理可以换算成R,S的统 计参数:
2 ln R ln 1 VR2
lnR=ln R ln 1 V lnS=ln S ln 1 V
2 R
1
2
2 ln S
ln V 1
2 S
2 S
1
2
所以得到:
如第一章所述,结构达到极限状态 的概率超过某一允许值,结构就失效。 所以极限状态是衡量结构是否失效的标 志,而极限状态可用极限状态方程来表 示:
Z=g(X1,X2,…,Xn)=0
Z=g(R,S)=R-S=0 当Z>0,结构处于可靠状态,当Z<0,结构处 于失效状态,当Z=0,结构恰处于极限状态。
从下图中可以清楚地看出,斜 线表示极限状态,即R=S;若点Z1 位于该线上面,即R1<S1,表示结构 失效;若点Z2位于该线下面,即 R2>S2,表示结构可靠。 Safe Region
Failure Region Limit State Surface (Failure Surface)
下面推导失效概率Pf和可靠概率Ps的 公式:
设fR,S(r,s)为随机变量(R,S)的联 合概率密度函数,FR,S(r,s)为相应的联 合概率分布函数, FR(x), FS(x), fS(x), fS(x)分别为边缘分布函数和边 缘概率密度函数。R,S统计独立。 则结构失效概率Pf应为(如图示)
1 FS x f R x dx
所以,有
Pf FR x f S x dx
1 FS x f R x dx
按相同原则,可求得可靠概率为
第3章可靠性-1

R(t) N n(t) N
(3-1)
式中,R ( t ) 也称存活率。当 N 时,limR(t) R(t) ,即为该产品的可
R(t) dt
(3-9) (3-10)
将上式从0到 t 进行积分,则得
R(t) e0t(t)dt
(3-11)
上式称为可靠度函数 R(t) 的一般方程,当 (t) 为常数时,就是 常用到的指数分布可靠度函数表达式。
例3-2 有100个零件已工作了6年,工作满5年时共有3个零件失效, 工作满6年时共有6个零件失效。试计算这批零件工作满5年时的失效率。
靠度。
N
由于可靠度表示的是一个概率,所以 R ( t ) 的取值范围为:
0R(t)1
(3-2)
可靠度是评价产品可靠性的最重要的定量指标之一。
例3-1 某批电子器件有1000个,开始工作至500h内有100个失效, 工作至1000h 共有500个失效,试求该批电子器件工作到500h 和
1000h 的可靠度。
(1)研究对象 产品即为可靠性的研究对象,它可以是系统、整机、部件,也可 以是组件、元件或零件等。 (2)规定的条件 它包括使用时的: 环境条件(如温度、湿度、气压等);
工作条件(如振动、冲击、噪音等); 动力、负荷条件(如载荷、供电电压等); 贮存条件、使用和维护条件等。 “规定的条件”不同,产品的可靠性也不同。
(3)耗损失效期
耗损失效期出现在产品使用的后期。 其特点是失效率随工作时间的增加而上升。
耗损失效主要是产品经长期使用后,由于某些零件的疲劳、老 化、过度磨损等原因,已渐近衰竭,从而处于频发失效状态,使失 效率随时间推移而上升,最终回导致产品的功能终止。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
0.905
B: t B 900, 400
100 900 R B 100 1 1 2 0.9772 400
对数正态分布
2 0
2
1
指数分布性质
• 指数分布性质
–指数分布的一个重要性质是无记忆性。无记忆性是产
品在经过一段时间t0工作之后的剩余寿命仍然具有原来 工作寿命相同的分布,而与t无关。这个性质说明,寿
命分布为指数分布的产品,过去工作了多久对现在和
将来的寿命分布不发生影响 –在“浴盆曲线”中,它是属于偶发期这一时段的
0.99999
思考:假如只有两个轮胎, 安全着陆的概率?
连续型随机变量的几种常见分布
• 正态分布
• 对数正态分布
• 指数分布 • 伽玛分布 • 威布尔分布
指数分布
1.指数分布
• • • • • 在数学上易处理成直观的曲线 失效率反映了特征参数 单参数分布 最基本最常用的分布 若产品的寿命或某一特征值t的故障密度为
对数正态分布的特征量
– 不可靠度函数
lnt - F t f t dt
t
– 可靠度函数
lnt R t 1
– 故障率函数
t
f t R t
泊松分布
• 泊松分布,经过适当的处理可成为指数分布。假 定:
在互不相交的时间区间内所发生的失效是统计独立的; 单位时间内的平均失效次数为常数,而与所考虑的时间区 间无关。
•
泊松过程有下面两个重要性质:
(1)设t是时间区间的长度,则在此区间内发生失效的次数X 是一个整数型的随机变量,在此时间区间内,发生k次失效的概 率服从一个均值为λ t的泊松分布:
f (t )
1 2
(t ) 2 2 2 e
(t 0, 0, 0)
正态分布
•
正态分布的特征量函数: – 不可靠度
t F( t ) f ( t )dt
t
查附表2
– 可靠度
t R t 1 Ft 1
R(2000 ) e2000 0.8187
t 0 .5
t 0 .9
0.6971
1
6931小时
ln
1 1048小时 0. 9
指数分布例题
例:一元件寿命服从指数分布,其平均寿命 (θ) 为2000小时,求故障率λ及求可靠度R (100)=? R(1000)=? 解: 1 1 5 10 4 2000
0 0
1
中位寿命:r=0.5
0.5 e t
t 0 .5 ln0.5 0.6971
特征寿命:
r e 1 0.368
e 1 e t
t 0.368 1
0.7E
1
寿命方差: 标准差:
t 2 f t dt - E 2
正态分布 截尾正态分布 对数正态分布 指数分布 伽玛分布 威布尔分布
可靠性的概率分布
可靠性工程以产品的寿命特征为主要研究对象。产品 的寿命特征一般是连续的随机变量,例如产品故障时间和 维修时间等。处理这种问题可利用概率统计方法,找出它 们的概率分布和概率密度函数,有了确定的分布就可以求 出该分布特征统计量,如正态分布的均值及标准差。即使 不知道具体的分布函数,也可以通过对分布的参数估计求 得某些特征量的估计值。这些分布及概率密度函数,不仅 描述了寿命的内在规律,而且分布的参数还决定了产品的 寿命特征。因此必须对失效分布作较深入的研究
个元件失效的概率比较小的情况
二项分布实例
例:有人打靶,每次命中率均为0.7,现独立射击5次,求恰 好命中2次的概率? 解:每次射击有“击中”和“未击中”两个可能,设 Ai "第i次击中 " ,“恰好有两次几种”的情况有
A1A 2 A3 A4 A5 , A1 A2 A3 A4 A5 , A1 A2 A3 A 4 A5 ,...共有C5 种
二项分布
(k 0,1,2,n)
上式为二项概率公式。若用X表示在n次重复试验中事件A发 生的次数,显然,X是一个随机变量,X的可能取值为 0,1,2,…n,则 • 随机变量X的分布律为:
P( X k ) Cnk pk qnk
(k 0,1,2,n)
此时,称随机变量X服从二项分布B(n,p)。 当n=1时,二项分布简化为两点分布即:
•
指数分布的特点
只含单一参数,形式简单 1 平均寿命、特征寿命、标准离差相等,为 故障率越小,平均寿命越大,但越大,分布 越分散 平均寿命大于中位寿命
•
发动机中有四种故障的寿命概率分布属于指数分布
受随机性冲击时产生的故障:故障与使用时间无关, 仅与外界超强度的冲击力随机到来和内部潜伏的隐患 偶然爆发有关,它们是随机性偶然发生故障,如内燃 机超载下工作或过热造成的故障 正常使用下的突发故障:常载下往复运动零件损伤, 或人为失误造成的故障,或偶然性操作不当 浴盆曲线的Ⅱ阶段(使用寿命期) 发动机返复多次维修期间所发生的故障可考虑为指数 分布故障
P(A1A 2 A3 A4 A5 ) P( A1 ) P( A2 ) P( A3 ) P( A4 ) P( A5 ) 0.7 0.7 0.3 0.3 0.3 0.7 2 0.33
P( A) C n P k q n k C5 0.7 2 0.33 0.1323
k!
(k 0,1,2,, n, 0)
F ( k ) P( X k )
r 0
k
r
r!
e
• X的期望与方差分别为:
E ( X ) kP( X k )
k 0
D( X ) [k E ( X )]2 P( X K )
k 0
2 k
2
如果要求命中不少于2次的概率?
二项分布实例
例:一架飞机有三个着陆轮胎,若不多于一个轮胎爆破,飞 机便能安全着陆。试验表明,每一千次着陆发生一次轮 胎爆破。求飞机安全着陆的概率? 解:
P(安全着陆) P(没有轮胎着陆 ) P(只有一个轮胎爆破 )
0 3 1 2 C( 0 . 001 ) ( 0 . 999 ) ( 0 . 001 ) ( 0 . 999 ) C3 3 0 1
(2)在任意两次相邻的失效之间的时间T是独立的连续型的随机 变量,服从参数为λ 的指数分布 :
(t ) k t P( X k ) e k!
(k 0)
P(T t ) R(t ) e t
泊松分布
两次失效的平均时间为
1
合于建模有较多的元件倾向于失效,而每
,泊松过程适
所谓独立试验是指将试验A重复做n次,若 各次试验的结果互不影响,即每次试验结果出 现的概率都与其他各次试验结果无关,则称这n 次试验是独立的,并称它们构成一个序列
•
在二项分布中,若一次试验中,P( A) p, P( A) 1 p , 则在n次独立地重复试验中,试验A发生的概率为:
k k n k Pn (k ) Cn pq
• 则称t服从参数λ的指数分布
f (t ) e
t
( 0, t 0)
指数分布
• 指数分布的特征量函数:
不可靠度(失效)函数
F (t ) f (t )dt 1 e t
0
t
可靠度函数
R(t ) et
平均寿命
E tf (t )dt te t dt
离散型随机变量的几种常见分布
可靠性抽样试验以及产品质量保证等大量工 程实际问题需要用到离散模型。主要有
两点分布 二项分布
泊松分布
几何分布与负二项分布 超几何分布
两点分布
• 数字特征:
E ( X ) 1 p 0 q p D( X ) p p 2 p(1 p) pq
例:内燃机增压器处于使用寿命期中工作,根据以
往经验知,寿命服从指数分布,在100小时工作 内有1%发生故障,求可靠度R(2000), t 0.5和 t 0.9 的使用寿命?
解:先求λ F(100)=0.01
1 e 100 0.01
1 1 ln 0.0001005 100 0.99
R(100) e
5104100
e
0.05
0.95
0.60
R(1000) e
5104 1000
e
0.5
此元件在100小时时的可靠度为0.95,而在 1000小时时的可靠度为0.60
正态分布
• 正态分布在机械可靠性设计中大量应用,如材料强度、
磨损寿命、齿轮轮齿弯曲、疲劳强度以及难以判断其分布 的场合。属于递增型故障率的概率分布。它的分布曲线处 于浴盆曲线的耗损阶段 • 若产品寿命或某特征值有故障密度
– 如气缸、活塞、齿轮和轴类零件
• 因磨损引起的故障,以及管、阀系统的腐蚀性故障,燃油 传给系统沉淀性故障都属正态分布
例:有两种内燃机配套机构,A种寿命分布是指数型, 其平均寿命为1000h;B种寿命分布是正态型,其平 均寿命为900h,标准离差σ = 400h,求:在100小 时使用期内,尽量不发生故障,求哪种设计为好?
• 对数正态分布是自变量取对数时,其故障密度函数符合正 态分布的一种偏态性概率分布。它的故障率其本属于递增 型的,但递增的速度是变化的,先快后慢然后趋于平稳
