汉明码的编码和译码算法
【doc】Hamming码编译码的算法及其实现

Hamming码编译码的算法及其实现总第64期海军工程太学电子工程学院HAIJUNGONGCHENGDAXUEDIANZIGONGCHENGXUEYUANXUEBAO27 Hamming码编译码的算法及其实现胡贵生王珍(海军工程大学电子工程学院,南京2¨800)摘要本文结出了一种Hamming码编译码的算法.本算法已在[利用超短波电台进行数据传辅]项目中得到应用关键诃Hamming码编译码算法TheAlgorithmandRealizationoftheCodingandDecodingofHammingCode Guisheng,WangZhen(ElectronicsEngineer[ragCollege,NavalUniversityofEngineering,Naniing,211800) Abatr~ct:ThispaperprovidesatypeofalgorithmforthecodinganddecodingofHammingCo de.TbisaJgoritbm hasbeeappliedintheresearchprojectDataTransmissionthroughvHF.Ke3noo~s:Hammingcode,codee,algorithm1.引言当今信息社会,信息的传输,信息的存储和信息的交换随时都在我们周围进行着.如何保证信息的可靠传输和可靠存储,已越来越引起人们的重视采用纠错编码技术,已从多方面被证实是一种提高信息传输可靠性的关键技术.1.1通信系统模型:无论在何种类型的计算机系统,数据存储和数据通信系统中,各部件或子系统,通信收发之间的数据交换处理,数据存储器中数据的读写,都可以用下图所示的通信系统模型表示其中信源:数据传输过程中数据的出发地.在计算机系统中,一般由k位二进制信息构成一个信息组MM=(mk—l,mk_¨,……,ml,m0)纠错编码:信息组M经过纠错编码后,被按一定规律附加上n—k位的校验信息,成为一组长为n位的编码码组CC一(cn一1,c一2,……,cI,Co)信道:编码码组C从发送端出发经过信道到达接收端.噪声或干扰:由于部件缺陷或系统故障等各种原因所引起的数据错误,都可等效为由于信道上的噪声或干扰所造成的错误序列E对编码码组C作用的结果E一(e~e,……,e1,e.)因此,编码码组C经过信道后到达接收端时已变成了R—C+ER一(rr一2,……rr.),rl—c.+e纠错译码:利用发送端所加的校验元和信息元之间的约束关系,对接收到的R进行纠错译码,恢复出k收藕日期2O0O—l2—2O28Hamming码编译码的算法厦其实现益第64期个信息元M.M一般等于M,但如果R中错误很多,已超出了纠错码的纠错能力,则M不等于M.信宿:数据传输过程中数据的目的地.1.2系统要求:通信系统模型中信道部分容许的传输速率必须比系统要求的信息传输速率高.这是采用纠错编码技术提高信息传输可靠性所必须具备的条件.2.Hamming码的定义Hamming码中文称作汉明码.汉明码是由汉明于1950年提出的,具有纠正一位错误能力的线性分组码它的突出特点是:编译码电路简单,易于硬件实现;用软件实现编译码算法时,软件效率高;而且性能比较好21汉明码的定义:若一致校验矩阵H的列是由不全为0且互不相同的所有二进制m(m≥2的正整数)重组成,则由此H矩阵得到的线性分组码称为有限城GF(2)上的[2一1+2一1一m,3]汉明码.2.2汉明码的构造特点:1.绐定一个m,在有限域GF(2)上,我们由二进制m重组成线性分组码的校验矩阵H,由二进制m重来标定一个发生错误的位置.由此可知,二进制m重共有2种位组合,去掉一个全为0的位组合,则余下共有2一1种位组合.故,汉明码的最大码长n=2一l.2.由上面分析,我们可以知道:m即是汉明码校验位的位数.故一个汉明码中,信息位的位数k—n—m=2一1一m3.汉明码的距离一3,因此可以纠正一位错误,发现两位错误.3.Hamming码编译码算法的实现1.在本系统具体实现时,取m=4,即在一个编码的码字中包含4位校验位,则汉明码的码长:nK2一1=15码字中有效信息的位数:k=n—m≤l5—4—11结合计算机信息存储与信息处理的特点,我们取码字中有效信息位的位数k=8,即在一个编码的码字中.实际传送有效信息的长度为一个字节2.综上所述,我们采用如下的汉明码编码结构:信息位位数:k一8位校验位位数:m一4位码长:n:k+m一12位00001001一[PIj阵OlOn矩lO00.o矩OO验0ll0校致0;一1OO1的式l0lnl};统n¨●系=H2001总第64新海军工程大学电子工程学院HAIJUNGONGCHENGDAXUEDtANZrGONGCHENGXUEYUANXUEBAo29相应的系统码形式的生成矩阵G矩阵G4.汉明码的编码已知M=(m,IT*……,IT*,mo)是由k位有效信息组成的信息组,则汉明码编码码宇c 由下式求出C—M?O例如:已知M=(0011101O),则汉明码编码的码字C—M—G一(001110100001)注:这里的所有运算均为定义在有限域GF(2)上的运算.汉明码的编码过程就是:从信源取出由k位有效信息组成的信息组M,进行M?G 的编码运算,产生n位已编码的信息即码字C,即可提交给信道发向信宿.5.汉明码的译码(1)由线性分组码理论可知,线性分组码的每一码字c都必须满足下式:C—H一0(2)因此,设接收端收到的N重码宇为R=(,_I'……,r1,)R=C——E,.一f+P.,,0,P.∈GF(2)则有R?H一(C+E)?H一C?+E?=E?H得出结论:若E一0则R?H一0若E≠O则R?H≠O即;R?H仅与错误图样有关,而与发送的是什么码竽无关(3)令S=R?H一E?H称S为对应于E的伴随式或称为校正子(4)本系统的校正子s一错误图样E对照表如下校正子S位图错误图样E位图0000000000000000000100000000000100100000000000100Oll0000000l00000100000000000100O10100000010000001100000010000000111000010000000l00000000000100010010001000000000l0llOl1O11O1101】000lllOllll0000OOO0O001OOOO00l000000lO00O0olO000OO1OO000o1oOO00O1O00000】OO0000O3OHamming码编译码舶算j击厦其实现总第64期(5)汉明码检错/纠错性能分析例一假设:已编码的码字为c一001110]00001B=3AlH经过信道的传输后,在接收端收到的码字为R=001l10110001B=3BIH即经过信道的传输,码字的bit4由0变成了l译码步骤如下:I计算:S—R?H一001lⅡ查S—E对照表可知E=000000010000BⅢ计算:R@E=001]10]l0001B0000000010000B一001]10100001B=3AlHⅣ结论:对于由于信道传输而5i起的Bit4的错误,汉明码可以对其进行成功的纠正.例二假设:已编码的码字为C一001110100001B=3AIH经过信道的传输后,在接收端收到的码字为R一00]l10100l11B=3A7H即经过信道的传输,码字的bit2由0变成了l,Bitl由0变成了l译码步骤如下:I计算:S=R?H一0110Ⅱ查S—E对照表可知E=0000O1000000BⅡ计算:R0E一001110100111B0000001000000B一001lII10011IB=3E7HⅣ结论:对于由于信道传输而引起的bit2,bitl两位的错误,计算结果表明:汉明码没有将错误纠正过来,发进的码字是3AIH,接收端译码后的码字为3E7H.这是由于错误的程度已经超出了汉明码的纠错能力,汉明码仅能纠正一位错误. 由S=011050可知,汉明码检测到了错误,但汉明码没有能力纠正这种错误.4.结束语本文在介绍了Hamming码定义的基础上,结出了一种Hamming码编译码的算法,本算法已在[利用超短波电台进行数据传输]项目中得到应用.实践证明:该算法对于由信道传输引起的差错具有很好的纠正作用,能够有效降低信道的误码率,从而提高传输的可靠性和传输效率.参考文献1.王新梅编着纠错码与差错控制人民邮电出版社,19892吴怕修.祝宗泰,钱霖君编信息论与编码东南大学出版社.19913[美]R.E.B]ahut着徐秉铮欧阳景正冯贵良译差错控制码的理论与实践华南理工大学出版社.19884.万哲先编着代数和编码科学出版社.1980墨。
汉明码编译码文档

第一章 绪论1.1差错控制编码差错控制编码 1.1 1.1 概述概述数字信号在传输过程中,数字信号在传输过程中,由于受到干扰的影响,由于受到干扰的影响,码元波形将变坏。
码元波形将变坏。
接收端收接收端收到后可能发生错误判决。
到后可能发生错误判决。
由于乘性干扰引起的码间串扰,由于乘性干扰引起的码间串扰,可以采用均衡的办法来可以采用均衡的办法来纠正。
纠正。
而加性干扰的影响则需要用其他办法解决。
而加性干扰的影响则需要用其他办法解决。
在设计数字通信系统时,在设计数字通信系统时,应该应该首先从合理选择调制制度,首先从合理选择调制制度,解调方法以及发送功率等方面考虑,解调方法以及发送功率等方面考虑,使加性干扰不足使加性干扰不足以影响到误码率要求。
在仍不能满足要求时,就要考虑采用差错控制措施了。
从差错控制角度看,按加性干扰引起的错码分布规律不同,信道可以分为3类,即随机信道,突发信道和混合信道。
在随机信道中,错码的出现是随机的,而且错码之间是统计独立的。
而且错码之间是统计独立的。
在突发信道中,在突发信道中,错码是成串集中出现的,错码是成串集中出现的,而且在短而且在短促的时间段之间存在较长的无错码区间。
把既存在随机错码又存在突发错码的的信道称为混合信道。
对于不同类型的信道,应该采用不同的差错控制技术。
1.2 1.2 纠错编码原理纠错编码原理我们把信息码分组,为每组信息码附加若干监督码的编码称为分组码为每组信息码附加若干监督码的编码称为分组码(block (block code).code).在分组码中,在分组码中,监督码元仅监督本码组中的信息码元。
分组码一般用符号(n ,k )表示,其中n 是码组的总位数,又称为码组的长度(码长),k 是码组中信息码元的数目,码元的数目,n-k=r n-k=r 为码组中的监督码元的数目,或者称为监督位数目,分组码的结构如图2示,图中前k 位为信息位,后面附加r 个监督位。
其中a n-1到a r 为k 个信息位,个信息位,a a r-1到a 0为r 个监督位。
汉明码的编码和译码(含有源程序)

目录序言 (1)第1章 QuartusⅡ与VHDL简介 (2)1.1 QuartusⅡ软件简介 (2)1.2 VHDL简介 (3)第2章 (7,4)汉明码的原理 (4)2.1 基本概念 (4)2.2 监督矩阵H.. 52.3 生成矩阵G.. 52.4 伴随式(校正子)S. 6第3章 (7,4)汉明码编解码器的设计 (7)3.1 (7,4)汉明码的编码思路及程序设计 (7)3.1.1 (7,4)汉明码的编码思路 (7)3.1.2 (7,4)汉明码的编码程序设计 (7)3.2 (7,4)汉明码的译码思路及程序设计 (8)3.2.1 (7,4)汉明码的译码思路 (8)3.2.2 (7,4)汉明码的译码程序设计 (10)第4章编译程序的调试与分析 (12)4.1 (7,4)汉明码的编码程序调试与分析 (12)4.1.1 (7,4)汉明码的编码程序的编译 (12)4.1.2 (7,4)汉明码的编码程序的仿真分析 (12)4.2 (7,4)汉明码的编译码程序分析及调试 (13)4.2.1 (7,4)汉明码的译码程序的编译 (13)4.2.2 (7,4)汉明码的译码程序的仿真分析 (13)参考文献 (15)体会与建议 (16)附录 (17)序言EDA ( Elect ronics Design Automation) 技术是随着集成电路和计算机技术飞速发展应运而生的一种高级、快速、有效的电子设计自动化工具。
目前,VHDL语言已经成为EDA的关键技术之一,VHDL 是一种全方位的硬件描述语言,具有极强的描述能力,能支持系统行为级、寄存器传输级和逻辑门级三个不同层次的设计,支持结构、数据流、行为三种描述形式的混合描述,覆盖面广,抽象能力强,因此在实际应用中越来越广泛。
VHDL语言具有功能强大的语言结构,可用明确的代码描述复杂的控制逻辑设计,并且具有多层次的设计描述功能,支持设计库和可重复使用的元件的生成。
近几十年来,EDA技术获得了飞速发展。
二元(7,4)汉明码的编译码分析与实验研究

设计(论文)题目:二元(7,4)汉明码的编译码分析与实验研究摘要汉明码(Hamming Code)在电信领域内属于线性分组码,或者可以称为线性调试码。
它是以发明者理查德·卫斯里·汉明的名字命名的。
汉明码在传输信息序列时插入校验码,当计算机存储或传输数据时,或者在信道传输的过程中,可能会产生误码,即信息错位,以检测并纠正一个比特错误。
由于汉明编码简单,它们被广泛应用于实际传输中。
本文主要涉及二元(7,4)汉明码的编码、译码及实现,以及信息论与编码的相关知识。
对于二元(7,4)汉明码C,其校验矩阵为H,汉明距离d(C)=3的充要条件是校验矩阵H的任意2个列矢量线性无关,且任意3个列向量是线性相关。
监督矩阵H生成的码是(7,4,3)码。
所以接下来问题是构建监督矩阵H和生成矩阵G,找出编码器和译码器输入和输出对应的逻辑关系,画出汉明码的编码电路图和译码电路图,通过VHDL语言实现汉明码的编码过程和译码过程,观察仿真波形,来观察实验结果。
关键字:二元(7,4)汉明码;生成矩阵;监督矩阵;编码;译码;AbstractHamming code field belongs to the linear block codes in the telecommunications, or you could be called linear debugging code. It is the inventor, Richard Wesley Hamming named after. Hamming code inserted into the check code in information transmission sequence, when the computer refers for data storage,or in the process of channel transmission. it may produce error, namely the informational burst-error, and Hamming Code could detect and correct errors one bit. Due to its simple hamming coding, they are widely used in the actual transmission.This paper mainly relates to binary (7, 4) hamming code about coding, decoding and realization, as well as the related knowledge of Information Theory and Coding. For binary (7, 4) hamming code called C, its supervision matrix of the H, hamming distance d (C) = 3 of any two of the sufficient and necessary condition is checking matrix H column vector linearly independent, and arbitrary three column vector is linearly dependent. Supervision of matrix H generated code is (7, 3) code. So the next problem is to build the generator matrix G and supervision matrix H, generate the encoder and decoder ,inputs and outputs corresponding logical relationship, as well as,draw the circuit diagram of hamming code encoding and decoding circuit diagram, using VHDL language realization of hamming code encoding and decoding process, observing the simulation waveform and the result of the experiment.Keywords:binary (7, 4) hamming code ;generator matrix;supervision matrix;encoding ;decoding ;引言汉明码是最早提出来的用于纠错的编码,它是一类可以纠正一位错误的高效的线性分组码。
实验三 汉明码编码与译码
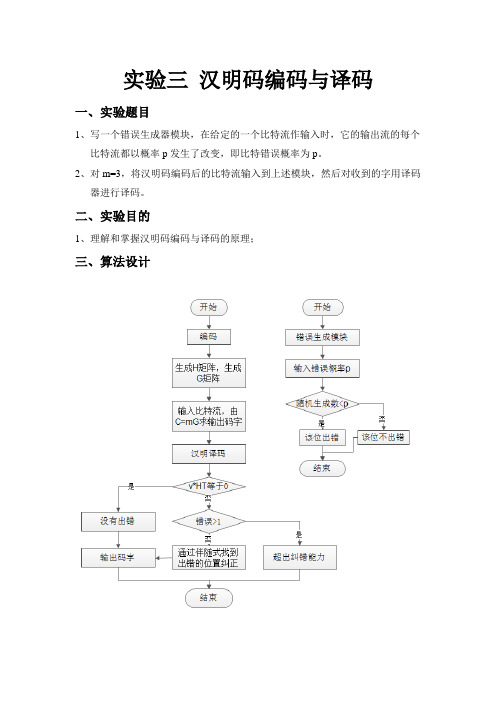
实验三汉明码编码与译码一、实验题目1、写一个错误生成器模块,在给定的一个比特流作输入时,它的输出流的每个比特流都以概率p发生了改变,即比特错误概率为p。
2、对m=3,将汉明码编码后的比特流输入到上述模块,然后对收到的字用译码器进行译码。
二、实验目的1、理解和掌握汉明码编码与译码的原理;三、算法设计四、程序分析1、错误生成模块:任一给以p,系统任意生成一数,若比p小则让其出错,否则不出错。
2、编码:首先随机生成H矩阵,由H矩阵生成G矩阵,利用C=mG编码。
3、解码:若v*H’=0,则没有出错,直接输出v中前k位;若v*H’!=0,列出所有的e和e*H’得到伴随阵s,若能在s中找到s=v*H则c0=v-e,输出c0中前k位;若找不到s,则输出“错误位数大于纠错能力,无法解码”。
五、程序代码#include <iostream>#include <string> // 字符串处理头文件#include <iomanip> // 输入输出控制头文件#include <math.h>#include <stdlib.h>#include <time.h>using namespace std;void Err_Pro();void Hamming_Decode();intm,n,k,t,err,r,R[100],N[100],COUNT[100],num[100][100],Th[100][100],PT_S[100][100],PT_D[1 00][100];intH[100][100],HT[100][100],Ig[100][100],P[100][100],G[100][100],Ibit[100],Cbit[100],Err_Cbit[1 00],V[100];/**************************************************************************//*函数名:void Binary_Conversion(int i) *//*功能:十-二进制转换*//*说明:该函数输出二进制数为低位在前,高位在后*//**************************************************************************/ void Binary_Conversion(int i){int j=0,temp=0;do // 生成完整n个二进制{temp = i % 2; // 判断相应最低位为0或1(若为2的倍数则为0,否则为1)i = i / 2; // 为考虑前一位为0或1做准备if(j < m) // m确定二进制的位数{N[j] = temp;j++;}}while(i != 0); // 等待i等于0(即等待十进制数为0时不进行二进制转换)}/**************************************************************************/ /*函数名:void Random_Array() */ /*功能:将数组的列随机排放*/ /**************************************************************************/ void Random_Array(){srand(unsigned(time(NULL))); // 随机生成条件(抵消rand函数伪随机效果)cout << endl << "产生随机数为:" << endl;for(int j=0;j<n;j++){loop:r= rand() % n; // 随机生成范围为0~n-1的正整数for(int i=0;i<j;i++){if(R[i] == r) // 如果随机产生的数与已产生的数相等,则重新随机产生数{goto loop;}}R[j] = r; // 产生不重复的随机数cout << setw(4) << r + 1;for(int i=0;i<m;i++){PT_D[i][j] = PT_S[i][r]; // 顺序转置系数矩阵->随机转置系数矩阵}}}/**************************************************************************/ /*函数名:void Creat_H() */ /*功能:创建系统型奇偶校验矩阵H */ /*说明:系统型奇偶校验矩阵H由转置负系数矩阵和单位矩阵组成*/ /**************************************************************************/ void Creat_H(){int i,j,count0=0,count1=0,count2=0,count3=0;/*************生成单位矩阵Ih************/ //教材P101for(i=0;i<m;i++) //i表示行j表示列{for(j=0;j<n;j++){if((j >= k) && (i+k == j))Ih[i][j] = 1;elseIh[i][j] = 0;}}/*********生成转置负系数矩阵PT**********/for(i=0;i<m;i++) // 转置二进制转换数组到PT_S{for(j=0;j<n;j++){PT_S[i][j] = num[j][i]; // 生成顺序转置系数矩阵}}Random_Array();//将数组的列随机排放for(j=0;j<n;j++){for(i=0;i<m;i++){if(PT_D[i][j] == 0)count0 ++;}count1 = count0; // count1记录每一列1的个数count0 = 0;if(count1 == (m-1)) // 将只有一位为1其余位为0的列的所有位置0{for(i=0;i<m;i++){PT_D[i][j] = 0;}}else// COUNT数组记录只有一位为1其余位为0的列为0,其余位的值为PT_D列的位置值+1 COUNT[count2] = j + 1;count2 ++;}for(int q=0;q<n;q++) // 将PT_D的至少有两个1的列赋给PT{if(COUNT[q] > 0){for(i=0;i<m;i++)PT[i][count3] = PT_D[i][q];count3 ++;}}cout << endl;/********生成系统型奇偶校验矩阵H********/for(i=0;i<m;i++){for(j=0;j<n;j++){H[i][j] = PT[i][j] + Ih[i][j];}}cout << endl << "系统型奇偶校验矩阵H为:" << endl;for(i=0;i<m;i++) // 显示系统型奇偶校验矩阵H{for(j=0;j<n;j++){cout << setw(2) << H[i][j] << setw(2);}cout << endl;}}/**************************************************************************/ /*函数名:void Creat_G() *//*功能:创建系统型生成矩阵G */ /*说明:系统型生成矩阵G由单位矩阵和系数矩阵组成*/ /**************************************************************************/ void Creat_G(){int i,j;/*************生成单位矩阵Ig************/for(i=0;i<k;i++){for(j=0;j<n;j++){if(i == j)Ig[i][j] = 1;elseIg[i][j] = 0;}}/*************生成系数矩阵P*************/for(j=0;j<n;j++){for(i=0;i<k;i++){if(j>k-1)P[i][j] = PT[j-k][i];}}/**********生成系统型生成矩阵G**********/for(i=0;i<k;i++){for(j=0;j<n;j++){G[i][j] = P[i][j] + Ig[i][j];}}cout << endl << "系统型生成矩阵G为:" << endl;for(i=0;i<k;i++) // 显示系统型奇偶校验矩阵H{for(j=0;j<n;j++){cout << setw(2) << G[i][j] << setw(2);}cout << endl;}}/*******************************主函数*************************************/ int main(){int i,j;cout << setw(30) << "汉明码" << endl;cout << "请输入校验元位数m = ";cin >> m;n = pow(2,m) - 1; //码长k = pow(2,m) - 1 -m; //信息源位数cout << "提示:" << setw(10) << "您输入的为(" <<n<< "," <<k<< ")汉明码,可纠正" << t << "个错误" << endl;cout << endl;for(i=0;i<n;i++) // 将n个转换二进制数组存入二维数组{Binary_Conversion(i+1);for(j=0;j<m;j++){num[i][j] = N[j];//num[i][m-j-1] = N[j]; // m-j-1意义在于将二进制高位在前,低位在后}}cout << "n个二进制转换表为:" << endl;for(i=0;i<n;i++) // 输出二进制转换对应表低位在前高位在后{for(j=0;j<m;j++){cout << num[i][j] << setw(2);}cout << setw(4);}cout << endl;Creat_H();Creat_G();cout << endl << "请输入" << k << "位信息比特流:" << endl;for(i=0;i<k;i++)cin >> Ibit[i];for(i=0;i<n;i++){for(j=0;j<k;j++){Cbit[i] += (Ibit[j] * G[j][i]); // 十进制加法Cbit[i] = Cbit[i] % 2; // 将十进制转换二进制}}cout << endl << "输出" << n << "位码字比特流:" << endl;for(i=0;i<n;i++) //输出编码后的码字cout << setw(3) << Cbit[i];cout << endl;Err_Pro(); //错误概率函数Hamming_Decode(); //汉明译码return 0;}/**************************************************************************/ /*函数名:void Err_Pro() */ /*功能:产生错误概率函数*/ /**************************************************************************/ void Err_Pro(){float p;cout << endl << "请输入错误概率p = ";cin >> p;for(int x=0;x<n;x++){if((float)((rand() % 1001) * 0.001) < p) // 如果小于概率,则原码0与1互换{err ++;Err_Cbit[x] = (Cbit[x] + 1) % 2;}elseErr_Cbit[x] = Cbit[x]; // 如果大于错误概率,则赋值原码}cout << endl << "输出" << n << "位码字比特流(每位等概出错):" << endl;for(int y=0;y<n;y++)cout << setw(3) << Err_Cbit[y];cout << endl;}/**************************************************************************/ /*函数名:void Hamming_Decode() */ /*功能:汉明译码函数*//**************************************************************************/ void Hamming_Decode(){int i,j,flag=0,d;for(i=0;i<n;i++) // 得到H的转置矩阵HT{for(j=0;j<m;j++){HT[i][j] = H[j][i];}cout << endl << "输出转置奇偶校验矩阵HT为:" << endl;for(i=0;i<n;i++){for(j=0;j<m;j++){cout << setw(3) << HT[i][j] << setw(3);}cout << endl;}for(i=0;i<m;i++) // 计算伴随矩阵{for(j=0;j<n;j++){V[i] += Err_Cbit[j] * HT[j][i];}if(V[i] % 2 == 0) // 将十进制转换二进制V[i] = 0;elseV[i] = 1;}cout << endl << "输出伴随矩阵为:" << endl;for(i=0;i<m;i++)cout << V[i] << setw(2);cout << endl;for(i=0;i<m;i++){if(V[i] == 0) // 如果伴随矩阵为零矩阵,则直接输出原码流{if(i == m-1){cout << endl << "<译码正确!>输出码流为:" << endl;for(j=0;j<n;j++)cout << Err_Cbit[j] << setw(3);cout << endl;}}else{flag ++; // 如果伴随矩阵为非零矩阵,则标志位自加1break;}if(flag != 0){if(err == 1) // 伴随矩阵为非零矩阵时执行{for(i=0;i<n;i++){for(j=0;j<m;j++){if(V[j] == HT[i][j]){if(j == (m-1)) d = i;//d记录行}elsebreak;}}cout << endl << "<译码正确!>输出码流为:"<< endl;Err_Cbit[d] = (Err_Cbit[d] + 1) % 2;for(i=0;i<n;i++)cout << setw(3) << Err_Cbit[i] << setw(3);cout << endl;}elsecout << endl << "由于本次编码有" << err << "个错误位,大于纠错能力" << t << ",故<译码错误!>" << endl;}}六、程序运行结果。
74汉明码编码译码函数matlab

74汉明码编码译码函数matlab73汉明码简介73汉明码(Hamming Code),是由理查德·哈明(Richard W. Hamming)于1950年提出的一种能够纠错的编码方式。
在数据的通信和储存中,由于比特位(Bit)的传输或存储可能出错,使用汉明码可以检测和纠正错误,保证数据的可靠性。
而且,它具有编码效率高、纠错能力强等优越性。
74汉明码编码原理74汉明码是由7个数据位加上3个校验位组成的码。
通过在7个数据位中插入3个校验位,使得每个校验位都对特定的数据位进行检验,并在校验位位上调整,使其满足校验规则。
74汉明码编码规则如下:1. 将数据位插入到编码位中:将数据位a1、a2、a3、a4、a5、a6、a7插入到编码位b1、b2、b3、c1、c2、c3、c4中,并按照如下公式进行计算:b1 = a1b2 = a2b3 = a3c1 = a4c2 = a5c3 = a6c4 = a72. 计算每个校验位的值:每个校验位都要对特定的数据位进行检验,并在校验位位上调整,使其满足校验规则。
校验位p1:检验b1、 b2、 c1 是否为1的个数是否为奇数。
校验位p2:检验b1、 b3、 c2 是否为1的个数是否为奇数。
校验位p3:检验b2、 b3、 c3 是否为1的个数是否为奇数。
3. 将所有编码位合并得到74汉明码:将校验位及数据位组成新的编码位,形成74汉明码。
74汉明码译码原理74汉明码译码的规则如下:1. 监测码:检测接受到的数据中是否存在错误。
利用4个校验位检测数据中的错误。
校验位p1:检验b1、 b2、 c1 是否为1的个数是否为奇数。
校验位p2:检验b1、 b3、 c2 是否为1的个数是否为奇数。
校验位p3:检验b2、 b3、 c3 是否为1的个数是否为奇数。
校验位p4:检验数据位a1、 a2、 a3、 a4、 a5、 a6、 a7以及校验位p1、 p2、 p3是否为1的个数是否为奇数。
汉明码编码原理介绍

汉明码编码原理介绍汉明码是在电信领域的一种线性调试码,以发明者理查德·卫斯里·汉明的名字命名。
汉明码在传输的消息流中插入验证码,以侦测并更正单一比特错误。
由于汉明编码简单,它们被广泛应用于内存(RAM)。
其SECDED版本另外加入一检测比特,可以侦测两个或以下同时发生的比特错误,并能够更正单一比特的错误。
1940年,汉明于贝尔实验室工作,运用贝尔模型电脑,输入端依靠打孔卡,这不免有些读取错误。
在平日,特殊代码将发现错误并闪灯,使得操作者能够纠正这个错误。
在周末和下班期间,在没有操作者的情况下,机器只会简单地转移到下一个工作,汉明在周末工作,他对于不可靠的读卡机发生错误后,总是必须重新开始方案变得愈来愈沮丧。
在接下来的几年中,他为了解决调试的问题,开发了功能日益强大的调试算法。
在1950年,他发表了今日所称的汉明码。
现在汉明码有着广泛的应用。
人们在汉明码出现之前使用过多种检查错误的编码方式,但是没有一个可以在和汉明码在相同空间消耗的情况下,得到相等的效果。
汉明码原理介绍:奇偶校验是一种添加一个奇偶位用来指示之前的数据中包含有奇数还是偶数个1的检验方式。
如果在传输的过程中,有奇数个位发生了改变,那么这个错误将被检测出来(注意奇偶位本身也可能改变)。
一般来说,如果数据中包含有奇数个1的话,则将奇偶位设定为1;反之,如果数据中有偶数个1的话,则将奇偶位设定为0。
换句话说,原始数据和奇偶位组成的新数据中,将总共包含偶数个1.奇偶校验并不总是有效,如果数据中有偶数个位发生变化,则奇偶位仍将是正确的,因此不能检测出错误。
而且,即使奇偶校验检测出了错误,它也不能指出哪一位出现了错误,从而难以进行更正。
数据必须整体丢弃并且重新传输。
在一个噪音较大的媒介中,成功传输数据可能需要很长时间甚至不可能完成。
虽然奇偶校验的效果不佳,但是由于他只需要一位额外的空间开销,因此这是开销最小的检测方式。
并且,如果知道了发生错误的位,奇偶校验还可以恢复数据。
74循环汉明码编码及译码

74循环汉明码编码及译码clear all;close all;%-------------(7,4)循环汉明码的编码----------------- n=7;k=4;p=cyclpoly(n,k,'all');[H,G]=cyclgen(n,p(1,:));Msg=[0 0 0 0;0 0 0 1;0 0 1 0;0 1 0 0;0 1 0 1];C=rem(Msg*G,2)M=input('M=');disp( '输入信源序列:');Msg=input('Msg=');C=rem(Msg*G,2) %编码结果R=7/4*log2(2) %计算码元信息率%----------- (7,4)循环码的译码------------------- M=input('M=');disp( '输入接收序列:');Msg=input('Msg=');S=mod(Msg*H',2)for i=1:Mif S(i)==[0 0 0]disp('接收码元无错');Rsg=Msgelseif S(i)==[1 0 0]disp('监督元a0位错');if Msg(0)==0Msg(0)=1;elseif Msg(0)==1Msg(0)=0;endRsg=Msgelseif S(i)==[0 1 0] disp('监督元a1位错'); if Msg(1)==0Msg(1)=1;elseif Msg(1)==1 Msg(1)=0;endRsg=Msgelseif S(i)==[0 0 1] disp('监督元a2位错'); if Msg(2)==0Msg(2)=1;elseif Msg(2)==1 Msg(2)=0;endRsg=Msgelseif S(i)==[1 0 1] disp('信息元第1位错'); if Msg(3)==0Msg(3)=1;elseif Msg(3)==1 Msg(3)=0;endRsg=Msgelseif S(i)==[1 1 1] disp('信息元第2位错'); if Msg(4)==0Msg(4)=1;elseif Msg(4)==1 Msg(4)=0;endRsg=Msgelseif S(i)==[1 1 0] disp('信息元第3位错'); if Msg(5)==0Msg(5)=1;elseif Msg(5)==1 Msg(5)=0;endRsg=Msgelseif S(i)==[0 1 1] disp('信息元第4位错'); if Msg(6)==0Msg(6)=1;elseif Msg(6)==1 Msg(6)=0;endRsg=Msgelsedisp('无法纠错');Rsg=MsgendendH =1 0 0 1 1 1 00 1 0 0 1 1 10 0 1 1 1 0 1G =1 0 1 1 0 0 0 1 1 1 0 1 0 0 1 1 0 0 0 1 0 0 1 1 0 0 0 1。
汉明码的编码和译码算法

汉明码(Hamming)的编码和译码算法本文所讨论的汉明码是一种性能良好的码,它是在纠错编码的实践中较早发现的一类具有纠单个错误能力的纠错码,在通信和计算机工程中都有应用。
例如:在“计算机组成原理”课程中,我们知道当计算机存储或移动数据时,可能会产生数据位错误,这时可以利用汉明码来检测并纠错。
简单的说,汉明码是一个错误校验码码集,由Bell实验室的R.W.Hamming发明,因此定名为汉明码。
如果对汉明码作进一步推广,就得出了能纠正多个错误的纠错码,其中最典型的是BCH码,而且汉明码是只纠1bit错误的BCH码,可将它们都归纳到循环码中。
各种码之间的大致关系显示如下。
一、汉明码的编码算法输入:信源消息u(消息分组u)输出:码字v处理:信源输出为一系列二进制数字0和1。
在分组码中,这些二进制信息序列分成固定长度的消息分组(message blocks)。
每个消息分组记为u,由k个信息位组成。
因此共有2k种不同的消息。
编码器按照一定的规则将输入的消息u转换为二进制n 维向量v ,这里n >k 。
此n 维向量v 就叫做消息u 的码字(codeword )或码向量(code vector )。
因此,对应于2k 种不同的消息,也有2k 种码字。
这2k 个码字的集合就叫一个分组码(block code )。
若一个分组码可用,2k 个码字必须各不相同。
因此,消息u 和码字v 存在一一对应关系。
由于n 符号输出码字只取决于对应的k 比特输入消息,即每个消息是独立编码的,从而编码器是无记忆的,且可用组合逻辑电路来实现。
定义:一个长度为n ,有2k 个码字的分组码,当且仅当其2k 个码字构成域GF(2)上所有n 维向量组成的向量空间的一个K 维子空间时被称为线性(linear )(n, k)码。
汉明码(n ,k ,d )就是线性分组(n, k)码的一种。
其编码算法即为使用生成矩阵G :v = u ·G 。
hammin(汉明)码编码规则

hammin(汉明)码编码规则计算机汉明码编码规则若编成的海明码为Hm,Hm-1…H2H1,则海明码的编码规律为:(1)校验位分布:在m位的海明码中,各校验位Pi分布在位号为2^(i-1)的位置,即校验位的位置分别为1,2,4,8,…,其余为数据位;数据位按原来的顺序关系排列。
如有效信息码为…D5D4D3D2D1,则编成的海明码为…D5P4D4D3D2P3D1P2P1。
(2)校验关系:校验关系指海明码的每一位Hi要有多个校验位校验,其关系是被校验位的位号为校验位的位号之和。
如D1(位号为3)要由P2(位号为2) 与P1(位号为1)两个校验位校验,D2(位号为5)要由P3(位号为4)与P1两个校验位校验,D3(位号为6)要由P2与P3两个校验位校验,D4(位号为7)要由P1,P2,P3三个校验位校验,……。
这样安排的目的是希望校验的结果能正确反映出出错位的位号。
(3)在增大合法码的码距时,使所有码的码距尽量均匀增大,以保证对所有码的校验能力平衡提高。
汉明距离在一个码组集合中,任意两个码字之间对应位上码元取值不同的位的数目定义为这两个码字之间的汉明距离。
即d(x,y)=∑x[i]⊕y[i],这里i=0,1,..n-1,x,y都是n位的编码,⊕表示异或例如,(00)与(01)的距离是1,(110)和(101)的距离是2。
在一个码组集合中,任意两个编码之间汉明距离的最小值称为这个码组的最小汉明距离。
最小汉明距离越大,码组越具有抗干扰能力。
下面我们用d表示码组的最小汉明距离。
1。
当码组用于检测错误时,设可检测e个位的错误,则d >=e + 1设有两个距离为d的码字A和B,如果A出现了e个错误,则A变成了以A为圆心,e位半径的球体表面的码字。
为了能够准确地分辨出这些码字既不是A也不是B,那么A 误码后变成的球面上的点与B至少应该有一位距离(如果B在球面上或在球面内部则无法分辨出到底B是不是A的错误码),即A与B之间的最小距离d >= e+1。
通信原理课程设计--汉明码的编码和译码

兰州理工大学课程设计报告课程名称:通信系统课程设计设计名称:汉明码的编码和译码姓名:学号:班级:指导教师:起止日期:2014.4.7-2014.4.9课程设计任务书学生班级:学生姓名:学号:设计名称:汉明码的编译和译码起止日期:2012.6.11-2012.6.25 指导教师:课程设计学生日志课程设计评语表汉明码的编码和译码一、 设计目的和意义1. 学习汉明码的编码和译码;2. 学习Matlab 的相关使用,学会用Malab 解决实际问题;3. 培养自己全面、独立思考的能力。
二、 设计原理2.1汉明码编码原理一般来说,若汉明码长为n ,信息位数为k ,则监督位数r=n-k 。
若希望用r 个监督位构造出r 个监督关系式来指示一位错码的n 种可能位置,则要求21r n -≥或211rk r -≥++ (1)下面以(7,4)汉明码为例说明原理:设汉明码(n,k )中k=4,为了纠正一位错码,由式(1)可知,要求监督位数r ≥3。
若取r=3,则n=k+r=7。
我们用6543210a a a a a a a 来表示这7个码元,用123s s s 的值表示3个监督关系式中的校正子,则123s s s 的值与错误码元位置的对应关系可以规定如表1所列。
表1 校正子和错码位置的关系则由表1可得监督关系式: 16542s a a a a =⊕⊕⊕()226531s a a a a =⊕⊕⊕ ()3 36430s a a a a =⊕⊕⊕()4 在发送端编码时,信息位6543a a a a 的值决定于输入信号,因此它们是随机的。
监督位2a 、1a、a 应根据信息位的取值按监督关系来确定,即监督位应使式(2)~式(4)中1s、2s 、3s 的值为0(表示编成的码组中应无错码)654265316430000a a a a a a a a a a a a ⊕⊕⊕=⎧⎪⊕⊕⊕=⎨⎪⊕⊕⊕=⎩ (5)式(5)经过移项运算,接触监督位265416530643a a a a a a a a a a a a=⊕⊕⎧⎪=⊕⊕⎨⎪=⊕⊕⎩ (6)式(5)其等价形式为:6543210111010001101010010110010a a a a a a a ⎡⎤⎢⎥⎢⎥⎢⎥⎡⎤⎡⎤⎢⎥⎢⎥⎢⎥=⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦⎢⎥⎢⎥⎢⎥⎣⎦(7)式(6)还可以简记为0T T H A •=或0TA H •= (8)其中111010011010101011001H ⎡⎤⎢⎥=⎢⎥⎢⎥⎣⎦[]6543210A a a a a a a a =[]0000=111011011011P ⎡⎤⎢⎥=⎢⎥⎢⎥⎣⎦100010001r I ⎡⎤⎢⎥=⎢⎥⎢⎥⎣⎦ 所以有[]r H PI = (9)式(6)等价于[][][]21065436543111110101011a a a a a a a a a a a Q⎡⎤⎢⎥⎢⎥==⎢⎥⎢⎥⎣⎦(10)其中Q 为P 的转置,即T Q P = (11)式(10)表示,信息位给定后,用信息位的行矩阵乘矩阵Q 就产生出监督位。
汉明码

汉明码译码方法汉明码,(Hamming Code)是由RichadHamming1950年提出的,它属于线性分组编码方式。
设原代码的码长为k比特,附加纠错编码部分为r比特,当码字n=2r-1,r=n-k,r=1,2⋯时就称这种线性分组码为汉明码。
其基本原理是,将信息码元与监督码元通过线性方程式联系起来,每一个监督位被编在传输码字的特定比特位置上。
系统对于错误的数位无论是原有信息位中的,还是附加监督位中的都能把它分离出来。
设数据位数为m,校验位数为k,则总编码位数为n,n=m+k,有Hamming不等式:对于这个不等式可以理解为:由于n位码长中有一位出错,可能产生n个不正确的代码(错误位也可能发生在校验位),所以加上k 位校验后,就需要定位昭m+k(=n)个状态。
用2k个状态中的一个状态指出“有无错”,其余2k-1个状态便可用于错误的定位。
要能充分地进行错误定位,则须满足式(10-1)的关系。
由此不等式得到校验位数与可校验的最大信息位之间的关系见表。
表Hamming校验位数与可校验的最大信息位数之间的关系Hamming码无法实现2位或2位以上的纠错,Hamming码只能实现一位纠错。
下面介绍汉明码距与编码纠错能力的关系。
汉明码距指的是长度相同的两个符号序列(码字)a和b之间对应位置上不同码元的个数,用符号D(a,b)表示,如两个二元序列:a=101111b=111100则得D(a,b)=3。
有了汉明码距的概念,我们就可以用汉明码距来描述码的纠错检测能力。
如果一组编码的码长为n,将这些资源全部利用上,可以对2n个符号进行编码,但这样一来这个编码就没有任何抗干扰能力,因为合法码字之间的最小汉明码距为1,任何一个符号的编码的任意一位发生错误,就变成了另外一个符号的编码,它也是一个合法的码字。
接收端不能判断是不是有错误发生。
我们可以在2n个可用的码字中间选择一些码字来对信源符号进行编码,把这些码字称为合法码字,而其他没有使用的码字称为非法码字。
对语音进行74汉明码编译码

对语音进行74汉明码编译码汉明码是一种用于检错的编码方式,常用于数据传输和存储领域。
它可以通过在数据中添加冗余的校验位来检测和纠正传输或存储过程中出现的错误。
汉明码的编码过程如下:1. 确定要传输的数据。
假设我们要传输一个k位的消息。
2. 确定校验位的数量。
校验位的数量r可以通过以下公式进行计算:2^r >= k + r + 1。
这个公式确保了校验位足够多以检测和纠正错误。
3. 将数据位和校验位进行排列。
将k位的数据位和r位的校验位按照某种方式进行排列。
一种常见的排列方式是将校验位插入到数据位的特定位置。
4. 计算校验位的值。
校验位的值可以通过以下步骤来计算:a. 将每一个校验位作为一个索引。
b. 对于每一个校验位,将目标位中索引所指的位进行异或运算。
c. 将异或结果作为校验位的值。
5. 将数据位和校验位传输或存储。
汉明码的解码过程如下:1. 接收数据位和校验位。
2. 计算每一个校验位的值。
校验位的值可以通过以下步骤来计算:a. 将每一个校验位作为一个索引。
b. 对于每一个校验位,将接收到的数据位中索引所指的位进行异或运算。
c. 将异或结果作为校验位的值。
3. 比较计算得到的校验位的值与接收到的校验位的值。
如果两者相等,则说明传输或存储过程中没有错误发生。
如果两者不相等,则说明可能存在错误。
4. 如果存在错误,根据所在位置的校验位的索引,进行纠正。
将该位的值进行翻转即可。
需要注意的是,汉明码可以检测错误的位置,并在发生错误时进行纠正,但是它有限制和缺陷。
它只能检测和纠正1位的错误,并且无法检测多位错误。
此外,汉明码的编码和解码过程相对复杂,可能会增加传输或存储的开销。
总结起来,汉明码是一种用于检错的编码方式,可以在数据传输或存储过程中检测和纠正错误。
通过添加校验位并进行异或运算,可以实现错误的检测和纠正。
然而,汉明码只能检测和纠正1位的错误,且编码和解码过程相对复杂。
汉明码编译码

汉明码编译码汉明码编译码一设计思想汉明码是一种常用的纠错码,具有纠一位错误的能力。
本实验使用Matlab平台,分别用程序语言和simulink来实现汉明码的编译码。
用程序语言实现就是从原理层面,通过产生生成矩阵,错误图样,伴随式等一步步进行编译码。
用simulink实现是用封装好的汉明码编译码模块进行实例仿真,从而验证程序语言中的编译码和误码性能分析结果。
此外,在结合之前信源编码的基础上,还可实现完整通信系统的搭建。
二实现流程1.汉明码编译码生成矩阵G信息序列M产生码字C信道计算伴随式S接收码流R校验矩阵H解码码流C2解码信息序列M2图 1 汉明码编译码框图1)根据生成多项式,产生指定的生成矩阵G2)产生随机的信息序列M3)由C MG得到码字4)进入信道传输5) 计算=TS RH 得到伴随式 6) 得到解码码流7) 得到解码信息序列2. 汉明码误码性能分析误码率(SER )是指传输前后错误比特数占全部比特数的比值。
误帧率(FER )是指传输前后错误码字数占全部码字数的比值。
通过按位比较、按帧比较可以实现误码率和误帧率的统计。
3. 构建完整通信系统图 2 完整通信系统框图 输入信息序列Huffman 编码Hamming 编码信道Hamming 译码Huffman 译码输出信息序列噪声三 结论分析1. 汉明码编译码编写了GUI 界面方便呈现过程和结果。
图 3 汉明码编译码演示GUI 界面以产生(7,4)汉明码为例说明过程的具体实现。
1) 根据生成多项式,产生指定的生成矩阵G 用[H,G,n,k] = hammgen(3,'D^3+D+1')函数得到系统码形式的校验矩阵H 、G 以及码字长度n 和信息位数k100101101011100010111H ⎡⎤⎢⎥=⎢⎥⎢⎥⎣⎦ 1101000011010011100101010001G ⎡⎤⎢⎥⎢⎥=⎢⎥⎢⎥⎣⎦2) 产生随机的信息序列M0010=01000111M ⎡⎤⎢⎥⎢⎥⎢⎥⎣⎦3) 由C MG =得到码字010001101101000010111C ⎡⎤⎢⎥=⎢⎥⎢⎥⎣⎦4) 进入信道传输假设是BSC 信道,错误转移概率设定为0.1 传输后接收端得到的码流为000011110100000111101R ⎡⎤⎢⎥=⎢⎥⎢⎥⎣⎦红色表示错误比特。
汉明码的编码和译码算法

汉明码(Hamming)的编码和译码算法本文所讨论的汉明码是一种性能良好的码,它是在纠错编码的实践中较早发现的一类具有纠单个错误能力的纠错码,在通信和计算机工程中都有应用。
例如:在“计算机组成原理”课程中,我们知道当计算机存储或移动数据时,可能会产生数据位错误,这时可以利用汉明码来检测并纠错。
简单的说,汉明码是一个错误校验码码集,由Bell实验室的R.W.Hamming发明,因此定名为汉明码。
如果对汉明码作进一步推广,就得出了能纠正多个错误的纠错码,其中最典型的是BCH码,而且汉明码是只纠1bit错误的BCH码,可将它们都归纳到循环码中。
各种码之间的大致关系显示如下。
一、汉明码的编码算法输入:信源消息u(消息分组u)输出:码字v处理:信源输出为一系列二进制数字0和1。
在分组码中,这些二进制信息序列分成固定长度的消息分组(message blocks)。
每个消息分组记为u,由k个信息位组成。
因此共有2k种不同的消息。
编码器按照一定的规则将输入的消息u转换为二进制n 维向量v ,这里n >k 。
此n 维向量v 就叫做消息u 的码字(codeword )或码向量(code vector )。
因此,对应于2k 种不同的消息,也有2k 种码字。
这2k 个码字的集合就叫一个分组码(block code )。
若一个分组码可用,2k 个码字必须各不相同。
因此,消息u 和码字v 存在一一对应关系。
由于n 符号输出码字只取决于对应的k 比特输入消息,即每个消息是独立编码的,从而编码器是无记忆的,且可用组合逻辑电路来实现。
定义:一个长度为n ,有2k 个码字的分组码,当且仅当其2k 个码字构成域GF(2)上所有n 维向量组成的向量空间的一个K 维子空间时被称为线性(linear )(n, k)码。
汉明码(n ,k ,d )就是线性分组(n, k)码的一种。
其编码算法即为使用生成矩阵G :v = u ·G 。
(7,4)汉明码编译码程序说明资料

(7,4)汉明码编译码原理程序说明书1、线性分组码假设信源输出为一系列二进制数字0和1.在分组码中,这些二进制信息序列分成固定长度的消息分组(message blocks )。
每个消息分组记为u ,由k 个信息位组成。
因此共有2k种不同的消息。
编码器按照一定的规则将输入的消息u 转换为二进制n 维向量v ,这里n>k 。
此n 维向量v 就叫做消息u 的码字(codeword )或码向量(code vector )。
因此,对应于2k种不同的消息,也有2k种码字。
这2k个码字的集合就叫一个分组码(block code )。
一个长度为n ,有2k个码字的分组码,当且仅当其2k个码字构成域GF (2)上所有n维向量空间的一个k 维子空间时被称为线性(linear )(n ,k )码。
对于线性分组码,希望它具有相应的系统结构(systematic structure ),其码字可分为消息部分和冗余校验部分两个部分。
消息部分由k 个未经改变的原始信息位构成,冗余校验部分则是n-k 个奇偶校验位(parity-check )位,这些位是信息位的线性和(linear sums )。
具有这样的结构的线性分组码被称为线性系统分组码(linear systematic block code )。
本实验以(7,4)汉明码的编译码来具体说明线性系统分组码的特性。
其主要参数如下:码长:21mn =- 信息位:21m k m =-- 校验位:m n k =-,且3m ≥ 最小距离:min 03d d ==由于一个(n ,k )的线性码C 是所有二进制n 维向量组成的向量空间n V 的一个k 维子空间,则可以找到k 个线性独立的码字,0,1,1k g g g -…… ,使得C 中的每个码字v 都是这k 个码字的一种线性组合。
(7,4)汉明码的生成矩阵如下,前三位为冗余校验部分,后四位为消息部分。
0123 1 1 0 1 0 0 00 1 1 0 1 0 01 1 1 0 0 1 01 0 1 0 0 0 1g g G g g ⎧⎫⎧⎫⎪⎪⎪⎪⎪⎪⎪⎪==⎨⎬⎨⎬⎪⎪⎪⎪⎪⎪⎪⎪⎩⎭⎩⎭如果()0123u u u u u =是待编码的消息序列,则相应的码字可如下给出:()0101230011223323g g v u G u u u u u g u g u g u g g g ⎧⎫⎪⎪⎪⎪===+++⎨⎬⎪⎪⎪⎪⎩⎭编码结构即码字()0123456v v v v v v v v =,对于(7,4)线性分组码汉明码而言,3456,,,v v v v 为所提供的消息序列,而0356v v v v =⊕⊕,1345v v v v =⊕⊕,2456v v v v =⊕⊕。
汉明编码和译码讲解

实验十五汉明编码和译码实验一、实验前的准备(1)预习本实验的相关内容。
(2)熟悉实验指导书附录B 和附录C中实验箱面板分布及测试孔位置相关模块的跳线状态。
(3)实验前重点熟悉的内容:汉明码的编码规则、汉明码的纠错能力。
二、实验目的(1)掌握汉明码编译码原理。
(2)掌握汉明码纠错检错原理。
(3)通过纠错编解码实验,加深对纠错编解码理论的理解。
三、实验仪器1. ZH5001A通信原理综合实验系统2. 20MHz双踪示波器四、基本原理差错控制编码的基本原理是:由发送端的信道编码器在信息码元序列中增加一些监督码元。
这冗余的码元与信息之间以某种确定的规则建立校验关系,使接收端可以利用这种关系由信道译码器来发现或纠正可能存在的错码。
不同的编码方法有不同的检错或纠错能力。
为了纠正位错码,在分组码中最少要加入多少监督位才可行呢?编码效率能否提高呢?从这种思想出发进行研究,便导致了汉明码的诞生。
汉明码是一种能够纠正一位错码且编码效率较高的线性分组码。
下面介绍汉明码的编码原理。
般来说,若码长为 n,信息位数为k ,记作(n,k)码,则监督位数r n k,如果希望用r 个监督位构造出r个监督关系式来指示一位错码的 n种可能位置,则要求2r 1 n或 2r k r 1通信原理综合实验系统中的纠错码系统采用(7,4)汉明码。
用a6a5⋯a0 表示这7 个码元,用S1、S2、S3表小3 个监督关系式中的校正子,则S1S2S3 的值与码元间构成偶数监督关系:S1 a6 a5 a4 a2S2 a4 a4 a3 a1S3 a6 a5 a3 a0在发送端编码时,信息位a6、a5、a4和a3的值决定于输入信号,因此它们是随机的。
监督位a2、a1和a0 应根据信息位的取值按监督关系来确定,即监督位应使以上=式中S1、S2、S3 的值为零(表示变成的码组中应无错码),即a6 a5 a4 a2 0 a5 a4 a3 a1 0a6 a5 a3 a0 0上式经移项运算,解出监督位a2 a6 a5 a4a1 a5 a4 a3a0 a6 a5 a3给定信息位后,可直接按上式算出监督位,其结果如下表通信原理实验第页0011 101 1011 0000100 111 1100 0100101 100 1101 0010110 001 1110 1000111 010 1111 111 接收端收到每个码组后,先计算出S1、S2、S3 ,再按上表判断错码情况。
汉明码编码译码实验报告(信息论与编码)及源程序

}
printf("经过译码后变为: \n");
for(i=0;i<N/4;i++)
{for(j=0;j<3;j++)
{f[j]=0;
for(k=A;k<A+7;k++)
f[j]+=w[k]*H[k-A][j];/////计算伴随式
}
for(m=0;m<7;m++)
{for(j=0;j<3;j++)
printf("%d",ww[A+m]);//没有出错的地方
}
}
A=A+7;//向后移动7位
L=8;//复位
M=0;///清零,复位
printf("\n");
}
}
4
5
这次的实验是实现汉明码的编码与译码,达到纠错功能。通过信息论的课程,我基本了解了汉明码编译的原理和方法,但在编程的过程中遇到了不小的困难。首先还是理解汉明码概念的问题,因为还存在纠错的功能,所以汉明码的编码方式和以前学的哈夫曼编码或Fano编码比起来要复杂不少,开始的时候理解起来有些困难。不过通过仔细看PPT,很快就弄懂了汉明码的原理。但是最开始编出来的程序运行的结果总是不正确,和书上的码字不一样,后来发现是在校验矩阵上出了问题,自己对矩阵方面的知识一直把握得不是很好。经过调试,程序很快就能够正确运行了。
if((f[j]%2)==H[m][j])M=M+1;
if(M==3)L=m ;
M=0;//清零
} ///根据伴随式找到出错的位置
for(m=0;m<7;m{ww[A+m]=(w[A+m]+1)%2;//将出错的地方更正
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
汉明码(Hamming)的编码和译码算法本文所讨论的汉明码是一种性能良好的码,它是在纠错编码的实践中较早发现的一类具有纠单个错误能力的纠错码,在通信和计算机工程中都有应用。
例如:在“计算机组成原理”课程中,我们知道当计算机存储或移动数据时,可能会产生数据位错误,这时可以利用汉明码来检测并纠错。
简单的说,汉明码是一个错误校验码码集,由Bell实验室的R.W.Hamming发明,因此定名为汉明码。
如果对汉明码作进一步推广,就得出了能纠正多个错误的纠错码,其中最典型的是BCH码,而且汉明码是只纠1bit错误的BCH码,可将它们都归纳到循环码中。
各种码之间的大致关系显示如下。
一、汉明码的编码算法输入:信源消息u(消息分组u)输出:码字v处理:信源输出为一系列二进制数字0和1。
在分组码中,这些二进制信息序列分成固定长度的消息分组(message blocks)。
每个消息分组记为u,由k个信息位组成。
因此共有2k种不同的消息。
编码器按照一定的规则将输入的消息u转换为二进制n 维向量v ,这里n >k 。
此n 维向量v 就叫做消息u 的码字(codeword )或码向量(code vector )。
因此,对应于2k 种不同的消息,也有2k 种码字。
这2k 个码字的集合就叫一个分组码(block code )。
若一个分组码可用,2k 个码字必须各不相同。
因此,消息u 和码字v 存在一一对应关系。
由于n 符号输出码字只取决于对应的k 比特输入消息,即每个消息是独立编码的,从而编码器是无记忆的,且可用组合逻辑电路来实现。
定义:一个长度为n ,有2k 个码字的分组码,当且仅当其2k 个码字构成域GF(2)上所有n 维向量组成的向量空间的一个K 维子空间时被称为线性(linear )(n, k)码。
汉明码(n ,k ,d )就是线性分组(n, k)码的一种。
其编码算法即为使用生成矩阵G :v = u ·G 。
例1-1:针对汉明码Hamming (7,4,3)而言,u =(u 0,u 1,u 2,u 3),v =(v 0,v 1,v 2,v 3,v 4,v 5,v 6),则我们有 (v 0,v 1,v 2,v 3,v 4,v 5,v 6)=(u 0,u 1,u 2,u 3) ·G 。
Hamming (7,4,3) 的生成矩阵G 为:G =⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡111011010011100101010001, (v 0,v 1,v 2,v 3,v 4,v 5,v 6) =(u 0,u 1,u 2,u 3) ·⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡111011010011100101010001, 所以我们有: v 0= u 0, v 1= u 1, v 2= u 2, v 3= u 3, v 4= u 0+u 1+u 2, v 5= u 1+u 2+u 3, v 6=u 0+u 1+u 3,例如u =1101,对应→v =1101001。
处理完毕。
■其他汉明码照此处理,甚至其他线性分组(n, k)码都照此办理即可。
线性分组(n, k)码的校正子(伴随式)有2n-k 个,设该码的纠错能力为t ,那么重量小于或者等于t 的所有错误模式(图样)都要有唯一的校正子(伴随式)与之对应,因而,对于二进制(n, k)码,有汉明限:2n-k≥∑=⎪⎪⎭⎫ ⎝⎛ti i n 0 ,当2n-k =∑=⎪⎪⎭⎫ ⎝⎛ti i n 0时,(n, k)码称为完备码(Perfect Code )。
完备码的伴随式得到了充分的利用,不存在解码不唯一的问题,然而完备码不一定是纠错能力强的码,因为它的最小距离d min 未必最大。
完备码也是稀少的,已知的二进制完备码有t=1的汉明码(Hamming Code )和t=3的格雷码(Golay Code ),以及n 为奇数的简单重复(n,1)码。
三进制完备码有t=2的(11,6,5)格雷码。
纠错能力t=1的完备码统称为汉明码。
由定义可知,(n, k)汉明码应当满足下列条件:2n-k =1+n ,令校验位长m=n-k ,那么容易知道:n=2m -1, k=2m -1-m, d min =3 。
汉明码的校验矩阵H 具有特殊的性质:它的m 维列向量正好是除零向量以外的所有可能的向量组合,共有2m -1个,恰好构成了H 矩阵的列数n 。
格雷码通常是指线性分组(23,12)码,最小距离d min =7,纠错能力 t=3。
由于223-12=2048=1+⎪⎪⎭⎫⎝⎛+⎪⎪⎭⎫ ⎝⎛+⎪⎪⎭⎫ ⎝⎛323223123 ,所以格雷码是完备码,其码重(码的重量)分布见下面表0-1。
表0-1 格雷码的码重分布备注:1、汉明码的生成矩阵:Hamming (7,4,3) 的生成矩阵G⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡111011010011100101010001 Hamming (17,12,3) 的生成矩阵G⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎣⎡1011010101001011101101010111100011111001011101001111101111111111110111 Hamming (13,9,3) 的生成矩阵G⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎣⎡1110110100111110111010101011111010111111111Hamming (15,11,3) 的生成矩阵G⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎣⎡11101101001111101110101010111110101111111111011110011 Hamming (16,11,4) 的生成矩阵G⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎣⎡11111011011001110110111101011010110111010011111111110101111100112、除了分组码之外,还有卷积码。
卷积码编码器同样接受k 比特分组的信息序列u ,并产生n 符号组的编码序列(码序列)v (卷积码编码中,符号u 和v 用来表示分组的序列而非单个分组)。
但是,每一个编码分组不仅取决于当前单位时间对应的k 比特消息组,而且与前m 个消息组有关。
此时,编码器的存储级数(memory order)为m 。
编码器所产生的所有可能的输出编码序列的集合构成了一个码。
比值R=k/n 称为码率(code rate )。
由于编码器有存储单元,因而必须采用时序逻辑电路实现。
二、汉明码的译码算法输入:接收向量r输出:译码所得码字v*处理:考虑一个(n,k)线性分组码,其生成矩阵为G,奇偶校验矩阵为H。
令v=( v0,v1, … ,v n-1)表示要通过有噪信道传输的码字,r = (r0,r1, … ,r n-1)为信道输出端接收到的码字。
由于信道中的噪声,r可能与v不同。
向量和e= r +v=( e0,e1,…,e n-1)是一个n维向量,其中r i≠v i时,e i=1,而r i= v i时,e i=0。
该n维向量e称为差错向量(error vector)或错误模式或错误图样(error pattern), 它直接指出接收向量r不同于传输码字v的位置。
e中的1表示由于信道噪声引起的传输差错(transmission errors)。
接收向量r的译码包括如下三个步骤:1、计算r的校正子(伴随式)s = r·H T;2、确定校正子(伴随式)s = r·H T对应的陪集首e l,于是e l被假定为由信道引起的错误模式(错误图样);3、将接收向量r译为码字v*=r+ e l。
上述译码方案被称为校正子(伴随式)译码(syndrome decoding)或查表译码(table lookup decoding)。
例2-1:Hamming (7,4,3) 的生成矩阵G = [ I k P ]k ×n=⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡111011010011100101010001, 则奇偶校验矩阵H 为H = [ P T I n-k ](n-k)×n =⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡1011101011100010111,这里n=7, k=3。
该码有23=8个陪集:假设传输码字为v =1110100,接收向量为r =0110100(错1位),其校正子s =r ·H T =101, 对应e =1000000,v *=r + e=1110100,所以译码正确!假设传输码字为v =1110100,接收向量为r =0110000(错2位),其校正子s = r ·H T =001, 对应e =0000001,v *=r + e=0110101,所以译码错误!可以看出:汉明码Hamming (7,4,3)可以纠正含单个差错的错误模式或者检测出含两个差错的错误模式(而不能纠正含两个或两个以上差错的错误模式)。
例2-2:Hamming (17,12,3) 的生成矩阵G = [ I k P ]k ×n =⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎣⎡1011010101001011101101010111100011111001011101001111101111111111110111奇偶校验矩阵H = [ P T I n-k ](n-k)×n =⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎣⎡111111111010010110011110110011111010101100111111001011001111该码有25=32个陪集:例2-3:Hamming (13,9,3) 的生成矩阵G = [ I k P ]k ×n =⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎣⎡1110110100111110111010101011111010111111111 奇偶校验矩阵H = [ P T I n-k ](n-k)×n =⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡111111111010111110110101111001101011 该码有24=16个陪集:例2-4:Hamming (15,11,3) 的生成矩阵G = [ I k P ]k ×n =⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎣⎡11101101001111101110101010111110101111111111011110011 奇偶校验矩阵H = [ P T I n-k ](n-k)×n =⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡11111111111010111100101101011110100110101111 该码有24=16个陪集:例2-5:Hamming (16,11,4) 的生成矩阵G 为G = [ I k P ]k ×n =⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎣⎡1111101101100111011011110101101011011101001111111111010111110011 奇偶校验矩阵H = [ P T I n-k ](n-k)×n :⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎣⎡11111111110011010111111010111100101101011110100110101111 该码有25=32个陪集:备注:Hamming (7,4,3) 的生成矩阵G 1 0 0 0 1 0 1 0 1 0 0 1 1 1 0 0 1 0 1 1 0 0 0 0 1 0 1 1⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡111011010011100101010001 Hamming (17,12,3) 的生成矩阵G 1 0 0 0 0 0 0 0 0 0 0 0 1 1 0 1 1 0 1 0 0 0 0 0 0 0 0 0 0 1 1 1 1 1 0 0 1 0 0 0 0 0 0 0 0 0 1 1 1 0 1 0 0 0 1 0 0 0 0 0 0 0 0 1 1 1 0 0 0 0 0 0 1 0 0 0 0 0 0 0 0 1 1 1 0 0 0 0 0 0 1 0 0 0 0 0 0 0 0 1 1 10 0 0 0 0 0 1 0 0 0 0 0 1 0 0 0 1 0 0 0 0 0 0 0 1 0 0 0 0 1 1 0 1 0 0 0 0 0 0 0 0 0 1 0 0 0 0 1 1 0 1 0 0 0 0 0 0 0 0 0 1 0 0 1 0 1 0 0 0 0 0 0 0 0 0 0 0 0 1 0 0 1 0 1 0 0 0 0 0 0 0 0 0 0 0 0 1 0 0 1 0 1⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎣⎡1011010101001011101101010111100011111001011101001111101111111111110111 Hamming (13,9,3) 的生成矩阵G 1 0 0 0 0 0 0 0 0 1 1 1 1 0 1 0 0 0 0 0 0 0 1 1 1 0 0 0 1 0 0 0 0 0 0 0 1 1 1 0 0 0 1 0 0 0 0 0 1 0 1 0 0 0 0 0 1 0 0 0 0 0 1 0 1 0 0 0 0 0 1 0 0 0 1 0 1 1 0 0 0 0 0 0 1 0 0 1 1 0 0 0 0 0 0 0 0 0 1 0 0 1 1 0 0 0 0 0 0 0 0 0 1 0 0 1 1⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎣⎡1110110100111110111010101011111010111111111 Hamming (15,11,3) 的生成矩阵G1 0 0 0 0 0 0 0 0 0 0 1 0 0 1 0 1 0 0 0 0 0 0 0 0 0 1 1 0 1 0 0 1 0 0 0 0 0 0 0 0 1 1 1 1 0 0 0 1 0 0 0 0 0 0 0 1 1 1 0 0 0 0 0 1 0 0 0 0 0 0 0 1 1 1 0 0 0 0 0 1 0 0 0 0 0 1 0 1 0 0 0 0 0 0 0 1 0 0 0 0 0 1 0 1 0 0 0 0 0 0 0 1 0 0 0 1 0 1 1 0 0 0 0 0 0 0 0 1 0 0 1 1 0 0 0 0 0 0 0 0 0 0 0 1 0 0 1 1 0 0 0 0 0 0 0 0 0 0 0 1 0 0 1 1⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎣⎡11101101001111101110101010111110101111111111011110011Hamming (16,11,4) 的生成矩阵G 1 0 0 0 0 0 0 0 0 0 0 1 0 0 1 1 0 1 0 0 0 0 0 0 0 0 0 1 1 0 1 0 0 0 1 0 0 0 0 0 0 0 0 1 1 1 1 1 0 0 0 1 0 0 0 0 0 0 0 1 1 1 0 0 0 0 0 0 1 0 0 0 0 0 0 0 1 1 1 0 0 0 0 0 0 1 0 0 0 0 0 1 0 1 0 1 0 0 0 0 0 0 1 0 0 0 0 0 1 0 1 1 0 0 0 0 0 0 0 1 0 0 0 1 0 1 1 0 0 0 0 0 0 0 0 0 1 0 0 1 1 0 0 1 0 0 0 0 0 0 0 0 0 1 0 0 1 1 0 1 0 0 0 0 0 0 0 0 0 0 1 0 0 1 1 1G = [ I k P ]k ×n =⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎣⎡1111101101100111011011110101101011011101001111111111010111110011参考文献:[1] Lin S and Costello D J. “Error Control Coding (Second Edition).” Pearson Education Inc., 2004.[2]Robert H. Morelos-Zaragoza. “The Art of Error Correcting Coding (Second Edition).” John Wiley & Sons, Ltd., 2006.[3] ETSI TS 102 361-1: "Electromagnetic compatibility and Radio spectrum Matters (ERM); Digital Mobile Radio (DMR) Systems; Part 1: DMR Air Interface (AI) protocol".V1.4.5 (2007-12)[S]。
