弹性力学及有限元法：第7章 等参数单元G2
合集下载
弹性力学的有限元求法
形态函数的几何意义
1 Ni 2A (ai bi x ci y)
1x y
Ni
11 2A
xj
yj
1 xm ym
Ni
SPJM SMIJ
Nj
SPMI SIJM
Nm
SPIJ SIJM
任意一点P的形态函数Ni是点P与结点I的对边所构 成的三角形面积与整个单元面积之比。
2.3单元载荷移置
有限元法的求解对象是单元的组合体，待求解 的未知变量都定义在单元的结点上，因此作用 在弹性体上的外力，需要移置到相应的单元结 点上成为结点载荷。
)T {P}
( xp, yp)
由于虚位移是任意的，
{R}e ([N ]
)T {P}
( xp, yp)
(2-16)
例2.3、在均质，等厚的三角形单元ijm的一点p （0.25a, 0.5a）上作用有集中载荷Px, Py。
Rxi Ni
Ryi
0
Rxj Ryj
Nj 0
Rxm
N
a1 a4
a2 a5
x x
a3 a6
y y
(2-6)
将3个结点上的坐标和位移分量代入公式（2-6） 就可以将六个待定系数用结点坐标和位移分量 表示出来。首先计算位移分量u的系数，
ui a1 a2 xi a3 yi u j a1 a2 x j a3 y j um a1 a2 xm a3 ym
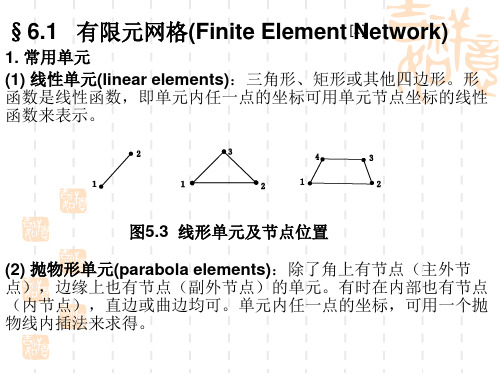
图5.4 抛物线形单元及节点位置
2. 单元划分要注意的几个问题 (1) 相邻两个单元的节点要与节点重合（外节点与外节点、内节点 与内节点），不能与无节点边重合。
( ,)
(2) 单元不必是相同尺寸，应力有突变的地方，单元划分应较小。 (3) 任何一个单元必须只能在一种材料区，即它不能跨越两种材料
弹性力学及有限单元法_河海大学中国大学mooc课后章节答案期末考试题库2023年
弹性力学及有限单元法_河海大学中国大学mooc课后章节答案期末考试题库2023年1.建立平衡微分方程时，用到了下列哪些假定（）、（）。
参考答案:连续性_小变形2.有限单元法中的单元仍然满足（）、（）、（）、（）的理想弹性体。
参考答案:完全弹性_均匀性_各向同性_连续性3.应力边界条件是指在边界上（）之间的关系式。
参考答案:应力与面力4.面力是指分布在物体的力。
参考答案:表面上##%_YZPRLFH_%##表面5.位移是指一点的移动。
参考答案:位置6.线应变（或正应变）以为正。
参考答案:伸长7.极坐标系下的几何方程有（）。
参考答案:3个8.极坐标系下的平衡微分方程有（）。
参考答案:2个9.应力是指上的内力。
参考答案:单位面积##%_YZPRLFH_%##单位截面10.地面的沉陷与地基的弹性模量无关。
（）参考答案:错误11.弹性力学问题中，仅对位移分量要求单值。
（）参考答案:错误12.在小边界上按圣维南原理列写的三个边界条件是方程。
参考答案:代数##%_YZPRLFH_%##积分13.在大边界上按精确的应力边界条件，列出的两个边界条件是方程。
参考答案:函数14.精确的应力边界条件可理解为，边界上的应力分量应等于对应的。
参考答案:面力分量15.当体力为常量时，按应力求解可简化为按求解。
参考答案:应力函数16.常体力，是指。
参考答案:体力是常量##%_YZPRLFH_%##体力等于常量##%_YZPRLFH_%##体力为常量17.体力是指分布在物体的力。
参考答案:体积内##%_YZPRLFH_%##体积18.在弹性力学中，可以应用叠加原理。
参考答案:正确19.逆解法先假设应力分量的函数形式进行求解。
参考答案:错误20.应力的量纲与面力的量纲是一样的。
参考答案:正确21.弹性力学中应力的符号与面力的符号规定，在正、负坐标面上是一致的。
参考答案:错误22.弹性力学和材料力学中关于切应力的符号规定是一样的。
参考答案:错误23.小变形假定可简化（）、（）为线性方程。
(同济大学)第1讲_弹性力学及有限元方法概述
有限元分析
的一般规律物体在空间的位置随时间的改变
对象内容
任务
对象内容
任务
概述
ANSYS 静力分析z起重机械有限元应用
整机模态分析
车辆安全性
工件淬火3.06 min 时的温度、组织分布(NSHT3D)
同济大学
同济大学
金属反挤压成型：温度分布和变化铸造成型：温度变化和气泡
速度
压力导流管分析
超音速飞行压力分布汽车气动分析
高速导弹气动
同济大学
两根热膨胀系数不同的棒焊接在一起，加热后的变形情况
子结构方法分析大型结构的早期应用法
梁单元
建模时充分利用重复性。
《弹性力学及有限元》教学大纲教程文件
《弹性力学及有限元》教学大纲《弹性力学及有限元》教学大纲大纲说明课程代码：5125004总学时：40学时（讲课32学时，上机8学时）总学分：2.5学分课程类别：必修适用专业：土木工程专业（本科）预修要求：高等数学、理论力学、材料力学课程的性质、目的、任务：本课程是土木工程专业限选修的一门专业基础课。
本课程的教学目的，是使学生在理论力学和材料力学等课程的基础上进一步掌握弹性力学的基本概念、原理和方法，了解弹性力学问题的求解思路、方法和解答，为学习相关专业课程打下初步的弹性力学基础。
在此基础上，使学生掌握有限单元法的基本概念、理论、方法，了解和应用ANSYS大型结构分析程序求解简单的弹性力学问题。
课程教学的基本要求：本课程教学环节主要包括：课堂讲授、习题课、作业、答疑、上机计算、考试。
采用课堂授课方式，重点章节安排习题课。
课后布置一定量的习题，以便掌握弹性力学与有限单元法的基本概念、原理和方法，用弹性力学的求解方法及大型结构分析有限单元程序求解简单的弹性力学问题。
考试采用开卷方式。
大纲的使用说明：本大纲适用于土木工程本科专业40课时的《弹性力学及有限元》课程.大纲正文第一章绪论学时：6学时（讲课6学时）本章讲授要点：了解弹性力学的研究内容，理解体力、面力、应力、应变和位移等基本概念，熟悉体力、面力、应力、应变、位移等力学量的记号和符号的有关规定，理解弹性力学的基本假定；了解有限单元法的发展，掌握泛函、变分和泛函极值等基本概念；了解加权残值、里兹与伽辽金等方法。
重点：弹性力学中的应力、应变和位移等基本概念；泛函、变分、驻值等基本概念；加权残值、里兹与伽辽金等方法。
难点：应力、应变；泛函、变分、驻值；加权残值法、里兹法与伽辽金法。
第一节弹性力学的内容第二节弹性力学中的几个基本概念第三节弹性力学中的基本假定第四节有限单元法的发展简介第五节变分原理.泛函.变分.驻值第六节加权残值法、里兹法与伽辽金法第二章弹性力学的基本理论学时：12学时（讲课12学时）本章讲授要点：掌握平面应力、平面应变与平面轴对称问题的特点及其它们的基本方程，了解按位移或者应力求解平面应力、平面应变与平面轴对称问题的求解思路，了解以多项式解法求解平面问题的基本思路与方法，了解以应力函数求解简支梁受均布荷载弯曲问题的思路和方法。
弹性力学及有限元法：第7章 等参数单元G2
上式写成矩阵形式
Ni x y
Ni
x
y
Ni
Ni
x
J
x
Ni
Ni
y
y
其中，J称为雅可比矩阵（Jacobian matrix）
(7.7)
x y
J
x y
(7.8)
将式(7.5)的表达式代入雅可比矩阵式(7.8)，求得雅可比矩阵。对于
荷移置的方法。假设单元作用有集中载荷F、体积力P和表面力Q
等，对上述载荷进行移植
对于集中载荷，设单元任意点c作用有集中载荷 F {Fx Fy}T
7.1 等参元的基本概念
则移置到单元有关节点上的等效节点载荷为
Fie {Fixe
Fiye}T
Ni
F
c
i 1, 2, n
对于体积力，设单元上作用的体力为 P {px py}T
表达的位移模式如下（位移插值）
n
n
u Ni , ui ,v Ni , vi n 4, 8
(7.4)
i 1
i 1
可以按照形函数的性质快速获得形函数
7.1 等参元的基本概念
（2）等参坐标变换
等参元需要用坐标变换把形状规整的母单元转换成具有曲线（面） 边界的、形状复杂的单元。转换后的单元称为子单元。子单元在几 何上可以适应实际结构的各种复杂外形。即可以采用各种形状复杂
的子单元在整体坐标系中对实际结构进行划分。映射 子单元通过坐标变换映射成一个局部坐标系下的规整的母单元。坐
标变换是指在局部坐标 ,, 和整体坐标 x, y, z 之间建立一一对应
关系。在这里，坐标变换关系 利用形函数建立起来。例如，对于上述4节点线性四边形单元，有
4
弹性力学及其有限元法
弹性力学及有限元分析1、 设试件两定点之间的长度为L 0，其截面积为F 0，加上拉力P 后，L 0 伸长了△L 。
我们把P/ F 0 称为拉伸应力（σ），△L/ L 0 称为拉伸应变（ε），于是有σ＝P/ F 0 ，ε＝ △L/ L 0某种材料的拉伸应力和拉伸应变的比，称为该材料的杨氏模量或弹性模量(E)，即 LF PL E ∆==00εσ，弹性模量E 表征了材料的物理性质。
2、 根据力学特性，固体通常分为韧性固体和脆性固体。
首先分析韧性材料，材料在受力变形过程中，明显地有四个特性点划分三各阶段。
a. 弹性阶段，这一阶段的明显特征是，当外力逐渐去掉时，变形也逐渐消失，物体能够恢复到原来的形状，物体的这种性质称为弹性，存在一个应力极限称为弹性极限。
随着外力的消失而消失的变形称为弹性变形；去掉外力后仍然保留的变形称为残余变形或永久变形。
弹性阶段另一个明显特征是，应力与应变保持线性关系。
设受力方向为x 方向，x xE εσ=，这就是简单拉伸时的虎克定律，弹性模量E 为常数，表示应力与应变成正比例。
通常把弹性极限和比例极限规定为一个值。
b. 塑性阶段，超过弹性极限后，材料开始失去弹性，进入塑性阶段，这时产生较大的永久变形，应力应变关系不再是线性的。
当曲线超过s 点（屈服极限）后，材料开始屈服，即在应力几乎不增加的情况下，应变会不断的增加，称s 点为屈服极限；当变形大到一定程度后，材料开始强化，要继续增加变形必须再增加外力，到达b 点后产生颈缩。
从弹性极限到b 的变形范围统称为塑性阶段，属于塑性力学的研究范畴。
c. 断裂阶段，试件产生颈缩后，开始失去抵抗外力的能力，最后发生断裂，相对于b点的应力称为强度极限。
脆性材料：它的拉伸曲线图没有明显的三个阶段之分，也没有明显的屈服应力点，材料亦不再满足虎克定律。
为了分析上的需要，往往以切线斜率作为弹性模量，即εσd d E =。
如果对脆性固体材料加载，应力应变曲线将沿着OA 上升，若到A 点后即行卸载，应力应变曲线并不沿着原来的途径回复到原点，而是沿着直线AB 下降，当全部载荷卸去之后，试件中尚残存一部分永久变形''ε。
弹性力学及有限元
• 研究方法的差别造成弹性力学与材料 力学问题的最大不同。
• 材料力学:常微分方程，数学求解没有困难。 • 弹性力学:偏微分方程边值问题，在数学上 求解困难重重，除了少数特殊问题，一般 弹性体问题很难得到解析解。
§1.2 弹性力学基本概念(重点) •外力、应力、形变、位移
•外力分为：体积力（体力） 表面力（面力）
3、弹性力学基本假定：
•连续性
•均匀性
•各向同性
•完全弹性
•小变形假定
（符合前四条假设的物体称为理想弹性体）
4、弹性力学的研究方法：
•已知：边界形状，材料性质，体力，面力，约束 •求解：应力、形变和位移 •解法： （1）根据力的平衡条件建立平衡微分方程； （2）根据应变和位移间的几何条件建立几何方程； （3）根据应力和应变间的物理条件建立物理方程；
——忽略位移、形变和应力等分量的高阶小 量，使基本方程成为线性的偏微分方程组。
＊弹性力学的发展
弹性力学是一门有悠久历史的学科，早期 研究可以追溯到1678年，胡克（R.Hooke） 发现胡克定律。 这一时期的研究工作主要是通过实验方法 探索物体的受力与变形之间的关系。
•近代弹性力学的研究是 从19世纪开始的。
轴正方向为正,沿坐标轴负方向为负。
单位：N/m2, 量纲是L-1MT-2(N=LT-2M)
•内力：物体受外力作用后，内部不同部分之
间相互作用的力。
应力
弹性体内任一点 P 其邻近面积为 A
A 上的内力为 F
F lim p A0 A
•和体力、面力不同，应力通常不用它沿坐标 轴的分量(进行某些公式推导时除外)，原因： 这些分量与物体的形变或材料强度没有直接的 关系。 •与物体的形变或材料强度直接相关的则是截 面法线方向和切线方向的分量，即正应力和 切应力，分别记为 σ，τ
等参数单元
(6.18)
三个节点的等效载荷为
Qi {Q
e e ix
式中, Γ是单元作用有面力的边界域, ds是边界域内的微段弧长。 在上述分析的基础上，利用结构中所有等参元的单元刚度矩阵集成 结构整体刚度矩阵。列写结构有限元方程、引入约束条件，进而进 行结构整体分析。
qx Q } Ni tds q y
6.1 等参元的基本概念 等参数单元（Isoparametric elements）简称等参元，是根据特 定方法设定的一大类单元，不一定具有相同的几何形状。因为等参 元具有规范的定义原理和较强的适应复杂几何形状的能力。在有限 元理论中占有重要的地位。采用等参元，一方面能够很好地适应曲 线边界和曲面边界，准确地模拟结构形状；另一方面，等参元一般 具有高阶位移模式，能够较好地反映结构的复杂应力分布情况，即 使单元网格划分比较稀疏，也可以得到比较好的计算精度。 等参元的基本思想是：首先导出关于局部坐标系（Local coordinate, 或Natural coordinate, 自然坐标系）的规整形状的单 元（母单元）的高阶位移模式，然后利用形函数多项式进行坐标变 换，得到关于整体坐标系(Global coordinate)的复杂形状的单元 （子单元），其中子单元的位移函数插值节点数与其位置坐标变换 的节点数相等，位移函数插值公式与位置坐标变换式都采用相同的 形函数与节点参数，这样的单元称为等参元。
x N i , xi , y Ni , yi
i 1 i 1 8 8
(6.11)
将上述等参元的位移模式代入弹性力学平面问题的几何方程，将会 得到如下形式的、用应变矩阵B表示的单元应变分量计算式
6.2 等参元的单元分析
u x x v e ε y Bδ B1 B2 y xy u v y x
弹性力学基础及有限元法-7
I t d ti of Introduction f ANSYS
3. Features of ANSYS（特点）
The individual physical field analysis such as structural, thermal, etc. and the coupled field analysis are both possible. possible Unified Database Powerful non-linear analysis Friendly interface and easy to use A strong function of the secondary development A variety of automatic meshing tools
O tli Outline 概要
1 R 1. Review i 回顾 2. ANSYS简介 3.静力学分析实例—平面桁架
Review 回顾
Finite Element Method FEM （有限元法）
1. Model and concept 模型和概念 1 2. FEM basic idea 有限元法的基本思想 3. 基本步骤 本步
Finite element method (FEM)
FEM procedure The Th body b d i is di divided id d i into some fi finite i elements. l to get the stiffness matrix of every element in th single the i l element l t analysis l i . The whole stiffness matrix is integrated from all element matrixes. matrixes To solve the equation and to obtain displacements of the nodes. nodes To draw the unknown values from the values of the nodes.
弹性力学及有限元
热传导案例
总结词
热传导是有限元分析中用于模拟物体内部热量传递规律的应用之一。
详细描述
在电子、机械、化工和材料等领域，热传导分析用于研究材料的热性能、热应力和热变形等。通过有 限元方法，可以模拟物体内部的热量传递过程，预测温度分布和热应力分布，优化材料和系统的热设 计。
06
结论展望
结论
01
02
有限元分析
有限元分析是一种数值分析方法，通过将复杂的物体或系统离散 化为有限个小的单元（或称为元素），并分析这些单元的应力、 应变和位移，从而对整个物体或系统的行为进行预测和分析。
主题的重要性
工程应用
弹性力学和有限元分析在工程领域中具有广泛的应用，如结 构分析、机械设计、航空航天、土木工程等。通过这些方法 ，工程师可以更准确地预测和分析结构的性能，优化设计， 提高安全性。
03
04
研究意义
弹性力学及有限元分析在工程 领域具有广泛应用，为复杂结 构的分析提供了有效方法。
主要成果
本文系统地介绍了弹性力学的 基本原理和有限元分析的方法 ，并通过实例验证了其有效性 。
研究限制
由于时间和资源的限制，本研 究未能涵盖所有相关领域，未 来研究可进一步拓展。
对实践的指导意义
本文为实际工程中的结构分析 提供了理论依据和实践指导， 有助于提高结构的安全性和稳 定性。
优势
有限元方法具有广泛的适用性，可以用于求解各种复杂的物理问题；能够处理 复杂的几何形状和边界条件；可以通过增加单元数目来提高解的精度；可以方 便地处理非线性问题和材料非均质性问题等。
局限性
有限元方法需要较大的计算资源和时间，尤其对于大规模问题；对于某些特殊 问题（如高速冲击、爆炸等），需要采用特殊处理方法；对于多物理场耦合问 题，需要采用多场耦合有限元方法等。
弹性力学及有限单元法
b.简化几何方程：在几何方程中，由于 (ε,γ)>>(ε,γ)2>>(ε,γ)3... ， 可 略 去 (ε,γ)2 等 项 , 使 几何方程成为线性的方程。
目录
34
§1.3 弹性力学中的基本假定 弹力基本假定，确定了弹力的研究范围:
理想弹性体的小变形问题。
目录
35
Mechanics forms the backbone of science and engineering.
Mechanics paves the foundation for the infrastructures of numerous cities in the word.
目录
5
第一章 绪 论
即应力与应变关系可用胡克定律表示（物 理线性）。
目录
31
§1.3 弹性力学中的基本假定
（3）均匀性 ─ 假定物体由同种材料组成。由 此得出 E、μ等与位置(x,y,z)无关。 （4）各向同性 ─ 假定物体各向同性。由此得 出 E、μ等与方向无关。
由（3）,（4）得出 E、μ等为常数。 符合（1）-（4）假定的称为理想弹性体。
目录
9
§1.1 弹性力学的内容
材力也考虑这几方面的条件，但不是十分严 格的：常常引用近似的计算假设（如平面截 面假设）来简化问题，并在许多方面进行了 近似的处理。
因此材力建立的是近似理论，得出的是近 似的解答。从其精度来看，材力解法只能 适用于杆件形状的结构。
目录
10
§1.1 弹性力学的内容
研究方法的差别造成弹性力学与材料力 学问题的最大不同。
目录
7
§1.1 弹性力学的内容
结构力学─在材料力学基础上研究杆系结 构(如桁架、刚架等)。
目录
34
§1.3 弹性力学中的基本假定 弹力基本假定，确定了弹力的研究范围:
理想弹性体的小变形问题。
目录
35
Mechanics forms the backbone of science and engineering.
Mechanics paves the foundation for the infrastructures of numerous cities in the word.
目录
5
第一章 绪 论
即应力与应变关系可用胡克定律表示（物 理线性）。
目录
31
§1.3 弹性力学中的基本假定
（3）均匀性 ─ 假定物体由同种材料组成。由 此得出 E、μ等与位置(x,y,z)无关。 （4）各向同性 ─ 假定物体各向同性。由此得 出 E、μ等与方向无关。
由（3）,（4）得出 E、μ等为常数。 符合（1）-（4）假定的称为理想弹性体。
目录
9
§1.1 弹性力学的内容
材力也考虑这几方面的条件，但不是十分严 格的：常常引用近似的计算假设（如平面截 面假设）来简化问题，并在许多方面进行了 近似的处理。
因此材力建立的是近似理论，得出的是近 似的解答。从其精度来看，材力解法只能 适用于杆件形状的结构。
目录
10
§1.1 弹性力学的内容
研究方法的差别造成弹性力学与材料力 学问题的最大不同。
目录
7
§1.1 弹性力学的内容
结构力学─在材料力学基础上研究杆系结 构(如桁架、刚架等)。
七不可(或接近不可)压缩弹性力学问题的有限单元法
m mm mm 偏斜应变： ε d = ε − ~ ε v = ε − ~ ~ ε = ( I − ~ ~ ) ε ~ 3 ~ ~ 3 ~ ~ ~ 3
σ d 和 ε d 之间存在如下关系
T T
T
T
~
~
2 mm T T ) ε = G (C0 − m m ) ε σ d = G C0 ε d = G C0 ( I − ~ 3 ~ ~ 3~~ ~ ~ ~ ~ ~
对三维问题 d1 ＝5， 对轴对称问题 d1 ＝3， 对平面应变问题 d1 ＝2，
不可（或接近不可）压缩弹性力学问题 一般网格情况的单元形式和积分方案：
• 对
K 只给予必要的刚体运动约束，
~
• 对于
K 2 奇异性，则应给网格加以更多的约束，
~
通常采用一种简单的方法估算 K 2 的奇异性。 如下图，在已有的二维网格基础上增加一个单元。
上式可理解为：对偏斜应变能部分采用最小位能原理， 对体积应变能采用H-R变分原理相结合的泛函。
对上式进行有限元离散，且
u = Nu a ~ ~~
e
p = Np b ~~
e
N u 和 N p 分别是对位移和压力的插值函数， ~ ~
a 和b ~ ~
e
e
分别是单元的结点位移和结点压力向量，
u 将上式代入 Πp (u, p) 并对 Πp (~, p) 变分， ~
Sσ
∫T ~
T
u ds ~
偏斜应变能
1 应变能 2 σε
体积应变能
应力和应变均可分为各自的两部分
1.应力， 已知： p = −
σx +σ y +σz
3
= [1 1 1
m =−~ σ 3 ~
σ d 和 ε d 之间存在如下关系
T T
T
T
~
~
2 mm T T ) ε = G (C0 − m m ) ε σ d = G C0 ε d = G C0 ( I − ~ 3 ~ ~ 3~~ ~ ~ ~ ~ ~
对三维问题 d1 ＝5， 对轴对称问题 d1 ＝3， 对平面应变问题 d1 ＝2，
不可（或接近不可）压缩弹性力学问题 一般网格情况的单元形式和积分方案：
• 对
K 只给予必要的刚体运动约束，
~
• 对于
K 2 奇异性，则应给网格加以更多的约束，
~
通常采用一种简单的方法估算 K 2 的奇异性。 如下图，在已有的二维网格基础上增加一个单元。
上式可理解为：对偏斜应变能部分采用最小位能原理， 对体积应变能采用H-R变分原理相结合的泛函。
对上式进行有限元离散，且
u = Nu a ~ ~~
e
p = Np b ~~
e
N u 和 N p 分别是对位移和压力的插值函数， ~ ~
a 和b ~ ~
e
e
分别是单元的结点位移和结点压力向量，
u 将上式代入 Πp (u, p) 并对 Πp (~, p) 变分， ~
Sσ
∫T ~
T
u ds ~
偏斜应变能
1 应变能 2 σε
体积应变能
应力和应变均可分为各自的两部分
1.应力， 已知： p = −
σx +σ y +σz
3
= [1 1 1
m =−~ σ 3 ~
弹性力学_第7章_平面问题的有限单元法
Sc
(d* )T p {ε* }T σdxdy {δ* }T F L
5. 建立有限单元法的基本方程： 在各个节点处，列出内力和外力的平衡方程，就得到有限 单元法的总体劲度方程
Kδ FL
其中：K FL
— 总体劲度矩阵， — 位移列阵，各个节点的位移， — 荷载列阵，将荷载化为节点力列阵
《弹塑性力学》课件
内容提要 平 面 问 题 的 有 限 单 元 法
2012/5/10
§7-1 §7-2 §7-3 §7-4 §7-5 §7-6 §7-7
基本量及基本方程的矩阵表示 有限单元法的概念 单元的位移模式与解答的收敛性 单元的应变列阵和应力列阵 单元的结点力列阵与劲度矩阵 载荷向结点移置 等效节点荷载 结构的整体分析 节点平衡方程组
有限单元法的基本解题步骤为： 1. 划分单元； 2. 建立位移模式。即建立单元内任一点位移与节点位移之间的 关系，设三角形单元三个节点的位移分别为：(ui,vi), (uj,vj), (um,vm)，三角形单元任何一点的位移 u 与 v用结点位移表示。 ui ui 结点位移列阵 v u [ N , N , N ] i i j m u j δi u j um 人为设计 δe δ j δ v j 的表达式。 v i m u m v [ N i , N j , N m ]v j v m v m 这种表示是人为设计的，每种单元都有不同表示方法，本 课程仅讲三结点三角形单元。
2 56
1、有限元法（Finite Element Method）
简称FEM，是弹性力学的一种近似解法。 首先将连续体变换为离散化结构，然后再利用分片插值技术与虚功原 理或变分方法进行求解。
(d* )T p {ε* }T σdxdy {δ* }T F L
5. 建立有限单元法的基本方程： 在各个节点处，列出内力和外力的平衡方程，就得到有限 单元法的总体劲度方程
Kδ FL
其中：K FL
— 总体劲度矩阵， — 位移列阵，各个节点的位移， — 荷载列阵，将荷载化为节点力列阵
《弹塑性力学》课件
内容提要 平 面 问 题 的 有 限 单 元 法
2012/5/10
§7-1 §7-2 §7-3 §7-4 §7-5 §7-6 §7-7
基本量及基本方程的矩阵表示 有限单元法的概念 单元的位移模式与解答的收敛性 单元的应变列阵和应力列阵 单元的结点力列阵与劲度矩阵 载荷向结点移置 等效节点荷载 结构的整体分析 节点平衡方程组
有限单元法的基本解题步骤为： 1. 划分单元； 2. 建立位移模式。即建立单元内任一点位移与节点位移之间的 关系，设三角形单元三个节点的位移分别为：(ui,vi), (uj,vj), (um,vm)，三角形单元任何一点的位移 u 与 v用结点位移表示。 ui ui 结点位移列阵 v u [ N , N , N ] i i j m u j δi u j um 人为设计 δe δ j δ v j 的表达式。 v i m u m v [ N i , N j , N m ]v j v m v m 这种表示是人为设计的，每种单元都有不同表示方法，本 课程仅讲三结点三角形单元。
2 56
1、有限元法（Finite Element Method）
简称FEM，是弹性力学的一种近似解法。 首先将连续体变换为离散化结构，然后再利用分片插值技术与虚功原 理或变分方法进行求解。
弹性力学与有限元分析98页PPT
➢ 当物体的厚度有突变或物体由不同材料组成时，不 要把厚度不同或材料不同的区域划分在统一单元。
➢ 节点编号，原则上可任意，但它影响基本方程系数 矩阵的带宽，所以单元的两个相邻节点编号之差 应尽可能小。
五、位移插值函数与形函数
结构离散化后，要对单元进行力学特性分析，即 确定单元节点力与节点位移之间的关系。为分析并确 定这一关系，需要把单元中任一点的位移分量表示为 坐标的某种函数，这一函数称为单元的位移插值函数。 它反映了单元的位移形态并决定着单元的力学特性。 由于这种函数关系在解题前是未知的，而在单元分析 时又必须用到，因此要事先假定，所假定的位移插值 函数须满足以下两个条件：
二、有限元法的分类与求解步骤
从选择基本未知量的角度来看，有限元法分为以下三类： ❖ 位移法——以节点位移作为基本未知量 ❖ 力法——以节点力作为基本未知量 ❖ 混合法——取一部分节点位移和一部分节点力作为
基本未知量 由于位移法比较简单，计算规律性强，便于编写 计算机通用程序，因此在用有限元法进行结构分析时，
弹性力学与有限元分析
41、实际上，我们想要的不是针对犯 罪的法 律，而 是针对 疯狂的 法律。 ——马 克·吐温 42、法律的力量应当跟随着公民，就 像影子 跟随着 身体一 样。— —贝卡 利亚 43、法律和制度必须跟上人类思想进 步。— —杰弗 逊 44、人类受制于法律，法律受制于情 理。— —托·富 勒
1、平面应力问题
在这类问题的应力分量中，凡带某一脚标的（如z） 都为零。其特点是： 几何形状特点：物体在一个方向（如z向）上的尺寸远
小于其他两个方向的几何尺寸，如薄 板。 所受外力特点：在薄板的两Z个侧面上无面力作用，只 在其边缘受到平行于板面且沿板厚均 匀分布的面力（面力分量中Z 0 ）作 用，同时体力也平行于板面且不沿板 厚变化（体力分量中Z0）。
弹塑性力学与有限元-等参元数值分析
《弹塑性力学与有限元》
弹塑性力学与有限元 —等参元和数值积分
等参元和数值积分
等参元和数值积分
等参元
➢ 等参单元的基本概念和单元矩阵的变换 ➢ 等参变换的条件和等参元的收敛性 ➢ 等参元用于分析弹性力学问题的一般格式
数值积分
➢ 数值积分方法 ➢ 等参元计算中数值积分阶次的选择
《弹塑性力学与有限元》
x a 2 b c
y d 2 e f
（4-13）
可见在整体坐标系中，单元的边是一条抛物线或退化为一条直线。
《弹塑性力学与有限元》
等参元和数值积分
等参单元的矩阵变换
图4-6 ANSYS提供的Plane82单元
《弹塑性力学与有限元》
等参元和数值积分
等参单元的矩阵变换
如图4-6所示，ANSYS提供的PLANE82单元是一个四边形八结 点等参单元，局部坐标定义为s和t，如图4-7所示。PLANE82单元可 以退化为三角形六结点单元。
《弹塑性力学与有限元》
等参元和数值积分
等参单元的基本概念和单元矩阵的变换
形函数为，
1x y
Ni
(1 4
)(1 a
) b
Nj
1 (1 4
x )(1 y ) ab
Nm
1 (1 4
x )(1 a
y) b
Np
1 (1 4
x )(1 a
y) b
上述单元位移模式满足位移模式选择的基本要求：反映了单元的刚体位
因此给出任意四边形单元的结点位移就能得到整个单元上的位移，上 式给出的位移模式就是所要找的正确的位移模式。把局部坐标与整体坐 标的变换式也取为:
x N1x1 N2 x2 N3x3 N4 x4 （4-8） y N1 y1 N2 y2 N3 y3 N4 y4
弹塑性力学与有限元 —等参元和数值积分
等参元和数值积分
等参元和数值积分
等参元
➢ 等参单元的基本概念和单元矩阵的变换 ➢ 等参变换的条件和等参元的收敛性 ➢ 等参元用于分析弹性力学问题的一般格式
数值积分
➢ 数值积分方法 ➢ 等参元计算中数值积分阶次的选择
《弹塑性力学与有限元》
x a 2 b c
y d 2 e f
（4-13）
可见在整体坐标系中，单元的边是一条抛物线或退化为一条直线。
《弹塑性力学与有限元》
等参元和数值积分
等参单元的矩阵变换
图4-6 ANSYS提供的Plane82单元
《弹塑性力学与有限元》
等参元和数值积分
等参单元的矩阵变换
如图4-6所示，ANSYS提供的PLANE82单元是一个四边形八结 点等参单元，局部坐标定义为s和t，如图4-7所示。PLANE82单元可 以退化为三角形六结点单元。
《弹塑性力学与有限元》
等参元和数值积分
等参单元的基本概念和单元矩阵的变换
形函数为，
1x y
Ni
(1 4
)(1 a
) b
Nj
1 (1 4
x )(1 y ) ab
Nm
1 (1 4
x )(1 a
y) b
Np
1 (1 4
x )(1 a
y) b
上述单元位移模式满足位移模式选择的基本要求：反映了单元的刚体位
因此给出任意四边形单元的结点位移就能得到整个单元上的位移，上 式给出的位移模式就是所要找的正确的位移模式。把局部坐标与整体坐 标的变换式也取为:
x N1x1 N2 x2 N3x3 N4 x4 （4-8） y N1 y1 N2 y2 N3 y3 N4 y4
弹性力学及有限元法chapter7精品PPT课件
e
i
j
m
v
j
w j
u
m
i
m
p
vm
wm
j y
u
p
x
vp
w p
第七章 空间问题和空间轴对称问题
7-2-1 位移函数
单元内任一点的位移 {f}假定为座标的线性函数
u
f
v
N
e
w
u 1 2x3y 4z v 5 6x7 y 8z w9 10x 11y 12z
节点i, j, m及 p的坐标分别为(xi,yi,zi),(xj,yj,zj),(xm,ym,zm) 及 (xp,yp,zp)，把它们代入上式的第一式，得出各节点在x方 向的位移
第七章 空间问题和空间轴对称问题
ui 1 2 xi 3 yi 4 zi u j 1 2x j 3 y j 4z j um 1 2 xm 3 ym 4 zm up 1 2xp 3 yp 4zp
解方程组，求得 1,2,3,4，代入第一式，整理后得到
u N iu i N ju j N m u m N p u p
其中
Ni 61 Vaibixciydiz
N j 6 1 Vajbjxcjydjz
Nm61 Vambmxcmydmz
Np61 Vapbpxcpydpz
称为形函数，其系数是
第七章 空间问题和空间轴对称问题
xj yj zj ai xm ym zm
xp yp zp
1 xj zj ci 1 xm zm
同样，可以得到
vNivi Njvj NmvmNpvp wNiwi Njwj NmwmNpwp
单元内任一点的位移可以写成如下形式：
f N 0 i N 0 i 0 0
七不可(或接近不可)压缩弹性力学问题的有限单元法
体积应变能
采用Lagrange乘子法，得到下面修正泛函：
2 T 1 2 1 T p T T Πp(u, p, λ) = ∫[ ε G(C0− mm )ε + p ]dv+ ∫ λ(εv + )dv− ∫ f udv− ∫T uds ~ 2 ~ ~ 3 ~ ~ ~ 2k k ~ ~ Sσ ~ ~ V V V
r >1是奇异性的必要条件。但为了使方程度解保持良好的 精度，理想的单元和积分方案应使 r=2~3。 一般建议采用(a)、 (b)和(d)，而避免采用(c) 。
另一方面，为保证 K 的非奇异性，建议在计算 K1 时， ~
~
• 对于(a)中的6结点单元采用3或4点的Hammer积分； • 对于(b)中的4结点单元采用2×2点的Gauss积分； • 对于(d)中的9结点单元采用3×3点的Gauss积分。
得到有限元求解方程
⎡ Kuu − Kup ⎤⎧a⎫ ⎧P⎫ ~ ⎥⎪~⎪ = ⎪~⎪ ⎢ ~ T ⎢− Kup − Kpp⎥⎨b⎬ ⎨0 ⎬ ⎪~⎪ ⎪~⎪ ⎢ ~ ⎥⎩ ⎭ ⎩ ⎭ ~⎦ ⎣
其中，
2 K uu = ∑ ∫ G B (C0 − m mT ) B dv ~ ~ 3~ ~ ~ ~ e Ve
Sσ
∫T ~
T
u ds ~
偏斜应变能
1 应变能 2 σε
体积应变能
应力和应变均可分为各自的两部分
1.应力， 已知： p = −
σx +σ y +σz
3
= [1 1 1
m =−~ σ 3 ~
0 0 0]
T
p 是平均压应力，
m ~
T
2.应变， 已知： ε v = ε x + ε y + ε z = m ε ~ ~
采用Lagrange乘子法，得到下面修正泛函：
2 T 1 2 1 T p T T Πp(u, p, λ) = ∫[ ε G(C0− mm )ε + p ]dv+ ∫ λ(εv + )dv− ∫ f udv− ∫T uds ~ 2 ~ ~ 3 ~ ~ ~ 2k k ~ ~ Sσ ~ ~ V V V
r >1是奇异性的必要条件。但为了使方程度解保持良好的 精度，理想的单元和积分方案应使 r=2~3。 一般建议采用(a)、 (b)和(d)，而避免采用(c) 。
另一方面，为保证 K 的非奇异性，建议在计算 K1 时， ~
~
• 对于(a)中的6结点单元采用3或4点的Hammer积分； • 对于(b)中的4结点单元采用2×2点的Gauss积分； • 对于(d)中的9结点单元采用3×3点的Gauss积分。
得到有限元求解方程
⎡ Kuu − Kup ⎤⎧a⎫ ⎧P⎫ ~ ⎥⎪~⎪ = ⎪~⎪ ⎢ ~ T ⎢− Kup − Kpp⎥⎨b⎬ ⎨0 ⎬ ⎪~⎪ ⎪~⎪ ⎢ ~ ⎥⎩ ⎭ ⎩ ⎭ ~⎦ ⎣
其中，
2 K uu = ∑ ∫ G B (C0 − m mT ) B dv ~ ~ 3~ ~ ~ ~ e Ve
Sσ
∫T ~
T
u ds ~
偏斜应变能
1 应变能 2 σε
体积应变能
应力和应变均可分为各自的两部分
1.应力， 已知： p = −
σx +σ y +σz
3
= [1 1 1
m =−~ σ 3 ~
0 0 0]
T
p 是平均压应力，
m ~
T
2.应变， 已知： ε v = ε x + ε y + ε z = m ε ~ ~
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
体坐标是连续的，且在公共节点上具有相同的坐标，即相邻单元是
连续的。
（3） 两种坐标系的关系——雅可比矩阵（Jacobian matrix）
局部坐标系和整体坐标系之间具有如下偏导数的关系。根据复合
函数的求导法则，有 Ni Ni x Ni y Ni y
(7.6)
x y z
7.1 等参元的基本概念
式(7.5a)表示的双线性四边形单元，有
x
4 i1
Ni
,
Hale Waihona Puke xi,y
4 i1
Ni
,
yi
(7.9)
7.1 等参元的基本概念
因为
y
J 1
1
J
x
y
x
(7.10)
所以
x
J
1
(4)按等参元y思 想进行载 荷移置
(7.11)
以下以具有n个节点的平面单元为例，说明按等参元思想进行载
等参元的基本思想是：首先导出关于局部坐标系（Local coordinate, 或Natural coordinate, 自然坐标系）下的规整形状的 单元（母单元）的高阶位移模式，然后利用形函数多项式进行坐标 变换，得到关于整体坐标系(Global coordinate)的复杂形状的单元 （子单元），其中子单元的位移函数插值节点数与其位置坐标变换 的节点数相等，位移函数插值公式与位置坐标变换式都采用相同的 形函数与节点参数，这样的单元称为等参元。
y Ni , yi N1 , y1 N2 , y2 N8 , y8
i1
其中，Ni,是用局部坐标表示的形函数，xi, yi 是节点i的整体坐标上式即
为平面坐标变换公式。
如图7-1和图7-2所示的二维单元的平面坐标变换，其中母单元是
正方形，子单元变换成曲边四边形，且相邻子单元在公共边上的整
表达的位移模式如下（位移插值）
n
n
u Ni , ui ,v Ni , vi n 4, 8
(7.4)
i 1
i 1
可以按照形函数的性质快速获得形函数
7.1 等参元的基本概念
（2）等参坐标变换
等参元需要用坐标变换把形状规整的母单元转换成具有曲线（面） 边界的、形状复杂的单元。转换后的单元称为子单元。子单元在几 何上可以适应实际结构的各种复杂外形。即可以采用各种形状复杂
N , 1, ,,1 2
2
22
1 1
3 4
3 4
33 44
(7.1)
代入节点坐标值
Ni
1 0 10
4
（i=1, 2, 3, 4）
(7.2)
由于采用了等参元（自然坐标系），因而可以写出较为简洁 的形函数表达式
7.1 等参元的基本概念
其中0 ，i0.该形i函 数是定义成自然坐标下的归一化变量 的
的子单元在整体坐标系中对实际结构进行划分。映射 子单元通过坐标变换映射成一个局部坐标系下的规整的母单元。坐
标变换是指在局部坐标 ,, 和整体坐标 x, y, z 之间建立一一对应
关系。在这里，坐标变换关系 利用形函数建立起来。例如，对于上述4节点线性四边形单元，有
4
x Ni , xi N1 , x1 N2 , x2
7.1 等参元的基本概念
（a）母单元
（b）子单元
图7-1 线性矩形单元及其平面坐标变换
（a）母单元
（b）子单元
图7-2 二次矩形单元
7.1 等参元的基本概念
对于如图7-1所示的线性4节点四边形等参元（Bilinearisoparametric
element），它在局部坐标系形函数如下：
1 1 1 11 1
i1
4
y Ni , yi N1 , y1 N2 , y2
i1
N4 , x4 N4 , y4
(7.5a)
7.1 等参元的基本概念
对于上述8节点二次四边形单元，有
8
x Ni , xi N1 , x1 N2 , x2 N8 , x8
i1 8
已知自然坐标，求整体坐标；已知整体坐标，求自然坐标 (7.5b)
第七章 等参数单元
第7章 等参数单元
本章概述
本章主要介绍等参数单元的基本概念及应用方法。具体讨论 了4节点四边形等参元、8节点二次四边形等参元的单元分析方法。 针对等参元积分计算的需求，对高斯数值积分法也进行了简要介 绍。
第7章 等参数单元
7.1 等参元的基本概念
等参数单元（Isoparametric elements）简称等参元，是根据特 定方法设定的一大类单元，不一定具有相同的几何形状。等参元具 有规范的定义原理和较强的适应复杂几何形状的能力。在有限元理 论中占有重要的地位。采用等参元，一方面能够很好地适应曲线边 界和曲面边界，准确地模拟结构形状；另一方面，等参元一般具有 高阶位移模式，能够较好地反映结构的复杂应力分布情况，即使单 元网格划分比较稀疏，也可以得到比较好的计算精度。
上式写成矩阵形式
Ni x y
Ni
x
y
Ni
Ni
x
J
x
Ni
Ni
y
y
其中，J称为雅可比矩阵（Jacobian matrix）
(7.7)
x y
J
x y
(7.8)
将式(7.5)的表达式代入雅可比矩阵式(7.8)，求得雅可比矩阵。对于
函数。 ,
对于8节点二次四边单元，角点上的形函数为
Ni
1 4
1 0 10 0
0
1
（i=1, 2, 3, 4）
(7.3a)
边中点上的形函数为
Ni
1 2
1
2
1
0
（i = 5, 7）
（7. 3b）
Ni
1 2
1
2 1
0
（i = 6, 8）
（7.3c）
可见，线性四边形单元和8节点二次四边单元用局部坐标形函数
7.1 等参元的基本概念
下面以平面四边形单元为例说明等参元的基本概念。 (1) 局部坐标系下的位移模式 根据形函数的定义，在局部坐标系中，建立起几何形状简单且规整 的单元，称之为母单元。
母单元是 , 平面中的2×2正方形，1 1 1 1 ，如图7-1所示，
坐标原点在单位形心上。单元边界是四条直线： 1 1 为保证用形函数定义 的未知量在相邻单元之间的连续性， 单元节点数目应与形 函数阶次相适应。 对于具有线性形函数的四边形单元，共有四个节点，如图7-1所示。 如果是二次函数的四边形单元，单元每边的节点数为三个，如图7-2。
荷移置的方法。假设单元作用有集中载荷F、体积力P和表面力Q
等，对上述载荷进行移植