第三节_伽利略变换
3、伽利略变换

3、伽利略变换1、惯性系:力学的发展经牛顿总结成动力学三定律,牛顿三定律及其导出的各定理在伽利略变换下,对所有惯性系都有相同形式。
这一表述通常称为力学相对性原理,伽利略变换不同惯性系的时空变换导出基于两个基本假定:一是相对性原理,另一个是时间和尺长在不同惯性系是相同的。
惯性系族:相对作匀速运动的所有惯性系称为惯性系族设惯性系S 相对惯性系S 是同族惯性系,惯性系时空的均匀性决定了同一事件点在惯性系S 与S 中对应坐标矢()t z y x ,,,=r 与()t z y x ,,,=r 满足如下线性关系:t a z a y a x a t t a z a y a x a z t a z a y a x a y t a z a y a x a x 44434241343332312423222114131211+++=+++=+++=+++=(1-1)t a z a y a x a t t a z a y a x a z t a z a y a x a y t a z a y a x a x 44434241343332312423222114131211'+'+'+'='+'+'+'='+'+'+'='+'+'+'= (1-2)即Ar r = , r A r 1-=惯性系空间的各向同性要求同一个惯性系在空间转动下不变,也即惯性系的空间是Euclid 空间,为了适当简化推导过程我们选择t 在S 系的空间投影为S 系的x 轴,同样选择t 在S 系的空间投影为S 系的x 轴,各自建立正交性的时空坐标,也即有z z t y y t x x t x )()()(⋅+⋅+⋅=μ(2-1)z z t y y t x x t x )()()(⋅+⋅+⋅='μ(2-2)在(2-1)式两边同时点乘y 或z ,由时空标架的正交性易得0=y t ⋅,0=z t ⋅于是 042=a ,043=a ;042=a ',043='a 同理0=y t ⋅,0=z t ⋅024=a ,034=a ;024='a ,034='a t x t 4441a a += (3-1) t x t 4414a a '+'=(3-2)在(3-1)两边点乘y 或z 可得0=y x ⋅,0=z x ⋅即021=a ,031=a ;021=a ',031=a ' 在(3-2)两边点乘y 或z 可得0=y x ⋅,0=z x ⋅012=a ,013=a ;012=a ',013=a ' 综上即有ta x a t t a x a x 44411411+=+=za y a z z a y a y 33322322+=+=即S 系到S 系的线性变换可分解为x -t 到x -t 的变换与y -z 到y -z 的变换。
伽利略变换

X1,Y1, Z1,t Y X1,Y1, Z1,t
y y u z z
X 2,Y2, Z2,t X 2 ,Y2, Z2 ,t
P
ut
x
X
O
X
x
Z
r 2 x2 y2 z2
所有惯性系中,空间任意两点的距离相等。
长度测量的绝对性
绝对时空观:时间的量度和空间的量度都与参照系无关, 时间与空间无关,时间、空间与物质运动无关。
t A
L 2
ut A
c u
2020/3/21
t tB tA 0 S系中观察光也同时到达A’、B’
tB
L 2c
t A
L 2c
2020/3/21
1
2020/3/21
二 十 世 纪 最 伟 大 的 科 学 家
2
第五章 狭 义 相 对 论
5.1 伽利略变换 5.2 狭义相对论基本假设 5.3 狭义相对论的时空观 5.4 洛仑兹变换 5.5 狭义相对论动力学简介 5.6 四维时空(*)
2020/3/21
3
§5.1 伽利略相对性原理和伽利略变换
O
是绝对的。
Z
O
Z
x
X
S系中: x x x ut x ut
S’系中: x x x ut x ut
x x ut
x x ut
S S y y
S S y y
z z
z z
t t
坐标变换
t t
2020/3/21
7
x x ut
Y
y y
z z
O
t t
Z
r2 x2 y2 z2
2020/3/21
8
x x ut
伽利略变换 公式推导

伽利略变换公式推导摘要:1.引言2.伽利略变换的定义和意义3.坐标系的选取和变换4.伽利略变换的公式推导5.实例分析6.结论正文:【引言】在经典力学中,伽利略变换是一种非常重要的数学工具,它描述了在不同惯性参考系中物理规律的相对性。
本文将详细介绍伽利略变换的定义、公式推导及实例分析。
【坐标系的选取和变换】在讨论伽利略变换之前,我们先了解一下坐标系的概念。
坐标系是用来描述物体运动状态的工具,选取合适的坐标系可以简化问题。
设有两个惯性坐标系S和S",其中S为原始坐标系,S"为变换后的坐标系。
【伽利略变换的定义和意义】伽利略变换是基于相对性原理推导出来的,它表示在两个惯性坐标系中物理规律的相互关系。
伽利略变换的意义在于揭示了物理规律的相对性,即物理规律在任何惯性坐标系中都是相同的。
【伽利略变换的公式推导】设有一物体在坐标系S中的坐标为(x,y,z),在坐标系S"中的坐标为(x",y",z")。
根据伽利略变换的定义,我们有以下关系:x" = γ(x - vt)y" = γ(y - vt)z" = γ(z - vt)其中,γ表示洛伦兹因子,v为S和S"之间的相对速度。
【实例分析】以电磁波为例,设电磁波在坐标系S中的频率为f,传播速度为c。
在坐标系S"中,电磁波的频率为f",传播速度为c"。
根据伽利略变换,我们有:f" = f / γc" = c * γ【结论】伽利略变换是描述惯性坐标系中物理规律相对性的重要工具,通过选取合适的坐标系,可以简化问题的求解。
通过本文的介绍,希望大家能够更好地理解伽利略变换的定义、公式及应用。
经典力学时空观伽利略变换.

5
与经典力学相对应的变换就是伽利略变换。
三、经典的时空观
时间是绝对的,空间是绝对的,时间和空间是 彼此独立,没有任何联系。从而同时也是绝对的。 绝对空间是指长度的量度与参照系无关,绝对时 间是指时间的量度与参照系无关。 同样两点的距离或同样的前后两个事件之间的 时间间隔无论在哪个惯性系中测量都是一样的,而 且时间和空间是彼此独立、没有任何联系的。
经典力学时空观 伽利略变换
1
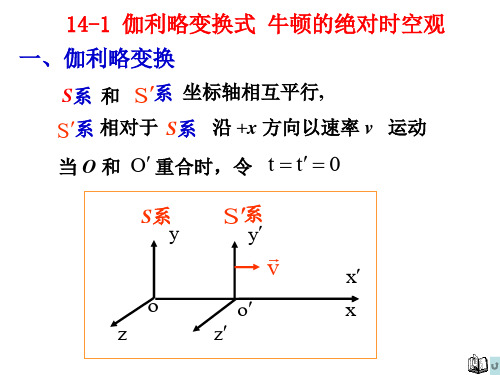
一、伽利略变换
设有两个参照系S系和S’系,各 坐标轴相互平行。 S’ 系相对S系沿 ox 轴以 u 运动。
坐标轴原点O与O’点重合时作为公共计 t 0时两坐标重合 x x' 0 时起点。 t时刻,物体在P点(看成一事件)
S
S'
y
o z
y'
u
o'
P
x x'
z'
2
1)伽利略坐标变换 正变换 逆变换
S
y
o
S'
y'
o' z'
x' x ut
y' y z' z t' t
2)伽利略速度变换
x x'ut y y' z z' t t'
逆
u P
x
x'
z
正
vx ' vx u
vy ' vy
vx vx 'u
vz ' vz
S F m a F ma 经典时空中牛顿第二定 S F m a F ma 律适用于任何惯性系。
1-5伽利略变换

运 动 描 述 的 相 对 性
伽利略(1566-1642)
意大利物理学家
§1-5 运动描述的相对性 伽利略坐标变换
一、伽利略坐标变换式 设 k ´ 相对于 k 沿 x 轴以速度 v 运动 y x ´= x v t y ´= y z ´= z t ´= t k z k´ vt
O
y´ v x´
O´
.P
x´ x
结束
z´
x
返回
伽利略坐标变换式 x = x ´+ v t x ´= x v t 逆 y y 正 y´ y = ´ = 变 z z 变 z´ z = ´ = 换 t = t´ 换 t ´= t 二、经典力学的时空观 在伽利略坐标变换式中 t = t ´ 这表明时 间的测量与坐标系无关。 间的测量与坐标系无关。即在不同参照系中 测量运动过程的时间是相同的。 测量运动过程的时间是相同的。 这一结论称为时间的绝对性。 这一结论称为时间的绝对性。
O
k´
y´ v
O´
vk ´
θ vk
x´
v x
vk = vk´ + v tg θ = v vk
或写成: 或写成:
vAk = v ´ + vk´k Ak
结束
返回
vAk = v ´ + vk´k Ak 例: v雨 , 地 = v雨 ,车 + v车 , 地 v 雨 ,车 v 雨 ,地 v 车 ,地 v车 ,地
返回
结束
三、速度变换 y k z z´ x ´= x v t y ´= y z ´= z t ´= t
O
y´ v k´
O´
x d x´ = dt dy´ = dt d z´ = dt
伽利略变换 公式推导

伽利略变换公式推导摘要:1.伽利略变换的概念2.伽利略变换的公式推导3.伽利略变换的应用正文:一、伽利略变换的概念伽利略变换,是物理学中一种描述不同惯性参考系下物体运动规律的坐标变换。
在经典力学中,伽利略变换主要用于研究在惯性参考系中运动的物体,在非惯性参考系中的运动规律。
这种变换方式由意大利物理学家伽利略提出,被广泛应用于经典力学和相对论的研究中。
二、伽利略变换的公式推导伽利略变换的公式推导过程如下:假设有一个物体在惯性参考系S 中运动,其速度为v,经过时间t 后,物体的位移为x。
现在我们考虑在非惯性参考系S"中观察该物体的运动。
在惯性参考系S 中,物体的位移可以表示为:x = vt。
在非惯性参考系S"中,由于存在加速度a,物体的位移需要考虑加速度的影响。
假设物体在S"系中的初速度为v",经过时间t"后,物体的位移为x"。
根据物理学的速度叠加原理,我们可以得到:x" = v"t" + 1/2 * a * t"^2.由于在非惯性参考系S"中,物体的初速度v"和加速度a 与惯性参考系S中的速度v 和时间t 之间存在关系。
根据伽利略变换的定义,我们可以得到:v" = v - a * t,a = a" - v^2 / r,其中,a"表示非惯性参考系S"中的加速度,r 表示物体在S 系中的半径。
将上述关系代入x"的公式中,我们可以得到伽利略变换的公式:x" = v(t - t") - 1/2 * (a" - v^2 / r) * (t - t")^2。
这就是伽利略变换的公式推导过程。
三、伽利略变换的应用伽利略变换在物理学中有广泛的应用,例如:1.研究在非惯性参考系中的物体运动,如地球表面附近自由落体的运动规律;2.在相对论中,伽利略变换是描述不同惯性参考系下物体运动规律的基础,是构建洛伦兹变换和闵可夫斯基变换的基础;3.在卫星导航系统中,由于卫星的运动速度非常快,需要考虑非惯性参考系下的物体运动规律,因此伽利略变换在卫星导航系统中有重要的应用。
力学相对性原理伽利略变换PPT课件

2.X射线:1895年,德国,伦琴
1901年获第一个诺贝尔物理奖
3.放射性:1896年,法国,贝克勒尔发现铀,居里 夫妇发现钋和镭,共同获得1903年诺贝尔物理奖
物理学还存在许多未知领域,有广阔的发展前景。
两朵乌云——暴风骤雨——20世纪初物理学危机
物理学正在临产中,它孕育着的新理论将要诞生了。
新理论:相对论、量子力学,
当物体运动时,两端坐标必须同时记录。
xA( t1 )
xB( t0 )
x (t ) A0
xB( t0 )
S系 S系
y y
u
o o x1
x x2 x
由伽利略变换:
x1 x1 ut1 x2 x2 ut2
设直尺相对于S系静止 直尺长度 x x2 x1 x2 x1 u( t2 t1 )
先验框架
• 时间间隔、空间距离的测量与参考系的选择无关。
四 . 力学相对性原理与伽利略变换相协调
要求力学定律在 是否协调 给出不同惯性
一切惯性系中数
系中对运动描
学形式相同
? 述的关联
由伽利略速度变换
得加速度变换:
a x ax a y ay az az
a
ห้องสมุดไป่ตู้
a
vx vx u
正变换
vv''xy
vx vy
u
v'z vz
逆变换
v v
x y
v'x v 'y
u
vz
v 'z
伽利略变换中已经隐含了时空观念 三 . 绝对时空观
1. 时间:用以表征物质存在的持续性,物质运动、 变化的阶段性和顺序性。
伽利略变换(课堂PPT)

O,O 重合时,t t 0 计时开始。 4
正变换:
x'xut y' y
z'z t't
r ' r u t
s y s'
y y'
ut
y'
u
x'
逆变换:
o
z z
o' z' z'
x
x x ut
y y z z
r r 'u t
t t
P(x, y, z) *(x', y', z')
x' x
解: 选定风为研究对象,摩托车(人)为运动参考系, 地面为基本参考系
绝对速度为: 风对地
相对速度为: 风对人 ' 满v 足 v ' u :
牵连速度为: 人对 地 u
16
由vv' u可得:
第一次:
y (北)
u v 1 v u '1 i u 11 i m 0 s 1
B 60 A
o'
o
平板车参考系为 S ' 系
r
r
相对运动:
O O
(x, y, z,t)
P
x
x
物体相对运动参考系(S’系)的运动.
牵连运动: S’系相对S系的运动.
牵u
12
2.伽利略速度变换
绝对速度
v绝
对
dr dt
yS
r r 'u t
y S (x, y, z,t)
相对速度 v相对ddrt'
牵连速度 v牵连 u
u
r r O O
(x, y, z,t)
3-1-伽利略变换和经典力学时空观PPT课件

(x', y', z')
F zz om va tz o'z ''a xa x'F ' m a xx''
在两相互作匀速直线运动的惯性
a'zaz 系中,牛顿-运动定律具有相同的形式6.
3.1 伽利略变换和经典力学时空观
第3章 相对论
注意
牛顿力学的相对性原理,在宏观、 低速的范围内,是与实验结果相一致的 .
三 理解狭义相对论中质量、动量与速度的 关系,以及质量与能量间的关系.
-
3
3.1 伽利略变换和经典力学时空观
第3章 相对论
3.1.1 伽利略变换式 经典力学的相对性原理
相对于不同的参考系 , 经典力学定律的形式是 完全一样的吗 ?
牛顿力学的回答: 对于任何惯性参照系 , 牛顿力学的规律都具有
相同的形式 . 这就是经典力学的相对性原理 .
理学的发展的文章中说到:
“在已经基本建成的科学大厦中, 后辈的物理学家只要做一些零碎的修补 工作就行了。”
-
1
3.1 伽利略变换和经典力学时空观
第3章 相对论
然而开尔文又说道:“但是,在物理学晴朗天空的远处,
还有两朵令人不安的乌云,----”
热事实证明,正是这两朵乌云发展为一埸革命的风暴,乌
o' z' z'
x
x'
x
经典力学认为:1)空间的
量度是绝对的,与参考系无关;
2)时间的量度也是绝对的,与
参考系无关 .
-
5
3.1 伽利略变换和经典力学时空观
第3章 相对论
伽利略速度变换公式
u'xuxv
伽利略变换PPT课件

v
vx
i
vy
j
v
vxi
vy
j
而:(vu21v0ix
)i
vy
vy
j
j
u1
y(北)
'
u2
对比 u2 vx u1 vx u1 u2 5 m/s
A 和点B。地面上人测得车通过A、B 两点间的距
离和时间与车上的人测量结果相同 .
v
B
A
经典力学认为:1)空间的量度是 绝对的,与参考系无关;2)时间的量度也 是绝对的,与参考系无关 .
三.伽利略速度变换
r r' ut
1、几个概念
y S y S (x, y, z,t)
绝对运动:
据伽利略坐标变换,可得到经典时空观 二.经典力学时空观
(1)同时的绝对性 在同一参照系中,两个事件同时发生 在其他惯性系中,两个事件也一定同时发生。
Y Y’
O O’ x1
X’
x2 X
(2)时间间隔的测量是绝对的 在同一参照系中,两个事件先后发生,其间隔为
t t2 t1 据伽利略变换,t t 在另一参照系中,
dt
du
牵连加速度 a牵连 dt
y S y S
u r r O O
v
v
'
u
a a'
(x, y, z,t)
(x, y, z,t)
P
x
x
加速度对伽利略变换具有不变性.
SUCCESS
THANK YOU
2019/8/9
伽利略变换

§2、2 伽利略变换2、2、1 伽利略变换(1) 如图2-2-1所示,有两个惯性 系S 和'S , 它们对应的坐标轴相互平行,且当t ='t =0时,两系的坐标原点'O 与O 重合。
设'S 系相对于S 系沿x 轴正方向以速度u 运动。
同一质点P 在某一时刻在S 系中的时空坐标为(x,y,z,t),在S`系中的时空坐标为 (x’,y’,z’,t’)⎪⎪⎩⎪⎪⎨⎧===-=t t zz y y ut x x '''' 即t u r r -='或 (1) x=x '+ut ⎪⎩⎪⎨⎧==='''t t z z y y 即 t u r r+='式(1)称为伽利略时空坐标变换公式。
(2)将式(1)中的空间坐标分别对时间求一次导数得:图2-2-1⎪⎪⎪⎩⎪⎪⎪⎨⎧====-=-==z z y y x x v dt dz v v dt dy v u v u dt dxdt dx v '''''' 即u v v -= ' 或⎪⎪⎪⎩⎪⎪⎪⎨⎧======+=+==z z y yx x v dt dz dt dz v v dt dy dt dy v u v u dt dx dt dx v '''''1即u v v '+'= (2)式(2)称为伽利略速度变换公式。
(3)将式(2)再对时间求一次导数得⎪⎪⎪⎩⎪⎪⎪⎨⎧=='='=='='=='='z z z z y y y y x x xxa dt dv dt v d a a dt dv dt v d a a dt dv dt v d a 即a a ='⎪⎩⎪⎨⎧'='='=z z y y x x a a a a a a a a'= (3) 式(3)表明在伽利略变换下加速度保持不变。
伽利略变换和经典力学时空观 优质课件

x x ut 1 (u c)2
t
t
u c2
x
1 (u c)2
t
t
u c2
x
1 (u c)2
对于洛仑兹变换的说明:
1、在狭义相对论中,洛仑兹变换占据中心地位;
2、洛仑兹变换是同一事件在不同惯性系中两组 时空坐标之间的变换方程;
3、各个惯性系中的时间、空间量度的基准必须一致;
u c
(1
u2 c2
)
1
有 x x ut y y z z t t
伽利略变换
例1:一短跑选手,在地球上以10s的时间跑完100m,在飞行速
率为0.98c的飞船中观测者看来,这个选手跑了多长时间和多长
距离(设飞船沿跑道的竞跑方向航行)?
1
1 2
1
1
u2 c2
y S
u
o x
P (x, y, z,t) (x, y, z, t) x x
二、洛仑兹变换式 时空变换关系
正变换 S S
x x ut
y y
z z
t
(t
u c2
x)
其中
1
1 2
1
1
牛顿力学 长度标度 质量的测量
与参考系无关
速度与参考系有关 (相对性)
狭义相对论 力学
光速不变
长度、时间、质量与 参考系有关(相对性)
二、洛仑兹变换式 时空变换关系
正变换 S S
x x ut
y y
z z
z
t
(t
u c2
x)
y S
ut o
x z
伽利略变换式

三、经典力学的时空观
经典时空观(绝对时空观):时间与空间是彼 此独立、互不相关,并且独立于物质和运动之外的 东西。
“绝对的真实的数学时间, 就其本质而言, 是永远均匀地 流逝着, 与任何外界无关.”
“绝对空间就其本质而言 是与任何外界事物无关的,它 从不运动, 并且永远不变.”
实践已证明 , 绝对时空观是不正确的.
理论预测 N 0.4 仪器可测量精度 N 0.01
实验结果
N 0
未观察到地球相对于“以太”的运动.
人们为维护“以太”观念作了种种努力, 提出了 各种理论 ,但这些理论或与天文观察,或与其它的实 验事实相矛盾,最后均以失败告终 .
o 与 o'重合
位置坐标变换公式
x' x vt
Hale Waihona Puke y' yz' z
t' t
s
y
y
s'
y'
y'
v
P(x, y, z)
*
(x', y', z')
vt
x'
o
z z
o' x
z' z'
x'
x
经典力学认为:1)空间的 量度是绝对的,与参考系无关; 2)时间的量度也是绝对的,与 参考系无关 .
伽利略速度变换公式
u'x ux v
u'y uy
u'z uz
s
y
y
s'
y'
y'
v
vt
x'
o
z z
o' x
伽利略变换.
s
y
y
s'
y'
y'
v
*P(x, y, z)
F
ay ay
az az
a
ma
a
F
vt
x'
o
o'x
zz z'z'
( x', y', z')
x'
x
ma 经典物理:m m
牛顿定律在一切惯性系中具有相同的 数学表达形式. ——力学相对性原理
4
二、力学相对性原理 力学定律在所有惯性系中都具有相
伽利略变换 中隐含了绝 对时空观念
1、绝对时间 伽利略变换 t t 或 t t
时钟的走时与运动无关,与惯性系无关
时间测量与运动无关,与惯性系选择无关
7
2、绝对空间 (1)、长度的测量: 长度 = 在与长度方向平行的坐标轴上,物体 两端坐标值之差。
注意:当物体运动时,两端坐标必须同时记录。
2
伽利略速度变换
ux ux v
uy u y
ax ax
ay ay
ቤተ መጻሕፍቲ ባይዱ
uz uz
az az
u
u
v
or
:
u
u
v
s y s' y' v
o
o'
*P(ux ,uy ,uz ) (ux' , uy' , uz' )
x x'
z z'
3
加速度变换
x
z z'
大学物理2012.9

l0 x 2 x1
在相对于物体运动的运动参照系中测得的物长
l x2 x1
s
s'
u
哥 . 哥
. a 弟
弟
x'1
x
x'2
x'
由洛仑兹正变换
x
x ut 1
2
得:
x1 l0 x2
x2 ut2 1
2
x1 ut1 1 2
在S 系中必须同时测量 x1和x2 须 t1 t2 x2 x1 l x1 于是 l0 x2 1 2 1 2
相 对 论
爱 因 斯 坦 假 设 洛 仑 兹 变 换
洛仑兹变换可以简化为伽利略变换: x x ut x x ut y y y y z z z z t t t t 即伽利略变换是洛仑兹变换在低速时的近似公
式。可见洛仑兹变换有更为普遍的意义。
一切惯性系中测得的长度都是相同的,即空 间是绝对的,与参照系无关。
2.时间的绝对性
设空间有两个事件在不同时间发生。 按伽利略变换有:
经 典 相 力 对 学 论 时 空 观
t1 t1 t2 t2 t1 \ t2 t1 t2
可见在两个参照系中时间和时间间隔也是相 同的,即时间是绝对相同,时间间隔绝对相等,
经 典 相 力 对 学 论 时 空 观
在一个孤立系统内(如一条封闭的船舱 里),人们不能根据所发生的任何力学现象来 判断所处系统是静止的还是作匀速直线运动。 如:在静止的船上你能跳三米远,在匀速 运动的船上也能跳三米远。无论你是向着船头、 还是向着船尾跳,尽管你在空中时船仍在运动。 水在静止的船上竖直下落,在匀速运动的 船上也同样竖直下落,尽管水在空中时船仍在 运动,水决不会有一滴落到容器之外。
相对运动伽利略变换

v甲乙 …..甲对乙的速度,甲是运动物体,乙是参照系.
a AB …..A相对B的加速度,A为运动物体,B是参照系.
研究的问题: 在两个有相互平动的参照系中考察同 一物理事件。 两个不同参照系对同一事件的描述存在怎样的关系?
2
一、运动相对性的描述
设有两个相互平动的参照系 S和S´。在S系中建立直角坐标 系o—xyz,在S´系中建立直角 坐标系o—x´y´z´。 设质点P在空间运动。 t时刻: P点相对于S系的位矢为: rPO 相对于S´系的位矢为: rPO ' 1)位矢的相对性 二者关系 rPO rPO' 2)位移的相对性
上式可以写作f-mA=ma
- m A 相当于一个附加的力,称为惯性力。
为相对加速度 a
17
在非惯性系中应用牛顿定律时,计算力要计入真 实力和假想的惯性力,加速度要用相对加速度。 这时牛顿定律的形式为: f f f 惯 =ma 惯性力:大小等于运动质点的质量与非惯性系加 速度的乘积;方向与非惯性系加速度的方向相反。 惯性力没有施力物体,所以不存在反作用力。 例1:超重与失重:台秤上显示的体 重读数是多少? 解:
二、伽利略变换
设有两个参照系S系和S’系,各 坐标轴相互平行。 S’ 系相对S系沿 ox 轴以 u 运动。
坐标轴原点O与O’点重合时作为公共计 t 0时两坐标重合 x x' 0 时起点。 t时刻,物体在P点(看成一事件)
S
S'
y
o z
y'
u
o'
P
x x'
z'
在S系看来,该事件的时空坐标为: r x, y , z , t 速度和加速度为: v x, y, z , t , a ( x, y , z , t ) 在S’系看来,该事件的时空坐标为: r x , y , z , t
伽利略变换

伽利略变换1.1 事件与参照系在自然界中发生的任何一件事,都称为一个事件,例如一次爆炸,一道光发出,一个声响,一个物体运动到某个位置等。
相对论中我们所关心的不是一个事件的具体内容,而是事件发生的地点和时间。
x图5.1 伽利略变换为了确定一个事件发生的地点的时间,必须建立一个参照系,并在该参照系中建立一个与参照系保持相对静止的坐标系,这样事件发生的地点即可以用这一地点所对应的位置坐标来表示。
为了测量事件发生的时间,还需要在该参照系中有一个钟。
伽利略变换描述从两个相对作匀速直线运动的参照系测量同一事件发生的地点(位置坐标)和时间,得到的两种测量结果之间的关系。
1.2 伽利略变换设有两个惯性系S和S',S'相对于S以速度u作匀速直线运动。
在两参照系建立坐标系O xy和O'x'y',其中x轴和x '轴相互重合且沿u 方向,y 、z 轴和y '、z '相互平行。
当t = t' =0时,O 和O'重合 ,如图5.1所示。
设有一事件在参照系S 中测得发生于(x ,y ,z ,t ),在 参照系S'中测得发生于(x ',y ',z ',t '),则x x ut y y z z t t '=-⎧⎪'=⎪⎨'=⎪⎪'=⎩ 或 x x uty y z z t t '=+⎧⎪'=⎪⎨'=⎪⎪'=⎩(5.1) 式(5.1)称为伽利略坐标变换 。
式(5.1)两边对时间求导,并考虑到t = t' ,可得伽利略速度变换x x y y z z v v u v v v v '⎧=-⎪'=⎨⎪'=⎩ 或 x x y yz z v v uv v v v '⎧=+⎪'=⎨⎪'=⎩(5.2) 式(5.2)称为伽利略速度变换。
2.8伽利略变换

上页
下页
返回
结束
第二章 质点运动学 [例题 一人骑自行车向东而行 在速度为 m/s时,觉得 例题2]一人骑自行车向东而行 在速度为10 例题 一人骑自行车向东而行,在速度为 时 觉得 有南风; 速度增至15m/s时, 觉得有东南风. 求风 的速度 东南风 的速度. 有南风 速度增至 时 觉得有东南 [解] 选地为基本坐标系 ,人为动坐标系 O′ 解 选地为基本坐标系O, 设风速为 v (1) 依题意: 依题意: 风相对于人 v ′
a ( x1 , t ), b ( x2 , t )
′ ′ a ( x1 , t1 ), b( x ′ , t 2 ) 2 ′
′ t1 = t
′ t2 = t
′ ′ t1 = t 2
参考系观测到两事件也是同时发生的. 即O‘参考系观测到两事件也是同时发生的 参考系观测到两事件也是同时发生的 同时具有绝对性. 同时具有绝对性
dr ' = dt
d rO ′ = dt
v绝对 = v相对 + v牵连
上页 下页 返回 结束
第二章 质点运动学
§2.8.4 加速度对伽利略变换为不变量
d v 牵连 d v 绝对 d v 相对 = + 加速度 a = dt dt dt d v 牵连 v牵连是常矢量 =0 dt
a绝 = a相
加速度对伽利略变换具有不变性. 加速度对伽利略变换具有不变性
−1
v y = v ′y
v′
y
????
u2
v ′ = v′ i + v′y j x
又风对人为东南风, 又风对人为东南风,所以
− v ′x = v ′y
x
v = v x i + v y j = ( u2 + v ′x )i + v ′y j
伽利略变换

伽利略变换伽利略变换(Galileo transformation)是牛顿力学中所使用的两个相对做等速直线运动的参考系中的时空变换,属于一种被动态变换。
伽利略变换中,直观上明显成立的公式在物体以接近光速运动时就会瓦解,这是相对论性效应造成的。
伽利略变换建基于人们加减物体速度的直觉,变换的核心是假设时间、空间是绝对的、彼此独立的,其中时间均匀流逝,空间均匀分布且各向同性。
外文名Galilean transformation力学牛顿力学算法等价属性概念算法公式目录1.平移变换2.三种伽利略变换3.变换的局限平移变换编辑伽利略变换是整个经典力学的支柱。
该理论认为空间是独立的,与在其中物体的运动无关,而时间是均匀流逝的,线性的。
它的数学表达式(如下图)。
伽利略变换是牛顿力学中所使用的两个相对做等速直线运动的参考系中的时空变换。
设有两个参考系S(Oxyz)及S'(O'x'y'z'),坐标轴相互平行且轴x与轴x'重合,S'相对S沿x轴以u做等速直线运动,且S系与S'系中各处有结构完全相同的时钟,记录的时刻为t与t',并以两坐标原点O及O'重合时刻为计时起点,则可得某质点m的运动在两参考系中的时空变换关系:x'=x-ut y'=y z'=z t'=t上式即为伽利略(坐标)变换。
最后一条方程式意味着时间是不受观测者的相对运动影响的。
如果将各式对时间求导,则得速度变换式:v x'=v x-u v y'=v y v z'=v z因此,如果S是惯性系,即不受外力作用的物体在其中做等速直线运动,则根据上式,它在S'中也一定做等速直线运动,所以S'也是惯性系。
如果将各式再一次对时间求导,则得加速度变换关系式:a x'=a x a y'=a y a z'=a z亦即a'=a。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
v
O’
( x1 , t1 ), (x2 , t 2 )
在O 观察测得
t1 t 2
Δx x2 x1 Δx x 2 x1
由伽利略坐标变换得
O
l0
( x '1 , t '1 ), (x '2 , t '2 )
x1 vt1 x1
t1 t2
x2 vt2 x2
V人地1
V雨人1
V雨地
地:基本参考系 人:动参考系 V雨地=V雨人1+V人地1 V雨地=V雨人2+V人地2 由右图
V人地2
V雨人2
V雨地
60° 120°
|V雨地|=|V人地2|= 36km/h
=90°--60°= 30° 即雨点的速度方向为向下偏东30°
§2.8.4 加速度对伽利略变换为不变量
1 2
t1 , t 2 t2 由伽利略坐标变换 t1
得
t1 t 2 t1 t2
意义:不同的参考系中,考察同一过程所经历的时间相同. 例:气体压缩过程. 例:火车手表的时间. 时间具静止,相对O以速度
v
运动
在O上观察,必须同时测出杆各端点坐标
§2.3 伽利略变换
§2.3.1 伽利略变换
§2.3.2 伽利略变换蕴含的时空观
§2.3.3 伽利略速度变换关系
§2.3.4 加速度对伽利略变换为不变量 例题
§2.3.1
伽利略变换
y ut y'
考虑两个相对平动的参照系
设O为基本参考系, O’为动参考系
u
P
t t 0; O与O重合 若O’系相对于O系沿x轴的正 方向以速 率 v 匀速运动:
v绝对 v '相对 v牵连
加速度
a绝对
dv绝对 dv '相对 dv牵连 dt dt dt
dv 牵 连 0 dt
v牵连是常矢量
a绝 a相
加速度对伽利略变换具有不变性.
用矢量讨论抛体运动
基本方程
v v0 gt
1 2 r v0 t gt 2
dr v绝 对 dt
相对速度
牵连速度
v '相对
v牵 连
dr ' dt ' drO dt
r r ' vt
v绝对 v '相对 v牵连
t't
例:一个人骑车以18km/h自西向东行进,他看见雨点垂直 下落.当他的速率增至36 km/h时,看见雨点与他前进的 方向成120°角下落,求雨点对地的速度. 绝对速度=相对速度+牵连速度 (速度变换公式) V1= 18km/h=V人地1 V2= 36km/h=V人地2 解:
所以
Δx Δx
t1 ' t2 '
意义:在不同参照系中,测量同一物体长度相同. 空间具有绝对性.
这一结论在我们写下 r R r 已包含其中了
§2.8.3 伽利略速度变换关系
绝对运动:物体相对基本参考系的运动. 相对运动:物体相对动参考系的运动. 牵连运动: O 相对O的运动. 绝对速度
r1
r
O O
r
r r2 2 '
P r
P
r2
作业:
2.30
2.32
v0t 2 v0 t
矢量图
v 0 t1
v0
O
1 2 1 2 1 2 gt 1 gt gt 2 2 2 2
r ( t1 ) r (t ) r (t2 )
[例题2] 如图表示一演示试验. 抛体发射前,瞄准高处
A的靶子,采取措施使靶子在抛体发射的同时开始自由 下落. 那么,不管抛体的初速率怎样,抛体都能够击中 靶子,这是为什么?
质点P: 一个气球爆炸 z
r
0
r
x' 0'
R
z'
x
O
P (r , t )
O ' P(r ', t )
r r ' R
R vti
t't
由人们的直觉得出
伽利略时空坐标变换
r r vt ' t t
x x vt ' y y z z t t
r r vt 逆变换 t t
x x vt y y 逆变换 z z t t
§2.8.2 伽利略变换蕴含的时空观
1.关于同时性
设有两事件a,b. 在O上看发生在 a( x1 , t1 ), b( x2 , t 2 )
如果 在 O 上看发生在 由伽利略坐标变换 得
t1 t2
, t1 ), b( x ) a( x1 2 , t2
t1 t1
t2 t2
= t2 t1
即两参考系观测到两事件是同时发生的. 同时具有绝对性.
2.关于时间间隔 设在O系中某点处发生二个事件 t1和 t2 在 O 上看,二事件发生于 t 和t
