湘教版数学八年级上册解题技巧专题:等腰三角形中辅助线的作法
等腰三角形辅助线的做法

专题:等腰三角形辅助线的作法类型一:利用三线合一作辅助线(1)等腰三角形中有底边中点时,常连底边上的中线1、如图ΔABC中,AB=AC,D是BC的中点,E、F分别是AB、AC上的点且AE= AF,求证:DE=DF2、如图,在ΔABC中,D是BC的中点,过A作EF‖BC且AE= AF,求证:DE=DF(2)没有底边中点时作底边上的高3、如图,在ΔABC中,AB=AC,BD⊥AC于D,求证:∠BAC=2∠DBC类型二:做平行线构造等腰三角形(1)作腰的平行线构造等腰三角形4、如图,ΔABC中,AB=AC,点D在AB上,点E在AC的延长线上,且BD=CE,DE交BC于F,求证:DF=EF(2)作底边的平行线构造等腰三角形5、如图,AB=AC,点D是BA的延长线上一点,E在AC上,且AD=AE,求证:DE⊥BC(3)利用“角平分线+平行线”构造等腰三角形6、如图,BD平分∠ABC交AC于D,点E为CD上一点,且AD=DE,EF‖BC交BD于F,求证:AB=EF类型三:用“截长补短法”构造等腰三角形7、如图,ΔABC中,∠BAC=120,AD⊥BC于D,且AB+BD=DC,求∠C 的度数。
8、如图,ΔABC中,∠BAC=108,AB=AC,BD平分∠ABC交AC于D,求证:BC=CD+AB类型四:运用角平分线作垂线9、如图,四边形AOBC中,AC=BC,∠A+∠OBC=180,CD⊥OA于D。
(1)求证:OC平分∠AOB;(2)若OD=3DA =6,求OB的长。
10、如图,已知等腰RTΔABC中,∠ACB=90,AC=BC=4,D为ΔABC的一个外角∠ABF的平分线上一点,且∠ADC=45,CD交AB于E,(1)求证:AD=CD(2)求AE的长。
【下载本文档,可以自由复制内容或自由编辑修改内容,更多精彩文章,期待你的好评和关注,我将一如既往为您服务】。
湘教版八年级数学上册阶段核心方法 等腰三角形中作辅助线的八种常用方法

探究培优
在△FBD 和△CDE 中,B∠FD=FDB= C,∠ECD, FD=CE,
∴△FBD≌△CDE(SAS), ∴DB=DE,∴△BDE 是等腰三角形. 又∵DG⊥BE 于 G, ∴G 为 BE 的中点,∴BG=EG.
探究培优
5.如图,AB∥CD,∠1=∠2,AD=AB+CD.求证: (1)BE=CE;
此页为防盗标记页(下载后可删)
1、谢谢大家听得这么专心。 2、大家对这些内容这么感兴趣,真让我高兴。 3、你们专注听讲的表情,使我快乐,给我鼓励。 4、我从你们的姿态上感觉到,你们听明白了。 5、我不知道我这样说是否合适。 6、不知我说清了没有,说明白了没有。 7、我的解释不知是否令你们满意,课后让我们大家再去找有关的书来读读。 8、你们的眼神告诉我,你们还是没有明白,想不想让我再讲一遍? 9、会“听”也是会学习的表现。我希望大家认真听好我下面要说的一段话。 10、从听课的情况反映出,我们是一个素质良好的集体。 1、谢谢你,你说的很正确,很清楚。 2、虽然你说的不完全正确,但我还是要感谢你的勇气。 3、你很有创见,这非常可贵。请再响亮地说一遍。 4、××说得还不完全,请哪一位再补充。 5、老师知道你心里已经明白,但是嘴上说不出,我把你的意思转述出来,然后再请你学说一遍。 6、说,是用嘴来写,无论是一句话,还是一段话,首先要说清楚,想好了再说,把自己要说的话在心里整理一下就能说清楚。 7、对!说得很好,我很高兴你有这样的认识,很高兴你能说得这么好! 8、我们今天的讨论很热烈,参与的人数也多,说得很有质量,我为你们感到骄傲。 9、说话,是把自己心里的想法表达出来,与别人交流。说时要想想,别人听得明白吗? 10、说话,是与别人交流,所以要注意仪态,身要正,不扭动,眼要正视对方。对!就是这样!人在小时候容易纠正不良习惯,经常 注意哦。
等腰三角形中的常见辅助线

等腰三角形中做辅助线的八种常用方法几何图形中添加辅助线,往往能把分散的条件集中,使隐蔽的条件显露,将复杂的问题简单化.例如:作“三线”中的一线或平行线证线段相等,利用截长补短证线段和差关系或求角的度数,利用加倍折半法证线段的倍分关系等,将不在同一个三角形的线段转移到同一个三角形(或两个全等三角形)中,然后运用等腰(或全等三角形)的性质来解决问题.方法1 等腰三角形中有底边上的中点时常作底边上的中线1.如图,在三角形ABC中,∠A=90°,AB=AC,D为BC的中点,E,F分别是AB,AC上的点,且BE=AF,求证:(1)DE=DF.(2)DE⊥DF方法2 等腰三角形中没有底边上的中点时常作底边上的高2.如图,△ABC中,AC=2AB,AD平分∠BAC交BC于D,E是AD上一点,且EA=EC,求证:EB⊥AB.方法3 等腰三角形中证与腰有关联的线段时常作腰的平行线或垂线3.如图,在△ABC中,AB=AC ,点P从点B出发沿线段BA移动(点P与A,B不重合),同时,点Q从点C出发沿线段AC的延长线移动,点P,Q移动的速度相同,PQ与直线BC相交于点D.(1)试说明:PD=QD(2)过点P作直线BC的垂线,垂足为E,P,Q在移动的过程中,线段BE,DE,CD中是否存在长度保持不变的线段?请说明理由.方法4 等腰三角形证与底有关的线段时常作底的平行线4.如图,等边三角形ABC中,D是边AC延长线上一点,延长BC至E,使CE=AD,DG⊥BE于G,求证:BG=EG.方法5补形法构造等腰三角形5.如图,AB∥CD,∠1=∠2,AD=AB+CD,求证:(1)BE=CE;(2)AE⊥DE;(3)AE平分∠BAD.方法6 倍长中线法构造等腰三角形6.如图,△ABC中,AD为中线,点E为AB上一点,AD,CE交于点F,且CE=EF,求证:AB=CF方法7 延长(或截长)法构造等腰三角形7.如图,在△ABC中,∠BAC=2∠B,CD平分∠ACB交AB于D,求证:AC+AD=BC.方法8 截长补短法构造等腰三角形8.如图,在△ABC中,∠BAC=120°,AD⊥BC于点D,且AB+BD=DC,求∠C的度数.。
八年级上册数学-等腰三角形(三)作辅助线构造等腰三角形
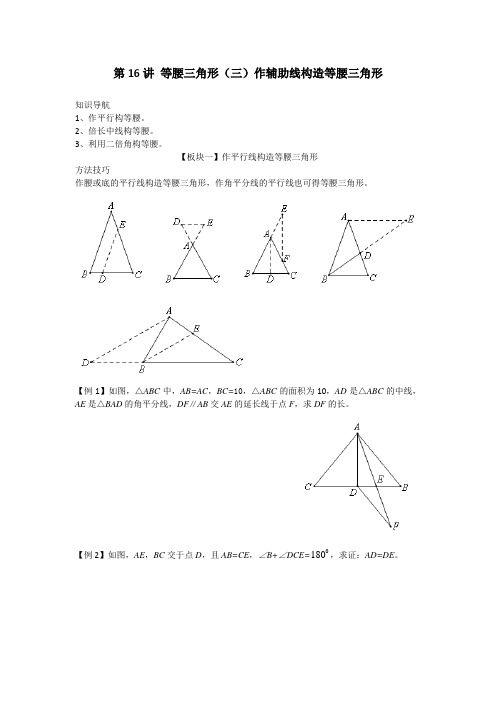
第16讲等腰三角形(三)作辅助线构造等腰三角形知识导航1、作平行构等腰。
2、倍长中线构等腰。
3、利用二倍角构等腰。
【板块一】作平行线构造等腰三角形方法技巧作腰或底的平行线构造等腰三角形,作角平分线的平行线也可得等腰三角形。
【例1】如图,△ABC中,AB=AC,BC=10,△ABC的面积为10,AD是△ABC的中线,AE是△BAD的角平分线,DF∥AB交AE的延长线于点F,求DF的长。
180,求证:AD=DE。
【例2】如图,AE,BC交于点D,且AB=CE,∠B+∠DCE=0针对练习11、如图,在△ABC 中,∠BAC=060,∠C=040,P ,Q 两点分别在BC ,CA 上,并且AP ,BQ 分别是∠BAC ,∠ABC 的角平分线,求证:BQ+AQ=AB+BP 。
2、如图1,在△ABC 中,∠ABC=2∠ACB ,AO ,BO 分别平分∠BAC ,∠ABC ,连接OC 。
(1)求证:OC 平分∠ACB ;(2)如图2,若AB=6,AC=10,求OB 的长。
【板块二】中线倍长构造等腰三角形方法技巧中线倍长,将相等的角或边集中到新的三角形中构成等腰三角形。
【例3】如图,AD 为△ABC 的中线,E 为AB 上一点,AD ,CE 交于点F ,且AB=CF ,过点E 作AF 的垂线交AC 于点P ,求证:AP=PF 。
针对练习21、如图,AB∥CD,BD与AC交于点E,DO平分∠CDE,若点O为AC的中点,试探究线段CD,AB,BD之间的数量关系。
2、如图,在△ABC中,D为CA的中点,∠ABD=2∠CBD,AO⊥BD于点O。
(1)若OD=3,OB=5,求AB的长;(2)求证:AB=2OD。
【板块三】利用∠α=2∠β构造等腰三角形方法技巧作角平分线或延长二倍角的一边。
【例4】如图,△ABC中,∠BAC=2∠C,BD为△ABC的角平分线,BC=6,AB=3.5,求AD的长。
针对练习31、如图,在△ABC 中,∠ABC=2∠C ,AD ⊥BC 于点D ,AE 为BC 边上的中线。
(完整)等腰三角形时常用的辅助线作法

有等腰三角形时常用的辅助线⑴作顶角的平分线,底边中线,底边高线例:已知,如图,AB = AC,BD⊥AC于D,求证:∠BAC = 2∠DBC⑵有底边中点时,常作底边中线例:已知,如图,△ABC中,AB = AC,D为BC中点,DE⊥AB于E,DF⊥AC于F,求证:DE = DF⑶将腰延长一倍,构造直角三角形解题例:已知,如图,△ABC中,AB = AC,在BA延长线和AC上各取一点E、F,使AE = AF,求证:EF⊥BC⑷常过一腰上的某一已知点做另一腰的平行线例:已知,如图,在△ABC中,AB = AC,D在AB上,E在AC延长线上,且BD = CE,连结DE交BC于F求证:DF = EF⑸常过一腰上的某一已知点做底的平行线例:已知,如图,△ABC中,AB =AC,F在AC上,E在BA延长线上,且AE = AF,连结DE求证:EF⊥BC⑹常将等腰三角形转化成特殊的等腰三角形---—--等边三角形例:已知,如图,△ABC中,AB = AC,∠BAC = 80o,P为形内一点,若∠PBC = 10o,∠PCB = 30o求∠PAB的度数。
有等腰三角形时常用的辅助线⑴作顶角的平分线,底边中线,底边高线例:已知,如图,AB = AC,BD⊥AC于D,求证:∠BAC = 2∠DBC证明:(方法一)作∠BAC的平分线AE,交BC于E,则∠1 = ∠2 = 12∠BAC又∵AB = AC∴AE⊥BC∴∠2+∠ACB = 90o∵BD⊥AC∴∠DBC+∠ACB = 90o∴∠2 = ∠DBC∴∠BAC = 2∠DBC(方法二)过A作AE⊥BC于E(过程略)(方法三)取BC中点E,连结AE(过程略)⑵有底边中点时,常作底边中线例:已知,如图,△ABC中,AB = AC,D为BC中点,DE⊥AB于E,DF⊥AC于F,求证:DE = DF21EDC BA证明:连结AD.∵D 为BC 中点, ∴BD = CD又∵AB =AC ∴AD 平分∠BAC ∵DE ⊥AB ,DF ⊥AC ∴DE = DF⑶将腰延长一倍,构造直角三角形解题例:已知,如图,△ABC 中,AB = AC,在BA 延长线和AC 上各取一点E 、F ,使AE = AF , 求证:EF ⊥BC证明:延长BE 到N ,使AN = AB ,连结CN ,则AB = AN = AC∴∠B = ∠ACB, ∠ACN = ∠ANC ∵∠B +∠ACB +∠ACN +∠ANC = 180o∴2∠BCA +2∠ACN = 180o ∴∠BCA +∠ACN = 90o 即∠BCN = 90o ∴NC ⊥BC ∵AE = AF ∴∠AEF = ∠AFE又∵∠BAC = ∠AEF +∠AFE ∠BAC = ∠ACN +∠ANC ∴∠BAC =2∠AEF = 2∠ANC ∴∠AEF = ∠ANCF E DCBAN FE CBA∴EF ∥NC ∴EF ⊥BC⑷常过一腰上的某一已知点做另一腰的平行线例:已知,如图,在△ABC 中,AB = AC,D 在AB 上,E 在AC 延长线上,且BD = CE ,连结DE 交BC 于F 求证:DF = EF证明:(证法一)过D 作DN ∥AE ,交BC 于N ,则∠DNB = ∠ACB,∠NDE = ∠E ,∵AB = AC, ∴∠B = ∠ACB ∴∠B =∠DNB ∴BD = DN 又∵BD = CE ∴DN = EC在△DNF 和△ECF 中 ∠1 = ∠2 ∠NDF =∠E DN = EC ∴△DNF ≌△ECF ∴DF = EF(证法二)过E 作EM ∥AB 交BC 延长线于M ,则∠EMB =∠B(过程略)⑸常过一腰上的某一已知点做底的平行线21NFED C BA21MFED CBA例:已知,如图,△ABC 中,AB =AC ,E 在AC 上,D 在BA 延长线上,且AD = AE ,连结DE求证:DE ⊥BC证明:(证法一)过点E 作EF ∥BC 交AB 于F ,则∠AFE =∠B ∠AEF =∠C ∵AB = AC ∴∠B =∠C ∴∠AFE =∠AEF ∵AD = AE∴∠AED =∠ADE又∵∠AFE +∠AEF +∠AED +∠ADE = 180o ∴2∠AEF +2∠AED = 90o 即∠FED = 90o∴DE ⊥FE 又∵EF ∥BC ∴DE ⊥BC(证法二)过点D 作DN ∥BC 交CA 的延长线于N,(过程略) (证法三)过点A 作AM ∥BC 交DE 于M ,(过程略)⑹常将等腰三角形转化成特殊的等腰三角形————--等边三角形例:已知,如图,△ABC 中,AB = AC,∠BAC = 80o ,P为形内一点,若∠PBC = 10o ∠PCB = 30o 求∠PAB 的度数. 解法一:以AB 为一边作等边三角形,连结CE则∠BAE =∠ABE = 60oN M FE D CBA PECBAAE = AB = BE∵AB = AC∴AE = AC ∠ABC =∠ACB ∴∠AEC =∠ACE∵∠EAC =∠BAC-∠BAE= 80o-60o = 20o∴∠ACE = 12(180o-∠EAC)= 80o∵∠ACB= 12(180o-∠BAC)= 50o∴∠BCE =∠ACE-∠ACB= 80o-50o = 30o∵∠PCB = 30o∴∠PCB = ∠BCE∵∠ABC =∠ACB = 50o, ∠ABE = 60o∴∠EBC =∠ABE-∠ABC = 60o-50o =10o ∵∠PBC = 10o∴∠PBC = ∠EBC在△PBC和△EBC中∠PBC = ∠EBCBC = BC∠PCB = ∠BCE∴△PBC≌△EBC∴BP = BE∵AB = BE∴AB = BP∴∠BAP =∠BPA∵∠ABP =∠ABC-∠PBC = 50o-10o = 40o∴∠PAB = 12(180o-∠ABP)= 70o解法二:以AC为一边作等边三角形,证法同一。
八年级数学上册 5 解题技巧专题 等腰三角形中辅助线的作法习题 湘教版

解题技巧专题:等腰三角形中辅助线的作法——形成精准思维模式,快速解题◆类型一利用“三线合一”作辅助线一、已知等腰作垂线(或中线、角平分线)1.如图,在△ABC中,AB=AC,D为BC边的中点,过点D作DE⊥AB,DF⊥AC,垂足分别为E,F.(1)求证:DE=DF;【方法11】(2)若∠A=90°,图中与DE相等的有哪些线段(不需说明理由)?2.如图,△ABC中,AC=2AB,AD平分∠BAC交BC于D,E是AD上一点,且EA =EC,求证:EB⊥AB.二、构造等腰三角形3.如图,△ABC的面积为1cm2,AP垂直∠ABC的平分线BP于P,则△PBC的面积为( )A.0.4cm2B.0.5cm2C.0.6cm2D.0.7cm2◆类型二巧用等腰直角三角形构造全等4.(xx·铜仁中考)如图,在△ABC 中,AC =BC ,∠C =90°,D 是AB 的中点,DE ⊥DF ,点E ,F 分别在AC ,BC 上,求证:DE =DF .◆类型三 等腰(边)三角形中截长补短构造全等5.如图,已知AB =AC ,∠A =108°,BD 平分∠ABC 交AC 于D ,求证:BC =AB +CD .参考答案与解析1.(1)证明:连接AD .∵AB =AC ,D 是BC 的中点,∴∠EAD =∠FAD .又∵DE ⊥AB ,DF ⊥AC ,∴∠AED =∠AFD =90°.∵AD =AD ,∴△ADE ≌△ADF ,∴DE =DF .(2)解:若∠BAC =90°,图中与DE 相等的线段有AE 、AF 、BE 、CF 、DF .2.证明:作EF ⊥A C 于F .∵EA =EC ,∴AF =FC =12AC .∵AC =2AB ,∴AF =AB .∵AD 平分∠BAC ,∴∠BAD =∠CAD .又∵AE =AE ,∴△ABE ≌△AFE (SAS),∴∠ABE =∠AFE =90°,∴EB ⊥AB .3.B 解析:延长AP 交BC 于点D .∵BP 平分∠ABC ,BP ⊥AD ,易得AB =BD ,AP=PD,∴S△ABP=S△BPD,S△ACP=S△CPD,∴S△PBC=12S△ABC=0.5cm2.故选B.4.证明:如图,连接CD.∵AC=BC,D是AB的中点,∴CD平分∠ACB,CD⊥AB ,∴∠CDB =90°.又∵∠ACB =90°,∴∠BCD =∠ACD =45°,∠B =45°,∴∠ECD =∠B =∠BCD ,∴CD =BD .∵ED ⊥DF ,∴∠EDF =∠EDC +∠CDF =90°.又∵∠CDF +∠BDF =90°,∴∠EDC =∠FDB ,∴△ECD ≌△FBD (ASA),∴DE =DF .5.证明:如图,在线段BC 上截取BE =BA ,连接DE .∵BD 平分∠ABC ,∴∠ABD =∠EBD =12∠ABC .又∵BD =BD ,∴△ABD ≌△EBD (SAS),∴∠BED =∠A =108°,∠ADB =∠EDB .又∵AB =AC ,∠A =108°,∴∠ACB =∠ABC =12×(180°-108°)=36°,∴∠CDE =∠DEB -∠C =108°-36°=72°,∠DEC =180°-∠DEB =180°-108°=72°.∴∠CDE =∠DEC ,∴CD =CE ,∴BC =BE +EC =AB +CD .如有侵权请联系告知删除,感谢你们的配合!。
技巧专题技巧专题等腰三角形7种常用辅助线添加方法

技巧专题等腰三角形7种常用辅助线添加方法方法1.三线合一法例1.如图,△ABC中,AB=AC,D是BC的中点,过A点的直线EF//BC,且AE=AF.求证: DE=DF.方法2.作一腰的平行线构造等腰三角形法例2.如图,AB=AC,F 为DE的中点,求证BD=CE.例3.如图,AABC中,AB=AC,点P从点B出发沿线段BA移动,同时,点Q从点C出发沿线段AC的延长线移动,已知点P, Q移动的速度相同,PQ与直线BC相交于点D.(1).如图①,当点P为AB的中点时,求证: PD=QD;(2).如图②,过点P作直线BC的垂线,垂足为E,当点P,Q在移动的过程中,线段BE、DE、CD中是否存在长度保持不变的线段?请说明理由.方法3.截长补短构造等腰三角形法例4.如图,在△ABC中,AB=AC, D是△ABC外一点,且∠ABD=60°,∠ACD=60°求证:BD+DC=AB例5.如图,在AABC中,∠BAC=120°, AD⊥BC于D,且AB+BD=DC,求∠C.方法4.证与底有关的线段时,通常作底的平行线例6.如图,等边△ABC中,D是边AB延长线上一点,延长BC至E点,使CE=AD, DG⊥BE 于G,求证BG=EG.方法5.加倍折半法,倍长中线法例7.如图,CE、CB分别是△ABC与△ADC的中线,且∠ACB=∠ABC.求证:CD=2CE.方法6.以底或腰为边作等边三角形,出三角形全等例8.如图,在△ABC中,∠ABC=∠ACB=40°,点P为三角形内一点,且∠PCA=∠PAB=20°.求∠PBC的度数方法7、将以腰为边的一个三角形绕顶角的顶点旋转例9.如图,△ABC中,点P是△ABC内一点,且∠APB>∠APC. 求证:PC> PB.课后培优练习题1.如图,在△ABC中,AB=AC, ∠A=90°,点D是BC的中点,点E、F分别在AB、AC上,且AE=CF.求证:△DEF 是等腰直角三角形.2.如图,等边△ABC的边BC上任取一点D,作∠ADE=60°,DE交∠C的外角平分线于点E,判断△ADE的形状,并证明你的结论.3.如图,△ABC中,AB=AC, D为BC边的中点,过点D作DE⊥AB, DF⊥AC,垂足分别为E, F.(1)求证: DE=DF;(2)若∠A=90°,图中与DE相等的有哪些线段? (不需说明理由)4.如图,△ABC中,AC=2AB, AD平分∠BAC交BC于D,E是AD上一点,且EA=EC,求证: EB⊥AB.5.如图,△ABC的面积为1cm2, AP垂直∠ABC的平分线BP于P,求△PBC的面积.6.如图,在△ABC中,AC=BC,∠C=90°,D是AB的中点,DE⊥DF,点E、F分别在AC、BC 上,求证: DE=DF.7.如图,已知AB=AC, ∠A=108°,BD平分∠ABC交AC于D.求证: BC=AB+CD.8.如图,在△ABC中,AB=AC, AE⊥BE于点E,且BC=2BE,若∠EAB=20°,求∠BAC的度数.9.如图,△ABC是等腰直角三角形,∠A=90°,BD平分∠ABC交AC于点D, CE ⊥BD. 求证: BD=2CE.10.如图,等边△ABC的边AB上一点P,作PE⊥AC于E,Q为BC延长线上一一点,且PA=CQ,连PQ交AC边于D.(1).求证: PD=DQ;(2).若△ABC的边长为1,求DE的长.。
初中数学等腰三角形辅助线添加方法及数学提分技巧

初中数学等腰三角形辅助线添加方法及数学提分技巧方法一:做三线合一中的一线三线合一,是等腰三角形里最重要的性质定理之一。
所谓三线,就是等腰三角形中,顶角的角平分线,底边的中线,底边的高线。
必然三线合一。
例题1,是三线合一的最基础的题型,D是BC的中点,那么连接AD,通过三线合一的性质,得出AD⊥BC.方法二:做平行线法这个一般是做一腰的平行线,得出两个角相等,从而得出三角形全等例题2中,这个题是非常常见的考试经典题型。
第①小题,得出三角形全等,得出PD=QD。
第②小题,过点P做PF∥AC,因为△PBF是等腰三角形,PE⊥BF,三线合一得出BE=EF。
又因为三角形全等,得出FD=CD。
所以,得出ED=BC的一半,即为定值。
方法三:截长补短法,或者叫截长取短法简单说,就是在某一条线段上截取一条线段,和已知线段相等。
或者,延长某一线段,使之等于某已知线段。
此解题方法常用,请大家细心钻研,平时多探索,勤学苦练。
例题3,就是一道延长某一线段,使之等于某已知线段,经典考试题型。
例题4,这就是一道在某一条线段上截取一条线段,和已知线段相等,通过等量转换,得出结论的经典考试题型。
方法四:加倍折半法,倍长中线法例题5,解析说过点B做BF∥AC,最后得出的还是线段相等。
其实,这个题还有一个更好的解题思路,就是倍长中线法先提示一下辅助线的添加方法。
因为CE是△ABC的中线,倍长中线CE。
延长CE 至F,使EF=CE,连接BF。
倍长中线,必出三角形全等,最后得出,△DBC≌△FBC,所以DC=CF,所以CD=2CE。
初中数学学习方法与提分技巧基本学习方法1.主动预习预习的目的是主动获取新知识的过程,有助于调动学习积极主动性,新知识在未讲解之前,认真阅读教材,养成主动预习的习惯,是获得数学知识的重要手段。
因此,要注意培养自学能力,学会看书。
如自学例题时,要弄清例题讲的什么内容,告诉了哪些条件,求什么,书上怎么解答的,为什么要这样解答,还有没有新的解法,解题步骤是怎样的。
等腰三角形常见的辅助线的做法

等腰三角形常见的辅助线的做法
如何快速解决好等腰三角形问题,做到孰能生巧?今天总结了以下四种和等腰三角形题型有关的常见辅助线添加方法
方法一:做三线合一中的一线
三线合一,是等腰三角形里最重要的性质定理之一。
所谓三线,就是等腰三角形中,顶角的角平分线,底边的中线,底边的高线。
必然三线合一。
方法二:做平行线法
这个一般是做一腰的平行线,得出两个角相等,从而得出三角形全等
方法三:截长补短法,或者叫截长取短法
简单说,就是在某一条线段上截取一条线段,和已知线段相等。
或者,延长某一线段,使之等于某已知线段。
此解题方法常用,请大家细心钻研
方法四:加倍折半法,倍长中线法。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
初中数学试卷
解题技巧专题:等腰三角形中辅助线的作法
——形成精准思维模式,快速解题
◆类型一利用“三线合一”作辅助线
一、已知等腰作垂线(或中线、角平分线)
1.如图,在△ABC中,AB=AC,D为BC边的中点,过点D作DE⊥AB,DF⊥AC,垂足分别为E,F.
(1)求证:DE=DF;【方法11】
(2)若∠A=90°,图中与DE相等的有哪些线段(不需说明理由)?
2.如图,△ABC中,AC=2AB,AD平分∠BAC交BC于D,E是AD上一点,且EA=EC,求证:EB⊥AB.
二、构造等腰三角形
3.如图,△ABC的面积为1cm2,AP垂直∠ABC的平分线BP于P,则△PBC的面积为( )
A.0.4cm2
B.0.5cm2
C.0.6cm2
D.0.7cm2
◆类型二巧用等腰直角三角形构造全等
4.(2016·铜仁中考)如图,在△ABC中,AC=BC,∠C=90°,D是AB的中点,DE⊥DF,点E,F分别在AC,BC上,求证:DE=DF.
◆类型三等腰(边)三角形中截长补短构造全等
5.如图,已知AB=AC,∠A=108°,BD平分∠ABC交AC于D,求证:BC=AB+CD.
参考答案与解析
1.(1)证明:连接AD.∵AB=AC,D是BC的中点,∴∠EAD=∠FAD.又∵DE⊥AB,DF⊥AC,∴∠AED=∠AFD=90°.∵AD=AD,∴△ADE≌△ADF,∴DE=DF.
(2)解:若∠BAC =90°,图中与DE 相等的线段有AE 、AF 、BE 、CF 、DF .
2.证明:作EF ⊥AC 于F .∵EA =EC ,∴AF =FC =12AC .∵AC =2AB ,∴AF =AB .∵AD 平分∠BAC ,∴∠BAD =∠CAD .又∵AE =AE ,∴△ABE ≌△AFE (SAS),∴∠ABE =∠AFE =90°,∴EB ⊥AB .
3.B 解析:延长AP 交BC 于点D .∵BP 平分∠ABC ,BP ⊥AD ,易得AB =BD ,AP =PD ,
∴S △ABP =S △BPD ,S △ACP =S △CPD ,∴S △PBC =12
S △ABC =0.5cm 2.故选B. 4.证明:如图,连接CD .∵AC =BC ,D 是AB 的中点,∴CD 平分∠ACB ,CD ⊥AB ,∴∠CDB =90°.又∵∠ACB =90°,∴∠BCD =∠ACD =45°,∠B =45°,∴∠ECD =∠B =∠BCD ,∴CD =BD .∵ED ⊥DF ,∴∠EDF =∠EDC +∠CDF =90°.又∵∠CDF +∠BDF =90°,∴∠EDC =∠FDB ,∴△ECD ≌△FBD (ASA),∴DE =DF .
5.证明:如图,在线段BC 上截取BE =BA ,连接DE .∵BD 平分∠ABC ,∴∠ABD =∠EBD =12
∠ABC .又∵BD =BD ,∴△ABD ≌△EBD (SAS),∴∠BED =∠A =108°,∠ADB =∠EDB .又∵AB =AC ,∠A =108°,∴∠ACB =∠ABC =12
×(180°-108°)=36°,∴∠CDE =∠DEB -∠C =108°-36°=72°,∠DEC =180°-∠DEB =180°-108°=72°.∴∠CDE =∠DEC ,∴CD =CE ,∴BC =BE +EC =AB +CD .。
