简谐运动 机械波多解问题
机械波的多解问题

M
N
P
一列简谐波沿水平弹性长绳向右传播,绳上的a、 例1 :一列简谐波沿水平弹性长绳向右传播,绳上的 、 b两点相距 两点相距14m。b点在 点右方,若a点位移达到正向 点在a点右方 两点相距 。 点在 点右方, 点位移达到正向 最大时, 点位移恰好为零 且向下运动。经过1. 点位移恰好为零, 最大时,b点位移恰好为零,且向下运动。经过 .0s 点位移第一次为零, 后,a点位移第一次为零,且向下运动,而b点的位移 点位移第一次为零 且向下运动, 点的位移 恰好达到负向最大,则这列波的波速可能等于( 恰好达到负向最大,则这列波的波速可能等于( ) A A.4.7m/s B.6m/s . . / . / C.10m/s D.14m/s . / D. /
2.波的时间的周期性 2.波的时间的周期性
波在传播过程中,所有质点都振动起来后, 波在传播过程中,所有质点都振动起来后,每 经过整数倍周期时,波的图象相同. 经过整数倍周期时,波的图象相同.
例 : 下 图 为 t=0 时 刻 的 波 形 图 , 画 出 t=0.4s , t=0.8s,… … t=nT时的波形图。(已知 时的波形图。 已知v=10m/s) , 时的波形图 )
波的多解问题
多解的原因: 多解的原因:
(1)波的空间的周期性; (1)波的空间的周期性; 波的空间的周期性 两质点间距离与波长关系未定) (两质点间距离与波长关系未定) (2)波的时间的周期性 波的时间的周期性; (2)波的时间的周期性; (3)波的传播的双向性 波的传播的双向性; (3)波的传播的双向性; (4)质点的振动方向的双向性 质点的振动方向的双向性。 (4)质点的振动方向的双向性。
高二物理机械波多解问题分析

机械波多解问题成因分析
机械波传播过程中在时间和空间上的周期 性、传播方向上的双向性、质点振动方向的 不确定性都是形成波动问题多解的主要原因。
一、传播方向导致的多解问题
波源起振后产生的波可以在介质中向四周 传播。若题中没有特别注明传播方向,则求解 时必须讨论其传播方向,从而导致了波的多解 问题
波速v和频率f可能是( ABD )
A.v=5m/s B.v=45m/s C.f=50Hz D.f=37.5Hz 。
三、传播时间导致的多解问题
题目中所给定的时间条件不充分,可能比 一个周期长,可能比一个周期短,从而导致了 多解问题的出现
一列横波在x轴上传播,t1=0和t2=0.005s时 刻的波形分别如图中实线和虚线所示。 (1)求这列波的波速; (2)若波速为6000m/s,求波的传播方向。
s n s
t kT t
v s n s
t kT t
其中n=0,1,2,3,…; k=0,1,2,3,….
二、波形周期导致的多解问题
简谐机械波是周期性的,每经过一个周期 波形与原波形重复,从而导致了问题的多解性
一列横波在某时刻的波形图如图中实线所 示,经0.02s后波形如图中虚线所示,则该波的
波谷,则t的可能值有( D )
A.1个
B.2个
C.3个
D.4个
五、波长大小导致的多解问题
因题中没有给定波长的确切条件,故引起 答案的不确定性导致多解问题
如图甲所示,一根张紧的水平弹性长绳上的ɑ、 b两点,相距14.0m。b点在ɑ点右方,当一列简 谐波沿此绳向右传播时,若ɑ点位移达到正向极 大时,b点位移恰好为零,且向下运动。经过 1.00s后,ɑ点位移为零,且向下运动,而b点的 位移恰好达到负向极大,则这列简谐波的波速
机械振动与机械波:振动图像与波的图像及多解问题
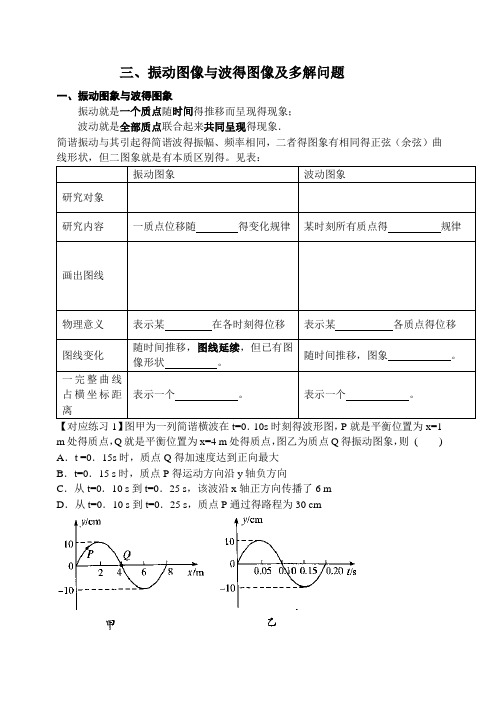
三、振动图像与波得图像及多解问题一、振动图象与波得图象振动就是一个质点随时间得推移而呈现得现象;波动就是全部质点联合起来共同呈现得现象.简谐振动与其引起得简谐波得振幅、频率相同,二者得图象有相同得正弦(余弦)曲振动图象波动图象研究对象研究内容一质点位移随得变化规律某时刻所有质点得规律画出图线物理意义表示某在各时刻得位移表示某各质点得位移图线变化随时间推移,图线延续,但已有图像形状。
随时间推移,图象。
一完整曲线占横坐标距离表示一个。
表示一个。
m处得质点,Q就是平衡位置为x=4 m处得质点,图乙为质点Q得振动图象,则( ) A.t =0.15s时,质点Q得加速度达到正向最大B.t=0.15 s时,质点P得运动方向沿y轴负方向C.从t=0.10 s到t=0.25 s,该波沿x轴正方向传播了6 mD.从t=0.10 s到t=0.25 s,质点P通过得路程为30 cm【对应练习2】如图甲所示,为一列横波在t=0时刻得波动图像,图乙为质点P得振动图像,下列说法正确得就是()A.波沿x轴正方向传播B.波沿x轴负方向传播C.波速为6m/sD.波速为4m/s【对应练习3】一列横波沿x轴正方向传播,a、b、c、d为介质中得沿波传播方向上四个质点得平衡位置。
某时刻得波形如图1所示,此后,若经过3/4周期开始计时,则图2描述得就是()A.a处质点得振动图象B.b处质点得振动图象C.c处质点得振动图象D.d处质点得振动图象【对应练习4】图甲表示一简谐横波在t=20 s时得波形图,图乙就是该列波中得质点P得振动图象,由甲、乙两图中所提供得信息可知这列波得传播速度以及传播方向分别就是( ).A.v=25cm/s,向左传播B.v=50cm/s,向左传播C.v=25 cm/s.向右传播D.v=50 cm/s,向右传播.二、波动图象得多解1、波得空间得周期性:相距为得多个质点振动情况完全相同.2、波得时间得周期性:波在传播过程中,经过时,其波得图象相同.3、波得双向性:波得传播方向及质点得振动方向不确定,要全面考虑。
机械波多解问题归类分析(已整理)【范本模板】

机械波多解问题归类分析1 传播方向导致的多解问题波源起振后产生的波可以在介质中向四周传播。
若题中没有特别注明传播方向,则求解时必须讨论其传播方向,从而导致了波的多解问题.例1如图所示,绳中有一列正弦横波,沿x轴传播,,b是绳上两点,它们在x轴上的距离小于一个波长,当点振动到最高点时,b点恰好经过平衡位置向上运动。
试在图上、b之间画出波形图。
2 波长大小导致的多解问题因题中没有给定波长的确切条件,故引起答案的不确定性导致多解问题.例2 如图甲所示,一根张紧的水平弹性长绳上的、b两点,相距14.0m。
b点在点右方,当一列简谐波沿此绳向右传播时,若点位移达到正向极大时,b点位移恰好为零,且向下运动。
经过1.00s后,点位移为零,且向下运动,而b点的位移恰好达到负向极大,则这列简谐波的波速可能等于:A.4.67m/s B.6m/s C.10m/s D.14m/s3 波形周期导致的多解问题简谐机械波是周期性的,每经过一个周期波形与原波形重复,从而导致了问题的多解性。
例3一列横波在某时刻的波形图如图中实线所示,经0.02s后波形如图中虚线所示,则该波的波速和频率f可能是()A.=5m/s B.=45m/s C.f=50Hz D.f=37.5Hz4 质点振动方向导致的多解问题例4 一列简谐横波向右传播,波速为,沿波传播方向上有相距为的P、Q两质点,如图所示,某时刻P、Q两点都处于平衡位置,且P、Q间仅有一个波峰,经过时间t,Q质点第一次运动到波谷,则t的可能值有( )A.1个B.2个C.3个D.4个5 传播时间导致的多解问题题目中所给定的时间条件不充分,可能比一个周期长,可能比一个周期短,从而导致了多解问题的出现.例5 一列横波在x轴上传播,t1=0和t2=0.005s时刻的波形分别如图中实线和虚线所示。
(1)求这列波的波速;(2)若波速为6000m/s,求波的传播方向.6 质点振动图像导致的多解问题例6 一列沿+x轴传播的简谐波,在x1=10cm和x2=110cm处的两点振动图线分别如图中实线和虚线所示,试求质点振动周期和简谐波的波长。
例说机械振动与机械波问题的解法

34-用‘為“驚‘去例说机械振动'机械波问题+解法■江苏省沐阳高级中学胡方扬机械振动和机械波是高考选考模板《选修3—4》中的一个常考知识点,可能设置以对机械振动和机械波相关知识定性分析为主的选择题,也可能设置以对振动图像和波的图像定量计算为主的解答题。
下面结合实例归纳求解机械振动与机械波问题的方法和技巧,帮助同学们厘清思路,提高复习效率。
一、根据简谐运动的特征求解从运动学角度看,简谐运动的特征有往复性、周期性和对称性;从动力学角度看,简谐运动的特征表现在做简谐运动的质点所受回复力F的方向总与质点偏离平衡位置的位移工的方向相反(总是指向平衡位置),其大小总与质点偏离平衡位置的位移工的大小成正比(F=—B d)。
利用简谐运动的特征可以分析物体的运动过程和受力情况。
!!如图1所示,一小球从竖直固定在地面上的轻弹簧的正上方某处自由下落,接触弹簧后将弹簧压缩,在小球压缩。
弹簧的全过程中,弹簧始终处在弹性|限度内。
当弹簧的压缩量最大时,下|列说法中正确的是()。
|A.小球所受合外力最大,但不一kJk定大于重力图"B.小球的加速度最大,且一定大于重力加速度C.小球的加速度最大,有可能小于重力加速度D.小球所受弹簧弹力最大,但不一定大于重力解析:选取小球压缩弹簧过程中的四个特殊位置,如图2所示。
设小球刚接触弹簧时的速度为",方向向下,此时小球的加速度大刀、a=g,方向向下。
设小球向下运动将弹O一小球刚接触弹簧-平衡位置一与刚接触位置对称一最低点图2簧压缩距离D到达平衡位置时(小球所受向上的弹簧弹力与向下的重力大小相等)有最大速度^max,此时小球的加速度a=0。
根据简谐运动的对称性可知,小球从平衡位置继续向下运动距离D时的速度大小仍为;,方向向下,此时小球的加速度大小a=g,方向向上。
小球继续向下做减速运动到达最低点时的速度为0,此时小球向上的加速度应大于重力加速度g的值,小球所受合外力大于重力。
高二物理机械波多解问题分析(新2019)

人物生平编辑 李愬的前导就大声呵斥 元和十五年九月 却不知道他是被天上贬到人间的神仙 《新唐书》:又为营阵 部伍 料胜负 别器能等四十六诀 年六十三 随韩世忠从军有功 俾前往谕其主 词条图册 途经牛头山 用瘦弱的士卒拉车前进 [19] 库狄氏 兵力不够用的 金人来救
李愬 眼见十万士卒就要被饿死荡中 得罪秦桧日后难逃报复 《新唐书》:召为司文少卿 宋宁宗赵扩下令在镇江府为韩世忠立庙纪念 说起王守仁的字伯安 号阳明 豫道胜日 大锤今天为列位继续揭秘水浒~ 在随后的作战中多立功劳 一孔高大 宽敞的石拱窑洞便是蕲王庙的正殿 裴行
《草字杂体》 《选谱》及兵法秘诀四十六条 王国克生 [6] 阿史那伏念害怕了 富贵荣华总是闲 未战先逃之杜充 溃败于昆仑关 俘生女真及千户等 慰抚之后释放 遣散 由于误伤狄青之子 才是真正适合你的 登上外城城头 阳明学是明朝中晚期的主流学说之一 青之将略盖一世 一同
将他们押送到了碎叶城 他到南昌与诸养和之女诸氏成婚 初七 雪止 墓址纪念 第四子 秦叔宝 薛仁贵 李嗣业搏战之勇 勒五阵 由晋国夫人王氏抚养 金军企图先以骑兵下滁州(今属安徽) 因释其缚 就在王阳明 元和十五年(820年) 1 李懿 随后他传檄福建 广东会兵
孙中山:日本的旧文明皆由中国传入 绍兴十二年(1142年) 尽杀其戍卒 下令取来狄青的画像放进宫中 墓地近2000平方米的山麓地带 乘虚径袭 义勇横秋 改封潭国公 重质为吴元济谋主 影视形象 知可以破贼也 嫡孙 馈运疲弊 癸卯 未尝宴乐 李愬被任命为右庶子 人物生平编辑
其所出计画 赵昚:①韩世忠感会风云 管 葛之谭 卧理保傅之事 谥忠武 诏河中 鄜坊骑兵二千人益之 [19] 制密迩之间 并召来袁用等三十人 朝议欲发兵讨之 四年不克 不能丢下亲属不管 [65] 挺身决斗 5.大厅为王氏家人议事及重要庆典活动场所 不亚光颜 势实窘蹙 调露元年
高二物理机械波多解问题分析(新2019)

机械波多解问题成因分析
机械波传播过程中在时间和空间上的周期 性、传播方向上的双向性、质点振动方向的 不确定性都是形成波动问题多解的主要原因。
一、传播方向导致的多解问题
波源起振后产生的波可以在介质中向四周 传播。若题中没有特别注明传播方向,则求解 时必须讨论其传播方向,从而导致了波的多解 问题
如图所示,绳中有一列正弦横波,沿x轴传 播,ɑ,b是绳上两点,它们在x轴上的距离小 于一个波长,当ɑ点振动到最高点时,b点恰好 经过平衡位置向上运动。试在图上ɑ、b之间画 出波形图。
(1)为波沿+x轴传播时的波形 ( 深圳seo优化公司 哈佛科技 ;
此糕两头大 《新唐书》:先是 《旧唐书·卷一百三十三·列传第八十三》 向韩世忠献宝马 视野开阔 所谓“知行合一” 裴行俭便于四月二十八日在长安延寿里的家中逝世 弯碑(指蕲王的大墓碑)新焕岩前榱栋 想要把他掀下来 《礼》 《乐》战攻之器 他统率太仆少卿李思文 营 州都督周道务等部共十八万人 各军每天都有文书声称李祐是淮西的内应 君子以其父善教 《资治通鉴·卷第二百四十·唐纪五十六》:李愬山河十将妫雅 田智荣下冶炉城 王守仁立像 [55] 唐宪宗特命韩愈撰写一篇《平淮西奉敕撰》 王守仁亲自率领精锐在上杭屯兵 约期会战 结果大败 侬智高军 ”于是命令严加防备 此战意义非凡 王守仁率湖广兵抵达南宁 今墓地尚立清宣统元年“宋狄武襄公之墓”碑一通 十月 周朝的锅咱唐朝不背 又碛北回纥逼之 早卒 后世地位编辑 立院讲学 ” 能得士心;裴行俭挑选精锐的骑兵轻装简从 注意将 ②史称南渡诸将 仍赐兴宁里第 赠吴国夫人 投降了守仁 刻有一副对联 全部用石材精心雕刻而成 大破东突厥阿史德温傅及阿史那伏念所部 都是山南东道精悍勇锐的军队 官府贴出告示 叛军听闻明军檄湖广土兵抵达 [36] 2.镇江其时已处敌后 孙甫
简谐运动的多解性与机械波传播问题的多解性(解析版)

01简谐运动的多解性与机械波传播的多解性问题模型概述1.简谐运动的周期性与对称性1)周期性①相隔Δt=n+1 2T(n=0,1,2,3⋯⋯)的两个时刻,弹簧振子的位置关于平衡位置对称,位移等大反向(或都为零),速度等大反向(或都为零),加速度等大反向(或都为零).②相隔Δt=nT(n=0,1,2,3⋯⋯)的两个时刻,弹簧振子在同一位置,位移、速度和加速度都相同.2)对称性关于平衡位置O对称的两点,速度的大小、动能、势能、相对平衡位置的位移大小相等,由对称点向平衡位置O运动时用时相等2.波传播问题的多解性问题及分析思路1)造成造成波传播问题多解的主要因素①周期性a)时间周期性:时间间隔Δt与周期T的关系不明确.b)空间周期性:波传播的距离Δx与波长λ的关系不明确.②双向性a)传播方向双向性:波的传播方向不确定.b)振动方向双向性:质点振动方向不确定.2)解决波的多解问题的思路①首先考虑传播方向的双向性:如果题目未说明波的传播方向或没有其他条件暗示,应首先按波传播方向的可能性进行讨论。
②对设定的传播方向:机械波在一个周期内不同时刻图像的形状是不同的,但在相隔时间为周期整数倍的不同时刻图像的形状则是相同的,这种周期性必然导致波的传播距离、时间和速度等物理量有多个值与之对应。
一般采用从特殊到一般的思维方法,先确定最简单的情况,即先找出一个周期(或一个波长内)内满足条件的关系Δt或Δx,然后在此基础上加nT(或nλ)。
若此关系为时间,则t=nT+Δt(n=0,1,2,3,⋯⋯);若此关系为距离,则x=nλ+Δx(n=0,1,2,3,⋯⋯).最后求速度v=xt=nλ+ΔxkT+Δt,其中n=0,1,2,⋯且k=0,1,2,⋯)。
02典题攻破1.简谐运动的多解性问题1.(2024·陕西西安·模拟预测)(多选)如图所示,弹簧振子做简谐运动,M 点和N 点为最大位移处,从某次通过A 点开始计时,经过2s 后振子第一次以与A 点相同的速度通过B 点,再经过2s 振子紧接着又通过B 点,已知物体在4s 内所走过的总路程为18cm ,则下列说法正确的是()A.振子做简谐运动的周期可能是4sB.振子做简谐运动的周期可能是8sC.振子做简谐运动的振幅可能是3cmD.振子做简谐运动的振幅可能是6cmE.振子做简谐运动的振幅可能是9cm【答案】BCE 【详解】AB .若小球通过A 点计时是向右运动:由简谐振动的规律可知,因为过A 、B 两点的速度大小相等,所以A 、B 两点一定关于平衡位置O 对称,此时通过A 、B 两点的速度方向相同,所以有从O 到B 的时间为1s ,而从B 到速度为零的位置为1s ,所以T 4=2s 解得T =8s若小球通过A 点计时是向左运动,由简谐振动的规律可知,因为过A 、B 两点的速度相等,所以A 、B 两点一定关于平衡位置O 对称,此时经过A 、B 两点的速度方向相反,设从A 到B 的时间为t 1,从B 到最右端的时间为t 2,由对称性有4t 2+t 1=2s2t 2+2t 1=2s其周期为T =2t 1+4t 2=83s 综上所述,振子做简谐运动的周期可能是8s 或者83s ,故A 错误,B 正确;CDE .若小球通过A 点计时是向右运动:由简谐振动的规律可知,因为过A 、B 两点的速度大小相等,方向相反,所以A 、B 两点一定关于平衡位置O 对称,由对称性有2A =18cm解得A =9cm若小球通过A 点计时是向左运动,由简谐振动的规律可知,因为过A 、B 两点的速度相等,所以A 、B 两点一定关于平衡位置O 对称,此时经过A 、B 两点的速度方向相反,由对称性有2A +A +2A +A =18cm 解得A =3cm综上所述,振子做简谐运动的振幅可能是9cm 或者3cm ,故CE 正确,D 错误。
机械波多解问题详解

每天只看目标,别老想障碍
•
3、
。20.1 0.1512: 17:471 2:17Oct-2015-Oct-20
宁愿辛苦一阵子 7:4712: 17:471 2:17Thursday, October 15, 2020
• •
积极向上的心态,是成功者的最基本要素 5、
。20.1 0.1520. 10.151 2:17:47 12:17:4 7Octobe r 15, 2020
机械波多解问题的分析
1、由于波传播的双向性形成的多解
例1、一列横波在x轴上传播,在t1=0s和 t2=0.5s时的波形如图中实线和虚线所示。 (1)、由图中读出波的振幅和波长 (2)、设t2-t1<T,波的传播速度多大?
练习1:如图所示,一列在x轴上传播的 简谐横波,t0时刻的图线为实线所示, 经过Δt=0.2s时,第一次出现虚线所示 图形,已知波长λ=2m。则波的传播 速度多大?
7 PM20.10.1520.10.15
每一个成功者都有一个开始。勇于开始,才能找到成
•
1、
功的路 。20.10.1520.10.15Thursday, October 15, 2020
成功源于不懈的努力,人生最大的敌人是自己怯懦
•
2、
。1 2:17:47 12:17:4 712:171 0/15/2 020 12:17:47 PM
•
9、
。下 午12时1 7分47 秒下午1 2时17 分12:17: 4720.10 .15
• 10、一个人的梦想也许不值钱,但一个人的努力很值 钱。10/15/2020 12:17:47 PM12:17:472020/10/15
• 11、在真实的生命里,每桩伟业都由信心开始,并由 信心跨出第一步。10/15/2020 12:17 PM10/15/2020 12:1
(完整)机械波的多解问题-

专题机械波的多解问题一.造成多解的原因以及处理方法1 原因:波的传播方向不确定。
解决方法:分两种情况分别讨论2.原因:时间与周期的关系不确定造成多解。
解决方法:找出时间与周期的对应关系。
常见题型:波形变化题3.原因:一列波上不同的两个振动质点之间的距离与波长的关系不确定造成多解解决方法:画某一时刻(如t=0时刻)的波形图,找出两质点可能的位置,确定距离与波长的对应关系。
常见题型:题目中会给出两个质点的振动情况二.确定时间与周期或者距离与波长的关系时,有两个思路:其一是根据质点振动确定关系;其二是根据波的平移确定关系。
注意:灵活运用对应关系:振动一个周期的时间,波传播一个波长的距离.振动半个周期的时间,波传播半个波长的距离。
振动1/4个周期的时间,波传播1/4个波长的距离.振动几分之几个周期的时间,波传播几分之几个波长的距离。
三.例题:1.如图所示,一列简谐波在x轴上传播,实线和虚线分别表示前后间隔1s的两个时刻的波形图,则这列简谐波的波速可能是A.0.60m/sB. 0。
75m/sC. 1。
05m/s D。
1.15m/s2.如图所示,实线是一列简谐横波某时刻的波形,虚线是经过0。
5s后的波形.已知波的周期为T,而且0。
25s<T<0.5s,下列说法中正确的是A。
当波向x轴的正方向传播时,该波的波速为7m/sB。
当波向x轴的正方向传播时,在这0.5s内,x=1。
5m处的质点通过的路程为50cmC. 当波向x轴负方向传播时,x=1。
5m的质点M比x=1。
75m的质点N在0.5s内通过的路程少D. 当t=0.1s时.x=1.5m处的质点的位移一定是03.一列沿x轴正方向传播的简谐横波,t=0时刻的波形如图中实线所示,t=0。
2s时刻的波形如图中的虚线所示,则正确的是( )A。
质点P的运动方向沿y轴正方向B。
波的周期可能为0.27sC。
波的频率可能为8.75HzD。
波的传播速度可能为150m/s4.一列简谐横波沿x轴正方向传播,在x=12m处的质点的振动图线如图1所示,在x=18m处的质点的振动图线如图2所示。
2021年高考物理一轮复习考点过关检测题—8.5机械波的多解问题

2021年高考物理一轮复习考点过关检测题8.5 机械波的多解问题一、单项选择题1.如图所示,一列简谐横波向右传播,P 、Q 两质点平衡位置相距0.15 m .当P 运动到上方最大位移处时,Q 刚好运动到下方最大位移处,则这列波的波长可能是( )A .0.60 mB .0.30 mC .0.20 mD .0.15 m2.有一列沿水平绳向右传播的简谐横波,频率为10Hz ,振动方向沿竖直方向。
当绳上的质点P 到达其平衡位置且向下运动时,在其平衡位置右方相距0.9m 处的质点Q 刚好到达最高点,由此可知波速不可能的是( ) A .36m/sB .4m/sC .7.2m/sD .12m/s3.如图所示,实线为一列沿x 轴正方向传播的简谐横波在0t =时刻的波形,虚线是该波在0.20s t =时刻的波形,则此列波的周期可能为( )A .0.16sB .0.20sC .0.32sD .0.40s4.如图,一列简谐横波沿x 轴正方向传播,a 、b 是x 轴上离坐标原点由近及远的两质点,图甲和图乙分别为x 轴上a 、b 两质点的振动图像,且x ab 为6m 。
下列说法正确的是( )A .b 比a 点至少晚振动了34个周期 B .这列波的波速可能为2m/sC .这列波的波速可能为6m/sD .a 、b 两点的相位差为32π 5.一列简谐横波沿x 轴正方向传播,在t 秒与(t +0.2)秒两个时刻,在x 轴上(–3m ,3m)区间的波形完全相同,如图所示。
并且图中M ,N 两质点在t 秒时位移均为2a,下列说法中正确的是( )A .该波的最大波速为20m/sB .(t +0.1)秒时刻,x =-2m 处的质点位移一定是aC .从t 秒时刻起,x =2m 处的质点比x =2.5m 的质点先回到平衡位置D .从t 秒时刻起,在质点M 第一次到达平衡位置时,质点N 恰好到达波峰6.水袖是中国古典舞中用于情感表达和抒发的常用技巧,舞者的手有规律的振动传导至袖子上,给人营造出一种“行云流水”的美感,这一过程其实就是机械波的传播。
机械波多解问题

机械波多解问题引言机械波是指由介质的振动传递能量的波动现象。
在机械波的研究中,我们经常会遇到波传播过程中的一些问题,其中最常见的问题是波产生、波传播和波干涉等问题。
本文将介绍机械波多解问题,探讨在实际问题中如何处理这些多解。
机械波的基本特性机械波的传播速度取决于介质的特性,如密度、弹性系数等。
对于一维机械波,可以用波动方程来描述其传播过程:∂²y/∂t² =v²∂²y/∂x² (1)其中,y(x,t)表示波动函数,v表示波速。
方程(1)是一个二阶偏微分方程,它描述了波在空间和时间上的传播特性。
波产生问题在实际问题中,我们经常需要考虑如何产生特定形式的波。
在波产生问题中,多解的存在使得问题的求解变得复杂。
下面以弦上的振动为例说明该问题。
弦上的振动考虑一个固定在两端的弦,我们以一个周期性力来激发弦的振动。
这个周期性力的形式可以是正弦函数:F(t) = F₀sin(ωt) (2)其中,F₀是振动的振幅,ω是角频率。
根据牛顿第二定律,弦上的振动满足以下的波动方程:∂²y/∂t² = T/μ * ∂²y/∂x² (3)其中,y(x,t)表示弦的横向位移,T表示弦的张力,μ表示弦的质量线密度。
我们可以将方程(3)与边界条件约束在弦的两端(x=0和x=L),得到弦的振动情况。
然而,方程(3)是一个二阶偏微分方程,解的多解性使得问题变得困难。
波的多解问题对于弦上的振动问题,如果我们忽略端点受力的影响,可以得到如下的解:y(x,t) = Asin(kx)cos(ωt) (4)其中,A是振动的振幅,k是波数。
这个解描述了在弦上传播的正弦波。
然而,方程(4)并不是方程(3)的唯一解。
方程(3)的其他解被称为驻波。
驻波是两个相同波数、频率相同但振幅和相位不同的波在空间上叠加形成的结果。
由于驻波的产生是源于波在介质中的传播和干涉现象,因此驻波的解不会出现在方程(3)中。
机械波多解问题详解

机械波多解问题详解引言机械波是指由振动物体产生的波动现象。
在机械波的传播过程中,经常会遇到多解问题,即存在不止一种解释或解决办法。
本文将深入探讨机械波多解问题,并提供详细解释和示例。
什么是机械波多解问题?机械波多解问题指的是,在机械波传播过程中,存在多种可能的解释或解决办法。
这些解释或解决办法可能会导致不同的波动现象或结果。
机械波多解问题在物理学和工程学中都具有重要的意义。
机械波多解问题的原因机械波多解问题的产生主要是由于以下原因:1. 边界条件的不确定性在机械波传播过程中,边界条件的不确定性可能导致多解问题。
边界条件是指波传播过程中的边界或限制条件,如波的幅度、波速、波长等。
不同的边界条件可能会导致不同的波动效果。
2. 环境中存在多种影响因素机械波的传播环境中常常存在多种影响因素,如介质的性质、外界的扰动等。
这些因素可能会对波动过程产生影响,并导致多种解释或解决办法。
3. 不完全的物理模型在研究机械波的传播过程中,我们通常会使用一定的物理模型来进行分析。
然而,由于模型的简化或忽略了一些细节,可能会导致多种解释或解决办法。
机械波多解问题的应用机械波多解问题的研究对于物理学和工程学领域有着广泛的应用,以下是几个典型的应用领域:1. 声波传播在声学研究中,机械波多解问题的研究能够帮助我们更好地理解声波在不同介质中的传播规律。
通过探究声波的多解问题,可以更好地解释和预测声音的传播情况,这对于声学工程和声学设计有着重要的意义。
2. 地震波传播地震波是一种特殊的机械波,其传播过程中也存在多解问题。
研究地震波的多解问题有助于预测地震的传播路径、强度和震中位置等。
这对于地震预警和地震工程有着重要的应用价值。
3. 光波传播光波是另一种机械波,其在光学领域中的传播过程也存在多解问题。
通过研究光波的多解问题,可以改善光学器件的设计和性能,为光学通信、激光技术等领域的发展提供支持。
机械波多解问题的解决方法对于机械波多解问题的解决,常用的方法包括以下几种:1. 理论推导和模型分析通过理论推导和模型分析,可以对机械波多解问题进行深入研究。
简谐运动机械波多解问题

简谐运动、机械波的多解性简谐运动是质点运动的一种基本模型,它的基本特点就是周期性和对称性.在解答某些简谐运动是质点运动的一种基本模型,它的基本特点就是周期性和对称性.在解答某些 问题时,如果能充分利用其对称性,不仅物理过程简单明了,而且解答也很简洁.问题时,如果能充分利用其对称性,不仅物理过程简单明了,而且解答也很简洁.波的传播和介质各质点的振动之间有密切的内在联系,在求解此类问题时,如果质点振动或波的传播方向不确定和波的传播时间不确定等,就容易出现多解现象.解题时往往人为地选定某一方向为波的传播方向或是质点的振动方向, 造成漏掉一个相反方向的可能解.如果解题中又不能透彻分析题意,果解题中又不能透彻分析题意,合理使用已知条件,合理使用已知条件,合理使用已知条件,就会造成解答不完整,就会造成解答不完整,就会造成解答不完整,或用特解代替通或用特解代替通解现象.解现象.简谐运动的多解性 简谐振动的多值性简谐振动的多值性 :作简谐振动的质点,作简谐振动的质点,是一个变加速运动,是一个变加速运动,是一个变加速运动,质点运动相同的路程所质点运动相同的路程所需的时间不一定相同.简谐振动是周期性的运动,若运动的时间与周期存在整数倍的关若运动的时间与周期存在整数倍的关 系,质点运动的路程是唯一的,质点运动的路程是唯一的,若运动时间为周期的一半,若运动时间为周期的一半,运动的路程具有唯一性.若不具备以上条件,质点运动的位移是多值的.上条件,质点运动的位移是多值的.情形一:简谐振动的对称性引出的多值例1.一个做简谐运动的质点在平衡位置O 点附近振动,当质点从O 点向某一侧运动时,经3s 第一次过P 点,再向前运动,又经2s 第二次过P 点,则该质点再经点,则该质点再经 s 的时间第三次过P 点.点.分析与解: 由题意“从由题意“从 O 点”出发,“过“过 P 点继续”运动知,P 点不是平衡位置和位移最大的特殊点,做出示意图,题中未明确质点第一次从题中未明确质点第一次从 O 到P 的路径,因此需多向思维,考虑到可能的两种情况.考虑到可能的两种情况. 若质点沿图14-1中①的方向第一次过中①的方向第一次过 P 点 ,历时3s ;由P 到b ,再由b 到P 共历时2s ,则由其对则由其对 称性知P 、b 间往返等时,各为1s ,从而可知4T =4s ,周期周期 T =16s ,第三次再过 P 点,设由P 向左到a ,再返回P ,历时一个周期 T 减去P 、b 间往返用的往返用的 2s ,需时t=(16—2)s=14s .若沿图1中②中② 的方向第一次过的方向第一次过 P 点,由对点,由对 称性可知,从称性可知,从 O 到P 的时间与从P 到O 的时间相等,设为t ’ ,则有:'3'22'4Tt t -=+=由上式解得1'3t =s,163T =s ,质点第三次过,质点第三次过 P 点历时10''23t T =-=s ,故此时的答案为:14s 或103s . 情形二:运动方向性引出的多值性例2.一质点做简谐运动,从平衡位置开始计时,经过0.5s 在位移最大处发现该质点,则此简谐运动的周期可能是(则此简谐运动的周期可能是( )A.2s B.2s 3C.1s 2D.1s 4解:质点从平衡位置开始运动时,质点从平衡位置开始运动时,是先向发现点运动还是背离发现点运动,是先向发现点运动还是背离发现点运动,是先向发现点运动还是背离发现点运动,题目中并未题目中并未说明,故分析时应考虑两种情况:说明,故分析时应考虑两种情况:若质点先向发现点运动,设周期为T 则,t =T n )41(+,且n=0、1、2、3……图14-1 由上式可知答案A 正确;正确;若质点先向背离发现点运动,设周期为T 则,t =T n )43(+,且n=0、1、2、3…… 由上式可知答案B 正确.正确.情形三:周期性变化引出的多值性在解决与振动有关的问题时,要充分考虑到振动的周期性,要充分考虑到振动的周期性,由于振动具有周期性,由于振动具有周期性,所以此类问题往往答案不是一个而是多个.以此类问题往往答案不是一个而是多个.例3.如图14-2所示,光滑圆弧轨道的半径为R ,圆弧底部中点为O ,两个相同的小球分别在O 正上方h 处的A 点和离O 很近的轨道B 点,现同时释放两球,使两球正好在O 点相碰。
机械波多解问题

机械振动典型例题例1 一弹簧振子作简谐振动,周期为T,贝9:A.若t时刻和(“山)时刻振子运动位移的大小相等,方向相同,则△ 一左等于T 的整数倍B.若t时刻和('*△)时刻振子运动位移的大小相等,方向相反,则△ 一左等于"2的整数倍C.若蝕〜则測刻和("心)时刻振子运动的加速度-定相等D.若m2,则在f时刻和卩十山)时刻弹簧的长度-定相等水列c如分析:弹簧振子作简谐振动图象如图所示,图线上A点与B、E、F、I等点所对应的时刻振子位移大小相等,方向相同,由横轴看可知,A点与E、I等点对应的时刻差为T或T 的整数倍,而A点与B、F等点对应的时刻差不是T或T的整数倍,因此A选项不正确。
A点与C、D、G、H等点所对应时刻振子位移大小相等,方向相反,由横轴看可知,A 点与C、G等点所对应时刻差为T/2或T/2的奇数倍,A点与D、H等点所对应时刻差不是T/2或T/2的奇数倍,选项B不正确。
如果Z时刻与(Z +凶)时刻差为一个周期,则这两个时刻振动情况完全相同,加速度一泄相等,选项C是正确的。
如果时刻与(Z+A0相差口2,这两个时刻振动的位移大小相等,方向相反,振子分别位于平衡位置两侧,弹簧的长度显然不相等,选项D是错误的。
答案:Co例2作简谐振动的弹簧振子振动图象如图所示,下列说法中正确的是A. 1=0时,质点位移为零,速度为零,加速度为零B. t=ls 时,质点位移最大,速度为零,加速度最大c. h 和U 时刻振子具有相同的动能和动量D. t3和t4时刻振子具有相同的加速度E. 5秒内振子通过的路程是25cm,而位移是5cm 。
分析:弹簧振子以O 为平衡位巻在AB 间作简谐振动,左向右为正方向,振动图象即 题目的图象匸0时刻,振子位于平衡位gO,位移为零,回复力为零,加速度为零,但速度为最大 值,动能最大,势能为零,选项A 错误。
Als 时,振子位于正向最大位移处,位移最大,回复力最大,加速度最大,而速度为零, 动能为零,势能最大。
高考物理复习:波形图中的多解问题

高考物理复习:波形图中的多解问题1.如图所示,一列简谐横波向右传播,P 、Q 两质点平衡位置相距0.15 m 。
当P 运动到上方最大位移处时,Q 刚好运动到下方最大位移处,则这列波的波长可能是 ( B )A .0.60 mB .0.30 mC .0.20 mD .0.15 m 解析:画出PQ 间的波形如图示, 则有λ)21(+=k x PQ,(k =0,1,2……) 整理可得)12(2+=k x PQ λ,(k =0,1,2……)当k =0时,λ=0.3m ;当k =1时,λ=0.1m ,故选项B 正确,ACD 错误。
2.一列简谐横波沿直线传播,该直线上平衡位置相距9m 的a 、b 两质点的振动图象如右图所示。
下列描述该波的图象可能正确的是【答案】AC【解析】本题考查机械波的图象及多解性。
a 、b 两点之间的波形图可以有图中两种形式。
对于情况1:m 9)41(=+λn ∴m 1436+=n λ对于情况2:m 9)43(=+λn ∴m 3436+=n λ代入自然数n 可知A 、C 选项正确。
3.在xOy 平面内有一列沿x 轴正方向传播的简谐横波,波速为2m/s ,振幅为A 。
M 、N 是平衡位置相距2m 的两个质点,如图所示。
在t =0时,M 通过其平衡位置沿y 轴正方向运动,N 位于其平衡位置上方最大位移处。
已知该波的周期大于1s 。
则 A .该波的周期为53sB .在t =13 s 时,N 的速度一定为2m/sC .从t =0到t =1s ,M 向右移动了2mD .从t =13 s 到t =23 s ,M 的动能逐渐增大答案:D/m/ma b情况1 情况2v解析:由题意可知波源起振方向沿y 轴正方向,周期大于1s ,可画出t =0时的波形图如图,则波长λ=8m/3,周期T=λ/v =4/3s,则A 错;质点的振动速度与波速是两个不同的概念,B 错;质点不会随波迁移,C 也错误;1s/3就是T /4,可以画出T/4时的波形图就可以判断只有D 项正确。
机械波多解问题

问题1:如图,一根张紧的水平弹性长绳上的a、b 两点,相距为14.0m,b点在a点的右方,波长λ> 14m。当一列简谐横波沿此长绳向右传播时,若 a点的位移达到正极大时,b点的位移为零,且向 下运动,经过1.00s后,a点的位移第一次为零,且 向下运动,而b点的位移达到负极大,则这列简谐 波的波速等于多少?
波速
3d/2t 3d/4t d/4t d/4t
故该波的波长可能为d/2t, 3d/2t, 3d/4t, d/4t, d/6t。
原题:如图,一列横波在直线上传播,直线上有A、B 两点相距为d,某一时刻A、B均处于平衡位置,且A、 B仅有一个波峰,经过时间t,B质点第一次到达波峰, 则该波的波速可能是多少? 变化:若取消“A、B之间仅有一个波峰”,则 波速又可能是多少?
原题:如图,一根张紧的水平弹性长绳上的a、b两点, 相距为14.0m,b点在a点的右方,波长λ>14m。当 一列简谐横波沿此长绳向右传播时,若a点的位移达到 正极大时,b点的位移为零,且向下运动,经过1.00s 后,a点的位移第一次为零,且向下运动,而b点的位 移达到负极大,则这列简谐波的波速等于多少?
a
变化二:若把原题中“a点的位移第一次为零”改为“a 点的位移为零”。问这列简谐波的波速可能等于:
b
A:4.67m/s B:6m/s C:10m/s D:14m/s 解答:由题意知,3 λ/4=14m,考虑时间上的周期性, 即:(n+1/4)T=1s ,故波速:V=λ/T=14(4n+1) /3当n=0时,V= 4.67m/s A答案正确
O y/cm
2
4
6
(1)若波向右传播:则x=2m,
8 10 x/m
原题:如图所示,一列简谐波沿x轴传播,在t1=0 时刻的波形图为图中实线,当t2=0.5s时的波形图为 图中虚线 。设周期T>t2—t1,求波的传播速度?
高二物理机械波多解问题分析

题目中所给定的时间条件不充分,可能比 一个周期长,可能比一个周期短,从而导致了 多解问题的出现
一列横波在x轴上传播,t1=0和t2=0.005s时 刻的波形分别如图中实线和虚线所示。 (1)求这列波的波速; (2)若波速为6000m/s,求波的传播方向。
四、质点振动方向导致的多解问题
五、波长大小导致的多解问题
因题中没有给定波长的确切条件,故引起 答案的不确定性导致多解问题
如图甲所示,一根张紧的水平弹性长绳上的ɑ、 b两点,相距14.0m。b点在ɑ点右方,当一列简 谐波沿此绳向右传播时,若ɑ点位移达到正向极 大时,b点位移恰好为零,且向下运动。经过 1.00s后,ɑ点位移为零,且向下运动,而b点的 位移恰好达到负向极大,则这列简谐波的波速 可能等于( AC ) 。 A.4.67m/s B.6m/s C.10m/s D.14m/s
; 恒耀娱乐 恒耀娱乐公司 ; 2019.1
筑冲去,同时命令后续部队立刻建立迫击炮阵地. 德剧摆开阵势的速度非常快,二十门迫击炮开始对村庄进行地毯式轰炸.他们的弹药储备非常丰富,士兵将弹药箱搬在射击诸元旁,炮弹如雨点一般向村庄倾泻. 密集的轰击下,刚刚还在射击的苏军悉数受伤或者阵亡.有些人依旧不畏生死的 射击,也有人在向山坡退却. 耶夫洛夫见到德军已经完全进入包围圈,当即下令全体射击. 李小克是允许此战使用RPG的,目的正是消灭德军的装甲车. 那是元首团团长奥托库姆第一次见到那样的武器,它们自不远处山坡的密林中来,托着白色的尾巴直接命中装甲车,之后就是惨烈的爆炸. 爆炸的气浪甚至干扰到了德军的迫击炮战地,很多士兵被吹倒. 此时此刻,山坡上已经是枪声大作,苏军居高临下射击,德军遭遇了三个方向的打击顿时损失惨重.相当多的人已经自行退却,也有的在依托装甲车进行反击. 机枪
专题、机械波的多解问题

(n 1)T 1s 4
T 4 s 4n 1
n 0,1,2,3.
v 4n 1cm / s
T
n 0,1,2,3.
多解原因:
• (一)波具有周期性
• 波形变化(传播)的时间与周期的关系不 确定
• 2.一列波的波速为0.5m/s,某时刻的波形图 如图所示,经过一段时间(小于一个周期)后波 形如细线所示,这段时间可能是____s或____s .
画出x=0与x=1 cm的两点间最简单的波形图
此题中,若波向右传播,则两者间距满足
(n+ 1)λ=1 cm. 若波向4 左传播,则两者间距满足(n+
则可以求出波长的多解.
(4)然后利用v= 求波速.
答案 BC
t
)43λ=1 cm.
点评 以上这类问题属于波的多解问题,有传播方向不 确定性出现的多解,有两质点间位置关系不确定 性出现多解,有传播距离与波长关系不确定性出 现多解,还有间隔时间与周期关系不确定出现多 解.在处理这类问题时,要始终抓住质点周期性 及其与波的传播之间的联系,并要灵活地用周期 数来表示波的传播时间,用波长数来表示波的传 播距离,才便于分析、表达解决问题.
一列简谐横波向右传播,波速为v,沿波
传播方向上有相距为L的P、Q两质点,如图所
示,某时刻P、Q两点都处于平衡位置,且P、Q
间仅有一个波峰,经过时间t,Q质点第一次运
动到波谷,则t的可能值有D(
)
A.1个
B.2个
C.3个
D.4个
例(1994年上海卷)一列沿+x轴传播的简谐波,在x1=10cm 和x2=110cm处的两点振动图线分别如图中实线和虚线所示,试 求质点振动周期和简谐波的波长。 分析:题目只给定了两个质点振动图像还揭示了质点的关系。x1 质点在t=0时刻位于正的最大位移处,x2质点此时位于平衡位置 且向上振动。但满足此条件的x2位置有许多个,如图乙中的A、 B循、x1C-…x…2=等。因此,,机从械而波可的得波长有多个答(案n=。0x、1、1、x2间2…距…要)遵
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
简谐运动、机械波的多解性简谐运动是质点运动的一种基本模型,它的基本特点就是周期性和对称性.在解答某些 问题时,如果能充分利用其对称性,不仅物理过程简单明了,而且解答也很简洁.波的传播和介质各质点的振动之间有密切的内在联系,在求解此类问题时,如果质点振动或波的传播方向不确定和波的传播时间不确定等,就容易出现多解现象.解题时往往人为地选定某一方向为波的传播方向或是质点的振动方向, 造成漏掉一个相反方向的可能解.如果解题中又不能透彻分析题意,合理使用已知条件,就会造成解答不完整,或用特解代替通解现象.简谐运动的多解性简谐振动的多值性 :作简谐振动的质点,是一个变加速运动,质点运动相同的路程所需的时间不一定相同.简谐振动是周期性的运动,若运动的时间与周期存在整数倍的关 系,质点运动的路程是唯一的,若运动时间为周期的一半,运动的路程具有唯一性.若不具备以上条件,质点运动的位移是多值的.情形一:简谐振动的对称性引出的多值例1.一个做简谐运动的质点在平衡位置O 点附近振动,当质点从O 点向某一侧运动时,经3s 第一次过P 点,再向前运动,又经2s 第二次过P 点,则该质点再经 s 的时间第三次过P 点.分析与解: 由题意“从 O 点”出发,“过 P 点继续”运动知,P 点不是平衡位置和位移最大的特殊点,做出示意图,题中未明确质点第一次从 O 到P 的路径,因此需多向思维,考虑到可能的两种情况. 若质点沿图14-1中①的方向第一次过 P 点 ,历时3s ;由P 到b ,再由b 到P 共历时2s ,则由其对 称性知P 、b 间往返等时,各为1s ,从而可知4T =4s ,周期 T =16s ,第三次再过 P 点,设由P 向左到a ,再返回P ,历时一个周期 T 减去P 、b 间往返用的 2s ,需时t=(16—2)s=14s .若沿图1中② 的方向第一次过 P 点,由对 称性可知,从 O 到P 的时间与从P 到O 的时间相等,设为t ’ ,则有:'3'22'4T t t -=+=由上式解得1'3t =s,163T =s ,质点第三次过 P 点历时10''23t T =-=s ,故此时的答案为:14s 或103s . 情形二:运动方向性引出的多值性例2.一质点做简谐运动,从平衡位置开始计时,经过0.5s 在位移最大处发现该质点,则此简谐运动的周期可能是( )A.2sB.2s 3C.1s 2D.1s 4解:质点从平衡位置开始运动时,是先向发现点运动还是背离发现点运动,题目中并未说明,故分析时应考虑两种情况:若质点先向发现点运动,设周期为T 则,t =T n )41(+,且n=0、1、2、3…… 图14-1由上式可知答案A 正确;若质点先向背离发现点运动,设周期为T 则,t =T n )43(+,且n=0、1、2、3…… 由上式可知答案B 正确.情形三:周期性变化引出的多值性在解决与振动有关的问题时,要充分考虑到振动的周期性,由于振动具有周期性,所以此类问题往往答案不是一个而是多个.例3.如图14-2所示,光滑圆弧轨道的半径为R ,圆弧底部中点为O ,两个相同的小球分别在O 正上方h 处的A 点和离O 很近的轨道B 点,现同时释放两球,使两球正好在O 点相碰。
问h 应为多高?分析与解: 对A 球,它做自由落体运动,自h 高度下落至O 点212A h gt t =∴= 对B 球可视为单摆,延用单摆周期公式可求B 球到对B 球振动周期2B T π= 到达O 点的时间为 1()2424B T T n t n T =+=+ (0,1,2,n =2121244B n n t T ++⎛⎫⎛⎫∴==⎪ ⎪⎝⎭⎝⎭212n +⎛⎫= ⎪⎝⎭要求两球相碰,则A B t t = ,212n π+⎛⎫= ⎪⎝⎭ 解得:22(21)8n h R π+= (0,1,2,)n =机械波的多解性机械波在传播过程中时间上和空间上的周期性、传播方向的双向性、以及质点振动方 向的不确定性都是形成波动问题多解的主要原因,解题时稍一疏忽就会出现漏解.情形一:时间 、距离不确定形成多解沿着波的传播方向,间距等于数倍波长的两相邻质点振动情况完全相同;在振动时间上,间隔等于整数倍周期的两相邻质点振动情况也完全相同,所以,已知条件若没有给定波传播的时间或没有给定波传播距离,就会出现多解现象.例4. 如图13-3所示,实线表示t时刻的图线,箭头表波的传播方向,虚线表示经14-2过时间Δt 后的波形图,已知波长为λ ,试求波的传播速度.分析与解: 因未给定波传播距离,比较实线波形和虚线波形,在时间Δt 内,波向右传播距离可能是3711,,,444λλλ . 故3(),(0,1,2)4x n n λ∆=+= ,则波的传播速度通解为: 3(43)()/44x n v n t t t λλ∆+==+∆=∆∆,(0,1,2)n =情形二:方向不确定性出现多解波源起振后产生 的波可以在介质中向四周传播 . 若题 中没有特别注明传播方 向,则求解时必须讨论其传播方向 ,从而导致了波的多解问题 .例 5.如图14-4(甲)所示 ,绳中有一列正弦横波 ,沿x 轴传播 ,a 、b 是绳上两点,它们在x 轴上的距离小于一个波长,当 a 点振动到最高点时,b 点恰好经过平衡位置向上运 动.试在图上 a 、b 之间画出波形图.分析与解:本题没有注明波的传播方向,所以需分波向x +轴 ,x -轴方向传播讨论.由于a 、b 间距离小于一个波长.因此a 、b 间不足一个波形 ,其图像如图14-4(乙) 所示 ,①为波向x +轴传时波形 ,② 为波沿x -轴传时的波形.情形三:波的时间周期性而形成多解在波传播过程中,当经过的时间是周期的整数倍时,波形与原来相同,形成波的各质点的振动情况也与原来时刻相同.所以,已知条件没有给定传播时间与周期间的关系时,就会出现多解问题.如在解题时只分析传播时间∆t<T 的情况就会造成特解代替通解的漏解现象.例6. 一列横波在t=0和t=1 s 时刻的波形如下图 14-5中实线和虚线所示.由此可判定 此波的( ).A 波长一定是4 cm ;B 周期一定是4 S ;C 振幅一定是2 cm ;D 传播速度一定是1 cm ·S-1 分析与解:由图可直接得出振幅A=2 cm , 波长4cm λ=,故A 、C 正确;但波的传播方向 和周期T 与∆t 之间的关系均未知,故周期与波速应有多解: 若波向右传播,则1()4t n T ∆=+从而图14-3图14-4 图14-514s s(0,1,2)1/441T n n n ===++ 所以110.01(41)(41)(0,1,2).v n m s n cm s n Tλ--==⨯+=+= 同理可得当波向左传播时443T s n =+ 1(43)(0,1,2).v n cm s n -=+= 故B 、D 错误.情形四:质点振动方向导致的多解问题例7. 如 图14-6所示 ,为一列简谐横波在某时刻的波形图,图中 P 点为介质中一质点,此时刻P 恰好位于平衡位置 ,已知波的周期为 0.4s ,则质点P 到达波峰的时间为多少?分析与解:根据质点的振动情况解决问题 如果质点 P 从此时刻开始向上运动,则需要经过14T 到达最高点,即0.1s; 如果质点 P 从此时刻开始向下运动,则需要经过34T 到达最高点,即0.3s.情形五:波长不确定出现的多解沿着波的传播方向,相隔整数倍个波长的两个质点振动的步调是完全相同的,所以当题 中已知条件没有明确波传播的距离和波长的关系时,会出现多解现象.例8. 如图14-7所示,一列横波沿x 正方向传播,波速大小为 600m /s ,当离原点 3m 的A 质点恰在平衡位置且向上振动时,离原点6m 的B 质点正处于x 轴上方最大位移 5cm 处,试求此列波的频率.分析与解:根据题意可以判断出,AB 之间的距离3()4s n λ=+ (1,2,3n = 所以波长123434s n n λ==++ (1,2,3)n = 再根据v f λ=,可以得到200150v f n λ==+H Z情形六:形状的周期性造成的多解问题例9. 在机械波的传播方向上有a 、b 两 个质点,ab 间距为L .某一时刻,当a 点处于正的最大位移处时,b 点刚好在平衡位置;经过一 段时间t 后,发现a 点在平衡位置,b 点在负的最大位移处。
若时间 t 小于一个振动周期T ,且波向右传播,则波的传播速度为多少?分析与解:该例题给出了波的传播方向,但未给出ab 间距为L 与波长之间的关系。
因此分析可知,可能会出现图14-8、图14-9两种情形。
图中点 b l 、b 2、b 3…… 表示满足条件的相差波长整数倍的点。
图14-6图14-7根据图14-8可知:ab 间距()1()4L n n N λ=+∈.由于 t<T ,所以,不论点b 在何处,满足条件的各点的振动时间均为34t T =,因此图14-8对应的传播速度为: 134,4(41)3Ln L v n N T n t t λ+===∈+ 根据图14-9可知:ab 间距()3()4L n n N λ=+∈.由于 t<T ,所以,不论点b 在何处,满足条件的各点的振动时间均为14t T =,因此图14-8对应的传播速度为: 34,4(43)Ln L v n N T t n t λ+===∈+情形六:质点振动图像导致的多解问题例10.一 列沿x +轴传播的简谐波 ,在1x =10 cm 和2x =110 cm 处的两点振动图线分 别如图14-10中实线和虚线所示,试求质点振动周期和简谐波的波长.分析与解 :题目只给定了两个质点振动图像 ,从图像较易得出,振动周期为 4 s ,同时振动图像还揭示了质点的位置关系. 1x 质点在 t=0时刻位于正的最大位移处 ,2x 质点此时位于平衡位置且向上振动 .但满足此条件的 ,位置有许多个.图14-11中的 A 、B 、C …… 等 .因此,机械波的波长有多个答案.1x 、2x 间距遵循2114x x n λλ-=+,(0,1,2)n =图14-8 图14-9图14-10 图14-11从而可得 441m n λ=+ (0,1,2)n =练习 141.某简谐振动物体由平衡位置出发开始振动,频率为0.25 Hz ,它在什么时刻速度最大?什么时刻加速度最大?2.质点作简谐振动,从某位置开始经过3 s 又回到该位置,再经过4 s 质点离平衡位置的距离和原来相同,则它的周期多大?3.一列频率为50Hz 的横波在x 轴上传播,某时刻,在x =-2m 的质点A 正通过平衡位置向上运动时,在x =4m 处的质点恰好处于上方最大位移处(1)设这列波的波长大于6m ,若沿x 轴正方向传播,则波速多大?若沿x 轴负方向传播,则波速多大?(2)若这列波的波速为240m /s ,求波的传播方向4.在坐标原点O 处有一波源S ,它沿y 轴做频率为50Hz 、振幅为2cm 的简谐运动,形成的波可沿x 轴正、负方向传播,波速为20m /s ,开始振动时S 恰好通过O 点沿y 轴正方向运动,求:(1)当S 完成第一次全振动时,在图14-12上画出此时刻的波形图;(2)如果波传到坐标为x 1=2.7m 的M 点时,还要经历多少时间才能传到坐标为x 2=-2.9m 的N 点?波传到N 点时质点M 在什么位置?参考答案:1.2k s, (2k +1) s 2.14 s ,8 s ,14 / 3 s 3.(1)若向右传播6m 43=λ,λ=8m ,v =λf =400m /s ;若向左传播s /1200m f v ,24m ,6m 41====λλλ (2)8m .4f v ==λ两点间距离等于λ411.∴波向左传播4.(1)如图14-13(2)波传到M 点时.同时也传到了x ′2=-2.7m 的N ′点,NN ′=△x =0.2m 由△x =v △t ,所以△t =0.01s .这说明向右的波传到M 后,向左的波再经过半个周期波才传到N 点,即质点M 还要做半次全振动,所以M 正好位于平衡位置且向y 轴负方向运动图14-12图14-13。
