安徽省滁州市高一下学期数学6月月考试卷
滁州市高中高一数学下学期第二次月考试题

关中地区民间饮食之营养剖析作者:段晓艳来源:《中国科技纵横》2012年第09期陕南东西部狭长的八百里秦川,也就是关中平原。
它东起潼关,西至宝鸡,南接秦岭,北抵陕北高原,号称“八百里秦川”,包括了宝鸡,咸阳、西安、铜川、渭南五个地市,古有“天府之国”的称誉,是陕西饮食民俗文化的代表性地区。
山不同景,水不同源,山水不同,则风情大异。
这方水土,也不例外,自有其风情风味所属。
对关中人来说最喜欢的主食莫过于麦面了。
当地平原的钙质黄土,兼之气候作用,生长的小麦相对其他地区受土时间要长,故而面粉筯道白晳、易揉易和。
儿时的记忆中就有“一天不吃面,就像没吃饭”的描述。
女孩子更是从小就要学会擀面,否则在旧时有“嫁不出去”的说法。
日常生活中食用的不止有“面条像裤带”所描述的又长又宽的面,也有“薄如纸,细如线,下到锅里莲花转,挑在筷上面不断,唏溜唏溜一大碗”的精细面。
现在回想起来,这种带有乡情的面条即使不调味也是香的。
从营养学的角度分析:小麦味甘性凉,入心、脾、肾经,常食有养心益肾、健脾厚肠、除热止渴的功效。
但是关中传统民风简谱,面条的吃法多为油泼,或者干拌,从膳食平衡的角度分析缺少蔬菜类,优质蛋白的摄入。
现如今人们的生活水平提高,面食的精细程度提高,微量营养物质和膳食纤维的量也显欠缺。
因此食用时若能搭配上焯水后的青菜,或者卤汁之类的配角,做到面菜合一,肉、蛋为辅,食用后再继承下梁宝生的经典吃法,喝上热乎乎的一份面汤,可谓是“原汤化原食”,不亦美哉!!小米米饭是另一个不得不提的关中美食。
所谓的小米米饭其实就是小米稠粥,盛到碗里需要用筷子夹着食用的。
也有吃稠玉米糁的。
冬天的早晨,一家人围坐在热乎乎的炕头,守着一锅烩菜,吃着小米饭,那种温馨,温情,无不增添了关中游子恋家的切切之心,无论走到哪里都忘不了家乡的味道,忘不了家乡饭的味道。
随着气候逐渐变暖,小米饭的稠度也在降低,到了炎热的夏季,就成了小米汤了。
关中人的早晚饭,基本上粘度不同的稀饭唱主角,不是小米的,就是玉米的,八宝的。
安徽省高一下学期数学6月月考联考试卷

安徽省高一下学期数学6月月考联考试卷姓名:________ 班级:________ 成绩:________一、选择题(本大题共12小题,共60分) (共12题;共60分)1. (5分) (2019高三上·涪城月考) 设集合,,则()A .B . {1}C .D .2. (5分),设,则下列判断中正确的是()A . 0<S<1B . 1<S<2C . 2<S<3D . 3<S<43. (5分) (2019高一下·上杭期中) 中,角的对边分别为,若,则角A为()A .B . 或C .D .4. (5分)各项都是正数的等比数列的公比,且成等差数列,则的值为()A .B .C .D . 或5. (5分)(2018·河北模拟) 某几何体的三视图如图所示,其中俯视图为半圆弧且点为下底面半圆弧上一点(异于点),则关于该几何体的说法正确的是()A .B .C . 平面D . 平面6. (5分) (2019高一下·长春期末) 等比数列中,,,则的值为()A .B .C . 128D . 或7. (5分) (2018高一上·会泽期中) 关于的不等式的解集为(x1 , x2),且,则=()A .B .C .D .8. (5分) (2017高一下·怀仁期末) 等差数列的前项和为,已知,,则()A . 38B . 20C . 10D . 910. (5分)边长为5,7,8的三角形的最大角与最小角的和是()A .B .C .D .11. (5分)(2018·重庆模拟) 某几何体的三视图如图所示,其正视图和侧视图是全等的正三角形,其俯视图中,半圆的直径是等腰直角三角形的斜边,若半圆的直径为2,则该几何体的体积等于()A .B .C .D .12. (5分)等差数列{}中,,则前10项和()A . 5B . 25C . 50D . 100二、填空题(本大题共4小题,共20分) (共4题;共20分)13. (5分) (2019高三上·淮南月考) 已知不等式组表示的平面区域为,是区域内任意两点,若,则的最大值是________.14. (5分) (2020高一下·湖北期末) 若正数a,b满足,则的最小值为________.15. (5分)(2020·新沂模拟) 等比数列中,,,则数列的前项和为________.16. (5分) (2020高一下·吉林期中) 已知台风中心位于城市A东偏北(为锐角)的150千米处,以v千米/时沿正西方向快速移动,2.5小时后到达距城市西偏北(为锐角)的200千米处,若,则 ________千米/时.三、解答题(本大题共6小题,17题10分,其它均为12分,共70 (共6题;共70分)17. (10分) (2016高一下·大庆期中) 在△ABC中,内角A,B,C对边的边长分别是a,b,c,已知c=2,C= .(1)若△ABC的面积等于,求a,b;(2)若sinC+sin(B﹣A)=2sin2A,求△ABC的面积.18. (12分)设等差数列的公差为d,前n项和为,等比数列的公比为q.已知,,,.(1)求数列,的通项公式;(2)当时,记,求数列的前项和.19. (12分) (2019高一下·浙江期中) 2018年5月21日5点28分,在我国西昌卫星发射中心,由中国航天科技集团有限公司抓总研制的嫦娥四号中继星“鹊桥”搭乘长征四号丙运载火箭升空,这标志着我国在月球探测领域取得新的突破。
滁州中学中学高一下第二次月考试卷

滁州中学高一下数学第二次月考试卷(试卷总分150分、考试时间120分钟)一、选择题(每小题5分共50分) 1、下列命题中正确的是(A)若a ,b ,c 是等差数列,则log 2a ,log 2b ,log 2c 是等比数列 (B)若a ,b ,c 是等比数列,则log 2a ,log 2b ,log 2c 是等差数列(C)若a ,b ,c 是等差数列,则2a ,2b ,2c是等比数列(D)若a ,b ,c 是等比数列,则2a ,2b ,2c是等差数列 2、在ABC ∆中,bc c b a++=222,则A 等于A ︒︒︒︒30.45.60.120.D C B3、已知数列{a n }是公比q ≠1的等比数列,则在 “(1){a n a n +1}, (2){a n +1-a n }, (3){a n 3},(4){na n }”这四个数列中,成等比数列的个数是 (A)1 (B)2 (C)3 (D)4 4、在⊿ABC 中,若222sin sin sin A B C =+,则△ABC 为(A)锐角三角形 (B) 直角三角形 (C)钝角三角形 (D)不能确定 5、在ABC ∆中,︒===452232B b a ,,,则A 为(A).︒︒︒︒︒︒30.15030.60.12060D C B 或或6、若a,b,c 成等比数列,m 是a,b 的等差中项,n 是b,c 的等差中项,则=+nc m a (A)4 (B)3 (C)2 (D)1 7、若三角形三边长之比为 3∶5∶7,那么这个三角形的最大角是 (A )60° (B )90° (C )120° (D )150°8、若 x ,x+1,x+2是钝角三角形的三边,则实数 x 的取值范围是(A )0<x<3 (B )1<x<3 (C )3<x<4 (D )4<x<6 9、等比数列{a n }中,已知对任意自然数n ,a 1+a 2+a 3+…+a n =2n-1,则 a 12+a 22+a 32+…+a n 2等于(A)2)12(-n(B))12(31-n (C)14-n(D) )14(31-n10、人朝正东方向走x 千米后,向右转o150并走3千米,结果他离出发点恰好3千米,那么x 的值为(A) 3 (B) 32 (C) 3或32 (D) 311、限数列 A={a 1,a 2,…,a n },S n 为其前 n 项和,定义12s ...nns s +++为 A 的“凯森和”;如有99项的数列{a 1,a 2,…,a 99}的“凯森和”为 1000,则有 100项的数列{1,a 1,a 2,…,a 99}的“凯森和”为(A )1001 (B )991 (C )999 (D )99012、图4所示的5×5正方形表格中尚有20个空格,若在每一个空格中填入一 个正整数,使得每一行和每一列都成等差数列,则字母a(A )16(B )17(C )18 (D )19二、填空题(每小题4分共16分)11、已知等比数列{a n }中,a 1+a 2=9,a 1a 2a 3=27,则{a n }的前n 项和S n = ___________ 12、在△ABC 中,BC=2,AC=2,C=1500,则△ABC 的面积为__________ 13、在△ABC 中,若CcB b A a cos cos cos ==,则△ABC 是 14、观察下列的图形中小正方形的个数,则第n 个图中有 个小正方形.滁州中学高一下数学第二次月考答题卷(2007、5)一、选择题:(请将正确答案的代号填在答题卡内,每小题5分,共60分)二、13、______⎥⎥⎦⎤⎢⎢⎣⎡⎪⎭⎫ ⎝⎛-=n n S 21112 14、_____1______15、___等边三角形_________ 16、____2)2)(1(++n n----------座位号--------------------------------------------------三.解答题(第17,18,19,20,21题每小题12分,第22题14分,共74分) 17、(满分12分)△ABC 中,内角A ,B ,C 的对边分别为a ,b ,c ,已知a ,b ,c 成等比数列,43cos =B . (Ⅰ)求CA tan 1tan 1+的值; (Ⅱ)设c a +=⋅求,3的值。
安徽省高一下学期数学6月月考试卷

安徽省高一下学期数学6月月考试卷姓名:________ 班级:________ 成绩:________一、单选题 (共12题;共24分)1. (2分)如果a<b<0,那么下列不等式成立的是()A . ﹣<﹣B . ab<b2C . ﹣ab<﹣a2D . |a|<|b|2. (2分) (2020·合肥模拟) 已知向量,,若,则与夹角的余弦值为()A .B .C .D .3. (2分)(2018·兰州模拟) 等比数列中各项均为正数,是其前项和,满足,则()A .B .C .4. (2分)(2012·江西理) 在中,如果,则满足上述条件的三角形有()A . 1个B . 2个C . 0个D . 无数个5. (2分)某次数学测试6位同学成绩的茎叶图如下,将这6位同学成绩作为总体,从总体中任取两位同学成绩作为一个样本,则样本平均数大于总体平均数的概率是()6 8A .B .C .D .6. (2分)若方程2x-3(x-2a)=0,则x等于()A .B . -6aC . 6aD .7. (2分)数列{an}的通项公式(),若前n项的和,则项数n为()B .C .D .8. (2分) (2018高二上·沧州期中) 某产品的广告费用 (单位:万元)与销售额 (单位:万元)的统计数据如下表:根据上表可得回归方程中的为9.4,据此模型预报广告费用为6万元时销售为()A . 63.6万元B . 65.5万元C . 67.7万元D . 72.0万元9. (2分)如图,在高速公路建设中需要确定隧道的长度,工程技术人员已测得隧道两端的两点A、B到点C 的距离AC=BC=1km,且∠ACB=120°,则A、B两点间的距离为()A . kmB . kmC . 1.5kmD . 2km10. (2分) (2017高一下·安庆期末) 设Sn为等差数列{an}的前n项的和,a1=﹣2016, =2,则S2016的值为()A . ﹣2015B . ﹣2016C . 2015D . 201611. (2分)(2020·菏泽模拟) 已知向量,满足,,若,则().A . 2B . -2C .D .12. (2分)已知x+2y+3z=6,则2x+4y+8z的最小值为()A .B .C . 12D .二、填空题 (共4题;共4分)13. (1分) (2019高一下·菏泽月考) 一支田径队有男运动员人,女运动员人,现按性别用分层抽样的方法从中抽取位运动员进行健康检查,则男运动员应抽取________人.14. (1分) (2019高一下·揭阳期中) 设向量,,则,的夹角等于________.15. (1分) (2019高二上·北京月考) 等比数列的首项,前n项和为,若,则公比 ________.16. (1分) (2018高二上·舒兰月考) 在三角形ABC中, 分别是内角A,B,C所对的边,,且满足,若点是三角形ABC外一点,,,,则平面四边形OACB面积的最大值是________.三、解答题 (共6题;共65分)17. (10分)(2018·广州模拟) 设为数列的前项和,已知,.(1)证明:数列为等比数列;(2)求数列的通项公式,并判断,,是否成等差数列?18. (10分)已知函数f(x)=sin( +x)sin(﹣x)+ sinxcosx(x∈R).(1)求f()的值;(2)在△ABC中,若f(A)=1,求sinB+sinC的最大值.19. (15分) (2018高二下·定远期末) 海水养殖场进行某水产品的新、旧网箱养殖方法的产量对比,收获时各随机抽取了100个网箱,测量各箱水产品的产量(单位:kg)其频率分布直方图如下:附:0.0500.0100.0013.841 6.63510.828(1)记表示事件“旧养殖法的箱产量低于50kg”,估计的概率;(2)填写下面联表,并根据列联表判断是否有%的把握认为箱产量与养殖方法有关:箱产量箱产量旧养殖法新养殖法(3)根据箱产量的频率分布直方图,对两种养殖方法的优劣进行比较.20. (10分) (2019高一下·诸暨期中) 已知数列的前项和为.(Ⅰ)当时,求数列的通项公式;(Ⅱ)当时,令,求数列的前项和.21. (10分)求f(x)=x2+ (x2>3)的最小值.22. (10分)(2017·厦门模拟) 在△ABC中,角A、B、C所对的边分别为a,b,c,满足(2a﹣c)cosB=bcosC.(1)求B的大小;(2)如图,AB=AC,在直线AC的右侧取点D,使得AD=2CD=4.当角D为何值时,四边形ABCD面积最大.参考答案一、单选题 (共12题;共24分)1-1、2-1、3-1、4-1、5-1、6-1、7-1、8-1、9-1、10-1、11-1、12-1、二、填空题 (共4题;共4分)13-1、14-1、15-1、16-1、三、解答题 (共6题;共65分) 17-1、17-2、18-1、18-2、19-1、19-2、19-3、20-1、21-1、22-1、22-2、。
安徽省高一月考数学试题(解析版)

【注意事项】1.本试卷共4页,总分150分,答题时长120分钟,请掌握好时间.2.请将自己的姓名、准考证号用钢笔或圆珠笔填写在答题卷的相应位置上.3.考生务必在答题卷上答题,在试卷上作答无效.考试结束后,请将试卷和答题卷一并交回.一、选择题(本大题共6小题,每小题5分,共30分.在每小题给出的四个选项中,只有一项是符合题目要求的)1. 甲、乙、丙三人比赛象棋,每局比赛后,若是和棋,则这两个人继续比赛,直到分出胜负,负者退下,由另一个与胜者比赛,比赛若干局后,甲胜4局,负2局;乙胜3局,负3局,如果丙负3局,那么丙胜( )A. 0局B. 1局C. 2局D. 3局 【答案】B【解析】【分析】根据题意,和局是不计入总局数的,那么三人胜局数总和与负局数总和是一样的,则即可求解答案.【详解】由题知,总负局数为,2338++=而甲乙胜局数为,437+=故丙胜局数为.871-=故选:B2. 已知实数满足,则的值是( ) x 22114x x x x ++-=21x x -A. 2或-3B. -2或3C. -2或1D. -1或2【答案】D【解析】 【分析】利用换元法可求的值. 21x x -【详解】可化为, 22114x x x x ++-=21120x x x x ⎛⎫-+--= ⎪⎝⎭故或,结合目标式,D 正确. 11x x -=12x x-=-故选:D.3. 若m 为实数,则函数的图像与坐标轴交点的个数为( )2(2)1y m x mx =-++A. 3B. 2C. 1或2D. 2或3【答案】C【解析】【分析】就和分类讨论,对于后者再结合判别式可判断交点的个数. 2m =2m ≠【详解】当时,,函数图象与轴的交点为, 2m =21y x =+x 1,02⎛⎫- ⎪⎝⎭当,,2m ≠()224(2)240m m m ∆=--=-+>故抛物线的图象与轴有两个交点,x 故选:C4. 如图,已知AB 和AC 是圆的两条弦,过点B 作圆的切线与AC 的延长线相交于点D , 过点C 作BD 的平行线与圆相交于点E ,与AB 相交于点F ,AF =3,FB =1,,则线段CD 的长为( ) 32EF =A. B. C. D. 65874354【答案】C 【解析】【分析】结合相交弦定理、切割线定理、平行线分线段成比例等知识求得正确答案.【详解】依题意, 3,31,22AF FB CF EF CF CF ⨯=⨯⨯=⨯=由于,所以, //CF BD 238,,43CF AF BD BD AB BD ===由切割线定理得, 264,9BD CD AD CD AD =⨯⨯=由于,所以, //CF BD 333,,,4444AC AF AC AD AD CD AD AD CD AD AB ===-==所以. 264444,93CD AD CD CD CD CD ⨯=⨯===故选:C 5. 若n 是正整数,定义! (例如:、),设m =1!()()!1221n n n n =⨯-⨯-⨯⨯⨯ 1!1=2!212=⨯=+2!+3!+4!+…+2011!+2012!,则m 的末位数字为( )A. 3B. 5C. 7D. 8 【答案】A【解析】【分析】利用阶乘的定义可判断当时,的末位数为0,从而可求的末位数字.5n ≥!n m 【详解】当时,必有一个2和5,故的末位数为0,5n ≥1,2,,2,1,n n n -- !n 而,1!2!3!4!1262433+++=+++=故求的末位数字为3,m 故选:A.6. 若一个三角形至少有两条边相等,则称它为“规则三角形”.用一个正方体的任意三个顶点构成的所有三角形中,“规则三角形”的个数为( )A. 24B. 28C. 32D. 56【答案】C【解析】【分析】先计算出正方体的顶点构成的三角形的个数,再排除对角面中的任意3个顶点构成的三角形的个数,从而可得正确的选项.【详解】正方体的8个顶点可构成三角形的个数为,38C 56=因任意3个顶点,必在由顶点确定的平面中,若它们不能构成 “规则三角形”,则它们必在对角面中,故这样的不规则三角形的个数为,346C 24⨯=故“规则三角形”的个数为32.故选:C. 二、填空题(本大题共7小题,每小题6分,共42分.将答案填在答题卷中相应横线上.) 7. 在实数范围内分解因式: ______________________.326114x x x -++【答案】(1)(34)(21)x x x --+【解析】【分析】利用因式分解相关知识点化简即可.【详解】原式322665544x x x x x =--+-+()()()2615141x x x x x =-----()()21654x x x =---()()()12134x x x =-+-故答案为:(1)(34)(21)x x x --+8. 两人进行乒乓球比赛,先赢三局者获胜,决出胜负为止,则所有可能出现的情形(各人输赢局次的不同视为不同情形)共有________________种.【答案】20【解析】【分析】利用分类计数原理及排列组合即可.【详解】第一类:三局为止,共有种情形,2第二类:四局为止,共有种情形,232C 6⨯=第三类:五局为止,共有种情形,242C 12⨯=故所有可能出现的情形共有2+6+12=20种情形,故答案为:20.9. 若关于的不等式只有一个整数解2,则实数的取值范围为 ____________. x 1222a a x -<-<a 【答案】314a ≤≤【解析】 【分析】求出不等式的解后可得端点满足的不等式组,从而可求参数的取值范围.【详解】的解为, 1222a a x -<-<1222a x a -<<+因为不等式的整数解只有2,故,故, 11222223a a ⎧≤-<⎪⎨⎪<+≤⎩314a ≤≤故答案为:. 314a ≤≤10. 若不等式有解,则a 的取值范围是____________13x x a ++-≤【答案】4a ≥【解析】 【分析】求出的最小值后可求的取值范围.13x x ++-a 【详解】,当且仅当时等号成立,13134x x x x ++-≥+-+=13x -≤≤故,故,()min 134x x ++-=4a ≥故答案为:.4a ≥11. 某校派出学生204人上山植树15301株,其中最少一人植树50株,最多一人植树100株,至少有_______人植树的株数相同.【答案】5【解析】【分析】利用抽屉原理可求相同株数的最小值.【详解】植树的株数分别为,共计51种,50,51,,100 而,而, 5010050511005138252++++=⨯= 153********=⨯+故至少有一种株数为至少5人所种,故答案为:5.12. 把抛物线平移得到抛物线m ,抛物线m 经过点和原点,它的顶点为P ,它212y x =()6,0A -()0,0O 的对称轴与抛物线交于点Q ,则图中阴影部分的面积为________________. 212y x =【答案】##13.5272【解析】 【分析】利用定积分可求阴影部分的面积.【详解】平移后抛物线的方程为:,其对称轴为,顶点坐标为. ()162y x x =+3x =-93,2P ⎛⎫-- ⎪⎝⎭在中令,则,故. 212y x =3x =-92y =93,2Q ⎛⎫- ⎪⎝⎭故阴影部分的面积为:, ()0022********d (3)d |13.5222x x x x x x x ---⎡⎤-+=-=-=⎢⎥⎣⎦⎰⎰故答案为:13.513. 如图,是的内心,,则_______I ABC A 40A ∠= CIB ∠=【答案】##110 11π18【解析】 【分析】先求出,在由三角形的内心的定义得出从ABC ACB ∠+∠()11802CIB ABC ACB ∠=-∠+∠ 而解决问题.【详解】因为,40A ∠= 所以,180140ABC ACB BAC ∠+∠=-∠= 因为是的内心,I ABC A 所以, ()1118018014011022CIB ABC ACB ∠=-∠+∠=-⨯= 故答案为:. 110 三、解答题(本大题共6小题,共78分.将答案填在答题卷中相应位置处,答题应写出文字说明、证明过程或演算步骤.)14. 先化简,再求值:,其中:. 32221052422x x x x x x x x --÷++--+-()02tan60cos45x =+︒-︒【答案】.1x -【解析】【分析】利用平方差化简后可求代数式的值.【详解】原式 2102(1)2(2)(2)5(2)(1)x x x x x x x x x --=-⨯+++-+-, 22(2)(1)1222x x x x x x x x -+-=+==-+++∵()2tan 60cos 451x =+-=+∴原式=15. 已知二次函数图象的顶点M 在第二象限,且经过点A (1,0)和点B (0,1),与x 轴的另一2y ax bx c =++个交点为C .(1)求实数的取值范围;a (2)当△ABC 面积等于时,求△ABM 的面积. 32【答案】(1)10a -<<(2) 316【解析】【分析】(1)根据题设可判断,求出顶点坐标后可得关于的不等式组,从而可求参数的取值范围. 0a <a (2)根据可求,利用割补法可求△ABM 的面积.0a <【小问1详解】由题意知.0a <因为图象过点,所以,又图象过点,所以,即,(0,1)1c =(1,0)10a b ++=1b a =--故, ()()2221111124a a y ax a x a x a a ++⎛⎫=+--+=-+- ⎪⎝⎭因为顶点在第二象限,故,故. ()21021104a a a a +⎧<⎪⎪⎨+⎪->⎪⎩10a -<<【小问2详解】由(1)得,,令,得, 2(1)1y ax a x =-++0y =121,1==x x a ∴,∴. 1,0C a ⎛⎫ ⎪⎝⎭11,1AC OA OB a =-==由,解得. 111311222ABC S AC OB a ⎛⎫=⨯=-⨯= ⎪⎝⎭△12a =-于是,,∴. 2211119122228y x x x ⎛⎫=--+=-++ ⎪⎝⎭19,28M ⎛⎫- ⎪⎝⎭连接,所以. OM ABM AOB BOM AOM S S S S =+-△△△△11119311112222816=⨯⨯+⨯⨯-⨯⨯=16. 如图,已知:矩形中,,菱形的三个顶点分别在矩形ABCD 79AD AB =,=EFGH E G H ,,的边上,,连接.ABCD AB CD DA ,,3AH =CF(1)当的面积为时,求DG 的长;△FCG 3(2)当的面积最小时,求DG 的长.△FCG 【答案】(1)7DG =(2)DG =【解析】【分析】(1)作,M 为垂足,连结,可证,从而可得点F 到直线FM DC ⊥GE AHE MFG △△≌CD 的距离始终为定值3,故可求DG 的长;(2)设,则可得,故可求面积的最小值. DG x =x ≤【小问1详解】作,M 为垂足,连结, FM DC ⊥GE∵,∴,∵,∴.//AB CD AEG MGE ∠=∠//HE GF HEG FGE ∠=∠∴.AEH MGF ∠=∠在和中,,AHE △MFG △90,A M HE FG ∠=∠=︒=∴.AHE MFG △△≌∴,即无论菱形如何变化,3FM HA ==EFGH 点F 到直线的距离始终为定值3.CD 因此,解得. 1332FCG S GC =⨯⨯=△2,7GC DG ==【小问2详解】设,则由第(1)小题得,, DG x =3(9)2FCG S x =-△又在中,,∴,AHE △9AE AB ≤=22290HE AH AE =+≤∴, 21690,x x +≤≤∴的最小值为,此时 FCG S △3(92-DG =17. 已知为实数,关于的方程有且仅有三个不同的实数根.a b 、x ()22160x ax b++-=(1)求证:; 2416a b -=(2的值.a b 、【答案】(1)证明见解析(2)a =-124b =【解析】【分析】(1)原方程等价于两个一元二次方程,故根据判别式可求. 2416a b -=(2)根据题设可得,结合(1)中结果可求的值. 22a ⎛⎫-=- ⎪⎝⎭a b 、【小问1详解】由原方程得或,240x ax b ++-=240x ax b +++=其判别式分别为,2212Δ416,Δ416a b a b =-+=--因原方程有三个不等的实数根,且两个方程无公共根,所以有一个方程有两个不等实数根,而另一个方程有两个相等实根,又显然,所以,即.12ΔΔ>2Δ0=2416a b -=【小问2详解】设方程的两个不等实数根为、,240x ax b ++-=1x 2x 方程的根为,不妨设,240x ax b +++=3x 12x x >由可知.1232x x a x +=-=132,0x x x a >><依题意,得,即,222123x x x -=()()212123x x x x x +-=由根与系数关系可得,, 22a ⎛⎫-=- ⎪⎝⎭因为,联立,解得.a<02416a b -=a =-124b =18. 如图,已知:中,,过、两点的圆分别交、于点、,设、ABC A AC BC =A C AB BC D E AE 相交于点,.CD F AC AF =(1)求证:;DF DB =(2)求的度数.ADC ∠【答案】(1)证明见解析(2)60︒【解析】【分析】(1)利用同一圆弧所对圆周角相等先证明,再结合等腰三角形性质证明; DE DF =DF DB =(2)利用四点共圆的特征及同一圆弧所对圆周角相等可求答案;或者利用待定系数法求解.【小问1详解】证明:连接,∵,∴,DE AC AF =ACF AFC ∠=∠∵四点共圆,故,而,,,,A D E C ACF DEF ∠=∠AFC DFE ∠=∠∴,∴.DEF DFE ∠=∠DE DF =又∵,∴,AC BC =CAB B ∠=∠∵,∴,∴,BED CAB ∠=∠BED B ∠=∠DB DE =∴.DF DB =【小问2详解】法1:连接,由(1)知,,∴点D 是的外心,BF DF DE DB ==BEF △∴, 11802BDF BEF ∠+∠=︒∴, ()()11801801802ADC AEC ︒-∠+︒-∠=︒∵,解得.ADC AEC ∠=∠60ADC ∠=︒法2:由(1),可设,,DEF DFE x B BED y ∠=∠=︒∠=∠=︒则,180218023602()BDF EDF BDE x y x y ∠=∠+∠=︒-︒+︒-︒=︒-+︒.()BEF x y ∠=+︒又,所以,ADC AEC ∠=∠BDF BEF ∠=∠即,解得,3602()x y x y -+=+120x y +=所以,,于是,.120BDF BEF ∠=∠=︒60ADC ∠=︒19. 已知m ,n ,p 都是正整数,求证:在三个数中,至多有一个数不小,,m n p a b c n p p m m n===+++于1.【答案】证明见解析【解析】【分析】至多一个的否定为至少两个,利用反证法假设a ,b ,c 中至少有两个数不小于1,推导出矛盾的结果即可得证.【详解】假设a ,b ,c 中至少有两个数不小于1,由m ,n ,p 都是正整数不妨设,则 1,1a b ≥≥,m n p ≥+.n p m ≥+两式相加,得, 20p ≤从而,0p ≤与条件p 是正整数矛盾. 所以命题成立.。
2022-2023学年安徽省滁州市定远县高一下册第一次月考数学模拟试题(含解析)

2022-2023学年安徽省滁州市定远县高一下册第一次月考数学模拟试题(含解析)一、单选题1.(34)(12)i i ++-=()A .42i +B .42i-C .14i+D .15i+【答案】A【分析】利用复数的加法法则直接计算即可.【详解】()()(34)(12)314242i i i i ++-=++-=+.故选:A.【点睛】本题考查复数的加法运算,属于基础题.2.下列说法错误的是()A .若非零向量a b c ,,有//a b ,//b c,则//a c B .零向量与任意向量平行C .已知向量a b ,不共线,且//a c ,//b c ,则0c =D .平行四边形ABCD 中,AB CD = 【答案】D【解析】根据共线向量的定义和性质逐一判断即可选出正确答案.【详解】选项A :因为a b c r r r ,,都不是零向量,所以由//a b ,可知向量a 与向量b 具有相同或相反方向.又由//b c ,可得向量c 与向量b 具有相同或相反方向,所以向量a与向量c 具有相同或相反方向,故//a c ,故本说法是正确的;选项B :零向量与任意向量平行这是数学规定,故本说法是正确的;选项C :由// a c ,//b c ,可知:c 与向量a 具有相同或相反方向,c 与向量b具有相同或相反方向,但是向量a b ,不共线,所以0c=,故本说法是正确的;选项D :平行四边形ABCD 中,应该有AB DC =,故本说法是错误的.故选:D【点睛】本题考查了共线向量的定义和性质,考查了相等向量的定义,考查了零向量的性质,属于基础题.3.已知正方形ABCD 的边长为6,M 在边BC 上且3BC BM =,N 为DC 的中点,则AM BN ⋅=A .-6B .12C .6D .-12【答案】A【分析】以向量,BA BC 为基底,将,AM BN用基底表示,结合向量数量积的运算律,即可求解.【详解】由M 在边BC 上且3BC BM =,N 为DC 的中点,13AM BM BA BC BA =-=- ,1122BN BC CN BC CD BC BA =+=+=+ ,11()()32AM BN BC BA BC BA ⋅=-⋅+ 2215112186362BC BC BA BA =-⋅-=-=-.故选:A.【点睛】本题考查向量基本定理以及向量的数量积运算,考查计算求解能力,属于基础题.4.若向量a ,b 满足1==a b r r ,且()12a ab ⋅-= ,则向量a 与b的夹角为()A .6πB .3πC .23πD .56π【答案】B【分析】由已知条件结合数量积公式化简即可求解.【详解】因为1==a b r r ,()12a ab ⋅-= ,即212a a b -⋅= ,21cos ,2a a b a b -⋅⋅= ,求得1cos ,2a b =,所以向量a 与b的夹角为3π.故选:B5.在ABC 中,AB c = ,AC b = .若点D 满足2BD DC = ,则AD =()A .2133b c+ B .5233c b-C .2133b c-D .1233b c+【答案】A【详解】试题分析:,故选A .6.已知i 是虚数单位,复数1232,14z i z i =-+=-,则复数12z z z =+在复平面内表示的点位于A .第一象限B .第二象限C .第三象限D .第四象限【答案】C【分析】根据复数的加法运算,表示出复数z ,进而得到其在复平面内表示的点坐标,即可得到所在象限.【详解】由复数加法运算可知12321422z z z i i i=+=-++-=--在复平面内表示的点坐标为()2,2--,所以所在象限为第三象限所以选C【点睛】本题考查了复数的简单加法运算,复平面内对应的点坐标及其象限,属于基础题.7.如图所示,隔河可以看到对岸两目标A ,B ,但不能到达,现在岸边取相距4km 的C ,D 两点,测得∠ACB =75°,∠BCD =45°,∠ADC =30°,∠ADB =45°(A ,B ,C ,D 在同一平面内),则两目标A ,B 间的距离为km.AB .3C .3D .【答案】B【分析】由已知可求30CAD ∠=︒,120ACD ∠=︒,由正弦定理可求AD 的值,在BCD ∆中,60CBD ∠=︒,由正弦定理可求BD 的值,进而由余弦定理可求AB 的值.【详解】由已知,ACD ∆中,30CAD ∠=︒,120ACD ∠=︒,由正弦定理,sin sin CD ADCAD ACD=∠∠,所以·sin 4·sin120sin sin30CD ACD AD CAD ∠︒===∠︒在BCD ∆中,60CBD ∠=︒,由正弦定理,sin sin CD BDCBD BCD=∠∠,所以·sin 4sin45sin sin60CD BCD BD CBD ∠︒===∠︒在ABD ∆中,由余弦定理,222802··3AB AD BD AD BD ADB =+-∠=,解得:3AB =.所以A 与B 的距离3AB =.故选B【点睛】本题主要考查了正弦定理,余弦定理在解三角形中的应用,考查了数形结合思想和转化思想,属于中档题.8.欧拉公式cos sin ix e x i x =+(i 为虚数单位)是由瑞士著名数学家欧拉发现的,他将指数函数的定义域扩大到复数集,建立了三角函数和指数函数的关系,它在复变函数理论中占有非常重要的地位,特别是当x π=时,10i e π+=被称为数学上的优美公式.根据欧拉公式,263i i e e π+表示复数z ,则z =()A .2+BC .2D .2【答案】B【分析】根据欧拉公式将263i i e e ππ+化简为1122z i =+,再利用复数模的计算公式计算即可.【详解】根据欧拉公式有26322cos sin cos sin 6633ii e e i i ππππππ+=+++1122i -+=,所以z =,||z =故选:B【点睛】本题主要考查复数模的计算,考查学生的数学运算能力,是一道容易题.9.三棱柱111ABC A B C -中,90BAC ∠= ,AB AC a ==,111160∠=∠= AA B AA C ,1190∠=BB C ,侧棱长为b ,则其侧面积为()A .4B .22ab C .abD .2ab 【答案】C【分析】先由题中条件,得到侧面11AA B B 和侧面11AAC C 为一般的平行四边形,侧面11BB C C 为矩形,根据题中数据,分别计算三个侧面的面积,即可求出结果.【详解】如图,由已知条件可知,侧面11AA B B 和侧面11AAC C 为一般的平行四边形,侧面11BB C C 为矩形.在ABC ∆中,90BAC ∠=︒,AB AC a ==,∴BC =,∴11BCC B S b =⋅=矩形.∵111160AA B AAC ∠=∠=︒,AB AC a ==,∴点B 到直线1AA 的距离为sin 60a ︒=.∴11112AA C C AA B B S S ab ==四边形四边形.∴22S ab ab =⨯=侧.故选C【点睛】本题主要考查棱柱的侧面积,熟记棱柱结构特征以及侧面积公式即可,属于常考题型.10.下列说法中正确的个数是()①空间中三条直线交于一点,则这三条直线共面;②平行四边形可以确定一个平面;③若一个角的两边分别平行于另一个角的两边,则这两个角相等;④若,A A αβ挝,且l αβ= ,则A 在l 上.A .1B .2C .3D .4【答案】B【解析】根据空间点、直线、平面之间的位置关系的公理及定理,对每项逐一判断,即可得到本题答案.【详解】对于①,两两相交的三条直线,若相交于同一点,则不一定共面,故①不正确;对于②,平行四边形两组对边分别平行,则平行四边形是平面图形,故②正确;对于③,若一个角的两边分别平行于另一个角的两边,则这两个角相等或互补,故③不正确;对于④,由公理可得,若,,A A l αβαβ∈∈⋂=,则∈A l ,故④正确.故选:B【点睛】本题主要考查空间点、直线、平面之间的位置关系的公理及定理的应用.11.一个圆柱的侧面展开图是一个正方形,则这个圆柱的表面积与侧面积的比值是()A .142ππ+B .122ππ+C .12ππ+D .142ππ+【答案】B【分析】根据圆柱的侧面展开图是一个正方形,得到圆柱的高和底面半径之间的关系,然后求出圆柱的表面积和侧面积即可得到结论.【详解】设圆柱的底面半径为r ,圆柱的高为h ,圆柱的侧面展开图是一个正方形,2r h π∴=,∴圆柱的侧面积为2224rh r ππ=,圆柱的两个底面积为22r π,∴圆柱的表面积为22222224r rh r r ππππ+=+,∴圆柱的表面积与侧面积的比为:22222241242r r r πππππ++=,故选:B .12.PA 垂直于正方形ABCD 所在平面,连接PB ,PC ,PD ,AC ,BD ,则下列垂直关系正确的个数是()①面PAB ⊥面PBC ②面PAB ⊥面PAD ③面PAB ⊥面PCD ④面PAB ⊥面PAC A .1B .2C .3D .4【答案】B【分析】根据题意,底面为正方形且PA ⊥平面ABCD ,则BC ⊥平面PAB ;即可判断【详解】证明:对于①,因为底面为正方形所以BC AB⊥由题意可知PA ⊥平面ABCD 所以BC PA ⊥,而PA AB A = 所以BC ⊥平面PAB 又因为BC ⊂平面PBC所以平面PAB ⊥平面PBC ,所以①正确;对于②,因为AD BC ∥故由①可得AD ⊥平面PAB ,而AD ⊂平面PAD所以平面PAD ⊥平面PAB ,所以②正确③④错误,不垂直.综上可知,正确的为①②故选:B【点睛】本题考查了平面与平面垂直的判定,属于基础题.二、填空题13.在平行四边形ABCD 中1AB e = ,2AC e = ,14NC AC = ,12BM MC =,则MN = ________.(用12,e e表示)【答案】1225312e e -+【分析】根据向量的线性运算性质及几何意义,由12BM MC = 得23MC BC =,利用向量的三角形法则得BC =AC -AB ,又14NC AC = ,MN =CN -CM ,最后将AC 和AB两个向量都用1e 和2e 表示即可求得结果.【详解】如图:MN =CN -CM=CN +2BM =CN +23BC=-14AC +23(AC-AB )=-214e+212()3e e - =1225312e e -+.故本题答案为1225312e e -+.【点睛】本题是一道关于向量运算的题目,考查平面向量的基本定理,解答本题的关键是熟练掌握向量的加法与减法的运算法则,属基础题.14.如图,设A 、B 两点在河的两岸,一测量者在A 的同侧所在的河岸边选定一点C ,测出AC 的距离为50m ,45ACB ∠=︒,105CAB ∠=︒后,就可以计算出A 、B 两点的距离为______【答案】502m【分析】由ACB ∠与BAC ∠,求出ABC ∠的度数,根据sin ACB ∠,sin ABC ∠,以及AC 的长,利用正弦定理即可求出AB 的长.【详解】解:在ABC ∆中,50AC m =,45ACB ∠=︒,105CAB ∠=︒,即30ABC ∠=︒,则由正弦定理sin sin AB ACACB ABC=∠∠,得:250sin 221sin 2AC ACBAB m ABC∠==∠.故答案为:2m .【点睛】本题考查正弦定理,以及特殊角的三角函数值,熟练掌握正弦定理是解本题的关键.15.如图所示,在上、下底面对应边的比为1:2的三棱台中,过上底面一边11A B 作一个平行于棱1C C 的平面11A B EF ,记平面分三棱台两部分的体积为1V (三棱柱111A B C FEC -),2V 两部分,那么12:V V =______.【答案】3:4【解析】设三棱台的高为h ,上底面的面积是S ,则下底面的面积是4S ,计算体积得到答案.【详解】设三棱台的高为h ,上底面的面积是S ,则下底面的面积是4S ,()174233V h S S S Sh ∴=++=台,1123,743V Sh V Sh V Sh Sh ∴=∴==-.故答案为:3:4.【点睛】本题考查了三棱台的体积问题,意在考查学生的计算能力.16.如图,S 为等边三角形ABC 所在平面外一点,且SA SB SC AB ===,,E F 分别为,SC AB 的中点,则异面直线EF 与AC 所成的角为______.【答案】45°【分析】由GE AC //,得GEF ∠等于异面直线EF 与AC 所成角,通过求GEF ∠的大小,即可得到本题答案.【详解】如图,取AS 的中点G ,连接,GE GF ,则,GE AC GF SB////GEF ∴∠等于异面直线EF 与AC 所成角.设2AB =,则1,1GE GF ==.取AC 的中点M ,连接,MS MB .SA SB SC AB ===Q ,,SAC ABC ∴∆∆为等边三角形,,,SM AC BM AC SM BM M ∴⊥⊥⋂=,AC ∴⊥平面BMS ,,AC SB EG GF ∴⊥∴⊥,45GEF ∴∠=︒.所以,异面直线EF 与AC 所成的角为45︒.故答案为:45︒【点睛】本题主要考查异面直线所成角,把异面直线平移到一个面上,然后通过解三角形求角,是解决此类题目的常用方法.三、解答题17.如图所示,在ABO ∆中,14OC OA =uuu r uu r ,12OD OB =uuu r uu u r ,AD与BC 相交于点M .设OA a = ,OB b =.(1)试用向量a 、b表示OM ;(2)在线段AC 上取一点E ,在线段BD 上取一点F ,使EF 过点M ,设OE OA λ= ,OF OB μ=,求证:137λμ+=.【答案】(1)1377OM a b =+;(2)证明见解析.【解析】(1)设OM ma nb =+,由A 、D 、M 三点共线以及B 、C 、M 三点共线可得出关于m 与n的方程组,解出这两个未知数,即可得出OM 关于a 、b的表达式;(2)设EM MF η= ,利用向量的减法运算可得出11OM a b λμηηη=+++ ,结合1377OM a b =+ 可建立等式,通过化简计算可得出137λμ+=,即可得出结论.【详解】(1)不妨设OM ma nb =+.由于A 、D 、M 三点共线,则存在()1αα≠-使得AM MD α= ,即()OM OA OD OM α-=- ,于是1OA ODOM αα+=+ .又12OD OB =uuu r uu u r ,所以()121121OA OB OM a b ααααα+==++++,则()1121m n ααα⎧=⎪+⎪⎨⎪=+⎪⎩,即21m n +=.①由于B 、C 、M 三点共线,则存在()1ββ≠-使得CM MB β=,即()OM OC OB OM β-=- ,于是1OC OB OM ββ+=+.又14OC OA =uuu r uu r ,所以()1141411OA OB OM a b βββββ+==++++ ,所以()1411m n βββ⎧=⎪+⎪⎨⎪=⎪+⎩,即41m n +=.②由①②可得17m =,37n =,所以1377OM a b =+ ;(2)由于E 、M 、F 三点共线,所以存在实数()1ηη≠-使得EM MF η= ,即()OM OE OF OM η-=- ,于是1OE OF OM ηη+=+ .又OE OA λ= ,OF OB μ= ,所以111OA OB OM a b λημλμηηηη+==++++ ,所以137711a b a b λμηηη+=+++ ,则117317λημηη⎧=⎪+⎪⎨⎪=⎪+⎩,可得171371ληημη⎧=⎪+⎪⎨⎪=⎪+⎩,两式相加得137λμ+=.【点睛】本题考查了平面向量的数乘,向量的线性运算及向量表示三点共线,属中档题.18.如图,一艘船从港口O 出发往南偏东75°方向航行了100km 到达港口A ,然后往北偏东60°方向航行了160km 到达港口B .试用向量分解知识求从出发点O 到港口B 的直线距离12.065≈≈,结果精确到0.1km ).(提示:将OA ,AB 分解为垂直的两个向量.)【答案】241.3km【分析】建立直角坐标系,利用平面向量的坐标表示公式,结合平面向量加法的几何意义和坐标表示公式进行求解即可.【详解】建立如图所示的坐标系:显然907515,906030,100,160AOC BAE OA AB ︒︒︒︒︒︒∠=-=∠=-===,于是有:sin15100sin15AC AC OA ︒︒=⇒=,cos15100cos15OC OC OA︒︒=⇒=,sin 30160sin 3080BE BE BA ︒︒=⇒==,cos 30160cos 30803AE AE BA︒︒=⇒==,所以(100cos15,100sin15),(803,80)OA AB ︒︒=-= ,因为(100cos15803,100sin1580)OB OA AB ︒︒=+=+-+ ,所以有:222222(100cos15803)(100sin1580)(100cos15)(803)(100sin15)80160003cos1516000sin153560032000cos 458940289401.414145.562012.065241.3OB︒︒︒︒︒︒︒=++-+=++-++-=+=+≈+⨯=≈⨯= 19.如图所示,圆形纸片的圆心为O ,半径为6cm ,该纸片上的等边三角形ABC 的中心为O ,点D ,E ,F 为圆O 上的点,,,DBC ECA FAB 分别是以BC,CA,AB 为底边的等腰三角形,沿虚线剪开后,分别以BC,CA,AB 为折痕折起,,DBC ECA FAB ,使得D ,E ,F 重合,得到三棱锥,则当ABC 的边长变化时,求三棱锥的表面积的取值范围.【答案】(0,543【分析】根据题意,设三棱锥的底面边长为a ,则063a <<,连接OD ,交BC 与点G ,则OD BC ⊥,从而可知36,6OD OG ==,则366DG =,根据三角形的面积分别求出三棱锥的底面积和侧面积,从而得出三棱锥的表面积9S a =,根据a 的取值范围,即可求出当ABC 的边长变化时,三棱锥的表面积的取值范围.【详解】解:由题可知,等边三角形ABC 的中心为O ,圆O 的半径为6,设三棱锥的底面边长为a ,即等边三角形ABC 的边长为a ,如图,连接OD ,交BC 与点G ,由题意可知,OD BC ⊥,则233323OA a a =⨯=,6OD =,可知OA OD <36<,则063a <<1336,326OD OG === ,则366DG OD OG =-=,∴三棱锥的底面积为:213sin 6024ABC S a a a =⨯⨯⨯= △,由题可知,,,DBC ECA FAB 全等,则面积相等,∴三棱锥的侧面积为:21133333692264DBC S BC DG a a a a ⎛⎫=⨯⨯⨯=⨯⨯⨯-=- ⎪ ⎪⎝⎭△,所以三棱锥的表面积为:223339944ABC DBC S S S a a =+=+=△△,03a << 093a ∴<<,即(0,543S ∈,所以当ABC 的边长变化时,求三棱锥的表面积的取值范围是(0,543.20.如图,长方体1111ABCD A B C D -中,12,3AB BC AA ===;(1)求异面直线1A B 和CD 所成角的正切值;(2)求三棱柱11A AB D DC -的体积和表面积.【答案】(1)32(2)体积6,表面积16213+.【分析】(1)因为//AB CD ,所以1A B 与CD 所成的角即为1A B 与AB 所成的角,从而得到结果;(2)根据三棱柱的体积公式和表面积公式即可得到结果.【详解】(1)在长方体中,因为//AB CD ,所以1A B 与CD 所成的角即为1A B 与AB 所成的角,即1A BA ∠(或补角),113tan 2A A A BA AB ∠==,所以异面直线1A B 和CD 所成角的正切值为32;(2)易知三棱柱11A AB D DC -是直三棱柱,底面1A AB 是直角三角形,所以111132322A AB S A A AB =⋅⋅=⨯⨯=.又11A D 为三棱柱的高,所以111326A AB V S A D =⋅=⨯=,又四边形11A D CB 为矩形,1112,A D A B ==所以1111224,236A D CB ABCD A D DA S S S ==⨯==⨯=四边形四边形四边形,故所求表面积111112A AB A D CB ABCD A D DAS S S S S =+++四边形四边形四边形234616=⨯++=+21.如图,四边形ABCD 中,,,642AB AD AD BC AD BC AB ^===,,P ,,E F 分别在,BC AD 上,EF AB ∥.现将四边形ABEF 沿EF 折起,使得平面ABEF ⊥平面EFDC .(1)当1BE =时,是否在折叠后的AD 上存在一点P ,使得CP P 平面ABEF ?若存在,求出P 点位置;若不存在,说明理由(2)设BE x =,问当x 为何值时,三棱锥A CDF -的体积有最大值?并求出这个最大值.【答案】(1)见解析;(2)当3x =时,三棱锥A CDF -的体积V 有最大值,最大值为3【分析】(1)先找到点32AP PD =,再证明此时CP P 平面ABEF .(2)BE x =,(04),6AF x x FD x =<<=-,体积的表达式为()21333V x =--+得到答案.【详解】(1)存在点P ,使得CP P 平面ABEF ,此时32AP PD =.当32AP PD =时,35AP AD =,过点P 作MP FD P ,交AF 于点M ,连接EM ,如图,则35MP FD =.∵在四边形ABCD 中,16BE AF AD ===,∴5FD =,∴3MP =.∵3,//EC EC FD =,∴//MP EC ,且MP EC =,故四边形MPCE 为平行四边形,∴//PC ME .∵CP Ë平面,ABEF ME Ì平面ABEF ,∴CP P 平面ABEF .(2)∵平面ABEF ⊥平面EFDC ,平面ABEF ⋂平面EFDC EF =,,AF EF AF ^^平面EFDC .∵BE x =,∴(04),6AF x x FD x =<<=-,故三棱锥A CDF -的体积()()21112633323V x x x =创�=--+,当3x =时,三棱锥A CDF -的体积V 有最大值,最大值为3【点睛】本题考查了线面平行,体积的最值,先找后证是一个常规的方法,找到体积的表达式是解题的关键.22.如图,正方体1111ABCD A B C D -中,E ,F 分别为11C D ,11B C 的中点.(1)求证:B ,D ,E ,F 四点共面;(2)若AC BD P =I ,11A C EF Q =I ,1AC 与平面EFBD 交于点R ,求证:,,P Q R 三点共线.【答案】(1)证明见解析;(2)证明见解析.【分析】(1)证明EF ∥BD 即可得出结论;(2)只需说明,,P Q R 三点都是平面BDEF 和平面ACC 1A 1的公共点即可得出结论.【详解】证明:(1)连接11B D ,在正方体1111ABCD A B C D -中,∵E ,F 分别为11C D ,11B C 的中点,∴EF 是111B C D △的中位线,∴11//EF B D ,又因为11//B D BD ,∴//EF BD∴四边形BDEF 为梯形,即B ,D ,E ,F 四点共面.(2)在正方体1111ABCD A B C D -中,AC BD P =I ,11A C EF Q =I ,AAC C与平面BDEF的交线,∴PQ是平面11AC交平面BDEF于点R,又因为1AAC C与平面BDEF的一个公共点.∴R是平面11因为两平面相交的所有公共点都在这两个平面的交线上,P Q R三点共线.∴,,。
安徽省高一下学期数学6月月考试卷

安徽省高一下学期数学6月月考试卷姓名:________ 班级:________ 成绩:________一、单选题 (共12题;共24分)1. (2分) (2016高二上·赣州期中) 如果a<b<0,那么下列不等式成立的是()A .B . ab<b2C . ﹣ab<﹣a2D .2. (2分)(2018·陕西模拟) 已知向量则()A . 1B .C . 2D . 33. (2分)(2017·金华模拟) 已知a,b为实常数,{ci}(i∈N*)是公比不为1的等比数列,直线ax+by+ci=0与抛物线y2=2px(p>0)均相交,所成弦的中点为Mi(xi , yi),则下列说法错误的是()A . 数列{xi}可能是等比数列B . 数列{yi}是常数列C . 数列{xi}可能是等差数列D . 数列{xi+yi}可能是等比数列4. (2分) (2020高三上·长沙月考) 为了测量西藏被誉称为“阿里之巅”冈仁波齐山峰的高度,通常采用人工攀登的方式进行,测量人员从山脚开始,直到到达山顶分段测量,最后将所有的高度差累加,得到珠峰的高度,在测量过程中,已知竖立在点处的测量觇标高10米,攀登者们在处测得到觇标底点和顶点的仰角分别为,,则、的高度差约为()(参考数据:,, )A . 10米B . 9.66米C . 9.40米D . 8.66米5. (2分) (2019高一下·武宁期末) 一组数据的茎叶图如图所示,则数据落在区间内的概率为()A . 0.2B . 0.4C . 0.5D . 0.66. (2分) (2020高一上·昆明期中) 已知一元二次不等式ax2+bx+c≤0的解集为[1,2],则cx2+bx+a≤0的解集为()A .B . [1,2]C . [-2,-1]D .7. (2分)在数列{an}中,如果存在常数,使得an+T=an对于任意正整数n均成立,那么就称数列{an}为周期数列,其中T叫做数列{an}的周期. 已知数列{xn}满足xn+2=|xn+1-xn|,若x1=1,x2=a (),当数列{xn}的周期为3时,则数列{xn}的前2012项的和S2012为()A . 1339 +aB . 1341+aC . 671 +aD . 672+a8. (2分) (2019高二下·兴宁期中) 设两个变量x和y之间具有线性相关关系,它们的相关系数是r,y关于x的回归直线的回归系数为,回归截距是,那么必有()A . 与r的符号相同B . 与r的符号相同C . 与r的符号相反D . 与r的符号相反9. (2分)在△ABC中,AB=AC,AC边上的中线长为9,当△ABC的面积最大时,AB的长为()A . 9B . 9C . 6D . 610. (2分)(2020·湛江模拟) 已知是等差数列的前项和.若,则的值为().A . 6B . 15C . 34D . 1711. (2分)非零向量,的夹角为,且,则的最小值为()A .B .C .D . 112. (2分) (2016高一下·岳池期末) 二次不等式ax2+bx+1>0的解集为{x|﹣1<x< },则ab的值为()A . ﹣5B . 5C . ﹣6D . 6二、填空题 (共4题;共4分)13. (1分) (2018高二上·南宁期中) 某单位200名职工的年龄分布情况如图所示,现要从中抽取40名职工作样本,用系统抽样法,将全体职工随机按1~200编号,并按编号顺序平均分为40组(1~5号为第1组,6~10号为第2组,…,196~200号为第40组).若第5组抽出的号码为22,则第8组抽出的号码是.若用分层抽样方法,则40岁以下年龄段应抽取人,则 ________.14. (1分)(2020·随县模拟) 已知向量,,与的夹角为,则实数________.15. (1分) (2019高二上·咸阳月考) 设数列{an}的前n项和为Sn(n∈N*),有下列三个命题:①若{an}既是等差数列又是等比数列,则an=an+1;②若Sn=an(a为非零常数),则{an}是等比数列;③若Sn=1-(-1)n ,则{an}是等比数列.其中真命题的序号是________.16. (1分) (2019高三上·黑龙江月考) 如图,设的内角A , B , C所对的边分别为a , b ,c ,,且若点D是外一点,,,则当四边形ABCD 面积最大值时, ________.三、解答题 (共6题;共65分)17. (10分)(2017·息县模拟) 已知在数列{an}中,a1=4,an>0,前n项和为Sn ,若.(1)求数列{an}的通项公式;(2)若数列的前n项和为Tn ,求Tn .18. (10分)(2017·南海模拟) 在△ABC中,内角A,B,C的对边长分别为a,b,c,且.(1)求角B的大小;(2)若,求△ABC面积的最大值.19. (15分) (2016高三上·沈阳期中) 2015年7月9日21时15分,台风“莲花”在我国广东省陆丰市甲东镇沿海登陆,造成165.17万人受灾,5.6万人紧急转移安置,288间房屋倒塌,46.5千公顷农田受灾,直接经济损失12.99亿元,距离陆丰市222千米的梅州也受到了台风的影响,适逢暑假,小明调查了梅州某小区的50户居民由于台风造成的经济损失,将收集的数据分成[0,2000],(2000,4000],(4000,6000],(6000,8000],(8000,10000]五组,并作出如图频率分布直方图:附:临界值参考公式:,n=a+b+c+d.(1)试根据频率分布直方图估计小区平均每户居民的平均损失(同一组中的数据用该组区间的中点值作代表);(2)小明向班级同学发出倡议,为该小区居民损款,现从损失超过4000元的居民中随机抽出2户进行捐款援助,投抽出损失超过8000元的居民为ξ户,求ξ的分布列和数学期望;(3)台风后区委会号召该小区居民为台风重灾区捐款,小明调查的50户居民捐款情况如表,在表格空白外填写正确数字,并说明是否有95%以上的把握认为捐款数额多于或少于500元和自身经济损失是否到4000元有关?经济损失不超过4000元经济损失超过4000元合计捐款超过500元30损款不超过500元6合计P(K2≥k)0.150.100.050.0250.0100.0050.001 k 2.072 2.706 3.841 5.024 6.6357.87910.82820. (10分) (2016高三下·娄底期中) 设等差数列{an}的公差为d,前n项和为Sn ,等比数列{bn}的公比为q,已知b1=a1 , b2=2,q=d,S10=100.(1)求数列{an},{bn}的通项公式(2)当d>1时,记cn= ,求数列{cn}的前n项和Tn .21. (10分) (2019高二上·郑州期中) 已知,,且 .(1)当,分别为何值时,取得最小值?并求出最小值;(2)当,分别为何值时,取得最小值?并求出最小值.22. (10分) (2019高一下·梅河口月考) 在中,角,,的对边分别为,,,,,且的面积为 .(1)求;(2)求的周长 .参考答案一、单选题 (共12题;共24分)答案:1-1、考点:解析:答案:2-1、考点:解析:答案:3-1、考点:解析:答案:4-1、考点:解析:答案:5-1、考点:解析:答案:6-1、考点:答案:7-1、考点:解析:答案:8-1、考点:解析:答案:9-1、考点:答案:10-1、考点:解析:答案:11-1、考点:解析:答案:12-1、考点:解析:二、填空题 (共4题;共4分)答案:13-1、考点:解析:答案:14-1、考点:解析:答案:15-1、考点:解析:答案:16-1、考点:解析:三、解答题 (共6题;共65分)答案:17-1、答案:17-2、考点:解析:答案:18-1、答案:18-2、考点:解析:答案:19-1、答案:19-2、答案:19-3、考点:解析:答案:20-1、答案:20-2、考点:解析:答案:21-1、答案:21-2、考点:解析:答案:22-1、答案:22-2、考点:解析:。
安徽省滁州市明光中学2019-2020学年高一下学期第二次月考数学试题(word无答案)

安徽省滁州市明光中学2019-2020学年高一下学期第二次月考数学试题一、单选题(★) 1 . 设a,,若,则A.B.C.D.(★) 2 . 已知向量,,若,则实数 a的值为A.B.2或C.或1D.(★) 3 . 已知集合,,则A.B.C.D.(★) 4 . 在中,,则∠ 等于( )A.30°或150°B.60°C.60°或120°D.30°(★) 5 . 已知数列是公比为的等比数列,且成等差数列,则公比的值为()A.B.1C.D.(★★★★) 6 . 在△ ABC中,内角 A、 B、 C所对的边分别为 a、 b、 c, S为△ ABC的面积,,且 A、 B、 C成等差数列,则 C的大小为()A.B.C.D.(★) 7 . 已知,则向量在方向上的投影为()A.B.C.D.(★★) 8 . 在中,角的对边分别为,若, ,则的面积为A.B.C.D.(★) 9 . 记为等差数列的前项和,若,,则为()A.B.C.D.(★) 10 . 等比数列的前项和为,若,,则()A.510B.255C.127D.6540(★) 11 . 已知向量,且∥ ,若均为正数,则的最小值是A.24B.8C.D.(★★) 12 . 在中,, G为的重心, H为的垂心.则( )A.4B.5C.-4D.-5二、填空题(★) 13 . 的三个内角所对的边分别是,则=__________.(★★) 14 . 在中,角所对的边分别为满足,,且,则的周长为__________.(★) 15 . 已知,则函数的最小值为_______.(★★) 16 . 等比数列的公比为,其前项和的积为,并且满足下面条件,,,.给出下列结论:① ;② ;③ 的值是中最大的;④ 成立最大的自然数等于198.其中正确的结论是__________.三、解答题(★★) 17 . 已知平面内三个向量:(1)若,求实数的值;(2)设,且满足,,求.(★★) 18 . 设的内角的对应边分别为且满足.(1)求角 B的大小;(2)若,求边上高 h的最大值.(★) 19 . 记公差不为0的等差数列的前项和为, S 3=9,成等比数列. (1)求数列的通项公式及;(2)若, n=1,2,3,,问是否存在实数,使得数列为单调递增数列?若存在,请求出的取值范围;不存在,请说明理由.(★★) 20 . 在四边形中,的面积为.(1)求;(2)若,求的长.(★★) 21 . 已知是等差数列的前 n项和,且,是数列的前 n项和,且.(1)求数列和的通项公式;(2)设,求数列的前 n项和.(★★) 22 .投资商到一开发区投资72万元建起一座蔬菜加工厂,经营中,第一年支出12万元,以后每年支出增加4万元,从第一年起每年蔬菜销售收入50万元,设表示前n年的纯利润总和(前年总收入-前年的总支出 -投资额72万元)(Ⅰ)该厂从第几年开始盈利?(Ⅱ)该厂第几年平均纯利润达到最大?并求出年平均纯利润的最大值.。
安徽省滁州市示范中学高一数学理月考试卷含解析

安徽省滁州市示范中学高一数学理月考试卷含解析一、选择题:本大题共10小题,每小题5分,共50分。
在每小题给出的四个选项中,只有是一个符合题目要求的1. 函数的零点所在的区间是()A. (0,1)B.C.D.参考答案:B【分析】首先判断出函数的单调性,根据零点存在定理求得结果.【详解】由题意知:在上单调递增当时,;;;;当时,可知:零点所在区间为:【点睛】本题考查利用零点存在定理判断零点所在区间,属于基础题.2. 已知集合A={1,16,4x},B={1,x2},若B?A,则x=()A.0 B.﹣4 C.0或﹣4 D.0或±4参考答案:C【考点】集合的包含关系判断及应用.【专题】集合.【分析】根据集合的包含关系与集合元素的互异性进行判断.【解答】解:∵A={1,16,4x},B={1,x2},若B?A,则x2=16或x2=4x,则x=﹣4,0,4.又当x=4时,4x=16,A集合出现重复元素,因此x=0或﹣4.故答案选:C.【点评】本题考查集合中子集的概念与集合中元素的互异性3. 将五个1,五个2,五个3,五个4,五个5共25个数填入一个5行5列的表格内(每格填入一个数),使得同一行中任何两数之差的绝对值不超过2,考察每行中五个数之和,记这五个和的最小值为,则的最大值为().A.8 B.9 C.10 D.11参考答案:C,5个1分在同列,,,5个1分在两列,则这两列出现最大数至多为,故,有,,个在三列,,∴,,若5个1在至少四列中,其中某一列至少有一个数大于,矛盾,∴,如图可取.故选.4. 已知直线l的方程为,则点关于l的对称点的坐标为()A.(-4,1)B.(-2,7)C. (-1,7)D. (-3,1)参考答案:B设是关于的对称点,则有,解得且,所以坐标为,即为所求的点的坐标,故选B.5. 设是两条不同的直线,是两个不同的平面,给出下列条件,能得到的是()A.B.C.D.参考答案:试题分析:从选项入手:中与可能平行,相交,或是垂直,错误;中与可能垂直或在平面内,错误;中与可能平行,相交,或是垂直,错误;故选.考点:排除法,线面垂直的判定.6. 在△ABC中,a2﹣c2+b2=ab,则角C的大小为()A.30°B.45°C.60°D.120°参考答案:C【考点】HR:余弦定理.【分析】利用余弦定理表示出cosC,将已知的等式代入求出cosC的值,由C为三角形的内角,利用特殊角的三角函数值即可求出C的度数.【解答】解:∵a2﹣c2+b2=ab,∴cosC===,又C为三角形的内角,则C=60°.故选C7. 函数的值域是( ).A.{-1,0,1,3}B.{-1,0,3}C.{-1,3}D.{-1,1}参考答案:C略8. 设直线过点,且与圆相切,直线的斜率是()A. B. C. D.参考答案:C9. 设,则使函数的定义域为R且为奇函数的所有值为()(A)(B)(C)(D)参考答案:A10. log52?log425等于()A.﹣1 B.C.1 D.2参考答案:C【考点】对数的运算性质.【分析】根据对数的运算性质计算即可.【解答】解:原式=?=1,故选:C二、填空题:本大题共7小题,每小题4分,共28分11. 已知函数是定义在R上的奇函数,当≥0时,=(+1),则函数= .参考答案:=12. (4分)已知A(2,3),B(4,﹣3),点P在线段AB的延长线上,且,则点P的坐标为.参考答案:P(6,﹣9)考点:线段的定比分点.专题:平面向量及应用.分析:根据题意,画出图形,结合图形,设出点P的坐标,利用向量的坐标表示以及向量相等,求出P点的坐标.解答:根据题意,画出图形,如图所示;设点P(x,y),∴=(x﹣2,y﹣3),=(x﹣4,y+3);又∵=2,∴(x﹣2,y﹣3)=2(x﹣4,y+3),即,解得;∴P(6,﹣9).故答案为:P(6,﹣9).点评:本题考查了平面向量的应用问题,也考查了平面向量的坐标运算问题,是基础题目.13. 设P是一个数集,且至少含有两个数,若对任意a、b∈P,都有a+b、a-b、ab、∈P(除数b≠0)则称P是一个数域,例如有理数集Q是数域,有下列命题:①数域必含有0,1两个数;②整数集是数域;③若有理数集Q M,则数集M必为数域;④数域必为无限集。
【期末提升】安徽省滁州市定远县育才学校2019-2020学年高一下学期6月月考数学试题(解析版) (1)
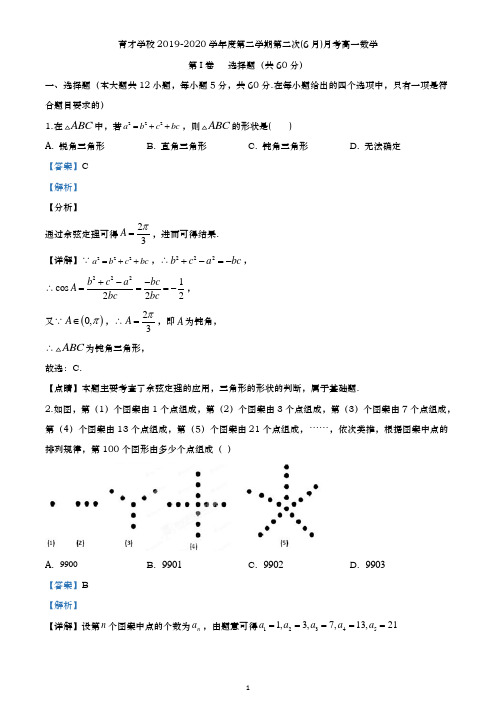
育才学校2019-2020学年度第二学期第二次(6月)月考高一数学第I 卷 选择题(共60分)一、选择题(本大题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的)1.在ABC 中,若222a b c bc =++,则ABC 的形状是( ) A. 锐角三角形 B. 直角三角形C. 钝角三角形D. 无法确定【答案】C 【解析】 【分析】通过余弦定理可得23A π=,进而可得结果. 【详解】∵222a b c bc =++,∴222b c a bc +-=-,∴2221cos 222b c a bc A bc bc +--===-,又∵()0,A π∈,∴23A π=,即A 为钝角, ∴ABC 为钝角三角形, 故选:C.【点睛】本题主要考查了余弦定理的应用,三角形的形状的判断,属于基础题.2.如图,第(1)个图案由1个点组成,第(2)个图案由3个点组成,第(3)个图案由7个点组成,第(4)个图案由13个点组成,第(5)个图案由21个点组成,⋅⋅⋅⋅⋅⋅,依次类推,根据图案中点的排列规律,第100个图形由多少个点组成( )A. 9900B. 9901C. 9902D. 9903【答案】B 【解析】【详解】设第n 个图案中点的个数为n a ,由题意可得123451,3,7,13,21a a a a a =====故213243542,4,6,8,...a a a a a a a a -=-=-=-=由此可得,()121n n a a n --=-,以上1n -各式子相加得()()()()()()213243541...2468...21n n a a a a a a a a a a n --+-+-+-++-=+++++-整理可得()()()()1001222111001001199012nn n a nn a -+--==-∴=⨯-+=3.在ABC中,1,AB AC =30A ∠=︒,则ABC 的面积等于 ( )A.2B.C.D.12【答案】B 【解析】 【分析】利用三角形的面积公式1sin 2S AB AC A =⋅⋅,即可求得结论.【详解】∵1AB AC ==,30A ∠=, ∴ABC的面积为1sin 2S AB AC A =⋅⋅ 11122=⋅=, 故选B .【点睛】本题考查三角形面积的计算,考查学生的计算能力,属于基础题.4.在相距4千米的A 、B 两点处测量目标C , 若75CAB ∠=︒,60CBA ∠=︒,则A 、C 两点之间的距离是( ) A. 4千米 B.C.D. 2千米【答案】B 【解析】 【分析】利用正弦定理列方程,解方程求得AC 的长度.【详解】由于75CAB ∠=︒,60CBA ∠=︒,所以180756045ACB ∠=︒-︒-︒=︒,由正弦定理得sin sin AC ABB ACB=∠2AC =⇒=. 故选:B【点睛】本小题主要考查正弦定理解三角形,属于基础题. 5.数列{}n a 中,11a =且121n n a a +=+,则{}n a 的通项为( ) A. 21n - B. 2n C. 21n + D. 12n +【答案】A 【解析】 【分析】等式两边同时加1,构造出数列{}1n a +为等比数列,即可得出结果. 【详解】∵121n n a a -=+,∴()1121n n a a ++=+, 由11a =得112a +=,故数列{}1n a +是以2为首项,2为公比的等比数列,∴11222n n n a -+=⋅=,即21nn a =-,故选:A.【点睛】本题主要考查了等比数列通项公式的求法,得到{}1n a +是等比数列是解题的关键,属于中档题.6.ABC ∆的两边长分别为2,3,其夹角的余弦值为13,则其外接圆的半径为( ) A.92B.92C.928D. 92【答案】C 【解析】 【分析】根据余弦定理得到3c =,再根据正弦定理得到答案.【详解】不妨设2,3a b ==,根据余弦定理:2222cos 9c a b ab C =+-=,故3c =.1cos 3C =,则sin 3C =,2sin c R C =,故8R =. 故选:C .【点睛】本题考查了余弦定理和正弦定理解三角形,意在考查学生的计算能力. 7.等差数列{}n a 中,a 3=7, a 9=19,则a 5= ( ) A. 10 B. 11C. 12D. 13【答案】B 【解析】由于a 3=7, a 9=19则93532,2741193a a d a a d -==∴=+=+=-. 故选B.8.已知ABC 的周长等于20,面积等于a ,b ,c 分别为ABC 内角A ,B ,C 的对边,60A ∠=︒,则a 为( )A. 5B. 6C. 7D. 8【答案】C 【解析】 【分析】由周长可得20b c a +=-,由三角形面积公式可得40bc =,最后由余弦定理可得a 的值. 【详解】由题意可得20a b c ++=,即20b c a +=-,∵sin 60112S bc =︒=40bc =, 由余弦定理可得()()222222cos60320120a b c bc b c bc a =+-︒=+-=--, 解得7a =, 故选:C.【点睛】本题主要考查了三角形的面积公式及余弦定理在求解三角形中的应用,属于基础题. 9.数列{}n a 的前n 项和为n S ,若()11n a n n =+,则5S 等于( )A. 1B.56 C.16D.130【答案】B 【解析】【分析】 化简()11111n a n n n n ==-++,利用裂项相消法可得结果.【详解】因为()11111n a n n n n ==-++,所以5111111111151122334455666S ⎛⎫⎛⎫⎛⎫⎛⎫⎛⎫=-+-+-+-+-=-= ⎪ ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭⎝⎭⎝⎭,故选B . 【点睛】裂项相消法是最难把握的求和方法之一,其原因是有时很难找到裂项的方向,突破这一难点的方法是根据式子的结构特点,常见的裂项技巧:(1)()1111n n k k n n k ⎛⎫=- ⎪++⎝⎭;(2) 1n k n ++()1n k n k=+-; (3)()()1111212122121n n n n ⎛⎫=- ⎪-+-+⎝⎭;(4)()()122121n n n +--()()()()1121212121n n n n ++---=--1112121n n +=---;此外,需注意裂项之后相消的过程中容易出现丢项或多项的问题,导致计算结果错误.10.已知{}n a 是等比数列,且0n a >,243546225a a a a a a ++=,那么35a a +=( ) A. 10 B. 15 C. 5 D. 6【答案】C 【解析】试题分析:()22224354633553535225225255a a a a a a a a a a a a a a ++=∴++=∴+=∴+=考点:等比数列性质11.在等比数列{a n }(n ∈N *)中,若 1411,8a a ==,则该数列的前10项和为() A. 8122-B. 9122-C. 10122-D. 11122-【答案】B 【解析】设等比数列{a n }的公比为q ,由1411,8a a ==得334118a a q q ===,故12q =.∴1010911()1221212S -==--.选B . 12.ABC ∆中,0,2,60a x b B ==∠=,则当ABC ∆有两个解时,x 的取值范围是( )A. x >B. 2x <或x >C. 2x <D. 2x <<【答案】D 【解析】试题分析:当ABC ∆有两个解时,则满足sin a B b a <<,因为0,2,60a x b B ==∠=,所以0sin 602x x <<,解得2x <<,故选D. 考点:三角形的个数的判定与应用.第II 卷 非选择题(共90分)二、填空题(本大题共4小题,每小题5分,共20分)13.已知等差数列{}n a 的前n 项和为n S ,若346518a a a a +=--,则8S =_________. 【答案】36 【解析】 【分析】根据等差数列的性质求得18a a +,由此求得8S 的值.【详解】由于数列{}n a 是等差数列,且346518a a a a +=--, 则()345618218a a a a a a +++=+=, 所以189a a +=, 所以1889883622a a S +=⨯=⨯=. 故答案为:36【点睛】本小题主要考查等差数列的性质,考查等差数列前n 项和公式,属于基础题. 14.在ABC ∆中,角A ,B ,C 所对的边分别为a ,b ,c ,已知6A π=,1a =,b =则B = ______.【答案】3π或23π. 【解析】 【分析】利用正弦定理列出关系式,将a ,sin A ,b 的值代入求出sin B 的值,即可确定出B 的度数. 【详解】解:在ABC ∆中,6A π=,1a =,b =∴由正弦定理sin sin a b A B=得:1sin 2sin 12b A B a ===, a b <,A B ∴<, 3B π∴=或23π. 故答案为:3π或23π. 【点睛】本题考查了正弦定理,以及特殊角的三角函数值,熟练掌握正弦定理是解本题的关键,属于基础题.15.已知数列()()1111,,,,,1335572121n n ⨯⨯⨯-+的前n 项和为n S ,计算得113S =,225S =,337S =,照此规律,n S =_________. 【答案】21nn + 【解析】 【分析】根据123,,S S S 的规律,猜想n S 的表达式. 【详解】由于113S =,225S =,337S =,其分子是正整数数列1,2,3,,,n ,分母是奇数列3,5,7,,21,n +,所以猜想21n nS n =+. 故答案为:21nn + 【点睛】本小题主要考查合情推理,属于基础题.16.在△ABC 中,若:3,则∠B 的大小为【答案】【解析】 试题分析:由sinA:sinB:sinC=1:7:3可知::1:73a b c =2221971cos 22132a cb B ac +-+-∴===⨯⨯3B π∴= 考点:正余弦定理解三角形三、解答题(本大题共6小题,共70分.解答应写出文字说明、证明过程或演算步骤) 17.在锐角△ABC 中,a 、b 、c 分别为A ∠、B 、C ∠32sin a c A =. (1)确定C ∠的大小;(2)若3c =,求△ABC 周长的取值范围. 【答案】(1)3π;(2)(33,33]+. 【解析】 【分析】32csin a A =,利用正弦定理化边为角可得. 由3c =,3C π∠=,由正弦定理得到2sin sin a bA B==,化边为角的正弦,利用正弦函数性质可得解.【详解】(132csin a A =变形得:3a c = 又正弦定理得:sin sin a Ac C=,sin sin 3A C =sin 0A ≠,3sin C ∴=, △ABC 是锐角三角形,3C π∴∠=(2)解:3c =,3sin C =, ∴由正弦定理得:32sin sin sin 32a b cA B C====,即2sin a A =,2sin b B =,又23A B C ππ+=-=,即23B A π=-,2(sin sin )a b c A B ∴++=++22[sin sin()]3A A π=+-+222(sin sincos cos sin )33A A A ππ=+-3sin A A =++A coscos Asin )66ππ=++)6A π=+, △ABC 是锐角三角形,62A ππ∴<<,sin()126A π<+≤,则△ABC 周长的取值范围是(3+【点睛】本题考查正弦定理的应用. 三角形中最值范围问题的解题思路:要建立所求量(式子)与已知角或边的关系,然后把角或边作为自变量,所求量(式子)的值作为函数值,转化为函数关系,将原问题转化为求函数的值域问题.要利用条件中的范围限制,以及三角形自身范围限制,要尽量把角或边的范围(也就是函数的定义域)找完善,避免结果的范围过大. 18.已知数列{}n a 是公差不为零的等差数列,1015a =,且3a 、4a 、7a 成等比数列. (1)求数列{}n a 的通项公式; (2)设2nn na b =,求数列{}n b 的前n 项和n T . 【答案】(1)()*25N n a n n =-∈;(2)()*211N 2n nn T n -=--∈. 【解析】 【分析】(1)由等比中项的性质可得2437a a a =,再将34710,,,a a a a 代入等差数列的通项公式,即可求得1,a d 的值,进而可求得{}n a 的通项公式;(2)代入n a 的通项公式,求得n b 的通项公式,利用错位相减法进行求和即可.【详解】(1)设数列{}n a 的公差为d ,0d ≠(),由已知得:10243715a a a a =⎧⎨=⎩,即()()()12111915326a d a d a d a d +=⎧⎪⎨+=++⎪⎩,解得:132a d =-⎧⎨=⎩, ()*25,N n a n n ∴=-∈.(2)2522n n n n a n b -==,1n ≥,*N n ∈. 23311252222n nT n ---=+++⋅⋅⋅+,① 234113112725222222n n n a n T +----=+++⋅⋅⋅++,② ①﹣②得:23111311125112222222222n n n n n n T ++---⎛⎫=+++⋅⋅⋅+-=-+ ⎪⎝⎭, ()*211N 2n nn T n -∴=--∈ 【点睛】本题考查等差数列的通项公式,等比中项的性质,错位相减法求和法,需熟记若{}n a 为等差数列,{}n b 为等比数列,则求n n n c a b =的前n 项和时,用错位相减法求和,考查学生化简计算的能力,属中档题.19.在ABC ∆中,角,,A BC 所对的边分别为,,a b c ,且cos sin a A B=. (1)求角A 的大小; (2)若a =4B π=,求b .【答案】(1)3π;(2)【解析】 试题分析:(1)由正弦定理边化角,结合三角函数的性质可得3A π=;(2)利用正弦定理可得:sin sin a Bb A== 试题解析:(1)由正弦定理可得,sin 3sin cos sin A B A B=, 所以tanA =. 因为A 为三角形的内角,所以A =.(2)a =2,A =,B =,由正弦定理得,b ==2. 20.已知{}n a 是一个等差数列,且21a =,55a =-.(1)求{}n a 的通项n a ;(2)求{}n a 前n 项和n S 的最大值.【答案】(1)25n a n =-+;(2)4.【解析】【分析】(1)设{}n a 的公差为d ,由已知条件列出关于1a 和d 的方程组,解出1a 和d 即可得结果;(2)由等差数列前n 项和公式可得n S ,结合二次函数的性质可得结果.【详解】(1)设{}n a 的公差为d ,由已知条件,11145a d a d +=⎧⎨+=-⎩, 解出13a =,2d =-,所以1(1)25n a a n d n =+-=-+.(2)221(1)44(2)2n n n S na d n n n -=+=-+=--. 所以2n =时,n S 取到最大值4.【点睛】本题主要考查了等差数列基本量的计算,考查了数列的函数特性,属于基础题.21.已知数列{}n a 的前n 项和为n S ,且*43()n n S a n N =-∈.(1)证明:数列{}n a 是等比数列;(2)若数列{}n b 满足*11(),2n n n b a b n N b +=+∈=且,求数列{}n b 的通项公式.【答案】(1)见解析;(2) 14313n n b -⎛⎫=⋅- ⎪⎝⎭.【解析】【分析】(1)先根据2n ≥时,43n n S a =-,1143n n S a --=-,求出144n n n a a a -=-,即143n n a a -=,根据定义即可证明{}n a 是等比数列; (2)先根据(1)求数列{}n a 的通项公式,代入1n n n b a b +=+,可得数列{}n b 的递推公式,即可求出数列{}n b 的通项公式.【详解】由43n n S a =-可知当1n =时1143a a =-,解得11a =.当2n ≥时,43n n S a =-,1143n n S a --=-,两式相减得144n n n a a a -=-,即143n n a a -=, ∴{}n a 是首项为1,公比为43的等比数列. (2)由(1)可知143n n a -⎛⎫= ⎪⎝⎭,由()1*n n n b a b n N +=+∈得1143n n n n b b a -+⎛⎫-== ⎪⎝⎭. 所以当2n ≥时,()()()121321n n n b b b b b b b b -=+-+-++-1141432314313n n --⎛⎫- ⎪⎛⎫⎝⎭=+=⋅- ⎪⎝⎭-.当1n =时上式也满足条件,故数列{}n b 的通项公式为14313n n b -⎛⎫=⋅- ⎪⎝⎭.22.已知数列{}n a 满足()1121,2n n a a n N a *+=-∈=. (1)求证:数列{}1n a -为等比数列,并求数列{}n a 的通项公式;(2)求数列{}n na 的前n 项和为()n S n N *∈. 【答案】(1)详见解析;(2)()()()11212n n n n S n n N *+=-++∈. 【解析】 试题分析:(1)由121n n a a +=-得()1121n n a a +-=-,故数列{}1n a -为公比为2的等比数列,所以112n n a --=,即()121n n a n N -*=+∈.(2)12n n na n n -=+,利用分组求和法,与错位相减法相结合,可求得n S 的值.试题解析:解:(1)()*121n n a a n N +=-∈,可得()()*1121n n a a n N +-=-∈,又111a -=,所以数列{}1n a -为公比为2的等比数列,所以112n n a --=,即()1*21n n a n N -=+∈. (2)12n n na n n -=+,设()01221122232...122n n n T n n --=⨯+⨯+⨯++-⨯+⨯,则()12312122232...122n n n T n n -=⨯+⨯+⨯++-⨯+⨯,所以()1221122...222n n n n T n --=--+++++⨯ ()221121n n n n n =⨯-+=-⨯+,()()()*11212n n n n S n n N +=-++∈. 【点睛】本题主要考查利用配凑法求数列的通项公式,考查了数列求和中的分组求和法与错位相减法.第一问已知条件是1n n a pa q -=+的形式,可以利用配凑法化简为111n n q q a p a p p -⎛⎫+=+ ⎪--⎝⎭,转化为等比数列来求得通项公式.如果一个数列的通项公式为一个等差数列乘以一个等比数列,可利用错位相减法求和.。
安徽省滁州市民办高中2020-2021学年高一数学下学期第三次月考试题

安徽省滁州市民办高中20212021学年高一数学下学期第三次月考试题高一数学注意事项:1.本卷分第I卷(选择题)和第II卷(非选择题),满分150分,考试时刻120分钟。
2.答题前,先将自己的姓名、准考证号填写在试题卷和答题卷上。
3.请将答案正确填写在答题卷上,写在其它地点无效。
4.本次考题要紧范畴:必修5等第I卷(选择题60分)一、选择题(本大题共12小题,每小题5分,满分60分。
)1.在中,已知,则的形状是( )A.等腰三角形B.直角三角形C.等腰直角三角形D.等腰三角形或直角三角形2.古希腊人常用小石子在沙滩上摆成各种性状来研究数,例如:他们研究过图1中的1,3,6,10,…,由于这些数能够表示成三角形,将其称为三角形数;类似地,称图2中的1,4,9,16…如此的数成为正方形数。
下列数中既是三角形数又是正方形数的是( )A. 1225B. 1024C. 289D. 13783.在△ABC中,若,且,则A=( )A. B. C. D.4.已知{a n }为等差数列,a 1+a 2=a 3=6,则a 2等于( ) A.2 B. C.3 D.45.在等比数列{}n a 中, 14a =,且1a , 2a , 31a -成等差数列,公比1q >,则n a 等于( ) A. 143n -⋅ B. 1342n -⎛⎫⋅ ⎪⎝⎭C. 4nD. 1542n -⎛⎫⋅ ⎪⎝⎭6.已知a , b , c R ∈,那么下列命题中正确的是( ). A. 若a b >,则22ac bc > B. 若a bc c>,则a b > C. 若33a b >且0ab <,则11a b > D. 若22a b >且0ab >,则11a b< 7.等差数列 共有项,若前项的和为200,前项的和为225,则中间项的和为( )A.50B.75C.100D.1258.等比数列{}n a 的前n 项和为n S ,若638a a =, 32S =,则6S =( ) A. 9 B. 16 C. 18 D. 219.已知,a b 是不相等的正数,且220a a b b ab -+-+=,则a b +的取值范畴是( ) A. 40,3⎛⎫ ⎪⎝⎭ B. 41,3⎛⎫ ⎪⎝⎭ C. 30,2⎛⎫ ⎪⎝⎭ D. 31,2⎛⎫⎪⎝⎭10.若实数,x y 满足240{10 1x y x y x +-≤--≤≥,则22x y +的最大值为 ( )A. 1B. 4C. 6D. 511.在ABC ∆中, 601A b ︒=,= ,其面积为3,则sin sin sin a b cA B C++++等于( )A. 33B.2393C. 833D. 39212.已知等比数列中,,,则的值为( )A.2B.4C.8D.16第II 卷(非选择题 90分)二、填空题(本大题共4小题,每小题5分,满分20分。
安徽省滁州市定远县民族中学2022_2022学年高一数学6月月考试题2022061403137

定远民族中学2022-2022学年度下学期6月月考试卷高一数学考前须知:1.答题前填写好自己的姓名、班级、考号等信息 2.请将答案正确填写在答题卡上第I 卷〔选择题 60分〕一、选择题〔本大题共12小题,每题5分,总分值60分。
〕 1.在ΔABC 中, 2sin 2A = (,,2c b a b c c-分别为角,,A B C 的对应边),那么ΔABC 的形状为〔 〕A. 正三角形B. 直角三角形C. 等腰直角三角形D. 等腰三角形 2.在ABC ∆中45A ︒∠=,60B ︒∠=, 2a =,那么b 等于〔 〕 A. 6 B. 2 C. 3 D. 26 3.数列3579,,,,24816--的一个通项公式为〔 〕A. ()2112n nn n a +=- B. ()2112n nnn a +=- C. ()12112n n n n a ++=- D. ()12112n n nn a ++=- 4.不等式y≥|x|表示的平面区域为〔 〕A. B. C. D.5.等差数列{}n a 的前n 项和为n S ,且22a =, 49S =,那么6a =〔 〕 A. 3 B. 4 C. 5 D. 66.等比数列{}n a 为递增数列,且()251021,25n n n a a a a a ++=+=,那么数列{}n a 的通项公式n a =〔 〕A. 2nB. 3nC. 2n -D. 3n-7.假设0a b >>,0c d <<,那么一定有〔 〕 A .a b d c > B .a b d c < C .a b c d > D . a b c d< 8.如下图,半圆的直径2AB =,点C 在AB 的延长线上, 1BC =,点P 为半圆上的一个动点,以DC 为边做等边PCD ∆,且点D 与圆心O 分别在PC 的两侧,那么四边形OPDC 面积的最大值为〔 〕 A.534 B. 5314+ C. 5324+ D. 5334+ 9.假设等比数列前n 项和为n S ,且满足963S S S =+,那么公比q 等于〔 〕 A. 1 B. -1 C. 1± D. 不存在 10.在中,, ,分别为角,,的对边,假设,,那么角的最大值为〔 〕 A.B.C.D.11.关于x 的不等式20x ax b -+<的解集为{}|12x x <<,那么不等式5bx a +>的解为 〔 〕A. ()1,4-B. ()4,1-C. ()(),41,-∞-⋃+∞D. ()(),14,-∞-⋃+∞12.点(),P x y 的坐标满足条件4{ 1x y y x x +≤≥≥,那么22x y +的最大值为〔 〕A. 10B. 8C. 10D. 16第II 卷〔非选择题 90分〕二、填空题〔本大题共4小题,每题5分,总分值20分。
2020年安徽省滁州市柳湖中学高一数学理月考试卷含解析

2020年安徽省滁州市柳湖中学高一数学理月考试卷含解析一、选择题:本大题共10小题,每小题5分,共50分。
在每小题给出的四个选项中,只有是一个符合题目要求的1. (5分)设集合A={1,2},B={1,2,3},C={2,3,4},则(A∩B)∪C=()A.{1,2,3} B.{1,2,4} C.{2,3,4} D.{1,2,3,4}参考答案:D考点:交、并、补集的混合运算.分析:属于集合简单运算问题.此类问题只要审题清晰、做题时按部就班基本上就不会出错.解答:∵集合A={1,2},B={1,2,3},∴A∩B=A={1,2},又∵C={2,3,4},∴(A∩B)∪C={1,2,3,4}故选D.点评:考查的是集合交、并、补的简单基本运算.2. (5分)若点A(﹣3,﹣4),B(6,3)到直线l:ax+y+1=0的距离相等,则实数a的值为()A.B.C.或D.﹣或﹣参考答案:D考点:点到直线的距离公式.专题:直线与圆.分析:利用点到直线的距离公式即可得出.解答:∵两点A(﹣3,﹣4),B(6,3)到直线l:ax+y+1=0的距离相等,∴=,化为|3a+3|=|6a+4|.∴6a+4=±(3a+3),解得a=﹣,或a=﹣,故选:D点评:本题考查了点到直线的距离公式的应用,属于基础题.3. 函数的图象是()参考答案:C略4. 已知定义在上的奇函数满足(其中),且在区间上是减函数,令,,则()A. B.C. D.参考答案:C略5. 若直线经过两点,则直线的倾斜角为A.B.C.D.参考答案:B略6. 下面的结论正确的是()A一个程序的算法步骤是可逆的B一个算法可以无止境地运算下去的C、完成一件事情的算法有且只有一种D、设计算法要本着简单方便的原则参考答案:D略7.A. B. C. D. 参考答案:D8. 下面是一个求10个数的平均数的程序,在横线上应填充的语句为 ( )A. i>10B. i<10C. i>=10D.i<=10参考答案:A略9. 关于x的方程有解,则m的取值范围是()A. B.C. D.参考答案:略10. 已有角的顶点与坐标原点重合,始边与x轴的非负半轴重合,终边经过点,则().A. B. C. D.参考答案:A由题意知,,故选A.二、填空题:本大题共7小题,每小题4分,共28分11. 函数的最小正周期是___________________。
安徽省滁州市定远县西片区高一数学6月月考试题

定远县西片区2017-2018学年下学期6月考试高一数学考生注意:1、本卷满分150分,考试时间120分钟;2、答题前请在答题卷上填写好自己的学校、姓名、班级、考号等信息;3、请将答案正确填写在答题卷指定的位置,在非答题区位置作答无效。
一、选择题(本大题共12小题, 满分60分)1.ABC ∆的内角A 、B 、C 的对边分别为a 、b 、c ,45A a b =︒==,B 等于A. 30︒B. 60︒C. 30︒或150︒D. 60︒或120︒2.在ABC ∆中, 120BAC ∠=︒, AD 为角A 的平分线, 2AC =, 4AB =,则AD 的长是A.43 B. 43或2 C. 1或2 D. 833.在△ABC 中, D 为BC 的中点,满足π2BAD C ∠+∠=,则△ABC 的形状一定是A. 直角三角形B. 等腰三角形C. 等边三角形D. 等腰三角形或直角三角形4.如图,某住宅小区的平面图呈圆心角为120°的扇形AOB ,C 是该小区的一个出入口,且小区里有一条平行于AO 的小路CD .已知某人从O 沿OD 走到D 用了2分钟,从D 沿着DC 走到C 用了3分钟.若此人步行的速度为每分钟50米,则该扇形的半径的长度为A. B. C. D.5.数列 的一个通项公式是A. B.C.D.6.等差数列{}n a 中, 4101630a a a ++=,则18142a a -的值为 A. 20 B. 20- C. 10 D. 10-7.设数列 的前 项和,若,则A.B.C. D.8.已知等差数列 ,且,则数列的前11项之和为A.84B.68C.52D.449.在等比数列中,,则A.28B.32C.35D.49 10.若对任意实数x ∈R,不等式恒成立,则实数m 的取值范围是A. [2,6]B. [-6,-2]C. (2,6)D. (-6,-2) 11.已知,0x y >,且112x y+=,则2x y +的最小值为A. 3- C. 3+12.不等式组表示的平面区域的面积为A.7B.5C.3D.14二、填空题(本大题共4小题, 满分20分)13.在中,角 , , 的对边分别为 , , ,若 ,,,,则角 的大小为 .14.在数列 中, = 若 = ,则 的值为 .15. , 时,若 ,则 的最小值为 .16.给出下列四个命题:(1)若,a b c d >>,则a d b c ->-;(2)若22a x a y >,则x y >;(3)a b >,则11a b a>-; (4)若110a b<<,则2ab b <. 其中正确命题的是 .(填所有正确命题的序号)三、解答题(本大题共6小题, 满分70分)17.已知函数 .(Ⅰ)解不等式 ;(Ⅱ)若不等式 的解集为,且满足,求实数 的取值范围.18.的内角A,B,C 的对边分别为a,b,c ,已知a=8,且.(1)求B ;(2)若 ,求的面积S .19.等差数列 的前 项和为 ,已知.(1)求 的通项公式;(2)求数列 的前 项和.20.如图,岛 、 相距 海里.上午9点整有一客轮在岛 的北偏西且距岛海里的 处,沿直线方向匀速开往岛 ,在岛 停留 分钟后前往 市.上午测得客轮位于岛 的北偏西且距岛海里的 处,此时小张从岛乘坐速度为 海里/小时的小艇沿直线方向前往 岛换乘客轮去 市.(Ⅰ)若,问小张能否乘上这班客轮?(Ⅱ)现测得,.已知速度为海里/小时( )的小艇每小时的总费用为( )元,若小张由岛直接乘小艇去市,则至少需要多少费用?21.已知是公差为3的等差数列,数列满足.(1)求的通项公式;(2)求的前n项和.22.已知函数 .(1)在给出的平面直角坐标系中作出函数的图像;(2)记函数的最大值为,是否存在正数,,使,且,若存在,求出,的值,若不存在,说明理由.参考答案及解析1.D0sin 60B B ==⇒=或120︒,选D. 2.A【解析】如图,由已知条件可得60,2,4DAC DAB AC AB ∠=∠===, ACD ABD ABC S S S ∆∆∆+=,1112424222AD AD ∴⨯⨯⨯⨯=⨯⨯,解得43AD =,故选A. 3.D【解析】如图,设BAD α∠=, DAC β∠=,则,22ACD ABD ππαβ∠=-∠=-,在三角形ABD ∆中,2sin sin 2aAD παβ=⎛⎫- ⎪⎝⎭, 2sin sin 2aAD πβα=⎛⎫- ⎪⎝⎭,故sin sin sin sin 22αβππβα=⎛⎫⎛⎫-- ⎪ ⎪⎝⎭⎝⎭,整理得到sin cos sin cos ααββ=,也就是sin2sin2αβ=, 因为()2,20,αβπ∈,故22αβ=或22αβπ+=,故αβ=或2παβ+=.若αβ=, AD也为角平分线,故ABC ∆为等腰三角形;若2παβ+=, ABC ∆为直角三角形,故选D.4.B【解析】设该扇形的半径为r 米,连接CO .由题意,得CD=150(米),OD=100(米),∠CDO=60°,在△CDO 中, ,即, ,解得 (米).5.B【解析】通过观察,各项分母是 的形式,符号与项数存在的关系.故答案为:B . 6.D【解析】由等差数列的性质得4101610330a a a a ++==,解得1010a =。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
安徽省滁州市高一下学期数学 6 月月考试卷
姓名:________
班级:________
成绩:________
一、 单选题 (共 10 题;共 20 分)
1. (2 分) (2016 高三上·鹰潭期中) 数列{an}:1,﹣ , ,﹣ ,…的一个通项公式是( )
A . an=(﹣1)n+1
(n∈N+)
B . an=(﹣1)n﹣1
(n∈N+)
C . an=(﹣1)n+1
(n∈N+)
D . an=(﹣1)n﹣1
(n∈N+)
2. (2 分) (2020 高一下·揭阳月考) 已知 A. B. C. D.
,向量
,则向量
()
3. (2 分) 设 , 为不共线向量, = +2 , ()
=4 - ,
=5 -3 , 则下列关系式中正确的是
A. =
B . =2
C . =-
D . =-2
4. (2 分) (2020 高一下·重庆期末) 在
中,角
的对边分别为
,
,
第1页共9页
则
()
A.
B.
C.
D. 5. (2 分) 在△ABC 中,A=60°,C=45°,b=2,则此三角形的最小边长为( ) A.2 B.
C.
D.
6. (2 分) (2018·广东模拟) 已知等比数列 ()
的首项为 ,公比
,且
,则
A.
B.
C.
D.
7. (2 分) (2019 高一下·吉林月考) 在△ABC 中,AB=5,BC=7,AC=8,则
的值为( )
A.5
B . -5
C . 15
第2页共9页
D . -15
8. (2 分) 已知平面直角坐标系 xOy 上的区域 D 由不等式组
A
, 则 Z=| |的最大值为 ( )
A.6
给定,若 M(x,y)为 D 上的动点,点
B. C.4 D.2
9. (2 分) (2018 高二下·遵化期中) 已知
且
,则
的最大值( )
A. B.2 C.1
D.
10. (2 分) 已知 M 是△ABC 内的一点,且
,
面积分别为 1, , ,则
的最小值是( )
A.2
B.8
C.6
D.9
二、 双空题 (共 3 题;共 3 分)
11. ( 1 分 ) (2019 高 一 下 · 上 海 期 中 )
的内角
第3页共9页
,若△MBC,△MCA 和△MAB 的
所对的边分别为
,已知
,
,则 =________.
12. (1 分) (2019·黄冈模拟) 正
中, 在
方向上的投影为
,且
,则
________.
13. (1 分) (2017 高三上·泰安期中) 已知{an}是公差为 1 的等差数列,Sn 为其前 n 项和,若 S8=4S4 , 则 a9=________.
三、 填空题 (共 4 题;共 4 分)
14. ( 1 分 ) (2014· 广 东 理 ) 若 等 比 数 列 {an} 的 各 项 均 为 正 数 , 且 a10a11+a9a12=2e5 , 则 lna1+lna2+…lna20=________.
15. (1 分) 已知{an}是等比数列,a2=2,a3= , 则 a1a2+a3a4+…+anan+1=________
16. (1 分) (2018 高三上·镇江期中) 在△ABC 中,a,b,c 分别为角 A,B,C 的对边,且 A=45°,C=75°, a=1,则 b=________.
17. (1 分) 已知函数 f(x)= 数 t 的取值范围是________.
四、 解答题 (共 5 题;共 40 分)
若对于任意 x∈R,不等式 f(x)≤ ﹣t+1 恒成立,则实
18. (10 分) 已知: 、 、 是同一平面上的三个向量,其中 =(1,2).
(1)若| |=2 , 且 ∥ , 求 的坐标.
(2)若| |= , 且 +2 与 2 ﹣ 垂直,求 与 的夹角 θ
19.(5 分)(2019 高二上·北京月考) 已知 是等差数列,满足
,
,数列 满足
,
,且
是等比数列.
(1) 求数列 和 的通项公式;
(2) 求数列 的前 项和.
第4页共9页
20. (5 分) (2019 高二上·分宜月考)
的内角
的对边分别为
,已知
.
(1) 求 A 的值;
(2) 若
的面积为
,求 的值.
21. (10 分) 已知等差数列{an}的前 n 项和记为 Sn , 公差为 2,且 a1 , a2 , a4 依次构成等比数列.
(1)求数列{an}的通项公式与 Sn
(2)数列{bn}满足 bn= , 求数列{bn}的前 n 项和 Tn .
22. (10 分) (2020·济宁模拟) 已知数列 为等差数列,且
,
(Ⅰ)求数列 的通项 ,及前 n 项和
(Ⅱ)请你在数列 的前 4 项中选出三项,组成公比的绝对值小于 1 的等比数列 的前 3 项,并记数列
的前 n 项和为
.若对任意正整数
,不等式
恒成立,试求 k 的最小值.
第5页共9页
一、 单选题 (共 10 题;共 20 分)
1-1、 2-1、 3-1、 4-1、 5-1、 6-1、 7-1、 8-1、 9-1、 10-1、
二、 双空题 (共 3 题;共 3 分)
11-1、 12-1、 13-1、
三、 填空题 (共 4 题;共 4 分)
14-1、
参考答案
第6页共9页
15-1、
16-1、
17-1、
四、 解答题 (共 5 题;共 40 分)
18-1
、
19-1、
19-2、 20-1、
第7页共9页
20-2、 21-1、
第8页共9页
22-1、
第9页共9页
。
