第5讲 信号流图
线性网络的信号流图分析法 习题

Ub
Uta
U
la
Ib
Ita
I
la
式中下标t、l分别表示树支、连支,下标a表示全部。再
将电压、电流向量的树支、连支分块分别按非源支路和
独立源支路分块,即
Uta
Ut UV
Ula
Ul UI
Ita
It IV
Ila
Il II
式中下标V、I分别表示电压源、电流源。Ut、It代表树支 中非源支路的电压向量、电流向量。
1 信号流图 2 Mason公式 3 线性网络SFG分析 4 习题讲解 5 修改后的SFG(闭合SFG)
一.信号流图
1.信号流图(SFG)定义:
信号流图(SFG)是一种表示线性代数方程组变量 关系的加权有向图,它由节点和连接在节点之间的有 向支路构成。
SFG用图的方法表示了各变量间的因果关系,能直 观的反映出系统中信号的传输情况和线性方程组的数 学运算。
Ul U I
BBtt12
BV1 Ut
BV
2
UV
(5-4-6)
写出非源支路的混合变量形式的支路电流电压关系,使 方程右端向量中的元素为连支电压和树支电流,左端向 量中的元素为连支电流和树支电压,即
Il Ut
Yl G21
G12 Ul
Zt
It
(5 4 7)
再将式(5-4-3)中的It和式(5-4-6)中的Ul代入式 (5-4-7)中,即得关系
线性网络的信号流图分析法 习题
PPT模板下载:/moban/ 节日PPT模板:/jieri/ PPT背景图片:/beijing/ 优秀PPT下载:/xiazai/ Word教程: /word/ 资料下载:/ziliao/ PPT课件下载:/kejian/ 范文下载:/fanwen/
《自动控制原理》专科课程标准

《自动控制原理》课程标准一、课程概述(一)课程性质地位自动控制原理是空间工程类、机械控制类、信息系统类等相关专业学历教育合训学员的大类技术基础课程。
由于自动控制原理在信息化武器装备中得到了广泛的应用,因此,将本课程设置为大类技术基础课,对培养懂技术的指挥人才有着十分重要的作用。
本课程所覆盖的知识面较宽,既有较深入的理论基础知识,也有较广泛的专业背景知识,因而,它在学员知识结构方面将起到加强理论深度和拓展知识广度的积极作用。
(二)课程基本理念为了贯彻素质教育和创新教育的思想,本课程将在注重自动控制原理的基本概念和基本分析与设计方法的基础上,适当引入自动控制发展中的、学员能够理解的新概念和新方法;贯彻理论联系实际的原则,科学取舍各种主要理论、方法的比例,正确处理好理论与案例的关系,以适应为部队培养应用复合型人才的需要;适当引入和利用Matlab工具来辅助自动控制原理中的复杂计算与作图、验证分析与设计的结果;本课程应该既使学员掌握必要的基础理论知识,并了解它们对实际问题的指导作用,又要促进学员养成积极思考、长于分析、善于推导的能力和习惯。
(三)课程设计思路本课程主要介绍自动控制原理的基本概念和基本的分析与设计方法。
课程采用“一纵三横”的设计思路,具体来说,“一纵”就是在课程讲授中要求贯彻自动控制系统的建模、分析及设计方法这条主线;“三横”就是在方法讲授中要求强调自动控制系统的稳定性、快速性和准确性,稳准快三个字是分析的核心,也是设计的归宿。
在课程讲授中,贯彻少而精的原则,即对重点、难点讲深讲透;注意理论联系专业实际,例子贴近生活,注重揭示抽象概念的物理意义;注意传统教法与现代教法的有机结合,充分运用各种教学手段,特别注重发挥课程教学网站的作用。
在课程学习中,注重阅读教材、完成作业、课程实验及讨论问题等四个环节,深刻理解课程内容中的重点和难点,重点掌握自动控制原理的基本概念和基本分析与设计方法。
二、课程目标(一)知识与技能通过本课程的学习,使学员掌握自动控制原理的基本概念和基本的分析与设计方法,重点培养学生利用自动控制的基本理论分析与解决工程实际问题的思维方式和初步能力,并为学习后续相关专业课程,以及进一步学习和应用自动控制方面的新知识、新技术打下必要基础。
自动控制原理第5讲

E
(s) R(s) H (s)C (s) 0
自动控制原理
13
(6)闭环系统的开环传递函数 将闭环回路在B(s)处断开,从输入R(s)到B(s)处的传递 函数,它等于此时B(s)与R(s)的比值。亦即前向通路传递函 数与反馈通路传递函数的乘积:
B( s ) G1 ( s)G2 ( s) H ( s) R( s )
自动控制原理
21
自动控制原理
12
2.6
控制系统的传递函数(续)
(5)闭环系统的特征方程 D(s)=1+G1(s)G2(s)H(s)=0 如果系统中控制装置的参数设置能满足 |G1(s)G2(s)H(s)|>>1及 | G1(s)H(s)|>>1 则系统的总输出表达式(结论P47)
C ( s) G1 ( s)G2 ( s) R( s) G2 ( s) N ( s) 1 G1 ( s)G2 ( s) H ( s) 1 G1 ( s)G2 ( s) H ( s) 1 R( s) 0 N ( s) H ( s)
自动控制原理
8
应用举例三(续)
特征式为
1 Li Li L j Li L j Lk
5 6 1 1 2 2 2 3 3 3 RCs R C s R C s
前向通路只有一条:
P1
1 R 3C 3 s 3
前向通路与各反馈回路均有接触,余子式: Δ1 = 1 则由梅逊公式可求得总传递函数: 1 3 3 3 U c P1Δ R C s 1 5 6 1 Ur 1 2 2 2 3 3 3 RCs R C s R C s 1 3 3 3 R C s 5R 2 C 2 s 2 6 RCs 1
2.4节信号流图自动控制原理(精)

R
=Δ∴有四个回路,分别是:
−它们都是互相接触的。
1G P =2G P =3G P =有九条前向通道,分别是:
对应的结构图为:
-
R
R
1
G 5
G
小结小结
第四节
一、信号流图及其等效变换
1、信号流图的概念:
信号流图
信号流图
信号流图
2、组成:
信号流图由
参见下图:
上图中,是输出支路,对输出节点信号流图的概念
信号流图的概念节点:
支路:z支路:传送方向,传递函数标在支路上箭头的旁边,称z节点:z示例:
3、几个术语:
输出节点有输入支路的节点。如:混合节点Q。混合节点相当于结构图中的信号相加点和分支点。的信号是所有输入支路引进信号的叠加。
注意:梅森公式只能求系统总增益,即输出对输入的增益。而输出对混合节点(中间变量的增益就不能直接应用梅森公式。
即对混合节点,不能简单地通过引出一条增益为1的支路,而把非输入节点变成输入节点。
对此问题有两种方法求其传递函数:
一、把该混合节点的所有其它输入支路去掉,然后再用梅森公式;
二、分别用梅森公式求取输出节点及该节点对输入节点的传递函数,然后把它们的结果相比,即可得到输出对该混合节点的传递函数。
b
(S R例1 :已知结构图如下,可在结构图上标出节点,如上图所示。然后按照对应关系画出信号流图如下图所示。
5、信号流图的绘制
信号流图的绘制
信号流图的绘制
2按微分方程拉氏变换后的代数方程所表示的变量间数学
关系绘制。
如前例所对应的代数方程为
按方程可绘制信号流图
二、梅逊公式的推导
信号流图在系统状态方程中的应用

收稿 日期 :0 61—6 2 0 —11
作者 简介 : 高继森( 9 7)男 , 1 5- , 河南郑 州人 , 副教授.
维普资讯
7 8
兰 州 交 通 大学 学 报 ( 然 科 学 版 ) 自
C 尺
一
第2 6卷
2 [ ] T] n 和[ I 的构成
如 图 1 示. 所
【 【r ZJ
出的方法 , 把符号形式的 2 信号流图[ , 6 3 采用矩阵 ]
运算 , 化简 成一 种简单 的状 态矩 阵流 图 , 流图仅 含 该 有独 立源 节点状 态变 量 及 导数 节 点 , 编写 状 态 方程 的方 法及 所需 的各状 态传 输 矩 阵全 部 给 出 , 些计 这 算公 式具有 一般性 , 它适 用 于线性 电路 .
关 键 词 : 号 流 图 ; 态 方 程 信 状
中 图分 类 号 : TM1 1 3
文献标识码 : A
信号 流图 是 基 于 图论 应 用 的方 向的 一 个 重 要 分 支 , 在很 多 工程 领 域 , 如 , 它 例 电子 、 电力 、 通信 和
K I方程为[ u 一 [] 即 V 阅[ ] 0 ,
… .[ ] … . ] 一 0 有 [ ]一一 ] ] [ () 4 电路 的 VAR为 [ ]= [ rlI] U Z - E () 5
[ J]一 [ ] ] [ () 6
[
控制等工程得到广泛应用. 信号流 图是线性 方程组
的图形 表示 , 由节 点 和 有 向支 路 构 成 的 一 种有 向 是 图. 对一个 具体 电路 , 文献 [3由信 号 流 图导 出 了状 1
维普资讯
第2卷 第 3 6 期 20 0 7年 6月
第5讲:大气数据计算机

自整角机同步信号/数字转换
电阻/数字转换
S/H
A/D
输入信号的传输
2020年4月18日6时1分
第15/共45
数字式大气数据计算机-----输入 接口(一)
2020年4月18日6时1分
二进制译码器
A B C D S0 S1
逻辑多路转 换器
第16/共45
数字式大气数据计算机-----输入接 口(二)
Ts
!0.2M
2 a
由于
a2 kRT
且
Ma
V a
考虑到总温探头误差
2020年4月18日6时1分
第5/共45
大气数据计算机
组成
传感器测量
静压传感器、全压传感器、总温传感器、 攻角传感器等
具有可进行误差修正和补偿的解算装置 座舱指示、显示装置及信号输出装置
2020年4月18日6时1分
第6/共45
2020年4月18日6时1分
第13/共45
全温探头
2020年4月18日6时1分
第14/共45
数字式大气数据计算机-----输入 接口
多路转换器
直流电压/数字转换
V-T式A/D转换
多 路
双积分式A/D转换
转 换
逐次逼近式A/D转换
器
交/直流转换原理
频率/数字转换原理
频率测量原理
周期测量原理
VDC1 sin VDC2 cos
自整角机
信号转换 方框图
将三相同步信号变换成传送角的正弦、余弦两相交流信号, 然后再变成直流信号,再通过A/D转换成相应的数字量。
2020年4月18日6时1分
第24/共45
角度信号的反变换
sinα cosα
《模拟电子技术》第5讲放大电路的分析方法I

例题一
2. 从输出电压上看,哪个Q点下最易产生截止失真? 哪个Q点下最易产生饱和失真?哪个Q点下Uom最大?
(1) Q2靠近截止区,最容易出现截止失真;
(2) Q3靠近饱和区,最容易出现饱和失真; (3) Q4距离饱和区和截止区最远,最大不失真电压Uom 最大;
例题二:已知放大电路如下图所示,电路参数都标 在电路中,并且已知三极管的输入特性曲线, 80 rbb' 200 求解放大电路的静态工作点Q。
解答:空载时Uom=5.3/2^1/2=3.75V,容易出现饱和 失真;带载时Uom=3/2^1/2=2.12V,容易出现截止 失真。
作业:
P138 2.2(a),(b) P138 2.4
饱和失真
饱和失真产生于晶体管的输出回路! 集电极电流ic顶部失真,输出电压uo底部失真!
消除饱和失真的方法
Rc↓或VCC↑
Q '''
Q''
Rb↑或 VBB ↓或 β↓
• 消除方法:增大Rb,减小VBB,减小β • 消除方法:减小Rc,增大VCC
一般不采 用!
4、图解法的特点
• 形象直观; • 适应于Q点分析、失真分析、最大不失真输出 电压的分析; • 能够用于大信号分析; • 不易准确求解; • 不能求解输入电阻、输出电阻、通频带等参数。
I BQ
VBB U BEQ Rb
分析静态工作点
ICQ I BQ
UCEQ VCC ICQ Rc
直流通路
基本共射放大电路的交流通路
交流通路绘制原则: VBB=0(短路),VCC=0(短路)
交流通路
阻容耦合单管共射放大电路的直流通路直流Biblioteka 路绘制原则:C1开路,C2开路
专题4-结构图与信号流图

图 RC无源网络结构图
2 结构图的等效变换和简化
复杂系统结构图,其方框间的连接是错综复杂的,但 方框间的基本连接方式只有串联、并联和反馈连接三种。 在简化过程中应遵循变换前后变量关系保持等效的原 则,
反馈连接方框的简化(等效)
R(s)
E(s)
C(s)
(ቤተ መጻሕፍቲ ባይዱ)
R(s)
B(s)
G(s)
H(s) (a)
名词术语
源节点(输入节点) 在该点上只 有信号输出支路,没有信号输入支 路,一般代表系统的输入量。
阱节点(输出节点)该点上只有输入支路而没有输出支路,代表输出量。 混合节点 在该点上既有输入支路又有输出支路。若从混合节点引出 一条具有单位增益的支路,可将混合节点变为阱节点.
4 信号流图的绘制
(1)由系统微分方程绘制信号流图
含有微分或积分的线性方程,应通过拉氏变换,变换为s的代 数方程后再画信号流图。绘制时首先要对系统的每个变量指定一 个节点,然后,用标明支路增益的支路,根据方程式将各节点变 量正确连接。
例 试绘制无源网络信号流图。
将各变量重新排列得下述方程式组:
(2)由结构图绘制信号流图 只需在结构图的信号线上用小圆圈标志出传递的信号, 便得到节点;用标有传递函数的线段代替结构图中的方框, 便得到支路,于是结构图就变换为相应的信号流图了。
G( s) 1 G( s) H ( s)
C(s)
方框的反馈连接及其简化
(b)
例 试简化如图的结构图,并求系统传递函数C(s)/R(s).
系统结构图
R(s)
_
_
G1 G2
H2
H1
G3
G4
C (s )
H3
图讲信号完整性

信号完整性基础信号完整性问题过冲(overshoot/undershoot)振铃(ringing/ring back)非单调性(non-monotonic)码间串扰(ISI)同步开关噪声(SSN)噪声余量(noise margin)串扰(crosstalk)信号完整性(Signal Integrity)主要包括以下几方面问题:1.过冲(Overshoot/Undershoot)一般IC对于过冲的高度和宽度的容忍度都有指标。
因为过冲会使IC内部的ESD防护二极管导通,通常电流有100mA左右。
信号长期的过冲会使IC器件降质,并是电源噪声和EMI的来源之一。
2. 振铃(Ringing/Ring Back)振铃会使信号的threshold域值模糊,而且容易引起EMI。
3.非单调性(Non-monotonic)电平上升过程中的平台会产生非单调性,这有可能对电路有危害,特别是针对异步信号如:Reset、Clock等会有影响。
4. 码间串扰(ISI)主要是针对高速串行信号。
其产生的本质是前一个波形还没有进入稳态,另外也有可能是传输线对不同频率衰减不同所造成的。
一般通过眼图来观察,方法是输入一伪随机码,观察输出眼图。
5. 同步开关噪声(SSN)同步开关噪声会使单根静止的信号线上出现毛刺?V,另外还会影响输入电平的判断。
SSN的另一种现象是SSO(同步开关输出),这会使得传输线的特性如阻抗、延时等特性发生改变。
6. 噪声裕量(Noise Margin)控制噪声余量的目的是防止外界干扰,用于克服仿真没有分析到的一些次要因素。
一般对于TTL信号应留有200~300mV的余量。
7. 串扰(Crosstalk)串扰主要有线间串扰、回路串扰、通过平面串扰(常见于数模混合电路)三种形式。
通常示波器所观察到的数字信号。
图中为各相关的信号完整性参数:•Overshoot、Undershoot指信号的过冲。
•Ringback 指信号的振铃。
第5讲:微波网络散射参数测量方法

现代微波与天线测量技术第5 讲:微波网络散射参数测量方法彭宏利博士2008.11微波与射频研究中心上海交通大学-电信学院-电子工程系第7节微波网络散射参数测量方法主要内容• 7. 1网络分析的基本概念• 7. 2网络分析系统• 7. 3反射参数测量• 7. 4传输参数测量• 7. 5S参数的全面测量及误差修正7.2. 现代网络分析系统设备:网络分析仪网络分析仪是通过测定线性网络的反射参数和传输参数,获得该网络参数频域、时域特性等几乎所有网络特性的测量仪器,S 参数是其中最基本的特性参数。
网络分析仪分为2 类:(1)标量网络分析仪:只测量线性系统的幅度信息;(2)矢量网络分析仪:可同时进行幅度传输特性和相位特性测量。
系统组成原理基本的网络分析仪:主要由信号源、S 参量测量装置及矢量电压表组成。
图7.2-1信号源:向被测网络提供入射信号或激励;S 参量测量装置:是反射测量电路与传输测量电路的组合,首先将入射、反射及传输信号分离开,然后通过转换开关分别进行测量;矢量电压表:测量入射、反射和传输信号的幅值及它们之间的相位差,也可以通过幅相接收机实现此功能。
标量网络分析仪组成图图7.2-2a1 为入射波、b1 为反射波、b2 为传输波,它们的测量通道分别为R(参考)、A、B。
通过这些信号可确定正向S 参数|S11|、|S21|。
将被测网络的激励端与测试端反接,同理可测得|S22|、|S12|。
外差式矢量网络分析仪组成图上图中PFD 为相频检波器,H(s)为环形滤波器,BPF 为带通滤波器。
基本结构与外差式接收机类似:扫频源一方面为DUT 提供激励,一方面可以作为单独的扫频源输出通道S。
参考信号即入射波,通过R 通道进行测量。
反射波、传输波所在的测试通道分别为A、B。
为获得复S 参数而进行的复数除法可用硬件完成,现在多采用对混频所得的中频信号采样和数字化,然后通过数字处理的方法来实现。
网络分析仪与频谱分析仪比较在电路结构方面,矢量网络分析仪与外差式频谱分析仪相似:在预定频率范围内自动测量电路幅度增益与相位,使用内部扫频源或可程控的外部信号源作激励,测量被激励电路的幅度增益与相位。
第2章 第4讲 信号流图及其梅逊公式

4
输入节点 输出节点 混合节点
混 合 节 点
X a X
输入节点 d 源点) (源点)
X
5
1
2
b
X
3
输入节点 源点) (源点)
c
输出节点 汇点) (汇点)
4
支路
连接两个节点的定向线段,用支路增益(传递函数)表示方 连接两个节点的定向线段,用支路增益(传递函数) 程式中两个变量的因果关系。支路相当于乘法器。信号在支 程式中两个变量的因果关系。支路相当于乘法器。 路上沿箭头单向传递。 路上沿箭头单向传递。
-1 Ui 1
1/R1
I1
1/sC1
UA
1
1/R2
I2 1/sC 2
1 Uo
-1
-1
23
(Mason)公式 6 梅逊 (Mason)公式
G —系统总传递函数或增益
1 n G ( s) = ∑ Pk k k =1
条前向通路的传递函数(通路增益) Pk—第k条前向通路的传递函数(通路增益) —特征式
自动控制原理
第4讲 信号流图及梅 逊公式
杨金显
yangjinxian@
河南理工大学电气工程与自动化学院
1
本节内容
信号流图及其术语 信号代数运算法则 根据微分方程绘制信号流图 根据结构图绘制信号流图 梅逊公式 根据梅逊闭环传递函数
2
1 信号流图概念 信号流图起源于梅逊( MASON) 信号流图起源于梅逊(S.J. MASON)利用图示法来 描述一个和一组线性代数方程, 描述一个和一组线性代数方程,是由节点和支路组成 的一种信号传递网络。 的一种信号传递网络。
步骤: 、画出前向通路(可能有多个 可能有多个); 步骤:1、画出前向通路 可能有多个 ; 2、确定节点(多画一个没有关系 ; 、确定节点 多画一个没有关系 多画一个没有关系); 3、连接各支路、回路 、连接各支路、
相对稳定性第十四讲

180 (c ) 180 104 76
方块图和信号流图
10-7-20
25
K 1 K 2.5
K 5.2
h(dB) h(dB) h(dB)
K c
方块图和信号流图
10-7-20
26
由题意知 Kg 10 G( j ) 0.1
K 0.1
(1 0.042 )(1 0.00252 )
方块图和信号流图
10-7-20
21
有关相位裕量和幅值裕量旳几点阐明
控制系统旳相位裕量和幅值裕量是系统旳极坐标图对 (-1,j0)点 接近程度旳度量。这两个裕量能够作为设计准则。
只用相位裕量和幅值裕量,都不足以阐明系统旳相对稳定 性。为了拟定系统旳相对稳定性,必须同步给出这两个量。
对于最小相位系统,只有当相位裕量和幅值裕量都是正值 时,系统才是稳定旳。负旳裕量表达系统不稳定。合适旳相位 裕量和幅值裕量能够预防系统中元件变化造成旳影响,而且指 明了频率值。
在极坐标图上旳临界点为0分贝和 180
方块图和信号流图
10-7-20
15
幅值裕量(Gain Margin) Kg
设系统旳相位穿越频率(Phase cross-over frequency)
( ) G( j )H ( j ) (2k 1) k 0,1,
定义幅值裕量为
Kg
1
G( j )H ( j )
方块图和信号流图
10-7-20
6
对照图如下:
正穿越
增长 时,相 角增大
负穿越 相角方向为正
1
L( )
( )
c
负穿越 正穿越
方块图和信号流图
10-7-20
7
例 1图5-37所示旳四种开环对数幅相频率特征,试鉴 别其闭环后旳稳定性。
自动控制原理第5讲(结构图化简)
C
C(s)
-
-
B
G5 G2 G3 G4
串联和并联
G7
G6
G5 1 G5 H 2
R(s) G1
G5
C(s)
反馈
-
H1G2
H2
1 G5
G1G5 G1G6 1 G5 H 2 G1G5 G7 1 GHG 1 G5 H 2 G1 H 1G2 1 G1G6 H 1G2 1 1 1 2 G5 1 G5 H 2
R(s) G(s) 比较点前移
+
C(s) Q(s)
R(s)
+
G(s)
C(s)
比较点后移 Q(s)
R(s)
+
G(s) C(s)
R(s) G(s)
+
C(s)
Q(s)
Q(s) G(s)
输 出 不 变 原 则
C ( s) R( s)G ( s) Q( s) Q( s ) [ R( s ) ]G ( s) G( s)
为了由系统的方块图方便地写出它的闭环传递 函数,通常需要对方块图进行等效变换。方块图的等 效变换必须遵守一个原则,即变换前后各变量之间的 传递函数保持不变。在控制系统中,任何复杂系统主 要由响应环节的方块经串联、并联和反馈三种基本形 式连接而成。三种基本形式的等效法则一定要掌握。 其他变化(比较点的移动、引出点的移动、比较点和 引出点之间不能互移)以此为基础(目标)。
G1G5 G1 (G2G3 G4 ) C (s) G7 R(s) 1 G7 1 G5 H 2 G1H1G2 G1G5 1 (G2G3 G4 )(G1 H 2 ) G1H1G2
第五讲状态机设计及其指导原则全篇

第五讲状态机设计及其指导原则1/ 38第五讲状态机设计及其指导原则1/ 38制作人:梁瑞宇单位:河海大学制作人:梁瑞宇单位:河海大学第五讲状态机设计及其指导原则1 状态机是一种设计思想方法2状态机结构3状态机设计的其他技巧4状态机设计步骤第五讲状态机设计及其指导原则2/ 38第五讲状态机设计及其指导原则2/ 38制作人:梁瑞宇单位:河海大学制作人:梁瑞宇单位:河海大学z 状态机是一种设计思想方法第五讲状态机设计及其指导原则3/ 38第五讲状态机设计及其指导原则3/ 38制作人:梁瑞宇单位:河海大学制作人:梁瑞宇单位:河海大学原语描述module noconditional (clk,nrst,state,event);input clk,nrst input state;output event;reg event;reg [2:0] CS; //CurrentState reg[2:0] NS; //NextStateparameter [2:0] //one hot with zero idleidle = 3’b000,dorm = 3'b001,diningroom = 3'b010,classroom = 3'b100;第五讲状态机设计及其指导原则4/ 38第五讲状态机设计及其指导原则4/ 38制作人:梁瑞宇单位:河海大学制作人:梁瑞宇单位:河海大学//sequential state transitionalways @ (posedge clk or negedge nrst)if (!nrst) CS <= idle; else CS <= NS; //combinational condition judgment always @ (nrst or CS)begincase (CS)idle:idle_task;NS = dorm;dorm:dorm_task;NS = diningroom;diningroom:diningroom_task;NS = classroom;classroom:classroom_task;NS = dorm;default:idle_task;NS = dorm;endcase end endmodule第五讲状态机设计及其指导原则5/ 38第五讲状态机设计及其指导原则5/ 38制作人:梁瑞宇单位:河海大学制作人:梁瑞宇单位:河海大学第五讲状态机设计及其指导原则6/ 38第五讲状态机设计及其指导原则6/ 38制作人:梁瑞宇单位:河海大学制作人:梁瑞宇单位:河海大学 状态机的本质--对具有逻辑顺序或时序规律事件的一种描述方法 状态机的两个应用思路:-从状态变量入手-明确电路的输出的关系第五讲状态机设计及其指导原则7/ 38第五讲状态机设计及其指导原则7/ 38制作人:梁瑞宇单位:河海大学制作人:梁瑞宇单位:河海大学对于逻辑电路而言,小到一个简单的时序逻辑,大到复杂的微处理器,都适合用状态机方法进行描述。
梅森公式-信号流图PPT课件
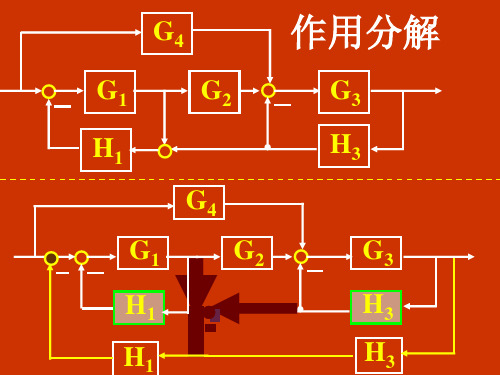
作用分解
G1
G2
G3
H1
G4
G1
G2
H3 G3
H1
H3
H1
H3
梅逊公式介绍 R-C : △称为系统特征式
C(s) R(s)
=
∑Pk△k △
△= 1 - ∑La + ∑LbLc -∑LdLeLf+…
其中:
—∑La 所有单独回路增益之和
∑LbLc—所有两两互不接触回路增益乘积之和
∑LdLeLf—所有三个互不接触回路增益乘积之和
1 - G1H1 + G2H2 + G1G2H3 -G1H1G2 H2
信号流图
e
g
R(s) 1
a
b
c
d
C(s)
f
h
前向通路两条
四个单独回路,两个回路互不接触
C(s) R(s)
=
1
abc d + e d (1 – bg) – af – bg – ch– eh g f +af ch
信号流图
• 信号流图是由节点和支路组成的一种信号传递网络。
Uo(s)
Ui(s)
-1
1/R1
1/C1s
IC(s)
-1
U(s)
1/R2
1/C2s
I2(s)
-1
Uo(s) Uo(s)
例3 已知系统信号流图,求传递函数。
解:三个回路:L1 G 2H 2
-H1
L2 G1G 2H2
L3 G 2G 3H1
• 回路相互均接触,则:
R
G1 G2 G3
C
H2 -H2
G4
L 3 a 44 互不接触 L 22 a 23 a 35 a 52 a 44
郑君里《信号与系统》(第3版)【教材精讲+考研真题解析】讲义 第11章 反馈系统 【圣才出品】

第11章反馈系统[视频讲解]11.1本章要点详解本章要点■反馈系统■信号流图重难点导学一、反馈系统反馈系统的研究是利用分解与互联概念而获得成功的典型范例。
1.连续时间信号反馈系统模型图11-1连续时间信号反馈系统模型2.离散时间信号反馈系统模型图11-2离散时间信号反馈系统模型3.反馈系统的基本特性及其应用(1)基本特性①前馈通路系统函数()A s (或()A z )对整个系统函数()H s (或()H z )的影响可忽略不计;②整个的系统函数()H s (或()H z )近似等于反馈通路系统函数()F s (或()F z )的倒数。
(2)应用①改善系统的灵敏度;②改善系统频响特性;③逆系统设计;④使不稳定系统成为稳定系统;⑤利用反馈系统产生自激振荡。
二、信号流图1.概述利用方框图可以描述系统(连续的或离散的),较微分方程或差分方程更为直观。
而将方框图进一步简化就可以得到流图。
其优点是系统模型的表示简明清楚、系统函数的计算过程明显简化。
2.系统的信号流图表示法信号流图是指用一些点和支路来描述系统,如图11-3所示。
图11-3用信号流图表示框图Y s称为结点。
线段表示信号传输的路径,称为支路。
信号的传输方向用箭X s、()()头表示,转移函数标在箭头附近,相当于乘法器。
3.流图术语(1)结点:表示系统中变量或信号的点。
(2)转移函数:两个结点之间的增益称为转移函数。
(3)支路:连接两个结点之间的定向线段,支路的增益即为转移函数。
(4)输入结点或源点:只有输出支路的结点,它对应的是自变量(即输入信号)。
(5)输出信号或阱点:只有输入支路的结点,它对应的是因变量(即输出信号)。
(6)混合结点:既有输入支路又有输出支路的结点。
(7)通路:沿支路箭头方向通过各相连支路的途径(不允许有相反方向支路存在)。
(8)开通路:通路与任一结点相交不多于一次。
(9)闭通路:如果通路的终点就是起点,并且与任何其他结点相交不多于一次。
信号与系统教案

信号与系统教案第1次课2学时授课时间课题(章节)第一章绪论引言信号概述教学目的与要求:了解信号与常用信号,熟练掌握信号描述的各种方法。
教学重点、难点:对该课程的认识,强调该课的研究方法和要求,以及该课程在今后课程中的作用。
信号的表示方法。
教学方法及师生互动设计:以通信系统为例,导入信号与系统的教学任务,简单介绍通信系统的知识,让学生逐渐进入专业研究,领会该课程在今后专业研究中所发挥的作用。
板书与PPT演示相结合介绍常见信号,并通过若干例子进一步阐述所讲内容,深化理解信号的表示方法。
课堂练、作业:课后小结:按计划完成内容,通过通信系统实例讲解信号与系统课程作用,使学生对专业有进一步了解。
讲解常见信号,使学生能运用表达式、图形等来描述信号。
第2次课2学时授课时间课题(章节)2信号运算教学目的与要求:熟练掌握信号描述的各种方法,及信号的基本变换,能熟练进行信号的运算。
教学重点、难点:信号的变换及计算。
教学方法及师生互动设计:板书与PPT演示相结合渐渐引见信号的加、减、乘、除,和时移、反转等变更。
通过部分题例子来讲解信号是如何变更及计算的,最后布置题,让学生进一步加强对知识的理解,并通过题对其加深理解。
课堂练、作业:补充题课后小结:本节是重点内容,讲解稍慢。
通过多举题,提高学生解题能力。
与学生互动发现学生接收过程偏慢,其缘故原由是学生的基本计算能力还需求提高,应讲解更详尽更慢。
第3次课2学时授课时间课题(章节)3系统概述教学目的与要求:了解系统分类的思路,熟练掌握连续﹑动态﹑时不变线性系统的描述方法和数学模型,对算子法表示系统应能正确运用。
教学重点、难点:掌握线性时不变系统的辨别,强调线性、时不变性、因果性的独立。
教学方法及师生互动设计:先列举部分系统,导入LTI系统,然后列举题,让学生判别LTI系统。
板书与PPT演示相结合介绍其系统的描述方法和数学模型。
课堂练、作业:课后小结:此部分内容稍易,大多数同学在研究过程中思路清晰,理解较为容易。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
x1
a12
变量因果关系
x2
函数运算关系 信号传递关系
2
下面通过一个例子,说明信号流图是如何构成的。 设有一系统,它由下列方程组描述:
x2 =a12 x1 + a32 x3 x3 = a23 x2 + a43 x4 x4 = a24 x2 + a34 x3 + a44 x4 x5 = a25 x2 + a45 x4
式中T — 总传输 (增益);
Tk k
k 1
n
n — 从源节点至汇节点前向通道总数;
Tk — 第K条前向通路的传输;
— 信号流图的特征式; k —第k条前向通路特征式的余因子式
12
二、梅逊增益公式
特征式的意义为
1 L1 L2 L3 (1) m Lm
3)信号在支路上沿箭头单向传递,后一节点变量依赖于前
一节点变量,即只有“前因后果”的因果关系。 4)支路相当于乘法器,信号流经支路时,被乘以支路增益 而变换为另一信号。 5)对于给定的系统,信号流图不唯一。
5.信号流图的绘制方法
1.直接法 2.翻译法
例1 画出下图所示系统的信号流图。 E1(s) E2(s) R(s) G2(s) G1(s) + C(s)
18
梅逊增益公式在结构图上的应用
由于一一对应的关系,可以直接根据结构图,利用梅逊公式直接写出传递函数。
例5 已知结构图如图所示,试用梅逊公式求C(s)/R(s)。 G2(s) R(s)
+
﹣
G1(s) H ( s)
G3(s) G4(s)
+ +
C(s)
G2 1 R
G1 -H 1
G3 G4
C
1 (G1 H G2 H ) T1 G1G3 , 1 1 T2 G2G3 , 2 1 T3 G1G4 , 1 1
本节课学习重点
了解信号流图中的术语
掌握由系统结构图绘制信号流图
掌握梅逊增益公式
2.6
一、 信号流图的基本概念
信号流图
1.定义:信号流图是表示一组联立线性代数方程的图。
先看最简单的例子。有一线性系统,它由下述方程式描述:
x2 = a12 x1
式中, x1为输入信号(变量);x2为输出信号(变量);a12为两信号
有向性
限定了信号传递方向。支路方向就是信
号传递的方向,用箭头表示。
有权性
限定了输入与输出两个变量之间的关系。
支路的权用它近旁标出的传输值(增益)表示。
3.信号流图的几个术语
节点及其类别
输入节点(源点) 只有输出支路的节点,它代表系统的输 入变量。如图中x1。
输出节点(汇点) 只有输入支路的节点,它代表系统的 输出变量。如图中x4。 混合节点 既有输入支路,又有输出支路的节点,如图中 x2 、x3 。
比较点与其输出线代表的是一个节点,但如果比较点前的输入线有分支点, 分支点和比较点就必须用两个节点表示!
规律:
系统结构图
变量 输入变量 比较点 引出点 方框 传输线 输出端 支路 汇节点
11
信号流图
节点 源节点
混合节点
二、梅逊增益公式
输入输出节点间总传输的一般式为
Xc 1 T Xr
R
解:
G2 1 G1 -H 1 G3 G4 C
T11 T2 2 T3 3 G1 (G3 G4 ) G2G3 T 1 (G1 G2 ) H
G2(s) R(s)
+
﹣
G1(s) H ( s)
G3(s) G4(s)
+ +
C(s)
作业:
P52
2-13
2-14
21
1 = 1 (gi + ghj) 2 = 1
T11 T2 2 T12
x1到x3的传输: T1 = 3 1 = 1 ( ac + abd ) T2 = 2ae 2 = 1 a c b e g x3 f d
2
x1 3
x2
h
j
T11 T2 2 T13
i
思考题1 求系统的总传输 -g
a32 ,a33 (自回环) 。
x1
a12 x2
a23 a32
x3
a33
a34
x4
a14
6
前向通路
是指从源点开始并终止于汇点且与其他节点相交不多于一 次的通路,该通路的各传输乘积称为前向通路增益。 不接触回环 如果一信号流图有多个回环,各回环之间没有任何公共 节点,就称为不接触回环,反之称为接触回环。
-f
Xr(s)
1
a
b
c
-e
d
Xc(s)
前向通路1条
3个单独回环,没有不接触回环
17
思考题2
1
e
g
Xr(s)
a f
b
c
h
d
Xc(s)
前向通路两条
四个单独回路,两个回路互不接触 ab c d + e d (1 – b g) Xc(s) = Xr(s) 1 – a f – b g – ch– e h g f + af c h
﹣ቤተ መጻሕፍቲ ባይዱ
解:
E1(s) R(s)
H ( s) G1(s) E2(s) G2(s)
C(s)
- H ( s)
9
例2 绘制结构图对应的信号流图
G2(s) R(s)
+
﹣
G1(s)
H ( s)
G3(s) G4(s)
+ +
C(s)
1.相加点处 的-记入反馈 支路增益中
G2 1 R G1 -H 1 G3 G4
2.相加点与其 输入线上的分 支点翻译成相 邻的2个节点, 增益为1,但代 C 表不同变量
a32 a43 a44 a45 x4 a25
3
x1
a12
x2
a23
a34
把内部变量结构 和相互关系描述的
x3 a24
x5
一清二楚
2.信号流图的基本元素
(1) 节点:用来表示变量,用符号“ O ”表示,并在近 旁标出所代表的变量。
(2) 支路:连接两节点的定向线段,用符号“”表
示。 支路具有两个特征:
例4
已知系统的信号 c a 2 g x3 i j
d b e
f h
流图如下,求输入x1至输出
x2和x3的传输。
解:单回路:x1 ac,abd,gi,ghj,
x2
aegh
3
两两互不接触回路: ac与gi,ghj; abd与gi,ghj x1到x2的传输: T1 = 2ab T2 = 3gfab
=1-(ac+gi+abd+ghj+aegf)+(acgi+acghj+abdgi+abdghj)
a
x0
b i
c
d
j m
e
f k
g
h x8
解:信号流图的组成:4个单回环,一条前向通道
=1 (bi + dj + fk + bcdefgm) + (bidj + bifk + djfk) bidjfk T1 = abcdefgh 1 = 1 0 = 1
x8 T1 Δ1 abcdefgh T x0 Δ Δ
a33
x1
a12 x2
a23
x3
a34
x4
a32
a14
5
通路及其类别
通路 从某一节点开始,沿着支路的箭头方向连续经 过一些支路而终止在另一节点的路径。用经过的支路传
输的乘积来表示。
开通路 如果通道从某一节点开始,终止在另一节点上,
而且通道中的每个节点只经过一次。如a12 a23 a34 。
闭通路(回环) 如果通道的终点就是起点的通道。如a23
回环增益 回环中各支路传输的乘积称为回环增益(或传输)。 a33 1 a12 a23 x3 a 34 x1 x4 x2 a32
a14
7
4.信号流图的基本性质
1)信号流图只能表示线性代数方程组。 2)节点表示系统的变量,表示所有流向该节点的信号之 (代数)和;而从该节点流向各支路的信号,均用该节点变 量表示。
L1 ——信号流图中所有不同回环的传输之和;
L2 ——信号流图中每两个互不接触回环的传输乘积之和;
……
Lm ——m个互不接触回环的传输乘积之和;
k 为在Δ中除去与第k条前向通路相接触的回路后的
特征式,称为第k条前向通路特征式的余因子。
13
例3 求图所示系统的信号流图输入x0至输出x8的总传输G。
