一次函数与几何综合-培优
第五讲 一次函数的图象与性质培优辅导含答案

第五讲 一次函数的图象与性质培优辅导知识点:一、一次函数和正比例函数的概念;正比例函数的一般形式是 ,一次函数的一般形式是 ; 正比例函数与一次函数的关系是 ;二、 一次函数y kx b =+的图象与性质一次函数y kx b =+的图象是经过( )和( )两点的一条直线.1.、.正比例函数.....y=kx ....(.k .≠.0.)的性质....:. 2.、.一次函数....y kx b =+(.k .≠.0.).的性质...(.1.).k .的正负决定直线的倾斜方向............:. (.2.).|k|...大小决定直线的倾斜程度...........:. |k|...越大,直线与......x .轴相交的锐角度数越大(直线陡),................|k|...越小,直线与......x .轴相交的锐角度数越小(直线缓);................ (.3.).b .的正、负决定直线与.........y .轴交点的位置;....... (.4.).由于..k .,.b .的符号不同,直线所经过的象限也不同;..................(.5.)由于...|k|...决定直线与.....x .轴相交的锐角的大小,..........k .相同,说明这两个锐角的大小相等,且.................它们是同位角,因此,它们是平行的.另外,从.....................平移的角度.....也可以分析,例如:直线...........y=x ...+.1.可以看作是正比例函数..........y=x ...向上平移一个单位得到的.............k .相同,...b .不同..,它们是平行的.......;.k .不.相同,...b .相同,相交于......y .轴的同一点。
......如:已知一次函数y kx b =+(k ≠0),求字母k 、b 为何值时:(1)y 随x 的增大而增大 ; (2)图象经过第一二三象限 (3)图象不经过第二象限 ; (4)图象经过原点 ;(5)图象平行于直线y=-4x+1 ; (6)图象与y 轴交点不在x 轴上方 .【思想方法】数形结合 【例题精讲】例1. 一次函数的定义当m 、n 为何值时,函数25(2)()m y m x n m -=-++(1)是正比例函数? (2)是一次函数?例2.求一次函数的解析式【思想方法】数形结合例1. 已知一次函数物图象经过A(-2,-3),B(1,3)两点. (1)求这个一次函数的解析式;(2)试判断点P(-1,1)是否在这个一次函数的图象上; (3)求此函数与x 轴、y 轴围成的三角形的面积.【变式题组】1、直线143+-=x y 向下平移2个单位,再向左平移1个单位得到直线________。
一次函数之几何综合专题培优
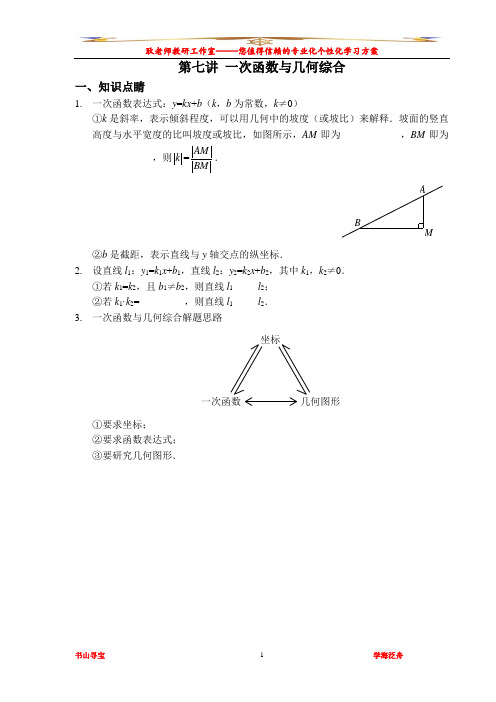
第七讲 一次函数与几何综合一、知识点睛1. 一次函数表达式:y =kx +b (k ,b 为常数,k ≠0)①k 是斜率,表示倾斜程度,可以用几何中的坡度(或坡比)来解释.坡面的竖直高度与水平宽度的比叫坡度或坡比,如图所示,AM 即为____________,BM 即为____________,则=AM k BM.MAB②b 是截距,表示直线与y 轴交点的纵坐标.2. 设直线l 1:y 1=k 1x +b 1,直线l 2:y 2=k 2x +b 2,其中k 1,k 2≠0.①若k 1=k 2,且b 1≠b 2,则直线l 1_____l 2; ②若k 1·k 2=_________,则直线l 1_____l 2. 3. 一次函数与几何综合解题思路坐标几何图形一次函数①要求坐标; ②要求函数表达式; ③要研究几何图形.二、精讲精练1.如图,点B,C分别在直线y=2x和y=kx上,A,D是x轴上的两点,若四边形ABCD是正方形,则k的值为________.第1题图第2题图2.如图,已知直线l:y x=+x轴交于点A,与y轴交于点B,将△AOB沿直线l折叠,点O落在点C处,则直线AC的表达式为__________________.3.如图,在平面直角坐标系xOy中放入一张长方形纸片ABCO,点D在AB边上,将CD所在直线的解析式为__________________.第3题图第4题图4.如图,直线l1交x轴、y轴于A,B两点,OA=m,OB=n,将△AOB绕点O逆时针旋转90°得到△COD.CD所在直线l2与直线l1交于点E,则l1____l2;若直线l1,l2的斜率分别为k1,k2,则k1·k2=_______.5.如图,直线483y x=-+分别交x轴、y轴于A,B两点,线段AB的垂直平分线交x 轴于点C,交AB于点D,则点C的坐标为____________.第5题图第6题图6.如图,在平面直角坐标系中,函数y=x的图象l是第一、三象限的角平分线.探索:若点A的坐标为(3,1),则它关于直线l的对称点A'的坐标为____________;猜想:若坐标平面内任一点P的坐标为(m,n),则它关于直线l的对称点P′的坐标为____________;应用:若已知两点B(-2,-5),C(-1,-3),试在直线l上确定一点Q,使点Q到B,C两点的距离之和最小,则此时点Q的坐标为____________.7.如图,已知直线l1:2833y x=+与直线l2:y=-2x+16相交于点C,直线l1,l2分别交x轴于A,B两点,矩形DEFG的顶点D,E分别在l1,l2上,顶点F,G都在x轴上,且点G与点B重合,那么S矩形DEFG:S△ABC=_________.8.如图,已知点A的坐标为(2,0),点B在直线y=-x上运动,当线段AB最短时,点B的坐标为()A.(-1,1)B.,C.(1,-1)D.(9.如图,在平面直角坐标系中,点A,B的坐标分别为A(4,0),B(0,-4),P为y轴上B点下方的一点,且PB=m(m>0),以点P为直角顶点,AP为腰在第四象限内作等腰Rt△APM.(1)求直线AB的解析式;(2)用含m的代数式表示点M的坐标;(3)若直线MB与x轴交于点Q,求点Q的坐标.。
一次函数应用及几何应用培优

BF=OE=2,OF= = ,
∴点B的坐标是( ,2)
设直线AB的解析式是y=kx+b(k≠0),则有 .
解得 .
∴直线AB的解析式是y= x+4;
(2)如图2,∵△ABD由△AOP旋转得到,
∴△ABD≌△AOP,
∴AP=AD,∠DAB=∠PAO,
解得a=b=6 ,c=12,
∵a2+b2=(6 )2+(6 )2=144=c2,
∴△ABC是直角三角形,
又∵a=b,
∴△ABC是等腰直角三角形;
(2)∵AB=c=12,
∴点B(12,0),
过点C作CD⊥x轴于D,则AD=CD= AB= ×12=6,
∴点C的坐标为(6,6);
(3)如图,把△ACM绕点C逆时针旋转90°得到△BCM′,连接M′N,
在△P′PC中,P′P2+P′C2=32+42=25=PC2,
∴∠PP′C=90°,
∴∠APB=∠AP′C=∠AP′P+∠PP′C=60°+90°=150°,
∴∠APB=150°;
故答案是:150°,△ABP;
(Ⅱ)(1)整理得,|a﹣6 |+(c﹣12)2+ =0,
由非负数的性质得,a﹣6 =0,c﹣12=0,b﹣6 =0,
解得x=2或x=10,
∴点C的坐标为(2,2)或(10,﹣2);
(3)用勾股定理+直线交点坐标做
综上所述,点C( ,3﹣ )或(﹣6,6)时,△BCD与△AOB全等.
2.已知直线y=﹣ x+4与x轴和y轴分别交与B、A两点,另一直线经过点B和点D(11,6).
一次函数与几何综合培优

一次函数与平面几何综合培优1.如图,在平面直角坐标系中,O是坐标原点,点A的坐标为(-4,0),点B的坐标为(0,b)(b>0). P是直线AB上的一个动点,作PC⊥x轴,垂足为C.记点P关于y轴的对称点为P'(点P'不在y轴上),连结PP',P'A,P'C.设点P的横坐标为a.(1)当b=3时,①求直线AB的解析式;②若点P'的坐标是(-1,m),求m的值;(2)是否同时存在a,b,使△P'CA为等腰直角三角形?若存在,请求出所有满足要求的a,b的值;若不存在,请说明理由.2如图,在平面直角坐标系中,O为坐标原点.A.B两点的坐标分别为A(m,0)、B(0,n)P从A出发,以每秒1个单位的速度沿射线AO匀速运动,设点P运动时间为t秒.(1)求m、n的值与OA、OB的长;(2)连接PB,若△POB的面积不大于3且不等于0,则t的取值范围是(请直接写出答案).(3)过P作直线AB的垂线,垂足为D,直线PD与y轴交于点E,在点P运动的过程中,是否存在这样的点P,使△EOP≌△AOB?若存在,请求出t的值;若不存在,请说明理由.3.如图,A(1,0),B(4,0),M(5,3).动点P从点A出发,沿x轴以每秒1个单位长的速度向右移动,且过点P的直线l:y=-x+b也随之移动.设移动时间为t秒.(1)当t=1时,求l的解析式;(2)若l与线段BM有公共点,确定t的取值范围;(3)直接写出t为何值时,点M关于l的对称点落在y轴上.如不存在,请说明理由.4.如图,已知在直角坐标系中,A(4,0),B(0,3),以线段AB为直角边在第一象限内作等腰Rt△ABC,∠BAC=90°.点P是x轴上的一个动点,设P(x,0)。
(1)求△ABC的面积;(2)若△ABP是等腰三角形,求点P的坐标;(3)是否存在这样的点P,使得|PC-PB|的值最大?如果不存在,请说明理由;如果存在,请在备用图中标出点P的位置。
2023年九年级数学下册中考综合培优测试卷:一次函数-动态几何问题【含答案】
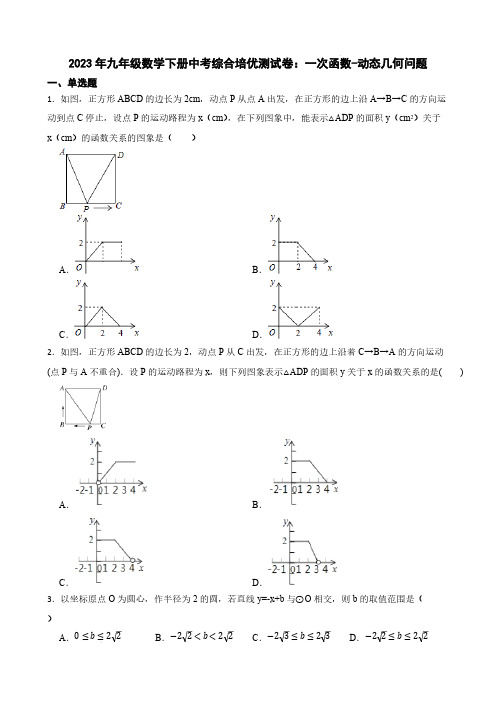
2023年九年级数学下册中考综合培优测试卷:一次函数-动态几何问题一、单选题1.如图,正方形ABCD的边长为2cm,动点P从点A出发,在正方形的边上沿A→B→C的方向运动到点C停止,设点P的运动路程为x(cm),在下列图象中,能表示△ADP的面积y(cm2)关于x(cm)的函数关系的图象是( )A.B.C.D.2.如图,正方形ABCD的边长为2,动点P从C出发,在正方形的边上沿着C→B→A的方向运动(点P与A不重合).设P的运动路程为x,则下列图象表示△ADP的面积y关于x的函数关系的是( )A.B.C.D.3.以坐标原点O为圆心,作半径为2的圆,若直线y=-x+b与⊙O相交,则b的取值范围是( )0≤b≤22−22<b<22−23≤b≤23−22≤b≤22 A.B.C.D.4.如图,在正方形ABCD中,点P从点A出发,沿着正方形的边顺时针方向运动一周,则△APC 的面积y与点P运动的路程x之间形成的函数关系图象大致是( )A.B.C.D.5.如图,正方形ABCD的边长为4cm,动点P从点A出发,沿A→D→C的路径以每秒1cm的速度运动(点P不与点A、点C重合),设点P运动时间为x秒,四边形ABCP的面积为ycm2,则下列图象能大致反映y与x的函数关系的是( )A.B.C.D.A B 4.P,QРA1 6.在数轴上,点表示-2,点表示为数轴上两点,点从点出发以每秒个单Q B2Q位长度的速度向左运动,同时点从点出发以每秒个单位长度的速度向左运动,点到达ОQ BРQР原点后,立即以原来的速度返回,当点回到点时,点与点同时停止运动.设点xРQ y y x运动的时间为秒,点与点之间的距离为个单位长度,则下列图像中表示与的函数关系的是( )A.B.C.D.7.已知点A为某封闭图形边界上一定点,动点P从点A出发,沿其边界顺时针匀速运动一周.设点P运动的时间为x,线段AP的长为y.表示y与x的函数关系的图象大致如图,则该封闭图形可能是( )A.B.C.D.8.如图,正方形ABCD的边长为4,点E是AB的中点,点P从点E出发,沿E→A→D→C移动至终点C,设P点经过的路径长为x,△CPE的面积为y,则下列图图能大致反映y与x函数关系的是( )A.B.C.D.9.如图1,在矩形MNPQ中,动点R从点N出发,沿N→P→Q→M方向运动至点M处停止。
北师大版八年级上册一次函数与几何解答题 培优专题(解析版)

2019-2020一次函数与几何解答题培优专题(解析版)1.如图,在平面直角坐标系中,一次函数y=kx+b的图象经过点A(﹣2,6),且与x轴相交于点B,与正比例函数y=3x的图象相交于点C,点C的横坐标为1.(1)求k、b的值;(2)若点D在y轴负半轴上,且满足S△COD=13S△BOC,求点D的坐标.2.如图,已知直线l1:y=2x+3,直线l2:y=﹣x+5,直线l1、l2分别交x轴于B、C两点,l1、l2相交于点A.(1)求A、B、C三点坐标;(2)求△ABC的面积.3.如图,已知一次函数y=mx+3的图象经过点A(2,6),B(n,-3).求:(1)m,n的值;(2)△OAB的面积.4.已知一次函数y=kx+b (k 、b 是常数)的图像平行于直线-3y x ,且经过点(2,-3). (1)求这个一次函数的解析式;(2)求这个一次函数与两坐标轴所围成的图形面积.5.长方形OABC ,O 为平面直角坐标系的原点,OA =5,OC =3,点B 在第三象限.(1)求点B 的坐标;(2)如图,若过点B 的直线BP 与长方形OABC 的边交于点P ,且将长方形OABC 的面积分为1:4两部分,求点P 的坐标.6.如图,在平面直角坐标系xOy 中,正比例函数y =x 的图象与一次函数y =kx -k 的图象的交点坐标为A(m ,2).(1)求m 的值和一次函数的解析式;(2)设一次函数y =kx -k 的图象与y 轴交于点B ,求△AOB 的面积;(3)直接写出使函数y =kx -k 的值大于函数y =x 的值的自变量x 的取值范围.7.如图,已知直线y =-2x +6与x 轴交于点A ,与y 轴交于点B.(1)点A 的坐标为________,点B 的坐标为________.(2)求△AOB 的面积.(3)直线AB 上是否存在一点C(点C 与点B 不重合),使△AOC 的面积等于△AOB 的面积?若存在,求出点C 的坐标;若不存在,请说明理由.8.已知:直线24y x =+与x 轴交于点A ,与y 轴交于点B ,坐标原点为O .(1)求点A ,点B 的坐标.(2)求直线24y x =+与x 轴、y 轴围成的三角形的面积.(3)求原点O 到直线24y x =+的距离.9.如图,一次函数y =2x +3与x 轴相交于点A ,与y 轴相交于点B.(1)求点A ,B 的坐标;(2)求当x =-2时,y 的值,当y =10时,x 的值;(3)过点B 作直线BP 与x 轴相交于点P ,且使OP =2OA ,求△ABP 的面积.10.如图,一次函数334y x =-+的图象与x 轴和y 轴分别交于点A 和点B ,将△AOB 沿直线CD 对折,使点A 与点B 重合,直线CD 与x 轴交于点C ,与AB 交于点D .(1)求A 、B 两点的坐标;(2)求OC 的长;(3)点P 是x 轴上一动点,若△P AB 是等腰三角形,写出点P 的坐标(不需计算过程).11.如图,直线l 1的解析式为33y x =-,且l 2与x 轴交于点D ,直线2l 经过点A 、B ,直线l 1,2l 相交于点C .()1求点D 的坐标;()2求ADC 的面积.12.如图,在平面直角坐标系xOy中,直线y=x+b与双曲线y=相交于A,B两点,已知A(2,5).求:(1)b和k的值;(2)△OAB的面积.13.已知:一次函数y=(1﹣m)x+m﹣3(1)若一次函数的图象过原点,求实数m的值.(2)当一次函数的图象经过第二、三、四象限时,求实数m的取值范围.14.如图,在平面直角坐标系中,为坐标原点,直线:与直线:交于点,与轴交于,与轴交于点.(1)求△的面积;(2)若点在直线上,且使得△的面积是△面积的,求点的坐标.15.已知一次函数y=(m﹣2)x﹣3m2+12,问:(1)m 为何值时,函数图象过原点?(2)m 为何值时,函数图象平行于直线y=2x ?(3)m 为何值时,函数图象过点(0,﹣15),且y 随x 的增大而减小?16.已知函数y =(m -2)x 3-|m|+m +7,当m 为何值时,y 是x 的一次函数.17.如图,一次函数y=-x+m 的图象与x 轴和y 轴分别交于点A 和点B ,与正比例函数32y x =图象交于点P(2,n).(1)求m 和n 的值;(2)求△POB 的面积;(3)在直线OP 上是否存在异与点P 的另一点C ,使得△OBC 与△OBP 的面积相等?若存在,请求出C 点的坐标;若不存在,请说明理由.18.如图,在平面直角坐标系中,直线3y x =-+过点(5,)A m 且与y 轴交于点B ,把点A 向左平移2个单位,再向上平移4个单位,得到点C .过点C 且与2y x =平行的直线交y 轴于点D .(1)求直线CD 的解析式;(2)直线AB 与CD 交于点E ,将直线CD 沿EB 方向平移,平移到经过点B 的位置结束,求直线CD 在平移过程中与x 轴交点的横坐标的取值范围.19.如图,直线1y x =-+与直线3y x =- ,两直线与x 轴的交点分别为A 、B .(1)求两直线交点C 的坐标;(2)求ABC ∆的面积.20.如图,已知一次函数y=kx+b 的图象经过A (﹣2,﹣1),B (1,3)两点,并且交x 轴于点C ,交y 轴于点D .(1)求一次函数的解析式;(2)求点C 和点D 的坐标;(3)求△AOB 的面积.21.已知一次函数y =kx +b 的图象经过点A (−1,−1)和点B (1,−3).求:(1)求一次函数的表达式;(2)求直线AB 与坐标轴围成的三角形的面积;(3)请在x轴上找到一点P,使得P A+PB最小,并求出P的坐标.22.如图,一次函数y=kx+b的图象经过点A(8,0),直线y=-3x+6与x轴交于点B,与y轴交于点D,且两直线交于点C(4,m).(1)求m的值及一次函数的解析式;(2)求△ACD的面积。
八年级数学竞赛培优 一次函数与几何综合 含解析

八年级数学竞赛培优 一次函数与几何综合 含解析【思维入门】1.如图4-15-1,已知A 点的坐标为(2,0),点B 在直线y =-x 上运动,当线段AB 最短时,点B 的坐标为( )图4-15-1A .(0,0)B .(2,-2)C .(1,-1)D .(-2,2)2.如图4-15-2,直线y =-43x +8与x 轴,y 轴交于A ,B 两点,∠BAO 的平分线所在的直线AM 的解析式是( )A .y =-12x +52 B .y =-12x +3 C .y =-12x +72D .y =-12x +4图4-15-23.如图4-15-3,在平面直角坐标系中,点A (0,4),B (3,0),连结AB .将△AOB 沿过点B 的直线折叠,使点A 落在x 轴上的点A ′处,折痕所在的直线交y 轴正半轴于点C ,则直线BC 的解析式为____.图4-15-34.如图4-15-4,直线y=-33x+2与x轴相交于点A,与y轴相交于点B,将△ABO沿着AB翻折,得到△ABC,则点C的坐标为____.图4-15-45.如图4-15-5,在平面直角坐标系中,一次函数y=-12x+1的图象与x轴,y轴分别交于A,B两点.(1)求点A,B的坐标;(2)点C在y轴上,当S△ABC=2S△AOB时,求点C的坐标.图4-15-5【思维拓展】6.如图4-15-6,是一对变量满足的函数关系的图象.有下列3个不同的问题情境:图4-15-6①小明骑车以400 m/min的速度匀速骑了5 min,在原地休息了4 min,然后以500 m/min的速度匀速骑回出发地,设时间为x min,离出发地的距离为y km;②有一个容积为6 L的开口空桶,小亮以1.2 L/min的速度匀速向这个空桶注水,注5 min后停止,等4 min后,再以2 L/min的速度匀速倒空桶中的水,设时间为x min,桶内的水量为y L;③矩形ABCD中,AB=4,BC=3,动点P从点A出发,依次沿对角线AC,边CD,边DA运动至点A停止,设点P的运动路程为x,当点P与点A不重合时,y=S△ABP;当点P与点A重合时,y=0.其中,符合图中所示函数关系的问题情境的个数为()A.0B.1C.2D.37.如图4-15-7,平面直角坐标系中,已知直线y=x上一点P(1,1),C为y轴上一点,连结PC,线段PC绕点P顺时针旋转90°至线段PD,过点D作直线AB⊥x轴,垂足为B,直线AB与直线y=x交于点A,且BD=2AD,连结CD,直线CD与直线y=x交于点Q,则点Q 的坐标为____.图4-15-7图4-15-88.已知点A(1,5),B(3,-1),点M在x轴上,当AM-BM最大时,点M的坐标为____.9.如图4-15-8,已知函数y=-12x+b的图象与x轴,y轴分别交于点A,B,与函数y=x的图象交于点M,点M的横坐标为2.在x轴上有一点P(a,0)(其中a>2),过点P作x轴的垂线,分别交函数y=-12x+b和y=x的图象于点C,D.(1)求点A的坐标;(2)若OB=CD,求a的值.【思维升华】10.若四条直线x=1,y=-1,y=3,y=kx-3所围成的凸四边形的面积等于12,则k的值为____.11.如图4-15-9,在平面直角坐标系中,直线AB由直线y=3x沿x轴向左平移3个单位长度所得,则直线AB与坐标轴所围成的三角形的面积为____.图4-15-94,0,P 12.直线y=kx+4分别与x轴,y轴相交于点A,B,O是坐标原点,A点的坐标为()是OB上(O,B两点除外)的一点,过P作PC⊥y轴交直线AB于C,过点C作CD⊥x轴,0,m.垂足为D,设线段PC的长为l,点P的坐标为()(1)求k的值;(2)如果点P在线段OB(O,B两点除外)上移动,求l与m的函数关系式,并写出自变量m的取值范围;(3)当点P运动到线段OB的中点时,四边形OPCD为正方形,将正方形OPCD沿着x轴的正0<a<4,正方形OPCD与△AOB重叠部分的面积为S.试求S 方向移动,设平移的距离为a()与a的函数关系式.一次函数与几何综合【思维入门】1.如图4-15-1,已知A点的坐标为(2,0),点B在直线y=-x上运动,当线段AB最短时,点B的坐标为(C)图4-15-1A.(0,0)B.(2,-2)C.(1,-1) D.(-2,2)【解析】如答图,当AB与直线y=-x垂直时,AB最短.∵直线y=-x是第二、四象限的角平分线,∴△OAB是等腰直角三角形.作BD⊥x轴,∴DO=BD=12OA=1,∴B的坐标是(1,-1).第1题答图2.如图4-15-2,直线y=-43x+8与x轴,y轴交于A,B两点,∠BAO的平分线所在的直线AM 的解析式是 ( B )A .y =-12x +52 B .y =-12x +3 C .y =-12x +72D .y =-12x +4图4-15-2【解析】 对于直线y =-43x +8,令x =0,求出y =8;令y =0,求出x =6, ∴A (6,0),B (0,8),即OA =6,OB =8, 根据勾股定理得AB =10.在x 轴上取一点B ′,使AB =AB ′,连结MB ′, ∵AM 为∠BAO 的平分线, ∴∠BAM =∠B ′AM , ∵在△ABM 和△AB ′M 中,⎩⎨⎧AB =AB ′,∠BAM =∠B ′AM ,AM =AM ,∴△ABM ≌△AB ′M (SAS ). ∴BM =B ′M ,设BM =B ′M =a ,则OM =OB -BM =8-a , 在Rt △B ′OM 中,B ′O =AB ′-OA =10-6=4, 根据勾股定理得a 2=42+(8-a )2, 解得a =5.∴OM =3,即M (0,3).设直线AM 的解析式为y =kx +b , 将点A 与点M 的坐标代入得⎩⎨⎧6k +b =0,b =3,第2题答图解得⎩⎪⎨⎪⎧k =-12,b =3,则直线AM 的解析式为y =-12x +3.3.如图4-15-3,在平面直角坐标系中,点A (0,4),B (3,0),连结AB .将△AOB 沿过点B 的直线折叠,使点A 落在x 轴上的点A ′处,折痕所在的直线交y 轴正半轴于点C ,则直线BC 的解析式为__y =-12x +32__.图4-15-3【解析】 ∵A (0,4),B (3,0), ∴OA =4,OB =3, 在Rt △OAB 中,AB =OA 2+OB 2=5.∵△AOB 沿过点B 的直线折叠,使点A 落在x 轴上的点A ′处,∴BA ′=BA =5,CA ′=CA , ∴OA ′=BA ′-OB =5-3=2, 设OC =t ,则CA =CA ′=4-t ,在Rt △OA ′C 中,∵OC 2+OA ′2=CA ′2, ∴t 2+22=(4-t )2,解得t =32, ∴C 点坐标为⎝ ⎛⎭⎪⎫0,32.设直线BC 的解析式为y =kx +b , 把B (3,0),C ⎝ ⎛⎭⎪⎫0,32代入得⎩⎪⎨⎪⎧3k +b =0,b =32.解得⎩⎪⎨⎪⎧k =-12,b =32,∴直线BC 的解析式为y =-12x +32.4.如图4-15-4,直线y=-33x+2与x轴相交于点A,与y轴相交于点B,将△ABO沿着AB翻折,得到△ABC,则点C的坐标为.图4-15-4 【解析】如答图,过点C作CD⊥y轴于D,∵直线y=-33x+2与x轴相交于点A,与y轴相交于点B,∴BC=OB=2,OA=23,AB=22+(23)2=4,∴∠BAO=30°,∠DBC=∠CBA=∠ABO=90°-30°=60°.∴Rt△DBC中,BD=12BC=12×2=1,∴OD=1+2=3,CD=22-12= 3.∴C(3,3).=-12x+15.如图4-15-5,在平面直角坐标系中,一次函数y 的图象与x轴,y轴分别交于A,B两点.(1)求点A,B的坐标;(2)点C在y轴上,当S△ABC=2S△AOB时,求点C的坐标.图4-15-5解:(1)令y=0,则-12x+1=0,∴x=2,∴点A(2,0).令x=0,则y=1,∴点B(0,1);(2)如答图,设点C的坐标为(0,y),∵S△ABC =2S△AOB,∴12OA ·BC =2×12OA ·OB , ∴BC =2OB , ∵B 点坐标为(0,1),∴OB =1,BC =2,∴C (0,3)或(0,-1).【思维拓展】6.如图4-15-6,是一对变量满足的函数关系的图象.有下列3个不同的问题情境:图4-15-6①小明骑车以400 m/min 的速度匀速骑了5 min ,在原地休息了4 min ,然后以500 m/min 的速度匀速骑回出发地,设时间为x min ,离出发地的距离为y km ;②有一个容积为6 L 的开口空桶,小亮以1.2 L/min 的速度匀速向这个空桶注水,注5 min 后停止,等4 min 后,再以2 L/min 的速度匀速倒空桶中的水,设时间为x min ,桶内的水量为y L ;③矩形ABCD 中,AB =4,BC =3,动点P 从点A 出发,依次沿对角线AC ,边CD ,边DA 运动至点A 停止,设点P 的运动路程为x ,当点P 与点A 不重合时,y =S △ABP ;当点P 与点A 重合时,y =0.其中,符合图中所示函数关系的问题情境的个数为( C )A .0B .1C .2D .37.如图4-15-7,平面直角坐标系中,已知直线y =x 上一点P (1,1),C 为y 轴上一点,连结PC ,线段PC 绕点P 顺时针旋转90°至线段PD ,过点D 作直线AB ⊥x 轴,垂足为B ,直线AB 与直线y =x 交于点A ,且BD =2AD ,连结CD ,直线CD 与直线y =x 交于点Q ,则点Q 的坐标为__⎝ ⎛⎭⎪⎫94,94__.图4-15-7【解析】 过P 作MN ⊥y 轴,交y 轴于M ,交AB 于N ,过D 作DH ⊥y 轴,交y 轴于H , ∠CMP =∠DNP =∠CPD =90°,∴∠MCP +∠CPM =90°,∠MPC +∠DPN =90°,∴∠MCP =∠DPN , ∵P (1,1),∴OM =BN =1,PM =1,在△MCP 和△NPD 中,⎩⎨⎧∠CMP =∠DNP ,∠MCP =∠DPN ,PC =PD ,∴△MCP ≌△NPD (AAS ), ∴DN =PM ,PN =CM ,∵BD =2AD ,∴设AD =a ,BD =2a , ∵P (1,1),∴DN =2a -1, 则2a -1=1,a =1,即BD =2. ∵直线y =x 过A 点,∴AB =OB =3, 在Rt △DNP 中,由勾股定理得PC =PD =(3-1)2+(2-1)2= 5. 在Rt △MCP 中,由勾股定理得CM =(5)2-12=2.则C 的坐标是(0,3), 设直线CD 的解析式是y =kx +3. 把D (3,2)代入得k =-13,即直线CD 的解析式是y =-13x +3, 解方程组⎩⎪⎨⎪⎧y =-13x +3,y =x ,得⎩⎪⎨⎪⎧x =94,y =94,即点Q 的坐标是⎝ ⎛⎭⎪⎫94,94.8.已知点A (1,5),B (3,-1),点M 在x 轴上,当AM -BM 最大时,点M 的坐标为__⎝ ⎛⎭⎪⎫72,0__.【解析】 如答图,作点B 关于x 轴的对称点B ′,连结AB ′并延长,与x 轴的交点,即为所求的M 点.此时AM -BM =AM -B ′M =AB ′.不妨在x 轴上任取另一点M ′,连结M ′A ,M ′B ,M ′B ′.则M ′A -M ′B =M ′A -M ′B ′<AB ′(三角形两边之差小于第三边). ∴M ′A -M ′B <AM -BM ,∴当M 在直线AB ′上时,AM -BM 最大.∵B ′是B (3,-1)关于x 轴的对称点,∴B ′(3,1).设直线AB ′的解析式为y =kx +b ,把A (1,5)和B ′(3,1)代入得⎩⎨⎧k +b =5,3k +b =1, 解得⎩⎨⎧k =-2,b =7,∴直线AB ′的解析式为y =-2x +7.令y =0,解得x =72,∴M 点坐标为⎝ ⎛⎭⎪⎫72,0.9.如图4-15-8,已知函数y =-12x +b 的图象与x 轴,y 轴分别交于点A ,B ,与函数y =x 的图象交于点M ,点M 的横坐标为2.在x图4-15-8轴上有一点P (a ,0)(其中a >2),过点P 作x 轴的垂线,分别交函数y =-12x +b 和y =x 的图象于点C ,D . (1)求点A 的坐标; (2)若OB =CD ,求a 的值.解:(1)∵点M 在函数y =x 的图象上,且横坐标为2,∴ 点M 的纵坐标为2. ∵点M (2,2)在一次函数y =-12x +b 的图象上, ∴-12×2+b =2,∴ b =3.∴ 一次函数的表达式为y =-12x +3. 令y =0,得x =6.∴ 点A 的坐标为(6,0); (2)由题意得C ⎝ ⎛⎭⎪⎫a ,-12a +3,D (a ,a ).第8题答图∵ OB =CD ,∴ a -⎝ ⎛⎭⎪⎫-12a +3=3,∴a =4.【思维升华】10.若四条直线x =1,y =-1,y =3,y =kx -3所围成的凸四边形的面积等于12,则k 的值为__1或-2__.【解析】 在y =kx -3中,令y =-1,解得x =2k ;令y =3,x =6k ;如答图,当k <0时,四边形的面积是12⎣⎢⎡⎦⎥⎤⎝ ⎛⎭⎪⎫1-2k +⎝ ⎛⎭⎪⎫1-6k ×4=12,解得k =-2.同理可得,当k >0时,k =1.即k 的值为-2或1.第10题答图11.如图4-15-9,在平面直角坐标系中,直线AB 由直线y =3x 沿x 轴向左平移3个单位长度所得,则直线AB 与坐标轴所围成的三角形的面积为__13.5__.图4-15-9【解析】 y =3x 的k =3,b =0,沿x 轴向左平移3个单位后,新直线解析式为y =3(x +3)=3x +9.易求A (0,9),B (-3,0), 则OA =9,OB =3,所以,直线AB 与坐标轴所围成的三角形的面积为12OA ·OB =12×9×3=13.5.12.直线y =kx +4分别与x 轴,y 轴相交于点A ,B ,O 是坐标原点,A 点的坐标为()4,0,P是OB 上(O ,B 两点除外)的一点,过P 作PC ⊥y 轴交直线AB 于C ,过点C 作CD ⊥x 轴,垂足为D ,设线段PC 的长为l ,点P 的坐标为()0,m . (1)求k 的值;(2)如果点P 在线段OB (O ,B 两点除外)上移动,求l 与m 的函数关系式,并写出自变量m 的取值范围;(3)当点P 运动到线段OB 的中点时,四边形OPCD 为正方形,将正方形OPCD 沿着x 轴的正方向移动,设平移的距离为a ()0<a <4,正方形OPCD 与△AOB 重叠部分的面积为S .试求S 与a 的函数关系式.解:(1)∵y =kx +4与x 轴相交于点A , 将A 点的坐标(4,0)代入y =kx +4,得 0=4k +4, ∴k =-1;(2)由k =-1,可知一次函数解析式为y =-x +4, ∴它与y 轴的交点坐标为(0,4), ∴OB =OA =4,根据已知可画出图象,如答图①所示:∵线段PC 的长为l ,点P 的坐标为(0,m ),PC ⊥y 轴, ∴PC ∥OA , ∴PC =BP ,∵PB =4-m ,PC =l , ∴l =-m +4,∵点P 在线段OB (O ,B 两点除外)上移动, ∴自变量m 的取值范围是0<m <4, ∴l =-m +4(0<m <4);(3)∵当点P 运动到线段OB 的中点时,四边形OPCD 为正方形, ∴正方形OPCD 的边长为2,面积为4; ①当0<a ≤2时,如答图②.设平移中PC 与直线y =-x +4交于E ,CD 与直线y =-x +4交于F , 由已知可得CE =CF =a ,第12题答图①S △EFC =12a 2,S =4-12a 2=-12a 2+4(0<a ≤2); ②当2<a <4时,如答图③.设平移中PO 与直线y =-x +4交于G , 由已知可得出OG =OA =4-a , S =12(4-a )2=12a 2-4a +8(2<a <4),∴S =⎩⎪⎨⎪⎧-12a 2+4(0<a ≤2),12a 2-4a +8(2<a <4).第12题答图② 第12题答图③。
一次函数与几何综合培优练习专题
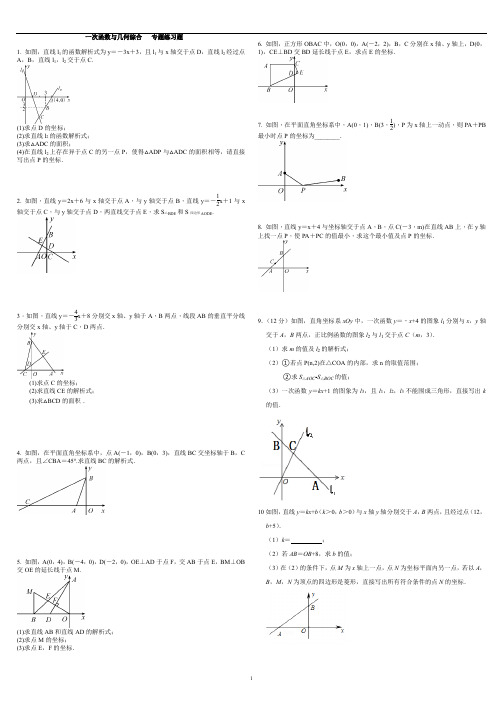
1一次函数与几何综合 专题练习题1. 如图,直线l 1的函数解析式为y =-3x +3,且l 1与x 轴交于点D ,直线l 2经过点A ,B ,直线l 1,l 2交于点C.(1)求点D 的坐标;(2)求直线l 2的函数解析式; (3)求△ADC 的面积;(4)在直线l 2上存在异于点C 的另一点P ,使得△ADP 与△ADC 的面积相等,请直接写出点P 的坐标.2. 如图,直线y =2x +6与x 轴交于点A ,与y 轴交于点B ,直线y =-12x +1与x轴交于点C ,与y 轴交于点D ,两直线交于点E ,求S △BDE 和S 四边形AODE .3.如图,直线y =-43x +8分别交x 轴、y 轴于A ,B 两点,线段AB 的垂直平分线分别交x 轴、y 轴于C ,D 两点.(1)求点C 的坐标;(2)求直线CE 的解析式; (3)求△BCD 的面积.4. 如图,在平面直角坐标系中,点A(-1,0),B(0,3),直线BC 交坐标轴于B ,C 两点,且∠CBA =45°.求直线BC 的解析式.5. 如图,A(0,4),B(-4,0),D(-2,0),OE ⊥AD 于点F ,交AB 于点E ,BM ⊥OB 交OE 的延长线于点M.(1)求直线AB 和直线AD 的解析式; (2)求点M 的坐标; (3)求点E ,F 的坐标.6. 如图,正方形OBAC 中,O(0,0),A(-2,2),B ,C 分别在x 轴、y 轴上,D(0,1),CE ⊥BD 交BD 延长线于点E ,求点E 的坐标.7. 如图,在平面直角坐标系中,A(0,1),B(3,12),P 为x 轴上一动点,则PA +PB最小时点P 的坐标为________.8. 如图,直线y =x +4与坐标轴交于点A ,B ,点C(-3,m)在直线AB 上,在y 轴上找一点P ,使PA +PC 的值最小,求这个最小值及点P 的坐标.9.(12分)如图,直角坐标系xOy 中,一次函数y =﹣x +4的图象l 1分别与x ,y 轴交于A ,B 两点,正比例函数的图象l 2与l 1交于点C (m ,3). (1)求m 的值及l 2的解析式;(2)①若点P(n,2)在△COA 的内部,求n 的取值范围;②求S △AOC -S △BOC 的值;(3)一次函数y =kx +1的图象为l 3,且l 1,l 2,l 3不能围成三角形,直接写出k 的值.10如图,直线y =kx +b (k >0,b >0)与x 轴y 轴分别交于A ,B 两点,且经过点(12,b +5).(1)k = ;(2)若AB =OB +8,求b 的值;(3)在(2)的条件下,点M 为x 轴上一点,点N 为坐标平面内另一点,若以A ,B ,M ,N 为顶点的四边形是菱形,直接写出所有符合条件的点N 的坐标.。
一次函数与几何综合-培优

一次函数与几何综合1.一次函数与全等三角形的综合以一次函数为背景的常见的几何模型如下:2.一次函数与面积的综合 解决在坐标系中的图形面积计算的常用方法:(1)割补法;(2)转化法;(3)加减法;(4)铅垂线法.有的问题还需要分类讨论. 3.一次函数与特殊图形的综合以一次函数为背景的常见的特殊图形有等腰三角形、直角三角形和平行四边形. (1)等腰三角形 ①确定点的位置如下图所示,在直线L 上找一点C ,使得△ABC 是等腰三角形.,:AC AB I =以A 点为圆心,AB 长为半径画圆,交直线L 于两点,,21C C ,:BC AB =X 以B 点为圆心,AB 长为半径画圆,交直线L 于两点,,43C CⅢ,:BC AC =作AB 的中垂线交直线L 于点⋅5C②求点的坐标:若△ABC 是等腰三角形,则分三种情况分类讨论:BC AC BC AB AC AB ===,, 然后利用等腰三角形的性质或勾股定理计算(或建立方程)解题.(2)直角三角形若△ABC 是直角三角形,则分三种情况分类讨论:.09,90,90ooC B A &ο=∠=∠=∠然后利用勾股定 理解题.(3)平行四边形 ①确定点的位置如右图所示,在△ABC 中,点A 、B 在直线L 上,点C 在x 轴上 ,在坐标平面内找一点D ,使得A 、B 、C 、D 围成的四边形是平行四边形.作法:分别为过A 、B 、C 的三个顶点作对边的平行线,交点即为平行四边形的第四个顶点,如右图所示.②求点的坐标:若四边形ABCD 是平行四边形,利用平行四边形的性质解题.基 础 演 练1.点P 是等边△ABC 的边上的一个作匀速运动的动点,点P 从点A 开始沿AB 边运动到B 再沿BC 边运动到C 为止,设运动时间为t ,△ACP 的面积为S ,S 与t 的大致图像是图19 -4—1中的( )2.(1)如图19-4-2所示,已知A 点坐标为(5,0),直线)0(>+=b b x y 与y 轴交于点B ,连接,75,ο=∠αAB 则b 的值为( ).3.A 335.B 4.C 435.D (2)如图19-4-3所示,直线233+-=x y 与x 轴、y 轴分别交于A 、B 两点,把△AOB 绕点A 顺时针旋转ο60后得到,//B AO ∆则点/B 的坐标是( ).)32,4.(A )4,32.(B )3,3.(C )32,232(+⋅D3.平面直角坐标系中,0是坐标原点,点A 的坐标是(4,O),点P 在直线m x y +-=上,且.4==OP AP 则m 的值为( ).322.+A 或322- 4.B 或4- 32.C 或32- 324.+D 或324-4.若函数4--=x y 与x 轴交于点A ,直线上有一点M ,若△AOM 的面积为8,则点M 的坐标5.(1)在平面直角坐标系中,0为坐标原点,已知A (1,a )在直线2+-=x y 上,在坐标轴上确定点P ,使△AOP 为等腰三角形,则符合条件的点P 的个数有 个. (2)如图19-4-4所示,直线133+-=x y 和x 轴、y 轴分别交于点A 、B ,点C 在坐标平面内,若以线段AB 为边作等边三角形ABC ,则点C 的坐标是6.(1)如图19-4-5所示,点A 的坐标为(-1,0),点B 在直线x y =上运动,当线段AB 最短时,点B 的坐标为(2)如图19-4-6所示,在平面直角坐标系中有两点A (-2,2),B(l ,4),P 为x 轴上一点.①当BP+AP 的值最小时,P 点的坐标为 ;②当BP-AP 的值最大时,P 点的坐标7.探索勾股定理时,我们发现“用不同的方式表示同一图形的面积”可以解决线段和(或差)的问题,这种方法称为面积法.请你运用面积法求解下列问题:在等腰△ABC 中,BD AC AB ,=为腰AC 上的高.(1)若M h BD ,=是直线BC 上的任意一点,M 到AB 、AC 的距离分别为ME 、MF .①若M 在线段BC 上,请你结合图形19-4-7(a)证明:h MF ME =+ ②当点M 在线段BC 的延长线上时ME 、MF 和h 之间的关系为 .(请直接写出结论,不必证明)(2)如图19-4-7(b)所示,在平面直角坐标系中有两条直线.63:;643:21+-=+=x y l x y l 若2l 上的一点M 到1l 的距离是3,请你利用以上结论求点M 的坐标.8.如图19-4-8所示,已知y AB b a A ⊥),,(轴于点B ,且满足.0)2(22=-+-b a(1)求直线AO 的解析式;(2)分别以AB 、AO 为边作等边三角形△ABC 和△AOD,试判定线段AC 和DC 的数量关系和位置关系.能 力 提 升9.在△ABC 中,BO 、CO 分别平分∠ABC 、∠ACB ,过点0作EF∥BC 分别交AB 、AC 于点E 、F ,已知a a BC (= 是常数),设△ABC 的周长为y ,△AEF 的周长为x ,在下列图像中,大致表示y 与x 之间的函数关系的是( ).10.如图19-4-9所示,在x 轴上有五个点,它们的横坐标依次为1,2,3,4,5.分别过这些点作x 轴的垂线与三条直线x a y x a y ax y )2(,)1(,+=+==相交,其中a>0.则图中阴影部分的面积是( ).5.12.A 25.B a C 5.12. a D 25.11.如图19 -4 -10所示,直线133+-=x y 分别交x 、y 轴于B 、C 两点,一边在x 轴上,另一个顶点在BC 边上的等边三角形分别是第1个,11B AA ∆第2个,221B A B ∆第3个,,332ΛB A B ∆则第n 个等边三角形的边长等于( ).n A 23.123.-n B nC 21. 123.+n D12.已知平面上四点A(O ,O),B(10,0),C(12,6),D(2,6),直线-=mx y 63+m 将四边形ABCD 分成面积相等的两部分,则m 的值为13.如图19 -4 -11所示,在平面直角坐标系中,点0为坐标原点,直线221+-=x y 与y 、x 轴分别交于A 、B 两点,点C 的坐标为(O ,1),过点C 作CD ⊥AO 交AB 于点D ,x 轴上的点P 和A 、B 、C 、D 、0中的两个点所构成的三角形与△ACD 全等,这样的三角形有 个.14.已知直线343+-=x y 交x 、y 轴于A 、B 两点,点C 的坐标为(6,3),在坐标平面内找一点D ,使得以A 、B 、C 、D 为顶点的四边形是平行四边形,则点D 的坐标为15.如图19 -4 -12所示,已知平行于y 轴的动直线a 的解析式为),0(<=⋅t t x 直线b 的解析式为,x y = 直线c 的解析式为,221+-=x y 且动直线a 分别交直线b 、c 于点D 、E ,P 是y 轴上一个动点,且满足△PDE 是等腰直角三角形,则点P 的坐标是16.如图19 -4 -13所示,在平面直角坐标系xOy 中,长方形OABC 的顶点A 、C 的坐标分别为(3,O),(0,5).(1)直接写出点B 的坐标;(2)若过点C 的直线CD 交AB 边于点D ,且把长方形OABC 的周长分为1:3两部分,求直线CD 的解析式; (3)设点P 沿O-A-B-C 的方向运动到点C (但不与点0、C 重合),求△OPC 的面积y 与点P 所行路程x之间的函数关系式及自变量x 的取值范围.17.如图19 -4 -14所示,在平面直角坐标系中,点A 的坐标为(2,O),以线段OA 为边在第四象限内作等边△AOB,点C 为x 正半轴上一动点(0C>1),连接BC ,以线段BC 为边在第四象限内作等边△CBD ,直线DA 交y 轴于点E.(1)△OBC 与△ABD 全等吗?判断并证明你的结论; (2)求直线AB 的解析式;(3)随着点C 位置的变化,点E 的位置是否会发生变化?若没有变化,求出点E 的坐标;若有变化,请说明理由.18.如图19 -4 -15所示,在平面直角坐标系xOy 中,点A 、B 、D 的坐标分别为),3,0()0,4()0,1(、、-,//BC AD 点E 在CD 上,且满足AE 、BE 分别平分.CBA DAB ∠∠、(1)求直线BC 的解析式;(2)请你判断下列哪个结论成立,并证明你的结论;.;BC AD AB DE CE +==②①(3)已知,60ο=∠DAB 直接写出线段BC 的长.19.如图19 -4 -16所示,在平面直角坐标系xOy 中,直线m x y +-=经过点A(2,0),交y 轴于点B.点D 为x 轴上一点,且.1=∆ADB s (1)求m 的值;(2)求线段OD 的长;(3)当点E 在直线AB 上(点E 与点B 不重合),且,EDA BDO ∠=∠求点E 的坐标.20.如图19 -4 -17所示,直线AB 交z 轴正半轴于点A (a ,0),交y 轴正半轴于点B(0,b),且a 、b 满足.0|4|4=-+-b a(1)求直线AB 的解析式;(2)如图19-4-17 (a)所示,D 为OA 的中点,连接BD ,过点0作BD OE ⊥于点F ,交AB 于点E , 求证:.EDA BDO ∠=∠ (3)如图19-4-17(b)所示,P 为x 轴上A 点右侧任意一点,以BP 为边作等腰Rt△PBM,其中,PM PB =,90ο=∠BPM 直线MA 交y 轴于点Q ,当点P 在x 轴上运动时,线段OQ 的长是否发生变化?若不变,求其值;若变化,求线段OQ 的取值范围,21.已知,A 点坐标为),0,23(-B 点坐标为(0,3). (1)求过A ,B 两点的直线解析式;(2)过B 点作直线BP 与x 轴交于点P ,且使,2OA OP =求△ABP 的面积.22.如图19 -4 -18所示,对于平面直角坐标系中的任意两点),,(),(222111y x P y x P 、我们把||||2121y y x x -+-叫做21p p 、两点间的直角距离,记作⋅).,(21p p d(1)已知0为坐标原点,动点P(x ,y)满足,1),(=p O d 请写出x 与y 之间满足的关系式,并在所给的直角坐标系中画出所有符合条件的点P 所组成的图形;(2)设),(000y x p 是一定点,Q(x ,y)是直线b ax y +=上的动点,我们把),(0Q P d 的最小值叫做0P 到直线b ax y +=的直角距离,试求点M(2,1)到直线2+=x y 的直角距离.23.如图19 -4 -19所示,正方形ABCO 的边OA 、OC 在坐标轴上,点B 坐标(3,3),将正方形ABCO 绕点A顺时针旋转角度),900(οο<<αα得到正方形ADEF ,ED 交线段OC 于点G ,ED 的延长 线交线段BC 于点P ,连AP 、AG. (1)求证:△AOG≌△ADG;(2)求∠PAG 的度数;并判断线段OG 、PG 、BP 之间的数量关系,说明理由; (3)当∠1= ∠2时,求直线PE 的解析式.24.如图19-4-20所示,△AOB 为正三角形,点B 的坐标为(2,0),过点C(-2,0)作直线L 交AO 于点D ,交AB 于点E ,且△ADE 与△DCO 的面积相等,求直线L 的解析式.25.已知,直线1:1-+=k kx y l 与直线k k x k y l ()1:2++=<是正整数)及x 轴围成的三角形的面积为⋅k S(1)求证:无论川取何值,直线21l l 与的交点均为定点;(2)求2013321s s s s ++++Λ的值.。
著名机构初中数学培优讲义一次函数与几何综合.第09讲(C级).教师版
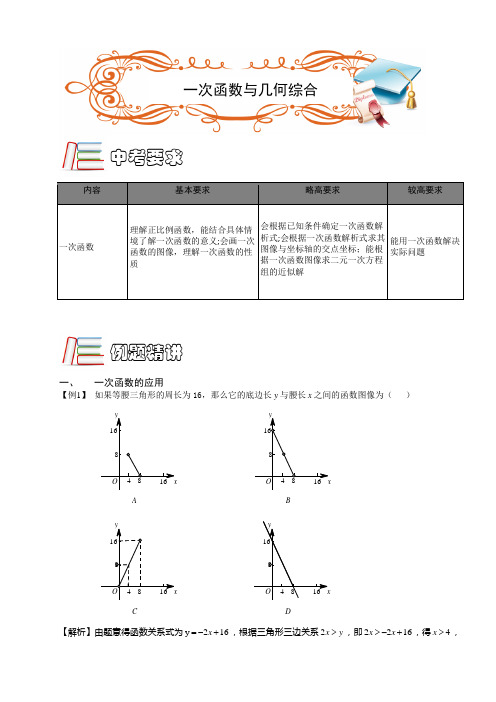
内容基本要求略高要求较高要求一次函数理解正比例函数,能结合具体情境了解一次函数的意义;会画一次函数的图像,理解一次函数的性质会根据已知条件确定一次函数解析式;会根据一次函数解析式求其图像与坐标轴的交点坐标;能根据一次函数图像求二元一次方程组的近似解能用一次函数解决实际问题一、 一次函数的应用【例1】 如果等腰三角形的周长为16,那么它的底边长y 与腰长x 之间的函数图像为( )A1684816y xOB1684816y xOC1684816y xOD1684816y xO【解析】由题意得函数关系式为y 216x =-+,根据三角形三边关系2x y >,即2216x x >-+,得4x >,例题精讲中考要求一次函数与几何综合又因为216x <,所以8x <,确定自变量的取值范围48x <<【答案】A【例2】 2007年5月,第五届中国宜昌长江三峡国际龙舟拉力赛在黄陵庙揭开比赛帷幕.20日上午9时,参赛龙舟从黄陵庙同时出发.其中甲、乙两队在比赛时,路程y (千米)与时间x (小时)的函数关系如图所示.甲队在上午11时30分到达终点黄柏河港. ⑴哪个队先到达终点?乙队何时追上甲队? ⑵在比赛过程中,甲、乙两队何时相距最远?时间/时【解析】⑴乙队先达到终点,对于乙队,1x =时,16y =,所以16y x =,对于甲队,出发1小时后,设y 与x 关系为y kx b =+, 将1x =,20y =和 2.5x =,35y =分别代入上式得: 2035 2.5k bk b =+⎧⎨=+⎩解得:1010y x =+ 解方程组161010y x y x =⎧⎨=+⎩ 得:53x =,即:出发1小时40分钟后(或者上午10点40分)乙队追上甲队.⑵1小时之内,两队相距最远距离是4千米,乙队追上甲队后,两队的距离是16(1010)610x x x -+=-,当x 为最大,即3516x =时,610x -最大,此时最大距离为35610 3.125416⨯-=<,(也可以求出AD CE 、的长度,比较其大小)所以比赛过程中,甲、乙两队在出发后1小时(或者上午10时)相距最远【答案】⑴乙队先达到终点,甲队出发1小时40分钟后(或者上午10点40分)乙队追上甲队;⑵甲、乙两队在出发后1小时(或者上午10时)相距最远【例3】 如图表示甲、乙两名选手在一次自行车越野赛中,路程y (km )随时间x (min )的变化的图像(全程),根据图像回答以下问题:⑴求比赛开始多少分钟时,两人第一次相遇?⑵求这次比赛的全程是多少?⑶求比赛开始多少分钟时,两人第二次相遇?【解析】⑴由图可知,线段OD 过点481200(,)(,,)可知其解析式为14y x =,他们相遇时6y =,此时24x =,故比赛开始24分钟时,两人第一次相遇. ⑵由图可知,这次比赛的全程为12km .⑶点B (33,7)、点C (43,12),故线段BC 的解析式为:()1192y x =-,而线段OD 的解析式为()10484y x =<<,故它们的交点坐标为(38,192),即比赛开始38分钟时,两人第二次相遇. 【答案】⑴24;⑵12;⑶38【例4】 为了保护环境,某企业决定购买10台污水处理设备,现有A B ,两种型号的设备,其中每台的价⑴求购买设备的资金y 万元与购买A 型x 台的函数关系,并设计该企业有几种购买方案; ⑵若企业每月产生的污水量为2040吨,利用函数的知识说明,应选择哪种购买方案;⑶在第⑵问的条件下,若每台设备的使用年限为10年,污水厂处理污水费为每吨10元,请你计算,该企业自己处理污水与将污水排到污水厂处理相比较,10年节约资金多少万元?(注:企业处理污水的费用包括购买设备的资金和消耗费)【解析】⑴购买污水处理设备A 型x 台,则B 型()10x -台,由题意知:()121010y x x =+- 即2100y x =+ 2100105y x =+≤ ∴ 2.5x ≤又∵x 是非负整数 ∴x 可取0,1,2∴有三种购买方案:①购A 型D 台,B 型10台;②购A 型1台,B 型9台;③购A 型2台,B 型8台;⑵由题意得()240200102040x x +-≥,解得1x ≥∴x 为1或2∵由2100y x =+得20k =>,y 随x 的增大而增大. 为了节约资金,应选购A 型1台,B 型9台.⑶10年企业自己处理污水的总资金为:1021010202+⨯=(万元) 若将污水排到污水厂处理,10年所需费用为: 20401210102448000⨯⨯⨯=(元)244.8=(万元)∵244.820242.8-=(万元) ∴能节约资金42.8万元.【答案】⑴2100105y x =+≤,有三种购买方案:①购A 型D 台,B 型10台;②购A 型1台,B 型9台;③购A 型2台,B 型8台; ⑶42.8【例5】 一次时装表演会预算中票价定位每张100元,容纳观众人数不超过2000人,毛利润y (百元)关于观众人数x (百人)之间的函数图象如图所示,当观众人数超过1000人时,表演会组织者需向保险公司交纳定额平安保险费5000元(不列入成本费用)请解答下列问题:⑴求当观众人数不超过1000人时,毛利润y (百元)关于观众人数x (百人)的函数解析式和成本费用s (百元)关于观众人数x (百人)的函数解析式;⑵若要使这次表演会获得36000元的毛利润,那么要售出多少张门票?需支付成本费用多少元? (注:当观众人数不超过1000人时,表演会的毛利润=门票收入—成本费用;当观众人数超过1000人时,表演会的毛利润=门票收入—成本费用—平安保险费)【解析】⑴由图象可知:当010x ≤≤时,设y 关于x 的函数解析100y kx =-,∵(10,400)在100y kx =-上,∴40010100k =-,解得50k = ∴50100y x =-,100(50100)s x x =--),∴50100s x =+ ⑵当1020x <≤时,设y 关于x 的函数解析式为y mx b =+, ∵(10,350),(20,850)在y mx b =+上, 1035020580m b m b +=⎧⎨+=⎩,解得50150m b =⎧⎨=-⎩∴50150y x =-,∴()100501505050100s x x s x ∴=---∴=+ ∴()()50100010501501020x x y x x ⎧-⎪=⎨-<⎪⎩≤≤≤令360y =当010x ≤≤时,50100360x -= 解得9.2x =50100509.2100560s x =+=⨯+=当1020x <≤时,50150360x -=解得10.2x = 501005010.2100610s x =+=⨯+=.要使这次表演会获得36000元的毛利润. 要售出920张或1020张门票,相应支付的成本费用分别为56000元或61000元.【答案】⑴50100s x =+;⑵要售出920张或1020张门票,相应支付的成本费用分别为56000元或61000元【例6】 某汽车运输公司根据实际需要计划购买大、中型两种客车共20辆,已知大型客车每辆62万元,中型客车每辆40万元,设购买大型客车x (辆),购车总费用为y (万元).(1)求y 与x 的函数关系式(不要求写出自变量x 的取值范围);(2)若购买中型客车的数量少于大型客车的数量,请你给出一种费用最省的方案,并求 出该方案所需费用. 【解析】略【答案】(1)因为购买大型客车x 辆,所以购买中型客车()20x -辆.()62402022800y x x x =+-=+. (2)依题意得()20x x -<.解得x >10.∵ 22800y x =+,y 随着x 的增大而增大,x 为整数,∴ 当x=11时,购车费用最省,为22×11+800=1 042(万元).此时需购买大型客车11辆,中型客车9辆.答:购买大型客车11辆,中型客车9辆时,购车费用最省,为1 042万元.二、 一次函数与几何综合【例7】 已知直线3y x =+的图象与x y 、轴交于A B 、两点,直线l 经过原点,与线段AB 交于点C ,把AOB ∆的面积分为2:1的两部分,求直线l 的解析式。
初中数学一次函数与全等三角形综合培优精讲及答案

3、一次函数与全等三角形综合题型切片题型一:一次函数与全等三角形综合思路导航例题精讲【引例】 平面直角坐标系内有两点()40A ,和()04B ,,点P 在直线AB 上运动.⑴ 若P 点横坐标为2P x =-,求以直线OP 为图象的函数解析式(直接写出结论);⑵ 若点P 在第四象限,作BM ⊥直线OP 于M ,AN ⊥直线OP 于N ,求证:MN BM AN =+; ⑶ 若点P 在第一象限,仍作直线OP 的垂线段BM 、AN ,试探究线段MN 、BM 、AN 所满足的数量关系式,直接写出结论,并画图说明.(实验中学单元测试)【解析】 ⑴ 设直线AB 函数解析式为y kx b =+04144k b k b b =+=-⎧⎧⇒⎨⎨==⎩⎩ 4y x =-+ 当x 为2-时,6y =,∴P 的坐标为()26-, ∵直线OP 过原点,∴解析式为3y x =-⑵ 如图1,由题意可证Rt Rt BMO ONA △≌△∴BM ON =,AN MO =,∴MN BM AN =+⑶ 如图2,证明Rt Rt BMO ONA △≌△ 可得结论MN BM AN =-图2图1 图2典题精练【例1】 如图,已知在平面直角坐标系xOy 中,点()04A ,,点B C ,在x 轴上,作BE AC ⊥,垂足为E (点E 在线段AC 上,且点E 与点A 不重合),直线BE 与y 轴交于点D ,若BD AC =. ⑴ 求点B 的坐标;⑵ 设OC 长为m ,BOD △的面积为S ,求S 与m 的函数关系式,并写出自变量m 的取值范围.【解析】 ⑴ 如图,由BOD AOC △≌△可知4BO AO ==∴B 点坐标为()40-,⑵ 由⑴可知DO OC m ==,∴142S m =⨯⋅,2S m =,m 的取值范围是04m <<【例2】 已知:如图,平面直角坐标系xOy 中,点A 、B 的坐标分别为()40A ,,()04B -,,P 为y 轴上B 点下方一点,()0PB m m =>,以AP 为边作等腰直角三角形APM ,其中PM PA =,点M 落在第四象限.⑴ 求直线AB 的解析式;⑵ 用m 的代数式表示点M 的坐标;⑶ 若直线MB 与x 轴交于点Q ,判断点Q 的坐标是否随m 的变化而变化,写出你的结论并说明理由. (西城期末)【解析】 ⑴ 4y x =-⑵ 作MC y ⊥轴,交y 轴于C ,9090AP PM MPC APO OAP APO PMC PMC MPC APO =⎫⎪∠=︒-∠=∠⇒⎬⎪∠=︒-∠=∠⎭△≌△ 由此可知()48M m m +--, ⑶ 由⑵中的全等可知4MC m =+,4BC m =+,∴MC BC = 45CBM ∠=︒,可得QO OB =()4,0Q - ∴Q 点坐标不随m 的变化而变化.【点评】 此题最关键一步是如何利用线段长表示点坐标,学生极易在此犯错!要记住线段长为正,而点坐标要根据其所在象限判断正负.【例3】 如图1,直线1:33l y x =+与x 轴交于B 点,与直线2l 交于y 轴上一点A ,且2l 与x 轴的交点为()10C ,.⑴ 求证:ABC ACB ∠=∠⑵ 如图2,过x 轴上一点()30D -,,作DE AC ⊥于E ,DE 交y 轴于F 点,交AB 于G 点,求G 点的坐标;⑶ 如图3,将ABC △沿x 轴向左平移,AC 边与y 轴交于点P (P 不同于A 和C 两点),过P 点作一直线与AB 的延长线交于Q 点,与x 轴交于点M ,且CP =BQ .在ABC △平移的过程中,线段OM 的长度是否发生变化?若不变,请求出它的长度.若变化,确定其变化范围.图3图2图1【解析】 ⑴ 由题意得()10B -,,BO OC =,又∵AO BC ⊥ ∴AB AC ABC ACB =∠=∠,⑵ 由题意得ABO DFO △≌△,∴1OF BO ==,∴()01F ,∴DE 解析式为113y x =+由11333y x y x ⎧=+⎪⎨⎪=+⎩ 解得3434x y ⎧=-⎪⎪⎨⎪=⎪⎩ ∴3344G ⎛⎫- ⎪⎝⎭, ⑶ 不变,1OM =如图过P 作PN AB ∥交BC 于N ,可知PN PC BQ ==,从而PNM QBM △≌△, ∴BM NM =,又NO CO =∴112OM BC ==【例4】 如图,在平面直角坐标系中,A (a ,0),B (0,b ),且a 、b 满足()220a -.⑴求直线AB 的解析式;⑵若点M 为直线y =mx 上一点,且△ABM 是以AB 为底的等腰直角三角形,求m 值; ⑶过A 点的直线y =kx -2k 交y 轴于负半轴于P ,N 点的横坐标为1-,过N 点的直线22k ky x =-交AP 于点M ,试证明PM PNAM-的值为定值. 【解析】 ⑴y =24x -+⑵易证阴影部分三角形全等,得到M (3,3)故而m =1⑶过N 点做直线垂直于y 轴,交PM 于G 点,另直线NM 与坐标轴交点分别为O 、I (如图所示),连接IG 并做MF ⊥x 轴于F ,易知N 、G 两点横坐标分别为1-和1,将其分别代入MN 、MP 的解析式中,求得两点坐标为N (1-,k -)G (1,k -), 易证△NHP ≌△GHP , ∴NP =GP易求I (1,0),∴IG ⊥x 轴 易证△IGA ≌△FMA , ∴MA =AG ∴2PM PN MGAM AM-==题型二:一次函数与面积综合思路导航解决平面直角坐标系中的图形面积问题通常可采用的方法有:1. 公式法:三角形、特殊四边形等面积公式;2. 割补法:通过“割补”转化为易求图形面积的和或差;3. 容斥法;4. 等积变换法:①平行线法:构造同底等高;②直角三角形:=ab ch ;5. 铅垂线法:如右图所示()1212ABC S AP h h =⋅+△,AP 称为铅垂高, 12h h +称为水平宽. 必要时需分类讨论.典题精练【例5】 已知:平面直角坐标系xOy 中,直线()0y kx b k =+≠与直线()0y mx m =≠交于点()24A -,.⑴求直线()0y mx m =≠的解析式;⑵若直线()0y kx b k =+≠与另一条直线2y x =交于点B ,且点B 的横坐标为4-,求ABO △的面积. (西城期末试题)【解析】 ⑴∵点(24)A -,在直线(0)y mx m ==/上,∴42m =-,2m =-∴2y x =-⑵ 解法一:作AM y ⊥轴于M ,BN y ⊥轴于N (如上图)∵点B 在直线y =2x 上,且点B 的横坐标为4-. ∴点B 的坐标为B (4-,8-) ∵1()2ABNM S AM BN MN =+⋅梯形1(24)(48)362=⨯+⨯+= 1124422AOM S AM MO =⋅=⨯⨯=△ 11481622BONS BN NO =⋅=⨯⨯=△ ∴ABO AOM BON ABNM S S S S =--△△△梯形3641616=--=解法二:设直线(0)y kx b k =+=/与x 轴交于点C (如下图). ∵点B 在直线y =2x 上,且点B 的横坐标为4-. ∴点B 的坐标为(4-,8-)∵直线()0y kx b k =+≠经过点A (2-,4)和点B (4-,8-), ∴4284k b k b =-+⎧⎨-=-+⎩,616k b =⎧⎨=⎩∴616y x =+令y =0.可得83x =-∴点C 的坐标为803C ⎛⎫- ⎪⎝⎭,∴181848162323ABO AOC BOC S S S =+=⨯⨯+⨯⨯=△△△.【教师备选】如图所示,直线OP 经过点P (4,),过x 轴上的点1、3、5、7、9、11······分别作x 轴的垂线,与直线OP 相交得x到一组梯形,其阴影部分梯形的面积从左至右依次记为1S 、2S 、3S ······n S ,则n S 关于n 的函数关系式是________.【解析】()843n S n =-⨯. 真题赏析【例6】 已知:一次函数132y x =+的图象与正比例函数y =kx 的图象相交于点A (a ,1). ⑴求a 的值及正比例函数y =kx 的解析式; ⑵点P 在坐标轴上(不与点O 重合),若P A =OA ,直接写出P 点的坐标;⑶直线x =m 与一次函数的图象交于点B ,与正比例函数图象交于点C ,若△ABC 的面积记为S ,求S 关于m 的函数关系式(写出自变量的取值范围).(2013西城期末)【解析】 ⑴∵一次函数132y x =+的图象与正比例函数y =kx 的图象相交于点A (a ,1), ∴1312a += ∴a =﹣4,即A (﹣4,1). ∴﹣4k =1 解得14k =-.∴正比例函数的解析式为14y x =-;⑵如图1,P 1(﹣8,0)或P 2(0,2);⑶依题意,得点B 的坐标为(m ,132m +),点C 的坐标为(m ,14m -).作AH ⊥BC 于点H ,H 的坐标为(m ,1). 以下分两种情况: ①当m <﹣4时,11342BC m m ⎛⎫=--+ ⎪⎝⎭=334m --.AH =4m --.则S △ABC =12BC ∙AH ()133424m m ⎛⎫=---- ⎪⎝⎭∴S=23368m m ++;②当m >4-时,11333244BC m m m ⎛⎫=++=+ ⎪⎝⎭.AH =m +4.则S △ABC =12BC∙AH =12(334m +)(4+m ) ∴S=23368m m ++;综上所述,()23S 3648m m m =++≠-.【教师备选】已知四条直线3y mx =-,1y =-,y =3,x =1所围成的四边形的面积为12,求m 的值. 【解析】 ∵3y mx =-,1y =-,x =1交于ABCDEF∴A (6m ,3),B (2m ,-1),C (1,-1),D (1,3),E (6m ,3),F (2m,-1) ① ()2ABCD CD BC AD S +=2621112mm ⎛⎫=-+- ⎪⎝⎭= ∴m =-2② ()2CFED CD ED CF S +=6221112mm ⎛⎫=-+- ⎪⎝⎭= ∴m =1综上说述,2m =-或m=1.-3y =3x思维拓展训练(选讲)训练1. 如图,AOB △为正三角形,点B 的坐标为()20,,过点()20C -,作直线l 交AO 于D ,交AB 于E ,且ADE △与DCO △的面积相等,求直线l 的解析式.【解析】 由ADE △与DCO △的面积相等可知,AOB BCE S S =△△.∵(20)C -,,设直线l 的解析式为y kx b =+,∴20k b -+=, ∴2b k =∴直线l 的解析式为:2y kx k =+又AB 的解析式为:323y x =-+,故点E 的坐标满足下式: 2433(2)3y kx kk y y x k =+⎧⎪⇒=⎨=--+⎪⎩, 故143134232273BCE AOB k S S k k =⨯⨯==⨯⨯⇒=+△△ 故直线l 的解析式为:3(2)7y x =+. 训练2. 在平面直角坐标系xOy 中,直线y x m =-+经过点()2,0A ,交y 轴于点B .点D 为x 轴上一点,且1ADB S =△.⑴ 求m 的值;⑵ 求线段OD 的长;⑶ 当点E 在直线AB 上(点E 与点B 不重合),且BDO EDA ∠=∠,求点E 的坐标.(备用图)(海淀期末试题) 【解析】 ⑴ ∵直线y x m =-+经过点()2,0A ,∴02m =-+.∴2m =.⑵ ∵直线2y x =-+交y 轴于点B , ∴点B 的坐标为()0,2. ∴2OB =.y xl ED CO B A∵112ADB S AD OB =⋅=△, ∴1AD =. ∵点A 的坐标为()2,0, ∴点D 的坐标为()1,0或()3,0. ∴1OD =或3OD =.⑶ ①当点D 的坐标为()1,0时,如图所示.取点()'0,2B -,连接'B D 并延长,交直线BA 于点E .∵'OB OB =,'AO BB ⊥于O , ∴OD 为'BB 的垂直平分线. ∴'DB DB =. ∴12∠=∠. 又∵23∠=∠, ∴13∠=∠.设直线'B D 的解析式为()20y kx k =-≠. ∵直线'B D 经过点()1,0D , ∴02k =-. ∴2k =.∴直线'B D 的解析式为22y x =-. 解方程组2,22,y x y x =-+⎧⎨=-⎩得 4,32.3x y ⎧=⎪⎪⎨⎪=⎪⎩∴点E 的坐标为42,33⎛⎫⎪⎝⎭.②当点D 的坐标为()3,0时,如图所示. 取点()'0,2B -,连接'B D ,交直线BA 于点E . 同①的方法,可得12∠=∠,直线'B D 的解析式 为223y x =-. 解方程组22,32,y x y x ⎧=-⎪⎨⎪=-+⎩得12,52.5x y ⎧=⎪⎪⎨⎪=-⎪⎩∴点E 的坐标为122,55⎛⎫- ⎪⎝⎭.综上所述,点E 的坐标为42,33⎛⎫ ⎪⎝⎭或122,55⎛⎫- ⎪⎝⎭.训练3. 已知:直线1l :1y kx k =+-与直线2l :(1)y k x k =++(k 是正整数)及x 轴围成的三角形的面积为k S .⑴ 求证:无论k 取何值,直线1l 与2l 的交点均为定点; ⑵ 求1232008S S S S ++++的值.(西城期末试题)【解析】 ⑴ 联立12l l ,的解析式,求得交点坐标为()11--,,∴交点为定点.⑵ 设直线12l l ,分别与x 轴交于A ,B 两点,则1001k k A B k k --⎛⎫⎛⎫⎪ ⎪+⎝⎭⎝⎭,,,,∴()1111k k AB k k k k --=-=++ ∴ ()11121k S k k =+×× 123200*********21223200820092009S S S S ⎛⎫++++=++⋅⋅⋅+=⎪⎝⎭×××训练4. 如图,在直角坐标系中,点A 的坐标为()10,,点B 在y 轴正半轴上,且AOB △是等腰直角三角形,点C 与点A 关于y 轴对称,过点C 的一条直线绕点C 旋转,交y 轴于点D ,交直线AB 于点()P x y ,,且点P 在第二象限内.⑴ 求B 点坐标及直线AB 的解析式;⑵ 设BPD △的面积为S ,试用x 表示BPD △的面积S .(朝阳期末试题)【解析】 ⑴ ∵AOB △是等腰直角三角形且()10A ,,∴()01B ,∴过点()10A ,、()01B ,的直线的解析式为1y x =-+ ⑵ ∵点C 与点A 关于y 轴对称,∴()10C -, 又点P 在直线AB 上,则()1P x x -+, 设过P 、C 两点的直线的解析式为y kx b =+ ∵()10C -,在直线y kx b =+上,∴0k b -+=. ∴k b =,y bx b =+ ∵点()1P x x -+,在直线y bx b =+上,∴1bx b x +=-+,解得b =11x x -++. ∴点D 的坐标为101x x -+⎛⎫ ⎪+⎝⎭,∵点P 在第二象限内,∴0x < ①当10x -<<时,如图.12P S BD x =⋅⋅=1(1)()2b x -⋅-11(1)()21x x x -+=-⋅-+12()21xx x -=⋅⋅-+21x x =+ ②当1x <-时,如图.12P S BD x =⋅⋅=1(1)()2b x -⋅-11(1)()21x x x -+=-⋅-+21x x =-+ 综上所述, 22(10),1(1).1xx x S x x x ⎧-<<⎪⎪+=⎨⎪-<-⎪+⎩复习巩固题型一 一次函数与全等三角形综合 巩固练习【练习1】如图,已知在平面直角坐标系xOy 中,点()04A ,,点B C ,在x 轴上,C 点坐标为()0m ,.作BE AC ⊥,垂足为E (点 E 在线段AC 上,且点E 与点A 不重合),直线BE 与y 轴 交于点D ,BD AC =.第一象限内有一点P ,坐标为()4m m +,,连接PA ,DC ,求证:PAC BDC ∠=∠.【解析】 如图,连接PC ,过A 作AH PC ⊥于H ,可知PH AH m ==45PAH APH ∠=∠=°由BOD AOC △≌△可知BDO ACO ∠=∠ 又∵AH OC ∥,∴ACO HAC ∠=∠,∴BDO HAC ∠=∠ 又由OD OC =可得45ODC ∠=°,∴ODC PAH ∠=∠∴BDC PAC ∠=∠【练习2】如图,在平面直角坐标系xOy 中,点A 、B 的坐标分别为()10-,、()40,,点D 在y轴上 AD BC ∥,点E 在CD 上,且满足AE 、BE 分别平分DAB ∠、CBA ∠. ⑴ 请你判断此时线段CE 与DE 是否相等,并证明你的结论;⑵ 已知60DAB ∠=°,直接写出线段BC 的长.【解析】 ⑴ 相等,证明如下如上右图,在AB 上取点D ',使AD AD '=,连接D E ', 可证ADE AD E '△≌△,∴DE D E '=由AD BC ∥,AE 、BE 平分DAB ∠与ABC ∠ 可得90AEB ∠=°从而可知D EB CEB '∠=∠由此,CEB D EB '△≌△,∴EC ED '= ∴DE EC =⑵ ∵60DAB ∠=°,∴30ADO ∠=°,∴22AD AO ==由⑵可知,2AD AD '== ∴523BC BD '==-=.【练习3】如图,已知直线OA 的解析式为y=x ,直线AC 垂直x 轴于点C ,点C 的坐标为()20,,4)直线OA 关于直线AC 的对称直线为AB 交x 轴于点B . ⑴ 写出点A 及点B 的坐标;⑵ 如图,直线AD 交x 轴于点D ,且ADB △的面积为1,求点D 的坐标;⑶ 若点D 为⑵中所求,作OE AD ⊥于点E ,交AC 于点H ,作BF AD ⊥于点F ,求证:OE AF =,并直接写出点H 的坐标.【解析】 ⑴ ()22A ,,()40B ,⑵ ∵AC BD ⊥于点C ,2AC =,1ADB S =△,∴112122ADB S BD AC BD =⋅=⨯=△.∴1BD =∴413OD OB BD =-=-= ∴()30D , ⑶ 由直线OA 的解析式为y x =,可知OC AC =.又90ACO ∠=°,∴45OAC AOC ∠=∠=°.∵直线OA 关于直线AC 的对称直线为AB , ∴45BAC OAC ∠=∠=°,OA BA =. ∴90OAB ∠=°.∴90BAF OAE ∠=-∠°. 在AOE △中,90OEA ∠=°, ∴90AOE OAE ∠=-∠°. ∴BAF AOE ∠=∠在AOE △与BAF △中, 90AOE BAF OEA AFB OA BA ∠=∠⎧⎪∠=∠=⎨⎪=⎩° ∴AOE BAF △≌△ ∴OE AF =又由OCH ACD △≌△可求得()21H ,题型二 一次函数与面积的综合 巩固练习【练习4】⑴如图,点A 、B 、C 在一次函数2y x m =-+的图象上,它们的横坐标依次为1-、1、2,分别过这些点作x 轴与y 轴的垂线,则图 中阴影部分的面积和是( ).A .1B .3C .3(1)m -D .3(2)2m -⑵ 如图1,在直角梯形ABCD 中,动点P 从点B 出发,沿BC , CD 运动至点D 停止.设点P 运动的路程为x ,ABP △的面积 为y ,如果y 关于x 的函数图象如图2所示,则BCD △的面 积是( ). A .3 B .4 C .5 D .6图1AB D 图2x【解析】 ⑴ B ⑵ A , 由图2可知23BC CD ==,.【练习5】直线23y x =+与x 轴交于点A ,与y 轴交于点B .若在x 轴上有一点Q ,并且满足:8:3BAQ AOB S S =△△,求Q 点坐标.【解析】 1393224AOB S =⨯⨯=△,∴98643BAQ S =⨯=△∵3BO =,∴4AQ =,又∵32A x =-∴35422Q x =-+=或311422Q x =--=-∴Q 坐标为502⎛⎫ ⎪⎝⎭,或1102⎛⎫- ⎪⎝⎭,。
2023年九年级数学下册中考数学综合培优测试卷:一次函数图像与几何变换【含答案】

2023年九年级数学下册中考数学综合培优测试卷:一次函数图像与几何变换一、单选题1.在平面直角坐标系中,把直线y=3x 向左平移2个单位长度,平移后的直线解析式是( )A .y=3x+2B .y=3x-2C .y=3x+6D .y=3x-62.若一次函数y=2x-3的图象平移后经过点(3,1),则下列叙述正确的是( )A .沿x 轴向右平移3个单位长度B .沿x 轴向右平移1个单位长度C .沿x 轴向左平移3个单位长度D .沿x 轴向左平移1个单位长度3.在平面直角坐标系中,将直线沿y 轴向下平移6个单位后,得到一条新的直线,该直y =−32x +3线与x 轴的交点坐标是( )A .B .C .D .(0,3)(−2,0)(4,0)(6,0)4.已知直线向下平移2个单位长度后得到直线,且直线与直线关于l 1:y =kx +3l 2l 2l 3:y =−x +1y 轴对称,则k 的值为( ).A .B .1C .2D .3−15.在平面直角坐标系中,将函数 的图象向上平移6个单位长度,则平移后的图象与x 轴的y =3x 交点坐标为( ) A .(2,0)B .(-2,0)C .(6,0)D .(-6,0)6.把直线y=-x+1向上平移3个单位长度后得到的直线的解析式为( )A .y=-x+4B .C .y=x+4D .y=x-27.将直线沿x 轴向左平移3个单位得到直线L ,则直线L 的解析式是( )y =2x +5A .y =2x +2B .y =2x +8C .y =2x -1D .y =2x +118.对于一次函数y =﹣2x+4,下列结论错误的是( )A .函数的图象不经过第三象限B .函数的图象与x 轴的交点坐标是(2,0)C .函数的图象向下平移4个单位长度得y =﹣2x 的图象D .若两点A(x 1,y 1),B(x 2,y 2)在该函数图象上,且x 1<x 2,则y 1<y 29.将一次函数y =﹣3x 的图象沿y 轴向下平移4个单位长度后,所得图象的函数表达式为( )A .y =﹣3(x ﹣4)B .y =﹣3x +4C .y =﹣3(x +4)D .y =﹣3x ﹣410.在平面直角坐标系中,将直线 先关于 轴作轴对称变换,再将所得直线关于y =−3x +4x y 轴作轴对称变换,则经两次变换后所得直线的表达式是( )A .B .C .D .y =4x−3y =−4x +3y =3x +4y =−3x−411.将直线向上平移2个单位长度,则平移后的直线所对应的函数解析式为( )y =−2x +3A .B .C .D .y =−2x +1y =−4x +5y =−2x +5y =−4x +112.将直线向上平移5个单位长度后得到直线,则下列关于直线的说y =x +1y =kx +b y =kx +b 法错误的是( )A .函数图象经过第一、二、三象限B .函数图象与轴的交点在轴的正半轴x xC .点在函数图象上(−2,4)D .随的增大而增大y x 二、填空题13.直线 +3的图像是由正比例函数 图像向 (填上或下)平移 y =3x 个单位得到或由正比例函数 图像向 (填左或右)平移 个单位得到可以得到的一条直线14.直线 沿 轴平移3个单位,则平移后直线与 轴的交点坐标为 .y =2x−1y y 15.在平面直角坐标系中,把直线y=2x 向左平移1个单位长度,平移后的直线解析式是 .16.将正比例函数y=﹣2x 的图象沿y 轴向上平移5个单位,则平移后所得图象的解析式是 .17.如图,在平面直角坐标系中,A (1,0),B (3,0),点C 在第一象限,∠ABC=90°,AC=25,直线l 的关系式为: .将△ABC 沿x 轴向左平移,当点C 落在直线l 上时,线段AC 扫y =−x−3过的面积为 平方单位.18.已知直线与直线关于y 轴对称,当时,,当y 1=ax +b(a ≠0)y 2=kx +5(k ≠0)x >−52y 1>0时,,则直线 .x >52y 2<0y 1=三、综合题19.如图,直线 与 轴、 轴交于点 、 ,直线 与 轴l 1:y =2x +1x y D A l 2:y =mx +4x y 轴分别交于点 、 ,两直线相交于点 .C B P(1,b)(1)求 , 的值; b m (2)求 的值;S △PDC −S △PAB (3)垂直于 轴的直线 与直线 , 分别交于点 , ,若线段 的长为x x =a l 1l 2M N MN 2,求 的值.a 20.如图,直线y =kx +4的图象与y 轴交于点A ,与x 轴交于点B (2,0),直线AF 交x 轴负半轴于点F ,且OF =2OA .(1)求出k 的值为 ,直线AF 的解析式为 ;(2)若将直线AB 沿y 轴向下平移,平移后的直线恰好经过C (﹣3,0),与y 轴相交于点D ,且直线CD 与直线AF 交于点E ,求点E 的坐标.21.如图,一次函数 的图象与反比例函数( 为常数且 )的图象相交于y =x +5y =kx k k ≠0 , 两点.A(−1,m)B(1)求反比例函数的表达式;(2)将一次函数 的图象沿 轴向下平移 个单位 ,使平移后的图象与反y =x +5y b (b >0)比例函数的图象有且只有一个交点,求 的值.y =kx b 22.已知反比例函数与正比例函数 相交于 .y 1=kx y 2=x A(2,2)(1)求 值.k (2)画出反比例函数的图象.(3)当 时,直接写出 的范围?y 1>y 2x (4)根据图象,解不等式 .kx <x−323.背景知识:已知两直线 , ,若 ,则m :y 1=k 1x +b 1n :y 2=k 2x +b 2(k 1k 2≠0)m ⊥n ;若 ,则 .k 1k 2=−1m//n k 1=k 2应用:在平面直线坐标系 中,直线 交x 轴于点C ,交y 轴于点D ,若 xoy l 1:y =x−1l 2⊥l 1于点 ,交y 轴于点A ,交x 轴于点B.P(2,1)(1)求直线 的表达式; l 2(2)求 的面积;△ABC (3)若将直线 向下平移 个单位,得到新的直线 ,交y 轴于点E ,交直线 于点F ,l 1q l 3l 2使得 ,求 的值.S △AEF =16q 24.已知:如图1,在平面直角坐标系中,一次函数y = x+3交x 轴于点A ,交y 轴于点B ,点C34是点A 关于y 轴对称的点,过点C 作y 轴平行的射线CD ,交直线AB 与点D ,点P 是射线CD 上的一个动点.(1)求点A ,B 的坐标.(2)如图2,将△ACP 沿着AP 翻折,当点C 的对应点C′落在直线AB 上时,求点P 的坐标. (3)若直线OP 与直线AD 有交点,不妨设交点为Q(不与点D 重合),连接CQ ,是否存在点P ,使得S △CPQ =2S △DPQ ,若存在,请求出对应的点Q 坐标;若不存在,请说明理由.答案解析部分1.【答案】C 2.【答案】B 3.【答案】B 4.【答案】B 5.【答案】B 6.【答案】A 7.【答案】D 8.【答案】D 9.【答案】D 10.【答案】D 11.【答案】C 12.【答案】B13.【答案】y=3x ;上;3;y=3x ;左;114.【答案】(0,2)或(0, )−415.【答案】y=2x+216.【答案】y =-2x+517.【答案】4018.【答案】或2x +55+2x19.【答案】(1)解:∵点 在直线 上,∴ ,P(1,b)l 1:y =2x +1b =2×1+1=3∵ 在直线 上,∴ ,∴P(1,3)l 2:y =mx +43=m +4m =−1(2)解:∵直线 与 轴、 轴交于点 、 ,l 2:y =−x +4x y D A ∴ ,,A(0,1)D(−12,0)∵直线 与 轴、 轴分别交于点 、 ,l 2:y =−x +4x y C B ∴ , ,B(0,4)C(4,0)∴S △PDC −S △PAB =12DC ⋅y P −12AB ⋅x P =12×(12+4)×3−12×(4−1)×1=214(3)解:设直线 与直线 , 分别交于点 , , x =a l 1l 2M N 当 时, ;当 时, ,x =a y M =2a +1x =a y N =4−a ∵ ,∴ ,解得或 ,MN =2|2a +1−(4−a)|=2a =13a =53所以 的值为 或 a 135320.【答案】(1)-2;y =+412x (2)解:∵直线AB 沿y 轴向下平移,平移后的直线恰好经过C (﹣3,0), ∴设直线DC 的解析式为y =﹣2x+d ,把C (﹣3,0)代入得d =﹣6,∴直线DC 的解析式为y =﹣2x﹣6.解得,{y =−2x−6y =12x +4{x =−4y =2∴E (﹣4,2).21.【答案】(1)解:由题意,将点 代入一次函数 得: A(−1,m)y =x +5m =−1+5=4∴A(−1,4)将点 代入得: ,解得 A(−1,4)y =k x k−1=4k =−4则反比例函数的表达式为;y =−4x (2)解:将一次函数 的图象沿 轴向下平移 个单位得到的一次函数的解析式为 y =x +5y b y =x +5−b 联立{y =x +5−by =−4x 整理得: x 2+(5−b)x +4=0一次函数 的图象与反比例函数 的图象有且只有一个交点∵y =x +5−b y =−4x 关于x 的一元二次方程 只有一个实数根∴x 2+(5−b)x +4=0 此方程的根的判别式 ∴Δ=(5−b)2−4×4=0解得 b 1=1,b 2=9则b 的值为1或9.22.【答案】(1)解:∵反比例函数y 1= 与正比例函数y 2=x 相交于A (2,2).kx ∴k=2×2=4(2)解:描出点(1,4),(2,2),(4,1), 用平滑的曲线连接,画出反比例函数的图象如图,(3)解:由图象可知,当0<x<2和x<-2时,y1>y2.(4)解:观察图象,直线y=x向下平移3个单位,与反比例函数的交点为(4,1)和(-1,-4),∴不等式 <x-3的解集为:-1<x <0和x >4.kx 23.【答案】(1)解:由 ,得 ,l 1:y =x−1k 1=1 , ,∵l 2⊥l 1∴k 2⋅k 1=−1,∴k 2=−1设 ,把 代入解析式得:b=3,l 2:y =−x +b P(2,1) ;∴l 2:y =−x +3(2)解:由图象可得:, 与x 轴交于点B 、C , 令y=0,则有 ∵l 2:y =−x +3l 1:y =x−1∴B(3,0),C(1,0),又 与y 轴交于点A , 令x=0,则有 ,∵l 2:y =−x +3∴A(0,3) OA=3,BC=2, ;∴∴S △ABC =12BC ⋅OA =3(3)解: 将直线 向下平移 个单位,得到新的直线 ,∵l 1q l 3 ,令x=0则 , ,∴l 3:y =x−1−q y =−1−q ∴E(0,−1−q) ,∴AE =3−(−1−q)=4+q 交直线 于点F , 解得,∵l 3l 2∴{y =−x +3y =x−1−q {x =4+q 2y =2−q 2 , ,∵S △AEF =12AE ⋅F x =16∴12×(4+q)⋅4+q 2=16解得 (不符题意,舍去).q 1=4,q 2=−12 .∴q =424.【答案】(1)解:令x=0,则y=3,∴B (0,3),令y=0,则 x+3=0,34∴x=﹣4,∴A (﹣4,0);(2)解:∵点C 是点A 关于y 轴对称的点, ∴C (4,0),∵CD ⊥x 轴,∴x=4时,y=6,∴D (4,6),∴AC=8,CD=6,AD=10,由折叠知,AC'=AC=8,∴C'D=AD﹣AC'=2,设PC=a ,∴PC'=a ,DP=6﹣a ,在Rt △DC'P 中,a2+4=(6﹣a )2,∴a= ,83∴P (4, );83(3)解:设P (4,m ), ∴CP=m ,DP=|m﹣6|,∵S △CPQ =2S △DPQ ,∴CP=2PD ,∴2|m﹣6|=m ,∴m=4或m=12,∴P (4,4)或P (4,12),∵直线AB 的解析式为y= x+3①,34当P (4,4)时,直线OP 的解析式为y=x ②,联立①②解得,x=12,y=12,∴Q (12,12),当P (4,12)时,直线OP 解析式为y=3x ③,联立①③解得,x= ,y=4,43∴Q ( ,4),43。
(lsl)培优专题:一次函数综合专题

专题: 一次函数图像及性质第一次课 一次函数与几何图形综合运用班级: 姓名:例题精讲:例1.已知一次函数的图象经过点(0,2),它与两坐标轴所围成的三角形的面积等于1,求这个一次函数的表达式.例2.如图,在平面直角坐标系中,直线y= 2x —6与x 轴、y 轴分别相交于点A 、B ,点C 在x 轴上,若△ABC 是等腰三角形,试求点C 的坐标.例3.在平面直角坐标系中,已知A (1,4)、B (3,1),P 是x 轴上一点,(1)当P 的坐标为多少时,AP+BP 取最小值,最小值为多少? 当P 的坐标为多少时,AP-BP 取最大值,最大值为多少?例4.如图所示,直线y =x +1与y 轴相交于点A 1,以OA 1为边作正方形OA 1B 1C 1,记作第一个正方形;然后延长C 1B 1与直线y =x +1相交于点A 2,再以C 1A 2为边作正方形C 1A 2B 2C 2,记作第二个正方形;同样延长C 2B 2与直线y =x +1相交于点A 3,再以C 2A 3为边作正方形C 2A 3B 3C 3,记作第三个正方形;…依此类推,则第n 个正方形的边长为__ _.xy ABO例5.直线y=-x+2与x 轴、y 轴交于A 、B 两点,C 在y 轴的负半轴上,且OC=OB. (1) 求AC 的解析式;(2) 在OA 的延长线上任取一点P,作PQ ⊥BP,交直线AC 于Q,试探究BP 与PQ 的数量关系,并证明你的结论. (3) 在(2)的前提下,作PM ⊥AC 于M,BP 交AC 于N,下面两个结论:①(MQ+AC)/PM 的值不变;②(MQ-AC)/PM的值不变,期中只有一个正确结论,请选择并加以证明。
例6.如图①所示,直线L :5y mx m =+与x 轴负半轴、y 轴正半轴分别交于A 、B 两点.(1)当OA=OB 时,试确定直线L 的解析式;(2)在(1)的条件下,如图②所示,设Q 为AB 延长线上一点,作直线OQ ,过A 、B 两点分别作AM ⊥OQ 于M ,BN ⊥OQ 于N ,若AM=4,BN=3,求MN 的长; (3)当m 取不同的值时,点B 在y 轴正半轴上运动,分别以OB 、AB 为边,点B 为直角顶点在第一、二象限内作等腰直角△OBF 和等腰直角△ABE ,连EF 交y 轴于P 点.如图③,问:当点B 在 y 轴正半轴上运动时,试猜想PB 的长是否为定值?若是,请求出其值.若不是,说明理由.xyo BA CPQ第2题图①第2题图②第2题图③xyo BA CPQM训练题一.选择题1.一次函数y=﹣3x ﹣2的图象不经过( ) A .第一象限 B .第二象限C .第三象限D .第四象限2.若函数,则当函数值y=8时,自变量x 的值是( )A .±B .4C .±或4D .4或﹣3.下列图形中,表示一次函数y=mx +n 与正比例函数y=mnx (m ,n 为常数,且mn ≠0)的图象的是( )A .B . D .4.如果一个正比例函数的图象经过不同象限的两点A (2,m ),B (n ,3),那么一定有( ) A .m >0,n >0 B .m >0,n <0 C .m <0,n >0 D .m <0,n <05.如图,在矩形ABCD 中,动点P 从点B 出发,沿BC 、CD 、DA 运动至点A 停止,设点P 运动的路程为x ,△ABP 的面积为y ,如果y 关于x 的函数图象如图所示,则△ABC 的面积是( )A .10B .16C .18D .20 第10题二.填空题(共13小题) 6.函数y=中自变量x 的取值范围是 .7.已知直线y=kx +b ,若k +b=﹣5,kb=6,那么该直线不经过第 象限. 8.把直线y=﹣x ﹣1沿x 轴向右平移2个单位,所得直线的函数解析式为 .9.已知直线y=2x +(3﹣a )与x 轴的交点在A (2,0)、B (3,0)之间(包括A 、B 两点),则a 的取值范围是 .10.(*)如图所示,直线y=33x+33与y 轴相交于点D ,点A 1在直线y=33x+33上,点B1在X 轴上,且△OA 1B 1是正三角形,记作第一个正三角形;然后过B 1作B 1A 2∥OA 1与直线y=33x+33相交于点A 2,点B 2在X 轴上,再以B 1A 2为边作正三角形A 2B 2B 1,记作第二个正三角形;同样过B 2作B 2A 3∥B 1A 2与直线y=33x+33相交于点A 3,点B 3在x 轴上,再以B 2A 3为边作正三角形A 3B 3B 2,记作第三个正三角形;…依此类推,则第n 个正三角形的顶点An 的纵坐标为 .三.解答题11. 已经正比例函数y=k 1x 的图像与一次函数y=k 2x-9的图像相交于点P(3,-6),求k 1,k 2的值.如果一次函数y=k 2x-9的图象与x 轴交于点A ,求点△AOP 的面积.12. (*)如图,直线1l 与x 轴、y 轴分别交于A 、B 两点,直线2l 与直线1l 关于x 轴对称,已知直线1l 的解析式为3y x =+.(1)求直线2l 的解析式;(2)过A 点在△ABC 的外部作一条直线3l ,过点B 作BE ⊥3l 于E,过点C 作CF ⊥3l 于F ,请画出图形并求证:BE +CF =EF ;(3)△ABC 沿y 轴向下平移,AB 边交x 轴于点P ,过P 点的直线与AC 边的延长线相交于点Q ,与y 轴相交于点M ,且BP =CQ ,在△ABC 平移的过程中,①OM 为定值;②MC 为定值.在这两个结论中,有且只有一个是正确的,请找出正确的结论,并求出其值.13. (**)如图,直线AB :y=-x-b 分别与x 、y 轴交于A (6,0)、B 两点,过点B 的直线交x 轴负半轴于C ,且OB :OC=3:1.(1)求直线BC 的解析式:(2)直线EF :y=kx-k (k ≠0)交AB 于E ,交BC 于点F ,交x 轴于D ,是否存在这样的直线EF ,使得S △EBD =S △FBD ?若存在,求出k 的值;若不存在,说明理由?(3)如图,P 为A 点右侧x 轴上的一动点,以P 为直角顶点,BP 为腰在第一象限内作等腰直角△BPQ ,连接QA 并延长交y轴于点K ,当P 点运动时,K 点的位置是否发现变化?若不变,请求出它的坐标;如果变化,请说明理由。
八年级数学培优专题一、一次函数培优训练经典题型精选全文完整版

可编辑修改精选全文完整版一次函数培优经典题型(最新)一、正比例函数的定义1、若y=(m+1)x+m2﹣1是关于x的正比例函数,则m的值为.2、已知函数y=(m+2)x﹣m2+4(m是常数)是正比例函数,则m=.二、一次函数的图象1、在同一平面直角坐标系中,函数y=kx﹣b与y=bx+k的图象不可能是()A.B.C.D.2、如果ab>0,bc<0,则一次函数y=﹣x+的图象的大致形状是()A.B.C.D.3、一次函数y=kx+k的图象可能是()A.B.C.D.4、如图,三个正比例函数的图象分别对应的解析式是:①y=ax,②y=bx,③y=cx,请用“>”表示a,b,c的不等关系.三、一次函数的性质1、已知直线y=kx+b过点A(﹣3,y1),B(4,y2),若k<0,则y1与y2大小关系为()A.y1>y2B.y1<y2C.y1=y2D.不能确定2、当1≤x≤10时,一次函数y=﹣3x+b的最大值为17,则b=.3、已知一次函数y=mx﹣2m(m为常数),当﹣1≤x≤3时,y有最大值6,则m的值为()A.﹣B.﹣2C.2或6D.﹣2或64、已知一次函数y=kx+b,当0≤x≤2时,对应的函数值y的取值范围是﹣2≤y≤4,则k的值为()A.3B.﹣3C.3或﹣3D.k的值不确定5、在平面直角坐标系中,已知一次函数y=kx+b(k,b为常数且k≠0).(1)当b=3k+6时,该函数恒经过一点,则该点的坐标为;(2)当﹣2≤x≤2时,﹣8≤y≤4,则该函数的解析式为.6、一次函数y=ax﹣a+1(a为常数,且a<0).(1)若点(2,﹣3)在一次函数y=ax﹣a+1的图象上,求a的值;(2)当﹣1≤x≤2时,函数有最大值2,求a的值.四、一次函数图象与系数的关系1、若一次函数y=(m﹣2)x+m+1的图象经过一、二、四象限,则m的取值范围是()A.m<﹣1B.m<2C.﹣1<m<2D.m>﹣12、一次函数y=(2k﹣1)x+k的图象不经过第三象限,则k的取值范围是()A.k>0B.C.k≥0D.3、关于x的一次函数y=(k﹣2)x+k2﹣4k+4,若﹣1≤x≤1时,y>0总成立,则k的取值范围是()A.k<1或k>3B.k>1C.k<3D.1<k<34、一次函数y=(3﹣a)x+b﹣2在直角坐标系中的图象如图所示,化简:﹣|2﹣b|=.5、关于x的一次函数y=(2a+1)x+a﹣2,若y随x的增大而增大,且图象与y轴的交点在原点下方,则实数a的取值范围是.6、函数y=3x+k﹣2的图象不经过第二象限,则k的取值范围是.7、设,则一次函数y=kx﹣k的图象一定过第_________象限.五、一次函数图象与几何变换1、直线y=﹣5x向上平移2个单位长度,得到的直线的解析式为()A.y=5x+2B.y=﹣5x+2C.y=5x﹣2D.y=﹣5x﹣2 2、在平面直角坐标系中,将正比例函数y=﹣2x的图象向右平移3个单位长度得到一次函数y=kx+b(k≠0)的图象,则该一次函数的解析式为()A.y=﹣2x+3B.y=﹣2x+6C.y=﹣2x﹣3D.y=﹣2x﹣63、若直线l1:y=kx+b(k≠0)是由直线l2:y=4x+2向左平移m(m>0)个单位得到,则下列各点中,可能在直线l1上的是()A.(0,1)B.(2,﹣1)C.(﹣1,2)D.(3,0)4、在平面直角坐标系中,将函数y=x的图象绕坐标原点逆时针旋转90°,再向上平移1个单位长度,所得直线的函数表达式为()A.y=﹣x+1B.y=x+1C.y=﹣x﹣1D.y=x﹣15、若一次函数y=kx+b与y=﹣2x+1的图象关于y轴对称,则k、b的值分别等于.六、待定系数法求一次函数解析式1、P(8,m),A(2,4),B(﹣2,﹣2)三点在同一直线上,则m的值为.2、已知y﹣2与x成正比例,且当x=﹣1时y=5,则y与x的函数关系式是.3、已知y﹣1与x成正比例,当x=﹣2时,y=4.(1)求出y与x的函数关系式;(2)设点(a,﹣2)在这个函数的图象上,求a的值.4、已知y=y1+y2,y1与x2成正比例,y2与x﹣2成正比例,当x=1时,y=5;当x=﹣1时,y=11,求y与x之间的函数表达式,并求当x=2时y的值.5、已知y﹣3与2x+4成正比例,且当x=﹣1时,y=7.(1)求y与x的函数关系式;(2)求此函数图象与坐标轴围成的面积.七、一次函数与一元一次方程1、如图,直线y=x+5和直线y=ax+b相交于点P,观察其图象可知方程x+5=ax+b的解()A.x=15B.x=25B.C.x=10D.x=202、如图,一次函数y=kx+b与y=x+2的图象相交于点P(m,4),则关于x的方程kx+b=4的解是()A.x=1B.x=2C.x=3D.x=43、如图,一次函数y=ax+b与正比例函数y=kx的图象交于点P(﹣2,﹣1),则关于x的方程ax+b=kx的解是.4、根据一次函数y=kx+b的图象,直接写出下列问题的答案:(1)关于x的方程kx+b=0的解;(2)代数式k+b的值;(3)关于x的方程kx+b=﹣3的解.八、一次函数中的面积问题1、若一次函数y=2x+b与坐标轴围成的三角形面积为9,则这个一次函数的解析式为.2、直线y=kx+b经过点(0,3),且与两坐标轴构成的直角三角形的面积是6,则k为.3、如图,一次函数y=x﹣4的图象与x轴,y轴分别交于点A,点B,过点A作直线l将△ABO分成周长相等的两部分,则直线l的函数解析式为.4、如图,在平面直角坐标系xOy中,A(2,0),B(2,4),C(0,4).若直线y=kx﹣2k+1(k是常数)将四边形OABC分成面积相等的两部分,则k的值为.5、如图所示,在直角坐标系中,矩形OABC的顶点B的坐标为(12,5),直线恰好将矩形OABC分成面积相等的两部分.那么b=.6、如图,在平面直角坐标系中,四边形ABCO是正方形,点B的坐标为(4,4),直线y=mx﹣2恰好把正方形ABCO的面积分成相等的两部分,则m=.九、一次函数的应用1、甲乙两人骑自行车分别从A,B两地同时出发相向而行,甲匀速骑行到B地,乙匀速骑行到A地,甲的速度大于乙的速度,两人分别到达目的地后停止骑行.两人之间的距离y(米)和骑行的时间x(秒)之间的函数关系图象如图所示,现给出下列结论:①a=450;②b=150;③甲的速度为10米/秒;④当甲、乙相距50米时,甲出发了55秒或65秒.其中正确的结论有()A.①②B.①③C.②④D.③④2、甲、乙两车从A地出发,沿同一路线驶向B地.甲车先出发匀速驶向B地,40min后乙出发,匀速行驶一段时间后,在途中的货站装货耗时半小时.由于满载货物,为了行驶安全,速度减少了50km/h,结果与甲车同时到达B地,甲乙两车距A地的路程y(km)与乙车行驶时间x(h)之间的函数图象如图所示.(1)a的值是,甲的速度是km/h.(2)求线段EF所表示的y与x的函数关系式;(3)若甲乙两车距离不超过10km时,车载通话机可以进行通话,则两车在行驶过程中可以通话的总时长为多少小时?十、一次函数综合题1、如图,直线与x轴,y轴分别交于点A,B,点C,D分别是AB,AO的中点,点P是y轴上一动点,则PC+PD的最小值是.2、若直线AB:y=x+4与x轴、y轴分别交于点B和点A,直线CD:y=﹣x+2与x轴、y轴分别交于点D和点C,线段AB与CD的中点分别是M,N,点P为x轴上一动点.(1)点M的坐标为;(2)当PM+PN的值最小时,点P的坐标为.3、如图,在平面直角坐标系中,一次函数的图象分别与x、y轴交于点A、B,点C在y轴上,AC平分∠OAB,则线段BC=.4、如图,点C的坐标是(2,2),A为坐标原点,CB⊥x轴于B,CD⊥y轴于D,点E是线段BC的中点,过点A的直线y=kx交线段DC于点F,连接EF,若AF平分∠DFE,则k的值为.5、如图,一次函数y=kx+b的图象经过点A(0,3)和点B(2,0),以线段AB为边在第一象限内作等腰直角△ABC使∠BAC=90°(1)求一次函数的解析式;(2)求出点C的坐标;(3)点P是y轴上一动点,当PC最小时,求点P的坐标.6、如图,直线l:y=kx+b(k≠0)与坐标轴分别交于点A,B,以OA为边在y=8.轴的右侧作正方形AOBC,且S△AOB(1)求直线l的解析式;(2)如图1,点D是x轴上一动点,点E在AD的右侧,∠ADE=90°,AD =DE.①当AE+CE最小时,求E点的坐标;②如图2,点D是线段OB的中点,另一动点H在直线BE上,且∠HAC=∠BAD,请求出点H的坐标.。
2019-20学年度北师大版八年级上册第四章一次函数与几何图形面积培优题( 解析版)

2019-2020一次函数与几何图形面积培优题(含解析)1.如图,正方形ABCD的边长为2cm,动点P从点A出发,在正方形的边上沿A→B→C的方向运动到点C停止,设点P的运动路程为x(cm),在下列图象中,能表示△ADP的面积y(cm2)关于x(cm)的函数关系的图象是()A.B.C.D.2.已知一次函数y=kx+b(k≠0)图象过点(0,2),且与两坐标轴围成的三角形面积为2,则一次函数的解析式为( )A.y= x+2 B.y= ﹣x+2 C.y= x+2或y=﹣x+2 D.y= - x+2或y = x-23.在平面直角坐标系中,过点(1,2)作直线l,若直线l与两坐标轴围成的三角形面积为4,则满足条件的直线l的条数是()A.5B.4C.3D.24.如图1,点F从菱形ABCD的顶点A出发,沿A→D→B以1cm/s的速度匀速运动到点B,图2是点F运动时,△FBC的面积y(cm2)随时间x(s)变化的关系图象,则a的值为()A.5B.2C.52D.255.直线y=﹣2x+b与两坐标轴围成的三角形的面积为1,则b的值为_________.6.已知一次函数y=kx+b(k≠0)的图象经过点(3,﹣3),且与直线y=﹣43x平行,求此一次函数的图象与两坐标轴围成的三角形的面积_____.7.如图,直线l1的函数解析式为y=﹣2x+4,且l1与x轴交于点D,直线l2经过点A、B,直线l1、l2交于点C.(1)求直线l2的函数解析式;(2)求△ADC的面积;(3)在直线l2上是否存在点P,使得△ADP面积是△ADC面积的2倍?如果存在,请求出P坐标;如果不存在,请说明理由.8.如图,平面直角坐标系中,直线AB:y=﹣x+b交y轴于点A,交x轴于点B,S△AOB=8.(1)求点B的坐标和直线AB的函数表达式;(2)直线a垂直平分OB交AB于点D,交x轴于点E,点P是直线a上一动点,且在点D的上方,设点P的纵坐标为m.①用含m的代数式表示△ABP的面积;②当S△ABP=6时,求点P的坐标;③在②的条件下,在坐标轴上,是否存在一点Q,使得△ABQ与△ABP面积相等?若存在,直接写出点Q的坐标,若不存在,请说明理由.9.如图,直线l1:y1=﹣x+2与x轴,y轴分别交于A,B两点,点P(m,3)为直线l1上一点,另一直线l2:y2=12x+b过点P.(1)求点P坐标和b的值;(2)若点C是直线l2与x轴的交点,动点Q从点C开始以每秒1个单位的速度向x轴正方向移动.设点Q的运动时间为t秒.①请写出当点Q在运动过程中,△APQ的面积S与t的函数关系式;②求出t为多少时,△APQ的面积小于3;③是否存在t的值,使△APQ为等腰三角形?若存在,请求出t的值;若不存在,请说明理由.10.已知:如图,一次函数334y x=+的图象分别与x轴、y轴相交于点A、B,且与经过点C(2,0)的一次函数y=kx+b的图象相交于点D,点D的横坐标为4,直线CD与y轴相交于点E.(1)直线CD的函数表达式为;(直接写出结果)(2)点Q为线段DE上的一个动点,连接BQ.①若直线BQ将△BDE的面积分为1:2两部分,试求点Q的坐标;②将△BQD沿着直线BQ翻折,使得点D恰好落在直线AB下方的坐标轴上,请直接写出点Q的坐标: .11.如图,在平面直角坐标系xOy中,已知正比例函数43y x=与一次函数7y x=-+的图像交于点A.(1)求点A的坐标;(2)在y轴上确定点M,使得△AOM是等腰三角形,请直接写出点M的坐标;(3)如图,设x轴上一点P(a,0),过点P作x轴的垂线(垂线位于点A的右侧),分别交43 y x =和7y x =-+的图像于点B 、C ,连接OC ,若BC =145OA ,求△ABC 的面积及点B 、点C 的坐标; (4)在(3)的条件下,设直线7y x =-+交x 轴于点D ,在直线BC 上确定点E ,使得△ADE 的周长最小,请直接写出点E 的坐标.12.如图,一次函数y=kx+b 的图象经过点A(8,0),直线y=-3x+6与x 轴交于点B,与y 轴交于点D,且两直线交于点C(4,m).(1)求m 的值及一次函数的解析式;(2)求△ACD 的面积。
《一次函数》培优题含答案解析

《一次函数》培优题含答案解析1.如图1,已知直线y=2某+2与y轴、某轴分别交于A、B两点,以B为直角顶点在第二象限作等腰Rt△ABC(1)求点C的坐标,并求出直线AC的关系式.(2)如图2,直线CB交y轴于E,在直线CB上取一点D,连接AD,若AD=AC,求证:BE=DE.(3)如图3,在(1)的条件下,直线AC交某轴于M,P(,k)是线段BC上一点,在线段BM上是否存在一点N,使直线PN平分△BCM的面积?若存在,请求出点N的坐标;若不存在,请说明理由.考点:一次函数综合题。
分析:(1)如图1,作CQ⊥某轴,垂足为Q,利用等腰直角三角形的性质证明△ABO≌△BCQ,根据全等三角形的性质求OQ,CQ的长,确定C点坐标;(2)同(1)的方法证明△BCH≌△BDF,再根据线段的相等关系证明△BOE≌△DGE,得出结论;(3)依题意确定P点坐标,可知△BPN中BN变上的高,再由S△PBN=S△BCM,求BN,进而得出ON.解答:解:(1)如图1,作CQ⊥某轴,垂足为Q,∵∠OBA+∠OAB=90°,∠OBA+∠QBC=90°,∴∠OAB=∠QBC,又∵AB=BC,∠AOB=∠Q=90°,∴△ABO≌△BCQ,∴BQ=AO=2,OQ=BQ+BO=3,CQ=OB=1,∴C(﹣3,1),由A(0,2),C(﹣3,1)可知,直线AC:y=某+2;(2)如图2,作CH⊥某轴于H,DF⊥某轴于F,DG⊥y轴于G,∵AC=AD,AB⊥CB,∴BC=BD,∴△BCH≌△BDF,∴BF=BH=2,∴OF=OB=1,∴DG=OB,∴△BOE≌△DGE,∴BE=DE;(3)如图3,直线BC:y=﹣某﹣,P(∴P(﹣,),由y=某+2知M(﹣6,0),∴BM=5,则S△BCM=.假设存在点N使直线PN平分△BCM的面积,则BN∴BN==某,,ON=,,k)是线段BC上一点,∵BN<BM,∴点N在线段BM上,∴N(﹣,0).点评:本题考查了一次函数的综合运用.关键是根据等腰直角三角形的特殊性证明全等三角形,利用全等三角形的性质求解.3.如图直线:y=k某+6与某轴、y轴分别交于点B、C,点B的坐标是(﹣8,0),点A的坐标为(﹣6,0)(1)求k的值.(2)若P(某,y)是直线在第二象限内一个动点,试写出△OPA的面积S与某的函数关系式,并写出自变量某的取值范围.(3)当点P运动到什么位置时,△OPA的面积为9,并说明理由.考点:一次函数综合题;待定系数法求一次函数解析式;三角形的面积。
一次函数综合培优(含解答题答案)

一次函数综合培优(含解答题答案)-CAL-FENGHAI.-(YICAI)-Company One1A B C D 第6题 第7题 一、选择题(每题3分,共36分) 1、点1(5,)A y -和2(2,)B y -都在直线231--=x y 上,则1y 与2y 的关系是( )A .12y y ≤B .12y y =C .12y y < D. 12y y > 2、若实数a ,b ,c 满足a+b+c=0,且a <b <c ,则函数y=cx+a 的图象可能是( )3、如图,在平面直角坐标系中,点A 的坐标为(0,3),△OAB 沿x 轴向右平移后得到△O ′A ′B ′,点A 的对应点在直线y=34x上一点,则点B 与其对应点B ′间的距离为( ) A .94B .3C .4D .54、若直线y=3x -1与y=x -k 的交点在第三象限,则k 的取值范围是( )A .k<13B .13<k<1 C .k>1 D .k>1或k<135、已知函数1225,23,y x y x =-=-+且12y y <,则x 的取值为( )A .0x >B .2x <C .x >2D .0x <6、如图,在平面直角坐标系中,▱OABC 的顶点A 在x 轴上,顶点B 的坐标为(6,4).若直线l 经过点(1,0),且将▱OABC 分割成面积相等的两部分,则直线l 的函数解析式是( )A .y=x+1B .y =13x+1 C .y=3x-3D .y=x-17、如图,直线L1:y=x+3与直线L2:y=ax+b 相交于点A (m ,4),则关于x 的不等式x+3≤ax+b 的解集是( ) A .x ≥4 B .x ≤4 C .x ≥m D .x ≤18、某校高一(1)班40名同学这“希望工程”捐款,共捐款100元,捐款情况如下表:表格中捐款2元和3元的人数不小心被墨水污染已看不清楚,若设捐款2元的有x 名同学,捐款3元的有y 名同学,假设(x ,y )是两个一次函数图象的交点,则这两个一次函数解析式分别是( )A .y=27-x 与y=23x+22B .y=27-x 与y=23x+1003C .y=27-x 与y=32x+33D .y=27-x 与y=23x+339、若直线y=-2x-4与直线y=4x+b 的交点在第三象限,则b 的取值范围是( ) A .-4<b <8 B .-4<b <0 C .b <-4或b >8 D .-4≤b ≤8第3题第10题 第11题5 2 0 xy(1) (2) 第16题 第15题10、如图,一次函数图象经过点A ,且与正比例函数y=-x 的图象交于点B ,则该一次函数的表达式为( )A .y=-x+2B .y=x+2C .y=x-2D .y=-x-211、如图所示,在平面直角坐标系中,直线OM 是正比例函数y=-3x 的图象,点A 的坐标为(1,0),在直线OM 上找点N ,使△ONA 是等腰三角形,符合条件的点N 的个数是( ) A .2个 B .3个 C .4个 D .5个12、如图,在平面直角坐标系中,直线y=23x-23与矩形ABCO 的边OC 、BC 分别交于点E 、F ,已知OA=3,OC=4,则△CEF 的面积是( )A .6B .3C .12D .43二、填空题(每题4分,共16分)13、函数y=ax+b (a >0,b <0)和y=kx (k <0)的图象交于点P ,那么点P 应该位于第 象限。
第十九章一次函数知识梳理及培优训练人教版2024—2025学年八年级下册

()()()321000.0k ⎪⎩⎪⎨⎧<=><b b b 第十九章一次函数知识梳理及培优训练人教版2024—2025学年八年级下册 一、知识梳理:1.一次函数的概念:函数(,为常数,)叫做的一次函数。
(1)作为一次函数自变量的最高次数是1,且其系数,这两个条件缺一不可。
(2)函数()中可以为任意常数, 当时,一次函数就成正比例函数(为常数,且) 因此正比例函数是一次函数的特例,但一次函数不一定是正比例函数。
2 一次函数的图象:(重点,请牢记)(1)正比例函数y=kx 的图象是经过(0,0),(1,k )的一条直线; (2)一次函数y=kx+b 的图象是经过(0,b )(—k/b ,0)的一条直线.3、一次函数的性质:(重点,请牢记) b=0 b<0 b>0k>0经过第一、三象限经过第一、三、四象限经过第一、二、三象限图象从左到右上升,y 随x 的增大而增大k<0经过第二、四象限经过第二、三、四象限经过第一、二、四象限图象从左到右下降,y 随x 的增大而减小4.两直线的位置关系设直线11b x k y +=(01≠k )与22b x k y +=(02≠k )则: (1)21k k =且21b b ≠ ⇔两直线 (2)21k k ≠ ⇔两直线(3)21k k =且21b b = ⇔两直线 (4)121-=k k ⇔两直线()()()321000.0k ⎪⎩⎪⎨⎧<=>>b b b图1 二、例题讲解【一】函数和一次函数的定义 (1)、下列各图中表示y 是x 的函数图像的是 ( )2.函数y=(k 2-1)x+3是一次函数,则k 的取值范围是( )A.k ≠1B.k ≠-1C.k ≠±1D.k 为任意实数. 3.2(3)9y m x m =-+-是正比例函数,则m= 4.已知关于x 的函数y=(m+3)x |m+2|是正比例函数,求m 值。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
一次函数与几何综合1.一次函数与全等三角形的综合以一次函数为背景的常见的几何模型如下:2.一次函数与面积的综合 解决在坐标系中的图形面积计算的常用方法:(1)割补法;(2)转化法;(3)加减法;(4)铅垂线法.有的问题还需要分类讨论. 3.一次函数与特殊图形的综合以一次函数为背景的常见的特殊图形有等腰三角形、直角三角形和平行四边形. (1)等腰三角形 ①确定点的位置如下图所示,在直线L 上找一点C ,使得△ABC 是等腰三角形.,:AC AB I =以A 点为圆心,AB 长为半径画圆,交直线L 于两点,,21C C ,:BC AB =X 以B 点为圆心,AB 长为半径画圆,交直线L 于两点,,43C CⅢ,:BC AC =作AB 的中垂线交直线L 于点⋅5C②求点的坐标:若△ABC 是等腰三角形,则分三种情况分类讨论:BC AC BC AB AC AB ===,, 然后利用等腰三角形的性质或勾股定理计算(或建立方程)解题.(2)直角三角形若△ABC 是直角三角形,则分三种情况分类讨论:.09,90,90ooC B A &ο=∠=∠=∠然后利用勾股定 理解题.(3)平行四边形 ①确定点的位置如右图所示,在△ABC 中,点A 、B 在直线L 上,点C 在x 轴上 ,在坐标平面内找一点D ,使得A 、B 、C 、D 围成的四边形是平行四边形.作法:分别为过A 、B 、C 的三个顶点作对边的平行线,交点即为平行四边形的第四个顶点,如右图所示.②求点的坐标:若四边形ABCD 是平行四边形,利用平行四边形的性质解题.基 础 演 练1.点P 是等边△ABC 的边上的一个作匀速运动的动点,点P 从点A 开始沿AB 边运动到B 再沿BC 边运动到C 为止,设运动时间为t ,△ACP 的面积为S ,S 与t 的大致图像是图19 -4—1中的( )2.(1)如图19-4-2所示,已知A 点坐标为(5,0),直线)0(>+=b b x y 与y 轴交于点B ,连接,75,ο=∠αAB 则b 的值为( ).3.A 335.B 4.C 435.D (2)如图19-4-3所示,直线233+-=x y 与x 轴、y 轴分别交于A 、B 两点,把△AOB 绕点A 顺时针旋转ο60后得到,//B AO ∆则点/B 的坐标是( ).)32,4.(A )4,32.(B )3,3.(C )32,232(+⋅D3.平面直角坐标系中,0是坐标原点,点A 的坐标是(4,O),点P 在直线m x y +-=上,且.4==OP AP 则m 的值为( ).322.+A 或322- 4.B 或4- 32.C 或32- 324.+D 或324-4.若函数4--=x y 与x 轴交于点A ,直线上有一点M ,若△AOM 的面积为8,则点M 的坐标5.(1)在平面直角坐标系中,0为坐标原点,已知A (1,a )在直线2+-=x y 上,在坐标轴上确定点P ,使△AOP 为等腰三角形,则符合条件的点P 的个数有 个. (2)如图19-4-4所示,直线133+-=x y 和x 轴、y 轴分别交于点A 、B ,点C 在坐标平面内,若以线段AB 为边作等边三角形ABC ,则点C 的坐标是6.(1)如图19-4-5所示,点A 的坐标为(-1,0),点B 在直线x y =上运动,当线段AB 最短时,点B 的坐标为(2)如图19-4-6所示,在平面直角坐标系中有两点A (-2,2),B(l ,4),P 为x 轴上一点.①当BP+AP 的值最小时,P 点的坐标为 ;②当BP-AP 的值最大时,P 点的坐标7.探索勾股定理时,我们发现“用不同的方式表示同一图形的面积”可以解决线段和(或差)的问题,这种方法称为面积法.请你运用面积法求解下列问题:在等腰△ABC 中,BD AC AB ,=为腰AC 上的高.(1)若M h BD ,=是直线BC 上的任意一点,M 到AB 、AC 的距离分别为ME 、MF .①若M 在线段BC 上,请你结合图形19-4-7(a)证明:h MF ME =+ ②当点M 在线段BC 的延长线上时ME 、MF 和h 之间的关系为 .(请直接写出结论,不必证明)(2)如图19-4-7(b)所示,在平面直角坐标系中有两条直线.63:;643:21+-=+=x y l x y l 若2l 上的一点M 到1l 的距离是3,请你利用以上结论求点M 的坐标.8.如图19-4-8所示,已知y AB b a A ⊥),,(轴于点B ,且满足.0)2(22=-+-b a(1)求直线AO 的解析式;(2)分别以AB 、AO 为边作等边三角形△ABC 和△AOD,试判定线段AC 和DC 的数量关系和位置关系.能 力 提 升9.在△ABC 中,BO 、CO 分别平分∠ABC 、∠ACB ,过点0作EF∥BC 分别交AB 、AC 于点E 、F ,已知a a BC (= 是常数),设△ABC 的周长为y ,△AEF 的周长为x ,在下列图像中,大致表示y 与x 之间的函数关系的是( ).10.如图19-4-9所示,在x 轴上有五个点,它们的横坐标依次为1,2,3,4,5.分别过这些点作x 轴的垂线与三条直线x a y x a y ax y )2(,)1(,+=+==相交,其中a>0.则图中阴影部分的面积是( ).5.12.A 25.B a C 5.12. a D 25.11.如图19 -4 -10所示,直线133+-=x y 分别交x 、y 轴于B 、C 两点,一边在x 轴上,另一个顶点在BC 边上的等边三角形分别是第1个,11B AA ∆第2个,221B A B ∆第3个,,332ΛB A B ∆则第n 个等边三角形的边长等于( ).n A 23.123.-n B nC 21. 123.+n D12.已知平面上四点A(O ,O),B(10,0),C(12,6),D(2,6),直线-=mx y 63+m 将四边形ABCD 分成面积相等的两部分,则m 的值为13.如图19 -4 -11所示,在平面直角坐标系中,点0为坐标原点,直线221+-=x y 与y 、x 轴分别交于A 、B 两点,点C 的坐标为(O ,1),过点C 作CD ⊥AO 交AB 于点D ,x 轴上的点P 和A 、B 、C 、D 、0中的两个点所构成的三角形与△ACD 全等,这样的三角形有 个.14.已知直线343+-=x y 交x 、y 轴于A 、B 两点,点C 的坐标为(6,3),在坐标平面内找一点D ,使得以A 、B 、C 、D 为顶点的四边形是平行四边形,则点D 的坐标为15.如图19 -4 -12所示,已知平行于y 轴的动直线a 的解析式为),0(<=⋅t t x 直线b 的解析式为,x y = 直线c 的解析式为,221+-=x y 且动直线a 分别交直线b 、c 于点D 、E ,P 是y 轴上一个动点,且满足△PDE 是等腰直角三角形,则点P 的坐标是16.如图19 -4 -13所示,在平面直角坐标系xOy 中,长方形OABC 的顶点A 、C 的坐标分别为(3,O),(0,5).(1)直接写出点B 的坐标;(2)若过点C 的直线CD 交AB 边于点D ,且把长方形OABC 的周长分为1:3两部分,求直线CD 的解析式; (3)设点P 沿O-A-B-C 的方向运动到点C (但不与点0、C 重合),求△OPC 的面积y 与点P 所行路程x之间的函数关系式及自变量x 的取值范围.17.如图19 -4 -14所示,在平面直角坐标系中,点A 的坐标为(2,O),以线段OA 为边在第四象限内作等边△AOB,点C 为x 正半轴上一动点(0C>1),连接BC ,以线段BC 为边在第四象限内作等边△CBD ,直线DA 交y 轴于点E.(1)△OBC 与△ABD 全等吗?判断并证明你的结论; (2)求直线AB 的解析式;(3)随着点C 位置的变化,点E 的位置是否会发生变化?若没有变化,求出点E 的坐标;若有变化,请说明理由.18.如图19 -4 -15所示,在平面直角坐标系xOy 中,点A 、B 、D 的坐标分别为),3,0()0,4()0,1(、、-,//BC AD 点E 在CD 上,且满足AE 、BE 分别平分.CBA DAB ∠∠、(1)求直线BC 的解析式;(2)请你判断下列哪个结论成立,并证明你的结论;.;BC AD AB DE CE +==②①(3)已知,60ο=∠DAB 直接写出线段BC 的长.19.如图19 -4 -16所示,在平面直角坐标系xOy 中,直线m x y +-=经过点A(2,0),交y 轴于点B.点D 为x 轴上一点,且.1=∆ADB s (1)求m 的值;(2)求线段OD 的长;(3)当点E 在直线AB 上(点E 与点B 不重合),且,EDA BDO ∠=∠求点E 的坐标.20.如图19 -4 -17所示,直线AB 交z 轴正半轴于点A (a ,0),交y 轴正半轴于点B(0,b),且a 、b 满足.0|4|4=-+-b a(1)求直线AB 的解析式;(2)如图19-4-17 (a)所示,D 为OA 的中点,连接BD ,过点0作BD OE ⊥于点F ,交AB 于点E , 求证:.EDA BDO ∠=∠ (3)如图19-4-17(b)所示,P 为x 轴上A 点右侧任意一点,以BP 为边作等腰Rt△PBM,其中,PM PB =,90ο=∠BPM 直线MA 交y 轴于点Q ,当点P 在x 轴上运动时,线段OQ 的长是否发生变化?若不变,求其值;若变化,求线段OQ 的取值范围,21.已知,A 点坐标为),0,23(-B 点坐标为(0,3). (1)求过A ,B 两点的直线解析式;(2)过B 点作直线BP 与x 轴交于点P ,且使,2OA OP =求△ABP 的面积.22.如图19 -4 -18所示,对于平面直角坐标系中的任意两点),,(),(222111y x P y x P 、我们把||||2121y y x x -+-叫做21p p 、两点间的直角距离,记作⋅).,(21p p d(1)已知0为坐标原点,动点P(x ,y)满足,1),(=p O d 请写出x 与y 之间满足的关系式,并在所给的直角坐标系中画出所有符合条件的点P 所组成的图形;(2)设),(000y x p 是一定点,Q(x ,y)是直线b ax y +=上的动点,我们把),(0Q P d 的最小值叫做0P 到直线b ax y +=的直角距离,试求点M(2,1)到直线2+=x y 的直角距离.23.如图19 -4 -19所示,正方形ABCO 的边OA 、OC 在坐标轴上,点B 坐标(3,3),将正方形ABCO 绕点A顺时针旋转角度),900(οο<<αα得到正方形ADEF ,ED 交线段OC 于点G ,ED 的延长 线交线段BC 于点P ,连AP 、AG. (1)求证:△AOG≌△ADG;(2)求∠PAG 的度数;并判断线段OG 、PG 、BP 之间的数量关系,说明理由; (3)当∠1= ∠2时,求直线PE 的解析式.24.如图19-4-20所示,△AOB 为正三角形,点B 的坐标为(2,0),过点C(-2,0)作直线L 交AO 于点D ,交AB 于点E ,且△ADE 与△DCO 的面积相等,求直线L 的解析式.25.已知,直线1:1-+=k kx y l 与直线k k x k y l ()1:2++=<是正整数)及x 轴围成的三角形的面积为⋅k S(1)求证:无论川取何值,直线21l l 与的交点均为定点;(2)求2013321s s s s ++++Λ的值.。
