最新梅森公式例子
梅森公式_精品文档

梅森公式
1. 简介
梅森公式(Mersenne formula),是指由法国数学家梅森(Marin Mersenne)在17世纪提出的一种用于生成素数的公式。
梅森公式的基本形式为2^n - 1,其中n是一个自然数。
如果2^n - 1是一个素数,则称之为梅森素数。
梅森公式产生的素数被广泛应用在密码学、计算机科学、通信领域等。
由于其计算简单、结构规律清晰,梅森公式较早被发现,至今为止已知的最大梅森素数为2^82,589,933 - 1。
本文将介绍梅森公式的原理、应用以及一些相关的数学定理。
2. 梅森公式的原理
梅森公式是基于二进制表示的思想,通过将2的幂次方相减得到一个整数,并判断该整数是否为素数。
其基本形式为:
M(n) = 2^n - 1
其中,M(n)为梅森素数。
梅森公式的原理是因为2^n - 1可以通过一种高效的算法进行计算,被称为。
梅森公式经典例题

梅森公式经典例题摘要:一、梅森公式简介二、梅森公式经典例题解析1.基本形式2.乘积形式3.复合形式4.应用场景三、梅森公式在实际问题中的应用四、总结与拓展正文:一、梅森公式简介梅森公式(Mason"s formula)是一种在概率论和统计学中广泛应用的公式,用于计算离散随机变量概率密度函数的积分。
梅森公式以数学家梅森(Mason)的名字命名,其一般形式如下:若离散随机变量X有n个可能的结果,对应的概率分别为p1, p2, ..., pn,则X的概率密度函数F(x)可以通过梅森公式计算:F(x) = Σ[pi * (1 - p1^(n-i))]二、梅森公式经典例题解析1.基本形式例题1:已知离散随机变量X有3个可能的结果,分别对应的概率为1/3,1/4,1/5。
求X的概率密度函数。
解:根据梅森公式,计算得到:F(x) = (1/3) * (1 - 1/3^2) + (1/4) * (1 - 1/4^2) + (1/5) * (1 - 1/5^2)2.乘积形式例题2:已知离散随机变量X有2个可能的结果,分别为A和B,对应的概率分别为1/2和1/3。
若事件A和事件B互斥,求X的概率密度函数。
解:根据梅森公式,计算得到:F(x) = (1/2) * (1 - 1/2^2) * (1 - 1/3^2)3.复合形式例题3:已知离散随机变量X有两个可能的结果A和B,对应的概率分别为1/2和1/3。
若随机变量Y = X + 1,求Y的概率密度函数。
解:根据梅森公式,计算得到:F(y) = (1/2) * (1 - 1/2^2) * (1 - 1/(y-1)^2)4.应用场景梅森公式在概率论和统计学中有广泛的应用,例如计算离散随机变量的累积分布函数、概率密度函数等。
此外,梅森公式还可以用于求解马尔可夫链、泊松分布等问题。
三、梅森公式在实际问题中的应用在实际问题中,梅森公式可以用于解决各种概率论和统计学问题。
梅森公式-信号流图

例4 已知系统信号流图, 解:三个回路
求传递函数 X4/X1及 X2/X1。
L
a
d eg bcg
c
有两个互不接触回路
L L
b
deg
f
则 1 d eg bcg deg
1. X 1 X 4 , p1 aef , p2 abcf 1 1 d , 2 1
x2
(g)
x2
x3
x5 L5 a23a35a52
a12 a23 a34 a45 (1 a44 )a12 a23 a35 P 1 (a23 a32 a23 a34 a42 a44 a23 a34 a52 a23 a35 a52 ) a23 a32 a44 a23 a35 a52 a44
2 1 a44
x3
a42 a12
a44 a34 x4 a35 a52 a45 x5
(a)
a23 x2 a32 x3
x1
(d)
x2
x3
互不接触
L1 a23a32
L12 a23a32a44 L2 a23a34a42
(e) (f)
x2
x4 x4 x5 L3 a44 互不接触 L22 a23a35a52a44 L4 a23a34a45a52
E(s)=
R(s)[ (1+G2H2) + (- G3G2H3) ] + (–G2H3) N(s)
1 - G1H1 + G2H2
+ G1G2H3 -G1H1G2 H2
信号流图
R(s) 1
e
g
a
f
b
自动控制原理第二章梅森公式-信号流图课件

ABCD
然后,通过分析梅森公式 的各项系数,确定系统的 极点和零点。
最后,将梅森公式的分析 结果转换为信号流图,进 一步明确系统各变量之间 的传递关系。
梅森公式在信号流图中的应用实例
假设一个控制系统的传递函数为 (G(s) = frac{s^2 + 2s + 5}{s^2 + 3s + 2})
在信号流图中,将极点和零点表示为相 应的节点,并根据梅森公式的各项系数 确定各节点之间的传递关系。
02
信号流图基础
信号流图定义与构成
信号流图定义
信号流图是一种用于描述线性动 态系统数学模型的图形表示方法 ,通过节点和支路表示系统中的 信号传递和转换过程。
信号流图构成
信号流图由节点和支路组成,节 点表示系统的动态方程,支路表 示输入输出之间的关系。
信号流图的绘制方法
确定系统动态方程
根据系统描述,列出系统的动态方程。
2
梅森公式与信号流图在描述和分析线性时不变系 统时具有互补性,二者可以相互转换。
3
信号流图能够直观地表示系统各变量之间的传递 关系,而梅森公式则提供了对系统频率特性的分 析手段。
如何使用梅森公式进行信号流图分析
首先,将系统的传递函数 转换为梅森公式的形式。
根据极点和零点的位置, 判断系统的稳定性、频率 响应特性等。
在未来研究中的可能发展方向
随着科技的不断进步和应用需求的不断变化,控制系统面临着越来越多的 挑战和机遇。
在未来研究中,可以利用梅森公式和信号流图进一步探索复杂系统的分析 和设计方法,提高系统的性能和稳定性。
同时,随着人工智能和大数据技术的应用,可以结合这些技术对控制系统 进行智能化分析和优化设计,提高系统的自适应和学习能力。
K1.24-梅森公式

1
i
pi i
1 Lj Lm Ln Lp Lq Lr 流图的特征行列式jm,np,q,r
Lj - 所有不同回路的增益之和; j
Lm Ln - 所有两两不接触回路的增益乘积之和;
m,n
Lp Lq Lr - 所有三三不接触回路的增益乘积之和;…
p,q,r
i 表示由源点到汇点的第i条前向通路的标号;
p1=2H1H2H3 p2=H1H4
1 H ( p11 p22 )
(4)求各前向通路的余因子:△1 =1 , △2 =1-GH3
3
Pi 是由源点到汇点的第i条前向通路增益;
△
i
称为第i条前向通路的剩余特征行列式。消去接触回路
2
梅森(Mason)公式
例: 求下列信号流图的系统函数。
H4
解: (1)首先找出所有回路:
L1=H3G
1 H1 H2 H3 2
1
L2=2H1H2H3H5
G
L3=H1H4H5
H5
(2)求特征行列式
△=1-(H3G+2H1H2H3H5+ H1H4H5)+ H3G H1H4H5 (3)然后找出所有的前向通路:
知识点K1.24
梅森(Mason)公式
梅森(Mason)公式
主要内容:
1.梅森公式及其各符号含义 2.梅森公式求解信号流图的系统函数步骤
基本要求:
1.掌握梅森公式 2.掌握由梅森公式求信号流图的系统函数
1
梅森(Mason)公式
K1.24 梅森公式
思考:意义?
系统函数H(s)记为H。梅森公式为: H
2-5 信号流图与梅森公式

G12 ( s ) R2 ( s )
G21 ( s )
C2 ( s ) G22 ( s )
G22 ( s )
+
+
C2 ( s )
5
2、根据线性代数方程组绘制。 设一组线性方程式如下:
x1 x1 x2 ax1 dx2 ex3 x3 x4 x5 bx2 cx3 x5
8
Σ Li:所有各回路的“回路传递函数”之和; Σ LiLj:两两互不接触的回路,其“回路传递 函数”乘积之和; Σ LiLjLk:所有三个互不接触的回路,其“回 路传递函数”乘积之和; n:前向通道数;
9
注意事项:
“回路传递函数”是指反馈回路的前 向通路和反馈回路的传递函数的乘积, 并且包含代表反馈极性的正、负号。
结论:开环传递函数等于前向通路传递函数G(s)和反馈 通路传递函数H(s)的乘积。
30
推广到一般情况:
b m s m b m 1s m 1 b1s b 0 G(s)H(s) a n s n a n 1s n 1 a 1s a 0
2 2 Π( τ i s 1) Π( τ di s 2ζ di τ d s 1) i 2 s ν Π(Ti s 1) Π(Tni s 2ζ ni Tni s 1) i 1 i 1 i 1 ρ i 1 σ u η
26
例3:画出信流图,并利用梅逊公式求取它 的传递函数C(s) / R(s)。
R (s)
+
A
_
1 R1
+
-
B
1 C1 s
C +
D _
1 R2
E
1 C2 s
梅森公式的理解

是包含于,你理解的有点偏差,举个例子如果有三个互不接触的回路,取两个不接触的回路应有三项,取三个互不接触回路就一项。
具体的应该是这样:
梅森公式G(s)=Σ(Ρκ*△κ)╱△G(s)= ——系统总传递函数;n——是前向通道数;Ρκ——第k条前向通路的传递函数,由输入端单向传递至输出端的信号通道称为前向通道;△——流图的特征式△=1-ΣLi+ΣLjLk-ΣLiLjLk+······
L A
bc为每两个不接触回路增益乘积之和
a为所有回路增益之和;L a L b
Li——所有单独回路的增益之和;
LjLk——所有互不接触的单独回路中,取其中两个不接触的回路增益乘积之和;LiLjLk——所有互不接触的单独回路中,取三个互不接触回路增益之和;
△κ——第k条前向通路特征式的余因子,即对于流图的特征式△,将与第k 条前向通路相接触的回路
增益代以零值,余下的即为△κ。
对于复杂的结构,理论上有很多项,但实际上△就取到前两三项。
信号与系统7_梅森公式的证明及应用

W=[wij],wij={ wij,i=j,wij是支路i的权,即支路传输 }
0,
i j
• 上述B,S,W三个矩阵完全描叙了信号流图。
梅森公式的推导
• 下面介绍一些定理和性质。
对于下列方程组: AX=Y ………………(1)
式中
A=
1
a a a a 21
...
12
1 ...
,Y=
y
回路传输乘积之和;
k 第k个前向通道的特征式的余子式;其值为 中除去与
第k个前向通道接触的回路后的剩余部分;
梅森公式的推导
梅森公式的推导(先 用一个一般性的图来证明)
如右图已知信号流图如图所 示,所对应的代数方程为
V1 mV1 lV3 bR
f
m
h
R1
Ⅰ
b
l
Ⅱ
V3
k
Ⅲ
Ⅳ
C
V1 d Ⅴ e V2 1
• 由定理6和7很容易推出梅森公式。
梅森公式
• 梅森公式不仅能求输入输出函数的比值的 (传输函数),对与流图中的任意一个节 点的信号与输入结点信号的比值也同样是 成立的。这个很好理解,因为输出节点并 没有什么特殊的地方,也仅仅是流图中的 一般点,只是我们赋予了它特殊的含义罢 了。下面就就举一例说明梅森公式对流图 中任一点与输入点的信号的比值的作用。
二、分别用梅森公式求取输出节点及该节点对输入节点的传递 函数,然后把它们的结果相比,即可得到输出对该混合节点的 传递函数。
mk e
于是传递函数为
(s) C(s) 2
bde f (1 m dl) bg
R(s) R 1 (m dl ke h gkl) mh dlh mke
梅森公式例子 PPT
-H1
-H2
-H3
第一条回路增益 L1= - G4 H1 第二条回路增益 L1= - G6 H2
第三条回路增益 L3= - G2 G3 G4 G5 G6 H3
第四条回路增益 L4= - G2 G3 G4 G9 G6 H3 第五条回路增益 L5= - G7 G4 G5 G6 H3
1 1 C(s)
G8
1 1 C(s)
G8
G7 G9
R(s) G1 G2 G3 G4
G5 G6
1
-H1
-H2
-H3
第一条前向通路增益 P1=G1 G2 G3 G4 G5 G6 第二条前向通路增益 P2=G1 G2 G8 第三条前向通路增益 P3=G1 G7 G4 G5 G6
1 1 C(s)
G8
G7 G9
R(s) G1 G2 G3 G4 G5
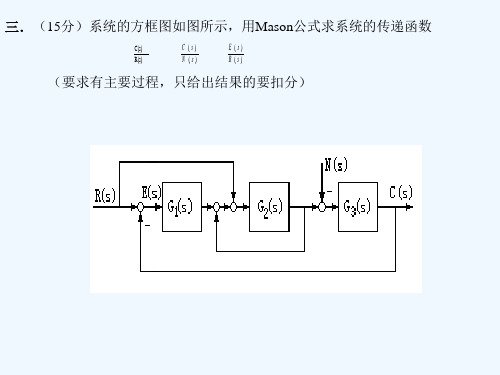
三.(15分)系统的方框图如图所示,用Mason公式求系统的传递函数
C(s)
C (s)
E (s)
R(s)
N (s)
R (s)
(要求有主要过程,只给出结果的要扣分)
R(s) G1
R(s) G1
G7 G2 G3
H3 G7 G2 G3 G4
G9
G4
G5
H1 G8
G8
G9
G5 G6
1
-H1
-H2
-H3
C(s) G6
1
-H1
-H2
-H3
第一条回路增益 L1= - G4 H1 第二条回路增益 L1= - G6 H2 第三条回路增益 L3= - G2 G3 G4 G5 G6 H3 第四条回路增益 L4= - G2 G3 G4 G9 G6 H3
(完整)系统的信号流图与梅森公式

6-5 系统的信号流图与梅森公式一、信号流图的定义由节点与有向支路构成的能表征系统功能与信号流动方向的图,称为系统的信号流图,简称信号流图或流图。
例如,图6—29(a)所示的系统框图,可用图6-29(b)来表示,图(b)即为图(a)的信号流图。
图(b)中的小圆圈“o”代表变量,有向支路代表一个子系统及信号传输(或流动)方向,支路上标注的H(s)代表支路(子系统)的传输函数.这样,根据图6—29(b),同样可写出系统各变量之间的关系,即图6—29二、三种运算器的信号流图表示三种运算器:加法器、数乘器、积分器的信号流图表示如表6-3中所列。
由该表中看出:在信号流图中,节点“o”除代表变量外,它还对流入节点的信号具有相加(求和)的作用,如表中第一行中的节点Y(s)即是。
三、模拟图与信号流图的相互转换规则模拟图与信号流图都可用来表示系统,它们两者之间可以相互转换,其规则是:(1) 在转换中,信号流动的方向(即支路方向)及正、负号不能改变。
(2) 模拟图(或框图)中先是“和点”后是“分点”的地方,在信号流图中应画成一个“混合”节点,如图6-30所示。
根据此两图写出的各变量之间的关系式是相同的,即。
(3) 模拟图(或框图)中先是“分点"后是“和点”的地方,在信号流图中应在“分点”与“和点”之间,增加一条传输函数为1的支路,如图6—31所示。
(4) 模拟图(或框图)中的两个“和点”之间,在信号流图中有时要增加一条传输函数为1的支路(若不增加,就会出现环路的接触,此时就必须增加),但有时则不需增加(若不增加,也不会出现环路的接触,此时即可以不增加。
见例6—17)。
(5) 在模拟图(或框图)中,若激励节点上有反馈信号与输入信号叠加时,在信号流图中,应在激励节点与此“和点"之间增加一条传输函数为1的支路(见例6—17).(6) 在模拟图(或框图)中,若响应节点上有反馈信号流出时,在信号流图中,可从响应节点上增加引出一条传输函数为1的支路(也可以不增加,见例6—17)。
第二章2-3系统方框图梅森公式及系统传递函数

? G (s)
综合点后移等效关系图
R(s)
Q(s)
C(s)
G(s)
R(s) G(s)
C(s)
Q(s)
G(s)
综合点前移
R(s)
G(s)
C(s)
Q(s)
R(s)
C(s)
G(s)
? Q(s)
综合点前移证明推导(移动前)
R(s)
C(s)
G(s)
Q(s)
C(s) R(s) G(s) Q(s)
3
-
-2
H1(s)
?
G3 ( s ) H3(s)
C(s)
G4 ( s )
例2 (解题方法一之步骤3)
R(s)
1
G1(s)
-
G2 ( s )
3
G2 ( s) H 2 ( s )
-
-2
G3 ( s )
H3(s)
H1(s)
C(s)
G4 ( s )
例2 (解题方法一之步骤4)
• 内反馈环节等效变换
1
R(s)
• 内反馈环节等效变换结果
R(s) 1
-
G1 ( s )G2 ( s )
G3 ( s )G4 ( s )
C(s)
1 G2(s)G3(s)H2(s) G3(s)G4(s)H3(s)
两个或两个以上的方框,具有同一个输入信号,并 以各方框输出信号的代数和作为输出信号,这种形
式的连接称为并联连接。
3. 反馈连接
R(s)
-
C(s) G(s)
H(s)
一个方框的输出信号输入到另一个方框后,得 到的输出再返回到这个方框的输入端,构成输 入信号的一部分。这种连接形式称为反馈连接。
matlab梅森公式

matlab梅森公式梅森公式,也称为梅森素数公式(Mersenne prime),是描述素数形式的一个公式,由法国数学家梅森(Marin Mersenne)在17世纪提出。
梅森公式可以按照以下形式表示:M = 2^p -1其中,M为梅森素数,p为素数。
梅森公式是一种简洁而有效的表达方式,可以很方便地生成梅森素数。
梅森素数是指满足梅森公式的素数。
例如,当p取2、3、5、7、13等值时,可以得到对应的梅森素数:3、7、31、127、8191等。
梅森素数在数论和计算机科学中有着重要的应用。
其中最为著名的应用之一就是在密码学领域。
RSA公钥加密算法中的素数选择和密钥生成就依赖于梅森素数。
此外,梅森素数还被广泛应用于快速傅里叶变换(FFT)和伪随机数生成等领域。
在数字计算中,梅森素数也用于帮助加快素数的测试和计算。
梅森素数的研究一直是数学家们的热点之一。
目前已知的梅森素数很少,大部分梅森素数都是通过计算机程序来生成的。
由于梅森公式的形式简单,计算机可以更快速地验证一个数是否是梅森素数。
但是这并不意味着每个满足梅森公式的数都是素数,只是方便验证。
在数学研究中,确定梅森素数的性质一直是一个重要的课题。
目前已知的梅森素数都是奇数,但是否所有的满足梅森公式的奇数都是素数,仍然是一个未解的问题。
数学家们一直在努力寻找更多的梅森素数,并且为梅森素数的性质和规律提供了许多重要的定理和猜想。
在实际计算中,由于梅森素数的位数非常大,大于几百甚至上千位,因此对梅森素数的计算和验证需要使用高效的算法和计算工具。
MATLAB是一种功能强大的数值计算和编程软件,可以用于计算和验证梅森素数。
MATLAB提供了丰富的数值计算库和函数,可以方便地进行大整数运算和素性测试,帮助研究人员寻找和验证梅森素数。
总之,梅森公式是描述素数形式的一种简洁有效的公式,可以方便地生成梅森素数。
梅森素数在密码学、计算机科学和数学研究中有着重要的应用。
通过使用MATLAB等计算工具,数学家们可以更方便地计算和验证梅森素数,推动梅森素数的研究和应用。
梅森公式——精选推荐

、 梅森公式(Mason ’s Formula)从系统的信号流图直接求系统函数()()()s F s Y s H =的计算公式,称为梅森公式。
该公式如下:()()()∑∆∆==k kk P 1s F s Y s H (6-34)此公式的证明甚繁,此处略去。
现从应用角度对此公式予以说明。
式中+-+-=∆∑∑∑r,q .p r q p n,m n m iI L L L L L L 1 (6-35)Δ称为信号流图的特征行列式。
式中:i L 为第i 个环路的传输函数, i i L 为所有环路传输函数之和;n m L L 为两个互不接触环路传输函数的乘积,n m L mL 为所有两个互不接触环路传输函数乘积之和;r q p L L L 为三个互不接触环路传输函数的乘积, ∑rq,p,rq p L L L 为所有三个互不接触环路传输函数乘积之和;k P 为由激励节点至所求响应节点的第k 条前向开通路所有支路传输函数的乘积;k ∆为除去第k 条前向通路中所包含的支路和节点后所剩子流图的特征行列式。
求k ∆的公式仍然是式(6-35)。
例6-19 图6-34(a)所示系统。
求系统函数()()()s F s Y s H =。
解:1 求Δ(1) 求∑iiL:该图共有5个环路,其传输函数分别为2L 1=,8,42L 2=⨯=()-11-1L 3=⨯= 2L 4=,()421-2L 5=⨯⨯-=故 ∑iiL15L L L L L 54321=++++=)s ()a ()b图6-34(2) 求 ∑nm,nmL L:该图中两两互不接触的环路共有3组:()1628L L 422L L 212L L 424131=⨯==⨯=-=-⨯=故 18L L L L L L L L424131nm,n m=++=∑该图中没有3个和3个以上互不接触的环路,故有 0LL L rrq,p,qp=∑;…。
故得418151L L L L L L -1r rq,p,q p n,m n m ii =+-=+-+=∆∑∑∑2 求∑∆kkk P(1) 求k P :该图共有3个前向通路,其传输函数分别为1111P 1=⨯⨯=()-41141-1P 2=⨯⨯⨯⨯= ()()2121-1P 3=⨯-⨯⨯=(2) 求k ∆:除去1P 前向通路中所包含的支路和节点后,所剩子图如图6-34(b)所示。
2.4 梅森公式

1 1
2 1 G2 H1
3 1 G4 H 2
由梅森公式求出传递函数:
C (s) 1 G( s) (P 11 P 22 P 3 3 ) R( s )
G1G2G3G4G5 G4G5G6 (1 G2 H1 ) G1G2G7 (1 G4 H 2 ) 1 G2 H1 G4 H 2 G1G2G3G4G5 H 3 G6G4G5 H 3 G1G2G7 H 3 G2G4 H1H 2 G2G4G5G6 H1H 3 G1G2G4G7 H 2 H 3
[ 例 2.21] 用梅逊增益公式求图所示的传递函数。
解 : 前向通道 P1=G1G2G3G4G5
回路,
三个 回路均与前向通道 接触,△1=1
L1=G2G3H1 L2=-G3G4H2 L3=-G1G2G3G4H3
C ( s) 1 G(s) P 11 R( s ) G1G2G3G4G5 1 G2G3 H1 G2G3 H 2 G1G2G3G4 H 3
G2(s)
C (s)
C(s) D (s) D(s)
G2 ( s) D( s ) 1 G1 ( s )G2 ( s ) H ( s )
3.给定输入和扰动输入同时作用下系统的总输出
C(s) (s) R(s) D (s) D(s)
G1 ( s)G2 ( s) G2 ( s) R( s ) D( s ) 1 G1 ( s)G2 ( s) H ( s) 1 G1 (s)G2 (s) H (s)
1
G2 ( s)
反馈通道: G2 (s)G3 (s)G1 ( s)
Y ( s) 1 D1 ( s ) D1 ( s) 1 G1G2G3
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
1
C(s) 1
G8
G7 G9
R(s) G1 G2 G3 G4
G5 G6
1
-H1
-H2
-H3
第一条回路增益 L1= - G4 H1 第二条回路增益 L1= - G6 H2 第三条回路增益 L3= - G2 G3 G4 G5 G6 H3 第四条回路增益 L4= - G2 G3 G4 G9 G6 H3 第五条回路增益 L5= - G7 G4 G5 G6 H3 第六条回路增益 L6= - GG7 G9
R(s) G1 G2 G3 G4
G5 G6
1
-H1
-H2
-H3
第一条回路增益 L1= - G4 H1 第二条回路增益 L1= - G6 H2
第三条回路增益 L3= - G2 G3 G4 G5 G6 H3
1
C(s) 1
G8
G7 G9
R(s) G1 G2 G3 G4
G5 G6
1
-H1
-H2
-H3
第一条回路增益 L1= - G4 H1 第二条回路增益 L1= - G6 H2 第三条回路增益 L3= - G2 G3 G4 G5 G6 H3 第四条回路增益 L4= - G2 G3 G4 G9 G6 H3
1
C(s) 1
G8
G7 G9
R(s) G1 G2 G3 G4
G5 G6
1
R(s) G1 G2 G3 G4 G5
G6
1
-H1
-H2
-H3
第一条前向通路增益 P1=G1 G2 G3 G4 G5 G6
第二条前向通路增益 P2=G1 G2 G8
第三条前向通路增益 P3=G1 G7 G4 G5 G6 第四条前向通路增益 P4=G1 G2 G3 G4 G9 G6
1
C(s) 1
G8
第七条回路增益 L7= - G2 G8 H3
1
C(s) 1
G8
G7 G9
R(s) G1 G2 G3 G4
G5 G6
1
1
C(s) 1
-H1
-H2
-H3
两两互不接触(没有公共的节点)回路增益乘积
L1 L2= G4 G6 H1 H2
G8
G7 G9
R(s) G1 G2 G3 G4
G5 G6
1
1
C(s) 1
G7 G9
R(s) G1 G2 G3 G4
G5 G6
1
-H1
-H2
-H3
第一条回路增益 L1= - G4 H1 第二条回路增益 L1= - G6 H2
第三条回路增益 L3= - G2 G3 G4 G5 G6 H3
第四条回路增益 L4= - G2 G3 G4 G9 G6 H3 第五条回路增益 L5= - G7 G4 G5 G6 H3 第六条回路增益 L6= - G7 G4 G9 G6 H3
G7 G9
R(s) G1 G2 G3 G4
G5 G6
1
1 1 C(s)
-H1
-H2
-H3
第一条前向通路增益 P1=G1 G2 G3 G4 G5 G6
第二条前向通路增益 P2=G1 G2 G8
还有没有前向通路啦?
第三条前向通路增益 P3=G1 G7 G4 G5 G6
第四条前向通路增益 P4=G1 G2 G3 G4 G9 G6 第五条前向通路增益 P5=G1 G7 G4 G9 G6
-H1
-H2
-H3
两两互不接触(没有公共的节点)回路增益乘积
L1 L2= G4 G6 H1 H2
L1 L7= G2 G4 G8 H1 H3
G8
G7 G9
R(s) G1 G2 G3 G4
G5 G6
1
1
C(s) 1
-H1
-H2
-H3
两两互不接触(没有公共的节点)回路增益乘积
L1 L2= G4 G6 H1 H2
G8
G7 G9
R(s) G1 G2 G3 G4
G5 G6
1
1
C(s) 1
-H1 -H3
第一条回路增益 L1= - G4 H1
-H2 注意:要考虑负号!
G8
G7 G9
R(s) G1 G2 G3 G4
G5 G6
1
-H1
-H2
-H3
第一条回路增益 L1= - G4 H1 第二条回路增益 L1= - G6 H2
L1 L7= G2 G4 G8 H1 H3 L2 L7= G2 G6 G8 H2 H3
G8
G7 G9
R(s) G1 G2 G3 G4
G5 G6
1
1
C(s) 1
-H1
-H2
-H3
三三互不接触回路增益乘积
L1 L2 L7= - G2 G4 G6 G8H1 H2 H3 =1-(L1+ L2 + L3+ L4 + L5+ L6 + L7)+ L1 L2+ L1 L7+ L2 L7- L1 L2 L7 =1+ G4 H1 + G6 H2 + G2 G3 G4 G5 G6 H3 + G2 G3 G4 G9 G6 H3
1 1 C(s)
-H1
-H2
-H3
第一条回路增益 L1= - G4 H1 第二条回路增益 L1= - G6 H2
第三条回路增益 L3= - G2 G3 G4 G5 G6 H3
第四条回路增益 L4= - G2 G3 G4 G9 G6 H3 第五条回路增益 L5= - G7 G4 G5 G6 H3
G8
第二条前向通路增益 P1=G1 G2 G8
G8
G7 G9
R(s) G1 G2 G3 G4
G5 G6
1
1 1 C(s)
-H1
-H2
-H3
第一条前向通路增益 P1=G1 G2 G3 G4 G5 G6
第二条前向通路增益 P2=G1 G2 G8
第三条前向通路增益 P3=G1 G7 G4 G5 G6
G8
G7 G9
+ G7 G4 G5 G6 H3 + G7 G4 G9 G6 H3 +G2 G8 H3 + G4 G6 H1 H2 + G2 G4 G8 H1 H3 + G2 G6 G8 H2 H3 + G2 G4 G6 G8H1 H2 H3
G8
G7 G9
R(s) G1 G2 G3 G4
G5 G6
1
-H1
-H2
-H3
梅森公式例子
G8
G7 G9
R(s) G1 G2 G3 G4
G5 G6
1
1
1C(s)
-H1
-H2
-H3
第一条前向通路增益 P1=G1 G2 G3 G4 G5 G6
G8
G7 G9
R(s) G1 G2 G3 G4
G5 G6
1
1 1 C(s)
-H1
-H2
-H3
第一条前向通路增益 P1=G1 G2 G3 G4 G5 G6
1
C(s) 1
G8
G7 G9
R(s) G1 G2 G3 G4
G5 G6
1
-H1
-H2
-H3
第一条前向通路增益 P1=G1 G2 G3 G4 G5 G6
第一条前向通路与各个回路都接触,
特征式的余因子 1=1
1
C(s) 1
G8
G7 G9
R(s) G1 G2 G3 G4
