射影几何入门
射影定理概念

射影定理的概念在数学中有两种不同的表述,分别对应于初等几何和代数几何两个不同领域。
1. 初等几何中的射影定理:
在平面几何中,尤其是直角三角形的背景下,射影定理(也称为欧几里得定理)表述为:在直角三角形ABC中,如果C是直角,则直角边AB上的高CD满足以下关系:
- CD² = AD × BD
- 同时,每一条直角边与其在斜边上的射影之间的乘积等于斜边的平方,即:
- AC × BC = AB²
换句话说,直角三角形斜边上的高是两直角边在斜边投影的比例中项,并且任意一直角边与它在斜边上的投影和斜边本身的长度之间也满足比例中项的关系。
2. 代数几何中的射影定理:
在更抽象的代数几何框架下,射影定理通常涉及射影空间和射影变换。
射影几何研究的是几何图形在无穷远点集合加入后的性质,以及这些图形经过投影变换后保持不变的特性。
例如,在代数几何中讨论射影
簇或射影变种时,射影定理可能指代将一个环上的代数集分解为其理想部分和闭点集的过程,这种分解有助于将复杂的代数问题转化为更容易处理的几何问题。
总结来说,射影定理在不同的数学分支中具有不同的意义,但都体现了射影思想的核心——通过投影操作来揭示几何对象间的深刻内在联系。
射影几何初步.doc
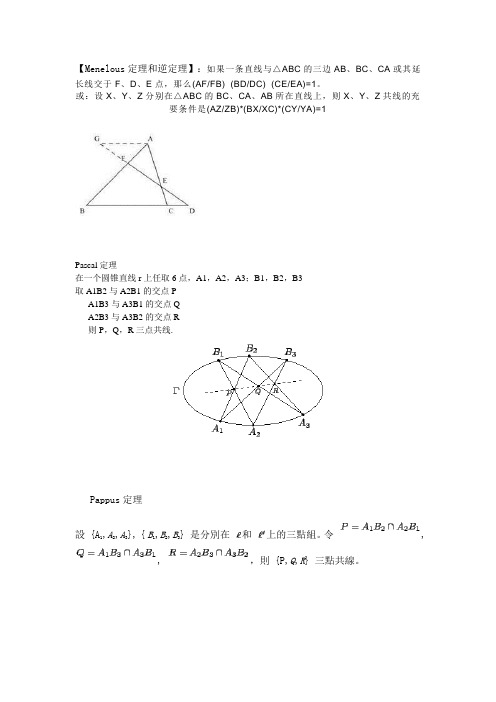
【Menelous定理和逆定理】:如果一条直线与△ABC的三边AB、BC、CA或其延长线交于F、D、E点,那么(AF/FB)×(BD/DC)×(CE/EA)=1。
或:设X、Y、Z分别在△ABC的BC、CA、AB所在直线上,则X、Y、Z共线的充要条件是(AZ/ZB)*(BX/XC)*(CY/YA)=1Pascal定理在一个圆锥直线r上任取6点,A1,A2,A3;B1,B2,B3取A1B2与A2B1的交点PA1B3与A3B1的交点QA2B3与A3B2的交点R则P,Q,R三点共线.Pappus定理,A2,A3}, { B1,B2,B3} 是分別在和上的三點組。
令,設 {A, ,則 {P,Q,R} 三點共線。
帕斯卡六边形定理:内接于二次曲线的六边形的三双对边的交点共线。
Ceva定理:在△ABC内任取一点O,直线AO、BO、CO分别交对边于D、E、F,则(BD/DC)*(CE/EA)*(AF/FB)=1 在△ABC内任取一点O,西姆松定理:过三角形外接圆上异于三角形顶点的任意一点作三边的垂线,则三垂足共线。
(此线常称为西姆松线)西姆松定理的逆定理若一点在三角形三边所在直线上的射影共线,则该点在此三角形的外接圆上。
托勒密定理:圆内接凸四边形两对对边乘积的和等于两条对角线的乘积Desargues(德沙格)定理:如果两个三角形的对应顶点的连线相交于一点, 则对应边的交点必定是共线的Desargues逆定理如果两个三角形的对应边的交点是共线的, 则对应顶点的连线必相交于同一点布立安香定理(Brianchon) 非退化的二次曲线的外切六点形的三对对顶点的连线必交于同一点。
布立安香逆定理如果一个六点形的三对对顶点的连线交于一点, 则这个六点形必为某一条二次曲线的外切六点形。
射影几何学

射影几何学射影几何是研究图形的射影性质,即它们经过射影变换后,依然保持不变的图形性质的几何学分支学科。
一度也叫做投影几何学,在经典几何学中,射影几何处于一种特殊的地位,通过它可以把其他一些几何学联系起来。
发展简况十七世纪,当笛卡儿和费尔马创立的解析几何问世的时候,还有一门几何学同时出现在人们的面前。
这门几何学和画图有很密切的关系,它的某些概念早在古希腊时期就曾经引起一些学者的注意,欧洲文艺复兴时期透视学的兴起,给这门几何学的产生和成长准备了充分的条件。
这门几何学就是射影几何学。
基于绘图学和建筑学的需要,古希腊几何学家就开始研究透视法,也就是投影和截影。
早在公元前200年左右,阿波罗尼奥斯就曾把二次曲线作为正圆锥面的截线来研究。
在4世纪帕普斯的著作中,出现了帕普斯定理。
在文艺复兴时期,人们在绘画和建筑艺术方面非常注意和大力研究如何在平面上表现实物的图形。
那时候,人们发现,一个画家要把一个事物画在一块画布上就好比是用自己的眼睛当作投影中心,把实物的影子影射到画布上去,然后再描绘出来。
在这个过程中,被描绘下来的像中的各个元素的相对大小和位置关系,有的变化了,有的却保持不变。
这样就促使了数学家对图形在中心投影下的性质进行研究,因而就逐渐产生了许多过去没有的新的概念和理论,形成了射影几何这门学科。
射影几何真正成为独立的学科、成为几何学的一个重要分支,主要是在十七世纪。
在17世纪初期,开普勒最早引进了无穷远点概念。
稍后,为这门学科建立而做出了重要贡献的是两位法国数学家——笛沙格和帕斯卡。
笛沙格是一个自学成才的数学家,他年轻的时候当过陆军军官,后来钻研工程技术,成了一名工程师和建筑师,他很不赞成为理论而搞理论,决心用新的方法来证明圆锥曲线的定理。
1639年,他出版了主要著作《试论圆锥曲线和平面的相交所得结果的初稿》,书中他引入了许多几何学的新概念。
他的朋友笛卡尔、帕斯卡、费尔马都很推崇他的著作,费尔马甚至认为他是圆锥曲线理论的真正奠基人。
射影几何学

在射影几何学中,把无穷远点看作是“理想点”。
通常的直线再加上一个无穷点就是无穷远直线,如果一个平面内两条直线平行,那么这两条直线就交于这两条直线共有的无穷远点。
通过同一无穷远点的所有直线平行。
德国数学家克莱因(图)在爱尔朗根大学提出著名的《爱尔朗根计划书》中提出用变换群对几何学进行分类在引入无穷远点和无穷远直线后,原来普通点和普通直线的结合关系依然成立,而过去只有两条直线不平行的时候才能求交点的限制就消失了。
由于经过同一个无穷远点的直线都平行,因此中心射影和平行射影两者就可以统一了。
平行射影可以看作是经过无穷远点的中心投影了。
这样凡是利用中心投影或者平行投影把一个图形映成另一个图形的映射,就都可以叫做射影变换了。
射影变换有两个重要的性质:首先,射影变换使点列变点列,直线变直线,线束变线束,点和直线的结合性是射影变换的不变性;其次,射影变换下,交比不变。
交比是射影几何中重要的概念,用它可以说明两个平面点之间的射影对应。
在射影几何里,把点和直线叫做对偶元素,把“过一点作一直线”和“在一直线上取一点”叫做对偶运算。
在两个图形中,它们如果都是由点和直线组成,把其中一图形里的各元素改为它的对偶元素,各运算改为它的对偶运算,结果就得到另一个图形。
这两个图形叫做对偶图形。
在一个命题中叙述的内容只是关于点、直线和平面的位置,可把各元素改为它的对偶元素,各运算改为它的对偶运算的时候,结果就得到另一个命题。
这两个命题叫做对偶命题。
这就是射影几何学所特有的对偶原则。
在射影平面上,如果一个命题成立,那么它的对偶命题也成立,这叫做平面对偶原则。
同样,在射影空间里,如果一个命题成立,那么它的对偶命题也成立,叫做空间对偶原则。
研究在射影变换下二次曲线的不变性质,也是射影几何学的一项重要内容。
如果就几何学内容的多少来说,射影几何学;仿射几何学;欧氏几何学,这就是说欧氏几何学的内容最丰富,而射影几何学的内容最贫乏。
比如在欧氏几何学里可以讨论仿射几何学的对象(如简比、平行性等)和射影几何学的对象(如四点的交比等),反过来,在射影几何学里不能讨论图形的仿射性质,而在仿射几何学里也不能讨论图形的度量性质。
数学射影定理公式

数学射影定理公式数学射影定理是解析几何中的基本定理之一,它描述了一个点在一个几何体上的射影位置。
射影是一种将一个高维空间中的对象映射到一个低维空间中的技术,它在计算机图形学、计算机视觉和几何学中有广泛的应用。
射影定理的公式可以简单表示为:P' = P / Pz,其中P'表示点的射影位置,P表示点的三维坐标,Pz表示点在Z轴上的坐标。
这个公式可以用来计算点在三维空间中的射影位置,即将点投影到二维平面上。
在几何学中,射影定理主要用于计算点在投影平面上的坐标。
例如,我们可以使用射影定理来计算三维物体在投影平面上的阴影位置,从而实现逼真的渲染效果。
此外,在计算机视觉中,射影定理也可以用于计算相机在三维空间中的位置和姿态。
射影定理还有一些重要的性质。
首先,如果一个点在投影平面上的射影位置为P',那么该点的任意倍数在投影平面上的射影位置也为P'。
其次,如果两个点在三维空间中的连线与投影平面平行,那么它们在投影平面上的连线也与投影平面平行。
射影定理的应用不仅限于几何学和计算机图形学领域,它还可以用于计算机视觉中的物体识别和姿态估计。
例如,当我们在图像中检测到一个物体时,我们可以使用射影定理来计算该物体在三维空间中的位置和姿态,进而实现对物体的准确定位和识别。
射影定理的公式简洁明了,但在应用中需要注意一些细节。
首先,由于射影定理涉及到除法运算,因此需要确保点的Z坐标不为零,否则会导致除零错误。
其次,射影定理只能用于计算点在投影平面上的射影位置,而不能用于计算点在其他平面上的射影位置。
数学射影定理公式是解析几何中的重要工具,它可以用于计算点在三维空间中的射影位置。
射影定理在计算机图形学、计算机视觉和几何学等领域有着广泛的应用,对于实现逼真的渲染效果和准确定位物体位置具有重要意义。
在应用射影定理时,需要注意除零错误和射影平面的选择,以确保计算结果的准确性和可靠性。
通过深入理解和灵活应用射影定理,我们可以在相关领域取得更好的研究和应用成果。
二维射影几何基本定理

二维射影几何基本定理
射影定理,又称“欧几里德定理”,定理内容是直角三角形中,斜边上的高是两直角边在斜边上射影的比例中项,每一条直角边是这条直角边在斜边上的射影和斜边的比例中项。
所谓射影,就是正投影。
直角三角形射影定理(又叫欧几里德定理):直角三角形中,斜边上的高的平方是两直角边在斜边上射影的比例中项。
每一条直角边是这条直角边在斜边上的射影和斜边的比例中项。
面积射影定理:“平面图形射影面积等于被射影图形的面积S乘以该图形所在平面与射影面所夹角的余弦。
”。
射影与射影变换的性质与应用

射影与射影变换的性质与应用射影几何是几何学的一个分支,主要研究高维空间中的射影与射影变换的性质与应用。
射影几何的研究对于空间形态的描述和数学建模具有重要的意义。
本文将介绍射影与射影变换的基本概念、性质以及在几何学和计算机图形学中的应用。
一、射影的基本概念射影是指从一个几何对象映射到另一个几何对象的操作。
在射影几何中,我们使用齐次坐标来描述几何对象。
齐次坐标是指用n+1个数表示n维空间中的点,通过对这些数进行比例变换可以得到等价的点。
例如,在二维平面中,一个点的齐次坐标可以表示为(x, y, 1),其中x和y是点在平面上的坐标。
二、射影变换的性质射影变换是指通过矩阵乘法对几何对象进行映射的操作。
射影变换具有以下性质:1. 保直线性:射影变换将直线映射为直线,保持直线上的所有点的次序关系。
2. 保比例性:射影变换将平行线段映射为平行线段,并且保持线段之间的比例关系。
3. 保交比性:射影变换可以保持射影空间中的交比关系,即一组点的交比在变换后保持不变。
4. 保角度性:射影变换可以保持两条直线之间的夹角不变。
5. 组合性:射影变换可以通过矩阵乘法的组合实现。
三、射影与射影变换在几何学中的应用1. 透视投影:透视投影是一种射影变换,将三维场景投影到二维平面上。
透视投影在计算机图形学中广泛应用于生成逼真的虚拟场景。
2. 图像处理:射影变换可以用于图像的旋转、缩放和扭曲等操作,以及图像的透视校正和纠正。
3. 几何建模:射影变换可以用于对三维几何模型进行旋转、平移和缩放等操作,以及模型的投影和透视变换。
四、射影与射影变换在计算机图形学中的应用1. 三维渲染:射影变换在三维渲染中用于将三维物体的坐标映射到二维屏幕上,实现真实感的显示。
2. 图形变换:射影变换在图形变换中用于对图形图像进行旋转、平移、缩放和扭曲等操作。
3. 图像合成:射影变换可以用于对多个图像进行叠加和融合,生成新的合成图像。
五、射影与射影变换的应用案例1. 虚拟现实:射影变换在虚拟现实中用于实现真实感的三维场景投影和交互。
交比(射影几何)

(
p1
p2 ,
p3
p4
)
(k1 (k2
k3 )(k2 k3 )(k1
k4 ) k4 )
.
交比 (2) 三角函数表示
设直线pi与x轴正向的夹角为i (i=1,2,3,4). 将ki=tani代入
上式, 利用三角恒等式化简可得
定理9 对于通常线束中以ki为斜率的四直线pi (i=1,2,3,4), 有
定理5 设线束S(p)中四直线pi的齐次坐标为a+ib (i=1,2,3,4).
则
(
p1
p2 (2
3 )(2 3 )(1
4 ) 4 )
.
(6)
注 上述定义、定理与点列的交比有相同的代数结构. 因此有 相同的组合性质, 并可类似定义调和直线组.
交比
a+1b=a', a+2b=b'.
从中解出a, b, 得
a a '2 b '1 , 2 1
b ' a '
b
.
2 1
于是, P1, P2, P3, P4的坐标可表示为 a ', b ', 2 3 a ' 3 1 b ', 2 4 a ' 4 1 b ' 2 1 2 1 2 1 2 1
(AG,OB) (AO, HB). 由交比的初等几何表示(2.4)式,有
AO GB AH OB GO AB OH AB
所以 GO OB AO OH
交比
推论4 设 P0 , P1, P* 为点列l(P)中取定的相异三点, Pl(P). 则
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
(一)1-1对应 11. 1-1对应的定义 12. 1-1对应的意义和性质 23. 1-1对应在数学中的应用 44. 无穷集之间的1-1对应 45. 部分和整体的1-1对应,无穷集的定义96.无穷远点. 点列和线束 10 7. 轴束. 基本形 118. 三种基本形的六种透视对应129. 射影关系1410. 1到无穷或无穷到1的对应1611. 平面点的无穷阶数 17 12. 一阶与二阶无穷集 1713. 通过空间一点的所有直线1714. 通过空间一点的所有平面 1815. 平面上所有的直线1816. 平面系和点系 1917. 空间中的所有平面1918. 空间中的所有点 2019. 空间系 2020. 空间中的所有直线2021. 点与数之间的对应2022. 无穷远元素 22(二)1-1对应基本形之间的关系2523. 七种基本形 2524.射影性 2525. Desargues 定理 2626. 关于二个完全四边形的基本定理 2727.定理的重要性2828. 定理的重述2829. 四调和点概念 2930. 调和共轭的对称性3031.概念的重要性3032. 四调和点的投影不变性 3133. 四调和线 3134. 四调和平面. 3135.结果的概要性总结 3236. 可射影性的定义 3337. 调和共轭点相互之间的对应3338. 调和共轭的元素的隔离 3439. 无穷远点的调和共轭34 40. 射影定理和度量定理, 线性作图法 3541. 平行线与中点3642. 将线段分成相等的n个部分 3743.数值上的关系3744.与四调和点关联的代数公式3745. 进一步的公式3846.非调和比(交比) 39(三)射影相关基本形的结合4147. 叠加的基本形,自对应元素4148. 无自对应点的情况4249. 射影对应的基本定理, 连续性假设 4350.定理应用于线束和平面束4451. 具有一公共自对应点的射影点列4452. 无公共自对应点的射影相关点列4553. 透视对应的两个射线束 4754. 透视对应的面束(轴束) 47 55. 二阶点列4756. 轨迹的退化 4857. 两阶线束4858.退化情况 4859. 二阶圆锥面 49(四) 二阶点列 4960. 二阶点列与二阶线束 4962. 切线 5063.轨迹生成问题的陈述 50 64.基本问题的解决 5165. 图形的不同构作法 5266. 将轨迹上四点连到第五点的直线 5267. 定理的另一种陈述形式 5368.更为重要的定理 5469. Pascal定理5470. Pascal定理中点的名称的替换5471. 在一个二阶点列上的调和点5672. 轨迹的确定5673.作为二阶点列的圆和圆锥线5674. 通过五点的圆锥曲线5775.圆锥线的切线 5876.内接四边形 5977. 内接的三角形6078. 退化圆锥线 61(五)二阶线束 6379. 已定义的二阶射线束63 80. 圆的切线6381. 圆锥曲线的切线6582. 系统的生成点列线 6583. 线束的确定6584. Brianchon定理6785. Brianchon定理中线的替换6886. 用Brianchon定理构造线束6887. 与一圆锥曲线相切的点 6888. 外切四边形 6989. 外切三边形 7090. Brianchon定理的应用 7091. 调和切线 7192.可射影性和可透视性7193. 退化情况7294.对偶律72(六)极点和极线 7595. 关于圆的极点和极线 7596. 圆锥曲线的内点的共轭点的轨迹7797. 更多的性质7898. 极点极线的定义 7899. 极点与极线的基本定理 78 100. 共轭点与共轭直线 79102. 自配极三角形 79103.射影相关的极点与极线 80 104. 对偶性 81105. 自对偶定理 81106. 其他对应关系 82(七) 圆锥曲线的度量性质83107. 直径与中心83108. 相关的几个定理 83109. 共轭直径 84110. 圆锥曲线的分类 84111. 渐近线 84112.有关的几个定理 85113. 关于渐近线的定理 85115. 由双曲线及其渐近线切割的弦86116.定理的应用86117.由二条渐近线和一条切线形成的三角形87118. 用渐近线来表示一个双曲线的方程 88119. 抛物线方程 88120. 参引共轭直径的有心圆锥线的方程 91(八)对合(Involution) 9512 1. 基本定理 95122. 线性作图法96123.直线上点的对合的定义97124. 对合中的二重点 97125.有关通过四点的圆锥曲线的Desargues定理99126. 退化圆锥线 100127. 通过四点并与一已知直线相切的圆锥线 100128. 二重对应100129.Steiner的作图方法101130. Steiner作图法在重对应中的应用 102131. 二阶点列中点的对合103132.射线的对合 104133.二重射线 105134. 通过一固定点与四线相切的圆锥线105135.双重对应105136.处于对合下的二阶射线束106137. 有关对合二阶射线束的定理106138. 由一圆锥曲线确定的射线的对合 106139.定理的陈述106140. 定理的对偶 107(九) 对合的度量性质109141. 无穷远点的引入; 对合的中心 109142. 基本度量定理109143. 二重点的存在110144. 二重射线的存在 112 145.通过圆来构筑对合112 146.圆点113147. 对合中的正交射线对, 圆对合114148. 圆锥线的轴 114149. 由一圆锥线确定的对合的点是圆点115150.圆点的性质 115151. 圆点的位置116152.寻找圆锥曲线的焦点 117153. 圆和抛物线117154. 圆锥线焦点性质118 155. 抛物线的情况 119 156.抛物面反射镜119157. 准线.主轴.顶点 119 158. 圆锥线的另一种定义120159. 离心率 120160. 焦距之和与差 121(十) 综合射影几何的历史123161. 早期成果 123162. 统一性原理124163.Desargues 124 164. 极点与极线 125165. 通过4点的二阶曲线的Des argues 定理125166. 推广到空间的极点与极线理论126167. 描述圆锥曲线的Desargues方法126168. Desargues工作的被接纳127169. Desargues时代的保守性127170. Desargues的写作风格 128171.Desargues工作缺乏欣赏129172. Pascal与他的定理129173. Pascal的短评130174. Pascal的独创性 130 175. De LaHire和他的工作131176.Descartes和他的影响132177. Newton和Maclaurin133178. Maclaurin的证法 133179.画法几何与综合几何的二次复兴134180. 对偶性, 同调性, 连续性, 偶然性联系 135181. Poncelet和Cauchy135182. Poncelet的工作 136 183. 解析几何妥欠综合几何的债137184. Steiner和他的工作137185. Von Staudt和他的工作138186. 近期的发展 139附录140参考文献148索引151第1章 1-1对应1.1-1 对应的定义【定义】任意给定两个集合,如果在它们之间能够建立一种对应,使得任意一个集合中的每一个元素,都对应到另一集合中的一个且仅一个元素,那么,这两个集合就称为能够建立1-1对应的集合,简称两个集合为1-1对应(One-to -One Correspondence)。
这里,1-1对应是定义两个集合之间的一种关系 ,而不是它们元素之间的关系,但要确定两个集合是否有这种关系,需要考察它们的元素之间是否能够建立一个具体的1-1对应。
【例】试问由三个数字组成的集合{1,2,3},和由三个字母组成的集合{A,B,C}之间是否1-1对应?【答】我们在这两个集合的元素之间建立下面这样的对应: 1 <-> A , 2 <-> B , 3 <-> C这里符号<->表示其左右两边元素为对应。
这样,两个集合中的每一个元素,都对应到了另一集合中的一个且仅一个元素。
所以集合{1,2,3}与集合{A,B,C}为 1-1 对应。
显然,包含两个数字的集合{1,2}或包含四个数字的集合{1,2,3,4}就不能与包含三个字母的集合{A,B,C}建立1-1 对应。
集合1-1对应的概念非常简单,但也非常重要,它在科研、生产或在日常生活中都频繁使用。
例如,我们通常进行的计数过程就是将被计数对象与数字'1'、'2'、'3'…之间在心中建立1-1对应;在人类尚未进入文明时代、尚未发明数字之前,也已利用他们的手指与被计数对象(如每天的掠物)建立1-1对应。
科学家们的神圣工作是对自然界各种事物进行命名与分类,本质上就是将这些事物及其属性与适当的word(单字)建立1-1对应。
这种过程虽然不像计数那样简单,需要反复,需要修正和深化,不可能一次完成,但在本质上,每一步无非就是对事物及其属性进行记录,并用一些word与它们建立1-1对应。
这些word开始只是少数人的专用语言,随着科学不断普及,这些专业术语也就逐步演变成人们的日常用语。
如果你仔细分析语言的各种成分,你将发现,人类语言的全部概念实际都是利用1-1对应这种简单想法(idea)生成的。
ﻫ2. 1-1 对应的进一步的意义和性质集合的1-1对应是定义在两个集合上的两个互逆的1-1变换所联合组合。
如集合{1,2,3}与集合{A,B,C}的 1-1 对应1 <-> A ,2 <-> B ,3 <-> C就是下列两个1-1变换的组合:f:( 1 -> A , 2 -> B , 3 ->C)g:( 1 <- A , 2 <- B, 3 <- C )其中f是{1,2,3}到{A,B,C}的变换,g是{A,B,C}到{1,2,3}的变换,且g与f互逆。
如果将二个变换改为f:( 1-> A , 2 -> B , 3 -> C )g:( 2 <- A , 1 <- B , 3 <- C )则尽管f和g都是1-1变换,使一个元素变到一个元素,但g与f不是互逆的两个变换,它们合在一起就不构成(同)一个1-1对应。
