§4-4 狭义相对论动力学基础
合集下载
狭义相对论动力学基础37页PPT

狭义相对论动力学基础
1、合法而稳定的权力在使用得当时很 少遇到 抵抗。 ——塞 ·约翰 逊 2、权力会使人渐渐失去温厚善良的美 德。— —伯克
3、最大限度地行使权力总是令人反感 ;权力 不易确 定之处 始终存 在着危 险。— —塞·约翰逊 4、权力会奴化一切。——塔西佗
5、虽然权力是一头固执的熊,可是金 子可以 拉着它 的鼻子 走。— —莎士 比
25、学习是劳动,是充满思想的夸大,也会招来人们的反感轻蔑和嫉妒。——培根 22、业精于勤,荒于嬉;行成于思,毁于随。——韩愈
23、一切节省,归根到底都归结为时间的节省。——马克思 24、意志命运往往背道而驰,决心到最后会全部推倒。——莎士比亚
1、合法而稳定的权力在使用得当时很 少遇到 抵抗。 ——塞 ·约翰 逊 2、权力会使人渐渐失去温厚善良的美 德。— —伯克
3、最大限度地行使权力总是令人反感 ;权力 不易确 定之处 始终存 在着危 险。— —塞·约翰逊 4、权力会奴化一切。——塔西佗
5、虽然权力是一头固执的熊,可是金 子可以 拉着它 的鼻子 走。— —莎士 比
25、学习是劳动,是充满思想的夸大,也会招来人们的反感轻蔑和嫉妒。——培根 22、业精于勤,荒于嬉;行成于思,毁于随。——韩愈
23、一切节省,归根到底都归结为时间的节省。——马克思 24、意志命运往往背道而驰,决心到最后会全部推倒。——莎士比亚
狭义相对论的

14
1 1 1 2 2 2 − 1 − 1 = 2 m 0 c Ek = m A0c − 1 + m B 0 c u2 u2 u2 1− 2 1− 2 1− 2 c c c
M= m A0 u 1− 2 c
2
−
mB 0 u 1− 2 c
2
=
2m0 u2 1− 2 c
这个过程中质量的增量为: 2m0 1 M − 2m0 = − 2m0 = 2m0 ( − 1) 2 2 u u 1− 2 1− 2 c c 显然这个过程质量不守恒,但质能守恒成立。增加的 能量来源于两质点的初动能。即:
c2 dm -u2dm- umdu=0
Ek = ∫(u2dm+mudu)
Ek = ∫ F dx = ∫ c 2 dm = c 2 (m − m0 ) = ∆mc 2
m0 m
以后把m称为质量 称为质量, 称为静止质量。 以后把 称为质量,m0称为静止质量。 1 2 Ek = m c −1 0 u2 1− 2 c
11
4)低速时
1 u2 3u 4 1 2 2 − 1 = m 0 c (1 + + 4 + ⋯ ⋯ − 1) = m 0 u 2 Ek = m0c 2 c 2 8c 2 u2 1− 2 c
相对论动能表示式过渡到经典力学的动能表示式。 2、动量与能量的关系 由质量与速度的关系式:
m= m0 u2 1− 2 c
上式两边取平方并改写为: m2(c2-u2)=m02c2 由 E=mc2、 P=mu 将上式两边乘上 c2 后得: m2c4-m2u2c2=m02c4
12
1 1 1 2 2 2 − 1 − 1 = 2 m 0 c Ek = m A0c − 1 + m B 0 c u2 u2 u2 1− 2 1− 2 1− 2 c c c
M= m A0 u 1− 2 c
2
−
mB 0 u 1− 2 c
2
=
2m0 u2 1− 2 c
这个过程中质量的增量为: 2m0 1 M − 2m0 = − 2m0 = 2m0 ( − 1) 2 2 u u 1− 2 1− 2 c c 显然这个过程质量不守恒,但质能守恒成立。增加的 能量来源于两质点的初动能。即:
c2 dm -u2dm- umdu=0
Ek = ∫(u2dm+mudu)
Ek = ∫ F dx = ∫ c 2 dm = c 2 (m − m0 ) = ∆mc 2
m0 m
以后把m称为质量 称为质量, 称为静止质量。 以后把 称为质量,m0称为静止质量。 1 2 Ek = m c −1 0 u2 1− 2 c
11
4)低速时
1 u2 3u 4 1 2 2 − 1 = m 0 c (1 + + 4 + ⋯ ⋯ − 1) = m 0 u 2 Ek = m0c 2 c 2 8c 2 u2 1− 2 c
相对论动能表示式过渡到经典力学的动能表示式。 2、动量与能量的关系 由质量与速度的关系式:
m= m0 u2 1− 2 c
上式两边取平方并改写为: m2(c2-u2)=m02c2 由 E=mc2、 P=mu 将上式两边乘上 c2 后得: m2c4-m2u2c2=m02c4
12
大学物理(下册) 14.3 狭义相对论动力学基础

4 m0 (2 H e ) 6.6425 1027 kg、 m0 (10 n) 1.6750 1027 kg
各粒子静止质量如上,若反应前粒子动能相对较小, 试计算反应后粒子所具有的总动能。 解:反应前、后粒子静止质量之和分别为:
2 3 m10 m0 (1 H ) m0 (1 H ) 8.3486 1027 kg 1 27 m20 m0 ( 4 H ) m ( n ) 8 . 3175 10 kg 2 e 0 0
2.相对论力学基本方程
m0 v dp d m0 v d F ( ) ( ) dt dt 1 2 dt 1 2 / c 2 dv dm m v dt dt
(3)
注意:
1. (3)式是 S.R. 基本方程; 2.当 v c 时, m m0
3.力并不总是与加速度同方向; a 4.当 v c 时dm dt , m 、 0 光速为极限;
我国于 1958 年建成的首座重水反应堆
原子弹爆炸
dv F m0 ; dt
14.3.3
质量与能量的关系
(1) (2)
质点相对论动能: Ek mc2 m0c2 质点相对论静能: E0 m0c 2
质点相对论总动能:E mc2 m0c 2 Ek (3) 注意: 1. 物体静止时所具有的能量=静能;
2. (3)式:相对论质能关系;
E (m)c
注意:
2
(4)
a. 质能关系式在原子核与基本粒子物理中已 被大量实验相当好的证实;
b. 质能关系式是原子能利用的主要理论根据; =核反应的理论基础;
例14.3.1 氢弹爆炸时其中一个聚变反应,及且已知
2 3 4 1 H H He 1 1 2 0n
各粒子静止质量如上,若反应前粒子动能相对较小, 试计算反应后粒子所具有的总动能。 解:反应前、后粒子静止质量之和分别为:
2 3 m10 m0 (1 H ) m0 (1 H ) 8.3486 1027 kg 1 27 m20 m0 ( 4 H ) m ( n ) 8 . 3175 10 kg 2 e 0 0
2.相对论力学基本方程
m0 v dp d m0 v d F ( ) ( ) dt dt 1 2 dt 1 2 / c 2 dv dm m v dt dt
(3)
注意:
1. (3)式是 S.R. 基本方程; 2.当 v c 时, m m0
3.力并不总是与加速度同方向; a 4.当 v c 时dm dt , m 、 0 光速为极限;
我国于 1958 年建成的首座重水反应堆
原子弹爆炸
dv F m0 ; dt
14.3.3
质量与能量的关系
(1) (2)
质点相对论动能: Ek mc2 m0c2 质点相对论静能: E0 m0c 2
质点相对论总动能:E mc2 m0c 2 Ek (3) 注意: 1. 物体静止时所具有的能量=静能;
2. (3)式:相对论质能关系;
E (m)c
注意:
2
(4)
a. 质能关系式在原子核与基本粒子物理中已 被大量实验相当好的证实;
b. 质能关系式是原子能利用的主要理论根据; =核反应的理论基础;
例14.3.1 氢弹爆炸时其中一个聚变反应,及且已知
2 3 4 1 H H He 1 1 2 0n
高二物理竞赛课件:狭义相对论质点动力学基础(共15张PPT)

与牛顿力学中 形式相同
质量
由力的定义式有:F 持续作用
P
m
持续
但 的上限是 c
m 随速率增大而增大
所以质量必须是 m m()的形式。
实验证明
相对论质量 m
m m0
1
υ2 c2
关系曲线
m0
o
Cv
相对论质量 m m0
m
m0--静止质量
讨论
1
υ2 c2
m0
o
Cv
1)合理性(速度愈大质量--惯性愈大) 加速就越难
•1克氘聚变释放能量是铀的4倍, 煤的1000万倍。
核反应堆
核 电 站
E mc2
E (m)c2
惯性质量的增加和能量的增加相联系,质 量的大小应标志着能量的大小,这是相对论 的又一极其重要的推论。
Ei mic2 常量
i
i
mi 常量
i
相对论把能量守恒和质量守恒这两条自
然规律统一起来了。
E EK m0c2 mc2
E mc 2 ----质能关系式
为开创原子能时代提供 了理论基础,被看作是 具有划时代意义的理论 公式,已成为纪念爱因 斯坦伟大功绩的标志。
讨论
E mc2
E静 m0c2 任何宏观静止的物体本身都蕴藏
着巨大的能量
1千克的物质所包含的静能 E0 91016 J
1
(1千克汽油的燃烧值为 4.6 107J ) 2109
相对论的质能关系为开创原子能时代提供 了理论基础, 这是一个具有划时代意义的理 论公式。
E mc2 相对论质能关系
相对论质量是能量的量度
E (m)c2
质量亏损 能量释放
质能关系预言:物质的质量就是能量的一种储藏
狭义相对论动力学基础

(14- 24)
狭义相对论动力学基础
这就是狭义相对论的质量- 能量关系式.将质量守恒定律式(14- 18)的
两边同乘以c2,可得
mvc2+m0c2=Muc2
(14- 25)
式(14- 25)表示在碰撞前两小球的总能量等于碰撞后物体的总能量,
质量- 速度关系是动量守恒定律满足洛伦兹协变性的条件,对质 量进行修正后,牛顿力学自然推广为狭义相对论力学.
狭义相对论动力学基础
按照定义,速度为v的物体,其相对论动量为
狭义相对论动力学基础
二、 相对论中的质量- 能量关系
将经典力学中的动能定理推广到 狭义相对论力学,便可得到相对论动 能表达式,进而得到相对论中的质量能量关系.
mv′A+mv′B=Mu′
(14- 14)
因此,为保证动量守恒定律的洛伦兹协变性,必须放弃“质量是
每个物体固有的恒量”这一概念.
狭义相对论动力学基础
质量是一个相对量,在不同的参考系中测量质量所得数值是不同的.
或者说,在同一个确定的参考系中测量,物体的质量将因其运动速度不
同而有不同的数值.一个物体相对于一个确定参考系的质量,只能与该运
狭义相对论动力学基础
狭义相对论动力学基础
我们知道,牛顿力学定律的形式在伽利略变换下是保持不变的.在牛 顿力学中,质量是被认为不变的物理量,则根据牛顿第二定律,给一个 质量不大的粒子施加一个较大的作用力时,在不太长的时间内粒子就可 以超过光速.事实上这是不可能的,是与狭义相对论的基本原理相违背的.
狭义相对论的基本原理可以总结为:在所有惯性系中,物理定律都 应该是洛伦兹协变的.也就是说,所有物理定律在洛伦兹变换下都应保持 相同的形式,为保证洛伦兹协变性,必须对牛顿力学定律做一些修正.下 面就通过分析动量守恒定律满足洛伦兹协变性所需要的条件,即质量- 速 度关系,来得到牛顿力学的修正——狭义相对论力学.
狭义相对论动力学基础
这就是狭义相对论的质量- 能量关系式.将质量守恒定律式(14- 18)的
两边同乘以c2,可得
mvc2+m0c2=Muc2
(14- 25)
式(14- 25)表示在碰撞前两小球的总能量等于碰撞后物体的总能量,
质量- 速度关系是动量守恒定律满足洛伦兹协变性的条件,对质 量进行修正后,牛顿力学自然推广为狭义相对论力学.
狭义相对论动力学基础
按照定义,速度为v的物体,其相对论动量为
狭义相对论动力学基础
二、 相对论中的质量- 能量关系
将经典力学中的动能定理推广到 狭义相对论力学,便可得到相对论动 能表达式,进而得到相对论中的质量能量关系.
mv′A+mv′B=Mu′
(14- 14)
因此,为保证动量守恒定律的洛伦兹协变性,必须放弃“质量是
每个物体固有的恒量”这一概念.
狭义相对论动力学基础
质量是一个相对量,在不同的参考系中测量质量所得数值是不同的.
或者说,在同一个确定的参考系中测量,物体的质量将因其运动速度不
同而有不同的数值.一个物体相对于一个确定参考系的质量,只能与该运
狭义相对论动力学基础
狭义相对论动力学基础
我们知道,牛顿力学定律的形式在伽利略变换下是保持不变的.在牛 顿力学中,质量是被认为不变的物理量,则根据牛顿第二定律,给一个 质量不大的粒子施加一个较大的作用力时,在不太长的时间内粒子就可 以超过光速.事实上这是不可能的,是与狭义相对论的基本原理相违背的.
狭义相对论的基本原理可以总结为:在所有惯性系中,物理定律都 应该是洛伦兹协变的.也就是说,所有物理定律在洛伦兹变换下都应保持 相同的形式,为保证洛伦兹协变性,必须对牛顿力学定律做一些修正.下 面就通过分析动量守恒定律满足洛伦兹协变性所需要的条件,即质量- 速 度关系,来得到牛顿力学的修正——狭义相对论力学.
狭义相对论的动力学

⑥ v > c时, m为虚数而无实际意义. 这阐明:真空中 旳光速c是一切物体运动速率旳极限.
2 动量与速度旳关系
p mv m0 v 1 v2 / c2
相对论中,质点所受旳力定义为:F
dp dt
d dt
mv
经典力学中,质点受力旳定义:
F
dp dt
m
d dt
v
显然,两者不再等效,因而用加速度表达旳牛顿 第二定律在相对论力学中不再成立.
A
B
2. 设有宇宙飞船A和B,固有长度均为l0 = 100m,沿 同一方向匀速飞行,在飞船B上观察到飞船A旳船头、
船尾经过飞船B船头旳时间间隔为0.6×10-7s,则飞船
B相对于飞船A旳速度是
。
解: 在B 船中观察A船旳长度
l l0 1 v c2
在B 船船头观察A船船头船尾飞过旳时间间隔
0
l v
• 爱因斯坦建立旳质能关系式被以为是一种具有划时
代意义旳理论公式,原子能旳利用使人类进入原子
时代。
E m0c2
这个关系式中 c2 旳数值很大,以至微小旳质量变化, 就相应着巨大旳能量变化。
在原子核裂变反应中,1g 235U裂变释放旳结合 能约 8.2 1010 J 。
在原子核聚变反应中,1g 氘和氚聚变释放旳结 合能大约是上述裂变反应释放能量旳3.5倍。
A
A 0.4kg B 0.8kg C 12×10-7kg D 1/12 ×10-7kg
m0c2 36 1015 J
m0
36 1015 9 1016
0.4kg
3. 一种立方体旳静质量为 m0,体积为 V0,当它相 对某惯性系S沿一边长方向以 v匀速运动时,静止在 S 中旳观察者测得其密度为多少?
第4章 狭义相对论基础

S系
m11 m2 2 m110 m2 20
利用伽利略变换
S 系
m11 m2 2 m110 m2 20
动量守恒定律在伽利略变换下形式不变。 在两相互作匀速直线运动的惯性系中,牛顿运 动定律具有相同的形式。
5
4.1 伽利略变换 经典力学的相对性原理
y' y
z' z
y y'
v x' c2 t 2 1 v 2 c t '
z z'
1) x ' , t '与 x, t成线性关系,但比例系数不等于1。 2) 时间不独立,t 和 x 变换相互交叉。 3)
v c
时,洛伦兹变换
伽利略变换。
13
4.2 狭义相对论的基本假设 洛仑兹变换
tt
'
t t 2 t1 t 2 t1 t '
6
4.1 伽利略变换 经典力学的相对性原理
空间间隔度量绝对不变
' x' x2 x1' ( x2 ut2 ) ( x1 ut1 )
x2 x1 x
t 2 t1
( S系中必须同时测量长度两端 ) 牛顿力学的相对性原理
1)满足相对性原理和光速不变原理。 2)当质点速率远小于真空光速 c 时,该变换应能
使伽利略变换重新成立。
o 设 : t ' 0 时, ,o' 重合 ; 事件 P 的时空坐标如图所示。 t
x' x vt v2 1 c
2
y' y
v x c2 t' 2 1 v 2 c t
第四章 相对论基础

2 2
)
F m
dv
dm v 与牛顿力学方程形式不同。 dt dt
v c0 m m0
当v c时
dv dm dv 牛顿力学方程 F m v F m0 dt dt dt
返回
退出
二、质量与能量的关系 1. 相对论动能
设质点在变力作用下,由静止开始沿x轴作一维 运动,由动能定理和动量定理: dp dE k Fdx dx vdp dt 2 vd( mv ) v dm mv dv m0 m0vdv m dm 2 2 2 2 2 32 1 v c c v c 1
根据洛仑兹变换,在K´系, 两事件发生的时间分别为:
t t1 vx1 c
2 2
v
t t2
v
vx2 c
2 2
o
o
x
x
1 v c
1 v c
t2 t1 c
2
( x1 x2 )
2
1 v c
0
在K系同时异地发生的两事件,在K´系中并不同时。 在K´系同时异地发生的两事件,在K系中也不同时。
绝对性:事件的因果关系有 绝对意义。
返回
退出
因果律与物质运动的最大速度
S系 原因 P1 ( x1 , t1 )
S 系
P1 ( x1 , t1 )
结果
P2 ( x 2 , t 2 )
t 2 t1
P2 ( x 2 , t 2 )
t 2 t1
1 1 u c
2 2
u (t t1 ) 2 ( x2 x1 ) 2 c
第四章 相对论基础
§4-1 狭义相对论基本原理 洛伦兹变换
)
F m
dv
dm v 与牛顿力学方程形式不同。 dt dt
v c0 m m0
当v c时
dv dm dv 牛顿力学方程 F m v F m0 dt dt dt
返回
退出
二、质量与能量的关系 1. 相对论动能
设质点在变力作用下,由静止开始沿x轴作一维 运动,由动能定理和动量定理: dp dE k Fdx dx vdp dt 2 vd( mv ) v dm mv dv m0 m0vdv m dm 2 2 2 2 2 32 1 v c c v c 1
根据洛仑兹变换,在K´系, 两事件发生的时间分别为:
t t1 vx1 c
2 2
v
t t2
v
vx2 c
2 2
o
o
x
x
1 v c
1 v c
t2 t1 c
2
( x1 x2 )
2
1 v c
0
在K系同时异地发生的两事件,在K´系中并不同时。 在K´系同时异地发生的两事件,在K系中也不同时。
绝对性:事件的因果关系有 绝对意义。
返回
退出
因果律与物质运动的最大速度
S系 原因 P1 ( x1 , t1 )
S 系
P1 ( x1 , t1 )
结果
P2 ( x 2 , t 2 )
t 2 t1
P2 ( x 2 , t 2 )
t 2 t1
1 1 u c
2 2
u (t t1 ) 2 ( x2 x1 ) 2 c
第四章 相对论基础
§4-1 狭义相对论基本原理 洛伦兹变换
高二物理竞赛课件:狭义相对论的动力学基础(共14张PPT)

当改造,否则与经典力学没有区别。
设作完有全两完非弹全相性碰同撞的,小球K’在系两沿惯X轴性以系速K、度Ku’中运沿动X轴
设在K系um中,u 两m球0 质X量X’ 分别为速m度m0 、为分m静别0止为质分量别为
u.0
m 为运动时的质量。
m m0 vx X
碰撞以后在K系中一起
以速度 vx 沿X轴运动
7 106V 7 106V
斯坦福加速器全貌
7 106V 7 106V
斯坦福加速器内貌
全长2英里
粒子加速器——重要工具
长达3.2公里的 斯坦福直线加 速器
7 106V 7 106V 7 106V 7 106V
依经典理论电子速达到 v 8.6 1010m / s C 而实测值为 v 0.999,999,9997c c
动量关系式
P mv
m0
v
1
v
2
c
1 1v 2 c2
实验数据:
质量随速率的变化 14
XX’
m m0 vx X
mu (m m0)vx (1)
下面u 从K’m系0来研u究m:X’
u
vx u
v'x
m
'm
m0 m
m0
(2)
X’
依动量守恒
mu (m m0)vx''(3)
(2)式(4)式对照:
u v'x'
m m0 (4) m
u
u
(5)
vx'' vx
即:vx v'x' (6)
u m
u
m0
XX’
m m0 vx X
依动量守恒定律
u
设作完有全两完非弹全相性碰同撞的,小球K’在系两沿惯X轴性以系速K、度Ku’中运沿动X轴
设在K系um中,u 两m球0 质X量X’ 分别为速m度m0 、为分m静别0止为质分量别为
u.0
m 为运动时的质量。
m m0 vx X
碰撞以后在K系中一起
以速度 vx 沿X轴运动
7 106V 7 106V
斯坦福加速器全貌
7 106V 7 106V
斯坦福加速器内貌
全长2英里
粒子加速器——重要工具
长达3.2公里的 斯坦福直线加 速器
7 106V 7 106V 7 106V 7 106V
依经典理论电子速达到 v 8.6 1010m / s C 而实测值为 v 0.999,999,9997c c
动量关系式
P mv
m0
v
1
v
2
c
1 1v 2 c2
实验数据:
质量随速率的变化 14
XX’
m m0 vx X
mu (m m0)vx (1)
下面u 从K’m系0来研u究m:X’
u
vx u
v'x
m
'm
m0 m
m0
(2)
X’
依动量守恒
mu (m m0)vx''(3)
(2)式(4)式对照:
u v'x'
m m0 (4) m
u
u
(5)
vx'' vx
即:vx v'x' (6)
u m
u
m0
XX’
m m0 vx X
依动量守恒定律
u
普通物理学chapter-4

绝对性:事件的因果关系有 绝对意义。
返回 退出
因果律与物质运动的最大速度
K系 原因 P1(x1, t1)
结果 P2 (x2 , t2 ) t2 t1
K系 P1(x1, t1)
P2 (x2 , t2 )
t2 t1
1
1
v2 c2
(t2
t1 )
v c2
( x2
x1
)
任何物质的运动速度都不能大于真空中的光速
x2
1 v c2
t2
t1
(t2
t1) 1
v c2
v
( x2
c 2
x1 )
t2
t1
v c2
( x2 x1)
1 v c2
v c2
(
x2
x1)
3 2 103 5.77 106 (s) 2c
返回 退出
例4-3 有两列火车同时从上海和北京发出,驶向对 方。有一艘飞船v=0.1C在天空中从上海往北京方向 飞行。问飞船中的观察者观察到这两列火车是不是 同时发出?哪列火车先发出?
符合光速不变原理。
返回 退出
例4-2 在地面上测到有两个飞船A、B分别以 +0.9c 和-0.9c的速度沿相反的方向飞行。求飞船A相对于 飞船B的速度有多大。
解:设K系被固定在飞船 B上,地面为K´系,K´对 K以v=0.9c的速度运动。 则飞船A 相对于K´系的速
度为 ux=0.9c 。
飞船A对K系的速度,亦即相对于飞船B的速度:
ux
ux 1
v
vux c2
0.9c 0.9c 1 0.9 0.9
1.80c 1.81
0.994c
返回 退出
§4-3 狭义相对论的时空观 狭义相对论利用洛伦兹变换对旧的绝对时空观进 行了根本性的变革, 认为时间、 空间都与物质的运 动有关,它们具有相对的意义——时空的相对性。 一、 “同时”的相对性(relativity of simultaneity)
返回 退出
因果律与物质运动的最大速度
K系 原因 P1(x1, t1)
结果 P2 (x2 , t2 ) t2 t1
K系 P1(x1, t1)
P2 (x2 , t2 )
t2 t1
1
1
v2 c2
(t2
t1 )
v c2
( x2
x1
)
任何物质的运动速度都不能大于真空中的光速
x2
1 v c2
t2
t1
(t2
t1) 1
v c2
v
( x2
c 2
x1 )
t2
t1
v c2
( x2 x1)
1 v c2
v c2
(
x2
x1)
3 2 103 5.77 106 (s) 2c
返回 退出
例4-3 有两列火车同时从上海和北京发出,驶向对 方。有一艘飞船v=0.1C在天空中从上海往北京方向 飞行。问飞船中的观察者观察到这两列火车是不是 同时发出?哪列火车先发出?
符合光速不变原理。
返回 退出
例4-2 在地面上测到有两个飞船A、B分别以 +0.9c 和-0.9c的速度沿相反的方向飞行。求飞船A相对于 飞船B的速度有多大。
解:设K系被固定在飞船 B上,地面为K´系,K´对 K以v=0.9c的速度运动。 则飞船A 相对于K´系的速
度为 ux=0.9c 。
飞船A对K系的速度,亦即相对于飞船B的速度:
ux
ux 1
v
vux c2
0.9c 0.9c 1 0.9 0.9
1.80c 1.81
0.994c
返回 退出
§4-3 狭义相对论的时空观 狭义相对论利用洛伦兹变换对旧的绝对时空观进 行了根本性的变革, 认为时间、 空间都与物质的运 动有关,它们具有相对的意义——时空的相对性。 一、 “同时”的相对性(relativity of simultaneity)
高中物理竞赛§4.5狭义相对论动力学基础PPT(课件)

——预言了“反粒子”的存在——后被实验证
光子实 的动量与质量m0 0
p E c
m E c2
已知 解法提要
电子的静止质量
31
9.1110
kg
31
16
9.1110 10
14
8.1910
电子的 静能
当电子以速度 0.99
运动时的 能量 动能
14
8.1910 0.99
13
5.8110
13
5.8110
14
●几个重要的狭义相对论效应 ——经典力学是相对论力学的低速近似
——此m仍叫为质量
质速关系与实验结果吻合的很好
当v<物<c时理,还学原为家牛顿笃第二信定律动量守恒总是成立的→导出
m
m0 1(v c)2
其中:m0——相对参考系静止物体的m——称为静止质量 m——……………运动…………——……运动……
§4.5 狭义相对论动力学基础(一质速关系)
说明 质速关系与实验结果吻合的很好
m
m0
1(v c)2
动质量恒大于静止质量 m>m0 v<<c时,m=m0 ——m0经典意义下的质量
——经典力学是相对论力学的低速近似
v=c时,m0 =0(m=∝无意义;如光子)
§4.5 狭义相对论动力学基础(一质速关系)
4相经.5对.典2 论:相F :对定论m 义的0动a基—量本—:方力p程 只m 改v变速度
§4.5 狭义相对论动力学基础
●力学相对性原理
——即太阳的质量损失率
——经典时空运动关系
●v一—5—位置<狭几高——<c义个 速 预 需时相重运言重,对要动了新m● ● ●论=的电“定m动狭几狭子反义0迈力—义,粒一学—相当子些 义个克基m对它”物0础耳论的的理相重经(效动存量典孙一应能在对要意质在——义速数—论的下关莫值后的系上被的狭质雷等实二量于验基基义实它证本验的实方本相程)假对—设论—效问洛应题伦兹—变—换新—关— 系下建的新结时论空运动关系
4 狭义相对论基础 (3)

2 27
9 10
16
2 . 799 10
12
1kg这种核燃料所释放的能量为:
E m1 m 2 2 . 799 10 8 . 3486 10
12 27
3 . 35 10
14
J/kg
这相当于同质量的优质煤燃烧所释放热量的1千多万倍!
【例题2】两个相同的粒子,静质量为 m0,粒子A静止, 粒子B以 0.6c 的速率向A碰撞,设碰撞是完全非弹性的, 求碰撞后复合粒子质量、动量及能量。
2
1
1 2
(v / c )
2
5 . 6 10
10
微观粒子速率接近光速如中子v=0.98c时
m 5 . 03 m 0
牛顿力学是相对论力学在低速情况下的近似
2、
m
m0 1 v c
2 2
v>c时,m成为虚数, 无意义所以光速是物体 运动的极限速度。
二. 狭义相对论运动方程
F dP dt
4 5
1 2
动能公式
m 0v
2
c
1 1 v c
2 2
1)
2 3
m 0c
2
当 v<<c 时:
1 1 v c
2 2
1
1 v 2 c
2 2
1
1 v 2 c
2 2
则: E K mc
2
m0c
2
2
v m 0 1 2 2c
m0c 1 2
2
2 2 c m 0c
i
Ei
(m
i
i
c ) 常量
9 10
16
2 . 799 10
12
1kg这种核燃料所释放的能量为:
E m1 m 2 2 . 799 10 8 . 3486 10
12 27
3 . 35 10
14
J/kg
这相当于同质量的优质煤燃烧所释放热量的1千多万倍!
【例题2】两个相同的粒子,静质量为 m0,粒子A静止, 粒子B以 0.6c 的速率向A碰撞,设碰撞是完全非弹性的, 求碰撞后复合粒子质量、动量及能量。
2
1
1 2
(v / c )
2
5 . 6 10
10
微观粒子速率接近光速如中子v=0.98c时
m 5 . 03 m 0
牛顿力学是相对论力学在低速情况下的近似
2、
m
m0 1 v c
2 2
v>c时,m成为虚数, 无意义所以光速是物体 运动的极限速度。
二. 狭义相对论运动方程
F dP dt
4 5
1 2
动能公式
m 0v
2
c
1 1 v c
2 2
1)
2 3
m 0c
2
当 v<<c 时:
1 1 v c
2 2
1
1 v 2 c
2 2
1
1 v 2 c
2 2
则: E K mc
2
m0c
2
2
v m 0 1 2 2c
m0c 1 2
2
2 2 c m 0c
i
Ei
(m
i
i
c ) 常量
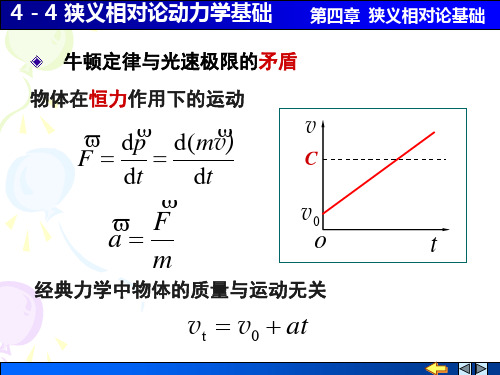
4-4 狭义相对论动力学基础
释放能量 E m0c2 2.799 10 12 J
1 kg 核燃料释放能量:
ΔE 3.351014 (J/kg) mD mT
4 - 4 狭义相对论动力学基础 第四章 狭义相对论基础
例2 求原子核的结合能 .
211H 201n42 He
解:已知实验测得的质子、中子、氦核的质量:
mH 1.00728u mHe 4.00150u
物理意义
E mc 2 m0c2 Ek
E m c2
惯性质量的增加和能量的增加相联系,质量的 大小应标志着能量的大小,这是相对论的又一极其 重要的推论 .
相对论的质能关系为开创原子能时代提供了理 论基础,这是一个具有划时代的意义的理论公式 .
4 - 4 狭义相对论动力学基础 第四章 狭义相对论基础
4 - 4 狭义相对论动力学基础 第四章 狭义相对论基础
相对论质能关系
E mc 2 m0c2 Ek
静能 m0c2 :物体静止时所具有的能量 .
电子的静质量
m0 0.9111030 kg
电子的静能 m0c2 8.19 1014 J 0.511MeV
质子的静质量
m0 1.6731027 kg
4 - 4 狭义相对论动力学基础 第四章 狭义相对论基础
氘核 (21H) 氚核 (31H)
mD 3.3437 1027 kg mT 5.0449 10 27 kg
氦核
(
4 2
He)
中子
(
1 0
n)
mHe 6.6425 10 27 kg mn 1.6750 10 27 kg
反应质量亏损 Δm0 (mD mT ) (mHe mn ) 0.03111027 (kg)
mn 1.00866 u 1u 1.660 1027 kg
狭义相对论动力学基础

结束
返回
三,相对论之能量 dE k= F . d s =F . v dt = d (m v ) . v = ( m dv + v dm ) . v = m v . dv + dm v . v
v . dv = vx dvx + vy dvy +vz dvz
1 d(v 2 v 2 v 2) = 2 x+ y+ z 1 d(v 2) =2 = v dv .v = v 2 v
2
时间膨胀公式: 时间膨胀公式:
t =
τ
1 v c
2 2
质速关系: 质速关系:
m= v v p = mv =
mo 1 v c
2 2
动量: 动量:
mo 1 v c
2 2
v v
v v v dp d(mv) 相对论基本方程: 相对论基本方程: F = = dt dt
相对论动能: 相对论动能: 相对论总能量: 相对论总能量:
结束
返回
三,相对论之能量 dE k= F . d s =F . v dt = d (m v ) . v = ( m dv + v dm ) . v = m v . dv + dm v . v 2 =m v dv + dm v
m0 m= 2 1 v )2 (1 c 2 m 0 v dv dm = 2 v 2 3 c (1 2 ) 2 c dm c 2(1 v 2 )32 v dv = m c2 0
静止能量的4倍时, 静止能量的 倍时,其质量为静止质量的 倍时 (A) 4倍. (B) 5倍. (C) 6倍. (D) 8倍
C B
v = 3c / 2 情况下粒子 3, (1) 在速度 在速度____________情况下粒子 ,
返回
三,相对论之能量 dE k= F . d s =F . v dt = d (m v ) . v = ( m dv + v dm ) . v = m v . dv + dm v . v
v . dv = vx dvx + vy dvy +vz dvz
1 d(v 2 v 2 v 2) = 2 x+ y+ z 1 d(v 2) =2 = v dv .v = v 2 v
2
时间膨胀公式: 时间膨胀公式:
t =
τ
1 v c
2 2
质速关系: 质速关系:
m= v v p = mv =
mo 1 v c
2 2
动量: 动量:
mo 1 v c
2 2
v v
v v v dp d(mv) 相对论基本方程: 相对论基本方程: F = = dt dt
相对论动能: 相对论动能: 相对论总能量: 相对论总能量:
结束
返回
三,相对论之能量 dE k= F . d s =F . v dt = d (m v ) . v = ( m dv + v dm ) . v = m v . dv + dm v . v 2 =m v dv + dm v
m0 m= 2 1 v )2 (1 c 2 m 0 v dv dm = 2 v 2 3 c (1 2 ) 2 c dm c 2(1 v 2 )32 v dv = m c2 0
静止能量的4倍时, 静止能量的 倍时,其质量为静止质量的 倍时 (A) 4倍. (B) 5倍. (C) 6倍. (D) 8倍
C B
v = 3c / 2 情况下粒子 3, (1) 在速度 在速度____________情况下粒子 ,
(2)狭义相对论动力学基础

vx v vx v x v S'系中观测:Mv x m v 1 2 vx c
质速 m m 0 关系式
1 v2 1 2 c
m0:静止质量 m:运动时的质量 v:运动速度
讨论 (1)m是相对量,与参照系选择有关, 随v增大而增大。 m (2)m–m0=mk 动质量 增加的质量 m0 O (3)v<<c:m m0 (4)v>c:无意义 光速是一切物体的极限速度 (5) v=c: 静质量为0 光子、中微子
1 五、相对论的能量 m m0 1. 动能 v2 1 2 v 1 2 c 经典:Ek F dr m v 0 2 相对论: v v d( m v ) dr E k F dr 0 0 dt 2 2 2 mc m 0 c mk c 动能公式 2. 能量 2 E 0 m0c 静止能量 质能关系式 2 总能量 E mc
六、动量与能量的关系 2 2 2 m 0v p v /c p mv 2 2 2 2 m0 c v 1 (v / c ) 1 2 c 2 2 m0c E 1 2 E mc 2 2 2 2 ( m c ) v 1 (v / c ) 0 1 2 c 2 2 2 2 2 E p E p c 2 2 1 2 4 2 4 1 2 4 m0 c m0 c m0 c m0 c
m0 v 2 1( ) c
小 结
1 (v / c ) d( m v ) dv dm m v (3)动力学方程 F dt dt dt
(4)质能关系 E mc m 0 c mk c
2 2 2
(2)动量 p m v
m 0v
2
(5)动量能量关系 E E0 ( pc ) 2
质速 m m 0 关系式
1 v2 1 2 c
m0:静止质量 m:运动时的质量 v:运动速度
讨论 (1)m是相对量,与参照系选择有关, 随v增大而增大。 m (2)m–m0=mk 动质量 增加的质量 m0 O (3)v<<c:m m0 (4)v>c:无意义 光速是一切物体的极限速度 (5) v=c: 静质量为0 光子、中微子
1 五、相对论的能量 m m0 1. 动能 v2 1 2 v 1 2 c 经典:Ek F dr m v 0 2 相对论: v v d( m v ) dr E k F dr 0 0 dt 2 2 2 mc m 0 c mk c 动能公式 2. 能量 2 E 0 m0c 静止能量 质能关系式 2 总能量 E mc
六、动量与能量的关系 2 2 2 m 0v p v /c p mv 2 2 2 2 m0 c v 1 (v / c ) 1 2 c 2 2 m0c E 1 2 E mc 2 2 2 2 ( m c ) v 1 (v / c ) 0 1 2 c 2 2 2 2 2 E p E p c 2 2 1 2 4 2 4 1 2 4 m0 c m0 c m0 c m0 c
m0 v 2 1( ) c
小 结
1 (v / c ) d( m v ) dv dm m v (3)动力学方程 F dt dt dt
(4)质能关系 E mc m 0 c mk c
2 2 2
(2)动量 p m v
m 0v
2
(5)动量能量关系 E E0 ( pc ) 2
相对论动力学

2,
r r E0 = m0c , P = mV
2
m=
2 2 m2 (1V 2 / c2 ) = m0 , m2c4 m2V 2c2 = m0 c4 1V 2 / c2 ,
m0
2 E2 c2P2 = E0
E
E = E +c P
2 2 0 2 2
cP
—— 相对论能量动量关系式
E0
( 讨论: ) 讨论: 1)
尾传到船头。 尾传到船头。飞船上的观察者测得飞船的长度为 90m
求:地球上的观察者测得光脉冲传播的距离和时间 解: 地球 S 系,飞船 S′ 系,u = 0.8c
“光脉冲从船尾发出”为事件1, 光脉冲从船尾发出” 事件1 光脉冲到达船头”为事件2 “光脉冲到达船头” 事件2 S′ : x′ = L0 , t′ = L0 / c
Ek = (m m0 )c2 = mc2 m0c2 = E E0
静止能量 E0 = m0c2 :静止能量
E = mc =
2
m0c
2 2
1V / c
2
=
E0 1V / c
2 2
:相对论总能量
E = E0 + Ek
E = mc2
:质能关系式
质量和能量是不可分割的, 质量和能量是不可分割的, E = mc2
2 2 令 x = V /c ,
x <1
,满足 x <1
2
α = 1/ 2
2
(1V / c )
2
2 1/ 2
=1+V /(2c ) +L
Ek = (m m0 )c2 =
2 2
m0c2 1V 2 / c2
2 1/ 2
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
m2v2
m02c2 1 v2 c2
1
m02v v2
2
c
2
m02
c2 1
v2
v2 c
2
m02c2
的动轻能核,聚足变以条克件服两温21度H要之达间到的1库08仑K 排时斥,力使.21H 具有10keV
三、动量与能量的关系
E mc2 m0c2 , 1 v2 c2
p
mv
m0
v
1 v2 c2
E c
2 Fra bibliotekp2m02c2 1 v2 c2
p2
m02c2 1 v2 c2
0.03111027 (kg) 释放能量 E mc2 2.799 1012 J
1kg核燃料释放能量 ΔE 3.35 1014(J/kg) mD mT
为1㎏优质煤燃烧所释放热量的1千多万倍!
相对论的质能关系为开创原子能时代提供了理论 基础 , 这是一个具有划时代的意义的理论公式 .
相对论质量:
P 0
p m0 v 1 v2 c2
p mv
v
1
c
m
m0 1 v2 c2
m
m m0
1 v2 c2
m0
m0 ——静止质量
0
1
v c
说明:
a.在 v c 时,m m0
b.当 v c 时, m 即不论对物体加多大的力,
也不可能再使它的速度增加。
c.当 v c 时,必须 m0 0 即以光速运动的物
E Ek E0
说明:
a. 物体处于静止状态时,物体也蕴涵着相当 可观的静能量。
b. 相对论中的质量不仅是惯性的量度,而且 还是总能量的量度。
c. 如果一个系统的质量发生变化,能量必有 相应的变化。
d. 对一个孤立系统而言,总能量守恒,总质 量也守恒。
相对论质能关系 E mc2 m0c2 Ek
vdp
vd(mv) v2dm mvdv
m
m0 1 v2 c2
dm
c2
m0vdv 1 v2 c2
32
c2
1
v2 c2
dm
m0vdv 1 v2 c2
c2
1
v2 c2
dm
m0vdv mvdv
1 v2 c2
代入动能式: dEk v2dm mvdv
电子的静能 m0c2 8.19 1014 J 0.511MeV
质子的静质量 m0 1.673 1027 kg
质子的静能 m0c2 1.5031010 J 938MeV
1千克的物体所包含的静能 9 1016 J
1千克汽油的燃烧值为 4.6 107 焦耳 .
质能关系预言:物质的质量就是能量的一种储藏。
m0c2
m0c2
1 1 v2
c2
1
1
v2 c2
1
2
1
1 2
v2 c2
3 8
v4 c4
Ek
1 2
m0v2
3 8 m0
v4 c4
c2
v c 时
Ek
1 2
m0v 2
得到牛顿力学的动能公式。
2.相对论总能量
mc2 Ek m0 c2 E mc2
质能关系预言:物质的质量就是能量的一种储藏 .
爱因斯坦认为(1905)
懒惰性
惯性 ( inertia )
活泼性
能量 ( energy )
物体的懒惰性就是 物体活泼性的度量 .
相对论质能关系 E mc 2 m0c2 Ek
静能m0c2 :物体静止时所具有的能量 .
电子的静质量 m0 0.9111030 kg
dEk v2dm c2 1 v2 c2 dm
v2dm c2dm v2dm c2dm
当 v 0时 , m m0 , Ek 0
Ek 0
dEk
m c2dm
m0
c2
m m0
相对论动能: Ek mc2 m0c2
讨论
Ek
mc2
质能公式在原子核裂变和聚变中的应用
1,重核裂变
235 92
U
01n15349
Xe
95 38
Sr
201
n
质量亏损 m 0.22u 原子质量单位 1u 1.66 1027 kg
放出的能量 Q E m c2 200MeV
1g 铀235 的原子裂变所释放的能量
Q 8.51010 J
我国于 1958 年建成的首座重水反应堆
2,轻核聚变
2 1
H
21H42
He
氘核 氦核 质量亏损
m0 (21H) 3.3437 1027 kg m0 (42He) 6.6425 1027 kg
m 0.026u 4.31029 kg
释放能量Q E (m)c2 3.87 1012 J 24MeV
H42
He
1 0
n
求:反应释放的能量。
氘核 (21H) mD 3.3437 1027 kg
氚核 (31H) mT 5.0449 1027 kg 氦核 (42He) mHe 6.6425 1027kg 中子 (01n) mn 1.6750 1027kg
反应质量亏损 Δm0 (mD mT ) (mHe mn )
例:m0 1kg , E0 m0c2 91016 J
现有 100 座楼,每楼 200 套房,每套房用电功率
10000 W ,总功率 2108 W,每天用电 10 小时 ,
年耗电量 2.72 1015 J,可用约 33 年。
例:在一种热核反应中,各种粒子的静质量如下:
2 1
H
3 1
§4-4 狭义相对论动力学基础
一、狭义相对论的基本方程
牛顿力学中,动量 p mv
m :不随物体运动状态而改变的恒量。
相对论动量必须满足以下两个条件: a.在洛氏变换下保持不变;
b.在 v c 0 的条件下,还原为牛顿力
学的动量形式。
由此,得相对论动量:
p m0 v 1 v2 c2
体是没有静止质量的。
d.
相对论力学基本方程
p mv
d
(
m0
v)
F
dt 1 v2 c2
上式方程满足相对性原理
在 v c 的条件下:
F
m0 a
二、质量与能量的关系
1. 相对论动能
设质点在变力作用下,由静止开始沿x轴做一维运
动,由动能定理和动量定理:
dEk
Fdx
dp dx dt
