探究线段数量关系与位置关系
专题21 三角形压轴题之线段数量与位置关系(解析版)

1专题21 三角形压轴题之线段数量与位置关系知识对接考点一、利用三角形全等判断线段的关系的方法 两条线段的关系要从数量关系和位置关系两个方面考虑.1.数量关系一般是相等,可通过证明三角形全等得到;位置关系一般是平行或垂直,从图中可直接看出.2.证线段平行时,通常转化为证明同位角相等、内错角相等或同旁内角互补,这些角的关系一般根据全等三角形的性质得到;证明线段垂直的方法通常是证明线段所在直线所夹的角是90°.专项训练一、单选题1.(2021·北京东城·九年级二模)在平面直角坐标系xOy 中,⊙O 的半径为2,点A (1,3与⊙O 的位置关系是( ) A .在⊙O 上 B .在⊙O 内 C .在⊙O 外 D .不能确定【答案】A 【分析】根据点A 的坐标,求出OA =2,根据点与圆的位置关系即可做出判断. 【详解】解:⊙点A 的坐标为(13, ⊙由勾股定理可得:OA ()221+3,又⊙⊙O 的半径为2, ⊙点A 在⊙O 上. 故选:A . 【点睛】本题考查了点和圆的位置关系,点和圆的位置关系是由点到圆心的距离d 和圆的半径r 间的大小关系确定的:(1)当d r 时,点在圆外;(2)当d r =时,点在圆上;(3)当d r <时,点在圆内.2.如图,Rt ABC ∆中,90C ∠=︒,5AB =,4cos 5A =,以点B 为圆心,r 为半径作B ,当3r =时,B 与AC 的位置关系是( )A .相离B .相切C .相交D .无法确定【答案】B 【分析】根据Rt ABC ∆中,90C ∠=︒, 4cos 5A =,求出AC 的值,再根据勾股定理求出BC 的值,比较BC 与半径r 的大小,即可得出B 与AC 的位置关系. 【详解】解:⊙Rt ABC ∆中,90C ∠=︒, 4cos 5A =, ⊙cosA=45AC AB = ⊙5AB =, ⊙AC=43当3r =时,B 与AC 的位置关系是:相切 故选:B 【点睛】本题考查了由三角函数解直角三角形,勾股定理以及直线和圆的位置关系等知识,利用勾股定理解求出BC 是解题的关键.3.(2021·陕西西安·交大附中分校九年级)如图,点A 的坐标为(2,1),将线段OA 绕O 点顺时针旋转90°.得到线段OB .若正比例函数y =kx 图象经过点B ,则k 的值为( )A .2B .1C .﹣1D .﹣2【答案】D 【分析】如图,过A 点作AC ⊙x 轴于C ,过B 点作BD ⊙x 轴于D ,先证明AOC △⊙OBD ,得到OD3=AC =1,BD =OC =2,则B 点坐标可求,最后将点B 的坐标代入函数y kx =,即可求解. 【详解】解:如图,过A 点作AC ⊙x 轴于C ,过B 点作BD ⊙x 轴于D ,⊙点A 的坐标为(2,1), ⊙OC =2,AC =1,⊙线段OA 绕O 点顺时针旋转90°得到线段OB , ⊙OA =OB ,⊙AOB =90°, ⊙⊙AOC +⊙BOD =90°, ⊙AC ⊙x 轴, BD ⊙x 轴, ⊙⊙ACO =⊙BDO =90°, ⊙⊙AOC +⊙OAC =90°, ⊙⊙BOD =⊙OAC . 在AOC △和OBD 中ACO BDO OAC BOD OA BO ∠=∠⎧⎪∠=∠⎨⎪=⎩, ⊙AOC △⊙OBD (AAS ), ⊙OD =AC =1,BD =OC =2, 又⊙点B 在第四象限, ⊙B 点坐标为(1,﹣2),将点B 的坐标代入函数y =kx ,得:﹣2=k , 解得:k =﹣2, 故选:D . 【点睛】本题考查的是旋转的性质,一次函数图象上点的坐标特征,全等三角形的判定与性质,证明AOC △⊙OBD 是解答此题的关键.4.(2021·江门市第二中学九年级)如图,在矩形ABCD 中,AB =10,BC =12,点M ,N 分别在AD ,BC 上,且AM BN =,3AD AM =,E 为BC 边上一动点,连接DE ,将DCE∆沿DE 所在直线折叠得到⊙DC E ',当C '点恰好落在线段MN 上时,NE 的长为( )A .B .5C .3D .【答案】A 【分析】设CE =x ,则C ′E =x ,证明四边形MNCD 是矩形,由矩形的性质得出⊙DMN =⊙MNC =90°,MN =CD =10,由折叠的性质得出C ′D =CD =10,求出6MC '=,则4NC '=,在Rt NEC '中,由勾股定理得出222(8)4x x --=,解方程可得出答案. 【详解】解:设CE =x ,则C ′E =x , ⊙矩形ABCD 中,AB =10,⊙CD =AB =10,AD =BC =12,AD∥BC ,⊙点M ,N 分别在AD ,BC 上,且3AM =AD ,BN =AM , ⊙DM =CN =8,⊙四边形CDMN 为平行四边形, ⊙⊙NCD =90°,⊙四边形MNCD 是矩形,⊙⊙DMN =⊙MNC =90°,MN =CD =10, 由折叠知,C ′D =CD ,10,⊙6MC '==, ⊙1064CN '=-=, ⊙EN =CN -CE =8-x , ⊙C ′E 2-NE 2=C ′N 2, ⊙222(8)4x x --=, 解得,5x =,即853NE CN CE =-=-=. 故选:C . 【点睛】本题主要考查了矩形的性质与判定,勾股定理,一元一次方程的应用,折叠的性质,熟练掌握折叠的性质是解题的关键.55.(2021·江苏九年级)已知线段a ,b ,c ,求作:ABC ,使BC a =,AC b =,AB c =.下面的作图顺序正确的是( )⊙以点A 为圆心,以b 为半径画弧,以点B 为圆心,以a 为半径画弧,两弧交于C 点; ⊙作线段AB 等于c ;⊙连接AC ,BC ,则ABC 就是所求作图形. A .⊙⊙⊙ B .⊙⊙⊙ C .⊙⊙⊙ D .⊙⊙⊙【答案】C 【分析】先画AB c =,确定A 、B 点位置,然后通过画弧确定C 点位置,从而得到ABC . 【详解】⊙先作线段AB 等于c ,⊙再以点A 为圆心,以b 为半径画弧,以点B 为圆心,以a 为半径画弧,两弧交于C 点,⊙然后连接AC ,BC ,则ABC 就是所求作图形. 故选:C . 【点睛】本题考查了作图,作一个三角形,使这个三角形的三边等于已知的三条线段,其实质是作一条线段等于已知线段,原理是全等三角形的边边边判定定理.解决此类题目的关键是熟悉基本几何图形的性质,结合几何图形的基本性质把复杂作图问题分解成基本作图来解决. 6.(2021·河北九年级)在平面直角坐标系中,点()3,4A ,()2,B m -,当线段AB 最短时,m 的值为( ) A .5 B .3 C .4 D .0【答案】C 【分析】根据两点之间的距离公式即可求得m 的值. 【详解】解:根据两点之间的距离公式得 222(32)(4)(4)25AB m m ++-=-+⊙当4m =时,AB 最小 故答案为C . 【点睛】此题考查了平面直角坐标系中动点问题,熟练掌握两点间的距离公式是解题的关键. 7.(2021·山东九年级模拟预测)如图,木工师傅在板材边角处作直角时,往往使用“三弧法”,其作法是:⊙作线段AB ,分别以A ,B 为圆心,以AB 长为半径作弧,两弧的交点为C ;⊙以C 为圆心,仍以AB 长为半径作弧交AC 的延长线于点D ;⊙连接BD ,BC .下列结论不正确的是( )A .30CBD ∠=︒B .点C 是ABD △的外心C .2ABDSAB =D .22sin cos 1A D +=【答案】D 【分析】根据等边三角形的判定方法,直角三角形的判定方法以及等边三角形的性质,直角三角形的性质一一判断即可. 【详解】解:由作图可知:AC AB BC ==, ⊙ABC 是等边三角形,60A ABC ∠=∠=︒, 由作图可知:CB CA CD ==,⊙点C 是ABD △的外心,90ABD ∠=︒,BD =,⊙30D CBD ∠=∠=︒,2ABD S AB =△,⊙AC CD =,⊙2BDC S AB =△,⊙22223sin cos 2A D +=+=⎝⎭⎝⎭, 故A 、B 、C 正确,不符合题意;D 不正确,符合题意, 故选:D . 【点睛】此题考查了等边三角形的性质,等腰三角形的性质,三角函数,三角形面积的求法等,根据作图找到相应的边角条件是解题的关键.8.(2021·山东九年级)如图,在平行四边形ABCD 中,AD =2,AB ,⊙B 是锐角,AE ⊙BC 于点E ,F 是AB 的中点,连接DF ,EF .若⊙EFD =90°,则线段AE 的长为( )7A .2B .1C 3D 5【答案】D 【分析】延长EF 交DA 的延长线于Q ,连接DE ,设BE x =,首先证明2DQ DE x ==+,利用勾股定理构建方程即可求解. 【详解】解:如图,延长EF 交DA 的延长线于Q ,连接DE ,设BE x =,四边形ABCD 是平行四边形, //DQ BC ∴,Q BEF ∴∠=∠,,AF EB AFQ BFE =∠=∠, ()QFA EFB AAS ∴≌, ,AQ BE x QF EF ∴===, 90,EFD DF QE ∠=︒∴⊥, 2DQ DE x ∴==+, ,//AE BC BC AD ⊥,,90AE AD AEB EAD ∴⊥∠=∠=︒,22222AE DE AD AB BE =-=-, 22(2)46x x ∴+-=-,解得:121,3x x ==-(舍去)1BE ∴=,22615AE AB BE ∴--=故选:D . 【点睛】本题考查了平行四边形的性质、线段的垂直平分线的性质、勾股定理、全等三角形的判定与性质,解题的关键是:掌握相关知识点,添加辅助线、构造全等三角形来解决问题.9.(2021·浙江九年级期末)如图,在边长为2的菱形ABCD中,按以下步骤作图:⊙以点B 为圆心,适当的长为半径作弧,交AB,BD于E,F两点;⊙分别以点E和点F为圆心,以大于12EF的长为半径作弧,两弧交于点P;⊙作射线BP,交线段AD于点M.此时点M恰好是线段AD的中点,则CM的长为()A B C.D.3【答案】B【分析】根据作图证明⊙ABD为等腰三角形,根据菱形的性质证明⊙ABD为等边三角形,再证明MBC∆是直角三角形,根据勾股定理求解即可.【详解】解:由作图步骤⊙⊙⊙步可得:BP为⊙ABD的平分线,又⊙M为AD的中点,⊙⊙ABD为等腰三角形,AB=BD⊙四边形ABCD是菱形,且边长为2⊙AB=BC=CD=DA=2⊙⊙ABD为等边三角形,⊙⊙ABD=⊙BAD=60°⊙⊙ABM=⊙DBM=30°,⊙DBC=60°⊙⊙MBC=⊙MBD+⊙DBC=30°+60°=90°又⊙AD=2,M为AD的中点,⊙ABD为等边三角形⊙AM=11 2AD=⊙BM在Rt⊙MBC中,CM==故选:B.【点睛】9此题主要考查了菱形的性质、等腰三角形和等边三角形的判定与性质,勾股定理等知识,证明⊙ABD 为等边三角形是解答此题的关键.10.(2021·广东广州·执信中学九年级模拟预测)如图,一次函数2y x =的图像与x 轴、y 轴分别交于点A 、B ,把直线AB 绕点B 顺时针旋转30交x 轴于点C ,则线段AC 长为( )A 62B .32C .23D 32【答案】A 【分析】根据一次函数表达式求出点A 和点B 坐标,得到⊙OAB 为等腰直角三角形和AB 的长,过点C 作CD ⊙AB ,垂足为D ,证明⊙ACD 为等腰直角三角形,设CD =AD =x ,结合旋转的度数,用两种方法表示出BD ,得到关于x 的方程,解之即可. 【详解】解:⊙一次函数2y x =的图像与x 轴、y 轴分别交于点A 、B , 令x =0,则y 2y =0,则x =2 则A (2-,0),B (02,则⊙OAB 为等腰直角三角形,⊙ABO =45°, ⊙AB ()()2222+,过点C 作CD ⊙AB ,垂足为D , ⊙⊙CAD =⊙OAB =45°,⊙⊙ACD 为等腰直角三角形,设CD =AD =x , ⊙AC 22AD CD +2, ⊙旋转, ⊙⊙ABC =30°, ⊙BC =2CD =2x ,⊙BD 22BC CD -3, 又BD =AB +AD =2+x , ⊙2+x 3, 解得:x 3,x)⊙AC故选A.【点睛】本题考查了一次函数与坐标轴的交点问题,等腰直角三角形的判定和性质,直角三角形的性质,勾股定理,二次根式的混合运算,知识点较多,解题的关键是作出辅助线,构造特殊三角形.二、填空题11.(2021·江苏省天一中学九年级)如图,直线y=x+b(b>0)与x轴、y轴分别交于点A、B,点P在第一象限内,⊙OPB=45o,则线段OP、AP、BP满足的数量关系式为______.【答案】BP2+2OP2=AP2【分析】以OP为边作等腰直角三角形OPQ,证明⊙AOP⊙⊙BOQ,得到AP=BQ,证明⊙BPQ为直角三角形,得到BP2+PQ2=BQ2,再利用等量代换即可得到结论.【详解】解:如图,以OP为边作等腰直角三角形OPQ,则OP=OQ,⊙POQ=90°,⊙OPQ=⊙OQP=45°=PQ,⊙直线y=x+b与x轴、y轴分别交于点A、B,令x=0,则y=b,令y=0,则x=-b,即A(-b,0),B(0,b),即OA=OB=b,⊙⊙OAB是等腰直角三角形,⊙OAB=⊙OBA=45°,⊙⊙AOB+⊙POB=⊙POQ+⊙POB,即⊙AOP=⊙BOQ,OA=OB,OP=OQ,11⊙⊙AOP ⊙⊙BOQ (SAS ), ⊙AP =BQ , ⊙⊙OPB =45°,⊙⊙BPQ =⊙OPB +⊙OPQ =90°, ⊙在⊙BPQ 中,BP 2+PQ 2=BQ 2, ⊙BP 2+2OP 2=AP 2,故答案为:BP 2+2OP 2=AP 2.【点睛】本题考查了等腰直角三角形的判定和性质,全等三角形的判定和性质,一次函数与坐标轴交点问题,勾股定理,有一定难度,解题的关键是添加辅助线,构造出全等三角形. 12.(2021·清远市清新区凤霞中学九年级一模)如图,点D 是锐角AOB ∠内一点,DE OA ⊥于点E ,点F 是线段OE 的一个动点,点G 是射线OB 的一个动点,连接DF 、FG 、GD ,当DFG 的周长最小时,FDG ∠与AOB ∠的数量关系式是________.【答案】2180FDG AOB ∠+∠=︒ 【分析】作D 关于OA 的对称点D ′,作D 关于OB 的对称得D ″,连接D ′D ″,交OA 、OB 于F 、G ,此时⊙DFG 的周长最小,最小值为D ′D ″,连OD 、OD ′、OD ″,根据轴对称的性质得出⊙GOD ⊙⊙GOD ″,⊙FOD ⊙⊙FOD ′,即可得出⊙BOD =⊙BOD ′,⊙ODG =⊙OD ″G ,⊙DOA =⊙AOD ′,⊙ODF =⊙ODF ′,由⊙D ′OD ″=2⊙AOB ,⊙GDF =⊙ODF ′+⊙ODG ″根据三角形内角和定理即可得出2⊙AOB +⊙GDF =180°. 【详解】解:作D关于OA的对称点D′,作D关于OB的对称得D″,连接D′D″,交OA、OB于F、G,此时⊙DFG的周长最小,最小值为D′D″,连OD、OD′、OD″,由轴对称的性质可知,⊙GOD⊙⊙GOD″,⊙FOD⊙⊙FOD′,⊙⊙BOD=⊙BOD″,⊙ODG=⊙OD″G,⊙DOA=⊙AOD′,⊙ODF=⊙OD′F,⊙⊙D′OD″=2⊙AOB,⊙GDF=⊙OD′F+⊙OD″G,⊙⊙D′OD″+⊙OD′F+⊙OD″G=180°,⊙2⊙AOB+⊙GDF=180°,故答案为2⊙AOB+⊙GDF=180°.【点睛】本题考查了轴对称-最短路线问题,熟练掌握轴对称的性质是解题的关键.13.(2021·石家庄市第二十八中学九年级)在数学探究活动中,敏敏进行了如下操作:如图,将四边形纸片ABCD沿过点A的直线折叠,使得点B落在CD上的点Q处.折痕为AP再将PCQ△,ADQ△分别沿PQ,AQ折叠,此时点C,D落在AP上的同一点R处.请完成下列探究:(1)AD与BC所在直线的位置关系______;(2)PAQ的大小为______°;(3)当四边形APCD是平行四边形时,ABQR的值为______.【答案】//AD BC30° 【分析】13(1)根据折叠性质和平角定义证得180D C ∠+∠=︒,再根据平行线的判定可得AD 与BC 所在直线的位置关系;(2)根据折叠性质和平角定义证得90B AQP ∠=∠=︒,再根据平行线的性质证得90B DAB ∠=∠=︒,进而由DAQ QAP PAB ∠=∠=∠求解即可;(3)根据折叠性质和平行四边形的性质证得AR PR =,再根据直角三角形斜边上的中线等于斜边的一半证得12QR AP =,然后根据直角三角形中30°角所对的直角边是斜边的一半和勾股定理求得2AP PB =, PB QR =,223AB AP PB PB -,进而求解即可. 【详解】解:(1)由折叠的性质可得:B AQP ∠=∠,DAQ QAP PAB ∠=∠=∠,DQA AQR ∠=∠,CQP PQR ∠=∠,D ARQ ∠=∠,C QRP ∠=∠,⊙180QRA QRP ∠+∠=︒, ⊙180D C ∠+∠=︒, ⊙//AD BC , 故答案是:AD ⊙BC ;(2)⊙180DQR CQR ∠+∠=︒,DQA AQR ∠=∠,CQP PQR ∠=∠, ⊙90DQA CQP ∠+∠=︒, ⊙90AQP ∠=︒, ⊙90B AQP ∠=∠=︒,由(1)结论知180B DAB ∠+∠=︒, ⊙90DAB ∠=︒,⊙30DAQ QAP PAB ∠=∠=∠=︒, 故答案为:30;(2)由折叠的性质可得:AD AR =,CP PR =, ⊙四边形APCD 是平行四边形, ⊙AD PC =, ⊙AR PR =, 又⊙90AQP ∠=︒,⊙12QR AP =, ⊙30PAB ∠=︒,90B ∠=︒, ⊙2AP PB =, ⊙PB QR =,⊙AB =,⊙AB ABQR PB==【点睛】本题考查折叠性质、平行线的判定与性质、平行四边形的性质、直角三角形斜边上的中线性质、含30°角的直角三角形的性质、勾股定理、平角定义,熟练掌握折叠性质和相关知识的联系是解答的关键.14.(2021·连云港市新海实验中学九年级)如图,正方形ABCD 中,AB =O 是BC 边的中点,点E 是正方形内一动点,OE =4,连接DE ,将线段DE 绕点D 逆时针旋转90°得DF ,连接AE 、CF ,则线段OF 长的最小值为_____【答案】4. 【分析】连接DO ,将线段DO 绕点D 逆时针旋转90°得DM ,连接OF ,FM ,OM ,证明⊙EDO ⊙⊙FDM ,可得FM =OE =4,由条件可得OM =OF +MF ≥OM ,即可得出OF 的最小值. 【详解】解:如图,连接DO ,将线段DO 绕点D 逆时针旋转90°得DM ,连接OF ,FM ,OM , ⊙⊙EDF =⊙ODM =90°, ⊙⊙EDO =⊙FDM , ⊙DE =DF ,DO =DM , ⊙⊙EDO ⊙⊙FDM (SAS ), ⊙FM =OE =4,⊙正方形ABCD 中,AB =O 是BC 边的中点,⊙OC =15⊙OD 22(45)(25)+10, ⊙OM 221010+102 ⊙OF +MF ≥OM , ⊙OF ≥24,⊙线段OF 长的最小值为1024. 故答案为:1024.【点睛】本题考查了图形旋转,全等三角形的判定和性质、正方形的性质和两点之间距离,熟练掌握并准确应用是解题的关键.15.(2021·哈尔滨市虹桥初级中学校九年级)已知.在ABC 中,42AB =45ABC ∠=︒,5AC =,则线段BC 的长为___________.【答案】7或1 【分析】作AD ⊙BC 于点D ,分类讨论点C 在BD 延长线上或BD 上,通过勾股定理进行求解即可. 【详解】解:作AD ⊙BC 于点D ,⊙当点C 在BD 延长线上时, ⊙45ABC ∠=︒,90ADB ∠=︒, ⊙ABD △为等腰直角三角形,⊙222AD BD AB +=,即(22242AD =, ⊙4=AD ,在Rt ACD △中,由勾股定理得:2222543CD AC AD -=-,⊙7BC BD CD =+=;⊙当点C '在BD 上时,同⊙可得:4AD BD ==,3C D '=, ⊙1BC BD C D ''=-=. 故答案为:7或1. 【点睛】本题考查了勾股定理的应用,熟练掌握勾股定理是解题的关键,无图形时注意考虑是否需要分类讨论. 三、解答题16.(2021·江苏南通市·)(1)甲厂每天加工的数量是乙厂每天加工数量的1.5倍,两厂各加工600套防护服,甲厂比乙厂要少用4天.求甲、乙两厂每天各加工多少套防护服? (2)如图,点C ,D 在线段AB 上,CE ⊙AB ,DF ⊙AB ,AC =BD ,AE =BF ,点G 为AB ,EF 的交点,求证CD 与EF 互相平分.【答案】(1)甲厂每天加工75套防护服,乙厂每天加工50套防护服;(2)见解析 【分析】(1)利用甲厂每天加工的数量是乙厂每天加工数量的1.5倍设乙厂每天加工x 套防护服,则甲厂每天加工1.5x 套防护服,根据等量关系是乙工作量除以以的工作效率-甲工作量除以甲工作效率=4天列方程解之即可;(2)连结ED ,CF ,CE ⊙AB ,DF ⊙AB ,可得⊙ECA =⊙FDB ,可证⊙ACE ⊙⊙BDF (HL )可得CE =DF ,且CE∥DF ,可证四边形CFDE 为平行四边形,可得CD 与EF 互相平分. 【详解】(1)解:设乙厂每天加工x 套防护服,则甲厂每天加工1.5x 套防护服, 根据题意,得60060041.5x x-=, 解得x =50,经检验:x =50是所列方程的解, 则1.5x =75.答:甲厂每天加工75套防护服,乙厂每天加工50套防护服.17(2)证明:连结ED ,CF , ⊙CE ⊙AB ,DF ⊙AB , ⊙⊙ECA =⊙FDB =90°, 在Rt ⊙ACE 与Rt ⊙BDF 中,AC BDAE BF =⎧⎨=⎩, ⊙⊙ACE ⊙⊙BDF (HL ), ⊙CE =DF ,又⊙⊙ECD =⊙FDC =90°, ⊙CE∥DF ,⊙四边形CFDE 为平行四边形, ⊙CD 与EF 互相平分.【点睛】本题考查列分式方程解应用题,与三角形全等判定与性质,平行四边形判定与性质,掌握列分式方程解应用题,与三角形全等判定与性质,平行四边形判定与性质是解题关键. 17.(2021·河南郑州外国语中学九年级)在ABC 中,3AC BC ==120ACB ∠=︒,在ADE 中,90DAE ∠=︒,30AED ∠=︒,1AD =,连接BD ,BE ,点F 是BD 的中点,连接CF . (1)如图1,当顶点D 在边AB 上时,线段BE 与线段CF 的数量关系是______,线段BE 与线段CF 的位置关系是 ;(2)将ADE 绕点A 旋转,转到图2的位置时,(1)中结论是否仍然成立?若成立,请给予证明,若不成立,请说明理由;(3)在ADE 绕点A 旋转的过程中,线段AF 的最大值为______;当//DE CF 时,线段CF 的长为______.【答案】(1)BE =,BE CF ⊥;(2)仍然成立,见解析;(3)12,2或1【分析】(1)过点A 作AG AB ⊥,交BC 延长线与点G ,连接GD 并延长交BE 于点H ,证明ADG⊙AEB ,得BE ABGD AG=AGD ABE ∠=∠,再证明CF 为BGD 的中位线即可证明结论; (2)与(1)同理可证明结论仍然成立;(3)延长AF 到点K ,使FK AF =,连接BK ,通过SAS 证明AFD ⊙KFB ,得1BK AD ==,在ABK 中,利用第三边小于两边之和,得AK AB BK <+,求出AK 最大为4,则AF 最大为2即可,当//DE CF 时,由(1)中证明可知//DG CF ,则G ,D ,E 三点共线,分点E 在D 下方,或点E 在点D 上方两种情形,分别画图进行计算即可. 【详解】解:(1)过点A 作AG AB ⊥,交BC 延长线与点G ,,连接GD 并延长交BE 于点H ,AC BC =,120ACB ∠=︒, 30CAB CBA ∴∠=∠=︒,60GAC AGC ∴∠=∠=︒, AC CG BC ∴==,∴点C 为BG 的中点,AG AD AB AE == 且DAG EAB ∠=∠,ADG ∴⊙AEB ,BE ABGD AG∴==AGD ABE ∠=∠,193BE DG ∴=,点C ,F 分别是BG ,BD 的中点,CF ∴为BGD 的中位线,//CF GD ∴,12CF GD =,3BE CF ∴=,又ADG BDH ∠=∠,90BHD GAD ∴∠=∠=︒, GH BE ∴⊥, //CF GD , CF BE ∴⊥,故答案为:23BE CF =,CF BE ⊥, (2)(1)中结论仍然成立,过点A 作AG AB ⊥,交BC 延长线与点G ,,连接GD 并延长交BE 于点H ,设GD 交AB 于点O ,由(1)同理可证ADG ⊙AEB , 3BE ABGD AG∴∴==AGD ABE ∠=∠, 3BE DG ∴=,点C ,F 分别是BG ,BD 的中点,CF ∴为BGD 的中位线,//CF GD ∴,12CF GD =,3BE CF ∴=,又AOG BOH ∠=∠,90BHD GAO ∴∠=∠=︒, GH BE ∴⊥, //CF GD , CF BE ∴⊥,故答案为:BE =,CF BE ⊥,(3)如图,延长AF 到点K ,使FK AF =,连接BK ,DF BF =,AF FK =,AFD BFK ∠=∠, AFD ∴⊙KFB , 1BK AD ∴==,在ABK 中, AK AB BK <+,4AK ∴<,∴当4AK =时,AF 最大为2,当//DE CF 时,由(2)中证明可知//DG CF ,G ∴,D ,E 三点共线,如图,当点E 在点D 下方时,AG AE ==30E ∠=︒,3GE ∴=,211GD ∴=,1122CF DG ∴==, 当点E 与G 重合时,此时//DE CF ,112CF DE ∴==, 综上:1CF =或12,故答案为:2,1或12.【点睛】本题是几何变换综合题,考查了含30角的直角三角形,相似三角形的判定与性质,全等三角形的判定与性质,中位线定理等知识,是作辅助线,构造三角形相似或者全等是解题的关键,综合性较强,难度较大.18.(2021·长沙市北雅中学)(1)如图1,正方形ABCD 和正方形DEFG (其中AB DE >),连接CE ,AG 交于点H ,请直接写出线段AG 与CE 的数量关系________,位置关系________; (2)如图2,矩形ABCD 和矩形DEFG ,2AD DG =,2AB DE =,AD DE =,连接AG ,CE 交于点H ,(1)中线段关系还成立吗?若成立,请写出理由;若不成立,请写出线段AG ,CE 的数量关系和位置关系,并说明理由;(3)矩形ABCD 和矩形DEFC ,26AD DG ==,28AB DE ==,直线AG ,CE 交于点H ,当点E 与点H 重合时,请直接写出线段AE 的长.【答案】(1)相等,垂直;(2)不成立,CE=2AG,AG⊙CE,理由见解析;(3)16 5【分析】(1)根据正方形的性质,证明⊙GDA⊙⊙EDC即可得到打啊;(2)证明⊙GDA⊙⊙EDC,即可求解;(3)分⊙当点E在线段AG上时;⊙当G在线段AE上时;两种情况进行讨论求解即可.【详解】解:(1)在正方形ABCD和正方形DEFG中,⊙ADC=⊙EDG=90°,⊙⊙ADE+⊙EDG=⊙ADC+⊙ADE,即⊙ADG=⊙CDE,⊙DG=DE,DA=DC,⊙⊙GDA⊙⊙EDC(SAS),⊙AG=CE,⊙GAD=⊙ECD,⊙⊙COD=⊙AOH,⊙⊙AHO=⊙CDO=90°,⊙AG⊙CE,故答案为:相等,垂直;(2)不成立,CE=2AG,AG⊙CE,理由如下:设AD与CE交于M,由(1)知⊙ADE+⊙EDG=⊙ADC+⊙ADE,即⊙ADG=⊙EDC,⊙AD=2DG,AB=2DE,AD=DE,又⊙四边形ABCD是矩形,⊙AB=CD,⊙12 DG DE DEAD AB CD===,⊙⊙GDA⊙⊙EDC,23⊙12AD AG CD CE ==,⊙ECD =⊙GAD , ⊙CE =2AG , ⊙⊙CMD =⊙AMH , ⊙⊙AHM =⊙CDM =90°, ⊙AG ⊙CE ;(3)⊙当点E 在线段AG 上时,如图所示, ⊙AD =2DG =6,AB =2DE =8, ⊙DG =3,ED =4, ⊙四边形DEFG 是矩形, ⊙⊙EDG =90°,⊙225EG DG DE +=, 过点D 作DP ⊙AG 于P ,⊙⊙DPG =⊙EDG =90°,⊙DGP =⊙EGD , ⊙⊙DGP ⊙⊙EGD , ⊙DG PG PDEG DG DE==即3534PG PD ==,⊙95PG =,125PD =,⊙22621AP AD PD =-=⊙62116AE AG GE AP GP GE -=-=+-=⊙当G 在线段AE 上时,如图所示, 过点D 作DP ⊙AG 于P ,⊙DPG =⊙EDG =90°,⊙DGP =⊙EGD ,同理得125PD =,AP =由勾股定理得165PE ==⊙AE AP PE =+=综上所述:AE =【点睛】本题主要考查了矩形的性质,全等三角形的性质与判定,相似三角形的性质与判定,勾股定理,旋转的性质,解题的关键在于能够熟练掌握相关知识进行求解.19.(2021·扬州中学教育集团树人学校)如图1,在⊙ABC 中,⊙ACB =90°,AC =BC =2,M 为AB 的中点.D 是射线BC 上一个动点,连接AD ,将线段AD 绕点A 顺时针旋转90°得到线段AE ,连接ED ,N 为ED 的中点,连接AN ,MN . (1)当BD =1时,AN = ,NM 与AB 的位置关系是 ; (2)当2<BD <4时,⊙依题意补全图2;⊙判断(1)中NM 与AB 的位置关系是否发生变化,并证明你的结论; (3)连接ME ,在点D 运动的过程中,当BD 的长为何值时,ME 的长最小?最小值是多少?请直接写出结果.25【答案】(110(2)⊙画图见分析;⊙不会发生变化,证明见分析;(3)BD 的长为3时,ME 的长最小,最小值为1. 【分析】(1)根据已知条件得到1CD =,根据勾股定理得到22125AD +到ADE 是等腰直角三角形,求得10DE =根据直角三角形的性质得到1102AN DE ==122AM AB ==ACD AMN ∽,根据相似三角形的性质即可得到结论; (2)⊙根据题意补全图形即可;⊙根据等腰直角三角形的性质得到45CAB B ∠=∠=︒,求得45CAN NAM ∠+∠=︒,根据旋转的性质得到AD AE =,90DAE ∠=︒,推出ACD AMN ∽,由相似三角形的性质得到AMN ACD ∠=∠,即可得到结论;(3)连接ME ,EB ,过M 作MG EB ⊥于G ,过A 作AK AB ⊥交BD 的延长线于K ,得到AKB △是等腰直角三角形,推出ADK ABE △≌△,根据全等三角形的性质得到45ABE K ∠=∠=︒,证得BMG △是等腰直角三角形,求出2BC =,22AB =2MB ,由ME MG ≥,于是得到当ME MG =时,ME 的值最小,根据等量代换即可得到结论. 【详解】解:(1)⊙90ACB ∠=︒,2AC BC ==,1BD =, ⊙2CD =,⊙225AD AC CD +⊙将线段AD 绕点A 顺时针旋转90°得到线段AE , ⊙ADE 是等腰直角三角形, ⊙210DE AD == ⊙N 为ED 的中点, ⊙1102AN DE ==⊙M 为AB 的中点,⊙12AM AB ==⊙AN AD ==,AM AC = ⊙AN AMAD AC=, ⊙45CAB DAN ∠=∠=︒, ⊙CAD BAN ∠=∠, ⊙ACD AMN ∽, ⊙90AMN C ∠=∠=︒, ⊙MN AB ⊥.(2)⊙补全图形如下图所示;⊙(1)中NM 与AB 的位置关系不会发生变化. 理由如下:⊙90ACB ∠=︒,AC BC =, ⊙45CAB B ∠=∠=︒, ⊙45CAN NAM ∠+∠=︒,⊙将线段AD 绕点A 顺时针旋转90°得到线段AE , ⊙AD AE =,90DAE ∠=︒, ⊙N 为ED 的中点,⊙1452DAN DAE ∠=∠=︒,AN DE ⊥,⊙45CAN DAC ∠+∠=︒ ⊙NAM DAC ∠=∠,在Rt AND △中,452AN cos DAN cos AD =∠=︒=,同理45AC cos AB =︒,27⊙AC ANAB AD=, ⊙45DAC CAN MAN ∠=︒-∠=∠, ⊙ACD AMN ∽, ⊙AMN ACD ∠=∠, ⊙D 在BC 的延长线上, ⊙18090ACD ACB ∠=︒-∠=︒, ⊙90AMN∠=︒,⊙MN AB ⊥.(3)连接ME ,EB ,过M 作MG EB ⊥于G ,过A 作AK AB ⊥交BD 的延长线于K ,则AKB △是等腰直角三角形, 在ADK △与ABE △中,AK ABKAD BAE AD AE =⎧⎪∠=∠⎨⎪=⎩, ⊙ADK ABE △≌△, ⊙45ABE K ∠=∠=︒, ⊙BMG △是等腰直角三角形, ⊙2BC =,⊙22AB =2MB ⊙451MG cos MB =︒=, ⊙90G ∠=︒, ⊙ME MG ≥,⊙当ME MG =时,ME 的值最小, ⊙1ME BE ==, ⊙1DK BE ==, ⊙2CK BC ==, ⊙1CD =, ⊙3BD =,⊙BD 的长为3时,ME 的长最小,最小值为1.【点睛】本题考查了旋转的性质,勾股定理,全等三角形的性质和判定,相似三角形的判定和性质,等腰直角三角形的判定和性质,直角三角形的性质,正确的作出辅助线是解题的关键. 20.(2021·湖北十堰市·九年级)如图,在Rt ABC 中,90BAC ∠=︒,AB AC =,点D ,E 分别在边AB ,AC 上,AD AE =,连接DC 、BE ,点P 为DC 的中点.(1)观察图1,猜想线段AP 与BE 的数量关系是______,位置关系是______;(2)把ADE 绕点A 逆时针方向旋转到图2的位置,(1)中的结论是否仍然成立,若成立请证明;若不成立,请写出新的结论并说明理由;(3)把ADE 绕点A 在平面内自由旋转,若6DE =,10BC =,请直接写出线段AP 长的取值范围. 【答案】(1)12AP BE =,AP BE ⊥;(2)12AP BE =,AP BE ⊥仍成立,理由见解析;(3)AP ≤ 【分析】(1)证明⊙BAE ⊙⊙CAD ,继而结合直角三角形中斜边中线的性质即可得答案; (2)延长PA 交BE 于N ,延长AP 到M 使PM AP =,连接CM ,用三角形全等推出12AP BE =,再得到//AD CM ,用平行线的性质和判定就可以证明AP BE ⊥. (3)利用三角形三边关系求出AM 的范围即可确定线段AP 长的取值范围. 【详解】 (1)12AP BE =,AP BE ⊥;理由如下: ⊙AB =AC ,⊙BAE =⊙CAD =90°,AD =AE , ⊙⊙BAE ⊙⊙CAD , ⊙BE =CD ,⊙ABE =⊙ACD , 又⊙P 为CD 中点, ⊙AP =CP =12CD ,29⊙12AP BE =,⊙ACD =⊙CAP , ⊙⊙ABE +⊙AEB =90°, ⊙⊙CAP +⊙AEB =90°, ⊙⊙ANE =90°, ⊙AP BE ⊥(2)成立.12AP BE =,AP BE ⊥. 理由如下:延长PA 交BE 于N ,延长AP 到M 使PM AP =,连接CM ,DPA CPM ∠=∠,⊙点P 为DC 的中点,⊙DP PC = 则ADP MCP ≅△△,⊙AD CM AE ==,DAP M ∠=∠, ⊙//AD CM ,⊙M DAP ∠=∠,180DAC ACM ∠+∠=︒. 又⊙90BAC DAE ∠=∠=︒, ⊙180DAC BAE ∠+∠=︒, ⊙ACM BAE ∠=∠, 又⊙AB AC =, ⊙BAE ACM ≅△△,⊙M AEB DAP ∠=∠=∠,BE AM =, ⊙12AP AM =, ⊙12AP BE =. 又⊙90EAN DAP ∠+∠=︒, ⊙90EAN AEB ∠+∠=︒, ⊙90ENA ∠=︒, 即AP BE ⊥.(3)⊙⊙AED ,⊙ABC 都是等腰直角三角形,6DE =,10BC =,⊙AD =AE ,AC =AB ,又由(2)知,CM =AD ⊙AM ≤⊙AM ≤ ⊙12AP AM =,AP ≤ 【点睛】此题考查的是三角形的旋转和相似三角形的综合题,熟悉掌握三角形旋转和相识三角形的性质和灵活的作品辅助线是解题的关键.21.(2021·北京市三帆中学)已知点P 为线段AB 上一点,将线段AP 绕点A 逆时针旋转α,得到线段AC ;再将线段BP 终点B 逆时针旋转180α︒-,得到线段BD ;连接AD ,取AD 中点M ,连接BM ,CM . (1)当60a =︒.⊙如图1,点P 为AB 中点时,补全图形,直接写出线段BM 与CM 的位置关系______.数量关系______.⊙如图2,当点P 不为AB 中点时,写出线段BM 与CM 的数量关系与位置关系,并证明.(2)如图3,当45α=︒,点P 为AB 中点时,直接写出线段AP ,BP ,BC 的数量关系______.【答案】(1)⊙BM ⊙CM ;;⊙BM ⊙CM ;,见解析;(2)22222BC BC AP BP ==+【分析】(1)⊙延长BM到点E,使得BM=ME,连接AE,CE,DE,通过证明⊙CAE⊙⊙CPB,证明⊙CEB是等边三角形,利用等腰三角形三线合一思想计算即可;⊙的结论不变,证明方法与⊙类似;(2)延长BM到点G,使得BM=MG,连接AG,CG,DG,证明三角形ACG是等腰直角三角形即可【详解】(1)⊙如图1, 延长BM到点E,使得BM=ME,连接AE,CE,DE,⊙M是AD的中点,⊙AM=MD,⊙BM=ME,⊙四边形AEDB是平行四边形,⊙AE=BD,AE∥BD,⊙PB=BD,⊙PB=AE,⊙⊙CAP=60°,AC=AP,⊙⊙APC是等边三角形,⊙AC=PC,⊙ACP=⊙APC=60°,⊙⊙CPB=120°,⊙⊙CAP=60°,⊙⊙PBD=120°,⊙⊙BAE=60°,⊙⊙CAE=120°,⊙⊙CAE=⊙CPB,⊙⊙CAE⊙⊙CPB,⊙CE=CB,⊙ACE=⊙PCB,⊙⊙ACE+⊙PCE=⊙PCB+⊙PCE,⊙⊙ACP=⊙BCE=60°,⊙⊙CEB是等边三角形,⊙BM=ME,31⊙BM⊙CM,⊙tan60°=CM BM,⊙CM;故答案为:BM⊙CM;CM;⊙关系为:BM⊙CM;CM;理由如下:如图2, 延长BM到点F,使得BM=MF,连接AF,CF,DF,⊙M是AD的中点,⊙AM=MD,⊙BM=MF,⊙四边形AFDB是平行四边形,⊙AF=BD,AF∥BD,⊙PB=BD,⊙PB=AF,⊙⊙CAP=60°,AC=AP,⊙⊙APC是等边三角形,⊙AC=PC,⊙ACP=⊙APC=60°,⊙⊙CPB=120°,⊙⊙CAP=60°,⊙⊙PBD=120°,⊙⊙BAF=60°,⊙⊙CAF=120°,⊙⊙CAF=⊙CPB,⊙⊙CAF⊙⊙CPB,⊙CF=CB,⊙ACF=⊙PCB,⊙⊙ACF+⊙PCF=⊙PCB+⊙PCF,⊙⊙ACP=⊙BCF=60°,⊙⊙CFB是等边三角形,33⊙BM =MF ,⊙BM ⊙CM , ⊙tan 60°=CMBM, ⊙CM 3;(2)如图3, 延长BM 到点G ,使得BM =MG ,连接AG ,CG ,DG , ⊙M 是AD 的中点, ⊙AM =MD , ⊙BM =MG ,⊙四边形AGDB 是平行四边形, ⊙AG =BD ,AG∥BD , ⊙PB =BD , ⊙PB =AG , ⊙AP =PB =AC⊙AP =PB =AG =AC =BD , ⊙⊙CAP =45°, ⊙⊙PBD =135°, ⊙⊙BAG =45°, ⊙⊙CAG =90°,⊙⊙CAN =⊙GAN ,⊙ANC =90°,⊙AN =NC =NG , ⊙在直角三角形BCN 中, 222CN BN BC +=,⊙222))PB PB BC ++=,⊙22222BC BC AP BP ==【点睛】本题考查了等边三角形的判定和性质,平行四边形的判定和性质,勾股定理,三角函数,熟练运用上面的知识,准确推理是解题的关键.22.(2021·河南信阳·)在ABC ∆中,BD AC ⊥于点D ,点Р为射线BD 上任一点(点B 除外)连接AP ,将线段PA 绕点Р顺时针方向旋转α︒,ABC α=∠,得到PE ,连接CE .(1)(观察发现)如图1,当BA BC =,且60ABC ∠=︒时,BP 与CE 的数量关系是___________,BC 与CE 的位置关系是___________.(2)(猜想证明)如图2,当BA BC =,且90ABC ∠=︒时,(1)中的结论是否成立?若成立,请予以证明;若不成立,请说明理由.(请选择图2,图3中的一种情况予以证明或说理)(3)(拓展探究)在(2)的条件下,若8AB =,AP =CE 的长. 【答案】(1)BP CE =,BC CE ⊥;(2)BC CE ⊥成立,BP CE =不成立,BP 与CE 的关系为CE =,见解析;(3)2或14 【分析】(1)连接AE ,证明⊙ABC 、⊙APE 为等边三角形, 再证明ABP ACE ∆∆≌,根据全等三角形的性质可得BP=CE ,ABP ACE ∠=∠,再求得30ABP ACE ∠=∠=︒,即可得90ACE ACB ∠+∠=︒,所有BC CE ⊥.(2)BC CE ⊥成立,BP CE =不成立,BP 与CE 的关系为CE =.选图2证明:连接AE ,易证BAP CAE ∆∆∽,根据相似三角形的性质可得CE CABP BA==ACE ABP ∠=∠,根据等腰直角三角形的性质可得45ABD CBD ACB ACE ∠==︒∠∠==∠,由此可得3590BCE BCA ACE ∠=∠+∠=︒,结论可证;选图3证明,类比图2的证明方法即可;(3)分图2和图3两种情况求CE 的长即可. 【详解】(1)如图,连接AE ,⊙BA BC =,且60ABC ∠=︒, ⊙⊙ABC 为等边三角形,⊙60ABC BAC ACB ∠=∠=∠=︒,AB =AC , ⊙PE PA =,且60APE α∠==︒, ⊙⊙APE 为等边三角形, ⊙60PAE ∠=︒,AP =AE ,⊙BAC PAC PAE PAC ∠-∠=∠-∠, ⊙BAP CAE ∠=∠; 在⊙BAP 和⊙CAE 中, AB AC BAP CAE AP AE =⎧⎪∠=∠⎨⎪=⎩, ⊙ABP ACE ∆∆≌,⊙BP=CE ,ABP ACE ∠=∠,⊙BD AC ⊥,BA BC =, 60ABC ∠=︒, ⊙⊙ABP =30°,⊙30ABP ACE ∠=∠=︒, ⊙90ACE ACB ∠+∠=︒, ⊙BC CE ⊥.故答案为:BP CE =,BC CE ⊥.(2)BC CE ⊥成立,BP CE =不成立,BP 与CE 的关系为2CE BP =. 理由如下:选图2证明:连接AE ,。
2022-2023学年九年级数学中考复习《几何图形变换综合压轴题》专题提升训练(附答案)

2022-2023学年九年级数学中考复习《几何图形变换综合压轴题》专题提升训练(附答案)1.如图,已知∠DAC=90°,△ABC是等边三角形,点P为射线AD上任意一点(点P与点A不重合),连接CP,将线段CP绕点C顺时针旋转60°得到线段CQ,连接QB并延长交直线AD于E.(1)如图1,猜想∠QEP=;(2)如图2,若当∠DAC是锐角时,其他条件不变,猜想∠QEP的度数,并证明;(3)如图3,若∠DAC=135°,∠ACP=15°,且AC=6,求BQ的长.2.如图1,在等腰△ABC中,AB=AC,AD为中线,将线段AC绕点A逆时针旋转90°,得到线段AE,连接BE交直线AD于点F,连接CF.(1)若∠BAC=30°,则∠FBC=°;(2)若∠BAC是钝角时,①请在图2中依题意补全图形,并标出对应字母;②探究图2中△BCF的形状,并说明理由;③若AB=5,BC=8,则EF=.3.在△ABC中,AB=AC,∠BAC=90°,点D在射线BC上(不与点B、点C重合),将线段AD绕A逆时针旋转90°得到线段AE,作射线BA与射线CE,两射线交于点F.(1)若点D在线段BC上,如图1,请直接写出CD与EF的关系.(2)若点D在线段BC的延长线上,如图2,(1)中的结论还成立吗?请说明理由.(3)在(2)的条件下,连接DE,G为DE的中点,连接GF,若tan∠AEC=,AB=,求GF的长.4.已知△ABC中,∠ABC=90°,将△ABC绕点B逆时针旋转90°后,点A的对应点为点D,点C的对应点为点E,直线DE与直线AC交于点F,连接FB.(1)如图1,当∠BAC<45°时,①求证:DF⊥AC;②求∠DFB的度数;(2)如图2,当∠BAC>45°时,①请依意补全图2;②用等式表示线段FC,FB,FE之间的数量关系,并证明.5.实验探究:如图,△ABC和△ADE是有公共顶点的等腰直角三角形,∠BAC=∠DAE=90°,BD、CE延长线交于点P.【问题发现】(1)把△ABC绕点A旋转到图1,BD、CE的关系是(“相等”或“不相等”),请直接写出答案;【类比探究】(2)若AB=3,AD=5,把△ABC绕点A旋转,当∠EAC=90°时,在图中作出旋转后的图形,并求出此时PD的长;【拓展延伸】(3)在(2)的条件下,请直接写出旋转过程中线段PD的最小值为.6.如图,在平面直角坐标系中,点O为坐标原点,点A(0,3)与点B关于x轴对称,点C(n,0)为x轴的正半轴上一动点.以AC为边作等腰直角三角形ACD,∠ACD=90°,点D在第一象限内.连接BD,交x轴于点F.(1)如果∠OAC=38°,求∠DCF的度数;(2)用含n的式子表示点D的坐标;(3)在点C运动的过程中,判断OF的长是否发生变化?若不变求出其值,若变化请说明理由.7.[问题背景]如图1所示,在△ABC中,AB=BC,∠ABC=90°,点D为直线BC上的一个动点(不与B、C重合),连接AD,将线段AD绕点D按顺时针方向旋转90°,使点A旋转到点E,连接EC.[问题初探]如果点D在线段BC上运动,通过观察、交流,小明形成了以下的解题思路:过点E作EF⊥BC交直线BC于F,如图2所示,通过证明△DEF≌△,可推证△CEF是三角形,从而求得∠DCE=°.[继续探究]如果点D在线段CB的延长线上运动,如图3所示,求出∠DCE的度数.[拓展延伸]连接BE,当点D在直线BC上运动时,若AB=,请直接写出BE的最小值.8.如图,在等边△ABC中,点D为BC的中点,点E为AD上一点,连EB、EC,将线段EB绕点E顺时针旋转至EF,使点F落在BA的延长线上.(1)在图1中画出图形:①求∠CEF的度数;②探究线段AB,AE,AF之间的数量关系,并加以证明;(2)如图2,若AB=4,点G为AC的中点,连DG,将△CDG绕点C顺时针旋转得到△CMN,直线BM、AN交于点P,连CP,在△CDG旋转一周过程中,请直接写出△BCP 的面积最大值为.9.在△ABC中,点P为BC边中点,直线a绕顶点A旋转,BM⊥直线a于点M.CN⊥直线a于点N,连接PM,PN.(1)如图1,若点B,P在直线a的异侧,延长MP交CN于点E.求证:PM=PE;(2)若直线a绕点A旋转到图2的位置时,点B,P在直线a的同侧,其它条件不变,此时S△BMP+S△CNP=7,BM=1,CN=3,求MN的长度.(3)若过P点作PG⊥直线a于点G,试探究线段PG、BM和CN的数量关系.10.在Rt△ABC中与Rt△DCE中,∠ACB=∠DCE=90°,∠BAC=∠DEC=30°,AC=DC=,将Rt△DCE绕点C顺时针旋转,连接BD,AE,点F,G分别是BD,AE的中点,连接CF,CG.(1)观察猜想如图1,当点D与点A重合时,CF与CG的数量关系是,位置关系是;(2)类比探究当点D与点A不重合时,(1)中的结论是否成立?如果成立,请仅就图2的情形给出证明;如果不成立,请说明理由.(3)问题解决在Rt△DCE旋转过程中,请直接写出△CFG的面积的最大值与最小值.11.如图1,Rt△ABC中,∠C=90°,点E是AB边上一点,且点E不与A、B重合,ED ⊥AC于点D.(1)当sin B=时,①求证:BE=2CD;②当△ADE绕点A旋转到如图2的位置时(60°<∠CAD<90°),BE=2CD是否成立?若成立,请给出证明;若不成立,请说明理由.(2)当sin B=时,将△ADE绕点A旋转到∠DEB=90°,若AC=10,AD=2,请直接写出线段CD的长.12.如图,已知点A(0,8),B(16,0),点P是x轴上的一个动点(不与原点O重合),连接AP,把△OAP沿着AP折叠后,点O落在点C处,连接PC,BC,设P(t,0).(1)如图1,当AP∥BC时,试判断△BCP的形状,并说明理由.(2)在点P的运动过程中,当∠PCB=90°时,求t的值.(3)如图2,过点B作BH⊥直线CP,垂足为点H,连接AH,在点P的运动过程中,是否存在AH=BC?若存在,求出t的值:若不存在,请说明理由.13.如图,点B,C,D在同一条直线上,△BCF和△ACD都是等腰直角三角形.连接AB,DF,延长DF交AB于点E.(1)如图1,若AD=BD,DE是△ABD的平分线,BC=1,求CD的长度;(2)如图2,连接CE,求证:DE=CE+AE;(3)如图3,改变△BCF的大小,始终保持点F在线段AC上(点F与点A,C不重合).将ED绕点E顺时针旋转90°得到EP.取AD的中点O,连接OP.当AC=2时,直接写出OP长度的最大值.14.综合与实践问题情境从“特殊到一般”是数学探究的常用方法之一,类比特殊图形中的数量关系和探究方法可以发现一般图形具有的普遍规律.如图1,在△ABC中,∠ACB=90°,AC=BC,AD为BC边上的中线,E为AD上一点,将△AEC以点C为旋转中心,逆时针旋转90°得到△BFC,AD的延长线交线段BF于点P.探究线段EP,FP,BP之间的数量关系.数学思考(1)请你在图1中证明AP⊥BF;特例探究(2)如图2,当CE垂直于AD时,求证:EP+FP=2BP;类比再探(3)请判断(2)的结论在图1中是否仍然成立?若成立,请证明;若不成立,请说明理由.15.在Rt△ABC中,AB=AC,OB=OC,∠A=90°,∠MON=α,分别交直线AB、AC于点M、N.(1)如图1,当α=90°时,求证:AM=CN;(2)如图2,当α=45°时,求证:BM=AN+MN;(3)当α=45°时,旋转∠MON至图3位置,请你直接写出线段BM、MN、AN之间的数量关系.16.教材呈现:如图是华师版八年级上册数学教材第94页的部分内容.2.线段垂直平分线我们已经知道线段是轴对称图形,线段的垂直平分线是线段的对称轴.如图,直线MN 是线段AB的垂直平分线,P是MN上任一点,连接P A、PB.将线段AB沿直线MN对折,我们发现P A与PB完全重合.由此即有:线段垂直平分线的性质定理线段:垂直平分线上的点到线段两端的距离相等.已知:如图,MN⊥AB,垂足为点C,AC=BC,点P是直线MN上的任意一点求证:P A=PB.分析:图中有两个直角三角形APC和BPC,只要证明这两个三角形全等,便可证得P A =PB.(1)请根据教材中的分析,结合图①,写出“线段垂直平分线的性质定理”完整的证明过程;(2)如图②,在△ABC中,直线l,m,n分别是边AB,BC,AC的垂直平分线.求证:直线l、m、n交于一点;(请将下面的证明过程补充完整)证明:设直线l,m相交于点O.(3)如图③,在△ABC中,AB=BC,边AB的垂直平分线交AC于点D,边BC的垂直平分线交AC于点E,若∠ABC=120°,AC=15,则DE的长为.17.如图,在平面直角坐标系中,点O为坐标原点,点A(x,y)中的横坐标x与纵坐标y 满足+|y﹣8|=0,过点A作x轴的垂线,垂足为点D,点E在x轴的负半轴上,且满足AD﹣OD=OE,线段AE与y轴相交于点F,将线段AD向右平移8个单位长度,得到线段BC.(1)直接写出点A和点E的坐标;(2)在线段BC上有一点G,连接DF,FG,DG,若点G的纵坐标为m,三角形DFG 的面积为S,请用含m的式子表示S(不要求写m的取值范围);(3)在(2)的条件下,当S=26时,动点P从D出发,以每秒1个单位的速度沿着线段DA向终点A运动,动点Q从A出发,以每秒2个单位的速度沿着折线AB→BC向终点C运动,P,Q两点同时出发,当三角形FGP的面积是三角形AGQ面积的2倍时,求出P点坐标18.如图1,在Rt△ACB中,AC=BC,过B点作BD⊥CD于D点,AB交CD于E.(1)如图1,若AC=6,tan∠ACD=2,求DE的长;(2)如图2,若CE=2BD,连接AD,在AD上找一点F,使CF=DF,在FD上取一点G,使∠EGF=∠CFG,求证:AF=EG;(3)如图3,D为线段BC上方一点,且∠BDC=90°,AC=6,连接AD,将AD绕A 点逆时针旋转90°,D点对应点为E点,H为DE中点,求当AH有最小值时,直接写出△ACH的面积.19.(1)问题发现:如图1,△ACB和△DCE均为等边三角形,当△DCE旋转至点A,D,E在同一直线上,连接BE.则:①∠AEB的度数为°;②线段AD、BE之间的数量关系是.(2)拓展研究:如图2,△ACB和△DCE均为等腰三角形,且∠ACB=∠DCE=90°,点A、D、E在同一直线上,若AD=a,AE=b,AB=c,求a、b、c之间的数量关系.(3)探究发现:图1中的△ACB和△DCE,在△DCE旋转过程中,当点A,D,E不在同一直线上时,设直线AD与BE相交于点O,试在备用图中探索∠AOE的度数,直接写出结果,不必说明理由.20.类比、转化、从特殊到一般等思想方法,在数学学习和研究中经常用到.小明在数学学习中遇到了这样一个问题:“如图1,Rt△ABC中,∠ACB=90°,∠CAB=α,点P在AB边上,过点P作PQ⊥AC于点Q,△APQ绕点A逆时针方向旋转,如图2,连接CQ.O 为BC边的中点,连接PO并延长到点M,使OM=OP,连接CM.探究在△APQ的旋转过程中,线段CM,CQ之间的数量关系和位置关系”小明计划采用从特殊到一般的方法探究这个问题.特例探究:(1)填空:如图3,当α=30°时,=,直线CQ与CM所夹锐角的度数为;如图4,当α=45°时,=,直线CQ与CM所夹锐角的度数为;一般结论:(2)将△APQ绕点A逆时针方向旋转的过程中,线段CQ,CM之间的数量关系如何(用含α的式子表示)?直线CQ与CM所夹锐角的度数是多少?请仅就图2所示情况说明理由;问题解决(3)如图4,在Rt△ABC中,若AB=4,α=45°,AP=3,将△APQ由初始位置绕点A逆时针方向旋转β角(0°<β<180°),当点Q到直线AC的距离为2时,请直接写出线段CM的值.参考答案1.解:(1)∠QEP=60°;证明:如图1,QE与CP的交点记为M,∵PC=CQ,且∠PCQ=60°,∴∠PCQ=∠ACB=60°,∴∠BCQ=∠ACP,则△CQB和△CP A中,,∴△CQB≌△CP A(SAS),∴∠CQB=∠CP A,在△PEM和△CQM中,∠EMP=∠CMQ,∴∠QEP=∠QCP=60°.故答案为:60°;(2)∠QEP=60°.理由如下:如图2,∵△ABC是等边三角形,∴AC=BC,∠ACB=60°,∵线段CP绕点C顺时针旋转60°得到线段CQ,∴CP=CQ,∠PCQ=6O°,∴∠ACB+∠BCP=∠BCP+∠PCQ,即∠ACP=∠BCQ,在△ACP和△BCQ中,,∴△ACP≌△BCQ(SAS),∴∠APC=∠Q,∵∠BOP=∠COQ,∴∠QEP=∠PCQ=60°;(3)作CH⊥AD于H,如图3,与(2)一样可证明△ACP≌△BCQ,∴AP=BQ,∵∠DAC=135°,∠ACP=15°,∴∠APC=30°,∠PCB=45°,∴∠HAC=45°,∴△ACH为等腰直角三角形,∴AH=CH=AC=3,在Rt△PHC中,PH=CH=3,∴P A=PH﹣AH=3﹣3,∴BQ=3﹣3.2.解:(1)如图1中,∵AB=AC,∠BAC=30°,∴∠ABC=∠ACB=(180°﹣30°)=75°,∵AE⊥AC,∴∠EAC=90°,∴∠BAE=30°+90°=120°,∵AB=AE,∴∠ABE=∠E=(180°﹣120°)=30°,∴∠FBC=∠ABC﹣∠ABF=75°﹣30°=45°.故答案为:45.(2)①图形如图2所示.②结论:△BCF是等腰直角三角形理由如下:如图2中,∵AB=AC,BD=CD,∴AD⊥BC,∴AD是BC的垂直平分线,∴FB=FC,又AB=AC,AF=AF,∴△ABF≌△ACF(SSS),∴∠1=∠2,由旋转可知AE=AC,又AB=AC,∴AB=AE,∴∠1=∠3,∴∠2=∠3.又∠4=∠5,∴∠CFE=∠CAE=90°即∠CFB=90°,又FB=FC,∴△BCF为等腰直角三角形.③如图3中,作EH⊥DF交DF的延长线于H.∵AB=AC=5,BD=CD=4,∴AD⊥BC,∴∠ADB=90°,∴AD===3,∵∠ADC=∠EAC=∠H=90°,∴∠DAC+∠ACD=90°,∠DAC+∠HAE=90°,∴∠ACD=∠HAE,∵AE=AC,∴△ADC≌△EHA(AAS),∴EH=AD=3,∵△BDF是等腰直角三角形,FD⊥BC,∴∠DFB=∠BFC=45°,∴∠HEF=∠HFE=45°,∵∠H=90°,∴∠EHF=∠HFE=45°,∴EH=FH=3,∴EF=EH=,故答案为:3.3.解:(1)CD=EF,CD⊥EF,理由如下:∵AB=AC,∠BAC=90°,∴∠ABC∠ACB=45°,∵将线段AD绕A逆时针旋转90°得到线段AE,∴AD=AE,∠DAE=90°=∠BAC,∴∠BAD=∠CAE,且AB=AC,AD=AE,∴△ABD≌△ACE(SAS)∴BD=CE,∠ABD=∠ACE=45°,∴∠BCF=∠ACB+∠ACE=90°,∴CD⊥EF,又∵∠ABC=45°,∴∠BFC=∠ABC,∴BC=CF,∴CD=EF;(2)结论仍然成立,理由如下:∵AB=AC,∠BAC=90°,∴∠ABC∠ACB=45°,∵将线段AD绕A逆时针旋转90°得到线段AE,∴AD=AE,∠DAE=90°=∠BAC,∴∠BAD=∠CAE,且AB=AC,AD=AE,∴△ABD≌△ACE(SAS)∴BD=CE,∠ABD=∠ACE=45°,∴∠BCF=∠ACB+∠ACE=90°,∴CD⊥EF,又∵∠ABC=45°,∴∠BFC=∠ABC,∴BC=CF,∴CD=EF;(3)如图,过点A作AN⊥CE于点N,过点G作GH⊥CE于H,∵AB=AC=,∴BC=CF=2,∵AN⊥CE,∠ACF=45°,∴AN=CN=1,∵tan∠AEC==,∴EN=2,∴EC=CN+EN=3,∴EF=EC﹣CF=1=CD,∵GH⊥CE,∠ECD=90°,∴HG∥CD,∴==,且EG=DG,∴HG=,EH=,∴FH=EH﹣EF=∴GF===4.解(1)①由旋转知,∠ABD=∠ABC=90°,∠D=∠A,∴∠D+∠BED=90°,∴∠A+∠BED=90°,∵∠BED=∠AEF,∴∠A+∠AEF=90°,∴∠AFE=90°,∴DF⊥AC;②如图1,过点B作BG⊥BF交DF于G,∴∠FBG=90°,由旋转知,∠D=∠A,BD=AB,∠ABD=90°,∴∠FBG=∠ABD,∴∠DBG=∠ABF,∴△BDG≌△BAF(ASA),∴BG=BF,∵∠FBG=90°,∴∠BFD=45°;(2)①如图2所示,②CF﹣EF=BF.过点B作BG⊥BF交AC于G,∴∠FBG=90°,由旋转知,∠C=∠E,BC=BE,∵∠ABC=90°,∴∠FBG=∠ABC,∴∠CBG=∠EBF,∴△BCG≌△BEF(ASA),∴CG=EF,BG=BF,∵∠FBG=90°,∴∠BFD=45°,∴FG=BF,∵CF=FG+CG,∴FG=CF﹣CG=CF﹣EF=BF,即:CF﹣EF=BF.5.解:(1)BD、CE的关系是相等.理由:∵△ABC和△ADE是有公共顶点的等腰直角三角形,∠BAC=∠DAE=90°,∴AB=AC,∠BAD=∠CAE,DA=EA,∴△ABD≌△ACE(SAS)∴BD=CE.故答案为:相等.(2)如图2,3即为旋转后的图形.①如图2,当C在AD上时,由(1)知△ABD≌△ACE,∴∠ADB=∠AEC又∵∠PCD=∠ACE,∴△PCD∽△ACE,∴又∵CE===CD=AD﹣AC=5﹣3=2∴,解得;如图3,当C在AD反向延长线上时,同理△PEB∽△ABD=∵BD=BE=AE﹣AB=5﹣3=2∴=解得PB=∴PD=DB+PB=+=.答:此时PD的长为或.(3)如图4所示,以点A为圆心,AC长为半径画圆,当CE在圆A下方与圆A相切时,PD的值最小.在Rt△ACE中,CE===4在Rt△ADE中,DE===5∵四边形ABPC是正方形,∴PC=AB=3∴PE=PC+CE=3+4=7在Rt△DEP中,PD===1∴线段PD的最小值为1.故答案为:1.6.解:(1)∵∠AOC=90°,∴∠OAC+∠ACO=90°,∵∠ACD=90°,∴∠DCF+∠ACO=90°,∴∠DCF=∠OAC,∵∠OAC=38°,∴∠DCF=38°;(2)如图,过点D作DH⊥x轴于H,∴∠CHD=90°∴∠AOC=∠CHD=90°,∵等腰直角三角形ACD,∠ACD=90°∴AC=CD,由(1)知,∠DCF=∠OAC,∴△AOC≌△CHD(AAS),∴OC=DH=n,AO=CH=3,∴点D的坐标(n+3,n);(3)不会变化,理由:∵点A(0,3)与点B关于x轴对称,∴AO=BO,又∵OC⊥AB,∴x轴是AB垂直平分线,∴AC=BC,∴∠BAC=∠ABC,又∵AC=CD,∴BC=CD,∴∠CBD=∠CDB,∵∠ACD=90°,∴∠ACB+∠DCB=270°,∴∠BAC+∠ABC+∠CBD+∠CDB=90°,∴∠ABC+∠CBD=45°,∵∠BOF=90°,∴∠OFB=45°,∴∠OBF=∠OFB=45°,∴OB=OF=3,∴OF的长不会变化.7.解:[问题初探]如图2,过点E作EF⊥BC交直线BC于F,∴∠DFE=90°=∠ABD,∴∠EDF+∠DEF=90°,由旋转知,AD=DE,∠ADE=90°,∴∠ADB+∠EDF=90°,∴∠ADB=∠DEF,∴△ABD≌△DFE(AAS),∴BD=EF,DF=AB,∵AB=BC,∴BC=DF,∴BD=CF,∴EF=CF,∴△CEF是等腰直角三角形,∴∠ECF=45°,∴∠DCE=135°,故答案为:ADB,等腰直角,135;[继续探究]如图3,过点E作EF⊥BC于F,∴∠DFE=90°=∠ABD,∴∠EDF+∠DEF=90°,由旋转知,AD=DE,∠ADE=90°,∴∠ADB+∠EDF=90°,∴∠ADB=∠DEF,∴△ABD≌△DFE(AAS),∴BD=EF,DF=AB,∵AB=BC,∴BC=DF,∴BD=CF,∴EF=CF,∴△CEF是等腰直角三角形,∴∠ECF=45°,∴∠DCE=45°;[拓展延伸]如图4,在△ABC中,∠ABC=90°,AB=BC=,∴∠ACB=45°当点D在射线BC上时,由[问题初探]知,∠BCM=135°,∴∠ACM=∠BCM﹣∠ACB=90°,当点D在线段CB的延长线上时,由[继续探究]知,∠BCE=45°,∴∠ACN=∠ACB+∠BCM=90°,∴点E是过点C垂直于AC的直线上的点,∴当BE⊥MN时,BE最小,∵∠BCE=45°,∴∠CBE=45°=∠BCE,∴BE=CE,∴BE最小=BC=,即:BE的最小值为.8.解:(1)如图1所示:延长BE,①∵等边△ABC中,点D为BC的中点,∴AD是BC的垂直平分线,∠BAD=∠CAD=30°,∴BE=CE,∴∠EBC=∠ECB,∵将线段EB绕点E顺时针旋转至EF,∴BE=EF,∴∠EBF=∠EFB,∵∠CEF=∠FEH+∠HEC=∠EBF+∠BFE+∠EBC+∠ECB=2∠ABE+2∠EBC,∴∠CEF=2∠ABC=120°;②AB=AF+AE,理由如下:如图1﹣1,在AB上截取BM=AF,连接ME,过点E作EN⊥AB于N,∵BM=AF,∠AFE=∠EBM,BE=EF,∴△BME≌△F AE(SAS),∴AE=EM,又∵EN⊥AB,∴AN=MN=AM,∵∠BAD=30°,∴AE=2NE,AN=NE,∴AN=AE,∴AM=AE,∴AB=BM+AM=AF+AE;(3)如图2,∵△ABC是等边三角形,AB=4,点G为AC的中点,∴AC=BC,∠ACB=60°,CG=CD=2,∵将△CDG绕点C顺时针旋转得到△CMN,∴CM=CN=CG=CD=2,∠MCN=∠ACB=60°,∴∠ACN=∠BCM,∴△BCM≌△ACN(SAS),∴∠CAN=∠CBM,∴点A,点B,点C,点P四点共圆,∴∠BPC=∠BAC=60°,∵将△CDG绕点C顺时针旋转得到△CMN,∴点M在以点C为圆心,CM为半径的圆上,∴当BM与⊙C相切于点M时,△BCP的面积有最大值,如图所示,过点P作PH⊥BC 于H,∵BM是⊙C的切线,∴∠BMC=90°=∠PMC,又∵∠BPC=60°,∴∠PCM=30°,∴CM=PM=2,∴MP=,∵BM===2,∴BP=BM+MP=,∵sin∠PBC=,∴PH==,∴△BCP的面积最大值=×4×=,故答案为.9.(1)证明:如图1中,∵BM⊥直线a于点M,CN⊥直线a于点N,∴∠BMA=∠CNM=90°,∴BM∥CN,∴∠MBP=∠ECP,又∵P为BC边中点,∴BP=CP,又∵∠BPM=∠CPE,∴△BPM≌△CPE(ASA),∴PM=PE(2)解:延长MP与NC的延长线相交于点E.∵BM⊥直线a于点M,CN⊥直线a于点N,∴∠BMN=∠CNM=90°∴∠BMN+∠CNM=180°,∴BM∥CN∴∠MBP=∠ECP,又∵P为BC中点,∴BP=CP,又∵∠BPM=∠CPE,∴△BPM≌△CPE(ASA),∴PM=PE,S△PBM=S△PCE,∴AE=CN+CE=4,∵S△BMP+S△CNP=7,∴S△PNE=7,∴S△MNE=2S△PNE=14,∴×MN×4=14,∴MN=7.(3)解:如图1﹣1中,当点B,P在直线a的异侧时,∵PG⊥a,CN⊥a,∴PG∥CN,∵PM=PE,∴MG=GN,∴PG=EN=(CN﹣EC),∵EC=BM,∴PG=(CN﹣BM).如图2﹣2中,当点B,P在直线a的同侧时,延长MP交NC的延长线于Q.∵PG⊥a,CN⊥a,∴PG∥CN,∵BM∥CQ,∴∠BMP=∠Q,∵∠BPM=∠CPQ,BP=CP,∴△PMB≌△PQC(AAS),∴PM=PQ,BM=CQ,∴MG=GN,∴PG=AQ=(CN+BM).综上所述,PG=(CN﹣BM)或PG=(CN+BM).10.解:(1)观察猜想∵在Rt△ABC中与Rt△DCE中,∠ACB=∠DCE=90°,∠BAC=∠DEC=30°,AC =DC=,∴AE=2DC=2,AC=BC=,AB=2BC,∠CDE=60°,∴BC=1,AB=2,∵点F,G分别是BD,AE的中点,∴CG=AE=,CG=AG,CF=AB=1,CF=AF,∴CG=CF,∠GDC=∠GCD=60°,∠ACF=∠F AC=30°,∴∠FCG=90°,∴CF⊥CG,故答案为:CG=CF,CF⊥CG;(2)类比探究仍然成立,理由如下:∵∠ACB=∠DCE=90°,∠BAC=∠DEC=30°,AC=DC=,∴∠BCD=∠ACE,AC=BC,CE=CD,∴=,∴△BCD∽△ACE,∴,∠CAE=∠CBD,∵点F,G分别是BD,AE的中点,∴BF=BD,AG=AE,∴∴△ACG∽△BCF,∴,∠BCF=∠ACG,∴CG=CF,∠ACB=∠FCG=90°,∴CF⊥CG;(3)问题解决如图,延长BC至H,使BC=CH=1,连接DH,∵点F是BD中点,BC=CH=1,∴CF=DH,由(2)可知,CF⊥CG,∴△CFG的面积=×CF×CG=CF2,∴△CFG的面积=DH2,∴当DH取最大值时,△CFG的面积有最大值,当DH取最小值时,△CFG的面积有最小值,∵CD=,∴点D在以点C为圆心,为半径的圆上,∴当点D在射线HC的延长线上时,DH有最大值为+1,∴△CFG的面积最大值=(+1)2=,当点D在射线CH的延长线上时,DH有最小值为﹣1,∴△CFG的面积最小值=(﹣1)2=.11.解:(1)∵Rt△ABC中,∠C=90°,sin B=,∴∠B=30°,∴∠A=60°,①如图1,过点E作EH⊥BC于点H,∵ED⊥AC∴∠ADE=∠C=90°,∴四边形CDEH是矩形,即EH=CD,∴在Rt△BEH中,∠B=30°,∴BE=2EH∴BE=2CD;②BE=2CD成立,理由:∵△ABC和△ADE都是直角三角形,∴∠BAC=∠EAD=60°,∴∠CAD=∠BAE,又∵,,∴,∴△ACD∽△ABE,∴,又∵Rt△ABC中,=2,∴=2,即BE=2CD;(2)∵sin B=,∴∠ABC=∠BAC=∠DAE=45°,∵ED⊥AD,∴∠AED=∠BAC=45°,∴AD=DE,AC=BC,将△ADE绕点A旋转∠DEB=90°,分两种情况:①如图3所示,过A作AF⊥BE交BE的延长线于F,则∠F=90°,当∠DEB=90°时,∠ADE=∠DEF=90°,又∵AD=DE,∴四边形ADEF是正方形,∴AD=AF=EF=2,∵AC=10=BC,根据勾股定理得,AB=10,在Rt△ABF中,BF==6,∴BE=BF﹣EF=4,又∵△ABC和△ADE都是直角三角形,且∠BAC=∠EAD=45°,∴∠CAD=∠BAE,∵,,∴,∴△ACD∽△ABE,∴=,即=,∴CD=2;②如图4所示,过A作AF⊥BE于F,则∠AFE=∠AFB=90°,当∠DEB=90°时,∠DEB=∠ADE=90°,又∵AD=ED,∴四边形ADEF是正方形,∴AD=EF=AF=2,又∵AC=10=BC,∴AB=10,在Rt△ABF中,BF==6,∴BE=BF+EF=8,又∵△ACD∽△ABE,∴=,即=,∴CD=4,综上所述,线段CD的长为2或4.12.解:(1)等腰直角三角形,理由如下:∵AP∥BC,∴∠APC=∠BCP,∠APO=∠CBP,∵△OAP沿着AP折叠,∴∠APO=∠APC,OP=PC,∴∠PCB=∠PBC,∴PC=PB=OP=8,∴△BCP是等腰三角形,∵OA=OP=8,∴∠OP A=∠APC=45°,∴∠OPC=90°,∴△BCP是等腰直角三角形;(2)当t>0时,如图,∵△OAP沿着AP折叠,∴∠AOP=∠ACP=90°,OP=PC=t,∴∠ACP+∠BCP=180°,∴点A,点C,点B三点共线,∵点A(0,8),B(16,0),∴OA=8,OB=16,∴AB===8,∵tan∠ABO=,∴,∴t=4﹣4;当t<0时,如图,同理可求:t=﹣4﹣4;(3)∵△OAP沿着AP折叠,∴AC=AO=8,∠ACP=∠AOP=90°,∵BH⊥CP,∴∠ACP=∠BHC=90°,∵AH=BC,CH=CH,∴Rt△ACH≌Rt△BHC(HL)∴AC=BH,∴四边形AHBC是平行四边形,如图2,当0≤t≤16时,点H在PC上时,连接AB交CH于G,∵四边形AHBC是平行四边形,∴AG=BG=4,HG=CG,AC=BH=8,∴HG===4,在Rt△PHB中,PB2=BH2+PH2,∴(16﹣t)2=64+(t﹣8)2,∴t=8;如图3,当0≤t≤16时,点H在PC的延长线上时,∵四边形AHBC是平行四边形,∴AG=BG=4,HG=CG,AC=BH=8,∴HG===4,在Rt△PHB中,PB2=BH2+PH2,∴(16﹣t)2=64+(t+8)2,∴t=;如图4,当t<0时,同理可证:四边形ABHC是平行四边形,又∵AH=BC,∴四边形ABHC是矩形,∴AC=BH=8,AB=CH=8,在Rt△PHB中,PB2=BH2+PH2,∴(16﹣t)2=64+(t+8)2,∴t=16﹣8;当t>16时,如图5,∵四边形ABHC是矩形,∴AC=BH=8,AB=CH=8,CP=OP=t,在Rt△PHB中,PB2=BH2+PH2,∴(t﹣16)2=64+(t﹣8)2,∴t=16+8.综上所述:当t=8或或16﹣8或16+8时,存在AH=BC.13.(1)解:∵△BCF和△ACD都是等腰直角三角形,∴AC=CD,FC=BC=1,FB=,∵AD=BD,DE是△ABD的平分线,∴DE垂直平分AB,∴F A=FB=,∴AC=F A+FC=,∴CD=;(2)证明:如图2,过点C作CH⊥CE交ED于点H,∵△BCF和△ACD都是等腰直角三角形,∴AC=DC,FC=BC,∠ACB=∠DCF=90°;∴△ABC≌△DFC(SAS),∴∠BAC=∠CDF,∵∠ECH=90°,∴∠ACE+∠ACH=90°,∵∠ACD=90°,∴∠DCH+∠ACH=90°,∴∠ACE=∠DCH.在△ACE和△DCH中,,∴△ACE≌△DCH(ASA),∴AE=DH,CE=CH,∴EH=CE.∵DE=EH+DH=CE+AE;(3)解:如图3,连接OE,将OE绕点E顺时针旋转90°得到EQ,连接OQ,PQ,则OQ=OE.由(2)知,∠AED=∠ABC+∠CDF=∠ABC+∠BAC=90°,在Rt△AED中,点O是斜边AD的中点,∴OE=OD=AD=AC=,∴OQ=OE=,在△OED和△QEP中,,∴△OED≌△QEP(SAS),∴PQ=OD=.∵OP≤OQ+PQ=,当且仅当O、P、Q三点共线时,取“=”号,∴OP的最大值是.14.证明:(1)如图1,∵将△AEC以点C为旋转中心,逆时针旋转90°得到△BFC,∴△AEC≌△BFC,∴∠CAE=∠CBF,∵∠ACB=90°,∴∠CAE+∠EAB+∠CBA=90°,∴∠CBF+∠EAB+∠CBA=90°,∴∠APB=90°,∴AP⊥BF;(2)如图2,∵CE⊥AD,∴∠AEC=90°=∠CEP,∵将△AEC以点C为旋转中心,逆时针旋转90°得到△BFC,∴△AEC≌△BFC,∠ECF=90°,∴∠AEC=∠BFC=90°,CE=CF,∴四边形CEPF是正方形,∴EP=PF=CE=CF,∠EPF=90°,∵AD为BC边上的中线,∴CD=BD,又∵∠CDE=∠BDP,∠CED=∠BPD=90°,∴△CDE≌△BDP(AAS),∴CE=BP,∴EP=PF=BP,∴EP+FP=2BP;(3)结论仍然成立,理由如下:如图1,过点C作CN⊥AD于N,作CM⊥BF,交BF的延长线于M,∵将△AEC以点C为旋转中心,逆时针旋转90°得到△BFC,∴∠CAE=∠CBF,CE=CF,∵∠ACB=90°,∴∠CAE+∠EAB+∠CBA=90°,∴∠CBF+∠EAB+∠CBA=90°,∴∠APB=90°,又∵CN⊥AD,CM⊥BM,∴四边形CNPM是矩形,∵∠CAE=∠CBF,∠ANC=∠BMC=90°,AC=BC,∴△ACN≌△BCM(AAS),∴CM=CN,∴四边形CNPM是正方形,∴CN=CM=NP=MP,∵AD为BC边上的中线,∴CD=BD,又∵∠CDN=∠BDP,∠CND=∠BPD=90°,∴△CDN≌△BDP(AAS),∴CN=BP,∴CN=BP=NP=MP,∴EP+FP=EN+NP+FP=NP+MF+PF=NP+MP=2BP.15.证明:(1)如图1,连接OA,∵AB=AC,∠BAC=90°,OB=OC,∴AO⊥BC,OA=OB=OC,∠ABO=∠ACO=∠BAO=∠CAO=45°,∴∠MON=∠AOC=90°,∴∠AOM=∠CON,且AO=CO,∠BAO=∠ACO=45°,∴△AOM≌△CON(ASA)∴AM=CN;(2)证明:如图2,在BA上截取BG=AN,连接GO,AO,∵AB=AC,∠BAC=90°,OB=OC,∴AO⊥BC,OA=OB=OC,∠ABO=∠ACO=∠BAO=∠CAO=45°,∵BG=AN,∠ABO=∠NAO=45°,AO=BO,∴△BGO≌△AON(SAS),∴OG=ON,∠BOG=∠AON,∵∠MON=45°=∠AOM+∠AON,∴∠AOM+∠BOG=45°,∵∠AOB=90°,∴∠MOG=∠MON=45°,∵MO=MO,GO=NO,∴△GMO≌△NMO(SAS),∴GM=MN,∴BM=BG+GM=AN+MN;(3)MN=AN+BM,理由如下:如图3,过点O作OG⊥ON,连接AO,∵AB=AC,∠BAC=90°,OB=OC,∴AO⊥BC,OA=OB=OC,∠ABO=∠ACO=∠BAO=∠CAO=45°,∴∠GBO=∠NAO=135°,∵MO⊥GO,∴∠NOG=90°=∠AOB,∴∠BOG=∠AON,且AO=BO,∠NAO=∠GBO,∴△NAO≌△GBO(ASA),∴AN=GB,GO=ON,∵MO=MO,∠MON=∠GOM=45°,GO=NO,∴△MON≌△MOG(SAS),∴MN=MG,∵MG=MB+BG,∴MN=AN+BM.16.证明:(1)如图①中,∵MN⊥AB,∴∠PCA=∠PCB=90°.在△P AC和△PBC中,,∴△P AC≌△PBC(SAS),∴P A=PB.(2)如图②中,设直线l、m交于点O,连接AO、BO、CO.∵直线l是边AB的垂直平分线,又∵直线m是边BC的垂直平分线,∴OB=OC,∴OA=OC,∴点O在边AC的垂直平分线n上,∴直线l、m、n交于点O.(3)解:如图③中,连接BD,BE.∵BA=BC,∠ABC=120°,∴∠A=∠C=30°,∵边AB的垂直平分线交AC于点D,边BC的垂直平分线交AC于点E,∴DA=DB,EB=EC,∴∠A=∠DBA=30°,∠C=∠EBC=30°,∴∠BDE=∠A+∠DBA=60°,∠BED=∠C+∠EBC=60°,∴△BDE是等边三角形,∴AD=BD=DE=BE=EC,∵AC=15,∴DE=AC=5.故答案为5.17.解:(1)∵+|y﹣8|=0,又∵≥0,|y﹣8|≥0,∴x=2,y=8,∴A(2,8),∵AD⊥x轴,∴OD=2,AD=8,∵AD﹣OD=OE,∴E(﹣6,0).(2)如图1中,连接OG.由题意G(10,m).∵AD=DE=8,∠ADE=90°,∴∠AED=45°,∴∠OEF=∠OFE=45°,∴OE=OF=6,∴F(0,6),∴S=S△ODG+S△OFG﹣S△OFD=×2×m+×6×10﹣×2×6=m+24(0≤m≤8).(3)如图2中,设FG交AD于J,P(2,t),当点P在DJ上,点Q在AB上时,当S=26时,m=2,∴G(10,2),∴直线FG的解析式为y=﹣x+6,∴J(2,),由题意,•(﹣t)×10=2××2t×6,解得t=,∴P(2,),当点P在AJ上,点Q在BG上时,同法可得,•(t﹣)×10=2××(14﹣2t)×8,解得t=,∴P(2,).综上所述,满足条件的点P的坐标为(2,)或(2,).18.解:(1)如图1中,过点E作EH⊥BC于H.∵BD⊥CD,∴∠D=90°,∵∠ACB=90°,∴∠ACD+∠DCB=90°,∠DCB+∠DBC=90°,∴∠ACD=∠DBC,∴tan∠DBC=tan∠ACD=2,∴=2,∵AC=BC=6,∴BD=,CD=,∵EH⊥BC,∠EBH=45°,∴∠EHB=90°,∠EHB=∠HBE=45°,∴EH=BH,设EH=BH=m,则HC=2EH=2m,∴3m=6,∴m=2,∴EH=2,CH=4,∴EC===2,∴DE=CD﹣CE=﹣2=.(2)如图2中,过点A作AT⊥CE于T,在AG上取一点J,使得EJ=EG.∵EJ=EG,∴∠EJG=∠EGJ,∵∠CFG=EGJ,∴∠CFG=∠EJG,∴∠AFC=∠AJE,∵∠ATC=∠CDB=∠ACB=90°,∴∠ACT+∠DCB=90°,∠DCB+∠CBD=90°,∴∠ACT=∠CBD,∵AC=BC,∴△ATC≌△CDB(AAS),∴CT=BD,∵EC=2BD,∴CT=ET,∵AT⊥EC,∴AC=AE,∴∠ACT=∠AEC,∴∠ACF+∠FCD=∠EAJ+∠FDC,∵FC=FD,∴∠FCD=∠FDC,∴∠ACF=∠EAJ,∴△ACF≌△EAJ(AAS),∴AF=EJ=EG.(3)如图3中,取BC的中点T,连接DT,AT.∵AC=BC=6,∠ACT=90°,CT=TB=3,∴AT===3,∵CD⊥BD,∴∠CDB=90°,∴DT=BC=3,∴AD≥AT﹣DT,∴AD≥3﹣3,∴AD的最小值为3﹣3,∵△ADE是等腰直角三角形,AH⊥DE,∴DH=EH,∴AH=DE=AD,∴AH的最小值为﹣,此时,A,D,T共线,如图3﹣1中,过点D作DQ⊥AC于Q,过点E作EP⊥CA交CA 的延长线于P,过点H作HJ⊥AC于J.∵DQ∥CT,∴==,∴==,∴DQ=,AQ=,由△AQD≌△EPQ,可得PE=AQ=,∵EP∥HJ∥DQ,EH=HD,∴PJ=JQ,∴JH=(PE+DQ)=∴△ACH的面积=×6×=.19.解:(1)①如图1,∵△ACB和△DCE均为等边三角形,∴CA=CB,CD=CE,∠ACB=∠DCE=60°,∴∠ACD=∠BCE,在△ACD和△BCE中,,∴△ACD≌△BCE(SAS).∴∠ADC=∠BEC.∵△DCE为等边三角形,∴∠CDE=∠CED=60°,∵点A,D,E在同一直线上,∴∠ADC=120°,∴∠BEC=120°,∴∠AEB=∠BEC﹣∠CED=60°,故答案为:60;②∵△ACD≌△BCE,∴AD=BE,故答案为:AD=BE;(2)∵△ACB和△DCE均为等腰直角三角形,∴CA=CB,CD=CE,∠ACB=∠DCE=90°.∴∠ACD=∠BCE,∴△ACD≌△BCE(SAS),∴BE=AD,∠ADC=∠BEC,∵△DCE为等腰直角三角形,∴∠CDE=∠CED=45°.∵点A,D,E在同一直线上,∴∠ADC=135°.∴∠BEC=135°,∴∠AEB=∠BEC﹣∠CED=90°,∴AD2+AE2=AB2,∵AD=a,AE=b,AB=c,∴a2+b2=c2;(3)如图3,由(1)知△ACD≌△BCE,∴∠CAD=∠CBE,∵∠CAB=∠CBA=60°,∴∠OAB+∠OBA=120°,∴∠AOE=180°﹣120°=60°,如图4,同理求得∠AOB=60°,∴∠AOE=120°,∴∠AOE的度数是60°或120°.20.解:(1)如图3中,连接PB,延长BP交CQ的延长线于J,延长QC到R,设AC交BJ于点K.∵∠P AQ=∠BAC,∴∠CAQ=∠BAP,∵==cos30°=,∴△QAC∽△P AB,。
探究与正方形有关的线段之间的数量关系
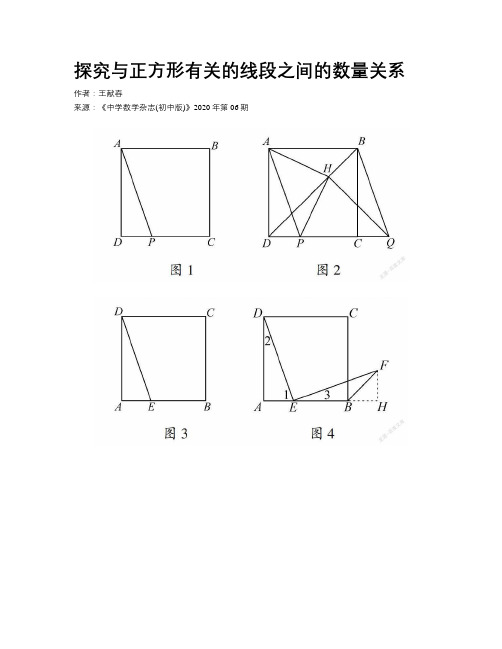
探究与正方形有关的线段之间的数量关系作者:***来源:《中学数学杂志(初中版)》2020年第06期正方形作为最特殊的四边形之一,具有平行四边形、矩形、菱形的所有性质,因而,以正方形为背景的几何综合题层出不穷.在题目中可以求线段之间的数量关系、位置关系、线段的长度、角的度数等等,解题时需要特别明确正方形的性质,善于动手操作、大胆猜想,联想学过的几何基本图形,恰当的添加辅助线,运用几何推理方可得出结论.1 与正方形有关的两条线段的相等关系例1 如图1,在正方形ABCD中,BD是一条对角线.点P在线段CD上(与点C,D不重合),连接AP,平移△ADP,使点D移动到点C,得到△BCQ,过点Q作QH⊥BD于点H,连接AH,PH.1.依题意补全图1;2.判断AH与PH的数量关系与位置关系并加以证明;分析 1.依题意补全图1,如图2,主要关注:(1)平移△ADP:平移的方向是沿着DC的方向,平移的距离是DC的长度;(2)过点Q作QH⊥BD于点H:明确过点Q,作QH⊥BD于点H,垂足是H;(3)连接AH,PH.2.判断AH与PH的数量关系与位置关系,这里包含两层意思(1)AH和PH的数量关系,是相等还是不相等,还是几倍的关系.(2)AH和PH的位置关系是平行还是垂直.本题解题时首先应该利用刻度尺和量角器度量后进行猜想,发现AH=PH,AH⊥PH.然后联想学过证明线段相等的方法:三角形全等、等角对等边、平行四边形对边相等.联想证明垂直的方法:直角三角形两锐角互余,矩形四个角为直角.结合本题条件,发现AH和PH所在的三角形,△HAD和△HPQ可以全等.因平移△ADP,使点D移动到点C得到△BCQ,知DC=PQ.由正方形ABCD可得DA=DC=PQ,∠BDA=∠BDC=45°.QH⊥BD于点H,∠HDQ=∠HQD=∠BDA=45°,HQ=HD,所以△HAD≌△HPQ,HA=HP、∠AHD=∠PHQ.由∠DHP+∠PHQ=90°,所以,∠DHP+∠AHD=90°,∠AHP=90°,HA⊥HP.反思本题中正方形ABCD提供了以下重要条件:边相等DA=DC、∠BDA=∠BDC=45°,然后再充分利用其他条件进行证明即可.2 与正方形有关的两条线段的倍数关系例2 如图3,在正方形ABCD中,E是边AB上的一动点(不与点A,B重合),连接DE,将线段ED绕点E顺时针旋转90°得到线段EF,连接BF.1.依题意补全图;2.用等式表示线段BF与AE的数量关系并证明.分析 1.依题意补全图形,如图4,主要关注:(1)将线段ED绕点E顺时针旋转90°:旋转中心是点E,旋转方向顺时针,旋转角度是90°;(2)连接BF.2.用等式表示线段BF与AE的数量关系.解题时首先应该利用刻度尺度量,发现BF和AE 不是相等关系.然后通过计算,猜想BF和AE具有 2倍的关系,因此,可以构造等腰直角三角形,让BF作为斜边,AE的长度作为直角边,可以过F做AB的延长线的垂线,通过证明△DAE≌△EHF从而达到目的.因四边形ABCD是正方形,则AB=AD,∠A=90°.由线段ED绕点E顺时针旋转90°得到线段EF,则DE=EF,∠DEF=90°.因∠1+∠2=90°,∠1+∠3=90°,所以∠2=∠3,△DAE≌△EHF,得出AE=FH,AD=EH,AB=EH,AE=BH,FH=BH,△BFH是等腰直角三角形,BF=2FH=2AE.反思本题中正方形ABCD提供了以下重要条件:AB=AD,∠A=90°,通过做辅助线,然后再充分利用其他条件进行证明即可.3 与正方形有关的三条线段的关系3.1 与正方形有关的三条线段的一次关系例3 如图5,在正方形ABCD中,点E是BC边上一动点(不与点B、C重合),过点B 作BF⊥DE,交射線DE于点F,连接CF.1.依题意补全图形;2.判断线段BF,CF,DF之间的数量关系,并证明.分析 1.依题意补全图,如图6,主要关注:(1)过点B作BF⊥DE,交射线DE于点F;(2)连接CF.2.判断线段BF,CF,DF之间的数量关系.解题时首先应该利用刻度尺度量,发现BF,CF,DF之间没有明确的两条线段之和等于第三条线段关系.然后通过计算,猜想DF大约等于BF加上CF的 2倍的关系,DF=DM+MF=BF+2CF.因此,可以在DF上截取DM=BF,连接CM,构造等腰直角三角形CMF,让CF作为直角边,再证明MF=2CF,从而达到目的.由正方形ABCD知BC=CD,∠BDC=∠DBC=45°,∠BCD=90°,∠CDM=∠CBF,△CDM≌△CBF(SAS).则DM=BF,CM=CF,∠DCM=∠BCF.∠MCF=∠BCF+∠MCE=∠DCM+∠MCE=∠BCD=90°所以MF= 2CF,DF=DM+MF=BF+2CF.反思本题中正方形ABCD提供了以下重要条件:BC=CD,∠BDC=∠DBC=45°,∠BCD=90°,通过添加辅助线,然后再充分利用其他条件进行证明即可.3.2 与正方形有关的三条线段的二次关系例4 如图7,正方形ABCD中,点P是线段AC上的一个动点,连接BP,将线段BP绕点B顺时针旋转90°得到线段BE,连接CE.1.依题意补全图形;2.求证:PA2+PC2=2PB2.分析 1.依题意补全图形如图8,主要关注:(1)将线段BP绕点B顺时针旋转90°得到线段BE,旋转中心是点B,旋转方向顺时针,旋转角度是90°;(2)连接CE.2.求证PA2+PC2=2PB2,发现是线段的平方关系,而且有2PB2,因此,猜想构造等腰直角三角形是关键.由四边形ABCD是正方形,得CB=AB,∠1=∠2=45°,∠3+∠4=90°.因将线段BP绕点B顺时针旋转90°得到线段BE,所以BE=BP,∠5+∠4=90°.PE=2PB,∠5=∠3.△CBE≌△ABP(SAS),因此EC=PA,∠6=∠1=45°.∠PCE=∠2+∠6=90°.得EC2+PC2=PE2,由EC=PA,PE=2PB,PA2+PC2=2PB2.反思本题中正方形ABCD提供了以下重要条件:BC=AB,∠1=∠2=45°,∠BCD=90°,通过添加辅助线,然后再充分利用其他条件进行证明即可.与正方形有关的线段之间的数量关系不止以上几种情况,在求解过程中,主要是动手操作,大胆猜想,积极验证.结合学习过的相关模型,巧妙运用正方形的相关性质,一定会顺利解题.作者简介王献春(1967—),男,北京延庆人,大学本科,正高级教师,主要从事初中教学研究.。
2023年九年级数学中考专题:几何探究压轴题

2023年九年级数学中考专题:几何探究压轴题一、解答题1.如图,在ABC 中,4AC =,3BC =,90ACB ∠=︒,D 是边AC 上一动点(不与点A 、C 重合),CE BD ⊥,垂足为E ,交边AB 于点F .(1)当点D 是边AC 中点时,求DE ,EC 的值;(2)设CD x =,AF y =,求y 关于x 的函数关系式,并写出定义域;(3)当EFD △与EFB △相似时,求线段CD 的长.2.【温故知新】黄金分割是一种最能引起美感的分割比例,具有严格的比例性、艺术性、和谐性,蕴藏着丰富的美学价值.我们知道:如图1,点C 把线段AB 分成两部分,如果BC AC AC AB=,那么称点C 为线段AB 的黄金分割点.(1)【问题发现】如图1,点C 为线段AB 的黄金分割点,且AC BC >,若2AB =,请直接写出CB 的值是__________.(2)【问题探究】如图2,在Rt ABC △中,90C ∠=︒,2AC =,1BC =,在BA 上截取BD BC =,再在AC 上截取AE AD =,则AE AC的值为__________. (3)【问题解决】如图3,用边长为6的正方形纸片进行如下操作:对折正方形ABDE 得折痕MN ,连接EN ,将AE 折叠到EN 上,点A 对应点H ,得折痕CE ,试说明:C 是AB 的黄金分割点.3.定义:若连接三角形一个顶点和对边上一点的线段能把该三角形分成一个等腰三角形和一个直角三角形,我们称这条线段为该三角形的智慧线,这个三角形叫做智慧三角形.(1)如图1,在智慧三角形ABC 中,AD BC ⊥,AD 为该三角形的智慧线,1CD =,则BD 长为_____,B ∠的度数为_____.(2)如图2,ABC 为等腰直角三角形,90BAC ∠︒=,2AB =,F 是斜边BC 延长线上一点,连接AF ,以AF为直角边作等腰直角三角形AFE (点A ,F ,E 按顺时针排列),90EAF ∠=︒, CF =AE 交BC 于点D ,连接EC ,EB .当2BDE BCE ∠=∠时,求线段ED 的长;(3)如图3,ABC 中,5AB AC ==,BC =BCD △是智慧三角形,且AC 为智慧线,求BCD △的面积.4.【问题提出】如图1,在等边三角形ABC 内部有一点P ,3PA=,4PB =,5PC =,求APB ∠的度数.(1)【尝试解决】将APC △绕点A 逆时针旋转60︒,得到AP B '△,连接PP ',则APP '为等边三角形. ∵3P P PA '==,4PB =,5P B PC '==,∴222=P P PB P B ''+∴BPP '为三角形∴APB ∠的度数为.(2)【类比探究】如图2,在等边三角形ABC 外部有一点P ,若∠BP A =30°,求证222PA PB PC +=.(3)【联想拓展】如图3,在ABC 中,90BAC ∠︒=,AB AC =.点P 在直线BC 上方且45APB ∠︒=,PC BC ==求PA 的长.5.已知正方形 ABCD 和正方形 CEFG ,连接 AF 交 BC 于点 O ,点 P 是 AF 的中点,过点 P 作 PH DG ⊥ 于 H ,2CD =,1CG =.(1)如图1,点 D ,C ,G 在同一直线上,点 E 在 BC 边上,求 PH 的长;(2)把正方形 CEFG 绕着点C 逆时针旋转 ()0180αα<<.①如图2,当点E 落在AF 上时,求CO 的长;②如图3,当DG =PH 的长.6.在ABC ∆中,点E 为AC 边上一动点,以CE 为边在CE 上方作等边CEN .(1)如图1,EN 与AB 交于点P ,连接PC ,若tan A =,1AE =,5CN =,求PC 的长: (2)如图2.当N 与B 重合时,在BC 上取一点D ,过点D 作DF AC ∥,连接BF ,EF ,过C 作CH EF ⊥交EF 于点H ,若30FBC DFE ︒∠-∠=,求证:CH BF +=;(3)如图3,若BC AB ⊥,且4AB BC ==,过点B 作BQ AC ∥,I 为射线.BQ 上一动点,取AC 中点M ,连接MI ,过点B 作BK MI ⊥交M 于点K ,连接NK ,直接写出NK 的最小值.7.问题情境:如图1,在Rt △ABC 和Rt △BEF 中,∠ACB =∠EFB =90°,AC =3,BC =4,且M ,N 分别为AE ,CF 的中点.(1)猜想证明:如图2,将Rt △BEF 绕点B 按逆时针方向旋转90°,其他条件不变.试判断54AM CN =是否成立?若成立,请写出证明过程;若不成立,请说明理由.(2)解决问题:如图3,将图2中的Rt △BEF 沿BF 所在直线折叠得到Rt BE F ',连接AE ',CF ,并分别取它们的中点P ,H ,连接CP ,FP ,PH .①试判断CP 与FP 之间的数量关系,并说明理由.②若AB =2BE ',BC =2BF ,请直接写出PH 的长.8.【方法尝试】(1)如图1,矩形ABFC 是矩形ADGE 以点A 为旋转中心,按逆时针方向旋转90︒所得的图形,CB ED 、分别是它们的对角线.则CB 与ED 数量关系________,位置关系________.【类比迁移】(2)如图2,在Rt ABC 和Rt ADE △中,90,9,6,3,2BAC DAE AC AB AE AD ∠=∠=︒====.将DAE 绕点A 在平面内逆时针旋转,设旋转角BAE ∠为()0360αα︒<︒,连接,CE BD .请判断线段CE 和BD 的数量关系和位置关系,并说明理由;【拓展延伸】(3)如图3,在Rt ABC 中,90,6ACB AB ∠=︒=,过点A 作AP BC ∥,在射线AP 上取一点D ,连结CD,使得3tan4ACD∠=,请求写出线段BD的最大值.9.如图①,在正方形ABCD中,点N、M分别在边BC、CD上,连接AM、AN、MN.∠MAN=45°,将△AMD 绕点A顺时针旋转90°,点D与点B重合,得到△ABE.易证:△ANM≌△ANE,从而得DM+BN=MN.【实践探究】(1)在图①条件下,若CN=6,CM=8,则正方形ABCD的边长是______.(2)如图②,点M、N分别在边CD、AB上,且BN=DM.点E、F分别在BM、DN上,∠EAF=45°,连接EF,猜想三条线段EF、BE、DF之间满足的数量关系,并说明理由.(3)【拓展应用】如图③,在矩形ABCD中,AB=6,AD=8,点M、N分别在边DC、BC上,连接AM,AN,已知∠MAN=45°,BN=2,求DM的长.10.小圆同学对图形旋转前后的线段之间、角之间的关系进行了拓展探究.(1)猜测探究:在△ABC中,AB=AC,M是平面内任意一点,将线段AM绕点A按顺时针方向旋转与∠BAC 相等的角度,得到线段AN,连接NB.①如图1,若M是线段BC上的任意一点,请直接写出∠NAB与∠MAC的数量关系是,NB与MC的数量关系是;②如图2,点E是AB延长线上点,若M是∠CBE内部射线BD上任意一点,连接MC,(1)中结论是否仍然成立?若成立,请给予证明,若不成立,请说明理由.(2)拓展应用:如图3,在△A 1B 1C 1中,A 1B 1=8,∠A 1B 1C 1=60°,∠B 1A 1C 1=75°,P 是B 1C 1上的任意点,连接A 1P ,将A 1P 绕点A 1按顺时针方向旋转75°,得到线段A 1Q ,连接B 1Q .求线段B 1Q 长度的最小值. 11.如图,在Rt ABC △中,90BAC ∠=︒,AB AC =,D 为AC 边上一点,连接BD ,作AP BD ⊥于点P ,过点C 作CE AC ⊥交AP 延长线于点E .(1)如图1,求证:AD CE =;(2)如图2,以AD ,BD 为邻边作ADBF ,连接EF 交BC 于点G ,连接AG ,①求证:AG EF ⊥;②若点D 为AC 中点,EF 、AB 交于点H ,求BH AB的值. 12.如图1,在ABC 中,90ACB ∠=︒,D 为AC 边上的一点,过点D 作DE AB ⊥,垂足为E ,连接BD ,P 为BD 中点,连接PC ,PE .(1)求证:PC PE =;(2)将图1中ADE 绕着点A 顺时针旋转如图2的位置,其他条件不变,(1)中的结论是否成立?若成立,请证明:若不成立,请说明理由;(3)若10AB =,6AD =,30BAC DAE ∠=∠=︒,在平面内,将Rt ADE △绕点A 旋转一周,当A ,C ,E 三点共线时,请直接写出PCE 的面积.13.如图1,在直角坐标系中,点()2,0A ,点()0,2C ,点D ,点E 分别为OA ,OC 的中点,ODE 绕原点O 顺时针旋转α角(090α︒<<︒)得11OD E ,射线1CD ,1AE 相交于点F .(1)求证:11OCD OAE △≌△;(2)如图2,在ODE 旋转过程中,当点1D 恰好落在线段CE 上时,求AF 的长;(3)如图3,在旋转α角从090α︒≤≤︒逐渐增大ODE 旋转过程中,求点F 的运动路线长.14.已知ABC 为等边三角形,边长为4,点D 、E 分别是BC 、AC 边上一点,连接AD 、BE .AE CD =.(1)如图1,若2AE =,求BE 的长度;(2)如图2,点F 为AD 延长线上一点,连接BF 、CF ,AD 、BE 相交于点G ,连接CG ,已知60,∠=︒=EBF CE CG ,求证:2+=BF GE CF ;(3)如图3,点P 是ABC 内部一动点,顺次连接PA PB PC 、、++的最小值.15.【问题提出】(1)如图1,在ABC 中,90C ∠=︒,BD 平分ABC ∠交AC 于点D ,设CD 的长为m ,点D 到边AB 的距离为n ,则m _______n ;(填“>”“<”或“=”)【问题探究】(2)如图2,在梯形ABCD 中,90A ∠=︒,AD BC ∥,(201AB =,BD 为对角线,且45BDC ∠=︒,求BCD △面积的最小值;【问题解决】(3)某景点有一个形状为菱形ABCD 的草坪,如图3,AB ==60B ∠︒,现欲将该草坪扩建为BEF △,使得点E 、F 分别在BA 、BC 的延长线上,且边EF 经过点D ,为了节省成本,要求扩建后的草坪面积(BEF △的面积)尽可能小,问BEF △的面积是否存在最小值?若存在,求出其最小值;若不存在,请说明理由.16.综合与实践:数学课外小组研究了两个问题,请你帮助解答.问题一:如图1,在矩形ABCD 中,6AB =,8AD =,E ,F 分别为AB ,AD 边的中点,四边形AEGF 为矩形,连接CG .问题二:数学小组对图形的旋转进行了拓展研究,如图4,在平行四边形ABCD 中,=60B ∠︒,6AB =,8AD =,E ,F 分别为AB ,AD 边的中点,四边形AEGF 为平行四边形,连接CG .数学小组发现DF 与CG 仍然存在着特定的数量关系.(1)请直接写出CG 的长是______.如图2,当矩形AEGF 绕点A 旋转(如顺时针旋转)至点G 落在边AB 上时,DF =______,CG =______,DF 与CG 之间的数量关系是______.(2)当矩形AEGF 绕点A 旋转至如图3的位置时,(1)中DF 与CG 之间的数量关系是否还成立?并说明理由.(3)如图5,当平行四边形ABCD 绕点A 旋转(如顺时针旋转),其它条件不变时,数学小组发现DF 与CG 仍然存在着这一特定的数量关系.请你直接写出这个特定的数量关系是______.17.如图,在四边形ABCD 中,AD ∥BC ,∠ABC =90°,AD =CD ,O 是对角线AC 的中点,连接BO 并延长交边AD 或边CD 于点E .(1)如图1,当点E 在AD 上时,连接CE ,求证:四边形ABCE 是矩形.(2)如图2,当点E 在CD 上时,当AC =4,BC =3时,求DAC S △与OBC S的比值.(3)若DE =2,OE =3,直接写出CD 的长.18.已知在正方形ABCD 中,E 是BC 边上一动点,作点B 关于AE 的对称点F ,BF 交AE 于点G ,连结DF .(1)如图1,求DFB ∠的度数;(2)如图2,过点D 作DM BF ⊥交BF 的延长线于点M ,连结,CM CF .若DF CM =,试探究四边形DFCM 的形状,并说明理由;(3)如图3,连结BD ,在AG 上截取=GT GB ,点P ,Q 分别是,AD BD 上的动点.若正方形ABCD 的面积为32,直接写出PTQ 周长的最小值.。
2022年春苏科版九年级数学中考复习几何压轴题专题训练(附答案)

2022年春苏科版九年级数学中考复习几何压轴题专题训练(附答案)1.如图,在Rt△ABC中,∠ACB=90°,∠A=30°,BD是△ABC的角平分线,DE⊥AB,垂足为E,点F在DE的延长线上,点G在线段AD上,且∠BGF=60°.(1)若DE=2,求AC的长;(2)证明:DF=AD+DG.2.在△ABC中,点D、E分别在AB、AC边上,设BE与CD相交于点F.(1)如图①,设∠A=60°,BE、CD分别平分∠ABC、∠ACB,证明:DF=EF.(2)如图②,设BE⊥AC,CD⊥AB,点G在CD的延长线上,连接AG、AF;若∠G=∠6,BD=CD,证明:GD=DF.3.已知:如图,在Rt△ABC中,∠C=90°,AB=5cm,AC=3cm,动点P从点B出发沿射线BC以1cm/s的速度移动,设运动的时间为t秒.(1)求BC边的长;(2)当△ABP为直角三角形时,求t的值;(3)当△ABP为等腰三角形时,求t的值.4.如图,已知A(a,b),AB⊥y轴于B,且满足+(b﹣2)2=0,(1)求A点坐标;(2)分别以AB,AO为边作等边三角形△ABC和△AOD,如图1试判定线段AC和DC 的数量关系和位置关系.(3)如图2过A作AE⊥x轴于E,F,G分别为线段OE,AE上的两个动点,满足∠FBG =45°,试探究的值是否发生变化?如果不变,请说明理由并求其值;如果变化,请说明理由.5.【阅读理解】课外兴趣小组活动时,老师提出了如下问题:如图1,△ABC中,若AB=8,AC=6,求BC边上的中线AD的取值范围.小明在组内经过合作交流,得到了如下的解决方法:延长AD到点E,使DE=AD,请根据小明的方法思考:(1)由已知和作图能得到△ADC≌△EDB的理由是.A.SSS B.SAS C.AAS D.HL(2)求得AD的取值范围是.A.6<AD<8 B.6≤AD≤8 C.1<AD<7 D.1≤AD≤7【感悟】解题时,条件中若出现“中点”“中线”字样,可以考虑延长中线构造全等三角形,把分散的已知条件和所求证的结论集合到同一个三角形中.【问题解决】(3)如图2,AD是△ABC的中线,BE交AC于E,交AD于F,且AE=EF.求证:AC =BF.6.在等边△ABC的两边AB、AC所在直线上分别有两点M、N,D为△ABC外一点,且∠MDN=60°,∠BDC=120°,BD=DC.探究:当M、N分别在直线AB、AC上移动时,BM、NC、MN之间的数量关系及△AMN的周长Q与等边△ABC的周长L的关系.(1)如图1,当点M、N在边AB、AC上,且DM=DN时,BM、NC、MN之间的数量关系是;此时=;(2)如图2,点M、N在边AB、AC上,且当DM≠DN时,猜想(I)问的两个结论还成立吗?若成立请直接写出你的结论;若不成立请说明理由.(3)如图3,当M、N分别在边AB、CA的延长线上时,探索BM、NC、MN之间的数量关系如何?并给出证明.7.已知△ABC为等边三角形,D为AC的中点,∠EDF=120°,DE交线段AB于E,DF 交直线BC于F.(1)如图(1),求证:DE=DF;(2)如图(2),若BE=3AE,求证:CF=BC.(3)如图(3),若BE=AE,则CF=BC;在图(1)中,若BE=4AE,则CF =BC.8.如图,在四边形ABCD中,AD=BC=4,AB=CD,BD=6,点E从D点出发,以每秒1个单位的速度沿DA向点A匀速移动,点F从点C出发,以每秒3个单位的速度沿C →B→C作匀速移动,点G从点B出发沿BD向点D匀速移动,三个点同时出发,当有一个点到达终点时,其余两点也随之停止运动.(1)证明:AD∥BC.(2)在移动过程中,小明发现当点G的运动速度取某个值时,有△DEG与△BFG全等的情况出现,请你探究当点G的运动速度取哪些值时,会出现△DEG与△BFG全等的情况.9.如图,已知凸五边形ABCDE中,EC,EB为其对角线,EA=ED.(1)如图1,若∠A=60°,∠CDE=120°,且CD+AB=BC.求证:CE平分∠BCD;(2)如图2,∠A与∠D互补,∠DEA=2∠CEB,若凸五边形ABCDE面积为30,且CD=AB=4.求点E到BC的距离.10.已知△ABC≌△ADE,且它们都是等腰直角三角形,∠ABC=∠ADE=90°.(1)如图1,当点D在边AC上时,连接BD并延长交CE于点F,①求证:∠CBD=∠EDF;②求证:点F为线段CE的中点;(2)△ADE绕着点A顺时针旋转,如图2所示,连接BD并延长交CE于点F,点F还是线段CE的中点吗?请说明理由.11.已知在△ABC与△CDE中,AB=CD,∠B=∠D,∠ACE=∠B,点B、C、D在同一直线上,射线AH、EI分别平分∠BAC、∠CED.(1)如图1,试说明AC=CE的理由;(2)如图2,当AH、EI交于点G时,设∠B=α,∠AGE=β,求β与α的数量关系,并说明理由;(3)当AH∥EI时,求∠B的度数.12.如图1,△ABC≌△DAE,∠BAC=∠ADE=90°.(1)连接CE,若AB=1,点B、C、E在同一条直线上,求AC的长;(2)将△ADE绕点A逆时针旋转α(0°<α<90°),如图2,BC与AD交于点F,BC 的延长线与AE交于点N,过点D,作DM∥AE交BC于点M.求证:①BM=DM;②MN2=NF•NB.13.如图1,2,3,将一个矩形ABCD绕点A顺时针旋转α(0°<α≤90°),得到矩形AB1C1D1,连接BD.(1)探究:①如图1,当α=90°时,点C1恰好在DB的延长线上,若AB=1,求BC的长;②如图2,连接AC1,过点D1作D1M∥AC1交BD于点M,线段D1M与DM相等吗?请说明理由.(2)在探究(1)②的条件下,射线DB分别交AD1、AC1于点P、N(如图3).求证:①MN=AN;②MN2=PN•DN.14.如图1,在矩形ABCD中,点E是CD上一动点,连接AE,将△ADE沿AE折叠,点D落在点F处,AE与DF交于点O.(1)射线EF经过点B,射线DF与BC交于点G.ⅰ)求证:△ADE∽△DCG;ⅱ)若AB=10,AD=6,求CG的长;(2)如图2,射线EF与AB交于点H,射线DF与BC交于点G,连接HG,若HG∥AE,AD=10,DE=5,求CE的长.15.如图1,在Rt△ABC中,∠ACB=90°,AB=10,BC=6.D、E分别是AB、AC边的中点,连接DE.现将△ADE绕A点逆时针旋转,连接BD,CE并延长交于点F.(1)如图2,点E正好落在AB边上,CF与AD交于点P.①求证:AE•AB=AD•AC;②求BF的长;(2)如图3,若AF恰好平分∠DAE,直接写出CE的长.16.如图,过⊙O外一点P作⊙Q的两条切线P A和PB,PD交⊙O于D和C,E在弦DC 上.且∠DAE=∠PBC.(1)求证:∠ADC=∠P AC;(2)求证:△ADE∽△BAC;(3)若AD=5,BC=3,AC=4,试求BD的长.17.如图,在△ABC中,AB=AC,AO⊥BC于点O,OE⊥AB于点E,以点O为圆心,OE 的长为半径作半圆,交AO于点F.(1)求证:AC是⊙O的切线;(2)若点F是AO的中点,OE=3,求图中阴影部分的面积;(3)在(2)的条件下,点P是BC边上的动点,当PE+PF取最小值时,求出BP的长.18.如图,△ABC为⊙O的内接三角形,AB为⊙O的直径,将△ABC沿BC翻折得到△DBC,过点D作⊙O的切线DF,与BC的延长线交于点E,F为切点,⊙O的半径为,∠ABD=30°.(1)求的长.(2)若DE∥AB,连接AE.①求证:四边形ABDE为菱形.②求DF的长.19.如图,AB是⊙O的直径,C是⊙O上一点,OD⊥AC于点D,过点C作⊙O的切线,交OD的延长线于点M,OM交⊙O于点N,连接AM.(1)求证:AM是⊙O的切线;(2)若DN=4,AC=8,求线段MN的长;(3)在(2)的条件下,求阴影部分的面积.20.如图,在Rt△ABC中,∠ABC=90°,以AB为直径的⊙O交AC于点D,连接BD,△ADE是以AD为斜边的直角三角形,且满足∠EAD=∠DAB,DE=DC.(1)求证:DE为⊙O的切线;(2)求证:DE2=EF•BD;(3)若AB=1,求BD的长.参考答案1.(1)解:在Rt△ABC中,∠ACB=90°,∠A=30°,∴∠ABC=60°,∵BD是△ABC的角平分线,DE⊥AB,∴CD=DE=2.∠CBD=∠ABD=30°,∴BD=2CD=4,∵DE⊥AB,∠CBD=∠ABD=30°,∴AD=BD=4,∴AC=AD+CD=4+2=6,∴AC的长为6;(2)证明:如图,在DE上截取DH=DG,连接GH,∵AD=BD,∠A=∠ABD=30°,∴∠BDE=∠ADE=60°,∴△DGH是等边三角形,∴∠DGH=∠DHG=60°,∵∠BGF=60°,∴∠1+∠HGB=∠2+∠HGB=60°,∴∠1=∠2,∵∠BDC=∠DHG=60°,∴∠BDG=∠FHG=120°,在△BDG和△FHG中,,∴△BDG≌△FHG(ASA),∵DF=FH+DH=BD+DG=AD+DG,∴DF=AD+DG.2.证明:(1)如图,在BC上截取BM=BD,连接FM,∵∠A=60,∴∠BFC=90°+60°÷2=120°,∴∠BFD=60°,∵BE平分∠ABC,∴∠1=∠2,在△BFD和△BFM中,,∴△BFD≌△BFM(SAS),∴∠BFM=∠BFD=60°,DF=MF,∴∠CFM=120°﹣60°=60°,∵∠CFE=∠BFD=60°,∴∠CFM=∠CFE,∵CD平分∠ACB,∴∠3=∠4,又CF=CF,在△ECF和△MCF中,,∴△ECF≌△MCF(ASA),∴EF=MF,(2)∵BE⊥AC,CD⊥AB,∴∠BDF=∠CDA=90°,∴∠1+∠BFD=90°,∠3+∠CFE=90°,∠BFD=∠CFE,∴∠1=∠3,∵BD=CD,在△BDF和△CDA中,,∴△BDF≌△CDA(ASA),∴DF=DA,∵∠ADF=90°,∴∠6=45°,∵∠G=∠6,∴∠5=45°∴∠G=∠5,∴GD=DA,∴GD=DF.3.解:(1)在Rt△ABC中,BC2=AB2﹣AC2=52﹣32=16,∴BC=4(cm);(2)由题意知BP=tcm,①当∠APB为直角时,点P与点C重合,BP=BC=4cm,即t=4;②当∠BAP为直角时,BP=tcm,CP=(t﹣4)cm,AC=3cm,在Rt△ACP中,AP2=32+(t﹣4)2,在Rt△BAP中,AB2+AP2=BP2,即:52+[32+(t﹣4)2]=t2,解得:t=,故当△ABP为直角三角形时,t=4或t=;(3)①当AB=BP时,t=5;②当AB=AP时,BP=2BC=8cm,t=8;③当BP=AP时,AP=BP=tcm,CP=(4﹣t)cm,AC=3cm,在Rt△ACP中,AP2=AC2+CP2,所以t2=32+(4﹣t)2,解得:t=,综上所述:当△ABP为等腰三角形时,t=5或t=8或t=.4.解:(1)根据题意得:a﹣2=0且b﹣2=0,解得:a=2,b=2,则A的坐标是(2,2);(2)AC=CD,且AC⊥CD.如图1,连接OC,CD,∵A的坐标是(2,2),∴AB=OB=2,∵△ABC是等边三角形,∴∠OBC=30°,OB=BC,∴∠BOC=∠BCO=75°,∵在直角△ABO中,∠BOA=45°,∴∠AOC=∠BOC﹣∠BOA=75°﹣45°=30°,∵△OAD是等边三角形,∴∠DOC=∠AOC=30°,即OC是∠AOD的角平分线,∴OC⊥AD,且OC平分AD,∴AC=DC,∴∠ACO=∠DCO=60°+75°=135°,∴∠ACD=360°﹣135°﹣135°=90°,∴AC⊥CD,故AC=CD,且AC⊥CD.(3)不变.延长GA至点M,使AM=OF,连接BM,∵在△BAM与△BOF中,,∴△BAM≌△BOF(SAS),∴∠ABM=∠OBF,BF=BM,∵∠OBF+∠ABG=90°﹣∠FBG=45°,∴∠MBG=45°,∵在△FBG与△MBG中,,∴△FBG≌△MBG(SAS),∴FG=GM=AG+OF,∴=1.5.(1)解:∵在△ADC和△EDB中,∴△ADC≌△EDB(SAS),故选B;(2)解:∵由(1)知:△ADC≌△EDB,∴BE=AC=6,AE=2AD,∵在△ABE中,AB=8,由三角形三边关系定理得:8﹣6<2AD<8+6,∴1<AD<7,故选C.(3)证明:延长AD到M,使AD=DM,连接BM,∵AD是△ABC中线,∴CD=BD,∵在△ADC和△MDB中∴△ADC≌△MDB,∴BM=AC,∠CAD=∠M,∵AE=EF,∴∠CAD=∠AFE,∵∠AFE=∠BFD,∴∠BFD=∠CAD=∠M,∴BF=BM=AC,即AC=BF.6.解:(1)如图1,BM、NC、MN之间的数量关系BM+NC=MN,此时,理由:∵DM=DN,∠MDN=60°,∴△MDN是等边三角形,∵△ABC是等边三角形,∴∠A=60°,∵BD=CD,∠BDC=120°,∴∠DBC=∠DCB=30°,∴∠MBD=∠NCD=90°,∵DM=DN,BD=CD,∴Rt△BDM≌Rt△CDN,∴∠BDM=∠CDN=30°,BM=CN,∴DM=2BM,DN=2CN,∴MN=2BM=2CN=BM+CN;∴AM=AN,∴△AMN是等边三角形,∵AB=AM+BM,∴AM:AB=2:3,∴=;(2)猜想:结论仍然成立,证明:在NC的延长线上截取CM1=BM,连接DM1,∵∠MBD=∠M1CD=90°,BD=CD,∴△DBM≌△DCM1,∴DM=DM1,∠MBD=∠M1CD,M1C=BM,∵∠MDN=60°,∠BDC=120°,∴∠M1DN=∠MDN=60°,∴△MDN≌△M1DN,∴MN=M1N=M1C+NC=BM+NC,∴△AMN的周长为:AM+MN+AN=AM+BM+CN+AN=AB+AC,∴=;(3)证明:在CN上截取CM1=BM,连接DM1,可证△DBM≌△DCM1,∴DM=DM1,可证∠M1DN=∠MDN=60°,∴△MDN≌△M1DN,∴MN=M1N,∴NC﹣BM=MN.7.证明:(1)如图1中,连接BD,作DM⊥AB于M,DN⊥BC于N,∵∠DMB=∠DNB=90°,∠ABC=60°,∴∠MDN=∠EDF=120°,∴∠MDE=∠NDF,∵△ABC是等边三角形,AD=DC,∴∠DBA=∠DBC,∴DM=DN,∴△DME≌△DNF,∴DE=DF.(2)如图2中,作DK∥BC交AB于K.设AE=a,则BE=3a,AB=AC=BC=4a,∵AD=DC,DK∥CB,∴AK=BK=2a,DK=BC=2a=AD=AK,∴AE=EK=a,∴DE⊥AK,∴∠BED=90°,∵∠BED+∠BFD=180°,∴∠DFB=90°,在Rt△CDF中,∵∠C=60°,∴CF=CD=a,∴CF=BC.(3)①如图3中,作DK∥BC交AB于K.设BE=a,则AE=3a,AK=BK=2a,△ADK是等边三角形,∴∠ADK=60°,∠EDF=∠KDC,∴∠KDE=∠CDF,∵DK=DC,DE=DF,∴△EDK≌△FDC,∴EK=CF=a,∵BC=4a,∴CF=BC.②如图4中,由(1)可知EM=FN,设AE=a,则BE=4a,AB=BC=AC=5a,AM=CN=a,EM=FN=a,∴CF=FN+CN=a,∴CF:BC=a:5a=3:10,∴CF=BC.故答案为,.8.(1)证明:在△ABD和△CDB中,,∴△ABD≌△CDB(SSS),∴∠ADB=∠CBD,∴AD∥BC;(2)解:设运动时间为t,点G的运动速度为v,当时,若△DEG≌△BGF,则,∴,∴,∴v=3;若△DEG≌△BGF,则,∴,∴(舍去);当时,若△DEG≌△BFG,则,∴,∴,∴;若△DEG≌△BGF,则,∴,∴,∴v=1.综上,当点G的速度为3或1.5或1时.会出现△DEG与△BFG全等的情况.9.(1)证明:延长CD到T,使得DT=BA,连接ET.∵∠CDE=120°,∴∠EDT=180°﹣120°=60°,∵∠A=60°,∴∠A=∠EDT,在△EAB和△EDT中,,∴△EAB≌△EDT(SAS),∴EB=ET,∴CB=CD+BA=CD+DT=CT,在△ECB和△ECT中,,∴△ECB≌△ECT(SSS),∴∠ECB=∠ECD,∴CE平分∠BCD.(2)解:延长CD到Q,使得∠QED=∠AEB,过点E作EH⊥BC于H.∵∠A+∠CDE=180°,∠CDE+∠EDQ=180°,∴∠A=∠EDQ,在△AEB和△DEQ中,,∴△AEB≌△DEQ(ASA),∴EB=EQ,∵∠AED=2∠BEC,∴∠AEB+∠CED=∠BEC,∴∠CED+∠DEQ=∠BEC,∴∠CEB=∠CEQ,在△CEB和△CEQ中,,∴△ECB≌△ECQ(SAS),∵S五边形ABCDE=S四边形EBCQ=2S△EBC=30,∴S△EBC=15,∵CD=AB=4,∴AB=6,CD=4,∴BC=CD+QD=CD+AB=10,∴×10×EH=15,∴EH=3,∴点E到BC的距离为3.10.(1)证明:①∵△ABC≌△ADE,∴AB=AD,BC=DE,AE=AC,∵△ABC,△ADE为等腰直角三角形,∴AD=DE,AB=BC,∠DAE=∠AED=∠BAC=∠BCA=45°,在△ABD中,AB=AD,∴∠ABD=∠ADB=67.5°,∴∠CBF=90°﹣∠ABD=22.5°,∠EDF=90°﹣∠CDF=90°﹣∠ADB=22.5°,∴∠CBF=∠EDF,∴∠CBD=∠EDF;②∵AE=AC,∠EAC=45°,∴∠ACE=∠AEC=67.5°,∵∠ADE=90°,∴∠DEC=22.5°,∵∠FDC=∠FCD=67.5°,∴EF=DF,DF=FC,∴EF=FC,∴点F为线段CE的中点;(2)解:点F还是线段CE的中点,理由如下:过点E作EG∥BC交BF延长线于G,∴∠EGF=∠CBF,∠FEG=∠FCB,∵AB=AD,∴∠ABD=∠ADB,∵∠ADE=∠ABC=90°,∴∠EDG=90°﹣∠ADB=90°﹣∠ABD=∠FBC,∴∠EDG=∠EGD,∴DE=EG,∵DE=BC,∴EG=BC,∵∠FEG=∠FCB,∠FGE=∠FBC,∴△EFG≌△CFB(ASA),∴EF=CF,∴F为EC的中点.11.(1)证明:∵∠ACD=∠ACE+∠ECD=∠A+∠B,又∠B=∠ACE,∴∠A=∠ECD.在△ABC和△CDE中,,∴△ABC≌△CDE(ASA).∴AC=CE.(2)解:3α﹣2β=180°.理由如下:如图1所示,连接GC并延长至点K.∵AH、EI分别平分∠BAC、∠DEC,则设∠CAH=∠BAH=a,∠CEI=∠DEI=b,∵∠ACK为△ACG的外角,∴∠ACK=a+∠AGC,同理可得∠ECK=b+∠EGC,∴∠ACE=∠ACK+∠ECK=∠B=α=(a+∠AGC)+(b+∠EGC)=a+b+∠AGE=a+b+β,即α=a+b+β,∴a+b=α﹣β.又由(1)中证明可知∠ECD=∠BAC=2a,由三角形内角和公式可得∠ECD+∠DEC+∠D=180°,即2a+2b+α=180°,∴2(a+b)+α=180°,∴3α﹣2β=180°.(3)当AH∥EI时,如图2所示,过点C作MN∥AH,则MN∥AH∥EI.∴∠CAH=∠ACM=a,∠CEI=∠ECM=b,∴∠ACE=∠ACM+∠ECM=a+b=α,即α=a+b.由(1)中证明可得∠ECD=∠BAC=2a,∠D=∠B=α.在△CED中,根据三角形内角和定理有∠ECD+∠CED+∠D=180°,即2a+2b+α=180°,即2(a+b)=180°﹣α,即3α=180°,解得:α=60°.故∠B=60°.12.(1)解:∵△ABC≌△DAE,∴AD=AB=1,AC=DE,∵∠BAC=∠ADE=90°,∴AB∥DE,∴△ABC∽△DEC,=,∴=,解得AC=;(2)证明:①连接BD,∵△ABC≌△DAE,∴∠ABC=∠DAE,AB=DA,∵DM∥AE,∴∠MDA=∠DAE,∴∠ABC=∠MDA,∵AB=DA,∴∠ABD=∠ADB,∴∠ABD﹣∠ABC=∠ADB﹣∠MDA,∴∠MBD=∠MDB,∴BM=DM;②连接MA,由①知,BM=DM,AB=DA,∵AM=AM,∴△AMB≌△AMD(SSS),∴∠BAM=∠DAM,由①知,∠ABC=∠DAE,∴∠ABC+∠BAM=∠DAE+∠DAM,∴∠AMN=∠NAM,∴MN=AN,∵∠BNA=∠ANF,∠ABC=∠DAE,∴△ANF∽△BNA,∴,∴AN2=BN•NF,∴MN2=NF•NB.13.(1)解:①如图1,∵四边形ABCD是矩形,∴CD=AB,BC=DA,∠BAD=90°,∵将矩形ABCD绕点A顺时针旋转90°得到矩形AB1C1D1,∴∠D1AD=∠BAD=90°,C1D1=CD=AB=1,∴AB与AD1重合,即点A、B、D1在同一条直线上,设BC=DA=D1A=x,则D1B=x﹣1,∵∠D1=∠BAD=90°,∠D1BC1=∠ABD,∴△D1BC1∽△∠ABD,∴=,∴=,解得x1=,x2=(不符合题意,舍去),∴BC=.②D1M=DM,理由如下:如图2,连结DD1,∵AD1=AD,∴∠AD1D=∠ADD1,∵D1C1=AB,∠C1D1A=∠BAD=90°,AD1=DA,∴△C1D1A≌△BAD(SAS),∴∠D1AC1=∠ADB,∵D1M∥AC1,∴∠AD1M=∠D1AC1,∴∠AD1M=∠ADB,∴∠AD1D﹣∠AD1M=∠ADD1﹣∠ADB,∴∠MD1D=∠MDD1,∴D1M=DM.(2)证明:如图3,连结AM,①∵AD1=AD,D1M=DM,AM=AM,∴△AD1M≌△ADM(SSS),∴∠AD1M=∠ADM,∠MAD1=∠MAD,∵∠AD1M=∠NAD1,∴∠NAD1=∠ADM,∴∠NAD1+∠MAD1=∠ADM+∠MAD,∵∠NAM=∠NAD1+∠MAD1,∠NMA=∠ADM+∠MAD,∴∠NAM=∠NMA,∴MN=AN.②∵∠NAD1=∠ADM,∴∠NAP=∠NDA,∵∠ANP=∠DNA,∴△ANP∽△DNA,∴=,∴AN2=PN•DN,∴MN2=PN•DN.14.解:(1)i)由翻折可得,△ADE≌△AFE,DF⊥AE于O,∴∠CDG+∠ADO=90°,∠ADO+∠EAD=90°,∴∠CDG=∠EAD,∵∠ADE=∠DCG=90°,∴△ADE∽△DCG;ii)∵AB=10△ADE≌△AFE,∴AF=AD=6,在Rt△ABF中,BF=,设DE=EF=x,CE=10﹣x,BC=AD=6,在Rt△BCE中,BE2=BC2+CE2,即(8+x)2=62+(10﹣x)2,解得:x=2,由i)可知△ADE∽△DCG,∴,∴,解得:CG=;(2)由i)可知,△ADE∽△DCG,∴,同理可得,△ADE∽△DOE,即,∵∠OAD=∠ODE,∠ADE=∠DOE=90°,∵HG∥AE,∴△HGF∽△EDF,∵△DOE≌△FOE,∴,∵∠BGH+∠CGD=90°,∠BHG+∠BGH=90°,∴∠CGD=∠BHG,∵∠B=∠C=90°,∴△BHG∽△CGD,∴,综上所述,△BHG∽△CGD∽△DEA∽△OED∽△GHF,设CE=x,DC=5+x,CG=,BG=10﹣CG=10﹣,BH=BG=,HG=BH=,∵HG:GF=1:2,∴GF=,在△ADE中,AD=10,DE=5,AE=5,DO=,∵,∵,∴OE=,DO=OF=2,在△DCG中,DC=5+x,CG=,DG=DF+FG=4,∵,∴DG=CG,即,解得:x=9,即CE=9.15.(1)①证明:∵D、E分别是AB、AC边的中点,∴DE∥BC,∴△ADE∽△ABC,∴=,∴AE•AB=AD•AC;②解:如图1,作CG⊥AB于G,作FH⊥AB于H,在Rt△ABC中,AB=10,BC=6,∴AC=8,∴AE=4,∴BE=AB﹣AE=6,∵BG=BC•cos∠ABC=6•=6×=,CG=BC•sin∠ABC=6×=,∴EG=BE﹣BG=6﹣=,∴tan∠FEH=tan∠CEG=,∴tan∠FEH=,设EH=a,FH=2a,∵tan∠FBE=,∴BH=4a,∵BH﹣EH=BE,∴4a﹣a=6,∴a=2,∴FH=4,BH=8,∴BF===4;(2)如图2,当AF平分∠DAE时,AF⊥BD,∴∠AFD=∠AED=90°,∴点A、E、F、D共圆,∴∠DEF=∠DAF,设AF与DE的交点为O,作OG⊥AD于G,作AH⊥CF于H,∵AF平分∠DAE,∴OG=OE,AG=AF=4,∴DG=AD﹣AG=1,设OG=OE=x,∴OD=3﹣x,在Rt△DOG中,(3﹣x)2﹣x2=12,∴x=,∴OG=OE=,∴tan∠DAF=,sin∠DAF=,cos∠DAF=,∵∠AED=90°,∴∠AEH+∠DEF=90°,∵∠AEH+∠EAH=90°,∴∠EAH=∠DEF=∠DAF,∴EH=AE•sin∠EAH=4×=,AH=AE•cos∠EAH=4×=,∴CH===,∴CE=EH+CH=.16.(1)证明:如图,过点A作直径AF,连接FC,则∠ACF=90°,∵P A是⊙O的切线,∴∠F AC+∠P AC=90°,∵∠AFC+∠F AC=90°,∴∠AFC=∠P AC,∵∠ADC=∠AFC,∴∠ADC=∠P AC,(2)如图,过点B作直径BG,连接GC,则∠GCB=90°,∴∠G+∠GBC=90°,∵PB是⊙O的切线,∠GBC+∠CBP=90°,∴∠G=∠CBP,又∠G=∠BAC,∴∠BAC=∠CBP,∵∠DAE=∠PBC,∴∠DAE=∠BAC,∵∠ADE=∠ABC,∴△ADE∽△BAC,(3)如图,过A作AN⊥PD于点N,过B作BM⊥PD于M,则AN=AD•sin∠ADC,BM =BD•sin∠BDC,∴==,又∵S△P AC=,S△PBC=,∴=,∵P A,PB是⊙O的切线,∴P A=PB,∴=,∴=,由(1)知:∠ADC=∠P AC,∠BDC=∠PBC,∴,∴,∴BD=.17.(1)证明:过O作OM⊥AC于M,如图:∵AB=AC,AO⊥BC,∴AO平分∠BAC,∵OE⊥AB,OM⊥AC,∴OE=OM,∵OE为⊙O半径,∴OM为⊙O半径,∴AC是⊙O的切线;(2)解:∵OM=OE=OF=3,且F是OA中点,∴OA=6,在Rt△AEO中,AE==3,∴S△AOE=AE•OE=,∵OE⊥AB,OA=6,OE=3,∴∠EAO=30°,∠AOE=60°,∴S扇形OEF==,∴S阴影=S△AOE﹣S扇形OEF=﹣;(3)解:作F关于BC的对称点G,连接EG交BC于P,连接EF,如图:此时PE+PF最小,最小值为EG的长度,∵F、G关于BC对称,∴∠FOP=∠GOP=90°,∴∠FOP+∠GOP=180°,即F、O、G共线,由(2)知∠EOF=60°,OG=OF=OE,∴∠G=30°,∠EOB=30°,∴∠GPO=∠B=60°,∴∠EPB=∠B=60°,∴△EBP是等边三角形,∴BP=BE,而Rt△BOE中,BE==,∴BP=.18.(1)解:如图,连接OC,∵△ABC沿BC翻折得到△DBC,∴AC=DC,∴OC为△ABD的中位线,∴OC∥BD,∴∠AOC=∠ABD=30°,∴的长;(2)①证明:∵△ABC沿BC翻折得到△DBC,∴∠ACB=∠DCB=90°,AC=DC.∵DE∥AB,∴∠ABC=∠DEC,∴∠BAC=∠EDC.在△ABC和△DEC中,,∴△ABC≌△DEC(AAS),∴AB=DE,∴四边形ABDE为平行四边形.∵AB为⊙O的直径,∴∠ACB=90°,即AC⊥BC,∴四边形ABDE是菱形.②解:如图,连接OF交BD于点G.∵DF为⊙O的切线,∴FO⊥EF.又∵DE∥AB,∴OF⊥OB.在Rt△BOG中,∠ABD=30°,∴,∴.∵DE∥AB,∴∠GDF=∠ABD=30°,在Rt△DFG中,.19.(1)证明:如图,连接OC,∵OD⊥AC,ON过圆心O,∴AD=CD.∴OM垂直平分AC.∴MA=MC.∴∠MAC=∠MCA.∵OA=OC,∴∠OAC=∠OCA.∴∠OAC+∠MAC=∠OCA+∠MCA,即∠MAO=∠MCO.∵CM为⊙O的切线,∴∠MCO=90°,∴∠MAO=90°.∴OA⊥AM.又∵点A在⊙O上,∴AM是⊙O的切线;(2)解:设⊙O的半径为r,则OD=r﹣4,AD=AC=4.∴(r﹣4)2+(4)2=r2,解得r=8.∴OD=4,OA=8,∴∠OAD=30°∴∠AOD=60°,∴∠AMO=30°.∴OM=2OA=16.∴MN=16﹣8=8;(3)解:∵∠COD=∠AOD=60°,∴∠AOC=120°,∴S阴影=S四边形AOCM﹣S扇形OAC=﹣=64﹣.20.解:(1)证明,连接OD,∵△ADE为直角三角形,AD为斜边,∴∠AED=90°,∴∠EAD+∠EDA=90°,∵∠EAD=∠DAB,∠OAD=∠ODA,∴∠ODA+∠EDA=90°,∵OD为⊙O半径,∴DE为⊙O的切线;(2)证明,如图,连接DF,∵∠DFE+∠DF A=180°,∠DF A+∠DBA=180°,∴∠DFE=∠DBA∵∠ABC=90°,∠DEA=90°,∴∠DBA+∠DBC=90°,∠DFE+∠EDF=90°,∴∠EDF=∠DBC,∴Rt△EDF∽Rt△DBC,∴=,∵DE=DC,∴DE2=EF•BD;(3)∵∠DBC+∠DBA=90°,∠DAB+∠DBA=90°,∴∠DBC=∠DAB,∵∠EAD=∠DAB,∴∠EAD=∠DBC,∵AB是⊙O的直径,∴∠ADB=∠BDC=90°,∴∠E=∠BDC,在Rt△ADE和Rt△BCD中,,∴△ADE≌△BCD(AAS),∴BC=AD,∵∠ADB=∠ABC=90°,∠C=∠C,∴△CDB∽△CBA,∴==,设CD=x,BC=y,则=,整理得x2+xy﹣y2=0,解得x1=y,x2=y(舍去),∵AB=1,∴=,即=,解得BD=,∴BD的长为.。
《利用线段图分析数量关系》教案范文

《利用线段图分析数量关系》教案《利用线段图分析数量关系》教案范文《利用线段图分析数量关系》教案范文【教学内容】:分数乘除法应用题【设计意图】:一直以来,分数应用题中的数量关系都较为抽象、难于理解,使学生对于“分数意义”的拓展认识,分数的意义不再仅仅局限于部分量与总量之间的对比关系,还引申为两种相关联的量在数量上的变化。
仅凭记忆题型确实可以使很多孩子迅速掌握这类问题的解决方法能够正确计算,但不利于培养学生分析问题和灵活应用知识能力的培养。
我认为,在教学分数应用题时,要求能结合具体情境,解决简单的分数实际问题,体会分数在现实生活中的应用。
学生通过前面的学习对于分数乘除法的意义及相应的问题已经有了一定的认识和理解。
在实践教学中,主要让学生通过将生活中的实际问题利用转化的思想抽象成数学问题,然后利用画线段图的方法分析数量关系,在逐层学习的过程中,通过分析交流和适量的练习使大部分学生能够掌握各自的方法。
利用画线段图的策略创设不同的问题情境,有助于学生理解分数应用题中各量之间的对比关系,从而能够轻松的根据分数乘除法意义的不同解决问题,帮助学生愉悦的学习数学,树立学好数学的信心。
【教学目标】:1、通过本课教学,使学生能够掌握分数应用题目中的单位“1”和各个量之间的数量关系,并能正确的对题目进行解答。
2、通过学习,培养学生学会用线段图表示数量关系,培养学生的分析能力和探究能力。
3、通过学习,培养学生认真、仔细的学习习惯。
【教学重点】:使学生掌握分数应用题的数量关系,较复杂的`题目能准确的画线段图,并做出正确的解答。
【教学难点】:使学生利用线段图,较准确地表示题目中的数量关系,并能正确的进行解答。
【教具】投影仪【教学过程】:课前互动:师:在上课之前,我们先来做一个小游戏。
输了的要完成我们的练习题。
介绍规则:轮流报分数,要求是分母比分子大一,按顺序说,如:1/2,2/3……。
一、谈话导入师:我们之前学习了分数应用题,在解决分数应用题时,你认为关键是什么?生:找准题目中的单位“1”,找对应的分率。
正方形与全等模型(含答案)

正方形与全等模型1.(垂直相等)如图,在正方形ABCD中.(1)若点E、F分别在AB、AD上,且AE=DF.试判断DE与CF的数量及位置关系,并说明理由;(2)若P、Q、M、N是正方形ABCD各边上的点,PQ与MN相交,且PQ=MN,问PQ⊥MN成立吗?为什么?2.(三垂)如图,直线MN不与正方形的边相交且经过正方形ABCD的顶点D,AM⊥MN于M,CN⊥MN于N,BR⊥MN于R.(1)求证:△ADM≌△DCN:(2)求证:MN=AM+CN;(3)试猜想BR与MN的数量关系,并证明你的猜想.3.(三垂)如图,在平的直角坐标系中,直线y=﹣2x+2与x轴、y轴分别相交于点A、B,四边形ABCD是正方形,曲线y=在第一象限经过点D.求双曲线表示的函数解析式.4.(三垂)如图,四边形ABCD是正方形,直线l1,l2,l3分别通过A,B,C三点,且l1∥l2∥l3,若l1与l2的距离为5,l2与l3的距离为7,则正方形ABCD的面积等于()A.70 B.74 C.144 D.1485.(三垂)如图在平面直角坐标系中正方形OABC的边OC,OA分别在x轴正半轴上和y轴的负半轴上,点B在双曲线y=﹣上,直线y=kx﹣k(k>0)交y轴与F.(1)求点B、E的坐标;(2)连接BE,CF交于M点,是否存在实数k,使得BE⊥CF?若存在,求出k的值;若不存在,请说明理由;(3)F在线段OA上,连BF,作OM⊥BF于M,AN⊥BF于N,当F在线段OA上运动时(不与O、A重合),的值是否变化.若变化,求出变化的范围;若不变,求其值.6.(对角互补)已知:如图,正方形ABCD中,对角线AC和BD相交于点O.E、F分别是边AB、BC上的点,若AE=4cm,CF=3cm,且OE⊥OF,则EF的长为_________cm.7.(对角互补)在图1到图3中,点O是正方形ABCD对角线AC的中点,△MPN为直角三角形,∠MPN=90°.正方形ABCD保持不动,△MPN沿射线AC向右平移,平移过程中P点始终在射线AC上,且保持PM垂直于直线AB于点E,PN垂直于直线BC于点F.(1)如图1,当点P与点O重合时,OE与OF的数量关系为_________;(2)如图2,当P在线段OC上时,猜想OE与OF有怎样的数量关系与位置关系?并对你的猜想结果给予证明;(3)如图3,当点P在AC的延长线上时,OE与OF的数量关系为_________;位置关系为_________.8.(对角互补)如图,正方形ABCD中,AC是对角线,今有较大的直角三角板,一边始终经过点B,直角顶点P 在射线AC上移动,另一边交DC于Q.(1)如图1,当点Q在DC边上时,猜想并写出PB与PQ所满足的数量关系;并加以证明;(2)如图2,当点Q落在DC的延长线上时,猜想并写出PB与PQ满足的数量关系,请证明你的猜想.9.(对角互补)如图,正方形ABCD,点P是对角线AC上一点,连接BP,过P作PQ⊥BP,PQ交CD于Q,连接BQ交AC于G,若AP=,Q为CD中点,则下列结论:①∠PBC=∠PQD;②BP=PQ;③∠BPC=∠BQC;④正方形ABCD的面积是16;其中正确结论的个数是()A.4B.3C.2D.110.(对角互补)如图1,直角∠EPF的顶点和正方形ABCD的顶点C重合,两直角边PE,PF分别和AB,AD所在的直线交于点E和F.易得△PBE≌△PDF,故结论“PE=PF”成立;(1)如图2,若点P在正方形ABCD的对角线AC上,其他条件不变,(1)中的结论是否仍然成立?说明理由;(2)如图(3)将(2)中正方形ABCD改为矩形ABCD其他条件不变,若AB=m,BC=n,直接写出的值.11.(对角互补)如图,边长一定的正方形ABCD,Q为CD上一个动点,AQ交BD于点M,过M作MN⊥AQ 交BC于点N,作NP⊥BD于点P,连接NQ,下列结论:①AM=MN;②MP=BD;③BN+DQ=NQ;④为定值.其中一定成立的是()A.①②③B.①②④C.②③④D.①②③④12.(等角共顶点)(1)如图①,△ABC中,AB=AC,∠BAC=90°,点D为BC边上一点(与点B、C不重合),连接AD,以AD为一边且在AD的右侧作正方形ADEF.可猜想线段CF,BD之间的数量关系是_________,位置关系是_________;(2)当点D在线段BC的延长线时,如图②,(1)中的结论是否仍然成立?如果成立,给出证明,如果不成立,说明理由.13.(等角共顶点)已知点O为正方形ABCD的中心,M为射线OD上一动点(M与点O,D不重合),以线段AM 为一边作正方形AMEF,连接FD.(1)当点M在线段OD上时(如图1),线段BM与DF有怎样的数量及位置关系?请判断并直接写出结果;(2)当点M在线段OD的延长线上时(如图2),(1)中的结论是否仍然成立?请结合图2说明理由.14.(等角共顶点)以△ABC的各边,在边BC的同侧分别作三个正方形.他们分别是正方形ABDI,BCFE,ACHG,试探究:(1)如图中四边形ADEG是什么四边形?并说明理由.(2)当△ABC满足什么条件时,四边形ADEG是矩形?(3)当△ABC满足什么条件时,四边形ADEG是正方形?15.(等角共顶点)在直角三角形ABC中,∠C=90°,BC=2,以AB为边作正方形ABDE,连接AD、BE交O,CO=,则AC的长为()A.2B.3C.4D.16.(等角共顶点)如图,已知正方形ABCD,点E是BC上一点,以AE为边作正方形AEFG.(1)连接GD,求证:△ADG≌△ABE;(2)连接FC,求证:∠FCN=45°;(3)请问在AB边上是否存在一点Q,使得四边形DQEF是平行四边形?若存在,请证明;若不存在,请说明理17.(等角共顶点)如图1,2,四边形ABCD是正方形,M是AB延长线上一点.直角三角尺的一条直角边经过点D,且直角顶点E在AB边上滑动(点E不与点A,B重合),另一条直角边与∠CBM的平分线BF相交于点F.(1)如图1,当点E在AB边的中点,N为AD边的中点位置时:①通过测量DE,EF的长度,猜想DE与EF满足的数量关系是_________;②请证明你的上述猜想.(2)如图2,当点E在AB边上的任意位置时,猜想此时DE与EF有怎样的数量关系,并证明你的结论.18.(对角互补分半)已知,四边形ABCD是正方形,∠MAN=45°,它的两边AM、AN分别交CB、DC与点M、N,连接MN,作AH⊥MN,垂足为点H(1)如图1,猜想AH与AB有什么数量关系?并证明;(2)如图2,已知∠BAC=45°,AD⊥BC于点D,且BD=2,CD=3,求AD的长;小萍同学通过观察图①发现,△ABM和△AHM关于AM对称,△AHN和△ADN关于AN对称,于是她巧妙运用这个发现,将图形如图③进行翻折变换,解答了此题.你能根据小萍同学的思路解决这个问题吗?19.(对角互补分半)(1)如图①,在正方形ABCD中,△AEF的顶点E,F分别在BC,CD边上,高AG与正方形的边长相等,求∠EAF的度数.(2)如图②,在Rt△ABD中,∠BAD=90°,AB=AD,点M,N是BD边上的任意两点,且∠MAN=45°,将△ABM 绕点A逆时针旋转90°至△ADH位置,连接NH,试判断MN,ND,DH之间的数量关系,并说明理由.(3)在图①中,连接BD分别交AE,AF于点M,N,若EG=4,GF=6,BM=3,求AG,MN的长.20.(对角互补分半)如图,将边长为4的正方形ABCD沿着折痕EF折叠,使点B落在边AD的中点G处,那么21.(等角共顶点拓展)如图,四边形ABCD是正方形,以CG为一边在正方形ABCD外作正方形CEFG,连接BG,DE.猜想图中线段BG、DE的数量和位置关系,并说明理由.22.(等角共顶点拓展)如图,正方形ABDE和ACFG是以△ABC的AB、AC为边的正方形,P、Q为它们的中心,M是BC的中点,试判断MP、MQ在数量和位置是有什么关系?并证明你的结论.23.如图所示,四边形ABCD为正方形,△BEF为等腰直角三角形(∠BFE=90°,点B、E、F按逆时针顺序),P 为DE的中点,连接PC、PF.(1)如图(1),E点在边BC上,则线段PC、PF的数量关系为_________,位置关系为_________(不需要证明).(2)如图(2),将△BEF绕B点顺时针旋转α°(0<α<45),则线段PC、PF有何数量关系和位置关系?请写出你的结论并证明.(3)如图(3),E点旋转到图中的位置,其它条件不变,完成图(3),则线段PC、PF有何数量关系和位置关系?直接写出你的结论,不需要证明.24.(等角共顶点拓展)如图甲,操作:把正方形CGEF的对角线,CE放在正方形ABCD的边BC的延长线上(CG >BC),取线段AE的中点M.(1)探究线段MD、MF的位置及数量关系,直接写出答案即可;(2)将正方形CGEF绕点C逆时针旋转45°(如图乙),令CG=2BC其他条件不变,结论是否发生变化,并加以证明;(2)将正方形CGEF绕点C旋转任意角度后(如图丙),其他条件不变.探究:线段MD,MF的位置及数量关系,并加以证明.【巩固练习】25.已知点E是正方形ABCD外的一点,EA=ED,线段BE与对角线AC相交于点F,(1)如图1,当BF=EF时,线段AF与DE之间有怎样的数量关系?并证明;(2)如图2,当△EAD为等边三角形时,写出线段AF、BF、EF之间的一个数量关系,并证明.26.如图1,四边形ABCD为正方形,E在CD上,∠DAE的平分线交CD于F,BG⊥AF于G,交AE于H.(1)如图1,∠DEA=60°,求证:AH=DF;(2)如图2,E是线段CD上(不与C、D重合)任一点,请问:AH与DF有何数量关系并证明你的结论;(3)如图3,E是线段DC延长线上一点,若F是△ADE中与∠DAE相邻的外角平分线与CD的交点,其它条件不变,请判断AH与DF的数量关系(画图,直接写出结论,不需证明).27.在直角坐标系中,直线y=2x+4交x轴于A,交y轴于D(1)以A为直角顶点作等腰直角△AMD,直接写出点M的坐标为_________(2)以AD为边作正方形ABCD,连BD,P是线段BD上(不与B、D重合)的一点,在BD上截取PG=,过G作GF⊥BD,交BC于F,连AP则AP与PF有怎样的数量关系和位置关系?并证明你的结论;(3)在(2)中的正方形中,若∠PAG=45°,试判断线段PD、PG、BG之间有何关系,并证明你的结论.28.如图,一个直角三角形的直角顶点P在正方形ABCD的对角线AC所在的直线上滑动,并使得一条直角边始终经过B点.(1)如图1,当直角三角形的另一条直角边和边CD交于Q点,=_________;(2)如图2,当另一条直角边和边CD的延长线相交于Q点时,=_________;(3)如图3或图4,当直角顶点P运动到AC或CA的延长线上时,请你在图3或图4中任选一种情形,求的值,并说明理由.29.已知,如图在正方形OADC中,点C的坐标为(0,4),点A的坐标为(4,0),CD的延长线交双曲线y=于点B.(1)求直线AB的解析式;(2)G为x轴的负半轴上一点连接CG,过G作GE⊥CG交直线AB于E.求证CG=GE;(3)在(2)的条件下,延长DA交CE的延长线于F,当G在x的负半轴上运动的过程中,请问的值是否为定值,若是,请求出其值;若不是,请说明你的理由.30.如图,四边形ABCD位于平面直角坐标系的第一象限,B、C在x轴上,A点函数上,且AB∥CD∥y轴,AD∥x轴,B(1,0)、C(3,0).(1)试判断四边形ABCD的形状;(2)若点P是线段BD上一点PE⊥BC于E,M是PD的中点,连EM、AM.求证:AM=EM;(3)在图(2)中,连接AE交BD于N,则下列两个结论:①值不变;②的值不变.其中有且仅有一个是正确的,请选择正确的结论证明并求其值.参考答案与试题解析一.选择题(共16小题)1.如图,在正方形ABCD中.(1)若点E、F分别在AB、AD上,且AE=DF.试判断DE与CF的数量及位置关系,并说明理由;(2)若P、Q、M、N是正方形ABCD各边上的点,PQ与MN相交,且PQ=MN,问PQ⊥MN成立吗?为什么?考点:正方形的性质.专题:探究型.分析:(1)由已知易得△DAE≌△CDF,故有DE=CF.(2)由点N,Q分别向AB,AD作垂线,构造两直角三角形全等,由角的等量代换,易得QP⊥MN.解答:解:(1)在正方形ABCD中,AD=DC,AE=DF,∠EAD=∠FDC,所以△EAD≌△FDC,故DE=CF,∴∠EDA=∠FCD,又∵∠DCF+∠DFC=90°,∴∠ADE+∠DFC=90°,∴∠DGF=90°即DE⊥CF.(2)由点N,Q∵PQ=MN,RN=SQ,∴△MNR≌△QPS(HL),∴∠PQS=∠MNR,又∠1+∠PQS=90°,所以∠1+∠MNR=90°,即MN⊥PQ.点评:解答本题要充分利用正方形的特殊性质.注意在正方形中的特殊三角形的应用,搞清楚矩形、菱形、正方形中的三角形的三边关系,可有助于提高解题速度和准确率.2.如图,直线MN不与正方形的边相交且经过正方形ABCD的顶点D,AM⊥MN于M,CN⊥MN于N,BR⊥MN 于R.(1)求证:△ADM≌△DCN:(2)求证:MN=AM+CN;(3)试猜想BR与MN的数量关系,并证明你的猜想.考点:正方形的性质;全等三角形的判定与性质.专题:证明题;探究型.分析:此题分三问进行,三问都与三角形全等直接相关,所以要紧扣三角形全等的判定方法进行思考.(1)要证△ADM≌△DCN,由于它们都是直角三角形,所以首先有直角相等,又由ABCD是正方形有AD=DC,再找一个条件即可,而由图形很容易分析得出∠ADM=∠DCN;(2)的关键是合理添加辅助线,通过等量代换等到结论;(3)首先结合前面的结论再结合图形合理猜想,然后再结合前面的结论认真推理,细致证明即可.解答:(1)证明:点M,CN⊥MN 于点N(已知),∴∠AMD=∠D NC=90°(垂直的定义).∴∠MAD+∠M DA=180°﹣90°=90°(三角形内角和定理).∵四边形ABCD是正方形(已知),∴∠ADC=90°,AD=DC.∴∠MDA+∠N DC=180°﹣90°=90°(平角的定义).∴∠MAD+∠M DA=∠NDC+∠NCD.∴∠MAD=∠N DC.在△AMB和△DNC中,∵∠AMD=∠D NC,∠MAD=∠ND C,AD=DC,∴△AMD≌△DNC(AAS).(2)证明:由(1)△AMD≌△DN C,∴AM=DN,MD=NC.(全等三角形对应边相等)∴MD+DN=AM +CN.即MN=AM+CN.(3)猜想BR=MN.证明如下:E.∵BR⊥MN,CN⊥MN(已知)∴BR∥CN(垂直于同一直线的两条直线平行)∴∠1=∠2(两直线平行同位角相等)又四边形ABCD是正方形∴AB⊥BC,DC⊥BC,∴∠ABE=∠D CN=90°﹣∠1,在△ABE和△DCN中,AB=DC,∠ABE=∠DCN ,∠AEB=∠DNC =90°∴△ABE≌△D CN(AAS)由(1)△ADM≌△DC N∴△ABE≌△A DM∴AM=AE(全等三角形对应边相等).又AE∥MR,AM∥ER,∴BR=BE+ER= CN+AM=DM+ DN=MN.点评:此题三问紧密相连,第一问正确解出后,后两问就顺理成章求出来了.3.如图,在平的直角坐标系中,直线y=﹣2x+2与x轴、y轴分别相交于点A、B,四边形ABCD是正方形,曲线y=在第一象限经过点D.求双曲线表示的函数解析式.考点:反比例函数综合题.专题:探究型.分析:过点D作DE⊥x轴于点E,先由直线y=﹣2x+2与x轴,y轴相交于点A、B求出OB及OA的长,再由全等三角形的判定定理得出△AOB≌△DEA,故可得出D点坐标,再由待定系数法即可求出反比例函数的解析式.解答:解:过点D作DE⊥x轴于点E,∵直线y=﹣2x+2与x轴,y轴相交于点A、B,∴当x=0时,y=2,即OB=2;当y=0时,x=1,即OA=1,∵四边形ABCD是正方形,∴∠BAD=90°,AB=AD.∴∠BAO+∠DAE=90°.∵∠ADE+∠DAE=90°,∴∠BAO=∠ADE,∵∠AOB=∠DEA=90°,∴△AOB≌△DEA,∴DE=AO=1,AE=BO=2,∴OE=3,DE=1.∴点D的坐标为(3,1)把(3,1)代入y=中,得k=3,故反比例函数的解析式为:y=.点评:本题考查的是反比例函数综合题,涉及到一次函数的性质、正方形的性质及全等三角形的判定与性质,根据题意作出辅助线,构造出全等三角形是解答此题的关键.4.如图,四边形ABCD是正方形,直线l1,l2,l3分别通过A,B,C三点,且l1∥l2∥l3,若l1与l2的距离为5,l2与l3的距离为7,则正方形ABCD的面积等于()A.70 B.74 C.144 D.148考点:勾股定理;全等三角形的判定与性质;正方形的性质.分析:画出L1到L2,L2到L3的距离,分别交L2,L3于E,F,通过证明△ABE≌△BCF,得出BF=AE,再由勾股定理即可得出结论.解答:解:过点A作AE⊥l1,过点C作CF⊥l2,∴∠CBF+∠BCF=90°,四边形ABCD是正方形,∴AB=BC=CD=AD,∴∠DAB=∠ABC=∠BCD=∠CDA=90°,∴∠ABE+∠CBF=90°,∵l1∥l2∥l3,∴∠ABE=∠BCF,在△ABE和△BCF中,∴△ABE≌△BCF(AAS)(画出L1到L2,L2到L3的距离,分别交L2,L3于E,F)∴BF=AE,∴BF2+CF2=BC2,∴BC2=52+72=74.故面积为74.故选B.点评:本题主要考查了正方形的性质,全等三角形的判定与性质以及正方形面积的求解方法,能够熟练掌握.5.如图在平面直角坐标系中正方形OABC的边OC,OA分别在x轴正半轴上和y轴的负半轴上,点B在双曲线y=﹣上,直线y=kx﹣k(k>0)交y轴与F.(1)求点B、E的坐标;(2)连接BE,CF交于M点,是否存在实数k,使得BE⊥CF?若存在,求出k的值;若不存在,请说明理由;(3)F在线段OA上,连BF,作OM⊥BF于M,AN⊥BF于N,当F在线段OA上运动时(不与O、A重合),的值是否变化.若变化,求出变化的范围;若不变,求其值.考点:反比例函数综合题.专题:开放型.分析:(1)把正方形的面积用B点坐标表示求解;(2)用分析法求解.根据直线解析式的特点,求k只需求满足条件时OF的长;(3)探索:,,,代换后得结论为1,所以不变化.解答:解:(1)根据题意,设B(x,﹣x),∵B在y=﹣的图象上,∴x2=4,x=±2,根据图形得B(2,﹣2),∵E在X轴上,∴kx﹣k=0,x=1,即E(1,0);(2)假设存在k,使BE⊥CF,∵∠OCF=∠CBE∠COF=∠BCE,OC=CB∴△OCF≌△CBE∴OF=CE=1∴k=1;(3)=1.证明:由已知条件易证:△OMF∽△BNA,△ANF∽△BNA,∴,∴===1.点评:此题运用了分析法解题探究,综合性很强,检验学生自主创新能力.6.(2008•安顺)已知:如图,正方形ABCD中,对角线AC和BD相交于点O.E、F分别是边AB、BC上的点,若AE=4cm,CF=3cm,且OE⊥OF,则EF的长为5cm.考点:正方形的性质;全等三角形的判定与性质;勾股定理.专题:计算题.分析:连接EF,作OM⊥AB于点M,根据条件可以证明△OED≌△OFC,则OE=OF,CF=DE=3Ccm,则AE=DF=4,根据勾股定理得到EF==5cm.解答:解:连接EF,作OM⊥AB于点M,∵OD=OC,∵OE⊥OF∴∠EOD+∠FOD=90°∵正方形ABCD∴∠COF+∠DOF=90°∴∠EOD=∠FOC而∠ODE=∠OCF=45°∴△OFC≌△OED,∴OE=OF,CF=DE=3cm,则AE=DF=4,根据勾股定理得到EF==5cm.故答案为5.点评:根据已知条件以及正方形的性质求证出两个全等三角形是解决本题的关键.7.在图1到图3中,点O是正方形ABCD对角线AC的中点,△MPN为直角三角形,∠MPN=90°.正方形ABCD 保持不动,△MPN沿射线AC向右平移,平移过程中P点始终在射线AC上,且保持PM垂直于直线AB于点E,PN垂直于直线BC于点F.(1)如图1,当点P与点O重合时,OE与OF的数量关系为OE=OF;(2)如图2,当P在线段OC上时,猜想OE与OF有怎样的数量关系与位置关系?并对你的猜想结果给予证明;(3)如图3,当点P在AC的延长线上时,OE与OF的数量关系为OE=OF;位置关系为OE⊥OF.考点:正方形的判定与性质;全等三角形的判定与性质;矩形的判定与性质;平移的性质.分析:(1)根据利用正方形的性质和直角三角形的性质即可判定四边形BEOF为正方形,从而得到结论;(2)当移动到点P的位置时,可以通过证明四边形BEPF为矩形来得到两条线段的数量关系;(3)继续变化,有相同的关系,其证明方法也类似.解答:(1)解:OE=OF(相等);(1分)(2)解:OE=OF,OE⊥OF;(3分)证明:连接BO,∵在正方形ABCD中,O为AC中点,∴BO=CO,BO⊥AC,∠BCA=∠ABO=45°,(4分)∵PF⊥BC,∠BCO=45°,∴∠FPC=45°,PF=FC.∵正方形ABCD,∠ABC=90°,∵PF⊥BC,PE⊥AB,∴∠PEB=∠PFB=90°.∴四边形PEBF是矩形,∴BE=PF.(5分)∴BE=FC.∴△OBE≌△OCF,∴OE=OF,∠BOE=∠COF,(7分)∵∠COF+∠BOF=90°,∴∠BOE+∠BOF=90°,∴∠EOF=90°,∴OE⊥OF.(8分)(3)OE=OF(相等),OE⊥OF(垂直).(10分)点评:本题考查了正方形的性质,解题的关键是抓住动点问题,化动为静,还要大胆的猜想.8.如图,正方形ABCD中,AC是对角线,今有较大的直角三角板,一边始终经过点B,直角顶点P在射线AC上移动,另一边交DC于Q.(1)如图1,当点Q在DC边上时,猜想并写出PB与PQ所满足的数量关系;并加以证明;(2)如图2,当点Q落在DC的延长线上时,猜想并写出PB与PQ满足的数量关系,请证明你的猜想.考点:正方形的判定与性质;全等三角形的判定与性质.分析:(1)过P作PE⊥BC,PF⊥CD,证明Rt△PQF≌Rt△PBE,即可;(2)证明思路同(1)解答:(1)PB=PQ,证明:过P作PE⊥BC,PF⊥CD,∵P,C为正方形对角线AC上的点,∴PC平分∠DCB,∠DCB=90°,∴PF=PE,∴四边形PECF为正方形,∵∠BPE+∠QPE=90°,∠QPE+∠QPF=90°,∴∠BPE=∠QPF,∴Rt△PQF≌Rt△PBE,∴PB=PQ;(2)PB=PQ,证明:过P作PE⊥BC,PF⊥CD,∵P,C为正方形对角线AC上的点,∴PC平分∠DCB,∠DCB=90°,∴PF=PE,∴四边形PECF为正方形,∵∠BPE+∠QPE=90°,∠QPE+∠QPF=90°,∴∠BPE=∠QPF,∴Rt△PQF≌Rt△PBE,∴PB=PQ.点评:此题考查了正方形,角平分线的性质,以及全等三角形判定与性质.此题综合性较强,注意数形结合思想.9.如图,正方形ABCD,点P是对角线AC上一点,连接BP,过P作PQ⊥BP,PQ交CD于Q,连接BQ交AC 于G,若AP=,Q为CD中点,则下列结论:①∠PBC=∠PQD;②BP=PQ;③∠BPC=∠BQC;④正方形ABCD的面积是16;其中正确结论的个数是()A.4B.3C.2D.1考点:正方形的性质;全等三角形的判定与性质.分析:根据对角互补的四边形,则四边形共圆,根据圆周角定理得出∠BPC=∠BQC,根据∠PBC=∠PQD,过P作PM⊥AD于M,PE⊥AB于E,PF⊥DC于F,则E、P、F三点共线,推出正方形AEPM,根据勾股定理求出AE=PE=PM=AM=DF=1,证△BEP≌△PFQ,推出PE=FQ=1,BP=PQ,求出DQ、DC,即可.解答:解:∵四边形ABCD是正方形,∴∠BCQ=90°,∵PQ⊥PB,∴∠BPQ=90°,∴∠BPQ+∠BC Q=180°,∴B、C、Q、P 四点共圆,∴∠PBC=∠PQ D,∠BPC=∠BQC ,∴①正确;③正确;过P作PM⊥AD 于M,PE⊥AB 于E,PF⊥DC 于F,则E、P、F三点共线,∵四边形ABCD是正方形,∴AB=AD=DC =BC,∠DAC=∠BAC ,∠DAB=90°,∴∠MAE=∠P EA=∠PMA=90°,PM=PE,∴四边形AMPE是正方形,∴AM=PM=PE =AE,∵AP=,∴在Rt△AEP 中,由勾股定理得:AE2+PE2=()2,解得:AE=AM=PE=P M=1,∴DF=1,设AB=BC=CD=A D=a,则BE=PF=a﹣1,∵∠BEP=∠PFQ=∠BPQ=90°,∴∠BPE+∠EBP=90°,∠EPB+∠FPQ=90°,∴∠EBP=∠FPQ,在△BEP和△PFQ中,∴△BEP≌△PFQ(ASA),∴PE=FQ=1,BP=PQ,∴②正确;∴DQ=1+1=2,∵Q为CD中点,∴DC=2DQ=4,∴正方形ABCD的面积是4×4=16,∴④正确;故选A.点评:本题考查了正方形的性质和判定,全等三角形的性质和判定,勾股定理,三角形的内角和定理等知识点,主要考查学生的推理能力,题目综合性比较强,有一定的难度.10.如图1,直角∠EPF的顶点和正方形ABCD的顶点C重合,两直角边PE,PF分别和AB,AD所在的直线交于点E和F.易得△PBE≌△PDF,故结论“PE=PF”成立;(1)如图2,若点P在正方形ABCD的对角线AC上,其他条件不变,(1)中的结论是否仍然成立?说明理由;(2)如图(3)将(2)中正方形ABCD改为矩形ABCD其他条件不变,若AB=m,BC=n,直接写出的值.考点:正方形的性质;垂线;全等三角形的判定与性质.分析:(1)过点P分别作AB、AD的垂线,垂足分别为G、H,有材料提供的证明思路可证明△PGE≌△PHF,再根据全等三角形的性质:对应边相等可得:PE=PF;(2)有(1)证题思路可知方形ABCD改为矩形ABCD其他条件不变,则△PGE∽△PHF,再根据相似三角形的性质:对应边的比值相等可得:的比值.解答:解:(1)成立.证明如下:如图,过点P分别作AB、AD的垂线,垂足分别为G、H,则∠GPH=90°,PG=PH,∠PGE=∠PHF=90°,∵∠EPF=90°,∴∠1=∠2,∴△PGE≌△PHF,∴PE=PF;(2).点评:本题是一个动态几何题,考查了正方形性质、矩形的性质、全等三角形的判定以及性质,三角形相似的条件和性质及进行有条理的思考和表达能力,还考查按要求画图能力.11.如图,边长一定的正方形ABCD,Q为CD上一个动点,AQ交BD于点M,过M作MN⊥AQ交BC于点N,作NP⊥BD于点P,连接NQ,下列结论:①AM=MN;②MP=BD;③BN+DQ=NQ;④为定值.其中一定成立的是()A.①②③B.①②④C.②③④D.①②③④考点:正方形的性质;全等三角形的判定与性质;确定圆的条件.专题:动点型.分析:由题可知A,B,N,M四点共圆,进而可得出∠ANM=∠NAM=45°,由等角对等边知,AM=MN,故①正确;由同角的余角相等知,∠HAM=∠PMN,所以Rt△AHM≌Rt△MPN,即可得出结论,故②正确;先由题意得出四边形SMWB是正方形,进而证出△AMS≌△NMW,因为AS=NW,所以AB+BN=SB+BW=2BW,而BW:BM=1:,所以==,故③正确.因为∠BAN+∠QAD=∠NAQ=45°,在∠NAM作AU=AB=AD,且使∠BAN=∠NAU,∠DAQ=∠QAU,所以△ABN≌△UAN,△DAQ≌△UAQ,有∠UAN=∠UAQ=90°,BN=NU,DQ=UQ,即可得出结论,故④正确;解答:解:如图:作AU⊥NQ于U,连接AN,AC,∵∠AMN=∠A BC=90°,∴A,B,N,M 四点共圆,∴∠NAM=∠D BC=45°,∠ANM=∠AB D=45°,∴∠ANM=∠N AM=45°,∴由等角对等边知,AM=MN,故①正确.由同角的余角相等知,∠HAM=∠PM N,∴Rt△AHM≌Rt△MPN∴MP=AH=A C=BD,故②正确,如图,作MS⊥AB,垂足为S,作MW⊥BC,垂足为W,点M是对角线BD上的点,∴四边形SMWB是正方形,有MS=MW=BS= BW,∴△AMS≌△NMW,∴AS=NW,∴AB+BN=SB+ BW=2BW,∵BW:BM=1:,∴==,故④正确.∵∠BAN+∠Q AD=∠NAQ=45°,∴在∠NAM作AU=AB=AD,且使∠BAN=∠NAU,∠DAQ=∠QAU,∴△ABN≌△UAN,△DAQ≌△UAQ,有∠UAN=∠UAQ,BN=NU,DQ=UQ,∴点U在NQ上,有BN+DQ=QU+UN=NQ,故③正确.故选D.点评:本题利用了正方形的性质,四点共圆的判定,圆周角定理,等腰直角三角形的性质,全等三角形的判定和性质求解.12.(1)如图①,△ABC中,AB=AC,∠BAC=90°,点D为BC边上一点(与点B、C不重合),连接AD,以AD为一边且在AD的右侧作正方形ADEF.可猜想线段CF,BD之间的数量关系是相等,位置关系是垂直;(2)当点D在线段BC的延长线时,如图②,(1)中的结论是否仍然成立?如果成立,给出证明,如果不成立,说明理由.考点:正方形的性质;全等三角形的判定与性质;等腰直角三角形.专题:几何综合题.分析:(1)可通过证明三角形ABD和三角形ACF全等来实现.因为AD=AF,AB=AC,只要证明∠BAD=∠CAF即可,∠BAD=90°﹣∠DAC=∠FAC,这样就构成了全等三角形判定中的SAS,△ABD≌△ACF,因此BC=CF,∠B=∠ACF,因为∠B+∠ACB=90°,那么∠ACF+ACD=90°,即FC⊥BC,也就是FC⊥BD.(2)当点D在BC的延长线上时①的结论仍成立.由正方形ADEF的性质可推出△DAB≌△FAC,所以CF=BD,∠ACF=∠ABD.结合∠BAC=90°,AB=AC,得到∠BCF=∠ACB+∠ACF=90度.即CF⊥BD.解答:解:(1)CF与BD的数量关系是:CF=BD;位置关系是:CF⊥BD;故答案为:相等、垂直.(2)当点D在BC的延长线上时(1)中的结论仍成立.(5分)理由如下:由正方形ADEF得AD=AF,∠DAF=90°.∵∠BAC=90°,∴∠DAF=∠BAC,∴∠DAB=∠FAC,又∵AB=AC,∴△DAB≌△FAC,(4分)∴CF=BD,∠ACF=∠ABD.(6分)∵∠BAC=90°,AB=AC,∴∠ABC=45°,∴∠ACF=45°,∴∠BCF=∠ACB+∠ACF=90°.即CF⊥BD.点评:本题中综合考查了正方形的性质,全等三角形的判定等知识,关键是证明三角形全等,判定两个三角形全等,先根据已知条件或求证的结论确定三角形,然后再根据三角形全等的判定方法,看缺什么条件,再去证什么条件.13.已知点O为正方形ABCD的中心,M为射线OD上一动点(M与点O,D不重合),以线段AM为一边作正方形AMEF,连接FD.(1)当点M在线段OD上时(如图1),线段BM与DF有怎样的数量及位置关系?请判断并直接写出结果;(2)当点M在线段OD的延长线上时(如图2),(1)中的结论是否仍然成立?请结合图2说明理由.考点:正方形的性质;全等三角形的判定与性质.专题:证明题;探究型.分析:(1)根据正方形性质求出AF=AM,AD=AB,∠FAM=∠DAB=90°,推出∠FAD=∠MAB,证△FAD≌△MAB,推出BM=DF,∠FDA=∠ABD=45°,求出∠ADB=45°即可;(2)根据正方形性质求出AF=AM,AD=AB,∠FAM=∠DAB=90°,推出∠FAD=∠MAB,证△FAD≌△MAB,推出BM=DF,∠FDA=∠ABD=45°,求出∠ADB=45°即可.解答:解:(1)BM=DF,BM⊥DF理由是:∵四边形ABCD、AMEF是正方形,∴AF=AM,AD=AB,∠FAM=∠DAB=90°,∴∠FAM﹣∠DAM=∠DAB﹣∠DAM,即∠FAD=∠MAB,∵在△FAD和△MAB中,∴△FAD≌△MAB,∴BM=DF,∠FDA=∠ABD=45°,∵∠ADB=45°,∴∠FDB=45°+45°=90°,∴BM⊥DF,即BM=DF,BM⊥DF.(2)解:成立,理由是:∵四边形ABCD和AMEF均为正方形,∴AB=AD,AM=AF,∠BAD=∠MAF=90°,∴∠FAM+∠DAM=∠DAB+∠DAM,即∠FAD=∠MAB,∵在△FAD和△MAB中,∴△FAD≌△MAB,∴BM=DF,∠ABM=∠ADF,由正方形ABCD知,∠ABM=∠ADB=45°,∴∠BDF=∠ADB+∠ADF=90°,即BM⊥DF,∴(1)中的结论仍成立.点评:本题考查了正方形的性质和全等三角形的性质和判定的应用,关键是求出△FAD≌△MAB,本题具有一定的代表性,主要培养学生运用性质进行推理的能力和猜想能力.14.以△ABC的各边,在边BC的同侧分别作三个正方形.他们分别是正方形ABDI,BCFE,ACHG,试探究:(1)如图中四边形ADEG是什么四边形?并说明理由.(2)当△ABC满足什么条件时,四边形ADEG是矩形?(3)当△ABC满足什么条件时,四边形ADEG是正方形?考点:正方形的判定与性质;全等三角形的判定与性质;平行四边形的判定;矩形的判定.分析:(1)根据全等三角形的判定定理SAS证得△BDE≌△BAC,所以全等三角形的对应边DE=AG.然后利用正方形对角线的性质、周角的定义推知∠EDA+∠DAG=180°,易证ED∥GA;最后由“一组对边平行且相等”的判定定理证得结论;(2)根据“矩形的内角都是直角”易证∠DAG=90°.然后由周角的定义求得∠BAC=135°;(3)由“正方形的内角都是直角,四条边都相等”易证∠DAG=90°,且AG=AD.由□ABDI和□ACHG的性质证得,AC=AB.解答:解:(1)图中四边形ADEG是平行四边形.理由如下:∵四边形ABDI、四边形BCFE、四边形ACHG都是正方形,∴AC=AG,AB=BD,BC=BE,∠GAC=∠EBC=∠DBA=90°.∴∠ABC=∠EBD(同为∠EBA的余角).在△BDE和△BAC中,,∴△BDE≌△BAC(SAS),∴DE=AC=AG,∠BAC=∠BDE.∵AD是正方形ABDI的对角线,∴∠BDA=∠BAD=45°.∵∠EDA=∠BDE﹣∠BDA=∠BDE﹣45°,∠DAG=360°﹣∠GAC﹣∠BAC﹣∠BAD=360°﹣90°﹣∠BAC﹣45°=225°﹣∠BAC∴∠EDA+∠DAG=∠BDE﹣45°+225°﹣。
人教版_部编版八年级数学上册第十二章第二节三角形全等的判定考试复习题二(含答案) (57)

人教版_部编版八年级数学上册第十二章第二节三角形全等的判定考试复习题二(含答案)如图,已知直线//AB 射线CD ,0100CEB ∠=。
P 是射线EB 上一动点,过点P 作//PQ EC 交射线CD 于点Q ,连结CP 。
作PCF PCQ ∠=∠,交直线AB 于点F ,CG 平分ECF ∠。
(1)若点,,P F G 都在点E 的右侧。
①求PCG ∠的度数;②若040EGC ECG ∠-∠=,求CPQ ∠的度数。
(2)在点P 的运动过程中,是否存在这样的情形,使32EGC EFC ∠=∠,若存在,求出CPQ ∠的度数;若不存在,请说明理由。
【答案】(1)①40°;②60°;(2)60°或15°.【解析】【分析】(1)①根据平行线的性质可知080ECQ ∠=,再结合角平分线的性质可求得1122PCG PCF FCG QCF FCE ∠=∠+∠=∠+∠,进而求解即可. ②根据平行线性质可得QCG EGC ∠=∠,结合已知条件040EGC ECG ∠-∠=且QCG ECG ECQ ∠+∠=∠可求得020EGC GCF FCP ∠=∠=∠=,根据平行线性质进而可求得060CPQ ECP EGC GCF FCP ∠=∠=∠+∠+∠=. (2)根据已知条件设3,2EGC x EFC x ∠=∠=,则GCF x ∠=,分①当点G F 、在点E 的右侧时②当点G F 、在点E 的左侧时两种情况,结合已知条件进行求解即可.【详解】(1)①∵0100CEB ∠=,//AB CD ,∴080ECQ ∠=,∵PCF PCQ ∠=∠,CG 平分ECF ∠, ∴1122PCG PCF FCG QCF FCE ∠=∠+∠=∠+∠ 01402ECQ =∠=②∵//AB CD∴QCG EGC ∠=∠,080QCG ECG ECQ ∠+∠=∠=,∴080EGC ECG ∠+∠=又∵040EGC ECG ∠-∠=,∴0060,20EGC ECG ∠=∠=∴020ECG GCF ∠=∠=()00018040202PCF PCQ ∠=∠=-= ∵//PQ CE ∴060CPQ ECP ∠=∠=(2)设3,2EGC x EFC x ∠=∠=,则GCF x ∠=,①当点G F 、在点E 的右侧时,则ECG PCF PCD x ∠=∠=∠=,∵080ECD ∠=,∴0480x =,解得020x =,∴0360CPQ x ∠==②当点G F 、在点E 的左侧时,则ECG GCF x ∠=∠=,∵01803CGF x ∠=-,080GCQ x ∠=+,∴00180380x x -=+,解得025x =,∴0005080130FCQ ECF ECQ ∠=∠+∠=+= ∴01652PCQ FCQ ∠=∠= ∴000655015CPQ ECP ∠=∠=-=【点睛】此题主要考查平行线的性质和角平分线的性质,解题在于熟练掌握平行线和角平分线的性质运用以及分情况讨论问题.62.如图,已知:OA OB =,OC OD =.(1)请找出图中一对全等的三角形,并说明理由;(2)若90O ︒∠=,25C ︒∠=,求BED ∠的度数.【答案】(1)△OAD ≌△OBC ,证明见解析;(2)∠BED=40°【解析】【分析】(1)由SAS 可以判定△OAD ≌△OBC(2)△OAD ≌△OBC 可得∠D=∠C=25°利用三角形内角和为180°可得∠OBC=65°利用三角形的外角等于与它不相邻的两个内角的和,可得∠BED 的度数.【详解】解(1)△OAD ≌△OBC理由:在△OAD 与△OBC 中OA=OB O=O OD=OC ⎧⎪∠∠⎨⎪⎩∴△OAD ≌△OBC (SAS )(2)由(1)可知:△OAD ≌△OBC∴∠D=∠C∵∠C=25°∴∠D=25°∵∠O=90°∴∠OBC=180°-∠O-∠C=180°-90°-25°=65°在△BDE中,∠OBC=∠D+∠BED∴∠BED=∠OBC-∠D=65°-25°=40°【点睛】本题考查了全等的判定及性质,以及三角形内角和和外角和的性质,掌握全等的判定是解题的关键.63.某段河流的两岸是平行的,数学兴趣小组在老师带领下不用涉水过河就测得河的宽度,他们是这样做的:①在河流的一侧岸边B点,选对岸正对的一棵树A;②沿河岸直走20米有一树C,继续前行20米到达D处;③从D处沿与河岸垂直的方向行走,当到达A树正好被C树遮挡住的E处停止行走;④测得DE的长为5米.求河流的宽度是多少?并说明理由.【答案】河流的宽度是5m ,证明见解析【解析】【分析】)根据全等三角形对应角相等可得AB=DE ;利用“角边角”证明Rt △ABC 和Rt △EDC 全等,再根据全等三角形对应边相等解答.【详解】解:河的宽度是5m ;证明如下:由作法知,BC=DC ,∠ABC=∠EDC=90°,在Rt △ABC 和Rt △EDC 中,ABC=EDC=90BC=DC ACB=ECD ⎧∠∠⎪⎨⎪∠∠⎩∴Rt △ABC ≌Rt △EDC (ASA ),∴AB=ED=5,即河流的宽度是5m【点睛】本题考查了全等三角形的应用,正确理解题中的测量距离是解题的关键.64.背景知识:如图,在Rt ABC 中,90ACB ∠=︒,若AC BC =,则:AB ==.(1)解决问题:如图(1),90ACD ∠=︒,AC DC =,MN 是过点A 的直线,过点D 作DB MN ⊥于点B ,连接CB ,现尝试探究线段BA 、BC 、BD 之间的数量关系:过点C 作CE CB ⊥,与MN 交于点E ,易发现图中出现了一对全等三角形,即 ≌,由此可得线段BA 、BC 、BD 之间的数量关系是: ;(2)类比探究:将图(1)中的MN 绕点A 旋转到图(2)的位置,其它条件不变,试探究线段BA 、BC 、BD 之间的数量关系,并证明;(3)拓展应用:将图(1)中的MN 绕点A 旋转到图 (3)的位置,其它条件不变,若2BD =,BC =AB 的长为 (直接写结果). 【答案】(1)△EAC ≌△BDC ;;(2)BD −,证明见解析;(3)4.【解析】【分析】(1)利用ASA 证明出△EAC ≌△BDC ,从而得出AE=BD ,EB=AE+AB=BD+AB ,根据EB =进一步得出答案即可;(2)过C 作EC ⊥CB 交MN 于E ,利用ASA 证明△ACE ≌△DCB ,进而求得线段之间的关系,进一步求证即可;(3)过C 作EC ⊥CB 于MN 于E ,利用ASA 证明△ACE ≌△DCB ,然后进一步即可求出AB 的长.【详解】(1)∵CE CB ⊥,∴∠ACE+∠ACB=90°,∵90ACD ∠=︒,∴∠BCD+∠ACB=90°∴∠ACE=∠BCD ,在四边形ACDB 中,∵DB MN ⊥,90ACD ∠=︒,∴∠CAB+∠D=180°,∵∠CAB+∠EAC=180°∴∠D=∠EAC ,在△EAC 与△BDC 中,∵∠EAC=∠D ,AC=DC ,∠ACE=∠DCB ,∴△EAC ≌△BDC(ASA),∴AE=BD ,EC=BC ,∴EB=AE+AB=BD+AB ,在Rt△ECB中,∵EC=BC,∴EB ,∴,故答案为:△EAC≌△BDC;;(2)BD−,证明:如图(2),过C作EC⊥CB交MN于E,则∠ECB=90°,∴∠ECB+∠BCA=∠ACD+∠BCA,∴∠ECA=∠BCD,∵DB⊥MN,∴∠ABD=∠ACD=90°,记AC与BD的交点为F,则∠BFA=∠DFC,∴∠BAF=∠FDC,在△ACE与△DCB中,∵∠BAF=∠FDC,AC=DC,∠ECA=∠BCD,∴△ACE≌△DCB(ASA),∴AE=BD,CE=CB,∴在Rt△BCE中,,∴,即:BD−;(3)如图(3)过C作EC⊥CB于MN于E,MN与CD相交于F,∵∠ACD=∠ACF=90°,∠ECB=90°,∴∠ACB+∠BCF=∠BCF+∠ECF,∴∠ACB=∠ECF,∴∠ACB+90°=∠ECF+90°,∴∠ACE=∠BCD,∵DB⊥MN,∴∠CAE=90°−∠AFC,∠D=90°−∠BFD,∵∠AFC=∠BFD,∴∠CAE=∠D,在△ACE与△DCB中,∵∠ACE=∠BCD,AC=DC,∠CAE=∠D,∴△ACE≌△DCB(ASA),∴AE=DB,CE=CB,∴△ECB为等腰直角三角形,∴,又∵BE=AB−AE=AB−BD,∴AB−,∵BD=2,,∴AB=4.【点睛】本题主要考查了全等三角形性质与判定的综合运用,熟练掌握相关概念是解题关键.65.如图,四边形ABCD中,AB=BC=2CD,AB∥CD,∠C=90°,E 是BC的中点,AE与BD相交于点F,连接DE.(1)求证:△ABE≌△BCD;(2)判断线段AE与BD的数量关系及位置关系,并说明理由;(3)若CD=1,试求△AED的面积.【答案】(1)见解析;(2)AE=BD,AE⊥BD,理由见解析;(3)△AED 的面积为3.2【解析】【分析】(1)由已知条件可推导得到AB BC ABE C BE CD =∠=∠=,,,由SAS 即可证明△ABE ≌△BCD ;(2)由(1)可得△ABE ≌△BCD 可得AE =BD ,再由角的转化可得∠AFB =90°,即可证明AE ⊥BD ;(3)因为 △AED 的面积=梯形ABCD 的面积﹣△ABE 的面积﹣△CDE 的面积,即可求解△AED 的面积.【详解】(1)证明:∵AB ∥CD ,∴∠ABE +∠C =180°,∵∠C =90°,∴∠ABE =90°=∠C ,∵E 是BC 的中点,∴BC =2BE ,∵BC =2CD ,∴BE =CD ,在△ABE 和△BCD 中,AB BC ABE C BE CD =⎧⎪∠=∠⎨⎪=⎩, ∴△ABE ≌△BCD (SAS );(2)解:AE =BD ,AE ⊥BD ,理由如下:由(1)得:△ABE ≌△BCD ,∴AE =BD ,∵∠BAE =∠CBD ,∠ABF +∠CBD =90°,∴∠ABF+∠BAE=90°,∴∠AFB=90°,∴AE⊥BD;(3)解:∵△ABE≌△BCD,∴BE=CD=1,∵AB=BC=2CD=2,∴CE=BC﹣BE=1,∴CE=CD,∴△AED的面积=梯形ABCD的面积﹣△ABE的面积﹣△CDE的面积=1 2(1+2)×2﹣12×2×1﹣12×1×1=32【点睛】此题考查全等三角形的判定与性质,解题关键在于掌握性质证明三角形全等.66.如图,△ABC 中,AB=BC,∠ABC=90°,F 为AB 延长线上一点,点E 在BC 上,且AE=CF.(1)求证:AE⊥CF;(2)若∠CAE=25°,求∠ACF 的度数.【答案】(1)见解析;(2)65°.【解析】【分析】(1)运用HL 定理直接证明△ABE ≌△CBF ,即可解决问题.(2)证明∠BAE=∠BCF=25°;求出∠ACB=45°,即可解决问题.【详解】如图,延长AE 交CF 于点H ,在Rt △ABE 与Rt △CBF 中,AE CF AB BC ⎧⎨⎩== ∴△ABE ≌△CBF (HL )∴∠BAE=∠BCF ,∵∠F+∠BCF=90°,∴∠BAE+∠F=90°,∴∠AHF=90°,∴AE ⊥CF(2)∵AB=BC ,∠ABC=90°,∴∠ACB=45°=∠BAC ,且∠CAE=25°,∴∠BAE=20°,∵△ABE ≌△CBF ,∴∠BAE=∠BCF=20°,∴∠ACF=65°.【点睛】此题考查全等三角形的判定及其性质的应用问题,准确找出图形中隐含的相等或全等关系是解题的关键.67.如图1,在△ABC中,点D、点E分别在边AB、BC上,DE=AE,且∠B=∠C=∠DEA=β。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
河北中考《操作与探究问题》专题复习 河北中考《操作与探究问题》
张北县第三中学
刘伟
A
D
A
D (A)
观察思考
A
B A
图1
D
B
图2
C(B) A B
E
E C
C
A
O
C D B
B
F B BF AD(C)图4E B OB
图3
E D
C
F
C
A
F
基本图形
图6
F
D 图5 C E
E
C
典例精析
A O E 2 图1
反思:你获得哪些知识与方法? 猜想:AE=BF,AE⊥BF , 如何证明呢? 反思:你获得哪些知识与方法? 猜想:BE=CF,AE=BF AE=B1F,如何证明呢? , ⊥
D F C
B1 B
转化思想 如图1, 已知正方形 如图1,已知正方形ABCD中, 如图 ,已知正方形 , 已知正方形ABCD中 , 中 中 F1 转化思想能够 BE=CF, 探究线段 与 使复杂的问题 AE⊥BF, 则线段BE 与CF 相 等 AE=BF , 探究线段AE与 BF的 ⊥ , 则线段BE与 CF相等 则线段 与 相等 的 数量关系和位置关系? 简单化 , 相等吗? 垂直吗? 吗?AE与BF相等吗? 数量关系和位置关系? 简单化, 陌生 与BF垂直吗 相等吗 垂直吗
O C E M B
D N F O/
B
M
E Q C N 图3 G 如图3,O为正方形 分别平移到 如图 , 为正方形ABCD内任意一点 内任意一点, 为正方形 内任意一点 如图4,若将MN、PQ分别平移到 , 如图 ,若将 、 MN⊥PQ于 则它们还相等吗? ⊥ 于 ,求证: . 图4 正方形外部,则它们还相等吗? 正方形外部,O,求证:MN=PQ.
的问题熟悉化, 的问题熟悉化 , 抽象的问题具 体化。 体化 。 例如将 图2中的问题 转化为我们相 对熟悉的图1, 进而获得解决 问题的转机。 问题的转机。
D P A 如图 2 , 若将 BF 平移到 B F P A 如图2 若将BF 平移到B1 BF平移到 O Q
位置, 位置 , 即 AE⊥B1F , 则线段 O F AE与 / 还相等吗? AE与B1F还相等吗?
截长补短法:上面问题中, ◆截长补短法:上面问题中,通过延长或截取的
方法, 方法 , 将三条线段的数量关系转化为两条线段的数 量关系,而解题关键就是要证明两个三角形全等。 量关系,而解题关键就是要证明两个三角形全等。
回顾反思
1.本堂课中复习到了哪些数学知识? 本堂课中复习到了哪些数学知识? 你学习到哪些新的题型,处理这类问题你有什么方法? 2.你学习到哪些新的题型,处理这类问题你有什么方法? 在解题的过程中你学习了哪些数学方法和数学思想? 3.在解题的过程中你学习了哪些数学方法和数学思想?
河北中考《操作与探究问题》 河北中考《操作与探究问题》专题复习
中考中的操作与探究问题, 中考中的操作与探究问题 , 绝大部分是研究几何图形变化过程 中性质的变化规律, 中性质的变化规律,尤其是相关图 形的不变性,常常体现在探究线段 形的不变性,常常体现在探究线段 的数量关系与位置关系, 的数量关系与位置关系,成为近年 中考的热点。 中考的热点。
深化提高
反思:你获得哪些证明方法? 反思:你获得哪些证明方法?
问题1 如图① 将等腰直角三角尺 AMN 的非直角顶点A ,AM与 AMN的非直角顶点 问题 1 : 如图 ① , ②,若三角尺AMN绕点A的非直角顶点 A 与正方形 问题2 如图② 若三角尺AMN绕点A继续逆时针旋转, AMN绕点 问题2:如图 将等腰直角三角尺AMN 继续逆时针旋转 AM与 ABCD的顶点 A 重合, 斜边 AN 与正方形的对角线 AC重合 F , 连 接 的顶点A AN与正方形的对角线 交 于 点 ABCD 的顶点长重合 ,于 点 E , AN 与 CD 的 延 长 线 AC 重合 . 若正方形 BC 的 延 线 交 斜边AN 与正方形的对角线AC 重合. ABCD保持不动 将三角尺AMN绕点A按逆时针方向旋转,当AM与BC交 保持不动, AMN绕点 ABCD保持不动,将三角尺AMN、 DF 、 EF 又有怎样的数量关系 ? 请 EF.此时,猜想线段BE DF、EF又有怎样的数量关系 BE、 又有怎样的数量关系? EF . 此时 , 猜想线段 BE 绕点A按逆时针方向旋转, AM与BC交 于点E,AN CD交于点 E,AN与 交于点F 连接EF BE+ 于点E,AN与CD交于点F 时, 连接EF.猜想 BE+DF与EF满足的数量关 写出你的猜想,并证明. 写出你的猜想,并证明. EF.猜想BE DF与EF满足的数量关 N 并证明. 系,并证明. A 1 D F F 32 D BE=0 N A 12 F / 4 DF=DCF B (E) C (F) E 3 EF=BC N / C E E B F M M M N 图② 图① 猜想: + 猜想:BE+DF=EF 猜想: M - 猜想:BE-DF=EF
未知 复杂 ●截长补短法 ●转化思想 一般 变中找不变, ●变中找不变,即在平移与 运动
已知 简单 特殊 静止
旋转过程中, 旋转过程中,抓住不变的边 和角。 和角。
结束寄语
下课了!
观察、操作、思考、 观察、操作、思考、感悟 是能否进入数学大门, 是能否进入数学大门,领略数 学奥妙的关键. 学奥妙的关键.
