列方程解应用题(和倍问题)例4PPT课件
西师大版五年级数学下册《列方程解应用题》教学PPT课件(4篇)

课后作业
1.从课后习题中选取; 2.完成练习册本课时的习题。
西师版五年级下数学
列方程解应用题
复习
1. X的8倍用字母表示( 8x ) 。 2.比y的15倍多3的数(15y+3 )。 3.比X的20倍少8的数( 20x-8 )。
等量关系
1.水果店运来一些苹果,每箱重 75kg,卖出去x箱,还剩5kg。 2.小丽有28张邮票,比小张的邮票少10张。
甲队铺了285平方米, 比乙队的2倍多5平方米。
解:设乙队铺了x平方米。 285-2x=5 x=140
答:乙队铺了140平方米。
乙队铺了多少 平方米呢?
2.小红家装修客厅,爸爸买了40块地砖,比买水 泥多花了280元。已知买水泥花了1400元,每块地 砖多少元?
解:设每块地砖x元,
40x-1400=280
解:设猴宝宝重x千克。
3x=24
x=8 答:猴宝宝重8千克。
(3)下面每个图形的面积都是24 dm2,算出每个 图形的高。
解:设四边形的高是xdm,三角形的高是ydm。
10x=24 x=2.4
12×y 24 2
y=4
课堂小结
通过这节课的学习活动,你 有什么收获?
课后作业
1.从课后习题中选取; 2.完成练习册本课时的习题。
探究新知
种植2天后, 还剩80棵。
平均每天种 植多少棵?
三峡小学的同学参加长 江上游种植天然防护林 活动,计划种植350棵树。
探究新知 你能列出哪些等量关系? 平均每天种植的颗数×2+80=总棵数 总棵数-平均每天种植的颗数×2=80 平均每天种植的颗数×2=总棵数-80
议一议
探究新知
列出一个方程,并解决。 平均每天种植的颗数×2+80=总棵数 解:设平均每天种植x棵。 2x+80=350 x=135
五年级列方程解和倍、差倍问题 PPT

姐姐邮票得张数是弟弟得3倍。
姐姐邮票得张数是弟弟得3倍。
姐姐、弟弟各有多少张?
姐姐、弟弟各有多少张?
和倍问题
关系式:
差倍问题
1、爸爸得年龄是淘气得5倍, 父子两人 共36岁。爸爸和淘气各多少岁?
解:设淘气χ岁, 则爸爸为5χ岁。
5χ+χ=36
2、爸爸得年龄是淘气得5倍, 爸爸比淘 气大40岁,爸爸和淘气各多少岁?
多少亿平方千米?
2、工程队挖一条400 m长得涵洞, 未挖得长度是已挖长度得3倍,还有多少米没有挖?
2、 姐姐比弟弟多90张邮票, 姐姐邮票得张数是弟弟得3倍。 差倍问题 姐姐、弟弟各有多少张?
列方程解和倍问题、差倍问题
基本思路和方法: ①先找出条件中得两个数量关系; ②再根据倍数关系设1倍量为X,则另一个量为几X;
4、
这幅画的长是宽的 2 倍。我做画 框用了 1.8 m 木条。
这幅画得长、宽分别是多少?
解: 设这幅画得宽是 x 米。 (x + 2 x)×2 = 1、8 3 x = 0、9 x = 0、3 0、3×2 = 0、6 (m) 0、3×0、6 = 0、18 (m2 )
答: 这幅画得长、宽、面积分别是 0、6 m、0、3 m、 0、18 m2。
五年级列方程解和倍、差倍问题
1、 弟弟和姐姐一共有180张邮票, 姐姐邮票得张数是弟弟得3倍。 和倍问题 姐姐、弟弟各有多少张?
列方程解和倍问题、差倍问题
基本思路和方法: ①先找出条件中得两个数量关系; ②再根据倍数关系设1倍量为X,则另一个量为几X;
③最后根据: 大数+小数=和 来列方程。
1、地球得表面积为5、1亿平方千米。其中,海洋面积 约为陆地面积得2、4 倍,海洋面积和陆地面积分别是
和倍问题PPT课件(沪科版)

3.4 二元一次方程组的应用 第1课时 和倍问题
提示:点击 进入习题
答案显示
基础巩固练
1 x+y=120;24x+36y=3 360;x2+ 4x+y=3162y=0,3 360
(1)(16-x);20x+(16-x)×50=590
2
x+y=16,
x+y=5.9,
(2)20x+50y=590(3)0x.2+0y.5=16
x+y=5.9, ____0_x.2_+__0_y._5_=__1_6___________________.
3.[中考·随州]小明到商店购买“五四青年节”活动奖品,
购买 20 支铅笔和 10 本笔记本共需 110 元,但购买
30 支铅笔和 5 本笔记本只需 85 元,设每支铅笔 x
元,每本笔记本 y 元,则可列方程组为( B )
人出八,盈三;人出七,不足四,问人数、物价各几何? 译文:今有人合伙购物,每人出 8 钱,会多 3 钱;每人出 7 钱,又会差 4 钱,问人数、物价各是多少.设合伙人为 x
人,物价为 y 钱,以下列出的方程组正确的是( C )
y-8x=3, A.y-7x=4
y-8x=3, B.7x-y=4
8x-y=3, C.y-7x=4
8x-y=3, D.7x-y=4
5.甲同学说:“(1)班与(5)班得分比为 6 5.”乙同
学说:“(1)班得分比(5)班得分的 2 倍少 40 分.”
若设(1)班得 x 分,(5)班得 y 分,根据题意所
列的方程组应为( D )
6x=5y, A.x=2y-40
6x=5y, B.x=2y+40
5x=6y, C.x=2y+40
签字笔
六年级数学和倍和差倍问题优秀课件.

六年级数学和倍和差倍问题优秀课件.一、教学内容本节课我们将学习《和倍与差倍问题》章节。
详细内容包括:理解什么是和倍问题,掌握和倍问题的解题方法;理解什么是差倍问题,掌握差倍问题的解题方法;通过实际例题的讲解,让学生能够灵活运用和倍与差倍问题的解法解决生活中的实际问题。
二、教学目标1. 理解并掌握和倍与差倍问题的概念及解法。
2. 能够运用和倍与差倍问题的解法解决实际问题。
3. 培养学生的逻辑思维能力和问题解决能力。
三、教学难点与重点教学难点:和倍与差倍问题的解题方法。
教学重点:理解并掌握和倍与差倍问题的概念,以及能够运用解题方法解决实际问题。
四、教具与学具准备1. 教具:PPT课件、黑板、粉笔。
2. 学具:练习本、铅笔。
五、教学过程1. 实践情景引入:通过一个关于分苹果的故事,引发学生对和倍与差倍问题的思考。
2. 讲解概念:详细讲解和倍问题与差倍问题的定义,并通过例题加深理解。
3. 例题讲解:精选两道和倍问题例题和两道差倍问题例题,逐步讲解解题思路和方法。
4. 随堂练习:让学生独立完成两道和倍问题练习题和两道差倍问题练习题,巩固所学知识。
5. 互动环节:邀请学生上台分享自己的解题过程和答案,共同讨论解题方法。
六、板书设计1. 和倍问题的定义和解法。
2. 差倍问题的定义和解法。
3. 例题及解题步骤。
4. 练习题及答案。
七、作业设计1. 作业题目:(1)一个数是另一个数的2倍,它们的和是63,求这两个数。
(2)一个数比另一个数大18,它们的和是63,求这两个数。
2. 答案:(1)这两个数分别是21和42。
(2)这两个数分别是22.5和40.5。
八、课后反思及拓展延伸1. 反思:本节课学生对和倍与差倍问题的掌握程度,以及解题方法的熟练程度。
2. 拓展延伸:引导学生思考,和倍与差倍问题在实际生活中的应用,激发学生的学习兴趣。
重点和难点解析1. 教学难点与重点的设定。
2. 例题讲解的详细步骤和思路。
3. 作业设计的题目难度和答案解析。
和倍问题ppt课件
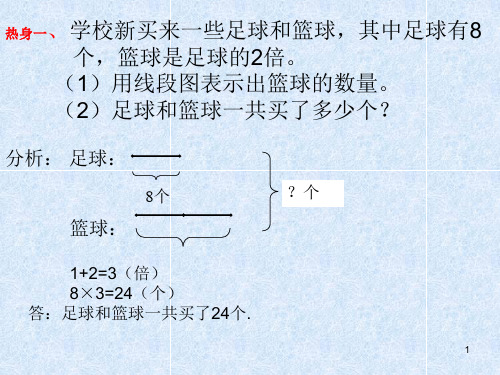
泡泡考考你1、
14
例5、光明小学有学生760人,其中男生比女生的3 为了规范事业单位聘用关系,建立和完善适应社会主义市场经济体制的事业单位工作人员聘用制度,保障用人单位和职工的合法权益 倍少40人,男、女生各有多少人?
黄纸鹤: ?个
40个
红纸鹤:
?个
24+16=40(只) 1+3=4(倍) 40÷4=10(只) 40-10=30(只) 答:红纸鹤30只,黄纸鹤10只。
7
例2
为了规范事业单位聘用关系,建立和 完善适 应社会 主义市 场经济 体制的 事业单 位工作 人员聘 用制度 ,保障 用人单 位和职 工的合 法权益
练习:泡泡教你学例2 泡泡考考你2、3、5
18
甲班有图书120本,乙班有图书30本,甲班给乙班 多少本,甲班的图书是乙班图书的2倍?
问题1、
问题2、 问题3、
这个题和前面两个题有什么不同? 做了内部调整,没有直接告诉和,告诉了调 整后的倍数关系。
调整前后什么没变,什么变了? 和没变,倍数变了
现在甲乙两班共有图书多少本? 120+30=150(本)
2、解答步骤: 1)仔细审题,找出两个数的和及倍数关系 2)总倍数=倍数+1 3)和÷总倍数=小数 小数×倍数=大数 或 和-小数=大数
6
为了规范事业单位聘用关系,建立和 完善适 应社会 主义市 场经济 体制的 事业单 位工作 人员聘 用制度 ,保障 用人单 位和职 工的合 法权益
热身三、小马用红纸和黄纸叠纸鹤,上午叠了24只,下午 又叠了16只,其中红纸鹤是黄纸鹤的3倍,她做的红纸鹤 和黄纸鹤各有多少只?
列方程解应用(题简单的和倍问题及差倍问题)

一、列方程解应用题
和倍问题
例1 图书馆买回来60本文艺书和科普书,其中文艺书的本数是科普书的3倍,文艺书有多少本?
例2 一个果园有荔枝、龙眼和芒果这三种果树108棵,其中荔枝的棵树是龙眼的3倍,芒果的棵树是龙眼的2倍,这三种果树各有多少棵?
例3 一个水池装有甲、乙两排水管,甲管每小时的排水量是乙管的3倍。
水池里有16吨水,打开两管5小时能把水排完,甲管每小时排水量多少吨?
例4 某粮店全天卖出大米、面粉和玉米面11520千克,卖出大米的千克数是面粉的6倍,面粉的千克数是玉米面的5倍,卖出的大米比玉米面多多少千克?
差倍问题
一个问题的已知条件是有关数量的差与数量之间的倍的关系,这种问题就是差倍问题。
列方程解差倍问题,可以吧问题中的一个未知数量用x表示,再根据问题中的“差”或“倍”的关系,把其他未知数量用含有x 的式子表示,再找出数量之间的等量关系列方程。
在设未知数x时,通常把倍的关系中作为1的数量设为x较好。
例1一张办公桌的价钱是一把椅子的4倍,办公桌的定价比椅子贵138元,一张办公桌的价钱是多少钱?
例2 一个书柜下层放的书的本数是上层的3倍,如果从下层取43本数放到上层,两层的书的本数相同,这个书柜一共放有多少本书?
例3 水果店购进的一批西瓜,分三天售完,其中第一天售出的千克数是第二天的2倍,第二天售出的千克数是第三天的1.5倍,第三天售出的比第一天少88千克,这批西瓜共有多少千克?。
列方程解决实际问题练习——和倍差倍问题PPT课件

第1页/共13页
解方程 6.6X-5X=64
0.7X+0.3X=9
第2页/共13页
丹顶鹤的只数+天鹅的只数=960只
x
2.2x
(1)300+660=960(只) (2)660÷3如00何=2.2
检验?
第3页/共13页
10.少先队员参加植树活动,六年级植树的棵树是 五年级的1.5倍,五年级比六年级少植树24棵。两 个年级各植树多少棵?
第11页/共13页
第12页/共13页
感谢您的欣赏!
第13页/共13页
六年级植树的棵数-五年级植树的棵数=24棵
- 1.5x
x =24
第4页/共13页
10.少先队员参加植树活动,六年级植树的棵树是 五年级的1.5倍,五年级比六年级少植树24棵。两 个年级各植树多少棵?
六年级植树的棵数-五年级植树的棵数=24棵
解:设五年级植树X棵,则六年级植树1.5X棵。
1.5x-x=24 0.5X=24 X=48
=45
14-9=5(年)
答:5年前父亲的年龄是儿子的5倍。
第10页/共13页
课堂总结:通过这节课的学习,你有什么收获?
1、题目中要求两个未知量,我们要根据两个未知量之间的关系,设标准量为x, 另一个未知量就用含有x的式子表示。
2、根据两个数量的和或差找出等量关系,列出 方程。 3、检验两个未知量之间关系是否符合题意, 未知量和已知量之间关系是否符合题意。
已知两个未知量的差与倍数关系
第6页/共13页
和倍问题:ax+x=和 差倍问题:ax-x=差
第7页/共13页
我会思考难不倒!
四-1、和倍问题(配PPT讲义)

第一讲和倍问题知识前奏:一、认识倍数提问:1、谁是1倍数?母鸡是几倍?公鸡和母鸡的和是几倍数?2、爷爷的年龄是孙子的5倍,谁是1倍数?爷爷年龄是几倍?3、“甲是乙的10倍”有几种表述方法?二、什么叫“和倍问题”例如:小明和爸爸年龄的和是45岁,爸爸的年龄是小明的4倍,小明和爸爸各多少岁?像这样,已知大、小两数的和,又知大数是小数的若干倍,求大、小两数各是多少的应用题,我们通常叫做“和倍”问题。
三、找寻倍数关系,并练习画线段图(画图先画1倍数)1、甲是乙的2倍2、甲÷乙=103. 甲比乙多3倍4. 甲是乙的2倍,乙是丙的3倍四、讲解例题,并练习例1:学校将360本图书分给二、三两个年级,已知三年级所分得的本数是二年级的2倍,问二、三两个年级各分得多少本图书?练习1、小红和小明共有压岁钱800元,小红的钱数是小明的3倍。
小红和小明各有压岁钱多少元?练习2.甲桶有油25千克,乙桶有油17千克,乙桶倒入多少千克油给甲桶后,甲桶油是乙桶的5倍?练习3、学校将360本图书分给二、三年级,已知三年级所得本数比二年级的2倍还多60本。
二、三年级各得图书多少本?例题2 小宁有圆珠笔芯30枝,小青有圆珠笔芯15枝,问小青给小宁多少枝后,小宁的圆珠笔芯枝数是小青的8倍?练习4、红红有邮票80张,佳佳有邮票60张,要使红红的邮票张数是佳佳的4倍,那么佳佳必须给红红多少张邮票?练习5、甲书架有图书18本,乙书架有图书8本,班图书管理员又买来图书16本,怎样分配才能使甲书架图书的本数是乙书架的2倍?例3 商店有红、黄气球共260只,如果卖出20只红气球后,红气球的只数就是黄气球只数的2倍。
这两种气球各有多少只?练习6、学校图书室有故事书和连环画共920本,如果借出20本故事书后,故事书的本数就是连环画的2倍。
这两种书各有多少本?练习7、饲养场有鸡和鸭共560只,如果卖出120只鸡后,鸡的只数就是鸭的3倍。
饲养场有鸡和鸭各多少只?练习8、水果店运进苹果和梨共72筐,如果卖出12筐苹果后,苹果的筐数就是梨的4倍。
《和倍和差倍问题》ppt课件

提高数学逻辑思维能 力和分析问题能力。
学会运用代数、几何 等知识解决实际问题。
02
CHAPTER
和倍问题
问题定义
总结词
和倍问题是指已知两个数的和以及它们的倍数关系,求这两个数分别是多少的 问题。
详细描述
这类问题通常涉及到两个未知数,它们的和以及它们的倍数关系已知。例如, 已知两个数的和是10,其中一个数是另一个数的2倍,求这两个数是多少。
解题方法
总结词
解题方法包括利用代数方程求解和利用算术方法求解两种。
详细描述
代数方程求解是通过设立代数方程来求解未知数。例如,设两个未知数分别为x和y,根据题目条件建立方程组, 然后解方程组得到未知数的值。算术方法求解则是通过逻辑推理和计算来求解未知数。例如,利用已知的倍数关 系和和的关系,通过计算得出未知数的值。
总结混合问题的常见解题技巧,如先分别 设立和倍和差倍的方程,再联立求解等, 帮助学生提高解题效率。
06
CHAPTER
总结与回顾
本课重点回顾
定义和倍、差倍问题的概念
和倍问题是指两个数的和与它们的倍数之间的关系问题, 差倍问题是指两个数的差与它们的倍数之间的关系问题。
解题思路和方法
解决和倍问题需要先求出两个数的和,再根据倍数关系求 出未知数;解决差倍问题需要先求出两个数的差,再根据 倍数关系求出未知数。
解法二:算术法
根据题目条件,两个 数的差是10,和是50, 可以列出方程:(x - y) = 10 和 (x + y) = 50。 解方程得到 x = 30, y = 20。
04
CHAPTER
混合问题
问题定义
问题定义
《列方程解应用题》(课件)-2021-2022学年数学五年级下册

2.列一列、解一解:根据等量关系式列出方程,并解方程。
西安大雁塔高64 米, 比小雁塔 高度的2倍少22 米。小雁塔高 多少米?
大雁塔
小组交流:
1.题中的关键句是哪一句?等量关系式是怎样的?
2.列出的方程是怎样的?你是怎样解方程的?
3.比较列出的方程与之前学过的方程有什么不同?
小雁塔
杭州湾跨海大桥全长约36千米,比香港青马大桥的16 倍还多0.8
答:宽应是96厘米。
1.列方程解决实际问题在格式上有什么特殊的要求?
先写“解:”,再把未知数设为“χ”。
2.列方程解决实际问题一般分几步来完成? 1.找关键句,确定数量关系 2.把问题设为χ 3.列方程并解答 4.检验 (先检查方程列得是否正确,再检验方程的解) 5.答
6. 在括号里填写含有字母的式子。
练习要求:
1.认真审题,独立完成在随练本上。 2.小组交流检查:
思考过程:题中的关键句是什么?根据怎样的等 量关系列方程? 解题过程:怎样设未知数,怎样列方程、解方程。 检验过程:如何证明计算结果是正确的。
钢琴的黑键有36 个, 比白键少16个。
白键有多少个?
白键的个数-16 = 黑键的个数 解:设白键有χ个。
千米。香港青马大桥全长大约多少千米?(先把数量间的相等关系
填写完整, 再列方程解答)
χ
(香港青)马大桥的长度×16+0.8=( 杭州湾)跨大海桥的长度
解:设香港青马大桥全长大约χ千米。
16χ + 0.8 = 36
16χ = 36-0.8 16χ = 35.2
χ = 35.2÷16 χ = 2.2 答:香港青马大桥全长大约2.2米。
李冶
700多年前,我国数学家李冶在解决问题的过程中系统地应用
列方程解和倍问题ppt课件

列方程解和倍问题
李兰
1
一、学思学疑,质疑课题。
1、科技组的男生人数是女生人数的3倍。
如果女生有x人,则男生有( 3x )人。
如果男生有x人,则女生有( x÷3 )人。
找到“一倍量”,设为x。
用“倍”的关系表示另一个未知数 用“和”的关系列方程
10
拓展延伸
爸爸比小红大27岁,他的年龄是小红的4倍, 爸爸和小红各是多少岁?
解:设小红今年x岁,爸爸今年4x岁。 4x-x=27 3x=27 x=9 4x=4×9=36
答:小红今年9岁,爸爸今年36岁。
11
师徒二人共同加工300个零件,完成任务时, 师傅加工的零件比徒弟的2倍多个60个,师傅、 徒弟分别加工了多少个?
比较:谁为x,另一个量就比较容易表示?
2、美术组一共有学生18人,若男生有x人, 则女生有(18-x )人。
3、学校书法组有女同学x人,男同学的人数 是女同学的2.5倍。男同学有(2.5x )人, 男女同学一共有( 2.35.x5+xx)人,男同学比女 同学多(21.5x—x)人。
2
妈妈的年龄是小磊的3倍,妈妈和 小磊的年龄之和为40岁,妈妈多少 岁?小磊多少岁?
解:设徒弟加工了x个,则师傅加工了(2 x +60)个。
(2 x +60)+ x=300
12
甲、乙两个食堂一共运进200袋大米,甲 食堂的袋数比乙食堂的3倍少16袋。甲乙 两食堂各运进多少袋?
解:设乙食堂运进x袋,则甲食堂运进 (3 x -16)袋。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2021
2
学校科技组共有36人,其中男生比女生多18 人,问男生和女生各有多少人?
男生人数+女生人数=总人数 解:设女生有x人,那么男生有(x+18)人。
2021
3
学校科技组共有36人,其中男生是女生的3 倍,问男生和女生各有多少人?
和倍问题
学校科技组的男生比女生多18人,而且男生 是女生的3倍,问男生和女生各有多少人?
20216人,其中男生比女生多 18人,问男生和女生各有多少人?
和差问题
2021
4
1、地球的表面积为5.1亿千米。 (和关系) 2、海洋面积约为陆地面积的2.4倍。(倍数关系)
3、海洋面积比陆地面积多2.1亿千米。(相差关系)
选择对应条件组合成“和倍问题”,“差倍问 题”,“和差问题”。
• 学校科技组共有36人,其中男生是女生的3 倍,问男生和女生各有多少人? 男生人数+女生人数=总人数
解:设女生有x人,那么男生有3x人。
2021
1
• 学校科技组的男生比女生多18人,而且男 生是女生的3倍,问男生和女生各有多少人?
男生人数——女生人数=总人数 解:设女生有x人,那么男生有3x人。
