第二章 静电场和稳恒磁场.
静电场与稳恒磁场的异同

静电场与稳恒磁场的异同
静电场和稳恒磁场是两种不同的物理场,它们具有一些相似之处,但也存在一些显著的差异。
相似之处:
1.无源性:静电场和稳恒磁场都是无源场,它们不依赖于电荷或电流的变化而产生。
差异之处:
1.作用粒子不同:静电场与电荷粒子(例如电子或质子)相互作用,而稳恒磁场则与运动带电粒子(电流)相互作用。
2.相关物理量不同:静电场与电荷的位置和电荷量有关,通常用电场强度(单位电荷受到的力)来描述;而稳恒磁场与电流的位置和大小有关,通常用磁感应强度(单位电流受到的力)来描述。
3.引力与斥力:静电场中的电荷之间可以相互吸引或排斥,根据电荷的正负性质决定;而稳恒磁场中的磁荷(即电流)之间不存在引力或斥力的作用。
4.能量流动方式:静电场中的能量流动是通过电磁辐射进行的,即光的形式;而稳恒磁场中的能量流动主要是通过电流在导体中的传输进行的。
总体而言,静电场和稳恒磁场在物理特性和相互作用方面存在一些重要的区别,但它们都是电磁场的重要组成部分,共同构成了电磁学的基础。
1/ 1。
电磁学复习

实际中常用μF(微法)和pF(皮法)
等SI量。纲:
C
Q U
IT ML2T 3I 1
M
1L2T 4 I 2
电容只与几何因素和介质有关, 固有的容电本领。
2024/8/27
28
二、电容器及其电容
两个互不连结导体构成的闭合导体空腔称 为电容器。
定义 C Q Q U A U B U
电容器的电容是使电容器两极板之间具有单位电 势差所需的电量。 描绘了电容器储存电能的能力。
相互作用能
2024/8/27
或:把这些带 电体从无限远 离的状态聚合 到状态 a 的过 程中,外力克 服静电力作的 功。
39
点电荷组的静电势能W等于克服电场力所做 的功A'
W 1
2
i
qiU i
Ui为除qi以外的电 荷在qi处的电势
2024/8/27
40
第三章 恒定磁场和磁介质
§3.1 磁的基本现象 §3.2 毕奥 —萨伐尔定律 §3.3 磁场的高斯定理和安培环路定理 §3.4 安培定律 §3.5 洛伦兹力 §3.6 磁介质
静电场力做功与路径无关
静电场中场强沿任意闭合环路的线积分恒等于零
E dl 0
L
无旋
2024/8/27
18
电势差(electric potential difference)
两点之间电势差可表为两点电势值之差
b b
Uab
a
E dl
a
E dl
E dl
U (a) U (b)
33
E0
S
dS
1
0
q0
内+
E dS
S
1
电动力学——精选推荐

电动⼒学电动⼒学第⼀章静电场⼀、考核知识点1、真空与介质中静电场场⽅程,场的性质、物理特征。
2、电场的边值关系、在两种介质分界⾯上电场的跃变性质。
3、由场⽅程、边值关系,通过电荷分布确定场分布及极化电荷的分布。
4、静电场的势描述。
由势分布确定场分布、荷分布;通过静电势的定解问题,确定静电势的分布、场分布及介质极化性质的讨论。
⼆、考核要求(⼀)、场⽅程、场的确定1、场⽅程,场的边值关系,体、⾯极化电荷密度的确定式等规律的推导。
2、识记:(1)、真空与介质静电场⽅程。
(2)、电场的边值关系。
(3)、体、⾯极化电荷密度的确定式。
3、领会与理解:(1)、静电场的物理特征。
12(2)、P D E ,,与电荷的关系,⼒线分布的区别与联系。
(3)、在介质分界⾯上场的跃变性质。
4、应⽤:通过对称性分析,运⽤静电场的⾼斯定理确定场,讨论介质的极化,正确地由电荷分布画出场的⼒线分布。
(⼆)、静电势1、静电势⽅程、边值关系的推导。
2、识记:静电势的积分表述、势⽅程、势的边值关系、势的边界条件、唯⼀性定理。
3、领会与理解:势的边值关系与边界条件,荷、势与场的关系,解的维数的确定,电像法的指导思想与像电荷的确定。
4、应⽤:求解静电势定解问题的⽅法(分离变量法、电像法)的掌握及应⽤,求解的准确性,场的特征分析及由势对介质极化问题的讨论。
第⼆章稳恒磁场⼀、考核知识点1、电荷守恒定律。
2、稳恒磁场场⽅程,场的性质特点。
3、由场⽅程,通过流分布确定场分布与磁化流。
4、磁场的边值关系。
5、稳恒磁场的⽮势。
6、由磁标势法确定场。
3⼆、考试要求1、规律的推导:真空、介质中稳恒磁场场⽅程,电荷守恒定律的微分表述,体、⾯磁化电流密度的确定式,磁场的边值关系,⽮势⽅程及其积分解,磁标势⽅程和边值关系等。
2、识记:电荷守恒定律,稳恒磁场场⽅程,体、⾯磁化电流密度的确定式,⽮势引⼊的定义式,磁标势引⼊条件,磁场的边值关系,0=f α情况磁标势的边值关系。
电动力学 知识点总结

第一章电磁现象的普遍规律一、主要内容:电磁场可用两个矢量—电场强度和磁感应强度来完全描写,这一章的主要任务是:在实验定律的基础上找出, 所满足的偏微分方程组—麦克斯韦方程组以及洛仑兹力公式,并讨论介质的电磁性质及电磁场的能量。
在电磁学的基础上从实验定律出发运用矢量分析得出电磁场运动的普遍规律;使学生掌握麦克斯韦方程的微分形式及物理意义;同时体会电动力学研究问题的方法,从特殊到一般,由实验定律加假设总结出麦克斯韦方程。
完成由普通物理到理论物理的自然过渡。
二、知识体系:三、内容提要:1.电磁场的基本实验定律:(1)库仑定律:对个点电荷在空间某点的场强等于各点电荷单独存在时在该点场强的矢量和,即:(2)毕奥——萨伐尔定律(电流决定磁场的实验定律)(3)电磁感应定律①生电场为有旋场(又称漩涡场),与静电场本质不同。
②磁场与它激发的电场间关系是电磁感应定律的微分形式。
(4)电荷守恒的实验定律,①反映空间某点与之间的变化关系,非稳恒电流线不闭合。
② 若空间各点与无关,则为稳恒电流,电流线闭合。
稳恒电流是无源的(流线闭合),,均与无关,它产生的场也与无关。
2、电磁场的普遍规律—麦克斯韦方程其中:1是介质中普适的电磁场基本方程,适用于任意介质。
2当,过渡到真空情况:3当时,回到静场情况:4有12个未知量,6个独立方程,求解时必须给出与,与的关系。
介质中:3、介质中的电磁性质方程若为非铁磁介质1、电磁场较弱时:均呈线性关系。
向同性均匀介质:,,2、导体中的欧姆定律在有电源时,电源内部,为非静电力的等效场。
4.洛伦兹力公式考虑电荷连续分布,单位体积受的力:洛伦兹认为变化电磁场上述公式仍然成立,近代物理实验证实了它的正确。
说明:①②5.电磁场的边值关系其它物理量的边值关系:恒定电流:6、电磁场的能量和能流能量密度:能流密度:三.重点与难点1.概念:电场强度、磁感应强度、电流密度、极化强度、磁化强度、能流密度。
2.麦克斯韦方程、电荷守恒定律、边值关系、极化强度与极化电荷的关系、磁化强度与磁化电流的关系、应用它们进行计算和证明。
麦克斯韦方程组的推导及说明

13-6麦克斯韦方程组关于静电场和稳恒磁场的基本规律,可总结归纳成以下四条基本定理:静电场的高斯定理:静电场的环路定理:稳恒磁场的高斯定理:磁场的安培环路定理:上述这些定理都是孤立地给出了静电场和稳恒磁场的规律,对变化电场和变化磁场并不适用。
麦克斯韦在稳恒场理论的基础上,提出了涡旋电场和位移电流的概念:1.麦克斯韦提出的涡旋电场的概念,揭示出变化的磁场可以在空间激发电场,并通过法拉第电磁感应定律得出了二者的关系,即上式表明,任何随时间而变化的磁场,都是和涡旋电场联系在一起的。
2.麦克斯韦提出的位移电流的概念,揭示出变化的电场可以在空间激发磁场,并通过全电流概念的引入,得到了一般形式下的安培环路定理在真空或介质中的表示形式,即上式表明,任何随时间而变化的电场,都是和磁场联系在一起的。
综合上述两点可知,变化的电场和变化的磁场彼此不是孤立的,它们永远密切地联系在一起,相互激发,组成一个统一的电磁场的整体。
这就是麦克斯韦电磁场理论的基本概念。
在麦克斯韦电磁场理论中,自由电荷可激发电场,变化磁场也可激发电场,则在一般情况下,空间任一点的电场强度应该表示为又由于,稳恒电流可激发磁场,变化电场也可激发磁场,则一般情况下,空间任一点的磁感强度应该表示为因此,在一般情况下,电磁场的基本规律中,应该既包含稳恒电、磁场的规律,如方程组(1),也包含变化电磁场的规律,根据麦克斯韦提出的涡旋电场和位移电流的概念,变化的磁场可以在空间激发变化的涡旋电场,而变化的电场也可以在空间激发变化的涡旋磁场。
因此,电磁场可以在没有自由电荷和传导电流的空间单独存在。
变化电磁场的规律是:1.电场的高斯定理在没有自由电荷的空间,由变化磁场激发的涡旋电场的电场线是一系列的闭合曲线。
通过场中任何封闭曲面的电位移通量等于零,故有:2.电场的环路定理由本节公式(2)已知,涡旋电场是非保守场,满足的环路定理是3.磁场的高斯定理变化的电场产生的磁场和传导电流产生的磁场相同,都是涡旋状的场,磁感线是闭合线。
稳恒磁场
安培定律
一、安培力
安培力:电流元在磁场中受到的磁力. 安培力:电流元在磁场中受到的磁力. 一个自由电子受的洛仑兹力为: 一个自由电子受的洛仑兹力为
f 洛 = qv × B = −ev × B
电流元所受磁力: 电流元所受磁力
方向: 方向:×
v
dl
B
I
设截面积为S,单位体积电子数为 设截面积为 单位体积电子数为n 单位体积电子数为
1 2 m = NISn = NI πR n 2
方向:与 B 成600夹角. 夹角. 方向: (2)此时线圈所受力矩的大小为: )此时线圈所受力矩的大小为:
)60
0
B
3 2 πR M = mB sin60 = NIB 4 方向: m× B 方向: ×
0
n
即垂直于 B向上,从上往下俯视,线圈是逆时针转动。 向上,从上往下俯视,线圈是逆时针转动。
1T = 1N ⋅ S ⋅ m−1 ⋅ C−1
磁通量
一、磁力(感)线 磁力( 直线电流的磁力线
磁场的高斯定理
圆电流的磁力线
通电螺线管的磁力线
I
I
I
I
通量(通过一定面积的磁力线数目) 二、磁通量(通过一定面积的磁力线数目)
v v dΦ = B ⋅ dS
v v Φ = ∫s B ⋅ dS
单位
1Wb= 1T ⋅ m
I
该式对任意形状的线圈都适用. 该式对任意形状的线圈都适用.
例1如图,求圆心O点的 B . 如图,求圆心 点的 I O
• × R
B=
µ0 I
4R
I
O• •
R
B=
µ0 I
8R
R
• •O
大学物理电磁学总结

大学物理电磁学总结电磁学部分总结静电场部分第一部分:静电场的基本性质和规律电场是物质的一种存在形态,它同实物一样也具有能量、动量、质量等属性。
静电场的物质特性的外在表现是:(1)电场对位于其中的任何带电体都有电场力的作用(2)带电体在电场中运动, 电场力要作功——电场具有能量1、描述静电场性质的基本物理量是场强和电势,掌握定义及二者间的关系。
电场强度 E =q 0∞ W a 电势 U a ==E ⋅d rq 0a2、反映静电场基本性质的两条定理是高斯定理和环路定理Φe =E ⋅d S =ε0∑qL E ⋅d r =0要掌握各个定理的内容,所揭示的静电场的性质,明确定理中各个物理量的含义及影响各个量的因素。
重点是高斯定理的理解和应用。
3、应用(1)、电场强度的计算1q E =r 02a) 、由点电荷场强公式 4πεr 及场强叠加原理 E = ∑ E 计i 0算场强一、离散分布的点电荷系的场强1q i E =∑E i =∑r 2i 0i i 4πεr 0i二、连续分布带电体的场强 d q E =⎰d E =⎰r 204πε0r其中,重点掌握电荷呈线分布的带电体问题b) 、由静电场中的高斯定理计算场源分布具有高度对称性的带电体的场强分布一般诸如球对称分布、轴对称分布和面对称分布,步骤及例题详见课堂笔记。
还有可能结合电势的计算一起进行。
c) 、由场强和电势梯度之间的关系来计算场强(适用于电势容易计算或电势分布已知的情形),掌握作业及课堂练习的类型即可。
(2)、电通量的计算a) 、均匀电场中S 与电场强度方向垂直b) 、均匀电场,S 法线方向与电场强度方向成θ角E =-gradU =-∇U∂U ∂U ∂U =-(i +j +k )∂x ∂y ∂zc) 、由高斯定理求某些电通量(3)、电势的计算a) 、场强积分法(定义法)——计算U P =⎰E ⋅d rb) 、电势叠加法——q i ⎰电势叠加原理计算⎰∑U i =∑4πεr⎰0iU =⎰dq ⎰dU =⎰⎰⎰4πε0r ⎰第二部分:静电场中的导体和电介质一、导体的静电平衡状态和条件导体内部和表面都没有电荷作宏观定向运动的状态称为静电平衡状态。
大学物理Ⅱ稳恒磁场知识点3

稳恒磁场小结1、磁感应强度 B 描写磁场大小和方向的物理量2、磁通量mΦ:穿过某一曲面的磁力线根数。
定义:θφcos ⋅⋅=⋅=⎰⎰⎰⎰S B S B d d ss m单位:韦伯, Wb nˆ NIS S NI P m == 3、磁矩m :描写线圈性质的物理量。
定义:单位:安培·米2方向:与电流满足右手定则。
一、基本概念n I二、磁感应强度B的计算20ˆ4rr l d I B d ⨯=πμ1)载流直导线的磁场aI B πμ20=)cos (cos 4210θθπμ-=aI B 无限长直导线的磁场1 利用毕萨定律求B PlId rθB1θIa P2θ二、磁感应强度B的计算20ˆ4rr l d I B d ⨯=πμ2)圆电流轴线上的磁场232220)(2x R R I B +=μ在圆弧电流圆心处:πθμ220R I B =在圆电流圆心处:RI B 20μ=1利用毕萨定律求B IB⊗θI⊗B l I d ROPxBiLI 1I 2I 3∑-=12I I Ii应用:分析磁场对称性;选定适当的安培环路。
各电流的正、负:I 与L呈右手螺旋时为正值;反之为负值。
⎰∑=⋅LIl d B 0μ2 利用安培环路定理计算磁场 B⎰∑=⋅LI l d B 0μ 1)、密绕长直螺线管内部nIB 0μ=rIN B πμ20=2) 螺绕环内部3)圆柱载流导体内部r < R 区域圆柱载流导体外一点r > R 区域r R IB 202πμ=rI B πμ20=4)圆柱面载流导体内部r < R 区域圆柱载流导体外一点r > R 区域I B μ0==B20 ˆ4rr v q B ⨯= πμ3 运动电荷的磁场Pqv+rθ大小 20 sin 4rv q B θπμ=三、两个重要定理1、磁场中的高斯定理0=⋅=Φ⎰⎰S m S d B2、磁场中的环路定理⎰∑=⋅LIl d B 0μ(1)磁场是“无源场”。
2024年度最新电动力学郭硕鸿版课件

磁介质中磁场分布
1 2
磁介质的分类
根据磁化率的大小和符号,可将磁介质分为抗磁 性物质、顺磁性物质和铁磁性物质。
磁化强度
描述磁介质磁化程度的物理量,其大小与磁介质 的性质、外磁场强度及温度等因素有关。
磁场强度
3
描述磁场和磁介质相互作用的物理量,其大小等 于磁感应强度B与磁化强度M之差与真空磁导率 μ0的比值。
2024/3/24
31
THANKS
感谢观看
2024/3/24
32
9
静电场中的导体和电介质
01
导体
在静电场中,导体内部电场为零,电荷分布在导体的外表面。导体能够
传导电流,具有导电性。
2024/3/24
02 03
电介质
在静电场中,电介质内部可以存在电场,且电介质中的正负电荷中心不 重合,形成电偶极子。电介质具有极化现象,即在外电场作用下产生感 应电荷的现象。
电容
描述导体或电介质储存电荷能力的物理量。在给定电位差下的电荷储藏 量,记为C,国际单位是法拉(F)。
质能关系
质量和能量之间存在等效 性,可以通过爱因斯坦质 能方程进行相互转换。
23
四维时空观与洛伦兹变换
四维时空观
时间和空间构成了一个统 一的四维时空,物质和能 量在其中传播和相互作用 。
2024/3/24
洛伦兹变换
描述不同惯性参照系之间 物理量变换的基本规律, 包括时间膨胀、长度收缩 和质量增加等效应。
电磁波接收原理
接收天线接收到空间中的电磁波 ,将其转换为电路中的电流或电 压信号。接收过程需要满足一定 的频率、极化等条件。
21
05 相对论性电动力 学基础
2024/3/24
电磁场与电磁波电子教案

电磁场与电磁波电子教案第一章:电磁场与电磁波概述1.1 电磁场的概念电场和磁场的基本性质电磁场的产生和变化1.2 电磁波的产生和传播电磁波的种类和特点电磁波的产生机制电磁波的传播特性1.3 电磁场与电磁波的应用电磁场在通信技术中的应用电磁波在医疗诊断中的应用第二章:静电场2.1 静电场的基本性质静电力和库仑定律电场强度和电势差2.2 静电场的能量和能量密度静电场的能量静电场的能量密度2.3 静电场的边界条件静电场的边界条件电场的连续性和跳跃性第三章:稳恒磁场3.1 稳恒磁场的基本性质磁场强度和磁感应强度安培环路定律3.2 磁场对电流的作用洛伦兹力和安培力磁场对电流的作用规律3.3 磁场的能量和能量密度磁场的能量磁场的能量密度第四章:电磁波的产生和传播4.1 电磁波的产生机制麦克斯韦方程组电磁波的产生过程4.2 电磁波的传播特性电磁波的波动方程电磁波的传播速度4.3 电磁波的能量和能量密度电磁波的能量电磁波的能量密度第五章:电磁波的应用5.1 电磁波在通信技术中的应用无线电通信和微波通信电磁波的天线原理5.2 电磁波在医疗诊断中的应用磁共振成像(MRI)微波热疗和电磁波治疗5.3 电磁波在其他领域的应用电磁波在能源传输中的应用电磁波在环境监测中的应用第六章:电磁波的波动方程与传播特性6.1 电磁波的波动方程电磁波的数学描述电磁波的波长、频率和波速6.2 电磁波的传播特性电磁波的直线传播电磁波的衍射和干涉6.3 电磁波的极化电磁波的偏振现象电磁波的圆极化和线极化第七章:电磁波的辐射与接收7.1 电磁波的辐射电磁波的发射过程天线辐射原理7.2 电磁波的接收电磁波的接收原理接收天线和放大器的设计7.3 电磁波的辐射和接收的应用无线电广播和电视传输卫星通信和导航系统第八章:电磁波的传播环境与衰减8.1 电磁波的传播环境自由空间中的电磁波传播导引波和波导传播8.2 电磁波的衰减电磁波在介质中的衰减电磁波的散射和反射8.3 电磁波的传播环境与衰减的影响因素天气和气候对电磁波传播的影响障碍物和遮挡对电磁波传播的影响第九章:电磁波的调制与解调9.1 电磁波的调制调幅和调频调相和复合调制9.2 电磁波的解调解调原理和方法解调电路的设计9.3 电磁波的调制与解调的应用无线通信和广播传输数据传输和网络通信第十章:电磁波的测量与监测10.1 电磁波的测量原理与方法电磁波的测量仪器和设备电磁波的测量技术和方法10.2 电磁波的监测与分析电磁波的监测原理和设备电磁波的频谱分析和信号处理10.3 电磁波的测量与监测的应用电磁兼容性分析和测试电磁环境监测和保护第十一章:电磁波在特定介质中的传播11.1 电磁波在均匀介质中的传播介质的电磁特性电磁波在介质中的传播方程11.2 电磁波在非均匀介质中的传播非均匀介质的特点电磁波在非均匀介质中的传播规律11.3 电磁波在特定介质中传播的应用电磁波在地球物理勘探中的应用电磁波在生物医学成像中的应用第十二章:电磁波的辐射与天线技术12.1 电磁波的辐射机制开放电荷和辐射场电磁波的辐射功率和辐射强度12.2 天线的基本原理与设计天线的作用和分类天线的辐射特性与设计方法12.3 电磁波的辐射与天线技术的应用无线通信和卫星通信的天线设计天线在雷达和导航系统中的应用第十三章:电磁波与物质的相互作用13.1 电磁波与物质的相互作用原理电磁波的吸收、反射和散射电磁波在物质中的传播过程13.2 电磁波在生物组织中的传播生物组织的电磁特性电磁波在医学成像中的应用13.3 电磁波与物质相互作用的应用电磁波在材料科学中的应用电磁波在环境监测中的应用第十四章:电磁波的安全与防护14.1 电磁波的安全性分析电磁波的生物效应电磁波的安全标准与规范14.2 电磁波的防护技术电磁屏蔽和吸波材料电磁波的防护设计与实施14.3 电磁波的安全与防护的应用电磁兼容性设计电磁环境保护和电磁辐射控制第十五章:电磁波的前沿领域与展望15.1 电磁波的前沿研究课题量子电动力学与高能电磁波极端条件下的电磁波传播15.2 电磁波技术的创新与发展新型天线技术与阵列处理智能材料与电磁波调控15.3 电磁波的应用前景与挑战未来通信系统的展望电磁波在可持续能源中的应用重点和难点解析重点:电磁场与电磁波的基本概念、原理、应用和发展前景。
静电场和稳恒磁场的区别与联系

静电场和稳恒磁场是两种不同的物理场,它们在性质和行为上有一些区别和联系。
区别:
物理本质:静电场是由电荷的分布所产生的电场,其基本单位是电荷。
而稳恒磁场是由电流的分布所产生的磁场,其基本单位是电流。
粒子属性:静电场作用于带电粒子,其力的方向与电荷的正负有关。
稳恒磁场则作用于带电粒子的运动,其力的方向与带电粒子运动的方向垂直。
动力学效应:静电场可以对电荷施加电场力,使其受力运动或产生势能。
而稳恒磁场作用于带电粒子时,不对其做功,只会改变其运动轨迹。
联系:
场的性质:静电场和稳恒磁场都是场,即它们都具有空间中某种物理量的分布特性。
数学描述:静电场和稳恒磁场都可以用物理学中的场论来描述,分别由静电场和稳恒磁场的场方程来表示。
应用:静电场和稳恒磁场在现实中有广泛的应用。
静电场的应用包括静电吸附、静电喷涂、静电除尘等。
稳恒磁场的应用包括电动机、磁共振成像、磁悬浮等。
需要注意的是,当电荷和电流随时间变化时,静电场和稳恒磁场的性质和行为将发生变化,此时需要考虑电磁场的动态效应,即电磁场理论。
电动力学判断题

判断题第一章 电磁现象的普遍规律1. 无论是稳恒磁场还是变化的磁场,磁感应强度总是无源的。
(√)2. 无论是静电场还是感应电场,都是无旋的。
(×)3. 在任何情况下电场总是有源无旋场。
(×)4. 在无电荷分布的区域内电场强度的散度总为零。
(√)5. 任何包围电荷的曲面都有电通量,但是散度只存在于有电荷分布的区域内。
(√)6. 电荷只直接激发其临近的场,而远处的场则是通过场本身的内部作用传递出去的。
(√)7. 稳恒传导电流的电流线总是闭合的。
(√)8. 在任何情况下传导电流总是闭合的。
(×)9. 非稳恒电流的电流线起自于正电荷减少的地方。
(√)10. 极化强度矢量p 的矢量线起自于正的极化电荷,终止于负的极化电荷。
(×)11. 均匀介质内部各点极化电荷为零,则该区域中无自由电荷分布。
(√)12. 在两介质的界面处,电场强度的切向分量总是连续的。
(√)13. 在两均匀介质分界面上电场强度的法向分量总是连续的。
(×)14. 在两介质的界面处,磁感应强度的法向分量总是连续的。
(√)15. 无论任何情况下,在两导电介质的界面处,电流线的法向分量总是连续的。
(×)16. 两不同介质表面的面极化电荷密度同时使电场强度和电位移矢量沿界面的法向分量不连续。
(×)17. 电介质中,电位移矢量D 的散度仅由自由电荷密度决定,而电场的散度则由自由电荷密度和束缚电荷密度共同决定。
(√)18. 两不同介质界面的面电流密度不改变磁场强度和磁感应强度的连续性。
(×)19. 关系式P E D +=0ε适用于各种介质。
(√)20. 静电场的能量密度为ρϕ21。
(×) 21. 稳恒电流场中,电流线是闭合的。
( √ )22. 电介质中E D ε=的关系是普遍成立的。
( × )23. 跨过介质分界面两侧,电场强度E 的切向分量一定连续。
《工程电磁场教案》

《工程电磁场教案》第一章:电磁场的基本概念1.1 电磁现象的发现1.2 电荷与电场1.3 电流与磁场1.4 电磁感应第二章:静电场2.1 静电场的定义与特性2.2 静电力与库仑定律2.3 电势与电势能2.4 电场强度与高斯定律第三章:稳恒电流场3.1 电流场的定义与特性3.2 欧姆定律3.3 电阻的计算3.4 电流场的分布与等势线第四章:稳恒磁场4.1 磁场的基本概念4.2 安培定律4.3 磁感应强度与磁场强度4.4 磁通量与磁通量密度第五章:电磁波5.1 电磁波的产生与传播5.2 电磁波的波动方程5.3 电磁波的极化与反射、折射5.4 电磁波的应用第六章:电磁场的数值计算方法6.1 有限差分法6.2 有限元法6.3 边界元法6.4 有限体积法第七章:电磁场的测量与检测7.1 电磁场测量的基础知识7.2 电磁场测量仪器与设备7.3 电磁兼容性测试7.4 电磁辐射的防护与控制第八章:电磁场在工程中的应用8.1 电机与变压器8.2 电磁兼容设计8.3 无线通信与雷达技术8.4 电力系统的电磁场问题第九章:电磁场相关的标准与规范9.1 国际电工委员会(IEC)标准9.2 北美电气和电子工程师协会(IEEE)标准9.3 欧洲电信标准协会(ETSI)标准9.4 我国电磁兼容性标准第十章:电磁场的环境保护与安全10.1 电磁污染与电磁干扰10.2 电磁场的生物效应10.3 电磁场的防护措施10.4 电磁场环境监测与管理重点和难点解析一、电磁场的基本概念难点解析:电磁现象的内在联系,电磁场的定量描述,电磁感应的数学表达。
二、静电场难点解析:静电场的能量分布,电势的计算,高斯定律在复杂几何形状中的应用。
三、稳恒电流场难点解析:电流场的散度,等势面的概念,复杂电路中的电流分布计算。
四、稳恒磁场难点解析:磁场的闭合性,安培定律的适用条件,磁通量的计算,磁场的能量。
五、电磁波难点解析:电磁波的麦克斯韦方程组,电磁波的产生机制,电磁波在不同介质中的传播特性。
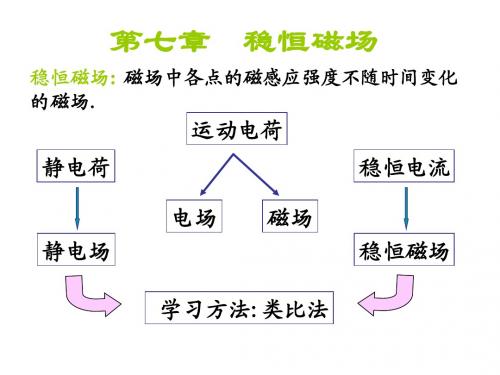
静电场与稳恒磁场的比较

静电场和稳恒磁场的比较[摘要][关键词]静电场电介质电场强度电通量高斯定理电场力的功电势导体电容电流电动势磁场磁感应强度安培环路定理磁介质在运动电荷周围,不但存在电场,而且还存在磁场。
稳恒电流产生的磁场是不随时间变化的,称为稳恒磁场。
稳恒磁场和静电场是两种性质不同的场,但在研究方法上有很多相似的地方,下面我们来比较:静电场是相对于观察者为静止的带电体周围存在的电场。
电场是一种特殊形态的物质,其物质性一方面体现在它的带电体的作用力,以及带电体在电场中运动时电场力对带电体做功;另一方面体现在电场具有能量。
动量和电磁质量等物质的基本属性。
电场强度和电动势是描述电场特性的两个物理量。
高斯定理和场强环流定理是反应静电场和稳恒电场性质的基本规律。
在电场作用下,导体和电介质的电荷分布会发生变化,这种变化了的电荷分布又会反过来影响电场分布,最后达到平衡。
稳恒磁场就是稳定的电流周围的磁场。
稳恒电流的磁场真空中的磁场主要分为两部分:一是电流激发的磁场;二是磁场对电流的作用。
稳恒电流激发静磁场,磁场是电场的相对论效应,若空间不止一个运动电荷,则空间某点总磁感应强度等于各场源电荷单独在该点激发的磁感应强度的矢量和。
运动的电荷产生磁场。
性质根据静电场的高斯定理,静电场的电场线起于正电荷或无穷远,终止于负电荷或无穷远,故静电场是有源场.从安培环路定理来说它是一个无旋场.根据环量定理,静电场中环量恒等于零,表明静电场中沿任意闭合路径移动电荷,电场力所做的功都为零,因此静电场是保守场.根据库仑定律,两个点电荷之间的作用力跟它们的电荷量的乘积成正比,和它们距离的平方成反比,作用力的方向在它们的连线上,即F=kq1q2/r,其中q1、q2为两电荷的电荷量、k为静电力常量,约为9.0e+09牛顿米2/库2,r为两电荷中心点连线的距离。
注意,点电荷是当带电体的距离比它们的大小大得多时,带电体的形状和大小可以忽略不计的电荷.静电感应如果电场中存在导体,在电场力的作用下出现静电感应现象,使原静电场来中和的正、负电荷分离,出现在导体表面上。
大学物理电磁学知识点总结

大学物理电磁学总结一、三大定律库仑定律:在真空中,两个静止的点电荷q1 和q2 之间的静电相互作用力与这两个点电荷所带电荷量的乘积成正比,与它们之间距离的平方成反比,作用力的方向沿着两个点电荷的连线,同号电荷相斥,异号电荷相吸。
uuu r q q ur F21 = k 1 2 2 er rur u r 高斯定理:a) 静电场:Φ e = E d S = ∫s∑qiiε0(真空中)b) 稳恒磁场:Φ m =u u r r Bd S = 0 ∫s环路定理:a) 静电场的环路定理:b) 安培环路定理:二、对比总结电与磁∫Lur r L E dl = 0 ∫ ur r B dl = 0 ∑ I i (真空中)L电磁学静电场稳恒磁场稳恒磁场电场强度:E磁感应强度:B 定义:B =ur ur F 定义:E = (N/C) q0基本计算方法:1、点电荷电场强度:E =ur r u r dF (d F = Idl × B )(T) Idl sin θ方向:沿该点处静止小磁针的N 极指向。
基本计算方法:urq ur er 4πε 0 r 2 1r ur u Idl × e r 0 r 1、毕奥-萨伐尔定律:d B = 2 4π r2、连续分布的电流元的磁场强度:2、电场强度叠加原理:ur n ur 1 E = ∑ Ei = 4πε 0 i =1r qi uu eri ∑ r2 i =1 inr ur u r u r 0 Idl × er B = ∫dB = ∫ 4π r 23、安培环路定理(后面介绍)4、通过磁通量解得(后面介绍)3、连续分布电荷的电场强度:ur ρ dV ur E=∫ e v 4πε r 2 r 0 ur σ dS ur ur λ dl ur E=∫ er , E = ∫ e s 4πε r 2 l 4πε r 2 r 0 04、高斯定理(后面介绍)5、通过电势解得(后面介绍)几种常见的带电体的电场强度公式:几种常见的磁感应强度公式:1、无限长直载流导线外:B = 2、圆电流圆心处:B = 3、圆电流轴线上:B =ur 1、点电荷:E =q ur er 4πε 0 r 2 10 I2R0 I 2π r2、均匀带电圆环轴线上一点:ur E=r qx i 2 2 32 4πε 0 ( R + x )R 2 IN 2 ( x 2 + R 2 )3 21 0α 23、均匀带电无限大平面:E =σ 2ε 0(N 为线圈匝数)4、无限大均匀载流平面:B =4、均匀带电球壳:E = 0( r < R )(α 是流过单位宽度的电流)ur E=q ur er (r > R ) 4πε 0 r 25、无限长密绕直螺线管内部:B = 0 nI (n 是单位长度上的线圈匝数)6、一段载流圆弧线在圆心处:B = (是弧度角,以弧度为单位)7、圆盘圆心处:B =r ur qr (r < R) 5、均匀带电球体:E = 4πε 0 R 3 ur E= q 4πε 0 r ur er (r > R ) 20 I 4π R0σω R2(σ 是圆盘电荷面密度,ω 圆盘转动的角速度)6、无限长直导线:E =λ 2πε 0 x λ 0(r > R ) 2πε 0 r7、无限长直圆柱体:E =E=λr (r < R) 4πε 0 R 2电场强度通量:N·m2·c-1)(磁通量:wb)(sΦ e = ∫ d Φ e = ∫ E cos θ dS = ∫s sur u r E d S通量u u r r Φ m = ∫ d Φ m = ∫ Bd S = ∫ B cos θ dS s s s若为闭合曲面:Φ e =∫sur u r E d S若为闭合曲面:u u r r Φ m = Bd S = B cos θ dS ∫ ∫s s均匀电场通过闭合曲面的通量为零。
静电场与稳恒磁场的对比浅析

静电场与稳恒磁场的对比浅析电磁学理论在现代物理学中占有重要的地位,它渗透到现代科学技术的各个领域,是许多学科和技术的理论基础。
而静电场和稳恒磁场是电磁学理论的两大重要组成部分,但这部分知识对学生来讲,是非常抽象的,要学好这部分内容,教师在讲授过程中要注意教学方法。
方法得当,学生就会激发学习的兴趣,收到很好的效果。
对有关大学物理教学改革方面的论文有很多,比如管薇写的关于工科大学物理教学改革[1]、张明霞浅谈大学物理教学改革[2]等等。
在本文,通过对静电场与稳恒磁场这两部分内容进行对比,再通过MATLAB程序模拟,有助于理解这两部分内容,让学生在学时少的情况下,很好的掌握这部分知识。
1 静电场与稳恒磁场物理量之间对比研究首先,从描述这两种场的某点性质和场强弱的物理量来进行对比。
描述静电场用电场强度矢量E和电位移矢量D,稳恒磁场用磁感应强度矢量B和磁场强度矢量H来描述。
D与E之间的关系和B与H之间的关系具有相似的公式,都可以用来表示,代表D或B,而代表E和H,在静电场中表示电介质的电容率,在稳恒磁场中表示磁介质的磁导率。
其次,这两种场的强弱还可以用电场线和磁感应线直观的观察到,众所周知,电磁学学习的难点在于对场的概念难以理解,这时我们讲授时可以利用MATLAB 强大的图形功能,使抽象的场的概念形象化,帮助学生理解这一问题。
在这里我们来模拟一下电偶极子电场线和等势线以及电流环产生的磁场分布。
(1)电偶极子的电场线和等势线,如图1所示。
(2)电流环产生的磁场分布,如图2所示。
从图1可以直观的看出:电场线是从正电荷出发,到负电荷终止,电场线密集的地方场强也比较强。
从图2可以看出电流环中心轴线的磁场强度方向向右,磁感线密集的地方场强强。
用这简单的模拟可以让学生直观的观察到,这样更能清晰的理解这两种场。
2 静电场和稳恒磁场相似的定理进行对比静电场和稳恒磁场都有高斯定理和环路定理,并且,有相似的表达式:静电场的高斯定理[3]:通过任意闭合曲面的电场强度通量,等于该闭合曲面所包含的电荷的电量除以,即∮,反映静电场是有源场。
《大学物理》第三篇电磁学

找比较对象 类象
重要作用: (1) 是提出科学假说的重要途径; (2) 是科学阐述或理论证明的辅助手段; (3) 在解决问题的过程中起启发思路、触类旁通的作用。
注意:类比推理所得结论是或然的,需证实或证伪。
3-15-2
磁场
静电场 电
感生 场 电场
一般 电场
高斯定理
SB dS 0
S D0 dS
物质存在的两种基本形式:实物和场
共性:能量、动量、质量
•场能对其中的物体做功 ——表明场有能量
•引力红移与偏折、光压等实验 ——表明场有质量和动量
可相互转化(如正负电子对湮没、同步辐射)
1、电磁场的能量密度与能量
电场能量密度
1 we 2 E D
磁场能量密度
wm
1 2
BH
电磁场能量密度
w
we
S D0 dS
ρdV
V
L E0 dl 0
SB dS 0
D
LH dl S ( j t ) dS
SB dS 0
LH dl S j dS
静电场 基本方程
静电场 基本方程
麦克斯韦方程组是对电磁场宏观规律的 全面总结和概括!
是经典物理三大支柱之一。
再看积分形式的麦克斯韦方程组
jE
2 t
由矢量运算公式: a (b c ) (a b) c b (a c )
(H E) ( H ) E H ( E)
1
(D E
BH)
(H
E)
jE
2 t
(E H ) j E
dW 1
dt
2 V t (D E B H )dV
jD πr 2
2) r >R
大学物理稳恒磁场教案

课时:2课时教学目标:1. 理解稳恒磁场的基本概念,包括磁感应强度、磁场中的高斯定理、毕奥-萨伐尔定律等。
2. 掌握毕奥-萨伐尔定律的应用,能够计算载流导线产生的磁场。
3. 理解安培环路定理,并能够运用其解决实际问题。
4. 了解磁矩、磁力矩、洛伦兹力等概念,并掌握其应用。
教学重点:1. 稳恒磁场的基本概念和公式。
2. 毕奥-萨伐尔定律的应用。
3. 安培环路定理的推导和应用。
教学难点:1. 毕奥-萨伐尔定律公式的推导和应用。
2. 安培环路定理的推导和应用。
教学过程:第一课时一、导入1. 回顾静电场的基本概念,引出稳恒磁场。
2. 介绍稳恒磁场的基本概念,如磁感应强度、磁场中的高斯定理等。
二、新课讲授1. 磁感应强度:- 定义磁感应强度,讲解其大小和方向。
- 举例说明磁感应强度在生活中的应用。
2. 磁场中的高斯定理:- 介绍高斯定理的概念,讲解其数学表达式。
- 举例说明高斯定理在解决实际问题中的应用。
三、课堂练习1. 计算一个载流直导线在空间某点产生的磁感应强度。
2. 计算一个载流圆形导线在中心轴线上某点产生的磁感应强度。
四、总结1. 回顾本节课所学内容,强调稳恒磁场的基本概念和公式。
2. 布置课后作业,巩固所学知识。
第二课时一、导入1. 回顾上一节课所学内容,引出毕奥-萨伐尔定律。
2. 介绍毕奥-萨伐尔定律的概念,讲解其数学表达式。
二、新课讲授1. 毕奥-萨伐尔定律:- 定义毕奥-萨伐尔定律,讲解其数学表达式。
- 举例说明毕奥-萨伐尔定律在解决实际问题中的应用。
2. 安培环路定理:- 介绍安培环路定理的概念,讲解其数学表达式。
- 推导安培环路定理,讲解其推导过程。
三、课堂练习1. 计算一个载流直导线在空间某点产生的磁场强度。
2. 计算一个载流圆形导线在中心轴线上某点产生的磁场强度。
四、总结1. 回顾本节课所学内容,强调毕奥-萨伐尔定律和安培环路定理的应用。
2. 布置课后作业,巩固所学知识。
教学反思:1. 本节课通过理论讲解和实例分析,帮助学生掌握了稳恒磁场的基本概念和公式。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
有 r >> l ,那么可以认为偶极子 − pr 到场点的距离等于 r − l cosθ
偶极子 − pr 在场点产生的电势为:
φ2
=
−1 4πε 0
p (r − l cosθ )2
cosα ′ ,其中 cosα ′ = cosϕ sinθ ′
= cosϕ
r
r − l cosθ
sinθ
那么场点的电势为:
解:
r E
=
−∇φ
=
−∇(
1
4πε 0
pr ⋅ err r2
)
= − 1 [ pv × ∇ × err + ( pr ⋅ ∇) err ]
4πε 0
r2
r2
= − 1 ( pr ⋅ ∇) err
4πε 0
r2
3.一对电量相等的正负电荷相距为 l ,求该系统在远处的电场强度。
解:具有偶极矩
pv z
=
r ql
σ
0 erz
球外电势为φ = 1 pr ⋅ rr 4πε 0 r 3
= R3 σ 0 cosθ 3ε 0 r 2
r 8.将一个半径为 R,介电常数为ε的无限长圆柱形均匀电介质放入均匀外电场 E0 中,圆
r 柱轴线与 E0 垂直。试求介质极化电荷所产生的电势和电场强度。 解:令柱外电势为φ1 ,柱内电势为φ2 ,由第 5 题容易知道它们的通解分别为:
电动力学习题解答参考
∫ 1.对电场强度的表示式
r E
=
1
4πε 0
V
ρ(rr′)(rr − rr′) rr − rr′ 3
dV
′
第二章 静电场和稳恒电磁场
进行直接微分。证明
∇
×
r E
=
0及 ∇
⋅
r E
=
ρ
ε0
∫ 证明:
∇
×
r E
=
1
4πε 0
v
ρ
(rv
′)∇
×
|
(rr − rr′) rr − rr′ |3
解:要求的定解问题为 ∇2φ = 0 (r > R)
φ |r=R = a(1 + cosθ )2
φ |∞ = 0
∞
∑ 根据题目条件,场具有轴对称性,那么φ 的通解为φ = (anr n + bn / r n+1 )Pn (cosθ ) n=0
代入边界条件解得:
φ
=
A0 r
+
A1 r2
P1 (cosθ ) +
∞
∑ φ1 = a0 + b0 ln r + [(amr m + bm / r m ) cos mθ + (cmr m + dm / r m ) sin mθ ] (r > R) m=1 ∞
∑ φ2 = a0 + b0 ln r + [(amr m + bm / r m ) cos mθ + (cmr m + dm / r m ) sin mθ ] (r < R) m=1 -3-
假定球外距球心为 b = R 2 处有一电量 q′ = − R q 的点电荷。
a
a
球壳本身带电,其上电势并不为 0,球内电势φ2
|r=R = φ1 |r=R =
1 4πε 0
q+Q R
那么 φ 2
=
1 4πε 0
q+Q R
+
1 4πε 0
[a 2
+ r2
q − 2ar cosθ ]1/ 2
−
1 4πε 0
两个(相等的)半球壳,为了使这两个半球壳不至于分开,需要加多大的外力? 解:易知球壳内部电场强度为 0,球外电势满足的定解问题为:
∇2φ = 0 (r > R)
φ |r=R = C
φ |∞ = −E0r cosθ
求得球壳外电势 φ
=
−E0r
cosθ
+
E0 R3 r2
cosθ
球壳上的电荷面密度为 σ
=
的电偶极子产生的电势为
φ
=
q 4πε 0
1 ( r+
−
1 )
r−
在远场处 1 r+
−1 r−
≈
1 r2
l cosθ
,故要求的电势为 φ
=
ql cosθ 4πε 0r 2
电场强度
r E
=
−∇φ
=
−∇(
1
ql cosθ )
4πε 0 r 2
-1-
电动力学习题解答参考
= 1 3ql cosθerr − qlerz
∫−
ε0
r=a
∂φ dl ∂r
=
λ
φ |r=a = C
φ |∞ = −E0r cosθ
根据题目条件,场与 z 无关,那么φ 的通解为:
∞
∑ φ = a0 + b0 ln r + [(amr m + bm / r m ) cos mθ + (cmr m + dm / r m ) sin mθ ] m=1
πε
0
E02
R
2
14.有一个半径为 R 的薄导体球壳,带电量为 Q。壳内距中心为 a (< R) 处有一点电荷 q.求
壳上的电荷分布。
解:根据高斯定理可知球外电场强度
r E
=
1
q + Q ,那么若确定无穷远处电势 为 0,可
4πε 0 r 2
得球外电势 φ1
=
1 4πε 0
q+Q r
对于球内的电势φ2 可以用电像法求得。考虑到导体球面上电势处处相等,由电像法可
[b 2
+ r2
Rq / a − 2br cosθ ]1/ 2
球壳上电荷分步 σ
=
ε
0
(
∂φ2 ∂r
−
∂φ1 ∂r
)
|r
=
R
= 1 [q +Q −
q(R − a cosθ )
− Rq / a(b cosθ − R)
4π R 2 [a 2 + R 2 − 2aR cosθ ]3/ 2 [b2 + R 2 − 2bR cosθ ]3/ 2
度。
∫ 解:磁偶极矩 mr
=
1 rr ×αrdS 2 r=a
=
4πa 3 3
α 0erz
磁感应强度
r B
=
−
µ0 4π
(mr
⋅ ∇)
rr r3
=
µ0α 0a 3 3r 3
(2 cosθerr
+ sinθerθ
)
-6-
0,作用在球壳上电荷的电场为
r E
=
3 2
cosθE0err
-4-
电动力学习题解答参考
第二章 静电场和稳恒电磁场
∫ r
那么电场作用在一个半球壳上的力 F =
Erσds
0<θ <π / 2
考虑到对称性
∫ F
=
π /2 0
3 2
cos 2
θE 0 err
3ε 0
cosθE0 R2πR sinθdθ
=
9 4
19. 一半径为 a 的无限长接地圆柱形导体,一线电荷密度为 λ 的无限长直线放在圆柱外且
与圆柱轴线平行,带电直线与圆柱轴线的距离为 d,求圆柱外任一点的电势。 解:如图,选择 A 点的电势为 0,则直线在场点 Q 产生的电势为
ϕ1
=
−
λ 2πε 0
ln
(ρ 2
+
d
2
− d
2ρd −a
cosθ )1/ 2
A3 r3
P2 (cosθ ) ,其中 A0
=
4R 3
a,
A1
=
2R 2a , A0
=
2R2 3
a
7.已知半径为 R 的球壳表面电荷面密度为σ = σ 0 cosθ ,求电偶极矩及球外电势。
∫ 解:电偶极矩 pr = σrvdS r=a = ∫∫σ 0 cosθ ⋅ rrr 2 sinθdθdφ
=
4πR 3 3
−ε 0
∂φ ∂r
|r=R
= 3ε 0 E0 cosθ
球外的电场强度
r E
=
−∇φ
=
∇(E0r cosθ
−
E0 R 3 r2
cosθ )
=
(E0
cosθ
+
2
E0 R 3 r3
cosθ )err
+ (−E0
sinθ
+
E0 R3 r3
sinθ )erθ
球壳外边界
r E
|r=R
=
3
cosθE0err
因为球壳内部电场强度为
φ
= φ1
+ φ2
=
p cosϕ sinθ 4πε 0
1 ( r2
−
r
)=− 1
(r − l cosθ )3
4πε 0
3 pl sinθ cosθ cosϕ r3
r 5.半径为 a 的无限长导体圆柱,带线电荷密度为λ,置于均匀电场 E0 中,电场和圆柱体轴
线垂直,求柱外电势。
解:要求的定解问题为 ∇2φ = 0 (r > a)
R2 r
E0 cosθ
,φ2
=
ε ε
−ε0 + ε0
E0r cosθ
r 柱外、柱内电场强度为: E1
