方差分析基本条件
合集下载
第七章方差分析与F检验
第七章 方差分析
• 方差分析又称做变异分析，它的主 要功能在于分析实验数据中不同来 源的变异对总变异的贡献大小，如 实验处理引起的变异、被试个体差 异带来的变异、实验误差带来的变 异等，从而确定实验中的自变量是 否对因变量有重要影响。
第一节 方差分析的基本原理
一、方差分析的基本原理：综合的F检验 （一）综合虚无假设与部分虚无假设 方差分析主要处理多于两个以上的平均数
1、建立假设：H0:μ1=μ2=…=μk H1:至少有两个总体平均数是不
同的，即处理效应不全为0 2、计算离差平方和 3、求均方 4、计算F值 5、进行F检验
6、列出方差分析表
变异来源
组间变异 （处理）
组内变异 （误差）
总变异
自由度 平方和 均方 F
dfb=k-1
SSb MSA MSA/
Dfw=∑(n-1) SSw MSE MSE
（六）陈列方差分析表
二、方差分析的基本条件
1、数据所代表的总体必须是正态分布， 即样本必须来自属于正态分布。
2、变异具有可分解性。
3、各组内的方差应无显著差异。因此 理论上在做方差分析之前应先对各 组方差的一致性进行检验。
第二节 单因素完全随机化设 计的方差分析
完全随机设计的方差分析，就是对单因素 组间设计的方差分析。在这种实验研究 设计中，各种处理的分类仅以单个实验 变量为基础，因而把它称为单因素方差 分析或单向方差分析。
③计算均方
MSb=MSA=SSb/dfb=43.33/2=21.67 MSw=MSE=SSw/dfw=30.00/12=2.50 ④计算F值,进行F检验,做出决断
F= MSb/ MSw=21.67/2.50=8.67 查F表,F0.05(2,12)=3.88 8.67>3.88,拒绝虚无假设,可以认为在
• 方差分析又称做变异分析，它的主 要功能在于分析实验数据中不同来 源的变异对总变异的贡献大小，如 实验处理引起的变异、被试个体差 异带来的变异、实验误差带来的变 异等，从而确定实验中的自变量是 否对因变量有重要影响。
第一节 方差分析的基本原理
一、方差分析的基本原理：综合的F检验 （一）综合虚无假设与部分虚无假设 方差分析主要处理多于两个以上的平均数
1、建立假设：H0:μ1=μ2=…=μk H1:至少有两个总体平均数是不
同的，即处理效应不全为0 2、计算离差平方和 3、求均方 4、计算F值 5、进行F检验
6、列出方差分析表
变异来源
组间变异 （处理）
组内变异 （误差）
总变异
自由度 平方和 均方 F
dfb=k-1
SSb MSA MSA/
Dfw=∑(n-1) SSw MSE MSE
（六）陈列方差分析表
二、方差分析的基本条件
1、数据所代表的总体必须是正态分布， 即样本必须来自属于正态分布。
2、变异具有可分解性。
3、各组内的方差应无显著差异。因此 理论上在做方差分析之前应先对各 组方差的一致性进行检验。
第二节 单因素完全随机化设 计的方差分析
完全随机设计的方差分析，就是对单因素 组间设计的方差分析。在这种实验研究 设计中，各种处理的分类仅以单个实验 变量为基础，因而把它称为单因素方差 分析或单向方差分析。
③计算均方
MSb=MSA=SSb/dfb=43.33/2=21.67 MSw=MSE=SSw/dfw=30.00/12=2.50 ④计算F值,进行F检验,做出决断
F= MSb/ MSw=21.67/2.50=8.67 查F表,F0.05(2,12)=3.88 8.67>3.88,拒绝虚无假设,可以认为在
医学统计学-8-方差分析
第二节 单因素方差分析
单因素方差分析
单因素方差分析：研究的是一个处理因素的 不同水平间效应的差别。
处 理 因 素
水平1 水平2 水平1 水平2 水平c
单因素方差分析
例1、某地用A、B和C三种方案治疗血红蛋 白含量不满10g的婴幼儿贫血患者，A方案 为每公斤体重每天口服2.5％硫酸亚铁1ml， B方案为每公斤体重每天口服2.5％硫酸亚 铁0.5ml，C方案为每公斤体重每天口服3g 鸡肝粉，治疗一月后，记录下每名受试者血 红蛋白的上升克数，资料见下表，问三种治 疗方案对婴幼儿贫血的疗效是否相同？
A、B、C三种方案治疗婴幼儿贫血的疗效观察表
治疗方案 A n=20
血红蛋白增加量（g） 1.8 1.4 0.5 1.2 2.3 2.3 3.7 0.7 2.4 0.5 2.0 1.4 1.5 1.7 2.7 3.0 1.1 3.2 0.9 2.5
B
n=19
0.2
0.0 2.1 -0.7
0.5
1.6 1.9 1.3
q XA XB
MSe 1 1 2 nA nB
ν=νe
一、q检验
例、在前面对某地用A、B和C三种方案治疗 血红蛋白含量不满10g的婴幼儿贫血患者的 例题（完全随机设计方差分析例1）进行了 方差分析，我们得出三组总体不等的结论。 究竟哪些总体均数之间存在着差别，我们需 要在前方差分析基础之上，再对该资料作两 两比较的q检验。
随机因素是无法避免的，而实质性差异是我们 需要得到的。 如何排除随机因素的干扰，利用样本信息对总 体均数间是否存在差异作出推断？
方差分析的基本思想
按照设计类型将总变异分解为处理因素引 起的变异和随机因素造成的变异； 以处理因素变异与随机因素变异之比来构 造检验统计量F。
第九章 方差分析
第九章方差分析前面介绍了两个样本均数比较的t检验，那么多个样本均数的比较应该采用什么方法？方差分析(analysis of variance, ANOV A)是20世纪20年代发展起来的一种统计方法，由英国著名统计学家R.A.Fisher提出，又称F检验，是通过对数据变异的分析来推断两个或多个样本均数所代表总体均数是否有差别的一种统计学方法。
本章首先介绍方差分析的基本思想和应用条件，然后结合研究设计类型分别介绍各类方差分析方法。
第一节方差分析的基本思想和应用条件一、方差分析的基本思想方差分析的基本思想是把全部观察值间的变异按设计类型的不同，分解成两个或多个组成部分，然后将各部分的变异与随机误差进行比较，以判断各部分的变异是否具有统计学意义。
例9.1 为研究大豆对缺铁性贫血的恢复作用，某研究者进行了如下实验：选取已做成贫血模型的大鼠36只，随机等分为3组，每组12只，分别用三种不同的饲料喂养：不含大豆的普通饲料、含10%大豆饲料和含15%大豆饲料。
喂养一周后，测定大鼠红细胞数(×1012/L)，试分析喂养三种不同饲料的大鼠贫血恢复情况是否不同？表9.1 喂养三种不同饲料的大鼠红细胞数(×1012/L)普通饲料10%大豆饲料15%大豆饲料合计X 4.78 4.65 6.80 4.65 6.92 5.913.984.447.284.04 6.167.51 3.445.997.51 3.776.677.743.65 5.298.194.91 4.707.154.795.058.185.316.01 5.534.055.677.795.16 4.688.03in12 12 12 36 (n)i X ∑ 52.53 66.23 87.62 206.38(X ∑)i X4.385.52 7.30 5.73 (X ) 2i X ∑ 234.2783373.2851647.73121255.2946(2X ∑)表9.1按完全随机设计获得的36个数据(X )中包含以下三种变异： 1. 总变异 36只大鼠喂养一周后测定红细胞数X 各不相同，即X 与总均数X 不同，这种变异称为总变异(total variation)。
方差分析(F检验)
10
因组间变异数大小与组数（组间自由度K-1）有关，故用 组间变异数除以自由度所得组间均方来表示组间变异。
ss 组间 ms 组间 k 1
k=组数
因组内变异数大小与各样本含量大小即组内自由度∑(ni –1) 有关，故用组内变异数除以组内自由度所得组内均方来表示 组内变异。
ms 组内
ss 组内 1 ) (n i
I
2019/2/11
23
15例患者体温降至正常 所需要的天数 甲法 乙法 丙法 5 5 7 5 5 9 5 7 9 7 7 9 7 7 9
[ 问题 2] 例 2 的总变异来源与例 1 有何异同点？ [ 答案 2] 共同点是其总变异来源都是来自于 处理因素变异和抽样误差变异，这不仅是它们 的共同点，而且是所有方差分析资料总变异来 源的共同点。
2019/2/11
17
随机区组设计资料 方差分析
研究酵解作用对血糖 受试者号 放置时间（分） 浓度的影响，从8名健康 45 90 135 人中抽取了血液并制备成 （区组） 0 1 5.27 5.27 4.94 4.61 血滤液，每个受试者的血 2 5.27 5.22 4.88 4.66 滤液分成四份，再随机把 3 5.88 5.83 5.38 5.00 4 5.44 5.38 5.27 5.00 4份血液分别放置0、45、 5 5.66 5.44 5.38 4.88 90、135分钟后测定其血 6 6.22 6.22 5.61 5.22 糖浓度，试分析放置不同 7 5.83 5.72 5.38 4.88 时间的血糖浓度有无变化。 8 5.27 5.11 5.00 4.44
2
2019/2/11
6
15例患者体温降至 正常所需要的天数 甲法 乙法 丙法 5 5 7 5 5 9 5 7 9 7 7 9 7 7 9
第七章 方差分析
第三节 平均数的多重比较
F检验是一种整体性检验，当经方差分析鉴别 多个正态总体的平均数有显著时，并不能说明 各组水平之间都存在显著差异，只是说至少有 一对差异显著，究竟哪些均数差异显著，哪些 差异不显著，则还需进行均数的多重比较。
一、图凯法
是一种能将所有各对平均值同时比较的方法。 设因素A分成两组，每组有相等的含量，并经
第二节 单因素方差分析
概念
观察的因素只有一个的实验叫单因素实验。对 此种实验结果进行方差分析的方法叫单因素方 差分析。
单因素方差分析所讨论的是k个总体标准差皆 相等的条件下，解决k个总体平均数是否相等 的问题。
一、计算步骤（见P140~142）
１、依据表中数据,计算各组内的 x,x2, xi,n ２、然后计算 x,x2,n, 并令
过方差分析判别各组之间存在显著性差异，为 了比较两者之间差异显著性，可按下式计算T
值： T QS x
其中Q值按预先确定的α水平，组数K和组内 自由度（N－k）查附表获得。
任何一对平均值之差，只要超过T值，就表明 这一对平均值之间的差别是显著的。
图凯法要求所有的样本含量都相等。
例题：P147~148 当各组被试不相等时，可采用S法检验进行两
X x, X 2 x2, N n
３、计算离差平方和：（总离差平方和、组间 离差平方和和组内离差平方和）
４、计算方差：（组间方差和组内方差） ５、计算F值
二、方差分析的计算
见课本P142~143
方差分析计算的两种情况：
当样本含量相等时：
当样本含量不等时： 例题7.2，P144~146
二、实验误差与条件误差
在方差分析的试验中，即使各水平的试验条件 完全相同，但由于随机抽样或试验过程中随机 因素的影响，其试验结果（指标）仍然会存在 偏差，我们称这种偏差为试验误差或随机误差。
方差分析
2
X
n
2
2
SST X
2
X
n
14
⑵ ．分解自由度
总自由度可以分解为组间自由度和组内自由度：
dfT dfB dfW
组间自由度
dfB k 1
dfW n k
组内自由度
总自由度
dfT n 1
15
⑶．计算方差
组间方差
SSB MS B dfB
随机区组设计的方差分析将变异来源分解为组间变异、区组变异和误差 变异三部分：
SST SSB SSR SSE
30
3．随机区组设计方差分析的计算公式
⑴．分解平方和
总平方和
SST X
2
X
n
2
组间平方和
SSB
X 2 X 2
n n
31
区组平方和
H0：μ1＝μ2＝μ3＝μ4 H1：至少有两个总体平均数不等
2．选择检验统计量并计算 假定四组记录数据是从四个正态总体中抽出的独立样本，对多 个独立样本平均数的差异进行显著性检验，应采用完全随机设计的 方差分析。
20
计算表
序号 X1 X2 X3 X4 治疗方案
1
2 3 4 5 6 7
30 900
28
总之，就区组来说，每一个区组都接受所有的各种实验处理；就实
验处理来说，每一种实验处理在各个区组中重复的次数相同。 随机区组设计的方差分析中，接受各种实验处理的是同一些区组，
故个别差异可以从组内差异中分离出来，从而减少由个别差异造成的误差， 增加实验的信息，提高实验的效率。
29
2．变异来源
5第六章方差分析
练习
• 以小鼠研究正常肝核糖核酸（RNA）对癌细 胞的生物学作用，试验分为对照组（生理 盐水）、水层 RNA组和酚层RNA组，分别用 此三种不同处理诱导肝细胞的FDP酶活力， 得数据如下。该三组资料均服从正态分布， 试比较三组均数有无差别?
ex_36.sas
表 6.1 对照组
2.79 2.69 3.11 3.47 1.77 2.44 2.83 2.52
复相关系数（确定系数），变异系数，均方根，总均数
对自变量的检验
R-Square:等于模型的平方和除以总 平方和，用于度量在因变量的变差 里能够由模型决定的比例有多少， 越接近1，效果越好。
检验的显著水平、自由度、 误差均方
具有相同字母的组间 均值差异没有统计学意义。
第2组具有A和B两个字母，所以 第二组和第三组，第一组均没有差异。
单因素方差分析
假设某单因素试验有k个处理，每个处理有n次重 复，共有nk个观测值。这类试验资料的数据模式
如下表所示。
（一）总平方和的分解 在上表中，反映全部观测值总变异的总平方和
是各观测值xij与总平均数的离均差平方和，记 为SST。即
kn
SST
( xij x.. ) 2
i1 j 1
nj 组内样本容量j 1,2,,n ki 组数，即水平数i 1,2,,k x.. 总平均数 xij i水平下第 j个样样本
变 差
组间 变差
总 变 差 组内 变差
组数（水平数）
（二）总自由度的剖分
在计算总平方和时，资料中的各个观测值要
kn
受 (xij x这..) 一0 条件的约束，故总自由度等于 i1 j1
资料中观测值的总个数减1，即kn-1。
dfT kn 1 df t k 1 df e dfT df t
方差分析
k
nkΒιβλιοθήκη 2总平方和：SST
实验中产生的总变异
组内平方和：SSW
实验误差（包括个体差异）由于不同的实验处理而造 造成的变异 成的变异
组间平方和：SSB
三者之间的关系如下：
SS 总 SS 组间 SS 组内
组间自由度： 组内自由度: 总体自由度： 书266：这样
df B = k-1
df W = k(n-1)
df T = nk-1
在方差分析中，比较组间变异与组内变异时，不 能直接比较各自的平方和。因为平方和的大小与 项数有关，应该将项数的影响去掉。因此用平方 和除以各自自由度得到均方，再进行比较。
SS B MS B df B
书266
MSW
SSW df W
方差分析就是通过比较组内均方MS组内 和组间均方 MS组间 的大小关系来判断处 理因素有无效应。
变异分解
SS 总(T) SS 组间(B) SS 区组(R) SS 误差(E)
SS R
1 n
( R ) 2 k
( R ) 2 nk
总自由度也被分为三部分： dfT = nk-1
df B k 1
dfE=(k-1)(n-1)
dfR=n-1
例4：5名被试在四种不同的环境条件下参加某一心理测验， 结果如下。问不同的测验环境是否对这一测验成绩有显著影 响。
SSB n ( X j X t ) 2
j 1 k
SSw ( X ij X j ) n s j
2 j 1
k
2
1、求平方和
Xt
X1 X 2 X 3 X 4 6.4 4
k
SSB n ( X j X t ) 2 30.08
第06章 方差分析
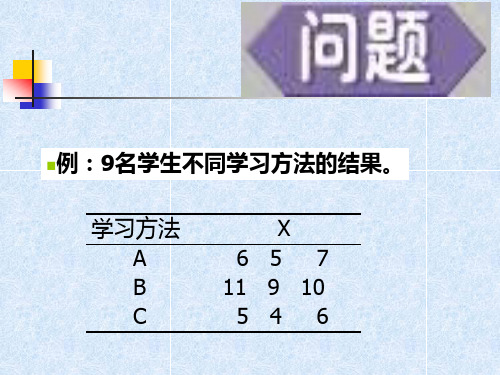
例：9名学生不同学习方法的结果。 学习方法 A B C X 6 5 7 11 9 10 5 4 6
1 Introduction: Why can not use multiple T test to conduct multiple comparison among groups?
• 若将显著性检验也视为两总体间“差异”检 验，则前面所讲t检验法主要适用于两总体间 均值差异的显著性检验，但在实践中经常会 遇到要比较多个处理优劣的问题，即需进行 多个均值间的差异显著性检验。这时若仍采 用t检验法有下列问题：
• More about F Test in ANOVA: • 方差分析假定各处理方差相等，则各处理样本方差S21、S22， S2m都是σ2的无偏估计量。各处理方差合成后估计精度更高。
SS e MS e df e (x ij x. j ) 2 m(n 1) SS1 SS 2 SS m m(n 1) df1 df 2 df m
分析
组内
完全随机化
组间效应显著 又意味着什么？
组间
意味着什么？
1.建立假设
• 单因素 完全随机化 设计模型
xij j ij i ij
j组均值 误差 总均值 j组效应
i i
1 k i k i 1
H 0 : 1 2 ... m
1、总变异的分解
总变异 = 组间变异 + 组内变异
SSt SSw SSb
SSt X X t SSw X X
2 2
2
SSb n X X t
2、自由度的计算
dft n 1
第六章 方差分析
9.0 9.4 8.0 69.7 608.69
ΣR 39.3 38.5 39.8 36.2 36.1 38
41.9 35.7 305.5
ΣR2 387.87 371.61 397.70 328.60 326.61 361.38 441.25 319.89
2934.91
SSt 18.34 SSw 9.44 SSs 8.06 SSe 0.84 Fw 78.75 Fs 28.75
15
方差分析原理例题
A 10 14 12 (n=5) 8 11
X j 11
实验处理
B
C
15
10
20
12
17
6
8
12
15
10
15
10
(K=3)
X t =12
任意一个数据与总平均数的离差 等于
这个数与该组平均数的离差
加上
该组平均数与总平均数的离差
(Xij Xt ) (Xij X j ) (X j Xt )
• 总自由度： dft = nk - 1
•
dft = dfb + dfw
F检验
SSb F MSb dfb
MSw SS w dfw
方差分析的一般步骤
1、计算离差平方和 2、确定自由度 3、F检验 4、列方差分析表
方差分析的基本条件
1、总体服从正态分布 2、变异的可加性（可分解性，即数据的总
人先后进行四种角度下的判断，结果如下，问不同夹角对错觉量是否有显著 影响。
被试
夹角
15°
30°
45°
60° ΣR
ΣR2
A
10.5
10.3
9.7
8.8 39.3
方差分析中的条件
方差分析中的条件
方差分析是统计学中非常重要的一种方法，它可以帮助我们准确地判断某种变量是否会对研究结果产生影响，从而帮助我们把握研究过程。
方差分析的核心是确定一个假设检验的阈值，以决定某种变量是否具有影响研究结果的能力。
本文将讨论方差分析的基本条件，以及应用方差分析的基本步骤，进而加深我们对方差分析的理解。
首先，介绍方差分析的基本条件。
方差分析中，主要有以下几个基本条件：
1.本容量：即研究中使用的样本量，一般来说，使用的样本量越大，分析结果就越准确可靠；
2.本与样本之间的独立性：即当一次实验在进行多次时，每个实验结果之间不受前次实验结果的影响；
3.察变量的独立性：即当我们观察不同的变量时，它的影响不能因为其他变量而出现变化；
4.测变量的正态分布：即观察变量在一定范围内必须服从正态分布；
5.本的一致性：即参加研究的样本必须有相应的特征，且与其他样本之间应是一致的。
其次，介绍方差分析的基本步骤。
一般来说，方差分析的步骤包括以下几点：
（1）建立假设：确定研究中使用的变量，以及其之间的关系；
（2）评估变量：收集样本变量以及相关信息，以及对变量进行
描述性统计；
（3）构建模型：使用回归方法，构建模型来衡量变量之间的关系；
（4）验证模型：通过检验模型的参数系数和方差分析，来验证模型是否有效；
（5）结果解释：解释模型的结果，对结果进行优化，并分析得出结论。
最后，总结本文。
方差分析是一种可以帮助我们准确判断某种变量是否会影响研究结果的重要方法，但是要想获得可靠的结果，必须要满足一定的基本条件，也必须遵循一定的基本步骤。
第十七章---方差分析(F检验)
误差的均方(组内均方)——个体差异 处理因素的均方(组间均方)——处理因素+个体因素 ○若处理因素有作用,则组间均方应大于组内均方. 即MS组间>MS误差, F=MS组间/MS组内>1 ○若处理因素不起作用,各样本均来自同一整体. 即MS组间≈MS误差, 则 F=MS组间/MS组内≈1 F值是方差分析的统计量,可查F界值表,求得F值,按所 取检验水平作统计判断.
#### #### #### ####
三 方差分析的条件
1 独立性 各随机样本相互独立。 2 随机性 各样本均是随机样本。 3 正态性 各样本均来自正态分布的整体。 （各因素每一水平的重复数椐均服从正态分 布。） 4 一致性 各处理组总体方差相等。
四 方差分析的基本思想
（一）方差分析的基本思想
1 从总变异中分出组间和组内变异,并用数量表 示变异程度。
❖ 求SS(总变异) ❖ 求SS组间 、 MS组间 ❖ 求SS组内 、 MS组内
1 求总变异的离均差平方和(SS总)
_
SS总 (xij X )2 ij
Xij表示第i组第j个观察值。 求32个观察值中每一观察值与总均数之差的平方 和。
总均数SS总=(22.6-18.51)2+ (22.8-18.51)2+……(16.2-18.51)2+
○例 如观察四种降脂药对4组动物动脉粥样硬化斑块 的影响，比较不同药物对动脉粥样硬化形成大小有 否影响。
处理
配伍
按体 Ⅰ 重高 Ⅱ 低分 Ⅲ
为四 Ⅳ
组
A(安妥明)
#### #### #### ####
B(降脂甲方) C(降脂乙方) D(降脂丙方)
#### #### #### ####
#### #### #### ####
#### #### #### ####
三 方差分析的条件
1 独立性 各随机样本相互独立。 2 随机性 各样本均是随机样本。 3 正态性 各样本均来自正态分布的整体。 （各因素每一水平的重复数椐均服从正态分 布。） 4 一致性 各处理组总体方差相等。
四 方差分析的基本思想
（一）方差分析的基本思想
1 从总变异中分出组间和组内变异,并用数量表 示变异程度。
❖ 求SS(总变异) ❖ 求SS组间 、 MS组间 ❖ 求SS组内 、 MS组内
1 求总变异的离均差平方和(SS总)
_
SS总 (xij X )2 ij
Xij表示第i组第j个观察值。 求32个观察值中每一观察值与总均数之差的平方 和。
总均数SS总=(22.6-18.51)2+ (22.8-18.51)2+……(16.2-18.51)2+
○例 如观察四种降脂药对4组动物动脉粥样硬化斑块 的影响，比较不同药物对动脉粥样硬化形成大小有 否影响。
处理
配伍
按体 Ⅰ 重高 Ⅱ 低分 Ⅲ
为四 Ⅳ
组
A(安妥明)
#### #### #### ####
B(降脂甲方) C(降脂乙方) D(降脂丙方)
#### #### #### ####
#### #### #### ####
方差分析(包括三因素)
2
15.1 17.5 20.1
3
15.8 17.1 18.9
4
14.8 15.9 18.2
5
17.1 18.4 20.5
6
15.0 17.7 19.7
A1 A2 A3
方差分析就是把总的 试验数据的波动分成
1、反映因素水平改变引起的波动。 2、反映随机因素所引起的波动。
然后加以比较进行统 计判断，得出结论。
2 ij 2 2 ij
m
n
m
n
T2 X mn i 1 j 1
m n 2 ij
12
同样可推出：
1 m 2 QE X Ti n i 1 i 1 j 1
2 ij
m
n
1 m 2 T2 QA Ti n i 1 mn
2、数据的简化： 试验数据经过变换
' X ij b( X ij a)
3
离差平方和 1.56 11.56 3.1 16.22
3
自由度 2 2 4 8
F值 FA=1.01 FB=7.46
F0.05(2,4) F0.01(2,4) 6.94 6.94 18.0 18.0
显著性
*
Q X
i 1 j 1
2 ij
T2 16.22 3 3
1 3 T2 2 QA Ti. 1.56 3 i 1 3 3
试验结果
假设：美中不足组合水平下服从正态分布、互相独立、方差相等。 所需要解决的问题是：所有Xij的均值是否相等。
18
假设检验：
1）在假设H0成立的条件下。 2）统计量
T2 Q X ml i 1 j 1
m l 2 ij
医学统计学(方差分析)
了解：
1、两因素方差分析
教学内容提要
重点讲解：
方差分析的基本思想 完全随机设计的单因素方差分析 多个样本均数间的多重比较
介绍：方差分析的原理与条件
与前面讲过的假设检验相同的是：
不同的是：方差分析用于多个均数的比较。
t检验是用 t值进行假设检验，方差分析则用 F值进行假设检验
方差分析的任务：统计量F的计算 F＝MS1/MS2
根据资料的性质选择不同的统计方法。注意都是在H0成 立的条件下进行计算。
计算概率值P：P的含义。
做出推论：统计学结论和专业结论。
单因素方差分析
方差分析表 （练习，完成该表。例题，写在黑板上）
变异来源 SS
MS
F
P
总变异 148
19-1
组间变异 57
4-1
组内变异
19-4
F0.05（3，15）＝3.29 F与它所对应的P值成反比
常取0.05，区分大小概率事件的标准。 计算统计量F：根据资料的性质选择不同的统计方
法。注意都是在H0成立的条件下进行计算。 计算概率值P：P的含义。 做出推论：统计学结论和专业结论。
四组不同摄入方式人的血浆游离吗啡水平
静脉点滴 肌肉注射 皮下注射 口服
12
12
10
16
7
15
8
9
9
14
均数
10
13
9
12
7
8
6
8
11
10
7
8
9.5
单因素方差分析
完整书写方差分析的过程
建立假设：
H0 ：4组病人血浆游离吗啡水平1 = 2 = 3= 4
H1 ： 4组病人血浆游离吗啡水平的总体均数全不相等或不全 相等
1、两因素方差分析
教学内容提要
重点讲解：
方差分析的基本思想 完全随机设计的单因素方差分析 多个样本均数间的多重比较
介绍：方差分析的原理与条件
与前面讲过的假设检验相同的是：
不同的是：方差分析用于多个均数的比较。
t检验是用 t值进行假设检验，方差分析则用 F值进行假设检验
方差分析的任务：统计量F的计算 F＝MS1/MS2
根据资料的性质选择不同的统计方法。注意都是在H0成 立的条件下进行计算。
计算概率值P：P的含义。
做出推论：统计学结论和专业结论。
单因素方差分析
方差分析表 （练习，完成该表。例题，写在黑板上）
变异来源 SS
MS
F
P
总变异 148
19-1
组间变异 57
4-1
组内变异
19-4
F0.05（3，15）＝3.29 F与它所对应的P值成反比
常取0.05，区分大小概率事件的标准。 计算统计量F：根据资料的性质选择不同的统计方
法。注意都是在H0成立的条件下进行计算。 计算概率值P：P的含义。 做出推论：统计学结论和专业结论。
四组不同摄入方式人的血浆游离吗啡水平
静脉点滴 肌肉注射 皮下注射 口服
12
12
10
16
7
15
8
9
9
14
均数
10
13
9
12
7
8
6
8
11
10
7
8
9.5
单因素方差分析
完整书写方差分析的过程
建立假设：
H0 ：4组病人血浆游离吗啡水平1 = 2 = 3= 4
H1 ： 4组病人血浆游离吗啡水平的总体均数全不相等或不全 相等
L2-第九章 方差分析
总 N 1 24 1 23
SS处理 ni X i X X i ni C
2 2 i
550.012 537.30 2 618.19 2 726.282 246398.0820 6 6 6 6 3742.5521
在实际运用中，往往将上述过程总结为如下的方差分析
表。
二、方差分析的应用条件 进行方差分析时，数据应满足以下两个应用条件： 1. 各样本是相互独立的随机样本，均服从正态分布。 当样本含量较小时，资料是否来自正态分布的总体难 于进行直观判断和检验，常常根据过去的经验；当样 本含量较大时，无论资料是否来自正态分布总体，数
变异、区组的变异和随机误差三个部分。
数理统计可以证明它们有如下的数量关系。
SS总 SS处理 SS区组 SS误差
总 处理 区组 误差
具体计算公式见下表：
二、随机区组设计资料方差分析的基本步骤 随机区组设计资料的方差分析步骤概括如下： ①. 建立假设 对于处理组 H0：4个总体均数全相等 H1：4个总体均数不等或不全相等 对于区组 H0：6个总体均数全相等 H1：6个总体均数不等或不全相等
bk个格子中，每个格子仅有一个数据Xij(i=1,2,3,,k; j=1,2,3,,b), 而无重复，因此其方差分析属无重复数据 的双向(因素)方差分析(two-way ANOVA)。
一、离均差平方和与自由度的分解 从该例数据表可以看出，随机区组设计资料的总变异 可以分解为：除处理的变异、随机误差外，还可分离 出区组变异。 区组变异 为6个不同窝别家兔血糖浓度值的样本均数
X j 各不相同，即 X j 与总均数 X 的不同。它既包含6个
区组的差异，也包含随机误差，其大小可用区组均方
方差分析
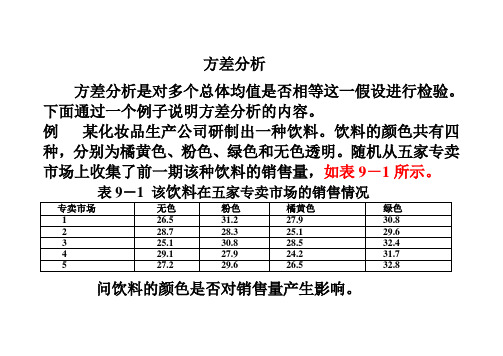
方差分析方差分析是对多个总体均值是否相等这一假设进行检验。
下面通过一个例子说明方差分析的内容。
例某化妆品生产公司研制出一种饮料。
饮料的颜色共有四种，分别为橘黄色、粉色、绿色和无色透明。
随机从五家专卖市场上收集了前一期该种饮料的销售量，如表9－1所示。
问饮料的颜色是否对销售量产生影响。
这是一个方差分析问题，即对四种不同颜色的饮料的销售量均值是否相等进行检验。
我们把四种不同颜色的饮料的销售量均值分别记为1234,,,μμμμ，由题意知，要检验假设0123:H μμμμ=== ； 11234:,,,H μμμμ不全相等如果检验结果为1234,,,μμμμ不全相等，则表明饮料颜色对销售量产生影响。
反之，如果检验结果为123,,μμμ不存在显著影响，则可以认为饮料颜色对销售量没有影响，他们来自于相同的总体。
1.1.2方差分析的基本概念在方差分析中，常常用到一些术语。
我们把要考察的对象的某种特征称为指标。
试验条件分为可控制的和不可控制的两类，称可控制的试验条件为因素；因素所处的状态称为该因素的水平。
如果在一项试验中只有一个因素在变化，称他为单因素试验。
若试验中变化因素多于一个，称他为双因素以及多因素试验。
在上例中，饮料的销售量为指标，饮料的颜色为因素，饮料的四种颜色为该因素的四个水平，该例是一个单因素四水平试验。
上一章所讲的对两个总体均值的比较，实际上就是单因素两水平试验。
下面，我们简单阐述单因素方差分析的基本原理。
1.2单因素方差分析1.2.1 单因素方差分析的基本原理单因素方差分析是研究一个因素的变化对试验指标的影响是否显著的统计分析方法，是方差分析中最简单的情形。
设因素A 有r 个水平12,,,,r A A A 在水平i A (1,2,,)i r = 下进行(2)i n i ≥次独立试验，试验记录如表9－2其中ij X 表示第i 水平i A 进行第j 次试验的可能结果。
假设2~(,)ij i X N μσ，(1,2,,)i r = 。
方差分析原理及应用
组内
78.750 28 2.813
总
268.875 31
F.01(3,28)=4.57
现在是16页\一共有162页\编辑于星期四
2.单因素完全随机区组实验设计
基本原理
研究问题:一个当要研究文章的生
a1 a2 a3 a4
字密度对学生阅读理解的影响。考 组1 3 4 8 9
24
虑到学生智力会对阅读理解产生影 组2 6 6 9 8
导言
方差分析是20世纪20年代英国统计学家发明的，用于两个 及0.9两56个=0以.73上5）样。本由均于数各差种别因的素显的著影性响检，验研（究C4所2=6得，的数据 呈现波动状，造成波动的原因可分成两类，一是不可控 的随机因素，另一是研究中施加的对结果形成影响的可 控因素。方差分析的基本思想是：通过分析研究中不同来
是否等与于A×B） 6.协方差（在一般方差分析中,要求除研究因素之外其他条件保
持不变.如作身高体重关系研究时要消除性别和年级的影响） 7.重复测验（同一文化的不同群体彼此不独立,采用重复测验的方差分析）
现在是10页\一共有162页\编辑于星期四
1.单因素完全随机实验设计
实验设计模式
1.当实验研究的自变量只有一个刺激变量（或由刺激
n
xij
xt
2
n
xij
xj
xj
xt
2
i1
i1
n
2n
2
n
n
2
xij xt xij xj 2xj xt xij xj xj xt
i1
i1
i1
i1
现在是5页\一共有162页\编辑于星期四
方差分析的基本原理
n
因 为 xij x j 0 i 1
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
…
X gng
…
ng X g
…
…
Sg
…
…
合计
X ij
N
X
S
X ij :第i个处理组第j个观察结果
记总均数为X X ij / N ，各处理组均
i 1 j 1
g
ni
数为 X i X ij / ni
j 1
ni
，总例数为N＝
nl+n2+…+ng，g为处理组数。
1.总变异:全部测量值大小不同，这种
计算公式为
( X ij )
j 1 ni 2
SS组间 ni ( X i X )
2 i 1 i 1
g
g
ni
C
组间 g 1
3．组内变异： 在同一处理组中，虽然
每个受试对象接受的处理相同，但测量值 仍各不相同，这种变异称为组内变异（误 差）。组内变异可用组内各测量值 Xij与其 所在组的均数的差值的平方和表示，记为 SS组内, 表示随机误差的影响。
背景
I型错误和II型错误
假设检验是利用小概率反证法思想，根 据P值判断结果，此推断结论具有概率性， 因而无论拒绝还是不拒绝 H0 ，都可能犯错 误。见表3-8。
2
表: 可能发生的两类错误
假设检验的结果 客观实际 拒绝 H0 H0 成立 H0 不成立 即 H1 成立 I 型错误 ( ) 推断正确 (1 ) “接受” H0 推断正确 (1 ) II 型错误 ( )
变异称为总变异。 总变异的大小可以用离均差平方和(sum of squares of deviations from mean，SS)表 示，即各测量值Xij与总均数差值的平方 和，记为SS总。 总变异SS总反映了所有测量值之间总的变 异程度。
计算公式为
SS总 X ij X X ij C
3
I 型错误：“实际无差别，但下了有差别 的结论”，假阳性错误。犯这种错误的概率 是（其值等于检验水准） II型错误：“实际有差别，但下了不拒绝H0 的结论”，假阴性错误。犯这种错误的概率 是（其值未知） 。
但 n 一定时， 增大， 则减少 。
1- ：检验效能（power）:当两总体确有差 别，按检验水准 所能发现这种差别的能力。
也可用于两个
方法：方差分析，即多个样本均数比较 的F检验。 基本思想：根据资料设计的类型及研究 目的，可将总变异分解为两个或多个部 分，每个部分的变异可由某因素的作用 来解释。通过比较可能由某因素所至的 变异与随机误差，即可了解该因素对测 定结果有无影响。
应用条件： 总体——正态且方差相等 2 2 N1 ( 1, ), N2 ( 2 , ), 样本——独立、随机 设计类型： 完全随机设计资料的方差分析 随机区组设计资料的方差分析
SS组内 ( X ij X i )
i 1 j 1
g ni
2
组内 N g
三种变异的关系：
SS总 SS组间 SS组内
总 组间 组内
均方差，均方(mean square，MS)。
MS组间 MS组内
SS组间
组间
SS组内
组内
检验统计量：
4
H1: <0 成立
1
1
界值
意图(以单侧u检验为例)
5
减少I型错误的主要方法：假设检验时设定 值。 减少II型错误的主要方法：提高检验效能。 提高检验效能的最有效方法：增加样本量。
如何选择合适的样本量：实验设计。
6
目的：推断多个总体均数是否有差别。
2 2 i 1 j 1 i 1 j 1
g
ni
g
ni
X C , N 1 总
i, j 2 ij
N
其中：
C
( X ij )
i 1 j 1
g ni
2
N
( X ij )
i, j
N
2
N
2．组间变异： 各处理组由于接受处理
的水平不同，各组的样本均数 (i＝1， 2，…，g)也大小不等，这种变异称为组 间变异。 其大小可用各组均数与总均数的离均差平 方和表示，记为SS组间 。
, N g ( g , )
2
完全随机设计资料的方差分析的基本思想
表 4-1
处理分组 1 水平 2 水平 X11 X21 X12 X22
g 个处理组的试验结果
测量值 … … X1j X2j … …
X 1n1 X 2 n2
统计量 n1 X1 n2
X2
S1 S2
…
g 水平
…
Xg1
…
Xg2
…
…
Xgj
…
MS组间 F , 1 组间 , 2 组内 MS组内 1 2 g ，则 如果 MS组间 , MS组内 都为随 机误差 2 的估计，F值应接近于1。
1, 2 , 如果
, g 不全相等，F值将明显大于1。
用F界值（单侧界值）确定P值。