PP02 电阻电路的等效变换.
电阻电路的等效变换.ppt

i R1
i1
R2
i2
如果两个电阻相等的话,i1=i2=i/2
返 回 上 页 下 页
④功率
p1=G1u2, p2=G2u2,, pn=Gnu2
p1: p2 : : pn= G1 : G2 : :Gn
总功率
p=Gequ2 = (G1+ G2+ …+Gn ) u2 =G1u2+G2u2+ +Gnu2 =p1+ p2++ pn
返 回
例 两个电阻的分压: R1 R2 u1 u u2 u R1 R2 R1 R2
R1 R2
上 页
下 页
④功率
p1=R1i2, p2=R2i2,, pn=Rni2 p1: p2 : : pn= R1 : R2 : :Rn p=Reqi2 = (R1+ R2+ …+Rn ) i2 =R1i2+R2i2+ +Rni2
u u1 uk un
返 回 上 页 下 页
②等效电阻 R1 i Rk Rn 等效 i u + _ Re q _
+ u1 _ + u k _ + un _
+ u 由欧姆定律
u R1i RK i Rni ( R1 Rn )i Reqi
返 回
上 页
下 页
2.2 电路的等效变换
1.两端电路(网络)
任何一个复杂的电路, 向外引出两个端钮,且 从一个端子流入的电流等于从另一端子流出的电流, 则称这一电路为二端网络 (或一端口网络)。 i
i
无 源
无 源 一 端 口
第02章电阻电路的等效变换 54页PPT文档

-
1/3k
1/3k R
1k
1k
+ 3k
E
R
- 3k 3k
例2 计算90电阻吸收的功率
1
10
1 +
20V
-
4 9 90
1
9 9
9
i+
i1
20V 90
-
1 +
4
3 3
3Req11 10 0 9 90 010 Ω
i 2/1 0 0 2 A
i2 =u23 /R23 – u12 /R12 (1) u23Y=R2i2Y – R3i3Y (2)
i3 =u31 /R31 – u23 /R23
u31Y=R3i3Y – R1i1Y i1Y+i2Y+i3Y = 0
由式(2)进行变换: u12Y=R1i1Y–R2i2Y u23Y=R2i2Y – R3i3Y u31Y=R3i3Y – R1i1Y i1Y+i2Y+i3Y = 0
1. 电阻的 、Y形连接
R1
R2
包含 a
R b
1
1 R3
R4
R12
R31
R1
2
3
R2
R3
三端 网络
R23
2
3
形网络
Y形网络
,Y 网络的变形:
型电路 ( 型)
T 型电路 (Y、星型)
注意 这两个电路当它们的电阻满足一定的关
系时,能够相互等效 。
2. —Y 变换的等效条件
+ 1– i1
u12Y=R1i1Y–R2i2Y u23Y=(R2+ R3)i2Y + R3i1Y
电阻电路的等效变换

三. 电阻星形联接、三角形联接旳等效互换 由三角形联接求等效星形联接旳公式
比较(1)式和(4)式,可得:
R1
R12
R31 R12 R23 R31
R2
R12
R23 R12 R23
R31
R3
R12
R23 R31 R23 R31
R12
1
i1
R1
2
R2
i2
R31
R3
R23
i3
3
若 R12=R23=R31=R ,则 R1=R2=R3=RT , 且 RT= (1/3) R 。
在分析含受控源旳电路时,也可用以上多 种等效变换措施化简电路。
但要注意:变换过程中不能让控制变量 消失。
例: 求图示二端 电路旳开路 电压Uab。
解:原电路
4Ω
2Ω
a
2A
+
5Ω
U1
-
2U1 b
4Ω
2Ω
+-
4U1
a
2A
+
5Ω
U1
-
b
Uab 4U1 2 (4 5) U1 2 5 10
Uab 4 10 18 22 (V )
第二章 电阻电路旳等效变换
❖ 2.1 等效二端网络 ❖ 2.2 电压源及电流源串、并联电路旳等效变换 ❖ 2.3 实际电源旳两种模型及其等效变换 ❖ 2.4 电阻星形连接与三角形连接旳等效变换 ❖ 2.5 例题
2.1 等效二端网络
电阻电路
仅由电源和线性电阻构成旳 电路
分析措施
(1)欧姆定律和基尔霍夫定律 是分析电阻电路旳根据;
2.1.2 单口网络端口伏安关系(VAR)旳求取
将单口网络从电路中分离出来,标好其端 口电流、电压旳参照方向;
电阻电路的等效变换(电路分析基础课件)

02
01
等效变换的目的
等效变换的基本原则
电压和电流保持不变
在等效变换过程中,电路中的电压和电流值应保持不变。
元件参数相同
等效变换后的元件参数应与原电路中的元件参数相同。
功率平衡
等效变换后的电路应满足功率平衡条件,即电源提供的功率等于负载消耗的功率。
02
电阻的串并联等效变换
总结词
当多个电阻以串联方式连接时,总电阻值等于各电阻值之和。
详细描述
在并联电阻的等效变换中,总电阻倒数1/R_eq等于各个并联电阻倒数1/R1、1/R2、...、1/Rn之和。这种等效变换在电路分析中非常有用,因为它可以帮助我们简化电路模型。
01
02
03
04
电阻并联的等效变换
串并联电阻的等效变换
总结词:串并联电阻的等效变换是电路分析中的重要概念,它涉及到将复杂的串并联电路简化为易于分析的形式。
等效变换方法:对于非线性电阻电路,可以采用分段线性化方法,将非线性电阻的伏安特性曲线分段近似为直线,然后进行等效变换。
05
等效变换在电路分析中的应用
在计算电流和电压中的应用
总结词:简化计算
详细描述:通过等效变换,可以将复杂的电阻电路简化为简单的电路,从而更容易计算电流和电压。
总结词:提高精度
总结词:扩展应用范围
电阻串联的等效变换
总结词
当多个电阻以并联方式连接时,总电阻值倒数等于各电阻值倒数之和。
详细描述
在电路中,如果多个电阻以并联方式连接,则总电阻的倒数等于各电阻倒数之和。这是因为多个电阻并联时,它们共享相同的电压,因此总电流等于各支路电流之和。
总结词
并联电阻的等效变换可以通过公式1/R_eq = 1/R1 + 1/R2 + ... + 1/Rn表示。
电阻电路的等效变换

B
A
C
A
①电明路确等效变换的条件:
两电路具有相同的VCR; ②电路等效变换的对象:
③电路等效变换的目的: 化简电路,方便计算。
2.2 电阻的等效变换
目的与要求
会对串、并联电路进行分析、计算
重点与 难点
重点: 1.串联分压原理 2.并联分流原理 3.串、并联电路的分析、计算
难点: 网络等效
2.2 电阻的等效变换
u31Y R2 u23Y R1 R1R2 R2R3 R3R1
i3 =u31 /R31 – u23 /R23
根据等效条件,比较式(3)与式(1),得 Y的变换条件:
R 12
R1
R2
R1R 2 R3
R 23
R2
R3
R2R3 R1
R 31
R3
R1
R3R1 R2
ik
inu R1 R2源自RkRn_
(a)各电阻两端为同一电压(KVL); (b)总电流等于流过各并联电阻的电流之和(KCL)。
i = i1+ i2+ …+ ik+ …+in
②等效电阻
i
i
+
i1 i2
ik
in
+
u R1 R2
Rk
Rn 等效 u
Req
_
_
由KCL:
i = i1+ i2+ …+ ik+ …+in
=R1i2+R2i2+ +Rni2
表明 =p1+ p2++ pn
(完整word版)电阻电路的等效变换(word文档良心出品)
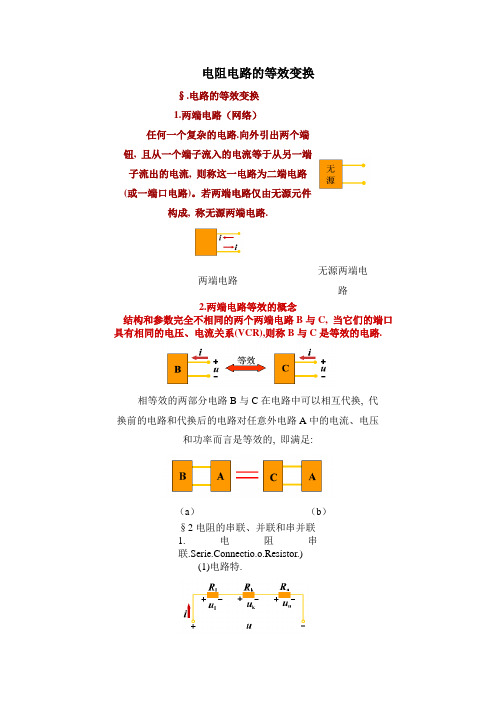
电阻电路的等效变换§.电路的等效变换1.两端电路(网络)任何一个复杂的电路.向外引出两个端钮, 且从一个端子流入的电流等于从另一端子流出的电流, 则称这一电路为二端电路(或一端口电路)。
若两端电路仅由无源元件构成, 称无源两端电路.两端电路无源两端电路2.两端电路等效的概念结构和参数完全不相同的两个两端电路B与C, 当它们的端口具有相同的电压、电流关系(VCR),则称B与C是等效的电路.相等效的两部分电路B与C在电路中可以相互代换, 代换前的电路和代换后的电路对任意外电路A中的电流、电压和功率而言是等效的, 即满足:(a)(b)§2电阻的串联、并联和串并联1.电阻串联.Serie.Connectio.o.Resistor.)(1)电路特.电阻串联图示为n个电阻的串联, 设电压、电流参考方向关联, 由基尔霍夫定律得电路特点:(a) 各电阻顺序连接, 根据KCL知, 各电阻中流过的电流相同;(b) 根据KVL, 电路的总电压等于各串联电阻的电压之和,即:(2)等效电阻把欧姆定律代入电压表示式中得:以上式子说明图(a)多个电阻的串联电路与图(b)单个电阻的电路具有相同的VCR, 是互为等效的电路。
其中等效电阻为:其中等效电阻为:结论:1)电阻串联, 其等效电阻等于各分电阻之和;2)等效电阻大于任意一个串联的分电阻。
(3)串联电阻的分压若已知串联电阻两端的总电压, 求各分电阻上的电压称分压。
由图(a )和图(b)知:满足:结论:电阻串联, 各分电阻上的电压与电阻值成正比, 电阻值大者分得的电压大。
因此串连电阻电路可作分压电路。
例求图示两个串联电阻上的电压。
解: 由串联电阻的分压公式得:(注意U2的方向)(4)功率各电阻的功率为:所以:总功率:从上各式得到结论:1)电阻串连时, 各电阻消耗的功率与电阻大小成正比, 即电阻值大者消耗的功率大;2)等效电阻消耗的功率等于各串连电阻消耗功率的总和。
电路原理02电阻电路的等效变换

12V
求 I1,I4,U4。 解:①分流方法
2R
U1 2R
U2 2R
U4
1 1 1 1 12 3 I 4 I 3 I 2 I1 2 4 8 8 R 2R
U4 I4 2R 3V
②分压方法
I1 12 R
3 I4 2R
def
结论:串联电路的总电阻等于各分电阻之和。
3. 串联电阻的分压(voltage division)公式
uk Rk i Rk Rk Rk n uk n u u Req i Req Rj Rj
j 1
j 1
u
i u1 un R1 Rn
串联电阻中的某个电阻的电压与该电阻成正比。 例1 两个电阻分压,如下图: u
二、电阻的串联(Series Connection of Resistors) R1 Rk Rn 等效 i i u1 uk un
1. 电路特点: (a)各电阻顺序连接,流过同一电流(KCL); (b)总电压等于各串联电阻的电压之代数和(KVL)。 2. 等效电阻Req 由欧姆定律 u
1 / R2 R1 i2 i i 1 / R1 1 / R2 R1 R2 (注意方向!)
4. 功率关系
p1 G1u2, ,pn Gnu2 p1: :pn G1: :Gn
总功率
p Geq u2 (G1 G2 Gn )u2 G1u2 G2 u2 Gn u2 p1 p2 pn
图(a)
R
uS
i
1
u
Req
电阻电路的等效变换

电阻电路的等效变换电阻电路的等效变换是指将一个电阻电路转化为另一个等效的电阻电路,使得两个电路在电学性质上完全相同。
等效变换在电路分析和设计中起着重要的作用,能够简化电路分析过程,提高计算效率。
一、串联电阻的等效变换串联电阻是指多个电阻按顺序连接在一起,电流依次通过每个电阻。
当电路中有多个串联电阻时,可以通过等效变换将其转化为一个等效电阻。
假设有两个串联电阻R1和R2,其等效电阻为Req。
根据欧姆定律可知,串联电阻中的电流相同。
根据电阻的定义可知,电阻与电流和电压之间存在线性关系,即R = U / I。
因此,R1和R2的电阻值可以表示为R1 = U / I1,R2 = U / I2。
在串联电路中,电流I1通过R1,电流I2通过R2,由于串联电路中电流只有一个路径,所以I1 = I2。
将上述两个等式相等,可得到R1 / I1 = R2 / I2,即R1 / R2 = I1 / I2。
由此可推导出串联电阻的等效电阻为Req = R1 + R2。
二、并联电阻的等效变换并联电阻是指多个电阻同时连接在一起,电流分别通过每个电阻。
当电路中有多个并联电阻时,可以通过等效变换将其转化为一个等效电阻。
假设有两个并联电阻R1和R2,其等效电阻为Req。
根据欧姆定律可知,电压在并联电路中相同。
根据电阻的定义可知,电阻与电流和电压之间存在线性关系,即R = U / I。
因此,R1和R2的电阻值可以表示为R1 = U1 / I,R2 = U2 / I。
在并联电路中,电压U1作用在R1上,电压U2作用在R2上,由于并联电路中电压相同,所以U1 = U2。
将上述两个等式相等,可得到R1 / U1 = R2 / U2,即R1 / R2 = U1 / U2。
由此可推导出并联电阻的等效电阻为1 / Req = 1 / R1 + 1 / R2。
三、星型-三角形转换星型电阻网络和三角形电阻网络是常见的电阻网络拓扑结构。
在电路分析中,有时需要将星型电阻网络转换为三角形电阻网络,或将三角形电阻网络转换为星型电阻网络,以便于进行电路分析。
第二章电阻电路的等效变换2019 32页PPT

返回 下页 上页
§ 2-3 电阻的串联和并联
一、 电阻串联 ( Series Connection of Resistors )
R1
Rk
Rn
i
+ u1 _ + uk _ + un _ 等效 i
+
u
_
Requ i iuk Rk
+
Req
u
_
串联电路的总电阻等于各分电阻之和。
返回 下页 上页
等效电阻Req具体求解思路:
13
3R
返回 下页 上页
应用举例:
1k
1k 1k
E
1k R
1KΩ
Req
35R 53R
1/3k 1/3k
1/3k
E
1k
R
1k 3k
R E
3k 3k
返回 下页 上页
§ 2-5 电压源、电流源的串联和并联
一. (理想)电压源的串、并联
串联
+
º
º
uS1 _
+
n
+
uS _
us usk
uSn _
k 1
并联
º
I º
º ( 注意参考方向)
I º
+
+
uS _ uS _
+ uS _
只有电压相等且极 性一致的电压源才
允许并联,而各个
º
º 电压源支路对应的
注意:电压源与任意元件的并联对外均可 电流无法确定。
等效为此电压源。
返回 下页 上页
二. (理想)电流源的串、并联
并联: 可等效成一个理想电流源 i S( 注意参考方向).
电阻电路的等效变换ppt课件

30
编辑版pppt
桥式电路:
a
R
Req R
R
R
b
R
(c)
a
R
RR
R
b
R R
a
R
R eq(RR )//(RR )R
R
R
R
b
31
编辑版pppt
2.4 电阻的Y— 等效变换
1
+
–
i1Y
u12Y
R1
u31Y
u12
+ i1
R12
1–
u31 R31
R2 – i2Y
2+
u23Y
R3
i3Y +
i2
–
–3
2+
9
9
ba
9
9
9
b
R a b(9//9//9 )91 2
21
编辑版pppt
a 20
b 100 10
40 80 60 50
(c)
ab
20 100 100
ab 20 100
60 120 60
ab 20 100
60 40
R a b (1 0 0//1 0 0 ) 2 0 7 0
22
编辑版pppt
5
15 6
ReqR2//(R1R3)R R2 2(R R 11 R R 3)3
Req
R1 R2 R3
ReqR1R2//R3R1RR 22RR 33
20
编辑版pppt
例2:求下图所示各电路ab端的等效电阻Rab
a
9
18
18
9
4
15
4
第2章电阻电路的等效变换

类似可得到由∆ 接的变换结果: 类似可得到由∆接→ Y接的变换结果: 接的变换结果
G12G31 G1 = G12 + G31 + G23 G23G12 G2 = G23 + G12 + G31 G31G23 G3 = G31 + G23 + G12
R R 12 31 R = 1 R + R23 + R 12 31
返回
§2.2 电路的等效变换
1
+ us 等效
1
+ us
Req
1′
-
1′
返回
§2.3 电阻的串联和并联
一、 电阻串联 ( Series Connection of Resistors ) 1. 电路特点 电路特点: i + R1 Rk Rn
+ u1 _ + uk _ + un _ u _
(a) 各电阻顺序连接,流过同一电流 (KCL); 各电阻顺序连接, ; (b) 总电压等于各串联电阻的电压之和 总电压等于各串联电阻的电压之和(KVL)。 。
1
U12
R2 2
R1 R3
Y-∆ 等效变换 ∆
1
U12
3
R12
2
R31 R23
3
当R1=R2=R3=RY
当R12 = R23 =R31 =R∆
R∆ = 3R Y
1 R = R∆ Y 3
例: 对图示电路求总电阻 12 对图示电路求总电阻R
1 1 2Ω Ω R12 2Ω Ω 2 1 0.8Ω Ω R12 2.4Ω Ω 1Ω Ω 2 1.4Ω Ω 2 1Ω Ω 1 2.684Ω Ω 1Ω Ω 2Ω Ω R12 1Ω Ω 2 0.4Ω Ω 0.8Ω Ω 0.4Ω Ω
【人大名师精品课件】电路第2讲电阻电路的等效变换

Req=( R1+ R2 +…+Rn) = Rk 结论: 串联电路的总电阻等于各分电阻之和。
电阻电路
的等效变换
3.串联电阻上电压的分配
由
uk Rk i Rk u Reqi Req
Rk
n
Rj
ºi +
+ u_1
R1
即 电压与电阻成正比
j1
故有
uk
Rk
n
u
u+ _ u_n
Rn
Rj
º
R R串 4 4 4 2 R串 4 4 4
电阻电路 的等效变换
例3. 40
º
R
30
º
30
R
40 2
30 3
30
40 º
40
30 R
30
º
30
电阻电路 的等效变换
例4.
+ 12V _
I1 I2 R I3 R
+
+
2R U_1 2R U_2 2R
总功率
p =p1+ p2++ pn =G1u2+G2u2+ +Gnu2 = (G1+ G2+ …+Gn ) u2 =Gequ2
电阻电路 的等效变换
四、电阻的串并联 (混联)
关键:弄清楚串、并联的概念
例2. º
4 2
3
R
6
º 63 R串 6 3 2 4
º 2
Hale Waihona Puke 4R6 3
Y形网络
下面要证明:这两个电路当它们的电阻满足一定的关系时, 是能够相互等效的。
大学物理-电阻电路的等效变换PPT课件

Rk
Rn
i
+ u1 _ + uk _ + un _ 等效 i
+
u
_
结论:串联电路的总电阻等于各分电阻之和。
2021/7/22
+
Req
u
_
8
串联电阻上电压的分配
uk
Rk u, Req
k1,2,n
例:两个电阻分压, 如下图
i
++
u
u1 +
R1
_
u2
R2
u1
R1 R1 R2
u
u2
R2 R1 R2
+ i3Y R3 3
–
R1
u12Y
u23Y
R2 i2Y –
2+
等效的条件: 如果 u12 = u12Y , u23 = u23Y , u31 = u31Y
有 i1 = i1Y , i2 = i2Y , i3 = i3Y ,
则两种结构可以相互变换
2021/7/22
17
– i1 u31 R31
+ 1
ik
in 等效 +
u R1 R2
Rk
Rn
u
Req
_
_
2021/7/22
11
并联电阻的电流分配
ik
Gk Geq
i
对于两电阻并联,
i
i1
i2
R1
R2
功率关系
i11/R 1 1/ R 11/R 2iR 1R 2R 2i i21/R 11/R 12/R2iR1R 1R2i
p1=G1u2, p2=G2u2,, pn=Gnu2
