奇偶性导学案普通班用导学案
2023年人教版数学五年级下册第6课奇数和偶数的运算性质导学案(精选3篇)

人教版数学五年级下册第6课奇数和偶数的运算性质导学案(精选3篇)〖人教版数学五年级下册第6课奇数和偶数的运算性质导学案第【1】篇〗《奇数和偶数的运算性质》教学设计【教学内容】数的奇偶性(教材第15页例2,以及第16~17页练习四第4~7题)。
【教学目标】1.经历探索加减法中数的奇偶性变化的过程,在活动中发现加法中的数的奇偶性的变化规律,在活动中体验研究方法,提高推理能力。
2.使学生体会到生活中处处有数学,增强学好数学的信心和应用数学的意识。
【重点难点】1.探索并理解数的奇偶性。
2.能应用数的奇偶性分析和解释生活中一些简单问题。
教学过程:【复习导入】师:在学习2、5的倍数特征时,我们已经知道什么是奇数和偶数,请看大屏。
把下面各数分别填在合适的圈里。
那么谁能回答一下,什么叫做奇数?奇数有什么特征?什么叫做偶数?偶数有什么特征?生说师大屏出示。
那么,奇数和偶数的运算会有那些特征呢?这节课我们就来进一步研究奇数和偶数。
板书课题《奇数和偶数的运算性质》【新课讲授】1.出示例2:奇数与偶数的和是奇数还是偶数?奇数与奇数的和是奇数还是偶数?偶数与偶数的和呢?这道题用算式怎么表示?奇数+偶数=?奇数+奇数=?偶数+偶数=?大屏出示:2、学生独立猜想,小组内汇报交流,然后统一意见进行验证(要求:验证时多选择几组进行证明)。
教师根据学生汇报总结方法如下:方法一:利用奇数和偶数的意义,奇数除以2都余1,而偶数除以2没有余数,奇数加偶数的和除以2还余1。
所以:奇数+偶数=奇数,奇数+奇数=偶数,偶数+偶数=偶数;方法二:利用算式寻找规律(大屏出示)例如:5+8=13, 7+8=15…… 5+7=12,7+9=16…… 8+12=20,12+24=36……通过上面的算式发现:奇数与偶数的和是奇数,奇数与奇数的和是偶数,偶数与偶数的和是偶数。
所以,奇数+偶数=奇数,奇数+奇数=偶数,偶数+偶数=偶数。
师:你能举几个例子说明一下吗?(学生的举例可以引导从正反两个角度进行)3、刚才我们探究出了奇数和偶数的和的奇偶性,那奇数和偶数的差的奇偶性有什么规律呢?你是怎么想的?你能举例说明你得出的结论吗?生说师大屏出示。
2023年人教版数学五年级下册奇数和偶数的运算性质导学案(优选3篇)

人教版数学五年级下册奇数和偶数的运算性质导学案(优选3篇)〖人教版数学五年级下册奇数和偶数的运算性质导学案第【1】篇〗《数的奇偶性》教学设计教学目标:1.通过观察、分析、讨论、归纳、猜想的研究方法,小组合作研究发现数的奇偶性。
2.经历探索加法中数的奇偶性变化过程,在活动重视学生体验探究方法。
3.培养学生分析、解决问题的能力。
教学重难点:探索加法中数的奇偶性变化规律。
教法:情境教学法学法:小组合作观察探究教具准备:教学挂图纸杯教学过程:课前活动游戏1:翻手腕活动。
游戏2:以开火车,各大组报数,记好各自的序号,以游戏的形式复述奇数和偶数的相关知识为本节课的教学做铺垫。
上课一、创生活情境,感受生活中的奇偶性1.谈话引入。
同学们,从开学那天起,我们每天都要在家到学校的路上来回走动,可就在来回走的过程中,只要你们用心观察,就能发现许多跟奇偶数相关的知识。
2.请一位同学来演示。
从讲台一端走(家)到另一端(学校),再按原路返回。
问:走5次后,这位同学在哪里?猜想:走12次后,这位同学会在哪里?师:光有猜想是不够的,我们还得想办法来验证一下自己的猜想是否正确。
3.尝试解答。
你是怎样想的?先各自在草稿上把自己的想法表示出来。
教师指导:用列表或画图的方法进行。
4.同桌交流。
5.全班反馈。
结论:走奇数次后,同学在(学校),走偶数次后,同学在(家里)。
二、解决生活中简单的奇偶性问题1.同桌翻纸杯游戏:游戏规则:(1)同桌合翻一个纸杯,第一位同学翻1次杯口朝下,第二位同学2次杯口朝上,这样轮流翻下去。
(2)每完成一个任务前,可先猜想一下纸杯可能在谁的手中,然后再动手验证。
(3)讨论时,同桌的交流不得让别的小组听到。
问题:翻动10后,杯口朝(),翻动19次后杯口朝()。
2.阅读课本上主题图。
快速作答:摆渡100次后,船在()岸。
摆渡133次后,船在()岸。
3.你能联系生活提出类似的问题吗?(上下楼梯、开关电灯、翻硬币、开关门、钓鱼、拉抽屉等)4.从刚才的几个活动中,你能解决类似的生活问题了吗?解决问题的关键是要弄清什么?(奇数次时是什么状况,偶数次时又是什么状况。
《函数的奇偶性》导学案

学习目标:1,初步理解奇函数、偶函数、函数的奇偶性的概念;2,掌握判断一些简单函数奇偶性的方法.《函数的奇偶性》导学案(一)一、课前预习1.画出函数()()xx f x x f 12==与,从对称的角度观察其图像特点.2.分析函数()2x x f =的图像,比较()()x f x f -与的关系.x……-3-2-10123……2x y =类比:()xx f 1=呢?3.给出奇函数、偶函数的概念:(1)偶函数一般地,对于函数()f x 的定义域内的,都有,那么函数()f x 就叫做偶函数.偶函数的图像关于对称(2)奇函数一般地,对于函数()f x 的定义域内的,都有,那么函数()f x 就叫做奇函数.奇函数的图像关于对称判断:①奇、偶函数的定义域都关于原点对称.()②对于定义在R 上的函数()f x ,若()()11f f -=-,则函数()f x 一定是奇函数.()由此,判断函数的奇偶性:图象法(形),定义法(数)二、项目一会判断函数的奇偶性1.判断下列函数的奇偶性:⑴()1f x x x =+⑵()11f x x x =+--()1,0x x -+<⎪⎩方法总结:用定义法判断函数的奇偶性:①先验证是否关于对称,②验证与的关系,③根据定义下结论.练习:判断下列函数的奇偶性:⑴()4223f x x x =+⑵()32f x x x =-⑶()21x f x x +=⑷()23f x x x =-+三、当堂检测1.对于定义域是R 的任意奇函数()f x 有().A.()()0f x f x --=B.()()0f x f x +-=C.()()0f x f x -= D.(0)0f ≠2.下列说法错误的是().A.1()f x x x =+是奇函数B.()|2|f x x =-是偶函数C.()0,[6,6]f x x =∈-既是奇函数,又是偶函数D.32()1x x f x x -=-既不是奇函数,又不是偶函数3.函数()|2||2|f x x x =-++的奇偶性是.项目总结:用定义法判断函数奇偶性的一般步骤:课后反思:。
3.2.2奇偶性(一)导学案高一上学期数学人教A版(2019)

【学习目标】1. 能结合具体函数,了解奇偶性的概念和几何意义2. 能根据函数奇偶性的定义判断和证明函数的奇偶性3. 了解奇偶函数图象的特征,掌握奇偶性的简单应用 【重、难点】重点: 函数奇偶性的概念与判断 难点: 函数奇偶性的应用 【学习过程】导:前面我们学习了函数单调性的概念,利用函数图象在定义域的某个区间上“上升”或“下降”研究了函数的单调性和最值,函数是否还有其他性质呢?我们继续研究函数的其他性质—奇偶性。
思:问题1 我们首先观察()2f x x =和()2g x x =-的图像,你能发现这两个函数有什么共同特征吗?类比函数单调性,你能用符号语言精确地描述“函数关于y 轴对称”这一特征吗? x ... 3 2 1 0 1 2 3 ... ()2f x x = ... ... ()2g x x =- ... ...偶函数:一般地,设函数()f x 的定义域为D,如果∀x ∈D ,都有______,且 ,那么函数()f x 叫做偶函数,函数图象关于 对称。
结论:1、偶函数)(x f 满足两个条件:(函数定义域为D )(1)∀x ∈D ,都有______⇔定义域关于 对称 (2)、=-)(x f2、函数()f x 是偶函数⇔()f x 的图象关于 对称 练习1.(1)()(1)(1),()y f x x R f f f x =∈-=函数,,是偶函数吗? (2)[]2(),1,2f x x x =∈-函数是偶函数吗?为什么?问题 2 观察函数()f x x =和1()f x x=的图象,你能发现这两个函数图象有什么共同特征吗?你能用符号语言精确地描述这一特征吗?我们取一些特殊值,观察一下相应的函数值:x ... 3 2 1 0 1 2 3 ... ()f x x = ... ... 1()f x x= ......f x ,那么函数()f x 叫做奇函数,函数图象关于 对称。
结论:奇函数)(x f 满足两个条件:(函数定义域为D )(1)∀x ∈D ,都有______⇔()f x 定义域关于 对称 (2)、=-)(x f(2)函数()f x 是奇函数⇔()f x 的图象关于 对称问题3判断函数奇偶性的一般步骤可归纳为: ① ;② 题型一 具体函数的奇偶性判断 例1.判断下列函数的奇偶性:(1) 21)(x x f =; (2) 1)(2+=x x f ; (3) ⎩⎨⎧<+->+=0,10,1)(x x x x x f题型二 抽象函数奇偶性判断例2.定义在[][]3113-,,上的函数(x f 是偶函数,且f(3)=3,f (1)=2,其部分图象如图所示:根据图像可知函数)(x f 的递增区间为 ;最大值= ;最小值= 题型三 奇偶函数图像及应用例 3.(1)已知)(x f y =是R 上的奇函数,且6)3(=f ,则)3-f 的值为________,f(0)= ______.(2)若函数b a x x f ++3)(2是偶函数,定义域为[]a a 2,1-,则b a +=______ ______题型四 利用函数的奇偶性求解析式例(1) 函数f (x )是定义域为R 的奇函数,当x >0时,f (x )=-x +1,求当x <0时,f (x )的解析式.(2)已知函数f (x )是定义域为R 的偶函数,当x ≥0时,f (x )=x 2-2x .求出函数f (x )在R 上的解析式;题型五 利用函数的奇偶性与单调性比较大小例 (1)设偶函数f (x )的定义域为R ,当x ∈[0,+∞)时,f (x )是增函数,则f (-2),f (π),f (-3)的大小关系是(2)已知偶函数f (x )在[0,+∞)上单调递减,则f (1)和f (-10)的大小关系为题型六 利用函数的奇偶性与单调性解不等式 例3 (1)已知f (x )是定义在R 上的偶函数,且在区间(-∞f (-3)=0,则f (x )x <0的解集为________. (2)已知函数f (xf (a -2)+f (3-2a )<0,试求a 的取值范围. 奇偶性课时作业 1.下列图象表示的函数具有奇偶性的是( ) 2.函数x x x f 1)(3+=的图象关于( ) A .原点对称 B .y 轴对称 C .x y =对称 D .x y -=对称 3.设函数f (x )=⎩⎨⎧x 2+x ,x ≥0,g (x ),x <0,且f (x )为偶函数,则g (-2)等于( ) A.6 B.-6 C.2 D.-2 3.已知奇函数f (x )在区间[0,+∞)上单调递增,则满足f (x )<f (1)的x 的取值范围是( ) A.(-∞,1) B.(-∞,-1) C.(0,1) D.[-1,1)4.已知f (x ),g (x )分别是定义在R 上的偶函数和奇函数,且f (x )-g (x )=x 3+x 2+1,则f (1)+g (1)等于( )5.若函数f (x )是R 上的偶函数,且在区间[0,+∞)上是增函数,则下列关系成立的是( ) A.f (-3)>f (0)>f (1) B.f (-3)>f (1)>f (0) C.f (1)>f (0)>f (-3) D.f (1)>f (-3)>f (0)6.已知函数y =f (x )是R 上的偶函数,且f (x )在[0,+∞)上是减函数,若f (a )≥f (-2),则a 的取值范围是( )A.a ≤-2B.a ≥2C.a ≤-2或a ≥2D.-2≤a ≤27.已知函数y =f (x )是偶函数,其图象与x 轴有4个交点,则方程f (x )=0的所有实根之和是( )8.设奇函数f (x )在(0,+∞)上为减函数,且f (1)=0,则不等式f (x )-f (-x )x<0的解集为( )A.(-1,0)∪(1,+∞)B.(-∞,-1)∪(0,1)C.(-∞,-1)∪(1,+∞)D.(-1,0)∪(0,1)9(多选).已知函数()f x 在[]5,5-上是奇函数,()f x 在[]0,5上是单调函数,且()()42f f -<-,则下列不等式一定成立的是( )11.已知)(x f 为奇函数,且当()().______1,102=-+=>f xx x f x 则时,12.若)4)(()(-+=x a x x f 为偶函数,则实数a =________. 13.若函数f (x )=(k -2)x 2+(k -1)x +3是偶函数,则f (x )的单调递减区间是______.14已知偶函数f (x )在区间[0,+∞)上单调递增,则满足f (2x -1)<f ⎝ ⎛⎭⎪⎫13的x 的取值范围是________.15(1).已知函数y =f (x )的图象关于原点对称,且当x >0时,f (x )=x 2-2x +3.(1)试求f (x )在R 上的解析式; (2)画出函数的图象,根据图象写出它的单调区间.16.已知函数f (x )=ax +b x +c (a ,b ,c 是常数)是奇函数,且满足f (1)=52,f (2)=174. (1)求a ,b ,c 的值; (2)试判断函数f (x )在区间⎝⎛⎭⎪⎫0,12上的单调性并证明.。
2024年人教版数学五年级下册奇数和偶数的运算性质导学案精选3篇

人教版数学五年级下册奇数和偶数的运算性质导学案精选3篇〖人教版数学五年级下册奇数和偶数的运算性质导学案第【1】篇〗教学内容:义务教育课程标准实验教科书北师大版数学五年级上册第14-15页。
教学目标:1、使学生尝试运用“列表”、“画示意图”等方法发现规律,运用数的奇偶性解决生活中的一些简单问题。
2、让学生经历探索加法运算中数的奇偶性变化的过程,发现数的奇偶性的变化规律。
3、在活动中培养等毛生的观察、推理和归纳能力。
4、学生通过自主探索发现规律,感受数学内在的魅力,培养学生学习数学的兴趣。
教学重点:探索数的奇偶性变化规律。
教具学具准备:数字卡片,盒子,奖品。
教学过程:复习引入新课。
(通过引导学生回忆、提问或列举等形式,复习奇、偶数的意义。
)活动1:数的奇偶性在生活中的应用。
(一)激趣导入。
清早,笑笑第一个走进了教室,像往常一样把门打开后就去开灯,结果灯未亮,于是,他自言自语地说了声“停电了”就走到座位上坐下。
不一会儿,同学们陆陆续续来到了教室,看到教室里光线有些暗,都下意识地伸手去按电灯开关,却都像笑笑一样无奈地走回自己的座位。
你知道第11个同学按过开关后,“开关”是打开的还是关闭了?(二)自主探究,发现规律。
1、学生独立思考后进行汇报交流。
方法:用文字列举出开、关的情况开、关;开、关;开、关;开、关;开、关;开、关……让学生数数,直观地发现第11个人按过开关后,开关是打开的。
2、增加人次,深入探究。
如果是第47个同学或第60个同学进去,用列举的方法判断“开关”的开、关情况还方便吗?你还能想出什么好方法?3、第二次汇报交流。
投影下表:用列表的方法启发学生总结规律并作答:当人数是1、3、5、7……的时候,开关处于开启状态,而当人数是2、4、6、8……的时候,开关处于关闭状态。
即,进来的是奇数个同学时,开关被打开;进来的是偶数个同学时,开关被关闭。
因为47是奇数,开关被打开;108是偶数,开关被关闭。
(三)巩固应用。
1.3.2奇偶性(1)导学案
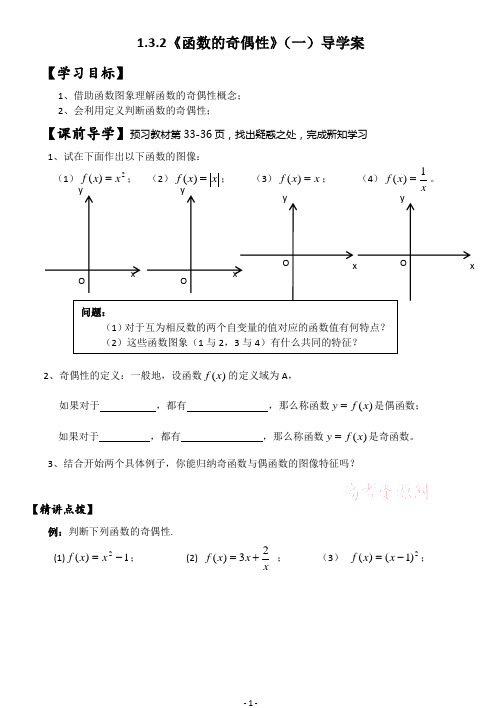
1.3.2《函数的奇偶性》(一)导学案【学习目标】1、借助函数图象理解函数的奇偶性概念;2、会利用定义判断函数的奇偶性;【课前导学】预习教材第33-36页,找出疑惑之处,完成新知学习1、试在下面作出以下函数的图像:(1)2)(x x f =; (2)x x f =)(; (3)x x f =)(; (4)x f 1)(=。
2、奇偶性的定义:一般地,设函数)(x f 的定义域为A ,如果对于 ,都有 ,那么称函数)(x f y =是偶函数; 如果对于 ,都有 ,那么称函数)(x f y =是奇函数。
3、结合开始两个具体例子,你能归纳奇函数与偶函数的图像特征吗?【精讲点拨】例:判断下列函数的奇偶性.(1)1)(2-=x x f ; (2) xx x f 23)(+= ; (3) 2)1()(-=x x f ;(4)2211(0)2()11(0)2x x g x x x ⎧+>⎪⎪=⎨⎪--<⎪⎩ ; (5) 1122-+-=x x y .1. 你能小结用定义判断函数奇偶性的方法步骤吗?2. 奇(偶)函数的性质:①f(x)为奇函数,定义域为D ,若0∈D ,则必有 ;② 在同一个关于原点对称的定义域上,奇函数+奇函数= ; 偶函数+偶函数= ;奇函数×奇函数= ; 偶函数×偶函数= 。
③对于分段函数的奇偶性的判断,须特别注意与-x 的对应关系。
【巩固练习】1、若函数()f x 为奇函数,且(2)3f =,则(2)f -=________;若函数()f x 为偶函数,且(1)3f -=,则(1)f =________。
2、已知定义在[-5,5]上的奇函数)(x f 的部分图像如右图所示,试画出函数在y 轴左侧的大致图像,且满足0)(>x f 的x 的集合为____ _____;满足不等式()0xf x <的集合为____ ____;满足不等式(2)0f x +<的集合为____ _____;3、对于定义域是R 的任意奇函数()f x 有( ).A .()()0f x f x --=B .()()0f x f x +-=C .()()0f x f x -=D .(0)0f ≠4、 已知()f x 是定义(,)-∞+∞上的奇函数,且()f x 在[)0,+∞上是减函数. 下列关系式中正确的是( )A. (5)(5)f f >-B.(4)(3)f f >C. (2)(2)f f ->D.(8)(8)f f -=5、下列说法错误的是( ). A. 1()f x x x=+是奇函数 B. ()|2|f x x =-是偶函数 C. ()0,[6,6]f x x =∈-既是奇函数,又是偶函数 D.32()1x x f x x -=-既不是奇函数,又不是偶函数 6、判断下面函数的奇偶性:(1)221)(x x x f +=; (2) x x x f 5)(3+=; (3) ⎩⎨⎧<-≥+=0),1(0),1()(x x x x x x x f ;。
《奇偶性》教学设计导学案

《奇偶性》教学设计导学案
活动二:
用图形说明,结合图形尝试用字母表示数,如用2n+1表示奇数,用2m表示偶数,将数与形结合起来理解。
所以,奇数+偶数=奇数奇数+奇数=偶数偶数+偶数=偶数
三、拓展提升,深化认识
◎教学笔记师:两个自然数相加,和的奇偶性我们可以确定,如果是
多个自然数相加呢?
(1)偶数+偶数+偶数+…+偶数
(2)奇数+奇数+奇数+…+奇数
发现:不管多少个偶数相加,和都是偶数;奇数个奇数相加和是奇数;偶数个奇数相加和是偶数。
师:如果一组自然数相加,其中有偶数,也有奇数,在确定和的奇偶性时,该怎么办?
小组讨论后交流探讨。
小结:多个自然数相加,就看加数中奇数的个数,如果加数中有奇数个奇数,和就是奇数;有偶数个奇数,和就是偶数。
四、运用规律,内化规律
1.解决基本问题。
学生自主解答。
全班交流展示,课件呈现解答过程。
《函数的奇偶性》导学案
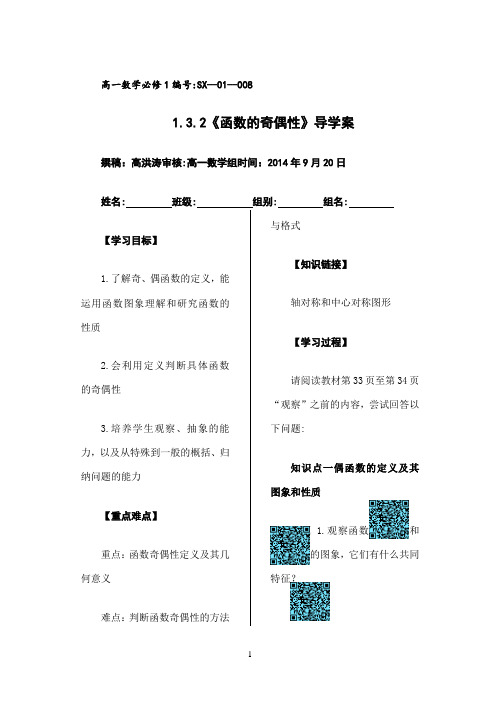
高一数学必修1编号:SX--01--0081.3.2《函数的奇偶性》导学案撰稿:高洪涛审核:高一数学组时间:2014年9月20日姓名: 班级: 组别: 组名:【学习目标】1.了解奇、偶函数的定义,能运用函数图象理解和研究函数的性质2.会利用定义判断具体函数的奇偶性3.培养学生观察、抽象的能力,以及从特殊到一般的概括、归纳问题的能力【重点难点】重点:函数奇偶性定义及其几何意义难点:判断函数奇偶性的方法与格式【知识链接】轴对称和中心对称图形【学习过程】请阅读教材第33页至第34页“观察”之前的内容,尝试回答以下问题:知识点一偶函数的定义及其图象和性质问题 1.观察函数和的图象,它们有什么共同特征?问题2:计算:,;,。
,;,。
通过计算,你有什么发现?问题3.通过对问题1和问题2的研究,回答什么样的函数叫做偶函数?其图象有何特征?问题4.观察图象并回答,下列哪些函数是偶函数?问题5.由问题4观察思考:函数为偶函数时定义域有何特征?请阅读教材第34页至第35页“例5”前面的内容,回答下列问题:知识点二奇函数的定义及其图象和性质问题 1.观察函数与的图象,它们有什么共同特征?问题 2.当自变量任取一对相反数时,函数值有什么特征?问题3.通过对问题1和问题2的研究,回答什么样的函数叫做奇函数?其图象有何特征?问题4.观察图象并回答,下列哪些函数是奇函数?问题5.由问题4思考:函数为奇函数时,定义域有何特征?请阅读教材35页例5,回答下列问题:知识点三定义法判断函数的奇偶性问题1:①若,其定义域为____,且_____,则_____,该函数为_____函数。
②若,其定义域为________,且_____,则_____,该函数为_____函数。
问题 2.尝试总结定义法判断函数奇偶性的一般步骤。
【基础自测】A1.尝试用定义法判断下列函数的奇偶性①;②;③;④.B2.设函数为奇函数,若,则_____.C3.已知偶函数在上为增函数,则和的大小关系是()A.B. C.= D.无法确定【课堂小结】1.知识小结:奇函数和偶函数的定义:奇函数和偶函数的图象特征:2.方法小结:定义法判断函数奇偶性的步骤:【当堂检测】判断下列函数的奇偶性:A1.B2.【课后反思】本节课我最大的收获是:_________________________________________ _____________________________ ______________________我还存在的疑惑是:_____________________________________________ _____________________________ ______________________我对导学案的建议是:____________________________________________ _____________________________ ______________________。
《函数的奇偶性》导学案

《函数的奇偶性》导学案一、学习目标1、理解函数奇偶性的概念,能够根据函数的解析式和图象判断函数的奇偶性。
2、掌握函数奇偶性的判定方法,会利用奇偶性的定义证明函数的奇偶性。
3、了解函数奇偶性的性质,能运用函数的奇偶性解决一些简单的问题。
二、学习重点1、函数奇偶性的概念和判定方法。
2、利用函数奇偶性的性质解决问题。
三、学习难点1、对函数奇偶性概念的理解。
2、函数奇偶性的判定和性质的综合应用。
四、知识回顾1、函数的定义:设 A、B 是非空的数集,如果按照某个确定的对应关系 f,使对于集合 A 中的任意一个数 x,在集合 B 中都有唯一确定的数 f(x)和它对应,那么就称 f:A→B 为从集合 A 到集合 B 的一个函数。
2、函数的图象:对于一个函数 y = f(x),如果把定义域内每一个自变量 x 的值和对应的函数值 y 组成的有序数对(x, y),都作为点的坐标,在平面直角坐标系中描出这些点,就得到函数 y = f(x) 的图象。
五、新课导入观察以下函数的图象:1、函数 f(x) = x²的图象关于 y 轴对称。
2、函数 f(x) = x³的图象关于原点对称。
思考:函数的图象具有这样的对称性,那么函数的解析式又有怎样的特点呢?六、概念讲解1、偶函数一般地,如果对于函数 f(x) 的定义域内任意一个 x,都有f(−x) =f(x),那么函数 f(x) 就叫做偶函数。
例如,函数 f(x) = x²,对于定义域内任意一个 x,都有f(−x) =(−(−x)²= x²= f(x),所以 f(x) = x²是偶函数。
2、奇函数一般地,如果对于函数 f(x) 的定义域内任意一个 x,都有f(−x) =−f(x),那么函数 f(x) 就叫做奇函数。
例如,函数 f(x) = x³,对于定义域内任意一个 x,都有f(−x) =(−x)³ =−x³ =−f(x),所以 f(x) = x³是奇函数。
函数奇偶性导学案

1.3.2函数的奇偶性导学案【学习目标】1.全部学生理解函数奇偶性的定义,了解什么是奇函数,什么是偶函数2.绝大部分学生能够根据函数图像及解析式判断函数的奇偶性3.绝大多数同学在快乐学习的过程中领会合作探究的精神,初步掌握研究问题的方法。
【学习过程】任务1:理解奇函数和偶函数的定义练习:根据下列函数图象,判断函数奇偶性.小结:由图像判断函数的奇偶性步骤:① ②]2,1[,)(2-∈=x x x f ]1,21()21,1[,)(3-∈=x x x f 112)(2+=x x f x任务3:根据奇偶函数定义,判断函数的奇偶性例2 利用定义判断下列函数中哪些是偶函数,哪些是奇函数练习:利用定义判断下列函数中哪些是奇函数,哪些是偶函数。
小结:由定义判断函数的奇偶性步骤:① ②()()()()()()()()()()1)(6 ]2,1[,)(5 14 1312 12223-=-∈=+==+==x x f x x x f x x x f x x f x x f x x f ()()()()()()()]1,1[,14 ),0(,312 ;12)1(2252-∈+=+∞∈=-=+-=x x x x f x x x f x x f x x f 【学习检测】1、下列函数中是偶函数的是?( )A.54+=x yB.13-=x yC. x y 3=D.)0(2>=x x y2、判断下列函数的奇偶性 (1)xx x f 1)(-= (2)1)(2+-=x x f (3)5)(=x f (4)0)(=x f(5)1)(+=x x f (6)]3,1[,)(2-∈=x x x f3、函数3)(x x f -=的大致图象可能是( )4.P36练习 1、2题5.(选作)你能猜想一下吗?偶函数+偶函数,奇函数+奇函数,奇函数+偶函数, 偶函数*偶函数,奇函数*奇函数,奇函数*偶函数… 它们各自的奇偶性是什么?举例说明。
新课程人教版 《3.2.2 奇偶性》教学设计、导学案全套

人教版 《3.2.2 奇偶性》教学设计、导学案全套第一部分 教学设计教材分析函数奇偶性是函数性质“ 两域三性”中又一个一个重要性质,它丰富了函数的性质,让函数的考查更加多层次、多维度,可以更好地让学生从数学的三种语言来理解认识数学,把握数学的本质,提升学生的思维能力水平。
本节内容承上启下,后续学习指数函数、对数函数、幂函数、三角函数的性质中都要用到函数的奇偶性. 教学目标1、理解函数的奇偶性及其几何意义;2、学会运用函数图象理解和研究函数的性质;3、学会判断函数的奇偶性. 数学学科素养1.数学抽象:用数学语言表示函数奇偶性;2.逻辑推理:证明函数奇偶性;3.数学运算:运用函数奇偶性求参数;4.数据分析:利用图像求奇偶函数;5.数学建模:在具体问题情境中,运用数形结合思想,利用奇偶性解决实际问题。
重点:函数奇偶性概念的形成和函数奇偶性的判断; 难点:函数奇偶性概念的探究与理解.教学方法:以学生为主体的导学式教学,精讲多练。
教学工具:多媒体课件,希沃白板。
教学过程 一、情境引入画出并观察函数21()()2||()()=f x x g x x f x x g x x==-=和、和的图像,你能发现这两个函数图像 有什么共同特征码?要求:引导学生观察思考,得到结论. 二、自主学习阅读课本82-84页,思考并完成以下问题 1.什么是偶函数?什么是奇函数?44()()(),f x x x f x -=-==2.奇偶函数各有什么性质?要求:学生独立完成,以小组为单位,组内可商量,最终选出代表回答问题。
三、重点讲解 1.奇函数、偶函数(1)偶函数(even function )一般地,对于函数f(x)的定义域内的任意一个x ,都有f(-x)=f(x),那么f(x)就叫做偶函数. (2)奇函数(odd function )一般地,对于函数f(x)的定义域内的任意一个x ,都有f(-x)=f(x),那么f(x)就叫做奇函数. 注意:(1)定义中隐含的条件,具有奇偶性的函数的定义域关于坐标原点对称.因此定义域关于原点对称是函数具有奇偶性的一个必要条件。
导学案006(函数的奇偶性

函数的奇偶性编号:006 一、考纲要求:函数的基本性质二、复习目标:1.理解函数奇偶性的定义2、会判断函数的奇偶性3、能证明函数的奇偶性三、重点难点:函数奇偶性的判断及证明四、要点梳理:1.奇、偶函数的概念一般地,如果对于函数f(x)的定义域内任意一个x,都有,那么函数f(x)就叫做偶函数.一般地,如果对于函数f(x)的定义域内任意一个x,都有,那么函数f(x)就叫做奇函数.奇函数的图象关于对称;偶函数的图象关于对称.2.奇、偶函数的性质(1)奇函数在关于原点对称的区间上的单调性相同,偶函数在关于原点对称的区间上的单调性相反.(2)在公共定义域内①两个奇函数的和是奇函数,两个奇函数的积是偶函数;②两个偶函数的和、积都是偶函数;③一个奇函数,一个偶函数的积是奇函数.3.一条规律奇、偶函数的定义域关于原点对称.函数的定义域关于原点对称是函数具有奇偶性的必要不充分条件.两个性质(1)若奇函数f(x)在x=0处有定义,则f(0)=0.(2)设f(x),g(x)的定义域分别是D1,D2,那么在它们的公共定义域上:奇+奇=奇,奇×奇=偶,偶+偶=偶,偶×偶=偶,奇×偶=奇.三种方法判断函数的奇偶性,一般有三种方法:(1)定义法;(2)图象法;(3)性质法.五、基础自测:1. 对于定义在R 上的函数()f x ,下列判断是否正确?(1)若(2)(2)f f -=,则函数()f x 是偶函数;(2)若(2)(2)f f -≠,则函数()f x 不是偶函数;(3)若(2)(2)f f -=,则函数()f x 不是奇函数.2. 已知()f x 是R 上的奇函数,且当(0,)x ∈+∞时,()(1f x x =,则()f x 的解析式为______________________3.给出4个函数:①241()3x f x x +=-;②()25f x x =-+;③1()lg 1x f x x-=+;④1()1x f x x -=+. 其中 是奇函数; 是偶函数; 既不是奇函数也不是偶函数.4.若函数()()(2)(,)f x x a bx a a b R =++∈常数是偶函数,且它的值域为(],4-∞,则该函数的解析式为_________________________5.若函数2()1x a f x x bx +=++在[1,1]-上是奇函数,则()f x =六、典例精讲例1 判断下列六个函数的奇偶性:(1)2(12)()2x x f x +=; (2)()lg(f x x =; (3)2lg(1)()|2|2x f x x -=--;(4)()(1f x x =- (5)2()|1|1f x x x =+-+;(6) ()f x =(7)22(0),()(0).x x x f x x x x ⎧-+⎪=⎨+<⎪⎩≥ (8) 11()()(212x f x x a a =++-为常数)例2、已知定义在R 上的偶函数()f x 满足:(1)()f x f x +=-,且当[]0,1x ∈时,3()31,(log 26)x f x f =-求的值七、千思百练:1.二次函数2(0)y ax bx c a =++≠是偶函数的充要条件是2.下列函数中是奇函数的是_______________(1) 1()lg 1x f x x +=- (2) 2()121x f x =+- (3) ()11f x x x =++-(4) ()f x x= (5) 2()33f x x x =+3.函数3()sin 1()f x x x x R =++∈,若2f =,则(f 的值为___________4.减函数()y f x =定义在[1,1]-上,且是奇函数,若2(1)(45)0f a a f a --+->,则实数a 的取值范围为___________________5. 若奇函数()f x 满足(3)1,(3)()(3),f f x f x f =+=+则3()2f =_____________ 6.已知定义在实数集R 上的偶函数()f x 在区间[)0,+∞上是单调增函数,若(1)(lg )f f x <,则x 的取值范围为________________七、反思感悟:(1) 判断函数奇偶性之前务必先考察定义域是否关于原点对称(2)确定函数奇偶性的常见方法:定义法,图像法,若所给函数的形式比较复杂,应先化简,再判断其奇偶性。
人教版数学五年级下册第6课奇数和偶数的运算性质导学案3篇2024

人教版数学五年级下册第6课奇数和偶数的运算性质导学案3篇2024〖人教版数学五年级下册第6课奇数和偶数的运算性质导学案第【1】篇〗教学目标:1、在实践活动中认识奇数和偶数,了解奇偶性的规律。
2、探索并掌握数的奇偶性,并能应用数的奇偶性分析和解释生活中一些简单问题。
3、通过本次活动,让学生经历猜想、实验、验证的过程,结合学习内容,对学生进行思想教育,使学生体会到生活中处处有数学,增强学好数学的信心和应用数学的意识。
教学重点:探索并理解数的奇偶性教学难点:能应用数的奇偶性分析和解释生活中一些简单问题教学过程:一、游戏导入,感受奇偶性1、游戏:换座位首先将全班45个学生分成6组,人数分别为5、6、7、8、9、10。
我们大家来做个换位置的游戏:要求是只能在本组内交换,而且每人只能与任意一个人交换一次座位。
(游戏后学生发现6人、8人、10人一组的均能按要求换座位,而5人、7人、9人一组的却有一人无法跟别人换座位)2、讨论:为什么会出现这种情况呢?学生能很直观的找出原因,并说清这是由于6、8、10恰好是双数,都是2的倍数;而5、7、9是单数,不是2的倍数。
(此时学生议论纷纷,正是引出偶数、奇数的最佳时机)3、小结:交换位置时两两交换,刚好都能换位置,像6、8、10……是2的倍数,这样的数就叫做偶数;而有人不能与别人换位置,像5、7、9……不时的倍数,这样的数就叫做奇数。
学生相互举例说说怎样的数是奇数,怎样的数是偶数。
二、猜想验证, 认识奇偶性1、设置悬念、激发思维现在我们继续来考虑六组人数:5人、6人、7人、8人、9人、10人,那么猜猜那些组合起来能够刚好换完?那些不能?2、学生猜想、操作验证学生独立猜想,小组内汇报交流,然后统一意见进行验证(要求:验证时多选择几组进行证明)。
汇报成果:奇数﹢奇数=偶数奇数-奇数=偶数 ?奇数+奇数+……+奇数=奇数奇数个偶数+偶数=偶数 ?偶数-偶数=偶数 ?奇数+奇数+……+奇数=偶数偶数个奇数+偶数=奇数 ?奇数-偶数=奇数 ?偶数+偶数+……+偶数=偶数你能举几个例子说明一下吗?(学生的举例可以引导从正反两个角度进行)3、深化请同学们闭上眼睛,想一想:2+4+6+8+……+98+100这么多偶数相加的和是偶数还是奇数?为什么?三、实践操作、应用奇偶性我们已经知道了奇偶数的一些特性,现在要用这些特性解决我们身边经常发生的问题。
函数奇偶性导学案

“导学案”高效课堂建设——数学学科导学案专题名 函数的基本性质课题名 1.3.2函数的奇偶性班级:________小组:________姓名:__________学号:______一、明确目标二、创设情境,引入定义(一)创设情景,揭示课题“对称”是大自然的一种美,这种“对称美”在数学中也有大量的反映,让我们看看下列各函数有什么共性?观察下列函数的图象,总结各函数之间的共性.2()f x x = ()||1f x x =- 21()f x=观察一对关于y 归纳:若点(,())x f x 在函数图象上,则相应的点(,())x f x -也在函数图象上,即函数图象上横坐标互为相反数的点,它们的纵坐标一定________.(二)研探新知函数的奇偶性定义:1.偶函数一般地,对于函数()f x 的定义域内的任意一个x ,都有()()f x f x -=,那么()f x 就叫做偶函数.(学生活动)依照偶函数的定义给出奇函数的定义.2.奇函数一般地,对于函数()f x 的定义域的任意一个x ,都有()()f x f x -=-,那么()f x 就叫做奇函数.注意:①函数是奇函数或是偶函数称为函数的奇偶性,函数的奇偶性是函数的整体性质; ②由函数的奇偶性定义可知,函数具有奇偶性的一个必要条件是,对于定义域内的任意一个x ,则x -也一定是定义域内的一个自变量(即定义域关于原点对称).3.具有奇偶性的函数的图象的特征偶函数的图象关于y 轴对称;奇函数的图象关于原点对称.三、师生合作,建构数学例1. 判断下列函数是否具有奇偶性:(1)()35f x x x x =++; (2)()21f x x =+; (3)()1f x x =+; (4)()[]2,1,3f x x x =∈- 练习.判断下列函数的奇偶性(1)4()f x x = (2)5()f x x = (3)1()f x x x =+ (4)21()f x x=小结:利用定义判断函数奇偶性的格式步骤:①首先确定函数的定义域,并判断其定义域是否关于原点对称;②确定()()f x f x -与的关系;③作出相应结论:若()()()()0,()f x f x f x f x f x -=--=或则是偶函数;若()()()()0,()f x f x f x f x f x -=--+=或则是奇函数.例3.利用函数的奇偶性补全函数的图象.教材35P 思考题:规律:偶函数的图象关于_______对称;奇函数的图象关于_______对称.说明:这也可以作为判断函数奇偶性的依据.例4.已知()f x 是奇函数,在(0,+∞)上是增函数.证明:()f x 在(-∞,0)上也是增函数.小结:偶函数在关于原点对称的区间上单调性相反;奇函数在关于原点对称的区间上单调性一致.四、巩固深化,反馈矫正判断下列函数是否具有奇偶性:(1(2(3(4)()()()()22100010x x f x x x x ⎧+>⎪==⎨⎪--<⎩.五、达标检测,及时巩固(由易到难分为A 、B 、C 组)A 组1.判断下列函数的奇偶性,并说明理由.①()0,[6,2][2,6];f x x =∈--②()|2||2|f x x x =-++③()|2||2|f x x x =--+2. 已知函数2()2||f x x x =-. (Ⅰ)判断并证明函数的奇偶性; (Ⅱ)判断函数()f x 在(1,0)-上的单调性并加以证明.3.函数()f x 和()g x 均为奇函数,()()()2h x af x bg x =++在区间()0,+∞上有最大值5,那么()h x 在(),0-∞的最小值为( )A .5-B .1-C .3-D .以上都不对4.已知()538f x x ax bx =++-,()210f -=,则()2f 等于( ) A .26- B .18- C .10- D .10B 组5. 已知函数()f x 是偶函数,0x 时,()224f x x x =-+,求0x <时()f x 的解析式。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
奇偶性导学案普通班用
导学案
-CAL-FENGHAI-(2020YEAR-YICAI)_JINGBIAN
《1.3.2奇偶性》导学案
【学习目标】其中2、3是重点和难点
1. 理解函数的奇偶性及其几何意义;
2. 学会判断函数的奇偶性;
3. 学会运用函数图象理解和研究函数的性质.
【课前导学】阅读教材第33-36页,找出疑惑之处,完成新知学习
1.偶函数:一般地,对于函数()f x 定义域内的任意一个x ,都有 ,那么函数()f x 叫偶函数(even function ).
2.奇函数:一般地,对于函数()f x 定义域内的任意一个x ,都有 ,那么函数()f x 叫奇函数(odd function ).
3.奇函数、偶函数的定义域关于 对称,奇函数图象关于 对称,偶函数图象关于 对称.
4.若奇函数的定义域包含数0,则f (0)= .
【预习自测】
1.奇函数y=f(x),x ∈R 的图象必经过点 ( )
A .(a,f (-a ))
B .(-a,f (a ))
C .(-a, -f (a ))
D .(a, f (a
1)) 2.已知函数f(x)在[-5,5]上是奇函数,且f(3) <f(1),则 ( )
(A )f(-1) <f(-3) (B )f(0) >f(1) (C )f(-1) <f(1) (D )f(-3) >f(-5)
3.如果二次函数y=ax 2+bx+c (a ≠0)是偶函数,则b=
【课中导学】
探究:奇函数、偶函数的概念
实践:在同一坐标系分别作出两组函数的图象:
(1)()f x x =、1
()f x x
=、3()f x x =; (2)2()f x x =、()||f x x =.
讨论:(1)观察各组图象有什么共同特征函数解析式在函数值方面有什么特征 (2)请给出偶函数的定义.
(3)仿照偶函数的定义给出奇函数(odd function )的定义.
反思:奇函数、偶函数的定义域有什么特征?
练习:已知函数2
1()f x x =在y 轴左边的图象如图所示, 画出它右边的图象.
例1 判别下列函数的奇偶性:P35页例5
小结:判别方法,先看定义域是否关于原点对称,再计算()f x -,并与()f x 进行比较.
【自我评价】你完成本节导学案的情况为( ).
A. 很好
B. 较好
C. 一般
D. 较差
练习案
1. 若函数f(x)是定义在R 上的奇函数,则 f(0)=
2. 已知()f x 是定义(,)-∞+∞上的奇函数,且()f x 在[)0,+∞上是减函数. 下列关系式中正确的是( )
A. (5)(5)f f >-
B.(4)(3)f f >
C. (2)(2)f f ->
D.(8)(8)f f -=
3. 下列说法错误的是( ). A. 1
()f x x x
=+是奇函数 B. ()|2|f x x =-是偶函数
C. ()0,[6,6]f x x =∈-既是奇函数,又是偶函数
D.32()1
x x f x x -=-既不是奇函数,又不是偶函数
4. 已知f (x )是奇函数,且在[3,7]是增函数且最大值为4,那么f (x )在[-7,-3]上是 函数,且最 值为 .
5.下列函数中既非奇函数又非偶函数的是 ( )
(A )y=
x 1 (B )y=112+x (C )y=0 , x ∈[-1,2] (D )y=1
2+x x
6如果奇函数f(x)在区间[3,7]上是增函数且最小值为5,那么f(x)在
区间[-7,-3]上是 ( )
(A )增函数且最小值为-5 (B )增函数且最大值为-5
(C )减函数且最大值为-5 (D )减函数且最小值为-5
7.已知8)(35-++=bx ax x x f 且f(-2)=0,那么f(2)等于
8.已知函数f(x)在(0, +∞)上单调递增,且为偶函数,则f(- ),f(-3
1), f(3)之间的大小关系是。
