等腰三角形常用辅助线专题练习(含答案)
专题13 等腰三角形常见辅助线的作法(原卷版)

专题13 等腰三角形常见辅助线的作法(原卷版)类型一作底边中线(连接顶角顶点与底边中点)1.(2023秋•万州区校级月考)如图,在等腰Rt△ABC中,∠C=90°;AC=8,F是AB边上的中点,点D、E分别在AC、BC边上运动,且保持AD=CE,连接DE、DF、EF.在此运动变化过程中,下列结论:①△DEF是等腰直角三角形,②四边形CDFE保持面积不变,③DF的长度处于最小值时,CD的长为4;④S△CDE=S△DEF;其中正确的结论是()A.①②③④B.①②C.①②④D.①②③2.(2023•成武县校级三模)如图,△ABC中,AB=AC,D是BC的中点,E、F分别是AB、AC上的点,且AE=AF,求证:DE=DF.3.(2020秋•新华区校级月考)如图,△ABC中,AB=AC,D是BC的中点,过A点的直线EF∥BC,且AE=AF,求证:DE=DF.4.(2018秋•邻水县校级期末)如图所示,△ABC中,AB=BC,DE⊥AB于点E,DF⊥BC于点D,交AC 于F.(1)若∠AFD=155°,求∠EDF的度数;(2)若点F是AC的中点,求证:∠CFD=12∠B.类型二作底边上的高5.(2022秋•西湖区校级期中)如图,在△ABC中,∠ABC=60°,BC=10,点D在BA的延长线上,CA =CD,BD=6,则AD=()A.1B.2C.3D.46.(2014•甘肃模拟)如图,已知AB=AC,BD⊥AC于点D,求证:∠DBC=12∠BAC.7.如图,点D、E分别在BA、AC的延长线上,且AB=AC,AD=AE,求证:DE⊥BC.8.(2019秋•河池期末)如图,在△ABC中,点D、点E在BC边上,且AB=AC,AD=AE.求证:DB=CE.9.(2022秋•晋江市期中)如图,△ABC中,AC=2AB,AD平分∠BAC交BC于D,E是AD上一点,且EA=EC,求证:EB⊥AB.10.(2023春•市中区期末)小明遇到这样一个问题如图1,△ABC中,∠ACB=90°,点D在AB上,且BD=BC,求证:∠ABC=2∠ACD.小明发现,除了直接用角度计算的方法外,还可以用下面两种方法:方法2:如图2,作BE⊥CD,垂足为点E.方法3:如图3,作CF⊥AB,垂足为点F.根据阅读材料,从三种方法中任选一种方法,证明∠ABC=2∠ACD.11.(2021秋•南通期中)如图,AD是△ABC的中线,BE交AC于E,交AD于F,且AE=a,EF=a,BF =b,则AC的长为()A.a+b B.2b C.1.5b D.b12.(2023•滕州市模拟)综合与实践小明遇到这样一个问题,如图1,△ABC中,AB=7,AC=5,点D为BC的中点,求AD的取值范围.小明发现老师讲过的“倍长中线法”可以解决这个问题,所谓倍长中线法,就是将三角形的中线延长一倍,以便构造出全等三角形,从而运用全等三角形的有关知识来解决问题的方法,他的做法是:如图2,延长AD到E,使DE=AD,连接BE,构造△BED≌△CAD,经过推理和计算使问题得到解决.请回答:(1)小明证明△BED≌△CAD用到的判定定理是:;(填入你选择的选项字母)A.SAS B.SSS C.AAS D.ASA(2)AD的取值范围是.小明还发现:倍长中线法最重要的一点就是延长中线一倍,完成全等三角形模型的构造.参考小明思考问题的方法,解决问题:如图3,在正方形ABCD中,E为AB边的中点,G、F分别为AD,BC边上的点,若AG=2,BF=4,∠GEF=90°,求GF的长.13.(2007•沈阳)如图,△ABC是边长为3的等边三角形,△BDC是等腰三角形,且∠BDC=120°.以D 为顶点作一个60°角,使其两边分别交AB于点M,交AC于点N,连接MN,则△AMN的周长为.14.(2021秋•龙亭区校级期中)如图,△ABC中,AB=AC,∠A=100°,CD平分∠ACB交AB于D,E 为BC上一点,BE=DE.求证:BC=CD+AD.类型五角平分线+平行线构造等腰三角形15.(2022春•驿城区校级期中)如图,已知∠AOB=30°,P是∠AOB的平分线OC上的任意一点,PD∥OA交OB于点D,PE⊥OA于点E,如果OD=8cm,求PE的长.16.(2020秋•秦淮区校级期中)在△ABC中,∠ABC=2∠C,BD平分∠ABC,交AC于D,AE⊥BD,垂足为E.求证:AC=2BE.17.(2022秋•淮滨县期末)已知A(﹣10,0),以OA为边在第二象限作等边△AOB.(1)求点B的横坐标;(2)如图,点M、N分别为OA、OB边上的动点,以MN为边在x轴上方作等边△MNE,连结OE,当∠EMO=45°时,求∠MEO的度数.类型六角平分线+垂直构造等腰三角形18.(2020秋•朝阳区校级期中)我们知道“对称补缺”的思想是解决与轴对称图形有关的问题的一种重要的添加辅助线的策略,参考这种思想解决下列问题如图,在△ABC中,D为△ABC外一点.(1)若AC平分∠BAD,CE⊥AB于点E,∠B+∠ADC=180°,求证:BC=CD;(2)若∠ACB=90°,AC=BC,F是AC上一点,AD⊥BF交BF延长线于点D,且BF是∠CBA的角平分线.求证:2AD=BF。
等腰三角形常用辅助线专题练习(含答案)汇总

等腰三角形常用辅助线专题练习(含答案)1.如图:已知,点D、E在三角形ABCの边BC上, AB=AC,AD=AE,求证:BD=CE。
证明:作AF⊥BC,垂足为F,则AF⊥DE。
∵AB=AC,AD=AE又∵AF⊥BC ,AF⊥DE,∴BF=CF,DF=EF (等腰三角形底边上の高与底边上の中线互相重合)。
∴BD=CE.2.如图,在三角形ABC中,AB=AC,AF平行BC于F, D是AC边上任意一点,延长BA到E,使AE=AD,连接 DE,试判断直线AF与DEの位置关系,并说明理由解:AF⊥DE.理由:延长ED交BC于G,∵AB=AC,AE=AD ∴∠B=∠C,∠E=∠ADE ∴∠B+∠E=∠C+∠ADE ∵∠ADE=∠CDG ∴∠B+∠E=∠C+∠CDG ∵∠B+∠E=∠DGC,∠C+∠CDG=∠BGE,∠BGE+∠CGD=180°∴∠BGE=∠CGD=90°∴EG⊥BC.∵AF∥BC ∴AF⊥DE.解法2:过A点作△ABC底边上の高,再用∠BAC=∠D+AED=∠2∠ADE, 即∠CAG=∠AED,证明AG∥DE 利用AF∥BC证明AF⊥DE3.如图,△ABC中,BA=BC,点D是AB延长线上一点, DF⊥AC交BC于E,求证:△DBE是等腰三角形。
证明:在△ABC中,∵BA=BC,∴∠A=∠C,∵DF⊥AC,∴∠C+∠FEC=90°,∠A+∠D=90°,∴∠FEC=∠D ∵∠FEC=∠BED,∴∠BED=∠D,∴BD=BE,即△DBE是等腰三角形.4. 如图,△ABC中,AB=AC,E在AC上,且AD=AE,DE の延长线与BC相交于F。
求证:DF⊥BC.证明:∵AB=AC,∴∠B=∠C,又∵AD=AE,∴∠D=∠AED,∴∠B+∠D=∠C+∠AED,∴∠B+∠D=∠C+∠CEF,∴∠EFC=∠BFE=180°× 1/2 = 90°,∴DF⊥BC;若把“AD =AE”与结论“DF⊥BC”互换,结论也成立。
八年级下册等腰三角形添辅助线的综合专题(含答案)
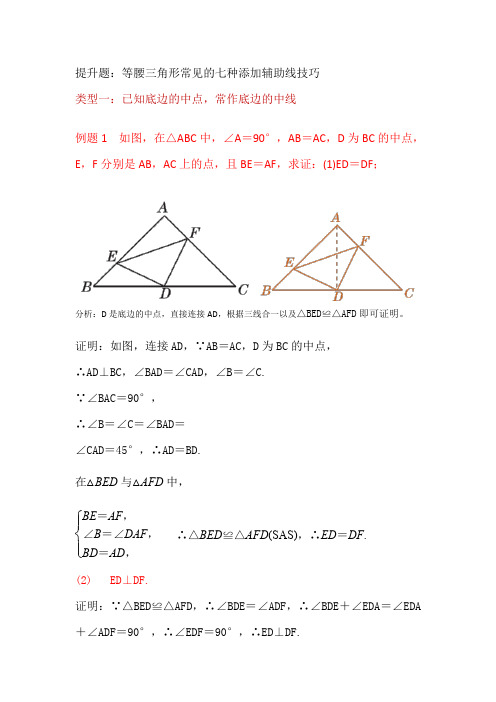
提升题:等腰三角形常见的七种添加辅助线技巧类型一:已知底边的中点,常作底边的中线例题1 如图,在△ABC 中,∠A =90°,AB =AC ,D 为BC 的中点,E ,F 分别是AB ,AC 上的点,且BE =AF ,求证:(1)ED =DF ;分析:D 是底边的中点,直接连接AD ,根据三线合一以及△BED ≌△AFD 即可证明。
证明:如图,连接AD ,∵AB =AC ,D 为BC 的中点,∴AD ⊥BC ,∠BAD =∠CAD ,∠B =∠C.∵∠BAC =90°,∴∠B =∠C =∠BAD =∠CAD =45°,∴AD =BD.在△BED 与△AFD 中,⎩⎪⎨⎪⎧BE =AF ,∠B =∠DAF ,BD =AD ,∴△BED ≌△AFD (SAS),∴ED =DF . (2) ED ⊥DF.证明:∵△BED ≌△AFD ,∴∠BDE =∠ADF ,∴∠BDE +∠EDA =∠EDA +∠ADF =90°,∴∠EDF =90°,∴ED ⊥DF.类型二:等腰三角形中没有底边中点时,常作底边上的高例题2 如图,在△ABC中,AC=2AB,AD平分∠BAC交BC于D,E是AD上一点,且EA=EC.求证:EB⊥AB.证明:如图,作EF⊥AC于点F,∵EA=EC,∴AF=FC.又∵AC=2AB,∴AF=AB.又∵AD平分∠BAC,∴∠BAE=∠FAE.又∵AE=AE,∴△ABE≌△AFE,∴∠ABE=∠AFE=90°,∴EB⊥AB.类型三等腰三角形中证与腰有关联的线段时,常作腰的平行线(或垂线)如图,在△ABC中,AB=AC,点P从点B出发沿线段BA移动(点P与A,B不重合),同时,点Q从点C出发沿线段AC的延长线移动,点P,Q移动的速度相同,PQ与直线BC相交于点D.求证:PD=QD.证明:如图,过点P作PF△AC交BC于点F.∵点P和点Q同时出发,且速度相同,∴BP=CQ.△PF//AQ,∴∠PFB=∠ACB,∠DPF=∠CQD.又△AB=AC,∴∠B=∠ACB.∴∠B=∠PFB. ∴BP=PF.∴PF=CQ.在△PFD和△QCD中,∠DPF=∠DQC,∠PDF=∠QDC,PF=CQ,∴△PFD≌△QCD(AAS),∴PD=QD.类型四:等腰三角形中证与底有关联的线段时,常作底的平行线。
等腰三角形中常见辅助线(中考)

等腰三角形中常见辅助线一、等腰三角形中底边中点常作底边的中线1.如图,在△ABC中,AB=AC,D是BC的中点,E,F分别是AB,AC上的点,且AE=AF.求证:DE=DF.证明:连接AD,∵AB=AC且BD=CD,∴∠BAD=∠CAD,又∵AE=AF,AD=AD,∴△AED≌△AFD(SAS),∴DE=DF二、利用“三线合一”作等腰三角形底边上的高2.如图,AB=2AC,AD平分∠BAC交BC于D,E是AD上一点,且AE=BE.求证:CE⊥AC.证明:作EH⊥AB于H,∵AE=BE,∴AH=BH,又∵AB=2AC,∴AC=AH,∵AD平分∠BAC,∴∠CAE=∠EAH,又∵AE=AE,∴△AHE≌△ACE(SAS),∴∠AHE=∠ACE=90°,∴CE⊥AC1.如图,在△ABC中,AB=AC,D是BC的中点,过点A作EF∥BC,且AE=AF.求证DE=DF.练习:证明:连接AD.∵AB=AC,D是BC的中点,∴AD⊥BC.∵EF∥BC,∴AD⊥EF.又∵AE=AF,∴AD垂直平分EF.∴DE=DF.三、作平行线构造等腰三角形如图,点D在等边三角形ABC的边AB上,点F在边AC上,连接DF并延长交BC的延长线于点E,EF=FD.求证:AD=CE.练习如图,在△ABC中,AB=AC,点P从点B出发沿线段BA移动(点P与A,B不重合),同时点Q从点C出发沿线段AC的延长线移动,点P,Q移动的速度相同,PQ与边BC相交于点D .(1)求证PD=QD.证明:如图,过点P 作PF ∥AC 交BC 于F .∵点P 和点Q 同时出发,且速度相同,∴BP =CQ .∵PF ∥AQ ,∴∠PFB =∠ACB ,∠DPF =∠CQD .又∵AB =AC ,(1)求证PD =QD.∴∠B =∠ACB ,∴∠B =∠PFB ,∴BP =PF ,∴PF =CQ .在△PFD 和△QCD 中,∴△PFD ≌△QCD (AAS).∴PD =QD .DPF DQC PDF QDC PF QC ∠∠⎧⎪∠∠⎨⎪⎩=,=,=,(2)过点P作直线BC的垂线,垂足为E,在P,Q移动的过程中,线段BE,DE,CD中是否存在长度保持不变的线段?请说明理由.解:ED的长度保持不变.理由如下:由(1)知PB=PF.∵PE⊥BF,∴BE=EF由(1)知△PFD≌△QCD,∴FD=DC,∴ED=EF+FD=BE+DC= BC∴ED为定值四、用截长补短法构造等腰三角形如图,已知AB=AC,∠A=108°,BD平分∠ABC交AC于点D.求证:BC=AB+CD.如图,在△ABC 中,AB =AC ,D 是△ABC 外一点,且∠ABD =60°,∠ACD =60°.求证BD +DC =AB.练习:证明:如图,延长BD至E,使BE=AB,连接CE,AE.∵∠ABE=60°,BE=AB,∴△ABE为等边三角形.又∵∠ACD=60°,∴∠ACD=∠AEB.∵AB=AC,AB=AE,∴AC=AE.∴∠ACE=∠AEC.∴∠DCE=∠DEC.∴DC=DE.∴AB=BE=BD+DE=BD+CD,即BD+DC=AB.五、作垂直构造K字型全等如图,将等腰Rt△ABC斜放在平面直角坐标系中,使直角顶点C与点(1,0)重合,点A的坐标为(-2,1).(1)求点B的坐标;(2)求△ABC的面积.六、常将等腰三角形转化为等边三角形如图,△ABC中,AB=AC,∠BAC=80°,P为形内一点,若∠PBC=10°,∠PCB=30°,求∠PAB的度数。
最新修订人教版八年级下册数学解题技巧专题练习:等腰三角形中辅助线的作法

解题技巧专题:等腰三角形中辅助线的作法——形成精准思维模式,快速解题◆类型一利用“三线合一”作辅助线一、已知等腰作垂线(或中线、角平分线)1.如图,在△ABC中,AB=AC,AE⊥BE于点E,且∠ABE=∠ABC.若BE=2,则BC=________.2.如图,在△ABC中,AB=AC,D是BC的中点,E、F分别是AB、AC上的点,且AE=AF.求证:DE=DF.二、构造等腰三角形3.如图,在△ABC中,BP平分∠BAC,且AP⊥BP于点P,连接CP.若△PBC的面积为2,则△ABC的面积为()A.3B.4C.5D.64.如图,已知△ABC是等腰直角三角形,∠A=90°,BD平分∠ABC交AC于点D,CE⊥BD,交BD的延长线于点E.求证:BD=2CE.◆类型二巧用等腰直角三角形构造全等5.如图,在△ABC中,AC=BC,∠C=90°,D是AB的中点,DE⊥DF,点E,F分别在AC,BC上.求证:DE=DF.◆类型三等腰(边)三角形中截长补短或作平行线构造全等6.如图,在△ABC中,AB=AC,∠A=108°,BD平分∠ABC交AC于点D.求证:BC=AB+CD.7.如图,过等边△ABC的边AB上一点P,作PE⊥AC于点E,Q为BC延长线上一点,且P A =CQ,连接PQ交AC于点D.(1)求证:PD=DQ;(2)若△ABC的边长为1,求DE的长.【方法8】参考答案与解析1.42.证明:连接AD .∵AB =AC ,D 是BC 的中点,∴∠EAD =∠F AD .在△AED 和△AFD 中,⎩⎪⎨⎪⎧AE =AF ,∠EAD =∠F AD ,AD =AD ,∴△AED ≌△AFD ,∴DE =DF .3.B4.证明:如图,延长BA 和CE 交于点M .∵CE ⊥BD ,∴∠BEC =∠BEM =90°.∵BD 平分∠ABC ,∴∠MBE =∠CBE .又∵BE =BE ,∴△MBE ≌△CBE ,∴EM =EC =12MC .∵△ABC 是等腰直角三角形,∴∠BAC =∠MAC =90°,BA =AC ,∴∠ABD +∠BDA =90°.∵∠BEC =90°,∴∠ACM +∠CDE =90°.∵∠BDA =∠EDC ,∴∠ABE =∠ACM .又∵AB =AC ,∴△ABD ≌△ACM (ASA),∴DB =MC ,∴BD =2CE .5.证明:连接CD .∵AC =BC ,∠C =90°,D 是AB 的中点,∴CD 平分∠ACB ,CD ⊥AB ,∴∠CDB =90°,∴∠BCD =∠ACD =45°,∠B =∠C =45°,∴∠ACD =∠B =∠BCD ,∴CD =BD .∵ED ⊥DF ,∴∠EDF =∠EDC +∠CDF =90°.又∵∠CDF +∠BDF =90°,∴∠EDC =∠FDB ,∴△ECD ≌△FBD ,∴DE =DF .6.证明:如图,在线段BC 上截取BE =BA ,连接DE .∵BD 平分∠ABC ,∴∠ABD =∠EBD .又∵BD =BD ,∴△ABD ≌△EBD (SAS),∴∠BED =∠A =108°,∴∠CED =180°-∠BED =72°.又∵AB=AC ,∠A =108°,∴∠ACB =∠ABC =12×(180°-108°)=36°,∴∠CDE =180°-∠ACB -∠CED =180°-36°-72°=72°.∴∠CDE =∠DEC ,∴CD =CE ,∴BC =BE +EC =AB +CD .7.(1)证明:过点P 作PF ∥BC 交AC 于点F ,∴∠AFP =∠ACB ,∠FPD =∠Q ,∠PFD =∠QCD .∵△ABC 为等边三角形,∴∠A =∠ACB =60°,∴∠AFP =60°,∴△APF 是等边三角形,∴PF=P A =CQ ,∴△PFD ≌△QCD ,∴PD =DQ .(2)解:由(1)知△APF 是等边三角形,∵PE ⊥AC ,∴AE =EF .由(1)知△PFD ≌△QCD ,∴DF =CD ,∴DE =EF +DF =12AF +12CF =12AC .又∵AC =1,∴DE =12.。
等腰三角形常用辅助线专题练习含答案

等腰三角形常用辅助线专题练习(含答案)1.如图:已知,点D、E在三角形ABC的边BC上, AB=AC,AD=AE,求证:BD=CE。
证明:作AF⊥BC,垂足为F,则AF⊥DE。
∵AB=AC,AD=AE又∵AF⊥BC ,AF⊥DE,∴BF=CF,DF=EF (等腰三角形底边上的高与底边上的中线互相重合)。
∴BD=CE.2.如图,在三角形ABC中,AB=AC,AF平行BC于F, D是AC边上任意一点,延长BA到E,使AE=AD,连接 DE,试判断直线AF与DE的位置关系,并说明理由解:AF⊥DE.理由:延长ED交BC于G,∵AB=AC,AE=AD ∴∠B=∠C,∠E=∠ADE ∴∠B+∠E=∠C+∠ADE ∵∠ADE=∠CDG ∴∠B+∠E=∠C+∠CDG ∵∠B+∠E=∠DGC,∠C+∠CDG=∠BGE,∠BGE+∠CGD=180°∴∠BGE=∠CGD=90°∴EG⊥BC.∵AF∥BC ∴AF⊥DE.解法2:过A点作△ABC底边上的高,再用∠BAC=∠D+AED=∠2∠ADE, 即∠CAG=∠AED,证明AG∥DE 利用AF∥BC证明AF⊥DE3.如图,△ABC中,BA=BC,点D是AB延长线上一点, DF⊥AC交BC于E,求证:△DBE是等腰三角形。
证明:在△ABC中,∵BA=BC,∴∠A=∠C,∵DF⊥AC,∴∠C+∠FEC=90°,∠A+∠D=90°,∴∠FEC=∠D ∵∠FEC=∠BED,∴∠BED=∠D,∴BD=BE,即△DBE是等腰三角形.4. 如图,△ABC中,AB=AC,E在AC上,且AD=AE,DE 的延长线与BC相交于F。
求证:DF⊥BC.证明:∵AB=AC,∴∠B=∠C,又∵AD=AE,∴∠D=∠AED,∴∠B+∠D=∠C+∠AED,∴∠B+∠D=∠C+∠CEF,∴∠EFC=∠BFE=180°× 1/2 = 90°,∴DF⊥BC;若把“AD =AE”与结论“DF⊥BC”互换,结论也成立。
(完整)等腰三角形时常用的辅助线作法

有等腰三角形时常用的辅助线⑴作顶角的平分线,底边中线,底边高线例:已知,如图,AB = AC,BD⊥AC于D,求证:∠BAC = 2∠DBC⑵有底边中点时,常作底边中线例:已知,如图,△ABC中,AB = AC,D为BC中点,DE⊥AB于E,DF⊥AC于F,求证:DE = DF⑶将腰延长一倍,构造直角三角形解题例:已知,如图,△ABC中,AB = AC,在BA延长线和AC上各取一点E、F,使AE = AF,求证:EF⊥BC⑷常过一腰上的某一已知点做另一腰的平行线例:已知,如图,在△ABC中,AB = AC,D在AB上,E在AC延长线上,且BD = CE,连结DE交BC于F求证:DF = EF⑸常过一腰上的某一已知点做底的平行线例:已知,如图,△ABC中,AB =AC,F在AC上,E在BA延长线上,且AE = AF,连结DE求证:EF⊥BC⑹常将等腰三角形转化成特殊的等腰三角形---—--等边三角形例:已知,如图,△ABC中,AB = AC,∠BAC = 80o,P为形内一点,若∠PBC = 10o,∠PCB = 30o求∠PAB的度数。
有等腰三角形时常用的辅助线⑴作顶角的平分线,底边中线,底边高线例:已知,如图,AB = AC,BD⊥AC于D,求证:∠BAC = 2∠DBC证明:(方法一)作∠BAC的平分线AE,交BC于E,则∠1 = ∠2 = 12∠BAC又∵AB = AC∴AE⊥BC∴∠2+∠ACB = 90o∵BD⊥AC∴∠DBC+∠ACB = 90o∴∠2 = ∠DBC∴∠BAC = 2∠DBC(方法二)过A作AE⊥BC于E(过程略)(方法三)取BC中点E,连结AE(过程略)⑵有底边中点时,常作底边中线例:已知,如图,△ABC中,AB = AC,D为BC中点,DE⊥AB于E,DF⊥AC于F,求证:DE = DF21EDC BA证明:连结AD.∵D 为BC 中点, ∴BD = CD又∵AB =AC ∴AD 平分∠BAC ∵DE ⊥AB ,DF ⊥AC ∴DE = DF⑶将腰延长一倍,构造直角三角形解题例:已知,如图,△ABC 中,AB = AC,在BA 延长线和AC 上各取一点E 、F ,使AE = AF , 求证:EF ⊥BC证明:延长BE 到N ,使AN = AB ,连结CN ,则AB = AN = AC∴∠B = ∠ACB, ∠ACN = ∠ANC ∵∠B +∠ACB +∠ACN +∠ANC = 180o∴2∠BCA +2∠ACN = 180o ∴∠BCA +∠ACN = 90o 即∠BCN = 90o ∴NC ⊥BC ∵AE = AF ∴∠AEF = ∠AFE又∵∠BAC = ∠AEF +∠AFE ∠BAC = ∠ACN +∠ANC ∴∠BAC =2∠AEF = 2∠ANC ∴∠AEF = ∠ANCF E DCBAN FE CBA∴EF ∥NC ∴EF ⊥BC⑷常过一腰上的某一已知点做另一腰的平行线例:已知,如图,在△ABC 中,AB = AC,D 在AB 上,E 在AC 延长线上,且BD = CE ,连结DE 交BC 于F 求证:DF = EF证明:(证法一)过D 作DN ∥AE ,交BC 于N ,则∠DNB = ∠ACB,∠NDE = ∠E ,∵AB = AC, ∴∠B = ∠ACB ∴∠B =∠DNB ∴BD = DN 又∵BD = CE ∴DN = EC在△DNF 和△ECF 中 ∠1 = ∠2 ∠NDF =∠E DN = EC ∴△DNF ≌△ECF ∴DF = EF(证法二)过E 作EM ∥AB 交BC 延长线于M ,则∠EMB =∠B(过程略)⑸常过一腰上的某一已知点做底的平行线21NFED C BA21MFED CBA例:已知,如图,△ABC 中,AB =AC ,E 在AC 上,D 在BA 延长线上,且AD = AE ,连结DE求证:DE ⊥BC证明:(证法一)过点E 作EF ∥BC 交AB 于F ,则∠AFE =∠B ∠AEF =∠C ∵AB = AC ∴∠B =∠C ∴∠AFE =∠AEF ∵AD = AE∴∠AED =∠ADE又∵∠AFE +∠AEF +∠AED +∠ADE = 180o ∴2∠AEF +2∠AED = 90o 即∠FED = 90o∴DE ⊥FE 又∵EF ∥BC ∴DE ⊥BC(证法二)过点D 作DN ∥BC 交CA 的延长线于N,(过程略) (证法三)过点A 作AM ∥BC 交DE 于M ,(过程略)⑹常将等腰三角形转化成特殊的等腰三角形————--等边三角形例:已知,如图,△ABC 中,AB = AC,∠BAC = 80o ,P为形内一点,若∠PBC = 10o ∠PCB = 30o 求∠PAB 的度数. 解法一:以AB 为一边作等边三角形,连结CE则∠BAE =∠ABE = 60oN M FE D CBA PECBAAE = AB = BE∵AB = AC∴AE = AC ∠ABC =∠ACB ∴∠AEC =∠ACE∵∠EAC =∠BAC-∠BAE= 80o-60o = 20o∴∠ACE = 12(180o-∠EAC)= 80o∵∠ACB= 12(180o-∠BAC)= 50o∴∠BCE =∠ACE-∠ACB= 80o-50o = 30o∵∠PCB = 30o∴∠PCB = ∠BCE∵∠ABC =∠ACB = 50o, ∠ABE = 60o∴∠EBC =∠ABE-∠ABC = 60o-50o =10o ∵∠PBC = 10o∴∠PBC = ∠EBC在△PBC和△EBC中∠PBC = ∠EBCBC = BC∠PCB = ∠BCE∴△PBC≌△EBC∴BP = BE∵AB = BE∴AB = BP∴∠BAP =∠BPA∵∠ABP =∠ABC-∠PBC = 50o-10o = 40o∴∠PAB = 12(180o-∠ABP)= 70o解法二:以AC为一边作等边三角形,证法同一。
专题 等腰三角形中常用的辅助线作法(原卷版)

(苏科版)八年级上册数学《第2章轴对称图形》专题等腰三角形中常用的辅助线作法解题技巧提炼当遇到等腰三角形时,常利用“三线合一”的性质,若已知图中无此线,可将其构造出来以辅助解决问题,通常是作底边上的高,再证底边上的中线或顶角的平分线.【例题1】(2022秋•秦淮区月考)如图所示,在五边形ABCDE中,AB=AE,∠B=∠E,BC=DE,F是CD的中点,连接AF.求证:AF⊥CD.【变式1-1】如图,△ABC中,CA=CB,D在AC的延长线上,E在BC上,且CD=CE,求证:DE⊥AB.【变式1-2】(2022秋•新洲区期中)如图.△ABC中,CA=CB.D是AB的中点.∠CED=∠CFD=90°,CE=CF,求证:∠ADF=∠BDE.【变式1-3】已知:如图,△ABC中,AB=AC,CE⊥AE于E,CE=12BC,E在△ABC外,求证:∠ACE=∠B.【变式1-4】(2022秋•晋江市期中)如图,△ABC中,AC=2AB,AD平分∠BAC交BC于D,E是AD上一点,且EA=EC,求证:EB⊥AB.【变式1-5】(2022秋•大足区期末)如图所示,△ABC中,AC=BC,点D是AB上一点,DE⊥BC于点E,过点E作EF⊥AC于点F.(1)若∠ADE=160°,求∠DEF的度数;(2)若点D是AB的中点,求证:∠BDE=12∠ACB.【变式1-6】(2022秋•南乐县月考)如图,在△ABC中,AB=AC,D、E是△ABC内两点,AD平分∠BAC,∠EBC=∠E=60°,且BE=4.(1)求∠D的度数;(2)若BC=5,求ED的长.【变式1-7】如图,AB∥CD,∠1=∠2,AD=AB+CD.(1)求证:BE=CE;(2)求证:AE⊥DE;(3)求证:AE平分∠DAB.【例题2】如图,在△ABC 中,AB =AC ,EF 交AB 于点E ,交BC 与点D .交AC 的延长线于点F ,且BE =CF .求证:DE =DF .【变式2-1】如图,△ABC 是等边三角形,D 为AC 延长线上一点,E 是BC 延长线上一点,CE =AD ,求证:DB =DE.【变式2-2】如图,BD平分∠ABC交AC于D,点E为CD上一点,且AD=DE,EF∥BC交BD于F.求证:AB=EF.【变式2-3】如图,在△ABC中,AB=AC,在AB上取一点E,在AC的延长线上取一点F,使BE=CF,EF交BC于点G.(1)试说明EG=FG;(2)试说明AB+AC>2EG.【变式2-4】如图,在△ABC中,AB=AC,E在线段AC上,D在AB的延长线,连DE交BC于F,过点E 作EG⊥BC于G.(1)若∠A=50°,∠D=30°,求∠GEF的度数;(2)若BD=CE,求证:FG=BF+CG.【变式2-5】如图所示,等边三角形ABC的边长是6,点P在边AB上,点Q在BC的延长线上,且AP=CQ,设PQ与AC相交于点D.(1)当∠DQC=30°时,求AP的长.(2)作PE⊥AC于E,试探究DE、AE、CD三条线段之间的数量关系,并证明你的结论.【变式2-6】已知,△ABC为等边三角形,点D为AC上的一个动点,点E为BC延长线上一点,且BD=DE.(1)如图1,若点D在边AC上,猜想线段AD与CE之间的关系,并说明理由;(2)如图2,若点D在AC的延长线上,(1)中的结论是否成立,请说明理由.【变式2-7】如图,AD为△ABC的平分线,E为BC的中点,EF∥AD交BA的延长线于F,交AC于G.(1)求证:AF=AG;(2)求证:BF=CG;(3)求AB AC CG的值.【例题3】如图,△ABC 中,CA =CB ,∠ACB =108°,BD 平分∠ABC 交AC 于D ,求证:AB =AD +BC .【变式3-1】如图,△ABC 中,AB =AC ,∠A =100°,CD 平分∠ACB 交AB 于D ,E 为BC 上一点,BE =DE .求证:BC =CD +AD.解题技巧提炼对于线段和差问题,利用“截长补短法”的思想,添加辅助线,可构造等腰三角形来实现边角之间的转化.【变式3-2】如图,在△ABC中,AD平分∠BAC,AD=AB,CM⊥AD交AD延长线于点M.求证:AM=12(AB+AC).【变式3-3】如图(1),线段AD∥BC,连接AB、CD,取CD中点E,连接AE,AE平分∠BAD.(1)线段AB与AD、BC之间存在怎样的等量关系?请说明理由.(2)如果点C在AB的左侧,其他条件不变,如图(2)所示,那么(1)中的结论还成立吗?如果成立,请说明理由;如果不成立,请写出新的结论,并说明理由.【变式3-4】(2022秋•崇川区校级月考)如图1,在△ABC中,∠BAC=75°,∠ACB=35°,∠ABC的平分线BD交边AC于点D.(1)求证:△BCD为等腰三角形;(2)若∠BAC的平分线AE交边BC于点E,如图2,求证:BD+AD=AB+BE;(3)若∠BAC外角的平分线AE交CB延长线于点E,请你探究(2)中的结论是否仍然成立?直接写出正确的结论.【变式3-5】在等边三角形ABC的两边AB、AC所在直线上分别有两点M、N,P为△ABC外一点,且∠MPN=60°,∠BPC=120°,BP=CP.探究:当点M、N分别在直线AB、AC上移动时,BM,NC,MN之间的数量关系.(1)如图①,当点M、N在边AB、AC上,且PM=PN时,试说明MN=BM+CN.(2)如图②,当点M、N在边AB、AC上,且PM≠PN时,MN=BM+CN还成立吗?答: .(请在空格内填“一定成立”“不一定成立”或“一定不成立”).(3)如图③,当点M、N分别在边AB、CA的延长线上时,请直接写出BM,NC,MN之间的数量关系.【例题4】阅读下面的题目及分析过程,并按要求进行证明.已知:如图,点E 是BC 的中点,点A 在DE 上,且∠BAE =∠CDE .求证:AB =CD .分析:证明两条线段相等,常用的方法是应用全等三角形或等腰三角形的判定和性质,观察本题中要证明的两条线段,它们不在同一个三角形中,且它们分别所在的两个三角形也不全等,因此,要证AB =CD ,必须添加适当的辅助线,构造全等三角形或等腰三角形.(1)现给出如下两种添加辅助线的方法,请任意选出其中一种,对原题进行证明.①如图1,延长DE 到点F ,使EF =DE ,连接BF ;②如图2,分别过点B 、C 作BF ⊥DE ,CG ⊥DE ,垂足分别为点F ,G .(2)请你在图3中添加不同于上述的辅助线,并对原题进行证明.【变式4-2】如图,在△ABC 中,点D 是BC 的中点,点E 是AD 上一点,BE =AC .若∠C =70°,∠DAC =50°,求∠EBD的度数.解题技巧提炼当题目中已知某线段的中点时,通过倍长中点处的线段构造全等三角形,从而将题目中的相等的角或边集中到新的三角形中构成等腰三角形.【变式4-3】(2022秋•文峰区月考)如图,已知△ABC中,AD是中线,AE是△ABD的中线,BA=BD,∠BAD =∠BDA,求证:AC=2AE.【变式4-4】阅读并完成以下填空:如图1,已知:AD为△ABC的中线,求证AB+AC>2AD.证明:延长AD至E使得DE=AD.连接EC,则AE=2AD.∵AD为△ABC的中线,∴BD=CD.在△ABD和△CED中,BD=CD, , .∴△ABD≌△CED.∴AB=EC.在△ACE中,根据三角形的三边关系有AC+EC AE.而AB=EC,AE=2AD,∴AB+AC>2AD.这种添加辅助线的方法,我们称为“倍长中线法”.请利用这种方法解决下列问题:问题1:如图2,在△ABC中,AC=5,AB=13,D为BC的中点,DA⊥AC.求△ABC的面积.问题2:如图3,在△ABC中,AD是三角形的中线.点F在中线AD上,且BF=AC,连接并延长BF 交AC于点E.求证AE=EF.【变式4-5】(2023春•汉寿县期中)已知:△ABC和△ADE均为等腰直角三角形,∠ABC=∠ADE=90°,AB=BC,AD=DE,按图1放置,使点E在AB上,取CE的中点F,连接DF,BF.(1)观察发现:图1中DF,BF的数量关系是 ,位置关系是 ;(2)探究证明:将图1中的△ADE绕点A顺时针转动45°,再连接CE,取CE的中点F(如图2),问(1)中的结论是否仍然成立?请证明你的结论;(3)拓展延伸:将图1中的△ADE绕点A顺时针转动任意角度(转动角度在0°到90°之间),再连接CE的中点F(如图3),问(1)中的结论是否仍然成立?请证明你的结论.【例题5】如图,在△ABC中,∠BAC=2∠B,CD平分∠ACB交AB于D,求证:AC+AD=BC.【变式5-1】在△ABC中,AD是BC边上的高,CD=AB+BD.求证:∠B=2∠C.【变式5-2】如图,在△ABC中∠ABC=2∠C,若AD⊥BC于D,BD=4,CD=16,求AB的长.【变式5-3】(2022•南京模拟)小明在完成一道几何证明问题时,往往会思考看是否会有不同的证明方法.例如:在如图1所示的△ABC中,∠ACB=90°,点D在AB上,且BD=BC,求证:∠ABC=2∠ACD.他发现,除了方法1直接用角度计算的方法外,还可以用下面两种方法:方法2:如图2,作BE⊥CD,垂足为点E.方法3:如图3,作CF⊥AB,垂足为点F.根据阅读材料,请你从三种方法中任选一种方法,证明∠ABC=2∠ACD,并写出其证明过程.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
等腰三角形常用辅助线专题练习
(含答案)
1.如图:已知,点D、E在三角形ABC的边BC上, AB=AC,AD=AE,求证:BD=CE。
证明:作AF⊥BC,垂足为F,则AF⊥DE。
∵AB=AC,AD=AE
又∵AF⊥BC ,AF⊥DE,∴BF=CF,DF=EF (等腰三角形底边上的高与底边上的中线互相重合)。
∴BD=CE.
2.如图,在三角形ABC中,AB=AC,AF平行BC于F, D是AC边上任意一点,延长BA到E,使AE=AD,连接 DE,试判断直线AF与DE的位置关系,并说明理由
解:AF⊥DE.理由:延长ED交BC于G,∵AB=AC,AE=AD ∴∠B=∠C,∠E=∠ADE ∴∠B+∠E=∠C+∠ADE ∵∠ADE=∠CDG ∴∠B+∠E=∠C+∠CDG ∵∠B+∠E=∠DGC,∠C+∠CDG=∠BGE,∠BGE+∠CGD=180°∴∠BGE=∠CGD=90°∴EG⊥BC.∵AF∥BC ∴AF⊥DE.
解法2:
过A点作△ABC底边上的高,
再用∠BAC=∠D+AED=∠2∠ADE, 即∠CAG=∠AED,证明AG∥DE 利用AF∥BC证明AF⊥DE
3.如图,△ABC中,BA=BC,点D是AB延长线上一点, DF⊥AC交BC于E,求证:△DBE是等腰三角形。
证明:在△ABC中,∵BA=BC,∴∠A=∠C,∵DF⊥AC,∴∠C+∠FEC=90°,∠A+∠D=90°,∴∠FEC=∠D ∵∠FEC=∠BED,∴∠BED=
∠D,∴BD=BE,即△DBE是等腰三角形.
4. 如图,△ABC中,AB=AC,E在AC上,且AD=AE,DE 的延长线与BC相交于F。
求证:DF⊥BC.
证明:∵AB=AC,∴∠B=∠C,又∵AD=AE,∴∠D=∠AED,
∴∠B+∠D=∠C+∠AED,∴∠B+∠D=∠C+∠CEF,
∴∠EFC=∠BFE=180°× 1/2 = 90°,∴DF⊥BC;
若把“AD =AE”与结论“DF⊥BC”互换,结论也成立。
若把条件“AB=AC”与结论“DF⊥BC”互换,结论依然成立。
5. 如图,AB=AE,BC=ED, ∠B=∠E,AM⊥CD, A 求证:CM=MD.
证明:连接AC,AD
∵AB=AE,∠B=∠E,BC=ED ∴△ABC≌△AED(SAS)
∴AC=AD
∵AM⊥CD ∴∠AMC=∠AMD=90°∵AM=AM (公共边) ∴RT△ACM≌RT△ADM (HL)
∴CM=DM
6.如图,已知AD是△ABC的中线,BE交AC于F, 且AE=EF,求证:BF=AC 证明:过B点做AC的平行线,交AD的延长线于G点
∵AD为中线,∴BD=CD ∵BG平行于AC,∴∠FGB=∠CAF,∠DBG=∠ACD 在△AFE和△GFB中,∵∠FGB=∠CAF,∠GFB=∠AFE ∴△AFE∽△GFB
∴∠FGB=∠FAE
∵AE=EF,∴∠FAE=∠AFE
∴∠BFG=∠G ∴△GFB为等腰三角形,且BF=BG 在△ADC和△GBD中∵∠DBG=∠ACD,BD=CD,∠BDG=∠CDA ∴△ADC≌△GBD ∴BG=AC
∴BF=AC
7.已知:如图,△ABC(AB≠AC)中,D、E在BC上,且DE=EC,过D点作DF∥BA,交AE于点F,DF=AC, 求证:AE平分∠BAC
证明:延长AE,过D作DM‖AC交AE延长线于M ∴∠M=∠1,∠C=∠2 在△DEM与△CEA中∠M=∠1,∠C=∠2, DE=CE ∴△DEM≌△CEA ∴DM=CA 又∵DF=CA,∴DM=DF,∴∠M=∠3 ∵AB‖FD,∴∠3=∠4,∴∠4=∠1 ∴AE 平分∠BAC
8. 已知:如图,△ABC中,AB=AC,在AB上取一点D,在延长线上取一点E,连接DE交BC于点F,若F是DE中点。
求证:BD=CE
证明:过D作DF∥AC交BC于F,∵DF∥AC(已知),∴∠DFC=∠FCE,∠DFB=∠ACB(平行线的性质)∵AB=AC(已知),∴∠B=∠ACB(等边对等角),∴∠B=∠DFB(等量代换),∴BD=DF(等角对等边),∵BD=CE(已知),∴DF=CE(等量代换),
∵∠DFC=∠FCE,∠DGF=∠CGE(已证),
∴△DFG≌△ECG(AAS),
∴DG=GE(对应边相等)
9. 已知:如图,在△ABC中,AB=AC=CE,B是AD上一点, BE⊥CB 交CD 于E,AC⊥DC, 求证:BE=1/2BC
证明:过点A作AF⊥BC交BC于点F
∵△ABC是等腰三角形,AB=AC,∠ABF=∠ACF…(1)∴AF是BC上的垂直平分线,AF⊥BC,BF=CF=BC/2……(2)∵BE⊥BC,∴BE//AF ∴∠DBE=∠BAF………………………………(3)∵∠CBE=90°∴∠DBE+∠ABF=90°=∠ACF+∠ECB…………(4)由(1)和(4)知道:∠DBE=∠ECB………………(5)由(3)和(5)知道:∠BAF=∠ECB 又∵AB=CE,∠BFA=∠EBC=90°∴RT△BFA≌RT△EBC(角角边)∴BF=EB…………………………(6)由(2)和(6)知道:BE=BC/2
10.如图,AD为△ABC的角平分线,M为BC的中点,ME∥DA交 BA延长线于E, 求证:BE=CF=1/2(AB+AC)
证明:(1)延长EM,使EM=MG,连接CG
∵点M是BC的中点 ,∴BM=CM ∵∠BME=∠CMG ∴△BME≌△CMG(SAS) ∴BE=CG,∠E=∠G
∵AD平分∠BAC ,∴∠BAD=∠CAD ∵ME∥DA,∴∠BAD=∠E,∠CAD=∠AFE ∴∠E=∠AFE,∴AE=AF ∵∠AFE=∠CFG ,∴∠G=∠CFG ∴CF=CG ,∴BE=CG,∴BE=CF
(2)∵BE=AB+AE,∴2BE=2AB+2AE
∵CF=BE,AC=CF+AF,AE=AF
∴2BE=2CF=AB+(AB+AE)+AE =AB+BE+AE=AB+(CF+AE) ∵AC=AF+CF ∴2BE=AB+AC ∴BE=CF=1/2(AB+AC)
11.如图,已知△ABC中,AD⊥BC,∠ABC=2∠C. 试说明AB+BD=CD的理由。
证明:在DC上截取DE=BD,连接AE ∵AD⊥BC,∴∠ADB=∠ADE=90°∵AD=AD ∴RT△ADB≌RT△ADE(SAS) ∴AB=AE ,∠ABC=∠AEB
∵∠AEB=∠C+∠EAC ∵∠ABC=2∠C(已知)∴∠EAC=∠C
∴AE=CE ,∴AB=CE ∵CD=CE+DE ,∴AB+BD=CD
12.已知:如图,AD是△ABC的角平分线,且AC=AB+BD. 求证:∠B=2∠C.
证明:在AC上作AE=AB,连结DE ∵AC=AB+BD=AE+CE ,∴BD=CE ∵AD是角平分线 ,∴∠BAD=∠EAD 又∵AB=AE,AD=AD ∴△ABD≌△EAD ∴∠B=∠AED,BD=DE=CE
∴∠EDC=∠C,∠AED=2∠C
即:∠B=2∠C
13.如图所示,已知在△ABC中AD是∠A的平分线,且∠B=2∠C. 求证:AC=AB+BD.
证明:延长AB到E,使AC=AE,连接DE
∵AD是∠BAC的角平分线∴∠BAD=∠DAC(角平分线的定义)∵公共边AD=AD AC=AE ∠BAD=∠DAC ∴△ACD≌△AED (SAS) ∴∠ACB=∠DEA (全等三角形形的对角相等)
∵∠BDE+∠DEB=∠CBA ∠CBA=2∠ACB ∠ACB=∠DEA ∴∠BDE=∠DEA ∴BD=BE(等角对等边)
∵AB+BE=AE,AC=AE,BD=BE
∴AB+BD=AC
14.如图,点E是等边△ABC内一点,且EA=EB, △ABC外一点D满足BD=AC,且BE平分∠BDE。
求∠BDE的度数解:连接CE,∵AC=BC,AE=BE,CE为公共边,∴△BCE≌△ACE,∴∠BCE=∠ACE=30° 又∵BD=AC=BC,∠DBE=∠CBE,BE为公共边,∴△BDE≌△BCE,∴∠BDE=∠BCE=30°
15.如图,已知在△ABC中,AB=BC=CA,E是AD上一点,并且 EB=BD=DE. 求证:BD+DC=AD. A
提示:证明△ABE≌△BCD即可 E B C
16.已知:如图,△ABC中,∠C=90°,CM⊥AB于M,AT平分∠BAC交CM于D,交BC于T,过D作DE∥AB交BC于E,求证:CT=BE
证明1:作DF∥BC交AB于F,则:
∵∠AFD=∠B=∠ACD, AT为∠BAC的角平分线,AD为公共边∴△AFD≌△ACD,AF=AC 连接TF ∵AF=AC, AT为∠BAC的角平分线,AT为公共边∴△ACT≌△AFT, TF⊥AF,TF∥CM ∵DF∥CT∥BE,TF∥CD,DE∥BF ∴四边形CTFD和四边形BEDF都是平行四边形∴CT=DF=BE
证明2:作TF⊥AB于F,则: ∵∠CDT=∠ADM=90°-∠DAM=90°-∠DAC=∠CTD ∴∠CDT =∠CTD , ∴CT=CD ∵AT为∠BAC的角平分线,TF⊥AB,AC⊥TC ∴CT=TF=CD ∵DE∥BF,TF∥CD, ∴∠DEC=∠B, ∠DCE=∠FTB 又∵TF=CD ∴△CDE≌△TFB, ∴CE=BT ∴CE-TE=BT-TE,CT=BE。
