单项式与多项式-课件ppt
合集下载
《单项式与多项式》课件
以上内容仅供参考，具体介绍可以根据您的需求和实际情况进行调整。
运算上的区别与联系
添加 标题
定义上的区别：单项式是由数字、字母或数字与字母的乘积组成的代数式；多项式是由若干个单项式通 过加减运算组成的代数式。
添加 标题
运算上的联系：多项式中的每一项都可以看作是一个单项式，因此多项式可以看作是多个单项式的组合； 同时，单项式也可以看作是只有一个项的多项式，因此单项式和多项式在运算上具有一定的联系。
多项式的运算
合并同类项：将多项式中的同类项合并成一个项 乘法分配律：将多项式中的每一项分别乘以括号内的数 乘法结合律：将多项式中的几项先乘起来，再与其他项相乘 乘法交换律：将多项式中的几项交换位置后，再相乘
单项式与多项式的
04
区别与联系
定义上的区别与联系
单项式的定义： 由数字、字母 或它们的乘积 组成的代数式
工程领域：用于设计、计 算和优化各种工程结构，
如桥梁、建筑、机械等
经济领域：用于描述成本、 收益、利润等经济指标之 间的关系
计算机科学：用于算法设 计和数据结构优化，如排
序、查找等
单项式与多项式的
06
练习题与解析
基础练习题
判断单项式和多项式的依据 单项式和多项式的加减运算 单项式和多项式的乘除运算 单项式和多项式的混合运算
提高练习题
基础练习：针对单项式与多项式的基本概念和运算规则进行练习 综合练习：结合实际应用场景，设计涉及多个知识点的练习题 拓展练习：增加难度，设计一些需要运用所学知识进行推理和解析的练习题 错题解析：针对学生在练习中容易出现的错误进行解析，帮助学生纠正错误理解和运用知 识
综合练习题
单项式与多项式的加减运算 单项式与多项式的乘除运算 单项式与多项式的混合运算 单项式与多项式的实际应用
2.1.2 单项式与多项式(2课时) (共34张PPT)
第3课时 多项式
说出下列单项式的系数和次数：
(1) 3a b2 3 (2)0.5 xyz (3)m3n4
ห้องสมุดไป่ตู้
(4) a
(5)R2
(7)23 ab5 (8)xy
(6) 2x2 y3 5
(9) 7 x2 y 13
指出下列式子中，哪些是单项式？
(1)abc
(2) x
3
(3) 4 R3
3
(4)0
例4 如图，用式子表示圆环的面积，当 R =15 cm,r =10 cm 时，求圆环的面积 （π取3.14）.
r R
例题讲解
解：外圆的面积减去内圆的面积就是圆环 的面积，所以圆环的面积是πR2- πr2 . 当R=15 cm, r=10 cm时， 圆环的面积是πR2- πr2
=3.14×152-3.14×102 =392.5（cm2）. 这个圆环的面积是392.5 cm2 .
新课讲授
多项式中次数最高的项的次数叫 做多项式的次数.同单项式一样，一 个多项式的次数是几，我们就称它为 几次式.如2x-3可以叫做一次二项式， 3x+5y+2z可以叫做一次三项式.
新课讲授
什么是整式？ 单项式和多项式统称为整式. 说一说单项式、多项式和整式三者之间的 关系.
整式
单项式 多项式
例题讲解
7
√
√x
√
单项式的系数、次数
观察单项式，6a2，2.5x，-n，2a2b ，它们
各由哪几部分组成？
7
单项式中的数字因数叫做这个单项式的系 数，应当注意的是，单项式的系数包括它前面 的性质符号.而如-n，a3这样的式子的系数分 别是-1和1，不能说没有系数.
单项式的系数、次数
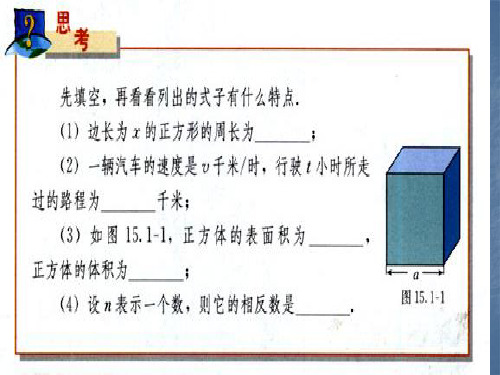
说出下列单项式的系数和次数：
(1) 3a b2 3 (2)0.5 xyz (3)m3n4
ห้องสมุดไป่ตู้
(4) a
(5)R2
(7)23 ab5 (8)xy
(6) 2x2 y3 5
(9) 7 x2 y 13
指出下列式子中，哪些是单项式？
(1)abc
(2) x
3
(3) 4 R3
3
(4)0
例4 如图，用式子表示圆环的面积，当 R =15 cm,r =10 cm 时，求圆环的面积 （π取3.14）.
r R
例题讲解
解：外圆的面积减去内圆的面积就是圆环 的面积，所以圆环的面积是πR2- πr2 . 当R=15 cm, r=10 cm时， 圆环的面积是πR2- πr2
=3.14×152-3.14×102 =392.5（cm2）. 这个圆环的面积是392.5 cm2 .
新课讲授
多项式中次数最高的项的次数叫 做多项式的次数.同单项式一样，一 个多项式的次数是几，我们就称它为 几次式.如2x-3可以叫做一次二项式， 3x+5y+2z可以叫做一次三项式.
新课讲授
什么是整式？ 单项式和多项式统称为整式. 说一说单项式、多项式和整式三者之间的 关系.
整式
单项式 多项式
例题讲解
7
√
√x
√
单项式的系数、次数
观察单项式，6a2，2.5x，-n，2a2b ，它们
各由哪几部分组成？
7
单项式中的数字因数叫做这个单项式的系 数，应当注意的是，单项式的系数包括它前面 的性质符号.而如-n，a3这样的式子的系数分 别是-1和1，不能说没有系数.
单项式的系数、次数
单项式与多项式相乘公开课课件
乘法分配律的运用
乘法分配律是数学中的一个基本定律，它指出一个数乘以 两个数的和等于这个数分别乘以这两个数再求和。在单项 式与多项式相乘时，乘法分配律是非常重要的。
例如，单项式$a^3$与多项式$b + c$相乘时，可以运用 乘法分配律进行计算：$(a^3)(b+c) = a^3b + a^3c$。 这样可以简化计算过程，提高计算效率。
单项式与多项式相乘公开课课件
contents
目录
• 单项式与多项式简介 • 单项式与多项式相乘的法则 • 单项式与多项式相乘的运算实例 • 单项式与多项式相乘的注意事项 • 习题与解答
01
单项式与多项式简介
单项式的定义与性质
定义
单项式是只包含一个项的代数式 ，通常表示为数字、字母的积。
性质
单项式具有加法封闭性、乘法交 换律和结合律等基本性质。
单项式的几何意义
在数轴上，单项式可以表示一个点或一个单位长度。例如，$3x$表示在x轴上， 每移动一个单位长度，坐标增加3。
多项式的几何意义
多项式可以表示一条曲线或曲面。例如，$y = x^2$表示一个开口向上的抛物线 。
02
单项式与多项式相乘的法则
单项式乘以多项式的法则
单项式乘以多项式的运算法则，是将单项式中的每一个因子 与多项式中的每一个项分别相乘，然后将所得的积相加。
多项式的定义与性质
定义
多项式是由有限个单项式通过加法运 算组成的代数式，表示为$P(x) = a_n x^n + a_{n-1} x^{n-1} + cdots + a_1换律 和结合律等基本性质，还具有分配律 和幂的运算法则等特殊性质。
单项式与多项式的几何意义
单项式与多项式课件
(3) 10a2b－5ab2＋ab;
(4)－18a3＋6a2＋4a.
5. (1) a2－9x＋18; (2)
;
(3) 3x2＋8x＋4; (4) 4y2－2y＋5;
(5) x3－2x2＋4x－8; (6) x3－y3.ቤተ መጻሕፍቲ ባይዱ
6. 原式=－2x2＋x,将x= 代入得0.
28
7. (1)－5x2－12x＋15; (2) 2x2－8. 8. 1.44×210 ×210=1.44×220(字节)。 9. 7.9×103 ×2×102=1.58×106 (米)。 10. 22a2m. 11. (1)x=1;(2)x＞ . 12.(1)m=13;(2) －20;(3)m=15;(4) －20;
16
化简求值：
yn(yn+9y-12)–3(3yn+1-4yn)，其中 y=2,n=1. 解： yn(yn+9y-12)–3(3yn+1-4yn)
=y2n+9yn-12–9yn+1+12yn =y3n-3–9yn+1+12yn
当y=2 ，n=1时，
原式=(2)0－9×4＋12×2=-11
17
例3 先化简,再求值： 2a(a-b)-b(2a-b)+2ab,其中a=2,b=
解3 : 原式=2a2 –2ab –2ab+b2+2ab = 2a2 – 2ab + b2
∵ a=2 ，b= 3
∴原式= 2a2 – 2ab + b2 =2×22－2×2×3＋32
=8－12＋9
=5
18
想一想
如图，为了扩大街心公园的绿地面积， 把一块原长a米、宽m米的长方形绿地，增长 了b米，加宽了n米。你能用几种方法求出扩 大后的绿地的面积？
单项式与多项式ppt
多项式
多项式是数学中的一个概念，它是一个由若干个单项式组成 的等式。例如，2x² + 3x + 4y²是一个二次多项式，因为它包 含两个变量的最高幂为2的单项式。
单项式与多项式的应用场景
代数
在代数中，单项式和多项式经常被用于表示和解决数学问题。例如，多项式可以用来解决 方程，而单项式可以用来表示一Βιβλιοθήκη 简单的数学关系。单项式与多项式
xx年xx月xx日
目 录
• 引言 • 单项式与多项式的定义及符号 • 单项式与多项式的运算 • 单项式与多项式的应用 • 单项式与多项式的关系 • 如何学习单项式与多项式
01
引言
定义与概念
单项式
在数学中，一个单项式是一个表示数量的简单形式，由一个 系数和一个变量的幂组成。例如，2x，3xy和4y²都是单项式 。
拓展数学视野
了解数学的历史、文化 和发展动态，拓展自己 的数学视野，增加数学 素养和人文素养。
THANKS
谢谢您的观看
些概念是数学中的基础。
02
解决问题
单项式和多项式可以帮助我们解决各种问题，从简单的代数问题到复
杂的科学问题。
03
发展思维
学习单项式和多项式可以发展我们的抽象思维和逻辑思维，这对我们
的学习和生活都有很大的帮助。
02
单项式与多项式的定义及符 号
单项式的定义及符号
定义
单项式是只由数字和字母乘积组成的代数式，其中数字因数叫做单项式的系 数，字母因数叫做单项式的次数。
降幂排列
将多项式按照次数从高到低的顺序排列，叫做降幂排列。例 如，$a^3 + 2a^2b + 3ab^2 + b^3$ 可以写成 $a^3 + 3ab^2 + 2a^2b + b^3$。
多项式是数学中的一个概念，它是一个由若干个单项式组成 的等式。例如，2x² + 3x + 4y²是一个二次多项式，因为它包 含两个变量的最高幂为2的单项式。
单项式与多项式的应用场景
代数
在代数中，单项式和多项式经常被用于表示和解决数学问题。例如，多项式可以用来解决 方程，而单项式可以用来表示一Βιβλιοθήκη 简单的数学关系。单项式与多项式
xx年xx月xx日
目 录
• 引言 • 单项式与多项式的定义及符号 • 单项式与多项式的运算 • 单项式与多项式的应用 • 单项式与多项式的关系 • 如何学习单项式与多项式
01
引言
定义与概念
单项式
在数学中，一个单项式是一个表示数量的简单形式，由一个 系数和一个变量的幂组成。例如，2x，3xy和4y²都是单项式 。
拓展数学视野
了解数学的历史、文化 和发展动态，拓展自己 的数学视野，增加数学 素养和人文素养。
THANKS
谢谢您的观看
些概念是数学中的基础。
02
解决问题
单项式和多项式可以帮助我们解决各种问题，从简单的代数问题到复
杂的科学问题。
03
发展思维
学习单项式和多项式可以发展我们的抽象思维和逻辑思维，这对我们
的学习和生活都有很大的帮助。
02
单项式与多项式的定义及符 号
单项式的定义及符号
定义
单项式是只由数字和字母乘积组成的代数式，其中数字因数叫做单项式的系 数，字母因数叫做单项式的次数。
降幂排列
将多项式按照次数从高到低的顺序排列，叫做降幂排列。例 如，$a^3 + 2a^2b + 3ab^2 + b^3$ 可以写成 $a^3 + 3ab^2 + 2a^2b + b^3$。
〔人教版〕单项式与多项式教学PPT课件
40、人生的旅途，前途很远，也很暗 。然而 不要怕 ，不怕 的人的 面前才 有路。 —— 鲁 迅 名人名言激励励志名言名语名句100句 （励志 古诗词 篇，附 出处）
41、人生像攀登一座山，而找寻出路 ，却是 一种学 习的过 程，我 们应当 在这过 程中， 学习稳 定、冷 静，学 习如何 从慌乱 中找到 生机。 席慕蓉 42、我们活着不能与草木同腐，不能 醉生梦 死，枉 度人生 ，要有 所作为 。 —— 方志敏
100、我无论做什么，始终在想着，只 要我的 精力允 许我的 话，我 就要首 先为我 的祖国 服务。 ——《 巴甫洛 夫选集 》 57、入于污泥而不染、不受资产阶级 糖衣炮 弹的侵 蚀，是 最难能 可贵的 革命品 质。 —— 周恩来
45、有谦和、愉快、诚恳的态度，而 同时又 加上忍 耐精神 的人， 是非常 幸运的 。 —— 塞涅卡
46、人的一生可能燃烧也可能腐朽， 我不能 腐朽， 我愿意 燃烧起 来！ —— 奥斯特洛夫斯基
98、喷泉的高度不会超过它的源头； 一个人 的事业 也是这 样，他 的成就 绝不会 超过自 己的信 念。—— 林 肯 99、朝着一定目标走去是“志”，一鼓 作气中 途绝不 停止是“气”，两 者合起 来就是 “志气”。一切 事业的 成败都 取决于 此。 —— 卡内基
40、对人不尊敬，首先就是对自己的 不尊敬 。 —— 惠特曼
41、一个人的真正伟大之处就在于他 能够认 识到自 己的渺 小。 —— 保 罗
42、自我控制是最强者的本能。 —— 萧伯纳
43、勿以恶小而为之，勿以善小而不 为。惟 贤惟德 ，能服 于人。 —— 刘备
44、要使别人喜欢你，首先你得改变 对人的 态度， 把精神 放得轻 松一点 ，表情 自然， 笑容可 掬，这 样别人 就会对 你产生 喜爱的 感觉了 。 —— 卡耐基
41、人生像攀登一座山，而找寻出路 ，却是 一种学 习的过 程，我 们应当 在这过 程中， 学习稳 定、冷 静，学 习如何 从慌乱 中找到 生机。 席慕蓉 42、我们活着不能与草木同腐，不能 醉生梦 死，枉 度人生 ，要有 所作为 。 —— 方志敏
100、我无论做什么，始终在想着，只 要我的 精力允 许我的 话，我 就要首 先为我 的祖国 服务。 ——《 巴甫洛 夫选集 》 57、入于污泥而不染、不受资产阶级 糖衣炮 弹的侵 蚀，是 最难能 可贵的 革命品 质。 —— 周恩来
45、有谦和、愉快、诚恳的态度，而 同时又 加上忍 耐精神 的人， 是非常 幸运的 。 —— 塞涅卡
46、人的一生可能燃烧也可能腐朽， 我不能 腐朽， 我愿意 燃烧起 来！ —— 奥斯特洛夫斯基
98、喷泉的高度不会超过它的源头； 一个人 的事业 也是这 样，他 的成就 绝不会 超过自 己的信 念。—— 林 肯 99、朝着一定目标走去是“志”，一鼓 作气中 途绝不 停止是“气”，两 者合起 来就是 “志气”。一切 事业的 成败都 取决于 此。 —— 卡内基
40、对人不尊敬，首先就是对自己的 不尊敬 。 —— 惠特曼
41、一个人的真正伟大之处就在于他 能够认 识到自 己的渺 小。 —— 保 罗
42、自我控制是最强者的本能。 —— 萧伯纳
43、勿以恶小而为之，勿以善小而不 为。惟 贤惟德 ，能服 于人。 —— 刘备
44、要使别人喜欢你，首先你得改变 对人的 态度， 把精神 放得轻 松一点 ，表情 自然， 笑容可 掬，这 样别人 就会对 你产生 喜爱的 感觉了 。 —— 卡耐基
《单项式与多项式》课件
2023 WORK SUMMARY
《单项式与多项式》 ppt课件
REPORTING
目录
• 单项式的定义与性质 • 多项式的定义与性质 • 单项式与多项式的运算 • 单项式与多项式的应用
PART 01
单项式的定义与性质
单项式的定义
单项式是由数字、字 母通过有限次乘法运 算得到的数学表达式 。
单项式可以表示为 $a_n x^n$ 的形式 ，其中 $a_n$ 是系 数，$x$ 是变量， $n$ 是非负整数。
PART 03
单项式与多项式的运算
单项式的加法与减法
总结词：简单明了
详细描述：单项式的加法与减法是基本的数学运算之一，主要涉及到同类项的合 并与分离。通过简单的数学公式和实例，可以让学生快速理解单项式之间的加法 与减法运算。
单项式的乘法与除法
总结词
乘法公式应用广泛
详细描述
单项式的乘法涉及到指数的加法和系数的乘法，而单项式的除法则涉及到指数的减法和系数的除法。通过具体的 乘法公式和除法公式，可以让学生更好地掌握单项式之间的乘法和除法运算。
单项式中只含有一个 项，可以是常数、变 量或变量的乘积。
单项式的系数与变量
单项式的系数是单项式中数字因子的 总和，通常表示为 $a_n$。
单项式的系数和变量共同决定了单项 式的值。
单项式的变量是单项式中字母因子的 标识，通常表示为 $x$。
单项式的次数
单项式的次数是单项式中所有字 母因子的指数之和。
例如，单项式 $3x^2 y^3$ 的 次数是 $2 + 3 = 5$。
次数的计算有助于确定单项式在 代数表达式中的位置和作用。
PART 02
多项式的定义与性质
多项式的定义
《单项式与多项式》 ppt课件
REPORTING
目录
• 单项式的定义与性质 • 多项式的定义与性质 • 单项式与多项式的运算 • 单项式与多项式的应用
PART 01
单项式的定义与性质
单项式的定义
单项式是由数字、字 母通过有限次乘法运 算得到的数学表达式 。
单项式可以表示为 $a_n x^n$ 的形式 ，其中 $a_n$ 是系 数，$x$ 是变量， $n$ 是非负整数。
PART 03
单项式与多项式的运算
单项式的加法与减法
总结词：简单明了
详细描述：单项式的加法与减法是基本的数学运算之一，主要涉及到同类项的合 并与分离。通过简单的数学公式和实例，可以让学生快速理解单项式之间的加法 与减法运算。
单项式的乘法与除法
总结词
乘法公式应用广泛
详细描述
单项式的乘法涉及到指数的加法和系数的乘法，而单项式的除法则涉及到指数的减法和系数的除法。通过具体的 乘法公式和除法公式，可以让学生更好地掌握单项式之间的乘法和除法运算。
单项式中只含有一个 项，可以是常数、变 量或变量的乘积。
单项式的系数与变量
单项式的系数是单项式中数字因子的 总和，通常表示为 $a_n$。
单项式的系数和变量共同决定了单项 式的值。
单项式的变量是单项式中字母因子的 标识，通常表示为 $x$。
单项式的次数
单项式的次数是单项式中所有字 母因子的指数之和。
例如，单项式 $3x^2 y^3$ 的 次数是 $2 + 3 = 5$。
次数的计算有助于确定单项式在 代数表达式中的位置和作用。
PART 02
多项式的定义与性质
多项式的定义
《单项式与多项式》课件
二次方程的解法
03
二次方程是代数方程的一种，单项式和多项式在求解二次方程时也起到重要作用。通过配方、因式分解等操作，可以将二次方程化简为一元二次方程，从而求解。
函数图像的绘制
在函数的学习中，单项式和多项式常常作为函数的表达式出现。通过将函数的表达式代入坐标系中，可以绘制出函数的图像，从而直观地了解函数的性质和变化规律。
单项式乘法是指将两个单项式相乘，根据分配律，将它们的系数相乘，并将相同的字母因子相加。例如，$2x^2y times 3xy = 6x^3y^2$。
详细描述
总结词
总结词
单项式相除的规则是将被除数的系数除以除数的系数，并将相同的字母因子相减。
详细描述
单项式除法是指将一个单项式除以另一个单项式，根据除法的定义，将被除数的系数除以除数的系数，并将相同的字母因子相减。例如，$frac{4x^2y}{2x} = 2xy$。
解析几何中的代数表达
解析几何是数学的一个重要分支，它通过代数方法来研究几何问题。在这个领域中，单项式和多项式是描述几何图形的基本工具。例如，直线的方程可以用一次多项式来表示，而圆的方程则可以用二次多项式来表示。
练习题与答案
对于进阶练习题中的第一题，根据多项式的定义，多项式是由一个或多个单项式组成的代数式，所以多项式的常数项就是多项式中不含字母的项，即$5$。
详细描述
单项式与多项式的应用
代数方程的解法
01
单项式和多项式在代数方程的解法中有着广泛的应用。通过合并同类项、移项、合并常数项等操作，可以简化方程，使其更容易求解。
线性方程的解法
02
线性方程是代数方程的一种，单项式和多项式在求解线性方程时起到关键作用。通过移项、合并同类项等操作，可以将线性方程化简为一元一次方程，从而求解。
03
二次方程是代数方程的一种，单项式和多项式在求解二次方程时也起到重要作用。通过配方、因式分解等操作，可以将二次方程化简为一元二次方程，从而求解。
函数图像的绘制
在函数的学习中，单项式和多项式常常作为函数的表达式出现。通过将函数的表达式代入坐标系中，可以绘制出函数的图像，从而直观地了解函数的性质和变化规律。
单项式乘法是指将两个单项式相乘，根据分配律，将它们的系数相乘，并将相同的字母因子相加。例如，$2x^2y times 3xy = 6x^3y^2$。
详细描述
总结词
总结词
单项式相除的规则是将被除数的系数除以除数的系数，并将相同的字母因子相减。
详细描述
单项式除法是指将一个单项式除以另一个单项式，根据除法的定义，将被除数的系数除以除数的系数，并将相同的字母因子相减。例如，$frac{4x^2y}{2x} = 2xy$。
解析几何中的代数表达
解析几何是数学的一个重要分支，它通过代数方法来研究几何问题。在这个领域中，单项式和多项式是描述几何图形的基本工具。例如，直线的方程可以用一次多项式来表示，而圆的方程则可以用二次多项式来表示。
练习题与答案
对于进阶练习题中的第一题，根据多项式的定义，多项式是由一个或多个单项式组成的代数式，所以多项式的常数项就是多项式中不含字母的项，即$5$。
详细描述
单项式与多项式的应用
代数方程的解法
01
单项式和多项式在代数方程的解法中有着广泛的应用。通过合并同类项、移项、合并常数项等操作，可以简化方程，使其更容易求解。
线性方程的解法
02
线性方程是代数方程的一种，单项式和多项式在求解线性方程时起到关键作用。通过移项、合并同类项等操作，可以将线性方程化简为一元一次方程，从而求解。
单项式与多项
《单项式与多项式ppt》xx年xx月xx日•单项式概述•多项式概述•单项式与多项式的应用目录•单项式与多项式的运算•单项式与多项式的例子•总结与展望01单项式概述单项式是由数字与字母的积组成的代数式，如：2x，3y等。
定义2x^3表示一个单项式，因为它是由数字2与字母x的三次方组成的。
示例单项式中不含加减号。
相同字母必须合并；字母的指数可以是0；特点：单项式具有以下特点单独一个数字也是单项式；单项式的分类数字与单个字母的积；分类：单项式可分为以下三类数字与多个字母的积。
相同字母的积；02多项式概述•定义：多项式是由若干个单项式组成的数学表达式。
它通常可以表示为$f(x) = a n x^n + a {n-1} x^{n-1} + \ldots + a_1 x + a_0$，其中$a n$、$a {n-1}$、$\ldots$、$a_1$、$a_0$是常数，$x$是变量。
多项式的定义•特点：多项式是一种特殊的函数，它具有次数、系数和项数等属性。
它的每个项都由一个单项式组成，并且每一项的次数从高到低排列。
多项式的次数等于最高次项的次数。
多项式的特点•分类：多项式可以分为实数多项式和复数多项式两大类。
实数多项式是指系数和常数都是实数的多项式，而复数多项式是指系数和常数中至少有一个是复数的多项式。
多项式的分类03单项式与多项式的应用1单项式在数学中的应用23单项式可以用来描述数学中的基本概念，例如数字、变量、幂等。
描述数学概念单项式可以用于计算中，例如加减乘除等基本运算。
计算单项式可以用来表达一些基本的数学公式，例如平方差公式等。
表达数学公式多项式可以用来描述复杂的函数，例如多项式函数、三角函数等。
描述复杂函数多项式可以用于解决方程中，例如求解高次方程。
解决方程多项式可以用来表达一些复杂的公式，例如泰勒公式等。
表达公式多项式在数学中的应用03经济学经济学中经常使用单项式与多项式来建立模型，例如成本函数、收益函数、价格函数等。
8.2.2 单项式与多项式相乘 (第2课时)课件(15张PPT)2023-2024学年沪科版七年级数
第 8 章 整式乘法与因式分解 8.2 整式乘法
8.2.2 单项式与多项式相乘 第2课时
学习导航
学习目标 新课导入 合作探究 当堂检测 课堂总结
一、学习目标
1.由单项式与多项式的乘法性质，探究多项式与单项式的除法； 2.能熟练运用多项式除以单项式的运算法则进行运算.(重点)
二、新课导入
复习回顾 1.单项式与多项式相乘，就是用单项式去 乘多项式的每一项 ， 再把所得的 积 相加.
解： (1)原式=6a2b÷a + 3a÷a (2)原式=4x3y2÷(-2x2y)-x2y2÷(-2x2y)
=6ab + 3.
=-2xy +
1 2
y.
(3)(20m4n3-12m3n3+3m2n) ÷(-4m2n)；
(3)原式=20m4n3÷(-4m2n)-12m3n3÷(-4m2n)+3m2n÷(-4m2n) =-5m2n2+3mn2 - 3 .
结论：多项式除以单项式，所得的商仍然是多项式，并且商的项数和原多项 式的项数相同.
三、合作探究
(4)如果某次多项式除以单项式计算得出的商乘以原单项式，得出的结果不 是原多项式，这次计算是否正确？ 小技巧：多项式除以单项式与单项式乘以多项式是互逆运算，因此可用单项 式乘以多项式来验证多项式除以单项式的结果是否正确． (5)如何计算[4(x+y)7+6(x+y)6]÷2(x+y)3呢？谈谈你的思路. 把(x+y)看作一个整体，再利用多项式除以单项式法则进行计算. 拓展：多项式除以单项式的法则，可用公式(am+bm+cm)÷m=a+b+c表示. 当这里的m表示一个多项式时，同样也能套用公式计算.
8.2.2 单项式与多项式相乘 第2课时
学习导航
学习目标 新课导入 合作探究 当堂检测 课堂总结
一、学习目标
1.由单项式与多项式的乘法性质，探究多项式与单项式的除法； 2.能熟练运用多项式除以单项式的运算法则进行运算.(重点)
二、新课导入
复习回顾 1.单项式与多项式相乘，就是用单项式去 乘多项式的每一项 ， 再把所得的 积 相加.
解： (1)原式=6a2b÷a + 3a÷a (2)原式=4x3y2÷(-2x2y)-x2y2÷(-2x2y)
=6ab + 3.
=-2xy +
1 2
y.
(3)(20m4n3-12m3n3+3m2n) ÷(-4m2n)；
(3)原式=20m4n3÷(-4m2n)-12m3n3÷(-4m2n)+3m2n÷(-4m2n) =-5m2n2+3mn2 - 3 .
结论：多项式除以单项式，所得的商仍然是多项式，并且商的项数和原多项 式的项数相同.
三、合作探究
(4)如果某次多项式除以单项式计算得出的商乘以原单项式，得出的结果不 是原多项式，这次计算是否正确？ 小技巧：多项式除以单项式与单项式乘以多项式是互逆运算，因此可用单项 式乘以多项式来验证多项式除以单项式的结果是否正确． (5)如何计算[4(x+y)7+6(x+y)6]÷2(x+y)3呢？谈谈你的思路. 把(x+y)看作一个整体，再利用多项式除以单项式法则进行计算. 拓展：多项式除以单项式的法则，可用公式(am+bm+cm)÷m=a+b+c表示. 当这里的m表示一个多项式时，同样也能套用公式计算.
单项式与多项式相乘课件
单项式与多项式相乘ppt 课件
欢迎来到这个关于单项式和多项式相乘的课件。在本次课件中，我们将探究 单项式和多项式的定义，以及它们相乘的各种规则和应用实例。
单项式和多项式的定义
1 单项式
只含有一个项的代数式，例如3x和4y。
2 多项式
含有两项或两项以上的代数式，例如3x+4y和2x^2+1。
单项式与单项式相乘的规则
步骤一
2
3x×x^2=3x^3
3
步骤二
3x×(-2x)=-6x^2
步骤三
4
3x×1=3x
5
步骤四
2×x^2=2x^2
步骤五
6
2×(-2x)=-4x
7
步骤六
2×1=2
答案
8
3x^3ቤተ መጻሕፍቲ ባይዱ4x^2+x+2
总结和要点
1 单项式
只含有一个项的代数式。
2 多项式
含有两项或两项以上的代数式。
3 乘法规则
分别计算单项式与单项式、单项式与多项式以及多项式与多项式相乘。
多项式与多项式相乘的规则
使用分配律
将多项式展开成单项式的和，然后按照“多项式与单项式相乘”的规则计算。
例如：
(3x+4)(2x-1) = 6x^2+5x-4
应用实例1：计算单项式与多项式相乘
问题
计算3x(2x^2+4y-3)
答案
6x^3+12xy-9x
应用实例2：计算多项式与多项式相乘
1
问题
计算(3x+2)(x^2-2x+1)
乘法原理
将系数相乘，同时将字母部分相乘并将幂次相加。
例如：
欢迎来到这个关于单项式和多项式相乘的课件。在本次课件中，我们将探究 单项式和多项式的定义，以及它们相乘的各种规则和应用实例。
单项式和多项式的定义
1 单项式
只含有一个项的代数式，例如3x和4y。
2 多项式
含有两项或两项以上的代数式，例如3x+4y和2x^2+1。
单项式与单项式相乘的规则
步骤一
2
3x×x^2=3x^3
3
步骤二
3x×(-2x)=-6x^2
步骤三
4
3x×1=3x
5
步骤四
2×x^2=2x^2
步骤五
6
2×(-2x)=-4x
7
步骤六
2×1=2
答案
8
3x^3ቤተ መጻሕፍቲ ባይዱ4x^2+x+2
总结和要点
1 单项式
只含有一个项的代数式。
2 多项式
含有两项或两项以上的代数式。
3 乘法规则
分别计算单项式与单项式、单项式与多项式以及多项式与多项式相乘。
多项式与多项式相乘的规则
使用分配律
将多项式展开成单项式的和，然后按照“多项式与单项式相乘”的规则计算。
例如：
(3x+4)(2x-1) = 6x^2+5x-4
应用实例1：计算单项式与多项式相乘
问题
计算3x(2x^2+4y-3)
答案
6x^3+12xy-9x
应用实例2：计算多项式与多项式相乘
1
问题
计算(3x+2)(x^2-2x+1)
乘法原理
将系数相乘，同时将字母部分相乘并将幂次相加。
例如：
相关主题
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
错
⑵ 单项式 1 R2 的系数是 1 ，次数是 3
2
2
⑶ 单项式 3 x2 y 的系数是-3，次数是 2 8
⑷单项式 3102 a2b2 的系数是 -3 ，次数是 4
⑸单项式的 9x2 y2 系数是-9，次数是 4
对
⑹单项式的 3a2b3c2 对字母 b 是三次单项式
注意问题：（1） 圆周率 是常数；
小试身手
1.找出下列代数式中哪些是整式？（写题号）
（1√）a2 2ab （2） 2n 1
3m 2
（5√） a2 b2 （6√） 5 4a
（√9） 1 x2 7
3
（1√0）
x
2 3
（√3） 21
（4） 2 ab
（√7） a （8） 3
2a
（1√1） 3x （1√2）1.05a
注意：除式中含有字母的代数式不是整式。
单项式的次数
单项式中 所有 字母 指数的和
叫
做单项式的次数。
ab c 例如，单项式
次数是2， 2
3x 2 的次数是2，
的次数是4。
1 ah 3
的
有几个字母 x 、 y 、
z，各字母的指数分别
是 2 、 3 、1
，则单项式 2 x2 y3z
的次数 6 。
3
练习：填写表格
单项式
系数
次数
2x2
2
2
a3b
注意：多项式中的每一项都包含它前面的符号。
多项式的次数： 多项式中 次数最高的项的次数 ，
叫做这个多项式的次数。
例如， x2 3x 2 有三项，其中次数最高的项的 次数为2，所以多项式 x2 3x 2 为二次三项式。
演示
多项式 2a a3b有两项为2a， a3b，项的次数分
别为 1，4 ，所以，多项式 次数是 4，系数是 1
（3）这个多项式2有常数项吗？如果有，是哪一2 项？
有常数项，常数项为
2 3
训练
1、下列代数式中，1_、__2_、_3_、__6是单项式，___4___是多项式，1_、__2_、_3_、__4_、__6是整式。
① －3x
② 1 mn 2
③a
④
1 mn +5m
2
⑤1 x
2、指出下列单项式的系数和次数
①
1 ab
② -4x2y ③
m
½，22
3、① －x2-xy-2y
-4，3 1，1 ② 5a2-7b2 － 1 ab
2
1、指出以上各式每一项的系数和次数
④ 12
12，0
③ 2πx2-7x－6
2、指出以上各式是几次几项式
⑥ 107
4.判断
⑴ 单项式 x 的系数是 0 ，次数是 0
2.观察1题中的代数式，哪些是单项式？ 归纳：单项式为只含乘、乘方运算的整式。
单项式的系数和次数
单项式的系数
单项式中的 数字因数 叫单项式的系数。
3x2, 1 ah, ab2c 3
的系数分别为：
3, 1 ,1 3
。
注意：1.单项式系数包括它前面的符号；
2.单项式系数是1或-1时，1可省略不写，但 “-1”时，“-”号不可省略。
单项式与多项式
学习目标：
1.了解整式的有关概念，会识别单项式、多 项式和整式。
2.能说出一个单项式的系数和次数，多项式 的项的系数和次数，以及多项式的项数和 次数。
3.在参与对单项式、多项式识别的过程中， 培养观察、归纳、概括和语言表达的能力。
探究一
ab 1 a2 8
1.05a
（0.50b-0.35a）
多项式中次数最高项的次数叫多项式的次数。
谢谢
观察下面的代数式，它们分别都含有哪些运算？
1.05a
r 2 a2
0.50b 0.35a
ab
1
8
a2
4
n 3
abc2
对于字母来说，只含 加、减、乘、乘方
运
算的 代数式 叫做整式。
探究二
其中，不含有 加、减
运算的整式叫单项式。
12，0，a，b 是单项式吗？
特别地，单独的 一个字母
或 一个数
也是单项式。
3
2
（1） 这个多项式有几项？
四项
（2） 这个多项式的最高次项是哪一项？写出它的次数和系数； 2x2 y2 四次 ，2
（3） 这个多项式有常数项吗？如果有，是哪一项？ 有 1
2
只含有加、减、乘、乘方运算的代数式叫做整式。 不含有加、减运算的整式叫单项式。 单项式中的数字因数叫单项式的系数。 单项式中所有字母指数的和叫做单项式的次数。 几个单项式的和叫多项式。 多项式中的每个单项式叫多项式的项。 多项式中不含字母的项叫常数项。
（2）
m2
xy
（5）
2
（3） 0.1x2 y
（6） a2bc
能力提升：
已知多项式
1 x3 y 3x2 2xy 2
2
3
，回答下列
问题：
（1）这个多项式有几项？指出它所有的项；
这个多项式有 4项，分别是 1 x3 y,3x2 ,2xy2 , 2
2
3
（2）这个多项式的次数最高项是哪一项？写出它的系数和次数；
牛刀小试
1. 说出下列多项式是由哪几项组成的，它们分别是几次多项式？
（1） 3x 2y 1 （2） 2a2 3a 5 （3） 2a a3b
（4） 7 3xy2 （5） a3 a2b ab2 b3 （6） 3x2 xy y3
2. 说出下列单项式的系数和次数：
（1） ab
（4） 2abc2 3
1
4
3xy 4
3 4
2
a
1
1
1 x2 y 4
6
1 6
6
探究三
多项式的有关概念
多项式：几个单项式的 和 叫做多项式。
例如， 0.5b
0.35a，a
0.05a，ab
1a2，r 2
8
a2
等都是多项式。
项与常数项： 多项式中的每个单项式 叫做这个多项式的项。
不含字母 的项叫做常数项。
例如， x2 3x 2 有三项，它们分别是 x2,3x,2,其中 2是常数项。
（2）当一个单项式的系数是 1 或－1 时，“1”通常省略不写，如 ab2 ，－abc；
（3） 单项式的系数是带分数时，通常写成假分数．如11 x2 y 写成 5 x2 y ．
4
4
本资料来自于资源最齐全的２１世纪教育网
5、（2 分）已知多项式 － 1 x2y+3x2+2x2y2－ 1 ,回答下列问题：